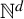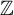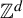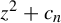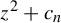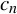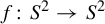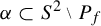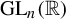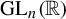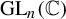Open access
Original Article
Poissonian pair correlation for directions in multi-dimensional affine lattices and escape of mass estimates for embedded horospheres
- Part of:
-
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Hausdorff dimension of invariant measures of piecewise smooth circle homeomorphisms
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Entropy, virtual Abelianness and Shannon orbit equivalence
- Part of:
-
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity of pressures of Hölder potentials and the fitting of analytic functions through them
- Part of:
-
- Published online by Cambridge University Press:
- 18 March 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximate homomorphisms and sofic approximations of orbit equivalence relations
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bohr chaoticity of principal algebraic actions and Riesz product measures
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An embedding theorem for subshifts over amenable groups with the comparison property
- Part of:
-
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tracial weights on topological graph algebras
- Part of:
-
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant measures of Toeplitz subshifts on non-amenable groups
- Part of:
-
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shifts of finite type on locally finite groups
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the stochastic bifurcations regarding random iterations of polynomials of the form
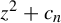 $z^{2} + c_{n}$
$z^{2} + c_{n}$
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measures of maximal entropy of bounded density shifts
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On denseness of horospheres in higher rank homogeneous spaces
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2024, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a self-embedding problem for self-similar sets
- Part of:
-
- Published online by Cambridge University Press:
- 14 February 2024, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eliminating Thurston obstructions and controlling dynamics on curves
- Part of:
-
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Levy and Thurston obstructions of finite subdivision rules
- Part of:
-
- Published online by Cambridge University Press:
- 15 December 2023, pp. 1-51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bracket words along Hardy field sequences
- Part of:
-
- Published online by Cambridge University Press:
- 14 December 2023, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A dynamical classification for crossed products of fiberwise essentially minimal zero-dimensional dynamical systems
- Part of:
-
- Published online by Cambridge University Press:
- 11 December 2023, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random and mean Lyapunov exponents for
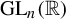 $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
- Part of:
-
- Published online by Cambridge University Press:
- 11 December 2023, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Constructing Birkhoff sections for pseudo-Anosov flows with controlled complexity
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2023, pp. 1-53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation