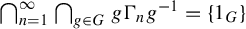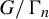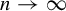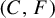FirstView articles
Original Article
Quasisymmetrically rigid self-similar carpets
- Part of:
-
- Published online by Cambridge University Press:
- 22 October 2024, pp. 1-14
-
- Article
-
- You have access
- HTML
- Export citation
Global rigidity of smooth
 ${\mathbb{Z}}\ltimes _{\unicode{x3bb}}{\mathbb{R}}$-actions on
${\mathbb{Z}}\ltimes _{\unicode{x3bb}}{\mathbb{R}}$-actions on  ${\mathbb{T}}^{2}$
${\mathbb{T}}^{2}$
- Part of:
-
- Published online by Cambridge University Press:
- 14 October 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
Rigidity of Lyapunov exponents for derived from Anosov diffeomorphisms
- Part of:
-
- Published online by Cambridge University Press:
- 14 October 2024, pp. 1-17
-
- Article
-
- You have access
- HTML
- Export citation
Effective dynamical systems beyond dimension zero and factors of SFTs
- Part of:
-
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1-41
-
- Article
-
- You have access
- HTML
- Export citation
Geometric properties of disintegration of measures
- Part of:
-
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1-30
-
- Article
-
- You have access
- HTML
- Export citation
Construction of smooth isomorphic and finite-to-one extensions of irrational rotations which are not almost automorphic
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Birkhoff attractors of dissipative billiards
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1-59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperbolic actions of higher rank lattices come from rank-one factors
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Marked length pattern rigidity for arithmetic manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On algebraic dependencies between Poincaré functions
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rank-one non-singular actions of countable groups and their odometer factors
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1-51
-
- Article
-
- You have access
- HTML
- Export citation
Uniform Diophantine approximation and run-length function in continued fractions
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1-35
-
- Article
-
- You have access
- HTML
- Export citation
On the critical regularity of nilpotent groups acting on the interval: the metabelian case
- Part of:
-
- Published online by Cambridge University Press:
- 24 September 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
A parameter ASIP for the quadratic family
- Part of:
-
- Published online by Cambridge University Press:
- 24 September 2024, pp. 1-41
-
- Article
-
- You have access
- HTML
- Export citation
Shub’s example revisited
- Part of:
-
- Published online by Cambridge University Press:
- 23 September 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
Multifractal analysis of homological growth rates for hyperbolic surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-35
-
- Article
-
- You have access
- HTML
- Export citation
Non-concentration property of Patterson–Sullivan measures for Anosov subgroups
- Part of:
-
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum
On the quasi-ergodicity of absorbing Markov chains with unbounded transition densities, including random logistic maps with escape – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-5
-
- Article
-
- You have access
- HTML
- Export citation
Original Article
A recurrence-type strong Borel–Cantelli lemma for Axiom A diffeomorphisms
- Part of:
-
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-20
-
- Article
-
- You have access
- HTML
- Export citation
Rigidity of flat holonomies
- Part of:
-
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation










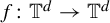




 meromorphic on
meromorphic on 
 ,
,  and
and  In this paper, we study the following problem: given Poincaré functions
In this paper, we study the following problem: given Poincaré functions  and
and  , find out if there is an algebraic relation
, find out if there is an algebraic relation  between them and, if such a relation exists, describe the corresponding algebraic curve
between them and, if such a relation exists, describe the corresponding algebraic curve 
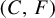
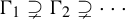 of cofinite subgroups in
of cofinite subgroups in