Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Huang, Lingling
and
Wu, Jun
2019.
Uniformly non–improvable Dirichlet set via continued fractions.
Proceedings of the American Mathematical Society,
Vol. 147,
Issue. 11,
p.
4617.
Bakhtawar, Ayreena
Bos, Philip
and
Hussain, Mumtaz
2020.
Hausdorff dimension of an exceptional set in the theory of continued fractions.
Nonlinearity,
Vol. 33,
Issue. 6,
p.
2615.
Huang, Lingling
Wu, Jun
and
Xu, Jian
2020.
Metric properties of the product of consecutive partial quotients in continued fractions.
Israel Journal of Mathematics,
Vol. 238,
Issue. 2,
p.
901.
SONG, TENG
and
ZHOU, QINGLONG
2020.
ON THE LONGEST BLOCK FUNCTION IN CONTINUED FRACTIONS.
Bulletin of the Australian Mathematical Society,
Vol. 102,
Issue. 2,
p.
196.
Feng, Jing
and
Xu, Jian
2021.
Sets of Dirichlet non-improvable numbers with certain order in the theory of continued fractions
*
.
Nonlinearity,
Vol. 34,
Issue. 3,
p.
1598.
Hu, Hui
Hussain, Mumtaz
and
Yu, Yueli
2021.
Limit theorems for sums of products of consecutive partial quotients of continued fractions.
Nonlinearity,
Vol. 34,
Issue. 12,
p.
8143.
Hu, Hui
Hussain, Mumtaz
and
Yu, Yueli
2021.
Metrical properties for continued fractions of formal Laurent series.
Finite Fields and Their Applications,
Vol. 73,
Issue. ,
p.
101850.
BAKHTAWAR, AYREENA
2021.
METRICAL PROBLEMS IN DIOPHANTINE APPROXIMATION.
Bulletin of the Australian Mathematical Society,
Vol. 104,
Issue. 3,
p.
519.
HUANG, LINGLING
and
MA, CHAO
2022.
A DIMENSIONAL RESULT ON THE PRODUCT OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS.
Journal of the Australian Mathematical Society,
Vol. 113,
Issue. 3,
p.
357.
Kim, Taehyeong
and
Kim, Wooyeon
2022.
Hausdorff measure of sets of Dirichlet non-improvable affine forms.
Advances in Mathematics,
Vol. 403,
Issue. ,
p.
108353.
Brown-Sarre, Adam
and
Hussain, Mumtaz
2023.
A note on the relative growth of products of multiple partial quotients in the plane.
Canadian Mathematical Bulletin,
Vol. 66,
Issue. 2,
p.
544.
Bos, Philip
Hussain, Mumtaz
and
Simmons, David
2023.
The generalised Hausdorff measure of sets of Dirichlet non-improvable numbers.
Proceedings of the American Mathematical Society,
LI, BIXUAN
WANG, BAOWEI
and
XU, JIAN
2023.
Hausdorff dimension of Dirichlet non-improvable set versus well-approximable set.
Ergodic Theory and Dynamical Systems,
Vol. 43,
Issue. 8,
p.
2707.
Hussain, Mumtaz
and
Shulga, Nikita
2024.
Hausdorff dimension for sets of continued fractions of formal Laurent series.
Finite Fields and Their Applications,
Vol. 95,
Issue. ,
p.
102377.
Fang, Lulu
Ma, Jihua
Song, Kunkun
and
Yang, Xin
2024.
Multifractal analysis of convergence exponents for products of consecutive partial quotients in continued fractions.
Acta Mathematica Scientia,
Vol. 44,
Issue. 4,
p.
1594.
Tan, Bo
and
Zhou, Qing-Long
2024.
Metrical properties of the large products of partial quotients in continued fractions.
Nonlinearity,
Vol. 37,
Issue. 2,
p.
025008.
CHEN, XIAO
FANG, LULU
LI, JUNJIE
SHANG, LEI
and
ZENG, XIN
2024.
ASYMPTOTIC BEHAVIOUR FOR PRODUCTS OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS.
Bulletin of the Australian Mathematical Society,
p.
1.
Wang, Bo
Li, Bing
and
Li, Ruofan
2024.
Uniform Diophantine approximation with restricted denominators.
Journal of Number Theory,
Vol. 260,
Issue. ,
p.
232.
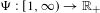 $\unicode[STIX]{x1D6F9}:[1,\infty )\rightarrow \mathbb{R}_{+}$ be a non-decreasing function,
$\unicode[STIX]{x1D6F9}:[1,\infty )\rightarrow \mathbb{R}_{+}$ be a non-decreasing function, 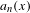 $a_{n}(x)$ the
$a_{n}(x)$ the  $n$th partial quotient of
$n$th partial quotient of  $x$ and
$x$ and 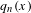 $q_{n}(x)$ the denominator of the
$q_{n}(x)$ the denominator of the  $n$th convergent. The set of
$n$th convergent. The set of  $\unicode[STIX]{x1D6F9}$-Dirichlet non-improvable numbers,
$\unicode[STIX]{x1D6F9}$-Dirichlet non-improvable numbers, 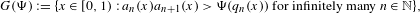 $$\begin{eqnarray}G(\unicode[STIX]{x1D6F9}):=\{x\in [0,1):a_{n}(x)a_{n+1}(x)>\unicode[STIX]{x1D6F9}(q_{n}(x))\text{ for infinitely many }n\in \mathbb{N}\},\end{eqnarray}$$
$$\begin{eqnarray}G(\unicode[STIX]{x1D6F9}):=\{x\in [0,1):a_{n}(x)a_{n+1}(x)>\unicode[STIX]{x1D6F9}(q_{n}(x))\text{ for infinitely many }n\in \mathbb{N}\},\end{eqnarray}$$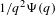 $1/q^{2}\unicode[STIX]{x1D6F9}(q)$-approximable numbers
$1/q^{2}\unicode[STIX]{x1D6F9}(q)$-approximable numbers 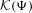 ${\mathcal{K}}(\unicode[STIX]{x1D6F9})$ in the sense that
${\mathcal{K}}(\unicode[STIX]{x1D6F9})$ in the sense that 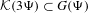 ${\mathcal{K}}(3\unicode[STIX]{x1D6F9})\subset G(\unicode[STIX]{x1D6F9})$. Both of these sets enjoy the same
${\mathcal{K}}(3\unicode[STIX]{x1D6F9})\subset G(\unicode[STIX]{x1D6F9})$. Both of these sets enjoy the same  $s$-dimensional Hausdorff measure criterion for
$s$-dimensional Hausdorff measure criterion for 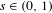 $s\in (0,1)$. We prove that the set
$s\in (0,1)$. We prove that the set 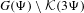 $G(\unicode[STIX]{x1D6F9})\setminus {\mathcal{K}}(3\unicode[STIX]{x1D6F9})$ is uncountable by proving that its Hausdorff dimension is the same as that for the sets
$G(\unicode[STIX]{x1D6F9})\setminus {\mathcal{K}}(3\unicode[STIX]{x1D6F9})$ is uncountable by proving that its Hausdorff dimension is the same as that for the sets 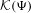 ${\mathcal{K}}(\unicode[STIX]{x1D6F9})$ and
${\mathcal{K}}(\unicode[STIX]{x1D6F9})$ and 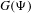 $G(\unicode[STIX]{x1D6F9})$. This gives an affirmative answer to a question raised by Hussain et al [Hausdorff measure of sets of Dirichlet non-improvable numbers. Mathematika 64(2) (2018), 502–518].
$G(\unicode[STIX]{x1D6F9})$. This gives an affirmative answer to a question raised by Hussain et al [Hausdorff measure of sets of Dirichlet non-improvable numbers. Mathematika 64(2) (2018), 502–518].


