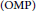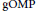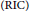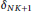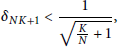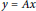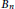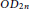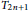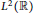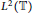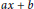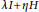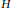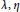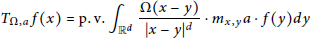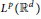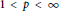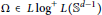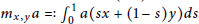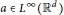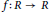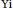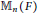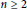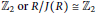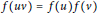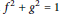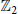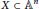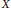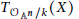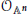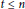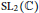Research Article
Periodic Steady-state Solutions of a Liquid Film Model via a Classical Method
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-15
-
- Article
-
- You have access
- Export citation
Classification of Simple Weight Modules over the Schrödinger Algebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 16-39
-
- Article
-
- You have access
- Export citation
A Sharp Bound on RIC in Generalized Orthogonal Matching Pursuit
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 40-54
-
- Article
-
- You have access
- Export citation
Enumerating Unlabelled Embeddings of Digraphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 55-69
-
- Article
-
- You have access
- Export citation
Hilbert Transformation and Representation of the ax + b Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 70-84
-
- Article
-
- You have access
- Export citation
On Subcritically Stein Fillable 5-manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 85-96
-
- Article
-
- You have access
- Export citation
On a Singular Integral of Christ–Journé Type with Homogeneous Kernel
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 97-113
-
- Article
-
- You have access
- Export citation
A Characterization of C*-normed Algebras via Positive Functionals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 114-123
-
- Article
-
- You have access
- Export citation
The Jordan Curve Theorem via Complex Analysis
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 124-129
-
- Article
-
- You have access
- Export citation
Additive Maps on Units of Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 130-141
-
- Article
-
- You have access
- Export citation
An Equivalent Form of Picard’s Theorem and Beyond
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 142-148
-
- Article
-
- You have access
- Export citation
Global Phase Portraits for the Abel Quadratic Polynomial Differential Equations of the Second Kind With Z2-symmetries
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 149-165
-
- Article
-
- You have access
- Export citation
A Module-theoretic Characterization of Algebraic Hypersurfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 166-173
-
- Article
-
- You have access
- Export citation
A Factorization Result for Classical and Similitude Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 174-190
-
- Article
-
- You have access
- Export citation
The Fefferman–Stein Type Inequalities for Strong and Directional Maximal Operators in the Plane
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 191-200
-
- Article
-
- You have access
- Export citation
Projective Plane Bundles Over an Elliptic Curve
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 201-210
-
- Article
-
- You have access
- Export citation
The Asymptotics of the Higher Dimensional Reidemeister Torsion for Exceptional Surgeries Along Twist Knots
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 211-224
-
- Article
-
- You have access
- Export citation