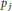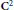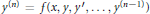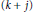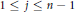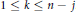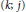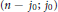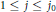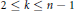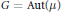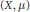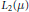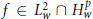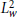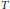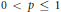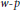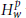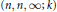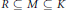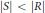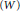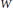Research Article
Limit Sets of Typical Homeomorphisms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-232
-
- Article
-
- You have access
- Export citation
On Algebraically Maximal Valued Fields and Defectless Extensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 233-241
-
- Article
-
- You have access
- Export citation
Convergence in Capacity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 242-248
-
- Article
-
- You have access
- Export citation
Description of Entire Solutions of Eiconal Type Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 249-259
-
- Article
-
- You have access
- Export citation
A Note on the Antipode for Algebraic Quantum Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 260-270
-
- Article
-
- You have access
- Export citation
On the Existence of the Graded Exponent for Finite Dimensional ℤp-graded Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 271-284
-
- Article
-
- You have access
- Export citation
Uniqueness Implies Existence and Uniqueness Conditions for a Class of (k + j)-Point Boundary Value Problems for n-th Order Differential Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 285-296
-
- Article
-
- You have access
- Export citation
The Group Aut (μ) is Roelcke Precompact
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 297-302
-
- Article
-
- You have access
- Export citation
Atomic Decomposition and Boundedness of Operators on Weighted Hardy Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 303-314
-
- Article
-
- You have access
- Export citation
A Note on the Vanishing of Certain Local Cohomology Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 315-318
-
- Article
-
- You have access
- Export citation
The Verdier Hypercovering Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 319-328
-
- Article
-
- You have access
- Export citation
Non-Discrete Complex Hyperbolic Triangle Groups of Type (n, n, ∞; k)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 329-338
-
- Article
-
- You have access
- Export citation
From Matrix to Operator Inequalities
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 339-350
-
- Article
-
- You have access
- Export citation
Rational Homogeneous Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 351-354
-
- Article
-
- You have access
- Export citation
Convolution Inequalities in lp Weighted Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 355-367
-
- Article
-
- You have access
- Export citation
The Secondary Chern–Euler Class for a General Submanifold
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 368-377
-
- Article
-
- You have access
- Export citation
On Modules Whose Proper Homomorphic Images Are of Smaller Cardinality
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 378-389
-
- Article
-
- You have access
- Export citation
Automorphisms of Iterated Wreath Product p-Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 390-399
-
- Article
-
- You have access
- Export citation
Eisenstein Series and Modular Differential Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 400-409
-
- Article
-
- You have access
- Export citation
A Ramsey Theorem with an Application to Sequences in Banach Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 410-417
-
- Article
-
- You have access
- Export citation