Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-26T16:19:17.217Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational Homogeneous Algebras

Published online by Cambridge University Press:  20 November 2018

J. A. MacDougall  and
L. G. Sweet
J. A. MacDougall
Affiliation:
School of Mathematical and Physical Sciences, University of Newcastle, Callaghan, NSW 2308, Australiae-mail: Jim.MacDougall@newcastle.edu.au
L. G. Sweet
Affiliation:
Dept. of Mathemetics, University of Prince Edward Island, Charlottetown, PEI C1A 4P3e-mail: sweet@upei.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An algebra 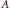$A$ is homogeneous if the automorphism group of 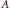$A$ acts transitively on the one-dimensional subspaces of 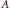$A$. The existence of homogeneous algebras depends critically on the choice of the scalar field. We examine the case where the scalar field is the rationals. We prove that if 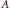$A$ is a rational homogeneous algebra with 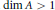$\dim\,A\,>\,1$, then 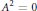${{A}^{2}}\,=\,0$.

Keywords

17D9917A36non-associative algebrahomogeneousautomorphism
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 2 , 01 June 2012 , pp. 351 - 354
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Djokovič, D. Ž., Real homogeneous algebras. Proc. Amer. Math. Soc. 41(1973), 457–462.Google Scholar
[2] Djokovič, D. Ž. and Sweet, L. G., Infinite homogeneous algebras are anticommutative. Proc. Amer. Math. Soc. 127(1999), no. 11, 3169–3174. http://dx.doi.org/10.1090/S0002-9939-99-04910-2 Google Scholar
[3] Djokovič, D. Ž. and Zhao, K., Real homogeneous algebras as truncated division algebras and their automorphism groups. Algebra Colloq. 11(2004), no. 1, 11–20.Google Scholar
[4] Gross, F., Finite automorphic algebras over GF(2) . Proc. Amer. Math. Soc. 31(1972), 10–14.Google Scholar
[5] Ivanov, D. N., Homogeneous algebras over GF(2) . Vestnik Moskov. Univ. Ser. I Mat. Mekh. 1982(1982), 69–72.Google Scholar
[6] Kostrikin, A. I., On homogeneous algebras. Izvestiya Akad. Nauk, SSSR Ser. Mat. 29(1965), 471–484.Google Scholar
[7] Kubota, K. K., Factors of polynomials under composition. J. Number Theory 4(1972), 587–595. http://dx.doi.org/10.1016/0022-314X(72)90030-3 Google Scholar
[8] MacDougall, J. A. and Sweet, L. G., Three dimensional homogeneous algebras. Pacific J. Math. 74(1978), no. 1, 153–162.Google Scholar
[9] Shult, E. E., On the triviality of finite automorphic algebras. Illinois J. Math. 13(1969), 654–659.Google Scholar
[10] Sweet, L. G., On the triviality of homogeneous algebras over an algebraically closed field Proc. Amer. Math. Soc. 48(1975), 321–324. http://dx.doi.org/10.1090/S0002-9939-1975-0364382-7 Google Scholar
[11] Sweet, L. G., On homogeneous algebras. Pacific J.Math 59(1975), no. 2, 385–594.Google Scholar
[12] Sweet, L. G. and MacDougall, J. A., Four-dimensional homogeneous algebras. Pacific J. Math. 129(1987), no. 2, 375–383.Google Scholar
[13] Sweet, L. G. and MacDougall, J. A., A decomposition theorem for homogeneous algebras. J. Austral. Math. Soc. 72(2002), no. 1, 47–56. http://dx.doi.org/10.1017/S1446788700003578 Google Scholar