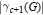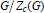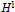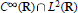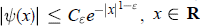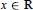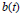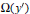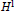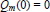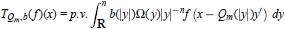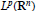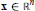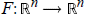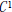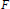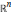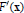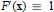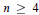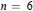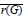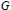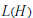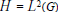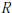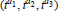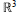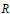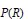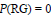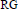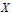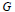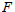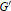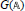Research Article
Inequalities for Baer Invariants of Finite Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 385-391
-
- Article
-
- You have access
- Export citation
A Note on H1 Multipliers for Locally Compact Vilenkin Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 392-397
-
- Article
-
- You have access
- Export citation
Band-Limited Wavelets with Subexponential Decay
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 398-403
-
- Article
-
- You have access
- Export citation
Lp-Boundedness of a Singular Integral Operator
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 404-412
-
- Article
-
- You have access
- Export citation
The Fixed Point Property in c0
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 413-422
-
- Article
-
- You have access
- Export citation
Free Products with Amalgamation and p-Adic Lie Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 423-433
-
- Article
-
- You have access
- Export citation
Linear Maps on Factors which Preserve the Extreme Points of the Unit Ball
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 434-441
-
- Article
-
- You have access
- Export citation
A Mountain Pass to the Jacobian Conjecture
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 442-451
-
- Article
-
- You have access
- Export citation
Dependent Automorphisms in Prime Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 452-462
-
- Article
-
- You have access
- Export citation
The Right Regular Representation of a Compact Right Topological Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 463-472
-
- Article
-
- You have access
- Export citation
Separating Singularities of Holomorphic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 473-477
-
- Article
-
- You have access
- Export citation
Convolution with Measures on Curves in ℝ3
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 478-480
-
- Article
-
- You have access
- Export citation
The Periodic Radical of Group Rings and Incidence Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-487
-
- Article
-
- You have access
- Export citation
Remarks on Certain Metaplectic Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 488-496
-
- Article
-
- You have access
- Export citation
On the Construction of Hölder and Proximal Subderivatives
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 497-507
-
- Article
-
- You have access
- Export citation
Other
Author Index for Volume 41, 1998
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 508-512
-
- Article
-
- You have access
- Export citation