Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
Hostname: page-component-5c569c448b-w5x57 Total loading time: 0.183 Render date: 2022-07-03T04:20:53.877Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "useRatesEcommerce": false, "useNewApi": true } hasContentIssue true
  • English
Canadian Mathematical Bulletin Canadian Mathematical Bulletin

Article contents

A Note on H1 Multipliers for Locally Compact Vilenkin Groups

Published online by Cambridge University Press:  20 November 2018

James E. Daly  and
Keith L. Phillips
James E. Daly
Affiliation:
Department of Mathematics University of Colorado Colorado Springs, CO 80907 USA, email: jedaly@math.uccs.edu
Keith L. Phillips
Affiliation:
Department of Mathematics University of Colorado Colorado Springs, CO 80907 USA, email: keith@pyramid.uccs.edu
Rights & Permissions[Opens in a new window]

Abstract

HTML view is not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Kitada and then Onneweer and Quek have investigated multiplier operators on Hardy spaces over locally compact Vilenkin groups. In this note, we provide an improvement to their results for the Hardy space 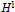${{H}^{1}}$ and provide examples showing that our result applies to a significantly larger group of multipliers.

Keywords

43A7044A35
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 4 , 01 December 1998 , pp. 392 - 397
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Chao, J. A. and Janson, S., A Note on H1 q-martingales. Pacific J. Math. 92 (1981), 307–317.Google Scholar
2. Daly, J. and Phillips, K., Walsh Multipliers and Square Functions for Hardy Spaces. Acta Math. Hungar. (4) 79 (1998), 311–327.Google Scholar
3. Daly, J. and Phillips, K., On Singular Integrals, Multipliers, H1, and Fourier Series—a Local Field Phenomenon. Math. Ann. 265 (1983), 181–219.Google Scholar
4. Kitada, T., Hp Multiplier Theorems on Certain Totally Disconnected Groups. Sci. Rep. Hirosaki Univ. 34 (1987), 1–7.Google Scholar
5. Onneweer, C. W. and Quek, T. S., Hp Multiplier Results on Locally Compact Vilenkin Groups. Quart. J. Math. Oxford Ser. 2 40 (1989), 313–323.Google Scholar
6. Simon, P., (L1, H)-Type Estimations for Some Operators with respect to the Walsh-Paley Systems. Acta. Math. Hungar. (3–4) 46 (1985), 307–310.Google Scholar
7. Young, W. S., Littlewood-Paley and Multiplier Theorems for Vilenkin-Fourier Series. Canad. J.Math (4) 46 (1994), 662–672.Google Scholar
You have Access
3
Cited by

Save article to Kindle

To save this article to your Kindle, first ensure coreplatform@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

A Note on H1 Multipliers for Locally Compact Vilenkin Groups
Available formats
×

Save article to Dropbox

To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.

A Note on H1 Multipliers for Locally Compact Vilenkin Groups
Available formats
×

Save article to Google Drive

To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.

A Note on H1 Multipliers for Locally Compact Vilenkin Groups
Available formats
×
×

Reply to: Submit a response

Please enter your response.

Your details

Please enter a valid email address.

Conflicting interests

Do you have any conflicting interests? *