Article contents
A Mountain Pass to the Jacobian Conjecture
Published online by Cambridge University Press: 20 November 2018
Abstract
This paper presents an approach to injectivity theorems via the Mountain Pass Lemma and raises an open question. The main result of this paper (Theorem 1.1) is proved by means of the Mountain Pass Lemma and states that if the eigenvalues of 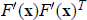 ${F}'(\text{x}){F}'{{(\text{x})}^{T}}\,$ are uniformly bounded away from zero for
${F}'(\text{x}){F}'{{(\text{x})}^{T}}\,$ are uniformly bounded away from zero for 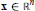 $\text{x}\,\in \,{{\mathbb{R}}^{n}}$, where
$\text{x}\,\in \,{{\mathbb{R}}^{n}}$, where 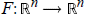 $F\,:\,{{\mathbb{R}}^{n}}\,\to \,{{\mathbb{R}}^{n}}$ is a class
$F\,:\,{{\mathbb{R}}^{n}}\,\to \,{{\mathbb{R}}^{n}}$ is a class 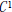 ${{C}^{1}}$ map, then F is injective. This was discovered in a joint attempt by the authors to prove a stronger result conjectured by the first author: Namely, that a sufficient condition for injectivity of class
${{C}^{1}}$ map, then F is injective. This was discovered in a joint attempt by the authors to prove a stronger result conjectured by the first author: Namely, that a sufficient condition for injectivity of class 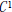 ${{C}^{1}}$ maps
${{C}^{1}}$ maps 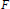 $F$ of
$F$ of 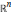 ${{\mathbb{R}}^{n}}$ into itself is that all the eigenvalues of
${{\mathbb{R}}^{n}}$ into itself is that all the eigenvalues of 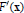 ${F}'\,(\text{x})$ are bounded away from zero on
${F}'\,(\text{x})$ are bounded away from zero on 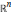 ${{\mathbb{R}}^{n}}$. This is stated as Conjecture 2.1. If true, it would imply (via Reduction-of-Degree) injectivity of polynomial maps
${{\mathbb{R}}^{n}}$. This is stated as Conjecture 2.1. If true, it would imply (via Reduction-of-Degree) injectivity of polynomial maps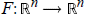 $F\,:\,{{\mathbb{R}}^{n}}\,\to \,{{\mathbb{R}}^{n}}$satisfying the hypothesis,
$F\,:\,{{\mathbb{R}}^{n}}\,\to \,{{\mathbb{R}}^{n}}$satisfying the hypothesis, 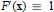 $\det F'(x)\equiv 1$, of the celebrated Jacobian Conjecture (JC) of Ott-Heinrich Keller. The paper ends with several examples to illustrate a variety of cases and known counterexamples to some natural questions.
$\det F'(x)\equiv 1$, of the celebrated Jacobian Conjecture (JC) of Ott-Heinrich Keller. The paper ends with several examples to illustrate a variety of cases and known counterexamples to some natural questions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998
Footnotes
The first author was partially supported by an NSERC Post-Doctoral Fellowship.
References
- 12
- Cited by


