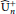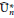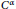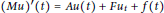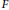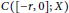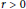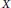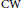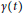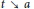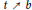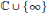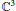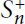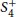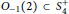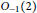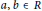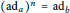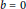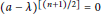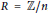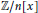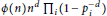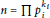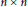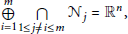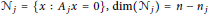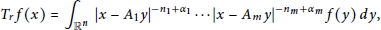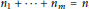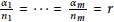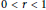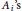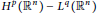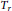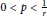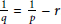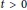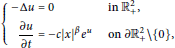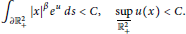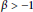Research Article
Higher ℓ2-Betti Numbers of Universal Quantum Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-235
-
- Article
-
- You have access
- Export citation
A Note on Uniformly Bounded Cocycles into Finite Von Neumann Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 236-239
-
- Article
-
- You have access
- Export citation
Hölder Continuous Solutions of Degenerate Differential Equations with Finite Delay
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 240-251
-
- Article
-
- You have access
- Export citation
Connectivity in Hypergraphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 252-271
-
- Article
-
- You have access
- Export citation
Symmetric Products of Equivariantly Formal Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 272-281
-
- Article
-
- You have access
- Export citation
The Initial and Terminal Cluster Sets of an Analytic Curve
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 282-288
-
- Article
-
- You have access
- Export citation
A Real-analytic Nonpolynomially Convex Isotropic Torus with no Attached Discs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 289-291
-
- Article
-
- You have access
- Export citation
A Note on a Unicity Theorem for the Gauss Maps of Complete Minimal Surfaces in Euclidean Four-space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 292-300
-
- Article
-
- You have access
- Export citation
Remarks on Hopf Images and Quantum Permutation Groups
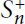 $S_{n}^{+}$
$S_{n}^{+}$
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 301-317
-
- Article
-
- You have access
- Export citation
Ad-nilpotent Elements of Semiprime Rings with Involution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 318-327
-
- Article
-
- You have access
- Export citation
Moduli of Space Sheaves with Hilbert Polynomial 4m + 1
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 328-345
-
- Article
-
- You have access
- Export citation
Counting Separable Polynomials in ℤ/n[x]
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 346-352
-
- Article
-
- You have access
- Export citation
Ground State and Multiple Solutions for Kirchhoff Type Equations With Critical Exponent
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 353-369
-
- Article
-
- You have access
- Export citation
A Remark on Certain Integral Operators of Fractional Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 370-375
-
- Article
-
- You have access
- Export citation
Elliptic Zeta Functions and Equivariant Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 376-389
-
- Article
-
- You have access
- Export citation
A Multiplier Theorem on Anisotropic Hardy Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 390-404
-
- Article
-
- You have access
- Export citation
Growth Rates of 3-dimensional Hyperbolic Coxeter Groups are Perron Numbers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 405-422
-
- Article
-
- You have access
- Export citation
Stability of Traveling Wavefronts for a Two-Component Lattice Dynamical System Arising in Competition Models
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 423-437
-
- Article
-
- You have access
- Export citation
Classification of Solutions for Harmonic Functions With Neumann Boundary Value
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 438-448
-
- Article
-
- You have access
- Export citation