Article contents
Counting Separable Polynomials in ℤ/n[x]
Published online by Cambridge University Press: 20 November 2018
Abstract
For a commutative ring 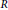 $R$, a polynomial
$R$, a polynomial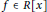 $f\,\in \,R[x]$ is called separable if
$f\,\in \,R[x]$ is called separable if 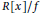 $R[x]/f$ is a separable
$R[x]/f$ is a separable 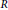 $R$-algebra. We derive formulae for the number of separable polynomials when
$R$-algebra. We derive formulae for the number of separable polynomials when 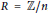 $R\,=\,\mathbb{Z}/n$, extending a result of L. Carlitz. For instance, we show that the number of polynomials in
$R\,=\,\mathbb{Z}/n$, extending a result of L. Carlitz. For instance, we show that the number of polynomials in 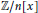 $\mathbb{Z}/n[x]$ that are separable is
$\mathbb{Z}/n[x]$ that are separable is 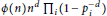 $\phi (n){{n}^{d}}{{\prod }_{i}}(1\,-\,p_{i}^{-d})$, where
$\phi (n){{n}^{d}}{{\prod }_{i}}(1\,-\,p_{i}^{-d})$, where 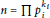 $n\,=\,\prod p_{i}^{{{k}_{i}}}$ is the prime factorisation of
$n\,=\,\prod p_{i}^{{{k}_{i}}}$ is the prime factorisation of  $n$ and
$n$ and 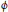 $\phi $ is Euler’s totient function.
$\phi $ is Euler’s totient function.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2018
References
- 2
- Cited by




