Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-26T11:00:52.727Z Has data issue: false hasContentIssue false
  • English
  • Français

A Remark on Certain Integral Operators of Fractional Type

Published online by Cambridge University Press:  20 November 2018

Pablo Alejandro Rocha
Pablo Alejandro Rocha*
Affiliation:
Universidad Nacional del Sur, Departamento de Matemáca, INMABB (Conicet), (8000) Bahía Blanca, Buenos Aires, Argentina, e-mail: alinorocha@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For 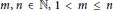$m,n\,\in \,\mathbb{N},\,1\,<\,m\le \,n$, we write 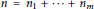$n={{n}_{1}}+\cdots +{{n}_{m}}$ where 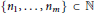$\{{{n}_{1}},\ldots \,,{{n}_{m}}\}\,\subset \,\mathbb{N}$. Let 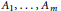${{A}_{1}}\,,\,\ldots \,,\,{{A}_{m}}$ be 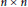$n\,\times \,n$ singular real matrices such that

$$\underset{i=1\,}{\overset{m}{\mathop{\oplus }}}\,\underset{1\le j\ne i\le m}{\mathop \bigcap }\,\,{{N}_{j}}\,=\,{{\mathbb{R}}^{n}},$$

where 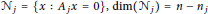${{N}_{j}}\,=\,\{x\,:\,{{A}_{j}}x\,=\,0\},\,\text{dim(}{{N}_{j}}\text{)}\,=\,n\,-\,{{n}_{j}}$, and 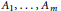${{A}_{1}}\,,\,\ldots \,,\,{{A}_{m}}$ is invertible. In this paper we study integral operators of the form

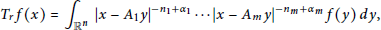$${{T}_{r}}f(x)\,=\,{{\int }_{{{\mathbb{R}}^{n}}}}|x\,-\,{{A}_{1y}}{{|}^{-{{n}_{1}}+{{\alpha }_{{{1}_{\ldots }}}}}}|x\,-\,{{A}_{m}}y{{|}^{-{{n}_{m}}+{{\alpha }_{m}}}}f(y)dy,$$

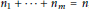${{n}_{1}}\,+\,\cdots \,+\,{{n}_{m}}\,=\,n$ , 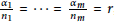$\frac{{{\alpha }_{1}}}{{{n}_{1}}}\,=\,\cdots \,=\,\frac{{{\alpha }_{m}}}{{{n}_{m}}}\,=\,r$, 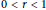$0\,<\,r\,<\,1$, and the matrices 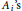${{A}_{i}}\text{ }\!\!'\!\!\text{ s}$ are as above. We obtain the 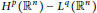${{H}^{p}}({{\mathbb{R}}^{n}})\,-\,{{L}^{q}}({{\mathbb{R}}^{n}})$ boundedness of 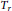${{T}_{r}}$ for 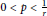$0\,<\,p\,<\,\frac{1}{r}$ and 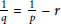$\frac{1}{q}\,=\,\frac{1}{p}\,-\,r$.

Keywords

42B2042B30integral operatorHardy space
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 2 , 01 June 2018 , pp. 370 - 375
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Godoy, T. and Urciuolo, M., About the Lp boundedness of some integral Operators. Rev. Un. Mat. Argentina 38 (1993), 192–195.Google Scholar
[2] Godoy, T. and Urciuolo, M., On certain integral Operators of fractional type. Acta Math. Hungar. 82 (1999), 99–105. http://dx.doi.Org/10.1023/A:1026437621978Google Scholar
[3] Krantz, S., Fractional 'Integration on Hardy Spaces. Studia Math. 73 (1982), no. 2, 87–94.Google Scholar
[4] Riveros, M. S. and Urciuolo, M., Weighted inequalities for integral Operators with some homogeneous kerneis. Czechoslovak Math. J. 55 (2005), 423–432. http://dx.doi.org/10.1007/s10587-005-0032-yGoogle Scholar
[5] Riveros, M. S. and Urciuolo, M., Weighted Hp — Lq boundedness of integral Operators with rough kerneis. Preprint. https://www.researchgate.net/publication/319511626Google Scholar
[6] Rocha, P., A note on Hardy Spaces and bounded linear Operators. To appear in Georgian Math. J.Google Scholar
[7] Rocha, P. and Urciuolo, M., On the Hp - Lp boundedness ofsome integral Operators. Georgian Math. J. 18 (2011) no. 4, 801–808. http://dx.doi.Org/10.1515/CMJ.2O11.0043Google Scholar
[8] Rocha, P. and Urciuolo, M., On the Hp - Lq boundedness of some fractional integral Operators. Czechoslovak Math. J. 62 (2012), 625–635. http://dx.doi.org/10.1007/s10587-012-0054-1Google Scholar
[9] Stein, E., Singular integrals and differentiability properties offunctions. Princeton Mathematical Series, 30. Princeton University Press, Princeton, NJ, 1970.Google Scholar
[10] Stein, E., Harmonie analysis, real variable methods, orthogonality and oscillatory integrals. Princeton Mathematical Series, 43. Princeton University Press, Princeton, NJ, 1993.Google Scholar
[11] Taibleson, M. H. and Weiss, G., The molecular characterization ofcertain Hardy Spaces. Asterisque, 77. Soc. Math. France, Paris, 1980, pp. 67–149.Google Scholar