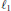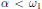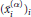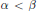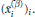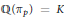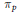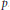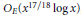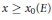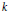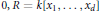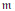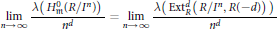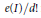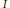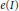Research Article
On the Structure of the Spreading Models of a Banach Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-707
-
- Article
-
- You have access
- Export citation
Enriques Diagrams and Adjacency of Planar Curve Singularities
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-16
-
- Article
-
- You have access
- Export citation
On the Sizes of Gaps in the Fourier Expansion of Modular Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-470
-
- Article
-
- You have access
- Export citation
On
 $\mathcal{C}\mathcal{R}$-Epic Embeddings and Absolute
$\mathcal{C}\mathcal{R}$-Epic Embeddings and Absolute  $\mathcal{C}\mathcal{R}$-Epic Spaces
$\mathcal{C}\mathcal{R}$-Epic Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1121-1138
-
- Article
-
- You have access
- Export citation
Unbounded Fredholm Operators and Spectral Flow
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-250
-
- Article
-
- You have access
- Export citation
Representation of Banach Ideal Spaces and Factorization of Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 897-940
-
- Article
-
- You have access
- Export citation
On Amenability and Co-Amenability of Algebraic Quantum Groups and Their Corepresentations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 17-60
-
- Article
-
- You have access
- Export citation
Some Transformations of Hausdorff Moment Sequences and Harmonic Numbers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 941-960
-
- Article
-
- You have access
- Export citation
Curvature Estimates in Asymptotically Flat Lorentzian Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 708-723
-
- Article
-
- You have access
- Export citation
Some New Results on L2 Cohomology of Negatively Curved Riemannian Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 251-266
-
- Article
-
- You have access
- Export citation
Small Coverings with Smooth Functions under the Covering Property Axiom
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 471-493
-
- Article
-
- You have access
- Export citation
Models in Which Every Nonmeager Set is Nonmeager in a Nowhere Dense Cantor Set
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1139-1154
-
- Article
-
- You have access
- Export citation
Partial Euler Products on the Critical Line
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 267-297
-
- Article
-
- You have access
- Export citation
On Operators with Spectral Square but without Resolvent Points
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 61-81
-
- Article
-
- You have access
- Export citation
Summation Formulae for Coefficients of L-functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 494-505
-
- Article
-
- You have access
- Export citation
Some Results on Surfaces of General Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 724-749
-
- Article
-
- You have access
- Export citation
Cone-Monotone Functions: Differentiability and Continuity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-982
-
- Article
-
- You have access
- Export citation
The Square Sieve and the Lang–Trotter Conjecture
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1155-1177
-
- Article
-
- You have access
- Export citation
Sur la structure transverse à une orbite nilpotente adjointe
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 750-770
-
- Article
-
- You have access
- Export citation
Asymptotic Behavior of the Length of Local Cohomology
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1178-1192
-
- Article
-
- You have access
- Export citation