Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
TOMATSU, Reiji
2006.
Amenable discrete quantum groups.
Journal of the Mathematical Society of Japan,
Vol. 58,
Issue. 4,
Tomatsu, Reiji
2007.
A Characterization of Right Coideals of Quotient Type and its Application to Classification of Poisson Boundaries.
Communications in Mathematical Physics,
Vol. 275,
Issue. 1,
p.
271.
Kyed, David
2011.
A cohomological description of property (T) for quantum groups.
Journal of Functional Analysis,
Vol. 261,
Issue. 6,
p.
1469.
NESHVEYEV, SERGEY
and
TUSET, LARS
2011.
ON SECOND COHOMOLOGY OF DUALS OF COMPACT GROUPS.
International Journal of Mathematics,
Vol. 22,
Issue. 09,
p.
1231.
GHANEI, MOHAMMAD REZA
and
NASR-ISFAHANI, RASOUL
2013.
INNER AMENABILITY OF LOCALLY COMPACT QUANTUM GROUPS.
International Journal of Mathematics,
Vol. 24,
Issue. 07,
p.
1350058.
Nemati, Mehdi
2014.
Ergodic properties and harmonic functionals on locally compact quantum groups.
International Journal of Mathematics,
Vol. 25,
Issue. 05,
p.
1450051.
Tomatsu, Reiji
2015.
Product type actions ofGq.
Advances in Mathematics,
Vol. 269,
Issue. ,
p.
162.
Akhtari, Fatemeh
and
Nasr-Isfahani, Rasoul
2016.
Voiculescu amenable Hopf von Neumann algebras with applications.
Journal of Algebra and Its Applications,
Vol. 15,
Issue. 06,
p.
1650079.
Daws, Matthew
Skalski, Adam
and
Viselter, Ami
2017.
Around Property (T) for Quantum Groups.
Communications in Mathematical Physics,
Vol. 353,
Issue. 1,
p.
69.
Jones, Corey
and
Penneys, David
2017.
Operator Algebras in Rigid C*-Tensor Categories.
Communications in Mathematical Physics,
Vol. 355,
Issue. 3,
p.
1121.
Ng, Chi-Keung
and
Viselter, Ami
2017.
Amenability of locally compact quantum groups and their unitary co-representations.
Bulletin of the London Mathematical Society,
Vol. 49,
Issue. 3,
p.
491.
Brannan, Michael
and
Kerr, David
2018.
Quantum Groups, Property (T), and Weak Mixing.
Communications in Mathematical Physics,
Vol. 360,
Issue. 3,
p.
1043.
Das, Biswarup
Daws, Matthew
and
Salmi, Pekka
2019.
Admissibility Conjecture and Kazhdan's Property (T) for quantum groups.
Journal of Functional Analysis,
Vol. 276,
Issue. 11,
p.
3484.
Chirvasitu, Alexandru
2021.
Fields of locally compact quantum groups: Continuity and pushouts.
International Journal of Mathematics,
Vol. 32,
Issue. 09,
p.
2150064.
Tomatsu, Reiji
2021.
Centrally Free Actions of Amenable $$\hbox {C}^*$$-Tensor Categories on von Neumann Algebras.
Communications in Mathematical Physics,
Vol. 383,
Issue. 1,
p.
71.
Tuset, Lars
2022.
Analysis and Quantum Groups.
p.
393.
 $*$-representations of algebraic quantum groups, which may be used to characterize amenability and co-amenability for such quantum groups. As a background for this study, we investigate the associated tensor
$*$-representations of algebraic quantum groups, which may be used to characterize amenability and co-amenability for such quantum groups. As a background for this study, we investigate the associated tensor 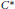 ${{C}^{*}}$-categories.
${{C}^{*}}$-categories.

