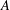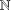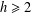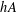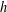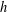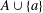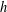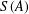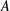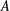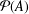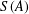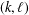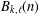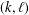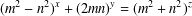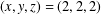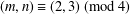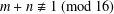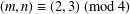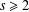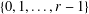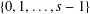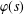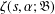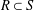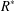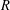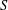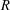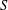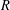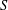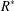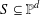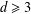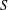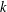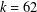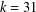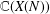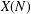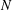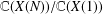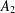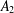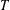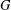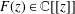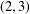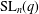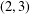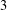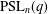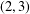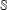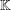Research Article
A NOTE ON ASYMPTOTIC NONBASES
- Part of:
-
- Published online by Cambridge University Press:
- 13 October 2016, pp. 1-4
-
- Article
-
- You have access
- Export citation
A FINITE-TO-ONE MAP FROM THE PERMUTATIONS ON A SET
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 177-182
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROPERTIES OF
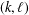 $(k,\ell )$-REGULAR BIPARTITIONS
$(k,\ell )$-REGULAR BIPARTITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2016, pp. 353-364
-
- Article
-
- You have access
- Export citation
MONOTONIC PHINOMIAL COEFFICIENTS
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2017, pp. 365-372
-
- Article
-
- You have access
- Export citation
A NOTE ON JEŚMANOWICZ’ CONJECTURE CONCERNING PRIMITIVE PYTHAGOREAN TRIPLES
- Part of:
-
- Published online by Cambridge University Press:
- 26 September 2016, pp. 5-13
-
- Article
-
- You have access
- Export citation
ON A PROBLEM OF ERDÖS AND MAHLER CONCERNING CONTINUED FRACTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 183-186
-
- Article
-
- You have access
- Export citation
ON THE EXPANSIONS OF REAL NUMBERS IN TWO MULTIPLICATIVELY DEPENDENT BASES
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2016, pp. 373-383
-
- Article
-
- You have access
- Export citation
REMARKS ON THE MIXED JOINT UNIVERSALITY FOR A CLASS OF ZETA FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 187-198
-
- Article
-
- You have access
- Export citation
WHEN IS THE INTEGRAL CLOSURE COMPARABLE TO ALL INTERMEDIATE RINGS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 14-21
-
- Article
-
- You have access
- Export citation
RANK TWO STABLE ULRICH BUNDLES ON ANTICANONICALLY EMBEDDED SURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 23 November 2016, pp. 22-37
-
- Article
-
- You have access
- Export citation
ON PAIRS OF GOLDBACH–LINNIK EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 199-208
-
- Article
-
- You have access
- Export citation
NORMAL BASES FOR MODULAR FUNCTION FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2017, pp. 384-392
-
- Article
-
- You have access
- Export citation
FIXED ELEMENTS OF NONINJECTIVE ENDOMORPHISMS OF POLYNOMIAL ALGEBRAS IN TWO VARIABLES
- Part of:
-
- Published online by Cambridge University Press:
- 20 October 2016, pp. 209-213
-
- Article
-
- You have access
- Export citation
A NOTE ON GROUPS WHOSE PROPER LARGE SUBGROUPS HAVE A TRANSITIVE NORMALITY RELATION
- Part of:
-
- Published online by Cambridge University Press:
- 04 November 2016, pp. 38-47
-
- Article
-
- You have access
- Export citation
TRANSCENDENCE OVER MEROMORPHIC FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2017, pp. 393-399
-
- Article
-
- You have access
- Export citation
THE
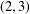 $(2,3)$-GENERATION OF THE SPECIAL LINEAR GROUPS OVER FINITE FIELDS
$(2,3)$-GENERATION OF THE SPECIAL LINEAR GROUPS OVER FINITE FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 26 September 2016, pp. 48-53
-
- Article
-
- You have access
- Export citation
EXPLICIT ZERO-COUNTING THEOREM FOR HECKE–LANDAU ZETA-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2017, pp. 400-411
-
- Article
-
- You have access
- Export citation
A PRIME ESSENTIAL RING THAT GENERATES A SPECIAL ATOM
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 214-218
-
- Article
-
- You have access
- Export citation
ON VARIETIES OF ABELIAN TOPOLOGICAL GROUPS WITH COPRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 54-65
-
- Article
-
- You have access
- Export citation
EXTENSIONS OF THE HERMITE–HADAMARD INEQUALITY FOR
 $r$-PREINVEX FUNCTIONS ON AN INVEX SET
$r$-PREINVEX FUNCTIONS ON AN INVEX SET
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2017, pp. 412-423
-
- Article
-
- You have access
- Export citation