Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-27T05:09:02.912Z Has data issue: false hasContentIssue false
  • English
  • Français

TRANSCENDENCE OVER MEROMORPHIC FUNCTIONS

Part of: Series expansions Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  13 March 2017

MICHAEL COONS  and
YOHEI TACHIYA
MICHAEL COONS*
Affiliation:
School of Mathematical and Physical Sciences, University of Newcastle, Callaghan, Australia email Michael.Coons@newcastle.edu.au
YOHEI TACHIYA
Affiliation:
Graduate School of Science and Technology, Hirosaki University, Hirosaki, Japan email tachiya@hirosaki-u.ac.jp
*
✉Michael.Coons@newcastle.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this short note, considering functions, we show that taking an asymptotic viewpoint allows one to prove strong transcendence statements in many general situations. In particular, as a consequence of a more general result, we show that if 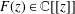$F(z)\in \mathbb{C}[[z]]$ is a power series with coefficients from a finite set, then 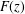$F(z)$ is either rational or it is transcendental over the field of meromorphic functions.

Keywords

transcendencealgebraic independenceradial asymptotics

MSC classification

Primary: 11J81: Transcendence (general theory)
Secondary: 11J91: Transcendence theory of other special functions 30B30: Boundary behavior of power series, over-convergence
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 3 , June 2017 , pp. 393 - 399
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

The research of M. Coons was supported by ARC grant DE140100223 and the research of Y. Tachiya was supported by JSPS, Grant-in-Aid for Young Scientists (B), 15K17504.

References

Allouche, J.-P., ‘Transcendence of formal power series with rational coefficients’, Theoret. Comput. Sci. 218(1) (1999), 143–160.Google Scholar
Allouche, J.-P. and Shallit, J., Automatic Sequences (Cambridge University Press, Cambridge, 2003).Google Scholar
Bézivin, J.-P., ‘Sur une classe d’équations fonctionnelles non linéaires’, Funkcial. Ekvac. 37(2) (1994), 263–271.Google Scholar
Borwein, P. and Coons, M., ‘Transcendence of power series for some number theoretic functions’, Proc. Amer. Math. Soc. 137(4) (2009), 1303–1305.CrossRefGoogle Scholar
Borwein, P., Erdélyi, T. and Littmann, F., ‘Polynomials with coefficients from a finite set’, Trans. Amer. Math. Soc. 360(10) (2008), 5145–5154.Google Scholar
Coons, M., ‘An asymptotic approach in Mahler’s method’, Preprint, 2015, available at arXiv:1511.07534, 15 pages.Google Scholar
Duffin, R. J. and Schaeffer, A. C., ‘Power series with bounded coefficients’, Amer. J. Math. 67 (1945), 141–154.Google Scholar
Fatou, P., ‘Séries trigonométriques et séries de Taylor’, Acta Math. 30(1) (1906), 335–400.Google Scholar
Knopp, K., ‘Über Lambertsche Reihen’, J. reine angew. Math. 142 (1913), 283–315.CrossRefGoogle Scholar
Randé, B., Équations fonctionnelles de Mahler et applications aux suites p-régulières (Institut National de Recherche en Informatique et en Automatique (INRIA), Rocquencourt, 1992); Thèse, Université de Bordeaux I, Talence, 1992.Google Scholar
Stein, E. M. and Shakarchi, R., Complex Analysis, Princeton Lectures in Analysis, II (Princeton University Press, Princeton, NJ, 2003).Google Scholar
Titchmarsh, E. C., The Theory of Functions (Oxford University Press, Oxford, 1958), reprint of the second (1939) edition.Google Scholar