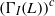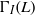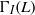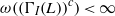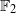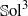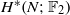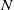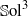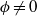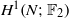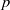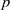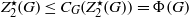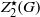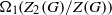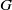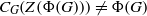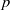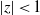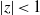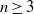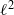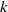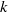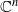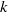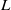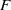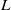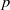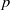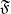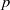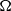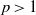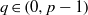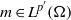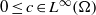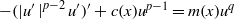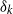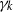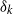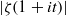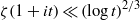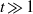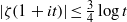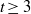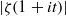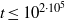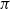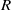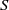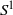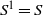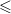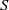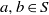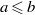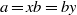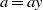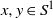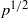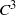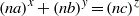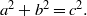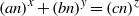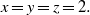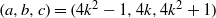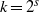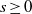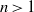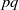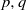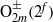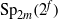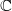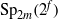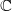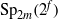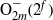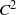Research Article
COMPLEMENT OF THE ZERO DIVISOR GRAPH OF A LATTICE
- Part of:
-
- Published online by Cambridge University Press:
- 11 June 2013, pp. 177-190
-
- Article
-
- You have access
- Export citation
THE
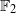 ${ \mathbb{F} }_{2} $-COHOMOLOGY RINGS OF
${ \mathbb{F} }_{2} $-COHOMOLOGY RINGS OF 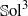 $ \mathbb{S} {\text{ol} }^{3} $-MANIFOLDS
$ \mathbb{S} {\text{ol} }^{3} $-MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2013, pp. 191-201
-
- Article
-
- You have access
- Export citation
ON NONINNER AUTOMORPHISMS OF FINITE NONABELIAN
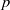 $p$-GROUPS
$p$-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 07 June 2013, pp. 202-209
-
- Article
-
- You have access
- Export citation
REMARKS ON THE UNIVALENCE CRITERION OF PASCU AND PASCU
- Part of:
-
- Published online by Cambridge University Press:
- 22 August 2013, pp. 210-216
-
- Article
-
- You have access
- Export citation
AN EXAMPLE CONCERNING BOUNDED LINEAR REGULARITY OF SUBSPACES IN HILBERT SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 12 September 2013, pp. 217-226
-
- Article
-
- You have access
- Export citation
WEAK CONTINUITY OF THE COMPLEX
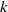 $k$-HESSIAN OPERATORS WITH RESPECT TO LOCAL UNIFORM CONVERGENCE
$k$-HESSIAN OPERATORS WITH RESPECT TO LOCAL UNIFORM CONVERGENCE
- Part of:
-
- Published online by Cambridge University Press:
- 11 June 2013, pp. 227-233
-
- Article
-
- You have access
- Export citation
CHARACTER CLUSTERS FOR LIE ALGEBRA MODULES OVER A FIELD OF NONZERO CHARACTERISTIC
- Part of:
-
- Published online by Cambridge University Press:
- 07 June 2013, pp. 234-242
-
- Article
-
- You have access
- Export citation
STRICTLY POSITIVE SOLUTIONS FOR ONE-DIMENSIONAL NONLINEAR PROBLEMS INVOLVING THE
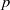 $p$-LAPLACIAN
$p$-LAPLACIAN
- Part of:
-
- Published online by Cambridge University Press:
- 06 September 2013, pp. 243-251
-
- Article
-
- You have access
- Export citation
CONCISENESS OF COPRIME COMMUTATORS IN FINITE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 18 July 2013, pp. 252-258
-
- Article
-
- You have access
- Export citation
A NEW UPPER BOUND FOR
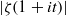 $\vert \zeta (1+ it)\vert $
$\vert \zeta (1+ it)\vert $
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2013, pp. 259-264
-
- Article
-
- You have access
- Export citation
COMPARISON OF MEASURES OF TOTALLY POSITIVE POLYNOMIALS
-
- Published online by Cambridge University Press:
- 22 August 2013, pp. 265-270
-
- Article
-
- You have access
- Export citation
ON A QUESTION OF HARTWIG AND LUH
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2013, pp. 271-278
-
- Article
-
- You have access
- Export citation
THE NATURAL PARTIAL ORDER ON SOME TRANSFORMATION SEMIGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 28 June 2013, pp. 279-292
-
- Article
-
- You have access
- Export citation
ON CONJUGACY OF SUPPLEMENTS OF NORMAL SUBGROUPS OF FINITE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2013, pp. 293-299
-
- Article
-
- You have access
- Export citation
ON SOLUTIONS TO SOME POLYNOMIAL CONGRUENCES IN SMALL BOXES
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2013, pp. 300-307
-
- Article
-
- You have access
- Export citation
ON SUMMABILITY CONDITIONS FOR INTERVAL MAPS
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2013, pp. 308-315
-
- Article
-
- You have access
- Export citation
A NOTE ON THE DIOPHANTINE EQUATION
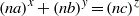 $\mathop{(na)}\nolimits ^{x} + \mathop{(nb)}\nolimits ^{y} = \mathop{(nc)}\nolimits ^{z} $
$\mathop{(na)}\nolimits ^{x} + \mathop{(nb)}\nolimits ^{y} = \mathop{(nc)}\nolimits ^{z} $
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2013, pp. 316-321
-
- Article
-
- You have access
- Export citation
SELF-COMPLEMENTARY VERTEX-TRANSITIVE GRAPHS OF ORDER A PRODUCT OF TWO PRIMES
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2013, pp. 322-330
-
- Article
-
- You have access
- Export citation
A REMARK ON THE PERMUTATION REPRESENTATIONS AFFORDED BY THE EMBEDDINGS OF
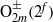 ${ \text{O} }_{2m}^{\pm } ({2}^{f} )$ IN
${ \text{O} }_{2m}^{\pm } ({2}^{f} )$ IN 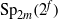 ${\text{Sp} }_{2m} ({2}^{f} )$
${\text{Sp} }_{2m} ({2}^{f} )$
- Part of:
-
- Published online by Cambridge University Press:
- 19 September 2013, pp. 331-336
-
- Article
-
- You have access
- Export citation
SOME REMARKS ON THE PIGOLA–RIGOLI–SETTI VERSION OF THE OMORI–YAU MAXIMUM PRINCIPLE
- Part of:
-
- Published online by Cambridge University Press:
- 19 August 2013, pp. 337-342
-
- Article
-
- You have access
- Export citation