Article contents
A NOTE ON THE DIOPHANTINE EQUATION 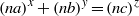 $\mathop{(na)}\nolimits ^{x} + \mathop{(nb)}\nolimits ^{y} = \mathop{(nc)}\nolimits ^{z} $
$\mathop{(na)}\nolimits ^{x} + \mathop{(nb)}\nolimits ^{y} = \mathop{(nc)}\nolimits ^{z} $
Published online by Cambridge University Press: 07 August 2013
Abstract
Let 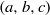 $(a, b, c)$ be a primitive Pythagorean triple satisfying
$(a, b, c)$ be a primitive Pythagorean triple satisfying 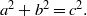 ${a}^{2} + {b}^{2} = {c}^{2} . $ In 1956, Jeśmanowicz conjectured that for any given positive integer
${a}^{2} + {b}^{2} = {c}^{2} . $ In 1956, Jeśmanowicz conjectured that for any given positive integer  $n$ the only solution of
$n$ the only solution of 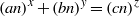 $\mathop{(an)}\nolimits ^{x} + \mathop{(bn)}\nolimits ^{y} = \mathop{(cn)}\nolimits ^{z} $ in positive integers is
$\mathop{(an)}\nolimits ^{x} + \mathop{(bn)}\nolimits ^{y} = \mathop{(cn)}\nolimits ^{z} $ in positive integers is 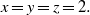 $x= y= z= 2. $ In this paper, for the primitive Pythagorean triple
$x= y= z= 2. $ In this paper, for the primitive Pythagorean triple 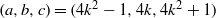 $(a, b, c)= (4{k}^{2} - 1, 4k, 4{k}^{2} + 1)$ with
$(a, b, c)= (4{k}^{2} - 1, 4k, 4{k}^{2} + 1)$ with 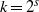 $k= {2}^{s} $ for some positive integer
$k= {2}^{s} $ for some positive integer 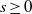 $s\geq 0$, we prove the conjecture when
$s\geq 0$, we prove the conjecture when 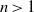 $n\gt 1$ and certain divisibility conditions are satisfied.
$n\gt 1$ and certain divisibility conditions are satisfied.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
- 10
- Cited by


