Research Article
On convergence in capacity
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-5
-
- Article
-
- You have access
- Export citation
On the orbit-sizes of permutation groups containing elements separating finite subsets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 7-10
-
- Article
-
- You have access
- Export citation
Duality for generalized problems in complex programming
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 11-22
-
- Article
-
- You have access
- Export citation
On certain non-archimedean functions analogous to complex analytic functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 23-36
-
- Article
-
- You have access
- Export citation
The ideals of the hurwitzean polynomial ring
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 37-61
-
- Article
-
- You have access
- Export citation
A note on locally finite varieties
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 63-70
-
- Article
-
- You have access
- Export citation
A case of boundedness in Littlewood's problem on oscillatory differential equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 71-93
-
- Article
-
- You have access
- Export citation
A class of modules over a locally finite group III
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 95-110
-
- Article
-
- You have access
- Export citation
Fibrations and Grothendieck topologies
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 111-128
-
- Article
-
- You have access
- Export citation
On the complex nonlinear complementary problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 129-136
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
Finite difference methods with application to the cavity problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 137-138
-
- Article
-
- You have access
- Export citation
Some problems concerning cluster processes and other point processes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 139-140
-
- Article
-
- You have access
- Export citation
Some theoretical aspects of dielectric absorption and dispersion in polar gases and liquids
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 141-143
-
- Article
-
- You have access
- Export citation
Analysis of functional relationships: old and new models
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 145-147
-
- Article
-
- You have access
- Export citation
Some number theoretic properties of arbitrary order recursive sequences
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 149-151
-
- Article
-
- You have access
- Export citation
Models with dimension
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 153-154
-
- Article
-
- You have access
- Export citation
Thermal convection at high Rayleigh number
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 155-156
-
- Article
-
- You have access
- Export citation
Maximum likelihood estimation for stochastic processes - a martingale approach
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 157-158
-
- Article
-
- You have access
- Export citation
On core flows
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 159-160
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 14 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation



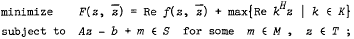
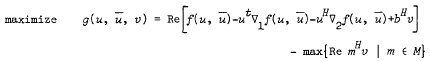
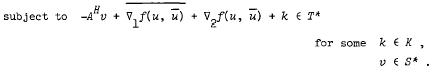
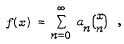
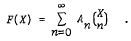
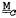 -module over
-module over 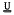 -groups, a class of locally finite groups similar in many ways to the class of finite soluble groups.
-groups, a class of locally finite groups similar in many ways to the class of finite soluble groups.