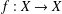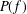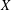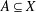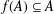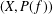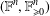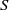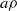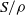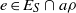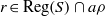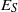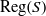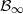27 results in 06Bxx
Semidistrim Lattices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 16 June 2023, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REFLEXIVITY INDEX OF THE PRODUCT OF SOME TOPOLOGICAL SPACES AND LATTICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 376-387
- Print publication:
- April 2024
-
- Article
- Export citation
REFLEXIVITY INDEX AND IRRATIONAL ROTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 29 March 2021, pp. 493-505
- Print publication:
- December 2021
-
- Article
- Export citation
THE DISTRIBUTIVITY SPECTRUM OF BAKER’S VARIETY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 26 October 2020, pp. 119-144
- Print publication:
- February 2021
-
- Article
- Export citation
Edwards' condition for quasitraces on C*-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 April 2020, pp. 525-547
- Print publication:
- April 2021
-
- Article
-
- You have access
- Open access
- Export citation
A MINIMAL CONGRUENCE LATTICE REPRESENTATION FOR
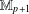 $\mathbb{M}_{p+1}$
$\mathbb{M}_{p+1}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 24 March 2020, pp. 332-340
- Print publication:
- June 2020
-
- Article
- Export citation
The Weak Order on Weyl Posets
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 867-899
- Print publication:
- August 2020
-
- Article
- Export citation
On the Weak Order of Coxeter Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 10 January 2019, pp. 299-336
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Lattice structure of Weyl groups via representation theory of preprojective algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1269-1305
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
Perforation conditions and almost algebraic order in Cuntz semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 18 April 2018, pp. 669-702
- Print publication:
- August 2018
-
- Article
- Export citation
REPRESENTING REGULAR PSEUDOCOMPLEMENTED KLEENE ALGEBRAS BY TOLERANCE-BASED ROUGH SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 57-78
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
HOMOGENEOUS FUNCTIONALLY ALEXANDROFF SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 08 November 2017, pp. 331-339
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
On a random search tree: asymptotic enumeration of vertices by distance from leaves
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 850-876
- Print publication:
- September 2017
-
- Article
- Export citation
FINITE-DIMENSIONAL ORDERED VECTOR SPACES WITH RIESZ INTERPOLATION AND EFFROS–SHEN’S UNIMODULARITY CONJECTURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 277-287
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
CHARACTERIZATION OF PROJECTIVE QUANTALES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 403-420
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
REGULAR CONGRUENCES ON AN IDEMPOTENT-REGULAR-SURJECTIVE SEMIGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 30 July 2013, pp. 190-196
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
IRREDUCIBLE QUASIORDERS OF MONOUNARY ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 01 March 2013, pp. 259-276
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
VARIETIES WHOSE TOLERANCES ARE HOMOMORPHIC IMAGES OF THEIR CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 08 August 2012, pp. 326-338
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Quasi-Birth-and-Death Processes, Lattice Path Counting, and Hypergeometric Functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 507-520
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
The Direct Decomposition of l-algebras into Products of Subdirectly Irreducible Factors
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 41-56
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation



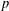
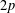
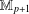
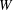
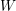
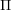
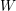

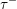
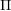
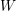
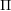
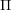
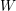
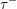
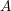
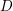
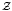 ) in terms of Cu(
) in terms of Cu(