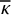1 Introduction
In this paper, all lattices are assumed to be finite. Two families of lattices that extend the family of distributive lattices are the family of semidistributive lattices and the family of trim lattices (see Section 2). The union of these two families contains several well-studied classes of lattices such as weak orders of finite Coxeter groups, facial weak orders of simplicial hyperplane arrangements [Reference Dermenjian, Hohlweg, McConville and Pilaud20], finite Cambrian lattices [Reference Reading37], biCambrian lattices [Reference Barnard and Reading7],
$\nu $
-Tamari lattices [Reference Préville-Ratelle and Viennot35], grid-Tamari lattices [Reference McConville33] and lattices of torsion classes of artin algebras [Reference Demonet, Iyama, Reading, Reiten and Thomas19, Reference Garver and McConville24, Reference Thomas and Williams50]. Although these two families are distinct (a semidistributive lattice that is not trim and a trim lattice that is not semidistributive are illustrated on the left and in the middle of Figure 1), they share many common properties. For example, the following hold for each lattice L in each of these families:
-
• there is a canonical bijection between join-irreducible and meet-irreducible elements of L;
-
• cover relations of L are canonically labeled by join-irreducible elements;
-
• each element in L is uniquely determined by the labels of its down-covers and also by the labels of its up-covers;
-
• the collection of down-cover label sets of the elements of L equals the collection of up-cover label sets of the elements of L, and each of these collections is equal to the collection of independent sets in a certain graph called the Galois graph;
-
• every interval of L is also in the family;
-
• there is a natural way of defining a certain bijective operator called rowmotion on L;
-
• L is crosscut simplicial; in particular, its order complex is either contractible or homotopy equivalent to a sphere.
Figure 1 Left: A semidistributive lattice that is not trim. Middle: A trim lattice that is not semidistributive. Right: A semidistrim lattice that is neither trim nor semidistributive.
In this paper, we develop a theory of semidistrim lattices, which we propose as a common generalization of semidistributive and trim lattices. An example of a semidistrim lattice that is neither semidistributive nor trim is illustrated on the right of Figure 1. The remainder of this introduction is devoted to sketching the definition of semidistrim lattices and outlining the theorems we will prove about these lattices in subsequent sections.
1.1 Semidistrim lattices
In Section 2, we recall basic notions from lattice theory, including the definitions of semidistributive lattices and trim lattices. If L is an arbitrary lattice, then the set
$\mathcal {J}_L$
of join-irreducible elements of L might not have the same cardinality as the set
$\mathcal {M}_L$
of meet-irreducible elements of L. However, these two sets do have the same size for several interesting lattices L. In Section 3, we define a pairing on L to be a bijection
$\mathcal {J}_L\to \mathcal {M}_L$
satisfying some additional natural desiderata. We say L is uniquely paired if it has a unique pairing; in this case, we let
$\kappa _L$
denote its unique pairing. We also define the Galois graph
$G_L$
of a uniquely paired lattice L to be the directed graph with vertex set
$\mathcal {J}_L$
in which there is an edge
$j\to j'$
whenever
$j\neq j'$
and
$j\not \leq \kappa _L(j')$
. We prove that semidistributive lattices and trim lattices are uniquely paired.
The purpose of Section 4 is to define and establish basic properties about a new family of lattices that we call compatibly dismantlable. Roughly speaking, a uniquely paired lattice is compatibly dismantlable if it can be broken into two disjoint intervals that are each compatibly dismantlable so that the join-irreducible elements, the meet-irreducible elements and the unique pairing of the entire lattice are compatible with those of the two intervals in a precise sense. Our terminology is inspired by the notion of an interval-dismantlable lattice [Reference Adaricheva, Hyndman, Lempp and Nation1]. We also prove that semidistributive lattices and trim lattices are compatibly dismantlable, which is not obvious from the definitions.
In Section 5, we define a uniquely paired lattice L to be overlapping if for each cover relation
$x\lessdot y$
, there is a unique join-irreducible element
$j_{xy}$
such that
$j_{xy}\leq y$
and
$\kappa _L(j_{xy})\geq x$
. If L is overlapping and
$x\in L$
, then we define the downward label set
$\mathcal {D}_L(x) = \{j_{yx} : y \lessdot x\}$
and the upward label set
$\mathcal {U}_L(x)=\{j_{xy} : x \lessdot y\}$
. These label sets are crucial for defining semidistrim lattices and their rowmotion operators. We also prove that every compatibly dismantlable lattice is overlapping. Moreover, we show that every element of a compatibly dismantlable lattice is uniquely determined by its downward label set and also by its upward label set.
Section 6 begins with the central definition of the paper: that of a semidistrim lattice. A lattice L is semidistrim if it is compatibly dismantlable and if for every
$x\in L$
, the label sets
$\mathcal {D}_L(x)$
and
$\mathcal {U}_L(x)$
are independent sets in the Galois graph
$G_L$
(this is an analogue of canonical join or meet representations for elements of semidistributive lattices). We prove that this class of lattices contains all semidistributive lattices and all trim lattices, thereby justifying the name semidistrim. Imposing the additional condition about independent sets on compatibly dismantlable lattices leads to several pleasant properties that we explore throughout the rest of the article. For instance, we prove that each of the maps
$\mathcal {D}_L$
and
$\mathcal {U}_L$
is actually a bijection from L to the collection of independent sets of
$G_L$
. We also describe how the sets
$\mathcal {D}_L(x)$
and
$\mathcal {U}_L(x)$
fit together inside
$G_L$
by proving that
$(\mathcal {D}_L(x),\mathcal {U}_L(x))$
is a tight orthogonal pair.
In Section 7, we prove that the class of semidistrim lattices is closed under taking products and intervals. While it is relatively straightforward to show that products of semidistrim lattices are semidistrim, the corresponding fact about intervals requires quite a bit of work to prove. However, the payoff is well worth the effort: knowing that intervals of semidistrim lattices are semidistrim allows us to establish several further results via induction. One of the other pleasant corollaries of the proof of this result states that if
$[u,v]$
is an interval in a semidistrim lattice L, then the unique pairing, the Galois graph, and the edge labels of L are compatible in a precise way with those of
$[u,v]$
. Intervals of compatibly dismantlable lattices need not be compatibly dismantlable; thus, the additional condition about independent sets is essential.
Section 8 is brief and is devoted to proving that semidistrim lattices are crosscut simplicial. This implies, in particular, that the order complex of a semidistrim lattice is contractible or homotopy equivalent to a sphere.
1.2 Rowmotion and pop-stack sorting
One of the most well-studied operators in the field of dynamical algebraic combinatorics is rowmotion, a certain invertible operator on the set of order ideals of a finite poset [Reference Brouwer and Schrijver9, Reference Cameron and Fon-der Flaass10, Reference Striker46]. Equivalently (by Birkhoff’s representation theorem), one can view rowmotion as a bijective operator on a distributive lattice. In recent years, there has been interest in extending the definition of rowmotion to more general classes of lattices. Barnard [Reference Barnard5] showed how to define rowmotion on semidistributive lattices, while Thomas and the second author [Reference Thomas and Williams50] defined rowmotion on trim lattices. We refer to [Reference Stanley45, Reference Thomas and Williams50] for a more thorough historical account of rowmotion. In Section 9, we define rowmotion for semidistrim lattices, thereby generalizing and unifying all previous definitions of rowmotion on lattices.
Given a lattice L, we define the pop-stack sorting operator
$\mathsf {Pop}^\downarrow _L\colon L\to L$
and the dual pop-stack sorting operator
$\mathsf {Pop}^\uparrow _L\colon L\to L$
by
$$\begin{align*}\mathsf{Pop}^\downarrow_L(x)=x\wedge\bigwedge\{y\in L:y\lessdot x\}\quad\text{and}\quad\mathsf{Pop}^\uparrow_L(x)=x\vee\bigvee\{y\in L:x\lessdot y\}.\end{align*}$$
When L is the right weak order on the symmetric group
$S_n$
, the pop-stack sorting operator coincides with the pop-stack sorting map, which acts by reversing the descending runs of a permutation. Recently, the pop-stack sorting map has received significant attention by combinatorialists [Reference Asinowski, Banderier and Hackl4, Reference Asinowski, Banderier, Billey, Hackl and Linusson3, Reference Elder and Goh21, Reference Claesson and Gumundsson12, Reference Pudwell and Smith36]. The first author has previously studied pop-stack sorting operators on weak orders of arbitrary Coxeter groups in [Reference Defant15] and on
$\nu $
-Tamari lattices in [Reference Defant14]. Mühle [Reference Mühle34] studied
$\mathsf {Pop}^\downarrow _L$
when L is congruence-uniform, where he called
$\mathsf {Pop}^\downarrow _L(x)$
the nucleus of x. The dual pop-stack sorting operator on the lattice of order ideals of a type A root poset is equivalent to the filling operator on Dyck paths analyzed in [43]. The authors have defined other variants of pop-stack sorting in [Reference Defant and Williams17, Reference Defant and Williams18].
The main purpose of Section 9 is to show that rowmotion, pop-stack sorting, and dual pop-stack sorting on a semidistrim lattice L are intimately connected. For example, we will show in Theorem 9.1 that if
$x\in L$
, then
$$\begin{align*}\mathsf{Pop}^\downarrow_L(x)=x\wedge\mathsf{Row}_L(x).\end{align*}$$
In fact, we will prove that
$\mathsf {Row}_L(x)$
is a maximal element of the set
$\{z\in L:\mathsf {Pop}^\downarrow _L(x)=x\wedge z\}$
. This naturally leads to a definition of rowmotion on meet-semidistributive lattices that need not be semidistrim; we prove that such a rowmotion operator is not invertible whenever the lattice is not semidistributive. It remains completely open to investigate the basic properties of these noninvertible operators.
Strengthening the links among rowmotion, pop-stack sorting and dual pop-stack sorting on a semidistrim lattice L, we ask how many times rowmotion on L ‘goes down’. More precisely, we are interested in the number of elements
$x\in L$
such that
$\mathsf {Row}_L(x)\leq x$
. It turns out that this quantity is equal to the size of the image of
$\mathsf {Pop}^\downarrow _L$
, which is also equal to the size of the image of
$\mathsf {Pop}^\uparrow _L$
:
$$\begin{align*}|\{ x \in L : \mathsf{Row}_L(x) \leq x\}|=|\mathsf{Pop}^\downarrow_L(L)|=|\mathsf{Pop}^\uparrow_L(L)|;\end{align*}$$
moreover, each of these three quantities is equal to the number of independent dominating sets of (the undirected version of) the Galois graph
$G_L$
. Even the equality
$|\mathsf {Pop}^\downarrow _L(L)|=|\mathsf {Pop}^\uparrow _L(L)|$
is interesting and nontrivial here because this equality does not hold for arbitrary lattices. This result motivates the study of the sizes of the images of the pop-stack sorting operators on interesting classes of lattices. This investigation was already initiated in [Reference Asinowski, Banderier, Billey, Hackl and Linusson3, Reference Claesson, Gumundsson and Pantone13] for the weak order on
$S_n$
(where
$\mathsf {Pop}^\downarrow _L$
is the classical pop-stack sorting map) and in [43] for the lattice of order ideals of a type A root poset. In Section 11.2, we state several enumerative conjectures about the sizes of the images of pop-stack sorting operators on other specific lattices such as Tamari lattices, bipartite Cambrian lattices and distributive lattices of order ideals in positive root posets.
1.3 Further directions
In Section 10, we show that there is analogy between join-prime elements of semidistrim lattices and the basic hyperplanes in Reading’s theory of shards. It would be interesting if this analogy could be tightened, and we indicate a few possible directions to pursue in Section 11.4. In Section 11, we collect several open questions about semidistrim lattices to help guide future research.
2 Background
In this section, we review notions from lattice theory, and we briefly discuss the two families of lattices that we will later unify with a common generalization.
2.1 Posets and lattices
We assume basic familiarity with standard terminology from the theory of posets, as discussed in [Reference Sapounakis, Tasoulas and Tsikouras44, Chapter 3]). For example, we write
$x\lessdot y$
(or
$y\gtrdot x$
) to indicate that an element y covers an element x. Given elements x and y in a poset P with
$x\leq y$
, the interval
$[x,y]$
is defined to be the set
$[x,y]=\{z\in P:x\leq z\leq y\}$
. The dual of the poset P is the poset
$P^*$
that has the same underlying set as P but with all order relations reversed; that is,
$x\leq y$
in P if and only if
$y\leq x$
in
$P^*$
. We write
$\min (P)$
and
$\max (P)$
for the set of minimal elements of P and the set of maximal elements of P, respectively. The order complex of P is the abstract simplicial complex whose faces are the chains of P.
A lattice is a poset L such that any two elements
$x,y\in L$
have a unique greatest lower bound, which is called their meet and denoted
$x\wedge y$
, and a unique least upper bound, which is called their join and denoted
$x\vee y$
. The meet and join operations are associative and commutative, so it makes sense to consider the meet and join of an arbitrary subset
$X\subseteq L$
; we denote these by
$\bigwedge X$
and
$\bigvee X$
, respectively. Each lattice has a unique minimal element, which we denote by
$\hat 0$
, and a unique maximal element, which we denote by
$\hat 1$
. An atom of L is an element that covers
$\hat 0$
, and a coatom of L is an element that is covered by
$\hat 1$
.
2.2 Irreducibles and primes
Let L be a lattice. An element
$j\in L$
is called join-irreducible if it covers exactly one element; if this is the case, we denote by
$j_*$
the unique element covered by j. An element
$m\in L$
is called meet-irreducible if it is covered by exactly one element; if this is the case, we denote by
$m^*$
the unique element covering m. We write
$\mathcal {J}_L$
and
$\mathcal {M}_L$
for the set of join-irreducible elements of L and the set of meet-irreducible elements of L, respectively. An element
$j \in L$
is called join-prime if for all
$x,y \in L$
satisfying
$x\vee y\geq j$
, we have
$x \geq j$
or
$y \geq j$
. Similarly, an element
$m \in L$
is called meet-prime if for all
$x,y \in L$
satisfying
$x\wedge y\leq m$
, we have
$x \leq m$
or
$y \leq m$
. Join-prime elements are necessarily join-irreducible, and meet-prime elements are necessarily meet-irreducible.
Proposition 2.1 ([Reference Markowsky31, Theorem 6]).
Let L be a lattice. An element
$j_0\in L$
is join-prime if and only if there exists
$m_0\in L$
such that
$L=[\hat 0,m_0]\sqcup [j_0,\hat 1]$
. An element
$m_0\in L$
is meet-prime if and only if there exists
$j_0\in L$
such that
$L=[\hat 0,m_0]\sqcup [j_0,\hat 1]$
.
If we can write
$L=[\hat 0,m_0]\sqcup [j_0,\hat 1]$
(so that
$j_0$
is join-prime and
$m_0$
is meet-prime), then we call the pair
$(j_0,m_0)$
a prime pair for L.
2.3 Semidistributive lattices
A lattice L is join-semidistributive if for all
$x,y,z \in L$
satisfying
$x \vee y = x\vee z$
, we have
$x \vee (y \wedge z) = x \vee y$
. Equivalently, L is join-semidistributive if for all
$a,b\in L$
with
$a\leq b$
, the set
$\{w\in L:w\vee a=b\}$
has a unique minimal element. Join-semidistributive lattices are characterized among finite lattices as those lattices having a certain canonical join representation for their elements [Reference Freese, Ježek and Nation23, Theorem 2.24], [Reference Barnard5, Theorem 3.1]; the canonical join representations
$x=\bigvee A$
are irredundant in the sense that
$\bigvee A' < \bigvee A$
for every proper subset
$A' \subset A$
, and the elements of A are taken to be as small as possible in the partial order.
Dually, L is called meet-semidistributive if for all
$x,y,z \in L$
satisfying
$x \wedge y = x\wedge z$
, we have
$x \wedge (y \vee z) = x \wedge y$
. The lattice L is meet-semidistributive if and only if for all
$a,b\in L$
with
$a\leq b$
, the set
$\{w\in L:w\wedge b=a\}$
has a unique maximal element. Meet-semidistributive lattices are characterized among finite lattices as having canonical meet representations
$x=\bigwedge A$
– these representations are irredundant, and the elements of A are taken to be as large as possible.
A lattice is semidistributive if it is both join-semidistributive and meet-semidistributive. It is known that in a semidistributive lattice, every atom is join-prime and every coatom is meet-prime [Reference Gaskill and Nation25].
2.4 Trim lattices
We say a lattice L is extremal if it has a maximum-length chain
$\hat 0=x_0\lessdot x_1\lessdot x_2\lessdot \cdots \lessdot x_n=\hat 1$
such that
$|\mathcal {J}_L|=|\mathcal {M}_L|=n$
[Reference Markowsky31]. An element
$x\in L$
is called left modular if for all
$y,z\in L$
with
$y \leq z$
, we have the equality
$(y \vee x) \wedge z = y \vee (x \wedge z)$
. A lattice is called left modular if it has a maximal chain of left modular elements [Reference Liu29]. A lattice is called trim if it is extremal and left modular [Reference Thomas48, Reference Thomas and Williams50]. Every trim lattice has at least one atom that is join-prime.
Figure 1 shows a semidistributive lattice that is not trim and a trim lattice that is not semidistributive. It was shown in [Reference Thomas and Williams50, Theorem 1.4] that an extremal semidistributive lattice is necessarily trim.
3 Uniquely Paired Lattices and Galois Graphs
As before, we write
$\mathcal {J}_L$
and
$\mathcal {M}_L$
for the set of join-irreducible elements and the set of meet-irreducible elements, respectively, of a lattice L.
3.1 Uniquely paired lattices
For
$j\in \mathcal {J}_L$
and
$m\in \mathcal {M}_L$
, let us write
$\mathcal {M}_L(j)=\max \{z\in L : j_*=j \wedge z\}$
and
$\mathcal {J}_L(m)=\min \{z\in L : m^*=m \vee z\}$
. Note that
$\mathcal {M}_L(j)$
is nonempty because it contains
$j_*$
and that
$\mathcal {J}_L(m)$
is nonempty because it contains
$m^*$
. One can show that L is meet-semidistributive if and only if
$\mathcal {M}_L(j)$
is a singleton set for every
$j\in \mathcal {J}_L$
(see [Reference Freese, Ježek and Nation23, Theorem 2.56]). Similarly, L is join-semidistributive if and only if
$\mathcal {J}_L(m)$
is a singleton set for every
$m\in \mathcal {M}_L$
.
Lemma 3.1. For
$j\in \mathcal {J}_L$
and
$m\in \mathcal {M}_L$
, we have
$\mathcal {J}_L(m)\subseteq \mathcal {J}_L$
and
$\mathcal {M}_L(j)\subseteq \mathcal {M}_L$
.
Proof. Suppose
$y \in \mathcal {J}_L(m)$
is not join-irreducible. Then
$y=\bigvee X$
for some set
$X\subseteq L$
with
$y \not \in X$
. Consider some
$x\in X$
. We have
$y> x$
, so
$m^*=y \vee m \geq x\vee m \geq m$
. This implies that
$x\vee m$
is either m or
$m^*$
. But we know that
$x\vee m\neq m^*$
because y is a minimal element of
$\{z\in L: m\vee z = m^*\}$
. Hence,
$x\leq m$
. As x was arbitrary, it follows that
$y=\bigvee X\leq m$
. However, this implies that
$y\vee m=m$
, which contradicts the fact that
$y\vee m=m^*$
. This proves that
$\mathcal {J}_L(m)\subseteq \mathcal {J}_L$
. A dual argument proves that
$\mathcal {M}_L(j)\subseteq \mathcal {M}_L$
.
Definition 3.2. A pairing on a lattice L is a bijection
$\kappa : \mathcal {J}_L \to \mathcal {M}_L$
such that
$\kappa (j) \in \mathcal {M}_L(j)$
for every
$j\in \mathcal {J}_L$
and
$\kappa ^{-1}(m) \in \mathcal {J}_L(m)$
for every
$m\in \mathcal {M}_L$
. We say L is paired if it has a pairing, and we say L is uniquely paired if it has a unique pairing.
When L is uniquely paired, we will use the symbol
$\kappa _L$
for its unique pairing. Figure 2 gives an example of a paired lattice that is not uniquely paired.
Figure 2 A paired lattice that is not uniquely paired.
If
$\kappa $
is a pairing on L and
$j\in \mathcal {J}_L$
, then
$j \not \leq \kappa (j)$
. Indeed, this is immediate from the fact that
$\kappa (j)\wedge j =j_*\neq j$
. In fact, the elements
$m=\kappa (j)$
and j can only be comparable if
$m = j_*$
and
$j = m^*$
.
Lemma 3.3. Let L be a lattice. A bijection
$\kappa \colon \mathcal {J}_L\to \mathcal {M}_L$
is a pairing if and only if the following hold for all
$j\in \mathcal {J}_L$
and
$m\in \mathcal {M}_L$
with
$m=\kappa (j)$
:
-
•
$m\geq j_*$
; -
•
$m^*\geq j$
; -
•
$m\not \geq j$
.
Proof. Let
$\kappa \colon \mathcal {J}_L\to \mathcal {M}_L$
be a bijection. Let
$j\in \mathcal {J}_L$
, and write
$m=\kappa (j)$
. Suppose
$m\geq j_*$
,
$m^*\geq j$
, and
$m\not \geq j$
. Since
$j \geq j \wedge m \geq j_*$
and
$m \not \geq j$
, we must have
$j \wedge m=j_*$
. The element m is maximal among elements z with
$j \wedge z = j_*$
because we have
$j\wedge x\geq j \wedge m^* = j$
for all
$x>m$
. Therefore,
$m \in \mathcal {M}_L(j)$
. An analogous argument shows that
$j \in \mathcal {J}_L(m)$
. Hence,
$\kappa $
is a pairing.
Conversely, suppose that
$\kappa $
is a pairing. Fix
$j\in \mathcal {J}_L$
and let
$m=\kappa (j)$
. Since
$m \in \mathcal {M}_L(j)$
, we have
$j \wedge m = j_*$
. This implies that
$m \geq j_*$
and
$m \not \geq j$
. We also have
$m^*\wedge j\geq m\wedge j=j_*$
. The maximality of m coming from the definition of
$\mathcal {M}_L(j)$
guarantees that
$m^*\wedge j\neq j_*$
, so
$m^*\wedge j\geq j$
. Hence,
$m^* \geq j$
.
Proposition 3.4. If
$\kappa $
is a pairing on a lattice L and
$(j_0,m_0)$
is a prime pair for L, then
$\kappa (j_0)=m_0$
.
Proof. Since
$m_0^* \not \in [\hat {0},m_0]$
, we have
$m_0^* \in [j_0,\hat {1}]$
, so
$m_0^* \geq j_0$
. It follows that
$m_0 \vee j_0 = m_0^*$
. Since
$m_0\vee (j_0)_*=m_0$
, we find that
$j_0 \in \mathcal {J}_L(m_0)$
. Since
$L=[\hat {0},m_0]\sqcup [j_0,\hat {1}]$
, any z satisfying
$m_0^*=m_0\vee z $
must satisfy
$z \geq j_0$
. Therefore,
$\mathcal {J}_L(m) = \{j_0\}$
. By the definition of a pairing, we must have
$\kappa (j_0)=m_0$
.
3.2 Galois graphs
In this subsection, we specialize Markowsky’s poset of irreducibles for general lattices to uniquely paired lattices. The term Galois graph in the following definition is inspired by the related notion of a Galois connection, which appears in Markowski’s work [Reference Markowsky30]. The following definition is new in the level of generality that we have presented it, but it has already been considered for trim lattices in [Reference Thomas and Williams50] and for semidistributive lattices in [Reference Reading, Speyer and Thomas39].
Definition 3.5. Let L be uniquely paired with unique pairing
$\kappa _L\colon \mathcal {J}_L\to \mathcal {M}_L$
. The Galois graph of L, denoted
$G_L$
, is the directed graph with vertex set
$\mathcal {J}_L$
such that for all
$j,j'\in \mathcal {J}_L$
, there is an edge
$j \to j'$
if and only if
$j \not \leq \kappa _L(j')$
and
$j\neq j'$
.
Slightly abusing notation, we write
$j \to j'$
to mean that there is a directed edge from j to
$j'$
in
$G_L$
, and we define
$$ \begin{align*}\mathrm{Out}(j) &= \{ j' \in \mathcal{J}_L : j \to j'\} \quad \text{and} \\ \mathrm{In}(j) &= \{ j' \in \mathcal{J}_L : j' \to j \}.\end{align*} $$
Proposition 3.6 [Reference Markowsky31, Remark 2].
Let L be a uniquely paired lattice with Galois graph
$G_L$
. A join-irreducible element j of L is join-prime if and only if
$j'\to j"$
whenever we have
$j' \to j$
and
$j \to j"$
.
Proposition 3.7. Let L be a uniquely paired lattice with Galois graph
$G_L$
. If
$j\in L$
is join-prime, then there is no join-irreducible element
$j'$
with
$j \to j'$
and
$j' \to j$
.
Proof. Suppose that j is join-prime and that
$j'\in \mathcal {J}_L$
satisfies
$j\to j'$
. Write
$m=\kappa _L(j)$
and
$m'=\kappa _L(j')$
. Then
$j\not \leq m'$
. Theorem 3.4 tells us that
$(j,m)$
is a prime pair, so
$L=[\hat 0,m]\sqcup [j,\hat 1]$
. Consequently,
$m'< m$
. Because
$m'$
is a maximal element of
$\{z\in L: j^{\prime }_*=j'\wedge z\}$
, we cannot have
$j'\wedge m=j^{\prime }_*$
. We know that
$j' \wedge m \geq j' \wedge m' = j^{\prime }_*$
, so we must have
$j' \wedge m> j^{\prime }_*$
. Hence,
$j'\wedge m=j'$
. This means that
$j'\leq m$
, so there is no edge
$j'\to j$
in
$G_L$
.
3.3 Semidistributive and extremal lattices are uniquely paired
In this subsection, we prove that two important families of lattices are uniquely paired.
Proposition 3.8. Semidistributive lattices are uniquely paired.
Proof. Let L be a semidistributive lattice. Then
$\mathcal {M}_L(j)$
and
$\mathcal {J}_L(m)$
are singleton sets for all
$j\in \mathcal {J}_L$
and
$m\in \mathcal {M}_L$
. Furthermore, one readily checks that m is the unique element of
$\mathcal {M}_L(j)$
if and only if j is the unique element of
$\mathcal {J}_L(m)$
. Therefore, we obtain a pairing
$\kappa \colon \mathcal {J}_L\to M_L$
by declaring
$\kappa (j)$
to be the unique element of
$\mathcal {M}_L(j)$
. This is the only pairing on L.
Even though
$\mathcal {J}_L(m)$
and
$\mathcal {M}_L(j)$
can contain multiple elements in extremal lattices, such lattices are still uniquely paired. An example is given in Figure 3.
Figure 3 An extremal (but not trim) lattice; by Theorem 3.9, this lattice is uniquely paired. Even though both
$m_3$
and
$m_4$
are maximal elements of the set
$\{z : (j_3)_*=j_3 \wedge z\}$
, the element
$m_4$
must be paired with
$j_4$
because
$m_4$
is the only element of
$\{z : (j_4)_*=j_4 \wedge z\}$
; this then forces
$m_3$
to be paired with
$j_3$
.
Proposition 3.9. Extremal lattices are uniquely paired.
Proof. Let L be an extremal lattice and fix a maximum-length chain
$\hat {0}=x_0\lessdot x_1\lessdot x_2\lessdot \cdots \lessdot x_n=\hat {1}$
. For each
$i\in [n]$
, there is a unique
$j_i\in \mathcal {J}_L$
such that
$j_i \vee x_{i-1}=x_i$
, and there is a unique
$m_i\in \mathcal {M}_L$
such that
$m_i \wedge x_i = x_{i-1}$
. This gives rise to a bijection
$\kappa \colon \mathcal {J}_L\to \mathcal {M}_L$
defined by
$\kappa (j_i)=m_i$
. Let us check that
$\kappa $
is a pairing. Fix
$i\in [n]$
. First, suppose j is a join-irreducible with
$j\leq (j_i)_*$
. Then
$j\vee x_{i-1}\leq j_i\vee x_{i-1}=x_i$
. By the uniqueness of
$j_i$
, we know that
$j\vee x_{i-1}\neq x_i$
. This shows that
$j\vee x_{i-1}=x_{i-1}$
, so
$j\leq x_{i-1}$
. As this is true for every join-irreducible j satisfying
$j\leq (j_i)_*$
, we conclude that
$(j_i)_*\leq x_{i-1}$
. Because
$j_i\vee x_{i-1}=x_i$
, we have
$j_i\not \leq x_{i-1}$
, so
$$\begin{align*}j_i\neq x_{i-1} \wedge j_i = (m_i \wedge x_i) \wedge j_i = m_i \wedge (x_i \wedge j_i) = m_i \wedge j_i.\end{align*}$$
Consequently,
$m_i\wedge j_i<j_i$
. But since
$(j_i)_* \leq x_{i-1}$
, we have
$m_i \wedge j_i = x_{i-1}\wedge j_i= (j_i)_*$
. This shows that
$m_i\geq (j_i)_*$
and that
$m_i\not \geq j_i$
. A similar argument shows that
$m_i^*\geq j_i$
. As this is true for all i, Lemma 3.3 tells us that
$\kappa $
is a pairing.
We now show that
$\kappa $
is the only pairing on L. Suppose instead that there is some pairing
$\kappa '\colon \mathcal {J}_L\to \mathcal {M}_L$
with
$\kappa '\neq \kappa $
. There must be some
$i,k\in [n]$
with
$i<k$
such that
$\kappa '(j_i)=m_k$
. Then
$x_k> x_{k-1} \geq x_i \geq j_i$
, so
$m_k \wedge j_i = m_k \wedge (x_k \wedge j_i) = (m_k\wedge x_k)\wedge j_i=x_{k-1} \wedge j_i = j_i$
. This contradicts the fact that
$\kappa '(j_i)\wedge j_i=(j_i)_*$
by the definition of a pairing.
Since trim lattices are extremal by definition, we have the following corollary.
Corollary 3.10. Trim lattices are uniquely paired.
4 Compatibly Dismantlable Lattices
As a next step toward semidistrim lattices, we impose additional structure on uniquely paired lattices to obtain the family of compatibly dismantlable lattices. This new structure is an analogue of interval-dismantlability (see [Reference Adaricheva, Hyndman, Lempp and Nation1]) that additionally requires a certain compatibility condition for join-irreducible elements and for meet-irreducible elements.
4.1 Compatibly dismantlable lattices
Definition 4.1. A uniquely paired lattice L is compatibly dismantlable if it has cardinality
$1$
or if it contains a prime pair
$(j_0,m_0)$
such that the following compatibility conditions hold:
-
•
$[j_0,\hat {1}]$
is compatibly dismantlable, and there is a bijection given by
$$\begin{align*}\alpha\colon\{j\in \mathcal{J}_L : j_0 \leq \kappa_L(j)\} \to \mathcal{J}_{[j_0,1]}\end{align*}$$
$\alpha (j)=j_0\vee j$
such that
$\kappa _{[j_0,\hat 1]}(\alpha (j))=\kappa _L(j)$
for all
$j\in \mathcal {J}_L$
with
$j_0\leq \kappa _L(j)$
;
-
•
$[\hat {0},m_0]$
is compatibly dismantlable, and there is a bijection given by
$$\begin{align*}\beta\colon\{m\in \mathcal{M}_L : \kappa_L^{-1}(m) \leq m_0\} \to \mathcal{M}_{[0,m_0]}\end{align*}$$
$\beta (m)=m_0\wedge m$
such that
$\kappa _{[\hat 0,m_0]}^{-1}(\beta (m))=\kappa _L^{-1}(m)$
for all
$m\in \mathcal {M}_L$
with
$\kappa _L^{-1}(m)\leq m_0$
.
We call such a prime pair
$(j_0,m_0)$
a dismantling pair for L and write
$L_0 = [\hat {0},m_0]$
and
$L^0 = [j_0,\hat {1}]$
.
Example 4.2. Figure 4 illustrates a compatibly dismantlable lattice L with dismantling pair
$(j_0,m_0)$
. The join-irreducible and meet-irreducible elements are named in such a way that
$\kappa _L(j_i)=m_i$
for all
$0\leq i\leq 4$
. The join-irreducible elements
$j\in \mathcal {J}_L$
satisfying
$j_0\leq \kappa _L(j)$
are
$j_2,j_3,j_4$
. These elements correspond bijectively to the join-irreducible elements of
$L^0$
: we have
$\alpha (j_2)=j_0\vee j_2=\hat 1$
,
$\alpha (j_3)=j_0\vee j_3=j_3$
and
$\alpha (j_4)=j_0\vee j_4=j_4$
. The meet-irreducible elements
$m\in \mathcal {M}_L$
satisfying
$\kappa _L^{-1}(m)\leq m_0$
are
$m_1$
and
$m_2$
. These elements correspond bijectively to the meet-irreducible elements of
$L_0$
: we have
$\beta (m_1)=m_0\wedge m_1=m_1$
and
$\beta (m_2)=m_0\wedge m_2=j_1$
. Notice how
$\alpha $
and
$\beta $
are compatible with the pairings
$\kappa _L$
,
$\kappa _{[\hat 0, m_0]}$
, and
$\kappa _{[j_0,\hat 1]}$
, as required by Theorem 4.1. For example,
$\kappa _{[j_0,\hat 1]}(\alpha (j_2))=\kappa _{[j_0,\hat 1]}(\hat 1)=m_2=\kappa _L(j_2)$
.
Figure 4 Left: A compatibly dismantlable lattice. Right: The corresponding Galois graph.
Remark 4.3. The lattice in Figure 4 has the undesirable property that the cover relations on its elements do not yield irredundant (as in Section 2.3) join or meet representations: for example,
$\hat {0}$
is covered by
$j_0$
,
$j_1$
, and
$j_2$
so that
$\hat {0} = m_0 \wedge m_1 \wedge m_2$
– but it also has the meet representation
$\hat {0} = m_1 \wedge m_2$
.
In Section 6, we will define semidistrim lattices by imposing a mild additional condition on compatibly dismantlable lattices to eliminate such occurrences. This extra condition is shared by both semidistributive and trim lattices, and it will have drastic consequences concerning intervals and compatibility conditions. It will turn out that every prime pair in a semidistrim lattice is a dismantling pair. More generally, we will find that every interval
$[u,v]$
in a semidistrim lattice L is semidistrim and that there is a compatibility condition for its join-irreducible and meet-irreducible elements generalizing the condition from Theorem 4.1 for the intervals
$[j_0,\hat 1]$
or
$[\hat 0,m_0]$
.
Suppose L is a compatibly dismantlable lattice with dismantling pair
$(j_0,m_0)$
. Let us write
$L_0=[\hat 0,m_0]$
and
$L^0=[j_0,\hat 1]$
. The first compatibility condition in Theorem 4.1 allows us to use the bijection
$\alpha $
to identify
$\mathcal {J}_{L^0}$
, which is the vertex set of the Galois graph
$G_{L^0}$
, with the subset
$\{j\in \mathcal {J}_L:j_0\leq \kappa _L(j)\}$
of the vertex set of
$G_L$
. Furthermore, we can naturally view
$\mathcal {J}_{L_0}$
, the vertex set of
$G_{L_0}$
, as a subset of the vertex set of
$G_L$
(since every join-irreducible element of
$L_0$
is also join-irreducible in L). The next proposition tells us that
$G_{L^0}$
and
$G_{L_0}$
can be identified with genuine induced subgraphs of
$G_L$
.
Proposition 4.4. Let L be a compatibly dismantlable lattice with a dismantling pair
$(j_0,m_0)$
and let
$L_0=[\hat 0,m_0]$
and
$L^0=[j_0,\hat 1]$
.
-
• Under the bijection
$\alpha \colon \{j\in \mathcal {J}_L : j_0 \leq \kappa _L(j)\}\to \mathcal {J}_{L^0}$
from Theorem 4.1, the Galois graph
$G_{L^0}$
corresponds to the induced subgraph of
$G_L$
on the vertex set
$\mathcal {J}_L\setminus (\{j_0\}\cup \mathrm {Out}(j_0))$
. -
• The Galois graph
$G_{L_0}$
is the induced subgraph of
$G_L$
on the vertex set
$\mathcal {J}_L\setminus (\{j_0\}\cup \mathrm {In}(j_0))$
.
Proof. It is immediate from the definition of the edges in the Galois graph that
$\{j\in \mathcal {J}_L:j_0\leq \kappa _L(j)\}=\mathcal {J}_L\setminus (\{j_0\}\cup \mathrm {Out}(j_0))$
. Now suppose
$j',j"\in \mathcal {J}_L$
are such that
$j_0\leq \kappa _L(j'),\kappa _L(j")$
. Then we have
$j'\to j"$
in
$G_{L}$
if and only if
$j'\not \leq \kappa _L(j")$
, and this occurs if and only if
$j_0\vee j'\not \leq \kappa _L(j")$
. The first compatibility condition in Theorem 4.1 tells us that
$\kappa _L(j")=\kappa _{L^0}(j_0\vee j")$
, so it follows that
$j'\to j"$
in
$G_{L}$
if and only if
$\alpha (j')\to \alpha (j")$
in
$G_{L^0}$
.
Now observe that
$\mathcal {J}_{L_0}=\{j\in \mathcal {J}_L: j\leq m_0\}=\{j\in \mathcal {J}_L:j\leq \kappa _L(j_0)\}=\mathcal {J}_L\setminus (\{j_0\}\cup \mathrm {In}(j_0))$
. Suppose
$j',j"\in \mathcal {J}_{L_0}$
. We have
$j'\to j"$
in
$G_L$
if and only if
$j'\not \leq \kappa _L(j")$
, and this occurs if and only if
$j'\not \leq m_0\wedge \kappa _L(j")$
. The second compatibility condition in Theorem 4.1 tells us that
$\kappa _{L_0}(j")=m_0\wedge \kappa _{L}(j")$
, so it follows that
$j'\to j"$
in
$G_{L}$
if and only if
$j'\to j"$
in
$G_{L_0}$
.
4.2 Semidistributive and trim lattices are compatibly dismantlable
Proposition 4.5. Semidistributive lattices are compatibly dismantlable.
Proof. Let L be a semidistributive lattice of cardinality at least
$2$
. We know by Theorem 3.8 that L is uniquely paired; let
$\kappa _L\colon \mathcal {J}_L\to \mathcal {M}_L$
be its unique pairing. Let
$j_0$
be an atom of L. By [Reference Gaskill and Nation25, Lemma 1],
$j_0$
is necessarily join-prime. Let
$L_0=[\hat 0,m_0]$
and
$L^0=[j_0,\hat 1]$
, where
$m_0=\kappa (j_0)$
so that
$(j_0,m_0)$
is a prime pair. Since intervals of semidistributive lattices are semidistributive, it follows by induction on the size of L that
$L_0$
and
$L^0$
are both compatibly dismantlable. Suppose
$j\in \mathcal {J}_L$
is such that
$j_0\leq \kappa _L(j)$
, and let
$m=\kappa _L(j)$
. We want to show that
$j_0\vee j$
is join-irreducible in
$L^0$
. Because L is semidistributive, j is the unique element of the singleton set
$\mathcal {J}_L(m)=\min \{z\in L: m^*=m\vee z\}$
. Since
$L^0$
is semidistributive, the set
$\{z\in L^0 : m^*=m \vee z \}$
has a unique minimal element. Certainly
$j_0 \vee j$
is in this set since
$m \vee (j_0 \vee j) = m \vee j = m^*$
. Suppose there is some
$x\in L^0$
with
$x< j\vee j_0$
and
$m\vee x=m^*$
. We have
$m\vee x=j\vee x=m^*$
, so it follows from the fact that L is join-semidistributive that
$m\vee (x\wedge j)= m^*$
. Now
$j\in \mathcal {J}_L(m)$
, so we must have
$x \wedge j = j$
, meaning
$x\geq j$
. But
$x\geq j_0$
, so this contradicts the assumption that
$x<j\vee j_0$
. This shows that no such x exists, so
$j_0\vee j$
is the unique minimal element of
$\{z\in L^0 : m^*=m \vee z \}$
. In other words,
$j_0\vee j\in \mathcal {J}_{L^0}(m)$
. By Lemma 3.1,
$j_0\vee j\in \mathcal {J}_{L^0}$
.
We now have a map
$\alpha \colon \{j\in \mathcal {J}_L:j_0\leq \kappa _L(j)\}\to \mathcal {J}_{L^0}$
given by
$\alpha (j)=j_0\vee j$
. Let us show that
$\alpha $
is injective. Suppose
$j,j'\in \mathcal {J}_L$
are such that
$j_0\leq \kappa _L(j),\kappa _L(j')$
and
$j_0\vee j=j_0\vee j'$
. Let
$m=\kappa _L(j)$
and
$m'=\kappa _L(j')$
. Then
$(j_0\vee j)\vee m=j\vee (j_0\vee m)=j\vee m=m^*$
, so
$j'\vee m=j'\vee (j_0\vee m)=(j_0\vee j')\vee m=(j_0\vee j)\vee m=m^*$
. Since j is the unique minimal element of
$\{z\in L:m^*=m\vee z\}$
, we must have
$j'\geq j$
. Reversing the roles of j and
$j'$
shows that
$j\geq j'$
. Hence,
$j=j'$
.
We now show that
$\alpha $
is surjective and that
$\kappa _{L^0}(\alpha (j))=\kappa _L(j)$
for every
$j\in \mathcal {J}_L$
with
$j_0\leq \kappa _L(j)$
. Suppose
$j'\in \mathcal {J}_{L^0}$
. Let
$m'=\kappa _{L^0}(j')$
. Then
$m'$
is meet-irreducible in
$L^0$
, so it is meet-irreducible in L. Let
$j=\kappa _L^{-1}(m')$
. We aim to show that
$j_0\vee j=j'$
. Since
$m'\vee j'=(m')^*$
and j is the unique minimal element of
$\{z\in L:(m')^*=m'\vee z\}$
, we have
$j'\geq j$
. Thus,
$j'\geq j_0\vee j$
. However, we have
$(j_0\vee j)\vee m'=(m')^*$
. Since
$j'$
is the unique minimal element of the set
$\{z\in L^0:(m')^*=m'\vee z\}$
, we must have
$j'\leq j_0\vee j$
. This proves that
$j'=j_0\vee j$
. Moreover,
$\kappa _L(j)=m'=\kappa _{L^0}(j')=\kappa _{L^0}(\alpha (j))$
.
Proposition 4.6. Trim lattices are compatibly dismantlable.
Proof. By Theorem 3.9, trim lattices are uniquely paired. [Reference Thomas and Williams50, Theorem 2.4] states that the Galois graph
$G_L$
of a trim lattice is acyclic. Let
$j_0$
be a sink of
$G_L$
. Then [Reference Markowsky31, Theorem 15] tells us that
$j_0$
is a join-prime atom of L; let
$m_0$
be the corresponding meet-prime element so that
$(j_0,m_0)$
is a prime pair. The proof of [Reference Thomas and Williams50, Proposition 3.13] (following the proof of [Reference Thomas48, Theorem 1]) shows that the compatibility conditions in Theorem 4.1 hold for this choice of prime pair.
Remark 4.7. Depending on the lattice L, the inductive dismantling
$L=[\hat {0},m_0] \sqcup [j_0,\hat {1}]$
has been called various names:
-
• if L is the weak order of a finite Coxeter group W and
$j_0$
is an atom (a simple reflection), then L is semidistributive and
$[\hat {0},m_0]$
is a maximal parabolic quotient; -
• if L is a c-Cambrian lattice for a finite Coxeter group W with Coxeter element c, then L is both trim and semidistributive. If s is a simple reflection that is initial in c, then for
$j_0=s$
, the interval
$[\hat {0},m_0]$
is the Cambrian lattice for a parabolic subgroup of W, and we obtain the Cambrian recurrence [Reference Reading38]; -
• when L is trim and
$j_0$
is taken to be a join-prime atom (i.e., a sink of the Galois graph), this decomposition was called the trim recurrence in [Reference Thomas and Williams50]; it was used there to establish many structural properties of trim lattices.
Remark 4.8. Although intervals of semidistributive lattices are again semidistributive and intervals of trim lattices are again trim, the same does not hold for compatibly dismantlable lattices. An example of this failure is given in Figure 5. We will address this deficiency in Section 6 by imposing one final condition on compatibly dismantlable lattices to form our titular semidistrim lattices. The fact that the family of semidistrim lattices is closed under taking intervals will have several notable consequences.
Figure 5
Left: A compatibly dismantlable lattice L with a lower interval (in red) that is not compatibly dismantlable. Right: The corresponding Galois graph
$G_L$
with the Galois graph of the interval indicated as a subgraph (in red).
5 Overlapping Lattices
Throughout this section, we assume L is uniquely paired with unique pairing
$\kappa _L\colon \mathcal {J}_L\to \mathcal {M}_L$
. Recall that for
$x\in L$
, we write
$J_L(x)=\{j\in \mathcal {J}_L:j\leq x\}$
and
$M_L(x)=\{j\in \mathcal {J}_L:\kappa _L(j)\geq x\}$
. Note that
$M_L(x)\cap J_L(x)=\emptyset $
because if there were some
$j\in M_L(x)\cap J_L(x)$
, then we would have
$j\leq \kappa _L(j)$
, which is impossible.
Definition 5.1. A uniquely paired lattice L is overlapping if for every cover
$x \lessdot y$
in L,
$M_L(x) \cap J_L(y)$
contains a single element, which we denote
$j_{xy}$
. If L is overlapping and
$x\in L$
, then we define the downward label set
$\mathcal {D}_L(x) = \{j_{yx} : y \lessdot x\}$
and the upward label set
$\mathcal {U}_L(x)=\{j_{xy} : x \lessdot y\}$
.
By [Reference Reading, Speyer and Thomas39, Lemma 4.4] and [Reference Thomas and Williams50, Theorem 3.4], both semidistributive and trim lattices are overlapping. In fact, it was shown in [Reference Thomas and Williams50] that an extremal lattice is trim if and only if it is overlapping; in particular, extremal semidistributive lattices are trim. Figure 6 gives an example of an overlapping uniquely paired lattice that is not compatibly dismantlable.
Figure 6
Left: An overlapping lattice that is not compatibly dismantlable; the map
$\mathrm {Ind}(G_L) \to L$
given by
$I \mapsto \bigvee I$
is a bijection. Right: The corresponding Galois graph.
Lemma 5.2. Let L be an overlapping lattice with unique pairing
$\kappa _L$
. If a cover relation
$x \lessdot y$
is labeled by
$j_{xy}$
, then
$x \vee j_{xy} = y$
and
$y \wedge \kappa _L(j_{xy}) = x$
.
Proof. Since
$j_{xy}$
is in
$M_L(x)$
, it is not in
$J_L(x)$
. But
$j_{xy}\in J_L(y)$
, so
$x\vee j_{xy}=y$
. A similar argument establishes that
$y \wedge \kappa _L(j_{xy}) = x$
.
We now show that every compatibly dismantlable lattice is overlapping. This will provide the edge-labeling needed for the definition of a semidistrim lattice; it will also be crucial for defining rowmotion on semidistrim lattices.
Proposition 5.3. Compatibly dismantlable lattices are overlapping.
Proof. Suppose L is compatibly dismantlable and let
$(j_0,m_0)$
be a dismantling pair for L. Write
$L_0=[\hat 0,m_0]$
and
$L^0=[j_0,\hat 1]$
. Then
$L_0$
and
$L^0$
are compatibly dismantlable, and
$L=L_0\sqcup L^0$
. By induction on the size of L, we know that
$L_0$
and
$L^0$
are overlapping. Let
$x \lessdot y$
be a cover relation in L.
First, suppose
$x,y\in L_0$
. Then
$J_{L_0}(y)=J_L(y)$
, and we can use the second compatibility condition in Theorem 4.1 to see that
$\kappa _{L_0}(j)=m_0\wedge \kappa _L(j)$
for every
$j\in J_{L_0}(y)$
. It follows that
$M_L(x)\cap J_L(y)=M_{L_0}(x)\cap J_{L_0}(y)$
, and this set is a singleton because
$L_0$
is overlapping.
Now suppose
$x,y\in L^0$
. An argument similar to the one used in the previous paragraph allows us to see that the map
$\alpha $
from Theorem 4.1 yields a bijection from
$M_L(x)\cap J_L(y)$
to
$M_{L^0}(x)\cap J_{L^0}(y)$
. As
$L^0$
is overlapping, we have
$|M_L(x)\cap J_L(y)|=|M_{L^0}(x)\cap J_{L^0}(y)|=1$
.
We may now assume that
$x \in L_0$
and
$y \in L^0$
. Since
$\kappa _L(j_0)=m_0$
by Theorem 3.4, we have that
$j_0 \in M_L(x) \cap J_L(y)$
. Suppose by way of contradiction that there is some
$j \in M_L(x) \cap J_L(y)$
with
$j\neq j_0$
. Let
$m=\kappa _L(j)$
so that
$m \geq x$
and
$j \leq y$
. We have
$x \leq x \vee j \leq y$
and
$y \geq y \wedge m \geq x$
. If
$x \vee j = x$
, then
$j\leq x \leq m$
, which is impossible. Therefore,
$x \vee j = y$
. Similarly,
$y \wedge m = x$
. We have
$x \leq m_0$
, so if
$j \leq m_0$
, then
$x \vee j = y \leq m_0$
, which is a contradiction. Consequently,
$j\not \leq m_0=\kappa _L(j_0)$
. A similar argument shows that
$\kappa _L(j)=m\not \geq j_0$
. This shows that we have edges
$j\to j_0$
and
$j_0\to j$
in the Galois graph
$G_L$
, which contradicts Theorem 3.7 because
$j_0$
is join-prime. Hence,
$M_L(x)\cap J_L(y)=\{j_0\}$
.
Corollary 5.4. Suppose L is a compatibly dismantlable lattice with dismantling pair
$(j_0,m_0)$
. Let
$x\lessdot y$
be a cover relation in L. If
$x\leq m_0$
and
$y\geq j_0$
, then the label
$j_{xy}$
of the cover
$x\lessdot y$
is
$j_0$
.
Corollary 5.5. Suppose L is a compatibly dismantlable lattice with dismantling pair
$(j_0,m_0)$
. If
$x \leq m_0$
, then
$\mathcal {D}_{L_0}(x) = \mathcal {D}_{L}(x)$
and
$\mathcal {U}_{L_0}(x)=\mathcal {U}_L(x)\setminus \{j_0\}$
. If
$x\geq j_0$
, then the map
$\alpha $
given by
$\alpha (j)=j_0\vee j$
induces bijections
$\mathcal {D}_L(x) \setminus \{j_0\}\to \mathcal {D}_{L^0}(x)$
and
$\mathcal {U}_{L}(x)\to \mathcal {U}_{L^0}(x)$
.
Proof. We prove the case in which
$x\geq j_0$
; the proof when
$x\leq m_0$
is similar. It follows from Theorem 5.4 that
$\mathcal {D}_L(x)\setminus \{j_0\}$
is the set of labels of covers of the form
$y\lessdot x$
with
$y\in L^0$
. If j is the label of such a cover
$y\lessdot x$
in L, then
$j\leq x$
and
$\kappa _L(j)\geq y$
. This implies that
$\alpha (j)\leq x$
and
$\kappa _{L^0}(\alpha (j))=\kappa _L(j)\geq y$
, so
$\alpha (j)$
is the label of
$y\lessdot x$
in
$L^0$
. This proves that
$\alpha $
induces a bijection
$\mathcal {D}_L(x)\setminus \{j_0\}\to \mathcal {D}_{L^0}(x)$
. A similar argument shows that
$\alpha $
induces a bijection
$\mathcal {U}_L(x)\to \mathcal {U}_{L^0}(x)$
.
When we define rowmotion on semidistrim lattices in Section 9, we will use the downward and upward label sets of the elements. In order for the definition to work, we will need to know that every element is uniquely determined by its downward label set and also by its upward label set; this is the content of the next theorem.
Theorem 5.6. Let L be a compatibly dismantlable lattice. Every element
$x \in L$
is uniquely determined by its downward label set
$\mathcal {D}_L(x)$
, and it is also uniquely determined by its upward label set
$\mathcal {U}_L(x)$
. More precisely,
$$\begin{align*}x = \bigvee \mathcal{D}_L(x) = \bigwedge\kappa_L(\mathcal{U}_L(x)).\end{align*}$$
Proof. We show that
$x = \bigvee \mathcal {D}_L(x)$
; the proof that
$x = \bigwedge \kappa _L(\mathcal {U}_L(x))$
follows from a completely analogous dual argument. Let
$(j_0,m_0)$
be a dismantling pair for L. By Theorem 4.1, the intervals
$L_0=[\hat 0,m_0]$
and
$L^0=[j_0,\hat 1]$
are compatibly dismantlable. We will make use of the containment
$\mathcal {J}_{L_0}\subseteq \mathcal {J}_L$
and the bijection
$\alpha \colon \{j\in \mathcal {J}_L:j_0\leq \kappa _L(j)\}\to \mathcal {J}_{L^0}$
. If
$x\in L_0$
, then we can use Theorem 5.5 and induction on the size of the lattice to see that
$x=\bigvee \mathcal {D}_{L_0}(x)=\bigvee \mathcal {D}_L(x)$
. Therefore, in what follows, we may assume
$x \in L^0$
.
If
$j_0 \in \mathcal {D}_L(x)$
, then we can use Theorem 5.5 and induction on the size of the lattice to see that
$$\begin{align*}x=\bigvee\mathcal{D}_{L^0}(x)=\bigvee_{j\in \mathcal{D}_L(x)\setminus\{j_0\}}\alpha(j)=\bigvee_{j\in \mathcal{D}_L(x)\setminus\{j_0\}}(j_0\vee j)=j_0\vee\bigvee(\mathcal{D}_L(x)\setminus\{j_0\}) \end{align*}$$
$$\begin{align*}=\bigvee\mathcal{D}_L(x). \end{align*}$$
Now suppose
$j_0\not \in \mathcal {D}_L(x)$
. In particular,
$x\neq j_0$
, so there is some element of
$L^0$
covered by x. Let
$y = \bigvee \mathcal {D}_L(x)$
. Our goal is to show that
$y=x$
, so assume otherwise. As in the previous case, we can use Theorem 5.5 and induction to find that
$$\begin{align*}x=\bigvee\mathcal{D}_{L^0}(x)=\bigvee_{j\in \mathcal{D}_L(x)}\alpha(j)=\bigvee_{j\in \mathcal{D}_L(x)}(j_0\vee j)=j_0\vee\bigvee\mathcal{D}_L(x)=j_0\vee y. \end{align*}$$
Since
$x\neq y$
, this implies that
$y\not \geq j_0$
. Hence,
$y\in L_0$
. There exist elements
$a\in L_0$
and
$b\in L^0$
such that
$y\leq a\lessdot b\leq x$
. The label
$j_{ab}$
of the cover
$a\lessdot b$
is equal to
$j_0$
by Theorem 5.4. Since
$j_0\not \in \mathcal {D}_L(x)$
, this implies that
$b<x$
. However, this shows that
$y\vee j_0\leq b<x$
, which contradicts the fact that
$y\vee j_0=x$
.
The next lemma will be handy when we prove that intervals in semidistrim lattices are semidistrim.
Lemma 5.7. Let L be a compatibly dismantlable lattice and let
$x \in L$
. Let
$j\in \mathcal {J}_L$
and let
$m=\kappa _L(j)\in \mathcal {M}_L$
. If
$j \leq x$
, then
$j \in \mathcal {U}_L(x \wedge m)$
. If
$m \geq x$
, then
$j \in \mathcal {D}_L(x \vee j)$
.
Proof. We only prove the first statement, as the second follows from an analogous dual argument. Thus, suppose
$j\leq x$
. Our goal is to show that there exists an element y covering
$x\wedge m$
such that
$j\leq y$
. Indeed, if we can do this, then (since
$m\geq x\wedge m$
) the cover relation
$x\wedge m\lessdot y$
will have label j. Let
$(j_0,m_0)$
be a dismantling pair for L and let
$L_0=[\hat 0,m_0]$
and
$L^0=[j_0,\hat 1]$
. Then
$L_0$
and
$L^0$
are compatibly dismantlable.
Assume first that
$x\in L_0$
. By Theorem 4.1, we have
$\kappa _{L_0}(j)=\kappa _{L_0}(\kappa _L^{-1}(m))=\beta (m)=m_0\wedge m$
, so we can use induction on the size of the lattice to see that
$j\in \mathcal {U}_{L_0}(x\wedge (m_0\wedge m))=\mathcal {U}_{L_0}(x\wedge m)$
. This means that there exists an element
$y\in L_0$
covering
$x\wedge m$
such that the cover relation
$x\wedge m\lessdot y$
is labeled by j in
$L_0$
. But then
$j\leq y$
, as desired.
We may now assume that
$x\in L^0$
. If
$m\in L^0$
, then we can use the first compatibility condition in Theorem 4.1 to see that
$\alpha (j)$
is a join-irreducible element of the compatibly dismantlable lattice
$L^0$
with
$\kappa _{L^0}(\alpha (j))=m$
and
$\alpha (j)\leq x$
. By induction on the size of the lattice, we have
$\alpha (j)\in \mathcal {U}_{L^0}(x\wedge m)$
, so there exists an element y covering
$x\wedge m$
such that the cover relation
$x\wedge m\lessdot y$
is labeled by
$\alpha (j)$
in
$L^0$
. But then
$j\leq j_0\vee j= \alpha (j)\leq y$
.
If
$m=m_0$
(so
$j=j_0$
), then there exist
$y,z$
such that
$x\wedge m\leq z\lessdot y\leq x$
with
$z\in L_0$
and
$y\in L^0$
. But then
$z = x \wedge m_0$
and
$j_0\leq y$
, as desired.
Finally, suppose
$m < m_0$
. This means that the edge
$j_0\to j$
appears in
$G_L$
, so Theorem 3.7 guarantees that the edge
$j\to j_0$
does not appear. That is,
$j \leq m_0$
. The second compatibility condition in Theorem 4.1 tells us that
$\kappa _{L_0}(j)=\beta (m)=m_0\wedge m=m$
. Since
$j\leq m_0\wedge x$
, we can use induction on the size of the lattice to see that
$j\in \mathcal {U}_{L_0}((m_0\wedge x)\wedge m)=\mathcal {U}_{L_0}(x\wedge m)$
. This means that there exists an element
$y\in L_0$
covering
$x\wedge m$
such that the cover relation
$x\wedge m\lessdot y$
is labeled by j in
$L_0$
. Then
$j\leq y$
.
6 Semidistrim Lattices
An independent set of a (directed or undirected) graph G is a subset I of the vertex set of G such that no two vertices of I are adjacent. Let
$\mathrm {Ind}(G)$
denote the collection of independent sets of G. The extra condition we impose on compatibly dismantlable lattices to obtain semidistrim lattices is that the downward label sets and upward label sets of all of the elements are independent sets in the Galois graph.
Definition 6.1. A lattice L is semidistrim if it is compatibly dismantlable and
$\mathcal {D}_L(x),\mathcal {U}_L(x)\in \mathrm {Ind}(G_L)$
for all
$x \in L$
.
Note that there are compatibly dismantlable lattices that are not semidistrim; Figure 4 shows an example. We remark that semidistrim lattices are distinct from congruence normal (and hence congruence uniform) lattices.
The next theorem, most of which we already proved in Section 4.2, justifies the name semidistrim.
Theorem 6.2. Semidistributive lattices are semidistrim, and trim lattices are semidistrim.
Proof. We already know that semidistributive lattices and trim lattices are compatibly dismantlable by Theorems 4.5 and 4.6. If x is an element in a semidistributive lattice L, then
$\mathcal {D}_L(x)$
is its canonical join representation, and
$\mathcal {U}_L(x)$
is its canonical meet representation. It is known that these sets are independent sets in the Galois graph [Reference Barnard5]. If x is an element in a trim lattice L, then
$\mathcal {D}_L(x)$
and
$\mathcal {U}_L(x)$
are independent sets in the Galois graph by [Reference Thomas and Williams50, Corollary 5.6].
Lemma 6.3. If L is a semidistrim lattice with dismantling pair
$(j_0,m_0)$
, then the intervals
$L_0=[\hat 0,m_0]$
and
$L^0=[j_0,\hat 1]$
are semidistrim.
Proof. We know these intervals are compatibly dismantlable by Theorem 4.1. Theorem 4.4 tells us that
$G_{L_0}$
is an induced subgraph of
$G_L$
and that
$G_{L^0}$
is isomorphic to an induced subgraph of
$G_L$
, where the isomorphism is the restriction of
$\alpha ^{-1}$
to the vertex set of
$G_{L^0}$
. Suppose
$x\in L_0$
and
$y\in L^0$
; we need to show that
$\mathcal {D}_{L_0}(x),\mathcal {U}_{L_0}(x)\in \mathrm {Ind}(G_{L_0})$
and that
$\mathcal {D}_{L^0}(y),\mathcal {U}_{L^0}(y)\in \mathrm {Ind}(G_{L^0})$
. Since L is semidistrim, all of the sets
$\mathcal {D}_L(x),\mathcal {U}_L(x),\mathcal {D}_L(y),\mathcal {U}_L(y)$
are independent sets in
$G_L$
. Theorem 5.5 tells us that
$\mathcal {D}_{L_0}(x)$
and
$\mathcal {U}_{L_0}(x)$
are subsets of
$\mathcal {D}_L(x)$
and
$\mathcal {U}_L(x)$
, respectively, so they are independent sets in
$G_{L_0}$
. The same proposition tells us that
$\alpha ^{-1}(\mathcal {D}_{L^0}(y))\subseteq \mathcal {D}_L(y)$
and
$\alpha ^{-1}(\mathcal {U}_{L^0}(y))\subseteq \mathcal {U}_L(y)$
. This shows that
$\mathcal {D}_{L^0}(y)$
and
$\mathcal {U}_{L^0}(y)$
are independent sets in
$G_{L^0}$
.
The next theorem will allow us to define rowmotion on semidistrim lattices in Section 9.
Theorem 6.4. Let L be a semidistrim lattice. The maps
$\mathcal {D}_L\colon L\to \mathrm {Ind}(G_L)$
and
$\mathcal {U}_L\colon L\to \mathrm {Ind}(G_L)$
are bijections.
Proof. The result is trivial if
$|L|=1$
, so we may assume
$|L|\geq 2$
and proceed by induction on
$|L|$
. Let us prove that
$\mathcal {D}_L$
is bijective; the proof that
$\mathcal {U}_L$
is bijective follows from a completely analogous dual argument. We know that
$\mathcal {D}_L$
is injective by Theorem 5.6, so it suffices to show that it is surjective. Let
$(j_0,m_0)$
be a dismantling pair for L and let
$L_0=[\hat 0,m_0]$
and
$L^0=[j_0,\hat 1]$
. The intervals
$L_0$
and
$L^0$
are semidistrim by Lemma 6.3.
Fix
$I\in \mathrm {Ind}(G_L)$
. If
$I\cap (\mathrm {In}(j_0)\cup \{j_0\})=\emptyset $
, then Theorem 4.4 implies that I is an independent set of
$G_{L_0}$
, so it follows by induction that there exists
$z\in L_0$
such that
$\mathcal {D}_{L_0}(z)=I$
. But
$\mathcal {D}_{L_0}(z)=\mathcal {D}_L(z)$
by Theorem 5.5, so I is in the image of
$\mathcal {D}_L$
.
We may now assume that
$I\cap (\mathrm {In}(j_0)\cup \{j_0\})\neq \emptyset $
. If
$j_0\in I$
, then
$I\cap \mathrm {Out}(j_0)=\emptyset $
because I is an independent set. Theorem 3.6 tells us that every vertex in
$\mathrm {In}(j_0)$
is adjacent to every vertex in
$\mathrm {Out}(j_0)$
; therefore, if I contains an element of
$\mathrm {In}(j_0)$
, then
$I\cap \mathrm {Out}(j_0)=\emptyset $
. In either case,
$I\cap \mathrm {Out}(j_0)=\emptyset $
. According to Theorem 4.4,
$\alpha (I\setminus \{j_0\})\in \mathrm {Ind}(G_{L^0})$
, so we can use induction on the size of L to see that there exists
$y\in L^0$
with
$\mathcal {D}_{L^0}(y)=\alpha (I\setminus \{j_0\})$
. But Theorem 5.5 tells us that
$\alpha ^{-1}(\mathcal {D}_{L^0}(y))=\mathcal {D}_L(y)\setminus \{j_0\}$
, so
$\mathcal {D}_L(y)\setminus \{j_0\}=I\setminus \{j_0\}$
. We will prove that
$\mathcal {D}_L(y)=I$
, which will show that I is in the image of
$\mathcal {D}_L$
, as desired. So assume by way of contradiction that
$\mathcal {D}_L(y)\neq I$
. This implies that either
$I=\mathcal {D}_L(y)\sqcup \{j_0\}$
or
$\mathcal {D}_L(y)=I\sqcup \{j_0\}$
.
If
$I=\mathcal {D}_L(y)\sqcup \{j_0\}$
, then
$\mathcal {D}_L(y)$
is an independent set in
$G_L$
that does not intersect
$\mathrm {In}(j_0)\cup \{j_0\}$
, so we know from an earlier case of this proof that
$\mathcal {D}_L(y)=\mathcal {D}_L(z)$
for some
$z\in L_0$
. However, this contradicts the fact that
$\mathcal {D}_L$
is injective (since
$y\in L^0$
and
$z\in L_0$
).
If
$\mathcal {D}_L(y)=I\sqcup \{j_0\}$
, then since we have assumed
$I\cap (\mathrm {In}(j_0)\cup \{j_0\})\neq \emptyset $
, the set I must contain an element of
$\mathrm {In}(j_0)$
. However, this contradicts the fact that
$\mathcal {D}_L(y)$
is an independent set in
$G_L$
.
Remark 6.5. Semidistrim lattices do not form the most general class of lattices for which the map
$\mathrm {Ind}(G_L) \to L$
given by
$I \mapsto \bigvee I$
is a bijection. Figure 6 gives an example of an overlapping – but not compatibly dismantlable – lattice with this property.
If L is semidistrim and
$x\in L$
, then the sets
$\mathcal {D}_L(x)$
and
$\mathcal {U}_L(x)$
are independent sets in
$G_L$
by definition. The next theorem tells us more precisely how these sets fit together within the Galois graph.
Suppose G is a directed graph. An orthogonal pair of G is a pair
$(X,Y)$
such that X and Y are disjoint independent sets of G and such that there does not exist an edge of the form
$j\to j'$
with
$j\in X$
and
$j'\in Y$
. An orthogonal pair
$(X,Y)$
is called tight if the following additional conditions hold:
-
• If j is a vertex of G that is not in
$X\cup Y$
, then the pairs
$(X\cup \{j\},Y)$
and
$(X,Y\cup \{j\})$
are not orthogonal pairs. -
• If
$j\to j'$
is an edge in G such that
$j\not \in X\cup Y$
and
$j'\in X$
, then the pair
$((X\setminus \{j'\})\cup \{j\},Y)$
is not an orthogonal pair. -
• If
$j'\to j$
is an edge in G such that
$j\not \in X\cup Y$
and
$j'\in Y$
, then the pair
$(X,(Y\setminus \{j'\})\cup \{j\})$
is not an orthogonal pair.
Theorem 6.6. Let L be a semidistrim lattice. For every
$x\in L$
, the pair
$(\mathcal {D}_L(x),\mathcal {U}_L(x))$
is a tight orthogonal pair of
$G_L$
.
Proof. Fix
$x\in L$
. If
$j\in \mathcal {D}_L(x)$
and
$j'\in \mathcal {U}_L(x)$
, then
$j\leq x\leq \kappa _L(j')$
, so there is no edge
$j\to j'$
in
$G_L$
. This shows that
$(\mathcal {D}_L(x),\mathcal {U}_L(x))$
is an orthogonal pair. We need to show that this pair is tight.
First, suppose j is a vertex of
$G_L$
that is not in
$\mathcal {D}_L(x)\cup \mathcal {U}_L(x)$
. To prove that
$(\mathcal {D}_L(x)\cup \{j\},\mathcal {U}_L(x))$
and
$(\mathcal {D}_L(x),\mathcal {U}_L(x)\cup \{j\})$
are not orthogonal pairs, it suffices to show that one of the sets
$\mathrm {In}(j)\cap \mathcal {D}_L(x)$
or
$\mathrm {Out}(j)\cap \mathcal {U}_L(x)$
is nonempty. Suppose instead that both of these sets are empty. Since
$\mathrm {Out}(j)\cap \mathcal {U}_L(x)=\emptyset $
, we have
$j\leq \kappa _L(j')$
for all
$j'\in \mathcal {U}_L(x)$
, so it follows from Theorem 5.6 that
$j\leq x$
. Since
$\mathrm {In}(j)\cap \mathcal {D}_L(x)=\emptyset $
, we have
$j'\leq \kappa _L(j)$
for all
$j'\in \mathcal {D}_L(x)$
, so it follows from Theorem 5.6 that
$x\leq \kappa _L(j)$
. Putting these together, we find that
$j\leq x\leq \kappa _L(j)$
, which is impossible. This proves that
$(\mathcal {D}_L(x)\cup \{j\},\mathcal {U}_L(x))$
and
$(\mathcal {D}_L(x),\mathcal {U}_L(x)\cup \{j\})$
are not orthogonal pairs.
Now suppose there is an edge
$j\to j'$
in
$G_L$
with
$j\not \in \mathcal {D}_L(x)\cup \mathcal {U}_L(x)$
and
$j'\in \mathcal {D}_L(x)$
. Our goal is to show that
$((\mathcal {D}_L(x)\setminus \{j'\})\cup \{j\},\mathcal {U}_L(x))$
is not an orthogonal pair. Suppose instead that this pair is orthogonal. Then
$(\mathcal {D}_L(x)\setminus \{j'\})\cup \{j\}$
is an independent set in
$G_L$
, so Theorem 6.4 tells us that there exists
$x'\in L$
with
$\mathcal {D}_L(x')=(\mathcal {D}_L(x)\setminus \{j'\})\cup \{j\}$
. Furthermore, we have
$\mathrm {Out}(j)\cap \mathcal {U}_L(x)=\emptyset $
, so
$j\leq \kappa _L(j")$
for all
$j"\in \mathcal {U}_L(x)$
. By Theorem 5.6, this implies that
$j\leq x$
. We also know that
$j"\leq x$
for all
$j"\in \mathcal {D}_L(x)$
, so Theorem 5.6 tells us that
$x'=\bigvee ((\mathcal {D}_L(x)\setminus \{j'\})\cup \{j\})\leq x$
. Because
$\mathcal {D}_L(x)\neq \mathcal {D}_L(x')$
, we must have
$x'<x$
. Let y be an element such that
$x'\leq y\lessdot x$
and consider the label
$j_{yx}$
of the cover relation
$y\lessdot x$
. We have
$x'\leq y\leq \kappa _L(j_{yx})$
. If
$j_{yx}=j'$
, then
$j\leq x'\leq \kappa _L(j_{yx})=\kappa _L(j')$
, contradicting the assumption that the edge
$j\to j'$
appears in
$G_L$
. However, if
$j_{yx}$
is not
$j'$
, then
$j_{yx}\in \mathcal {D}_L(x)\setminus \{j'\}\subseteq \mathcal {D}_L(x')$
, so
$j_{yx}\leq x'\leq \kappa _L(j_{yx})$
, which is impossible.
Finally, we must show that if there is an edge
$j'\to j$
in
$G_L$
such that
$j\not \in \mathcal {D}_L(x)\cup \mathcal {U}_L(x)$
and
$j'\in \mathcal {U}_L(x)$
, then
$(\mathcal {D}_L(x),(\mathcal {U}_L(x)\setminus \{j'\})\cup \{j\})$
is not an orthogonal pair. This follows from an argument that is dual to the one used in the previous paragraph.
Remark 6.7. Given a semidistrim lattice L, Theorem 6.6 yields a map
$x\mapsto (\mathcal {D}_L(x),\mathcal {U}_L(x))$
from L to the set of tight orthogonal pairs of
$G_L$
. Theorem 5.6 implies that this map is injective. Thomas and the second author [Reference Thomas and Williams49] proved that if L is trim, then this map is actually a bijection. However, for arbitrary semidistrim lattices, the map can fail to be surjective. An example is given in Figure 7.
Figure 7
Left: A semidistrim lattice L. Right: The corresponding Galois graph, with a tight orthogonal pair
$(X,Y)$
that is not
$(\mathcal {D}(x),\mathcal {U}(x))$
for any element
$x \in L$
(the elements of X are shaded blue, whereas the elements of Y are shaded yellow).
Remark 6.8. Even though semidistributive lattices and trim lattices have join-prime atoms and meet-prime coatoms (not necessarily corresponding to each other under the pairing), the same is not generally true of semidistrim lattices. A counterexample is given in Figure 8.
Figure 8 A semidistrim lattice with no join-prime atom or meet-prime coatom (in contrast to semidistributive and trim lattices).
7 Products and Intervals of Semidistrim Lattices
The goal of this section is to show that products of semidistrim lattices are semidistrim and that intervals in semidistrim lattices are semidistrim. The proof of the statement about products is more straightforward, so we will begin with that.
7.1 Products
Recall that if P and
$P'$
are two posets, then their product is the poset
$P\times P'$
whose underlying set is the Cartesian product of P and
$P'$
, where
$(x,x')\leq (y,y')$
if and only if
$x\leq y$
in P and
$x'\leq y'$
in
$P'$
. We will actually show that the classes of uniquely paired lattices, compatibly dismantlable lattices and semidistrim lattices are each closed under taking products.
In what follows, L and
$L'$
are lattices. The product
$L\times L'$
is also a lattice, and its meet and join operations are given by
$(x,y)\wedge (x',y')=(x\wedge y,x'\wedge y')$
and
$(x,y)\vee (x',y')=(x\vee y,x'\vee y')$
. We write
$\hat 0$
and
$\hat 1$
(respectively,
$\hat 0'$
and
$\hat 1'$
) for the minimum and maximum elements of L (respectively,
$L'$
). It is straightforward to check that
$$ \begin{align}\mathcal{J}_{L\times L'}=(\mathcal{J}_L\times\{\hat 0'\})\sqcup(\{\hat 0\}\times\mathcal{J}_{L'})\quad\text{and}\quad\mathcal{M}_{L\times L'}=(\mathcal{M}_L\times\{\hat 1'\})\sqcup(\{\hat 1\}\times\mathcal{M}_{L'}). \end{align} $$
Proposition 7.1. If L and
$L'$
are uniquely paired, then
$L\times L'$
is uniquely paired.
Proof. Suppose
$\lambda \colon \mathcal {J}_{L\times L'}\to \mathcal {M}_{L\times L'}$
is a pairing. If
$j\in \mathcal {J}_L$
, then since
$(j,\hat 0')\not \leq \lambda (j,\hat 0')$
, it follows from (7.1) that
$\lambda (j,\hat 0')=(\mu (j),\hat 1')$
for some
$\mu (j)\in \mathcal {M}_L$
. Similarly, if
$j'\in \mathcal {J}_{L'}$
, then
$\lambda (\hat 0,j')=(\hat 1,\mu '(j'))$
for some
$\mu '(j')\in \mathcal {M}_{L'}$
. It is straightforward to check that the resulting maps
$\mu \colon \mathcal {J}_L\to \mathcal {M}_L$
and
$\mu '\colon \mathcal {J}_{L'}\to \mathcal {M}_{L'}$
are pairings on L and
$L'$
, respectively. Since L and
$L'$
are uniquely paired, we have
$\mu =\kappa _L$
and
$\mu '=\kappa _{L'}$
. This shows that if
$L\times L'$
is paired, then it is uniquely paired. However, one can readily check that the map
$\kappa _{L\times L'}\colon \mathcal {J}_{L\times L'}\to \mathcal {M}_{L\times L'}$
given by
$\kappa _{L\times L'}(j,\hat 0')=(\kappa _L(j),\hat 1')$
and
$\kappa _{L\times L'}(\hat 0,j')=(\hat 1,\kappa _{L'}(j'))$
is indeed a pairing on
$L\times L'$
.
Proposition 7.2. If L and
$L'$
are compatibly dismantlable, then
$L\times L'$
is compatibly dismantlable.
Proof. Theorem 7.1 tells us that
$L\times L'$
is uniquely paired, and the proof shows how to compute
$\kappa _{L\times L'}$
in terms of
$\kappa _L$
and
$\kappa _{L'}$
. Let
$(j_0,m_0)$
and
$(j_0',m_0')$
be dismantling pairs for L and
$L'$
, respectively. One readily checks that
$((j_0,\hat 0'),(m_0,\hat 1'))$
is a dismantling pair for
$L\times L'$
. Using the easily-verified decomposition
$$\begin{align*}\{(a,b)\in \mathcal{J}_{L\times L'}:(j_0,\hat 0')\leq \kappa_{L\times L'}(a,b)\}=\{(j,\hat 0'):j_0\leq\kappa_L(j)\}\sqcup(\{\hat 0\}\times\mathcal{J}_{L'}),\end{align*}$$
one can check that the map
$$\begin{align*}\alpha\colon\{(a,b)\in \mathcal{J}_{L\times L'}:(j_0,\hat 0')\leq \kappa_{L\times L'}(a,b)\}\to\mathcal{J}_{[(j_0,\hat 0'),(\hat 1,\hat 1')]}\end{align*}$$
given by
$\alpha (a,b)=(j_0,\hat 0')\vee (a,b)$
is a bijection such that
$$\begin{align*}\kappa_{[(j_0,\hat 0'),(\hat 1,\hat 1')]}(\alpha(a,b))=\kappa_{L\times L'}(a,b)\end{align*}$$
for all
$(a,b)\in \mathcal {J}_{L\times L'}$
with
$(j_0,\hat 0')\leq \kappa _{L\times L'}(a,b)$
. In other words, the first compatibility condition in Theorem 4.1 holds for
$L\times L'$
. The second compatibility condition also holds similarly.
Theorem 7.3. If L and
$L'$
are semidistrim, then
$L\times L'$
is semidistrim.
Proof. Theorem 7.2 tells us that
$L\times L'$
is compatibly dismantlable. Using (7.1) and the description of
$\kappa _{L\times L'}$
given in the proof of Theorem 7.1, it is straightforward to show that the Galois graph
$G_{L\times L'}$
is naturally isomorphic to
$G_L\sqcup G_{L'}$
, the disjoint union of
$G_L$
and
$G_{L'}$
(with no vertices in
$G_L$
adjacent to any vertices in
$G_{L'}$
). More precisely, the isomorphism sends
$(j,\hat 0')\in \mathcal {J}_L\times \{\hat 0'\}$
to j and sends
$(\hat 0,j')\in \{\hat 0\}\times \mathcal {J}_{L'}$
to
$j'$
.
Consider
$(y,y')\in L\times L'$
. The elements covered by
$(y,y')$
in
$L\times L'$
are precisely the elements of the form
$(x,y')$
with
$x\lessdot y$
in L or of the form
$(y,x')$
with
$x'\lessdot y'$
in
$L'$
. Moreover, the label of
$(x,y')\lessdot (y,y')$
is
$(j_{xy},\hat 0')$
, while the label of
$(y,x')\lessdot (y,y')$
is
$(\hat 0,j_{x'y'})$
. It follows that under the aforementioned isomorphism between
$G_{L\times L'}$
and
$G_L\sqcup G_{L'}$
, the set
$\mathcal {D}_{L\times L'}(y,y')$
corresponds to
$\mathcal {D}_L(y)\sqcup \mathcal {D}_{L'}(y')$
. Since
$\mathcal {D}_L(y)\in \mathrm {Ind}(G_L)$
and
$\mathcal {D}_{L'}(y')\in \mathrm {Ind}(G_{L'})$
, we have
$\mathcal {D}_{L\times L'}(y,y')\in \mathrm {Ind}(G_{L\times L'})$
. A similar argument shows that
$\mathcal {U}_{L\times L'}(y,y')\in \mathrm {Ind}(G_{L\times L'})$
.
7.2 Intervals
We now show that intervals in semidistrim lattices are again semidistrim. The strategy is to prove that lower intervals of semidistrim lattices are again semidistrim – the result will then follow because the dual of a semidistrim lattice is again semidistrim.
Lemma 7.4. Let L be a semidistrim lattice and let
$v\in L$
. Let
$L_v=[\hat 0,v]$
. For
$j\in \mathcal J_{L_v}$
, let
$\kappa ^{\wedge v}(j)=\kappa _L(j)\wedge v$
. Then
$\kappa ^{\wedge v}\colon \mathcal {J}_{L_v}\to \mathcal {M}_{L_v}$
is a pairing on
$L_v$
.
Proof. Let
$(j_0,m_0)$
be a dismantling pair for L and let
$L_0=[\hat 0,m_0]$
and
$L^0=[j_0,\hat 1]$
. First, suppose
$v\in L_0$
. Lemma 6.3 tells us that
$L_0$
is semidistrim, and the second compatibility condition in Theorem 4.1 states that
$\kappa _{L_0}(j)=m_0\wedge \kappa _L(j)$
for all
$j\in \mathcal {J}_{L}$
with
$j\leq m_0$
. In particular, for
$j\in \mathcal {J}_{L_v}$
, we have
$\kappa ^{\wedge v}(j)=\kappa _L(j)\wedge v=\kappa _{L_0}(j)\wedge v$
. Since
$L_v$
is a lower interval in
$L_0$
, we can use induction on the size of the lattice to see that
$\kappa ^{\wedge v}$
is a pairing on
$L_v$
.
Now assume
$v\in L^0$
. Let
$j\in \mathcal {J}_{L_v}$
. By Lemma 5.7, we have
$j \in \mathcal {U}_{L}(\kappa ^{\wedge v}(j))$
. In other words, there is some cover relation
$\kappa ^{\wedge v}(j)\lessdot y$
with label j. Note that
$y=\kappa ^{\wedge v}(j)\vee j\leq v$
. Suppose by way of contradiction that there is some element
$z\in L_v$
with
$z\neq y$
and
$\kappa ^{\wedge v}(j)\lessdot z$
. Let
$j'$
be the label of the cover
$\kappa ^{\wedge v}(j)\lessdot z$
. Then
$j'\not \leq \kappa ^{\wedge v}(j)=\kappa _L(j)\wedge v$
. We have
$j'\leq v$
, so
$j'\not \leq \kappa _L(j)$
. This means that
$j'\to j$
is an edge in
$G_L$
, which contradicts the fact that
$\mathcal {U}_L(\kappa ^{\wedge v}(j))$
is an independent set in
$G_L$
(because L is semidistrim). This shows that no such element z exists, which implies that y is the only element of
$L_v$
that covers
$\kappa ^{\wedge v}(j)$
. Hence,
$\kappa ^{\wedge v}(j)\in \mathcal {M}_{L_v}$
. This shows that
$\kappa ^{\wedge v}$
maps
$\mathcal {J}_{L_v}$
to
$\mathcal {M}_{L_v}$
. We have also seen that
$\kappa ^{\wedge v}$
is injective because we can recover j as the label of the cover
$\kappa ^{\wedge v}\lessdot y$
.
To see that
$\kappa ^{\wedge v}$
is surjective, consider some
$m\in \mathcal {M}_{L_v}$
. Let
$m^*$
be the unique element of
$L_v$
that covers m. Consider the label
$j_{mm^*}$
of the cover
$m\lessdot m^*$
. Then
$\kappa ^{\wedge v}(j_{mm^*})=\kappa _L(j_{mm^*})\wedge v\geq m$
. If we had
$\kappa ^{\wedge v}(j_{mm^*})\geq m^*$
, then we would have
$j_{mm^*}\leq m^*\leq \kappa ^{\wedge v}(j_{mm^*})\leq \kappa _L(j_{mm^*})$
, which is impossible. Therefore,
$\kappa ^{\wedge v}(j_{mm^*})=m$
.
We now know that
$\kappa ^{\wedge v}$
is a bijection, so we need to check that it is a pairing. To do this, we will use Lemma 3.3. Fix
$j'\in \mathcal {J}_{L_v}$
and let
$m'=\kappa ^{\wedge v}(j')$
. We need to show that
$m'\geq j^{\prime }_*$
,
$(m')^*\geq j'$
, and
$m'\not \geq j'$
. We saw above that
$j'$
is the label of the cover
$m'\lessdot (m')^*$
, so
$(m')^*=m'\vee j'$
. This proves that
$(m')^*\geq j'$
and
$m'\not \geq j'$
. Since
$\kappa _L$
is a pairing, we have
$\kappa _L(j')\geq j^{\prime }_*$
. We also know that
$v\geq j^{\prime }_*$
, so
$m'=\kappa _L(j')\wedge v\geq j^{\prime }_*$
.
Our next step is to show that the pairing
$\kappa ^{\wedge v}$
defined in Lemma 7.4 is the only pairing on
$L_v$
.
Lemma 7.5. Let L be a semidistrim lattice and fix
$v\in L$
. The interval
$L_v= [\hat {0},v]$
is uniquely paired; its unique pairing is the map
$\kappa ^{\wedge v}\colon \mathcal J_{L_v}\to \mathcal M_{L_v}$
defined by
$\kappa ^{\wedge v}(j)=\kappa _L(j)\wedge v$
.
Proof. We know by Lemma 7.4 that
$\kappa ^{\wedge v}$
is a pairing on
$L_v$
, so we just need to show that it is the unique pairing. Let
$\lambda \colon \mathcal J_{L_v}\to \mathcal M_{L_v}$
be a pairing on
$L_v$
and define
$\sigma \colon \mathcal J_{L_v}\to \mathcal J_{L_v}$
by
$\sigma =(\kappa ^{\wedge v})^{-1}\circ \lambda $
. Our goal is to show that
$\lambda =\kappa ^{\wedge v}$
or, equivalently, that
$\sigma $
is the identity map on
$\mathcal J_{L_v}$
. Define a map
$\widetilde \kappa \colon \mathcal J_L\to \mathcal M_L$
by
$$\begin{align*}\widetilde\kappa(j) = \begin{cases} \kappa_L(j) & \text{ if } j \not\in L_v \\ \kappa_L(\sigma(j)) & \text{ if } j\in L_{v}. \end{cases}\end{align*}$$
We will prove that
$\widetilde \kappa $
is a pairing on L. Since L is uniquely paired, this will imply that
$\widetilde \kappa =\kappa _L$
. It will then follow that
$\kappa _L(j)=\kappa _L(\sigma (j))$
for all
$j\in \mathcal J_{L_v}$
. Because
$\kappa _L$
is injective, this will imply that
$\sigma $
is the identity, as desired.
It is straightforward to check that
$\widetilde \kappa $
is a bijection. Now fix
$j\in \mathcal J_L$
and let
$m=\widetilde \kappa (j)$
. According to Lemma 3.3, we need to check that
$m\geq j_*$
,
$m^*\geq j$
and
$m\not \geq j$
. If
$j\not \in L_v$
, then
$m=\kappa _L(j)$
, so these conditions follow from the fact that
$\kappa _L$
is a pairing on L. Thus, we may assume
$j\in L_v$
.
Note that
$$\begin{align*}m\wedge v=\widetilde\kappa(j)\wedge v=\kappa_L((\kappa^{\wedge v})^{-1}(\lambda(j)))\wedge v=\kappa^{\wedge v}((\kappa^{\wedge v})^{-1}(\lambda(j)))=\lambda(j).\end{align*}$$
We have
$$\begin{align*}m\wedge j=m\wedge(v\wedge j)=(m\wedge v)\wedge j=\lambda(j)\wedge j=j_*,\end{align*}$$
where the last equality is due to the fact that
$\lambda $
is a pairing on
$L_v$
. This proves that
$m\geq j_*$
and
$m\not \geq j$
.
We are left to show that
$m^*\geq j$
. As above, note that
$m\wedge v =\lambda (j)$
. Because
$\lambda $
is a pairing on
$\mathcal {M}_{L_v}$
, the element
$\lambda (j)$
is meet-irreducible in
$L_v$
. Let y be the unique element of
$L_v$
that covers
$\lambda (j)$
. Since
$\lambda (j)=\kappa ^{\wedge v}(\sigma (j))$
and
$\kappa ^{\wedge v}$
is a pairing on
$L_v$
, we have
$y=\lambda (j)\vee \sigma (j)$
. Since
$m=\kappa _L(\sigma (j))$
and
$\kappa _L$
is a pairing on L, we have
$m^*\geq \sigma (j)$
. We also have
$m^*\gtrdot m\geq m\wedge v=\lambda (j)$
, so
$m^*\geq \lambda (j)\vee \sigma (j)=y$
. Since
$\lambda $
is a pairing on
$L_v$
and y is the unique element of
$L_v$
covering
$\lambda (j)$
, we must have
$y\geq j$
. Thus,
$m^*\geq y\geq j$
, as desired.
We now know that the interval
$L_v=[\hat 0,v]$
of L is uniquely paired, so we will usually write
$\kappa _{L_v}$
instead of
$\kappa ^{\wedge v}$
for its unique pairing. One should keep in mind that
$\kappa _{L_v}$
is described explicitly in terms of
$\kappa _L$
by the formula
$\kappa _{L_v}(j)=\kappa _L(j)\wedge v$
.
Lemma 7.6. If L is semidistrim and
$v\in L$
, then the interval
$L_v= [\hat {0},v]$
is compatibly dismantlable.
Proof. We know by Lemma 7.5 that
$L_v$
is uniquely paired with its pairing
$\kappa _{L_v}\colon \mathcal J_{L_v}\to \mathcal M_{L_v}$
given by
$\kappa _{L_v}(j)=\kappa _L(j)\wedge v$
. Let
$(j_0,m_0)$
be a dismantling pair for L and let
$L_0=[\hat 0,m_0]$
and
$L^0=[j_0,\hat 1]$
. According to Lemma 6.3, the intervals
$L_0$
and
$L^0$
are semidistrim. Therefore, if
$v\in L_0$
, then the desired result follows by induction on the size of L.
We may now assume
$v\in L^0$
. Note that
$j_0$
is also join-prime in
$L^0$
. Let
$m_0^v=m_0\wedge v$
so that
$(j_0,m_0^v)$
is a dismantling pair for
$L_v$
. Since
$L_0$
and
$L^0$
are semidistrim, they have unique pairings
$\kappa _{L_0}\colon \mathcal J_{L_0}\to \mathcal M_{L_0}$
and
$\kappa _{L^0}\colon \mathcal J_{L^0}\to \mathcal M_{L^0}$
. By induction, the intervals
$(L_v)_0=[\hat {0},m_0^v]\subseteq L_0$
and
$(L_v)^0=[j_0,v]\subseteq L^0$
are compatibly dismantlable. Moreover, it follows from Lemma 7.5 that the unique pairings on these intervals are the bijections
$\kappa _{(L_v)_0}\colon \mathcal J_{(L_v)_0}\to \mathcal M_{(L_v)_0}$
and
$\kappa _{(L_v)^0}\colon \mathcal J_{(L_v)^0}\to \mathcal M_{(L_v)^0}$
defined by
$\kappa _{(L_v)_0}(j)=\kappa _{L_0}(j)\wedge m_0^v$
and
$\kappa _{(L_v)^0}(j)=\kappa _{L^0}(j)\wedge v$
.
Because L is compatibly dismantlable, there is a bijection
$\alpha _L\colon \{j\in \mathcal {J}_L:j_0\leq \kappa _L(j)\}\to \mathcal {J}_{L^0}$
given by
$\alpha _L(j)=j_0\vee j$
. We want to show that there is a bijection
$\alpha _{L_v}\colon \{j \in \mathcal {J}_{L_v}:j_0\leq \kappa _{L_v}(j)\}\to \mathcal {J}_{(L_v)^0}$
given by
$\alpha _{L_v}(j)=j_0\vee j$
. To this end, suppose j is a join-irreducible element of
$L_v$
with
$j_0\leq \kappa _{L_v}(j)$
. Then we have
$j\in \mathcal {J}_L$
and
$j_0\leq \kappa _L(j)$
, so
$j_0 \vee j=\alpha _L(j)\in \mathcal {J}_{L^0}$
. Because
$j_0 \vee j \leq v$
, the element
$j_0\vee j$
is actually in
$\mathcal {J}_{(L_v)^0}$
. This shows that
$\alpha _{L_v}$
does actually map
$\{j \in \mathcal {J}_{L_v}:j_0\leq \kappa _{L_v}(j)\}$
to
$\mathcal {J}_{(L_v)^0}$
. Noting that
$$\begin{align*}\{ j \in \mathcal{J}_{L_v} : j_0\leq \kappa_{L_v}(j)\}= \{j \in \mathcal{J}_L : j_0\leq \kappa_L(j)\}\cap L_v,\\[-15pt]\end{align*}$$
we see that the injectivity of
$\alpha _{L_v}$
follows immediately from the injectivity of
$\alpha _L$
.
To see that
$\alpha _{L_v}$
is surjective, let us choose a join-irreducible element
$j'$
of
$\mathcal {J}_{(L_v)^0}$
. Then
$j'$
is join-irreducible in
$L^0$
, so it is of the form
$\alpha _L(j")$
for some
$j" \in \mathcal {J}_L$
with
$j_0\leq \kappa _L(j")$
. But then
$j"\leq j'\leq v$
, so
$j"\in \{j \in \mathcal {J}_L : j_0\leq \kappa _L(j)\}\cap L_v=\{j \in \mathcal {J}_{L_v} : j_0\leq \kappa _{L_v}(j)\}$
.
We also need to check that if
$j\in \mathcal J_{L_v}$
satisfies
$j_0\leq \kappa _{L_v}(j)$
, then
$$\begin{align*}\kappa_{(L_v)^0}(\alpha_{L_v}(j))=\kappa_{L_v}(j).\\[-15pt]\end{align*}$$
We know by Theorem 4.1 that
$\kappa _{L^0}(\alpha _L(j))=\kappa _L(j)$
. Hence,
$$\begin{align*}\kappa_{(L_v)^0}(\alpha_{L_v}(j))=\kappa_{L^0}(\alpha_{L_v}(j))\wedge v=\kappa_{L^0}(\alpha_{L}(j))\wedge v=\kappa_L(j)\wedge v=\kappa_{L_v}(j).\\[-15pt]\end{align*}$$
To finish the proof, we need to show that there is a bijection
$$\begin{align*}\beta_{L_v}\colon\{ m \in \mathcal{M}_{L_v} : \kappa_{L_v}^{-1}(m) \leq m_0^v\}\to\mathcal M_{(L_v)_0}\\[-15pt]\end{align*}$$
given by
$\beta _{L_v}(m)=m_0^v\wedge m$
such that
$\kappa _{(L_v)_0}^{-1}(\beta _{L_v}(m))=\kappa ^{-1}_{L_v}(m)$
for all
$m\in \mathcal M_{L_v}$
with
$\kappa _{L_v}^{-1}(m)\leq m_0^v$
. Choose
$m\in \mathcal M_{L_v}$
with
$\kappa _{L_v}^{-1}(m)\leq m_0^v$
and let
$j=\kappa _{L_v}^{-1}(m)$
. Then
$m = \kappa _L(j) \wedge v$
, so
$$ \begin{align} m_0^v\wedge m = (m_0 \wedge v)\wedge (\kappa_L(j) \wedge v) = m_0^v\wedge \kappa_L(j)=\kappa_{(L_v)_0}(j)=\kappa_{(L_v)_0}(\kappa_{L_v}^{-1}(m)),\\[-15pt]\nonumber \end{align} $$
where the equality
$m_0^v\wedge \kappa _L(j)=\kappa _{(L_v)_0}(j)$
follows from the description of the unique pairing
$\kappa _{(L_v)_0}$
on the interval
$(L_v)_0=[\hat 0,m_0^v]$
given by Lemma 7.5. This proves that
$m_0^v\wedge m\in \mathcal M_{(L_v)_0}$
and that
$\kappa _{(L_v)_0}^{-1}(m_0^v\wedge m)=\kappa _{L_v}^{-1}(m)$
. This yields the map
$\beta _{L_v}$
; we still need to prove that this map is a bijection.
The map
$\beta _{L_v}$
is injective because we can use (7.2) to see that
$$\begin{align*}m=\kappa_{L_v}(\kappa_{(L_v)_0}^{-1}(\beta_{L_v}(m)))\\[-15pt]\end{align*}$$
for every
$m\in \mathcal {M}_{L_v}$
with
$\kappa _{L_v}^{-1}(m)\leq m_0^v$
. To prove that
$\beta _{L_v}$
is surjective, consider
$m'\in \mathcal {M}_{(L_v)_0}$
and let
$m=\kappa _{L_v}(\kappa _{(L_v)_0}^{-1}(m'))$
. Then
$m\in \mathcal {M}_{L_v}$
and
$\kappa _{L_v}^{-1}(m)\leq m_0^v$
. According to (7.2), we have
$\beta _{L_v}(m)=m_0^v\wedge m=\kappa _{(L_v)_0}(\kappa _v^{-1}(m))=m'$
, as desired.
Lemma 7.7. If L is a semidistrim lattice and
$v\in L$
, then the Galois graph
$G_{L_v}$
of the interval
$L_v = [\hat {0},v]$
is the induced subgraph of
$G_L$
with vertex set
$\mathcal J_{L_v}$
.
Proof. Consider
$j,j' \in \mathcal {J}_{L_v}$
. We must show that
$j\to j'$
in
$G_L$
if and only if
$j\to j'$
in
$G_{L_v}$
. This is equivalent to showing that
$j\leq \kappa _L(j')$
if and only if
$j\leq \kappa _{L_v}(j')$
. We know by Lemma 7.5 that
$\kappa _{L_v}(j')=\kappa _L(j')\wedge v$
. Since
$j'\leq v$
, the desired result follows.
Theorem 7.8. Intervals in semidistrim lattices are semidistrim.
Proof. We first argue that if
$v\in L$
, then the interval
$L_v=[\hat {0},v]$
is semidistrim. We know by Lemma 7.6 that
$L_v$
is compatibly dismantlable. Now suppose
$y\in L_v$
. We know by Lemma 7.7 that the Galois graph
$G_{L_v}$
of
$L_v$
is an induced subgraph of
$G_L$
. The sets
$\mathcal {D}_{L_v}(y)$
and
$\mathcal {U}_{L_v}(y)$
are the intersections of
$\mathcal {D}_L(y)$
and
$\mathcal {U}_L(y)$
, respectively, with the vertex set of
$G_{L_v}$
. Since
$\mathcal {D}_L(y)$
and
$\mathcal {U}_L(y)$
are independent sets in
$G_L$
, the sets
$\mathcal {D}_{L_v}(y)$
and
$\mathcal {U}_{L_v}(y)$
must be independent sets in
$G_{L_v}$
. Hence,
$L_v$
is semidistrim.
Now fix an interval
$[u,v]$
in L. It is immediate from the definition of a semidistrim lattice that a lattice is semidistrim if and only if its dual is semidistrim, so it follows from the preceding paragraph that
$[u,\hat {1}]$
is semidistrim. We can now apply the preceding paragraph again to see that the interval
$[u,v]$
of the semidistrim lattice
$[u,\hat {1}]$
is semidistrim.
Suppose L is a compatibly dismantlable lattice with dismantling pair
$(j_0,m_0)$
. By Theorem 4.1, the unique pairings
$\kappa _{L_0}$
and
$\kappa _{L^0}$
on the intervals
$L_0=[\hat 0,m_0]$
and
$L^0=[j_0,\hat 1]$
are compatible with the pairing
$\kappa _L$
via the maps
$\alpha $
and
$\beta $
. If we additionally assume that L is semidistrim, then the preceding theorem tells us that every interval in L is semidistrim; the next corollary tells us that the pairings on the intervals of L are compatible with
$\kappa _L$
.
Corollary 7.9. Let L be a semidistrim lattice and let
$[u,v]$
be an interval in L. There are bijections
$\alpha _{u,v}\colon J_L(v)\cap M_L(u)\to \mathcal {J}_{[u,v]}$
and
$\beta _{u,v}\colon \kappa _L(J_L(v)\cap M_L(u))\to \mathcal {M}_{[u,v]}$
given by
$\alpha _{u,v}(j)=u\vee j$
and
$\beta _{u,v}(m)=v\wedge m$
, respectively. Moreover,
$\kappa _{[u,v]}(\alpha _{u,v}(j))=\beta _{u,v}(\kappa _L(j))$
for all
$j\in J_L(v)\cap M_L(u)$
.
Proof. If
$u=\hat 0$
, then this follows from Lemma 7.5. There is a natural dual version of Lemma 7.5 that yields the desired result when
$v=\hat 1$
. The general result then follows from combining these two cases (for example, by viewing
$[u,v]$
as a lower interval in
$[u,\hat 1]$
).
Note that it follows from the preceding corollary that every prime pair in a semidistrim lattice is a dismantling pair.
To end this section, let us record how the Galois graph and the edge labels of an interval in a semidistrim lattice relate to those of the entire lattice.
Corollary 7.10. Let
$[u,v]$
be an interval in a semidistrim lattice L. The bijection
$\alpha _{u,v}\colon J_L(v)\cap M_L(u)\to \mathcal {J}_{[u,v]}$
given by
$\alpha _{u,v}(j)=u\vee j$
is an isomorphism from an induced subgraph of the Galois graph
$G_L$
to the Galois graph
$G_{[u,v]}$
. If
$u\leq x\lessdot y\leq v$
and
$j_{xy}$
is the label of the cover relation
$x\lessdot y$
in L, then
$\alpha _{u,v}(j_{xy})$
is the label of the same cover relation in
$[u,v]$
.
Proof. Suppose
$j,j'\in J_L(v)\cap M_L(u)$
. This means that
$$\begin{align*}j,j'\leq v\quad\text{and}\quad\kappa_L(j),\kappa_L(j')\geq u.\end{align*}$$
We must show that
$j\to j'$
in
$G_L$
if and only if
$\alpha _{u,v}(j)\to \alpha _{u,v}(j')$
in
$G_{[u,v]}$
. Equivalently, we must show that
$j\leq \kappa _L(j')$
if and only if
$\alpha _{u,v}(j)\leq \kappa _{[u,v]}(\alpha _{u,v}(j'))$
. We have
$\alpha _{u,v}(j)=u\vee j$
by definition, and we have
$\kappa _{[u,v]}(\alpha _{u,v}(j'))=\beta _{u,v}(\kappa _L(j'))=v\wedge \kappa _L(j')$
by Theorem 7.9. The assumptions
$j\leq v$
and
$\kappa _L(j')\geq u$
imply that
$j\leq \kappa _L(j')$
if and only if
$u \vee j\leq v\wedge \kappa _L(j')$
.
To prove the last statement, note that
$j_{xy}\leq y$
and
$\kappa _L(j_{xy})\geq x$
by Theorem 5.1. Since
$y\geq u$
, this implies that
$\alpha _{u,v}(j_{xy})=u\vee j_{xy}\leq y$
. Also, since
$x\leq v$
, we have (by Theorem 7.9)
$\kappa _{[u,v]}(\alpha _{u,v}(j_{xy}))=v\wedge \kappa _L(j_{xy})\geq x$
. Hence,
$\alpha _{u,v}(j_{xy})$
is the label of
$x\lessdot y$
in
$[u,v]$
.
Remark 7.11. In the time since we released the initial preprint of this article, the first author and Li inserted randomness into the definition of rowmotion in order to define rowmotion Markov chains on semidistrim lattices [Reference Defant and Li16]. That article relies heavily on Theorem 7.8 and Theorems 7.9 and 7.10 to prove that rowmotion Markov chains are irreducible.
8 Poset Topology
The crosscut complex of a lattice L is the abstract simplicial complex whose faces are the sets A of atoms of L such that
$\bigvee A\neq \hat 1$
. We say L is crosscut simplicial if for all
$u,v\in L$
with
$u\leq v$
, the crosscut complex of the interval
$[u,v]$
contains all proper subsets of the set of atoms of
$[u,v]$
as faces. It is known [Reference Björner8, Theorem 10.8] that the order complex of a lattice is homotopy equivalent to its crosscut complex; it follows that if L is crosscut simplicial, then every interval in L has an order complex that is either contractible or homotopy equivalent to a sphere. McConville [Reference McConville32] proved that semidistributive lattices are crosscut simplicial; in fact, Barnard [Reference Barnard5] showed that a lattice is semidistributive if and only if it is join-semidistributive and crosscut simplicial. In his initial work on trim lattices, Thomas [Reference Thomas48] proved that the order complex of a trim lattice must be contractible or homotopy equivalent to a sphere. We generalize these results to semidistrim lattices in the following theorem.
Theorem 8.1. Semidistrim lattices are crosscut simplicial.
Proof. Let L be a semidistrim lattice. Because intervals of semidistrim lattices are semidistrim (Theorem 7.8), it is enough to show that every proper subset of the set of atoms of L is a face of the crosscut complex of L. Note that
$\mathcal {U}_L(\hat 0)$
is the set of atoms of L. Let A be a proper subset of
$\mathcal {U}_L(\hat 0)$
. By the definition of a semidistrim lattice, the set
$\mathcal {U}_L(\hat 0)$
is an independent set in
$G_L$
. Hence, A is also an independent set in
$G_L$
. It follows from Theorem 6.4 that there exist distinct
$x,x'\in L$
such that
$\mathcal {D}_L(x)=\mathcal {U}_L(\hat 0)$
and
$\mathcal {D}_L(x')=A$
. According to Theorem 5.6, we have
$x=\bigvee \mathcal {U}_L(\hat 0)$
and
$x'=\bigvee A$
. Then
$x'<x$
, so
$\bigvee A<\hat 1$
.
Corollary 8.2. The order complex of a semidistrim lattice is either contractible or homotopy equivalent to a sphere.
9 Pop-Stack Sorting and Rowmotion
9.1 Relationships between pop-stack sorting and rowmotion
Let L be a lattice. Following [Reference Defant14], we define the pop-stack sorting operator
$\mathsf {Pop}^\downarrow _L\colon L\to L$
and the dual pop-stack sorting operator
$\mathsf {Pop}^\uparrow _L\colon L\to L$
by
$$\begin{align*}\mathsf{Pop}^\downarrow_L(x)=x\wedge\bigwedge\{y\in L:y\lessdot x\}\quad\text{and}\quad\mathsf{Pop}^\uparrow_L(x)=x\vee\bigvee\{y\in L:x\lessdot y\}. \end{align*}$$
In particular,
$\mathsf {Pop}^\downarrow _L(\hat 0)=\hat 0$
, and
$\mathsf {Pop}^\uparrow _L(\hat 1)=\hat 1$
. As mentioned in the introduction,
$\mathsf {Pop}^\downarrow _L$
coincides with the classical pop-stack sorting map (see [Reference Claesson and Gumundsson12, Reference Elder and Goh21]) when L is the right weak order on the symmetric group
$S_n$
. Pop-stack sorting operators on lattices were introduced in [Reference Defant15, Reference Defant14] as generalizations of the pop-stack sorting map.
Now suppose L is semidistrim. Theorem 6.4 tells us that the maps
$\mathcal {D}_L\colon L\to \mathrm {Ind}(G_L)$
and
$\mathcal {U}_L\colon L\to \mathrm {Ind}(G_L)$
are bijections. We define rowmotion to be the bijection
$\mathsf {Row}_L\colon L\to L$
defined by declaring
$\mathsf {Row}_L(x)$
to be the unique element of L that satisfies
$\mathcal {U}_L(\mathsf {Row}(x))=\mathcal {D}_L(x)$
. This definition of rowmotion extends the rowmotion operators on distributive, semidistributive and trim lattices considered recently by several authors [Reference Thomas and Williams50, Reference Thomas and Williams49, Reference Barnard5, Reference Stanley45].
Our goal in this section is to show that pop-stack sorting, dual pop-stack sorting and rowmotion are closely related. While discussing the connections among these operators, we will be led to questions and results that are new even for distributive lattices.
Theorem 9.1. Let L be a semidistrim lattice. For
$x\in L$
, we have
$$ \begin{align*}\mathsf{Row}_L(x) = \bigwedge\kappa_L(\mathcal{D}_L(x)) &\text{ and } \mathsf{Row}_L^{-1}(x) = \bigvee \mathcal{U}_L(x); \\ \mathsf{Pop}^\downarrow_L(x) = x \wedge \bigwedge\kappa_L(\mathcal{D}_L(x)) &\text{ and } \mathsf{Pop}^\uparrow_L(x) = x \vee \bigvee\mathcal{U}_L(x).\end{align*} $$
In particular,
$$\begin{align*}\mathsf{Pop}^\downarrow_L(x) = x \wedge \mathsf{Row}_L(x) \text{ and } \mathsf{Pop}^\uparrow_L(x) = x \vee \mathsf{Row}_L^{-1}(x).\end{align*}$$
Proof. The statements about rowmotion follow from Theorem 5.6. For the statements about pop-stack sorting and dual pop-stack sorting, we compute
$$\begin{align*}\mathsf{Pop}^\downarrow_L(x)=x\wedge\bigwedge\{y\in L:y\lessdot x\}=x\wedge\bigwedge_{y\lessdot x}(x\wedge \kappa_L(j_{xy}))=x\wedge\bigwedge\kappa_L(\mathcal{D}_L(x))\end{align*}$$
and
$$\begin{align*}\mathsf{Pop}^\uparrow_L(x)=x\vee\bigvee\{y\in L:x\lessdot y\}=x\vee\bigvee_{x\lessdot y}(x\vee j_{xy})=x\vee\bigvee\mathcal{U}_L(x). \\[-46pt]\end{align*}$$
The identity
$\mathsf {Pop}^\downarrow _L(x)=x\wedge \mathsf {Row}_L(x)$
in the preceding theorem gives our first glance at the connection between pop-stack sorting and rowmotion. However, there might be several elements z such that
$\mathsf {Pop}^\downarrow _L(x)=x\wedge z$
, so we would like to know that there is something special about
$\mathsf {Row}_L(x)$
. We will see that
$\mathsf {Row}_L(x)$
is actually a maximal element of the set of all z satisfying
$\mathsf {Pop}^\downarrow _L(x)=x\wedge z$
. First, we need the following lemma. Recall from Theorem 7.8 that intervals in semidistrim lattices are semidistrim.
Lemma 9.2. Let L be a semidistrim lattice. Consider
$v\in L$
and let
$L_v=[\hat {0},v]$
. For every
$x\in L_v$
, we have
$\mathsf {Row}_{L_v}(x)=v\wedge \mathsf {Row}_L(x)$
.
Proof. We know by Lemma 7.4 that
$\kappa _{L_v}(j)=\kappa _L(j)\wedge v$
for all
$j\in \mathcal {J}_{L_v}$
. Now consider
$x\in L_v$
. We have
$\mathcal {D}_{L_v}(x)=\mathcal {D}_L(x)$
by Theorem 7.10. Using Theorem 9.1, we find that
$$\begin{align*}\mathsf{Row}_{L_v}(x)=\bigwedge\kappa_{L_v}(\mathcal{D}_L(x))=\bigwedge_{j\in\mathcal{D}_L(x)}(\kappa_L(j)\wedge v)=v\wedge\bigwedge_{j\in\mathcal{D}_L(x)}\kappa_L(j)=v\wedge\mathsf{Row}_L(x).\\[-36pt] \end{align*}$$
Our next theorem tightens the relationship between pop-stack sorting and rowmotion beyond Theorem 9.1; it is new and nontrivial even for semidistributive and trim lattices.
Theorem 9.3. Let L be a semidistrim lattice. If
$x\in L$
, then
$\mathsf {Row}_L(x)$
is a maximal element of the set
$\{z\in L:\mathsf {Pop}^\downarrow _L(x)= x\wedge z\}$
, and
$\mathsf {Row}_L^{-1}(x)$
is a minimal element of the set
$\{z\in L:\mathsf {Pop}^\uparrow _L(x)= x\vee z\}$
.
Proof. We prove that
$\mathsf {Row}_L(x)\in \max \{z\in L:\mathsf {Pop}^\downarrow _L(x)= x\wedge z\}$
; the second statement follows from this one by taking duals. Let
$(j_0,m_0)$
be a dismantling pair for L and let
$L_0=[\hat {0},m_0]$
and
$L^0=[j_0,\hat {1}]$
. We consider three cases.
Case 1. Assume
$x\in L_0$
. Note that
$\mathsf {Pop}^\downarrow _L(x)=\mathsf {Pop}^\downarrow _{L_0}(x)$
. It follows by induction on the size of the lattice that
$\mathsf {Row}_{L_0}(x)\in \max \{z\in L_0:\mathsf {Pop}^\downarrow _L(x)=x\wedge z\}$
. Suppose by way of contradiction that there exists
$w\in L$
satisfying
$w>\mathsf {Row}_L(x)$
and
$\mathsf {Pop}^\downarrow _L(x)=x\wedge w$
. Let
$y\in L$
be such that
$\mathsf {Row}_L(x)\lessdot y\leq w$
. Then
$$\begin{align*}\mathsf{Pop}^\downarrow_L(x)=x\wedge\mathsf{Row}_L(x)\leq x\wedge y\leq x\wedge w=\mathsf{Pop}^\downarrow_L(x),\end{align*}$$
so
$\mathsf {Pop}^\downarrow _L(x)=x\wedge y$
. We have
$x\wedge (y\wedge m_0)=(x\wedge m_0)\wedge y=x\wedge y=\mathsf {Pop}^\downarrow _L(x)$
. Applying Lemma 9.2 with
$v=m_0$
, we find that
$\mathsf {Row}_{L_0}(x)=\mathsf {Row}_L(x)\wedge m_0\leq y\wedge m_0$
. We have seen that
$\mathsf {Row}_{L_0}(x)$
is maximal in the set
$\{z\in L_0:\mathsf {Pop}^\downarrow _L(x)=x\wedge z\}$
and that
$y\wedge m_0$
is in this set, so
$y\wedge m_0=\mathsf {Row}_{L_0}(x)$
. Let j be the join-irreducible element of L that labels the cover relation
$\mathsf {Row}_L(x)\lessdot y$
. Then
$j\leq y$
, and
$j\not \leq \mathsf {Row}_L(x)$
. Now
$j\in \mathcal {U}_L(\mathsf {Row}_L(x))=\mathcal {D}_L(x)$
, so
$j\leq x\leq m_0$
. This shows that
$j\leq y\wedge m_0=\mathsf {Row}_{L_0}(x)=\mathsf {Row}_L(x)\wedge m_0\leq \mathsf {Row}_L(x)$
, which is our desired contradiction.
Case 2. Now assume
$x\in L^0$
and
$\mathsf {Row}_L(x)\in L^0$
. For each
$j\in \mathcal {D}_L(x)=\mathcal {U}_L(\mathsf {Row}_L(x))$
, we have
$\kappa _L(j)\geq \mathsf {Row}_L(x)\geq j_0$
. In particular,
$j_0\not \in \mathcal {D}_L(x)$
because
$\kappa _L(j_0)\not \geq j_0$
. Theorem 5.5 tells us that the map
$\alpha $
given by
$\alpha (j)=j_0\vee j$
gives a bijection from
$\mathcal {D}_L(x)$
to
$\mathcal {D}_{L^0}(x)$
. Furthermore, Theorem 4.1 ensures that
$\kappa _{L^0}(\alpha (j))=\kappa _L(j)$
for all
$j\in \mathcal {D}_L(x)$
. Hence, by Theorem 9.1,
$$\begin{align*}\mathsf{Row}_{L_0}(x)=\bigwedge\kappa_{L^0}(\mathcal{D}_{L^0}(x))=\bigwedge\kappa_{L^0}(\alpha(\mathcal{D}_L(x)))=\bigwedge\kappa_L(\mathcal{D}_L(x))=\mathsf{Row}_L(x).\end{align*}$$
Also, note that
$\mathsf {Pop}^\downarrow _L(x)=x\wedge \mathsf {Row}_L(x)\in L^0$
. This means that all of the elements covered by x in L are in
$L^0$
, so
$\mathsf {Pop}^\downarrow _{L^0}(x)=\mathsf {Pop}^\downarrow _L(x)$
. Consequently,
$\{z\in L:\mathsf {Pop}^\downarrow _L(x)=x\wedge z\}=\{z\in L^0:\mathsf {Pop}^\downarrow _{L^0}(x)=x\wedge z\}$
. We know by induction that
$\mathsf {Row}_{L^0}(x)$
is a maximal element of
$\{z\in L^0:\mathsf {Pop}^\downarrow _{L^0}(x)=x\wedge z\}$
. We have seen that
$\mathsf {Row}_{L^0}(x)=\mathsf {Row}_L(x)$
, so
$\mathsf {Row}_L(x)$
is a maximal element of
$\{z\in L:\mathsf {Pop}^\downarrow _L(x)=x\wedge z\}$
.
Case 3. Finally, assume
$x\in L^0$
and
$\mathsf {Row}_L(x)\in L_0$
. Then
$\mathsf {Pop}^\downarrow _L(x)=x\wedge \mathsf {Row}_L(x)\in L_0$
, so there must be an element
$w\in L_0$
that is covered by x. Theorem 5.4 tells us that this element w is unique and that the label of the cover relation
$w\lessdot x$
is
$j_0$
. Because L is semidistrim, the set
$\mathcal {D}_L(x)$
is an independent set in the Galois graph
$G_L$
. Therefore,
$\mathcal {D}_L(x)\setminus \{j_0\}$
is also an independent set in
$G_L$
. Theorem 6.4 guarantees that there exists a unique
$x'\in L$
such that
$\mathcal {D}_L(x')=\mathcal {D}_L(x)\setminus \{j_0\}$
. Then
$x'\neq x$
, and Theorem 5.6 implies that
$x=x'\vee j_0$
. Hence,
$x'\in L_0$
. Appealing to Case 1, we find that
$\mathsf {Row}_{L_0}(x')\in \max \{z\in L_0:\mathsf {Pop}^\downarrow _{L_0}(x')=x'\wedge z\}$
. Suppose by way of contradiction that
$\mathsf {Row}_L(x)\not \in \max \{z\in L:\mathsf {Pop}^\downarrow _L(x)=x\wedge z\}$
. Then there exists
$y\in L$
satisfying
$\mathsf {Row}_L(x)\lessdot y$
and
$\mathsf {Pop}^\downarrow _L(x)=x\wedge y$
. We will prove that
$\mathsf {Row}_{L_0}(x')\lessdot y$
and
$\mathsf {Pop}^\downarrow _L(x')=x'\wedge y$
, which will contradict the fact that
$\mathsf {Row}_{L_0}(x')\in \max \{z\in L_0:\mathsf {Pop}^\downarrow _{L_0}(x')=x'\wedge z\}$
.
Since
$x'\in L_0$
, we can apply Lemma 9.2 with
$v=m_0$
to find that
$\mathsf {Row}_{L_0}(x')=\mathsf {Row}_L(x')\wedge m_0$
. Appealing to Theorem 9.1 yields
$$\begin{align*}\mathsf{Row}_{L_0}(x')=m_0\wedge \mathsf{Row}_L(x')=m_0\wedge\bigwedge\kappa_L(\mathcal{D}_L(x'))\end{align*}$$
$$\begin{align*}=\kappa_L(j_0)\wedge\bigwedge\kappa_L(\mathcal{D}_L(x)\setminus\{j_0\})=\bigwedge\kappa_L(\mathcal{D}_L(x))=\mathsf{Row}_L(x).\end{align*}$$
It follows that
$\mathsf {Row}_{L_0}(x')\lessdot y$
. Finally, since
$x'<x$
, we can use Theorem 9.1 again to find that
$$\begin{align*}x'\wedge y=x'\wedge x\wedge y=x'\wedge\mathsf{Pop}^\downarrow_L(x)=x'\wedge x\wedge\bigwedge\kappa_L(\mathcal{D}_L(x))=x'\wedge\bigwedge\kappa_L(\mathcal{D}_L(x))\end{align*}$$
$$\begin{align*}=x'\wedge\kappa_L(j_0)\wedge\bigwedge\kappa_L(\mathcal{D}_L(x'))=(x'\wedge m_0)\wedge\bigwedge\kappa_L(\mathcal{D}_L(x'))=x'\wedge\bigwedge\kappa_L(\mathcal{D}_L(x'))\end{align*}$$
$$\begin{align*}=\mathsf{Pop}^\downarrow_L(x').\\[-36pt] \end{align*}$$
If L is a meet-semidistributive lattice and
$a,b\in L$
are such that
$a\leq b$
, then the set
$\{z\in L:a=b\wedge z\}$
has a unique maximal element. Therefore, if L is both meet-semidistributive and semidistrim, then Theorem 9.3 tells us that for every
$x \in L$
,
$\mathsf {Row}_L(x)$
is the unique maximal element of
$\{z \in L: \mathsf {Pop}^\downarrow _L(x)=x\wedge z\}$
. This is interesting because it provides a natural way to extend the definition of rowmotion to arbitrary meet-semidistributive lattices that might not be semidistrim. More precisely, if L is a meet-semidistributive lattice, then we define rowmotion to be the operator
$\mathsf {Row}_L\colon L\to L$
such that for every
$x\in L$
, the element
$\mathsf {Row}_L(x)$
is the unique maximal element of
$\{z \in L: \mathsf {Pop}^\downarrow _L(x)=x\wedge z\}$
. Let us remark that this rowmotion operator is not necessarily bijective in general (see Figure 9). In fact, we have the following proposition.
Figure 9
Left: A meet-semidistributive lattice L that is not semidistrim. Right: The action of rowmotion, defined by the condition
$\max \{z\in L : \mathsf {Pop}^\downarrow _L(x)=x\wedge z\}=\{\mathsf {Row}_L(x)\}$
.
Proposition 9.4. A lattice L is semidistributive if and only if it is meet- semidistributive and the rowmotion operator
$\mathsf {Row}_L\colon L\to L$
is bijective.
Proof. We know already that rowmotion on a semidistributive lattice is bijective, so we only need to prove one direction of the proposition. Suppose L is a meet-semidistributive lattice such that
$\mathsf {Row}_L$
is bijective. We want to show that L is join-semidistributive. By [Reference Freese, Ježek and Nation23, Theorem 2.56], it suffices to show that
$|\mathcal {J}_L(m)|=1$
for every
$m\in \mathcal M_L$
. Suppose
$m\in \mathcal {M}_L$
and
$j\in \mathcal {J}_L(m)$
. Then
$m^*=m\vee j\neq m\vee j_*$
. This forces us to have
$m\geq j_*$
and
$m\not \geq j$
, so
$m\wedge j=j_*$
. Furthermore,
$m^*\wedge j=j\neq j_*$
. It follows that
$m\in \mathcal {M}_L(j)=\max \{z\in L:\mathsf {Pop}^\downarrow _L(j)=j\wedge z\}$
. Hence,
$m=\mathsf {Row}_L(j)$
. This proves that the only element of
$\mathcal {J}_L(m)$
is
$\mathsf {Row}^{-1}(m)$
.
Theorem 9.4 implies that a lattice is semidistributive if and only if it is meet-semidistributive and semidistrim.
Let us now turn back to semidistrim lattices. The next proposition will be crucial for establishing further connections among pop-stack sorting, dual pop-stack sorting and rowmotion. Although the proof of this proposition is quite short, let us stress that this is only because we already did most of the heavy lifting in Section 7.2 when we proved that the class of semidistrim lattices is closed under taking intervals.
Proposition 9.5. If L is a semidistrim lattice and
$x \in L$
, then
$$\begin{align*}\mathcal{D}_L(x) \subseteq \mathcal{U}_L(\mathsf{Pop}^\downarrow_L(x))\quad\text{and}\quad\mathcal{U}_L(x) \subseteq \mathcal{D}_L(\mathsf{Pop}^\uparrow_L(x)).\end{align*}$$
Proof. The second containment follows from the first by considering the dual lattice, so we will only prove the first containment. The proof is by induction on
$|L|$
. Let
$u=\mathsf {Pop}^\downarrow _L(x)$
. Let
$\alpha _{u,x}\colon J_L(x)\cap M_L(u)\to \mathcal {J}_{[u,x]}$
be the bijection from Theorem 7.9. Since every element covered by x is in
$[u,x]$
, it follows from Theorem 7.10 that
$\mathcal {D}_{[u,x]}(x)=\alpha _{u,x}(\mathcal {D}_L(x))$
and that
$\mathcal {U}_{[u,x]}(x)\subseteq \alpha _{u,x}(\mathcal {U}_L(u))$
. The interval
$[u,x]$
is semidistrim by Theorem 7.8. If
$[u,x]$
is a proper interval of L, then we can use induction to see that
$\mathcal {D}_{[u,x]}(x)\subseteq \mathcal {U}_{[u,x]}(u)$
. In this case, we have
$\mathcal {D}_L(x)=\alpha _{u,x}^{-1}(\mathcal {D}_{[u,x]}(x))\subseteq \alpha _{u,x}^{-1}(\mathcal {U}_{[u,x]}(u))\subseteq \mathcal {U}_L(u)$
, as desired. Now suppose
$[u,x]=L$
. This means that
$x=\hat 1$
and
$u=\mathsf {Pop}^\downarrow _L(\hat 1)=\hat 0$
. Then
$\mathsf {Row}_L(\hat {1}) = \mathsf {Row}_L(\hat {1}) \wedge \hat {1} = \mathsf {Pop}^\downarrow _L(\hat {1})$
, so
$\mathcal {D}_L(\hat {1}) =\mathcal {U}_L(\mathsf {Row}_L(\hat 1))= \mathcal {U}_L(\mathsf {Pop}^\downarrow _L(\hat {1}))$
by the definition of rowmotion.
9.2 Popping pairs
We are now in a position to discuss deeper connections among
$\mathsf {Row}_L$
,
$\mathsf {Pop}^\downarrow _L$
and
$\mathsf {Pop}^\uparrow _L$
. Let us begin with a fairly innocent question about rowmotion on a semidistrim lattice L. How many times does rowmotion on L ‘go down’? More precisely, how many elements
$x\in L$
have the property that
$\mathsf {Row}_L(x)\leq x$
? This question appears to be new even when L is distributive. We will see that the answer is intimately related to
$\mathsf {Pop}^\downarrow _L$
and
$\mathsf {Pop}^\uparrow _L$
, as well as independent dominating sets in the Galois graph
$G_L$
. Before giving more details, let us consider a natural process where we alternately apply
$\mathsf {Pop}^\downarrow _L$
and
$\mathsf {Pop}^\uparrow _L$
.
Begin with some element
$z\in L$
. Let
$x_1=\mathsf {Pop}^\downarrow _L(z)$
,
$y_1=\mathsf {Pop}^\uparrow _L(x_1)$
,
$x_2=\mathsf {Pop}^\downarrow _L(y_1)$
,
$y_2=\mathsf {Pop}^\uparrow _L(x_2)$
and so on. In general,
$y_i=\mathsf {Pop}^\uparrow _L(x_i)$
, and
$x_{i+1}=\mathsf {Pop}^\downarrow _L(y_i)$
. It follows from Theorem 9.5 that
$\mathcal {D}_L(z)\subseteq \mathcal {U}_L(x_1)\subseteq \mathcal {D}_L(y_1)\subseteq \mathcal {U}_L(x_2)\subseteq \mathcal {D}_L(y_2)\subseteq \cdots $
. Appealing to Theorem 5.6, we find that we have a chain
$$ \begin{align} \cdots\leq x_2\leq x_1\leq z\leq y_1\leq y_2\leq\cdots. \end{align} $$
This chain is obviously finite because L is finite. Therefore, there exists a positive integer k such that
$\mathsf {Pop}^\uparrow _L(x_k)=y_k$
and
$\mathsf {Pop}^\downarrow _L(y_k)=x_k$
. This motivates the following definition.
Definition 9.6. Let L be a semidistrim lattice and let
$x,y\in L$
. We say that
$(x,y)$
is a popping pair if
$\mathsf {Pop}^\uparrow _L(x)=y$
and
$\mathsf {Pop}^\downarrow _L(y)=x$
.
The next lemma shows how popping pairs relate to our question about rowmotion going down.
Lemma 9.7. Let L be a semidistrim lattice and let
$x,y\in L$
. Then
$(x,y)$
is a popping pair if and only if
$x \leq y$
and
$\mathcal {U}_L(x)=\mathcal {D}_L(y)$
, and this occurs if and only if
$x\leq y$
and
$\mathsf {Row}_L(y)=x$
.
Proof. It is immediate from the definition of rowmotion that
$\mathcal {U}_L(x)=\mathcal {D}_L(y)$
if and only if
$\mathsf {Row}_L(y)=x$
. If
$(x,y)$
is a popping pair, then certainly
$x\leq y$
, and we have
$\mathcal {U}_L(x)\subseteq \mathcal {D}_L(\mathsf {Pop}^\uparrow _L(x))=\mathcal {D}_L(y)\subseteq \mathcal {U}_L(\mathsf {Pop}^\downarrow _L(y))=\mathcal {U}_L(x)$
by Theorem 9.5. Hence,
$\mathcal {U}_L(x)=\mathcal {D}_L(y)$
.
Now suppose
$x\leq y$
and
$\mathcal {U}_L(x)=\mathcal {D}_L(y)$
. Then
$y=x\vee y=x\vee \bigvee \mathcal {D}_L(y)=x\vee \bigvee \mathcal {U}_L(x)=\mathsf {Pop}^\uparrow _L(x)$
, where we have used Theorem 5.6 and Theorem 9.1. Similarly,
$x=y\wedge x=y\wedge \bigwedge \kappa _L(\mathcal {U}_L(x))=y\wedge \bigwedge \kappa _L(\mathcal {D}_L(y))=\mathsf {Pop}^\downarrow _L(y)$
.
In general, when one is faced with a set X and a noninvertible operator
$f\colon X\to X$
, it is natural to ask for a description or enumeration of the image of f. For example, the structural and enumerative properties of the image of the classical pop-stack sorting map on
$S_n$
were studied in [Reference Asinowski, Banderier, Billey, Hackl and Linusson3, Reference Claesson, Gumundsson and Pantone13]. The next proposition connects the images of
$\mathsf {Pop}^\downarrow _L$
and
$\mathsf {Pop}^\uparrow _L$
with popping pairs.
Proposition 9.8. Let L be a semidistrim lattice and let
$z\in L$
. Then z is in the image of
$\mathsf {Pop}^\downarrow _L$
if and only if there exists
$y\in L$
such that
$(z,y)$
is a popping pair. Similarly, z is in the image of
$\mathsf {Pop}^\uparrow _L$
if and only if there exists
$x\in L$
such that
$(x,z)$
is a popping pair.
Proof. We prove only the first statement since the second statement is dual to it. Certainly if there exists
$y\in L$
such that
$(z,y)$
is a popping pair, then
$z=\mathsf {Pop}^\downarrow _L(y)$
is in the image of
$\mathsf {Pop}^\downarrow _L$
.
To prove the converse, suppose z is in the image of
$\mathsf {Pop}^\downarrow _L$
, say
$z=\mathsf {Pop}^\downarrow _L(x)$
. Let
$y=\mathsf {Row}_L^{-1}(z)$
. Then
$y=\bigvee \mathcal {U}_L(z)$
by Theorem 9.1. We know from Theorem 5.6 that
$x=\bigvee \mathcal {D}_L(x)$
. Then Theorem 9.5 tells us that
$\mathcal {D}_L(x)\subseteq \mathcal {U}_L(z)$
, so
$z\leq x=\bigvee \mathcal {D}_L(x)\leq y$
. This shows that
$z\leq y$
and
$z=\mathsf {Row}_L(y)$
, so we deduce from Lemma 9.7 that
$(z,y)$
is a popping pair.
Remark 9.9. Theorem 9.8 implies that when we constructed the chain
$\cdots \leq x_2\leq x_1\leq z\leq y_1\leq y_2\leq \cdots $
in (9.1), the process actually stabilized after at most two steps. In other words,
$$\begin{align*}x_1=x_2=x_3=\cdots\quad\text{and}\quad y_1=y_2=y_3=\cdots. \end{align*}$$
Corollary 9.10. If L is a semidistrim lattice, then
$$\begin{align*}|\{x\in L:\mathsf{Row}_L(x)\leq x\}|=|\mathsf{Pop}^\downarrow_L(L)|=|\mathsf{Pop}^\uparrow_L(L)|. \end{align*}$$
Proof. It follows from Lemma 9.7 and Theorem 9.8 that each of the three quantities involved in the statement of the corollary is equal to the number of popping pairs of L.
Remark 9.11. The equality
$|\mathsf {Pop}^\downarrow _L(L)|=|\mathsf {Pop}^\uparrow _L(L)|$
, which holds when L is semidistrim, is interesting in its own right and is not a simple consequence of the definitions of
$\mathsf {Pop}^\downarrow _L$
and
$\mathsf {Pop}^\uparrow _L$
. Indeed, this equality fails for many lattices. Figure 10 shows a lattice L such that
$|\mathsf {Pop}^\downarrow _L(L)|=2$
and
$|\mathsf {Pop}^\uparrow _L(L)|=1$
.
Figure 10 A non-semidistrim lattice L with
$2=|\mathsf {Pop}^\downarrow _L(L)|\neq |\mathsf {Pop}^\uparrow _L(L)|=1$
.
We now want to relate the quantities appearing in Theorem 9.10 with a notion from graph theory. A set I of vertices in an undirected graph G is called dominating if every vertex of G is either in I or is adjacent to a vertex in I. An independent dominating set of G is an independent set of G that is dominating. We write
$\mathrm {Ind}^{\mathrm {dom}}(G)$
for the collection of independent dominating sets of G. See [Reference Goddard and Henning26] for a survey of independent dominating sets. We are going to show that each of the quantities in Theorem 9.10 is equal to the number of independent dominating sets in the undirected version of the Galois graph
$G_L$
. First, we need a lemma.
Lemma 9.12. Let L be semidistrim lattice and let
$x \in L$
. If
$j \in \mathcal {U}_L(\mathsf {Pop}^\downarrow _L(x)) \setminus \mathcal {D}_L(x)$
, then
$j \leq \mathsf {Row}_L(x)$
.
Proof. Fix
$j\in \mathcal {U}_L(\mathsf {Pop}^\downarrow _L(x)) \setminus \mathcal {D}_L(x)$
. Because L is semidistrim,
$\mathcal {U}_L(\mathsf {Pop}^\downarrow _L(x))$
is an independent set in
$G_L$
. This implies that
$j \leq \kappa _L(j')$
for every
$j' \in \mathcal {U}_L(\mathsf {Pop}^\downarrow _L(x))$
with
$j'\neq j$
. Since
$\mathcal {D}_L(x) \subseteq \mathcal {U}_L(\mathsf {Pop}^\downarrow _L(x))$
, this implies that
$j \leq \kappa _L(j')$
for all
$j'\in D_L(x)$
. Therefore,
$$\begin{align*}j \leq \bigwedge\kappa_L(\mathcal{D}_L(x)) = \bigwedge\kappa_L(\mathcal{U}_L(\mathsf{Row}_L(x))) = \mathsf{Row}_L(x),\end{align*}$$
where the last equality follows from Theorem 5.6.
Given a directed simple graph G, let us write
$\widetilde G$
for the undirected simple graph obtained by forgetting the orientations of the edges in G.
Theorem 9.13. Let L be a semidistrim lattice and let
$x \in L$
. Then
$\mathsf {Row}_L(x) \leq x$
if and only if
$\mathcal {D}_L(x)$
is an independent dominating set of
$\widetilde {G}_L$
. Therefore,
$$\begin{align*}|\{ x \in L : \mathsf{Row}_L(x) \leq x\}|=|\mathsf{Pop}^\downarrow_L(L)|=|\mathsf{Pop}^\uparrow_L(L)|=|\mathrm{Ind}^{\mathrm{dom}}(\widetilde{G}_L)|.\end{align*}$$
Proof. The chain of equalities follows from the first statement and from Theorem 9.10, so we will focus on proving the first statement. Fix
$x\in L$
. Since L is semidistrim,
$\mathcal {D}_L(x)$
is an independent set of
$\widetilde {G}_L$
. Therefore, we just need to show that
$\mathcal {D}_L(x)$
is dominating if and only if
$\mathsf {Row}_L(x)\leq x$
.
Suppose
$j\in \mathcal {J}_L\setminus \mathcal {D}_L(x)$
. Saying that j is not adjacent to any element of
$\mathcal {D}_L(x)$
is equivalent to saying that
$j \leq \kappa _L(j')$
and
$j' \leq \kappa _L(j)$
for every
$j' \in \mathcal {D}_L(x)$
. By Theorem 5.6 and Theorem 9.1, this is equivalent to saying
$j \leq \mathsf {Row}_L(x)$
and
$\kappa _L(j) \geq x$
.
Suppose
$\mathsf {Row}_L(x) \leq x$
. If
$j\in \mathcal {J}_L\setminus \mathcal {D}_L(x)$
is not adjacent to any element of
$\mathcal {D}_L(x)$
, then
$j \leq \mathsf {Row}_L(x) \leq x \leq \kappa _L(j)$
, which is impossible. Hence,
$\mathcal {D}_L(x)$
is an independent dominating set.
Now suppose
$\mathsf {Row}_L(x) \not \leq x$
. We want to show that
$\mathcal {D}_L(x)$
is not a dominating set, which is equivalent to showing that there is a join-irreducible element
$j\in \mathcal {J}_L\setminus \mathcal {D}_L(x)$
with
$j \leq \mathsf {Row}_L(x)$
and
$\kappa _L(j) \geq x$
. Let
$v=\mathsf {Pop}^\uparrow _L(\mathsf {Pop}^\downarrow _L(x))$
. Since
$\mathsf {Pop}^\downarrow _L(x)$
is in the image of
$\mathsf {Pop}^\downarrow _L$
, it follows from Theorem 9.8 that
$(\mathsf {Pop}^\downarrow _L(x),v)$
is a popping pair. Theorem 9.5 tells us that
$\mathcal {D}_L(x)\subseteq \mathcal {U}_L(\mathsf {Pop}^\downarrow _L(x))\subseteq \mathcal {D}_L(v)$
, so
$x\leq v$
by Theorem 5.6. According to Lemma 9.7, we have
$\mathcal {U}_L(\mathsf {Pop}^\downarrow _L(x))=\mathcal {D}_L(v)$
and
$\mathsf {Row}_L(v)=\mathsf {Pop}^\downarrow _L(x)\leq x$
. Since we have assumed
$\mathsf {Row}_L(x)\not \leq x$
, this forces
$x\neq v$
. Consequently, there exists an element y such that
$x \leq y \lessdot v$
. Let
$j=j_{yv}$
be the label of the cover relation
$y \lessdot v$
. Then
$j \in \mathcal {D}_L(v)= \mathcal {U}_L(\mathsf {Pop}^\downarrow _L(x))$
. Note that
$\kappa _L(j) \geq y \geq x$
. This implies that
$j \not \leq x$
. It follows that
$j \not \in \mathcal {D}_L(x)$
, so we can use Lemma 9.12 to see that
$j \leq \mathsf {Row}_L(x)$
.
Theorem 9.13 further motivates us to ask about the sizes of the images of pop-stack sorting operators on specific interesting semidistrim lattices. This analysis was carried out in [Reference Asinowski, Banderier, Billey, Hackl and Linusson3, Reference Claesson, Gumundsson and Pantone13] when L is the weak order on
$S_n$
and in [43] when L is the lattice of order ideals of a type A root poset. In Section 11, we list some conjectures about these images for other specific semidistrim lattices.
Remark 9.14. There is very little known about the behavior of rowmotion on the weak order of
$S_n$
; the only nontrivial result we know is a certain instance of the homomesy phenomenon due to Hopkins [Reference Hopkins28, Corollary 6.16]. Combining Theorem 9.13 with the results of [Reference Asinowski, Banderier, Billey, Hackl and Linusson3, Reference Claesson, Gumundsson and Pantone13] yields some information by telling us about the number of times rowmotion goes down.
10 Shards
Let
$\mathcal {H}$
be a real simplicial hyperplane arrangement with fixed base region B; its poset of regions is a semidistributive lattice. In [Reference Reading40], Reading defined a geometric analogue of join-irreducible elements called shards; these are certain connected components of hyperplanes, and there is a natural bijection between shards and join-irreducible elements of the poset of regions.
The construction proceeds as follows. A hyperplane H in a subarrangement of
$\mathcal {H}$
is called basic if H bounds the region of the subarrangement containing B. Given
$H,H' \in \mathcal {H}$
, form the rank-two subarrangement
$\mathcal {H}(H,H')$
consisting of all hyperplanes containing the intersection
$H \cap H'$
and remove from each nonbasic hyperplane of
$\mathcal {H}(H,H')$
the points contained in the basic hyperplanes. The closures of the resulting connected components are shards, and for a region R, we write
$\mathcal {D}(R)$
for the set of shards that bound R and separate it from B. Regions turn out to be in bijection with intersections of shards – a region R corresponds to the intersection
$\bigcap \mathcal {D}(R)$
. Because the join-irreducible elements are those regions with
$|\mathcal {D}(R)|=1$
, join-irreducible elements are in bijection with shards themselves. We refer to [Reference Reading41] for further details.
We now indicate an analogy that carries over to semidistrim lattices. Recall that atoms of a semidistributive lattice are join-prime, so that basic hyperplanes are necessarily join-prime elements. Having fixed a region R, we observe that the subarrangement of
$\mathcal {H}$
whose basic hyperplanes correspond to the shards in
$\mathcal {D}(R)$
consists of those hyperplanes separating
$\mathsf {Pop}^\downarrow (R)$
from R, since
$\mathsf {Pop}^\downarrow (R)$
corresponds to the region of the subarrangement containing the base region B. This motivates the following definition.
Definition 10.1. For L a finite lattice, define the face determined by an element
$b \in L$
to be the interval
$\mathrm {Face}(b)=[\mathsf {Pop}^\downarrow _L(b),b]$
.
The following proposition strengthens the analogy between join-prime elements of semidistrim lattices and basic hyperplanes.
Proposition 10.2. Let L be a semidistrim lattice. Let
$j\in \mathcal {J}_L$
be join-prime and let
$b\in L$
. If j appears as a label of a cover relation in
$\mathrm {Face}(b)$
, then it appears in
$\mathcal {D}_L(b)$
and
$\mathcal {U}_L(\mathsf {Pop}^\downarrow _L(b))$
.
Proof. Let m be the meet-prime element such that
$(j,m)$
is a prime pair. Then
$m=\kappa _L(j)$
by Theorem 3.4. Suppose j is the label of a cover relation
$y \lessdot z$
, where
$\mathsf {Pop}^\downarrow _L(b)\leq y\lessdot z\leq b$
. Then
$y \leq m$
, and
$z\geq j$
. This implies that
$b \geq j$
and that
$\mathsf {Pop}^\downarrow _L(b) \leq m$
. Hence,
$j\not \leq \mathsf {Pop}^\downarrow _L(b)$
. Since
$\mathsf {Pop}^\downarrow _L(b)$
is the meet of the elements covered by b, there must be some element w covered by b such that
$j\not \leq w$
. Because
$(j,m)$
is a prime pair, we have
$w\leq m$
. The edge
$w \lessdot b$
has label j, so
$j\in \mathcal {D}_L(b)$
. Finally,
$\mathcal {D}_L(b)\subseteq \mathcal {U}_L(\mathsf {Pop}^\downarrow _L(b))$
by Theorem 9.5.
It would be interesting if the converse to Theorem 10.2 held. If b is an element of a semidistrim lattice L, then the interval
$\mathrm {Face}(b)$
is a semidistrim lattice by Theorem 7.8. It follows that join-prime elements of the lattice
$\mathrm {Face}(b)$
appear as labels in
$\mathcal {D}_L(b)$
and
$\mathcal {U}_L(\mathsf {Pop}^\downarrow _L(b))$
(we are identifying labels of edges in
$\mathrm {Face}(b)$
with the labels of the corresponding edges in L via Theorem 7.10). When L is the poset of regions of a simplicial hyperplane arrangement
$\mathcal H$
, this corresponds to the fact that
$\mathsf {Pop}^\downarrow _L(R)$
is bounded by the basic hyperplanes in the subarrangement of
$\mathcal {H}$
consisting of those hyperplanes containing
$\bigcap \mathcal {D}(R)$
. We address further analogies between semidistrim lattices and shards in Section 11.4.
11 Further Directions
In this section, we collect several open problems that we hope will stimulate further development of the theory of semidistrim lattices.
11.1 Properties of semidistrim lattices
As the reader may have realized, our definition of a semidistrim lattice is somewhat long and cumbersome. Is there a simpler definition?
Birkhoff’s representation theorem characterizes the Galois graphs of finite distributive lattices as the (directed) comparability graphs of finite posets. The recent article [Reference Reading, Speyer and Thomas39] characterizes the Galois graphs of finite semidistributive lattices, while a graph-theoretic description of the Galois graphs of trim lattices was given in [Reference Thomas and Williams50, Theorem 4.11]. It would be interesting and useful to have a characterization of the Galois graphs of semidistrim lattices.
In Section 7, we proved that products and intervals of semidistrim lattices are semidistrim, generalizing the corresponding statements for semidistributive and trim lattices. While sublattices of semidistributive lattices are again semidistributive, the same is not true for sublattices of trim lattices. Figure 11 gives an example showing that sublattices of semidistrim lattices are not necessarily semidistrim. It would be interesting to have other lattice operations that preserve the family of semidistrim lattices. In particular, we have the following question that, if answered affirmatively, would generalize the corresponding statement for trim lattices proven in [Reference Thomas and Williams50, Lemma 3.10].
Figure 11 A sublattice of a semidistrim lattice that is not semidistrim (indicated in red). This also serves as an example of a trim lattice with a non-trim sublattice (compare with [Reference Thomas48, Theorem 3]).
Question 11.1. Is every quotient of a semidistrim lattice necessarily semidistrim?
In Section 9, we showed how the pop-stack sorting operator can be used to define rowmotion on a meet-semidistributive lattice L that need not be semidistrim; namely, for
$x\in L$
, we defined
$\mathsf {Row}_L(x)$
to be the unique maximal element of
$\{z\in L:\mathsf {Pop}^\downarrow _L(x)=x\wedge z\}$
. We saw in Theorem 9.4 that this rowmotion operator is noninvertible whenever L is meet-semidistributive but not semidistributive. Virtually all reasonable questions that one might wish to ask about these operators are open. For example, it would be interesting to describe the periodic points or the image of rowmotion on such a lattice. What can be said about the maximum number of preimages that an element can have under rowmotion? Perhaps there are interesting families of meet-semidistributive lattices where these noninvertible rowmotion operators have desirable properties.
11.2 Enumeration
The image of the classical pop-stack sorting map on
$S_n$
, which coincides with
$\mathsf {Pop}^\downarrow _L$
when L is the right weak order on
$S_n$
, was studied in [Reference Asinowski, Banderier, Billey, Hackl and Linusson3, Reference Claesson, Gumundsson and Pantone13]. Theorem 9.13 motivates the investigation of the image of
$\mathsf {Pop}^\downarrow _L$
for other nice families of semidistrim lattices L. It is also natural to refine the enumeration by considering the generating function
$$\begin{align*}\mathsf{Pop}(L;q) = \sum_{b\in\mathsf{Pop}^\downarrow_L(L)}q^{|\mathcal{U}_L(b)|}=\sum_{b\in\mathsf{Pop}^\uparrow_L(L)}q^{|\mathcal{D}_L(b)|},\end{align*}$$
where the second equality follows from Lemma 9.7 and Theorem 9.8. It follows from Theorem 9.13 that
$\mathsf {Pop}(L;q)$
enumerates the independent dominating sets in
$\widetilde G_L$
according to cardinality. We write
$[q^i]\mathsf {Pop}(L;q)$
for the coefficient of
$q^i$
in
$\mathsf {Pop}(L;q)$
.
When
$L=\mathrm {Weak}(A_{n-1})$
is the right weak order on
$S_n$
,
$\mathsf {Pop}(L;q)$
enumerates permutations in the image of the pop-stack sorting map according to the number of ascending runs, which is one of the primary focuses of the article [Reference Asinowski, Banderier, Billey, Hackl and Linusson3]. For example, Proposition 5 of that article proves that
$$\begin{align*}[q^{n-2}]\mathsf{Pop}(\mathrm{Weak}(A_{n-1});q)=2^n-2n.\end{align*}$$
The article [43] considers a certain filling operator on Dyck paths, which is equivalent to the dual pop-stack sorting operator on the lattice of order ideals of a type A root poset. Therefore, it follows from [43, Proposition 4.3] that the sizes of the images of dual pop-stack sorting operators (equivalently, the images of pop-stack sorting operators) on lattices of order ideals of type A root posets are given by the OEIS sequence A086581:
$$\begin{align*}\mathsf{Pop}(J(\Phi^+_{A_n});1) = \sum_{k=0}^n \frac{1}{k+1}\binom{2k}{k} \binom{n+k}{3k}.\end{align*}$$
In the same spirit as the above results, we make the following conjectures, with accompanying data given in Figures 12 to 14. Write
$\mathrm {Weak}(W)$
for the right weak order on a finite Coxeter group W. Write
$\mathrm {Tamari}(W)$
for a Cambrian lattice corresponding to a Coxeter element obtained by taking the product of simple reflections in some linear orientation of the Dynkin diagram (defined only when W has a Dynkin diagram that is a path). Write
$\mathrm {Camb}_{\mathrm {bi}}(W)$
for a Cambrian lattice arising from a bipartite Coxeter element. Write
$J(\Phi ^+_W)$
for the distributive lattice of order ideals in the positive root poset of type W.
Conjecture 11.2. The following equalities hold:
The parts of Theorem 11.2 concerning the lattices
$\text {Tamari}(A_n)$
,
$\text {Tamari}(B_n)$
,
$\text {Camb}_{\text {bi}}(A_n)$
and
$J(\Phi _{B_n}^+)$
are open even when we specialize
$q=1$
.
Figure 12 Some data for
$\mathsf {Pop}(\mathrm {Weak}(W);q)$
, where
$\mathrm {Weak}(W)$
is the weak order on the finite Coxeter group W (we did not compute the data for
$E_7$
and
$E_8$
). As stated in Theorem 11.2, the coefficient of
$q^{n-1}$
in
$\mathsf {Pop}(\mathrm {Weak}(B_n);q)$
appears to be
$ 3^n - 2n - 1$
.
Figure 13 Some data supporting Theorem 11.2 for
$\mathsf {Pop}(\mathrm {Tamari}(W);q)$
for Cambrian lattices coming from linearly-oriented Coxeter elements of types A and B.
Figure 14 Some data supporting Theorem 11.2 for
$\mathsf {Pop}(\mathrm {Camb}_{\mathrm {bi}}(W);q)$
and
$\mathsf {Pop}(J(\Phi ^+_W);q)$
, where
$\mathrm {Camb}_{\mathrm {bi}}(W)$
is a Cambrian lattice for a bipartite Coxeter element and
$J(\Phi ^+_W)$
is the distributive lattice of order ideals of the positive root poset of type W (nonnesting partitions). For the noncrystallographic types
$I_2(m)$
and
$H_3$
, Armstrong’s root posets are used for the nonnesting partitions [Reference Armstrong2, Figure 5.15].
Remark 11.3. In the time since we released the initial preprint of this article, several parts of Theorem 11.2 have been resolved. The part of the conjecture concerning
$\text {Tamari}(A_n)$
was settled by Hong in [Reference Hong27]. The parts of the conjecture concerning
$\text {Weak}(B_n)$
,
$\text {Tamari}(B_n)$
,
$J(\Phi ^+_{A_n})$
and
$J(\Phi ^+_{B_n})$
were settled by Choi and Sun in [Reference Choi and Sun11].
11.3 Uniquely completely paired lattices
Let L be a lattice. Note that if
$j\in \mathcal {J}_L$
and
$m\in \mathcal {M}_L$
, then we have
$\mathsf {Pop}^\downarrow _L(j)=j_*$
and
$\mathsf {Pop}^\uparrow _L(m)=m^*$
, so the sets
$\mathcal {M}_L(j)$
and
$\mathcal {J}_L(m)$
defined in Section 3.1 satisfy
$\mathcal {M}_L(j)=\max \{z\in L:\mathsf {Pop}^\downarrow _L(j)=j\wedge z\}$
and
$\mathcal {J}_L(m)=\min \{z \in L: \mathsf {Pop}^\uparrow _L(j)=j\vee z\}$
. It is reasonable to extend the notion of uniquely paired in Theorem 3.2 to every element of L as follows.
Definition 11.4. A lattice L is completely uniquely paired if there is a unique bijection
$\lambda : L \to L$
so that
$\lambda (x) \in \max \{z\in L:\mathsf {Pop}^\downarrow _L(x)=x\wedge z\}$
and
$\lambda ^{-1}(x) \in \min \{z \in L: \mathsf {Pop}^\uparrow _L(x)=x\vee z\}$
for every
$x\in L$
.
By Theorem 9.3, if L is both semidistrim and completely uniquely paired, then the bijection
$\lambda $
must be rowmotion – and so it makes sense to use the name rowmotion for the bijection
$\lambda $
in a completely uniquely paired lattice. While completely uniquely paired lattices have some desired properties, they generally lack others common to semidistributive and trim lattices – for example, not all completely uniquely paired lattices have join-prime elements, which are useful tools for working with semidistrim lattices. Figure 15 illustrates a completely uniquely paired lattice that does not have a join-prime or meet-prime element. While not every completely uniquely paired lattice is semidistrim, we expect the converse should hold.
Figure 15 A uniquely completely paired lattice with no join-prime or meet-prime elements. See also Figure 8.
Conjecture 11.5. Every semidistrim lattice is completely uniquely paired.
11.4 Core label orders
In this section, we closely follow the ideas of [Reference Mühle34] in the setting of our semidistrim lattices. For L a semidistrim lattice and
$b\in L$
, write
$$\begin{align*}\mathrm{Shard}_{\mathsf{Pop}}(b)=J_L(b)\cap M_L(\mathsf{Pop}^\downarrow_L(b)), \end{align*}$$
so that
$\mathrm {Shard}_{\mathsf {Pop}}(b)$
is the set of join-irreducibles that label the cover relations in the interval
$\mathrm {Face}(b)$
(by Theorem 7.9 and Theorem 7.10). It is reasonable to think of the set
$\mathrm {Shard}_{\mathsf {Pop}}(b)$
as an extension of the edge labeling to faces, since when
$j \in \mathcal {J}_L$
with the cover
$j_* \lessdot j$
labeled by j itself, we recover
$\mathrm {Shard}(j)=\{j\}$
. Similarly, we define
$$\begin{align*}\mathrm{Shard}_{\mathsf{Row}}(b)=J_L(b)\cap M_L(\mathsf{Row}_L(b)). \end{align*}$$
By Theorem 9.5, we have that
$\mathrm {Shard}_{\mathsf {Row}}(b) \subseteq \mathrm {Shard}_{\mathsf {Pop}}(b)$
.
Question 11.6. For which semidistrim lattices L do we have
$\mathrm {Shard}_{\mathsf {Row}}(b) = \mathrm {Shard}_{\mathsf {Pop}}(b)$
for all
$b \in L$
? Does this hold when L is the lattice of regions of a real simplicial hyperplane arrangement?
Define the pop-core label order to be the partial order
$\preceq _{\mathsf {Pop}}$
on L given by
$x \preceq _{\mathsf {Pop}} y$
if and only if
$\mathrm {Shard}_{\mathsf {Pop}}(x) \subseteq \mathrm {Shard}_{\mathsf {Pop}}(y)$
. This definition extends Mühle’s definition of the core label order [Reference Mühle34], which was formulated as a generalization of Reading’s shard intersection order [Reference Reading40]. Define the row-core label order by
$x \preceq _{\mathsf {Row}} y$
if and only if
$\mathrm {Shard}_{\mathsf {Row}}(x) \subseteq \mathrm {Shard}_{\mathsf {Row}}(y)$
. In general, we do not have that
$\preceq _{\mathsf {Pop}}=\preceq _{\mathsf {Row}}$
– [Reference Mühle34, Figure 7] gives an example for which
$\preceq _{\mathsf {Pop}}$
is not a lattice but
$\preceq _{\mathsf {Row}}$
is a lattice.
It would be interesting to see what properties one can say about the row-core label orders of semidistrim lattices. In particular, we have the following question.
Question 11.7. When is the pop-core or row-core label order on a semidistrim lattice a meet-semilattice?
In order to approach the preceding question, it could be useful to understand graph-theoretically what the sets
$\mathrm {Shard}_{\mathsf {Pop}}(b)$
and/or
$\mathrm {Shard}_{\mathsf {Row}}(b)$
are when we view them as subsets of the vertex set of the Galois graph. For example, when L is distributive, the pop-core label order and the row-core label order are equal to each other, and each is a meet-semilattice because
$$\begin{align*}\{\mathrm{Shard}_{\mathsf{Pop}}(b):b\in L\}=\{\mathrm{Shard}_{\mathsf{Row}}(b):b\in L\}=\mathrm{Ind}(G_L).\end{align*}$$
Remark 11.8. After we released the original preprint of this article, the preprint [Reference Enomoto22] independently defined the pop-core and row-core label orders for semidistributive lattices. See also [Reference Barnard and Hanson6].
Acknowledgements
We thank Henri Mühle for useful correspondence. We thank the anonymous referees for very helpful feedback. This work benefited from computations in Sage [Reference Striker and Williams47] and the combinatorics features developed by the Sage-Combinat community [42].
Competing Interest
The authors have no conflicts of interest to declare.
Financial Support
Colin Defant was supported by the National Science Foundation under Award No. DGE–1656466 and Award No. 2201907, by a Fannie and John Hertz Foundation Fellowship and by a Benjamin Peirce Fellowship at Harvard University. Nathan Williams was partially supported by Simons Foundation Collaboration Grant No. 585380.
Open access
