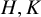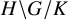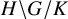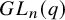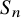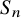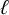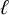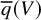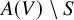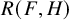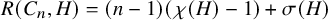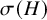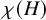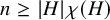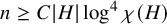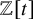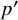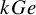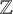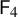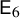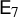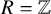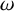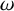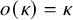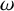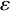Differential Equations
Branch points for (almost-)minimizers of two-phase free boundary problems
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2023, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probability
Double coset Markov chains
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2023, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topology
Equivariant Brill–Noether theory for elliptic operators and superrigidity of J-holomorphic maps
- Part of:
-
- Published online by Cambridge University Press:
- 16 January 2023, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Virasoro constraints for moduli spaces of sheaves on surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 23 January 2023, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Generalized Bockstein maps and Massey products
- Part of:
-
- Published online by Cambridge University Press:
- 23 January 2023, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Noninjectivity of the cycle class map in continuous
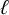 $\ell $
-adic cohomology
$\ell $
-adic cohomology
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2023, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effective characterization of quasi-abelian surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 02 February 2023, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Automorphy lifting with adequate image
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2023, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
Mutation-finite quivers with real weights
- Part of:
-
- Published online by Cambridge University Press:
- 10 February 2023, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ramsey numbers of cycles versus general graphs
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2023, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mathematical Physics
On Duclos–Exner’s conjecture about waveguides in strong uniform magnetic fields
- Part of:
-
- Published online by Cambridge University Press:
- 23 February 2023, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Grassmanniennes affines tordues sur les entiers
- Part of:
-
- Published online by Cambridge University Press:
- 23 February 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structure of blocks with normal defect and abelian
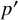 $p'$
inertial quotient
$p'$
inertial quotient
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2023, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Heights on stacks and a generalized Batyrev–Manin–Malle conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 03 March 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
On the derived Lusztig correspondence
-
- Published online by Cambridge University Press:
- 07 March 2023, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Decompositions of moduli spaces of vector bundles and graph potentials
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2023, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differential Equations
Global Asymptotics of the Sixth Painlevé Equation in Okamoto’s Space
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2023, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Albert algebras over
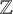 $\mathbb {Z}$
and other rings
$\mathbb {Z}$
and other rings
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2023, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Foundations
On
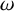 $\omega $
-Strongly Measurable Cardinals
$\omega $
-Strongly Measurable Cardinals
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2023, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computational Mathematics
Approximate and discrete Euclidean vector bundles
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2023, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation