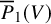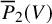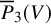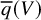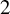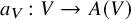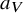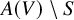1 Introduction
Let V be a smooth complex quasi-projective variety. By Hironaka’s theorem on the resolution of singularities, we can write
![]() $V=X\backslash D$
, where X is a smooth projective variety and D is a reduced divisor on X with simple normal crossings support (in fact, in the case of surfaces, our main interest here, V is automatically quasi-projective since it is smooth).
$V=X\backslash D$
, where X is a smooth projective variety and D is a reduced divisor on X with simple normal crossings support (in fact, in the case of surfaces, our main interest here, V is automatically quasi-projective since it is smooth).
Denoting by
![]() $K_X$
the canonical divisor of X, one defines the following invariants of V:
$K_X$
the canonical divisor of X, one defines the following invariants of V:
-
• for m a positive integer, the m-th log-plurigenus of V is
 $\overline {P}_m(V):=h^0(X,m(K_X+D))$
;
$\overline {P}_m(V):=h^0(X,m(K_X+D))$
; -
• the log-Kodaira dimension of V is
 $\overline {\kappa }(V):=\kappa (X,K_X+D);$
$\overline {\kappa }(V):=\kappa (X,K_X+D);$
-
• the log-irregularity of V is
 $\overline {q}(V):=h^0(X,\Omega ^1_X(\log D))$
.
$\overline {q}(V):=h^0(X,\Omega ^1_X(\log D))$
.
In addition, we say that the irregularity
![]() $q(V)$
of V is the irregularity of X, that is,
$q(V)$
of V is the irregularity of X, that is,
It easy to see that these invariants do not depend on the choice of the compactification X.
Similarly to what happens for projective varieties, to V we can associate a quasi-abelian variety (i.e., an algebraic group which does not contain
![]() $\mathbb {G}_a$
)
$\mathbb {G}_a$
)
![]() $A(V)$
, called the quasi-Albanese variety of V. This comes equipped with a morphism
$A(V)$
, called the quasi-Albanese variety of V. This comes equipped with a morphism
![]() $a_V\colon V\rightarrow A(V)$
which is called the quasi-Albanese morphism. Iitaka in [Reference Iitaka12] characterizes quasi-abelian surfaces as surfaces of log-Kodaira dimension 0 and log-irregularity 2. More precisely, he proves the following.
$a_V\colon V\rightarrow A(V)$
which is called the quasi-Albanese morphism. Iitaka in [Reference Iitaka12] characterizes quasi-abelian surfaces as surfaces of log-Kodaira dimension 0 and log-irregularity 2. More precisely, he proves the following.
Theorem (Iitaka, [Reference Iitaka12]).
Let V be a smooth complex algebraic surface. Then
![]() $\overline {\kappa }(V)=0$
and
$\overline {\kappa }(V)=0$
and
![]() $\overline {q}(V)=2$
if and only if the quasi-Albanese morphism
$\overline {q}(V)=2$
if and only if the quasi-Albanese morphism
![]() $a_V\colon V\rightarrow A(V)$
is birational and there are an open subset
$a_V\colon V\rightarrow A(V)$
is birational and there are an open subset
![]() $V^0\subseteq V$
and finitely many points
$V^0\subseteq V$
and finitely many points
![]() $\{p_1,\ldots p_t\}\subseteq A(V)$
such that the restriction
$\{p_1,\ldots p_t\}\subseteq A(V)$
such that the restriction
![]() $a_{V|_{V^0}}\colon V^0\rightarrow A(V)\backslash \{p_1,\ldots p_t\}$
is proper.
$a_{V|_{V^0}}\colon V^0\rightarrow A(V)\backslash \{p_1,\ldots p_t\}$
is proper.
In this paper, we give a characterization of quasi-abelian surfaces using the three first logarithmic plurigenera instead of the logarithmic Kodaira dimension. Our main result is the following Theorem:
Theorem A. Let V be a smooth complex algebraic surface with
![]() $\overline {q}(V)=2$
. Assume that:
$\overline {q}(V)=2$
. Assume that:
-
(a)
 $\overline {P}_1(V)=\overline {P}_2(V)=1$
and
$\overline {P}_1(V)=\overline {P}_2(V)=1$
and
 $q(V)>0$
, or
$q(V)>0$
, or -
(b)
 $\overline {P}_1(V)=\overline {P}_3(V)=1$
and
$\overline {P}_1(V)=\overline {P}_3(V)=1$
and
 $q(V)=0$
.
$q(V)=0$
.
Then the quasi-Albanese morphism
![]() $a_V\colon V\rightarrow A(V)$
is birational. In addition, there are an open subset
$a_V\colon V\rightarrow A(V)$
is birational. In addition, there are an open subset
![]() $V^0\subseteq V$
and finitely many points
$V^0\subseteq V$
and finitely many points
![]() $\{p_1,\ldots p_t\}\subseteq A(V)$
such that the restriction
$\{p_1,\ldots p_t\}\subseteq A(V)$
such that the restriction
![]() $a_{V|_{V^0}}\colon V^0\rightarrow A(V)\backslash \{p_1,\ldots p_t\}$
is proper.
$a_{V|_{V^0}}\colon V^0\rightarrow A(V)\backslash \{p_1,\ldots p_t\}$
is proper.
Using the language of weakly weak proper birational (WWPB) equivalences introduced by Iitaka in [Reference Iitaka10], Theorem A above can be rephrased in the following manner.
Theorem A*. Let V be a smooth algebraic surface. Then V is WWPB equivalent to a quasi-abelian variety if and only if either
-
(a)
 $\overline q(V)=2$
,
$\overline q(V)=2$
,
 $\overline {P}_1(V)=\overline {P}_2(V)=1$
and
$\overline {P}_1(V)=\overline {P}_2(V)=1$
and
 $q(V)>0$
, or
$q(V)>0$
, or -
(b)
 $\overline q(V)=2$
,
$\overline q(V)=2$
,
 $\overline {P}_1(V)=\overline {P}_3(V)=1$
and
$\overline {P}_1(V)=\overline {P}_3(V)=1$
and
 $q(V)=0$
.
$q(V)=0$
.
As WWPB-maps between normal affine varieties are actually isomorphisms (see [Reference Iitaka10, Corollary on p. 498]), we have:
Corollary B. A smooth complex affine surface V is isomorphic to
![]() $\mathbb {G}_m^2$
if and only if it has
$\mathbb {G}_m^2$
if and only if it has
![]() $\overline {P}_1(V)=\overline {P}_3(V)=1$
and
$\overline {P}_1(V)=\overline {P}_3(V)=1$
and
![]() $\overline {q}(V)=2$
.
$\overline {q}(V)=2$
.
We remark that Kawamata, in his celebrated work [Reference Kawamata14], proved in any dimension a weaker form of Iitaka’s theorem, showing that the quasi-Albanese morphism of an algebraic variety of log-Kodaira dimension 0 and log-irregularity equal to the dimension is birational. In the compact case, effective versions of this result have been given in [Reference Chen and Hacon3] and [Reference Pareschi, Popa and Schnell19]: in [Reference Chen and Hacon3], it is proven that the Albanese map of a projective variety X is surjective and birational iff
![]() $\dim X=q(X)$
and
$\dim X=q(X)$
and
![]() $P_1(X)=P_2(X)=1$
; in [Reference Pareschi, Popa and Schnell19], the analogous statement is proven for compact Kähler manifolds.
$P_1(X)=P_2(X)=1$
; in [Reference Pareschi, Popa and Schnell19], the analogous statement is proven for compact Kähler manifolds.
So we are led to formulate the following conjecture:
Conjecture. Let V a smooth complex quasi-projective variety with
![]() $\overline {q}(V)=\dim V$
, then there exists a positive integer k, independent of the dimension of V such that
$\overline {q}(V)=\dim V$
, then there exists a positive integer k, independent of the dimension of V such that
![]() $\overline {P}_1(V)=\overline {P}_k(V)=1$
implies that the quasi-Albanese morphism of V is birational (and there exist an open set
$\overline {P}_1(V)=\overline {P}_k(V)=1$
implies that the quasi-Albanese morphism of V is birational (and there exist an open set
![]() $V^0\subseteq V$
and a closed set
$V^0\subseteq V$
and a closed set
![]() $W\subseteq A(V)$
of codimension
$W\subseteq A(V)$
of codimension
![]() $>1$
such that
$>1$
such that
![]() $a_{V|_{V^0}}\colon V^0\rightarrow A(V)\backslash W$
is proper).
$a_{V|_{V^0}}\colon V^0\rightarrow A(V)\backslash W$
is proper).
In view of the results recalled above, one might hope that
![]() $k=2$
is the right bound also in the open setting, but in fact our Theorem A is sharp because there is a surface V with
$k=2$
is the right bound also in the open setting, but in fact our Theorem A is sharp because there is a surface V with
![]() $\overline P_1(V)=\overline P_2(V)=1$
,
$\overline P_1(V)=\overline P_2(V)=1$
,
![]() $\overline q(V)=2$
and the quasi-Albanese map not dominant (see Example 4.18).
$\overline q(V)=2$
and the quasi-Albanese map not dominant (see Example 4.18).
Our argument is completely independent of Iitaka’s theorem and its proof. The first step consists in showing that the assumptions on the logarithmic irregularity and on the logarithmic plurigenera imply that the quasi-Albanese map of V is dominant. When
![]() $ q(V)=2$
, one obtains as an immediate consequence of the work of Chen and Hacon [Reference Chen and Hacon3] that the quasi-Albanese map of V is birational. When
$ q(V)=2$
, one obtains as an immediate consequence of the work of Chen and Hacon [Reference Chen and Hacon3] that the quasi-Albanese map of V is birational. When
![]() $q(V)=0$
, the lengthy proof uses a fine analysis of the boundary divisor and classical arguments from the theory of surfaces. However, when
$q(V)=0$
, the lengthy proof uses a fine analysis of the boundary divisor and classical arguments from the theory of surfaces. However, when
![]() $q(V)=1$
, we get a considerably shorter proof leveraging on the fact that the Albanese map of a compactification of V is nontrivial, using techniques coming from Green–Lazarsfeld generic vanishing theorems [Reference Green and Lazarsfeld8] and their more recent extensions to pairs (see [Reference Popa and Schnell20] and [Reference Shibata21]).
$q(V)=1$
, we get a considerably shorter proof leveraging on the fact that the Albanese map of a compactification of V is nontrivial, using techniques coming from Green–Lazarsfeld generic vanishing theorems [Reference Green and Lazarsfeld8] and their more recent extensions to pairs (see [Reference Popa and Schnell20] and [Reference Shibata21]).
Once we know that the quasi-Albanese map of V is dominant, then we get that its extension to the compactifications of V and
![]() $A(V)$
respectively is generically finite. Then we use Iitaka’s logarithmic ramification formula (see 2.3 for more details) together with some geometric considerations to conclude that the quasi-Albanese map is birational.
$A(V)$
respectively is generically finite. Then we use Iitaka’s logarithmic ramification formula (see 2.3 for more details) together with some geometric considerations to conclude that the quasi-Albanese map is birational.
The last step of our argument consists in proving that the quasi-Albanese map is proper outside a finite set of points. This is done by showing that the boundary divisor D gets contracted by the quasi-Albanese map. Again, the key tool here is the logarithmic ramification formula together with some more classical arguments exploiting the geometry of the divisor D.
The paper is organized as follows. In §2, we recall the necessary prerequisites; §3 contains some results that hold in arbitrary dimension for
![]() $q(V)>0$
(see in particular Corollary 3.2). Then we focus on surfaces. Section 4 is devoted to proving that the quasi-Albanese map is dominant: here the results of §3 are crucial in case
$q(V)>0$
(see in particular Corollary 3.2). Then we focus on surfaces. Section 4 is devoted to proving that the quasi-Albanese map is dominant: here the results of §3 are crucial in case
![]() $q(V)>0$
. In §5 we complete the proof of Theorem A.
$q(V)>0$
. In §5 we complete the proof of Theorem A.
Notation. We work over the complex numbers. If X is a smooth projective variety, we denote by
![]() $K_X$
the canonical class, by
$K_X$
the canonical class, by
![]() $q(X):=h^0(X,\Omega ^1_X)=h^1(X,\mathcal O_X)$
the irregularity and by
$q(X):=h^0(X,\Omega ^1_X)=h^1(X,\mathcal O_X)$
the irregularity and by
![]() $p_g(X):=h^0(X,K_X)$
the geometric genus.
$p_g(X):=h^0(X,K_X)$
the geometric genus.
We identify invertible sheaves and Cartier divisors, and we use the additive and multiplicative notation interchangeably. Linear equivalence is denoted by
![]() $\sim $
. Given two divisors
$\sim $
. Given two divisors
![]() $D_1$
and
$D_1$
and
![]() $D_2$
on X, we write
$D_2$
on X, we write
![]() $D_1\succeq D_2$
(respectively
$D_1\succeq D_2$
(respectively
![]() $D_1\succ D_2$
) if the divisor
$D_1\succ D_2$
) if the divisor
![]() $D_1-D_2$
is (strictly) effective.
$D_1-D_2$
is (strictly) effective.
Finally, note that, throughout this paper, we use the term (-1)-curve to indicate the total transform E of a point
![]() $q\in Y$
via a birational morphism
$q\in Y$
via a birational morphism
![]() $g\colon X\to Y$
of smooth projective surfaces such that
$g\colon X\to Y$
of smooth projective surfaces such that
![]() $g^{-1}$
is not defined at q; so one has
$g^{-1}$
is not defined at q; so one has
![]() $E^2=K_XE=-1$
but E may be reducible and/or nonreduced.
$E^2=K_XE=-1$
but E may be reducible and/or nonreduced.
2 Preliminaries
Our proof of Theorem A combines different arguments and techniques; in this section, we recall briefly the necessary prerequisites and set the notation.
2.1 Log varieties
Let X be a smooth complex projective variety of dimension n. A reduced effective divisor
![]() $D=\sum D_i$
on X is said to have simple normal crossings (in short we say D is snc) if all the
$D=\sum D_i$
on X is said to have simple normal crossings (in short we say D is snc) if all the
![]() $D_i$
are smooth and for every
$D_i$
are smooth and for every
![]() $p\in \operatorname {Supp} D$
there are local coordinates
$p\in \operatorname {Supp} D$
there are local coordinates
![]() $(x_1,\ldots ,x_n)$
around p such that D is cut out by the equation
$(x_1,\ldots ,x_n)$
around p such that D is cut out by the equation
![]() $x_1\cdots x_r=0$
, for some
$x_1\cdots x_r=0$
, for some
![]() $r\leq n$
.
$r\leq n$
.
Given a smooth projective n-dimensional variety X together with a snc divisor D, we can define the sheaf of logarithmic 1-forms along D by setting
 $$ \begin{align*}\Omega^1_X(\log D)_p:=\sum_{i=1}^r\mathcal{O}_{X,p}\frac{dx_i}{x_i}+\sum_{i=r+1}^n\mathcal{O}_{X,p}dx_i \subset(\Omega^1_X\otimes k(X))_p \end{align*} $$
$$ \begin{align*}\Omega^1_X(\log D)_p:=\sum_{i=1}^r\mathcal{O}_{X,p}\frac{dx_i}{x_i}+\sum_{i=r+1}^n\mathcal{O}_{X,p}dx_i \subset(\Omega^1_X\otimes k(X))_p \end{align*} $$
where
![]() $(x_1,\ldots ,x_n)$
are local coordinates around p such that
$(x_1,\ldots ,x_n)$
are local coordinates around p such that
![]() $D=\{x_1\cdots x_r=0\}$
. It is a locally free sheaf of rank equal to n. The sheaf of logarithmic m-forms is defined as
$D=\{x_1\cdots x_r=0\}$
. It is a locally free sheaf of rank equal to n. The sheaf of logarithmic m-forms is defined as
and, in particular, we have that
We recall the following condition for the existence of logarithmic 1-forms with prescribed poles.
Proposition 2.1. Let D be a simple normal crossing divisor on a smooth projective variety X, and let
![]() $D_1, \dots D_k$
be a subset of the irreducible components of D.
$D_1, \dots D_k$
be a subset of the irreducible components of D.
There exists
![]() $\sigma \in H^0(X,\Omega ^1_X(\log D))$
with poles precisely on
$\sigma \in H^0(X,\Omega ^1_X(\log D))$
with poles precisely on
![]() $D_1 \dots D_k$
if and only if in
$D_1 \dots D_k$
if and only if in
![]() $H^2(X,\mathbb Z)$
there is a relation
$H^2(X,\mathbb Z)$
there is a relation
![]() $\sum _i a_i [D_i ]=0$
between the classes
$\sum _i a_i [D_i ]=0$
between the classes
![]() $[D_1],\dots [D_k]$
such that
$[D_1],\dots [D_k]$
such that
![]() $a_i\ne 0$
for
$a_i\ne 0$
for
![]() $i=1,\dots k$
.
$i=1,\dots k$
.
Proof. Let
![]() $D_1, \dots D_t$
be the irreducible components of D; consider the residue sequence
$D_1, \dots D_t$
be the irreducible components of D; consider the residue sequence
The claim follows from the fact that the associated coboundary map
![]() $\delta \colon \oplus _{i=1}^tH^0(X,{\mathcal O}_{D_i})\to H^1(X,\Omega ^1_X)$
sends
$\delta \colon \oplus _{i=1}^tH^0(X,{\mathcal O}_{D_i})\to H^1(X,\Omega ^1_X)$
sends
![]() $1\in H^0(X,{\mathcal O}_{D_i})$
to the class
$1\in H^0(X,{\mathcal O}_{D_i})$
to the class
![]() $[D_i]\in H^1(X,\Omega ^1_X)$
.
$[D_i]\in H^1(X,\Omega ^1_X)$
.
Given a smooth quasi-projective variety V, by Hironaka’s resolution of singularities, we can embed it in a smooth projective variety X such that
![]() $X\backslash V$
is a snc divisor D, called the boundary of V. Then we can use the sheaves of logarithmic forms to define logarithmic (in short ‘log’) invariants on V, as explained in the introduction. In the case when V is a curve, we call
$X\backslash V$
is a snc divisor D, called the boundary of V. Then we can use the sheaves of logarithmic forms to define logarithmic (in short ‘log’) invariants on V, as explained in the introduction. In the case when V is a curve, we call
![]() $\overline {P}_1(V)=\overline {q}(V)$
the logarithmic genus of V.
$\overline {P}_1(V)=\overline {q}(V)$
the logarithmic genus of V.
While the usual plurigenera and irregularity are birational invariants, this is not the case for logarithmic invariants. For example, an abelian variety X and
![]() $X\backslash D$
, where
$X\backslash D$
, where
![]() $D\succ0$
is a smooth ample divisor, are birational but they have different logarithmic Kodaira dimensions. For this reason, Iitaka in [Reference Iitaka10] introduced the notion of WPB-equivalence (weakly proper birational equivalence). It is the equivalence relation generated by the proper birational morphisms and by the open inclusions
$D\succ0$
is a smooth ample divisor, are birational but they have different logarithmic Kodaira dimensions. For this reason, Iitaka in [Reference Iitaka10] introduced the notion of WPB-equivalence (weakly proper birational equivalence). It is the equivalence relation generated by the proper birational morphisms and by the open inclusions
![]() $V\subset V'$
such that
$V\subset V'$
such that
![]() $V'\setminus V$
has codimension at least 2.
$V'\setminus V$
has codimension at least 2.
WPB-equivalent varieties have the same plurigenera and log irregularity: this is obvious for open immersions as above, and it is proven for proper birational morphisms in [Reference Iitaka11, Prop. 1]. Therefore, it would seem that WPB-equivalence is the right notion of equivalence when studying the birational geometry of open varieties. However, the set of WPB-maps is not saturated; namely, it is possible, for instance, to have rational maps
![]() $g\colon U\dashrightarrow V$
and
$g\colon U\dashrightarrow V$
and
![]() $f\colon V\dashrightarrow W$
such that
$f\colon V\dashrightarrow W$
such that
![]() $f\circ g$
is WPB, but f or g is not. In order to get around this kind of difficulty, Iitaka in [Reference Iitaka10] defines the notion of WWPB-equivalence, proving that WWPB-equivalent varieties have the same logarithmic plurigenera and irregularity.
$f\circ g$
is WPB, but f or g is not. In order to get around this kind of difficulty, Iitaka in [Reference Iitaka10] defines the notion of WWPB-equivalence, proving that WWPB-equivalent varieties have the same logarithmic plurigenera and irregularity.
2.2 Quasi-abelian varieties and the quasi-Albanese map
Here, we introduce one of the main characters of our story: quasi-abelian varieties, which for many aspects can be thought of as a nonprojective analogue of abelian varieties. We recall briefly the facts that we need.
Definition 2.2. A quasi-abelian variety—in some sources also called a semiabelian variety—is a connected algebraic group G that is an extension of an abelian variety A by an algebraic torus. More precisely, G sits in the middle of an exact sequence of the form
We call A the compact part and
![]() $\mathbb {G}_m^r$
the linear part of G.
$\mathbb {G}_m^r$
the linear part of G.
Over the complex numbers,
![]() $G\simeq \mathbb {C}^{\dim G}/\pi _1(G)$
. Observe that
$G\simeq \mathbb {C}^{\dim G}/\pi _1(G)$
. Observe that
![]() $\pi _1(G)$
is a finitely generated free abelian group. When the rank of
$\pi _1(G)$
is a finitely generated free abelian group. When the rank of
![]() $\pi _1(G)$
is equal to
$\pi _1(G)$
is equal to
![]() $2\dim (G)$
, then G is an abelian variety.
$2\dim (G)$
, then G is an abelian variety.
For later use, we recall the following from [Reference Iitaka9, §10]:
Proposition 2.3. Let G be a quasi abelian variety, let A be its compact part and let
![]() $r:=\dim G-\dim A$
. Then there exists a compactification
$r:=\dim G-\dim A$
. Then there exists a compactification
![]() $G\subset Z$
such that:
$G\subset Z$
such that:
-
(a) Z is a
 $\mathbb P^r$
-bundle over A;
$\mathbb P^r$
-bundle over A; -
(b)
 $\Delta :=Z\setminus G$
is a simple normal crossing divisor and
$\Delta :=Z\setminus G$
is a simple normal crossing divisor and
 $\Omega ^1_{Z}(\log \Delta )$
is a trivial bundle of rank equal to
$\Omega ^1_{Z}(\log \Delta )$
is a trivial bundle of rank equal to
 $\dim G$
.
$\dim G$
.
In particular,
![]() $\overline q(G)=\dim G$
and
$\overline q(G)=\dim G$
and
![]() $\overline P_m (G)=1$
for all
$\overline P_m (G)=1$
for all
![]() $m>0$
.
$m>0$
.
We are especially interested in the following particular case of Proposition 2.3:
Corollary 2.4. Let G be a quasi-abelian variety of dimension 2 with compact part A of dimension 1. Then there is a compactification
![]() $G\subset Z$
, where
$G\subset Z$
, where
![]() $Z=\mathbb P ({\mathcal O}_A\oplus L)$
with
$Z=\mathbb P ({\mathcal O}_A\oplus L)$
with
![]() $L\in \operatorname {\mathrm {Pic}}^0(A)$
and the boundary
$L\in \operatorname {\mathrm {Pic}}^0(A)$
and the boundary
![]() $\Delta $
is the disjoint union of two sections
$\Delta $
is the disjoint union of two sections
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
of
$\Delta _2$
of
![]() $Z\to A$
.
$Z\to A$
.
Proof. By Proposition 2.3, we may find a compactification Z which is a
![]() $\mathbb P^1$
-bundle over A and such that
$\mathbb P^1$
-bundle over A and such that
![]() $\Delta $
is a normal crossing divisor. The divisor
$\Delta $
is a normal crossing divisor. The divisor
![]() $\Delta $
meets every fiber of
$\Delta $
meets every fiber of
![]() $Z\to A$
in exactly two points, so it is a smooth bisection. By Proposition 2.3, there is a nonregular logarithmic 1-form of Z with poles contained in
$Z\to A$
in exactly two points, so it is a smooth bisection. By Proposition 2.3, there is a nonregular logarithmic 1-form of Z with poles contained in
![]() $\Delta $
, hence by Proposition 2.1
$\Delta $
, hence by Proposition 2.1
![]() $\Delta $
is reducible and its components satisfy a nontrivial relation in cohomology. Since
$\Delta $
is reducible and its components satisfy a nontrivial relation in cohomology. Since
![]() $\Delta $
is a smooth bisection of
$\Delta $
is a smooth bisection of
![]() $Z\to A$
, we have
$Z\to A$
, we have
![]() $\Delta =\Delta _1+\Delta _2$
with
$\Delta =\Delta _1+\Delta _2$
with
![]() $\Delta _i$
disjoint sections. So
$\Delta _i$
disjoint sections. So
![]() $Z={\mathbf {P}} ({\mathcal O}_A\oplus L)$
for some
$Z={\mathbf {P}} ({\mathcal O}_A\oplus L)$
for some
![]() $L\in \operatorname {\mathrm {Pic}}(A)$
. Since in
$L\in \operatorname {\mathrm {Pic}}(A)$
. Since in
![]() $\operatorname {\mathrm {Pic}}(Z)$
, we have
$\operatorname {\mathrm {Pic}}(Z)$
, we have
![]() $\Delta _2=\Delta _1+p^*L$
, where
$\Delta _2=\Delta _1+p^*L$
, where
![]() $p\colon Z\to A$
is the natural projection,
$p\colon Z\to A$
is the natural projection,
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
are independent in
$\Delta _2$
are independent in
![]() $H^2(Z,\mathbb Z)$
unless
$H^2(Z,\mathbb Z)$
unless
![]() $p^*L=0$
in
$p^*L=0$
in
![]() $H^2(Z,\mathbb Z)$
; namely, unless
$H^2(Z,\mathbb Z)$
; namely, unless
![]() $p^*L\in \operatorname {\mathrm {Pic}}^0(Z)$
. So Proposition 2.1 implies that L is an element of
$p^*L\in \operatorname {\mathrm {Pic}}^0(Z)$
. So Proposition 2.1 implies that L is an element of
![]() $\operatorname {\mathrm {Pic}}^0(A)$
.
$\operatorname {\mathrm {Pic}}^0(A)$
.
Finally we recall some fundamental properties of abelian varieties that extend verbatim to the quasi-abelian case:
Proposition 2.5. Let G be a quasi-abelian variety. Then:
-
1. if
 $G'$
is a quasi-abelian variety and
$G'$
is a quasi-abelian variety and
 $\phi \colon G'\to G$
is a morphism with
$\phi \colon G'\to G$
is a morphism with
 $\phi (0)=0$
, then
$\phi (0)=0$
, then
 $\phi $
is a homomorphism;
$\phi $
is a homomorphism; -
2. if
 $G'\to G$
is a finite étale cover, then
$G'\to G$
is a finite étale cover, then
 $G'$
is a quasi-abelian variety;
$G'$
is a quasi-abelian variety; -
3. if
 $H\subset G$
is closed and
$H\subset G$
is closed and
 $\overline \kappa (H)=0$
, then H is a quasi-abelian variety.
$\overline \kappa (H)=0$
, then H is a quasi-abelian variety.
Proof. Item 1. is [Reference Noguchi and Winkelmann17, Thm. 5.1.37], 2. is [Reference Fujino7, Thm. 4.2] and 3. is [Reference Iitaka9, Thm. 4].
2.2.1 The quasi-Albanese map
The classical construction of the Albanese variety of a projective variety can be extended to the nonprojective case by replacing regular 1-forms by logarithmic ones and abelian varieties by quasi-abelian ones. The key fact is that by Deligne [Reference Deligne4] logarithmic 1-forms are closed (for the details of the construction see [Reference Iitaka9], [Reference Fujino7, Section 3]).
Theorem 2.6. Let V be a smooth algebraic variety. Then there exists a quasi-abelian variety
![]() $A(V)$
and a morphism
$A(V)$
and a morphism
![]() $a_V\colon V\to A(V)$
such that:
$a_V\colon V\to A(V)$
such that:
-
1. if
 $h\colon V\rightarrow G$
is a morphism to a quasi-abelian variety, then h factors through
$h\colon V\rightarrow G$
is a morphism to a quasi-abelian variety, then h factors through
 $a_V$
in a unique way;
$a_V$
in a unique way; -
2. if X is a compactification of V with snc boundary D, then we have the following exact sequence:
(2.2) $$ \begin{align}1\rightarrow \mathbb{G}_m^r\longrightarrow A(V)\longrightarrow A(X)\rightarrow 0, \end{align} $$
$$ \begin{align}1\rightarrow \mathbb{G}_m^r\longrightarrow A(V)\longrightarrow A(X)\rightarrow 0, \end{align} $$
where
 $r=\overline q(V)-q(V)$
.
$r=\overline q(V)-q(V)$
.
Proof. Item 1. is proven in [Reference Iitaka9] in the discussion immediately after Proposition 4. Item 2. is [Reference Fujino7, p. 13].
The variety
![]() $A(V)$
is called the quasi-Albanese variety of V and
$A(V)$
is called the quasi-Albanese variety of V and
![]() $a_V$
the quasi-Albanese map. Note that the compact part of
$a_V$
the quasi-Albanese map. Note that the compact part of
![]() $A(V)$
is
$A(V)$
is
![]() $A(X)$
. We note the following logarithmic version of Abel’s Theorem:
$A(X)$
. We note the following logarithmic version of Abel’s Theorem:
Proposition 2.7. Let C be a smooth curve with
![]() $\overline P_1(C)>0$
. Then the quasi-Albanese map
$\overline P_1(C)>0$
. Then the quasi-Albanese map
![]() $a_C\colon C\to A(C)$
is an embedding.
$a_C\colon C\to A(C)$
is an embedding.
Proof. Denote by
![]() $\overline C$
the compactification of C. If
$\overline C$
the compactification of C. If
![]() $g(\overline C)>0$
, then the Abel–Jacobi map
$g(\overline C)>0$
, then the Abel–Jacobi map
![]() $\overline C\to A(\overline C)$
factorizes through
$\overline C\to A(\overline C)$
factorizes through
![]() $a_C$
, so the claim follows by Abel’s theorem. If
$a_C$
, so the claim follows by Abel’s theorem. If
![]() $g(\overline C)=0$
, we have
$g(\overline C)=0$
, we have
![]() $C:=\overline C\setminus \{p_0,\dots p_k\}$
, where
$C:=\overline C\setminus \{p_0,\dots p_k\}$
, where
![]() $k:=\overline P_1(C)$
. By the universal property, the inclusion
$k:=\overline P_1(C)$
. By the universal property, the inclusion
![]() $C\to \overline C\setminus \{p_0,p_1\}\simeq \mathbb G_m$
factorizes through
$C\to \overline C\setminus \{p_0,p_1\}\simeq \mathbb G_m$
factorizes through
![]() $a_C$
, which therefore is an isomorphism.
$a_C$
, which therefore is an isomorphism.
2.3 Logarithmic ramification formula
Let V, W be smooth varieties of dimension n, and let
![]() $h\colon V\to W$
be a dominant morphism. Let
$h\colon V\to W$
be a dominant morphism. Let
![]() $g\colon X\to Z$
be a morphism extending h, where X, Z are smooth compactifications of V, respectively W, such that
$g\colon X\to Z$
be a morphism extending h, where X, Z are smooth compactifications of V, respectively W, such that
![]() $D:=X\setminus V$
and
$D:=X\setminus V$
and
![]() $\Delta :=Z\setminus W$
are snc divisors. Then the pullback of a logarithmic n-form on Z is a logarithmic n-form on X, and a local computation shows that there is an effective divisor
$\Delta :=Z\setminus W$
are snc divisors. Then the pullback of a logarithmic n-form on Z is a logarithmic n-form on X, and a local computation shows that there is an effective divisor
![]() $\overline R_g$
of X—the logarithmic ramification divisor—such that the following linear equivalence holds:
$\overline R_g$
of X—the logarithmic ramification divisor—such that the following linear equivalence holds:
Equation (2.3) is called the logarithmic ramification formula (cf. [Reference Iitaka13, §11.4]).
We note the following for later use:
Lemma 2.8. In the above setup, denote by
![]() $R_g$
the (usual) ramification divisor of g. Let
$R_g$
the (usual) ramification divisor of g. Let
![]() $\Gamma $
be an irreducible divisor such that
$\Gamma $
be an irreducible divisor such that
![]() $g(\Gamma )\not \subseteq \Delta $
. Then
$g(\Gamma )\not \subseteq \Delta $
. Then
![]() $\Gamma $
is a component of
$\Gamma $
is a component of
![]() $\overline R_g$
if and only if
$\overline R_g$
if and only if
![]() $\Gamma $
is a component of
$\Gamma $
is a component of
![]() $D+R_g$
.
$D+R_g$
.
Proof. Let
![]() $x\in \Gamma $
be a general point so that
$x\in \Gamma $
be a general point so that
![]() $y=g(x)$
does not lie on
$y=g(x)$
does not lie on
![]() $\Delta $
. Then
$\Delta $
. Then
![]() $K_Z+\Delta $
is generated locally near y by a nowhere vanishing regular n-form, while
$K_Z+\Delta $
is generated locally near y by a nowhere vanishing regular n-form, while
![]() $K_X+D$
is generated locally near x either by an n-form with a logarithmic pole on
$K_X+D$
is generated locally near x either by an n-form with a logarithmic pole on
![]() $\Gamma $
or by a regular n-form, according to whether
$\Gamma $
or by a regular n-form, according to whether
![]() $\Gamma $
is a component of D or not. In the former case,
$\Gamma $
is a component of D or not. In the former case,
![]() $\Gamma $
is always a component of
$\Gamma $
is always a component of
![]() $\overline R_g$
; in the latter case, it is a component of
$\overline R_g$
; in the latter case, it is a component of
![]() $\overline R_g$
if and only if g is ramified along
$\overline R_g$
if and only if g is ramified along
![]() $\Gamma $
.
$\Gamma $
.
2.4 Generic vanishing
The theory of generic vanishing was introduced by Green–Lazarsfeld in [Reference Green and Lazarsfeld8]. It has since developed in a powerful tool to study the geometry of projective varieties via their Albanese morphism (see, for example, [Reference Pareschi18] for a nice survey). We are going to see in Section 3 that these techniques can be useful instruments also in the quasi-projective setting.
Let X be a smooth projective variety. Given a coherent sheaf
![]() $\mathcal {F}$
on X, the cohomological support loci of
$\mathcal {F}$
on X, the cohomological support loci of
![]() $\mathcal {F}$
are the subsets
$\mathcal {F}$
are the subsets
We say that
![]() $\mathcal {F}$
is a
$\mathcal {F}$
is a
![]() $GV$
-sheaf if, for every
$GV$
-sheaf if, for every
![]() $i>0$
, we have that
$i>0$
, we have that
When all the
![]() $V^i(X,\mathcal {F})$
are empty for
$V^i(X,\mathcal {F})$
are empty for
![]() $i>0$
, one says, following the original terminology of Mukai [Reference Mukai16], that
$i>0$
, one says, following the original terminology of Mukai [Reference Mukai16], that
![]() $\mathcal {F}$
is a IT(0)-sheaf.
$\mathcal {F}$
is a IT(0)-sheaf.
We recall the following well-known useful observation:
Lemma 2.9. Let X be a smooth projective variety and L a line bundle of X.
If
![]() $V^0(X,L)\cap (-V^0(X,L))$
has positive dimension, then
$V^0(X,L)\cap (-V^0(X,L))$
has positive dimension, then
![]() $h^0(X, 2L)\ge 2$
.
$h^0(X, 2L)\ge 2$
.
Proof. For
![]() $\alpha \in V^0(X,L)\cap (-V^0(X,L))$
, consider the multiplication map
$\alpha \in V^0(X,L)\cap (-V^0(X,L))$
, consider the multiplication map
As
![]() $\alpha $
varies, the image of the map must vary since a divisor can be written as the sum of two effective divisors only in finitely many ways. As a consequence,
$\alpha $
varies, the image of the map must vary since a divisor can be written as the sum of two effective divisors only in finitely many ways. As a consequence,
![]() $h^0(X,2L)\ge 2$
.
$h^0(X,2L)\ge 2$
.
2.5 Curves on smooth surfaces
Let
![]() $D\succ 0$
be a divisor (a ‘curve’) on a smooth projective surface X. The arithmetic genus of D is
$D\succ 0$
be a divisor (a ‘curve’) on a smooth projective surface X. The arithmetic genus of D is
![]() $p_a(D):=1-\chi ({\mathcal O}_D)$
and can be computed by means of the adjunction formula
$p_a(D):=1-\chi ({\mathcal O}_D)$
and can be computed by means of the adjunction formula
By Serre duality, one also has
![]() $p_a(D)-1= h^0(D,\omega _D)-h^0(D, {\mathcal O}_D)$
, hence
$p_a(D)-1= h^0(D,\omega _D)-h^0(D, {\mathcal O}_D)$
, hence
![]() $h^0(D, \omega _D)\ge p_a(D)$
.
$h^0(D, \omega _D)\ge p_a(D)$
.
For
![]() $m\in \mathbb N$
, we say that D is m-connected if, for every decomposition
$m\in \mathbb N$
, we say that D is m-connected if, for every decomposition
![]() $D=D_1+D_2$
, with
$D=D_1+D_2$
, with
![]() $D_1$
and
$D_1$
and
![]() $D_2$
effective, one has
$D_2$
effective, one has
![]() $D_1D_2\ge m$
.
$D_1D_2\ge m$
.
We recall some well-known facts.
Lemma 2.10. Let D be a
![]() $1$
-connected divisor, then:
$1$
-connected divisor, then:
-
1.
 $h^0(D,{\mathcal O}_D)=1$
(so in particular,
$h^0(D,{\mathcal O}_D)=1$
(so in particular,
 $p_a(D)=h^0(D, \omega _D)\ge 0$
);
$p_a(D)=h^0(D, \omega _D)\ge 0$
); -
2. if L is a line bundle on D that has degree 0 on every component of D, then
 $h^0(D,L)\le 1$
, and
$h^0(D,L)\le 1$
, and
 $h^0(D,L)=1$
if and only if
$h^0(D,L)=1$
if and only if
 $L= {\mathcal O}_D$
.
$L= {\mathcal O}_D$
.
Proof. See [Reference Barth, Hulek, Peters and Van de Ven2, Lem. II 12.2].
Lemma 2.11. Let
![]() $D_1$
,
$D_1$
,
![]() $D_2$
be two effective nonzero divisors on a smooth projective surface X. Then
$D_2$
be two effective nonzero divisors on a smooth projective surface X. Then
-
1.
 $p_a(D_1+D_2)=p_a(D_1)+p_a(D_2)+D_1D_2-1$
;
$p_a(D_1+D_2)=p_a(D_1)+p_a(D_2)+D_1D_2-1$
; -
2. if
 $D_1\prec D_2$
, then
$D_1\prec D_2$
, then
 $h^0(D_1,\omega _{D_1})\le h^0(D_2, \omega _{D_2})$
.
$h^0(D_1,\omega _{D_1})\le h^0(D_2, \omega _{D_2})$
.
Proof. 1. Use the adjunction formula (2.4).
2. Write
![]() $D_2=D_1+A$
, and consider the decomposition sequence:
$D_2=D_1+A$
, and consider the decomposition sequence:
Twisting by
![]() $K_X+D_2$
and taking cohomology gives the result.
$K_X+D_2$
and taking cohomology gives the result.
Lemma 2.12. Let D be an effective nonzero divisor on a smooth projective surface X. Then we have the following formulae:
-
1.
 $h^0(X, K_X+D)= p_a(D)+ p_g(X)-q(X)+h^1(X,-D)$
;
$h^0(X, K_X+D)= p_a(D)+ p_g(X)-q(X)+h^1(X,-D)$
; -
2.
 $h^0(X, K_X+D)= h^0(D,\omega _D)+ p_g(X)-q(X)+d$
,
$h^0(X, K_X+D)= h^0(D,\omega _D)+ p_g(X)-q(X)+d$
,where d is the dimension of the kernel of the restriction map
 $H^1(X, {\mathcal O}_X)\to H^1(D, {\mathcal O}_D)$
.
$H^1(X, {\mathcal O}_X)\to H^1(D, {\mathcal O}_D)$
.
Proof. 1. follows from the Riemann–Roch theorem, the adjunction formula (2.4) and Serre duality.
Taking cohomology in the restriction sequence
one obtains
![]() $h^1(X,-D)= h^0(D, {\mathcal O}_D)-1+d$
. Plugging this relation and the equality
$h^1(X,-D)= h^0(D, {\mathcal O}_D)-1+d$
. Plugging this relation and the equality
![]() $p_a(D)-1= h^0(D,\omega _D)-h^0(D, {\mathcal O}_D)$
in 1. one obtains 2.
$p_a(D)-1= h^0(D,\omega _D)-h^0(D, {\mathcal O}_D)$
in 1. one obtains 2.
Remark 2.13. Note that by Serre duality d is exactly the codimension of the image of the map
![]() $t\colon H^0(D, \omega _D)\to H^1(X, K_X)$
.
$t\colon H^0(D, \omega _D)\to H^1(X, K_X)$
.
3 Results in arbitrary dimension via generic vanishing
Let V be a smooth quasi-projective variety, and let X be a smooth compactification of V with snc boundary. In this section, we investigate the geometric constraints imposed on the Albanese map
![]() $a_X$
of X, and on the image of V via
$a_X$
of X, and on the image of V via
![]() $a_X$
, by the fact the logarithmic plurigenera of V are small. Our main tool will be the theory of generic vanishing (§2.4), and its recent extensions to the ‘log-canonical’ setting by Popa–Schnell [Reference Popa and Schnell20] and Shibata [Reference Shibata21].
$a_X$
, by the fact the logarithmic plurigenera of V are small. Our main tool will be the theory of generic vanishing (§2.4), and its recent extensions to the ‘log-canonical’ setting by Popa–Schnell [Reference Popa and Schnell20] and Shibata [Reference Shibata21].
Proposition 3.1. Let V be a smooth quasi-projective variety, and denote by X a compactification of V with simple normal crossing boundary divisor D.
If
![]() $\overline P_1(V)=\overline {P}_{2}(V)=1$
, then the Albanese morphism
$\overline P_1(V)=\overline {P}_{2}(V)=1$
, then the Albanese morphism
![]() $a_X\colon X\to A(X)$
is surjective.
$a_X\colon X\to A(X)$
is surjective.
Proof. Since
![]() $V^0(X,\mathcal {O}_X(K_X+D))$
is a union of translates of subtori of
$V^0(X,\mathcal {O}_X(K_X+D))$
is a union of translates of subtori of
![]() $A(X)$
(cf. [Reference Shibata21, Theorem 1.3]), Lemma 2.9 implies that
$A(X)$
(cf. [Reference Shibata21, Theorem 1.3]), Lemma 2.9 implies that
![]() ${\mathcal O}_X$
is an isolated point of
${\mathcal O}_X$
is an isolated point of
![]() $V^0(X,{\mathcal O}_X(K_X+D))$
. Thus, by the projection formula
$V^0(X,{\mathcal O}_X(K_X+D))$
. Thus, by the projection formula
![]() ${\mathcal O}_{A(X)}$
is an isolated point of
${\mathcal O}_{A(X)}$
is an isolated point of
![]() $V^0(A(X),a_{X,*}{\mathcal O}_X(K_X+D))$
. Thanks to [Reference Popa and Schnell20, Variant 5.5], we know that
$V^0(A(X),a_{X,*}{\mathcal O}_X(K_X+D))$
. Thanks to [Reference Popa and Schnell20, Variant 5.5], we know that
![]() $a_{X,*}{\mathcal O}_X(K_X+D)$
is a
$a_{X,*}{\mathcal O}_X(K_X+D)$
is a
![]() $GV$
-sheaf on
$GV$
-sheaf on
![]() $A(X)$
, and therefore by [Reference Pareschi18, Lemma 1.8] we know that
$A(X)$
, and therefore by [Reference Pareschi18, Lemma 1.8] we know that
![]() ${\mathcal O}_{A(X)}$
is a component of
${\mathcal O}_{A(X)}$
is a component of
![]() $V^{q(X)}(A(X),a_{X,*}{\mathcal O}_X(K_X+D))$
. In particular,
$V^{q(X)}(A(X),a_{X,*}{\mathcal O}_X(K_X+D))$
. In particular,
![]() $h^{q(X)}(A(X),a_{X,*}{\mathcal O}_X(K_X+D))\neq 0$
, and we deduce that the dimension of the Albanese image of X is equal the dimension of
$h^{q(X)}(A(X),a_{X,*}{\mathcal O}_X(K_X+D))\neq 0$
, and we deduce that the dimension of the Albanese image of X is equal the dimension of
![]() $A(X)$
. We conclude because X and
$A(X)$
. We conclude because X and
![]() $A(X)$
are projective.
$A(X)$
are projective.
As an immediate consequence we have:
Corollary 3.2. Let V an n-dimensional smooth quasi-projective variety, X a compactification of V such that
![]() $D:=X\setminus V$
is a snc divisor. If
$D:=X\setminus V$
is a snc divisor. If
![]() $\overline {P}_1(V)=\overline {P}_2(V)=1$
and
$\overline {P}_1(V)=\overline {P}_2(V)=1$
and
![]() $\overline {q}(V)=q(X)=n$
, then the quasi-Albanese morphism
$\overline {q}(V)=q(X)=n$
, then the quasi-Albanese morphism
![]() $a_V\colon V\rightarrow A(V)$
is birational.
$a_V\colon V\rightarrow A(V)$
is birational.
Proof. By Proposition 3.1, we know that
![]() $a_X$
is generically finite, and so X is of maximal Albanese dimension. In particular, we have that
$a_X$
is generically finite, and so X is of maximal Albanese dimension. In particular, we have that
We conclude that
![]() $h^0(X,K_X)=1$
. Similarly, we see that
$h^0(X,K_X)=1$
. Similarly, we see that
![]() $h^0(X,2K_X)=1$
, and so by the characterization Theorem of Chen–Hacon [Reference Chen and Hacon3] we conclude that
$h^0(X,2K_X)=1$
, and so by the characterization Theorem of Chen–Hacon [Reference Chen and Hacon3] we conclude that
![]() $a_X$
is a birational morphism. In addition, by Theorem 2.6 there is a commutative diagram
$a_X$
is a birational morphism. In addition, by Theorem 2.6 there is a commutative diagram

and so also
![]() $a_V$
is birational.
$a_V$
is birational.
The next result refines Proposition 3.1:
Proposition 3.3. Let V be a smooth quasi-projective variety, X a compactification of V such that
![]() $D:=X\setminus V$
is a snc divisor. Let
$D:=X\setminus V$
is a snc divisor. Let
![]() $a_X\colon X\to A(X)$
be the Albanese morphism, and let
$a_X\colon X\to A(X)$
be the Albanese morphism, and let
![]() $E\succ0$
be a divisor on
$E\succ0$
be a divisor on
![]() $A(X)$
.
$A(X)$
.
If
![]() $\overline P_1(V)>0$
and D contains the support of
$\overline P_1(V)>0$
and D contains the support of
![]() $a_X^*E$
, then
$a_X^*E$
, then
![]() $\overline P_2(V)\ge 2$
.
$\overline P_2(V)\ge 2$
.
Proof. The divisor E is of the form
![]() $\pi ^*H$
, where
$\pi ^*H$
, where
![]() $\pi \colon A\to B$
is a morphism onto a positive dimensional abelian variety, and H is an ample divisor on B. Set
$\pi \colon A\to B$
is a morphism onto a positive dimensional abelian variety, and H is an ample divisor on B. Set
![]() $f:=\pi \circ a_X$
; by assumption there is a positive integer N such that
$f:=\pi \circ a_X$
; by assumption there is a positive integer N such that
![]() $ND\succeq f^*H$
. Set
$ND\succeq f^*H$
. Set
![]() $\Delta :=D-\frac {1}{N}f^*H$
: by assumption the
$\Delta :=D-\frac {1}{N}f^*H$
: by assumption the
![]() $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
![]() $\Delta $
has snc support and
$\Delta $
has snc support and
![]() $\Delta =\sum _id_i\Delta _i$
, with
$\Delta =\sum _id_i\Delta _i$
, with
![]() $\Delta _i$
irreducible divisors and
$\Delta _i$
irreducible divisors and
![]() $0\le d_i\le 1$
. Given
$0\le d_i\le 1$
. Given
![]() $\alpha \in \operatorname {\mathrm {Pic}}^0(B)$
, the divisor
$\alpha \in \operatorname {\mathrm {Pic}}^0(B)$
, the divisor
![]() $K_X+D+f^*(\alpha )$
is
$K_X+D+f^*(\alpha )$
is
![]() $\mathbb Q$
-linearly equivalent to
$\mathbb Q$
-linearly equivalent to
![]() $K_X+\Delta +f^*(\frac {1}{N}H+\alpha )$
. Since
$K_X+\Delta +f^*(\frac {1}{N}H+\alpha )$
. Since
![]() $\frac {1}{N}H+\alpha $
is ample if H is, the assumptions of [Reference Fujino6, Thm. 6.3] or [Reference Ambro1, Thm. 3.2] are satisfied and we have
$\frac {1}{N}H+\alpha $
is ample if H is, the assumptions of [Reference Fujino6, Thm. 6.3] or [Reference Ambro1, Thm. 3.2] are satisfied and we have
So
![]() $f_*(K_X+D)$
is an IT(0)-sheaf, and therefore for all
$f_*(K_X+D)$
is an IT(0)-sheaf, and therefore for all
![]() $\alpha \in \operatorname {\mathrm {Pic}}^0(B)$
we have
$\alpha \in \operatorname {\mathrm {Pic}}^0(B)$
we have
![]() $h^0(B, f_*\mathcal O_X(K_X+D)\otimes \alpha )=h^0(B, f_*(K_X+D))=\overline P_1(V)>0$
. So
$h^0(B, f_*\mathcal O_X(K_X+D)\otimes \alpha )=h^0(B, f_*(K_X+D))=\overline P_1(V)>0$
. So
![]() $V^0(X, K_X+D)$
contains the positive dimensional abelian subvariety
$V^0(X, K_X+D)$
contains the positive dimensional abelian subvariety
![]() $f^*\operatorname {\mathrm {Pic}}^0(B)=\pi ^*\operatorname {\mathrm {Pic}}^0(B)$
and
$f^*\operatorname {\mathrm {Pic}}^0(B)=\pi ^*\operatorname {\mathrm {Pic}}^0(B)$
and
![]() $\overline P_2(V)\ge 2$
by Lemma 2.9.
$\overline P_2(V)\ge 2$
by Lemma 2.9.
When
![]() $q(V)$
is equal to 1, Proposition 3.3 gives:
$q(V)$
is equal to 1, Proposition 3.3 gives:
Corollary 3.4. Let V be a smooth quasi-projective variety, X a compactification of V such that
![]() $D:=X\setminus V$
is a snc divisor. Let
$D:=X\setminus V$
is a snc divisor. Let
![]() $a_X\colon X\to A(X)$
be the Albanese morphism.
$a_X\colon X\to A(X)$
be the Albanese morphism.
If
![]() $q(V)=\overline P_1(V)=\overline P_2(V)=1$
, then
$q(V)=\overline P_1(V)=\overline P_2(V)=1$
, then
![]() $a_X(V)=A(X)$
.
$a_X(V)=A(X)$
.
Remark 3.5. Observe that, by Proposition 3.1, we can deduce that if
![]() $\overline P_1(V)=\overline P_2(V)=1$
then the map
$\overline P_1(V)=\overline P_2(V)=1$
then the map
![]() $ a_X|_V$
is dominant. In addition, as a consequence of Proposition 3.3, we know that the complement of
$ a_X|_V$
is dominant. In addition, as a consequence of Proposition 3.3, we know that the complement of
![]() $a_X(V)$
in
$a_X(V)$
in
![]() $A(X)$
does not contain a divisor. Notice that, if
$A(X)$
does not contain a divisor. Notice that, if
![]() $q(X)>1$
, this does not mean that the complement of
$q(X)>1$
, this does not mean that the complement of
![]() $a_X(V)$
has codimension
$a_X(V)$
has codimension
![]() $>1$
, since the image of V is not necessarily open in
$>1$
, since the image of V is not necessarily open in
![]() $A(X)$
.
$A(X)$
.
4 The geometry of the quasi-Albanese morphism
The aim of this section is to establish the following fundamental step in the proof of Theorem A:
Proposition 4.1. Let V be a smooth complex algebraic surface with
![]() $\overline {q}(V)=2$
. Assume that:
$\overline {q}(V)=2$
. Assume that:
-
(a)
 $\overline {P}_1(V)=\overline {P}_2(V)=1$
and
$\overline {P}_1(V)=\overline {P}_2(V)=1$
and
 $q(V)>0$
; or
$q(V)>0$
; or -
(b)
 $\overline {P}_1(V)=\overline {P}_3(V)=1$
and
$\overline {P}_1(V)=\overline {P}_3(V)=1$
and
 $q(V)=0$
.
$q(V)=0$
.
Then the quasi-Albanese morphism
![]() $a_V\colon V\rightarrow A(V)$
is dominant.
$a_V\colon V\rightarrow A(V)$
is dominant.
We use different approaches for the case
![]() $q(V)=0$
and
$q(V)=0$
and
![]() $q(V)>0$
, so we treat them separately. In fact, Proposition 4.1 is just the combination of Propositions 4.2 and 4.3 below.
$q(V)>0$
, so we treat them separately. In fact, Proposition 4.1 is just the combination of Propositions 4.2 and 4.3 below.
4.1 The quasi-Albanese map when
 $q(V)\ge 1$
$q(V)\ge 1$
Proposition 4.2. Let V be a smooth algebraic surface such that
![]() $\overline {P}_1(V)=\overline {P}_2(V)=1$
,
$\overline {P}_1(V)=\overline {P}_2(V)=1$
,
![]() $\overline {q}(V)=2$
and
$\overline {q}(V)=2$
and
![]() $q(V)\ge 1$
. Then the quasi-Albanese morphism of V is dominant and, hence, generically finite.
$q(V)\ge 1$
. Then the quasi-Albanese morphism of V is dominant and, hence, generically finite.
Proof. When
![]() $q(V)=\overline q(V)=2$
, the map
$q(V)=\overline q(V)=2$
, the map
![]() $a_V$
is dominant by Corollary 3.2.
$a_V$
is dominant by Corollary 3.2.
Assume now that
![]() $q(V)=1$
and, by contradiction, that the image of
$q(V)=1$
and, by contradiction, that the image of
![]() $a_V$
is a curve C. Denote by
$a_V$
is a curve C. Denote by
![]() $\overline C$
the smooth projective model of C; since
$\overline C$
the smooth projective model of C; since
![]() $\overline C$
dominates the elliptic curve
$\overline C$
dominates the elliptic curve
![]() $A(X)$
, the curve
$A(X)$
, the curve
![]() $\overline C$
has positive genus and
$\overline C$
has positive genus and
![]() $a_V$
extends to a morphism
$a_V$
extends to a morphism
![]() $f\colon X \to \overline C$
such that the Albanese morphism factorizes through
$f\colon X \to \overline C$
such that the Albanese morphism factorizes through
![]() $\overline C$
. By the universal property of the Albanese map, the map
$\overline C$
. By the universal property of the Albanese map, the map
![]() $\overline C\to A(X)$
is an isomorphism. Now, Corollary 3.4 implies that
$\overline C\to A(X)$
is an isomorphism. Now, Corollary 3.4 implies that
![]() $C=\overline C$
. In particular, by Proposition 2.5 up to translation C is an algebraic subgroup of
$C=\overline C$
. In particular, by Proposition 2.5 up to translation C is an algebraic subgroup of
![]() $A(V)$
. On the other hand, C must generate
$A(V)$
. On the other hand, C must generate
![]() $A(V)$
as an algebraic group, so it follows
$A(V)$
as an algebraic group, so it follows
![]() $C=A(V)$
, a contradiction.
$C=A(V)$
, a contradiction.
4.2 The quasi-Albanese map when
 $q(V)=0$
$q(V)=0$
In this section, we prove the following
Proposition 4.3. Let V be a smooth algebraic surface such that
![]() $\overline {P}_1(V)=\overline {P}_3(V)=1$
,
$\overline {P}_1(V)=\overline {P}_3(V)=1$
,
![]() $\overline {q}(V)=2$
, and
$\overline {q}(V)=2$
, and
![]() $q(V)=0$
. Then the quasi-Albanese morphism of V is dominant and, hence, generically finite.
$q(V)=0$
. Then the quasi-Albanese morphism of V is dominant and, hence, generically finite.
The proof is based on numerical arguments and is quite intricate, so we break it into several steps. We start by proving two results on curves on smooth projective surfaces.
Lemma 4.4. Let X be a nonsingular projective surface and A a 1-connected effective divisor with
![]() $p_a(A)=1$
.
$p_a(A)=1$
.
Then A contains a 2-connected divisor B such that
![]() $p_a(B)=1$
.
$p_a(B)=1$
.
Proof. If A is 2-connected, there is of course nothing to prove. Otherwise, take any decomposition
![]() $A=A_1+A_2$
with
$A=A_1+A_2$
with
![]() $A_1A_2=1$
and
$A_1A_2=1$
and
![]() $A_1$
minimal with respect to
$A_1$
minimal with respect to
![]() $A_1A_2=1$
.
$A_1A_2=1$
.
![]() $A_2$
is 1-connected,
$A_2$
is 1-connected,
![]() $A_1$
is 2-connected, and by Lemma 2.11
$A_1$
is 2-connected, and by Lemma 2.11
![]() $p_a(A_1)+p_a(A_2)=1$
,
$p_a(A_1)+p_a(A_2)=1$
,
![]() $p_a(A_1)\geq 0$
,
$p_a(A_1)\geq 0$
,
![]() $p_a(A_2)\geq 0$
. If
$p_a(A_2)\geq 0$
. If
![]() $p_a(A_1)=1$
, we have proved the statement; if not, we repeat the argument on
$p_a(A_1)=1$
, we have proved the statement; if not, we repeat the argument on
![]() $A_2$
.
$A_2$
.
Lemma 4.5. Let X be a nonsingular projective surface and B a 2-connected effective divisor with
![]() $p_a(B)=1$
. Then:
$p_a(B)=1$
. Then:
-
1. if B is not irreducible, then every component
 $\Gamma $
of B is smooth rational and satisfies
$\Gamma $
of B is smooth rational and satisfies
 $(K_X+B)\Gamma =0$
;
$(K_X+B)\Gamma =0$
; -
2.
 $\omega _B=\mathcal O_B$
;
$\omega _B=\mathcal O_B$
; -
3. if
 $\Gamma $
is an irreducible component of B and
$\Gamma $
is an irreducible component of B and
 $B-\Gamma \succ 0$
, then
$B-\Gamma \succ 0$
, then
 $B-\Gamma $
is 1-connected.
$B-\Gamma $
is 1-connected.
Proof. 1. Since
![]() $p_a(B)=1$
,
$p_a(B)=1$
,
![]() $(K_X+B)B=0$
. On the other hand, for every irreducible component
$(K_X+B)B=0$
. On the other hand, for every irreducible component
![]() $\Gamma $
of B, one has
$\Gamma $
of B, one has
![]() $(K_X+B)\Gamma =(K_X+\Gamma )\Gamma + (B-\Gamma )\Gamma \geq 0$
because
$(K_X+B)\Gamma =(K_X+\Gamma )\Gamma + (B-\Gamma )\Gamma \geq 0$
because
![]() $(K_X+\Gamma )\Gamma \geq -2$
by adjunction and
$(K_X+\Gamma )\Gamma \geq -2$
by adjunction and
![]() $(B-\Gamma )\Gamma \geq 2$
since B is 2-connected and reducible. So necessarily
$(B-\Gamma )\Gamma \geq 2$
since B is 2-connected and reducible. So necessarily
![]() $(K_X+B)\Gamma =0$
, and
$(K_X+B)\Gamma =0$
, and
![]() $\Gamma $
is smooth rational.
$\Gamma $
is smooth rational.
2. Since, by 1.
![]() $\omega _B$
has degree
$\omega _B$
has degree
![]() $0$
on every component of B and
$0$
on every component of B and
![]() $h^0(B, \omega _B)=1$
, by Lemma 2.10
$h^0(B, \omega _B)=1$
, by Lemma 2.10
![]() $\omega _B={\mathcal O}_B$
.
$\omega _B={\mathcal O}_B$
.
3. By the proof of 1. one has
![]() $\Gamma (B-\Gamma )=2$
. Let
$\Gamma (B-\Gamma )=2$
. Let
![]() $B-\Gamma =A_1+A_2$
with
$B-\Gamma =A_1+A_2$
with
![]() $A_1>0,A_2>0$
. Then because B is 2-connected,
$A_1>0,A_2>0$
. Then because B is 2-connected,
![]() $A_i(A_j+\Gamma )\geq 2$
for
$A_i(A_j+\Gamma )\geq 2$
for
![]() $\{i,j\}=\{1,2\}$
. Since
$\{i,j\}=\{1,2\}$
. Since
![]() $(A_1+A_2)\Gamma =2$
necessarily
$(A_1+A_2)\Gamma =2$
necessarily
![]() $A_1A_2\geq 1$
and so
$A_1A_2\geq 1$
and so
![]() $B-\Gamma $
is 1-connected.
$B-\Gamma $
is 1-connected.
Lemma 4.6. Let X be a nonsingular projective surface with
![]() $q(X)=0$
, and let B be an effective 2-connected divisor satisfying
$q(X)=0$
, and let B be an effective 2-connected divisor satisfying
![]() $p_a(B)=1$
. Then one of the following occurs:
$p_a(B)=1$
. Then one of the following occurs:
-
(a)
 $h^0(X, 2K_X+2B)\geq 2$
;
$h^0(X, 2K_X+2B)\geq 2$
; -
(b) X is rational, and there is a blow-down morphism
 $\rho \colon X\to T$
with exceptional divisor
$\rho \colon X\to T$
with exceptional divisor
 $\sum _{j=1}^nE_j$
(where the
$\sum _{j=1}^nE_j$
(where the
 $E_j$
are
$E_j$
are
 $-1$
-curves) such that
$-1$
-curves) such that
 $K_X+B\sim \sum _{j=1}^nE_j$
and B is disjoint from
$K_X+B\sim \sum _{j=1}^nE_j$
and B is disjoint from
 $\sum _{j=1}^nE_j$
.
$\sum _{j=1}^nE_j$
.
Proof. From Lemma 2.12, we obtain
![]() $h^0(X, K_X+B)=p_g(X)+1\geq 1$
.
$h^0(X, K_X+B)=p_g(X)+1\geq 1$
.
Assume that
![]() $K_X+B$
is nef. Then since
$K_X+B$
is nef. Then since
![]() $(K_X+B)B=0$
, we have
$(K_X+B)B=0$
, we have
![]() $K_X(K_X+B)=(K_X+B)^2\geq 0$
and
$K_X(K_X+B)=(K_X+B)^2\geq 0$
and
![]() $(2K_X+B) (K_X+B)=2K_X(K_X+B)\geq 0$
. So we have two possibilities: either
$(2K_X+B) (K_X+B)=2K_X(K_X+B)\geq 0$
. So we have two possibilities: either
![]() $K_X+B\sim 0$
(and
$K_X+B\sim 0$
(and
![]() $p_g(X)=0$
) or there is a nonzero effective divisor
$p_g(X)=0$
) or there is a nonzero effective divisor
![]() $B_1$
in
$B_1$
in
![]() $|K_X+B|$
, and
$|K_X+B|$
, and
![]() $p_a(B_1)\geq 1 $
implying by Lemma 2.12 that
$p_a(B_1)\geq 1 $
implying by Lemma 2.12 that
![]() $h^0(X, K_X+B_1)\geq 1+p_g$
, that is,
$h^0(X, K_X+B_1)\geq 1+p_g$
, that is,
![]() $h^0(X, 2K_X+B)\geq 1$
.
$h^0(X, 2K_X+B)\geq 1$
.
In the second case, the restriction map
![]() $H^0(X, K_X+B)\to H^0(B, \omega _B)$
is surjective because
$H^0(X, K_X+B)\to H^0(B, \omega _B)$
is surjective because
![]() $q(X)=0$
. Since
$q(X)=0$
. Since
![]() $\omega _B=\mathcal O_B$
, the map
$\omega _B=\mathcal O_B$
, the map
![]() $ H^0(X, 2K_X+2B)\to H^0(B, \omega _B^{\otimes 2})$
is also nonzero. So the exact sequence
$ H^0(X, 2K_X+2B)\to H^0(B, \omega _B^{\otimes 2})$
is also nonzero. So the exact sequence
gives
![]() $h^0(X, 2K_X+2B)\geq 2$
.
$h^0(X, 2K_X+2B)\geq 2$
.
Assume now that
![]() $B_1$
is not nef, and let
$B_1$
is not nef, and let
![]() $\theta $
be an irreducible curve with
$\theta $
be an irreducible curve with
![]() $B_1\theta <0$
. Since
$B_1\theta <0$
. Since
![]() $B_1$
is effective,
$B_1$
is effective,
![]() $\theta $
is a component of
$\theta $
is a component of
![]() $B_1$
with
$B_1$
with
![]() $\theta ^2<0$
. In addition, for every component
$\theta ^2<0$
. In addition, for every component
![]() $\Gamma $
of B, we have, by Lemma 4.5,
$\Gamma $
of B, we have, by Lemma 4.5,
![]() $B_1\Gamma = 0$
, so
$B_1\Gamma = 0$
, so
![]() $\theta $
is not a component of B, and thus
$\theta $
is not a component of B, and thus
![]() $B\theta \ge 0$
. Then the only possibility is that
$B\theta \ge 0$
. Then the only possibility is that
![]() $\theta $
is an irreducible
$\theta $
is an irreducible
![]() $-1$
-curve disjoint from B. We contract
$-1$
-curve disjoint from B. We contract
![]() $\theta $
and replace B by its image under the contraction; repeating this process, we eventually end up with a birational morphism of smooth surfaces
$\theta $
and replace B by its image under the contraction; repeating this process, we eventually end up with a birational morphism of smooth surfaces
![]() $ \rho \colon X\to T$
such that
$ \rho \colon X\to T$
such that
![]() $K_{T}+\rho (B)$
is nef, and
$K_{T}+\rho (B)$
is nef, and
![]() $\rho (B)$
is still a 2-connected divisor with
$\rho (B)$
is still a 2-connected divisor with
![]() $p_a=1$
.
$p_a=1$
.
By the discussion in the previous case, we see that either
![]() $h^0(T, 2K_T+2\rho (B))\ge 2$
or
$h^0(T, 2K_T+2\rho (B))\ge 2$
or
![]() $K_T+\rho (B)\sim 0$
. In the former case
$K_T+\rho (B)\sim 0$
. In the former case
![]() $h^0(X, 2K_X+2B)\ge h^0(T, 2K_T+2\rho (B))\ge 2$
. In the latter case, taking pullbacks we get
$h^0(X, 2K_X+2B)\ge h^0(T, 2K_T+2\rho (B))\ge 2$
. In the latter case, taking pullbacks we get
![]() $\rho ^*(K_T)+B=K_X-\sum _{j=1}^nE_j+B \sim 0$
. So, if L is an ample divisor on T, then
$\rho ^*(K_T)+B=K_X-\sum _{j=1}^nE_j+B \sim 0$
. So, if L is an ample divisor on T, then
![]() $\rho ^*L$
is nef and big and it satisfies
$\rho ^*L$
is nef and big and it satisfies
![]() $K_X\rho ^*L=-B\rho ^*L<0$
, so
$K_X\rho ^*L=-B\rho ^*L<0$
, so
![]() $\kappa (X)=-\infty $
. Since
$\kappa (X)=-\infty $
. Since
![]() $q(X)=0$
, the surface X is rational.
$q(X)=0$
, the surface X is rational.
For the rest of the section, we refer to the following situation:
Setting 4.7. We let V be a smooth open algebraic surface with
![]() $\overline {q}(V)=2$
,
$\overline {q}(V)=2$
,
![]() $q(V)=0$
and
$q(V)=0$
and
![]() $\overline P_1(V)=\overline P_3(V)=1$
. We consider the standard compactification
$\overline P_1(V)=\overline P_3(V)=1$
. We consider the standard compactification
![]() $Z=\mathbb P^1\times \mathbb P^1$
of
$Z=\mathbb P^1\times \mathbb P^1$
of
![]() $A(V)=\mathbb G_m^2$
, and we denote by
$A(V)=\mathbb G_m^2$
, and we denote by
![]() $\Delta :=Z\setminus A(V)$
the boundary. Finally, we fix a compactification X of V with snc boundary D such that the quasi-Albanese map
$\Delta :=Z\setminus A(V)$
the boundary. Finally, we fix a compactification X of V with snc boundary D such that the quasi-Albanese map
![]() $a_V\colon V\to A(V)$
extends to a morphism
$a_V\colon V\to A(V)$
extends to a morphism
![]() $g\colon X \to Z$
.
$g\colon X \to Z$
.
We exploit the previous results to gain more information on the pair
![]() $(X,D)$
.
$(X,D)$
.
Lemma 4.8. There is a blow-down morphism
![]() $\rho \colon X\to T$
with exceptional divisor
$\rho \colon X\to T$
with exceptional divisor
![]() $\sum _{j=1}^n E_j$
(where the
$\sum _{j=1}^n E_j$
(where the
![]() $E_j$
are
$E_j$
are
![]() $-1$
-curves) such that one of the following holds:
$-1$
-curves) such that one of the following holds:
-
(a)
 $p_g(X)=0$
,
$p_g(X)=0$
,
 $h^0(D,\omega _D)=1$
, X is a rational surface, and there is a 2-connected divisor
$h^0(D,\omega _D)=1$
, X is a rational surface, and there is a 2-connected divisor
 $B\preceq D$
such that
$B\preceq D$
such that
 $K_X+B\sim \sum _{j=1}^n E_j$
and B is disjoint from
$K_X+B\sim \sum _{j=1}^n E_j$
and B is disjoint from
 $\sum _{j=1}^n E_j$
;
$\sum _{j=1}^n E_j$
; -
(b)
 $p_g(X)=1$
,
$p_g(X)=1$
,
 $h^0(D,\omega _D)=0$
, and T is a K3 surface.
$h^0(D,\omega _D)=0$
, and T is a K3 surface.
In either case, there is a divisor
![]() $B\succeq 0$
such that
$B\succeq 0$
such that
![]() $K_X+B\sim \sum _{j=1}^n E_j$
.
$K_X+B\sim \sum _{j=1}^n E_j$
.
Proof. The assumption
![]() $\overline P_1(V)=1$
implies that either
$\overline P_1(V)=1$
implies that either
![]() $p_g(X)=0$
or
$p_g(X)=0$
or
![]() $ p_g(X)=1$
; in either case, the value of
$ p_g(X)=1$
; in either case, the value of
![]() $h^0(D,\omega _D)$
can be computed by Lemma 2.12.
$h^0(D,\omega _D)$
can be computed by Lemma 2.12.
Assume first
![]() $p_g(X)=0$
. Then, by Lemma 2.12,
$p_g(X)=0$
. Then, by Lemma 2.12,
![]() $q(X)=0$
implies that
$q(X)=0$
implies that
![]() $h^0(D,\omega _D)=1$
. So there is a connected component A of D such that
$h^0(D,\omega _D)=1$
. So there is a connected component A of D such that
![]() $p_a(A)=h^0(A,\omega _A)=1$
, and by Lemma 4.4 there is a 2-connected divisor
$p_a(A)=h^0(A,\omega _A)=1$
, and by Lemma 4.4 there is a 2-connected divisor
![]() $B\preceq A$
with
$B\preceq A$
with
![]() $p_a(B)=1$
. By Lemma 4.6 and the hypothesis
$p_a(B)=1$
. By Lemma 4.6 and the hypothesis
![]() $\overline P_2(V)=1$
, X is rational and there is a blow-down morphism
$\overline P_2(V)=1$
, X is rational and there is a blow-down morphism
![]() $\rho \colon X\to T$
as in (a).
$\rho \colon X\to T$
as in (a).
Assume now
![]() $p_g(X)=1$
. In this case, X has nonnegative Kodaira dimension and we take
$p_g(X)=1$
. In this case, X has nonnegative Kodaira dimension and we take
![]() $\rho \colon X\to T$
to be the morphism to the minimal model. If X is of general type,
$\rho \colon X\to T$
to be the morphism to the minimal model. If X is of general type,
![]() $K_T^2>0$
and
$K_T^2>0$
and
![]() $h^0(X, 2K_X)=h^0(T, 2K_T)=K_T^2+\chi (\mathcal O_X)\geq 2$
, contradicting
$h^0(X, 2K_X)=h^0(T, 2K_T)=K_T^2+\chi (\mathcal O_X)\geq 2$
, contradicting
![]() $\overline P_2(V)=1$
.
$\overline P_2(V)=1$
.
If X is properly elliptic, then, because
![]() $p_g(T)=1$
and
$p_g(T)=1$
and
![]() $K_T\neq \mathcal O_T$
,
$K_T\neq \mathcal O_T$
,
![]() $h^0(T, -K_T)=0$
, and so by duality
$h^0(T, -K_T)=0$
, and so by duality
![]() $h^2(T, 2K_T)=0$
. Since
$h^2(T, 2K_T)=0$
. Since
![]() $K_T^2=0$
, by the Riemann–Roch theorem, we obtain
$K_T^2=0$
, by the Riemann–Roch theorem, we obtain
![]() $h^0(T, 2K_T)=h^1(T,2K_T)+\chi (\mathcal O_X)\geq 2$
.
$h^0(T, 2K_T)=h^1(T,2K_T)+\chi (\mathcal O_X)\geq 2$
.
So
![]() $\kappa (X)=0$
and by the classification of projective surfaces we conclude that T is a
$\kappa (X)=0$
and by the classification of projective surfaces we conclude that T is a
![]() $K3$
-surface. We have
$K3$
-surface. We have
![]() $K_X=\sum _{j=1}^n E_j$
, so in this case the last claim holds with
$K_X=\sum _{j=1}^n E_j$
, so in this case the last claim holds with
![]() $B=0$
.
$B=0$
.
Lemma 4.9. One has:
-
1.
 $h^0(X, 2K_X+D)=h^0(X, 3K_X+2D)=p_g(X)$
;
$h^0(X, 2K_X+D)=h^0(X, 3K_X+2D)=p_g(X)$
; -
2. if
 $D_i$
is the unique divisor in
$D_i$
is the unique divisor in
 $|i(K_X+D)|$
,
$|i(K_X+D)|$
,
 $i=1,2$
, then
$i=1,2$
, then
 $h^0(D_i, \omega _{D_i})=0$
.
$h^0(D_i, \omega _{D_i})=0$
.
Proof. 1. Since
![]() $D\succ 0$
and
$D\succ 0$
and
![]() $\overline P_i(V)=1$
for
$\overline P_i(V)=1$
for
![]() $i=1,2,3$
by assumption, we have
$i=1,2,3$
by assumption, we have
![]() $p_g(X)\le h^0(X, 2K_X+D) \le h^0(X, 3K_X+2D)\le 1$
. So if
$p_g(X)\le h^0(X, 2K_X+D) \le h^0(X, 3K_X+2D)\le 1$
. So if
![]() $p_g(X)=1$
the assertion is trivial.
$p_g(X)=1$
the assertion is trivial.
For
![]() $p_g(X)=0$
and
$p_g(X)=0$
and
![]() $m\ge 1$
, consider the exact sequence:
$m\ge 1$
, consider the exact sequence:
The second map in equation (4.1) is an isomorphism for
![]() $m=1$
since
$m=1$
since
![]() $q(X)=0$
, so it is nonzero for all
$q(X)=0$
, so it is nonzero for all
![]() $m\ge 1$
since D is a reduced divisor. Then
$m\ge 1$
since D is a reduced divisor. Then
![]() $\overline P_2(V)=1$
and
$\overline P_2(V)=1$
and
![]() $\overline P_3(V)=1$
imply that
$\overline P_3(V)=1$
imply that
![]() $h^0(X, 2K_X+D)=h^0(X, 3K_X+2D)=0$
.
$h^0(X, 2K_X+D)=h^0(X, 3K_X+2D)=0$
.
2. is an immediate consequence of
![]() $q(X)=0$
and of 1. (see Lemma 2.12).
$q(X)=0$
and of 1. (see Lemma 2.12).
We now turn to the study of the quasi-Albanese map.
Lemma 4.10. If the image of
![]() $a_V$
is a curve, then it is isomorphic to
$a_V$
is a curve, then it is isomorphic to
![]() $\mathbb P^1\setminus \{0,1,\infty \}$
and the general fiber of
$\mathbb P^1\setminus \{0,1,\infty \}$
and the general fiber of
![]() $a_V$
is connected.
$a_V$
is connected.
Proof. Let g as in Setting 4.7. By assumption, the image
![]() $\Gamma $
of g is a curve. Let
$\Gamma $
of g is a curve. Let
![]() $X\to \widetilde \Gamma \to \Gamma $
be the Stein factorization of g, and let
$X\to \widetilde \Gamma \to \Gamma $
be the Stein factorization of g, and let
![]() $\Gamma _0\subset \widetilde \Gamma $
be the image of V. Then by the universal property of the quasi-Albanese map,
$\Gamma _0\subset \widetilde \Gamma $
be the image of V. Then by the universal property of the quasi-Albanese map,
![]() $A(V)$
is isomorphic to
$A(V)$
is isomorphic to
![]() $A(\Gamma _0)$
. In addition, the image of
$A(\Gamma _0)$
. In addition, the image of
![]() $a_V$
is isomorphic to
$a_V$
is isomorphic to
![]() $\Gamma _0$
by Proposition 2.7. It follows that g has connected fibers; hence, the general fiber of
$\Gamma _0$
by Proposition 2.7. It follows that g has connected fibers; hence, the general fiber of
![]() $a_V$
is also connected. Finally,
$a_V$
is also connected. Finally,
![]() $\Gamma _0$
is rational, since
$\Gamma _0$
is rational, since
![]() $q(X)=0$
, and has logarithmic genus 2; hence, it is isomorphic to
$q(X)=0$
, and has logarithmic genus 2; hence, it is isomorphic to
![]() $\mathbb P^1\setminus \{0,1,\infty \}$
.
$\mathbb P^1\setminus \{0,1,\infty \}$
.
We get immediately:
Corollary 4.11. If the image of
![]() $a_V$
is a curve, then there is a fibration
$a_V$
is a curve, then there is a fibration
![]() $f\colon X\to \mathbb P^1$
such that D contains the supports
$f\colon X\to \mathbb P^1$
such that D contains the supports
![]() $F_1^s$
,
$F_1^s$
,
![]() $F_2^s$
and
$F_2^s$
and
![]() $F_3^s$
of three distinct fibers
$F_3^s$
of three distinct fibers
![]() $F_1$
,
$F_1$
,
![]() $F_2$
and
$F_2$
and
![]() $F_3$
of f.
$F_3$
of f.
Lemma 4.12. Let
![]() $E_j$
,
$E_j$
,
![]() $j=1,\dots n$
, be the
$j=1,\dots n$
, be the
![]() $-1$
-curves contracted by the blow-down morphism
$-1$
-curves contracted by the blow-down morphism
![]() $\rho \colon X\to T$
of Lemma 4.8.
$\rho \colon X\to T$
of Lemma 4.8.
Then
![]() $ E_jF_i^s\geq 0$
for all
$ E_jF_i^s\geq 0$
for all
![]() $j,i$
.
$j,i$
.
Proof. Assume by contradiction that
![]() $E_jF_1^s< 0$
. Then
$E_jF_1^s< 0$
. Then
![]() $E_j$
and
$E_j$
and
![]() $F_1^s$
have common components. Write
$F_1^s$
have common components. Write
![]() $E_j=A+C_1$
and
$E_j=A+C_1$
and
![]() $F_1^s=A+C_2$
, where
$F_1^s=A+C_2$
, where
![]() $A\succ 0$
and
$A\succ 0$
and
![]() $C_1,C_2 \succeq 0$
have no common components. Note that
$C_1,C_2 \succeq 0$
have no common components. Note that
![]() $C_2\succ 0$
otherwise blowing down
$C_2\succ 0$
otherwise blowing down
![]() $E_j$
we would contract the whole fiber. Now,
$E_j$
we would contract the whole fiber. Now,
![]() $E_jF_1^s< 0$
yields
$E_jF_1^s< 0$
yields
![]() $A^2+AC_1+AC_2+C_1C_2<0$
. But, because
$A^2+AC_1+AC_2+C_1C_2<0$
. But, because
![]() $E_j$
is a
$E_j$
is a
![]() $(-1)$
-curve,
$(-1)$
-curve,
![]() $E_jA=A^2+AC_1\geq -1$
(see [Reference Lorenzo, Mendes Lopes and Pardini15, Prop. 3.2]) and because
$E_jA=A^2+AC_1\geq -1$
(see [Reference Lorenzo, Mendes Lopes and Pardini15, Prop. 3.2]) and because
![]() $F_1^s$
is 1-connected
$F_1^s$
is 1-connected
![]() $AC_2\geq 1$
. Since
$AC_2\geq 1$
. Since
![]() $C_1C_2\geq 0$
, we have a contradiction.
$C_1C_2\geq 0$
, we have a contradiction.
Lemma 4.13. Let
![]() $E_j$
,
$E_j$
,
![]() $j=1,\dots n$
, be the
$j=1,\dots n$
, be the
![]() $-1$
-curves contracted by the blow down-morphism
$-1$
-curves contracted by the blow down-morphism
![]() $\rho \colon X\to T$
of Lemma 4.8.
$\rho \colon X\to T$
of Lemma 4.8.
Then
![]() $\sum _{j=1}^n E_j+D$
has at most one component transversal to f.
$\sum _{j=1}^n E_j+D$
has at most one component transversal to f.
Proof. Let
![]() $ M_1,M_2$
be two distinct components of
$ M_1,M_2$
be two distinct components of
![]() $\sum _{j=1}^n E_j+D$
tranversal to f. Then because
$\sum _{j=1}^n E_j+D$
tranversal to f. Then because
![]() $F_i^s$
is the support of a full fiber
$F_i^s$
is the support of a full fiber
![]() $M_k(\sum _{i=1}^3 F_i^s)\geq 3$
for
$M_k(\sum _{i=1}^3 F_i^s)\geq 3$
for
![]() $k=1,2$
yielding
$k=1,2$
yielding
![]() $p_a(M_1+M_2+\sum _{i=1}^3 F_i^s) \geq 2$
and so, by Lemma 2.12,
$p_a(M_1+M_2+\sum _{i=1}^3 F_i^s) \geq 2$
and so, by Lemma 2.12,
![]() $h^0(X, K_X+M_1+M_2+\sum _{i=1}^3 F_i^s)\geq 2$
.
$h^0(X, K_X+M_1+M_2+\sum _{i=1}^3 F_i^s)\geq 2$
.
By Lemma 4.8, there is a divisor
![]() $0\preceq B\preceq D$
such that
$0\preceq B\preceq D$
such that
![]() $K_X+B\sim \sum _j E_j$
. Since
$K_X+B\sim \sum _j E_j$
. Since
![]() $M_1+M_2+\sum _{i=1}^3 F_i^s \leq \sum _{j=1}^n E_j+D\in |K_X+B+D|$
, we obtain
$M_1+M_2+\sum _{i=1}^3 F_i^s \leq \sum _{j=1}^n E_j+D\in |K_X+B+D|$
, we obtain
![]() $h^0(X, 2K_X+B+D)\geq 2$
, which contradicts
$h^0(X, 2K_X+B+D)\geq 2$
, which contradicts
![]() $\overline P_2(V)=1$
.
$\overline P_2(V)=1$
.
Corollary 4.14. Assume
![]() $p_g(X)=0$
, and let
$p_g(X)=0$
, and let
![]() $0\prec B\preceq D$
be the divisor such that
$0\prec B\preceq D$
be the divisor such that
![]() $K_X+B\sim \sum _j E_j$
(cf. Lemma 4.8). If B has components in common with
$K_X+B\sim \sum _j E_j$
(cf. Lemma 4.8). If B has components in common with
![]() $\sum _{i=1}^3 F_i^s$
, then one of the following happens:
$\sum _{i=1}^3 F_i^s$
, then one of the following happens:
-
(a)
 $B\leq F_i^s$
for some
$B\leq F_i^s$
for some
 $i\in \{1,2,3\}$
, or
$i\in \{1,2,3\}$
, or -
(b) B has a unique component H transversal to f and
 $B-H$
is contained in, say,
$B-H$
is contained in, say,
 $F_1^s$
. Furthermore,
$F_1^s$
. Furthermore,
 $HF_1^s=2$
and
$HF_1^s=2$
and
 $HF_i^s=1$
for
$HF_i^s=1$
for
 $i=2,3$
.
$i=2,3$
.
Proof. Suppose no component of B is transversal to f. Then because B is connected and we are assuming that B has common components with
![]() $\sum F_i^s$
, we have statement (a).
$\sum F_i^s$
, we have statement (a).
If there is a component H of B transversal to f, the assumption that
![]() $ B$
has common components with
$ B$
has common components with
![]() $\sum _{i=1}^3 F_i^s$
implies
$\sum _{i=1}^3 F_i^s$
implies
![]() $B-H\neq 0$
. Recall that, by Lemma 4.8, the divisor B is
$B-H\neq 0$
. Recall that, by Lemma 4.8, the divisor B is
![]() $2$
-connected and
$2$
-connected and
![]() $p_a(B)=1$
, so, by Lemma 4.5,
$p_a(B)=1$
, so, by Lemma 4.5,
![]() $H\simeq \mathbb P^1$
and
$H\simeq \mathbb P^1$
and
![]() $B-H$
is connected. From Lemma 4.13,
$B-H$
is connected. From Lemma 4.13,
![]() $B-H$
is contained in fibers of f, and since
$B-H$
is contained in fibers of f, and since
![]() $B-H$
is connected, we obtain
$B-H$
is connected, we obtain
![]() $B-H$
contained in
$B-H$
contained in
![]() $F_i^s$
for one of
$F_i^s$
for one of
![]() $i=1,2,3$
, say
$i=1,2,3$
, say
![]() $F_1^s$
.
$F_1^s$
.
In this case,
![]() $HF_1^s\geq 2$
(since B is 2-connected) and
$HF_1^s\geq 2$
(since B is 2-connected) and
![]() $HF_i^s\geq 1$
for
$HF_i^s\geq 1$
for
![]() $i=2,3$
because
$i=2,3$
because
![]() $F_i^s$
is the support of a full fiber. Now,
$F_i^s$
is the support of a full fiber. Now,
![]() $p_a(H+\sum _{i=1}^3 F_i^s)\geq p_a(H)+\sum _{i=1}^3 p_a(F_i^s) + H(\sum _{i=1}^3F_i^s)-3$
. Since
$p_a(H+\sum _{i=1}^3 F_i^s)\geq p_a(H)+\sum _{i=1}^3 p_a(F_i^s) + H(\sum _{i=1}^3F_i^s)-3$
. Since
![]() $h^0(D,\omega _D)=1$
(cf. Lemma 4.8), D cannot contain an effective divisor with
$h^0(D,\omega _D)=1$
(cf. Lemma 4.8), D cannot contain an effective divisor with
![]() $p_a\geq 2$
and so necessarily
$p_a\geq 2$
and so necessarily
![]() $HF_1^s=2$
and
$HF_1^s=2$
and
![]() $HF_i^s= 1$
for
$HF_i^s= 1$
for
![]() $i=2,3$
.
$i=2,3$
.
Lemma 4.15. Let
![]() $E_j$
,
$E_j$
,
![]() $j=1,\dots n$
, be the
$j=1,\dots n$
, be the
![]() $-1$
-curves contracted by the blow-down morphism
$-1$
-curves contracted by the blow-down morphism
![]() $\rho \colon X\to T$
, and let
$\rho \colon X\to T$
, and let
![]() $B\preceq D$
be the divisor such that
$B\preceq D$
be the divisor such that
![]() $K_X+B\sim \sum _j E_j$
(cf. Lemma 4.8):
$K_X+B\sim \sum _j E_j$
(cf. Lemma 4.8):
-
1. if
 $F_i^s\leq D-B$
, then
$F_i^s\leq D-B$
, then
 $ E_jF_i^s\leq 1$
for all
$ E_jF_i^s\leq 1$
for all
 $E_j$
;
$E_j$
; -
2. the general fiber F of f satisfies
 $F\sum _{j=1}^nE_j=0$
.
$F\sum _{j=1}^nE_j=0$
.
Proof. 1. Assume that
![]() $E_jF_i^s\geq 2$
. Then
$E_jF_i^s\geq 2$
. Then
![]() $h^0(E_j+F_i^s,\omega _{E_j+F_i^s})=p_a(E_j+F_i^s)\geq p_a(F_i^s)+1\geq 1$
, and so since by the assumption
$h^0(E_j+F_i^s,\omega _{E_j+F_i^s})=p_a(E_j+F_i^s)\geq p_a(F_i^s)+1\geq 1$
, and so since by the assumption
![]() $F_i^s\leq D-B$
, we have
$F_i^s\leq D-B$
, we have
![]() $E_j+F_i^s\leq D_1\in |K_X+D|$
, contradicting Lemma 4.9 (cf. Lemma 2.11).
$E_j+F_i^s\leq D_1\in |K_X+D|$
, contradicting Lemma 4.9 (cf. Lemma 2.11).
2. Suppose otherwise, that is, that there is an irreducible curve
![]() $M\preceq \sum _{j=1}^n E_j$
transversal to the fibration f. Since B and
$M\preceq \sum _{j=1}^n E_j$
transversal to the fibration f. Since B and
![]() $ \sum _{j=1}^n E_j$
are disjoint (cf. Lemma 4.8), by Lemma 4.13 the divisor B must be contained in a fiber of f.
$ \sum _{j=1}^n E_j$
are disjoint (cf. Lemma 4.8), by Lemma 4.13 the divisor B must be contained in a fiber of f.
Since each
![]() $F_i^s$
is the support of a whole fiber, we have
$F_i^s$
is the support of a whole fiber, we have
![]() $MF_i^s\geq 1$
. Since
$MF_i^s\geq 1$
. Since
![]() $M\preceq \sum _{j=1}^n E_j$
, we have
$M\preceq \sum _{j=1}^n E_j$
, we have
![]() $M^2=-l <0$
. Then among the
$M^2=-l <0$
. Then among the
![]() $E_j$
’s, there are
$E_j$
’s, there are
![]() $E_{p_1}, \ldots ,E_{p_{l-1}}$
such that
$E_{p_1}, \ldots ,E_{p_{l-1}}$
such that
![]() $E_m=M+\sum _{k=1}^{l-1} E_{p_k}$
is one of the
$E_m=M+\sum _{k=1}^{l-1} E_{p_k}$
is one of the
![]() $E_j$
. This is true by [Reference Lorenzo, Mendes Lopes and Pardini15, Lemma 3.2] if
$E_j$
. This is true by [Reference Lorenzo, Mendes Lopes and Pardini15, Lemma 3.2] if
![]() $l=1$
, by [Reference Lorenzo, Mendes Lopes and Pardini15, Prop. 4.1] if
$l=1$
, by [Reference Lorenzo, Mendes Lopes and Pardini15, Prop. 4.1] if
![]() $l=2$
and by [Reference Lorenzo, Mendes Lopes and Pardini15, Prop. 4.2] if
$l=2$
and by [Reference Lorenzo, Mendes Lopes and Pardini15, Prop. 4.2] if
![]() $l>2$
.
$l>2$
.
Since
![]() $E_{p_k}F_i^s\geq 0$
for all
$E_{p_k}F_i^s\geq 0$
for all
![]() $k=1,\dots l-1$
and
$k=1,\dots l-1$
and
![]() $i=1,2,3$
by Lemma 4.12, we obtain
$i=1,2,3$
by Lemma 4.12, we obtain
![]() $E_m(\sum F_i^s)\geq 3$
. Since
$E_m(\sum F_i^s)\geq 3$
. Since
![]() $E_m(E_m+\sum _{i=1}^3F_i^s)\geq 2$
, one obtains
$E_m(E_m+\sum _{i=1}^3F_i^s)\geq 2$
, one obtains
-
(a)
 $p_a(2E_m+\sum _{i=1}^3F_i^s)\geq 2$
if
$p_a(2E_m+\sum _{i=1}^3F_i^s)\geq 2$
if
 $p_g(X)=0$
and
$p_g(X)=0$
and
 $B\neq 0$
is contained in one of the
$B\neq 0$
is contained in one of the
 $F_i^s$
.
$F_i^s$
. -
(b)
 $p_a(2E_m+\sum _{i=1}^3F_i^s)\geq 1$
, if
$p_a(2E_m+\sum _{i=1}^3F_i^s)\geq 1$
, if
 $p_g(X)=1$
or
$p_g(X)=1$
or
 $p_g(X)=0$
and B is not contained in
$p_g(X)=0$
and B is not contained in
 $\sum _{i=1}^3F_i^s$
.
$\sum _{i=1}^3F_i^s$
.
Since
![]() $E_m\leq K_X+B$
, we have
$E_m\leq K_X+B$
, we have
![]() $2E_m+\sum F_i^s\leq 2K_X+2B+D$
, which in case (a) yields
$2E_m+\sum F_i^s\leq 2K_X+2B+D$
, which in case (a) yields
![]() $h^0(X, 3K_X+ 2B+ D)\geq 2$
, contradicting
$h^0(X, 3K_X+ 2B+ D)\geq 2$
, contradicting
![]() $\overline P_3(V)=1$
. In case (b), we have
$\overline P_3(V)=1$
. In case (b), we have
![]() $2E_m+\sum F_i^s\leq 2(K_X+B)+ (D-B)=2K_X+B+D$
, yielding
$2E_m+\sum F_i^s\leq 2(K_X+B)+ (D-B)=2K_X+B+D$
, yielding
![]() $h^0(X, 3K_X+B+ D)\geq p_g(X)+1$
and contradicting Lemma 4.9.
$h^0(X, 3K_X+B+ D)\geq p_g(X)+1$
and contradicting Lemma 4.9.
Corollary 4.16. The fibration
![]() $f\colon X\to \mathbb P^1$
descends to a fibration
$f\colon X\to \mathbb P^1$
descends to a fibration
![]() $\bar f\colon T\to \mathbb P^1$
.
$\bar f\colon T\to \mathbb P^1$
.
Lemma 4.17. The general fiber F of
![]() $\bar f$
has genus
$\bar f$
has genus
![]() $0$
.
$0$
.
Proof. Clearly, f and
![]() $\bar f$
have the same general fiber by construction. Since
$\bar f$
have the same general fiber by construction. Since
![]() $K_T+\rho (B)=0$
and F is nef, we have
$K_T+\rho (B)=0$
and F is nef, we have
![]() $FK_T=-F\rho (B)\le 0$
, so either
$FK_T=-F\rho (B)\le 0$
, so either
![]() $FK_T=0$
and F has genus 1, or
$FK_T=0$
and F has genus 1, or
![]() $K_TF=-2$
and F is smooth rational.
$K_TF=-2$
and F is smooth rational.
Assume by contradiction that F has genus
![]() $1$
. In case
$1$
. In case
![]() $p_g(X)=0$
, all the components of B are contracted by f since
$p_g(X)=0$
, all the components of B are contracted by f since
![]() $F\rho (B)=0$
, so B, being connected, is contained in a fiber of f and we may assume that B and
$F\rho (B)=0$
, so B, being connected, is contained in a fiber of f and we may assume that B and
![]() $F_2^s+F_3^s$
are disjoint. The divisor
$F_2^s+F_3^s$
are disjoint. The divisor
![]() $D_0=B+F_2^s+F_3^s$
satisfies
$D_0=B+F_2^s+F_3^s$
satisfies
![]() $h^0(D_0,\omega _{D_0})=p_a(B)+p_a(F_2^s)+p_a(F_3^s)=1+p_a(F_2^s)+p_a(F_3^s)$
. Since
$h^0(D_0,\omega _{D_0})=p_a(B)+p_a(F_2^s)+p_a(F_3^s)=1+p_a(F_2^s)+p_a(F_3^s)$
. Since
![]() $h^0(D_0,\omega _{D_0})\le h^0(D,\omega _{D})=\overline P_1(V)=1$
(cf. Lemma 2.12), we conclude that
$h^0(D_0,\omega _{D_0})\le h^0(D,\omega _{D})=\overline P_1(V)=1$
(cf. Lemma 2.12), we conclude that
![]() $p_a(F_2^s)=p_a(F_3^s)=0$
. If
$p_a(F_2^s)=p_a(F_3^s)=0$
. If
![]() $p_g(X)=1$
, applying the same argument to
$p_g(X)=1$
, applying the same argument to
![]() $D_0:=F_1^s+F_2^s+F_3^s$
, we obtain
$D_0:=F_1^s+F_2^s+F_3^s$
, we obtain
![]() $p_a(F_i^s)=0$
for
$p_a(F_i^s)=0$
for
![]() $i=1,2,3$
.
$i=1,2,3$
.
Denote by
![]() $\overline F_i$
the full fiber of
$\overline F_i$
the full fiber of
![]() $\bar f$
corresponding to
$\bar f$
corresponding to
![]() $F_i^s$
for
$F_i^s$
for
![]() $i=1,2,3$
. If
$i=1,2,3$
. If
![]() $p_g(X)=1$
, then T is minimal by Lemma 4.8; hence,
$p_g(X)=1$
, then T is minimal by Lemma 4.8; hence,
![]() $\overline F_i$
does not contain
$\overline F_i$
does not contain
![]() $-1$
-curves for
$-1$
-curves for
![]() $i=1,2,3$
. If
$i=1,2,3$
. If
![]() $p_g(X)=0$
and E is an irreducible
$p_g(X)=0$
and E is an irreducible
![]() $-1$
curve of T, then
$-1$
curve of T, then
![]() $\rho (B)E=-K_TE=1$
; namely, E meets
$\rho (B)E=-K_TE=1$
; namely, E meets
![]() $\rho (B)$
. So, in this case, there is no
$\rho (B)$
. So, in this case, there is no
![]() $-1$
-curve contained in
$-1$
-curve contained in
![]() $\overline F_2+\overline F_3$
.
$\overline F_2+\overline F_3$
.
By Lemmas 4.12 and 4.15, we know that
![]() $0\leq F_i^s E_j\leq 1$
for
$0\leq F_i^s E_j\leq 1$
for
![]() $i=2,3$
and also for
$i=2,3$
and also for
![]() $i=1$
if
$i=1$
if
![]() $p_g(X)=1$
. Therefore,
$p_g(X)=1$
. Therefore,
![]() $\rho ^*(\rho (F_i^s))\leq F_i^s+\sum _{j=1}^n E_j$
. So the reduced divisor
$\rho ^*(\rho (F_i^s))\leq F_i^s+\sum _{j=1}^n E_j$
. So the reduced divisor
![]() $\rho (F_i^s)$
still has
$\rho (F_i^s)$
still has
![]() $p_a=0$
for
$p_a=0$
for
![]() $i=1,2,3$
in the case
$i=1,2,3$
in the case
![]() $p_g(X)=1$
and for
$p_g(X)=1$
and for
![]() $i=2,3$
in the case
$i=2,3$
in the case
![]() $p_g(X)=0$
.
$p_g(X)=0$
.
For
![]() $i=1,2,3$
in the case
$i=1,2,3$
in the case
![]() $p_g(X)=1$
and for
$p_g(X)=1$
and for
![]() $i=2,3$
in the case
$i=2,3$
in the case
![]() $p_g(X)=0$
, the elliptic fibers
$p_g(X)=0$
, the elliptic fibers
![]() $\overline F_i$
, since they do not contain
$\overline F_i$
, since they do not contain
![]() $-1$
-curves and have support with
$-1$
-curves and have support with
![]() $p_a=0$
, must be of type
$p_a=0$
, must be of type
![]() $^*$
(see [Reference Barth, Hulek, Peters and Van de Ven2, Chp.V, §7]). Note that, in particular, the
$^*$
(see [Reference Barth, Hulek, Peters and Van de Ven2, Chp.V, §7]). Note that, in particular, the
![]() $\overline F_i$
cannot be multiple fibers of
$\overline F_i$
cannot be multiple fibers of
![]() $\bar f$
(see [Reference Barth, Hulek, Peters and Van de Ven2, Chp.V, §7]). So, if
$\bar f$
(see [Reference Barth, Hulek, Peters and Van de Ven2, Chp.V, §7]). So, if
![]() $\overline F$
is a fiber of type
$\overline F$
is a fiber of type
![]() $^*$
with support
$^*$
with support
![]() $F_0$
, we have
$F_0$
, we have
![]() $2F_0\geq \overline F$
if
$2F_0\geq \overline F$
if
![]() $\overline F$
is of type
$\overline F$
is of type
![]() $I_b^*$
(
$I_b^*$
(
![]() $=\tilde D_{4+b}$
) and
$=\tilde D_{4+b}$
) and
![]() $3F_0\geq \overline F$
if
$3F_0\geq \overline F$
if
![]() $\overline F$
is of type
$\overline F$
is of type
![]() $IV^*$
(
$IV^*$
(
![]() $=\tilde E_6$
).
$=\tilde E_6$
).
On the other hand, if
![]() $p_g(X)=0$
, note that the sum of the Euler numbers
$p_g(X)=0$
, note that the sum of the Euler numbers
![]() $e(\overline F_2)+e(\overline F_3)$
cannot exceed 12 since a relatively minimal elliptic fibration on a rational surface has
$e(\overline F_2)+e(\overline F_3)$
cannot exceed 12 since a relatively minimal elliptic fibration on a rational surface has
![]() $c_2=12$
. Since the Euler numbers of fibers of type
$c_2=12$
. Since the Euler numbers of fibers of type
![]() $^*$
are always bigger than
$^*$
are always bigger than
![]() $6$
except for type
$6$
except for type
![]() $I_0^*$
,
$I_0^*$
,
![]() $\overline F_2$
and
$\overline F_2$
and
![]() $\overline F_3$
must be of type
$\overline F_3$
must be of type
![]() $I_0^*$
, and so, for instance,
$I_0^*$
, and so, for instance,
![]() $ 2(F_2^s+\sum _{j=1}^n E_j)$
contains
$ 2(F_2^s+\sum _{j=1}^n E_j)$
contains
![]() $\rho ^*(\overline F_2)=F_2$
. Since
$\rho ^*(\overline F_2)=F_2$
. Since
![]() $h^0(X,F_2)=2$
, we obtain
$h^0(X,F_2)=2$
, we obtain
![]() $h^0(X, 2K_X+2B+2F_2^s)\geq 2$
, contradicting
$h^0(X, 2K_X+2B+2F_2^s)\geq 2$
, contradicting
![]() $h^0(X, 2K_X+2D)=1$
.
$h^0(X, 2K_X+2D)=1$
.
Similarly, if
![]() $p_g(X)=1$
, then the sum of the Euler numbers
$p_g(X)=1$
, then the sum of the Euler numbers
![]() $e(\overline F_1)+e(\overline F_2)+e(\overline F_3)$
cannot exceed 24. If one of the
$e(\overline F_1)+e(\overline F_2)+e(\overline F_3)$
cannot exceed 24. If one of the
![]() $\overline F_i$
is of type
$\overline F_i$
is of type
![]() $I_b^*$
, we have a contradiction as above, and if one of the
$I_b^*$
, we have a contradiction as above, and if one of the
![]() $\overline F_i$
is of type
$\overline F_i$
is of type
![]() $IV^*$
(
$IV^*$
(
![]() $=\tilde E_6$
), then
$=\tilde E_6$
), then
![]() $F_i\preceq 3F_i^s+3\sum _{j=1}^n E_j\preceq 3K_X+3D$
, contradicting
$F_i\preceq 3F_i^s+3\sum _{j=1}^n E_j\preceq 3K_X+3D$
, contradicting
![]() $h^0(X, 3K_X+3D)=1$
. On the other hand if all the
$h^0(X, 3K_X+3D)=1$
. On the other hand if all the
![]() $\overline F_i$
are of type
$\overline F_i$
are of type
![]() $II^*$
(
$II^*$
(
![]() $=\tilde E_8$
) or type
$=\tilde E_8$
) or type
![]() $III^*$
(
$III^*$
(
![]() $=\tilde E_7$
), the sum of the Euler numbers is larger than 24.
$=\tilde E_7$
), the sum of the Euler numbers is larger than 24.
Proof of Proposition 4.3.
By Lemma 4.17, the general fiber F of f has genus
![]() $0$
, and in particular, we have
$0$
, and in particular, we have
![]() $p_g(X)=0$
. Since
$p_g(X)=0$
. Since
![]() $K_XF=-2$
, we have
$K_XF=-2$
, we have
![]() $BF=2$
, and so B has a component H transversal to f. If B has no common component with
$BF=2$
, and so B has a component H transversal to f. If B has no common component with
![]() $F_i^s$
,
$F_i^s$
,
![]() $i=1,2,3$
, then we set
$i=1,2,3$
, then we set
![]() $D_0=B+F_1^s+F_2^s+F_3^s$
and we compute
$D_0=B+F_1^s+F_2^s+F_3^s$
and we compute
Since
![]() $D_0$
is reduced and connected, we have
$D_0$
is reduced and connected, we have
![]() $p_a(D_0)=h^0(D_0,\omega _{D_0})\le h^0(D,\omega _D) = \overline P_1(V)=1$
(cf. Lemma 2.11 and 2.12) and we conclude that
$p_a(D_0)=h^0(D_0,\omega _{D_0})\le h^0(D,\omega _D) = \overline P_1(V)=1$
(cf. Lemma 2.11 and 2.12) and we conclude that
![]() $p_a(F_i^s)=0$
,
$p_a(F_i^s)=0$
,
![]() $BF_i^s=1$
for
$BF_i^s=1$
for
![]() $i=1,2,3$
. On the other hand, if B and
$i=1,2,3$
. On the other hand, if B and
![]() $F_1^s+F_2^s+F_3^s$
have common components, then by Corollary 4.14 at least two of the
$F_1^s+F_2^s+F_3^s$
have common components, then by Corollary 4.14 at least two of the
![]() $F_i^s$
, say
$F_i^s$
, say
![]() $F_2^s$
and
$F_2^s$
and
![]() $F_3^s$
, have no common components with B and satisfy
$F_3^s$
, have no common components with B and satisfy
![]() $F_i^s B=1$
for
$F_i^s B=1$
for
![]() $i=2,3$
.
$i=2,3$
.
So in any case,
![]() $F_2^s$
contains a unique irreducible curve
$F_2^s$
contains a unique irreducible curve
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\Gamma B\neq 0$
. Since
$\Gamma B\neq 0$
. Since
![]() $BF=2$
for a general fiber of F and
$BF=2$
for a general fiber of F and
![]() $BF_2^s=1$
,
$BF_2^s=1$
,
![]() $\Gamma $
appears with multiplicity
$\Gamma $
appears with multiplicity
![]() $2$
in the full fiber
$2$
in the full fiber
![]() $F_2$
containing
$F_2$
containing
![]() $F_2^s$
. The curve
$F_2^s$
. The curve
![]() $\Gamma $
is not contracted by
$\Gamma $
is not contracted by
![]() $\rho $
since
$\rho $
since
![]() $B\Gamma =1$
and B does not meet the
$B\Gamma =1$
and B does not meet the
![]() $\rho $
-exceptional curves.
$\rho $
-exceptional curves.
Write
![]() $\rho ^*(\rho (\Gamma ))=\Gamma +Z$
, with Z an exceptional divisor. Since
$\rho ^*(\rho (\Gamma ))=\Gamma +Z$
, with Z an exceptional divisor. Since
![]() $B= \rho ^*(\rho (B))$
, the projection formula gives
$B= \rho ^*(\rho (B))$
, the projection formula gives
Since
![]() $K_T+\rho (B)=0$
, we have
$K_T+\rho (B)=0$
, we have
![]() $K_T\rho (\Gamma )=-1$
. The curve
$K_T\rho (\Gamma )=-1$
. The curve
![]() $\rho (\Gamma )$
is contained in a fiber of
$\rho (\Gamma )$
is contained in a fiber of
![]() $\bar f$
, so
$\bar f$
, so
![]() $\rho (\Gamma )^2\le 0$
and
$\rho (\Gamma )^2\le 0$
and
![]() $\rho (\Gamma )$
is a
$\rho (\Gamma )$
is a
![]() $-1$
-curve by the adjunction formula. So
$-1$
-curve by the adjunction formula. So
![]() $\overline F_2=2\rho (\Gamma ) +C$
, where C does not contain
$\overline F_2=2\rho (\Gamma ) +C$
, where C does not contain
![]() $\rho (\Gamma )$
. The components of C do not meet
$\rho (\Gamma )$
. The components of C do not meet
![]() $\rho (B)=-K_T$
; hence, they are all
$\rho (B)=-K_T$
; hence, they are all
![]() $-2$
-curves. From
$-2$
-curves. From
![]() $\rho (\Gamma ) \overline F_2=0$
, we get
$\rho (\Gamma ) \overline F_2=0$
, we get
![]() $C\rho (\Gamma )=2$
. If there are two distinct components
$C\rho (\Gamma )=2$
. If there are two distinct components
![]() $N_1$
and
$N_1$
and
![]() $N_2$
of C with
$N_2$
of C with
![]() $\rho (\Gamma )N_i=1$
, then
$\rho (\Gamma )N_i=1$
, then
![]() $N_1$
and
$N_1$
and
![]() $N_2$
are disjoint since the dual graph of
$N_2$
are disjoint since the dual graph of
![]() $\overline F_2$
is a tree. So
$\overline F_2$
is a tree. So
![]() $(2\rho (\Gamma )+N_1+N_2)^2=0$
and therefore
$(2\rho (\Gamma )+N_1+N_2)^2=0$
and therefore
![]() $\overline F_2=2\rho (\Gamma )+N_1+N_2$
. If there is only a component N of G with
$\overline F_2=2\rho (\Gamma )+N_1+N_2$
. If there is only a component N of G with
![]() $N\rho (\Gamma )=1$
, then
$N\rho (\Gamma )=1$
, then
![]() $N $
appears in
$N $
appears in
![]() $\overline F_2$
with multiplicity 2 and
$\overline F_2$
with multiplicity 2 and
![]() $M_1:=\rho (\Gamma )+N$
is a (reducible and reduced)
$M_1:=\rho (\Gamma )+N$
is a (reducible and reduced)
![]() $-1$
-curve such that
$-1$
-curve such that
![]() $\overline F_2=2M_1+C_1$
and
$\overline F_2=2M_1+C_1$
and
![]() $C_1$
and
$C_1$
and
![]() $M_1$
have no common component. So we may repeat the previous argument and either write
$M_1$
have no common component. So we may repeat the previous argument and either write
![]() $\overline F_2=2M_1+N_1+N_2$
, where
$\overline F_2=2M_1+N_1+N_2$
, where
![]() $N_1,N_2$
are disjoint
$N_1,N_2$
are disjoint
![]() $-2$
-curves contained in
$-2$
-curves contained in
![]() $C_1$
with
$C_1$
with
![]() $N_i M_1=1$
, or
$N_i M_1=1$
, or
![]() $\overline F_2=2(M_1+N)+C_2$
, where N is a component of C such that
$\overline F_2=2(M_1+N)+C_2$
, where N is a component of C such that
![]() $M_2:=M_1+N$
is a
$M_2:=M_1+N$
is a
![]() $-1$
-curve and
$-1$
-curve and
![]() $C_2$
and
$C_2$
and
![]() $M_2$
have no common component. This process must of course terminate, showing that
$M_2$
have no common component. This process must of course terminate, showing that
![]() $\overline F_2=2M_0+N_1+N_2$
, where
$\overline F_2=2M_0+N_1+N_2$
, where
![]() $M_0$
is a reduced
$M_0$
is a reduced
![]() $-1$
-curve, and
$-1$
-curve, and
![]() $N_1$
and
$N_1$
and
![]() $N_2$
are disjoint
$N_2$
are disjoint
![]() $-2$
-curves not contained in
$-2$
-curves not contained in
![]() $M_0$
. In particular, we have shown that
$M_0$
. In particular, we have shown that
![]() $\overline F_2$
has no component of multiplicity
$\overline F_2$
has no component of multiplicity
![]() $>2$
.
$>2$
.
Since (as in the proof of Lemma 4.17)
![]() $\rho ^*(\rho (F_2^s))\leq F_2^s+\sum _{j=1}^n E_j$
, we conclude that
$\rho ^*(\rho (F_2^s))\leq F_2^s+\sum _{j=1}^n E_j$
, we conclude that
![]() $2F_2^s+2\sum _{j=1}^n E_j$
contains the full fiber
$2F_2^s+2\sum _{j=1}^n E_j$
contains the full fiber
![]() $F_2$
of f, and as in the in the proof of Lemma 4.17, we obtain
$F_2$
of f, and as in the in the proof of Lemma 4.17, we obtain
![]() $h^0(X, 2K_X+ 2B+2F_2^s)\geq 2$
, contradicting
$h^0(X, 2K_X+ 2B+2F_2^s)\geq 2$
, contradicting
![]() $h^0(X, 2K_X+2D)=\overline P_2(V)=1$
.
$h^0(X, 2K_X+2D)=\overline P_2(V)=1$
.
So we have excluded all the possibilities for the genus of the general fiber F of the fibration induced by
![]() $a_V$
if
$a_V$
if
![]() $a_V$
is not dominant, and the proof is complete.
$a_V$
is not dominant, and the proof is complete.
Example 4.18. The hypothesis
![]() $\overline P_3(V)=1$
in Proposition 4.3 is necessary. A K3 surface with an elliptic fibration with three singular fibers of type
$\overline P_3(V)=1$
in Proposition 4.3 is necessary. A K3 surface with an elliptic fibration with three singular fibers of type
![]() $IV^*$
(cf. the proof of Lemma 4.17) does exist. Take for instance the elliptic curve C with an automorphism h of order 3. Let
$IV^*$
(cf. the proof of Lemma 4.17) does exist. Take for instance the elliptic curve C with an automorphism h of order 3. Let
![]() $\mathbb Z/3$
act on
$\mathbb Z/3$
act on
![]() $C \times C$
by
$C \times C$
by
![]() $(x,y)\mapsto (hx,h^2y)$
, and denote by
$(x,y)\mapsto (hx,h^2y)$
, and denote by
![]() $X_0$
the quotient surface. Then
$X_0$
the quotient surface. Then
![]() $X_0$
has nine singular points of type
$X_0$
has nine singular points of type
![]() $A_2$
, and the first projection
$A_2$
, and the first projection
![]() $C\times C\to C$
descends to an isotrivial elliptic fibration
$C\times C\to C$
descends to an isotrivial elliptic fibration
![]() $X_0\to C/\mathbb Z_3\cong \mathbb P^1$
with three ‘triple’ fibers, each containing three of the nine singular points. The minimal resolution X of
$X_0\to C/\mathbb Z_3\cong \mathbb P^1$
with three ‘triple’ fibers, each containing three of the nine singular points. The minimal resolution X of
![]() $X_0$
is a K3 surface with an isotrivial elliptic fibration with three fibers of type
$X_0$
is a K3 surface with an isotrivial elliptic fibration with three fibers of type
![]() $IV^*$
. Alternatively, X can be constructed as the minimal resolution of a simple
$IV^*$
. Alternatively, X can be constructed as the minimal resolution of a simple
![]() $\mathbb Z_3$
-cover of
$\mathbb Z_3$
-cover of
![]() $\mathbb P^1\times \mathbb P^1$
branched over three fibers of one of the fibrations plus three fibers of the other.
$\mathbb P^1\times \mathbb P^1$
branched over three fibers of one of the fibrations plus three fibers of the other.
Consider the surface
![]() $V:=X\backslash \{F_1^s,\;F_2^s,\;F_3^s\}$
, where the
$V:=X\backslash \{F_1^s,\;F_2^s,\;F_3^s\}$
, where the
![]() $F_i^s$
denote the supports of the three fibers of type IV*. Then V has
$F_i^s$
denote the supports of the three fibers of type IV*. Then V has
![]() $\overline P_1(V)=\overline P_2(V)=1$
and
$\overline P_1(V)=\overline P_2(V)=1$
and
![]() $\overline q(V)=2$
(see Proposition 2.1), and its quasi-Albanese map is the restriction of the elliptic fibration
$\overline q(V)=2$
(see Proposition 2.1), and its quasi-Albanese map is the restriction of the elliptic fibration
![]() $X\to \mathbb P^1$
, and so it is not dominant.
$X\to \mathbb P^1$
, and so it is not dominant.
5 Proof of Theorem A
Thanks to what we have proven in the previous section, we know that in the assumptions of Theorem A the quasi-Albanese map of V is dominant. Since V and
![]() $\operatorname {Alb}(V)$
have the same dimension, we can conclude that
$\operatorname {Alb}(V)$
have the same dimension, we can conclude that
![]() $a_V$
is generically finite. In particular, there is a generically finite morphism
$a_V$
is generically finite. In particular, there is a generically finite morphism
![]() $g:X\rightarrow Z$
, where Z is the compactification of
$g:X\rightarrow Z$
, where Z is the compactification of
![]() $\operatorname {Alb}(V)$
described in Proposition 2.3. Now, our proof boils down to the following two facts
$\operatorname {Alb}(V)$
described in Proposition 2.3. Now, our proof boils down to the following two facts
-
1. the morphism g has degree 1;
-
2. all the components of D that are not mapped to the boundary
 $\Delta $
of
$\Delta $
of
 $\operatorname {Alb}(V)$
are contracted by g.
$\operatorname {Alb}(V)$
are contracted by g.
When
![]() $q(V)=2$
, the first assertion is Corollary 3.2. The second statement can be proven by contradiction (see §5.2).
$q(V)=2$
, the first assertion is Corollary 3.2. The second statement can be proven by contradiction (see §5.2).
The situation is more involved when
![]() $q(V)<2$
. We start by proving a slightly weaker version of assertion 2 (Lemma 5.5), and we use it to show that the finite part of the Stein factorization of g is étale over
$q(V)<2$
. We start by proving a slightly weaker version of assertion 2 (Lemma 5.5), and we use it to show that the finite part of the Stein factorization of g is étale over
![]() $A(V)$
(in case
$A(V)$
(in case
![]() $q(V)=1$
this requires also a topological argument). Now, the universal property of the quasi-Albanese map implies that g has indeed degree 1. Finally, we complete the proof of assertion 2 by means of a local computation.
$q(V)=1$
this requires also a topological argument). Now, the universal property of the quasi-Albanese map implies that g has indeed degree 1. Finally, we complete the proof of assertion 2 by means of a local computation.
5.1 Preliminary steps
Notation 5.1. We let V be a smooth open algebraic surface V with
![]() $\overline {q}(V)=2$
. We assume
$\overline {q}(V)=2$
. We assume
![]() $\overline P_1(V)=\overline P_2(V)=1$
if
$\overline P_1(V)=\overline P_2(V)=1$
if
![]() $q(V)\ge 1$
and
$q(V)\ge 1$
and
![]() $\overline P_1(V)=\overline P_3(V)=1$
if
$\overline P_1(V)=\overline P_3(V)=1$
if
![]() $q(V)=0$
.
$q(V)=0$
.
If
![]() $q(V)\le 1$
fix a compactification Z with boundary
$q(V)\le 1$
fix a compactification Z with boundary
![]() $\Delta $
of the quasi-Albanese variety
$\Delta $
of the quasi-Albanese variety
![]() $A(V)$
of V as follows:
$A(V)$
of V as follows:
-
• if
 $q(V)=1$
, we take Z a
$q(V)=1$
, we take Z a
 $\mathbb P^1$
-bundle over the compact part A of
$\mathbb P^1$
-bundle over the compact part A of
 $A(V)$
as in Corollary 2.4, and we write
$A(V)$
as in Corollary 2.4, and we write
 $\Delta =\Delta _1+\Delta _2$
, where
$\Delta =\Delta _1+\Delta _2$
, where
 $\Delta _i$
are disjoint sections of
$\Delta _i$
are disjoint sections of
 $Z\to A$
;
$Z\to A$
; -
• if
 $q(V)=0$
(and thus
$q(V)=0$
(and thus
 $A(V)=\mathbb G_m^2$
), we take
$A(V)=\mathbb G_m^2$
), we take
 $Z=\mathbb P^1\times \mathbb P^1$
with the obvious choice of the boundary
$Z=\mathbb P^1\times \mathbb P^1$
with the obvious choice of the boundary
 $\Delta $
.
$\Delta $
.
We fix a compactification X of V with snc boundary D such that the quasi-Albanese map
![]() $a_V\colon V\to A(V)$
extends to a morphism
$a_V\colon V\to A(V)$
extends to a morphism
![]() $g\colon X \to Z$
. In addition, we write
$g\colon X \to Z$
. In addition, we write
![]() $H:=g^{-1} (\Delta )$
(set-theoretic inverse image), and in case
$H:=g^{-1} (\Delta )$
(set-theoretic inverse image), and in case
![]() $q(V)=1$
, we also write
$q(V)=1$
, we also write
![]() $H_i=g^{-1} (\Delta _i)$
,
$H_i=g^{-1} (\Delta _i)$
,
![]() $i=1,2$
. Note that
$i=1,2$
. Note that
![]() $D\succeq H$
by construction. When
$D\succeq H$
by construction. When
![]() $q(V)=1$
, we denote by
$q(V)=1$
, we denote by
![]() $a_X\colon X\to A=A(X)$
the Albanese map of X.
$a_X\colon X\to A=A(X)$
the Albanese map of X.
The proof is quite involved, so we break it into several smaller steps, and we examine the case
![]() $q(V)\leq 1$
since, by Corollary 3.2, for
$q(V)\leq 1$
since, by Corollary 3.2, for
![]() $q(V)=2$
we already know that
$q(V)=2$
we already know that
![]() $a_V$
is birational.
$a_V$
is birational.
Lemma 5.2. If
![]() $q(V)\le 1$
, then the divisor of poles of a generator of
$q(V)\le 1$
, then the divisor of poles of a generator of
![]() $H^0(X, K_X+D)$
is a nonzero subdivisor of H. In particular,
$H^0(X, K_X+D)$
is a nonzero subdivisor of H. In particular,
![]() $p_g(X)=0$
and
$p_g(X)=0$
and
![]() $h^0(X, K_X+H) =1$
.
$h^0(X, K_X+H) =1$
.
Proof. The vector space
![]() $H^0(Z,\Omega ^1_Z(\log \Delta ))$
is generated by two logarithmic
$H^0(Z,\Omega ^1_Z(\log \Delta ))$
is generated by two logarithmic
![]() $1$
-forms
$1$
-forms
![]() $\tau _1$
and
$\tau _1$
and
![]() $\tau _2$
such that
$\tau _2$
such that
![]() $\omega :=\tau _1\wedge \tau _2$
vanishes nowhere on
$\omega :=\tau _1\wedge \tau _2$
vanishes nowhere on
![]() $A(V)$
(cf. Proposition 2.3) and has poles exactly on
$A(V)$
(cf. Proposition 2.3) and has poles exactly on
![]() $\Delta $
. More precisely, if
$\Delta $
. More precisely, if
![]() $q(V)=1$
, then we can take
$q(V)=1$
, then we can take
![]() $\tau _1$
to be the pullback of a nonzero regular 1-form on
$\tau _1$
to be the pullback of a nonzero regular 1-form on
![]() $A=A(X)$
via the projection
$A=A(X)$
via the projection
![]() $Z\to A$
and
$Z\to A$
and
![]() $\tau _2$
a logarithmic
$\tau _2$
a logarithmic
![]() $1$
-form with poles on
$1$
-form with poles on
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
(cf. proof of Corollary 2.4); if
$\Delta _2$
(cf. proof of Corollary 2.4); if
![]() $q(V)=0$
, then we can take
$q(V)=0$
, then we can take
![]() $\tau _1$
and
$\tau _1$
and
![]() $\tau _2$
to be pullbacks of nonzero logarithmic forms via the two projections
$\tau _2$
to be pullbacks of nonzero logarithmic forms via the two projections
![]() $ \mathbb G_m^2\to \mathbb G_m$
.
$ \mathbb G_m^2\to \mathbb G_m$
.
Since g is surjective by Propositions 4.2 and 4.3,
![]() $g^*\omega $
is a nonzero logarithmic form on X and a local computation shows that, if
$g^*\omega $
is a nonzero logarithmic form on X and a local computation shows that, if
![]() $\Gamma $
is an irreducible component of H not contracted by g, then
$\Gamma $
is an irreducible component of H not contracted by g, then
![]() $g^*\omega $
has a pole along
$g^*\omega $
has a pole along
![]() $\Gamma $
. On the other hand, the poles of
$\Gamma $
. On the other hand, the poles of
![]() $\omega $
are contained in H by construction.
$\omega $
are contained in H by construction.
Since
![]() $\overline P_1(V)=h^0(X, K_X+D)=1$
, it follows immediately that
$\overline P_1(V)=h^0(X, K_X+D)=1$
, it follows immediately that
![]() $p_g(X)=0$
and
$p_g(X)=0$
and
![]() $h^0(X, K_X+H) =1$
.
$h^0(X, K_X+H) =1$
.
Lemma 5.3.
-
1. If
 $q(V)=0$
, then H is connected and
$q(V)=0$
, then H is connected and
 $h^0(\omega _H)=1$
;
$h^0(\omega _H)=1$
; -
2. if
 $q(V)=1$
, then for
$q(V)=1$
, then for
 $i=1,2$
the divisor
$i=1,2$
the divisor
 $H_i$
is connected and
$H_i$
is connected and
 $h^0(\omega _{H_i})=1$
.
$h^0(\omega _{H_i})=1$
.
Proof. 1. The divisor H is connected since it is the support of the nef and big divisor
![]() $g^*\Delta $
. Lemma 2.12 gives
$g^*\Delta $
. Lemma 2.12 gives
![]() $h^0(H,\omega _H)=1$
since
$h^0(H,\omega _H)=1$
since
![]() $p_g(X)=0$
by Lemma 5.2.
$p_g(X)=0$
by Lemma 5.2.
2. Consider the exact sequence
The second map in the sequence is nonzero, since H is mapped onto A by the Albanese map
![]() $a_X$
, so in this case Lemma 2.12 gives
$a_X$
, so in this case Lemma 2.12 gives
![]() $h^0(H, \omega _H)=2$
. The divisor H is the disjoint union of
$h^0(H, \omega _H)=2$
. The divisor H is the disjoint union of
![]() $H_1$
and
$H_1$
and
![]() $H_2$
, so
$H_2$
, so
![]() $2= h^0(H, \omega _H)=h^0(H_1,\omega _{H_1})+h^0(H_2,\omega _{H_2})$
. For
$2= h^0(H, \omega _H)=h^0(H_1,\omega _{H_1})+h^0(H_2,\omega _{H_2})$
. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $S_i$
be a component of
$S_i$
be a component of
![]() $H_i$
such that
$H_i$
such that
![]() $g(S_i)=\Delta _i$
. Since
$g(S_i)=\Delta _i$
. Since
![]() $\Delta _i$
has geometric genus 1, by Lemma 2.11 we have
$\Delta _i$
has geometric genus 1, by Lemma 2.11 we have
![]() $1\le h^0(S_i,\omega _{S_i})\le h^0(H_i,\omega _{H_i})$
. So we have
$1\le h^0(S_i,\omega _{S_i})\le h^0(H_i,\omega _{H_i})$
. So we have
![]() $h^0(S_i,\omega _{S_i})= h^0(H_i,\omega _{H_i})=1$
for
$h^0(S_i,\omega _{S_i})= h^0(H_i,\omega _{H_i})=1$
for
![]() $i=1,2$
and
$i=1,2$
and
![]() $S_i$
is the only component of H with
$S_i$
is the only component of H with
![]() $p_a>0$
. Assume now by contradiction that
$p_a>0$
. Assume now by contradiction that
![]() $H_i=B_i+C_i$
, where
$H_i=B_i+C_i$
, where
![]() $B_i$
and
$B_i$
and
![]() $C_i$
are disjoint nonzero effective divisors and
$C_i$
are disjoint nonzero effective divisors and
![]() $S_i\preceq B_i$
. Then all the components of
$S_i\preceq B_i$
. Then all the components of
![]() $C_i$
are rational, and so their images via g are contained in fibers of
$C_i$
are rational, and so their images via g are contained in fibers of
![]() $Z\to A$
. Since
$Z\to A$
. Since
![]() $g(C_i)\subset \Delta _i$
, it follows that
$g(C_i)\subset \Delta _i$
, it follows that
![]() $g(C_i)$
is a finite set. So the intersection form on the set of components of
$g(C_i)$
is a finite set. So the intersection form on the set of components of
![]() $C_i$
is negative definite, contradicting the fact that
$C_i$
is negative definite, contradicting the fact that
![]() $B_i+C_i$
is the support of the nef divisor
$B_i+C_i$
is the support of the nef divisor
![]() $g^*\Delta _i$
.
$g^*\Delta _i$
.
Since
![]() $K_Z+\Delta =0$
, the logarithmic ramification formula (2.3) gives
$K_Z+\Delta =0$
, the logarithmic ramification formula (2.3) gives
![]() $K_X+D\sim \overline R_g$
. We aim to show that the components of
$K_X+D\sim \overline R_g$
. We aim to show that the components of
![]() $\overline R_g$
not contained in H are contracted to points. We begin with a simple observation:
$\overline R_g$
not contained in H are contracted to points. We begin with a simple observation:
Lemma 5.4. If
![]() $\Gamma $
is an irreducible component of
$\Gamma $
is an irreducible component of
![]() $\overline R_g$
, then
$\overline R_g$
, then
![]() $h^0(X, K_X+H+\Gamma )\le 1$
.
$h^0(X, K_X+H+\Gamma )\le 1$
.
Proof. We have
![]() $(K_X+H)+\Gamma \preceq (K_X+D)+\overline R_g=2(K_X+D)$
. So
$(K_X+H)+\Gamma \preceq (K_X+D)+\overline R_g=2(K_X+D)$
. So
![]() $h^0(X, K_X+H+\Gamma )\le \overline P_2(V)=1$
.
$h^0(X, K_X+H+\Gamma )\le \overline P_2(V)=1$
.
Lemma 5.5. Let C be the union of all the components of
![]() $ \overline R_g$
that are not contained in H and are not contracted by g. Then:
$ \overline R_g$
that are not contained in H and are not contracted by g. Then:
-
1. if
 $q(V)=0$
, then
$q(V)=0$
, then
 $C=0$
;
$C=0$
; -
2. if
 $q(V)=1$
and
$q(V)=1$
and
 $C>0$
, then C is irreducible and
$C>0$
, then C is irreducible and
 $g(C)$
is a ruling of Z.
$g(C)$
is a ruling of Z.
Proof. 1. Let
![]() $\Gamma $
be an irreducible component of C. Since
$\Gamma $
be an irreducible component of C. Since
![]() $g(\Gamma )$
is a curve not contained in
$g(\Gamma )$
is a curve not contained in
![]() $\Delta $
and since
$\Delta $
and since
![]() $\Delta $
is the union of two fibers of the first projection
$\Delta $
is the union of two fibers of the first projection
![]() $\mathbb G^2_m\to \mathbb G_m$
and two fibers of the second projection,
$\mathbb G^2_m\to \mathbb G_m$
and two fibers of the second projection,
![]() $g(\Gamma )\cap \Delta $
contains at least two distinct points. So
$g(\Gamma )\cap \Delta $
contains at least two distinct points. So
![]() $\Gamma \cap H$
also contains at least two distinct points, and therefore,
$\Gamma \cap H$
also contains at least two distinct points, and therefore,
![]() $H\Gamma \ge 2$
and
$H\Gamma \ge 2$
and
![]() $p_a(H+\Gamma )= p_a(H)+p_a(\Gamma )+H\Gamma -1\ge p_a(H)+1$
. Since both the reduced divisors H and
$p_a(H+\Gamma )= p_a(H)+p_a(\Gamma )+H\Gamma -1\ge p_a(H)+1$
. Since both the reduced divisors H and
![]() $H+\Gamma $
are connected by Lemma 5.3, we have
$H+\Gamma $
are connected by Lemma 5.3, we have
![]() $p_a(H)=h^0(H,\omega _H)$
and
$p_a(H)=h^0(H,\omega _H)$
and
![]() $h^0(H+\Gamma , \omega _{H+\Gamma })=p_a(H+\Gamma )\ge h^0(H,\omega _H) +1=2$
, where the last equality follows from Lemma 5.3. Now, Lemma 2.12 gives
$h^0(H+\Gamma , \omega _{H+\Gamma })=p_a(H+\Gamma )\ge h^0(H,\omega _H) +1=2$
, where the last equality follows from Lemma 5.3. Now, Lemma 2.12 gives
![]() $h^0(X, K_X+H+\Gamma )= h^0(H+\Gamma , \omega _{H+\Gamma })\ge 2$
(recall that
$h^0(X, K_X+H+\Gamma )= h^0(H+\Gamma , \omega _{H+\Gamma })\ge 2$
(recall that
![]() $p_g(X)=0$
by Lemma 5.2), contradicting Lemma 5.4.
$p_g(X)=0$
by Lemma 5.2), contradicting Lemma 5.4.
2. Let again
![]() $\Gamma $
be a component of C such that
$\Gamma $
be a component of C such that
![]() $g(\Gamma )$
is not a ruling of Z. Then
$g(\Gamma )$
is not a ruling of Z. Then
![]() $\Gamma $
dominates A and therefore
$\Gamma $
dominates A and therefore
![]() $p_a(\Gamma )\ge 1$
. If
$p_a(\Gamma )\ge 1$
. If
![]() $\Gamma $
is disjoint from H, then
$\Gamma $
is disjoint from H, then
![]() $h^0(H+\Gamma , \omega _{H+\Gamma })=h^0(H,\omega _H)+h^0(\Gamma ,\omega _{\Gamma })\ge 3$
by Lemma 5.3. If
$h^0(H+\Gamma , \omega _{H+\Gamma })=h^0(H,\omega _H)+h^0(\Gamma ,\omega _{\Gamma })\ge 3$
by Lemma 5.3. If
![]() $\Gamma $
intersects H, then it intersects both
$\Gamma $
intersects H, then it intersects both
![]() $H_1$
and
$H_1$
and
![]() $H_2$
, since they support the numerically equivalent divisors
$H_2$
, since they support the numerically equivalent divisors
![]() $g^*\Delta _1$
and
$g^*\Delta _1$
and
![]() $g^*\Delta _2$
. So
$g^*\Delta _2$
. So
![]() $\Gamma +H$
is connected and
$\Gamma +H$
is connected and
![]() $h^0(\Gamma +H,\omega _{\Gamma +H})=p_a(\Gamma +H)\ge p_a(\Gamma )+p_a(H)+1=3$
. In either case, Lemma 2.12 gives
$h^0(\Gamma +H,\omega _{\Gamma +H})=p_a(\Gamma +H)\ge p_a(\Gamma )+p_a(H)+1=3$
. In either case, Lemma 2.12 gives
![]() $h^0(X, K_X+H+\Gamma )\ge 2$
, contradicting Lemma 5.4. So we conclude that
$h^0(X, K_X+H+\Gamma )\ge 2$
, contradicting Lemma 5.4. So we conclude that
![]() $g(\Gamma )$
is a ruling of Z. Assume that C has at least two components
$g(\Gamma )$
is a ruling of Z. Assume that C has at least two components
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
: then the same argument as above gives
$\Gamma _2$
: then the same argument as above gives
![]() $h^0(X, K_X+H+\Gamma _1+\Gamma _2)\ge 2$
, contradicting Lemma 5.4 again.
$h^0(X, K_X+H+\Gamma _1+\Gamma _2)\ge 2$
, contradicting Lemma 5.4 again.
Now, we consider the Stein factorization
![]() $X\overset {\nu }{\to } \overline X\overset {\overline g}{\to }Z$
of g.
$X\overset {\nu }{\to } \overline X\overset {\overline g}{\to }Z$
of g.
Lemma 5.6. The morphism
![]() $\overline g$
is étale over
$\overline g$
is étale over
![]() $A(V)$
.
$A(V)$
.
Proof. Let
![]() $m:=\deg g$
; if
$m:=\deg g$
; if
![]() $m=1$
, then
$m=1$
, then
![]() $\overline g$
is an isomorphism and the claim is of course true. So we may assume
$\overline g$
is an isomorphism and the claim is of course true. So we may assume
![]() $m>1$
.
$m>1$
.
The map
![]() $\overline g$
is finite by construction, so by purity of the branch locus it is enough to show that there is no component of the (usual) ramification divisor of g that is not contained in H and is not contracted to a point. By Lemma 2.8, such a curve is a component of the logarithmic ramification divisor
$\overline g$
is finite by construction, so by purity of the branch locus it is enough to show that there is no component of the (usual) ramification divisor of g that is not contained in H and is not contracted to a point. By Lemma 2.8, such a curve is a component of the logarithmic ramification divisor
![]() $\overline R_g$
. So if
$\overline R_g$
. So if
![]() $q(V)=0$
, the statement follows directly from Lemma 5.5. Therefore, we assume for the rest of the proof that
$q(V)=0$
, the statement follows directly from Lemma 5.5. Therefore, we assume for the rest of the proof that
![]() $q(V)=1$
.
$q(V)=1$
.
Again, by Lemma 5.5, if
![]() $\overline g$
is not étale, then there is exactly one irreducible curve
$\overline g$
is not étale, then there is exactly one irreducible curve
![]() $\Gamma $
in
$\Gamma $
in
![]() $R_g$
such that
$R_g$
such that
![]() $\Gamma $
is not contained in H and is not contracted by g, and the image of
$\Gamma $
is not contained in H and is not contracted by g, and the image of
![]() $\Gamma $
is a ruling
$\Gamma $
is a ruling
![]() $\Phi $
of Z. So
$\Phi $
of Z. So
![]() $\overline g$
restricts to a connected étale cover
$\overline g$
restricts to a connected étale cover
![]() $q\colon \widetilde W \to W:=A(V)\setminus \Phi $
. The preimage in X of a ruling of Z is a fiber of the Albanese map
$q\colon \widetilde W \to W:=A(V)\setminus \Phi $
. The preimage in X of a ruling of Z is a fiber of the Albanese map
![]() $a_X\colon X\to A(V)$
, and so it is connected. So q restricts to a connected cover of
$a_X\colon X\to A(V)$
, and so it is connected. So q restricts to a connected cover of
![]() $\mathbb G_m$
.
$\mathbb G_m$
.
Since algebraically trivial line bundles are topologically trivial, Corollary 2.4 implies that Z is homeomorphic to
![]() $A\times \mathbb P^1$
,
$A\times \mathbb P^1$
,
![]() $A(V)$
is homeomorphic to
$A(V)$
is homeomorphic to
![]() $A\times \mathbb G_m$
and W is homeomorphic to
$A\times \mathbb G_m$
and W is homeomorphic to
![]() $(A\setminus \{a\})\times \mathbb P^1$
, where
$(A\setminus \{a\})\times \mathbb P^1$
, where
![]() $a\in A$
is a point. Fix base points in
$a\in A$
is a point. Fix base points in
![]() $\widetilde W$
and W, and denote by N the subgroup of index m of
$\widetilde W$
and W, and denote by N the subgroup of index m of
![]() $\pi _1(W)\simeq \pi _1(A\setminus \{a\})\times \pi _1( \mathbb G_m)$
corresponding to the cover q. If
$\pi _1(W)\simeq \pi _1(A\setminus \{a\})\times \pi _1( \mathbb G_m)$
corresponding to the cover q. If
![]() $\gamma $
is a generator of
$\gamma $
is a generator of
![]() $\pi _1(\mathbb G_m)$
, we have
$\pi _1(\mathbb G_m)$
, we have
![]() $N\cap \pi _1(\mathbb G_m)=<\gamma ^m>$
. So the elements
$N\cap \pi _1(\mathbb G_m)=<\gamma ^m>$
. So the elements
![]() $1, \gamma ,\dots \gamma ^{m-1}$
represent distinct left cosets of
$1, \gamma ,\dots \gamma ^{m-1}$
represent distinct left cosets of
![]() $\pi _1(W)$
modulo N. Since
$\pi _1(W)$
modulo N. Since
![]() $\pi _1(\mathbb G_m)$
is a central subgroup of
$\pi _1(\mathbb G_m)$
is a central subgroup of
![]() $\pi _1(W)$
, it follows that left and right cosets modulo N coincide; namely, N is a normal subgroup of
$\pi _1(W)$
, it follows that left and right cosets modulo N coincide; namely, N is a normal subgroup of
![]() $\pi _1(W)$
and the quotient
$\pi _1(W)$
and the quotient
![]() $\pi _1(W)/N$
is cyclic of order m. Since the map
$\pi _1(W)/N$
is cyclic of order m. Since the map
![]() $\pi _1(W)\to \pi _1(A(V))$
is just abelianization, N is the preimage of an index m subgroup
$\pi _1(W)\to \pi _1(A(V))$
is just abelianization, N is the preimage of an index m subgroup
![]() $\overline N<\pi _1(A(V))$
. This shows that q extends to an étale cover
$\overline N<\pi _1(A(V))$
. This shows that q extends to an étale cover
![]() $q'\colon W'\to A(V)$
. Since by [Reference Dethloff and Grauert5, Thm. 3.4] both q and
$q'\colon W'\to A(V)$
. Since by [Reference Dethloff and Grauert5, Thm. 3.4] both q and
![]() $q'$
extend uniquely to an analytically branched covering of Z, it follows that
$q'$
extend uniquely to an analytically branched covering of Z, it follows that
![]() $\overline g\colon \overline X\to Z$
extends
$\overline g\colon \overline X\to Z$
extends
![]() $q'$
, that is,
$q'$
, that is,
![]() $\overline g$
is étale over
$\overline g$
is étale over
![]() $A(V)$
as claimed.
$A(V)$
as claimed.
5.2 Conclusion
We are finally ready to complete the proof of Theorem A.
Proof of Theorem A.
Consider the case
![]() $q(V)=2$
first. By Corollary 3.2, we only need to show that all components of D are contracted by
$q(V)=2$
first. By Corollary 3.2, we only need to show that all components of D are contracted by
![]() $a_X$
. So assume for contradiction that there is an irreducible component
$a_X$
. So assume for contradiction that there is an irreducible component
![]() $\Gamma $
of D that is not contracted by
$\Gamma $
of D that is not contracted by
![]() $a_X$
, and denote by
$a_X$
, and denote by
![]() $\overline \Gamma $
its image in
$\overline \Gamma $
its image in
![]() $A(X)$
; note that the map
$A(X)$
; note that the map
![]() $ \Gamma \to \overline \Gamma $
is birational. The geometric genus of
$ \Gamma \to \overline \Gamma $
is birational. The geometric genus of
![]() $ \overline \Gamma $
is positive, and if it is equal to 1, then
$ \overline \Gamma $
is positive, and if it is equal to 1, then
![]() $\overline \Gamma $
is a translate of an abelian subvariety of
$\overline \Gamma $
is a translate of an abelian subvariety of
![]() $A(X)$
, so in particular, it is smooth.
$A(X)$
, so in particular, it is smooth.
Assume first that
![]() $p_a(\Gamma )=1$
: then
$p_a(\Gamma )=1$
: then
![]() $\Gamma $
is smooth of genus 1 and
$\Gamma $
is smooth of genus 1 and
![]() $\Gamma \to \overline \Gamma $
is an isomorphism. It follows that
$\Gamma \to \overline \Gamma $
is an isomorphism. It follows that
![]() $a_X^*\overline \Gamma \preceq K_X+\Gamma \preceq K_X+D$
. Since
$a_X^*\overline \Gamma \preceq K_X+\Gamma \preceq K_X+D$
. Since
![]() $h^0(A(X), 2\overline \Gamma )=2$
, we have a contradiction to
$h^0(A(X), 2\overline \Gamma )=2$
, we have a contradiction to
![]() $\overline P_2(V)=2$
. If
$\overline P_2(V)=2$
. If
![]() $p_a(\Gamma )\ge 2$
, then by Serre duality and Riemann–Roch for all
$p_a(\Gamma )\ge 2$
, then by Serre duality and Riemann–Roch for all
![]() $\alpha \in \operatorname {\mathrm {Pic}}^0(X)$
we have
$\alpha \in \operatorname {\mathrm {Pic}}^0(X)$
we have
![]() $h^0(X, K_X+\Gamma +\alpha )\ge \chi (K_X+\Gamma )=p_a(\Gamma )-1\ge 1$
. Lemma 2.9 gives
$h^0(X, K_X+\Gamma +\alpha )\ge \chi (K_X+\Gamma )=p_a(\Gamma )-1\ge 1$
. Lemma 2.9 gives
![]() $h^0(X, 2(K_X+\Gamma ))\ge 2$
, contradicting again the assumption
$h^0(X, 2(K_X+\Gamma ))\ge 2$
, contradicting again the assumption
![]() $\overline P_2(V)=1$
. So all the components of D are
$\overline P_2(V)=1$
. So all the components of D are
![]() $a_X$
-exceptional.
$a_X$
-exceptional.
From now on, we assume
![]() $q(V)\le 1$
. By Lemma 5.6, the quasi-Albanese map
$q(V)\le 1$
. By Lemma 5.6, the quasi-Albanese map
![]() $a_V\colon V\to A(V)$
factors through an étale cover of degree
$a_V\colon V\to A(V)$
factors through an étale cover of degree
![]() $m:=\deg g$
. Since a finite étale cover of a quasi-abelian variety is also a quasi-abelian variety (Proposition 2.5) by the universal property of
$m:=\deg g$
. Since a finite étale cover of a quasi-abelian variety is also a quasi-abelian variety (Proposition 2.5) by the universal property of
![]() $a_V$
(cf. Theorem 2.6), we have
$a_V$
(cf. Theorem 2.6), we have
![]() $m=1$
; namely, g is birational. To complete the proof, we need to show that all the components of
$m=1$
; namely, g is birational. To complete the proof, we need to show that all the components of
![]() $D-H$
are contracted by g. Since
$D-H$
are contracted by g. Since
![]() $D-H\preceq \overline R_g$
by Lemma 2.8, in case
$D-H\preceq \overline R_g$
by Lemma 2.8, in case
![]() $q(V)=0$
the claim follows by Lemma 5.5.
$q(V)=0$
the claim follows by Lemma 5.5.
Assume
![]() $q(V)=1$
. By Lemma 5.5, there is at most an irreducible curve
$q(V)=1$
. By Lemma 5.5, there is at most an irreducible curve
![]() $\Gamma \preceq D-H$
such that
$\Gamma \preceq D-H$
such that
![]() $\Gamma $
is not contracted by g, and
$\Gamma $
is not contracted by g, and
![]() $g(\Gamma )$
is a ruling
$g(\Gamma )$
is a ruling
![]() $\Phi $
of Z. We are going to show that
$\Phi $
of Z. We are going to show that
![]() $g^*\Phi \preceq \overline R_g$
, hence
$g^*\Phi \preceq \overline R_g$
, hence
![]() $g^*(2\Phi )\preceq 2\overline R_g\sim 2(K_X+D)$
. Since
$g^*(2\Phi )\preceq 2\overline R_g\sim 2(K_X+D)$
. Since
![]() $h^0(Z, 2\Phi )=2$
, this contradicts the assumption
$h^0(Z, 2\Phi )=2$
, this contradicts the assumption
![]() $\overline P_2(V)=1$
.
$\overline P_2(V)=1$
.
Write
![]() $g^*\Phi =\Gamma + \sum _i\alpha _iC_i$
, where the
$g^*\Phi =\Gamma + \sum _i\alpha _iC_i$
, where the
![]() $C_i$
are distinct irreducible curves contracted by g and
$C_i$
are distinct irreducible curves contracted by g and
![]() $\alpha _i \in \mathbb N_{>0}$
. Let
$\alpha _i \in \mathbb N_{>0}$
. Let
![]() $u,v$
be local coordinates on Z centered at the point
$u,v$
be local coordinates on Z centered at the point
![]() $P_i:=g(C_i)$
such that
$P_i:=g(C_i)$
such that
![]() $u=0$
is the ruling
$u=0$
is the ruling
![]() $\Phi $
of Z; if, in addition
$\Phi $
of Z; if, in addition
![]() $P_i\in \Delta $
, we assume that v is a local equation of
$P_i\in \Delta $
, we assume that v is a local equation of
![]() $\Delta $
. At a general point of
$\Delta $
. At a general point of
![]() $C_i$
, we have
$C_i$
, we have
![]() $u=x^{\alpha _i}a$
,
$u=x^{\alpha _i}a$
,
![]() $v=x^{\beta _i}b$
, where x is a local equation for
$v=x^{\beta _i}b$
, where x is a local equation for
![]() $C_i$
,
$C_i$
,
![]() $a,b$
are nonzero regular functions and
$a,b$
are nonzero regular functions and
![]() $\beta _i>0$
is an integer. A simple computation gives
$\beta _i>0$
is an integer. A simple computation gives
 $$ \begin{align}g^*\frac{dv}{v}=\beta_i\frac{dx}{x}+\frac{db}{b}, \qquad g^*\left(\frac{du}{u}\wedge \frac{dv}{v}\right)=\frac{dx}{x}\wedge \left(\alpha_i\frac{db}{b}-\beta_i\frac{da}{a}\right). \end{align} $$
$$ \begin{align}g^*\frac{dv}{v}=\beta_i\frac{dx}{x}+\frac{db}{b}, \qquad g^*\left(\frac{du}{u}\wedge \frac{dv}{v}\right)=\frac{dx}{x}\wedge \left(\alpha_i\frac{db}{b}-\beta_i\frac{da}{a}\right). \end{align} $$
Note that
![]() $\alpha _i\frac {db}{b}-\beta _i\frac {da}{a}$
is a regular 1-form. So if
$\alpha _i\frac {db}{b}-\beta _i\frac {da}{a}$
is a regular 1-form. So if
![]() $P_i\in \Delta $
, then
$P_i\in \Delta $
, then
![]() $C_i\preceq D$
,
$C_i\preceq D$
,
![]() $K_Z+\Delta $
is locally generated by
$K_Z+\Delta $
is locally generated by
![]() $u\wedge \frac {dv}{v}$
,
$u\wedge \frac {dv}{v}$
,
![]() $K_X+D$
is locally generated by
$K_X+D$
is locally generated by
![]() $\frac {dx}{x}\wedge dy$
and
$\frac {dx}{x}\wedge dy$
and
![]() $C_i$
appears in
$C_i$
appears in
![]() $\overline R_g$
with multiplicity
$\overline R_g$
with multiplicity
![]() $\ge \alpha _i$
.
$\ge \alpha _i$
.
If
![]() $P_i\notin \Delta $
, then
$P_i\notin \Delta $
, then
![]() $K_Z+\Delta $
is locally generated by
$K_Z+\Delta $
is locally generated by
![]() $du\wedge dv$
,
$du\wedge dv$
,
![]() $K_X+D$
is locally generated by
$K_X+D$
is locally generated by
![]() $\frac {dx}{x}\wedge dy$
or by
$\frac {dx}{x}\wedge dy$
or by
![]() $dx\wedge dy$
according to whether
$dx\wedge dy$
according to whether
![]() $C_i\preceq D$
or not; in either case,
$C_i\preceq D$
or not; in either case,
![]() $C_i$
appears in
$C_i$
appears in
![]() $\overline R_g$
with multiplicity
$\overline R_g$
with multiplicity
![]() $\ge \alpha _i+\beta _i-1\ge \alpha _i$
. Summing up, we have shown
$\ge \alpha _i+\beta _i-1\ge \alpha _i$
. Summing up, we have shown
![]() $g^*\Phi \preceq \overline R_g$
, as promised.
$g^*\Phi \preceq \overline R_g$
, as promised.
Acknowledgments
We wish to thank the referee for the extremely careful reading of the paper. The third author would like to thank Yi Zhu for telling her about the Iitaka philosophy and planting the seed for this work.
This research was supported by grants from the FCT/Portugal through Centro de Análise Matemática, Geometria e Sistemas Dinâmicos (CAMGSD), IST-ID, projects UIDB/04459/2020 and UIDP/04459/; MIUR PRIN 2017SSNZAW
![]() $\_$
004 ‘Moduli Theory and Birational Classification’; Research Council of Norway, grant 261756, Knut och Alice Wallenberg Stifelse KAW 2019.0493.
$\_$
004 ‘Moduli Theory and Birational Classification’; Research Council of Norway, grant 261756, Knut och Alice Wallenberg Stifelse KAW 2019.0493.
In addition, R. Pardini is a member of GNSAGA (Gruppo Nazionale per le Strutture Algebriche e Geometriche e le loro Applicazioni) of INDAM (Instituto Nazionale di Alta Matematica).
Conflict of Interest
The authors have no conflict of interest to declare.
Data availability statement
No data were used; no code needs to be replicated.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Supplementary material
None.