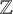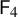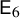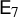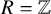1 Introduction
Albert algebras, which are a specific kind of Jordan algebra, are naturally distinguished objects among commutative nonassociative algebras and also arise naturally in the context of simple affine group schemes of type
![]() $\mathsf {F}_4$
,
$\mathsf {F}_4$
,
![]() $\mathsf {E}_6$
, or
$\mathsf {E}_6$
, or
![]() $\mathsf {E}_7$
. We study these objects over an arbitrary base ring R, with particular attention to the case
$\mathsf {E}_7$
. We study these objects over an arbitrary base ring R, with particular attention to the case
![]() $R = \mathbb {Z}$
. We prove in this generality results previously in the literature in the special case where R is a field of characteristic different from 2 and 3.
$R = \mathbb {Z}$
. We prove in this generality results previously in the literature in the special case where R is a field of characteristic different from 2 and 3.
Why Albert algebras?
In the setting of semisimple algebraic groups over a field, a standard technique for computing with elements of a group — especially an anisotropic group — is to interpret the group in terms of automorphisms of some algebraic structure, such as viewing an adjoint group of type
![]() $\mathsf {B}_n$
as the special orthogonal group of a quadratic form of dimension
$\mathsf {B}_n$
as the special orthogonal group of a quadratic form of dimension
![]() $2n+1$
, or an adjoint group of inner type
$2n+1$
, or an adjoint group of inner type
![]() $\mathsf {A}_n$
as the automorphism group of an Azumaya algebra of rank
$\mathsf {A}_n$
as the automorphism group of an Azumaya algebra of rank
![]() $(n+1)^2$
. This approach can be seen in many references, from [Reference WeilWeil], through [Reference Knus, Merkurjev, Rost and TignolKnMRT] and [Reference ConradConrad]. In this vein, Albert algebras appear as a natural tool for computations related to
$(n+1)^2$
. This approach can be seen in many references, from [Reference WeilWeil], through [Reference Knus, Merkurjev, Rost and TignolKnMRT] and [Reference ConradConrad]. In this vein, Albert algebras appear as a natural tool for computations related to
![]() $\mathsf {F}_4$
,
$\mathsf {F}_4$
,
![]() $\mathsf {E}_6$
, and
$\mathsf {E}_6$
, and
![]() $\mathsf {E}_7$
groups, as we do below.
$\mathsf {E}_7$
groups, as we do below.
In the setting of nonassociative algebras, Albert algebras also arise naturally. Among commutative not-necessarily-associative algebras under additional mild hypotheses (the field has characteristic
![]() $\ne 2, 3, 5$
and the algebra is metrized), every algebra satisfying a polynomial identity of degree
$\ne 2, 3, 5$
and the algebra is metrized), every algebra satisfying a polynomial identity of degree
![]() $\le 4$
is a Jordan algebra (see [Reference Chayet and GaribaldiChG, Proposition A.8]). Jordan algebras have an analogue of the Wedderburn-Artin theory for associative algebras [Reference JacobsonJ68, p. 201, Corollary 2], and one finds that all the simple Jordan algebras are closely related to associative algebras (more precisely, “are special”) except for one kind, the Albert algebras (see, for example [Reference JacobsonJ68, p. 210, Theorem 11] or [Reference McCrimmon and Zel’manovMcCZ]).
$\le 4$
is a Jordan algebra (see [Reference Chayet and GaribaldiChG, Proposition A.8]). Jordan algebras have an analogue of the Wedderburn-Artin theory for associative algebras [Reference JacobsonJ68, p. 201, Corollary 2], and one finds that all the simple Jordan algebras are closely related to associative algebras (more precisely, “are special”) except for one kind, the Albert algebras (see, for example [Reference JacobsonJ68, p. 210, Theorem 11] or [Reference McCrimmon and Zel’manovMcCZ]).
Our contribution
In the setting of nonassociative algebras, we prove a classification of Albert algebras over
![]() $\mathbb {Z}$
(Theorem 14.3), which was viewed as an open question in the context of nonassociative algebra; here, we see that it is equivalent to the classification of groups of type
$\mathbb {Z}$
(Theorem 14.3), which was viewed as an open question in the context of nonassociative algebra; here, we see that it is equivalent to the classification of groups of type
![]() $\mathsf {F}_4$
, which was known (see [Reference ConradConrad], which leverages [Reference GrossGr] and [Reference Elkies and GrossElkiesGr]). We also prove new results about ideals in Albert algebras (Theorem 8.2), about isotopy of Albert algebras over semilocal rings (Theorem 13.3), and about the number of generators of an Albert algebra (Proposition 12.1). We have not seen Lemma 15.1 in the literature, even in the case of a base field of characteristic different from 2 and 3.
$\mathsf {F}_4$
, which was known (see [Reference ConradConrad], which leverages [Reference GrossGr] and [Reference Elkies and GrossElkiesGr]). We also prove new results about ideals in Albert algebras (Theorem 8.2), about isotopy of Albert algebras over semilocal rings (Theorem 13.3), and about the number of generators of an Albert algebra (Proposition 12.1). We have not seen Lemma 15.1 in the literature, even in the case of a base field of characteristic different from 2 and 3.
In the setting of affine group schemes, the language of Albert algebras provides a way to give concrete descriptions of the affine group schemes over
![]() $\mathbb {Z}$
(see Section 18). In that language, a clever computation in [Reference Elkies and GrossElkiesGr] appears as an example of a general mechanism known as isotopy (see Definition 14.1). To facilitate these applications, we present the definition of Albert algebras in a streamlined way (see Definition 7.1). Note that they are defined as a type of what was formerly called a “quadratic” Jordan algebra — because instead of a bilinear multiplication, one has a quadratic map, the U-operator — and that the definition makes sense whether or not 2 is invertible in the base ring. Applying the definition here allows one to replace, in some proofs, “global” computations over
$\mathbb {Z}$
(see Section 18). In that language, a clever computation in [Reference Elkies and GrossElkiesGr] appears as an example of a general mechanism known as isotopy (see Definition 14.1). To facilitate these applications, we present the definition of Albert algebras in a streamlined way (see Definition 7.1). Note that they are defined as a type of what was formerly called a “quadratic” Jordan algebra — because instead of a bilinear multiplication, one has a quadratic map, the U-operator — and that the definition makes sense whether or not 2 is invertible in the base ring. Applying the definition here allows one to replace, in some proofs, “global” computations over
![]() $\mathbb {Z}$
as one finds in [Reference ConradConrad] with “local” computations over an algebraically closed field that exist in several places in the literature (see, for example, the proof of Lemma 9.1 and Section 18).
$\mathbb {Z}$
as one finds in [Reference ConradConrad] with “local” computations over an algebraically closed field that exist in several places in the literature (see, for example, the proof of Lemma 9.1 and Section 18).
A different definition
The definition of Albert algebra over a ring R given here (Definition 7.2) is in the context of para-quadratic algebras as recalled at the beginning of Section 5 — such an algebra is an R-module M with a distinguished element
![]() $1_M$
and a quadratic map
$1_M$
and a quadratic map
![]() $U \!: M \to \operatorname {\mathrm {End}}_R(M)$
such that
$U \!: M \to \operatorname {\mathrm {End}}_R(M)$
such that
![]() $U_{1_M} = \operatorname {\mathrm {Id}}_M$
. There are no other axioms to check. We then define a specific para-quadratic algebra,
$U_{1_M} = \operatorname {\mathrm {Id}}_M$
. There are no other axioms to check. We then define a specific para-quadratic algebra,
![]() $\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R))$
, in Definition 6.7, and define an Albert R-algebra J to be a para-quadratic R-algebra such that
$\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R))$
, in Definition 6.7, and define an Albert R-algebra J to be a para-quadratic R-algebra such that
![]() $J \otimes S \cong \operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R)) \otimes S$
for some faithfully flat R-algebra S.
$J \otimes S \cong \operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R)) \otimes S$
for some faithfully flat R-algebra S.
A different approach is taken by references such as [Reference PeterssonPe19, Section 6.1] or [Reference AlsaodyAls21]. They define an Albert R-algebra to be a cubic Jordan R-algebra (Definition 6.2) J whose underlying R-module is projective of rank 27 and
![]() $J \otimes F$
is a simple algebra for every homomorphism from R to a field F. This definition involves axioms that in principle need to be verified over all R-algebras. The two definitions give the same objects. Theorem 17 in [Reference PeterssonPe19] states that an Albert algebra in the sense of that paper is an Albert algebra in the sense of this paper by proving the existence of the required faithfully flat R-algebra; a detailed proof has not been published but closely follows an argument for octonion algebras from [Reference Loos, Petersson and RacineLoPR]. For the converse, an Albert algebra in the sense of this paper has a projective underlying module (because
$J \otimes F$
is a simple algebra for every homomorphism from R to a field F. This definition involves axioms that in principle need to be verified over all R-algebras. The two definitions give the same objects. Theorem 17 in [Reference PeterssonPe19] states that an Albert algebra in the sense of that paper is an Albert algebra in the sense of this paper by proving the existence of the required faithfully flat R-algebra; a detailed proof has not been published but closely follows an argument for octonion algebras from [Reference Loos, Petersson and RacineLoPR]. For the converse, an Albert algebra in the sense of this paper has a projective underlying module (because
![]() $\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R))$
does), is a cubic Jordan algebra (Proposition 10.1), and satisfies the simplicity condition (Corollary 8.5).
$\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R))$
does), is a cubic Jordan algebra (Proposition 10.1), and satisfies the simplicity condition (Corollary 8.5).
2 Notation
Rings, by definition, have a 1. We put
![]() ${\mathbb {Z}\text {-}\textbf {alg}}$
for the category of commutative rings, where
${\mathbb {Z}\text {-}\textbf {alg}}$
for the category of commutative rings, where
![]() $\mathbb {Z}$
is an initial object. For any
$\mathbb {Z}$
is an initial object. For any
![]() $R \in {\mathbb {Z}\text {-}\textbf {alg}}$
, we put
$R \in {\mathbb {Z}\text {-}\textbf {alg}}$
, we put
![]() ${R\text {-}\textbf {alg}}$
for the category of pairs
${R\text {-}\textbf {alg}}$
for the category of pairs
![]() $(S, f)$
with
$(S, f)$
with
![]() $S \in {\mathbb {Z}\text {-}\textbf {alg}}$
and
$S \in {\mathbb {Z}\text {-}\textbf {alg}}$
and
![]() $f \!: R \to S$
, that is, the coslice category
$f \!: R \to S$
, that is, the coslice category
![]() $R \downarrow {\mathbb {Z}\text {-}\textbf {alg}}$
. Below, R will typically denote an element of
$R \downarrow {\mathbb {Z}\text {-}\textbf {alg}}$
. Below, R will typically denote an element of
![]() ${\mathbb {Z}\text {-}\textbf {alg}}$
. (The interested reader is invited to mentally replace R by a base scheme
${\mathbb {Z}\text {-}\textbf {alg}}$
. (The interested reader is invited to mentally replace R by a base scheme
![]() $\mathbf {X}$
,
$\mathbf {X}$
,
![]() ${R\text {-}\textbf {alg}}$
with the category of schemes over
${R\text {-}\textbf {alg}}$
with the category of schemes over
![]() $\mathbf {X}$
, finitely generated projective R-modules with vector bundles over
$\mathbf {X}$
, finitely generated projective R-modules with vector bundles over
![]() $\mathbf {X}$
, etc., thereby translating results below into a language closer to that in [Reference Calmès and FaselCalF].) An R-algebra S is said to be fppf if it is faithfully flat and finitely presented.
$\mathbf {X}$
, etc., thereby translating results below into a language closer to that in [Reference Calmès and FaselCalF].) An R-algebra S is said to be fppf if it is faithfully flat and finitely presented.
We write
![]() $\operatorname {\mathrm {Mat}}_n(R)$
for the ring of n-by-n matrices with entries from R,
$\operatorname {\mathrm {Mat}}_n(R)$
for the ring of n-by-n matrices with entries from R,
![]() $\operatorname {\mathrm {Id}}$
for the identity matrix, and
$\operatorname {\mathrm {Id}}$
for the identity matrix, and
![]() ${\left \langle {\alpha _1, \ldots , \alpha _n}\right \rangle } \in \operatorname {\mathrm {Mat}}_n(R)$
for the diagonal matrix whose
${\left \langle {\alpha _1, \ldots , \alpha _n}\right \rangle } \in \operatorname {\mathrm {Mat}}_n(R)$
for the diagonal matrix whose
![]() $(i,i)$
-entry is
$(i,i)$
-entry is
![]() $\alpha _i$
. The transpose of a matrix x is denoted
$\alpha _i$
. The transpose of a matrix x is denoted
![]() $x^{\intercal }$
. We write
$x^{\intercal }$
. We write
![]() $\operatorname {\mathrm {GL}}_n(R)$
for the group of invertible elements in
$\operatorname {\mathrm {GL}}_n(R)$
for the group of invertible elements in
![]() $\operatorname {\mathrm {Mat}}_n(R)$
.
$\operatorname {\mathrm {Mat}}_n(R)$
.
Suppose now that
![]() $\mathbf {G}$
is a finitely presented group scheme over R. For each fppf
$\mathbf {G}$
is a finitely presented group scheme over R. For each fppf
![]() $S \in {R\text {-}\textbf {alg}}$
, we write
$S \in {R\text {-}\textbf {alg}}$
, we write
![]() $H^1(S/R, \mathbf {G})$
for Čech cohomology of the sheaf of groups
$H^1(S/R, \mathbf {G})$
for Čech cohomology of the sheaf of groups
![]() $\mathbf {G}$
relative to
$\mathbf {G}$
relative to
![]() $R \to S$
(see, for example [Reference GiraudGir, Section III.3.6] or [Reference WaterhouseWa, Chapter 17]). The set
$R \to S$
(see, for example [Reference GiraudGir, Section III.3.6] or [Reference WaterhouseWa, Chapter 17]). The set
![]() $H^1(S/R, \mathbf {G})$
does not depend on the choice of structure homomorphism
$H^1(S/R, \mathbf {G})$
does not depend on the choice of structure homomorphism
![]() $R \to S$
, and more is true: Every morphism
$R \to S$
, and more is true: Every morphism
![]() $S \to T$
in
$S \to T$
in
![]() ${k\text {-}\textbf {alg}}$
gives a morphism
${k\text {-}\textbf {alg}}$
gives a morphism
![]() $H^1(S/R, \mathbf {G}) \to H^1(T/R, \mathbf {G})$
that is injective and does not depend on the choice of arrow
$H^1(S/R, \mathbf {G}) \to H^1(T/R, \mathbf {G})$
that is injective and does not depend on the choice of arrow
![]() $S \to T$
[Reference GiraudGir, Remark III.3.6.5]. The subcategory of fppf elements of
$S \to T$
[Reference GiraudGir, Remark III.3.6.5]. The subcategory of fppf elements of
![]() ${R\text {-}\textbf {alg}}$
has a small skeleton, so the colimit
${R\text {-}\textbf {alg}}$
has a small skeleton, so the colimit
is a set. We call it the nonabelian fppf cohomology of
![]() $\mathbf {G}$
. In case
$\mathbf {G}$
. In case
![]() $\mathbf {G}$
is smooth, it agrees with étale
$\mathbf {G}$
is smooth, it agrees with étale
![]() $H^1$
. If additionally R is a field, then it agrees with the nonabelian Galois cohomology defined in, for example, [Reference SerreSerre].
$H^1$
. If additionally R is a field, then it agrees with the nonabelian Galois cohomology defined in, for example, [Reference SerreSerre].
Unimodular elements
Let M be an R-module. An element
![]() $m \in M$
is said to be unimodular if
$m \in M$
is said to be unimodular if
![]() $Rm$
is a free R-module of rank 1 and a direct summand of M, equivalently, if there is some
$Rm$
is a free R-module of rank 1 and a direct summand of M, equivalently, if there is some
![]() $\lambda \in M^*$
(the dual of M) such that
$\lambda \in M^*$
(the dual of M) such that
![]() $\lambda (m) = 1$
. When M is finitely generated projective, this is equivalent to:
$\lambda (m) = 1$
. When M is finitely generated projective, this is equivalent to:
![]() $m \otimes 1$
is not zero in
$m \otimes 1$
is not zero in
![]() $M \otimes F$
for every field
$M \otimes F$
for every field
![]() $F \in {R\text {-}\textbf {alg}}$
(see, for example [Reference LoosLo, 0.3]). If
$F \in {R\text {-}\textbf {alg}}$
(see, for example [Reference LoosLo, 0.3]). If
![]() $m \in M$
is unimodular, then so is
$m \in M$
is unimodular, then so is
![]() $m \otimes 1 \in M \otimes S$
for every
$m \otimes 1 \in M \otimes S$
for every
![]() $S \in {R\text {-}\textbf {alg}}$
. In the opposite direction, if M is finitely generated projective, S is a Zariski cover of R (i.e.,
$S \in {R\text {-}\textbf {alg}}$
. In the opposite direction, if M is finitely generated projective, S is a Zariski cover of R (i.e.,
![]() $\operatorname {\mathrm {Spec}} S \to \operatorname {\mathrm {Spec}} R$
is surjective), and
$\operatorname {\mathrm {Spec}} S \to \operatorname {\mathrm {Spec}} R$
is surjective), and
![]() $m \otimes 1$
is unimodular in
$m \otimes 1$
is unimodular in
![]() $M \otimes S$
, it follows that m is unimodular as an element of M.
$M \otimes S$
, it follows that m is unimodular as an element of M.
3 Background on polynomial laws
We may identify an R-module M with a functor
![]() $\mathbf {W}(M)$
from
$\mathbf {W}(M)$
from
![]() ${R\text {-}\textbf {alg}}$
to the category of sets defined via
${R\text {-}\textbf {alg}}$
to the category of sets defined via
![]() $S \mapsto M \otimes S$
. For R-modules M, N, a polynomial law (in the sense of [Reference RobyRoby] or [Reference BourbakiBouA2, Section IV.5, Exercise 9])
$S \mapsto M \otimes S$
. For R-modules M, N, a polynomial law (in the sense of [Reference RobyRoby] or [Reference BourbakiBouA2, Section IV.5, Exercise 9])
![]() $f \colon \mathbf {W}(M) \to \mathbf {W}(N)$
is a morphism of functors, that is, a collection of set maps
$f \colon \mathbf {W}(M) \to \mathbf {W}(N)$
is a morphism of functors, that is, a collection of set maps
![]() $f_S \colon M \otimes S \to N \otimes S$
varying functorially with S. We put
$f_S \colon M \otimes S \to N \otimes S$
varying functorially with S. We put
![]() $\mathscr {P}_R(M, N)$
for the collection of polynomial laws
$\mathscr {P}_R(M, N)$
for the collection of polynomial laws
![]() $\mathbf {W}(M) \to \mathbf {W}(N)$
, omitting the subscript R when it is understood. Note that
$\mathbf {W}(M) \to \mathbf {W}(N)$
, omitting the subscript R when it is understood. Note that
![]() $\mathscr {P}_R(M, N)$
is an R-module.
$\mathscr {P}_R(M, N)$
is an R-module.
Lemma 3.1. Let M be a finitely generated projective R-module, and suppose
![]() $f \in \mathscr {P}(M, N)$
is such that
$f \in \mathscr {P}(M, N)$
is such that
![]() $f_R(0) = 0$
. If
$f_R(0) = 0$
. If
![]() $m \in M$
has
$m \in M$
has
![]() $f_R(m)$
unimodular in N, then m is unimodular.
$f_R(m)$
unimodular in N, then m is unimodular.
In the case
![]() $N = R$
, the condition that
$N = R$
, the condition that
![]() $f_R(m)$
is unimodular means that
$f_R(m)$
is unimodular means that
![]() $f_R(m) \in R^{\times }$
.
$f_R(m) \in R^{\times }$
.
Proof. Replacing f with
![]() $\lambda f$
, where
$\lambda f$
, where
![]() $\lambda \in N^*$
is such that
$\lambda \in N^*$
is such that
![]() $\lambda (f_R(m)) = 1$
, we may assume
$\lambda (f_R(m)) = 1$
, we may assume
![]() $N = R$
and
$N = R$
and
![]() $f_R(m) = 1$
. If m is not unimodular, then there is a field
$f_R(m) = 1$
. If m is not unimodular, then there is a field
![]() $F \in {R\text {-}\textbf {alg}}$
, such that
$F \in {R\text {-}\textbf {alg}}$
, such that
![]() $m \otimes 1 = 0$
in
$m \otimes 1 = 0$
in
![]() $M \otimes F$
, and
$M \otimes F$
, and
![]() $f_F(m \otimes 1) = 0$
, whence
$f_F(m \otimes 1) = 0$
, whence
![]() $f_R(m)$
belongs to the kernel of
$f_R(m)$
belongs to the kernel of
![]() $R \to F$
a contradiction.
$R \to F$
a contradiction.
A polynomial law is homogeneous of degree
![]() $d \ge 0$
if
$d \ge 0$
if
![]() $f_S(sx) = s^d f_S(x)$
for every
$f_S(sx) = s^d f_S(x)$
for every
![]() $S \in {R\text {-}\textbf {alg}}$
,
$S \in {R\text {-}\textbf {alg}}$
,
![]() $s \in S$
, and
$s \in S$
, and
![]() $x \in M \otimes S$
(see [Reference RobyRoby, p. 226]). We put
$x \in M \otimes S$
(see [Reference RobyRoby, p. 226]). We put
![]() $\mathscr {P}^d_R(M, N)$
for the submodule of
$\mathscr {P}^d_R(M, N)$
for the submodule of
![]() $\mathscr {P}_R(M, N)$
of polynomial laws that are homogeneous of degree d. The polynomial laws that are homogeneous of degree 0 are constants, and those of degree 1 are linear transformations, that is, the natural maps
$\mathscr {P}_R(M, N)$
of polynomial laws that are homogeneous of degree d. The polynomial laws that are homogeneous of degree 0 are constants, and those of degree 1 are linear transformations, that is, the natural maps
are isomorphisms (see [Reference RobyRoby, pp. 230, 231]). For degree
![]() $2$
,
$2$
,
![]() $\mathscr {P}_R^2(M,N)$
is canonically identified with the maps
$\mathscr {P}_R^2(M,N)$
is canonically identified with the maps
![]() $f \colon M \to N$
that are quadratic in the sense that
$f \colon M \to N$
that are quadratic in the sense that
![]() $f(rm) = r^2f(m)$
and the map
$f(rm) = r^2f(m)$
and the map
![]() $M\times M \to N$
defined by
$M\times M \to N$
defined by
![]() $f(m_1,m_2) := f(m_1 + m_2) - f(m_1) - f(m_2)$
is bilinear [Reference RobyRoby, p. 236, Proposition II.1]. A form of degree d on M is a polynomial law
$f(m_1,m_2) := f(m_1 + m_2) - f(m_1) - f(m_2)$
is bilinear [Reference RobyRoby, p. 236, Proposition II.1]. A form of degree d on M is a polynomial law
![]() $\mathbf {W}(M) \to \mathbf {W}(R)$
that is homogeneous of degree d. The forms of degree 2 are commonly known as quadratic forms on M.
$\mathbf {W}(M) \to \mathbf {W}(R)$
that is homogeneous of degree d. The forms of degree 2 are commonly known as quadratic forms on M.
Directional derivatives
For
![]() $f \in \mathscr {P}(M, N)$
,
$f \in \mathscr {P}(M, N)$
,
![]() $v \in M$
, t an indeterminate, and
$v \in M$
, t an indeterminate, and
![]() $n \ge 0$
, we define a polynomial law
$n \ge 0$
, we define a polynomial law
![]() $\nabla _v^n f$
as follows. For
$\nabla _v^n f$
as follows. For
![]() $S \in {R\text {-}\textbf {alg}}$
and
$S \in {R\text {-}\textbf {alg}}$
and
![]() $x \in M \otimes S$
,
$x \in M \otimes S$
,
![]() $f_{S[t]}(x + v \otimes t)$
is an element of
$f_{S[t]}(x + v \otimes t)$
is an element of
![]() $N \otimes S[t]$
, and we define
$N \otimes S[t]$
, and we define
![]() $\nabla _v^n f_S(x) \in N \otimes S$
to be the coefficient of
$\nabla _v^n f_S(x) \in N \otimes S$
to be the coefficient of
![]() $t^n$
. This defines a polynomial law called the n-th directional derivative
$t^n$
. This defines a polynomial law called the n-th directional derivative
![]() $\nabla _v^n f$
of f in the direction v. One finds that
$\nabla _v^n f$
of f in the direction v. One finds that
![]() $\nabla ^0_v f = f$
regardless of v. We abbreviate
$\nabla ^0_v f = f$
regardless of v. We abbreviate
![]() $\nabla _v f := \nabla _v^1 f$
; it is linear in v.
$\nabla _v f := \nabla _v^1 f$
; it is linear in v.
If f is homogeneous of degree d and
![]() $0 \le n \le d$
, then
$0 \le n \le d$
, then
![]() $\nabla _v^n f(x)$
is homogeneous of degree
$\nabla _v^n f(x)$
is homogeneous of degree
![]() $d - n$
in x and degree n in v. The symmetry implicit in the definition of the directional derivative gives
$d - n$
in x and degree n in v. The symmetry implicit in the definition of the directional derivative gives
![]() $\nabla _v^n f(x) = \nabla _x^{d-n} f(v)$
for
$\nabla _v^n f(x) = \nabla _x^{d-n} f(v)$
for
![]() $x \in M$
.
$x \in M$
.
Lemma 3.2. Suppose M, N are R-modules and A is a unital associative R-algebra and
![]() $g \in \mathscr {P}(M , A)$
is a polynomial law such that there is an element
$g \in \mathscr {P}(M , A)$
is a polynomial law such that there is an element
![]() $m \in M$
such that
$m \in M$
such that
![]() $g_R(m) \in A$
is invertible. If
$g_R(m) \in A$
is invertible. If
![]() $f \in \mathscr {P}^d(M, N)$
satisfies
$f \in \mathscr {P}^d(M, N)$
satisfies
for all
![]() $S \in {R\text {-}\textbf {alg}}$
and
$S \in {R\text {-}\textbf {alg}}$
and
![]() $x \in M \otimes S$
, then
$x \in M \otimes S$
, then
![]() $f = 0$
.
$f = 0$
.
Proof. Since the hypotheses are stable under base change, it suffices to show that
![]() $f(v) = 0$
for all
$f(v) = 0$
for all
![]() $v \in M$
. Replacing g by
$v \in M$
. Replacing g by
![]() $L \circ g \in \mathscr {P}(M, A)$
, where
$L \circ g \in \mathscr {P}(M, A)$
, where
![]() $L \in \operatorname {\mathrm {End}}_R(A)$
is multiplication in A on the left by the inverse of
$L \in \operatorname {\mathrm {End}}_R(A)$
is multiplication in A on the left by the inverse of
![]() $g_R(m)$
, we may assume
$g_R(m)$
, we may assume
![]() $g_R(m) = 1_A$
. Set
$g_R(m) = 1_A$
. Set
![]() $S := R[\varepsilon ]/(\varepsilon ^{d+1})$
. For
$S := R[\varepsilon ]/(\varepsilon ^{d+1})$
. For
![]() $v \in M$
, the element
$v \in M$
, the element
 $$\begin{align*}g_S(m + \varepsilon v) = 1_A + \sum_{n=1}^d \varepsilon^n \nabla_v^n g_R(m) \end{align*}$$
$$\begin{align*}g_S(m + \varepsilon v) = 1_A + \sum_{n=1}^d \varepsilon^n \nabla_v^n g_R(m) \end{align*}$$
is invertible in
![]() $A_S$
, so by hypothesis,
$A_S$
, so by hypothesis,
 $$\begin{align*}0 = f_S(m+\varepsilon v) = \sum_{n = 0}^d \varepsilon^n \nabla_v^n f_R(m). \end{align*}$$
$$\begin{align*}0 = f_S(m+\varepsilon v) = \sum_{n = 0}^d \varepsilon^n \nabla_v^n f_R(m). \end{align*}$$
Focusing on the coefficient of
![]() $\varepsilon ^d$
in that equation gives
$\varepsilon ^d$
in that equation gives
as required.
While Lemma 3.2 has some similarity with the principle of extension of algebraic identities as in [Reference BourbakiBouA2, Section IV.2.3], that result imposes some hypothesis on R.
The module of polynomial laws
In the following, we write
![]() $\mathsf {S}^n M$
for the n-th symmetric power of M, that is, the R-module
$\mathsf {S}^n M$
for the n-th symmetric power of M, that is, the R-module
![]() $\otimes ^n M$
modulo the submodule generated by elements
$\otimes ^n M$
modulo the submodule generated by elements
![]() $x - \sigma (x)$
for
$x - \sigma (x)$
for
![]() $x \in \otimes ^n M$
and
$x \in \otimes ^n M$
and
![]() $\sigma $
a permutation of the n factors.
$\sigma $
a permutation of the n factors.
Lemma 3.3. Let M and N be finitely generated projective R-modules. Then for each
![]() $d \ge 0$
:
$d \ge 0$
:
-
1.
 $\mathscr {P}^d(M, N)$
is a finitely generated projective R-module.
$\mathscr {P}^d(M, N)$
is a finitely generated projective R-module. -
2. If
 $T \in {R\text {-}\textbf {alg}}$
is flat, the natural map
$T \in {R\text {-}\textbf {alg}}$
is flat, the natural map
 $\mathscr {P}^d_R(M, N) \otimes T \to \mathscr {P}^d_T(M \otimes T, N \otimes T)$
is an isomorphism.
$\mathscr {P}^d_R(M, N) \otimes T \to \mathscr {P}^d_T(M \otimes T, N \otimes T)$
is an isomorphism. -
3. The natural map
 $\mathsf {S}^d(M^*) \otimes N \to \mathscr {P}^d(M, N)$
is an isomorphism.
$\mathsf {S}^d(M^*) \otimes N \to \mathscr {P}^d(M, N)$
is an isomorphism. -
4. The natural map
 $\mathscr {P}^d(M, R) \otimes N \to \mathscr {P}^d(M, N)$
is an isomorphism.
$\mathscr {P}^d(M, R) \otimes N \to \mathscr {P}^d(M, N)$
is an isomorphism.
Proof. To establish notation, we write
![]() $R = \prod _{i=0}^n R_i$
for some n such that
$R = \prod _{i=0}^n R_i$
for some n such that
![]() $M = \prod _i M_i$
and
$M = \prod _i M_i$
and
![]() $N = \prod _i N_i$
with each
$N = \prod _i N_i$
with each
![]() $M_i$
,
$M_i$
,
![]() $N_i$
an
$N_i$
an
![]() $R_i$
-module of finite constant rank.
$R_i$
-module of finite constant rank.
Next write
![]() $\Gamma _d(M)$
for the module of degree d divided powers on M as defined in [Reference BourbakiBouA2, Section IV.5, Exercise 2]. We claim that it is finitely generated projective, and therefore, by [Stacks, Tag 00NX], finitely presented. If M is free, then
$\Gamma _d(M)$
for the module of degree d divided powers on M as defined in [Reference BourbakiBouA2, Section IV.5, Exercise 2]. We claim that it is finitely generated projective, and therefore, by [Stacks, Tag 00NX], finitely presented. If M is free, then
![]() $\Gamma _d(M)$
is free. If M is projective of constant rank, then there exists
$\Gamma _d(M)$
is free. If M is projective of constant rank, then there exists
![]() $S \in {R\text {-}\textbf {alg}}$
faithfully flat such that
$S \in {R\text {-}\textbf {alg}}$
faithfully flat such that
![]() $M \otimes S$
is free. Because
$M \otimes S$
is free. Because
![]() $\Gamma _d$
commutes with base change [Reference BourbakiBouA2, Section IV.5, Exercise 7],
$\Gamma _d$
commutes with base change [Reference BourbakiBouA2, Section IV.5, Exercise 7],
![]() $\Gamma _d(M) \otimes S \cong \Gamma _d(M \otimes S)$
is free, and we again find that
$\Gamma _d(M) \otimes S \cong \Gamma _d(M \otimes S)$
is free, and we again find that
![]() $\Gamma _d(M)$
is finitely generated projective [Stacks, Tags 03C4, 05A9]. In the general case,
$\Gamma _d(M)$
is finitely generated projective [Stacks, Tags 03C4, 05A9]. In the general case,
![]() $\Gamma _d(M) = \prod _i \Gamma _d(M_i)$
, and the claim is verified.
$\Gamma _d(M) = \prod _i \Gamma _d(M_i)$
, and the claim is verified.
To verify (2), we note that
![]() $\mathscr {P}^d_R(M, N)$
is naturally isomorphic to
$\mathscr {P}^d_R(M, N)$
is naturally isomorphic to
![]() $\operatorname {\mathrm {Hom}}_R(\Gamma _d(M), N)$
by [Reference RobyRoby, Theorem IV.1]. Then
$\operatorname {\mathrm {Hom}}_R(\Gamma _d(M), N)$
by [Reference RobyRoby, Theorem IV.1]. Then
![]() $\mathscr {P}^d_R(M, N) \otimes T \cong \operatorname {\mathrm {Hom}}_R(\Gamma _d(M), N) \otimes T$
, which in turn is
$\mathscr {P}^d_R(M, N) \otimes T \cong \operatorname {\mathrm {Hom}}_R(\Gamma _d(M), N) \otimes T$
, which in turn is
![]() $\operatorname {\mathrm {Hom}}_T(\Gamma _d(M) \otimes T, N \otimes T)$
because T is flat and
$\operatorname {\mathrm {Hom}}_T(\Gamma _d(M) \otimes T, N \otimes T)$
because T is flat and
![]() $\Gamma _d(M)$
is finitely presented [Reference BourbakiBouCA, Section I.2.10, Proposition 11]. Since
$\Gamma _d(M)$
is finitely presented [Reference BourbakiBouCA, Section I.2.10, Proposition 11]. Since
![]() $\Gamma _d$
commutes with base change, we have verified (2).
$\Gamma _d$
commutes with base change, we have verified (2).
(3): If M and N are free modules, then the map is an isomorphism by [Reference RobyRoby, p. 232]. If M and N have constant rank, then there is a faithfully flat
![]() $T \in {R\text {-}\textbf {alg}}$
such that
$T \in {R\text {-}\textbf {alg}}$
such that
![]() $M \otimes T$
and
$M \otimes T$
and
![]() $N \otimes T$
are free. Since (3) holds over T by the free case, (2) and faithfully flat descent give that (3) holds. In the general case,
$N \otimes T$
are free. Since (3) holds over T by the free case, (2) and faithfully flat descent give that (3) holds. In the general case,
![]() $\mathscr {P}^d(M, N) = \prod \mathscr {P}^d(M_i, N_i)$
and
$\mathscr {P}^d(M, N) = \prod \mathscr {P}^d(M_i, N_i)$
and
![]() $\mathsf {S}^d(M^*) \otimes N = \prod (\mathsf {S}^d(M_i^*) \otimes N_i)$
and the claim follows by the constant rank case.
$\mathsf {S}^d(M^*) \otimes N = \prod (\mathsf {S}^d(M_i^*) \otimes N_i)$
and the claim follows by the constant rank case.
(4) follows trivially from (3). For (1), note that
![]() $M^*$
is finitely generated projective, so are
$M^*$
is finitely generated projective, so are
![]() $\mathsf {S}^d(M^*)$
and the tensor product
$\mathsf {S}^d(M^*)$
and the tensor product
![]() $\mathsf {S}^d(M^*) \otimes N$
. Applying (3) gives the claim.
$\mathsf {S}^d(M^*) \otimes N$
. Applying (3) gives the claim.
One can create new polynomial laws from old by twisting by a line bundle, that is, by a rank 1 projective module.
Lemma 3.4. Let M and N be finitely generated projective R-modules. Then for every
![]() $d \ge 0$
and every line bundle L, we have:
$d \ge 0$
and every line bundle L, we have:
-
1. There is a natural isomorphism
 $\mathscr {P}^d(M, N) \otimes (L^*)^{\otimes d} \to \mathscr {P}^d(M \otimes L, N)$
.
$\mathscr {P}^d(M, N) \otimes (L^*)^{\otimes d} \to \mathscr {P}^d(M \otimes L, N)$
. -
2. There is a natural isomorphism
 $\mathscr {P}^d(M, N) \cong \mathscr {P}^d(M \otimes L, N \otimes L^{\otimes d})$
.
$\mathscr {P}^d(M, N) \cong \mathscr {P}^d(M \otimes L, N \otimes L^{\otimes d})$
.
Proof. For (1), since
![]() $L^*$
is a line bundle, the natural map
$L^*$
is a line bundle, the natural map
![]() $(L^*)^{\otimes d} \to \mathsf {S}^d(L^*)$
is an isomorphism because it is so after faithfully flat base change. Since
$(L^*)^{\otimes d} \to \mathsf {S}^d(L^*)$
is an isomorphism because it is so after faithfully flat base change. Since
![]() $\mathsf {S}^d(M^*) \otimes \mathsf {S}^d(L^*)$
is naturally identified with
$\mathsf {S}^d(M^*) \otimes \mathsf {S}^d(L^*)$
is naturally identified with
![]() $\mathsf {S}^d((M \otimes L)^*)$
, combining Lemma 3.3(3),(4) then gives (1).
$\mathsf {S}^d((M \otimes L)^*)$
, combining Lemma 3.3(3),(4) then gives (1).
For (2), there are isomorphisms
![]() $\mathscr {P}^d(M \otimes L, N \otimes L^{\otimes d}) \xrightarrow {\sim } \mathscr {P}^d(M, N) \otimes (L^*)^{\otimes d} \otimes L^{\otimes d}$
by (1) and Lemma 3.3(4). Since
$\mathscr {P}^d(M \otimes L, N \otimes L^{\otimes d}) \xrightarrow {\sim } \mathscr {P}^d(M, N) \otimes (L^*)^{\otimes d} \otimes L^{\otimes d}$
by (1) and Lemma 3.3(4). Since
![]() $L^{\otimes d} \otimes (L^*)^{\otimes d} \cong R$
, the claim follows.
$L^{\otimes d} \otimes (L^*)^{\otimes d} \cong R$
, the claim follows.
Example 3.5. (References: [Stacks, Tag 03PK], [Reference Calmès and FaselCalF, Section 2.4.3], [Reference KnusKn, Section III.3]) Suppose L is a line bundle and there is an isomorphism
![]() $h \colon L^{\otimes d} \to R$
for some
$h \colon L^{\otimes d} \to R$
for some
![]() $d \ge 1$
. We call such a pair
$d \ge 1$
. We call such a pair
![]() $[L, h]$
a d-trivialized line bundle. (In the case
$[L, h]$
a d-trivialized line bundle. (In the case
![]() $d = 2$
, they are sometimes called discriminant modules.) Applying h to identify
$d = 2$
, they are sometimes called discriminant modules.) Applying h to identify
![]() $N \otimes L^{\otimes d} \xrightarrow {\sim } N$
in Lemma 3.4(2) gives a construction that takes
$N \otimes L^{\otimes d} \xrightarrow {\sim } N$
in Lemma 3.4(2) gives a construction that takes
![]() $f \in \mathscr {P}^d(M, N)$
and gives an element of
$f \in \mathscr {P}^d(M, N)$
and gives an element of
![]() $\mathscr {P}^d(M \otimes L, N)$
, which we denote by
$\mathscr {P}^d(M \otimes L, N)$
, which we denote by
![]() $[L, h] \cdot (M, f)$
.
$[L, h] \cdot (M, f)$
.
For example, for each
![]() $\alpha \in R^{\times }$
, define
$\alpha \in R^{\times }$
, define
![]() ${\left \langle {\alpha }\right \rangle }$
to be
${\left \langle {\alpha }\right \rangle }$
to be
![]() $[L, h]$
as in the preceding paragraph, where
$[L, h]$
as in the preceding paragraph, where
![]() $L = R$
and h is defined by
$L = R$
and h is defined by
![]() $h(\ell _1 \otimes \cdots \otimes \ell _d) = \alpha \prod \ell _i$
. Clearly,
$h(\ell _1 \otimes \cdots \otimes \ell _d) = \alpha \prod \ell _i$
. Clearly,
![]() ${\left \langle {\alpha \beta ^d}\right \rangle } \cong {\left \langle {\alpha }\right \rangle }$
for all
${\left \langle {\alpha \beta ^d}\right \rangle } \cong {\left \langle {\alpha }\right \rangle }$
for all
![]() $\alpha , \beta \in R^{\times }$
. Applying the construction in the previous paragraph, we find
$\alpha , \beta \in R^{\times }$
. Applying the construction in the previous paragraph, we find
![]() ${\left \langle {\alpha }\right \rangle } \cdot (M, f) \cong (M, \alpha f)$
.
${\left \langle {\alpha }\right \rangle } \cdot (M, f) \cong (M, \alpha f)$
.
Every
![]() $[L, h]$
with
$[L, h]$
with
![]() $L = R$
is necessarily isomorphic to
$L = R$
is necessarily isomorphic to
![]() ${\left \langle {\alpha }\right \rangle }$
for some
${\left \langle {\alpha }\right \rangle }$
for some
![]() $\alpha \in R^{\times }$
. In particular, if
$\alpha \in R^{\times }$
. In particular, if
![]() $\operatorname {\mathrm {Pic}}(R)$
has no d-torsion elements other than zero — for example, if R is a semilocal ring or a UFD [Stacks, Tags 0BCH, 02M9] — then each
$\operatorname {\mathrm {Pic}}(R)$
has no d-torsion elements other than zero — for example, if R is a semilocal ring or a UFD [Stacks, Tags 0BCH, 02M9] — then each
![]() $[L, h]$
is isomorphic to
$[L, h]$
is isomorphic to
![]() ${\left \langle {\alpha }\right \rangle }$
for some
${\left \langle {\alpha }\right \rangle }$
for some
![]() $\alpha $
. The group scheme
$\alpha $
. The group scheme
![]() $\mu _d$
of d-th roots of unity is the automorphism group of each
$\mu _d$
of d-th roots of unity is the automorphism group of each
![]() $[L, h]$
, where
$[L, h]$
, where
![]() $\mu _d$
acts by multiplication on L. The group
$\mu _d$
acts by multiplication on L. The group
![]() $H^1(R, \mu _d)$
classifies pairs
$H^1(R, \mu _d)$
classifies pairs
![]() $[L, h]$
up to isomorphism.
$[L, h]$
up to isomorphism.
We say that homogeneous polynomial laws related by the isomorphism in Lemma 3.4(2) are projectively similar, imitating the language from [Reference Auel, Bernardara and BolognesiAuBB, Section 1.2] for the case of quadratic forms (
![]() $d = 2$
). (This relationship was called “lax-similarity” in [Reference Balmer and CalmèsBC].) We say that homogeneous degree d laws f and
$d = 2$
). (This relationship was called “lax-similarity” in [Reference Balmer and CalmèsBC].) We say that homogeneous degree d laws f and
![]() $[L, h] \cdot f$
for
$[L, h] \cdot f$
for
![]() $[L, h] \in H^1(R, \mu _d)$
as in the preceding example are similar. If
$[L, h] \in H^1(R, \mu _d)$
as in the preceding example are similar. If
![]() $\operatorname {\mathrm {Pic}}(R)$
is d-torsion, the two notions coincide.
$\operatorname {\mathrm {Pic}}(R)$
is d-torsion, the two notions coincide.
For
![]() $f \in \mathscr {P}^d(M, N)$
, we define
$f \in \mathscr {P}^d(M, N)$
, we define
![]() $\operatorname {\mathrm {Aut}}(f)$
to be the subgroup of
$\operatorname {\mathrm {Aut}}(f)$
to be the subgroup of
![]() $\operatorname {\mathrm {GL}}(M)$
consisting of elements g such that
$\operatorname {\mathrm {GL}}(M)$
consisting of elements g such that
![]() $fg = f$
as polynomial laws. In case M and N are finitely generated projective, so is
$fg = f$
as polynomial laws. In case M and N are finitely generated projective, so is
![]() $\mathscr {P}^d(M, N)$
, whence the functor
$\mathscr {P}^d(M, N)$
, whence the functor
![]() $\mathbf {Aut}(f)$
from
$\mathbf {Aut}(f)$
from
![]() ${R\text {-}\textbf {alg}}$
to groups defined by
${R\text {-}\textbf {alg}}$
to groups defined by
![]() $\mathbf {Aut}(f)(T) = \operatorname {\mathrm {Aut}}(f_T)$
is a closed sub-group-scheme of
$\mathbf {Aut}(f)(T) = \operatorname {\mathrm {Aut}}(f_T)$
is a closed sub-group-scheme of
![]() $\mathbf {GL}(M)$
.
$\mathbf {GL}(M)$
.
Lemma 3.6. Let f and
![]() $f'$
be homogeneous polynomial laws on finitely generated projective modules. If f and
$f'$
be homogeneous polynomial laws on finitely generated projective modules. If f and
![]() $f'$
are projectively similar, then their automorphism groups are isomorphic.
$f'$
are projectively similar, then their automorphism groups are isomorphic.
Proof. By hypothesis,
![]() $f \in \mathscr {P}^d(M, N)$
and
$f \in \mathscr {P}^d(M, N)$
and
![]() $f' \in \mathscr {P}^d(M \otimes L, N \otimes L^{\otimes d})$
for some modules M and N, line bundle L, and
$f' \in \mathscr {P}^d(M \otimes L, N \otimes L^{\otimes d})$
for some modules M and N, line bundle L, and
![]() $d \ge 0$
. The group scheme
$d \ge 0$
. The group scheme
![]() $\mathbf {Aut}(f)$
is the closed sub-group-scheme of
$\mathbf {Aut}(f)$
is the closed sub-group-scheme of
![]() $\mathbf {GL}(M)$
stabilizing the element f in
$\mathbf {GL}(M)$
stabilizing the element f in
![]() $\mathsf {S}^d(M^*) \otimes N$
. Now, any element of
$\mathsf {S}^d(M^*) \otimes N$
. Now, any element of
![]() $\mathbf {GL}(M)$
acts on
$\mathbf {GL}(M)$
acts on
![]() $\mathsf {S}^d((M \otimes L)^*) \otimes (N \otimes L^{\otimes d})$
by defining it to act as the identity on L. In this way, we find a homomorphism
$\mathsf {S}^d((M \otimes L)^*) \otimes (N \otimes L^{\otimes d})$
by defining it to act as the identity on L. In this way, we find a homomorphism
![]() $\mathbf {Aut}(f) \to \mathbf {Aut}(f')$
. Viewing M as
$\mathbf {Aut}(f) \to \mathbf {Aut}(f')$
. Viewing M as
![]() $(M \otimes L) \otimes L^*$
and N as
$(M \otimes L) \otimes L^*$
and N as
![]() $(N \otimes L^{\otimes d}) \otimes (L^*)^{\otimes d}$
, and repeating this construction, we find an inverse mapping
$(N \otimes L^{\otimes d}) \otimes (L^*)^{\otimes d}$
, and repeating this construction, we find an inverse mapping
![]() $\mathbf {Aut}(f') \to \mathbf {Aut}(f)$
.
$\mathbf {Aut}(f') \to \mathbf {Aut}(f)$
.
4 Background on composition algebras
A not-necessarily-associative R-algebra C is an R-module with an R-linear map
![]() $C \otimes _R C \to C$
, which we view as a multiplication and write as juxtaposition. Such a C is unital if it has an element
$C \otimes _R C \to C$
, which we view as a multiplication and write as juxtaposition. Such a C is unital if it has an element
![]() $1_C \in C$
such that
$1_C \in C$
such that
![]() $1_C c = c 1_C = c$
for all
$1_C c = c 1_C = c$
for all
![]() $c \in C$
(see, for example, [Reference SchaferSch]). A composition R-algebra as in [Reference PeterssonPe93] is such a C that is finitely generated projective as an R-module, is unital, and has a quadratic form
$c \in C$
(see, for example, [Reference SchaferSch]). A composition R-algebra as in [Reference PeterssonPe93] is such a C that is finitely generated projective as an R-module, is unital, and has a quadratic form
![]() $n_C \!: C \to R$
that allows composition (that is, such that
$n_C \!: C \to R$
that allows composition (that is, such that
![]() $n_C(xy) = n_C(x)n_C(y)$
for all
$n_C(xy) = n_C(x)n_C(y)$
for all
![]() $x, y \in C$
), satisfies
$x, y \in C$
), satisfies
![]() $n_C(1_C) = 1$
, and whose bilinearization defined by
$n_C(1_C) = 1$
, and whose bilinearization defined by
![]() $n_C(x, y) := n_C(x+y) - n_C(x) - n_C(y)$
gives an isomorphism
$n_C(x, y) := n_C(x+y) - n_C(x) - n_C(y)$
gives an isomorphism
![]() $C \to C^*$
via
$C \to C^*$
via
![]() $x \mapsto n_C(x, \cdot )$
. We say that a symmetric bilinear form with this property is regular. The quadratic form
$x \mapsto n_C(x, \cdot )$
. We say that a symmetric bilinear form with this property is regular. The quadratic form
![]() $n_C$
(which is unique by Proposition 4.3 below) is called the norm of C.
$n_C$
(which is unique by Proposition 4.3 below) is called the norm of C.
Remark 4.1. In the definition above, one can swap the condition
![]() $n_C(1_C) = 1$
with the requirement that the rank of C is nowhere zero, that is,
$n_C(1_C) = 1$
with the requirement that the rank of C is nowhere zero, that is,
![]() $C \otimes F \ne 0$
for every field
$C \otimes F \ne 0$
for every field
![]() $F \in {R\text {-}\textbf {alg}}$
.
$F \in {R\text {-}\textbf {alg}}$
.
We put
![]() $\operatorname {\mathrm {Tr}}_C(x) := n_C(x, 1_C)$
, a linear map
$\operatorname {\mathrm {Tr}}_C(x) := n_C(x, 1_C)$
, a linear map
![]() $C \to R$
, called the trace of C. Trivially,
$C \to R$
, called the trace of C. Trivially,
![]() $\operatorname {\mathrm {Tr}}_C(1_C) = 2$
. Lemma 3.1 gives that
$\operatorname {\mathrm {Tr}}_C(1_C) = 2$
. Lemma 3.1 gives that
![]() $1_C$
is unimodular, so we may identify R with
$1_C$
is unimodular, so we may identify R with
![]() $R1_C$
, and C is a faithful R-module. The unimodularity of
$R1_C$
, and C is a faithful R-module. The unimodularity of
![]() $1_C$
is equivalent to the existence of some
$1_C$
is equivalent to the existence of some
![]() $\lambda \in C^*$
such that
$\lambda \in C^*$
such that
![]() $\lambda (1_C) = 1$
, that is, some
$\lambda (1_C) = 1$
, that is, some
![]() $x \in C$
such that
$x \in C$
such that
![]() $\operatorname {\mathrm {Tr}}_C(x) = 1$
, whence
$\operatorname {\mathrm {Tr}}_C(x) = 1$
, whence
![]() $\operatorname {\mathrm {Tr}}_C \colon C \to R$
is surjective.
$\operatorname {\mathrm {Tr}}_C \colon C \to R$
is surjective.
The class of composition algebras is stable under base change. That is, if C is a composition R-algebra with norm
![]() $n_C$
, then for every
$n_C$
, then for every
![]() $S \in {R\text {-}\textbf {alg}}$
,
$S \in {R\text {-}\textbf {alg}}$
,
![]() $C \otimes S$
is a composition S-algebra with norm
$C \otimes S$
is a composition S-algebra with norm
![]() $n_C \otimes S$
. The following two results are essentially well known [Reference PeterssonPe93, 1.2
$n_C \otimes S$
. The following two results are essentially well known [Reference PeterssonPe93, 1.2
![]() $-$
1.4]. For convenience, we include their proof.
$-$
1.4]. For convenience, we include their proof.
Lemma 4.2 (“Cayley-Hamilton”)
Let C be a composition algebra with norm
![]() $n_C$
, and define
$n_C$
, and define
![]() $\operatorname {\mathrm {Tr}}_C$
as above. Then
$\operatorname {\mathrm {Tr}}_C$
as above. Then
for all
![]() $x \in C$
.
$x \in C$
.
Proof. Linearizing the composition law
![]() $n_C(xy) = n_C(x) n_C(y)$
, we find
$n_C(xy) = n_C(x) n_C(y)$
, we find
for all
![]() $x, y, z, w \in C$
. Setting
$x, y, z, w \in C$
. Setting
![]() $z = x$
and
$z = x$
and
![]() $w = 1_C$
in (4.2), we find:
$w = 1_C$
in (4.2), we find:
Combining these with (4.1), we find:
Since the bilinear form
![]() $n_C$
is regular, the claim follows.
$n_C$
is regular, the claim follows.
A priori, a composition algebra is a unital algebra together with a quadratic form, the norm. The next result shows that these data are redundant.
Proposition 4.3. If C is a composition algebra, then the norm
![]() $n_C$
is uniquely determined by the algebra structure of C.
$n_C$
is uniquely determined by the algebra structure of C.
Proof. Let
![]() $n' \colon C \to R$
be any quadratic form making C a composition algebra, and write
$n' \colon C \to R$
be any quadratic form making C a composition algebra, and write
![]() $\operatorname {\mathrm {Tr}}'$
for the corresponding trace
$\operatorname {\mathrm {Tr}}'$
for the corresponding trace
![]() $\operatorname {\mathrm {Tr}}'(x) := n'(x + 1_C) - n'(x) - n'(1_C)$
. Then
$\operatorname {\mathrm {Tr}}'(x) := n'(x + 1_C) - n'(x) - n'(1_C)$
. Then
![]() $\lambda := \operatorname {\mathrm {Tr}}_C - \operatorname {\mathrm {Tr}}'$
(respectively,
$\lambda := \operatorname {\mathrm {Tr}}_C - \operatorname {\mathrm {Tr}}'$
(respectively,
![]() $q := n_C - n'$
) is a linear (respectively, quadratic) form on C and the Cayley-Hamilton property yields
$q := n_C - n'$
) is a linear (respectively, quadratic) form on C and the Cayley-Hamilton property yields
We aim to prove that
![]() $q = 0$
. Because
$q = 0$
. Because
![]() $1_C$
is unimodular, it suffices to prove
$1_C$
is unimodular, it suffices to prove
![]() $\lambda = 0$
. This can be checked locally, so we may assume that R is local and, in particular,
$\lambda = 0$
. This can be checked locally, so we may assume that R is local and, in particular,
![]() $C = R1_C \oplus M$
for a free module M. Now,
$C = R1_C \oplus M$
for a free module M. Now,
![]() $\operatorname {\mathrm {Tr}}_C(1_C) = 2 = \operatorname {\mathrm {Tr}}'(1_C)$
, so
$\operatorname {\mathrm {Tr}}_C(1_C) = 2 = \operatorname {\mathrm {Tr}}'(1_C)$
, so
![]() $\lambda (1_C) = 0$
. For
$\lambda (1_C) = 0$
. For
![]() $m \in M$
a basis vector,
$m \in M$
a basis vector,
![]() $\lambda (m)m$
belongs to
$\lambda (m)m$
belongs to
![]() $M \cap R1_C$
by (4.3), so it is zero, whence
$M \cap R1_C$
by (4.3), so it is zero, whence
![]() $\lambda (m) = 0$
, proving the claim.
$\lambda (m) = 0$
, proving the claim.
Corollary 4.4. Let C be a unital R-algebra. If there is a faithfully flat
![]() $S \in {R\text {-}\textbf {alg}}$
such that
$S \in {R\text {-}\textbf {alg}}$
such that
![]() $C \otimes S$
is a composition S-algebra, then C is a composition algebra over R.
$C \otimes S$
is a composition S-algebra, then C is a composition algebra over R.
Proof. Because the norm
![]() $n_{C \otimes S}$
of
$n_{C \otimes S}$
of
![]() $C \otimes S$
is uniquely determined by the algebra structure, one obtains by faithfully flat descent a quadratic form
$C \otimes S$
is uniquely determined by the algebra structure, one obtains by faithfully flat descent a quadratic form
![]() $n_C \colon C \to R$
such that
$n_C \colon C \to R$
such that
![]() $n_C \otimes S = n_{C \otimes S}$
. Because
$n_C \otimes S = n_{C \otimes S}$
. Because
![]() $n_{C \otimes S}$
satisfies the properties required to make
$n_{C \otimes S}$
satisfies the properties required to make
![]() $C \otimes S$
a composition algebra and S is faithfully flat over R, it follows that the same properties hold for
$C \otimes S$
a composition algebra and S is faithfully flat over R, it follows that the same properties hold for
![]() $n_C$
.
$n_C$
.
The following facts are standard, see, for example [Reference KnusKn, Section V.7]: Composition algebras are alternative algebras. The map
![]() $\bar {\ } \!: C \to C$
defined by
$\bar {\ } \!: C \to C$
defined by
![]() $\overline {x} := \operatorname {\mathrm {Tr}}_C(x)1_C - x$
is an involution, that is, an R-linear antiautomorphism of period 2.
$\overline {x} := \operatorname {\mathrm {Tr}}_C(x)1_C - x$
is an involution, that is, an R-linear antiautomorphism of period 2.
Composition algebras of constant rank
In case R is connected — that is,
![]() $R \not \cong R_1 \times R_2$
, where neither
$R \not \cong R_1 \times R_2$
, where neither
![]() $R_1$
nor
$R_1$
nor
![]() $R_2$
are the zero ring — a composition R-algebra has rank
$R_2$
are the zero ring — a composition R-algebra has rank
![]() $2^e$
for
$2^e$
for
![]() $e \in \{ 0, 1, 2, 3 \}$
[Reference KnusKn, p. 206, Theorem V.7.1.6]. Therefore, specifying a composition R-algebra C is equivalent to writing
$e \in \{ 0, 1, 2, 3 \}$
[Reference KnusKn, p. 206, Theorem V.7.1.6]. Therefore, specifying a composition R-algebra C is equivalent to writing
 $$ \begin{align} R = \prod_{e=0}^3 R_e \quad \text{and} \quad C = \prod_{e=0}^3 C_e, \end{align} $$
$$ \begin{align} R = \prod_{e=0}^3 R_e \quad \text{and} \quad C = \prod_{e=0}^3 C_e, \end{align} $$
where
![]() $C_e$
is a composition
$C_e$
is a composition
![]() $R_e$
-algebra of constant rank
$R_e$
-algebra of constant rank
![]() $2^e$
.
$2^e$
.
If C is a composition algebra of rank 1, then since
![]() $1_C$
is unimodular, C is equal to R. The bilinear form
$1_C$
is unimodular, C is equal to R. The bilinear form
![]() $n_C(\cdot , \cdot )$
gives an isomorphism
$n_C(\cdot , \cdot )$
gives an isomorphism
![]() $C \to C^*$
and
$C \to C^*$
and
![]() $n_C(1_C, \alpha 1_C) = 2\alpha $
, and we deduce that
$n_C(1_C, \alpha 1_C) = 2\alpha $
, and we deduce that
![]() $2$
is invertible in R. Conversely, if 2 is invertible, then R is a composition algebra by setting
$2$
is invertible in R. Conversely, if 2 is invertible, then R is a composition algebra by setting
![]() $n_C(\alpha ) = \alpha ^2$
; in this case, we say that R is a split composition algebra.
$n_C(\alpha ) = \alpha ^2$
; in this case, we say that R is a split composition algebra.
A composition algebra whose rank is 2 is not just an associative and commutative ring, it is an étale algebra [Reference KnusKn, p. 43, Theorem I.7.3.6]. Conversely, every rank 2 étale algebra is a composition algebra. Among rank 2 étale algebras, there is a distinguished one,
![]() $R \times R$
, which is said to be split.
$R \times R$
, which is said to be split.
A composition algebra whose rank is 4 is associative and is an Azumaya algebra, commonly known as a quaternion algebra. (Note that our notion of quaternion algebra is more restrictive than the one in the books [Reference KnusKn, see p. 43] and [Reference VoightVo].) Among quaternion R-algebras, there is a distinguished one, the 2-by-2 matrices
![]() $\operatorname {\mathrm {Mat}}_2(R)$
, which is said to be split.
$\operatorname {\mathrm {Mat}}_2(R)$
, which is said to be split.
A composition algebras whose rank is 8 is known as an octonion algebra. Among octonion R-algebras, there is a distinguished one that is said to be split, called the Zorn vector matrices and denoted
![]() $\operatorname {\mathrm {Zor}}(R)$
(see [Reference Loos, Petersson and RacineLoPR, 4.2]). As a module, we view it as
$\operatorname {\mathrm {Zor}}(R)$
(see [Reference Loos, Petersson and RacineLoPR, 4.2]). As a module, we view it as
![]() $\left ( \begin {smallmatrix} R & R^3 \\ R^3 & R \end {smallmatrix} \right )$
with multiplication
$\left ( \begin {smallmatrix} R & R^3 \\ R^3 & R \end {smallmatrix} \right )$
with multiplication
where
![]() $\times $
is the ordinary cross product on
$\times $
is the ordinary cross product on
![]() $R^3$
. The quadratic form is
$R^3$
. The quadratic form is
One says that a composition R-algebra C is split if, when we write R and C as in (4.4),
![]() $C_e$
is isomorphic to the split composition
$C_e$
is isomorphic to the split composition
![]() $R_e$
-algebra for
$R_e$
-algebra for
![]() $e \ge 1$
.
$e \ge 1$
.
It is well known in the case where
![]() $R = \mathbb {R}$
, the real numbers, that a composition algebra is determined up to isomorphism by its dimension and whether it is split. That is, there are only seven isomorphism classes of composition
$R = \mathbb {R}$
, the real numbers, that a composition algebra is determined up to isomorphism by its dimension and whether it is split. That is, there are only seven isomorphism classes of composition
![]() $\mathbb {R}$
-algebras, consisting of four split ones and four division algebras, namely,
$\mathbb {R}$
-algebras, consisting of four split ones and four division algebras, namely,
![]() $\mathbb {R}$
,
$\mathbb {R}$
,
![]() $\mathbb {C}$
,
$\mathbb {C}$
,
![]() $\mathbb {H}$
, and
$\mathbb {H}$
, and
![]() $\mathbb {O}$
; note that both collections of four contain
$\mathbb {O}$
; note that both collections of four contain
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Example 4.5. The real octonions
![]() $\mathbb {O}$
are a composition
$\mathbb {O}$
are a composition
![]() $\mathbb {R}$
-algebra with basis
$\mathbb {R}$
-algebra with basis
![]() $1_{\mathbb {O}}$
,
$1_{\mathbb {O}}$
,
![]() $e_1$
,
$e_1$
,
![]() $e_2$
,
$e_2$
,
![]() $\ldots $
,
$\ldots $
,
![]() $e_7$
which is orthonormal with respect to the quadratic form
$e_7$
which is orthonormal with respect to the quadratic form
![]() $n_{\mathbb {O}}$
with multiplication table
$n_{\mathbb {O}}$
with multiplication table
for all r with subscripts taken modulo 7, and the displayed triple product is associative.
The
![]() $\mathbb {Z}$
-sublattice
$\mathbb {Z}$
-sublattice
![]() $\mathcal {O}$
of
$\mathcal {O}$
of
![]() $\mathbb {O}$
spanned by
$\mathbb {O}$
spanned by
![]() $1_{\mathbb {O}}$
, the
$1_{\mathbb {O}}$
, the
![]() $e_r$
, and
$e_r$
, and
 $$ \begin{align*} h_1 = (1 + e_1 + e_2 + e_4)/2, \quad h_2 = (1 + e_1 + e_3 + e_7)/2, \\ h_3 = (1 + e_1 + e_5 + e_6)/2 \quad \text{and} \quad h_4 = (e_1 + e_2 + e_3 + e_5)/2 \end{align*} $$
$$ \begin{align*} h_1 = (1 + e_1 + e_2 + e_4)/2, \quad h_2 = (1 + e_1 + e_3 + e_7)/2, \\ h_3 = (1 + e_1 + e_5 + e_6)/2 \quad \text{and} \quad h_4 = (e_1 + e_2 + e_3 + e_5)/2 \end{align*} $$
is a composition
![]() $\mathbb {Z}$
-algebra. It is a maximal order in
$\mathbb {Z}$
-algebra. It is a maximal order in
![]() $\mathcal {O} \otimes \mathbb {Q}$
, and all such are conjugate under the automorphism group of
$\mathcal {O} \otimes \mathbb {Q}$
, and all such are conjugate under the automorphism group of
![]() $\mathcal {O} \otimes \mathbb {Q}$
. (As a consequence, there is some choice in the way one presents this algebra. We have followed [Reference Elkies and GrossElkiesGr].) As a subring of
$\mathcal {O} \otimes \mathbb {Q}$
. (As a consequence, there is some choice in the way one presents this algebra. We have followed [Reference Elkies and GrossElkiesGr].) As a subring of
![]() $\mathbb {O}$
, it has no zero divisors. For more on this, see [Reference DicksonDi, Section 19], [Reference CoxeterCox], [Reference Conway and SmithConwS, Section 9], or [Reference ConradConrad, Section 5]. The nonuniqueness of this choice of maximal order and its relationship to other orders like
$\mathbb {O}$
, it has no zero divisors. For more on this, see [Reference DicksonDi, Section 19], [Reference CoxeterCox], [Reference Conway and SmithConwS, Section 9], or [Reference ConradConrad, Section 5]. The nonuniqueness of this choice of maximal order and its relationship to other orders like
![]() $\mathbb {Z} \oplus \mathbb {Z} e_1 \oplus \cdots \oplus \mathbb {Z} e_7$
can be understood in terms of the Bruhat-Tits building of the group
$\mathbb {Z} \oplus \mathbb {Z} e_1 \oplus \cdots \oplus \mathbb {Z} e_7$
can be understood in terms of the Bruhat-Tits building of the group
![]() $\operatorname {\mathrm {Aut}}(\operatorname {\mathrm {Zor}}(\mathbb {Q}_2))$
of type
$\operatorname {\mathrm {Aut}}(\operatorname {\mathrm {Zor}}(\mathbb {Q}_2))$
of type
![]() $\mathsf {G}_2$
over the 2-adic numbers, compare [Reference Gan and YuGanY, Section 9].
$\mathsf {G}_2$
over the 2-adic numbers, compare [Reference Gan and YuGanY, Section 9].
5 Background on Jordan algebras
Para-quadratic algebras
A (unital) para-quadratic algebra over a ring R is an R-module J together with a quadratic map
![]() $U \colon J \to \operatorname {\mathrm {End}}_R(J)$
— that is, U is an element of
$U \colon J \to \operatorname {\mathrm {End}}_R(J)$
— that is, U is an element of
![]() $\mathscr {P}^2(J, \operatorname {\mathrm {End}}_R(J))$
— called the U-operator, and a distinguished element
$\mathscr {P}^2(J, \operatorname {\mathrm {End}}_R(J))$
— called the U-operator, and a distinguished element
![]() $1_J \in J$
such that
$1_J \in J$
such that
![]() $U_{1_J} = \operatorname {\mathrm {Id}}_J$
. A homomorphism
$U_{1_J} = \operatorname {\mathrm {Id}}_J$
. A homomorphism
![]() $\phi \colon J \to J'$
of para-quadratic R-algebras is an R-linear map such that
$\phi \colon J \to J'$
of para-quadratic R-algebras is an R-linear map such that
![]() $\phi (1_J) = 1_{J'}$
and
$\phi (1_J) = 1_{J'}$
and
![]() $U^{\prime }_{\phi (x)} \phi (y) = \phi (U_x y)$
for all
$U^{\prime }_{\phi (x)} \phi (y) = \phi (U_x y)$
for all
![]() $x, y \in J$
, where
$x, y \in J$
, where
![]() $U'$
denotes the U-operator in
$U'$
denotes the U-operator in
![]() $J'$
.
$J'$
.
Jordan algebras
As a notational convenience, we define a linear map
![]() $J \otimes J \otimes J \to J$
denoted
$J \otimes J \otimes J \to J$
denoted
![]() $x \otimes y \otimes z \mapsto \{ xyz\}$
via
$x \otimes y \otimes z \mapsto \{ xyz\}$
via
Evidently,
![]() $\{ x y z \} = \{ z y x \}$
for all
$\{ x y z \} = \{ z y x \}$
for all
![]() $x, y, z \in J$
. A para-quadratic R-algebra J is a Jordan R-algebra if the identities
$x, y, z \in J$
. A para-quadratic R-algebra J is a Jordan R-algebra if the identities
hold for all
![]() $x, y, z \in J\otimes S$
for all
$x, y, z \in J\otimes S$
for all
![]() $S \in {R\text {-}\textbf {alg}}$
. (Alternatively, one can define a Jordan R-algebra entirely in terms of identities concerning elements of J, avoiding the “for all
$S \in {R\text {-}\textbf {alg}}$
. (Alternatively, one can define a Jordan R-algebra entirely in terms of identities concerning elements of J, avoiding the “for all
![]() $S \in {R\text {-}\textbf {alg}}$
”, at the cost of requiring a longer list of identities (see [Reference McCrimmonMcC66, Section 1]).) Note that if J is a Jordan R-algebra, then
$S \in {R\text {-}\textbf {alg}}$
”, at the cost of requiring a longer list of identities (see [Reference McCrimmonMcC66, Section 1]).) Note that if J is a Jordan R-algebra, then
![]() $J \otimes T$
is a Jordan T-algebra for every
$J \otimes T$
is a Jordan T-algebra for every
![]() $T \in {R\text {-}\textbf {alg}}$
(“Jordan algebras are closed under base change”). If J is a para-quadratic algebra and
$T \in {R\text {-}\textbf {alg}}$
(“Jordan algebras are closed under base change”). If J is a para-quadratic algebra and
![]() $J \otimes T$
is Jordan for some faithfully flat
$J \otimes T$
is Jordan for some faithfully flat
![]() $T \in {R\text {-}\textbf {alg}}$
, then J is Jordan.
$T \in {R\text {-}\textbf {alg}}$
, then J is Jordan.
For x in a Jordan algebra J and
![]() $n \ge 0$
, we define the n-th power
$n \ge 0$
, we define the n-th power
![]() $x^n$
via
$x^n$
via
An element
![]() $x \in J$
is invertible with inverse y if
$x \in J$
is invertible with inverse y if
![]() $U_x y = x$
and
$U_x y = x$
and
![]() $U_x y^2 = 1$
[Reference McCrimmonMcC66, Section 5]. It turns out that x is invertible if and only if
$U_x y^2 = 1$
[Reference McCrimmonMcC66, Section 5]. It turns out that x is invertible if and only if
![]() $U_x$
is invertible if and only if
$U_x$
is invertible if and only if
![]() $1$
is in the image of
$1$
is in the image of
![]() $U_x$
; when these hold, the inverse of x is
$U_x$
; when these hold, the inverse of x is
![]() $y = U_x^{-1} x$
, which we denote by
$y = U_x^{-1} x$
, which we denote by
![]() $x^{-1}$
. It follows from (5.2) that
$x^{-1}$
. It follows from (5.2) that
![]() $x,y \in J$
are both invertible if and only if
$x,y \in J$
are both invertible if and only if
![]() $U_xy$
is invertible, and in this case,
$U_xy$
is invertible, and in this case,
![]() $(U_xy)^{-1} = U_{x^{-1}}y^{-1}$
.
$(U_xy)^{-1} = U_{x^{-1}}y^{-1}$
.
Example 5.1. Let A be an associative and unital R-algebra. Define
![]() $U_xy := xyx$
for
$U_xy := xyx$
for
![]() $x, y \in A$
. Then
$x, y \in A$
. Then
![]() $\{ xyz\} = xyz + zyx$
and A endowed with this U-operator is a Jordan algebra denoted by
$\{ xyz\} = xyz + zyx$
and A endowed with this U-operator is a Jordan algebra denoted by
![]() $A^+$
. Note that for
$A^+$
. Note that for
![]() $x \in A$
and
$x \in A$
and
![]() $n \ge 0$
, the n-th powers of x in A and
$n \ge 0$
, the n-th powers of x in A and
![]() $A^+$
are the same.
$A^+$
are the same.
Relations with other kinds of algebras
Suppose for this paragraph and the next that 2 is invertible in R. Given a para-quadratic algebra J as in the preceding paragraph, one can define a commutative (bilinear) product
![]() $\bullet $
on J via
$\bullet $
on J via
(In the case where J is constructed from an associative algebra as in Example 5.1, one finds that
![]() $x \bullet y = \frac 12 (xy + yx)$
. If, additionally, the associative algebra is commutative,
$x \bullet y = \frac 12 (xy + yx)$
. If, additionally, the associative algebra is commutative,
![]() $\bullet $
equals the product in that associative algebra.) If J is Jordan, then
$\bullet $
equals the product in that associative algebra.) If J is Jordan, then
![]() $\bullet $
satisfies
$\bullet $
satisfies
which is the axiom classically called the “Jordan identity”.
In the opposite direction, given an R-module J with a commutative product
![]() $\bullet $
with identity element
$\bullet $
with identity element
![]() $1_J$
, we obtain a para-quadratic algebra by setting
$1_J$
, we obtain a para-quadratic algebra by setting
If the original product satisfied the Jordan identity, then the para-quadratic algebra so obtained satisfies (5.2), that is, is a Jordan algebra in our sense (see, for example [Reference JacobsonJ69, Section 1.4]).
Definition 5.2 (hermitian matrix algebras)
Let C be a composition R-algebra and
![]() $\Gamma = {\left \langle {\gamma _1, \gamma _2, \gamma _3}\right \rangle } \in \operatorname {\mathrm {GL}}_3(R)$
. We define
$\Gamma = {\left \langle {\gamma _1, \gamma _2, \gamma _3}\right \rangle } \in \operatorname {\mathrm {GL}}_3(R)$
. We define
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
to be the R-submodule of
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
to be the R-submodule of
![]() $\operatorname {\mathrm {Mat}}_3(C)$
consisting of elements fixed by the involution
$\operatorname {\mathrm {Mat}}_3(C)$
consisting of elements fixed by the involution
![]() $x \mapsto \Gamma ^{-1} \bar {x}^{\intercal } \Gamma $
and with diagonal entries in R. Note that, as an R-module,
$x \mapsto \Gamma ^{-1} \bar {x}^{\intercal } \Gamma $
and with diagonal entries in R. Note that, as an R-module,
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
is a sum of three copies of C and three copies of R, so it is finitely generated projective.
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
is a sum of three copies of C and three copies of R, so it is finitely generated projective.
In the special case where 2 is invertible in R, one can define a multiplication
![]() $\bullet $
on
$\bullet $
on
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
via
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
via
![]() $x \bullet y := \frac 12 (xy + yx)$
, where juxtaposition denotes the usual product of matrices in
$x \bullet y := \frac 12 (xy + yx)$
, where juxtaposition denotes the usual product of matrices in
![]() $\operatorname {\mathrm {Mat}}_3(C)$
. It satisfies the Jordan identity [Reference JacobsonJ68, p. 61, Corollary], and therefore, the U-operator defined via (5.6) makes
$\operatorname {\mathrm {Mat}}_3(C)$
. It satisfies the Jordan identity [Reference JacobsonJ68, p. 61, Corollary], and therefore, the U-operator defined via (5.6) makes
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
into a Jordan algebra.
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
into a Jordan algebra.
6 Cubic Jordan algebras
In this section, we define cubic Jordan algebras and the closely related notion of cubic norm structure. They provide a useful alternative language for computation.
Definition 6.1. Following [Reference McCrimmonMcC69] (see [Reference Petersson and RacinePeR86a, p. 212] for the terminology), we define a cubic norm R-structure as a quadruple
![]() $\mathbf {M} = (M,1_{\mathbf {M}},\sharp ,N_{\mathbf {M}})$
consisting of an R-module M; a distinguished element
$\mathbf {M} = (M,1_{\mathbf {M}},\sharp ,N_{\mathbf {M}})$
consisting of an R-module M; a distinguished element
![]() $1_{\mathbf {M}} \in M$
(the base point); a quadratic map
$1_{\mathbf {M}} \in M$
(the base point); a quadratic map
![]() $\sharp \colon M \to M$
, written
$\sharp \colon M \to M$
, written
![]() $x \mapsto x^{\sharp }$
(the adjoint) with (symmetric bilinear) polarization
$x \mapsto x^{\sharp }$
(the adjoint) with (symmetric bilinear) polarization
![]() $x \times y := (x + y)^{\sharp } - x^{\sharp } - y^{\sharp };$
and a cubic form
$x \times y := (x + y)^{\sharp } - x^{\sharp } - y^{\sharp };$
and a cubic form
![]() $N_{\mathbf {M}}\colon M \to R$
(the norm) such that the following axioms are fulfilled. Define a bilinear form
$N_{\mathbf {M}}\colon M \to R$
(the norm) such that the following axioms are fulfilled. Define a bilinear form
![]() $T_{\mathbf {M}}\colon M \times M \to R$
by
$T_{\mathbf {M}}\colon M \times M \to R$
by
(the bilinear trace), which is symmetric since the directional derivatives
![]() $\nabla _x$
,
$\nabla _x$
,
![]() $\nabla _y$
commute [Reference RobyRoby, p. 241, Proposition II.5], and a linear form
$\nabla _y$
commute [Reference RobyRoby, p. 241, Proposition II.5], and a linear form
![]() $\operatorname {\mathrm {Tr}}_{\mathbf {M}}\colon M \to R$
by
$\operatorname {\mathrm {Tr}}_{\mathbf {M}}\colon M \to R$
by
(the linear trace). For
![]() $\mathbf {M}$
to be a cubic norm structure, we require that the identities
$\mathbf {M}$
to be a cubic norm structure, we require that the identities
hold in all scalar extensions
![]() $M \otimes S$
,
$M \otimes S$
,
![]() $S\in {R\text {-}\textbf {alg}}$
.
$S\in {R\text {-}\textbf {alg}}$
.
For such a cubic norm structure
![]() $\mathbf {M}$
, we then define a U-operator by
$\mathbf {M}$
, we then define a U-operator by
which together with
![]() $1_{\mathbf {M}}$
converts the R-module M into a Jordan R-algebra
$1_{\mathbf {M}}$
converts the R-module M into a Jordan R-algebra
![]() $J = J(\mathbf {M})$
[Reference McCrimmonMcC69, Theorem 1]. In the sequel, we rarely distinguish carefully between the cubic norm structure
$J = J(\mathbf {M})$
[Reference McCrimmonMcC69, Theorem 1]. In the sequel, we rarely distinguish carefully between the cubic norm structure
![]() $\mathbf {M}$
and the Jordan algebra
$\mathbf {M}$
and the Jordan algebra
![]() $J(\mathbf {M})$
. By abuse of notation, we write
$J(\mathbf {M})$
. By abuse of notation, we write
![]() $1_J = 1_{\mathbf {M}}$
,
$1_J = 1_{\mathbf {M}}$
,
![]() $N_J = N_{\mathbf {M}}$
,
$N_J = N_{\mathbf {M}}$
,
![]() $T_J = T_{\mathbf {M}}$
, and
$T_J = T_{\mathbf {M}}$
, and
![]() $\operatorname {\mathrm {Tr}}_J:= \operatorname {\mathrm {Tr}}_{\mathbf {M}}$
if there is no danger of confusion, even though, in general, J does not determine
$\operatorname {\mathrm {Tr}}_J:= \operatorname {\mathrm {Tr}}_{\mathbf {M}}$
if there is no danger of confusion, even though, in general, J does not determine
![]() $\mathbf {M}$
uniquely [Reference Petersson and RacinePeR86a, p. 216].
$\mathbf {M}$
uniquely [Reference Petersson and RacinePeR86a, p. 216].
Definition 6.2. A Jordan R-algebra J is said to be cubic if there exists a cubic norm R-structure
![]() $\mathbf {M}$
as in Definition 6.1 such that (i)
$\mathbf {M}$
as in Definition 6.1 such that (i)
![]() $J = J(\mathbf {M})$
and (ii)
$J = J(\mathbf {M})$
and (ii)
![]() $J = M$
is a finitely generated projective R-module. With the quadratic form
$J = M$
is a finitely generated projective R-module. With the quadratic form
![]() $S_J\colon M \to R$
defined by
$S_J\colon M \to R$
defined by
![]() $S_J(x) := \operatorname {\mathrm {Tr}}_J(x^{\sharp })$
for
$S_J(x) := \operatorname {\mathrm {Tr}}_J(x^{\sharp })$
for
![]() $x \in J$
(the quadratic trace), the cubic Jordan algebra J satisfies the identities
$x \in J$
(the quadratic trace), the cubic Jordan algebra J satisfies the identities
for all
![]() $x \in J$
. For (6.6)–(6.8) and the first equation of (6.9), see [Reference McCrimmonMcC69, p. 499], while the second equation of (6.9) follows from the first, (6.7), and (6.8) via
$x \in J$
. For (6.6)–(6.8) and the first equation of (6.9), see [Reference McCrimmonMcC69, p. 499], while the second equation of (6.9) follows from the first, (6.7), and (6.8) via
![]() $x^4 = U_xx^2 = U_xx^{\sharp } + \operatorname {\mathrm {Tr}}_J(x)U_xx - S_J(x)U_x1_J = \operatorname {\mathrm {Tr}}_J(x)x^3 - S_J(x)x^2 + N_J(x)x$
.
$x^4 = U_xx^2 = U_xx^{\sharp } + \operatorname {\mathrm {Tr}}_J(x)U_xx - S_J(x)U_x1_J = \operatorname {\mathrm {Tr}}_J(x)x^3 - S_J(x)x^2 + N_J(x)x$
.
Remark 6.3. Note that the second equality of (6.9) derives from the first through formal multiplication by x. But, due to the para-quadratic character of Jordan algebras, this is not a legitimate operation unless
![]() $2$
is invertible in R. In fact, cubic Jordan algebras exist that contain elements x satisfying
$2$
is invertible in R. In fact, cubic Jordan algebras exist that contain elements x satisfying
![]() $x^2 = 0 \neq x^3$
[Reference JacobsonJ69, 1.31–1.32].
$x^2 = 0 \neq x^3$
[Reference JacobsonJ69, 1.31–1.32].
Example 6.4 (3-by-3 matrices)
We claim that
![]() $\operatorname {\mathrm {Mat}}_3(R)^+$
is a cubic Jordan algebra, in particular, it is
$\operatorname {\mathrm {Mat}}_3(R)^+$
is a cubic Jordan algebra, in particular, it is
![]() $J(\mathbf {M})$
for
$J(\mathbf {M})$
for
![]() $\mathbf {M} := (\operatorname {\mathrm {Mat}}_3(R), \operatorname {\mathrm {Id}}, \sharp , \det )$
, where
$\mathbf {M} := (\operatorname {\mathrm {Mat}}_3(R), \operatorname {\mathrm {Id}}, \sharp , \det )$
, where
![]() $\sharp $
denotes the classical adjoint. We first verify that
$\sharp $
denotes the classical adjoint. We first verify that
![]() $\mathbf {M}$
is a cubic norm structure. Computing directly from the definition (6.1), we find that
$\mathbf {M}$
is a cubic norm structure. Computing directly from the definition (6.1), we find that
![]() $T_{\mathbf {M}}(x,y) = \operatorname {\mathrm {Tr}}_{\operatorname {\mathrm {Mat}}_3(R)}(xy)$
, where the juxtaposition on the right is usual matrix multiplication. The formulas in (6.3) are obvious. For (6.4), the first two equations can be verified directly and the third equation is a standard property of the classical adjoint, completing the proof that
$T_{\mathbf {M}}(x,y) = \operatorname {\mathrm {Tr}}_{\operatorname {\mathrm {Mat}}_3(R)}(xy)$
, where the juxtaposition on the right is usual matrix multiplication. The formulas in (6.3) are obvious. For (6.4), the first two equations can be verified directly and the third equation is a standard property of the classical adjoint, completing the proof that
![]() $\mathbf {M}$
is a cubic norm structure. Similarly, one can check directly that the U-operator defined from the cubic norm structure by (6.5) equals the U-operator defined from the usual matrix product in Example 5.1, that is,
$\mathbf {M}$
is a cubic norm structure. Similarly, one can check directly that the U-operator defined from the cubic norm structure by (6.5) equals the U-operator defined from the usual matrix product in Example 5.1, that is,
![]() $J(\mathbf {M}) = \operatorname {\mathrm {Mat}}_3(R)^+$
.
$J(\mathbf {M}) = \operatorname {\mathrm {Mat}}_3(R)^+$
.
Lemma 6.5. Let J be a cubic Jordan R-algebra and
![]() $x,y \in J$
.
$x,y \in J$
.
-
1. x is invertible in J if and only if
 $N_J(x)$
is invertible in R. In this case
$N_J(x)$
is invertible in R. In this case  $$\begin{align*} x^{-1} = N_J(x)^{-1}x^{\sharp} \quad \text{and} \quad N_J(x^{-1}) = N_J(x)^{-1}. \end{align*}$$
$$\begin{align*} x^{-1} = N_J(x)^{-1}x^{\sharp} \quad \text{and} \quad N_J(x^{-1}) = N_J(x)^{-1}. \end{align*}$$
-
2. Invertible elements of J are unimodular.
-
3.
 $N_J(U_xy) = N_J(x)^2N_J(y)$
and
$N_J(U_xy) = N_J(x)^2N_J(y)$
and
 $N_J(x^2) = N_J(x)^2 = N_J(x^{\sharp })$
.
$N_J(x^2) = N_J(x)^2 = N_J(x^{\sharp })$
.
Proof. (1): If
![]() $N_J(x)$
is invertible in R, then (6.7) shows that so is x, with inverse
$N_J(x)$
is invertible in R, then (6.7) shows that so is x, with inverse
![]() $x^{-1} = N_J(x)^{-1}x^{\sharp }$
. Conversely, assume x is invertible in J. Then
$x^{-1} = N_J(x)^{-1}x^{\sharp }$
. Conversely, assume x is invertible in J. Then
![]() $y := (x^{-1})^2$
satisfies
$y := (x^{-1})^2$
satisfies
![]() $U_xy = 1_J$
, and (6.6) yields
$U_xy = 1_J$
, and (6.6) yields
![]() $1_J = N_J(U_xy)U_xy = N_J(x)^2N_J(y)1_J$
, hence
$1_J = N_J(U_xy)U_xy = N_J(x)^2N_J(y)1_J$
, hence
since
![]() $1_J$
is unimodular by Lemma 3.1 and (6.3). Thus,
$1_J$
is unimodular by Lemma 3.1 and (6.3). Thus,
![]() $N_J(x) \in R^{\times }$
. Before proving the final formula of (1), we deal with (2), (3).
$N_J(x) \in R^{\times }$
. Before proving the final formula of (1), we deal with (2), (3).
(2) follows immediately from Lemma 3.1 combined with the first part of (1).
(3): Applying Lemma 3.2 to the polynomial law
![]() $g\colon J \times J \to \operatorname {\mathrm {End}}_R(J)$
defined by
$g\colon J \times J \to \operatorname {\mathrm {End}}_R(J)$
defined by
![]() $g(x,y) := U_{U_xy}$
in all scalar extensions, we may assume that
$g(x,y) := U_{U_xy}$
in all scalar extensions, we may assume that
![]() $U_xy$
is invertible. By (2), therefore,
$U_xy$
is invertible. By (2), therefore,
![]() $U_xy$
is unimodular, and the first equality follows from (6.6). The second equality follows from the first for
$U_xy$
is unimodular, and the first equality follows from (6.6). The second equality follows from the first for
![]() $y = 1_J$
, while in the third equality, we may again assume that x is invertible, hence, unimodular. Then (6.7) combines with the first equality to imply
$y = 1_J$
, while in the third equality, we may again assume that x is invertible, hence, unimodular. Then (6.7) combines with the first equality to imply
![]() $N_J(x)^4 = N_J(N_J(x)x) = N_J(U_xx^{\sharp }) = N_J(x)^2N_J(x^{\sharp })$
, as desired.
$N_J(x)^4 = N_J(N_J(x)x) = N_J(U_xx^{\sharp }) = N_J(x)^2N_J(x^{\sharp })$
, as desired.
Now the second equality of (1) follows from the first and (3) via
Without the assumption that J is finitely generated projective as an R-module, Lemma 6.5 would be false [Reference Petersson and RacinePeR85, Theorem 10].
Example 6.6. We endow the R-module
![]() $M := \operatorname {\mathrm {Her}}_3(C,\Gamma )$
from Definition 5.2 with a cubic norm R-structure
$M := \operatorname {\mathrm {Her}}_3(C,\Gamma )$
from Definition 5.2 with a cubic norm R-structure
![]() $\mathbf {M}= (M,1_{\mathbf {M}},\sharp ,N_{\mathbf {M}})$
, where
$\mathbf {M}= (M,1_{\mathbf {M}},\sharp ,N_{\mathbf {M}})$
, where
![]() $1_{\mathbf {M}}$
is the 3-by-3 identity matrix. An element
$1_{\mathbf {M}}$
is the 3-by-3 identity matrix. An element
![]() $x \in \operatorname {\mathrm {Her}}_3(C, \Gamma )$
may be written as
$x \in \operatorname {\mathrm {Her}}_3(C, \Gamma )$
may be written as
 $$\begin{align*}x = \left( \begin{smallmatrix} \alpha_1 & \gamma_2 c_3 & \gamma_3 \bar{c}_2 \\ \gamma_1 \bar{c}_3 & \alpha_2 & \gamma_3 c_1 \\ \gamma_1 c_2 & \gamma_2 \bar{c}_1 & \alpha_3 \end{smallmatrix} \right) \end{align*}$$
$$\begin{align*}x = \left( \begin{smallmatrix} \alpha_1 & \gamma_2 c_3 & \gamma_3 \bar{c}_2 \\ \gamma_1 \bar{c}_3 & \alpha_2 & \gamma_3 c_1 \\ \gamma_1 c_2 & \gamma_2 \bar{c}_1 & \alpha_3 \end{smallmatrix} \right) \end{align*}$$
for
![]() $\alpha _i \in R$
and
$\alpha _i \in R$
and
![]() $c_i \in C$
. Because three of the entries are determined by symmetry, we may denote such an element by
$c_i \in C$
. Because three of the entries are determined by symmetry, we may denote such an element by
where
![]() $\varepsilon _i$
has a 1 in the
$\varepsilon _i$
has a 1 in the
![]() $(i, i)$
entry and zeros elsewhere, and
$(i, i)$
entry and zeros elsewhere, and
![]() $\delta _i^{\Gamma }(c)$
has
$\delta _i^{\Gamma }(c)$
has
![]() $\gamma _{i+2}c$
in the
$\gamma _{i+2}c$
in the
![]() $(i+1, i+2)$
entry — where the symbols
$(i+1, i+2)$
entry — where the symbols
![]() $i+1$
and
$i+1$
and
![]() $i+2$
are taken modulo 3 — and zeros in the other entries not determined by symmetry. In the literature on Jordan algebras, one finds the notation
$i+2$
are taken modulo 3 — and zeros in the other entries not determined by symmetry. In the literature on Jordan algebras, one finds the notation
![]() $c[(i+1)(i+2)]$
for what we denote
$c[(i+1)(i+2)]$
for what we denote
![]() $\delta _i^{\Gamma }(c)$
. We define the adjoint
$\delta _i^{\Gamma }(c)$
. We define the adjoint
![]() $\sharp $
by
$\sharp $
by
with indices modulo (mod) 3, and the norm
![]() $N_{\mathbf {M}}$
by
$N_{\mathbf {M}}$
by
in all scalar extensions, where the last summand on the right of (6.11) is unambiguous since
![]() $\mathrm {Tr}_C((c_1c_2)c_3) = \mathrm {Tr}_C(c_1(c_2c_3))$
[Reference McCrimmonMcC85, Theorem 3.5]. By [Reference McCrimmonMcC69, Theorem 3],
$\mathrm {Tr}_C((c_1c_2)c_3) = \mathrm {Tr}_C(c_1(c_2c_3))$
[Reference McCrimmonMcC85, Theorem 3.5]. By [Reference McCrimmonMcC69, Theorem 3],
![]() $\mathbf {M}$
is indeed a cubic norm structure. The corresponding cubic Jordan algebra will again be denoted by
$\mathbf {M}$
is indeed a cubic norm structure. The corresponding cubic Jordan algebra will again be denoted by
![]() $J := \operatorname {\mathrm {Her}}_3(C,\Gamma ) := J(\mathbf {M})$
.
$J := \operatorname {\mathrm {Her}}_3(C,\Gamma ) := J(\mathbf {M})$
.
(In case 2 is invertible in R, the commutative product
![]() $\bullet $
on
$\bullet $
on
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
defined from the U-operator by (5.4) equals the product
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
defined from the U-operator by (5.4) equals the product
![]() $x \bullet y := \frac 12 (xy + yx)$
from Definition 5.2. In order to see this, it suffices to note that the square of
$x \bullet y := \frac 12 (xy + yx)$
from Definition 5.2. In order to see this, it suffices to note that the square of
![]() $x \in \operatorname {\mathrm {Her}}_3(C, \Gamma )$
as defined in (5.3) is the same as the square of x in the matrix algebra
$x \in \operatorname {\mathrm {Her}}_3(C, \Gamma )$
as defined in (5.3) is the same as the square of x in the matrix algebra
![]() $\operatorname {\mathrm {Mat}}_3(C)$
. This in turn follows immediately from (6.8), (6.11), and the definition of the adjoint.)
$\operatorname {\mathrm {Mat}}_3(C)$
. This in turn follows immediately from (6.8), (6.11), and the definition of the adjoint.)
For x as above and
![]() $y = \sum (\beta _i\varepsilon _i + \delta _i^{\Gamma }(d_i))$
, with
$y = \sum (\beta _i\varepsilon _i + \delta _i^{\Gamma }(d_i))$
, with
![]() $\beta _i \in R$
,
$\beta _i \in R$
,
![]() $d_i \in C$
, evaluating the bilinear trace at
$d_i \in C$
, evaluating the bilinear trace at
![]() $x,y$
yields
$x,y$
yields
Since the bilinearization of
![]() $n_C$
is regular, so is
$n_C$
is regular, so is
![]() $T_J$
.
$T_J$
.
Here is an important special case.
Definition 6.7. For the special case where
![]() $\Gamma = \operatorname {\mathrm {Id}}$
, we define
$\Gamma = \operatorname {\mathrm {Id}}$
, we define
![]() $\operatorname {\mathrm {Her}}_3(C) := \operatorname {\mathrm {Her}}_3(C, \operatorname {\mathrm {Id}})$
and write
$\operatorname {\mathrm {Her}}_3(C) := \operatorname {\mathrm {Her}}_3(C, \operatorname {\mathrm {Id}})$
and write
![]() $\delta _i$
for
$\delta _i$
for
![]() $\delta _i^{\Gamma }$
. It can be useful to write elements of
$\delta _i^{\Gamma }$
. It can be useful to write elements of
![]() $\operatorname {\mathrm {Her}}_3(C)$
as
$\operatorname {\mathrm {Her}}_3(C)$
as
where
![]() $\cdot $
denotes an entry that is omitted because it is determined by symmetry. As an example of the triple product defined from (5.1) and (6.5), we mention that for
$\cdot $
denotes an entry that is omitted because it is determined by symmetry. As an example of the triple product defined from (5.1) and (6.5), we mention that for
![]() $x = \sum \alpha _i \varepsilon _i$
diagonal, we have
$x = \sum \alpha _i \varepsilon _i$
diagonal, we have
for
![]() $i \in 1, 2, 3$
taken mod 3 and
$i \in 1, 2, 3$
taken mod 3 and
![]() $a, b \in C$
.
$a, b \in C$
.
Note that, for the Jordan algebra
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
, if we multiply
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
, if we multiply
![]() $\Gamma $
by an element of
$\Gamma $
by an element of
![]() $R^{\times }$
or any entry in
$R^{\times }$
or any entry in
![]() $\Gamma $
by the square of an element of
$\Gamma $
by the square of an element of
![]() $R^{\times }$
, we obtain an algebra isomorphic to the original. Therefore, replacing
$R^{\times }$
, we obtain an algebra isomorphic to the original. Therefore, replacing
![]() $\Gamma $
by
$\Gamma $
by
![]() ${\left \langle { (\det \Gamma )^{-1} \gamma _1, (\det \Gamma )^{-1} \gamma _2, (\det \Gamma ) \gamma _3}\right \rangle }$
does not change the isomorphism class of
${\left \langle { (\det \Gamma )^{-1} \gamma _1, (\det \Gamma )^{-1} \gamma _2, (\det \Gamma ) \gamma _3}\right \rangle }$
does not change the isomorphism class of
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
, and we may assume that
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
, and we may assume that
![]() $\gamma _1 \gamma _2 \gamma _3 = 1$
.
$\gamma _1 \gamma _2 \gamma _3 = 1$
.
Example 6.8. When studying the Jordan R-algebras
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
in the special case
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
in the special case
![]() $R = \mathbb {R}$
, the preceding paragraph shows that it is sufficient to consider two choices for
$R = \mathbb {R}$
, the preceding paragraph shows that it is sufficient to consider two choices for
![]() $\Gamma $
, namely,
$\Gamma $
, namely,
![]() ${\left \langle {1, s, s}\right \rangle }$
for
${\left \langle {1, s, s}\right \rangle }$
for
![]() $s = \pm 1$
. We compute
$s = \pm 1$
. We compute
![]() $T_{\operatorname {\mathrm {Her}}_3(C, \Gamma )}$
for each choice of C and
$T_{\operatorname {\mathrm {Her}}_3(C, \Gamma )}$
for each choice of C and
![]() $\Gamma $
. Regular symmetric bilinear forms over
$\Gamma $
. Regular symmetric bilinear forms over
![]() $\mathbb {R}$
are classified by their dimension and signature (an integer), so it suffices to specify the signature. If
$\mathbb {R}$
are classified by their dimension and signature (an integer), so it suffices to specify the signature. If
![]() $C = \mathbb {R}$
,
$C = \mathbb {R}$
,
![]() $\mathbb {C}$
,
$\mathbb {C}$
,
![]() $\mathbb {H}$
, or
$\mathbb {H}$
, or
![]() $\mathbb {O}$
, the signature of
$\mathbb {O}$
, the signature of
![]() $n_C$
is
$n_C$
is
![]() $2^r$
for
$2^r$
for
![]() $r = 0$
, 1, 2, 3, respectively. By (6.12),
$r = 0$
, 1, 2, 3, respectively. By (6.12),
![]() $T_J$
has signature
$T_J$
has signature
![]() $3(1 + 2^r)$
for
$3(1 + 2^r)$
for
![]() $J = \operatorname {\mathrm {Her}}_3(C)$
and
$J = \operatorname {\mathrm {Her}}_3(C)$
and
![]() $3 - 2^r$
for
$3 - 2^r$
for
![]() $J = \operatorname {\mathrm {Her}}_3(C, {\left \langle {1, -1, -1}\right \rangle })$
. For
$J = \operatorname {\mathrm {Her}}_3(C, {\left \langle {1, -1, -1}\right \rangle })$
. For
![]() $C$
the split composition algebra of rank
$C$
the split composition algebra of rank
![]() $2^r$
for
$2^r$
for
![]() $r = 1$
, 2, or 3 and any
$r = 1$
, 2, or 3 and any
![]() $\Gamma$
, the signature of
$\Gamma$
, the signature of
![]() $n_C$
is 0 and the signature of
$n_C$
is 0 and the signature of
![]() $T_{\operatorname {\mathrm {Her}}_3(C, \Gamma)}$
is 3.
$T_{\operatorname {\mathrm {Her}}_3(C, \Gamma)}$
is 3.
Remark 6.9. Alternatively, one could define the Jordan algebra structure on
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
for an arbitrary ring R without referring to cubic norm structures as follows. Writing out the formulas for the U-operator from Definition 5.2 in case
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
for an arbitrary ring R without referring to cubic norm structures as follows. Writing out the formulas for the U-operator from Definition 5.2 in case
![]() $R = \mathbb {Q}$
, one finds that the formulas do not involve any denominators other than
$R = \mathbb {Q}$
, one finds that the formulas do not involve any denominators other than
![]() $\gamma _i$
terms and therefore make sense for any R regardless of whether 2 is invertible. This makes
$\gamma _i$
terms and therefore make sense for any R regardless of whether 2 is invertible. This makes
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
a para-quadratic algebra. Because it is a Jordan algebra in case
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
a para-quadratic algebra. Because it is a Jordan algebra in case
![]() $R = \mathbb {Q}$
as in Definition 5.2, we conclude that
$R = \mathbb {Q}$
as in Definition 5.2, we conclude that
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
is a Jordan algebra with no hypothesis on R by extension of identities [Reference BourbakiBouA2, Section IV.2.3, Theorem 2]. This alternative definition gives the same objects but is much harder to work with.
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
is a Jordan algebra with no hypothesis on R by extension of identities [Reference BourbakiBouA2, Section IV.2.3, Theorem 2]. This alternative definition gives the same objects but is much harder to work with.
7 Albert algebras are Freudenthal algebras are Jordan algebras
Definition 7.1. A split Freudenthal R-algebra is a Jordan algebra
![]() $\operatorname {\mathrm {Her}}_3(C)$
as in Definition 6.7 for some split composition R-algebra C. Because split composition algebras are determined up to isomorphism by their rank function, so are split Freudenthal algebras.
$\operatorname {\mathrm {Her}}_3(C)$
as in Definition 6.7 for some split composition R-algebra C. Because split composition algebras are determined up to isomorphism by their rank function, so are split Freudenthal algebras.
A para-quadratic R-algebra J is a Freudenthal algebra if
![]() $J \otimes S$
is a split Freudenthal S-algebra for some faithfully flat
$J \otimes S$
is a split Freudenthal S-algebra for some faithfully flat
![]() $S \in {R\text {-}\textbf {alg}}$
. It is immediate that every Freudenthal algebra is a Jordan algebra. Since every split Freudenthal R-algebra is finitely generated projective as an R-module for every R, the same is true for every Freudenthal R-algebra J, and by the same reasoning, we see that the identity element
$S \in {R\text {-}\textbf {alg}}$
. It is immediate that every Freudenthal algebra is a Jordan algebra. Since every split Freudenthal R-algebra is finitely generated projective as an R-module for every R, the same is true for every Freudenthal R-algebra J, and by the same reasoning, we see that the identity element
![]() $1_J$
is unimodular. Because the rank of a composition algebra takes values in
$1_J$
is unimodular. Because the rank of a composition algebra takes values in
![]() $\{ 1, 2, 4, 8 \}$
, the rank of a Freudenthal algebra takes values in
$\{ 1, 2, 4, 8 \}$
, the rank of a Freudenthal algebra takes values in
![]() $\{ 6, 9, 15, 27 \}$
.
$\{ 6, 9, 15, 27 \}$
.
We are now prepared to define the objects named in the title of this paper.
Definition 7.2. An Albert R-algebra is a Freudenthal R-algebra of rank 27.
We continue to prove results about Freudenthal algebras, rather than merely Albert algebras. The extra generality comes at a low cost.
Proposition 7.3. For every composition R-algebra C and every
![]() $\Gamma \in \operatorname {\mathrm {GL}}_3(R)$
,
$\Gamma \in \operatorname {\mathrm {GL}}_3(R)$
,
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
is a Freudenthal algebra.
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
is a Freudenthal algebra.
Proof. Replacing R with
![]() $R_e$
as in (4.4), we may assume that C has constant rank. There is a faithfully flat
$R_e$
as in (4.4), we may assume that C has constant rank. There is a faithfully flat
![]() $S \in {R\text {-}\textbf {alg}}$
such that
$S \in {R\text {-}\textbf {alg}}$
such that
![]() $C \otimes S$
is a split composition algebra.
$C \otimes S$
is a split composition algebra.
Consider
![]() $T := S[t_1, t_2, t_3] / (t_1^2 - \gamma _1, t_2^2 - \gamma _2, t_3^2 - \gamma _3)$
. It is a free S-module, so faithfully flat. Then
$T := S[t_1, t_2, t_3] / (t_1^2 - \gamma _1, t_2^2 - \gamma _2, t_3^2 - \gamma _3)$
. It is a free S-module, so faithfully flat. Then
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma ) \otimes T$
is isomorphic to
$\operatorname {\mathrm {Her}}_3(C, \Gamma ) \otimes T$
is isomorphic to
![]() $\operatorname {\mathrm {Her}}_3(C \otimes T)$
as Jordan algebras, and the latter is a split Freudenthal algebra.
$\operatorname {\mathrm {Her}}_3(C \otimes T)$
as Jordan algebras, and the latter is a split Freudenthal algebra.
A Freudenthal algebra is said to be reduced if it is isomorphic to
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
for some C and
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
for some C and
![]() $\Gamma $
.
$\Gamma $
.
Example 7.4. Let J be a Freudenthal R-algebra. If
![]() $x \in J$
has
$x \in J$
has
![]() $U_x = \operatorname {\mathrm {Id}}_J$
, then
$U_x = \operatorname {\mathrm {Id}}_J$
, then
![]() $x = \zeta 1_J$
for some
$x = \zeta 1_J$
for some
![]() $\zeta \in R$
such that
$\zeta \in R$
such that
![]() $\zeta ^2 = 1$
. To see this, first suppose that J is
$\zeta ^2 = 1$
. To see this, first suppose that J is
![]() $\operatorname {\mathrm {Her}}_3(C)$
for some composition algebra C and write
$\operatorname {\mathrm {Her}}_3(C)$
for some composition algebra C and write
![]() $x = \sum (\alpha _i \varepsilon _i + \delta _i(c_i))$
for
$x = \sum (\alpha _i \varepsilon _i + \delta _i(c_i))$
for
![]() $\alpha _i \in R$
and
$\alpha _i \in R$
and
![]() $c_i \in C$
. We find
$c_i \in C$
. We find
for each i, so
![]() $\alpha _i^2 = 1$
and
$\alpha _i^2 = 1$
and
![]() $c_{i+2} = 0$
for all i. Then
$c_{i+2} = 0$
for all i. Then
Since
![]() $1_C$
is unimodular,
$1_C$
is unimodular,
![]() $\alpha _{i+1} \alpha _{i+2} = 1$
for all i, proving the claim for this J.
$\alpha _{i+1} \alpha _{i+2} = 1$
for all i, proving the claim for this J.
For general J, let
![]() $S \in {R\text {-}\textbf {alg}}$
be faithfully flat such that
$S \in {R\text {-}\textbf {alg}}$
be faithfully flat such that
![]() $J \otimes S$
is split. Then
$J \otimes S$
is split. Then
![]() $x \in J$
maps to an element of
$x \in J$
maps to an element of
![]() $R1_J \otimes S \subseteq J \otimes S$
and so belongs to
$R1_J \otimes S \subseteq J \otimes S$
and so belongs to
![]() $R1_J \subseteq J$
. Since
$R1_J \subseteq J$
. Since
![]() $U_{\zeta 1_J} = \zeta ^2 \operatorname {\mathrm {Id}}_J$
for
$U_{\zeta 1_J} = \zeta ^2 \operatorname {\mathrm {Id}}_J$
for
![]() $\zeta \in R$
, the claim follows.
$\zeta \in R$
, the claim follows.
The following result is well known when R is a field or perhaps a local ring (see, for example [Reference PeterssonPe19, Proposition 20]). We impose no hypothesis on R.
Proposition 7.5. Suppose C is a split composition R-algebra of constant rank at least 2, that is, C is
![]() $R \times R$
,
$R \times R$
,
![]() $\operatorname {\mathrm {Mat}}_2(R)$
, or
$\operatorname {\mathrm {Mat}}_2(R)$
, or
![]() $\operatorname {\mathrm {Zor}}(R)$
. Then
$\operatorname {\mathrm {Zor}}(R)$
. Then
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma ) \cong \operatorname {\mathrm {Her}}_3(C)$
for all
$\operatorname {\mathrm {Her}}_3(C, \Gamma ) \cong \operatorname {\mathrm {Her}}_3(C)$
for all
![]() $\Gamma $
.
$\Gamma $
.
Proof. Define
![]() $\gamma _i$
via
$\gamma _i$
via
![]() $\Gamma = {\left \langle {\gamma _1, \gamma _2, \gamma _3}\right \rangle }$
. We may assume
$\Gamma = {\left \langle {\gamma _1, \gamma _2, \gamma _3}\right \rangle }$
. We may assume
![]() $\gamma _1\gamma _2\gamma _3 = 1$
. Since
$\gamma _1\gamma _2\gamma _3 = 1$
. Since
![]() $n_C$
is universal, there are invertible
$n_C$
is universal, there are invertible
![]() $p, q \in C$
such that
$p, q \in C$
such that
![]() $\gamma _2 = n_C(q^{-1})$
and
$\gamma _2 = n_C(q^{-1})$
and
![]() $\gamma _3 = n_C(p^{-1})$
, so
$\gamma _3 = n_C(p^{-1})$
, so
![]() $\gamma _1 = n_C(pq)$
. We define
$\gamma _1 = n_C(pq)$
. We define
![]() $C^{(p,q)}$
to be a not-necessarily-associative R-algebra with the same underlying R-module structure and with multiplication
$C^{(p,q)}$
to be a not-necessarily-associative R-algebra with the same underlying R-module structure and with multiplication
![]() $\cdot _{(p,q)}$
defined by
$\cdot _{(p,q)}$
defined by
where the multiplication on the right is the multiplication in C. Certainly
![]() $(pq)^{-1}$
is an identity element in
$(pq)^{-1}$
is an identity element in
![]() $C^{(p,q)}$
. The algebra
$C^{(p,q)}$
. The algebra
![]() $C^{(p,q)}$
is called an isotope of C and is studied in [Reference McCrimmonMcC71a], where it is proved to be alternative. One checks that it is a composition algebra with quadratic form
$C^{(p,q)}$
is called an isotope of C and is studied in [Reference McCrimmonMcC71a], where it is proved to be alternative. One checks that it is a composition algebra with quadratic form
![]() $n_{C^{(p,q)}} = n_C(pq) n_C$
(see [Reference McCrimmonMcC71a, Proposition 5] for a more general statement in case R is a field).
$n_{C^{(p,q)}} = n_C(pq) n_C$
(see [Reference McCrimmonMcC71a, Proposition 5] for a more general statement in case R is a field).
Define
![]() $\phi \!: \operatorname {\mathrm {Her}}_3(C^{(p,q)}) \to \operatorname {\mathrm {Her}}_3(C, \Gamma )$
via
$\phi \!: \operatorname {\mathrm {Her}}_3(C^{(p,q)}) \to \operatorname {\mathrm {Her}}_3(C, \Gamma )$
via
![]() $\phi (\sum x_i \varepsilon _i + \delta _i(c_i)) = \sum x_i \varepsilon _i + \delta _i^{\Gamma }(c^{\prime }_i)$
, where
$\phi (\sum x_i \varepsilon _i + \delta _i(c_i)) = \sum x_i \varepsilon _i + \delta _i^{\Gamma }(c^{\prime }_i)$
, where
It is evidently an isomorphism of R-modules, and one checks that it is an isomorphism of Jordan algebras, compare [Reference McCrimmonMcC71a, Theorem 3]. Therefore, we are reduced to verifying that
![]() $C^{(p,q)}$
is split.
$C^{(p,q)}$
is split.
If C is associative, then the R-linear map
is an isomorphism of R-algebras. So assume
![]() $C = \operatorname {\mathrm {Zor}}(R)$
.
$C = \operatorname {\mathrm {Zor}}(R)$
.
At the beginning, when we chose p and q, we were free to pick
![]() $\xi _i, \eta _i \in R^{\times }$
such that
$\xi _i, \eta _i \in R^{\times }$
such that
![]() $p = \left ( \begin {smallmatrix} \xi _1 & 0 \\ 0 & \xi _2 \end {smallmatrix} \right )$
and
$p = \left ( \begin {smallmatrix} \xi _1 & 0 \\ 0 & \xi _2 \end {smallmatrix} \right )$
and
![]() $q = \left ( \begin {smallmatrix} \eta _1 & 0 \\ 0 & \eta _2 \end {smallmatrix} \right )$
. Let
$q = \left ( \begin {smallmatrix} \eta _1 & 0 \\ 0 & \eta _2 \end {smallmatrix} \right )$
. Let
![]() $A \in \operatorname {\mathrm {Mat}}_3(R)$
be any matrix such that
$A \in \operatorname {\mathrm {Mat}}_3(R)$
be any matrix such that
![]() $\det A = (\xi _1 \xi _2^2 \eta _1^2 \eta )^{-1}$
and put
$\det A = (\xi _1 \xi _2^2 \eta _1^2 \eta )^{-1}$
and put
![]() $B := \xi _2 \eta _1 (A^{\sharp })^{\intercal }$
, where
$B := \xi _2 \eta _1 (A^{\sharp })^{\intercal }$
, where
![]() $\sharp $
denotes the classical adjoint. With
$\sharp $
denotes the classical adjoint. With
![]() $\zeta _i := (\xi _i \eta _i)^{-1}$
, one checks, using the formula
$\zeta _i := (\xi _i \eta _i)^{-1}$
, one checks, using the formula
![]() $(Sx) \times (Sy) = (S^{\sharp })^{\intercal }(x \times y)$
for
$(Sx) \times (Sy) = (S^{\sharp })^{\intercal }(x \times y)$
for
![]() $\times $
the usual cross product in
$\times $
the usual cross product in
![]() $R^3$
, that the assignment
$R^3$
, that the assignment
defines an isomorphism
![]() $C \xrightarrow {\sim } C^{(p,q)}$
.
$C \xrightarrow {\sim } C^{(p,q)}$
.
8 The ideal structure of Freudenthal algebras
It is a standard exercise to show that every (two-sided) ideal in the matrix algebra
![]() $\operatorname {\mathrm {Mat}}_n(R)$
is of the form
$\operatorname {\mathrm {Mat}}_n(R)$
is of the form
![]() $\operatorname {\mathrm {Mat}}_n(\mathfrak {a})$
for some ideal
$\operatorname {\mathrm {Mat}}_n(\mathfrak {a})$
for some ideal
![]() $\mathfrak {a}$
in R. More generally, every ideal in an Azumaya R-algebra A is of the form
$\mathfrak {a}$
in R. More generally, every ideal in an Azumaya R-algebra A is of the form
![]() $\mathfrak {a} A$
some ideal
$\mathfrak {a} A$
some ideal
![]() $\mathfrak {a}$
of R [Reference Knus and OjangurenKnO, p. 95, Corollary III.5.2].
$\mathfrak {a}$
of R [Reference Knus and OjangurenKnO, p. 95, Corollary III.5.2].
A similar result holds for every octonion R-algebra C: Every one-sided ideal in C is a two-sided ideal that is stable under the involution on C. The maps
![]() $I \mapsto I \cap R$
and
$I \mapsto I \cap R$
and
![]() are bijections between the set of ideals of C and ideals in R. See [Reference PeterssonPe21, Section 4] for a proof in this generality and the references therein for earlier results of this type going back to [Reference MahlerMa].
are bijections between the set of ideals of C and ideals in R. See [Reference PeterssonPe21, Section 4] for a proof in this generality and the references therein for earlier results of this type going back to [Reference MahlerMa].
We now prove a similar result for Freudenthal algebras.
Definition 8.1. An ideal in a para-quadratic R-algebra J is the kernel of a homomorphism, that is, an R-submodule I such that
where we have written
![]() $U_I J$
for the R-span of
$U_I J$
for the R-span of
![]() $U_x y$
with
$U_x y$
with
![]() $x \in I$
and
$x \in I$
and
![]() $y \in J$
. (This is sometimes written with a
$y \in J$
. (This is sometimes written with a
![]() $\subseteq $
instead of
$\subseteq $
instead of
![]() $=$
, but the two are equivalent since
$=$
, but the two are equivalent since
![]() $U_J I \supseteq U_{1_J} I = I$
.) An R-submodule I is an outer ideal if
$U_J I \supseteq U_{1_J} I = I$
.) An R-submodule I is an outer ideal if
Here are some observations about outer ideals:
-
1. Every ideal is an outer ideal.
-
2. If 2 is invertible in R, then for every
 $x \in I$
and
$x \in I$
and
 $y \in J$
,
$y \in J$
,
 $U_x y = \frac 12 \{ xyx \} \in \{ J J I \}$
, so the notions of ideal and outer ideal coincide, and both agree with the notion of ideal for the commutative bilinear product
$U_x y = \frac 12 \{ xyx \} \in \{ J J I \}$
, so the notions of ideal and outer ideal coincide, and both agree with the notion of ideal for the commutative bilinear product
 $\bullet $
defined in (5.4).
$\bullet $
defined in (5.4). -
3. For every ideal
 $\mathfrak {a}$
in R, the R-submodule
$\mathfrak {a}$
in R, the R-submodule
 $\mathfrak {a} J$
is an ideal of J.
$\mathfrak {a} J$
is an ideal of J. -
4. If
 $1_J$
is unimodular, then for every outer ideal I of J,
$1_J$
is unimodular, then for every outer ideal I of J,
 $I \cap R1_J$
is an ideal in R, for the trivial reason that I is an R-module.
$I \cap R1_J$
is an ideal in R, for the trivial reason that I is an R-module. -
5. If
 $\mathfrak {a}$
is an ideal in R and
$\mathfrak {a}$
is an ideal in R and
 $1_J$
is unimodular, then
$1_J$
is unimodular, then
 $\mathfrak {a} 1_J = (\mathfrak {a} J) \cap R 1_J$
. The containment
$\mathfrak {a} 1_J = (\mathfrak {a} J) \cap R 1_J$
. The containment
 $\subseteq $
is clear. To see the opposite containment, suppose
$\subseteq $
is clear. To see the opposite containment, suppose
 $\alpha 1_J \in \mathfrak {a} J \cap R1_J$
for some
$\alpha 1_J \in \mathfrak {a} J \cap R1_J$
for some
 $\alpha \in R$
and write
$\alpha \in R$
and write
 $\alpha 1_J = \sum \alpha _i y_i$
with
$\alpha 1_J = \sum \alpha _i y_i$
with
 $\alpha _i \in \mathfrak {a}$
and
$\alpha _i \in \mathfrak {a}$
and
 $y_i \in J$
. There is some R-linear
$y_i \in J$
. There is some R-linear
 $\lambda \!: J \to R$
such that
$\lambda \!: J \to R$
such that
 $\lambda (1_J) = 1$
. Then
$\lambda (1_J) = 1$
. Then
 $\alpha = \lambda (\alpha 1_J) = \sum \alpha _i \lambda (y_i)$
is in
$\alpha = \lambda (\alpha 1_J) = \sum \alpha _i \lambda (y_i)$
is in
 $\mathfrak {a}$
.
$\mathfrak {a}$
.
Theorem 8.2. Let J be a Freudenthal R-algebra. Every outer ideal of J is an ideal. The maps
![]() $I \mapsto I \cap R1_J$
and
$I \mapsto I \cap R1_J$
and
![]() are bijections between the set of outer ideals of J and the set of ideals of R.
are bijections between the set of outer ideals of J and the set of ideals of R.
Proof. It suffices to show that the stated maps are bijections, because then observation (3) implies that every outer ideal is of the form
![]() $\mathfrak {a} J$
and therefore an ideal. In view of (5) (noting that
$\mathfrak {a} J$
and therefore an ideal. In view of (5) (noting that
![]() $1_J$
is unimodular), it suffices to verify that
$1_J$
is unimodular), it suffices to verify that
![]() $(I \cap R1_J)J = I$
for every outer ideal I. First suppose that
$(I \cap R1_J)J = I$
for every outer ideal I. First suppose that
![]() $J = \operatorname {\mathrm {Her}}_3(C)$
for some composition R-algebra C and write
$J = \operatorname {\mathrm {Her}}_3(C)$
for some composition R-algebra C and write
![]() $\mathfrak {a} := I \cap R1_J$
. The Peirce projections relative to the diagonal frame of J, that is,
$\mathfrak {a} := I \cap R1_J$
. The Peirce projections relative to the diagonal frame of J, that is,
![]() $U_{\varepsilon _i}$
and
$U_{\varepsilon _i}$
and
![]() $x \mapsto \{\varepsilon _j x \varepsilon _l \}$
for
$x \mapsto \{\varepsilon _j x \varepsilon _l \}$
for
![]() $i, j, l = 1, 2, 3$
[Reference McCrimmonMcC66, p. 1074] stabilize I, and we find
$i, j, l = 1, 2, 3$
[Reference McCrimmonMcC66, p. 1074] stabilize I, and we find
Set
![]() $B := \{ c \in C \mid \delta _1(c) \in I \}$
. We claim that B is an ideal in C. Note that
$B := \{ c \in C \mid \delta _1(c) \in I \}$
. We claim that B is an ideal in C. Note that
![]() $U_{\delta _1(1_C)} \delta _1(b) = \delta _1(\bar {b})$
, so B is stable under the involution.
$U_{\delta _1(1_C)} \delta _1(b) = \delta _1(\bar {b})$
, so B is stable under the involution.
We leverage (6.13). Repeatedly applying this with
![]() $a = 1_C$
and using that B is stable under the involution, we conclude that
$a = 1_C$
and using that B is stable under the involution, we conclude that
![]() $\delta _i(B) = I \cap \delta _i(C)$
for all i. For
$\delta _i(B) = I \cap \delta _i(C)$
for all i. For
![]() $c \in C$
and
$c \in C$
and
![]() $b \in B$
, I contains
$b \in B$
, I contains
![]() $\{ 1_J \delta _2(\bar {c}) \delta _1(\bar {b}) \} = \delta _3(c b)$
, so
$\{ 1_J \delta _2(\bar {c}) \delta _1(\bar {b}) \} = \delta _3(c b)$
, so
![]() $cB \subseteq B$
, that is, B is an ideal in C and therefore
$cB \subseteq B$
, that is, B is an ideal in C and therefore
![]() $B = \mathfrak {a} C$
for some ideal
$B = \mathfrak {a} C$
for some ideal
![]() $\mathfrak {a}$
of R.
$\mathfrak {a}$
of R.
For
![]() $c \in C$
, I contains
$c \in C$
, I contains
![]() $\{ \delta _i(1_C) \varepsilon _{i+1} \delta _i(\mathfrak {a} c) \} = \operatorname {\mathrm {Tr}}_C(\mathfrak {a} c) \varepsilon _{i+2}$
. Since
$\{ \delta _i(1_C) \varepsilon _{i+1} \delta _i(\mathfrak {a} c) \} = \operatorname {\mathrm {Tr}}_C(\mathfrak {a} c) \varepsilon _{i+2}$
. Since
![]() $\operatorname {\mathrm {Tr}}_C$
is surjective,
$\operatorname {\mathrm {Tr}}_C$
is surjective,
![]() $\mathfrak {a} \varepsilon _j \subseteq I$
for all j.
$\mathfrak {a} \varepsilon _j \subseteq I$
for all j.
In the other direction, if
![]() $\alpha _i \varepsilon _i \in I$
, then so is
$\alpha _i \varepsilon _i \in I$
, then so is
It follows that
![]() $I \cap R\varepsilon _i = \mathfrak {a} R$
for all i and, in particular,
$I \cap R\varepsilon _i = \mathfrak {a} R$
for all i and, in particular,
![]() $I \cap R1_J = \mathfrak {a} R$
and
$I \cap R1_J = \mathfrak {a} R$
and
![]() $I = \mathfrak {a} J$
.
$I = \mathfrak {a} J$
.
We now treat the general case. Suppose I is an outer ideal in a Freudenthal R-algebra J. There is a faithfully flat
![]() $S \in {R\text {-}\textbf {alg}}$
, such that
$S \in {R\text {-}\textbf {alg}}$
, such that
![]() $J \otimes S$
is a split Freudenthal algebra. We have
$J \otimes S$
is a split Freudenthal algebra. We have
where the first equality is because S is flat and the second is by the previous case, since
![]() $I \otimes S$
is an outer ideal. It follows that
$I \otimes S$
is an outer ideal. It follows that
![]() $I = (I \cap R1_J)J$
as desired.
$I = (I \cap R1_J)J$
as desired.
Remark 8.3. In the proof above, the inclusion
![]() $(I \cap R1_J) J \subseteq I$
could instead have been argued as follows. Define
$(I \cap R1_J) J \subseteq I$
could instead have been argued as follows. Define
![]() $\operatorname {\mathrm {Sq}}(J)$
as the R-submodule of J generated by
$\operatorname {\mathrm {Sq}}(J)$
as the R-submodule of J generated by
![]() $x^2$
for
$x^2$
for
![]() $x \in J$
. Since
$x \in J$
. Since
![]() $1_J$
is unimodular, one finds that
$1_J$
is unimodular, one finds that
![]() $(I \cap R1_J) \operatorname {\mathrm {Sq}}(J) \subseteq I$
. Then, one argues that
$(I \cap R1_J) \operatorname {\mathrm {Sq}}(J) \subseteq I$
. Then, one argues that
![]() $\operatorname {\mathrm {Sq}}(J) = J$
for a split Freudenthal algebra, and that
$\operatorname {\mathrm {Sq}}(J) = J$
for a split Freudenthal algebra, and that
![]() $\operatorname {\mathrm {Sq}}(J \otimes S) = \operatorname {\mathrm {Sq}}(J) \otimes S$
for all flat
$\operatorname {\mathrm {Sq}}(J \otimes S) = \operatorname {\mathrm {Sq}}(J) \otimes S$
for all flat
![]() $S \in {R\text {-}\textbf {alg}}$
.
$S \in {R\text {-}\textbf {alg}}$
.
Corollary 8.4. Let
![]() $\phi \colon J \to A$
be a homomorphism of para-quadratic R algebras. If J is a Freudenthal algebra and
$\phi \colon J \to A$
be a homomorphism of para-quadratic R algebras. If J is a Freudenthal algebra and
![]() $1_A$
is unimodular in A, then
$1_A$
is unimodular in A, then
![]() $\phi $
is injective.
$\phi $
is injective.
In particular, the corollary applies to every homomorphism between Freudenthal R-algebras.
Proof. The kernel of
![]() $\phi $
is an ideal of J and therefore
$\phi $
is an ideal of J and therefore
![]() $\mathfrak {a} J$
for some ideal
$\mathfrak {a} J$
for some ideal
![]() $\mathfrak {a}$
of R. For
$\mathfrak {a}$
of R. For
![]() $\alpha \in \mathfrak {a}$
, we have
$\alpha \in \mathfrak {a}$
, we have
![]() $0 = \phi (\alpha 1_J) = \alpha \phi (1_J) = \alpha 1_A$
, so
$0 = \phi (\alpha 1_J) = \alpha \phi (1_J) = \alpha 1_A$
, so
![]() $\alpha = 0$
because
$\alpha = 0$
because
![]() $1_{A}$
is unimodular.
$1_{A}$
is unimodular.
Because a Freudenthal algebra J is a projective R-module of rank
![]() $\ge 3$
, the corollary says that there is no homomorphism of para-quadratic R-algebras
$\ge 3$
, the corollary says that there is no homomorphism of para-quadratic R-algebras
![]() $J \to R^+$
. This might be stated as J is not augmented or J has no counit.
$J \to R^+$
. This might be stated as J is not augmented or J has no counit.
A para-quadratic algebra J is said to be simple if the underlying module is not the zero module and if every ideal in J equals 0 or J. Theorem 8.2 immediately gives:
Corollary 8.5. If J is a Freudenthal R-algebra and R is a field, then J is simple.
![]() $\Box $
$\Box $
Remark 8.6. There is also the notion of an inner ideal in a Jordan algebra (see [Reference McCrimmonMcC71b, Theorem 8] for a description of them for
![]() $\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R))$
). The inner ideals are related to the projective homogeneous varieties associated with the group of isometries described in Section 15 and “outer automorphisms” relating these varieties (see [Reference RacineRac] and [Reference Carr and GaribaldiCarrG]).
$\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R))$
). The inner ideals are related to the projective homogeneous varieties associated with the group of isometries described in Section 15 and “outer automorphisms” relating these varieties (see [Reference RacineRac] and [Reference Carr and GaribaldiCarrG]).
9 Groups of type
 $\mathsf {F}_4$
and
$\mathsf {F}_4$
and
 $\mathsf {C}_3$
$\mathsf {C}_3$
In the following, for a Jordan R-algebra J, we write
![]() $\operatorname {\mathrm {Aut}}(J)$
for the ordinary group of R-linear automorphisms of J and
$\operatorname {\mathrm {Aut}}(J)$
for the ordinary group of R-linear automorphisms of J and
![]() $\mathbf {Aut}(J)$
for the functor from
$\mathbf {Aut}(J)$
for the functor from
![]() ${R\text {-}\textbf {alg}}$
to groups such that
${R\text {-}\textbf {alg}}$
to groups such that
![]() $S \mapsto \operatorname {\mathrm {Aut}}(J \otimes S)$
. Recall that for every simple root datum, there is a unique simple group scheme over
$S \mapsto \operatorname {\mathrm {Aut}}(J \otimes S)$
. Recall that for every simple root datum, there is a unique simple group scheme over
![]() $\mathbb {Z}$
called a Chevalley group [Reference Demazure and GrothendieckDemG, Corollary XXIII.5.4], and every split simple algebraic group over a field is obtained from a unique Chevalley group by base change [Reference MilneMilne, Section 23g].
$\mathbb {Z}$
called a Chevalley group [Reference Demazure and GrothendieckDemG, Corollary XXIII.5.4], and every split simple algebraic group over a field is obtained from a unique Chevalley group by base change [Reference MilneMilne, Section 23g].
Lemma 9.1. Let J be a Freudenthal algebra of rank 15 or 27 over a ring R. Then
![]() $\mathbf {Aut}(J)$
is a semisimple R-group scheme that is adjoint (i.e., its center is the trivial group scheme). Its root system has type
$\mathbf {Aut}(J)$
is a semisimple R-group scheme that is adjoint (i.e., its center is the trivial group scheme). Its root system has type
![]() $\mathsf {C}_3$
if J has rank 15 and type
$\mathsf {C}_3$
if J has rank 15 and type
![]() $\mathsf {F}_4$
if J has rank 27. If J is the split Freudenthal algebra, then the group scheme
$\mathsf {F}_4$
if J has rank 27. If J is the split Freudenthal algebra, then the group scheme
![]() $\mathbf {Aut}(J)$
is obtained from the Chevalley group over
$\mathbf {Aut}(J)$
is obtained from the Chevalley group over
![]() $\mathbb {Z}$
by base change.
$\mathbb {Z}$
by base change.
Proof. First suppose that
![]() $R = \mathbb {Z}$
and J is split. If J has rank 15, then the proof of 14.19 in [Reference SpringerSp73] shows that the automorphisms of
$R = \mathbb {Z}$
and J is split. If J has rank 15, then the proof of 14.19 in [Reference SpringerSp73] shows that the automorphisms of
![]() $J \otimes F$
for every field F are exactly the automorphisms of the algebra
$J \otimes F$
for every field F are exactly the automorphisms of the algebra
![]() $\operatorname {\mathrm {Mat}}_6(F)$
with the split symplectic involution, which is the split adjoint group
$\operatorname {\mathrm {Mat}}_6(F)$
with the split symplectic involution, which is the split adjoint group
![]() $\operatorname {\mathrm {PGSp}}_6$
of type
$\operatorname {\mathrm {PGSp}}_6$
of type
![]() $\mathsf {C}_3$
. For J of rank 27,
$\mathsf {C}_3$
. For J of rank 27,
![]() $\mathbf {Aut}(J) \times F$
is split of type
$\mathbf {Aut}(J) \times F$
is split of type
![]() $\mathsf {F}_4$
by [Reference JacobsonJ71, Section 6] (written for Lie algebras), [Reference FreudenthalFr85, Satz 4.11] (written for
$\mathsf {F}_4$
by [Reference JacobsonJ71, Section 6] (written for Lie algebras), [Reference FreudenthalFr85, Satz 4.11] (written for
![]() $\mathbb {R}$
), [Reference Springer and VeldkampSpV, Theorem 7.2.1] (if
$\mathbb {R}$
), [Reference Springer and VeldkampSpV, Theorem 7.2.1] (if
![]() $\operatorname {\mathrm {char}} F \ne 2, 3$
), or [Reference SpringerSp73, 14.24] in general.
$\operatorname {\mathrm {char}} F \ne 2, 3$
), or [Reference SpringerSp73, 14.24] in general.
Note that
![]() $\mathbf {Aut}(J) \times F$
is connected and smooth as a group scheme over F, and
$\mathbf {Aut}(J) \times F$
is connected and smooth as a group scheme over F, and
![]() $\mathbf {Aut}(J)$
is finitely presented (because
$\mathbf {Aut}(J)$
is finitely presented (because
![]() $\mathbb {Z}$
is noetherian and J is a finitely generated module), so it follows by [Reference Gan and YuGanY, Proposition 6.1] or [Reference Alsaody and GilleAlsG, Lemma B.1] that
$\mathbb {Z}$
is noetherian and J is a finitely generated module), so it follows by [Reference Gan and YuGanY, Proposition 6.1] or [Reference Alsaody and GilleAlsG, Lemma B.1] that
![]() $\mathbf {Aut}(J)$
is smooth as a scheme over the Dedekind domain
$\mathbf {Aut}(J)$
is smooth as a scheme over the Dedekind domain
![]() $\mathbb {Z}$
. In summary,
$\mathbb {Z}$
. In summary,
![]() $\mathbf {Aut}(J)$
is semisimple and adjoint of the specified type. Moreover, because
$\mathbf {Aut}(J)$
is semisimple and adjoint of the specified type. Moreover, because
![]() $\mathbf {Aut}(J) \times \mathbb {Q}$
is split,
$\mathbf {Aut}(J) \times \mathbb {Q}$
is split,
![]() $\mathbf {Aut}(J)$
is a Chevalley group [Reference ConradConrad, Theorem 1.4].
$\mathbf {Aut}(J)$
is a Chevalley group [Reference ConradConrad, Theorem 1.4].
In the case of general R and J, let
![]() $S \in {R\text {-}\textbf {alg}}$
be faithfully flat such that
$S \in {R\text {-}\textbf {alg}}$
be faithfully flat such that
![]() $J \otimes S$
is split. Then
$J \otimes S$
is split. Then
![]() $\mathbf {Aut}(J) \times S$
is semisimple adjoint of the specified type. Certainly,
$\mathbf {Aut}(J) \times S$
is semisimple adjoint of the specified type. Certainly,
![]() $\mathbf {Aut}(J)$
is also smooth. Moreover, for each
$\mathbf {Aut}(J)$
is also smooth. Moreover, for each
![]() $\mathfrak {p} \in \operatorname {\mathrm {Spec}} R$
, there is a
$\mathfrak {p} \in \operatorname {\mathrm {Spec}} R$
, there is a
![]() $\mathfrak {q} \in \operatorname {\mathrm {Spec}} S$
such that
$\mathfrak {q} \in \operatorname {\mathrm {Spec}} S$
such that
![]() $\mathfrak {q} \cap R = \mathfrak {p}$
. Then the field of fractions
$\mathfrak {q} \cap R = \mathfrak {p}$
. Then the field of fractions
![]() $R(\mathfrak {p})$
of
$R(\mathfrak {p})$
of
![]() $R/\mathfrak {p}$
embeds in the field
$R/\mathfrak {p}$
embeds in the field
![]() $S(\mathfrak {q})$
, so the algebraic closure
$S(\mathfrak {q})$
, so the algebraic closure
![]() $\overline {R(\mathfrak {p})}$
includes in the algebraic closure
$\overline {R(\mathfrak {p})}$
includes in the algebraic closure
![]() $\overline {S(\mathfrak {q})}$
. Because
$\overline {S(\mathfrak {q})}$
. Because
![]() $\mathbf {Aut}(J) \times \overline {S(\mathfrak {q})}$
is adjoint semisimple of the specified type and this property is unchanged by replacing one algebraically closed field by a smaller one, the same holds over
$\mathbf {Aut}(J) \times \overline {S(\mathfrak {q})}$
is adjoint semisimple of the specified type and this property is unchanged by replacing one algebraically closed field by a smaller one, the same holds over
![]() $\overline {R(\mathfrak {p})}$
. Since this holds for every
$\overline {R(\mathfrak {p})}$
. Since this holds for every
![]() $\mathfrak {p}$
, the claim is verified.
$\mathfrak {p}$
, the claim is verified.
Remark 9.2. In case R is a field, the automorphism group of the split Freudenthal algebra of rank 6 or 9 can be deduced in a similar manner, referring to 14.17 and 14.16 in [Reference SpringerSp73]. The automorphism group of the split Freudenthal algebra of rank 9 is
![]() $\operatorname {\mathrm {PGL}}_3 \rtimes \mathbb {Z}/2$
. The automorphism group of the split Freudenthal algebra of rank 6 is the special orthogonal group of the quadratic form
$\operatorname {\mathrm {PGL}}_3 \rtimes \mathbb {Z}/2$
. The automorphism group of the split Freudenthal algebra of rank 6 is the special orthogonal group of the quadratic form
![]() $x^2 + y^2 + z^2$
, that is, the group commonly denoted
$x^2 + y^2 + z^2$
, that is, the group commonly denoted
![]() $\mathrm {SO}(3)$
. In particular, it is not smooth when R is a field of characteristic 2, and indeed, one can give examples of Freudenthal algebras of rank 6 over a field F of characteristic 2 that are not split by any separable field extension of F. (From this, it follows that such an algebra is not split by any étale F-algebra R.)
$\mathrm {SO}(3)$
. In particular, it is not smooth when R is a field of characteristic 2, and indeed, one can give examples of Freudenthal algebras of rank 6 over a field F of characteristic 2 that are not split by any separable field extension of F. (From this, it follows that such an algebra is not split by any étale F-algebra R.)
Suppose J,
![]() $J_0$
are Jordan R-algebras and there is an fppf
$J_0$
are Jordan R-algebras and there is an fppf
![]() $S \in {R\text {-}\textbf {alg}}$
and an isomorphism
$S \in {R\text {-}\textbf {alg}}$
and an isomorphism
![]() $f \colon J \otimes S \to J_0 \otimes S$
. The isomorphism f gives a class in
$f \colon J \otimes S \to J_0 \otimes S$
. The isomorphism f gives a class in
![]() $H^1(S/R, \mathbf {Aut}(J_0))$
that depends only on the isomorphism class of J as a Jordan R-algebra. Analogous statements apply when the role of Jordan algebras is replaced with affine group schemes. This is the source of the diagonal arrows in the theorem below.
$H^1(S/R, \mathbf {Aut}(J_0))$
that depends only on the isomorphism class of J as a Jordan R-algebra. Analogous statements apply when the role of Jordan algebras is replaced with affine group schemes. This is the source of the diagonal arrows in the theorem below.
Theorem 9.3. Let
![]() $J_0$
be a Freudenthal R-algebra of rank
$J_0$
be a Freudenthal R-algebra of rank
![]() $r = 15$
or 27. In the diagram
$r = 15$
or 27. In the diagram

all arrows are bijections that are functorial in R.
Proof. The top arrow has the claimed codomain by Lemma 9.1.
Every Freudenthal algebra is split by some faithfully flat R-algebra by definition, so the discussion preceding the theorem of the statement yields the lower left arrow.
As another consequence of Lemma 9.1, the conjugation map
![]() $\mathbf {Aut}(J_0) \to \mathbf {Aut}(\mathbf {Aut}(J_0))$
is an isomorphism that we use to identify
$\mathbf {Aut}(J_0) \to \mathbf {Aut}(\mathbf {Aut}(J_0))$
is an isomorphism that we use to identify
![]() $H^1(R, \mathbf {Aut}(J_0)) \xrightarrow {\sim } H^1(R, \mathbf {Aut}(\mathbf {Aut}(J_0)))$
. Every semisimple group scheme is split by some faithfully flat R-algebra (even an étale cover) [Reference Demazure and GrothendieckDemG, Corollary XXIV.4.1.6], and the remarks before the statement of the theorem now define the lower right arrow.
$H^1(R, \mathbf {Aut}(J_0)) \xrightarrow {\sim } H^1(R, \mathbf {Aut}(\mathbf {Aut}(J_0)))$
. Every semisimple group scheme is split by some faithfully flat R-algebra (even an étale cover) [Reference Demazure and GrothendieckDemG, Corollary XXIV.4.1.6], and the remarks before the statement of the theorem now define the lower right arrow.
The facts that the diagram commutes and that the diagonal arrows are bijective are general features of the machinery of descent as in [Reference WaterhouseWa, Theorem 17.6] or see [Reference Calmès and FaselCalF, 2.2.4.5].
The machinery of descent shows a more refined statement, where each of the boxes in the theorem are replaced by groupoids and the arrows are equivalences of groupoids. In that statement, the bottom box is replaced by the groupoid of
![]() $\mathbf {Aut}(J_0)$
-torsors and the diagonal arrows are provided by [Reference GiraudGir, p. 151, Theorem III.2.5.1].
$\mathbf {Aut}(J_0)$
-torsors and the diagonal arrows are provided by [Reference GiraudGir, p. 151, Theorem III.2.5.1].
In the theorem, the set
![]() $H^1(R, \mathbf {Aut}(J_0))$
is naturally a pointed set and the bijections are actually of pointed sets, where the distinguished elements are
$H^1(R, \mathbf {Aut}(J_0))$
is naturally a pointed set and the bijections are actually of pointed sets, where the distinguished elements are
![]() $J_0$
in the upper left and
$J_0$
in the upper left and
![]() $\mathbf {Aut}(J_0)$
in the upper right.
$\mathbf {Aut}(J_0)$
in the upper right.
In case R is a field of characteristic different from 2, 3 and
![]() $r = 27$
, the theorem goes back to [Reference HijikataHij]. Or see [Reference Knus, Merkurjev, Rost and TignolKnMRT, 26.18]. The statement of the theorem is similar to various statements over a field that can be found in [Reference SerreSerre, Section III.1].
$r = 27$
, the theorem goes back to [Reference HijikataHij]. Or see [Reference Knus, Merkurjev, Rost and TignolKnMRT, 26.18]. The statement of the theorem is similar to various statements over a field that can be found in [Reference SerreSerre, Section III.1].
Corollary 9.4. For each Freudenthal R-algebra J of rank 15 or 27, there is an étale cover
![]() $S \in {R\text {-}\textbf {alg}}$
such that
$S \in {R\text {-}\textbf {alg}}$
such that
![]() $J \otimes S$
is a split Freudenthal algebra.
$J \otimes S$
is a split Freudenthal algebra.
Proof. Let
![]() $J_0$
be the split Freudenthal R-algebra of the same rank as J. The image
$J_0$
be the split Freudenthal R-algebra of the same rank as J. The image
![]() $\mathbf {Iso}(J, J_0)$
of J in
$\mathbf {Iso}(J, J_0)$
of J in
![]() $H^1(R, \mathbf {Aut}(J_0))$
is an
$H^1(R, \mathbf {Aut}(J_0))$
is an
![]() $\mathbf {Aut}(J_0)$
-torsor. Since
$\mathbf {Aut}(J_0)$
-torsor. Since
![]() $\mathbf {Aut}(J_0)$
is smooth (Lemma 9.1), there is an étale cover of R that trivializes
$\mathbf {Aut}(J_0)$
is smooth (Lemma 9.1), there is an étale cover of R that trivializes
![]() $\mathbf {Iso}(J, J_0)$
.
$\mathbf {Iso}(J, J_0)$
.
Note that exactly the same kind of argument gives analogues of Lemma 9.1 and Theorem 9.3 for composition algebras, where
![]() $r = 4$
or 8, and the group is of type
$r = 4$
or 8, and the group is of type
![]() $\mathsf {A}_1$
or
$\mathsf {A}_1$
or
![]() $\mathsf {G}_2$
, respectively.
$\mathsf {G}_2$
, respectively.
10 Generic minimal polynomial of a Freudenthal algebra
Polynomials with polynomial-law coefficients
Let J be a Jordan R-algebra,
![]() $\mathscr {P}(J, R)$
the R-algebra of polynomial laws from J to R, and t a variable. Consider a polynomial
$\mathscr {P}(J, R)$
the R-algebra of polynomial laws from J to R, and t a variable. Consider a polynomial
![]() $\mathbf {p}(t) = \sum _{i=0}^n f_it^i$
with
$\mathbf {p}(t) = \sum _{i=0}^n f_it^i$
with
![]() $f_i \in \mathscr {P}(J, R)$
for
$f_i \in \mathscr {P}(J, R)$
for
![]() $0 \leq i \leq n$
. For
$0 \leq i \leq n$
. For
![]() $S \in {R\text {-}\textbf {alg}}$
,
$S \in {R\text {-}\textbf {alg}}$
,
![]() $x \in J \otimes S$
, we have
$x \in J \otimes S$
, we have
![]() $\mathbf {p}(t,x) := \sum _{i=0}^nf_{iS}(x)t^i \in S[t]$
, and we define
$\mathbf {p}(t,x) := \sum _{i=0}^nf_{iS}(x)t^i \in S[t]$
, and we define
 $$\begin{align*}\mathbf{p}(x,x) := \sum_{i=0}^nf_{iS}(x)x^i \quad \in J \otimes S. \end{align*}$$
$$\begin{align*}\mathbf{p}(x,x) := \sum_{i=0}^nf_{iS}(x)x^i \quad \in J \otimes S. \end{align*}$$
The algebra J is said to satisfy
![]() $\mathbf {p}$
if
$\mathbf {p}$
if
![]() $\mathbf {p}(x,x) = 0 = (t\mathbf {p})(x,x)$
for all
$\mathbf {p}(x,x) = 0 = (t\mathbf {p})(x,x)$
for all
![]() $S \in {R\text {-}\textbf {alg}}$
and
$S \in {R\text {-}\textbf {alg}}$
and
![]() $x \in J \otimes S$
. Note that the second equation follows from the first if
$x \in J \otimes S$
. Note that the second equation follows from the first if
![]() $2$
is invertible in R but not in general (see Remark 6.3).
$2$
is invertible in R but not in general (see Remark 6.3).
The generic minimal polynomial
Let
![]() $J := \operatorname {\mathrm {Her}}_3(C, \Gamma )$
as in Example 6.6. With a variable t, we recall from (6.9) that J satisfies the monic polynomial
$J := \operatorname {\mathrm {Her}}_3(C, \Gamma )$
as in Example 6.6. With a variable t, we recall from (6.9) that J satisfies the monic polynomial
More precisely, by [Reference LoosLo, 2.4(b)], J is generically algebraic of degree
![]() $3$
in the sense of [Reference LoosLo, 2.2] and
$3$
in the sense of [Reference LoosLo, 2.2] and
![]() $\mathbf {m}_J$
is the generic minimal polynomial of J, that is, the unique monic polynomial in
$\mathbf {m}_J$
is the generic minimal polynomial of J, that is, the unique monic polynomial in
![]() $\mathscr {P}(J,R)[t]$
of minimal degree satisfied by J [Reference LoosLo, 2.7]. It follows that the Jordan algebra J determines the polynomial
$\mathscr {P}(J,R)[t]$
of minimal degree satisfied by J [Reference LoosLo, 2.7]. It follows that the Jordan algebra J determines the polynomial
![]() $\mathbf {m}_J$
uniquely. In particular, the generic norm
$\mathbf {m}_J$
uniquely. In particular, the generic norm
![]() $N_J$
, the generic trace
$N_J$
, the generic trace
![]() $T_J$
(or
$T_J$
(or
![]() $\operatorname {\mathrm {Tr}}_J$
) and, in fact, the cubic norm structure underlying J in the sense of Definition 6.2 are uniquely determined by J as a Jordan algebra. By faithfully flat descent, every Freudenthal algebra J has a uniquely determined generic minimal polynomial of the form (10.1), and a uniquely determined underlying cubic norm structure. We conclude:
$\operatorname {\mathrm {Tr}}_J$
) and, in fact, the cubic norm structure underlying J in the sense of Definition 6.2 are uniquely determined by J as a Jordan algebra. By faithfully flat descent, every Freudenthal algebra J has a uniquely determined generic minimal polynomial of the form (10.1), and a uniquely determined underlying cubic norm structure. We conclude:
Proposition 10.1. Every Freudenthal algebra J is a cubic Jordan algebra and the bilinear trace form
![]() $T_J$
is regular.
$T_J$
is regular.
![]() $\Box $
$\Box $
The preceding discussion shows that, for a Freudenthal R-algebra J, the Jordan algebra structure of J alone (ignoring that J is a cubic Jordan algebra) determines the bilinear form
![]() $T_J$
. (For example, the 11 Freudenthal
$T_J$
. (For example, the 11 Freudenthal
![]() $\mathbb {R}$
-algebras discussed in Example 6.8 have distinct trace forms and therefore are distinct.) When R is a field of characteristic
$\mathbb {R}$
-algebras discussed in Example 6.8 have distinct trace forms and therefore are distinct.) When R is a field of characteristic
![]() $\ne 2, 3$
and J and
$\ne 2, 3$
and J and
![]() $J'$
are reduced Freudenthal algebras, Springer proved that the converse also holds, that is,
$J'$
are reduced Freudenthal algebras, Springer proved that the converse also holds, that is,
![]() $J \cong J'$
if and only if
$J \cong J'$
if and only if
![]() $T_J \cong T_{J'}$
[Reference Springer and VeldkampSpV, Theorem 5.8.1]. We do not use Springer’s result in this paper.
$T_J \cong T_{J'}$
[Reference Springer and VeldkampSpV, Theorem 5.8.1]. We do not use Springer’s result in this paper.
The following result can also be found in [Reference PeterssonPe19, Corollary 18(b)], based on the definition of Albert algebra appearing there.
Lemma 10.2. Let J and
![]() $J'$
be Freudenthal R-algebras. An R-linear map
$J'$
be Freudenthal R-algebras. An R-linear map
![]() $\phi \!: J \to J'$
is an isomorphism of para-quadratic algebras if and only if
$\phi \!: J \to J'$
is an isomorphism of para-quadratic algebras if and only if
![]() $\phi $
is surjective,
$\phi $
is surjective,
![]() $\phi (1_J) = 1_{J'}$
, and
$\phi (1_J) = 1_{J'}$
, and
![]() $N_{J'} = N_J \phi $
as polynomial laws.
$N_{J'} = N_J \phi $
as polynomial laws.
Proof. The “only if” direction follows from the uniqueness of the generic minimal polynomial as in (10.1), so we show “if”. The equality
![]() $N_{J'} = N_J \phi $
of polynomial laws and the definition of the directional derivative in Section 3 gives formulas, such as
$N_{J'} = N_J \phi $
of polynomial laws and the definition of the directional derivative in Section 3 gives formulas, such as
Since
![]() $\phi (1_J) = 1_{J'}$
, the definition of the bilinear forms
$\phi (1_J) = 1_{J'}$
, the definition of the bilinear forms
![]() $T_J$
and
$T_J$
and
![]() $T_{J'}$
in (6.1) give:
$T_{J'}$
in (6.1) give:
for all
![]() $x, y$
. Therefore, on the one hand we have
$x, y$
. Therefore, on the one hand we have
On the other hand, we have
Therefore,
![]() $\phi (x^{\sharp }) = \phi (x)^{\sharp }$
for all x. In summary,
$\phi (x^{\sharp }) = \phi (x)^{\sharp }$
for all x. In summary,
![]() $\phi $
commutes with
$\phi $
commutes with
![]() $\sharp $
and preserves
$\sharp $
and preserves
![]() $T_J$
. Therefore, by (6.5),
$T_J$
. Therefore, by (6.5),
![]() $\phi $
is a homomorphism of Jordan algebras.
$\phi $
is a homomorphism of Jordan algebras.
Suppose that x is in
![]() $\ker \phi $
. Then for all
$\ker \phi $
. Then for all
![]() $y \in J$
,
$y \in J$
,
![]() $T_J(x, y) = T_{J'}(\phi (x), \phi (y)) = 0$
, so
$T_J(x, y) = T_{J'}(\phi (x), \phi (y)) = 0$
, so
![]() $x = 0$
since the bilinear form
$x = 0$
since the bilinear form
![]() $T_J$
is regular. Since
$T_J$
is regular. Since
![]() $\phi $
is both surjective and injective, it is an isomorphism.
$\phi $
is both surjective and injective, it is an isomorphism.
Example 10.3. We claim that
![]() $\operatorname {\mathrm {Her}}_3(R \times R)$
, the split Freudenthal algebra of rank 9, is isomorphic to
$\operatorname {\mathrm {Her}}_3(R \times R)$
, the split Freudenthal algebra of rank 9, is isomorphic to
![]() $\operatorname {\mathrm {Mat}}_3(R)^+$
. To see this, define
$\operatorname {\mathrm {Mat}}_3(R)^+$
. To see this, define
![]() $\pi _i \!: R \times R \to R$
to be the projection on the i-th coordinate and define
$\pi _i \!: R \times R \to R$
to be the projection on the i-th coordinate and define
![]() $\phi \colon \operatorname {\mathrm {Her}}_3(R \times R) \to \operatorname {\mathrm {Mat}}_3(R)^+$
by sending
$\phi \colon \operatorname {\mathrm {Her}}_3(R \times R) \to \operatorname {\mathrm {Mat}}_3(R)^+$
by sending
 $$\begin{align*}\left( \begin{smallmatrix} \alpha_1 & c_3 & \cdot \\ \cdot & \alpha_2 & c_1 \\ c_2 & \cdot & \alpha_3 \end{smallmatrix} \right) \mapsto \left( \begin{smallmatrix} \alpha_1 & \pi_1(c_3) & \pi_2(c_2)\\ \pi_2(c_3) & \alpha_2 & \pi_1(c_1) \\ \pi_1(c_2) & \pi_2(c_2) & \alpha_3 \end{smallmatrix} \right) \quad \text{for } \alpha_i \in R \text{ and } c_i \in R \times R. \end{align*}$$
$$\begin{align*}\left( \begin{smallmatrix} \alpha_1 & c_3 & \cdot \\ \cdot & \alpha_2 & c_1 \\ c_2 & \cdot & \alpha_3 \end{smallmatrix} \right) \mapsto \left( \begin{smallmatrix} \alpha_1 & \pi_1(c_3) & \pi_2(c_2)\\ \pi_2(c_3) & \alpha_2 & \pi_1(c_1) \\ \pi_1(c_2) & \pi_2(c_2) & \alpha_3 \end{smallmatrix} \right) \quad \text{for } \alpha_i \in R \text{ and } c_i \in R \times R. \end{align*}$$
This map is obviously R-linear and surjective and sends the identity to the identity. One checks directly that
![]() $\phi $
preserves norms, that is, that
$\phi $
preserves norms, that is, that
![]() $\det (\phi (x))$
equals
$\det (\phi (x))$
equals
![]() $N(x)$
according to (6.11). Because
$N(x)$
according to (6.11). Because
![]() $\operatorname {\mathrm {Her}}_3(R \times R)$
and
$\operatorname {\mathrm {Her}}_3(R \times R)$
and
![]() $\operatorname {\mathrm {Mat}}_3(R)^+$
are both cubic Jordan algebras with regular trace bilinear forms, the proof of the “if” direction of Lemma 10.2 shows that
$\operatorname {\mathrm {Mat}}_3(R)^+$
are both cubic Jordan algebras with regular trace bilinear forms, the proof of the “if” direction of Lemma 10.2 shows that
![]() $\varphi $
is an isomorphism of Jordan algebras.
$\varphi $
is an isomorphism of Jordan algebras.
11 Basic classification results for Albert algebras
In the case where R is a field, such as the real numbers, a finite field, a local field, or a global field, one can find in many places in the literature classifications of Albert algebras proved using techniques involving algebras as in [Reference Springer and VeldkampSpV, Section 5.8]. For such an R, groups of type
![]() $\mathsf {F}_4$
can be classified using techniques from algebraic groups, such as in [Reference Platonov and RapinchukPlRap, Chapter 6] or [Reference GilleGil19]. The two approaches are equivalent by Theorem 9.3.
$\mathsf {F}_4$
can be classified using techniques from algebraic groups, such as in [Reference Platonov and RapinchukPlRap, Chapter 6] or [Reference GilleGil19]. The two approaches are equivalent by Theorem 9.3.
Example 11.1 (Albert algebras over
 $\mathbb {R}$
)
$\mathbb {R}$
)
Up to isomorphism, there are three Albert
![]() $\mathbb {R}$
-algebras, namely, the split one
$\mathbb {R}$
-algebras, namely, the split one
![]() $\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {R}))$
,
$\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {R}))$
,
![]() $\operatorname {\mathrm {Her}}_3(\mathbb {O}, {\left \langle {1, -1, -1}\right \rangle })$
, and
$\operatorname {\mathrm {Her}}_3(\mathbb {O}, {\left \langle {1, -1, -1}\right \rangle })$
, and
![]() $\operatorname {\mathrm {Her}}_3(\mathbb {O})$
. Rather than proving this in the language of Jordan algebras as in [Reference Albert and JacobsonAlbJ, Theorem 10], one may leverage Theorem 9.3 as follows. The three algebras are pairwise nonisomorphic because their trace forms are (Example 6.8). At the same time, a computation in the Weyl group of
$\operatorname {\mathrm {Her}}_3(\mathbb {O})$
. Rather than proving this in the language of Jordan algebras as in [Reference Albert and JacobsonAlbJ, Theorem 10], one may leverage Theorem 9.3 as follows. The three algebras are pairwise nonisomorphic because their trace forms are (Example 6.8). At the same time, a computation in the Weyl group of
![]() $\mathsf {F}_4$
as in [Reference SerreSerre, Section III.4.5], [Reference Borovoi and EvenorBorE, 14.1], or [Reference Adams and TaïbiAdT, Table 3] shows that
$\mathsf {F}_4$
as in [Reference SerreSerre, Section III.4.5], [Reference Borovoi and EvenorBorE, 14.1], or [Reference Adams and TaïbiAdT, Table 3] shows that
![]() $H^1(\mathbb {R}, \mathbf {Aut}(\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {R}))))$
has three elements. That is, there are exactly three isomorphism classes of simple affine group schemes over
$H^1(\mathbb {R}, \mathbf {Aut}(\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {R}))))$
has three elements. That is, there are exactly three isomorphism classes of simple affine group schemes over
![]() $\mathbb {R}$
of type
$\mathbb {R}$
of type
![]() $\mathsf {F}_4$
, so we have found all of them.
$\mathsf {F}_4$
, so we have found all of them.
Example 11.2 (Albert algebras over global fields)
Let A be an Albert F-algebra for F a global field. Put
![]() $\Omega $
for the (finite) set of inequivalent embeddings
$\Omega $
for the (finite) set of inequivalent embeddings
![]() $\omega \colon F \hookrightarrow \mathbb {R}$
. Since
$\omega \colon F \hookrightarrow \mathbb {R}$
. Since
![]() $\mathbf {Aut}(A)$
is a simple and simply connected affine group scheme, the natural map
$\mathbf {Aut}(A)$
is a simple and simply connected affine group scheme, the natural map
 $$\begin{align*}H^1(F, \mathbf{Aut}(A)) \xrightarrow{\prod \omega} \prod_{\omega \in \Omega} H^1(\mathbb{R}, \mathbf{Aut}(A)) \end{align*}$$
$$\begin{align*}H^1(F, \mathbf{Aut}(A)) \xrightarrow{\prod \omega} \prod_{\omega \in \Omega} H^1(\mathbb{R}, \mathbf{Aut}(A)) \end{align*}$$
is a bijection by [Reference HarderHa66] or [Reference Platonov and RapinchukPlRap, p. 286, Theorem 6.6]. Because
![]() $H^1(\mathbb {R}, \mathbf {Aut}(A))$
has three elements by the preceding example, there are exactly
$H^1(\mathbb {R}, \mathbf {Aut}(A))$
has three elements by the preceding example, there are exactly
![]() $3^{|\Omega |}$
isomorphism classes of Albert F-algebras. This result, for number fields and with a proof in the language of Albert algebras, dates back to [Reference Albert and JacobsonAlbJ, p. 417, Corollary of Theorem 12].
$3^{|\Omega |}$
isomorphism classes of Albert F-algebras. This result, for number fields and with a proof in the language of Albert algebras, dates back to [Reference Albert and JacobsonAlbJ, p. 417, Corollary of Theorem 12].
The same argument goes through for octonion algebras, and one finds that there are
![]() $2^{|\Omega |}$
isomorphism classes of octonion F-algebras. This result, for number fields and with a proof in the language of octonion algebras, dates back to [Reference ZornZ, p. 400].
$2^{|\Omega |}$
isomorphism classes of octonion F-algebras. This result, for number fields and with a proof in the language of octonion algebras, dates back to [Reference ZornZ, p. 400].
In the special case where F has a unique real embedding (e.g.,
![]() $F = \mathbb {Q}$
), the two isomorphism classes of octonion algebras are
$F = \mathbb {Q}$
), the two isomorphism classes of octonion algebras are
![]() $\operatorname {\mathrm {Zor}}(F)$
and
$\operatorname {\mathrm {Zor}}(F)$
and
![]() $\mathcal {O} \otimes F$
, and the three isomorphism classes of Albert algebras are
$\mathcal {O} \otimes F$
, and the three isomorphism classes of Albert algebras are
![]() $\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(F))$
and
$\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(F))$
and
![]() $\operatorname {\mathrm {Her}}_3(\mathcal {O} \otimes F, {\left \langle {1, s, s}\right \rangle })$
for
$\operatorname {\mathrm {Her}}_3(\mathcal {O} \otimes F, {\left \langle {1, s, s}\right \rangle })$
for
![]() $s = \pm 1$
.
$s = \pm 1$
.
Below, we will focus our attention on classification results in the case where R is not a field. We translate known results about cohomology of affine group schemes into the language of Albert algebras.
Proposition 11.3. If R is: (1) a complete discrete valuation ring whose residue field is finite or (2) a finite ring, then every Freudenthal R-algebra of rank 15 or 27 and every quaternion or octonion R-algebra is split.
Proof. In view of Theorem 9.3 and its analogue for composition algebras, it suffices to prove that
![]() $H^1(R, \mathbf {G}) = 0$
for
$H^1(R, \mathbf {G}) = 0$
for
![]() $\mathbf {G}$
a simple R-group scheme of type
$\mathbf {G}$
a simple R-group scheme of type
![]() $\mathsf {F}_4$
or
$\mathsf {F}_4$
or
![]() $\mathsf {C}_3$
obtained by base change from a Chevalley group over
$\mathsf {C}_3$
obtained by base change from a Chevalley group over
![]() $\mathbb {Z}$
. In case (1), this is [Reference ConradConrad, Proposition 3.10]. In case (2), we apply the following lemma.
$\mathbb {Z}$
. In case (1), this is [Reference ConradConrad, Proposition 3.10]. In case (2), we apply the following lemma.
Lemma 11.4. If R is a finite ring and
![]() $\mathbf {G}$
is a smooth connected R-group scheme, then
$\mathbf {G}$
is a smooth connected R-group scheme, then
![]() $H^1(R, \mathbf {G}) = 0$
.
$H^1(R, \mathbf {G}) = 0$
.
Proof. If R is not connected, then it is a finite product
![]() $R = \prod R_i$
, where each ring
$R = \prod R_i$
, where each ring
![]() $R_i$
is finite, so
$R_i$
is finite, so
![]() $H^1(R, \mathbf {G}) = \prod H^1(R_i, \mathbf {G} \times R_i)$
. Therefore, it suffices to assume that R is connected.
$H^1(R, \mathbf {G}) = \prod H^1(R_i, \mathbf {G} \times R_i)$
. Therefore, it suffices to assume that R is connected.
Suppose
![]() $\mathbf {X}$
is a
$\mathbf {X}$
is a
![]() $\mathbf {G}$
-torsor. Our aim is to show that
$\mathbf {G}$
-torsor. Our aim is to show that
![]() $\mathbf {X}$
is the trivial torsor, that is,
$\mathbf {X}$
is the trivial torsor, that is,
![]() $\mathbf {X}(R)$
is nonempty. Put
$\mathbf {X}(R)$
is nonempty. Put
![]() $\mathfrak {a}$
for the nil radical
$\mathfrak {a}$
for the nil radical
![]() $\operatorname {\mathrm {Nil}}(R)$
of R. Because R is finite, there is some minimal
$\operatorname {\mathrm {Nil}}(R)$
of R. Because R is finite, there is some minimal
![]() $m \ge 1$
such that
$m \ge 1$
such that
![]() $\mathfrak {a}^m = 0$
. We proceed by induction on m. If
$\mathfrak {a}^m = 0$
. We proceed by induction on m. If
![]() $m = 1$
, then R is reduced and connected, so it is a finite field and
$m = 1$
, then R is reduced and connected, so it is a finite field and
![]() $H^1(R, \mathbf {G}) = 0$
by Lang’s theorem. For the case
$H^1(R, \mathbf {G}) = 0$
by Lang’s theorem. For the case
![]() $m \ge 2$
, put
$m \ge 2$
, put
![]() $I := \mathfrak {a}^{m-1}$
. The ring
$I := \mathfrak {a}^{m-1}$
. The ring
![]() $R/I$
has
$R/I$
has
![]() $\operatorname {\mathrm {Nil}}(R/I)^{m-1} = (\operatorname {\mathrm {Nil}}(R)/I)^{m-1} = 0$
, so by induction,
$\operatorname {\mathrm {Nil}}(R/I)^{m-1} = (\operatorname {\mathrm {Nil}}(R)/I)^{m-1} = 0$
, so by induction,
![]() $\mathbf {X}(R/I)$
is nonempty. On the other hand,
$\mathbf {X}(R/I)$
is nonempty. On the other hand,
![]() $I^2 = \mathfrak {a}^{2m-2} = \mathfrak {a}^m \cdot \mathfrak {a}^{m-2} = 0$
and
$I^2 = \mathfrak {a}^{2m-2} = \mathfrak {a}^m \cdot \mathfrak {a}^{m-2} = 0$
and
![]() $\mathbf {X}$
is smooth, so the natural map
$\mathbf {X}$
is smooth, so the natural map
![]() $\mathbf {X}(R) \to \mathbf {X}(R/I)$
is surjective.
$\mathbf {X}(R) \to \mathbf {X}(R/I)$
is surjective.
Example 11.5. Suppose R is a Dedekind domain, and write F for its field of fractions. For
![]() $\mathbf {G}$
a Chevalley group of type
$\mathbf {G}$
a Chevalley group of type
![]() $\mathsf {G}_2$
,
$\mathsf {G}_2$
,
![]() $\mathsf {F}_4$
, or
$\mathsf {F}_4$
, or
![]() $\mathsf {E}_8$
, the map
$\mathsf {E}_8$
, the map
![]() $H^1(R, \mathbf {G}) \to H^1(F, \mathbf {G})$
has zero kernel [Reference HarderHa67, Satz 3.3]. Consequently, if A is an Albert or octonion R-algebra and
$H^1(R, \mathbf {G}) \to H^1(F, \mathbf {G})$
has zero kernel [Reference HarderHa67, Satz 3.3]. Consequently, if A is an Albert or octonion R-algebra and
![]() $A \otimes F$
is split, then the R-algebra A is split.
$A \otimes F$
is split, then the R-algebra A is split.
In particular, if F is a global field with no real embeddings, then every Albert or octonion F-algebra is split, so every Albert or octonion R-algebra is split.
In the case where F is a number field with a real embedding, we provide the following partial result, which relies on Example 11.1.
Proposition 11.6. Suppose F is a number field and R is a localization of its ring of integers at finitely many primes. If A is an Albert (respectively, octonion) F-algebra such that
![]() $A \otimes \mathbb {R}$
is not isomorphic to
$A \otimes \mathbb {R}$
is not isomorphic to
![]() $\operatorname {\mathrm {Her}}_3(\mathbb {O})$
(respectively,
$\operatorname {\mathrm {Her}}_3(\mathbb {O})$
(respectively,
![]() $\mathbb {O}$
) for every embedding
$\mathbb {O}$
) for every embedding
![]() $F \hookrightarrow \mathbb {R}$
, then there is an Albert (respectively, octonion) R-algebra B such that
$F \hookrightarrow \mathbb {R}$
, then there is an Albert (respectively, octonion) R-algebra B such that
![]() $B \otimes F \cong A$
and B is uniquely determined up to R-isomorphism.
$B \otimes F \cong A$
and B is uniquely determined up to R-isomorphism.
Proof. Write
![]() $\mathbf {G}$
for the automorphism group of the split Albert (respectively, octonion) F-algebra. Write
$\mathbf {G}$
for the automorphism group of the split Albert (respectively, octonion) F-algebra. Write
![]() $H^1_{\mathrm {ind}}(R, \mathbf {G}) \subseteq H^1(R, \mathbf {G})$
for the isomorphism classes of R-algebras B such that
$H^1_{\mathrm {ind}}(R, \mathbf {G}) \subseteq H^1(R, \mathbf {G})$
for the isomorphism classes of R-algebras B such that
![]() $B \otimes F_v$
is not
$B \otimes F_v$
is not
![]() $\operatorname {\mathrm {Her}}_3(\mathbb {O})$
(respectively,
$\operatorname {\mathrm {Her}}_3(\mathbb {O})$
(respectively,
![]() $\mathbb {O}$
), that is, such that
$\mathbb {O}$
), that is, such that
![]() $\mathbf {Aut}(B) \times F_v$
is not compact, for all real places v of F. Since
$\mathbf {Aut}(B) \times F_v$
is not compact, for all real places v of F. Since
![]() $\mathbf {G}$
is simply connected, Strong Approximation gives that the natural map
$\mathbf {G}$
is simply connected, Strong Approximation gives that the natural map
![]() $H^1_{\mathrm {ind}}(R, \mathbf {G}) \to H^1_{\mathrm {ind}}(F, \mathbf {G})$
is an isomorphism [Reference HarderHa67, Satz 4.2.4], which is what is claimed.
$H^1_{\mathrm {ind}}(R, \mathbf {G}) \to H^1_{\mathrm {ind}}(F, \mathbf {G})$
is an isomorphism [Reference HarderHa67, Satz 4.2.4], which is what is claimed.
12 The number of generators of an Albert algebra
The goal of this section is to prove Proposition 12.1, which is inspired by the work of First-Reichstein [Reference First and ReichsteinFiR] generalizing the Forster-Swan theorem. Let J be a para-quadratic R-algebra. By a (para-quadratic) subalgebra of J, we mean a submodule
![]() $J' \subseteq J$
containing
$J' \subseteq J$
containing
![]() $1_J$
and closed under the U-operator, that is, such that
$1_J$
and closed under the U-operator, that is, such that
![]() $U_x y \in J'$
for all
$U_x y \in J'$
for all
![]() $x,y \in J'$
. For any subset
$x,y \in J'$
. For any subset
![]() $S \subseteq J$
, the smallest subalgebra of J containing S is called the subalgebra generated by S; if this subalgebra is all of J, we say that S generates J.
$S \subseteq J$
, the smallest subalgebra of J containing S is called the subalgebra generated by S; if this subalgebra is all of J, we say that S generates J.
Proposition 12.1. For every noetherian ring R, every Albert R-algebra can be generated in the sense of the preceding paragraph by
![]() $3 + \dim \operatorname {\mathrm {Max}} R$
elements.
$3 + \dim \operatorname {\mathrm {Max}} R$
elements.
In the statement,
![]() $\operatorname {\mathrm {Max}} R$
is the topological space whose points are the maximal ideals of R, endowed with the subspace topology inherited from
$\operatorname {\mathrm {Max}} R$
is the topological space whose points are the maximal ideals of R, endowed with the subspace topology inherited from
![]() $\operatorname {\mathrm {Spec}} R$
. It is evident that
$\operatorname {\mathrm {Spec}} R$
. It is evident that
![]() $\dim \operatorname {\mathrm {Max}} R \le \dim \operatorname {\mathrm {Spec}} R$
, also known as the Krull dimension. Beyond this inequality, the two numbers may be quite different (e.g., for a local ring,
$\dim \operatorname {\mathrm {Max}} R \le \dim \operatorname {\mathrm {Spec}} R$
, also known as the Krull dimension. Beyond this inequality, the two numbers may be quite different (e.g., for a local ring,
![]() $\dim \operatorname {\mathrm {Max}} R = 0$
and
$\dim \operatorname {\mathrm {Max}} R = 0$
and
![]() $\dim \operatorname {\mathrm {Spec}} R$
can be any number).
$\dim \operatorname {\mathrm {Spec}} R$
can be any number).
If 2 is invertible in R, the bound in the proposition is Corollary 4.2c in [Reference First and ReichsteinFiR]. The contribution here is to remove the hypothesis on 2. In the special case where R contains an infinite field of characteristic
![]() $\ne 2$
, a different (and possibly smaller) upper bound is given in [Reference First, Reichstein and WilliamsFiRW, Section 13].
$\ne 2$
, a different (and possibly smaller) upper bound is given in [Reference First, Reichstein and WilliamsFiRW, Section 13].
The results in [Reference First and ReichsteinFiR] reduce the proof of the proposition to the case where R is a field. For a field of characteristic not
![]() $2$
, a proof may be read off from [Reference McCrimmonMcC04, p. 112]; we give a characteristic-free proof using the first Tits construction of cubic Jordan algebras [Reference McCrimmonMcC69, pp. 507–509]. We briefly recall its details.
$2$
, a proof may be read off from [Reference McCrimmonMcC04, p. 112]; we give a characteristic-free proof using the first Tits construction of cubic Jordan algebras [Reference McCrimmonMcC69, pp. 507–509]. We briefly recall its details.
The first Tits construction
Let A be a (finite-dimensional) separable associative algebra of degree
![]() $3$
over a field F, so its generic norm
$3$
over a field F, so its generic norm
![]() $N_A$
is a cubic form on A and its trace
$N_A$
is a cubic form on A and its trace
![]() $T_A\colon A \times A \to F$
defined as in (6.1) is a nondegenerate symmetric bilinear form. Given any nonzero scalar
$T_A\colon A \times A \to F$
defined as in (6.1) is a nondegenerate symmetric bilinear form. Given any nonzero scalar
![]() $\mu \in F$
, we obtain a cubic norm structure
$\mu \in F$
, we obtain a cubic norm structure
by defining
for all
![]() $x = (x_0,x_1,x_2)$
in all scalar extensions of
$x = (x_0,x_1,x_2)$
in all scalar extensions of
![]() $A \times A \times A$
. By [Reference McCrimmonMcC69, Theorem 6],
$A \times A \times A$
. By [Reference McCrimmonMcC69, Theorem 6],
![]() $\mathbf {M}$
is a cubic norm structure, so
$\mathbf {M}$
is a cubic norm structure, so
![]() $J(\mathbf {M})$
is a cubic Jordan F-algebra which we denote by
$J(\mathbf {M})$
is a cubic Jordan F-algebra which we denote by
![]() $J(A, \mu )$
.
$J(A, \mu )$
.
Example 12.2. (a): Let E be a cubic étale F-algebra. If E is either split — that is, isomorphic to
![]() $F \times F \times F$
— or a cyclic cubic field extension of F, then
$F \times F \times F$
— or a cyclic cubic field extension of F, then
![]() $J(E,1) \cong \operatorname {\mathrm {Her}}_3(F \times F, {\left \langle {1, -1, -1}\right \rangle })$
[Reference Petersson and RacinePeR84b, Theorem 3], that is, is the split Freudenthal algebra of rank 9 (Proposition 7.5), which is
$J(E,1) \cong \operatorname {\mathrm {Her}}_3(F \times F, {\left \langle {1, -1, -1}\right \rangle })$
[Reference Petersson and RacinePeR84b, Theorem 3], that is, is the split Freudenthal algebra of rank 9 (Proposition 7.5), which is
![]() $\operatorname {\mathrm {Mat}}_3(F)^+$
by Example 10.3.
$\operatorname {\mathrm {Mat}}_3(F)^+$
by Example 10.3.
(b): Let A be a central simple associative F-algebra of degree
![]() $3$
. Then
$3$
. Then
![]() $J(A,1)$
is a split Albert algebra [Reference Petersson and RacinePeR84a, Corollary 4.2].
$J(A,1)$
is a split Albert algebra [Reference Petersson and RacinePeR84a, Corollary 4.2].
Lemma 12.3. Let A be a separable associative F-algebra of degree
![]() $3$
and
$3$
and
![]() $\mu \in F^{\times }$
. Then the first Tits construction
$\mu \in F^{\times }$
. Then the first Tits construction
![]() $J(A,\mu )$
is generated by
$J(A,\mu )$
is generated by
![]() $A^+$
(identified in
$A^+$
(identified in
![]() $J(A,\mu )$
through the initial summand) and
$J(A,\mu )$
through the initial summand) and
![]() $(0,1_A,0)$
.
$(0,1_A,0)$
.
Proof. Let
![]() $J'$
be the subalgebra of
$J'$
be the subalgebra of
![]() $J(A, \mu )$
generated by
$J(A, \mu )$
generated by
![]() $A^+$
and
$A^+$
and
![]() $w := (0,1_A,0)$
. As a subalgebra, it is closed under
$w := (0,1_A,0)$
. As a subalgebra, it is closed under
![]() $\sharp $
by (6.8), that is,
$\sharp $
by (6.8), that is,
![]() $x^{\sharp } \in J'$
and
$x^{\sharp } \in J'$
and
![]() $x \times y \in J'$
for all
$x \times y \in J'$
for all
![]() $x, y \in J'$
. Since
$x, y \in J'$
. Since
![]() $w^{\sharp } = \mu (0,0,1_A)$
and
$w^{\sharp } = \mu (0,0,1_A)$
and
![]() $x_0 \times (0,x_1,x_2) = (0,-x_0x_1,-x_2x_0)$
for all
$x_0 \times (0,x_1,x_2) = (0,-x_0x_1,-x_2x_0)$
for all
![]() $x_i \in A$
by (12.2), it follows that
$x_i \in A$
by (12.2), it follows that
![]() $J'$
must be all of
$J'$
must be all of
![]() $J(A, \mu )$
.
$J(A, \mu )$
.
Proof of Proposition 12.1
Theorem 1.2 in [Reference First and ReichsteinFiR] reduces the proof to the case where R is a field F, in which case
![]() $\dim \operatorname {\mathrm {Max}} R = 0$
, so the task is to prove that three elements suffice to generate an Albert algebra J. If F is infinite, then Proposition 4.1 in [Reference First and ReichsteinFiR] reduces us to considering the case where J is split. If F is finite, then J is split by Proposition 11.3.
$\dim \operatorname {\mathrm {Max}} R = 0$
, so the task is to prove that three elements suffice to generate an Albert algebra J. If F is infinite, then Proposition 4.1 in [Reference First and ReichsteinFiR] reduces us to considering the case where J is split. If F is finite, then J is split by Proposition 11.3.
If
![]() $F \ne \mathbb {F}_2$
, then the split cubic étale F-algebra
$F \ne \mathbb {F}_2$
, then the split cubic étale F-algebra
![]() $E := F \times F \times F$
can be generated by a single element x as an associative algebra. On the other hand, if
$E := F \times F \times F$
can be generated by a single element x as an associative algebra. On the other hand, if
![]() $F = \mathbb {F}_2$
, let
$F = \mathbb {F}_2$
, let
![]() $E := \mathbb {F}_8$
be the cyclic cubic extension of F, which is again generated by one element, call it x. In either case, x also generates the Jordan algebra
$E := \mathbb {F}_8$
be the cyclic cubic extension of F, which is again generated by one element, call it x. In either case, x also generates the Jordan algebra
![]() $E^+$
, because the powers of x in
$E^+$
, because the powers of x in
![]() $E^+$
and E are the same.
$E^+$
and E are the same.
Hence, Example 12.2 (a) and Lemma 12.3 show that
![]() $\operatorname {\mathrm {Mat}}_3(F)^+$
is generated by two elements. Lemma 12.3 combined with Example 12.2 (b) shows that the split Albert algebra
$\operatorname {\mathrm {Mat}}_3(F)^+$
is generated by two elements. Lemma 12.3 combined with Example 12.2 (b) shows that the split Albert algebra
![]() $J(\operatorname {\mathrm {Mat}}_3(F),1)$
is generated by three elements.
$J(\operatorname {\mathrm {Mat}}_3(F),1)$
is generated by three elements.
Remark 12.4. That the Jordan algebra
![]() $\operatorname {\mathrm {Mat}}_3(F)^+$
, for any field F, is generated by two elements doesn’t seem too surprising, but one should keep in mind that the analogous result for 2-by-2 matrices is false: the minimal number of generators for the Jordan algebra
$\operatorname {\mathrm {Mat}}_3(F)^+$
, for any field F, is generated by two elements doesn’t seem too surprising, but one should keep in mind that the analogous result for 2-by-2 matrices is false: the minimal number of generators for the Jordan algebra
![]() $\operatorname {\mathrm {Mat}}_2(F)^+$
is three.
$\operatorname {\mathrm {Mat}}_2(F)^+$
is three.
Remark 12.5 (dichotomy of fields and the Tits construction)
The classification of Albert algebras over a field F of characteristic
![]() $\ne 3$
has a fundamentally different flavor depending on whether or not
$\ne 3$
has a fundamentally different flavor depending on whether or not
![]() $H^3(F, \mathbb {Z}/3)$
is zero, as indicated by [Reference RostRost], [Reference Petersson and RacinePeR96], or [Reference GaribaldiGar09, Section 8]. If
$H^3(F, \mathbb {Z}/3)$
is zero, as indicated by [Reference RostRost], [Reference Petersson and RacinePeR96], or [Reference GaribaldiGar09, Section 8]. If
![]() $H^3(F, \mathbb {Z}/3) = 0$
— as is the case for global fields, p-adic fields, and the real numbers — every Albert F-algebra is reduced, that is, of the form
$H^3(F, \mathbb {Z}/3) = 0$
— as is the case for global fields, p-adic fields, and the real numbers — every Albert F-algebra is reduced, that is, of the form
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
for some C and
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
for some C and
![]() $\Gamma $
, and is not a division algebra. (It is natural to speculate that this is the reason it took many years after Albert algebras were defined — all the way until 1958 — for the first Albert division algebra to be exhibited in [Reference AlbertAlb58].) In the other case, when
$\Gamma $
, and is not a division algebra. (It is natural to speculate that this is the reason it took many years after Albert algebras were defined — all the way until 1958 — for the first Albert division algebra to be exhibited in [Reference AlbertAlb58].) In the other case, when
![]() $H^3(F, \mathbb {Z}/3) \ne 0$
, as happens when
$H^3(F, \mathbb {Z}/3) \ne 0$
, as happens when
![]() $F = \mathbb {Q}(t)$
, for example, one can construct an Albert division algebra via the first Tits construction described above as
$F = \mathbb {Q}(t)$
, for example, one can construct an Albert division algebra via the first Tits construction described above as
![]() $J(A \otimes \mathbb {Q}(t), t)$
for A an associative division algebra of dimension 9 over
$J(A \otimes \mathbb {Q}(t), t)$
for A an associative division algebra of dimension 9 over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
It is known that every Albert algebra over a field is obtained by the first Tits construction or second Tits construction (which we have not described here) (see [Reference McCrimmonMcC70, Theorem 10] or [Reference Petersson and RacinePeR86b, Theorem 3.1(i)]). Both constructions have been extended from the case of algebras over a field to an arbitrary base ring [Reference Petersson and RacinePeR86a]. However, in this more general setting, the Tits constructions do not produce all Albert algebras [Reference Parimala, Sridharan and ThakurPaST].
13 Isotopy
The aim of this section is to discuss the notion of isotopy of Jordan algebras, which will pay off later in the paper when we discuss groups of type
![]() $\mathsf {E}_6$
in Section 15 and
$\mathsf {E}_6$
in Section 15 and
![]() $\mathsf {E}_7$
in Section 17. We include this material at this point in the paper because Corollary 13.6 is needed in the following section.
$\mathsf {E}_7$
in Section 17. We include this material at this point in the paper because Corollary 13.6 is needed in the following section.
Definition 13.1. Let J be a Jordan R-algebra, and suppose
![]() $u \in J$
is invertible. We define a Jordan algebra
$u \in J$
is invertible. We define a Jordan algebra
![]() $J^{(u)}$
with the same underlying R-module, with U-operator
$J^{(u)}$
with the same underlying R-module, with U-operator
![]() $U^{(u)}_x := U_x U_u$
(where the unadorned U on the right denotes the U-operator in J), and with identity element
$U^{(u)}_x := U_x U_u$
(where the unadorned U on the right denotes the U-operator in J), and with identity element
![]() $1^{(u)} := u^{-1}$
. One checks that
$1^{(u)} := u^{-1}$
. One checks that
![]() $J^{(u)}$
is indeed a Jordan algebra, and for
$J^{(u)}$
is indeed a Jordan algebra, and for
![]() $u, v$
invertible, we have
$u, v$
invertible, we have
![]() $(J^{(u)})^{(v)} = J^{(U_u v)}$
. A Jordan R-algebra
$(J^{(u)})^{(v)} = J^{(U_u v)}$
. A Jordan R-algebra
![]() $J'$
is an isotope of J if it is isomorphic to
$J'$
is an isotope of J if it is isomorphic to
![]() $J^{(u)}$
for some invertible
$J^{(u)}$
for some invertible
![]() $u \in J$
; equivalently, one says that J and
$u \in J$
; equivalently, one says that J and
![]() $J'$
are isotopic. This defines an equivalence relation on Jordan algebras that is a priori weaker than isomorphism.
$J'$
are isotopic. This defines an equivalence relation on Jordan algebras that is a priori weaker than isomorphism.
We have presented the notion of isotopy for Jordan algebras. However, there are analogous notions for other classes of algebras, which go back at least to [Reference AlbertAlb42]. For associative algebras, isotopy is the same as isomorphism. For octonion algebras, isotopy amounts to norm equivalence [Reference Alsaody and GilleAlsG, Corollary 6.7], which is a weaker condition than isomorphism (see [Reference GilleGil14] and [Reference Asok, Hoyois and WendtAsHW]).
Isotopes of cubic Jordan algebras
If J is a cubic Jordan R-algebra and
![]() $u \in J$
is invertible, then [Reference McCrimmonMcC69, Theorem 2] and its proof show that the isotope
$u \in J$
is invertible, then [Reference McCrimmonMcC69, Theorem 2] and its proof show that the isotope
![]() $J^{(u)}$
is a cubic Jordan algebra as well whose identity element, adjoint and norm are given by
$J^{(u)}$
is a cubic Jordan algebra as well whose identity element, adjoint and norm are given by
Moreover, the (bi-)linear and quadratic trace of
![]() $J^{(u)}$
have the form
$J^{(u)}$
have the form
The first equation of (13.2) is in [Reference McCrimmonMcC69, p. 500], while the second one follows from (13.1), the first, and Lemma 6.5 (1) via
![]() $\operatorname {\mathrm {Tr}}_{J^{(u)}}(x) = T_{J^{(u)}}(u^{-1},x) = T_J(U_uu^{-1},x) = T_J(u,x)$
. Similarly,
$\operatorname {\mathrm {Tr}}_{J^{(u)}}(x) = T_{J^{(u)}}(u^{-1},x) = T_J(U_uu^{-1},x) = T_J(u,x)$
. Similarly,
Example 13.2.
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
is isotopic to
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
is isotopic to
![]() $\operatorname {\mathrm {Her}}_3(C)$
for every
$\operatorname {\mathrm {Her}}_3(C)$
for every
![]() $\Gamma $
. Indeed, for
$\Gamma $
. Indeed, for
 $$\begin{align*}u := \left( \begin{smallmatrix} \gamma_1 & 0 & 0 \\ 0 & \gamma_2 & 0 \\ 0 & 0 & \gamma_3 \end{smallmatrix} \right) \quad \in \operatorname{\mathrm{Her}}_3(C, \Gamma), \end{align*}$$
$$\begin{align*}u := \left( \begin{smallmatrix} \gamma_1 & 0 & 0 \\ 0 & \gamma_2 & 0 \\ 0 & 0 & \gamma_3 \end{smallmatrix} \right) \quad \in \operatorname{\mathrm{Her}}_3(C, \Gamma), \end{align*}$$
the map
![]() $\phi \!: \operatorname {\mathrm {Her}}_3(C, \Gamma )^{(u)} \to \operatorname {\mathrm {Her}}_3(C)$
defined by
$\phi \!: \operatorname {\mathrm {Her}}_3(C, \Gamma )^{(u)} \to \operatorname {\mathrm {Her}}_3(C)$
defined by
 $$\begin{align*}\phi \left( \begin{smallmatrix} \alpha_1 & \gamma_2 c_3 & \gamma_3 \bar{c}_2 \\ \gamma_1 \bar{c}_3 & \alpha_2 & \gamma_3 c_1 \\ \gamma_1 c_2 & \gamma_2 \bar{c}_1 & \alpha_3 \end{smallmatrix} \right) = \left( \begin{smallmatrix} \gamma_1 \alpha_1 & \gamma_1 \gamma_2 c_3 & \cdot \\ \cdot & \gamma_2 \alpha_2 & \gamma_2 \gamma_3 c_1 \\ \gamma_1 \gamma_3 c_2 & \cdot & \gamma_3 \alpha_3 \end{smallmatrix} \right) \end{align*}$$
$$\begin{align*}\phi \left( \begin{smallmatrix} \alpha_1 & \gamma_2 c_3 & \gamma_3 \bar{c}_2 \\ \gamma_1 \bar{c}_3 & \alpha_2 & \gamma_3 c_1 \\ \gamma_1 c_2 & \gamma_2 \bar{c}_1 & \alpha_3 \end{smallmatrix} \right) = \left( \begin{smallmatrix} \gamma_1 \alpha_1 & \gamma_1 \gamma_2 c_3 & \cdot \\ \cdot & \gamma_2 \alpha_2 & \gamma_2 \gamma_3 c_1 \\ \gamma_1 \gamma_3 c_2 & \cdot & \gamma_3 \alpha_3 \end{smallmatrix} \right) \end{align*}$$
is an isomorphism of Jordan algebras. One can also turn this around:
Jordan algebras isotopic to a reduced Freudenthal algebra
In the special case where R is a field, a Jordan algebra that is isotopic to the split Albert algebra
![]() $\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R))$
is necessarily isomorphic to it (see, for example [Reference JacobsonJ71, p. 53, Theorem 9]). This need not hold for general R: Alsaody has shown in [Reference AlsaodyAls21, Theorem 2.7] that there exists a ring R finitely generated over
$\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R))$
is necessarily isomorphic to it (see, for example [Reference JacobsonJ71, p. 53, Theorem 9]). This need not hold for general R: Alsaody has shown in [Reference AlsaodyAls21, Theorem 2.7] that there exists a ring R finitely generated over
![]() $\mathbb {C}$
and an Albert R-algebra that is isotopic to the split Albert R-algebra but is not isomorphic to it. Here we show that it is sufficient to assume that R is a semilocal ring (Corollary 13.4), as a consequence of a more general result (Theorem 13.3) from which we also obtain the key Corollary 13.6.
$\mathbb {C}$
and an Albert R-algebra that is isotopic to the split Albert R-algebra but is not isomorphic to it. Here we show that it is sufficient to assume that R is a semilocal ring (Corollary 13.4), as a consequence of a more general result (Theorem 13.3) from which we also obtain the key Corollary 13.6.
We work in a slightly more general context than semilocal rings. For the following statements, see [Reference Estes and GuralnickEsG] and [Reference McDonald and WaterhouseMcDW]. We say that R is an LG ring if whenever a polynomial
![]() $f \in R[x_1, \ldots , x_n]$
represents a unit over
$f \in R[x_1, \ldots , x_n]$
represents a unit over
![]() $R_{\mathfrak {m}}$
for every maximal ideal
$R_{\mathfrak {m}}$
for every maximal ideal
![]() $\mathfrak {m}$
of R, then f represents a unit over R. Every semilocal ring is an LG ring. It is easy to see that rings
$\mathfrak {m}$
of R, then f represents a unit over R. Every semilocal ring is an LG ring. It is easy to see that rings
![]() $R_1$
,
$R_1$
,
![]() $R_2$
are both LG if and only if their product
$R_2$
are both LG if and only if their product
![]() $R_1 \times R_2$
is LG. The ring of all algebraic integers and the ring of all real algebraic integers are LG rings. Every integral extension of an LG ring is LG [Reference Estes and GuralnickEsG, Corollary 2.3].
$R_1 \times R_2$
is LG. The ring of all algebraic integers and the ring of all real algebraic integers are LG rings. Every integral extension of an LG ring is LG [Reference Estes and GuralnickEsG, Corollary 2.3].
Theorem 13.3. Suppose J is a Jordan R-algebra that is isotopic to
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
for some composition R-algebra C and some
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
for some composition R-algebra C and some
![]() $\Gamma $
. If R is an LG ring, then J is isomorphic to
$\Gamma $
. If R is an LG ring, then J is isomorphic to
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma ')$
for some
$\operatorname {\mathrm {Her}}_3(C, \Gamma ')$
for some
![]() $\Gamma '$
.
$\Gamma '$
.
Proof. As in previous proofs, we reduce to the case where C has constant rank.
In view of Example 13.2, J is isotopic to
![]() $\operatorname {\mathrm {Her}}_3(C)$
, that is,
$\operatorname {\mathrm {Her}}_3(C)$
, that is,
![]() $J \cong \operatorname {\mathrm {Her}}_3(C)^{(u^{-1})}$
for some invertible
$J \cong \operatorname {\mathrm {Her}}_3(C)^{(u^{-1})}$
for some invertible
![]() $u \in \operatorname {\mathrm {Her}}_3(C)$
. The same example shows we are done if u is diagonal.
$u \in \operatorname {\mathrm {Her}}_3(C)$
. The same example shows we are done if u is diagonal.
Write N for the cubic form on
![]() $\operatorname {\mathrm {Her}}_3(C)$
. In case u is not diagonal, we will apply successive elements
$\operatorname {\mathrm {Her}}_3(C)$
. In case u is not diagonal, we will apply successive elements
![]() $\eta \in \operatorname {\mathrm {GL}}(\operatorname {\mathrm {Her}}_3(C))$
such that
$\eta \in \operatorname {\mathrm {GL}}(\operatorname {\mathrm {Her}}_3(C))$
such that
![]() $N \eta = N$
as polynomial laws. (In the notation of Section 15 below,
$N \eta = N$
as polynomial laws. (In the notation of Section 15 below,
![]() $\eta \in \mathbf {Isom}(\operatorname {\mathrm {Her}}_3(C))(R)$
.) Note that each such
$\eta \in \mathbf {Isom}(\operatorname {\mathrm {Her}}_3(C))(R)$
.) Note that each such
![]() $\eta $
defines an isomorphism of R-modules
$\eta $
defines an isomorphism of R-modules
We have
so we have by (13.1) that
Since
![]() $\eta $
is a norm isometry that maps the identity element
$\eta $
is a norm isometry that maps the identity element
![]() $u^{-1}$
in the domain of (13.3) to the identity element in the codomain, it is an isomorphism of algebras by Lemma 10.2. Thus, if successive elements
$u^{-1}$
in the domain of (13.3) to the identity element in the codomain, it is an isomorphism of algebras by Lemma 10.2. Thus, if successive elements
![]() $\eta $
transform u into a diagonal element, the proof will be complete.
$\eta $
transform u into a diagonal element, the proof will be complete.
We employ the transformation
![]() $\tau _{st}(q)$
for
$\tau _{st}(q)$
for
![]() $1 \le s \ne t \le 3$
and
$1 \le s \ne t \le 3$
and
![]() $q \in C$
defined by
$q \in C$
defined by
where
![]() $I_3$
is the identity matrix,
$I_3$
is the identity matrix,
![]() $E_{st}$
is the 3-by-3 matrix with a 1 in the
$E_{st}$
is the 3-by-3 matrix with a 1 in the
![]() $(s, t)$
-entry and 0 elsewhere, and juxtaposition defines naive multiplication of 3-by-3 matrices with entries in C. For example,
$(s, t)$
-entry and 0 elsewhere, and juxtaposition defines naive multiplication of 3-by-3 matrices with entries in C. For example,
These transformations appear in [Reference JacobsonJ61, Section 5] and [Reference KrutelevichKr02, Section 2]; the argument in either reference shows that
![]() $\tau _{st}(q)$
preserves N for all choices of s, t, and q. For
$\tau _{st}(q)$
preserves N for all choices of s, t, and q. For
![]() $e = 2, 3$
, define polynomial functions
$e = 2, 3$
, define polynomial functions
![]() $\nu _e$
from
$\nu _e$
from
![]() $C^e$
to the group scheme
$C^e$
to the group scheme
![]() $\mathbf {G}$
of linear transformations stabilizing the norm N via
$\mathbf {G}$
of linear transformations stabilizing the norm N via
Additionally, for every permutation
![]() $\pi $
of
$\pi $
of
![]() $\{ 1, 2, 3 \}$
, there is a linear transformation of
$\{ 1, 2, 3 \}$
, there is a linear transformation of
![]() $\operatorname {\mathrm {Her}}_3(C)$
that we denote also by
$\operatorname {\mathrm {Her}}_3(C)$
that we denote also by
![]() $\pi $
, for example, the transposition
$\pi $
, for example, the transposition
![]() $(1\,2)$
acts via
$(1\,2)$
acts via
(see, for example, [Reference KrutelevichKr02, p. 282]). The other transpositions are constructed analogously and each evidently preserves the norm. In this way, we obtain a representation of the permutation group on
![]() $\operatorname {\mathrm {Her}}_3(C)$
.
$\operatorname {\mathrm {Her}}_3(C)$
.
Case: R is local: We collect some observations in the case where R is a local ring. Write
By hypothesis,
![]() $N(u)$
is invertible, that is, does not lie in the maximal ideal
$N(u)$
is invertible, that is, does not lie in the maximal ideal
![]() $\mathfrak {m}$
of R.
$\mathfrak {m}$
of R.
If
![]() $\alpha _1 \in R^{\times }$
or
$\alpha _1 \in R^{\times }$
or
![]() $\alpha _2, \alpha _3 \notin R^{\times }$
, then after modifying u by a transformation in the image of
$\alpha _2, \alpha _3 \notin R^{\times }$
, then after modifying u by a transformation in the image of
![]() $\nu _3$
, we may assume that
$\nu _3$
, we may assume that
![]() $\alpha _1 \in R^{\times }$
and
$\alpha _1 \in R^{\times }$
and
![]() $c_2 = c_3 = 0$
. Indeed, if
$c_2 = c_3 = 0$
. Indeed, if
![]() $\alpha _1 \notin R^{\times }$
, then by (6.11) we have
$\alpha _1 \notin R^{\times }$
, then by (6.11) we have
whence
![]() $c_3 \notin \mathfrak {m} C$
. Since
$c_3 \notin \mathfrak {m} C$
. Since
![]() $n_C$
continues to be regular when changing scalars to
$n_C$
continues to be regular when changing scalars to
![]() $R/\mathfrak {m}$
, some
$R/\mathfrak {m}$
, some
![]() $q \in C$
has
$q \in C$
has
![]() $n_C(q,c_3) \notin \mathfrak {m}$
. Applying
$n_C(q,c_3) \notin \mathfrak {m}$
. Applying
![]() $\tau _{12}(q)$
, we may arrange
$\tau _{12}(q)$
, we may arrange
![]() $\alpha _1 \in R^{\times }$
. Then note that
$\alpha _1 \in R^{\times }$
. Then note that
![]() $\tau _{21}(q) \left ( \begin {smallmatrix} \alpha _1 & c_3 & \cdot \\ \cdot & \alpha _2 & c_1 \\ c_2 & \cdot & \alpha _3 \end {smallmatrix} \right )$
has top row entries
$\tau _{21}(q) \left ( \begin {smallmatrix} \alpha _1 & c_3 & \cdot \\ \cdot & \alpha _2 & c_1 \\ c_2 & \cdot & \alpha _3 \end {smallmatrix} \right )$
has top row entries
![]() $\alpha _1$
,
$\alpha _1$
,
![]() $c_3 + \alpha _1 \bar {q}$
,
$c_3 + \alpha _1 \bar {q}$
,
![]() $\bar {c_2}$
. Taking
$\bar {c_2}$
. Taking
![]() $q = -\bar {c}_3 \alpha _1^{-1}$
shows that we may assume
$q = -\bar {c}_3 \alpha _1^{-1}$
shows that we may assume
![]() $c_3 = 0$
. The argument that we may assume
$c_3 = 0$
. The argument that we may assume
![]() $c_2 = 0$
is similar, with the role of
$c_2 = 0$
is similar, with the role of
![]() $\tau _{21}$
replaced by
$\tau _{21}$
replaced by
![]() $\tau _{31}$
.
$\tau _{31}$
.
Now suppose that
![]() $\alpha _1 \in R^{\times }$
and
$\alpha _1 \in R^{\times }$
and
![]() $c_2 = c_3 = 0$
. If
$c_2 = c_3 = 0$
. If
![]() $\alpha _2 \in R^{\times }$
or
$\alpha _2 \in R^{\times }$
or
![]() $\alpha _3 \notin R^{\times }$
, then after modifying u by a transformation in the image of
$\alpha _3 \notin R^{\times }$
, then after modifying u by a transformation in the image of
![]() $\nu _2$
, we may assume that u is diagonal. Indeed, since u has norm
$\nu _2$
, we may assume that u is diagonal. Indeed, since u has norm
![]() $\alpha _1 (\alpha _2 \alpha _3 - n_C(c_1)) \not \in \mathfrak {m}$
, at least one of
$\alpha _1 (\alpha _2 \alpha _3 - n_C(c_1)) \not \in \mathfrak {m}$
, at least one of
![]() $\alpha _2$
,
$\alpha _2$
,
![]() $\alpha _3$
, or
$\alpha _3$
, or
![]() $n_C(c_1)$
is not in
$n_C(c_1)$
is not in
![]() $\mathfrak {m}$
. The same argument as in the preceding paragraph, with
$\mathfrak {m}$
. The same argument as in the preceding paragraph, with
![]() $\tau _{12}$
replaced by
$\tau _{12}$
replaced by
![]() $\tau _{23}$
, shows that we may assume that
$\tau _{23}$
, shows that we may assume that
![]() $\alpha _2 \not \in \mathfrak {m}$
. The same argument as in the preceding paragraph, with
$\alpha _2 \not \in \mathfrak {m}$
. The same argument as in the preceding paragraph, with
![]() $\tau _{21}$
replaced by
$\tau _{21}$
replaced by
![]() $\tau _{32}$
, shows that we may assume that
$\tau _{32}$
, shows that we may assume that
![]() $c_1 = 0$
. Thus, we have transformed u into a diagonal element, as required.
$c_1 = 0$
. Thus, we have transformed u into a diagonal element, as required.
General case: Return to the setting of R as in the statement of the theorem. We combine the transformations
![]() $\nu _3$
,
$\nu _3$
,
![]() $\nu _2$
, and permutations together into a polynomial function
$\nu _2$
, and permutations together into a polynomial function
![]() $C^{21} \to \mathbf {G}$
, namely
$C^{21} \to \mathbf {G}$
, namely
where the arguments to the various
![]() $\nu _2$
,
$\nu _2$
,
![]() $\nu _3$
are assigned independently. Combining this with the polynomial function on
$\nu _3$
are assigned independently. Combining this with the polynomial function on
![]() $\mathbf {G}$
that sends
$\mathbf {G}$
that sends
![]() $g \in \mathbf {G}(R)$
to the product of the diagonal entries of
$g \in \mathbf {G}(R)$
to the product of the diagonal entries of
![]() $gu$
, we obtain a polynomial law in
$gu$
, we obtain a polynomial law in
![]() $\mathscr {P}(C^{21}, R)$
. But more is true. Because R is LG and C is projective of constant rank, C is a free module (see [Reference Estes and GuralnickEsG, Theorem 2.10] or [Reference McDonald and WaterhouseMcDW, p. 457]). Choosing a basis for C expresses this polynomial law as a polynomial with coefficients in R.
$\mathscr {P}(C^{21}, R)$
. But more is true. Because R is LG and C is projective of constant rank, C is a free module (see [Reference Estes and GuralnickEsG, Theorem 2.10] or [Reference McDonald and WaterhouseMcDW, p. 457]). Choosing a basis for C expresses this polynomial law as a polynomial with coefficients in R.
We claim that this polynomial represents a unit over
![]() $R_{\mathfrak {m}}$
for every maximal ideal
$R_{\mathfrak {m}}$
for every maximal ideal
![]() $\mathfrak {m}$
of R. For a given
$\mathfrak {m}$
of R. For a given
![]() $\mathfrak {m}$
, here is how to pick the element of
$\mathfrak {m}$
, here is how to pick the element of
![]() $C^{21}$
that produces a unit. If
$C^{21}$
that produces a unit. If
![]() $\alpha _1 \in R_{\mathfrak {m}}^{\times }$
or
$\alpha _1 \in R_{\mathfrak {m}}^{\times }$
or
![]() $\alpha _2, \alpha _3 \notin R_{\mathfrak {m}}^{\times }$
, applying
$\alpha _2, \alpha _3 \notin R_{\mathfrak {m}}^{\times }$
, applying
![]() $\nu _3$
to u, with arguments chosen as in the second paragraph of the local case, we obtain an element with
$\nu _3$
to u, with arguments chosen as in the second paragraph of the local case, we obtain an element with
![]() $\alpha _1 \in R_{\mathfrak {m}}^{\times }$
and
$\alpha _1 \in R_{\mathfrak {m}}^{\times }$
and
![]() $c_3 = c_2 = 0$
. We take this to be the rightmost term in (13.5). If that element has
$c_3 = c_2 = 0$
. We take this to be the rightmost term in (13.5). If that element has
![]() $\alpha _2 \in R_{\mathfrak {m}}^{\times }$
or
$\alpha _2 \in R_{\mathfrak {m}}^{\times }$
or
![]() $\alpha _3 \notin R_{\mathfrak {m}}^{\times }$
, the next
$\alpha _3 \notin R_{\mathfrak {m}}^{\times }$
, the next
![]() $\nu _2$
term can be chosen to produce a diagonal u; one takes the remaining
$\nu _2$
term can be chosen to produce a diagonal u; one takes the remaining
![]() $\nu $
terms in (13.5) to have argument 0. Otherwise,
$\nu $
terms in (13.5) to have argument 0. Otherwise,
![]() $\alpha _3$
is invertible in
$\alpha _3$
is invertible in
![]() $R_{\mathfrak {m}}$
, and we plug 0 into the rightmost
$R_{\mathfrak {m}}$
, and we plug 0 into the rightmost
![]() $\nu _2$
, pick the argument for the next
$\nu _2$
, pick the argument for the next
![]() $\nu _2$
as in the proof of the local case, and plug 0 into the remaining
$\nu _2$
as in the proof of the local case, and plug 0 into the remaining
![]() $\nu $
terms to the left in (13.5). The claim is verified if
$\nu $
terms to the left in (13.5). The claim is verified if
![]() $\alpha _1 \in R_{\mathfrak {m}}^{\times }$
or
$\alpha _1 \in R_{\mathfrak {m}}^{\times }$
or
![]() $\alpha _2, \alpha _3 \notin R_{\mathfrak {m}}^{\times }$
.
$\alpha _2, \alpha _3 \notin R_{\mathfrak {m}}^{\times }$
.
The next case of the claim is where
![]() $\alpha _2 \in R_{\mathfrak {m}}^{\times }$
. In that case, we plug 0 into the rightmost three
$\alpha _2 \in R_{\mathfrak {m}}^{\times }$
. In that case, we plug 0 into the rightmost three
![]() $\nu $
terms in (13.5). After applying the permutation
$\nu $
terms in (13.5). After applying the permutation
![]() $(2\,3)$
and then
$(2\,3)$
and then
![]() $(1\,3)$
, we obtain an element of
$(1\,3)$
, we obtain an element of
![]() $\operatorname {\mathrm {Her}}_3(C)$
with
$\operatorname {\mathrm {Her}}_3(C)$
with
![]() $\alpha _1$
invertible, and a well-chosen argument for the next
$\alpha _1$
invertible, and a well-chosen argument for the next
![]() $\nu _3$
term will assure that
$\nu _3$
term will assure that
![]() $c_3 = c_2 = 0$
. As in the preceding paragraph, choosing the arguments for the leftmost two
$c_3 = c_2 = 0$
. As in the preceding paragraph, choosing the arguments for the leftmost two
![]() $\nu _2$
terms in the middle product in (13.5) suffices to transform u into a diagonal element, verifying the claim in this case.
$\nu _2$
terms in the middle product in (13.5) suffices to transform u into a diagonal element, verifying the claim in this case.
The last case of the claim is when
![]() $\alpha _3 \in R_{\mathfrak {m}}^{\times }$
. Plug 0 in the
$\alpha _3 \in R_{\mathfrak {m}}^{\times }$
. Plug 0 in the
![]() $\nu $
terms in the middle and right parenthetical expressions in (13.5). After applying all permutations in (13.5) besides the leftmost transposition to u, we obtain an element of
$\nu $
terms in the middle and right parenthetical expressions in (13.5). After applying all permutations in (13.5) besides the leftmost transposition to u, we obtain an element of
![]() $\operatorname {\mathrm {Her}}_3(C)$
with
$\operatorname {\mathrm {Her}}_3(C)$
with
![]() $\alpha _1 \in R_{\mathfrak {m}}^{\times }$
and the argument in the preceding paragraph, again, transforms u into a diagonal element, completing the proof of the claim.
$\alpha _1 \in R_{\mathfrak {m}}^{\times }$
and the argument in the preceding paragraph, again, transforms u into a diagonal element, completing the proof of the claim.
Since R is an LG ring, the claim provides an element
![]() $g \in \mathbf {G}(R)$
such that
$g \in \mathbf {G}(R)$
such that
![]() $gu$
has
$gu$
has
![]() $(1,1)$
-entry a unit. That is, we may assume that in the element u,
$(1,1)$
-entry a unit. That is, we may assume that in the element u,
![]() $\alpha _1$
is invertible. Applying now
$\alpha _1$
is invertible. Applying now
![]() $\tau _{21}(q)$
and
$\tau _{21}(q)$
and
![]() $\tau _{31}(q)$
to u for values of q chosen as in the local case, we may assume that
$\tau _{31}(q)$
to u for values of q chosen as in the local case, we may assume that
![]() $c_3 = c_2 = 0$
.
$c_3 = c_2 = 0$
.
Applying now an argument as in the preceding five paragraphs, with the function
we conclude that we may transform u to further assume that
![]() $\alpha _2$
is invertible, and therefore, apply a transformation
$\alpha _2$
is invertible, and therefore, apply a transformation
![]() $\tau _{32}(q)$
to transform it into a diagonal element, as required.
$\tau _{32}(q)$
to transform it into a diagonal element, as required.
Corollary 13.4. Suppose J is a Jordan R-algebra over an LG ring R. If J is isotopic to a split Freudenthal algebra whose rank does not take the value 6, then J is itself a split Freudenthal algebra.
Proof. As in previous proofs, one is reduced to the case where J has constant rank, which is not 6. The theorem and Proposition 7.5 give the claim.
The hypothesis that the rank is not 6 is necessary, because
![]() $\operatorname {\mathrm {Her}}_3(\mathbb {R}, {\left \langle {1, -1, -1}\right \rangle })$
is isotopic to the split Freudenthal algebra
$\operatorname {\mathrm {Her}}_3(\mathbb {R}, {\left \langle {1, -1, -1}\right \rangle })$
is isotopic to the split Freudenthal algebra
![]() $\operatorname {\mathrm {Her}}_3(\mathbb {R})$
(Example 13.2) but is not isomorphic to it (Example 6.8).
$\operatorname {\mathrm {Her}}_3(\mathbb {R})$
(Example 13.2) but is not isomorphic to it (Example 6.8).
Example 13.5 (isotopy over global fields)
For
![]() $F = \mathbb {R}$
or a global field, there is a bijection between the isomorphism classes of octonion algebras and isotopy classes of Albert algebras given by
$F = \mathbb {R}$
or a global field, there is a bijection between the isomorphism classes of octonion algebras and isotopy classes of Albert algebras given by
![]() $C \leftrightarrow \operatorname {\mathrm {Her}}_3(C)$
. Indeed, every Albert F-algebra is reduced (Example 11.2), so
$C \leftrightarrow \operatorname {\mathrm {Her}}_3(C)$
. Indeed, every Albert F-algebra is reduced (Example 11.2), so
![]() $C \mapsto \operatorname {\mathrm {Her}}_3(C)$
touches every isotopy class. For injectivity, if
$C \mapsto \operatorname {\mathrm {Her}}_3(C)$
touches every isotopy class. For injectivity, if
![]() $C, C'$
are distinct octonion algebras, there is a real embedding
$C, C'$
are distinct octonion algebras, there is a real embedding
![]() $F \hookrightarrow \mathbb {R}$
such that
$F \hookrightarrow \mathbb {R}$
such that
![]() $C \otimes \mathbb {R} \not \cong C' \otimes \mathbb {R}$
, and Corollary 13.4 shows that
$C \otimes \mathbb {R} \not \cong C' \otimes \mathbb {R}$
, and Corollary 13.4 shows that
![]() $\operatorname {\mathrm {Her}}_3(C) \otimes \mathbb {R}$
and
$\operatorname {\mathrm {Her}}_3(C) \otimes \mathbb {R}$
and
![]() $\operatorname {\mathrm {Her}}_3(C') \otimes \mathbb {R}$
are not isotopic.
$\operatorname {\mathrm {Her}}_3(C') \otimes \mathbb {R}$
are not isotopic.
Corollary 13.6. Every isotope of a Freudenthal algebra is itself a Freudenthal algebra.
Proof. Suppose J is an isotope of a Freudenthal algebra. After base change to a faithfully flat extension, J is an isotope of a split Freudenthal algebra.
The R-algebra
![]() $S := \prod _{\mathfrak {m}} R_{\mathfrak {m}}$
, where
$S := \prod _{\mathfrak {m}} R_{\mathfrak {m}}$
, where
![]() $\mathfrak {m}$
ranges over maximal ideals of R, is faithfully flat. For each
$\mathfrak {m}$
ranges over maximal ideals of R, is faithfully flat. For each
![]() $\mathfrak {m}$
,
$\mathfrak {m}$
,
![]() $J \otimes R_{\mathfrak {m}}$
is
$J \otimes R_{\mathfrak {m}}$
is
![]() $\operatorname {\mathrm {Her}}_3(C, \Gamma )$
for C a split composition
$\operatorname {\mathrm {Her}}_3(C, \Gamma )$
for C a split composition
![]() $R_{\mathfrak {m}}$
-algebra and some
$R_{\mathfrak {m}}$
-algebra and some
![]() $\Gamma $
by Theorem 13.3. By Proposition 7.3, there is a faithfully flat
$\Gamma $
by Theorem 13.3. By Proposition 7.3, there is a faithfully flat
![]() $R_{\mathfrak {m}}$
-algebra T such that
$R_{\mathfrak {m}}$
-algebra T such that
![]() $J \otimes T$
is a split Freudenthal algebra. The product of these T’s is a faithfully flat R-algebra over which J is the split Freudenthal algebra.
$J \otimes T$
is a split Freudenthal algebra. The product of these T’s is a faithfully flat R-algebra over which J is the split Freudenthal algebra.
We close this section by making explicit the relationship between isotopy and norm similarity between Freudenthal algebras, extending Lemma 10.2.
Proposition 13.7. Let J and
![]() $J'$
be Freudenthal R-algebras. For an R-linear map
$J'$
be Freudenthal R-algebras. For an R-linear map
![]() $\phi \!: J \to J'$
, the following are equivalent:
$\phi \!: J \to J'$
, the following are equivalent:
-
1.
 $\phi $
is an isomorphism
$\phi $
is an isomorphism
 $J \to (J')^{(u)}$
for some invertible
$J \to (J')^{(u)}$
for some invertible
 $u \in J'$
(“
$u \in J'$
(“
 $\phi $
is an isotopy”).
$\phi $
is an isotopy”). -
2.
 $N_{J'} \phi = \alpha N_J$
as polynomial laws for some
$N_{J'} \phi = \alpha N_J$
as polynomial laws for some
 $\alpha \in R^{\times }$
, and
$\alpha \in R^{\times }$
, and
 $\phi $
is surjective (“
$\phi $
is surjective (“
 $\phi $
is a norm similarity”).
$\phi $
is a norm similarity”).
Proof. Since
![]() $(J^{\prime })^{(u)}$
is a Freudenthal algebra by Corollary 13.6, condition (2) follows from (1) by Lemma 10.2 and (13.1). Conversely, we assume (2) and prove (1). Because
$(J^{\prime })^{(u)}$
is a Freudenthal algebra by Corollary 13.6, condition (2) follows from (1) by Lemma 10.2 and (13.1). Conversely, we assume (2) and prove (1). Because
![]() $N_{J'}(\phi (1_J)) = \alpha $
, the element
$N_{J'}(\phi (1_J)) = \alpha $
, the element
![]() $\phi (1_J)$
is invertible in
$\phi (1_J)$
is invertible in
![]() $J'$
. We set
$J'$
. We set
![]() $u := \phi (1_J)^{-1}$
and
$u := \phi (1_J)^{-1}$
and
![]() $J'' := (J')^{(u)}$
. We have
$J'' := (J')^{(u)}$
. We have
Also,
![]() $N_{J'}(u) = N_{J'}(\phi (1_J))^{-1} = \alpha ^{-1}$
. Then
$N_{J'}(u) = N_{J'}(\phi (1_J))^{-1} = \alpha ^{-1}$
. Then
as polynomial laws. Lemma 10.2 implies that
![]() $\phi $
is an isomorphism
$\phi $
is an isomorphism
![]() $J \xrightarrow {\sim } J''$
, as desired.
$J \xrightarrow {\sim } J''$
, as desired.
14 Classification of Albert algebras over
 $\mathbb {Z}$
$\mathbb {Z}$
In this section, we study Albert algebras over the integers.
Definition 14.1. In the notation of Example 4.5, consider the element
as was done in [Reference Elkies and GrossElkiesGr, (5.2)]. That element has
Put
 $$\begin{align*}v := \left( \begin{smallmatrix} 2 & \beta & \cdot \\ \cdot & 2 & \beta \\ \beta & \cdot & 2 \end{smallmatrix} \right) \quad \in \operatorname{\mathrm{Her}}_3(\mathcal{O}). \end{align*}$$
$$\begin{align*}v := \left( \begin{smallmatrix} 2 & \beta & \cdot \\ \cdot & 2 & \beta \\ \beta & \cdot & 2 \end{smallmatrix} \right) \quad \in \operatorname{\mathrm{Her}}_3(\mathcal{O}). \end{align*}$$
Since
![]() $\operatorname {\mathrm {Tr}}_{\mathcal {O}}(\beta ^3) = 5$
, we find that
$\operatorname {\mathrm {Tr}}_{\mathcal {O}}(\beta ^3) = 5$
, we find that
![]() $N_{\operatorname {\mathrm {Her}}_3(\mathcal {O})}(v) = 1$
. In particular, v is invertible with inverse
$N_{\operatorname {\mathrm {Her}}_3(\mathcal {O})}(v) = 1$
. In particular, v is invertible with inverse
![]() $v^{\sharp }$
. We define
$v^{\sharp }$
. We define
![]() $\Lambda := \operatorname {\mathrm {Her}}_3(\mathcal {O})^{(v)}$
; it is an Albert algebra by Corollary 13.6.
$\Lambda := \operatorname {\mathrm {Her}}_3(\mathcal {O})^{(v)}$
; it is an Albert algebra by Corollary 13.6.
Proposition 14.2.
![]() $\operatorname {\mathrm {Her}}_3(\mathcal {O}) \not \cong \Lambda $
as Jordan
$\operatorname {\mathrm {Her}}_3(\mathcal {O}) \not \cong \Lambda $
as Jordan
![]() $\mathbb {Z}$
-algebras, but
$\mathbb {Z}$
-algebras, but
![]() $\operatorname {\mathrm {Her}}_3(\mathcal {O}) \otimes \mathbb {Q} \cong \Lambda \otimes \mathbb {Q}$
as Jordan
$\operatorname {\mathrm {Her}}_3(\mathcal {O}) \otimes \mathbb {Q} \cong \Lambda \otimes \mathbb {Q}$
as Jordan
![]() $\mathbb {Q}$
-algebras.
$\mathbb {Q}$
-algebras.
Proof. We first prove the claim over
![]() $\mathbb {Z}$
, which amounts to a computation from [Reference Elkies and GrossElkiesGr]. The isomorphism class of a Freudenthal algebra determines its cubic norm form and also its trace linear form. From (13.1), we deduce for
$\mathbb {Z}$
, which amounts to a computation from [Reference Elkies and GrossElkiesGr]. The isomorphism class of a Freudenthal algebra determines its cubic norm form and also its trace linear form. From (13.1), we deduce for
![]() $x \in \operatorname {\mathrm {Her}}_3(\mathcal {O})$
that
$x \in \operatorname {\mathrm {Her}}_3(\mathcal {O})$
that
![]() $x^{\sharp (v)} = 0$
if and only if
$x^{\sharp (v)} = 0$
if and only if
![]() $x^{\sharp } = 0$
. Hence, [Reference Elkies and GrossElkiesGr, Proposition 5.5] says that
$x^{\sharp } = 0$
. Hence, [Reference Elkies and GrossElkiesGr, Proposition 5.5] says that
![]() $\operatorname {\mathrm {Her}}_3(\mathcal {O})$
contains exactly three elements x such that
$\operatorname {\mathrm {Her}}_3(\mathcal {O})$
contains exactly three elements x such that
![]() $x^{\sharp } = 0$
and
$x^{\sharp } = 0$
and
![]() $\operatorname {\mathrm {Tr}}_{\operatorname {\mathrm {Her}}_3(\mathcal {O})}(x) = 1$
, whereas
$\operatorname {\mathrm {Tr}}_{\operatorname {\mathrm {Her}}_3(\mathcal {O})}(x) = 1$
, whereas
![]() $\Lambda $
has no elements x such that
$\Lambda $
has no elements x such that
![]() $x^{\sharp (v)} = 0$
and
$x^{\sharp (v)} = 0$
and
where the left side is
![]() $\operatorname {\mathrm {Tr}}_{\Lambda }(x)$
by (13.2). This proves that
$\operatorname {\mathrm {Tr}}_{\Lambda }(x)$
by (13.2). This proves that
![]() $\operatorname {\mathrm {Her}}_3(\mathcal {O}) \not \cong \Lambda $
.
$\operatorname {\mathrm {Her}}_3(\mathcal {O}) \not \cong \Lambda $
.
Now consider
![]() $\operatorname {\mathrm {Her}}_3(\mathcal {O}) \otimes \mathbb {R}$
. It is called a “euclidean” Jordan algebra or, in older references, a “formally real” Jordan algebra, because every sum of nonzero squares is not zero [Reference Braun and KoecherBrK, p. 331]. The element v has generic minimal polynomial, in the sense of (10.1),
$\operatorname {\mathrm {Her}}_3(\mathcal {O}) \otimes \mathbb {R}$
. It is called a “euclidean” Jordan algebra or, in older references, a “formally real” Jordan algebra, because every sum of nonzero squares is not zero [Reference Braun and KoecherBrK, p. 331]. The element v has generic minimal polynomial, in the sense of (10.1),
![]() $(t-1)(t^2 - 5t + 1)$
, which has three positive real roots. Therefore, there is some
$(t-1)(t^2 - 5t + 1)$
, which has three positive real roots. Therefore, there is some
![]() $u \in \operatorname {\mathrm {Her}}_3(\mathcal {O}) \otimes \mathbb {R}$
such that
$u \in \operatorname {\mathrm {Her}}_3(\mathcal {O}) \otimes \mathbb {R}$
such that
![]() $u^2 = v$
[Reference Braun and KoecherBrK, Section XI.3, S. 3.6 and 3.7]. From this, it is trivial to see that
$u^2 = v$
[Reference Braun and KoecherBrK, Section XI.3, S. 3.6 and 3.7]. From this, it is trivial to see that
and Example 11.2 gives that
![]() $\Lambda \otimes \mathbb {Q} \cong \operatorname {\mathrm {Her}}_3(\mathcal {O}) \otimes \mathbb {Q}$
.
$\Lambda \otimes \mathbb {Q} \cong \operatorname {\mathrm {Her}}_3(\mathcal {O}) \otimes \mathbb {Q}$
.
Theorem 14.3. Over
![]() $\mathbb {Z}$
:
$\mathbb {Z}$
:
-
a. There are exactly two isomorphism classes of octonion algebras:
 $\operatorname {\mathrm {Zor}}(\mathbb {Z})$
and
$\operatorname {\mathrm {Zor}}(\mathbb {Z})$
and
 $\mathcal {O}$
.
$\mathcal {O}$
. -
b. There are exactly four isomorphism classes of Albert algebras:
 $\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Z}))$
,
$\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Z}))$
,
 $\operatorname {\mathrm {Her}}_3(\mathcal {O}, {\left \langle {1, -1, -1}\right \rangle })$
,
$\operatorname {\mathrm {Her}}_3(\mathcal {O}, {\left \langle {1, -1, -1}\right \rangle })$
,
 $\operatorname {\mathrm {Her}}_3(\mathcal {O})$
, and
$\operatorname {\mathrm {Her}}_3(\mathcal {O})$
, and
 $\Lambda $
.
$\Lambda $
. -
c. There are exactly two isotopy classes of Albert algebras:
 $\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Z}))$
and
$\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Z}))$
and
 $\operatorname {\mathrm {Her}}_3(\mathcal {O})$
.
$\operatorname {\mathrm {Her}}_3(\mathcal {O})$
.
Proof. We first prove (a) and (b). No pair of the algebras listed are isomorphic to each other. For
![]() $\operatorname {\mathrm {Her}}_3(\mathcal {O})$
and
$\operatorname {\mathrm {Her}}_3(\mathcal {O})$
and
![]() $\Lambda $
, this is Proposition 14.2. For any other pair, base change to
$\Lambda $
, this is Proposition 14.2. For any other pair, base change to
![]() $\mathbb {Q}$
yields nonisomorphic
$\mathbb {Q}$
yields nonisomorphic
![]() $\mathbb {Q}$
-algebras. To complete the proof, it suffices to show that every octonion or Albert
$\mathbb {Q}$
-algebras. To complete the proof, it suffices to show that every octonion or Albert
![]() $\mathbb {Z}$
-algebra B is isomorphic to one of the ones listed.
$\mathbb {Z}$
-algebra B is isomorphic to one of the ones listed.
If B is indefinite — that is,
![]() $B \otimes \mathbb {R}$
is not isomorphic to
$B \otimes \mathbb {R}$
is not isomorphic to
![]() $\mathbb {O}$
nor
$\mathbb {O}$
nor
![]() $\operatorname {\mathrm {Her}}_3(\mathbb {O})$
— then the isomorphism class of B is determined by
$\operatorname {\mathrm {Her}}_3(\mathbb {O})$
— then the isomorphism class of B is determined by
![]() $B \otimes \mathbb {Q}$
as a
$B \otimes \mathbb {Q}$
as a
![]() $\mathbb {Q}$
-algebra (Proposition 11.6). Since the indefinite octonion or Albert
$\mathbb {Q}$
-algebra (Proposition 11.6). Since the indefinite octonion or Albert
![]() $\mathbb {Q}$
-algebras are
$\mathbb {Q}$
-algebras are
![]() $\operatorname {\mathrm {Zor}}(\mathbb {Q})$
,
$\operatorname {\mathrm {Zor}}(\mathbb {Q})$
,
![]() $\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Q}))$
, and
$\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Q}))$
, and
![]() $\operatorname {\mathrm {Her}}_3(\mathcal {O} \otimes \mathbb {Q}, {\left \langle {1, -1, -1}\right \rangle })$
by Example 11.2, B is isomorphic to one of the algebras listed in the statement.
$\operatorname {\mathrm {Her}}_3(\mathcal {O} \otimes \mathbb {Q}, {\left \langle {1, -1, -1}\right \rangle })$
by Example 11.2, B is isomorphic to one of the algebras listed in the statement.
If B is definite, then
![]() $\mathbf {Aut}(B)$
is a
$\mathbf {Aut}(B)$
is a
![]() $\mathbb {Z}$
-form of the compact real group of type
$\mathbb {Z}$
-form of the compact real group of type
![]() $\mathsf {G}_2$
or
$\mathsf {G}_2$
or
![]() $\mathsf {F}_4$
. Gross’s mass formula [Reference GrossGr, Proposition 5.3] shows that, up to
$\mathsf {F}_4$
. Gross’s mass formula [Reference GrossGr, Proposition 5.3] shows that, up to
![]() $\mathbb {Z}$
-isomorphism, there is only one group of type
$\mathbb {Z}$
-isomorphism, there is only one group of type
![]() $\mathsf {G}_2$
and two groups of type
$\mathsf {G}_2$
and two groups of type
![]() $\mathsf {F}_4$
with this property. Using the equivalence between these groups and octonion or Albert algebras (Theorem 9.3), we conclude that up to isomorphism
$\mathsf {F}_4$
with this property. Using the equivalence between these groups and octonion or Albert algebras (Theorem 9.3), we conclude that up to isomorphism
![]() $\mathcal {O}$
is the unique definite octonion
$\mathcal {O}$
is the unique definite octonion
![]() $\mathbb {Z}$
-algebra and
$\mathbb {Z}$
-algebra and
![]() $\operatorname {\mathrm {Her}}_3(\mathcal {O})$
and
$\operatorname {\mathrm {Her}}_3(\mathcal {O})$
and
![]() $\Lambda $
are the two isomorphism classes of definite Albert
$\Lambda $
are the two isomorphism classes of definite Albert
![]() $\mathbb {Z}$
-algebras, completing the proof of (a) and (b).
$\mathbb {Z}$
-algebras, completing the proof of (a) and (b).
For (c), note that the three algebras in (b) that are not
![]() $\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Z}))$
are all isotopic, see Example 13.2, so the two algebras listed in (c) represent all of the isotopy classes of Albert
$\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Z}))$
are all isotopic, see Example 13.2, so the two algebras listed in (c) represent all of the isotopy classes of Albert
![]() $\mathbb {Z}$
-algebras. The base change of these two algebras to
$\mathbb {Z}$
-algebras. The base change of these two algebras to
![]() $\mathbb {Q}$
are not isotopic (Example 13.5), so they are not isotopic as
$\mathbb {Q}$
are not isotopic (Example 13.5), so they are not isotopic as
![]() $\mathbb {Z}$
-algebras.
$\mathbb {Z}$
-algebras.
Note that part (a) of the theorem can be proved entirely in the language of octonion algebras (see [Reference van der Blij and SpringervdBS]).
In view of Theorem 9.3, part (b) is equivalent to a classification of the group schemes of type
![]() $\mathsf {F}_4$
over
$\mathsf {F}_4$
over
![]() $\mathbb {Z}$
, which was done in Sections 6 and 7 of [Reference ConradConrad], especially Examples 6.7 and 7.4. The innovation, here, is that we can use the language of Albert algebras also in the case of
$\mathbb {Z}$
, which was done in Sections 6 and 7 of [Reference ConradConrad], especially Examples 6.7 and 7.4. The innovation, here, is that we can use the language of Albert algebras also in the case of
![]() $\mathbb {Z}$
where
$\mathbb {Z}$
where
![]() $2$
is not invertible. Because of this extra flexibility, we can substitute results from the literature over algebraically closed fields (including characteristic 2) for some of the computations over
$2$
is not invertible. Because of this extra flexibility, we can substitute results from the literature over algebraically closed fields (including characteristic 2) for some of the computations over
![]() $\mathbb {Z}$
done in [Reference ConradConrad].
$\mathbb {Z}$
done in [Reference ConradConrad].
Part (c) corresponds to the classification of groups of type
![]() $\mathsf {E}_6$
over
$\mathsf {E}_6$
over
![]() $\mathbb {Z}$
up to isogeny (see Section 18).
$\mathbb {Z}$
up to isogeny (see Section 18).
15 Groups of type
 $\mathsf {E}_6$
$\mathsf {E}_6$
Roundness of the norm
We note that the cubic norm of a Freudenthal algebra has the following special property. A quadratic form with this property is called “round” (see [Reference Elman, Karpenko and MerkurjevElKM, Section 9.A]).
Lemma 15.1 (roundness)
For every Freudenthal R-algebra J,
Proof. If
![]() $\alpha \in R^{\times }$
and
$\alpha \in R^{\times }$
and
![]() $\phi \in \operatorname {\mathrm {GL}}(J)$
are such that
$\phi \in \operatorname {\mathrm {GL}}(J)$
are such that
![]() $\alpha N_J = N_J \phi $
, then for
$\alpha N_J = N_J \phi $
, then for
![]() $x := \phi (1_J)$
, we have
$x := \phi (1_J)$
, we have
![]() $N_J(x) = \alpha $
. Conversely, if x is invertible in J, put
$N_J(x) = \alpha $
. Conversely, if x is invertible in J, put
![]() $\alpha := N_J(x)$
and define
$\alpha := N_J(x)$
and define
![]() $\phi := \alpha U_{x^{-1}}$
. Then
$\phi := \alpha U_{x^{-1}}$
. Then
![]() $N_J \phi = \alpha ^3 N_J(x^{-1})^2 N_J$
by Lemma 6.5(3), so
$N_J \phi = \alpha ^3 N_J(x^{-1})^2 N_J$
by Lemma 6.5(3), so
![]() $N_J \phi = \alpha N_J$
.
$N_J \phi = \alpha N_J$
.
Example 15.2. For
![]() $J = \operatorname {\mathrm {Her}}_3(C, \Gamma )$
, the sets displayed in Lemma 15.1 equal
$J = \operatorname {\mathrm {Her}}_3(C, \Gamma )$
, the sets displayed in Lemma 15.1 equal
![]() $R^{\times }$
. To see this for the right side, take
$R^{\times }$
. To see this for the right side, take
![]() $\alpha \in R^{\times }$
and note that
$\alpha \in R^{\times }$
and note that
![]() $N_J(\alpha \varepsilon _1 + \varepsilon _2 + \varepsilon _3) = \alpha $
. For the left side, consider
$N_J(\alpha \varepsilon _1 + \varepsilon _2 + \varepsilon _3) = \alpha $
. For the left side, consider
![]() $\phi \in \operatorname {\mathrm {GL}}(J)$
defined by
$\phi \in \operatorname {\mathrm {GL}}(J)$
defined by
 $$ \begin{align*} \phi(\varepsilon_i) = \alpha \varepsilon_i \quad \text{and} \quad \phi(\delta_i(c)) = \delta_i(c) \quad \text{for } i = 1, 2, \\ \phi(\varepsilon_3) = \alpha^{-1} \varepsilon_3 \quad \text{and} \quad \phi(\delta_3(c)) = \delta_3(\alpha c). \end{align*} $$
$$ \begin{align*} \phi(\varepsilon_i) = \alpha \varepsilon_i \quad \text{and} \quad \phi(\delta_i(c)) = \delta_i(c) \quad \text{for } i = 1, 2, \\ \phi(\varepsilon_3) = \alpha^{-1} \varepsilon_3 \quad \text{and} \quad \phi(\delta_3(c)) = \delta_3(\alpha c). \end{align*} $$
Then
![]() $N_J \phi = \alpha N_J$
as polynomial laws.
$N_J \phi = \alpha N_J$
as polynomial laws.
Example 15.3. In contrast to the preceding example, we now show that the sets displayed in Lemma 15.1 may be properly contained in
![]() $R^{\times }$
. Suppose F is a field and J is a Freudenthal F-algebra such that
$R^{\times }$
. Suppose F is a field and J is a Freudenthal F-algebra such that
![]() $N_J$
is anisotropic, that is,
$N_J$
is anisotropic, that is,
![]() $N_J(x) = 0$
if and only if
$N_J(x) = 0$
if and only if
![]() $x = 0$
. (For example, such a J exists if F is Laurent series or rational functions in one variable over a global field, see Remark 12.5.) We claim that, for t an indeterminate, every nonzero element in the image of
$x = 0$
. (For example, such a J exists if F is Laurent series or rational functions in one variable over a global field, see Remark 12.5.) We claim that, for t an indeterminate, every nonzero element in the image of
![]() $N_{J \otimes F((t))}$
has lowest term of degree divisible by 3. Because the norm is a homogeneous form, it suffices to prove this claim for
$N_{J \otimes F((t))}$
has lowest term of degree divisible by 3. Because the norm is a homogeneous form, it suffices to prove this claim for
![]() $J \otimes F[[t]]$
.
$J \otimes F[[t]]$
.
Let
![]() $x \in J \otimes F[[t]]$
be nonzero, so
$x \in J \otimes F[[t]]$
be nonzero, so
![]() $x = \sum _{j \ge j_0} x_j t^j$
for some
$x = \sum _{j \ge j_0} x_j t^j$
for some
![]() $j_0 \ge 0$
with
$j_0 \ge 0$
with
![]() $x_{j_0} \ne 0$
. Since
$x_{j_0} \ne 0$
. Since
![]() $N_J$
is anisotropic,
$N_J$
is anisotropic,
![]() $N_J(x_{j_0}) \ne 0$
. If
$N_J(x_{j_0}) \ne 0$
. If
![]() $j_0 = 0$
, then the homomorphism
$j_0 = 0$
, then the homomorphism
![]() $F[[t]] \to F$
such that
$F[[t]] \to F$
such that
![]() $t \mapsto 0$
sends
$t \mapsto 0$
sends
![]() $x \mapsto x_0$
and
$x \mapsto x_0$
and
![]() $N_{J\otimes F[[t]]}(x) \mapsto N_J(x_0) \ne 0$
, therefore
$N_{J\otimes F[[t]]}(x) \mapsto N_J(x_0) \ne 0$
, therefore
![]() $N_{J \otimes F[[t]]}(x)$
has lowest degree term
$N_{J \otimes F[[t]]}(x)$
has lowest degree term
![]() $N_J(x_0)t^0$
. If
$N_J(x_0)t^0$
. If
![]() $j_0> 0$
, then
$j_0> 0$
, then
proving the claim.
Corollary 15.4. For Freudenthal R-algebras J and
![]() $J'$
, the following are equivalent:
$J'$
, the following are equivalent:
-
1. J and
 $J'$
are isotopic.
$J'$
are isotopic. -
2.
 $N_J \cong \alpha N_{J'}$
for some
$N_J \cong \alpha N_{J'}$
for some
 $\alpha \in R^{\times }$
.
$\alpha \in R^{\times }$
. -
3.
 $N_J \cong N_{J'}$
.
$N_J \cong N_{J'}$
.
Proof. The equivalence of (1) and (2) is Proposition 13.7.
Supposing (2), let
![]() $\phi \colon J' \to J$
be an R-module isomorphism such that
$\phi \colon J' \to J$
be an R-module isomorphism such that
![]() $\alpha N_{J'} = N_J \phi $
. Take
$\alpha N_{J'} = N_J \phi $
. Take
![]() $x := \phi (1_{J'})$
. Since
$x := \phi (1_{J'})$
. Since
![]() $N_J(x) = \alpha $
, Lemma 15.1 gives that
$N_J(x) = \alpha $
, Lemma 15.1 gives that
![]() $\alpha N_J \cong N_J$
. As
$\alpha N_J \cong N_J$
. As
![]() $N_J$
is also isomorphic to
$N_J$
is also isomorphic to
![]() $\alpha N_{J'}$
, we conclude (3). The converse is trivial.
$\alpha N_{J'}$
, we conclude (3). The converse is trivial.
In the corollary, the inclusion of (3) seems to be new, even in the case where R is a field. Omitting that, in the special case where R is a field of characteristic
![]() $\ne 2, 3$
, the equivalence of (1) and (2) and Proposition 15.6 below can be found as Theorems 7 and 10 in [Reference JacobsonJ71].
$\ne 2, 3$
, the equivalence of (1) and (2) and Proposition 15.6 below can be found as Theorems 7 and 10 in [Reference JacobsonJ71].
Albert algebras and groups of type
 $\mathsf {E}_6$
$\mathsf {E}_6$
The stabilizer of the cubic form
![]() $N_J$
in
$N_J$
in
![]() $\mathbf {GL}(J)$
is a closed sub-group-scheme denoted
$\mathbf {GL}(J)$
is a closed sub-group-scheme denoted
![]() $\mathbf {Isom}(J)$
. It contains
$\mathbf {Isom}(J)$
. It contains
![]() $\mathbf {Aut}(J)$
as a natural sub-group-scheme, namely, it is the stabilizer of
$\mathbf {Aut}(J)$
as a natural sub-group-scheme, namely, it is the stabilizer of
![]() $1_J$
by Lemma 10.2. Arguing as in the proof of Lemma 9.1, one finds that
$1_J$
by Lemma 10.2. Arguing as in the proof of Lemma 9.1, one finds that
![]() $\mathbf {Isom}(J)$
is a simple affine group scheme that is simply connected of type
$\mathbf {Isom}(J)$
is a simple affine group scheme that is simply connected of type
![]() $\mathsf {E}_6$
. (In the case where R is an algebraically closed field, this claim is verified in [Reference SpringerSp73, 11.20, 12.4], or see [Reference Springer and VeldkampSpV, Theorem 7.3.2] for the case where R is a field of characteristic different from 2, 3.) Compare [Reference AlsaodyAls21, Lemma 2.3] or [Reference ConradConrad, Appendix C]. Moreover,
$\mathsf {E}_6$
. (In the case where R is an algebraically closed field, this claim is verified in [Reference SpringerSp73, 11.20, 12.4], or see [Reference Springer and VeldkampSpV, Theorem 7.3.2] for the case where R is a field of characteristic different from 2, 3.) Compare [Reference AlsaodyAls21, Lemma 2.3] or [Reference ConradConrad, Appendix C]. Moreover,
![]() $\mathbf {Isom}(J)$
is a “pure inner form” in the sense of [Reference ConradConrad, Section 3], respectively, “strongly inner” in [Reference Calmès and FaselCalF, Definition 2.2.4.9], meaning that it is an inner twist of
$\mathbf {Isom}(J)$
is a “pure inner form” in the sense of [Reference ConradConrad, Section 3], respectively, “strongly inner” in [Reference Calmès and FaselCalF, Definition 2.2.4.9], meaning that it is an inner twist of
![]() $\mathbf {Isom}(J_0)$
for the split Albert algebra
$\mathbf {Isom}(J_0)$
for the split Albert algebra
![]() $J_0$
. We note that the center of
$J_0$
. We note that the center of
![]() $\mathbf {Isom}(J)$
is the group scheme
$\mathbf {Isom}(J)$
is the group scheme
![]() $\mu _3$
of cube roots of unity operating on J by scalar multiplication.
$\mu _3$
of cube roots of unity operating on J by scalar multiplication.
Faithfully flat descent shows that the set
![]() $H^1(R, \mathbf {Isom}(J))$
is in bijection with isomorphism classes of pairs
$H^1(R, \mathbf {Isom}(J))$
is in bijection with isomorphism classes of pairs
![]() $(M, f)$
, where M is a projective module of the same rank as J and f is a cubic form on M — that is, an element of
$(M, f)$
, where M is a projective module of the same rank as J and f is a cubic form on M — that is, an element of
![]() $\mathsf {S}^3(M^*)$
— such that
$\mathsf {S}^3(M^*)$
— such that
![]() $f \otimes S$
is isomorphic to the norm on
$f \otimes S$
is isomorphic to the norm on
![]() $\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(S))$
for some faithfully flat
$\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(S))$
for some faithfully flat
![]() $S \in {R\text {-}\textbf {alg}}$
. For every Albert R-algebra J and every
$S \in {R\text {-}\textbf {alg}}$
. For every Albert R-algebra J and every
![]() $\alpha \in R^{\times }$
,
$\alpha \in R^{\times }$
,
![]() $(J, \alpha N_J)$
is such a pair by Example 15.2. In the special case where R is a field, every such pair
$(J, \alpha N_J)$
is such a pair by Example 15.2. In the special case where R is a field, every such pair
![]() $(M, f)$
— that is, every element of
$(M, f)$
— that is, every element of
![]() $H^1(R, \mathbf {Isom}(J))$
— is of the form
$H^1(R, \mathbf {Isom}(J))$
— is of the form
![]() $(J, \alpha N_J)$
for some J and
$(J, \alpha N_J)$
for some J and
![]() $\alpha \in R^{\times }$
(see [Reference GaribaldiGar09, 9.12] in general or [Reference SpringerSp62] for the case of characteristic
$\alpha \in R^{\times }$
(see [Reference GaribaldiGar09, 9.12] in general or [Reference SpringerSp62] for the case of characteristic
![]() $\ne 2, 3$
).
$\ne 2, 3$
).
Outer automorphism of
 $\mathbf {Isom}(J)$
$\mathbf {Isom}(J)$
Suppose J and
![]() $J'$
are Freudenthal R-algebras and
$J'$
are Freudenthal R-algebras and
![]() $\phi \colon J \to J'$
is an isomorphism of R-modules. Since the bilinear form
$\phi \colon J \to J'$
is an isomorphism of R-modules. Since the bilinear form
![]() $T_{J'}$
is regular, there is a unique R-linear map
$T_{J'}$
is regular, there is a unique R-linear map
![]() $\phi ^{\dagger } \colon J \to J'$
such that
$\phi ^{\dagger } \colon J \to J'$
such that
![]() $T_{J'}(\phi x, \phi ^{\dagger } y) = T_J(x, y)$
for all
$T_{J'}(\phi x, \phi ^{\dagger } y) = T_J(x, y)$
for all
![]() $x, y \in J$
. Because
$x, y \in J$
. Because
![]() $T_J$
and
$T_J$
and
![]() $T_{J'}$
are symmetric, we have
$T_{J'}$
are symmetric, we have
![]() $(\phi ^{\dagger })^{\dagger } = \phi $
for all
$(\phi ^{\dagger })^{\dagger } = \phi $
for all
![]() $\phi $
. If
$\phi $
. If
![]() $J''$
is another Freudenthal R-algebra and
$J''$
is another Freudenthal R-algebra and
![]() $\psi \colon J' \to J''$
is an R-linear bijection, then
$\psi \colon J' \to J''$
is an R-linear bijection, then
![]() $(\phi \psi )^{\dagger } = \phi ^{\dagger } \psi ^{\dagger }$
.
$(\phi \psi )^{\dagger } = \phi ^{\dagger } \psi ^{\dagger }$
.
Proposition 15.5. Let J be a Freudenthal R-algebra.
-
1. If
 $\phi \in \operatorname {\mathrm {GL}}(J)$
is such that
$\phi \in \operatorname {\mathrm {GL}}(J)$
is such that
 $N_J \phi = \alpha N_J$
for some
$N_J \phi = \alpha N_J$
for some
 $\alpha \in R^{\times }$
, then
$\alpha \in R^{\times }$
, then
 $N_J \phi ^{\dagger } = \alpha ^{-1} N_J$
.
$N_J \phi ^{\dagger } = \alpha ^{-1} N_J$
. -
2. The map
 $\phi \mapsto \phi ^{\dagger }$
is an automorphism of
$\phi \mapsto \phi ^{\dagger }$
is an automorphism of
 $\mathbf {Isom}(J)$
of order 2 that is not an inner automorphism.
$\mathbf {Isom}(J)$
of order 2 that is not an inner automorphism. -
3. For
 $\phi $
as in (1) or in
$\phi $
as in (1) or in
 $\mathbf {Isom}(J)(R)$
,
$\mathbf {Isom}(J)(R)$
,
 $\phi ^{\dagger } = \phi $
if and only if
$\phi ^{\dagger } = \phi $
if and only if
 $\phi $
is an automorphism of J.
$\phi $
is an automorphism of J.
Proof. (1): Put
![]() $u := \phi (1_J)^{-1}$
. On the one hand,
$u := \phi (1_J)^{-1}$
. On the one hand,
for all
![]() $x, y \in J$
, because
$x, y \in J$
, because
![]() $\phi $
is an isomorphism
$\phi $
is an isomorphism
![]() $J \to J^{(u)}$
by Proposition 13.7. On the other hand, (13.2) yields
$J \to J^{(u)}$
by Proposition 13.7. On the other hand, (13.2) yields
Therefore,
To complete the proof of (1), we note by Lemma 6.5(3) that
For (2), we only have to check that the map is not an inner automorphism. Let
![]() $S \in {R\text {-}\textbf {alg}}$
be such that there exists
$S \in {R\text {-}\textbf {alg}}$
be such that there exists
![]() $\zeta \in \mu _3(S)$
such that
$\zeta \in \mu _3(S)$
such that
![]() $\zeta \ne 1$
. Then
$\zeta \ne 1$
. Then
![]() $\zeta ^{\dagger } = \zeta ^{-1} \ne \zeta $
and
$\zeta ^{\dagger } = \zeta ^{-1} \ne \zeta $
and
![]() $\zeta $
is in the center of
$\zeta $
is in the center of
![]() $\mathbf {Iso}(J)(R)$
, proving that the automorphism is not inner (and not the identity).
$\mathbf {Iso}(J)(R)$
, proving that the automorphism is not inner (and not the identity).
For (3), suppose
![]() $\phi ^{\dagger } = \phi $
. Then
$\phi ^{\dagger } = \phi $
. Then
![]() $N_J \phi = N_J$
. By (15.1),
$N_J \phi = N_J$
. By (15.1),
![]() $U_{\phi (1_J)^{-1}} = \operatorname {\mathrm {Id}}_J$
, so
$U_{\phi (1_J)^{-1}} = \operatorname {\mathrm {Id}}_J$
, so
![]() $\phi (1_J) = \zeta 1_J$
for some
$\phi (1_J) = \zeta 1_J$
for some
![]() $\zeta \in R$
with
$\zeta \in R$
with
![]() $\zeta ^2 = 1$
(Example 7.4). Yet
$\zeta ^2 = 1$
(Example 7.4). Yet
![]() $1 = N_J(1_J) = N_J \phi (1_J)$
, so
$1 = N_J(1_J) = N_J \phi (1_J)$
, so
![]() $\zeta ^3$
also equals 1, whence
$\zeta ^3$
also equals 1, whence
![]() $\phi (1_J) = 1_J$
. Lemma 10.2 shows that
$\phi (1_J) = 1_J$
. Lemma 10.2 shows that
![]() $\phi $
is an automorphism of J. Conversely, if
$\phi $
is an automorphism of J. Conversely, if
![]() $\phi $
is an automorphism of J, then
$\phi $
is an automorphism of J, then
![]() $u = 1_J$
, so
$u = 1_J$
, so
![]() $\phi ^{\dagger } = \phi $
by (15.1).
$\phi ^{\dagger } = \phi $
by (15.1).
Proposition 15.6. Let J and
![]() $J'$
be Albert R-algebras. Among the statements
$J'$
be Albert R-algebras. Among the statements
-
1.
 $\mathbf {Isom}(J) \cong \mathbf {Isom}(J')$
,
$\mathbf {Isom}(J) \cong \mathbf {Isom}(J')$
, -
2. There is a line bundle L and isomorphism
 $h \colon L^{\otimes 3} \to R$
such that
$h \colon L^{\otimes 3} \to R$
such that
 $(J', N_{J'}) \cong [L, h] \cdot (J, N_J)$
for
$(J', N_{J'}) \cong [L, h] \cdot (J, N_J)$
for
 $\cdot $
as defined in Section 3,
$\cdot $
as defined in Section 3, -
3. J and
 $J'$
are isotopic,
$J'$
are isotopic,
we have the implications (1)
![]() $\Leftrightarrow $
(2)
$\Leftrightarrow $
(2)
![]() $\Leftarrow $
(3). If
$\Leftarrow $
(3). If
![]() $\operatorname {\mathrm {Pic}} R$
has no 3-torsion other than zero, then all three statements are equivalent.
$\operatorname {\mathrm {Pic}} R$
has no 3-torsion other than zero, then all three statements are equivalent.
Proof. Suppose (1); we prove (2). We may assume R is connected.
The conjugation action gives a homomorphism
![]() $\mathbf {Isom}(J) \to \mathbf {Aut}(\mathbf {Isom}(J))$
, which gives a map of pointed sets
$\mathbf {Isom}(J) \to \mathbf {Aut}(\mathbf {Isom}(J))$
, which gives a map of pointed sets
where the second set is in bijection with isomorphism classes of R-group schemes that become isomorphic to
![]() $\mathbf {Isom}(J)$
after base change to an fppf R-algebra. By hypothesis, the class of
$\mathbf {Isom}(J)$
after base change to an fppf R-algebra. By hypothesis, the class of
![]() $N_{J'} \in H^1(R, \mathbf {Isom}(J))$
is in the kernel of (15.2).
$N_{J'} \in H^1(R, \mathbf {Isom}(J))$
is in the kernel of (15.2).
There is an exact sequence
of fppf sheaves by [Reference Demazure and GrothendieckDemG, Theorem XXIV.1.3]. Since R is connected,
![]() $(\mathbb {Z}/2)(R)$
has one nonidentity element, and it is the image of the map
$(\mathbb {Z}/2)(R)$
has one nonidentity element, and it is the image of the map
![]() $\dagger $
from Lemma 15.5. That is, in the exact sequence
$\dagger $
from Lemma 15.5. That is, in the exact sequence
the first map is surjective, so the third map has zero kernel, and we deduce that the image of
![]() $N_{J'}$
in
$N_{J'}$
in
![]() $H^1(R, \mathbf {Isom}(J)/\mu _3)$
is the zero class. It follows that
$H^1(R, \mathbf {Isom}(J)/\mu _3)$
is the zero class. It follows that
![]() $N_{J'}$
is in the image of the map
$N_{J'}$
is in the image of the map
which is the orbit of the zero class
![]() $N_J$
under the action of the group
$N_J$
under the action of the group
![]() $H^1(R, \mu _3)$
, which is (2).
$H^1(R, \mu _3)$
, which is (2).
That (2) implies (1) is Lemma 3.6. The claimed implications between (3) and (2) are Corollary 15.4.
16 Freudenthal triple systems
In this section, we define Freudenthal triple systems, also known as FT systems. We will see in Theorem 17.4 in the next section that they play the same role relative to groups of type
![]() $\mathsf {E}_7$
that forms of the norm on an Albert algebra play for groups of type
$\mathsf {E}_7$
that forms of the norm on an Albert algebra play for groups of type
![]() $\mathsf {E}_6$
.
$\mathsf {E}_6$
.
For any Albert R-algebra J, define
![]() $Q(J)$
to be the rank 56 projective R-module
$Q(J)$
to be the rank 56 projective R-module
![]() $R \oplus R \oplus J \oplus J$
endowed with a 4-linear form
$R \oplus R \oplus J \oplus J$
endowed with a 4-linear form
![]() $\Psi $
and an alternating bilinear form b, defined as follows.
$\Psi $
and an alternating bilinear form b, defined as follows.
We write an element of
![]() $Q(J)$
as
$Q(J)$
as
![]() $\left ( \begin {smallmatrix} \alpha & x \\ x' & \alpha ' \end {smallmatrix} \right )$
for
$\left ( \begin {smallmatrix} \alpha & x \\ x' & \alpha ' \end {smallmatrix} \right )$
for
![]() $\alpha , \alpha ' \in R$
and
$\alpha , \alpha ' \in R$
and
![]() $x, x' \in J$
. Define
$x, x' \in J$
. Define
As an intermediate step to defining
![]() $\Psi $
, define a quartic form
$\Psi $
, define a quartic form
compare [Reference BrownBrown, p. 87] or [Reference KrutelevichKr07, p. 940].
To define the 4-linear form, consider first the case
![]() $R = \mathbb {Z}$
and
$R = \mathbb {Z}$
and
![]() $J := \operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Z}))$
. (The following definitions are inspired by [Reference LurieLur, Section 6].) Putting
$J := \operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Z}))$
. (The following definitions are inspired by [Reference LurieLur, Section 6].) Putting
![]() $X_i$
for an element of
$X_i$
for an element of
![]() $Q(J)$
and
$Q(J)$
and
![]() $t_i$
for an indeterminate, the coefficient of
$t_i$
for an indeterminate, the coefficient of
![]() $t_1 t_2 t_3 t_4$
in
$t_1 t_2 t_3 t_4$
in
![]() $q(\sum t_i X_i)$
, equivalently, the 4-linear form
$q(\sum t_i X_i)$
, equivalently, the 4-linear form
on
![]() $Q(J)$
, equals
$Q(J)$
, equals
![]() $2\Theta $
for a symmetric 4-linear form
$2\Theta $
for a symmetric 4-linear form
![]() $\Theta $
. Define 4-linear forms
$\Theta $
. Define 4-linear forms
![]() $\Phi _i$
via
$\Phi _i$
via
 $$ \begin{align} \Phi_1(X_1, X_2, X_3, X_4) &= b(X_1, X_2)\, b(X_3, X_4) \notag \\ \Phi_2(X_1, X_2, X_3, X_4) &= b(X_1, X_3)\, b(X_4, X_2) \\ \Phi_3(X_1, X_2, X_3, X_4) &= b(X_1, X_4)\, b(X_2, X_3). \notag \end{align} $$
$$ \begin{align} \Phi_1(X_1, X_2, X_3, X_4) &= b(X_1, X_2)\, b(X_3, X_4) \notag \\ \Phi_2(X_1, X_2, X_3, X_4) &= b(X_1, X_3)\, b(X_4, X_2) \\ \Phi_3(X_1, X_2, X_3, X_4) &= b(X_1, X_4)\, b(X_2, X_3). \notag \end{align} $$
Then
![]() $\Theta + \sum \Phi _i$
is divisible by 2 as a 4-linear function on
$\Theta + \sum \Phi _i$
is divisible by 2 as a 4-linear function on
![]() $Q(\operatorname {\mathrm {Zor}}(\mathbb {Z}))$
, and we set
$Q(\operatorname {\mathrm {Zor}}(\mathbb {Z}))$
, and we set
As
![]() $\Theta $
is symmetric,
$\Theta $
is symmetric,
![]() $\Psi $
is evidently stable under even permutations of its arguments, and we have:
$\Psi $
is evidently stable under even permutations of its arguments, and we have:
For any ring R, we define
![]() $\Psi _{\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R))} := \Psi _{\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Z}))} \otimes R$
, and we define
$\Psi _{\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R))} := \Psi _{\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Z}))} \otimes R$
, and we define
![]() $\Psi _J$
for an Albert R-algebra J by descent.
$\Psi _J$
for an Albert R-algebra J by descent.
Definition 16.1. A Freudenthal triple system
Footnote
1
or FT system
![]() $(M, \Psi , b)$
is an R-module M endowed with a 4-linear form
$(M, \Psi , b)$
is an R-module M endowed with a 4-linear form
![]() $\Psi $
and an alternating bilinear form b such that
$\Psi $
and an alternating bilinear form b such that
![]() $(M, \Psi , b) \otimes S$
is isomorphic (in an obvious sense) to
$(M, \Psi , b) \otimes S$
is isomorphic (in an obvious sense) to
![]() $Q(J)$
for some faithfully flat
$Q(J)$
for some faithfully flat
![]() $S \in {R\text {-}\textbf {alg}}$
and some Albert S-algebra J.
$S \in {R\text {-}\textbf {alg}}$
and some Albert S-algebra J.
Comparison with other definitions
Suppose for this paragraph that 6 is invertible in R. Given an FT system
![]() $(M, \Psi , b)$
, we may define 4-linear forms
$(M, \Psi , b)$
, we may define 4-linear forms
![]() $\Phi _i$
on M via (16.3) and recover
$\Phi _i$
on M via (16.3) and recover
![]() $\Theta $
and q via
$\Theta $
and q via
as polynomial laws in X. (This last is a special case of the general fact that going from a homogeneous form of degree d to a d-linear form and back to a homogeneous form of degree d equals multiplication by
![]() $d!$
[Reference BourbakiBouA2, Section IV.5.8, Proposition 12(i)].) Since the form b is regular and
$d!$
[Reference BourbakiBouA2, Section IV.5.8, Proposition 12(i)].) Since the form b is regular and
![]() $\Theta $
is symmetric, the equation
$\Theta $
is symmetric, the equation
implicitly defines a symmetric 3-linear form
![]() $t \colon M \times M \times M \to M$
, and
$t \colon M \times M \times M \to M$
, and
![]() $\mathbf {Aut}(M, \Psi , b)$
equals
$\mathbf {Aut}(M, \Psi , b)$
equals
![]() $\mathbf {Aut}(M, t, b)$
. That is, under the hypothesis that 6 is invertible in R, we would obtain an equivalent class of objects if we replaced the asymmetric 4-linear form
$\mathbf {Aut}(M, t, b)$
. That is, under the hypothesis that 6 is invertible in R, we would obtain an equivalent class of objects if we replaced the asymmetric 4-linear form
![]() $\Psi $
in the definition of FT systems with the quartic form q (the version studied in [Reference BrownBrown]) or with the trilinear form t (the version studied in [Reference MeybergMey]).
$\Psi $
in the definition of FT systems with the quartic form q (the version studied in [Reference BrownBrown]) or with the trilinear form t (the version studied in [Reference MeybergMey]).
Similarity of FT systems
For a d-linear form f on an R-module M, that is, an R-linear map
![]() $f \colon M^{\otimes d} \to R$
, and a d-trivialized line bundle
$f \colon M^{\otimes d} \to R$
, and a d-trivialized line bundle
![]() $[L, h] \in H^1(R, \mu _d)$
, we define a d-linear form
$[L, h] \in H^1(R, \mu _d)$
, we define a d-linear form
![]() $[L, h] \cdot f$
on
$[L, h] \cdot f$
on
![]() $M \otimes L$
via the composition
$M \otimes L$
via the composition
For
![]() $Q := (M, \Psi , b)$
, an FT system and a discriminant module
$Q := (M, \Psi , b)$
, an FT system and a discriminant module
![]() $[L, h] \in H^1(R, \mu _2)$
, we define
$[L, h] \in H^1(R, \mu _2)$
, we define
![]() $[L, h] \cdot Q$
to be the triple consisting of the module
$[L, h] \cdot Q$
to be the triple consisting of the module
![]() $M \otimes L$
, the 4-linear form
$M \otimes L$
, the 4-linear form
![]() $[L, h^{\otimes 2}] \cdot \Psi $
for
$[L, h^{\otimes 2}] \cdot \Psi $
for
![]() $[L, h^{\otimes 2}] \in H^1(R, \mu _4)$
, and the bilinear form
$[L, h^{\otimes 2}] \in H^1(R, \mu _4)$
, and the bilinear form
![]() $[L, h] \cdot b$
. Since
$[L, h] \cdot b$
. Since
![]() ${\left \langle {1}\right \rangle } \cdot Q$
is Q itself, we deduce that
${\left \langle {1}\right \rangle } \cdot Q$
is Q itself, we deduce that
![]() $[L, h] \cdot Q$
is also an FT system. We say that FT systems Q,
$[L, h] \cdot Q$
is also an FT system. We say that FT systems Q,
![]() $Q'$
are similar if
$Q'$
are similar if
![]() $Q' \cong [L, h] \cdot Q$
for some
$Q' \cong [L, h] \cdot Q$
for some
![]() $[L, h] \in H^1(R, \mu _2)$
. For example, for any FT system
$[L, h] \in H^1(R, \mu _2)$
. For example, for any FT system
![]() $(M, \Psi , b)$
and any
$(M, \Psi , b)$
and any
![]() $\alpha \in R^{\times }$
,
$\alpha \in R^{\times }$
,
![]() $(M, \Psi , b)$
and
$(M, \Psi , b)$
and
![]() $(M, \alpha ^2 \Psi , \alpha b)$
are similar.
$(M, \alpha ^2 \Psi , \alpha b)$
are similar.
Example 16.2. Suppose
![]() $(M, \Psi , b) = Q(J)$
for some Albert R-algebra J. Then for every
$(M, \Psi , b) = Q(J)$
for some Albert R-algebra J. Then for every
![]() $\mu \in R^{\times }$
, the map
$\mu \in R^{\times }$
, the map
is an isomorphism
![]() ${\left \langle {\mu }\right \rangle } \cdot Q(J) \xrightarrow {\sim } Q(J)$
. One checks this for
${\left \langle {\mu }\right \rangle } \cdot Q(J) \xrightarrow {\sim } Q(J)$
. One checks this for
![]() $R = \mathbb {Z}$
and
$R = \mathbb {Z}$
and
![]() $J = \operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Z}))$
using (16.1) and (16.2). It follows for general R and J by base change and twisting.
$J = \operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Z}))$
using (16.1) and (16.2). It follows for general R and J by base change and twisting.
17 Groups of type
 $\mathsf {E}_7$
$\mathsf {E}_7$
We will now relate FT systems as defined in the previous section to affine group schemes of type
![]() $\mathsf {E}_7$
. Here is a tool that allows us to work with the quartic form q as in (16.2) rather than the less convenient 4-linear form
$\mathsf {E}_7$
. Here is a tool that allows us to work with the quartic form q as in (16.2) rather than the less convenient 4-linear form
![]() $\Psi $
, while still getting results that hold when 6 is not invertible.
$\Psi $
, while still getting results that hold when 6 is not invertible.
Lemma 17.1. Let
![]() $(M, \Psi , b)$
be an FT system over
$(M, \Psi , b)$
be an FT system over
![]() $\mathbb {Z}$
, let
$\mathbb {Z}$
, let
![]() $\mathbf {G}$
be a closed subgroup of
$\mathbf {G}$
be a closed subgroup of
![]() $\mathbf {GL}(M)$
, and let F be a field of characteristic zero. If
$\mathbf {GL}(M)$
, and let F be a field of characteristic zero. If
![]() $\mathbf {G}(F)$
is dense in
$\mathbf {G}(F)$
is dense in
![]() $\mathbf {G}$
(which holds if
$\mathbf {G}$
(which holds if
![]() $\mathbf {G}$
is connected) and
$\mathbf {G}$
is connected) and
![]() $\mathbf {G}(F)$
preserves
$\mathbf {G}(F)$
preserves
![]() $b \otimes F$
and the quartic form q over F defined by (16.5), then
$b \otimes F$
and the quartic form q over F defined by (16.5), then
![]() $\mathbf {G}$
is a closed sub-group-scheme of
$\mathbf {G}$
is a closed sub-group-scheme of
![]() $\mathbf {Aut}(M, \Psi , b)$
.
$\mathbf {Aut}(M, \Psi , b)$
.
Proof. Since
![]() $\mathbf {G}(F)$
is dense in
$\mathbf {G}(F)$
is dense in
![]() $\mathbf {G}$
, the group scheme
$\mathbf {G}$
, the group scheme
![]() $\mathbf {G} \times F$
preserves
$\mathbf {G} \times F$
preserves
![]() $b \otimes F$
and q, whence also
$b \otimes F$
and q, whence also
![]() $\Psi \otimes F$
. Viewing b and
$\Psi \otimes F$
. Viewing b and
![]() $\Psi $
as elements of the representation
$\Psi $
as elements of the representation
![]() $V := (M^*)^{\otimes d}$
of
$V := (M^*)^{\otimes d}$
of
![]() $\mathbf {G}$
for
$\mathbf {G}$
for
![]() $d = 2$
or 4, the natural map
$d = 2$
or 4, the natural map
![]() $V^{\mathbf {G}} \otimes F \to (V \otimes F)^{\mathbf {G} \times F}$
is an isomorphism because F is flat over
$V^{\mathbf {G}} \otimes F \to (V \otimes F)^{\mathbf {G} \times F}$
is an isomorphism because F is flat over
![]() $\mathbb {Z}$
[Reference SeshadriSes, Lemma 2], so
$\mathbb {Z}$
[Reference SeshadriSes, Lemma 2], so
![]() $\mathbf {G}$
preserves b and
$\mathbf {G}$
preserves b and
![]() $\Psi $
.
$\Psi $
.
Corollary 17.2. For every Freudenthal R-algebra J, there is an inclusion
![]() $f \colon \mathbf {Isom}(J) \hookrightarrow \mathbf {Aut}(Q(J))$
via
$f \colon \mathbf {Isom}(J) \hookrightarrow \mathbf {Aut}(Q(J))$
via
Proof. Consider the case
![]() $J = \operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Z}))$
. For
$J = \operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {Z}))$
. For
![]() $\phi \in \mathbf {Isom}(J)(\mathbb {Q})$
, it follows from the definition of
$\phi \in \mathbf {Isom}(J)(\mathbb {Q})$
, it follows from the definition of
![]() $\phi ^{\dagger }$
and Proposition 15.5(1) that
$\phi ^{\dagger }$
and Proposition 15.5(1) that
![]() $f(\phi )$
is an isomorphism of the bilinear and quartic forms
$f(\phi )$
is an isomorphism of the bilinear and quartic forms
![]() $b \otimes \mathbb {Q}$
and q defined by (16.2) for
$b \otimes \mathbb {Q}$
and q defined by (16.2) for
![]() $J \otimes \mathbb {Q}$
. The lemma gives the claim in this case. Base change and twisting give the claim for every R and every Albert R-algebra J.
$J \otimes \mathbb {Q}$
. The lemma gives the claim in this case. Base change and twisting give the claim for every R and every Albert R-algebra J.
Corollary 17.3. Suppose J and
![]() $J'$
are Albert R-algebras. If J and
$J'$
are Albert R-algebras. If J and
![]() $J'$
are isotopic, then
$J'$
are isotopic, then
![]() $\mathbf {Aut}(Q(J)) \cong \mathbf {Aut}(Q(J'))$
.
$\mathbf {Aut}(Q(J)) \cong \mathbf {Aut}(Q(J'))$
.
Proof. The inclusions
![]() $\mathbf {Aut}(J) \hookrightarrow \mathbf {Isom}(J) \hookrightarrow \mathbf {Aut}(Q(J))$
induce maps
$\mathbf {Aut}(J) \hookrightarrow \mathbf {Isom}(J) \hookrightarrow \mathbf {Aut}(Q(J))$
induce maps
where the last set classifies FT systems over R. The class of
![]() $J'$
in
$J'$
in
![]() $H^1(R, \mathbf {Aut}(J))$
maps to the class of
$H^1(R, \mathbf {Aut}(J))$
maps to the class of
![]() $N_{J'}$
in
$N_{J'}$
in
![]() $H^1(R, \mathbf {Isom}(J))$
, and by hypothesis and by Proposition 15.6, this is the trivial class. Therefore, the image of
$H^1(R, \mathbf {Isom}(J))$
, and by hypothesis and by Proposition 15.6, this is the trivial class. Therefore, the image of
![]() $J'$
in
$J'$
in
![]() $H^1(R, \mathbf {Aut}(Q(J)))$
, which is
$H^1(R, \mathbf {Aut}(Q(J)))$
, which is
![]() $Q(J')$
, is the trivial class.
$Q(J')$
, is the trivial class.
In case R is a field of characteristic
![]() $\ne 2, 3$
, the converse of Corollary 17.3 is true by [Reference FerrarFe72, Corollary 6.9]. That is, if
$\ne 2, 3$
, the converse of Corollary 17.3 is true by [Reference FerrarFe72, Corollary 6.9]. That is, if
![]() $Q(J) \cong Q(J')$
, then J and
$Q(J) \cong Q(J')$
, then J and
![]() $J'$
are isotopic. The paper [Reference AlsaodyAls22] provides an example related to this construction over rings.
$J'$
are isotopic. The paper [Reference AlsaodyAls22] provides an example related to this construction over rings.
Theorem 17.4. The group scheme
![]() $\mathbf {Aut}(Q(\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R))))$
over R is obtained from the simply connected Chevalley group of type
$\mathbf {Aut}(Q(\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R))))$
over R is obtained from the simply connected Chevalley group of type
![]() $\mathsf {E}_7$
over
$\mathsf {E}_7$
over
![]() $\mathbb {Z}$
by base change. Every strongly inner and simply connected simple R-group scheme of type
$\mathbb {Z}$
by base change. Every strongly inner and simply connected simple R-group scheme of type
![]() $\mathsf {E}_7$
over R is of the form
$\mathsf {E}_7$
over R is of the form
![]() $\mathbf {Aut}(Q)$
for some FT system Q. For FT systems Q and
$\mathbf {Aut}(Q)$
for some FT system Q. For FT systems Q and
![]() $Q'$
,
$Q'$
,
![]() $\mathbf {Aut}(Q) \cong \mathbf {Aut}(Q')$
if and only if Q and
$\mathbf {Aut}(Q) \cong \mathbf {Aut}(Q')$
if and only if Q and
![]() $Q'$
are similar.
$Q'$
are similar.
Proof. Put
![]() $J_R := \operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R))$
and
$J_R := \operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(R))$
and
![]() $Q_R := Q(J_R)$
. We will show that
$Q_R := Q(J_R)$
. We will show that
![]() $\mathbf {Aut}(Q_R)$
is isomorphic to the base change to R of the simply connected Chevalley group
$\mathbf {Aut}(Q_R)$
is isomorphic to the base change to R of the simply connected Chevalley group
![]() $E_7$
over
$E_7$
over
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
In addition to the sub-group-scheme
![]() $\mathbf {Isom}(J_R)$
of
$\mathbf {Isom}(J_R)$
of
![]() $\mathbf {Aut}(Q_R)$
provided by Corollary 17.2, we consider a rank 1 torus
$\mathbf {Aut}(Q_R)$
provided by Corollary 17.2, we consider a rank 1 torus
![]() $\mathbb {G}_{\mathrm {m}}$
defined by
$\mathbb {G}_{\mathrm {m}}$
defined by
and two copies of
![]() $J_R$
(as group schemes under addition) through which an element
$J_R$
(as group schemes under addition) through which an element
![]() $y \in J_R$
acts via
$y \in J_R$
acts via
These preserve b and q, see, for example, [Reference BrownBrown, p. 95] or [Reference KrutelevichKr07, p. 942], and so by Lemma 17.1 do belong to
![]() $\mathbf {Aut}(Q_R)$
. Considering the Lie algebras of
$\mathbf {Aut}(Q_R)$
. Considering the Lie algebras of
![]() $\mathbf {Isom}(J_R)$
,
$\mathbf {Isom}(J_R)$
,
![]() $\mathbb {G}_{\mathrm {m}}$
, and the two copies of J, as subalgebras of
$\mathbb {G}_{\mathrm {m}}$
, and the two copies of J, as subalgebras of
![]() $\operatorname {\mathrm {Lie}}(\mathbf {GL}(Q_R))$
, one can identify the subalgebra
$\operatorname {\mathrm {Lie}}(\mathbf {GL}(Q_R))$
, one can identify the subalgebra
![]() $L_R$
they generate with the Lie algebra of
$L_R$
they generate with the Lie algebra of
![]() $E_7 \times R$
by picking out specific root subalgebras and so on as in [Reference FreudenthalFr54] or [Reference SeligmanSel], or see [Reference GaribaldiGar01, Section 7] for partial information. Note that
$E_7 \times R$
by picking out specific root subalgebras and so on as in [Reference FreudenthalFr54] or [Reference SeligmanSel], or see [Reference GaribaldiGar01, Section 7] for partial information. Note that
![]() $\operatorname {\mathrm {Lie}}(\mathbf {Aut}(Q_R)) \supseteq L_R$
. For F any algebraically closed field, we may identify the smooth closed subgroup of
$\operatorname {\mathrm {Lie}}(\mathbf {Aut}(Q_R)) \supseteq L_R$
. For F any algebraically closed field, we may identify the smooth closed subgroup of
![]() $\mathbf {Aut}(Q_F)$
generated by
$\mathbf {Aut}(Q_F)$
generated by
![]() $\mathbf {Isom}(J_F)$
,
$\mathbf {Isom}(J_F)$
,
![]() $\mathbb {G}_{\mathrm {m}}$
, and the two copies of
$\mathbb {G}_{\mathrm {m}}$
, and the two copies of
![]() $J_F$
with
$J_F$
with
![]() $E_7 \times F$
.
$E_7 \times F$
.
In [Reference LurieLur], Lurie begins with
![]() $L_{\mathbb {Z}}$
and defines
$L_{\mathbb {Z}}$
and defines
![]() $L_{\mathbb {Z}}$
-invariant 4-linear forms
$L_{\mathbb {Z}}$
-invariant 4-linear forms
![]() $\Theta ^L$
,
$\Theta ^L$
,
![]() $\Phi _i^L$
, and
$\Phi _i^L$
, and
![]() $\Psi ^L$
and alternating bilinear form
$\Psi ^L$
and alternating bilinear form
![]() $b^L$
on the 56-dimensional Weyl module of
$b^L$
on the 56-dimensional Weyl module of
![]() $L_{\mathbb {Z}}$
. Over
$L_{\mathbb {Z}}$
. Over
![]() $\mathbb {C}$
,
$\mathbb {C}$
,
![]() $\mathbf {Aut}(Q_{\mathbb {C}})$
is simply connected of type
$\mathbf {Aut}(Q_{\mathbb {C}})$
is simply connected of type
![]() $\mathsf {E}_7$
by the references in the previous paragraph, so it preserves the base change of Lurie’s forms
$\mathsf {E}_7$
by the references in the previous paragraph, so it preserves the base change of Lurie’s forms
![]() $\Theta ^L \otimes \mathbb {C}$
, etc. Because
$\Theta ^L \otimes \mathbb {C}$
, etc. Because
![]() $\mathbf {Aut}(Q_{\mathbb {C}})(\mathbb {C})$
is dense in
$\mathbf {Aut}(Q_{\mathbb {C}})(\mathbb {C})$
is dense in
![]() $\mathbf {Aut}(Q_{\mathbb {C}})$
, Lemma 17.1 shows that
$\mathbf {Aut}(Q_{\mathbb {C}})$
, Lemma 17.1 shows that
![]() $\mathbf {Aut}(Q_{\mathbb {Z}})$
preserves
$\mathbf {Aut}(Q_{\mathbb {Z}})$
preserves
![]() $\Theta ^L$
, the
$\Theta ^L$
, the
![]() $\Phi _i^L$
,
$\Phi _i^L$
,
![]() $\Psi ^L$
, and
$\Psi ^L$
, and
![]() $b^L$
. By the uniqueness of
$b^L$
. By the uniqueness of
![]() $E_7$
invariant bilinear and symmetric 4-linear forms on M (which follows from the uniqueness over
$E_7$
invariant bilinear and symmetric 4-linear forms on M (which follows from the uniqueness over
![]() $\mathbb {C}$
as in the proof of Lemma 17.1), we find that
$\mathbb {C}$
as in the proof of Lemma 17.1), we find that
![]() $b^L = \pm b$
and
$b^L = \pm b$
and
![]() $\Theta ^L = \pm \Theta $
. Note that regardless of the sign on b in the preceding sentence, we find
$\Theta ^L = \pm \Theta $
. Note that regardless of the sign on b in the preceding sentence, we find
![]() $\Phi ^L_i = \Phi _i$
for all i and
$\Phi ^L_i = \Phi _i$
for all i and
![]() $\mathbf {Aut}(Q_F)$
preserves
$\mathbf {Aut}(Q_F)$
preserves
![]() $b^L$
. Now let F be an algebraically closed field. If F has characteristic different from 2, then
$b^L$
. Now let F be an algebraically closed field. If F has characteristic different from 2, then
![]() $\mathbf {Aut}(Q_F)$
preserves
$\mathbf {Aut}(Q_F)$
preserves
![]() $2 \Psi = \Theta + \sum \Phi _i$
and the
$2 \Psi = \Theta + \sum \Phi _i$
and the
![]() $\Phi _i$
, so it preserves
$\Phi _i$
, so it preserves
![]() $\Theta $
, hence
$\Theta $
, hence
![]() $\Theta ^L$
, hence
$\Theta ^L$
, hence
![]() $\Psi ^L$
. If F has characteristic 2, then although
$\Psi ^L$
. If F has characteristic 2, then although
![]() $\Psi ^L = \frac 12 (\pm \Theta + \sum \Phi _i)$
for some choice of sign as polynomials over
$\Psi ^L = \frac 12 (\pm \Theta + \sum \Phi _i)$
for some choice of sign as polynomials over
![]() $\mathbb {Z}$
, we have
$\mathbb {Z}$
, we have
![]() $\Psi ^L \otimes F = \Psi \otimes F$
. In either case,
$\Psi ^L \otimes F = \Psi \otimes F$
. In either case,
![]() $\mathbf {Aut}(Q_F)$
preserves
$\mathbf {Aut}(Q_F)$
preserves
![]() $b^L \otimes F$
and
$b^L \otimes F$
and
![]() $\Psi ^L \otimes F$
, whence so does its Lie algebra, so
$\Psi ^L \otimes F$
, whence so does its Lie algebra, so
![]() $\dim \operatorname {\mathrm {Lie}} \mathbf {Aut}(Q_F) \le \dim L_F$
by [Reference LurieLur, Theorem 6.2.3]. Putting this together with the previous paragraph, we see that
$\dim \operatorname {\mathrm {Lie}} \mathbf {Aut}(Q_F) \le \dim L_F$
by [Reference LurieLur, Theorem 6.2.3]. Putting this together with the previous paragraph, we see that
![]() $\mathbf {Aut}(Q_F)$
, an affine group scheme over the field F, is smooth with identity component
$\mathbf {Aut}(Q_F)$
, an affine group scheme over the field F, is smooth with identity component
![]() $E_7 \times F$
.
$E_7 \times F$
.
We claim that
![]() $\mathbf {Aut}(Q_F)$
is connected. Since its identity component
$\mathbf {Aut}(Q_F)$
is connected. Since its identity component
![]() $E_7$
has no outer automorphisms, every element of
$E_7$
has no outer automorphisms, every element of
![]() $\mathbf {Aut}(Q_F)(F)$
is a product of an element of
$\mathbf {Aut}(Q_F)(F)$
is a product of an element of
![]() $E_7(F)$
and a linear transformation centralizing
$E_7(F)$
and a linear transformation centralizing
![]() $E_7$
. The action of
$E_7$
. The action of
![]() $E_7 \times F$
on
$E_7 \times F$
on
![]() $Q_F$
is irreducible (it is the 56-dimensional minuscule representation), so the centralizer of
$Q_F$
is irreducible (it is the 56-dimensional minuscule representation), so the centralizer of
![]() $E_7$
consists of scalar transformations. Finally, we note that the intersection of
$E_7$
consists of scalar transformations. Finally, we note that the intersection of
![]() $\mathbf {Aut}(Q_F)$
and the scalar transformations is the group scheme
$\mathbf {Aut}(Q_F)$
and the scalar transformations is the group scheme
![]() $\mu _2$
of square roots of unity, which is contained in
$\mu _2$
of square roots of unity, which is contained in
![]() $E_7$
. In summary,
$E_7$
. In summary,
![]() $\mathbf {Aut}(Q_F) = E_7 \times F$
for every algebraically closed field F.
$\mathbf {Aut}(Q_F) = E_7 \times F$
for every algebraically closed field F.
As in the proof of Lemma 9.1, it follows that
![]() $\mathbf {Aut}(Q_{\mathbb {Z}})$
is a simple affine group scheme that is simply connected of type
$\mathbf {Aut}(Q_{\mathbb {Z}})$
is a simple affine group scheme that is simply connected of type
![]() $\mathsf {E}_7$
, and we deduce from the fact that
$\mathsf {E}_7$
, and we deduce from the fact that
![]() $\mathbf {Aut}(Q_{\mathbb {R}})$
is split that
$\mathbf {Aut}(Q_{\mathbb {R}})$
is split that
![]() $\mathbf {Aut}(Q_{\mathbb {Z}})$
is in fact the Chevalley group.
$\mathbf {Aut}(Q_{\mathbb {Z}})$
is in fact the Chevalley group.
The second claim now follows by descent.
The third claim is proved in the same manner as Proposition 15.6, although the current situation is somewhat easier due to the absence of nontrivial automorphisms of the Dynkin diagram of
![]() $\mathsf {E}_7$
and therefore the absence of outer automorphisms for semisimple groups of that type. The sequence
$\mathsf {E}_7$
and therefore the absence of outer automorphisms for semisimple groups of that type. The sequence
is exact, where
![]() $\mu _2$
is the center of
$\mu _2$
is the center of
![]() $\mathbf {Aut}(Q)$
and
$\mathbf {Aut}(Q)$
and
![]() $\mathbf {Aut}(\mathbf {Aut}(Q)) \cong \mathbf {Aut}(Q)/\mu _2$
is the adjoint group. We have
$\mathbf {Aut}(\mathbf {Aut}(Q)) \cong \mathbf {Aut}(Q)/\mu _2$
is the adjoint group. We have
![]() $\mathbf {Aut}(Q') \cong \mathbf {Aut}(Q)$
if and only if the element
$\mathbf {Aut}(Q') \cong \mathbf {Aut}(Q)$
if and only if the element
![]() $Q'$
in
$Q'$
in
![]() $H^1(R, \mathbf {Aut}(Q))$
is in the kernel of the second map in (17.1), if and only if
$H^1(R, \mathbf {Aut}(Q))$
is in the kernel of the second map in (17.1), if and only if
![]() $Q'$
is in the image of the first map. To complete the proof, it suffices to calculate by descent that the action of
$Q'$
is in the image of the first map. To complete the proof, it suffices to calculate by descent that the action of
![]() $H^1(R, \mu _2)$
on
$H^1(R, \mu _2)$
on
![]() $H^1(R, \mathbf {Aut}(Q))$
is exactly by the similarity action defined in Section 16.
$H^1(R, \mathbf {Aut}(Q))$
is exactly by the similarity action defined in Section 16.
A partial rephrasing of the second statement of the theorem is that, for any FT system Q, the set
![]() $H^1(R, \mathbf {Aut}(Q))$
is in bijection with the set of isomorphism classes of FT systems over R.
$H^1(R, \mathbf {Aut}(Q))$
is in bijection with the set of isomorphism classes of FT systems over R.
Corollary 17.5. If R is: (1) a complete discrete valuation ring whose residue field is finite; (2) a finite ring; or (3) a Dedekind domain whose field of fractions F is a global field with no real embeddings, then the split FT system is the only one over R, up to isomorphism.
Proof. Imitate the arguments in Proposition 11.3 or Example 11.5, where
![]() $\mathbf {G}$
is the base change to R of the simply connected Chevalley group
$\mathbf {G}$
is the base change to R of the simply connected Chevalley group
![]() $\mathbf {Aut}(Q(\operatorname {\mathrm {Zor}}(\mathbb {Z})))$
.
$\mathbf {Aut}(Q(\operatorname {\mathrm {Zor}}(\mathbb {Z})))$
.
Remarks 17.6. A previous work that considered groups of type
![]() $\mathsf {E}_7$
over rings is [Reference LuzgarevLuz]. Aschbacher [Reference AschbacherAsch] studied the 4-linear form in the case where R is a field of characteristic 2. The paper [Reference Mühlherr and WeissMüW] studied the case of fields of any characteristic, organized around a polynomial law
$\mathsf {E}_7$
over rings is [Reference LuzgarevLuz]. Aschbacher [Reference AschbacherAsch] studied the 4-linear form in the case where R is a field of characteristic 2. The paper [Reference Mühlherr and WeissMüW] studied the case of fields of any characteristic, organized around a polynomial law
![]() $\Theta \in \mathscr {P}(Q, R)$
that is not homogeneous. For a field F of characteristic
$\Theta \in \mathscr {P}(Q, R)$
that is not homogeneous. For a field F of characteristic
![]() $\ne 2, 3$
, FT systems have been studied in this century in [Reference ClercCl], [Reference HeleniusHel], [Reference KrutelevichKr07], [Reference SpringerSp06], and [Reference Borsten, Duff, Ferrara, Marrani and RubensBDFMR] to name a few. They arise naturally in the context of the bottom row of the magic triangle from [Reference Deligne and GrossDelG, Table 2], in connection with the existence of extraspecial parabolic subgroups as in [Reference RöhrleRöh] or [Reference GaribaldiGar09, Section 12], or from groups with a
$\ne 2, 3$
, FT systems have been studied in this century in [Reference ClercCl], [Reference HeleniusHel], [Reference KrutelevichKr07], [Reference SpringerSp06], and [Reference Borsten, Duff, Ferrara, Marrani and RubensBDFMR] to name a few. They arise naturally in the context of the bottom row of the magic triangle from [Reference Deligne and GrossDelG, Table 2], in connection with the existence of extraspecial parabolic subgroups as in [Reference RöhrleRöh] or [Reference GaribaldiGar09, Section 12], or from groups with a
![]() $\mathsf {B}\mathsf {C}_1$
grading [Reference Gross and GaribaldiGrG, p. 995]. For every Albert F-algebra J, the group scheme
$\mathsf {B}\mathsf {C}_1$
grading [Reference Gross and GaribaldiGrG, p. 995]. For every Albert F-algebra J, the group scheme
![]() $\mathbf {Aut}(Q(J))$
is isotropic (see, for example [Reference SpringerSp06, Lemma 5.6(i)]). Yet there exist strongly inner groups of type
$\mathbf {Aut}(Q(J))$
is isotropic (see, for example [Reference SpringerSp06, Lemma 5.6(i)]). Yet there exist strongly inner groups of type
![]() $\mathsf {E}_7$
that are anisotropic, see [Reference TitsT, 3.1] or [Reference GaribaldiGar09, Appendix A], and therefore, there exist FT systems Q that are not isomorphic to
$\mathsf {E}_7$
that are anisotropic, see [Reference TitsT, 3.1] or [Reference GaribaldiGar09, Appendix A], and therefore, there exist FT systems Q that are not isomorphic to
![]() $Q(J)$
for any J. A construction that produces all FT systems can be obtained by considering a subgroup
$Q(J)$
for any J. A construction that produces all FT systems can be obtained by considering a subgroup
![]() $\mathbf {Isom}(J) \rtimes \mu _4$
of
$\mathbf {Isom}(J) \rtimes \mu _4$
of
![]() $\mathbf {Aut}(Q(J))$
, which leads to a surjection
$\mathbf {Aut}(Q(J))$
, which leads to a surjection
![]() $H^1(F, \mathbf {Isom}(J) \rtimes \mu _4) \to H^1(F, \mathbf {Aut}(Q(J)))$
(see [Reference GaribaldiGar09, 12.13], [Reference GaribaldiGar01, Lemma 4.15] or [Reference SpringerSp06, Section 4]).
$H^1(F, \mathbf {Isom}(J) \rtimes \mu _4) \to H^1(F, \mathbf {Aut}(Q(J)))$
(see [Reference GaribaldiGar09, 12.13], [Reference GaribaldiGar01, Lemma 4.15] or [Reference SpringerSp06, Section 4]).
18 Exceptional groups over
 $\mathbb {Z}$
$\mathbb {Z}$
We now record explicit descriptions of the isomorphism classes of semisimple affine group schemes over
![]() $\mathbb {Z}$
of types
$\mathbb {Z}$
of types
![]() $\mathsf {F}_4$
,
$\mathsf {F}_4$
,
![]() $\mathsf {G}_2$
,
$\mathsf {G}_2$
,
![]() $\mathsf {E}_6$
, and
$\mathsf {E}_6$
, and
![]() $\mathsf {E}_7$
.
$\mathsf {E}_7$
.
There are four such group schemes of type
![]() $\mathsf {F}_4$
, namely,
$\mathsf {F}_4$
, namely,
![]() $\mathbf {Aut}(J)$
for each of the four Albert
$\mathbf {Aut}(J)$
for each of the four Albert
![]() $\mathbb {Z}$
-algebras listed in Theorem 14.3(b). The proof of this fact is intertwined with the proof of that theorem. Similarly, there are two such group schemes of type
$\mathbb {Z}$
-algebras listed in Theorem 14.3(b). The proof of this fact is intertwined with the proof of that theorem. Similarly, there are two such group schemes of type
![]() $\mathsf {G}_2$
, namely,
$\mathsf {G}_2$
, namely,
![]() $\mathbf {Aut}(C)$
for
$\mathbf {Aut}(C)$
for
![]() $C = \operatorname {\mathrm {Zor}}(\mathbb {Z})$
or
$C = \operatorname {\mathrm {Zor}}(\mathbb {Z})$
or
![]() $\mathcal {O}$
.
$\mathcal {O}$
.
Proposition 18.1. For
![]() $R = \mathbb {Z}$
,
$R = \mathbb {Z}$
,
![]() $\mathbb {R}$
or a number field with a unique real embedding, and
$\mathbb {R}$
or a number field with a unique real embedding, and
![]() $J_i = \operatorname {\mathrm {Her}}_3(C_i)$
for
$J_i = \operatorname {\mathrm {Her}}_3(C_i)$
for
![]() $C_0 = \operatorname {\mathrm {Zor}}(R)$
and
$C_0 = \operatorname {\mathrm {Zor}}(R)$
and
![]() $C_1 = \mathcal {O} \otimes R$
:
$C_1 = \mathcal {O} \otimes R$
:
-
1. there are exactly two isomorphism classes of R-forms of the cubic norm on
 $J_0$
, namely,
$J_0$
, namely,
 $N_{J_i}$
for
$N_{J_i}$
for
 $i = 0, 1$
.
$i = 0, 1$
. -
2. there are exactly two isomorphism classes of FT systems over R, namely,
 $Q(J_i)$
for
$Q(J_i)$
for
 $i = 0, 1$
.
$i = 0, 1$
.
Proof. For
![]() $n = 6$
or 7, put
$n = 6$
or 7, put
![]() $E_n$
for the semisimple simply connected Chevalley group scheme over
$E_n$
for the semisimple simply connected Chevalley group scheme over
![]() $\mathbb {Z}$
of type
$\mathbb {Z}$
of type
![]() $\mathsf {E}_n$
. The set
$\mathsf {E}_n$
. The set
![]() $H^1(\mathbb {R}, E_n)$
has two elements (see [Reference Borovoi and EvenorBorE], [Reference Borovoi and TimashevBorT, esp. Section 15] or [Reference Adams and TaïbiAdT, Table 3]). For F a number field with a unique real embedding, the map
$H^1(\mathbb {R}, E_n)$
has two elements (see [Reference Borovoi and EvenorBorE], [Reference Borovoi and TimashevBorT, esp. Section 15] or [Reference Adams and TaïbiAdT, Table 3]). For F a number field with a unique real embedding, the map
![]() $H^1(F, E_n) \to H^1(\mathbb {R}, E_n)$
is a bijection, a fact we have already used in Example 11.2.
$H^1(F, E_n) \to H^1(\mathbb {R}, E_n)$
is a bijection, a fact we have already used in Example 11.2.
By [Reference ConradConrad, Remark 4.8],
![]() $\mathbb {Z}$
forms of absolutely simple and simply connected
$\mathbb {Z}$
forms of absolutely simple and simply connected
![]() $\mathbb {Q}$
-group schemes are purely inner forms, that is, in this case they are obtained by twisting
$\mathbb {Q}$
-group schemes are purely inner forms, that is, in this case they are obtained by twisting
![]() $E_n$
by a class
$E_n$
by a class
![]() $\xi \in H^1(\mathbb {Z}, E_n)$
. Now the compact real form of type
$\xi \in H^1(\mathbb {Z}, E_n)$
. Now the compact real form of type
![]() $\mathsf {E}_n$
is not a pure inner form, so
$\mathsf {E}_n$
is not a pure inner form, so
![]() $(E_n)_{\xi } \times \mathbb {R}$
is not compact for all
$(E_n)_{\xi } \times \mathbb {R}$
is not compact for all
![]() $\xi \in H^1(\mathbb {Z}, E_n)$
. Therefore, the natural map
$\xi \in H^1(\mathbb {Z}, E_n)$
. Therefore, the natural map
![]() $H^1(\mathbb {Z}, E_n) \to H^1(\mathbb {Q}, E_n)$
is a bijection by [Reference HarderHa67, Satz 4.2.4].
$H^1(\mathbb {Z}, E_n) \to H^1(\mathbb {Q}, E_n)$
is a bijection by [Reference HarderHa67, Satz 4.2.4].
We have observed that the set
![]() $H^1(R, E_n)$
has two elements for each choice of R, and we have already noted that this set is in bijection with the isomorphism classes in (1) for
$H^1(R, E_n)$
has two elements for each choice of R, and we have already noted that this set is in bijection with the isomorphism classes in (1) for
![]() $n = 6$
and (2) for
$n = 6$
and (2) for
![]() $n = 7$
(Theorem 17.4). It suffices to prove that the two exhibited elements are distinct, for which it suffices to consider the case
$n = 7$
(Theorem 17.4). It suffices to prove that the two exhibited elements are distinct, for which it suffices to consider the case
![]() $R = \mathbb {R}$
.
$R = \mathbb {R}$
.
In case (1),
![]() $\operatorname {\mathrm {Her}}_3(\mathcal {O})$
is not split (Example 11.1), so it is not isotopic to
$\operatorname {\mathrm {Her}}_3(\mathcal {O})$
is not split (Example 11.1), so it is not isotopic to
![]() $\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {R}))$
(Cor. 13.4) and the cubic norms on the two algebras are not isomorphic (Corollary 15.4). In case (2), one can invoke Ferrar’s converse to Corollary 17.3. Alternatively, one can use the methods used to calculate
$\operatorname {\mathrm {Her}}_3(\operatorname {\mathrm {Zor}}(\mathbb {R}))$
(Cor. 13.4) and the cubic norms on the two algebras are not isomorphic (Corollary 15.4). In case (2), one can invoke Ferrar’s converse to Corollary 17.3. Alternatively, one can use the methods used to calculate
![]() $H^1(\mathbb {R}, E_n)$
to observe that the nontrivial element of
$H^1(\mathbb {R}, E_n)$
to observe that the nontrivial element of
![]() $H^1(\mathbb {R}, E_7)$
is in the image of
$H^1(\mathbb {R}, E_7)$
is in the image of
![]() $H^1(\mathbb {R}, E_6)$
.
$H^1(\mathbb {R}, E_6)$
.
(Apart from the case
![]() $R = \mathbb {Z}$
, the proposition is well known. Analogous statements for any number field can be deduced from the result over
$R = \mathbb {Z}$
, the proposition is well known. Analogous statements for any number field can be deduced from the result over
![]() $\mathbb {R}$
via Harder’s local-global principle as in Example 11.2, see, for example [Reference FerrarFe76] and [Reference FerrarFe78].)
$\mathbb {R}$
via Harder’s local-global principle as in Example 11.2, see, for example [Reference FerrarFe76] and [Reference FerrarFe78].)
The proof provides the following corollary.
Corollary 18.2. Regarding isomorphism classes of semisimple and simply connected affine group schemes over
![]() $\mathbb {Z}$
:
$\mathbb {Z}$
:
-
1. there are two of type
 $\mathsf {E}_6$
, namely,
$\mathsf {E}_6$
, namely,
 $\mathbf {Isom}(\operatorname {\mathrm {Her}}_3(C))$
and
$\mathbf {Isom}(\operatorname {\mathrm {Her}}_3(C))$
and -
2. there are two of type
 $\mathsf {E}_7$
, namely,
$\mathsf {E}_7$
, namely,
 $\mathbf {Aut}(Q(\operatorname {\mathrm {Her}}_3(C)))$
$\mathbf {Aut}(Q(\operatorname {\mathrm {Her}}_3(C)))$
for
![]() $C = \operatorname {\mathrm {Zor}}(\mathbb {Z})$
or
$C = \operatorname {\mathrm {Zor}}(\mathbb {Z})$
or
![]() $\mathcal {O}$
.
$\mathcal {O}$
.
![]() $\Box $
$\Box $
We have addressed now all the simple types that are usually called “exceptional”, apart from
![]() $\mathsf {E}_8$
. A classification of
$\mathsf {E}_8$
. A classification of
![]() $\mathbb {Z}$
-groups of type
$\mathbb {Z}$
-groups of type
![]() $\mathsf {E}_8$
like Proposition 18.2 appears currently out of reach, because among those group schemes
$\mathsf {E}_8$
like Proposition 18.2 appears currently out of reach, because among those group schemes
![]() $\mathbf {G}$
over
$\mathbf {G}$
over
![]() $\mathbb {Z}$
such that
$\mathbb {Z}$
such that
![]() $\mathbf {G} \times \mathbb {R}$
is the compact group of type
$\mathbf {G} \times \mathbb {R}$
is the compact group of type
![]() $\mathsf {E}_8$
, there are at least 13,935 distinct isomorphism classes [Reference GrossGr, Proposition 5.3]. Among those
$\mathsf {E}_8$
, there are at least 13,935 distinct isomorphism classes [Reference GrossGr, Proposition 5.3]. Among those
![]() $\mathbf {G}$
over
$\mathbf {G}$
over
![]() $\mathbb {Z}$
of type
$\mathbb {Z}$
of type
![]() $\mathsf {E}_8$
such that
$\mathsf {E}_8$
such that
![]() $\mathbf {G} \times \mathbb {R}$
is not compact, the same argument as in the proof of Proposition 18.2 shows that there are two isomorphism classes.
$\mathbf {G} \times \mathbb {R}$
is not compact, the same argument as in the proof of Proposition 18.2 shows that there are two isomorphism classes.
Acknowledgments
We thank the many kind readers who provided suggestions or comments, including Asher Auel, Brian Conrad, Uriya First, Wee Teck Gan, Erhard Neher, Zinovy Reichstein, Ben Williams and anonymous referees. The development of this paper was influenced in various ways by [Reference ConradConrad], even when it is not explicitly cited. The authors have no support or funding to report.
Conflict of Interest
The authors have no conflict of interest to declare.