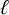1 Introduction
Let k be a field,
![]() $k_s\subset \overline {k}$
be a separable and an algebraic closure of k, respectively,
$k_s\subset \overline {k}$
be a separable and an algebraic closure of k, respectively,
![]() $\ell $
be a prime number invertible in k and X be a smooth projective k-variety. For all integers i and j, we denote by
$\ell $
be a prime number invertible in k and X be a smooth projective k-variety. For all integers i and j, we denote by
![]() $CH^i(X)$
the Chow group of codimension i cycles modulo rational equivalence and by
$CH^i(X)$
the Chow group of codimension i cycles modulo rational equivalence and by
![]() $H^{i}(X,\mathbb {Q}_{\ell }(j))$
the continuous
$H^{i}(X,\mathbb {Q}_{\ell }(j))$
the continuous
![]() $\ell $
-adic cohomology defined by Jannsen [Reference Jannsen17] (or equivalently, the pro-étale cohomology defined by Bhatt and Scholze [Reference Bhatt and Scholze3]). Motivated by the Bloch–Beilinson conjecture on the existence of a certain functorial filtration on
$\ell $
-adic cohomology defined by Jannsen [Reference Jannsen17] (or equivalently, the pro-étale cohomology defined by Bhatt and Scholze [Reference Bhatt and Scholze3]). Motivated by the Bloch–Beilinson conjecture on the existence of a certain functorial filtration on
![]() $CH^i(X)\otimes _{\mathbb {Z}}\mathbb {Q}$
and its relation to the conjectural theory of mixed motives, Jannsen [Reference Jannsen18, Question 2.8] asked the following question.
$CH^i(X)\otimes _{\mathbb {Z}}\mathbb {Q}$
and its relation to the conjectural theory of mixed motives, Jannsen [Reference Jannsen18, Question 2.8] asked the following question.
Question 1.1 (Jannsen).
Suppose that k is of finite type over its prime field. Is the
![]() $\ell $
-adic cycle class map
$\ell $
-adic cycle class map
injective?
A positive answer to Question 1.1 would imply the Bloch–Beilinson conjecture [Reference Jannsen18, Conjecture 2.1] over k. More precisely, consider the Hochschild-Serre spectral sequence in continuous
![]() $\ell $
-adic cohomology [Reference Jannsen17, Corollary 3.4]:
$\ell $
-adic cohomology [Reference Jannsen17, Corollary 3.4]:
The spectral sequence degenerates at the
![]() $E_2$
page, and so gives a filtration
$E_2$
page, and so gives a filtration
where
![]() $F^p/F^{p+1}\simeq H^p(k,H^{2i-p}(X_{k_s},\mathbb {Q}_{\ell }(i)))$
for all
$F^p/F^{p+1}\simeq H^p(k,H^{2i-p}(X_{k_s},\mathbb {Q}_{\ell }(i)))$
for all
![]() $p\geq 0$
. If Question 1.1 had a positive answer, then the inverse image of
$p\geq 0$
. If Question 1.1 had a positive answer, then the inverse image of
![]() $F^{\cdot }$
would be a filtration on
$F^{\cdot }$
would be a filtration on
![]() $CH^i(X)$
with all properties predicted by Bloch and Beilinson, proving the Bloch–Beilinson conjecture (see [Reference Jannsen18, Lemma 2.7]).
$CH^i(X)$
with all properties predicted by Bloch and Beilinson, proving the Bloch–Beilinson conjecture (see [Reference Jannsen18, Lemma 2.7]).
Of course, there is no reason to expect Question 1.1 to have an affirmative answer over an arbitrary field. For example, if k is algebraically closed, the kernel of the cycle class map is the group of homologically trivial cycles modulo rational equivalence, and it is often nontrivial: in particular, the cycle class map factors through algebraic equivalence. However, the situation when k is of finite type over its prime field is very different. Indeed, in this case, Jannsen observed that, as a consequence of the Mordell-Weil theorem, the integral codimension
![]() $1$
cycle class map
$1$
cycle class map
![]() $\operatorname {Pic}(X)\otimes _{\mathbb {Z}}\mathbb {Z}_{\ell }\to H^2(X,\mathbb {Z}_\ell (1))$
is injective (see [Reference Jannsen17, Remark 6.15 (a)]). This naturally leads to the following variant of Jannsen’s question.
$\operatorname {Pic}(X)\otimes _{\mathbb {Z}}\mathbb {Z}_{\ell }\to H^2(X,\mathbb {Z}_\ell (1))$
is injective (see [Reference Jannsen17, Remark 6.15 (a)]). This naturally leads to the following variant of Jannsen’s question.
Question 1.2. Suppose that k is of finite type over its prime field. Is the
![]() $\ell $
-adic cycle class map
$\ell $
-adic cycle class map
injective?
As noted by Jannsen, Question 1.2 has an affirmative answer for
![]() $i=1$
. Question 1.2 is also implicit in work of Saito [Reference Saito36], who obtained some positive results for
$i=1$
. Question 1.2 is also implicit in work of Saito [Reference Saito36], who obtained some positive results for
![]() $i=2$
. Colliot-Thélène–Sansuc–Soulé [Reference Colliot-Thélène, Sansuc and Soulé12] showed that the
$i=2$
. Colliot-Thélène–Sansuc–Soulé [Reference Colliot-Thélène, Sansuc and Soulé12] showed that the
![]() $\ell $
-adic cycle class map is injective on torsion when
$\ell $
-adic cycle class map is injective on torsion when
![]() $i=2$
and the field k is finite.
$i=2$
and the field k is finite.
Question 1.2 fits into a constellation of conjectural integral refinements of well-known rational cycle conjectures. These questions go back at least to Totaro [Reference Totaro46], who suggested that certain Lefschetz-hyperplane properties for Chow groups, originally conjectured rationally by Hartshorne, Nori and Paranjape, should also hold for integral Chow groups. Totaro also showed that Nori connectivity for Chow groups fails on torsion cycles. Later, Soulé–Voisin [Reference Soulé and Voisin42] showed that Voevodsky’s smash nilpotence conjecture fails integrally.
In contrast to these negative results, Schreieder [Reference Schreieder38] recently proved that some aspects of the rational conjectures hold in fact integrally. For example, Schreieder proved a torsion analogue of a certain conjecture of Jannsen, asserting that cycles in the kernel of the Abel-Jacobi map have coniveau one (see [Reference Schreieder38, Corollary 1.3]). In his talk at the conference “Géométrie Algébrique en l’honneur de Claire Voisin,” held in May 2022 in Paris, he used this result to motivate the general and natural question of to which extent rational cycle conjectures hold integrally, and in particular, Question 1.2.
The purpose of the present work is to show that Question 1.2 has a negative answer in general. We offer examples of very different natures: topological (Atiyah–Hirzebruch-style approximations of classifying spaces), geometric (products of a Kummer threefold and an elliptic curve) and arithmetic (quadrics, norm varieties). As we explain below, our examples exhibit new and interesting behaviour of the coniveau filtration on Chow groups and of Schreieder’s transcendental Abel-Jacobi map over finitely generated fields.
Theorem 1.3 (Theorem 2.3).
There exist a finite field (respectively, a number field) k and a smooth complete intersection
![]() $Y\subset \mathbb {P}^N_k$
of dimension
$Y\subset \mathbb {P}^N_k$
of dimension
![]() $15$
with a free action of a finite
$15$
with a free action of a finite
![]() $2$
-group G, such that, letting
$2$
-group G, such that, letting
![]() , the cycle class map
, the cycle class map
is not injective.
The aforementioned result of Colliot-Thélène–Sansuc–Soulé [Reference Colliot-Thélène, Sansuc and Soulé12] shows that
![]() $3$
is the least possible codimension in which one can find a torsion counterexample over a finite field.
$3$
is the least possible codimension in which one can find a torsion counterexample over a finite field.
The dimension of the examples of Theorem 1.3 is quite large. The following theorem yields examples of smaller dimension over a number field.
Theorem 1.4 (Theorem 4.3).
There exist a number field k and a fourfold product
![]() $X=Y\times E$
over k, where Y is a Kummer threefold and E is an elliptic curve, such that the cycle class map
$X=Y\times E$
over k, where Y is a Kummer threefold and E is an elliptic curve, such that the cycle class map
is not injective.
The examples of Theorem 1.4 are the counterexamples of smallest dimension that we could find over number fields. Over a field of transcendence degree
![]() $1$
over
$1$
over
![]() $\mathbb {Q}$
, we provide examples of one dimension lower, in one codimension lower. Recall that a number field is said to be totally imaginary if it admits no real places.
$\mathbb {Q}$
, we provide examples of one dimension lower, in one codimension lower. Recall that a number field is said to be totally imaginary if it admits no real places.
Theorem 1.5 (Theorem 6.3).
Let k be a totally imaginary number field and
![]() $k(t)$
be a purely transcendental extension of k of transcendence degree
$k(t)$
be a purely transcendental extension of k of transcendence degree
![]() $1$
. There exists a smooth quadric hypersurface
$1$
. There exists a smooth quadric hypersurface
![]() $X\subset \mathbb {P}^4_{k(t)}$
, such that the cycle class map
$X\subset \mathbb {P}^4_{k(t)}$
, such that the cycle class map
is not injective.
We also show that, if
![]() $\ell $
is an odd prime invertible in k, there exists a norm variety X of dimension
$\ell $
is an odd prime invertible in k, there exists a norm variety X of dimension
![]() $\ell ^2-1$
over
$\ell ^2-1$
over
![]() $k(t)$
, such that
$k(t)$
, such that
![]() $\operatorname {\mathrm {cl}}\colon CH^2(X)[\ell ]\rightarrow H^4(X,\mathbb {Z}_\ell (2))$
is not injective. Thus, Question 1.2 has a negative answer for all prime numbers
$\operatorname {\mathrm {cl}}\colon CH^2(X)[\ell ]\rightarrow H^4(X,\mathbb {Z}_\ell (2))$
is not injective. Thus, Question 1.2 has a negative answer for all prime numbers
![]() $\ell $
.
$\ell $
.
We now explain the relation of our examples to Schreieder’s results on the coniveau filtration on Chow groups. By now, we have a good understanding of the filtration over the complex numbers, especially for codimension
![]() $\leq 3$
(see, for example, [Reference Schreieder38, Corollary 1.2]). Our examples show that this filtration is still interesting when k is of finite type over its prime field. We also relate our examples to the transcendental Abel-Jacobi map on torsion cycles constructed by Schreieder [Reference Schreieder38, Section 7.5].
$\leq 3$
(see, for example, [Reference Schreieder38, Corollary 1.2]). Our examples show that this filtration is still interesting when k is of finite type over its prime field. We also relate our examples to the transcendental Abel-Jacobi map on torsion cycles constructed by Schreieder [Reference Schreieder38, Section 7.5].
Remark 1.6. We denote by
![]() $N^{\cdot }CH^i(X)$
the coniveau filtration on Chow groups [Reference Schreieder38, Section 1.1], and by
$N^{\cdot }CH^i(X)$
the coniveau filtration on Chow groups [Reference Schreieder38, Section 1.1], and by
![]() $H^i_{j,\operatorname {nr}}(X,-)$
Schreieder’s refined unramified cohomology [Reference Schreieder38, Section 5], which for
$H^i_{j,\operatorname {nr}}(X,-)$
Schreieder’s refined unramified cohomology [Reference Schreieder38, Section 5], which for
![]() $j=0$
coincides with the ordinary unramified cohomology:
$j=0$
coincides with the ordinary unramified cohomology:
![]() $H^i_{0,\operatorname {nr}}=H^i_{\operatorname {nr}}$
. In the following, we assume that k is of finite type over its prime field.
$H^i_{0,\operatorname {nr}}=H^i_{\operatorname {nr}}$
. In the following, we assume that k is of finite type over its prime field.
(a) We have
![]() $N^{i-1}CH^i(X)\otimes _{\mathbb {Z}}{\mathbb {Z}_\ell }=0$
for all smooth projective k-varieties X by Jannsen’s result (see [Reference Schreieder38, Lemma 7.5(2)]). The examples of Theorem 1.5 show that
$N^{i-1}CH^i(X)\otimes _{\mathbb {Z}}{\mathbb {Z}_\ell }=0$
for all smooth projective k-varieties X by Jannsen’s result (see [Reference Schreieder38, Lemma 7.5(2)]). The examples of Theorem 1.5 show that
![]() $N^{i-2}CH^{i}(X)\otimes _{\mathbb {Z}} \mathbb {Z}_{\ell }$
can be nonzero for
$N^{i-2}CH^{i}(X)\otimes _{\mathbb {Z}} \mathbb {Z}_{\ell }$
can be nonzero for
![]() $i=2$
(in this case,
$i=2$
(in this case,
![]() $N^{0}CH^{2}(X)\otimes _{\mathbb {Z}}\mathbb {Z}_{\ell }$
is exactly the kernel of the cycle class map). One can further analyse the torsion part of the stage of the filtration on the examples using the transcendental Abel-Jacobi map, and [Reference Schreieder38, Corollary 9.5, Proposition 7.16] yields
$N^{0}CH^{2}(X)\otimes _{\mathbb {Z}}\mathbb {Z}_{\ell }$
is exactly the kernel of the cycle class map). One can further analyse the torsion part of the stage of the filtration on the examples using the transcendental Abel-Jacobi map, and [Reference Schreieder38, Corollary 9.5, Proposition 7.16] yields
In other words, there is a cohomology class in
![]() $H^3(X,\mathbb {Q}_2/\mathbb {Z}_2(2))$
of coniveau
$H^3(X,\mathbb {Q}_2/\mathbb {Z}_2(2))$
of coniveau
![]() $1$
, which lifts to a rational class but not to a rational class of coniveau
$1$
, which lifts to a rational class but not to a rational class of coniveau
![]() $1$
.
$1$
.
(b) By [Reference Schreieder38, Theorem 1.8], the kernel of the cycle class map is given by
Question 1.1 asks whether this group is torsion. Our examples of Theorems 1.3, 1.4 and 1.5 show that it can be nonzero for
![]() $i=2,3$
. In the case
$i=2,3$
. In the case
![]() $i=2$
, we get an explicit statement on ordinary unramified cohomology: the examples of Theorem 1.5 have an unramified class of degree
$i=2$
, we get an explicit statement on ordinary unramified cohomology: the examples of Theorem 1.5 have an unramified class of degree
![]() $3$
which does not extend to a class on all of X. In fact, using a restriction-corestriction argument, one sees that in this case, the inclusion
$3$
which does not extend to a class on all of X. In fact, using a restriction-corestriction argument, one sees that in this case, the inclusion
has cokernel of finite torsion order
![]() $>1$
, a phenomenon that does not seem to have been observed before (in contrast,
$>1$
, a phenomenon that does not seem to have been observed before (in contrast,
![]() $H^3_{\operatorname {nr}}(X,\mathbb {Z}_2(2))$
is torsion-free and
$H^3_{\operatorname {nr}}(X,\mathbb {Z}_2(2))$
is torsion-free and
![]() $H^3(k,\mathbb {Z}_2(2))$
is a direct summand of
$H^3(k,\mathbb {Z}_2(2))$
is a direct summand of
![]() $H^3_{\operatorname {nr}}(X,\mathbb {Z}_2(2))$
if
$H^3_{\operatorname {nr}}(X,\mathbb {Z}_2(2))$
if
![]() $X(k)\neq \emptyset $
).
$X(k)\neq \emptyset $
).
(c) In our setting, Schreieder’s transcendental Abel-Jacobi map is of the form:
![]() $\lambda _{\text {tr}}\colon CH^{i}_{0}(X)\{\ell \}\rightarrow H^{2i-1}(X,\mathbb {Q}_{\ell }/\mathbb {Z}_{\ell }(i))/N^{i-1}H^{2i-1}(X,\mathbb {Q}_{\ell }(i))$
, where
$\lambda _{\text {tr}}\colon CH^{i}_{0}(X)\{\ell \}\rightarrow H^{2i-1}(X,\mathbb {Q}_{\ell }/\mathbb {Z}_{\ell }(i))/N^{i-1}H^{2i-1}(X,\mathbb {Q}_{\ell }(i))$
, where
![]() $CH^{i}_{0}(X)\{\ell \}$
is the kernel of
$CH^{i}_{0}(X)\{\ell \}$
is the kernel of
![]() $\operatorname {\mathrm {cl}}\colon CH^{i}(X)\{\ell \}\rightarrow H^{2i}(X,\mathbb {Z}_{\ell }(i))$
. For
$\operatorname {\mathrm {cl}}\colon CH^{i}(X)\{\ell \}\rightarrow H^{2i}(X,\mathbb {Z}_{\ell }(i))$
. For
![]() $i=2$
, the transcendental Abel-Jacobi map is injective by [Reference Schreieder38, Corollary 9.5]. In particular, the torsion cycles in the examples of Theorem 1.5 do not lie in the kernel of
$i=2$
, the transcendental Abel-Jacobi map is injective by [Reference Schreieder38, Corollary 9.5]. In particular, the torsion cycles in the examples of Theorem 1.5 do not lie in the kernel of
![]() $\lambda _{\text {tr}}$
. This also shows that
$\lambda _{\text {tr}}$
. This also shows that
![]() $\lambda _{\text {tr}}$
can be nonzero. In contrast, Theorems 1.3 and 1.4 provide examples where
$\lambda _{\text {tr}}$
can be nonzero. In contrast, Theorems 1.3 and 1.4 provide examples where
![]() $\lambda _{\text {tr}}$
is not injective for
$\lambda _{\text {tr}}$
is not injective for
![]() $i=3$
(see Remark 3.3).
$i=3$
(see Remark 3.3).
We now comment on the proofs of the main theorems. In view of the discussion around Question 1.1, it is natural to approach Question 1.2 by considering the filtration
![]() $F^{\cdot }$
on
$F^{\cdot }$
on
![]() $H^{2i}(X,\mathbb {Z}_\ell (i))$
induced by the Hochschild-Serre spectral sequence
$H^{2i}(X,\mathbb {Z}_\ell (i))$
induced by the Hochschild-Serre spectral sequence
We start with a nonzero torsion cycle
![]() $\alpha \in CH^i(X)$
(producing such examples is generally quite difficult) and try to show that
$\alpha \in CH^i(X)$
(producing such examples is generally quite difficult) and try to show that
![]() $\operatorname {\mathrm {cl}}(\alpha )\in F^p$
for all
$\operatorname {\mathrm {cl}}(\alpha )\in F^p$
for all
![]() $p\geq 0$
. To show that
$p\geq 0$
. To show that
![]() $\operatorname {\mathrm {cl}}(\alpha )\in F^1$
, we only need to show that
$\operatorname {\mathrm {cl}}(\alpha )\in F^1$
, we only need to show that
![]() $\operatorname {\mathrm {cl}}(\alpha )$
is geometrically trivial, but the subsequent steps of the filtration are more difficult because the groups appearing in the spectral sequence are typically huge and the image of
$\operatorname {\mathrm {cl}}(\alpha )$
is geometrically trivial, but the subsequent steps of the filtration are more difficult because the groups appearing in the spectral sequence are typically huge and the image of
![]() $\operatorname {\mathrm {cl}}(\alpha )\in F^p/F^{p+1}$
often seems hard to compute (see [Reference Jannsen19] for the case
$\operatorname {\mathrm {cl}}(\alpha )\in F^p/F^{p+1}$
often seems hard to compute (see [Reference Jannsen19] for the case
![]() $p=2$
). In the examples used to prove Theorems 1.3 and 1.5, we get around this by showing that all
$p=2$
). In the examples used to prove Theorems 1.3 and 1.5, we get around this by showing that all
![]() $F^p/F^{p+1}$
are torsion free, which forces
$F^p/F^{p+1}$
are torsion free, which forces
![]() $\operatorname {\mathrm {cl}}(\alpha )=0$
.
$\operatorname {\mathrm {cl}}(\alpha )=0$
.
Theorem 1.4 lies deeper. A key result (Proposition 3.1), relating injectivity of the
![]() $\ell $
-adic cycle class map to that of Bloch’s map, reduces Theorem 1.4 to finding fourfold examples defined over a number field where the Deligne cycle class map is not injective on torsion in codimension
$\ell $
-adic cycle class map to that of Bloch’s map, reduces Theorem 1.4 to finding fourfold examples defined over a number field where the Deligne cycle class map is not injective on torsion in codimension
![]() $3$
. We then achieve this in two steps: a result of Bloch–Esnault yields examples defined over a number field with nonvanishing fourth unramified cohomology group
$3$
. We then achieve this in two steps: a result of Bloch–Esnault yields examples defined over a number field with nonvanishing fourth unramified cohomology group
![]() $H^4_{\operatorname {\mathrm {nr}}}(X_{\mathbb {C}},\mathbb {Q}_\ell /\mathbb {Z}_\ell (3))$
, where, with extra care, one can find such examples with a small Chow group of zero-cycles; then using the Bloch–Kato conjecture and a result of Voisin and Ma relating
$H^4_{\operatorname {\mathrm {nr}}}(X_{\mathbb {C}},\mathbb {Q}_\ell /\mathbb {Z}_\ell (3))$
, where, with extra care, one can find such examples with a small Chow group of zero-cycles; then using the Bloch–Kato conjecture and a result of Voisin and Ma relating
![]() $H^4_{\operatorname {\mathrm {nr}}}(X_{\mathbb {C}},\mathbb {Q}_\ell / \mathbb {Z}_\ell (3))$
to the kernel of the Deligne cycle class map on torsion in codimension
$H^4_{\operatorname {\mathrm {nr}}}(X_{\mathbb {C}},\mathbb {Q}_\ell / \mathbb {Z}_\ell (3))$
to the kernel of the Deligne cycle class map on torsion in codimension
![]() $3$
, one deduces the desired noninjectivity. The construction is inspired by the work of Diaz.
$3$
, one deduces the desired noninjectivity. The construction is inspired by the work of Diaz.
Our work leads us to the following questions.
Question 1.7. (a) Is there a smooth projective d-dimensional variety X over a field of finite type over its prime field, such that the
![]() $\ell $
-adic map
$\ell $
-adic map
![]() $\operatorname {\mathrm {cl}}\colon CH^d(X)\otimes _{\mathbb {Z}}\mathbb {Z}_{\ell }\to H^{2d}(X,\mathbb {Z}_{\ell }(d))$
is not injective?Footnote
1
$\operatorname {\mathrm {cl}}\colon CH^d(X)\otimes _{\mathbb {Z}}\mathbb {Z}_{\ell }\to H^{2d}(X,\mathbb {Z}_{\ell }(d))$
is not injective?Footnote
1
(b) Let i be either
![]() $2$
or
$2$
or
![]() $3$
. Is there a smooth projective threefold over a number field k, such that the
$3$
. Is there a smooth projective threefold over a number field k, such that the
![]() $\ell $
-adic map
$\ell $
-adic map
![]() $\operatorname {\mathrm {cl}}\colon CH^i(X)\otimes _{\mathbb {Z}}\mathbb {Z}_{\ell }\to H^{2i}(X,\mathbb {Z}_{\ell }(i))$
is not injective? What happens over
$\operatorname {\mathrm {cl}}\colon CH^i(X)\otimes _{\mathbb {Z}}\mathbb {Z}_{\ell }\to H^{2i}(X,\mathbb {Z}_{\ell }(i))$
is not injective? What happens over
![]() $k=\mathbb {Q}$
?
$k=\mathbb {Q}$
?
The paper is organised as follows. In Section 2, we prove Theorem 1.3. In Section 3, we prove a key result (Proposition 3.1), relating the injectivity of the
![]() $\ell $
-adic cycle class map to that of Bloch’s map, which is useful in Sections 4 and 5. As first application, we give a second proof of Theorem 1.3. In Section 4, we prove Theorem 1.4. In Section 5, we construct further examples in codimension
$\ell $
-adic cycle class map to that of Bloch’s map, which is useful in Sections 4 and 5. As first application, we give a second proof of Theorem 1.3. In Section 4, we prove Theorem 1.4. In Section 5, we construct further examples in codimension
![]() $3$
using nontorsion type counterexamples to the integral Hodge and Tate conjectures. Finally, in Section 6, we prove Theorem 1.5.
$3$
using nontorsion type counterexamples to the integral Hodge and Tate conjectures. Finally, in Section 6, we prove Theorem 1.5.
Notation
If k is a field, we write
![]() $H^i(k,-)$
for continuous Galois cohomology. If X is a smooth projective k-variety, we write
$H^i(k,-)$
for continuous Galois cohomology. If X is a smooth projective k-variety, we write
![]() $H^i(X,-)$
for the continuous étale cohomology, as defined by Jannsen [Reference Jannsen17],
$H^i(X,-)$
for the continuous étale cohomology, as defined by Jannsen [Reference Jannsen17],
![]() $CH^i(X)$
for the Chow group of codimension i cycles modulo rational equivalence and
$CH^i(X)$
for the Chow group of codimension i cycles modulo rational equivalence and
![]() $\operatorname {\mathrm {cl}}$
for the cycle class map in continuous
$\operatorname {\mathrm {cl}}$
for the cycle class map in continuous
![]() $\ell $
-adic cohomology; when k is algebraically closed, we write
$\ell $
-adic cohomology; when k is algebraically closed, we write
![]() $\lambda $
for Bloch’s map. If
$\lambda $
for Bloch’s map. If
![]() $k=\mathbb {C}$
, we denote by
$k=\mathbb {C}$
, we denote by
![]() $H^i_{\mathcal {D}}(X,\mathbb {Z}(j))$
the Deligne cohomology group and by
$H^i_{\mathcal {D}}(X,\mathbb {Z}(j))$
the Deligne cohomology group and by
![]() $\operatorname {\mathrm {cl}}_{\mathcal D}$
the Deligne cycle class map; for
$\operatorname {\mathrm {cl}}_{\mathcal D}$
the Deligne cycle class map; for
![]() $A\in \{\mathbb {Z},\mathbb {Q}/\mathbb {Z},\mathbb {Z}/2\}$
, we denote by
$A\in \{\mathbb {Z},\mathbb {Q}/\mathbb {Z},\mathbb {Z}/2\}$
, we denote by
![]() $H^i_{\operatorname {nr}}(X,A)$
the i-th unramified cohomology group.
$H^i_{\operatorname {nr}}(X,A)$
the i-th unramified cohomology group.
For an abelian group A, an integer
![]() $n\geq 1$
and a prime number
$n\geq 1$
and a prime number
![]() $\ell $
, we denote
$\ell $
, we denote
![]() , by
, by
![]() $A\{\ell \}$
the subgroup of
$A\{\ell \}$
the subgroup of
![]() $\ell $
-primary torsion elements of A, by
$\ell $
-primary torsion elements of A, by
![]() $A_{\operatorname {\mathrm {tors}}}$
the subgroup of torsion elements of A and
$A_{\operatorname {\mathrm {tors}}}$
the subgroup of torsion elements of A and
![]() .
.
2 Proof of Theorem 1.3
In order to prove Theorem 1.3, we will make use of a construction due to Totaro [Reference Totaro46]. Totaro’s construction is stated over the complex numbers but works over an arbitrary field of characteristic zero. It has been generalised to fields of characteristic not
![]() $2$
by Quick [Reference Quick32].
$2$
by Quick [Reference Quick32].
Let
![]() $k_0$
be a field of characteristic different from
$k_0$
be a field of characteristic different from
![]() $2$
. Let H be the Heisenberg group of order
$2$
. Let H be the Heisenberg group of order
![]() $32$
(see [Reference Totaro46, Section 5]), and set
$32$
(see [Reference Totaro46, Section 5]), and set
. We have a group homomorphism
where the map on the right is the Heisenberg representation of H (see [Reference Totaro46, Section 5]) (Totaro works in characteristic zero, but as observed during the proof of [Reference Quick32, Theorem 7.2], the Heisenberg representation is defined over any field of characteristic different from
![]() $2$
). Let
$2$
). Let
![]() $A:\operatorname {SO}_4\to \operatorname {GL}_3$
be the representation given by the composition
$A:\operatorname {SO}_4\to \operatorname {GL}_3$
be the representation given by the composition
and
![]() $B:\operatorname {SO}_4\to \operatorname {GL}_4$
be the natural
$B:\operatorname {SO}_4\to \operatorname {GL}_4$
be the natural
![]() $4$
-dimensional representation of
$4$
-dimensional representation of
![]() $\operatorname {SO}_4$
. Define
$\operatorname {SO}_4$
. Define
let
![]() $c_1\in CH^1(BG)$
be the pullback along the second projection
$c_1\in CH^1(BG)$
be the pullback along the second projection
![]() $\operatorname {pr}_2:G\to \mathbb {Z}/2$
of the first Chern-class of the nontrivial character of
$\operatorname {pr}_2:G\to \mathbb {Z}/2$
of the first Chern-class of the nontrivial character of
![]() $\mathbb {Z}/2$
, and set
$\mathbb {Z}/2$
, and set
We have
![]() $2\alpha =0$
because
$2\alpha =0$
because
![]() $2c_1=0$
.
$2c_1=0$
.
Finally, let V be a G-representation of finite dimension over
![]() $k_0$
,
$k_0$
,
![]() $U\subset V$
be a G-invariant open subscheme of V, such that G acts freely on U and the codimension of
$U\subset V$
be a G-invariant open subscheme of V, such that G acts freely on U and the codimension of
![]() $V-U$
in V is at least
$V-U$
in V is at least
![]() $4$
.
$4$
.
Lemma 2.1. Let
![]() $(k_0)_s$
be a separable closure of
$(k_0)_s$
be a separable closure of
![]() $k_0$
.
$k_0$
.
-
(a) We have
 $\operatorname {\mathrm {cl}}(\alpha _{(k_0)_s})=0$
in
$\operatorname {\mathrm {cl}}(\alpha _{(k_0)_s})=0$
in
 $H^6((U/G)_{(k_0)_s},\mathbb {Z}_2(3))$
.
$H^6((U/G)_{(k_0)_s},\mathbb {Z}_2(3))$
. -
(b) There exists a finite field subextension
 $k_0\subset k\subset (k_0)_s$
, such that
$k_0\subset k\subset (k_0)_s$
, such that
 $\operatorname {\mathrm {cl}}(\alpha _k)=0$
in
$\operatorname {\mathrm {cl}}(\alpha _k)=0$
in
 $H^6((U/G)_k,\mathbb {Z}_2(3))$
.
$H^6((U/G)_k,\mathbb {Z}_2(3))$
.
Proof. Since the codimension of
![]() $V-U$
in V is at least
$V-U$
in V is at least
![]() $4$
, we have
$4$
, we have
(see [Reference Totaro47, Definition 1.2]).
(a) By the invariance of étale cohomology under purely inseparable field extensions, it suffices to show that
![]() $\operatorname {\mathrm {cl}}(\alpha _{\overline {k}_0})=0$
in
$\operatorname {\mathrm {cl}}(\alpha _{\overline {k}_0})=0$
in
![]() $H^6((U/G)_{\overline {k}_0},\mathbb {Z}_2(3))$
, where
$H^6((U/G)_{\overline {k}_0},\mathbb {Z}_2(3))$
, where
![]() $\overline {k}_0$
is an algebraic closure of
$\overline {k}_0$
is an algebraic closure of
![]() $k_0$
containing
$k_0$
containing
![]() $(k_0)_s$
. If
$(k_0)_s$
. If
![]() $k_0=\mathbb {C}$
, the map
$k_0=\mathbb {C}$
, the map
![]() $U/G\to BG$
corresponding to the principal G-bundle
$U/G\to BG$
corresponding to the principal G-bundle
![]() $U\to U/G$
induces an isomorphism
$U\to U/G$
induces an isomorphism
![]() $H^6((U/G)_{\mathbb {C}},\mathbb {Z})\xrightarrow {\sim } H^6(BG,\mathbb {Z})$
, and the cycle class of
$H^6((U/G)_{\mathbb {C}},\mathbb {Z})\xrightarrow {\sim } H^6(BG,\mathbb {Z})$
, and the cycle class of
![]() $\alpha $
in
$\alpha $
in
![]() $H^6(BG,\mathbb {Z})$
is zero as stated in [Reference Totaro46, p. 485], hence, the cycle class of
$H^6(BG,\mathbb {Z})$
is zero as stated in [Reference Totaro46, p. 485], hence, the cycle class of
![]() $\alpha $
in
$\alpha $
in
![]() $H^6((U/G)_{\mathbb {C}},\mathbb {Z})$
vanishes. Since Artin’s comparison isomorphism is compatible with cycle classes in singular and
$H^6((U/G)_{\mathbb {C}},\mathbb {Z})$
vanishes. Since Artin’s comparison isomorphism is compatible with cycle classes in singular and
![]() $\ell $
-adic cohomology, this implies that (a) holds for
$\ell $
-adic cohomology, this implies that (a) holds for
![]() $k_0=\mathbb {C}$
. If
$k_0=\mathbb {C}$
. If
![]() $k_0$
is an arbitrary field of characteristic zero, then (a) follows from the case
$k_0$
is an arbitrary field of characteristic zero, then (a) follows from the case
![]() $k_0=\mathbb {C}$
and the invariance of
$k_0=\mathbb {C}$
and the invariance of
![]() $\ell $
-adic cohomology under extensions of algebraically closed fields. Finally, if
$\ell $
-adic cohomology under extensions of algebraically closed fields. Finally, if
![]() $k_0$
is an arbitrary field of characteristic different from
$k_0$
is an arbitrary field of characteristic different from
![]() $2$
, the arguments of Totaro have been adapted by Quick using étale cobordism (see the proof of [Reference Quick32, Proposition 5.3]). One could also argue more directly via a specialisation argument from the characteristic zero case. This completes the proof of (a).
$2$
, the arguments of Totaro have been adapted by Quick using étale cobordism (see the proof of [Reference Quick32, Proposition 5.3]). One could also argue more directly via a specialisation argument from the characteristic zero case. This completes the proof of (a).
(b) The morphism
![]() $U_{(k_0)_s}\to (U/G)_{(k_0)_s}$
is a Galois G-cover, hence, we have the Hochschild-Serre spectral sequence in
$U_{(k_0)_s}\to (U/G)_{(k_0)_s}$
is a Galois G-cover, hence, we have the Hochschild-Serre spectral sequence in
![]() $\ell $
-adic cohomology
$\ell $
-adic cohomology
Here,
![]() $H^i(G,-)$
denotes group cohomology. Since U is an open subscheme of a vector space whose complement has codimension
$H^i(G,-)$
denotes group cohomology. Since U is an open subscheme of a vector space whose complement has codimension
![]() $\geq 4$
, we have
$\geq 4$
, we have
![]() $H^0(U_{(k_0)_s},\mathbb {Z}_2(3))=\mathbb {Z}_2(3)$
and
$H^0(U_{(k_0)_s},\mathbb {Z}_2(3))=\mathbb {Z}_2(3)$
and
![]() $H^j(U_{(k_0)_s},\mathbb {Z}_2(3))=0$
for all
$H^j(U_{(k_0)_s},\mathbb {Z}_2(3))=0$
for all
![]() $1\leq j\leq 6$
. We deduce that the natural map
$1\leq j\leq 6$
. We deduce that the natural map
![]() $H^i(G,\mathbb {Z}_2(3))\to H^i((U/G)_{(k_0)_s},\mathbb {Z}_2(3))$
is an isomorphism for all
$H^i(G,\mathbb {Z}_2(3))\to H^i((U/G)_{(k_0)_s},\mathbb {Z}_2(3))$
is an isomorphism for all
![]() $1\leq i\leq 6$
. Since the group G is finite, the group
$1\leq i\leq 6$
. Since the group G is finite, the group
is finite for all
![]() $i\geq 1$
, hence
$i\geq 1$
, hence
For every finite field subextension
![]() $k_0\subset k\subset (k_0)_s$
, the Hochschild-Serre spectral sequence in continuous
$k_0\subset k\subset (k_0)_s$
, the Hochschild-Serre spectral sequence in continuous
![]() $\ell $
-adic cohomology
$\ell $
-adic cohomology
yields a filtration
where
![]() $F^i/F^{i+1}$
is a subquotient of
$F^i/F^{i+1}$
is a subquotient of
![]() $H^i(k,H^{6-i}((U/G)_{(k_0)_s},\mathbb {Z}_2(3)))$
. When
$H^i(k,H^{6-i}((U/G)_{(k_0)_s},\mathbb {Z}_2(3)))$
. When
![]() $i=0,1$
,
$i=0,1$
,
![]() $F^i/F^{i+1}$
is even a submodule of
$F^i/F^{i+1}$
is even a submodule of
![]() $H^i(k,H^{6-i}((U/G)_{(k_0)_s},\mathbb {Z}_2(3)))$
.
$H^i(k,H^{6-i}((U/G)_{(k_0)_s},\mathbb {Z}_2(3)))$
.
It is a consequence of [Reference Serre41, I.2.2, Corollary 1] that for all
![]() $i\geq 1$
and all finite continuous
$i\geq 1$
and all finite continuous
![]() $\operatorname {Gal}((k_0)_s/k)$
-modules M, any element of
$\operatorname {Gal}((k_0)_s/k)$
-modules M, any element of
![]() $H^i(k,M)$
is killed by passage to a suitable finite extension of k. Thus, (2.2) implies that for all
$H^i(k,M)$
is killed by passage to a suitable finite extension of k. Thus, (2.2) implies that for all
![]() $1\leq i\leq 6$
, any element of
$1\leq i\leq 6$
, any element of
![]() $H^i(k,H^{6-i}((U/G)_{(k_0)_s},\mathbb {Z}_2(3)))$
vanishes after base change to a suitable finite extension of k. By (a), we know that
$H^i(k,H^{6-i}((U/G)_{(k_0)_s},\mathbb {Z}_2(3)))$
vanishes after base change to a suitable finite extension of k. By (a), we know that
![]() $\operatorname {\mathrm {cl}}(\alpha _{(k_0)_s})=0$
, that is,
$\operatorname {\mathrm {cl}}(\alpha _{(k_0)_s})=0$
, that is,
![]() $\operatorname {\mathrm {cl}}(\alpha )\in F^1$
. Using the fact that
$\operatorname {\mathrm {cl}}(\alpha )\in F^1$
. Using the fact that
![]() $F^i/F^{i+1}$
is a subquotient of
$F^i/F^{i+1}$
is a subquotient of
![]() $H^i(k,H^{6-i}((U/G)_{(k_0)_s},\mathbb {Z}_2(3)))$
, we may now construct finite field extensions
$H^i(k,H^{6-i}((U/G)_{(k_0)_s},\mathbb {Z}_2(3)))$
, we may now construct finite field extensions
such that
![]() $\operatorname {\mathrm {cl}}(\alpha _{k_i})\in F^i$
for all i. In particular,
$\operatorname {\mathrm {cl}}(\alpha _{k_i})\in F^i$
for all i. In particular,
![]() $\operatorname {\mathrm {cl}}(\alpha _{k_7})=0$
, hence,
$\operatorname {\mathrm {cl}}(\alpha _{k_7})=0$
, hence,
![]() $k=k_7$
satisfies the conclusion of the lemma.
$k=k_7$
satisfies the conclusion of the lemma.
Remark 2.2. It is important to note that continuous
![]() $\ell $
-adic cohomology does not commute with inverse limits of schemes, so (b) is not a formal consequence for (a).
$\ell $
-adic cohomology does not commute with inverse limits of schemes, so (b) is not a formal consequence for (a).
Here is a generalised version of Theorem 1.3.
Theorem 2.3. Let
![]() $k_0$
be a field of characteristic different from
$k_0$
be a field of characteristic different from
![]() $2$
. There exist a finite
$2$
. There exist a finite
![]() $2$
-group G, a smooth complete intersection
$2$
-group G, a smooth complete intersection
![]() $Y\subset \mathbb {P}_{k_0}^N$
of dimension
$Y\subset \mathbb {P}_{k_0}^N$
of dimension
![]() $15$
with a free G-action and finite extension
$15$
with a free G-action and finite extension
![]() $k/k_0$
, such that, letting
$k/k_0$
, such that, letting
![]() , the cycle class map
, the cycle class map
is not injective.
Proof. Let Y be a smooth complete intersection of dimension
![]() $15$
over
$15$
over
![]() $k_0$
on which
$k_0$
on which
acts freely, and set
: (see [Reference Serre40, Proposition 15]). Letting G act diagonally on
![]() $Y\times U$
, the projections of
$Y\times U$
, the projections of
![]() $Y\times U$
onto its factors are G-equivariant: we write
$Y\times U$
onto its factors are G-equivariant: we write
![]() $\pi _1\colon (Y\times U)/G\to X$
and
$\pi _1\colon (Y\times U)/G\to X$
and
![]() $\pi _2\colon (Y\times U)/G\to U/G$
for the induced morphisms. We have a commutative diagram
$\pi _2\colon (Y\times U)/G\to U/G$
for the induced morphisms. We have a commutative diagram

The projection
![]() $Y\times V\to Y$
is a G-equivariant vector bundle and the G-action on Y is free, therefore, by descent and Grothendieck’s version of Hilbert’s Theorem 90 (see [Reference Milne28, Proposition III.4.9]), the induced morphism
$Y\times V\to Y$
is a G-equivariant vector bundle and the G-action on Y is free, therefore, by descent and Grothendieck’s version of Hilbert’s Theorem 90 (see [Reference Milne28, Proposition III.4.9]), the induced morphism
![]() $(Y\times V)/G\to X$
is also a vector bundle. Since
$(Y\times V)/G\to X$
is also a vector bundle. Since
![]() $Y\times U\to Y$
is a G-invariant dense open subscheme of the G-equivariant vector bundle
$Y\times U\to Y$
is a G-invariant dense open subscheme of the G-equivariant vector bundle
![]() $Y\times V\to Y$
,
$Y\times V\to Y$
,
![]() $\pi _1$
is a dense open subscheme of a vector bundle. Moreover, since
$\pi _1$
is a dense open subscheme of a vector bundle. Moreover, since
![]() $V-U$
has codimension
$V-U$
has codimension
![]() $\geq 4$
in V, the codimension of the complement
$\geq 4$
in V, the codimension of the complement
![]() $(Y\times U)/G$
inside
$(Y\times U)/G$
inside
![]() $(Y\times V)/G$
is also
$(Y\times V)/G$
is also
![]() $\geq 4$
, hence, by [Reference Jannsen17, Theorem 3.23] and homotopy invariance, the maps
$\geq 4$
, hence, by [Reference Jannsen17, Theorem 3.23] and homotopy invariance, the maps
![]() $\pi _1^*$
are isomorphisms. We get a well-defined element
$\pi _1^*$
are isomorphisms. We get a well-defined element
By Lemma 2.1(b), we have
![]() $\operatorname {\mathrm {cl}}(\beta )=0$
. In order to complete the proof, it remains to show that
$\operatorname {\mathrm {cl}}(\beta )=0$
. In order to complete the proof, it remains to show that
![]() $\beta \neq 0$
.
$\beta \neq 0$
.
Suppose first that
![]() $k=\mathbb {C}$
. Then Totaro showed in [Reference Totaro46] that the class of
$k=\mathbb {C}$
. Then Totaro showed in [Reference Totaro46] that the class of
![]() $\beta $
in the complex cobordism group
$\beta $
in the complex cobordism group
![]() $MU^6(X)\otimes _{MU^*(X)}\mathbb {Z}$
is not zero, hence,
$MU^6(X)\otimes _{MU^*(X)}\mathbb {Z}$
is not zero, hence,
![]() $\beta \neq 0$
. If k is a field of characteristic zero, the rigidity of the
$\beta \neq 0$
. If k is a field of characteristic zero, the rigidity of the
![]() $2$
-torsion subgroup of the Chow group [Reference Lecomte25] implies
$2$
-torsion subgroup of the Chow group [Reference Lecomte25] implies
![]() $\beta _{\overline {k}}\neq 0$
, hence,
$\beta _{\overline {k}}\neq 0$
, hence,
![]() $\beta \neq 0$
. If k has positive characteristic (different from
$\beta \neq 0$
. If k has positive characteristic (different from
![]() $2$
), the arguments of Totaro have been adapted by Quick (see the proof of [Reference Quick32, Proposition 5.3(b)]). We conclude that
$2$
), the arguments of Totaro have been adapted by Quick (see the proof of [Reference Quick32, Proposition 5.3(b)]). We conclude that
![]() $\beta \neq 0$
, as desired.
$\beta \neq 0$
, as desired.
3
 $\ell $
-adic cycle class map and Bloch’s map
$\ell $
-adic cycle class map and Bloch’s map
In this section, we explain the relation between the cycle class map in continuous
![]() $\ell $
-adic cohomology and a certain map defined by Bloch. The main result of this section (Proposition 3.1) will be used to produce counterexamples to Question 1.2 in Sections 4 and 5.
$\ell $
-adic cohomology and a certain map defined by Bloch. The main result of this section (Proposition 3.1) will be used to produce counterexamples to Question 1.2 in Sections 4 and 5.
Let
![]() $k_0$
be a field,
$k_0$
be a field,
![]() $i\geq 0$
be an integer,
$i\geq 0$
be an integer,
![]() $\ell $
be a prime number invertible in
$\ell $
be a prime number invertible in
![]() $k_0$
and X be a smooth projective
$k_0$
and X be a smooth projective
![]() $k_0$
-variety. For every finite extension
$k_0$
-variety. For every finite extension
![]() $k/k_0$
, we have the cycle class map
$k/k_0$
, we have the cycle class map
![]() $\operatorname {\mathrm {cl}}_k\colon CH^i(X_k)\otimes _{\mathbb {Z}}\mathbb {Z}_{\ell }\rightarrow H^{2i}(X_k,\mathbb {Z}_\ell (i))$
and the Bockstein homomorphism
$\operatorname {\mathrm {cl}}_k\colon CH^i(X_k)\otimes _{\mathbb {Z}}\mathbb {Z}_{\ell }\rightarrow H^{2i}(X_k,\mathbb {Z}_\ell (i))$
and the Bockstein homomorphism
It will be important for us that
![]() $CH^i(X_{\overline {k}_0})=\varinjlim _{k/k_0}CH^i(X_k)$
and
$CH^i(X_{\overline {k}_0})=\varinjlim _{k/k_0}CH^i(X_k)$
and
where the direct limits are over all finite extensions
![]() $k/k_{0}$
contained in
$k/k_{0}$
contained in
![]() $\overline {k}_0/k_0$
. Finally, recall that Bloch [Reference Bloch4] (also see [Reference Colliot-Thélène10]) defined a map
$\overline {k}_0/k_0$
. Finally, recall that Bloch [Reference Bloch4] (also see [Reference Colliot-Thélène10]) defined a map
which, for
![]() $\overline {k}_{0}=\mathbb {C}$
, coincides with the Deligne cycle class map on torsion [Reference Bloch4, Proposition 3.7]. Note that
$\overline {k}_{0}=\mathbb {C}$
, coincides with the Deligne cycle class map on torsion [Reference Bloch4, Proposition 3.7]. Note that
![]() $\lambda $
is rigid, that is, it does not change under algebraically closed field extensions, because the rigidity property holds for the torsion part of Chow groups [Reference Lecomte25] and for étale cohomology with torsion coefficients.
$\lambda $
is rigid, that is, it does not change under algebraically closed field extensions, because the rigidity property holds for the torsion part of Chow groups [Reference Lecomte25] and for étale cohomology with torsion coefficients.
Proposition 3.1. The composition
 $$\begin{align*}CH^i(X_{\overline{k}_0}) \{\ell\}\xrightarrow{\lambda}H^{2i-1}(X_{\overline{k}_0},\mathbb{Q}_\ell/\mathbb{Z}_\ell(i)) \xrightarrow{\varinjlim_{k/k_0}\beta_k}\varinjlim_{k/k_0} H^{2i}(X_k,\mathbb{Z}_\ell(i)) \end{align*}$$
$$\begin{align*}CH^i(X_{\overline{k}_0}) \{\ell\}\xrightarrow{\lambda}H^{2i-1}(X_{\overline{k}_0},\mathbb{Q}_\ell/\mathbb{Z}_\ell(i)) \xrightarrow{\varinjlim_{k/k_0}\beta_k}\varinjlim_{k/k_0} H^{2i}(X_k,\mathbb{Z}_\ell(i)) \end{align*}$$
coincides with
![]() $\varinjlim _{k/k_0} \operatorname {\mathrm {cl}}_k$
on torsion. If
$\varinjlim _{k/k_0} \operatorname {\mathrm {cl}}_k$
on torsion. If
![]() $k_{0}$
is of finite type over its prime field,
$k_{0}$
is of finite type over its prime field,
![]() $\varinjlim _{k/k_0}\beta _k$
induces an isomorphism
$\varinjlim _{k/k_0}\beta _k$
induces an isomorphism
 $$\begin{align*}H^{2i-1}(X_{\overline{k}_0},\mathbb{Q}_\ell/\mathbb{Z}_\ell(i))\xrightarrow{\sim}\left(\varinjlim_{k/k_0} H^{2i}(X_k,\mathbb{Z}_\ell(i))\right)\{\ell\}, \end{align*}$$
$$\begin{align*}H^{2i-1}(X_{\overline{k}_0},\mathbb{Q}_\ell/\mathbb{Z}_\ell(i))\xrightarrow{\sim}\left(\varinjlim_{k/k_0} H^{2i}(X_k,\mathbb{Z}_\ell(i))\right)\{\ell\}, \end{align*}$$
hence,
![]() $\varinjlim _{k/k_0}\operatorname {\mathrm {cl}}_k$
is injective on torsion if and only if
$\varinjlim _{k/k_0}\operatorname {\mathrm {cl}}_k$
is injective on torsion if and only if
![]() $\lambda $
is injective.
$\lambda $
is injective.
Remark 3.2. For
![]() $i\in \{1,2,\dim X\}$
,
$i\in \{1,2,\dim X\}$
,
![]() $\lambda $
is injective: the case of
$\lambda $
is injective: the case of
![]() $i=1$
is elementary using the Kummer sequence [Reference Bloch4, Proposition 3.6], the case of
$i=1$
is elementary using the Kummer sequence [Reference Bloch4, Proposition 3.6], the case of
![]() $i=\dim X$
is due to Rojtman [Reference Rojtman33] (see also [Reference Bloch4, Theorem 4.2]) and the case of
$i=\dim X$
is due to Rojtman [Reference Rojtman33] (see also [Reference Bloch4, Theorem 4.2]) and the case of
![]() $i=2$
is a consequence of a theorem of Merkurjev–Suslin [Reference Merkurjev and Suslin27, Section 18]. In these cases, if
$i=2$
is a consequence of a theorem of Merkurjev–Suslin [Reference Merkurjev and Suslin27, Section 18]. In these cases, if
![]() $k_0$
is of finite type over its prime field,
$k_0$
is of finite type over its prime field,
![]() $\varinjlim _{k/k_{0}}\operatorname {\mathrm {cl}}_{k}$
is injective on torsion by Proposition 3.1. For
$\varinjlim _{k/k_{0}}\operatorname {\mathrm {cl}}_{k}$
is injective on torsion by Proposition 3.1. For
![]() $i=1$
, this is also a direct consequence of the observation of Jannsen [Reference Jannsen17, Remark 6.15 (a)] that
$i=1$
, this is also a direct consequence of the observation of Jannsen [Reference Jannsen17, Remark 6.15 (a)] that
![]() $\operatorname {\mathrm {cl}}_k\colon CH^1(X_k)\otimes _{\mathbb {Z}} \mathbb {Z}_\ell \rightarrow H^2(X_k,\mathbb {Z}_\ell (1))$
is injective. Remarkably, the kernel of
$\operatorname {\mathrm {cl}}_k\colon CH^1(X_k)\otimes _{\mathbb {Z}} \mathbb {Z}_\ell \rightarrow H^2(X_k,\mathbb {Z}_\ell (1))$
is injective. Remarkably, the kernel of
![]() $\operatorname {\mathrm {cl}}_k\colon CH^2(X_k)\{\ell \}\rightarrow H^4(X_k,\mathbb {Z}_\ell (2))$
might be nonzero, as we will see in Section 6.
$\operatorname {\mathrm {cl}}_k\colon CH^2(X_k)\{\ell \}\rightarrow H^4(X_k,\mathbb {Z}_\ell (2))$
might be nonzero, as we will see in Section 6.
For
![]() $3\leq i\leq \dim X-1$
, there are several known examples [Reference Rosenschon and Srinivas34, Reference Schoen37, Reference Schreieder39, Reference Soulé and Voisin42, Reference Totaro46, Reference Totaro49] where
$3\leq i\leq \dim X-1$
, there are several known examples [Reference Rosenschon and Srinivas34, Reference Schoen37, Reference Schreieder39, Reference Soulé and Voisin42, Reference Totaro46, Reference Totaro49] where
![]() $\lambda $
is not injective; among them, [Reference Rosenschon and Srinivas34, Reference Schoen37, Reference Schreieder39, Reference Totaro49] even showed that the kernel of
$\lambda $
is not injective; among them, [Reference Rosenschon and Srinivas34, Reference Schoen37, Reference Schreieder39, Reference Totaro49] even showed that the kernel of
![]() $\lambda $
may be infinite. Note that fields of definition for [Reference Rosenschon and Srinivas34, Reference Schoen37, Reference Schreieder39, Reference Soulé and Voisin42, Reference Totaro49] have positive transcendence degree over
$\lambda $
may be infinite. Note that fields of definition for [Reference Rosenschon and Srinivas34, Reference Schoen37, Reference Schreieder39, Reference Soulé and Voisin42, Reference Totaro49] have positive transcendence degree over
![]() $\mathbb {Q}$
, while Totaro’s
$\mathbb {Q}$
, while Totaro’s
![]() $15$
-dimensional examples in [Reference Totaro46] may be defined over
$15$
-dimensional examples in [Reference Totaro46] may be defined over
![]() $\mathbb {Q}$
or
$\mathbb {Q}$
or
![]() $\mathbb {F}_p$
with
$\mathbb {F}_p$
with
![]() $p\neq 2$
. In Section 4, we exhibit the first fourfold examples defined over
$p\neq 2$
. In Section 4, we exhibit the first fourfold examples defined over
![]() $\mathbb {Q}$
where
$\mathbb {Q}$
where
![]() $\lambda $
is not injective over
$\lambda $
is not injective over
![]() $\overline {\mathbb {Q}}$
(
$\overline {\mathbb {Q}}$
(
![]() $4$
is the least possible dimension in which one can find such an example). In Section 5, we give further instances of noninjectivity of
$4$
is the least possible dimension in which one can find such an example). In Section 5, we give further instances of noninjectivity of
![]() $\lambda $
in relation to the integral Hodge and Tate conjectures. Using Proposition 3.1 and the rigidity property of
$\lambda $
in relation to the integral Hodge and Tate conjectures. Using Proposition 3.1 and the rigidity property of
![]() $\lambda $
, all of these provide counterexamples to Question 1.2 over all sufficiently large finite extensions of fields of definition.
$\lambda $
, all of these provide counterexamples to Question 1.2 over all sufficiently large finite extensions of fields of definition.
Proof of Proposition 3.1.
The second assertion follows by observing that if
![]() $k_{0}$
is of finite type over its prime field, then for every finite extension
$k_{0}$
is of finite type over its prime field, then for every finite extension
![]() $k/k_0$
contained in
$k/k_0$
contained in
![]() $\overline {k}_0/k_0$
, the map
$\overline {k}_0/k_0$
, the map
![]() $H^{2i-1}(X_{k},\mathbb {Q}_\ell (i))\rightarrow H^{2i-1}(X_{\overline {k}_0},\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$
is zero, because it factors through
$H^{2i-1}(X_{k},\mathbb {Q}_\ell (i))\rightarrow H^{2i-1}(X_{\overline {k}_0},\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$
is zero, because it factors through
![]() $H^{2i-1}(X_{\overline {k}_0},\mathbb {Q}_\ell (i))^{\operatorname {\mathrm {Gal}}(\overline {k}_0/k)}$
which vanishes by weight reasons.
$H^{2i-1}(X_{\overline {k}_0},\mathbb {Q}_\ell (i))^{\operatorname {\mathrm {Gal}}(\overline {k}_0/k)}$
which vanishes by weight reasons.
It remains to show the first assertion. By construction,
![]() $\lambda $
fits into the commutative diagram:
$\lambda $
fits into the commutative diagram:

where f is the surjection given in [Reference Colliot-Thélène, Sansuc and Soulé12, Proposition 1],
![]() $H^{i-1}(X_{\overline {k}_0},\mathcal {H}(\mathbb {Q}_\ell /\mathbb {Z}_\ell (i)))$
is the
$H^{i-1}(X_{\overline {k}_0},\mathcal {H}(\mathbb {Q}_\ell /\mathbb {Z}_\ell (i)))$
is the
![]() $E^{i-1,i}_2$
term of the Bloch-Ogus spectral sequence [Reference Bloch and Ogus7] and g is the edge homomorphism. Hence, the proof will follow once we show the anticommutativity of the following diagram:
$E^{i-1,i}_2$
term of the Bloch-Ogus spectral sequence [Reference Bloch and Ogus7] and g is the edge homomorphism. Hence, the proof will follow once we show the anticommutativity of the following diagram:

Here,
![]() $H^{i-1}(X_{\overline {k}_0},\mathcal {H}^i(\mathbb {Q}_\ell /\mathbb {Z}_\ell (i)))=\varinjlim _{k/k_0}H^{i-1}(X_{k},\mathcal {H}^i(\mathbb {Q}_{\ell }/\mathbb {Z}_{\ell }(i)))$
, because the Gersten complex of
$H^{i-1}(X_{\overline {k}_0},\mathcal {H}^i(\mathbb {Q}_\ell /\mathbb {Z}_\ell (i)))=\varinjlim _{k/k_0}H^{i-1}(X_{k},\mathcal {H}^i(\mathbb {Q}_{\ell }/\mathbb {Z}_{\ell }(i)))$
, because the Gersten complex of
![]() $\mathcal {H}^i(\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$
on
$\mathcal {H}^i(\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$
on
![]() $X_{\overline {k}_0}$
is the direct limit of Gersten complexes on
$X_{\overline {k}_0}$
is the direct limit of Gersten complexes on
![]() $X_k$
. Hence, the anticommutativity of (3.1) is reduced to showing, for every finite extension
$X_k$
. Hence, the anticommutativity of (3.1) is reduced to showing, for every finite extension
![]() $k/k_0$
and every integer
$k/k_0$
and every integer
![]() $\nu \geq 1$
, the anticommutativity of
$\nu \geq 1$
, the anticommutativity of

To prove that (3.2) anticommutes, we proceed as in the proof of [Reference Colliot-Thélène, Sansuc and Soulé12, Proposition 1]. Recall that each element
![]() $\alpha \in H^{i-1}(X_{k},\mathcal {H}^i(\mu _{l^\nu }^{\otimes i}))$
is represented by a class
$\alpha \in H^{i-1}(X_{k},\mathcal {H}^i(\mu _{l^\nu }^{\otimes i}))$
is represented by a class
![]() $a\in H^{2i-1}_Z(X_k-Z',\mu _{l^\nu }^{\otimes i})$
, where
$a\in H^{2i-1}_Z(X_k-Z',\mu _{l^\nu }^{\otimes i})$
, where
![]() $(Z,Z')$
is a pair of closed subsets of
$(Z,Z')$
is a pair of closed subsets of
![]() $X_k$
of codimension
$X_k$
of codimension
![]() $i-1$
and i, respectively, with
$i-1$
and i, respectively, with
![]() $Z'\subset Z$
, that vanishes under the connecting homomorphism
$Z'\subset Z$
, that vanishes under the connecting homomorphism
![]() $H^{2i-1}_{Z-Z'}(X_k-Z',\mu _{l^\nu }^{\otimes i})\rightarrow H^{2i}_{Z'}(X_k,\mu _{l^\nu }^{\otimes i})$
. We may now associate to the class a two classes
$H^{2i-1}_{Z-Z'}(X_k-Z',\mu _{l^\nu }^{\otimes i})\rightarrow H^{2i}_{Z'}(X_k,\mu _{l^\nu }^{\otimes i})$
. We may now associate to the class a two classes
![]() $b,c\in H^{2i}_Z(X_k,\mathbb {Z}_\ell (i))$
whose images in
$b,c\in H^{2i}_Z(X_k,\mathbb {Z}_\ell (i))$
whose images in
![]() $H^{2i}(X_{k},\mathbb {Z}_{\ell }(i))$
are
$H^{2i}(X_{k},\mathbb {Z}_{\ell }(i))$
are
![]() $\beta _k\circ g(\alpha )$
,
$\beta _k\circ g(\alpha )$
,
![]() $-\operatorname {\mathrm {cl}}_k\circ f(\alpha )$
respectively. The argument is as follows, using the diagram:
$-\operatorname {\mathrm {cl}}_k\circ f(\alpha )$
respectively. The argument is as follows, using the diagram:

Here, the horizontal arrows are from the long exact sequences for cohomology with supports and the vertical arrows are from the long exact sequences for
![]() $H^*_{Z'}(X_k,-)$
,
$H^*_{Z'}(X_k,-)$
,
![]() $H^*_{Z}(X_k,-)$
and
$H^*_{Z}(X_k,-)$
and
![]() $H^*_{Z-Z'}(X_k,-)$
induced by the short exact sequence of inverse systems of abelian sheaves on
$H^*_{Z-Z'}(X_k,-)$
induced by the short exact sequence of inverse systems of abelian sheaves on
![]() $X_{{\acute{\rm e}\text {t}}}$
:
$X_{{\acute{\rm e}\text {t}}}$
:

By the choice on a, there exists
![]() $a_1\in H^{2i-1}_Z(X_k,\mu _{\ell ^\nu }^{\otimes i})$
, such that
$a_1\in H^{2i-1}_Z(X_k,\mu _{\ell ^\nu }^{\otimes i})$
, such that
![]() $j(a_1)=a$
. Set
$j(a_1)=a$
. Set
. Meanwhile, after possibly enlarging
![]() $Z'\subset Z$
, a lifts along p to a class
$Z'\subset Z$
, a lifts along p to a class
![]() $a_2\in H^{2i-1}_{Z-Z'}(X_k-Z',\mathbb {Z}_\ell (i))$
. Indeed, we may assume that:
$a_2\in H^{2i-1}_{Z-Z'}(X_k-Z',\mathbb {Z}_\ell (i))$
. Indeed, we may assume that:
![]() $Z-Z'$
is smooth, thus
$Z-Z'$
is smooth, thus
 $$ \begin{align*} H^{2i-1}_{Z-Z'}(X_k-Z',\mu_{\ell^\nu}^{\otimes i})&=H^{1}(Z-Z', \mu_{\ell^{\nu}}),\\ H^{2i-1}_{Z-Z'}(X_k-Z',\mathbb{Z}_\ell(i))&=H^{1}(Z-Z',\mathbb{Z}_{\ell}(1)) \end{align*} $$
$$ \begin{align*} H^{2i-1}_{Z-Z'}(X_k-Z',\mu_{\ell^\nu}^{\otimes i})&=H^{1}(Z-Z', \mu_{\ell^{\nu}}),\\ H^{2i-1}_{Z-Z'}(X_k-Z',\mathbb{Z}_\ell(i))&=H^{1}(Z-Z',\mathbb{Z}_{\ell}(1)) \end{align*} $$
by [Reference Jannsen17, Theorem 3.17];
![]() $a\in H^{1}(Z-Z', \mu _{\ell ^{\nu }})$
lifts along the composition
$a\in H^{1}(Z-Z', \mu _{\ell ^{\nu }})$
lifts along the composition
where
![]() $\Delta $
is the connecting homomorphism for the short exact sequence of inverse systems of abelian sheaves on
$\Delta $
is the connecting homomorphism for the short exact sequence of inverse systems of abelian sheaves on
![]() $X_{{\acute{\rm e}\text {t}}}$
$X_{{\acute{\rm e}\text {t}}}$

(to see this, note that
![]() $p\circ \Delta $
at the direct limit over all
$p\circ \Delta $
at the direct limit over all
![]() $Z'\subset Z$
corresponds to the surjection
$Z'\subset Z$
corresponds to the surjection
![]() $\oplus k(x)^{\times }\twoheadrightarrow \oplus k(x)^{\times }/\ell ^{\nu }$
, where the direct sums are over the generic points of Z). Let
$\oplus k(x)^{\times }\twoheadrightarrow \oplus k(x)^{\times }/\ell ^{\nu }$
, where the direct sums are over the generic points of Z). Let
![]() $a_3=\delta (a_2)$
. Then there exits
$a_3=\delta (a_2)$
. Then there exits
![]() $a_4\in H^{2i}_{Z'}(X_k,\mathbb {Z}_\ell (i))$
, such that
$a_4\in H^{2i}_{Z'}(X_k,\mathbb {Z}_\ell (i))$
, such that
![]() $a_3=l^\nu a_4$
. Set
$a_3=l^\nu a_4$
. Set
. It is now direct to see that
![]() $b,c$
satisfy the required properties.
$b,c$
satisfy the required properties.
To complete the proof, it is enough to show that
![]() $b=c$
. As the category of inverse systems of abelian sheaves on
$b=c$
. As the category of inverse systems of abelian sheaves on
![]() $X_{{\acute{\rm e}\text {t}}}$
is an abelian category with enough injectives by [Reference Jannsen17, Proposition 1.1], we may take a Cartan-Eilenberg injective resolution of (3.3). Now an argument analogous to [Reference Colliot-Thélène, Sansuc and Soulé12, p. 771] concludes the proof.
$X_{{\acute{\rm e}\text {t}}}$
is an abelian category with enough injectives by [Reference Jannsen17, Proposition 1.1], we may take a Cartan-Eilenberg injective resolution of (3.3). Now an argument analogous to [Reference Colliot-Thélène, Sansuc and Soulé12, p. 771] concludes the proof.
Second Proof of Theorem 2.3.
As in Section 2, let
![]() , where H is the Heisenberg group of order
, where H is the Heisenberg group of order
![]() $32$
, let
$32$
, let
![]() $Y\subset \mathbb {P}^N_{k_0}$
be a smooth complete intersection of dimension
$Y\subset \mathbb {P}^N_{k_0}$
be a smooth complete intersection of dimension
![]() $15$
on which G acts freely, and
$15$
on which G acts freely, and
![]() . By means of Proposition 3.1 and the rigidity property of
. By means of Proposition 3.1 and the rigidity property of
![]() $\lambda $
, it is enough for us to show that
$\lambda $
, it is enough for us to show that
![]() $\lambda \colon CH^3(X_{F})\{2\}\rightarrow H^5(X_{F},\mathbb {Q}_2/\mathbb {Z}_2(3))$
is not injective for some algebraically closed field extension F of a field of definition.
$\lambda \colon CH^3(X_{F})\{2\}\rightarrow H^5(X_{F},\mathbb {Q}_2/\mathbb {Z}_2(3))$
is not injective for some algebraically closed field extension F of a field of definition.
The assertion in characteristic zero follows from [Reference Totaro46, Theorem 7.2]. In positive characteristic different from
![]() $2$
, the assertion follows from [Reference Quick32, Proposition 5.3 (b)], because the group
$2$
, the assertion follows from [Reference Quick32, Proposition 5.3 (b)], because the group
![]() $H^5(X_{\overline {k}_0},\mathbb {Z}_2(3))$
is torsion by construction and the composition
$H^5(X_{\overline {k}_0},\mathbb {Z}_2(3))$
is torsion by construction and the composition
coincides with the cycle class map. This concludes the proof.
We conclude this section by a remark on Schreieder’s transcendental Abel-Jacobi map [Reference Schreieder38, Section 7.5].
Remark 3.3. Suppose that
![]() $k_{0}$
is of finite type over its prime field. For every finite extension
$k_{0}$
is of finite type over its prime field. For every finite extension
![]() $k/k_{0}$
, we have the transcendental Abel-Jacobi map:
$k/k_{0}$
, we have the transcendental Abel-Jacobi map:
where
![]() $CH^{i}_{0}(X_{k})\{\ell \}$
is the kernel of
$CH^{i}_{0}(X_{k})\{\ell \}$
is the kernel of
![]() $\operatorname {\mathrm {cl}}_{k}\colon CH^{i}(X_{k})\{\ell \}\rightarrow H^{2i}(X_{k},\mathbb {Z}_{\ell }(i))$
. Then one can observe that
$\operatorname {\mathrm {cl}}_{k}\colon CH^{i}(X_{k})\{\ell \}\rightarrow H^{2i}(X_{k},\mathbb {Z}_{\ell }(i))$
. Then one can observe that
![]() $\varinjlim _{k/k_0}\lambda _{\text {tr},k}=0$
by [Reference Schreieder38, Proposition 7.16] and weight arguments. This shows that if
$\varinjlim _{k/k_0}\lambda _{\text {tr},k}=0$
by [Reference Schreieder38, Proposition 7.16] and weight arguments. This shows that if
 $$\begin{align*}\varinjlim_{k/k_{0}}CH^{i}_{0} (X_{k})\{\ell\}=\operatorname{\mathrm{Ker}}\left(CH^{i} (X_{\overline{k}_{0}})\{\ell\}\xrightarrow{\varinjlim_{k/k_{0}}\operatorname{\mathrm{cl}}_{k}}\varinjlim_{k/k_{0}}H^{2i}(X_{k},\mathbb{Z}_{\ell}(i))\right) \end{align*}$$
$$\begin{align*}\varinjlim_{k/k_{0}}CH^{i}_{0} (X_{k})\{\ell\}=\operatorname{\mathrm{Ker}}\left(CH^{i} (X_{\overline{k}_{0}})\{\ell\}\xrightarrow{\varinjlim_{k/k_{0}}\operatorname{\mathrm{cl}}_{k}}\varinjlim_{k/k_{0}}H^{2i}(X_{k},\mathbb{Z}_{\ell}(i))\right) \end{align*}$$
is not zero, or equivalently by Proposition 3.1, if
![]() $\lambda $
is not injective over
$\lambda $
is not injective over
![]() $\overline {k}_0$
, then
$\overline {k}_0$
, then
![]() $\lambda _{\text {tr},k}$
is not injective for all sufficiently large finite extensions
$\lambda _{\text {tr},k}$
is not injective for all sufficiently large finite extensions
![]() $k/k_{0}$
contained in
$k/k_{0}$
contained in
![]() $\overline {k}_0/k_0$
. As described in Remark 3.2, we already have several examples with the property, and we will give further such examples in Sections 4 and 5. In Section 6, we will provide examples with
$\overline {k}_0/k_0$
. As described in Remark 3.2, we already have several examples with the property, and we will give further such examples in Sections 4 and 5. In Section 6, we will provide examples with
![]() $\lambda _{\text {tr},k}\neq 0$
.
$\lambda _{\text {tr},k}\neq 0$
.
4 Proof of Theorem 1.4
Let
![]() $k_0$
be a number field. Let B (respectively, E) be an abelian threefold (respectively, an elliptic curve) over
$k_0$
be a number field. Let B (respectively, E) be an abelian threefold (respectively, an elliptic curve) over
![]() $k_0$
, and set
$k_0$
, and set
![]() . Suppose that A has good ordinary reduction at some prime dividing
. Suppose that A has good ordinary reduction at some prime dividing
![]() $2$
. For instance, one can take
$2$
. For instance, one can take
![]() $k_0=\mathbb {Q}$
and A to be the product of
$k_0=\mathbb {Q}$
and A to be the product of
![]() $4$
copies of the elliptic curve
$4$
copies of the elliptic curve
Let
![]() $\iota $
be an involution acting on B by
$\iota $
be an involution acting on B by
![]() $-1$
and Y be the Kummer threefold associated to B, that is, the blow up of
$-1$
and Y be the Kummer threefold associated to B, that is, the blow up of
![]() $B/\iota $
at the
$B/\iota $
at the
![]() $64$
singular points, so that Y is smooth and contains
$64$
singular points, so that Y is smooth and contains
![]() $64$
disjoint copies of
$64$
disjoint copies of
![]() $\mathbb {P}^2$
. Finally, set
$\mathbb {P}^2$
. Finally, set
![]() . Note that the action of
. Note that the action of
![]() $\iota $
lifts to A where
$\iota $
lifts to A where
![]() $\iota $
acts trivially on E, and X can also be obtained by blowing up the quotient variety
$\iota $
acts trivially on E, and X can also be obtained by blowing up the quotient variety
![]() $A/\iota $
along the singular locus.
$A/\iota $
along the singular locus.
In the following, we fix an embedding
![]() $k_0\hookrightarrow \mathbb {C}$
.
$k_0\hookrightarrow \mathbb {C}$
.
Lemma 4.1.
![]() $H^4_{\operatorname {nr}}(X_{\mathbb {C}},\mathbb {Z}/2)\neq 0$
.
$H^4_{\operatorname {nr}}(X_{\mathbb {C}},\mathbb {Z}/2)\neq 0$
.
Proof. We follow the method of Diaz in [Reference Diaz15, Section 2.1]. In this proof, we write
![]() $A, B, E, X$
for
$A, B, E, X$
for
![]() $A_{\mathbb {C}}, B_{\mathbb {C}}, E_{\mathbb {C}}, X_{\mathbb {C}}$
. Letting
$A_{\mathbb {C}}, B_{\mathbb {C}}, E_{\mathbb {C}}, X_{\mathbb {C}}$
. Letting
![]() ,
,
![]() and
and
![]() $\pi \colon A^\circ \rightarrow U$
be the quotient map, we have the following commutative diagram:
$\pi \colon A^\circ \rightarrow U$
be the quotient map, we have the following commutative diagram:

Here, the vertical arrows are the restriction maps and the horizontal arrows are the pullback maps, the injectivity of
![]() $H^4_{\operatorname {nr}}(A,\mathbb {Z}/2)\to H^4_{\operatorname {nr}}(A^\circ ,\mathbb {Z}/2)$
and
$H^4_{\operatorname {nr}}(A,\mathbb {Z}/2)\to H^4_{\operatorname {nr}}(A^\circ ,\mathbb {Z}/2)$
and
![]() $H^4_{\operatorname {nr}}(X,\mathbb {Z}/2)\to H^4_{\operatorname {nr}}(U,\mathbb {Z}/2)$
is by definition of unramified cohomology, the map
$H^4_{\operatorname {nr}}(X,\mathbb {Z}/2)\to H^4_{\operatorname {nr}}(U,\mathbb {Z}/2)$
is by definition of unramified cohomology, the map
![]() $H^4(A,\mathbb {Z}/2)\to H^4(A^{\circ },\mathbb {Z}/2)$
is an isomorphism because
$H^4(A,\mathbb {Z}/2)\to H^4(A^{\circ },\mathbb {Z}/2)$
is an isomorphism because
![]() $\operatorname {codim}(B[2]\times E,A)=3$
.
$\operatorname {codim}(B[2]\times E,A)=3$
.
We need to check that (i)
![]() $\pi ^*\colon H^4(U,\mathbb {Z}/2)\twoheadrightarrow H^4(A^\circ ,\mathbb {Z}/2)$
and (ii)
$\pi ^*\colon H^4(U,\mathbb {Z}/2)\twoheadrightarrow H^4(A^\circ ,\mathbb {Z}/2)$
and (ii)
![]() $H^4(U,\mathbb {Z}/2)\rightarrow H^4_{\operatorname {nr}}(U,\mathbb {Z}/2)$
factors through
$H^4(U,\mathbb {Z}/2)\rightarrow H^4_{\operatorname {nr}}(U,\mathbb {Z}/2)$
factors through
![]() $H^4_{\operatorname {nr}}(X,\mathbb {Z}/2)$
. As for (i), note that
$H^4_{\operatorname {nr}}(X,\mathbb {Z}/2)$
. As for (i), note that
![]() $A^{\circ }=(B-B[2])\times E$
and
$A^{\circ }=(B-B[2])\times E$
and
![]() $U=(B-B[2])/\iota \times E$
. Letting
$U=(B-B[2])/\iota \times E$
. Letting
![]() $\rho \colon B-B[2]\rightarrow (B-B[2])/\iota $
be the quotient map, it is enough for us to show that
$\rho \colon B-B[2]\rightarrow (B-B[2])/\iota $
be the quotient map, it is enough for us to show that
![]() $\rho ^*\colon H^i((B-B[2])/\iota ,\mathbb {Z}/2)\rightarrow H^i(B-B[2],\mathbb {Z}/2)$
is surjective for
$\rho ^*\colon H^i((B-B[2])/\iota ,\mathbb {Z}/2)\rightarrow H^i(B-B[2],\mathbb {Z}/2)$
is surjective for
![]() $i=2, 3,4$
. Since
$i=2, 3,4$
. Since
![]() $\operatorname {codim}(B[2],B)=3$
, the restriction map
$\operatorname {codim}(B[2],B)=3$
, the restriction map
is an isomorphism for
![]() $i\leq 4$
. So it suffices to show that
$i\leq 4$
. So it suffices to show that
![]() $\rho ^*\colon H^1((B-B[2])/\iota ,\mathbb {Z}/2)\rightarrow H^1(B-B[2],\mathbb {Z}/2)$
is surjective, which follows from the fact that the short exact sequence
$\rho ^*\colon H^1((B-B[2])/\iota ,\mathbb {Z}/2)\rightarrow H^1(B-B[2],\mathbb {Z}/2)$
is surjective, which follows from the fact that the short exact sequence
splits. Here, the splitting is given by the nontrivial element in the fundamental group of
![]() $\mathbb {RP}^5$
that appears as the quotient of the boundary
$\mathbb {RP}^5$
that appears as the quotient of the boundary
![]() $\mathbb {S}^5$
of an open ball neighborhood of a
$\mathbb {S}^5$
of an open ball neighborhood of a
![]() $2$
-torsion point in B, as observed in the first paragraph of the proof of [Reference Spanier43, Theorem 1] (see also [Reference Diaz15, p. 267]). Alternatively, (i) directly follows from [Reference Diaz15, Corollary 2.8], because the assumptions for the statement are satisfied:
$2$
-torsion point in B, as observed in the first paragraph of the proof of [Reference Spanier43, Theorem 1] (see also [Reference Diaz15, p. 267]). Alternatively, (i) directly follows from [Reference Diaz15, Corollary 2.8], because the assumptions for the statement are satisfied:
![]() $B[2]\times E$
is smooth,
$B[2]\times E$
is smooth,
![]() $\operatorname {codim}(B[2]\times E,A)=3$
,
$\operatorname {codim}(B[2]\times E,A)=3$
,
![]() $\iota $
acts by
$\iota $
acts by
![]() $-1$
on the normal bundle
$-1$
on the normal bundle
![]() $N_{B[2]\times E/A}$
and
$N_{B[2]\times E/A}$
and
![]() $\iota $
acts trivially on
$\iota $
acts trivially on
![]() $H^1(A,\mathbb {Z}/2)$
. As for (ii), the direct computation of the unramified cohomology group using the Gersten complex reduces it to the vanishing
$H^1(A,\mathbb {Z}/2)$
. As for (ii), the direct computation of the unramified cohomology group using the Gersten complex reduces it to the vanishing
![]() $H^3_{\operatorname {\mathrm {nr}}}(X-U,\mathbb {Z}/2)=0$
(see [Reference Diaz15, Lemma 2.10]). The vanishing indeed holds because
$H^3_{\operatorname {\mathrm {nr}}}(X-U,\mathbb {Z}/2)=0$
(see [Reference Diaz15, Lemma 2.10]). The vanishing indeed holds because
![]() $X-U$
is
$X-U$
is
![]() $64$
disjoint copies of
$64$
disjoint copies of
![]() $\mathbb {P}^2\times E$
and
$\mathbb {P}^2\times E$
and
Finally, a theorem of Bloch–Esnault [Reference Bloch and Esnault6, Theorem 1.2] shows that
![]() $H^4(A,\mathbb {Z}/2)\rightarrow H^4_{\operatorname {nr}}(A,\mathbb {Z}/2)$
is nonzero (here, we use the rigidity property for unramified cohomology with torsion coefficients [Reference Colliot-Thélène8, Theorem 4.4.1]). This, with (4.1), concludes the proof.
$H^4(A,\mathbb {Z}/2)\rightarrow H^4_{\operatorname {nr}}(A,\mathbb {Z}/2)$
is nonzero (here, we use the rigidity property for unramified cohomology with torsion coefficients [Reference Colliot-Thélène8, Theorem 4.4.1]). This, with (4.1), concludes the proof.
Proposition 4.2.
![]() $\operatorname {\mathrm {cl}}_{\mathcal {D}}\colon CH^3(X_{\mathbb {C}})\{2\}\rightarrow H^6_{\mathcal {D}}(X_{\mathbb {C}},\mathbb {Z}(3))$
is not injective.
$\operatorname {\mathrm {cl}}_{\mathcal {D}}\colon CH^3(X_{\mathbb {C}})\{2\}\rightarrow H^6_{\mathcal {D}}(X_{\mathbb {C}},\mathbb {Z}(3))$
is not injective.
Proof. One needs to relate the fourth unramified cohomology group to the kernel of the Deligne cycle class map on torsion in codimension
![]() $3$
. We start with a short exact sequence given by [Reference Voisin51, Theorem 0.2] and [Reference Ma26, Remark 4.2 (1)]:
$3$
. We start with a short exact sequence given by [Reference Voisin51, Theorem 0.2] and [Reference Ma26, Remark 4.2 (1)]:
where

(the notation
![]() $/\operatorname {\mathrm {alg}}$
in the above equation means quotient by the algebraically trivial cycles in the kernel). It is important for us that
$/\operatorname {\mathrm {alg}}$
in the above equation means quotient by the algebraically trivial cycles in the kernel). It is important for us that
![]() $CH_0(X_{\mathbb {C}})$
is supported in dimension
$CH_0(X_{\mathbb {C}})$
is supported in dimension
![]() $\leq 3$
, because
$\leq 3$
, because
![]() $CH_0(Y_{\mathbb {C}})$
is supported in dimension
$CH_0(Y_{\mathbb {C}})$
is supported in dimension
![]() $\leq 2$
by [Reference Bloch and Srinivas5, Section 4 (1)]. By decomposition of the diagonal and the Bloch–Kato conjecture proved by Voevodsky, we have
$\leq 2$
by [Reference Bloch and Srinivas5, Section 4 (1)]. By decomposition of the diagonal and the Bloch–Kato conjecture proved by Voevodsky, we have
(see [Reference Colliot-Thélène and Voisin14, Proposition 3.3 (i)]). Moreover, [Reference Suzuki45, Theorem 1.1] yields
 $$ \begin{align*} &\operatorname{\mathrm{Coker}}\left(H^5(X_{\mathbb{C}},\mathbb{Z})_{\operatorname{\mathrm{tors}}}\rightarrow \Lambda^5(X_{\mathbb{C}})_{\operatorname{\mathrm{tors}}}\right)\\ &\simeq \operatorname{\mathrm{Ker}}\left(\operatorname{\mathrm{cl}}_{\mathcal{D}}\colon CH^3(X_{\mathbb{C}})_{\operatorname{\mathrm{alg}},\operatorname{\mathrm{tors}}}\rightarrow H^6_{\mathcal{D}}(X_{\mathbb{C}},\mathbb{Z}(3)) \right), \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{Coker}}\left(H^5(X_{\mathbb{C}},\mathbb{Z})_{\operatorname{\mathrm{tors}}}\rightarrow \Lambda^5(X_{\mathbb{C}})_{\operatorname{\mathrm{tors}}}\right)\\ &\simeq \operatorname{\mathrm{Ker}}\left(\operatorname{\mathrm{cl}}_{\mathcal{D}}\colon CH^3(X_{\mathbb{C}})_{\operatorname{\mathrm{alg}},\operatorname{\mathrm{tors}}}\rightarrow H^6_{\mathcal{D}}(X_{\mathbb{C}},\mathbb{Z}(3)) \right), \end{align*} $$
where we write
![]() $CH^3(X_{\mathbb {C}})_{\operatorname {\mathrm {alg}},\operatorname {\mathrm {tors}}}\subset CH^3(X_{\mathbb {C}})$
for the subgroup of algebraically trivial torsion cycles. Note that
$CH^3(X_{\mathbb {C}})_{\operatorname {\mathrm {alg}},\operatorname {\mathrm {tors}}}\subset CH^3(X_{\mathbb {C}})$
for the subgroup of algebraically trivial torsion cycles. Note that
![]() $H^5(X_{\mathbb {C}},\mathbb {Z})$
is in fact torsion free, because
$H^5(X_{\mathbb {C}},\mathbb {Z})$
is in fact torsion free, because
![]() $Y_{\mathbb {C}}$
and
$Y_{\mathbb {C}}$
and
![]() $E_{\mathbb {C}}$
have torsion free cohomology (use [Reference Spanier43, Theorem 2] for the Kummer threefold
$E_{\mathbb {C}}$
have torsion free cohomology (use [Reference Spanier43, Theorem 2] for the Kummer threefold
![]() $Y_{\mathbb {C}}$
), hence
$Y_{\mathbb {C}}$
), hence
By (4.2), (4.3) and (4.4), it remains to show that
![]() $H^4_{\operatorname {\mathrm {nr}}}(X_{\mathbb {C}},\mathbb {Q}/\mathbb {Z})\{2\}\neq 0$
. This can be deduced from Lemma 4.1, because the natural map
$H^4_{\operatorname {\mathrm {nr}}}(X_{\mathbb {C}},\mathbb {Q}/\mathbb {Z})\{2\}\neq 0$
. This can be deduced from Lemma 4.1, because the natural map
is injective, again, by the Bloch–Kato conjecture (see [Reference Auel, Colliot-Thélène and Parimala2, Theorem 1.1]). The proof is now complete.
We prove a strengthened version of Theorem 1.4.
Theorem 4.3. Let
![]() $k_0$
be a field of characteristic zero. Then there exist a fourfold product
$k_0$
be a field of characteristic zero. Then there exist a fourfold product
![]() $X=Y\times E$
over
$X=Y\times E$
over
![]() $k_0$
, where Y is a Kummer threefold and E is an elliptic curve, and a finite extension
$k_0$
, where Y is a Kummer threefold and E is an elliptic curve, and a finite extension
![]() $k/k_0$
, such that the cycle class map
$k/k_0$
, such that the cycle class map
is not injective.
Proof. Let
![]() $X=Y\times E$
be a fourfold product over a subfield
$X=Y\times E$
be a fourfold product over a subfield
![]() $\widetilde {k}_{0}\subset k_{0}$
that is finite over
$\widetilde {k}_{0}\subset k_{0}$
that is finite over
![]() $\mathbb {Q}$
, as given at the beginning of this section. Fixing an embedding
$\mathbb {Q}$
, as given at the beginning of this section. Fixing an embedding
![]() $\widetilde {k}_{0}\hookrightarrow \mathbb {C}$
, Proposition 4.2 shows that
$\widetilde {k}_{0}\hookrightarrow \mathbb {C}$
, Proposition 4.2 shows that
is not injective, hence, by the rigidity property of
![]() $\lambda $
, the same result holds over
$\lambda $
, the same result holds over
![]() $\overline {\widetilde {k}}_0$
, then over
$\overline {\widetilde {k}}_0$
, then over
![]() $\overline {k}_0$
. Proposition 3.1 now shows that there exists a finite extension
$\overline {k}_0$
. Proposition 3.1 now shows that there exists a finite extension
![]() $k/k_0$
, such that
$k/k_0$
, such that
is not injective. This finishes the proof.
5 Further examples in codimension three
In this section, we provide further counterexamples to Question 1.2 in codimension
![]() $3$
. By Proposition 3.1, this is reduced to finding examples for which Bloch’s map
$3$
. By Proposition 3.1, this is reduced to finding examples for which Bloch’s map
![]() $\lambda $
is not injective over some algebraically closed field extension of a field of definition. To achieve this, we use nontorsion type counterexamples to the integral Hodge and Tate conjectures, inspired by the work of Soulé–Voisin [Reference Soulé and Voisin42].
$\lambda $
is not injective over some algebraically closed field extension of a field of definition. To achieve this, we use nontorsion type counterexamples to the integral Hodge and Tate conjectures, inspired by the work of Soulé–Voisin [Reference Soulé and Voisin42].
Let
![]() $k_0$
be a field,
$k_0$
be a field,
![]() $\ell $
be a prime number invertible in
$\ell $
be a prime number invertible in
![]() $k_0$
,
$k_0$
,
![]() $i\geq 0$
be an integer and Y be a smooth projective variety over
$i\geq 0$
be an integer and Y be a smooth projective variety over
![]() $k_0$
. We define
$k_0$
. We define
where
![]() $H^{2i}(Y_{(k_{0})_s},\mathbb {Z}_\ell (i))^{(1)}\subset H^{2i}(Y_{(k_{0})_s},\mathbb {Z}_\ell (i))$
is the
$H^{2i}(Y_{(k_{0})_s},\mathbb {Z}_\ell (i))^{(1)}\subset H^{2i}(Y_{(k_{0})_s},\mathbb {Z}_\ell (i))$
is the
![]() $\operatorname {\mathrm {Gal}}((k_{0})_s/k_0)$
-submodule consisting of elements with open stabiliser and
$\operatorname {\mathrm {Gal}}((k_{0})_s/k_0)$
-submodule consisting of elements with open stabiliser and
![]() $H^{2i}_{\operatorname {\mathrm {alg}}}(Y_{(k_{0})_s},\mathbb {Z}_\ell (i))$
is the image of the cycle class map
$H^{2i}_{\operatorname {\mathrm {alg}}}(Y_{(k_{0})_s},\mathbb {Z}_\ell (i))$
is the image of the cycle class map
![]() $\operatorname {\mathrm {cl}}\colon CH^i(Y_{(k_{0})_s})\otimes _{\mathbb {Z}} \mathbb {Z}_\ell \rightarrow H^{2i}(Y_{(k_{0})_s},\mathbb {Z}_\ell (i))$
. The group
$\operatorname {\mathrm {cl}}\colon CH^i(Y_{(k_{0})_s})\otimes _{\mathbb {Z}} \mathbb {Z}_\ell \rightarrow H^{2i}(Y_{(k_{0})_s},\mathbb {Z}_\ell (i))$
. The group
![]() $\widetilde {Z}^{2i}_{{\acute{\rm e}\text {t}},\ell }(Y_{(k_{0})_s})$
is well-defined because
$\widetilde {Z}^{2i}_{{\acute{\rm e}\text {t}},\ell }(Y_{(k_{0})_s})$
is well-defined because
![]() $H^{2i}(Y_{(k_{0})_s},\mathbb {Z}_\ell (i))^{(1)}\subset H^{2i}(Y_{(k_{0})_s},\mathbb {Z}_\ell (i))$
is saturated by [Reference Colliot-Thélène and Kahn11, Lemma 4.1]. Note that
$H^{2i}(Y_{(k_{0})_s},\mathbb {Z}_\ell (i))^{(1)}\subset H^{2i}(Y_{(k_{0})_s},\mathbb {Z}_\ell (i))$
is saturated by [Reference Colliot-Thélène and Kahn11, Lemma 4.1]. Note that
![]() $\widetilde {Z}^{2i}_{{\acute{\rm e}\text {t}},\ell }(Y_{(k_{0})_s})_{\operatorname {\mathrm {tors}}}=0$
if and only if the sublattice
$\widetilde {Z}^{2i}_{{\acute{\rm e}\text {t}},\ell }(Y_{(k_{0})_s})_{\operatorname {\mathrm {tors}}}=0$
if and only if the sublattice
is saturated. When
![]() $k\subset \mathbb {C}$
, we similarly define
$k\subset \mathbb {C}$
, we similarly define
where
![]() $\operatorname {Hdg}^{2i}(Y_{\mathbb {C}},\mathbb {Z})\subset H^{2i}(Y_{\mathbb {C}},\mathbb {Z})$
is the subgroup of integral Hodge classes and
$\operatorname {Hdg}^{2i}(Y_{\mathbb {C}},\mathbb {Z})\subset H^{2i}(Y_{\mathbb {C}},\mathbb {Z})$
is the subgroup of integral Hodge classes and
. Note that
![]() $\widetilde {Z}^{2i}(Y_{\mathbb {C}})_{\operatorname {\mathrm {tors}}}=0$
if and only if the sublattice
$\widetilde {Z}^{2i}(Y_{\mathbb {C}})_{\operatorname {\mathrm {tors}}}=0$
if and only if the sublattice
is saturated.
Lemma 5.1. With the same notation as above, suppose either:
![]() $\widetilde {Z}^{2i}_{{\acute{\rm e}\text {t}},\ell }(Y_{(k_{0})_s})\{\ell \}\neq 0$
, or
$\widetilde {Z}^{2i}_{{\acute{\rm e}\text {t}},\ell }(Y_{(k_{0})_s})\{\ell \}\neq 0$
, or
![]() $k_0\subset \mathbb {C}$
and
$k_0\subset \mathbb {C}$
and
![]() $\widetilde {Z}^{2i}(Y_{\mathbb {C}})\{\ell \}\neq 0$
. Then there exist a finitely generated extension
$\widetilde {Z}^{2i}(Y_{\mathbb {C}})\{\ell \}\neq 0$
. Then there exist a finitely generated extension
![]() $K_0/k_0$
with
$K_0/k_0$
with
![]() $\operatorname {tr\, deg}_{k_0} K_0= 1$
and an elliptic curve E over
$\operatorname {tr\, deg}_{k_0} K_0= 1$
and an elliptic curve E over
![]() $K_0$
, such that, letting
$K_0$
, such that, letting
![]() , the map
, the map
![]() $\lambda \colon CH^{i+1}(X_{\overline {K}_0})\{\ell \}\rightarrow H^{2i+1}(X_{\overline {K}_0},\mathbb {Q}_\ell / \mathbb {Z}_\ell (i+1))$
is not injective.
$\lambda \colon CH^{i+1}(X_{\overline {K}_0})\{\ell \}\rightarrow H^{2i+1}(X_{\overline {K}_0},\mathbb {Q}_\ell / \mathbb {Z}_\ell (i+1))$
is not injective.
Proof. We only do the first case, the second case is similar (also see [Reference Suzuki45, Proposition 3.1]). After tensor
![]() $\mathbb {Q}_{\ell }/\mathbb {Z}_{\ell }$
, the short exact sequence
$\mathbb {Q}_{\ell }/\mathbb {Z}_{\ell }$
, the short exact sequence
yields an exact sequence
From the assumption, we now see that there exists a nonzero
![]() $\alpha \in CH^i(Y_{(k_{0})_s})\otimes \mathbb {Q}_\ell /\mathbb {Z}_\ell $
that vanishes in
$\alpha \in CH^i(Y_{(k_{0})_s})\otimes \mathbb {Q}_\ell /\mathbb {Z}_\ell $
that vanishes in
![]() $H^{2i}(Y_{(k_{0})_s},\mathbb {Z}_\ell (i))\otimes \mathbb {Q}_\ell /\mathbb {Z}_\ell $
. Note that, by passing to the algebraic closure, we get isomorphisms
$H^{2i}(Y_{(k_{0})_s},\mathbb {Z}_\ell (i))\otimes \mathbb {Q}_\ell /\mathbb {Z}_\ell $
. Note that, by passing to the algebraic closure, we get isomorphisms
Let
![]() $\alpha '\in CH^i(X_{\overline {k}_0})\otimes \mathbb {Q}_\ell /\mathbb {Z}_\ell $
be the image of
$\alpha '\in CH^i(X_{\overline {k}_0})\otimes \mathbb {Q}_\ell /\mathbb {Z}_\ell $
be the image of
![]() $\alpha $
.
$\alpha $
.
Let
![]() $K_0/k_0$
be a finitely generated field extension with
$K_0/k_0$
be a finitely generated field extension with
![]() $\operatorname {tr\, deg}_{k_0} K_0=1$
and E be an elliptic curve over
$\operatorname {tr\, deg}_{k_0} K_0=1$
and E be an elliptic curve over
![]() $K_0$
with
$K_0$
with
![]() $j(E)\not \in \overline {k}_0$
. Fixing a component
$j(E)\not \in \overline {k}_0$
. Fixing a component
![]() $\mathbb {Q}_\ell /\mathbb {Z}_\ell $
of
$\mathbb {Q}_\ell /\mathbb {Z}_\ell $
of
![]() $CH^1(E_{\overline {K}_0})\{\ell \}=(\mathbb {Q}_\ell /\mathbb {Z}_\ell )^2$
, we indentify
$CH^1(E_{\overline {K}_0})\{\ell \}=(\mathbb {Q}_\ell /\mathbb {Z}_\ell )^2$
, we indentify
![]() $\alpha '$
with an element in
$\alpha '$
with an element in
![]() $CH^{i}(Y_{\overline {k}_0})\otimes CH^1(E_{\overline {K}_0})\{\ell \}$
. Letting
$CH^{i}(Y_{\overline {k}_0})\otimes CH^1(E_{\overline {K}_0})\{\ell \}$
. Letting
, a theorem of Schoen [Reference Schoen37, Theorem 0.2] shows that the image
![]() $\beta $
of
$\beta $
of
![]() $\alpha '$
under the exterior product map
$\alpha '$
under the exterior product map
is nonzero. Now it remains for us to show that
![]() $\beta \in CH^{i+1}(X_{\overline {K}_0})\{\ell \}$
is in the kernel of
$\beta \in CH^{i+1}(X_{\overline {K}_0})\{\ell \}$
is in the kernel of
![]() $\lambda $
. This follows from the commutative diagram:
$\lambda $
. This follows from the commutative diagram:

The proof is complete.
Lemma 5.1 can be applied to nontorsion type counterexamples to the integral Hodge conjecture [Reference Colliot-Thélène and Voisin14, Reference Diaz15, Reference Kollár22, Reference Ottem and Suzuki30, Reference Totaro48] or the integral Tate conjecture [Reference Pirutka and Yagita31, Reference Totaro48]. One may take
![]() $k_0=\mathbb {Q}$
for the examples in [Reference Colliot-Thélène and Voisin14, Reference Diaz15, Reference Kollár22, Reference Ottem and Suzuki30, Reference Totaro48] and
$k_0=\mathbb {Q}$
for the examples in [Reference Colliot-Thélène and Voisin14, Reference Diaz15, Reference Kollár22, Reference Ottem and Suzuki30, Reference Totaro48] and
![]() $k_0$
to be a finite field for the examples in [Reference Pirutka and Yagita31].
$k_0$
to be a finite field for the examples in [Reference Pirutka and Yagita31].
Proposition 3.1 then produces various examples of fields K of finite type over the prime fields of transcendence degree
![]() $1$
, prime numbers
$1$
, prime numbers
![]() $\ell $
invertible in K and smooth projective K-varieties X, such that
$\ell $
invertible in K and smooth projective K-varieties X, such that
![]() $\operatorname {\mathrm {cl}}\colon CH^3(X)[\ell ]\rightarrow H^6(X,\mathbb {Z}_\ell (3))$
is not injective. Those with the best bounds are: fourfolds in characteristic zero; eightfolds in positive characteristic.
$\operatorname {\mathrm {cl}}\colon CH^3(X)[\ell ]\rightarrow H^6(X,\mathbb {Z}_\ell (3))$
is not injective. Those with the best bounds are: fourfolds in characteristic zero; eightfolds in positive characteristic.
6 Proof of Theorem 1.5
Lemma 6.1. Let k be a field and
![]() $\ell $
be a prime invertible in k. Then
$\ell $
be a prime invertible in k. Then
![]() $H^2(k,\mathbb {Z}_{\ell }(1))\simeq T_{\ell }(\operatorname {Br}(k))$
. In particular,
$H^2(k,\mathbb {Z}_{\ell }(1))\simeq T_{\ell }(\operatorname {Br}(k))$
. In particular,
![]() $H^2(k,\mathbb {Z}_{\ell }(1))$
is torsion free.
$H^2(k,\mathbb {Z}_{\ell }(1))$
is torsion free.
Proof. By [Reference Neukirch, Schmidt and Wingberg29, Theorem 2.7.5], we have a short exact sequence
The Kummer sequence
gives natural identifications
The induced maps
![]() $k^{\times }/k^{\times \ell ^{m+1}}\to k^{\times }/k^{\times \ell ^m}$
are the natural quotient maps, and, in particular, they are surjective. It follows that the sequence of the
$k^{\times }/k^{\times \ell ^{m+1}}\to k^{\times }/k^{\times \ell ^m}$
are the natural quotient maps, and, in particular, they are surjective. It follows that the sequence of the
![]() $H^1(k,\mu _{\ell ^m})$
satisfies the Mittag-Leffler condition, and so
$H^1(k,\mu _{\ell ^m})$
satisfies the Mittag-Leffler condition, and so
![]() ${\varprojlim }^1H^1(k,\mu _{\ell ^m})=0$
. The induced maps
${\varprojlim }^1H^1(k,\mu _{\ell ^m})=0$
. The induced maps
![]() $\operatorname {Br}(k)[\ell ^{m+1}]\to \operatorname {Br}(k)[\ell ^m]$
are given by multiplication by
$\operatorname {Br}(k)[\ell ^{m+1}]\to \operatorname {Br}(k)[\ell ^m]$
are given by multiplication by
![]() $\ell $
, hence,
$\ell $
, hence,
![]() $\varprojlim H^2(k,\mu _{\ell ^m})=T_{\ell }(\operatorname {Br}(k))$
.
$\varprojlim H^2(k,\mu _{\ell ^m})=T_{\ell }(\operatorname {Br}(k))$
.
Lemma 6.2. Let k be a global field,
![]() $\ell $
be a prime number invertible in k and
$\ell $
be a prime number invertible in k and
![]() $k(t)/k$
be a purely transcendental extension of transcendence degree
$k(t)/k$
be a purely transcendental extension of transcendence degree
![]() $1$
. If
$1$
. If
![]() $\ell =2$
, suppose that k is a totally imaginary number field or a function field. Then
$\ell =2$
, suppose that k is a totally imaginary number field or a function field. Then
![]() $H^4(k(t),\mathbb {Z}_{\ell }(2))=0$
.
$H^4(k(t),\mathbb {Z}_{\ell }(2))=0$
.
Proof. By [Reference Neukirch, Schmidt and Wingberg29, Theorem 2.7.5], we have a short exact sequence
By [Reference Serre41, II.4.4, Proposition 13], we have
![]() $\operatorname {\mathrm {cd}}_{\ell }(k)\leq 2$
, and so [Reference Serre41, II.4.2, Proposition 11] implies
$\operatorname {\mathrm {cd}}_{\ell }(k)\leq 2$
, and so [Reference Serre41, II.4.2, Proposition 11] implies
![]() $\operatorname {\mathrm {cd}}_\ell (k(t))\leq 3$
. It follows that the group
$\operatorname {\mathrm {cd}}_\ell (k(t))\leq 3$
. It follows that the group
![]() $H^4(k(t),\mu _{\ell ^n}^{\otimes 2})$
is trivial for all
$H^4(k(t),\mu _{\ell ^n}^{\otimes 2})$
is trivial for all
![]() $n\geq 0$
, hence,
$n\geq 0$
, hence,
![]() $\varprojlim _n H^4(k(t),\mu _{\ell ^n}^{\otimes 2})=0$
. In view of (6.1), the proof will be complete once we show that
$\varprojlim _n H^4(k(t),\mu _{\ell ^n}^{\otimes 2})=0$
. In view of (6.1), the proof will be complete once we show that
![]() $\varprojlim _n^1H^3(k(t),\mu _{\ell ^n}^{\otimes 2})=0$
.
$\varprojlim _n^1H^3(k(t),\mu _{\ell ^n}^{\otimes 2})=0$
.
We regard
![]() $k(t)$
as the function field of
$k(t)$
as the function field of
![]() $\mathbb {P}^1_k$
. By [Reference Serre41, p. 113], we have an exact sequence
$\mathbb {P}^1_k$
. By [Reference Serre41, p. 113], we have an exact sequence
which is functorial in
![]() $n\geq 0$
. Since
$n\geq 0$
. Since
![]() $\operatorname {\mathrm {cd}}_{\ell }(k)\leq 2$
, the first term
$\operatorname {\mathrm {cd}}_{\ell }(k)\leq 2$
, the first term
![]() $H^3(k,\mu _{\ell ^n}^{\otimes 2})$
vanishes. The surjective map C is the direct sum of the corestriction maps along the field extensions
$H^3(k,\mu _{\ell ^n}^{\otimes 2})$
vanishes. The surjective map C is the direct sum of the corestriction maps along the field extensions
![]() $k(x)/k$
, and so the point at infinity
$k(x)/k$
, and so the point at infinity
![]() $\infty \in \mathbb {P}^1_k$
determines a section of C. We obtain a decomposition
$\infty \in \mathbb {P}^1_k$
determines a section of C. We obtain a decomposition
The isomorphism on the right comes from the Kummer short exact sequence. The isomorphism (6.2) is functorial in n, where on the right, the transition maps
![]() $\operatorname {Br}(k(x))[\ell ^{n+1}]\to \operatorname {Br}(k(x))[\ell ^n]$
are given by multiplication by
$\operatorname {Br}(k(x))[\ell ^{n+1}]\to \operatorname {Br}(k(x))[\ell ^n]$
are given by multiplication by
![]() $\ell $
.
$\ell $
.
Suppose first that k is a totally imaginary number field or a function field. Then for every closed point x of
![]() $\mathbb {A}^1_k$
, the residue field
$\mathbb {A}^1_k$
, the residue field
![]() $k(x)$
is also totally imaginary. It follows from the celebrated theorem of Albert, Brauer, Hasse and Noether [Reference Neukirch, Schmidt and Wingberg29, Theorem 8.1.17] that
$k(x)$
is also totally imaginary. It follows from the celebrated theorem of Albert, Brauer, Hasse and Noether [Reference Neukirch, Schmidt and Wingberg29, Theorem 8.1.17] that
![]() $\operatorname {Br}(k(x))$
is divisible. Thus, the maps
$\operatorname {Br}(k(x))$
is divisible. Thus, the maps
![]() $\operatorname {Br}(k(x))[\ell ^{n+1}]\to \operatorname {Br}(k(x))[\ell ^n]$
given by multiplication by
$\operatorname {Br}(k(x))[\ell ^{n+1}]\to \operatorname {Br}(k(x))[\ell ^n]$
given by multiplication by
![]() $\ell $
are surjective, hence, by (6.2) so are the transition maps
$\ell $
are surjective, hence, by (6.2) so are the transition maps
![]() $H^3(k(t),\mu _{\ell ^{n+1}}^{\otimes 2})\to H^3(k(t),\mu _{\ell ^n}^{\otimes 2})$
. This shows that the inverse system
$H^3(k(t),\mu _{\ell ^{n+1}}^{\otimes 2})\to H^3(k(t),\mu _{\ell ^n}^{\otimes 2})$
. This shows that the inverse system
![]() $\{H^3(k(t),\mu _{\ell ^n}^{\otimes 2})\}_{n\geq 0}$
satisfies the Mittag-Leffler condition, and so
$\{H^3(k(t),\mu _{\ell ^n}^{\otimes 2})\}_{n\geq 0}$
satisfies the Mittag-Leffler condition, and so
![]() $\varprojlim _n^1H^3(k(t),\mu _{\ell ^n}^{\otimes 2})=0$
by [Reference Neukirch, Schmidt and Wingberg29, Proposition 2.7.4], as desired.
$\varprojlim _n^1H^3(k(t),\mu _{\ell ^n}^{\otimes 2})=0$
by [Reference Neukirch, Schmidt and Wingberg29, Proposition 2.7.4], as desired.
Suppose now that k admits at least one real embedding. Then under our assumptions,
![]() $\ell \neq 2$
. By [Reference Neukirch, Schmidt and Wingberg29, Theorem 8.1.17], the group
$\ell \neq 2$
. By [Reference Neukirch, Schmidt and Wingberg29, Theorem 8.1.17], the group
![]() $\operatorname {Br}(k(x))$
is the direct sum of a divisible group and a finite elementary
$\operatorname {Br}(k(x))$
is the direct sum of a divisible group and a finite elementary
![]() $2$
-group. Then, since
$2$
-group. Then, since
![]() $\ell $
is odd, the maps
$\ell $
is odd, the maps
![]() $\operatorname {Br}(k(x))[\ell ^{n+1}]\to \operatorname {Br}(k(x))[\ell ^n]$
given by multiplication by
$\operatorname {Br}(k(x))[\ell ^{n+1}]\to \operatorname {Br}(k(x))[\ell ^n]$
given by multiplication by
![]() $\ell $
are surjective and the conclusion follows as in the previous case.
$\ell $
are surjective and the conclusion follows as in the previous case.
Theorem 1.5 is a special case of the following more general statement.
Theorem 6.3. Let k be a global field,
![]() $k(t)$
be a purely transcendental extension of k of transcendence degree
$k(t)$
be a purely transcendental extension of k of transcendence degree
![]() $1$
and
$1$
and
![]() $\ell $
be a prime invertible in k. If
$\ell $
be a prime invertible in k. If
![]() $\ell =2$
, suppose that k is a totally imaginary number field or a function field, and if
$\ell =2$
, suppose that k is a totally imaginary number field or a function field, and if
![]() $\ell $
is odd, suppose that
$\ell $
is odd, suppose that
![]() $\operatorname {char}(k)=0$
. Then there exists a norm variety X of dimension
$\operatorname {char}(k)=0$
. Then there exists a norm variety X of dimension
![]() $\ell ^2-1$
over
$\ell ^2-1$
over
![]() $k(t)$
, such that
$k(t)$
, such that
is not injective.
Proof. By (6.2) and the theorem of Albert, Brauer, Hasse and Noether [Reference Neukirch, Schmidt and Wingberg29, Theorem 8.1.17], we have
![]() $H^3(k(t),\mu _{\ell }^{\otimes 2})\neq 0$
. Let X be a norm variety associated to a nontrivial symbol
$H^3(k(t),\mu _{\ell }^{\otimes 2})\neq 0$
. Let X be a norm variety associated to a nontrivial symbol
![]() $s\in H^3(k(t),\mu _{\ell }^{\otimes 2})$
, as constructed by Rost [Reference Suslin and Joukhovitski44] (see also [Reference Karpenko and Merkurjev21, Section 5d]). The k-variety X is a smooth projective of dimension
$s\in H^3(k(t),\mu _{\ell }^{\otimes 2})$
, as constructed by Rost [Reference Suslin and Joukhovitski44] (see also [Reference Karpenko and Merkurjev21, Section 5d]). The k-variety X is a smooth projective of dimension
![]() $\ell ^2-1$
. The pure Chow motive with
$\ell ^2-1$
. The pure Chow motive with
![]() $\mathbb {Z}_{(\ell )}$
-coefficients
$\mathbb {Z}_{(\ell )}$
-coefficients
![]() $M(X;\mathbb {Z}_{(\ell )})$
of X contains the Rost motive
$M(X;\mathbb {Z}_{(\ell )})$
of X contains the Rost motive
![]() $\mathcal {R}$
of s as a direct summand. By [Reference Karpenko and Merkurjev21, Theorem RM.10], we have
$\mathcal {R}$
of s as a direct summand. By [Reference Karpenko and Merkurjev21, Theorem RM.10], we have
![]() $CH^2(\mathcal {R})=\mathbb {Z}/\ell $
, hence,
$CH^2(\mathcal {R})=\mathbb {Z}/\ell $
, hence,
![]() $CH^2(X)[\ell ]\neq 0$
(we apply [Reference Karpenko and Merkurjev21, Theorem RM.10] with
$CH^2(X)[\ell ]\neq 0$
(we apply [Reference Karpenko and Merkurjev21, Theorem RM.10] with
![]() $p=\ell $
,
$p=\ell $
,
![]() $n=2$
,
$n=2$
,
![]() $k=1$
and
$k=1$
and
![]() $i=1$
. By definition
$i=1$
. By definition
![]() $b=1+p$
, hence,
$b=1+p$
, hence,
![]() $j=bk-p^i+1=2$
). Let
$j=bk-p^i+1=2$
). Let
![]() $\alpha \in CH^2(\mathcal {R})[\ell ]$
be a nonzero element.
$\alpha \in CH^2(\mathcal {R})[\ell ]$
be a nonzero element.
If
![]() $\ell =2$
, we may construct X and
$\ell =2$
, we may construct X and
![]() $\alpha $
in any characteristic different from
$\alpha $
in any characteristic different from
![]() $2$
as follows. Let
$2$
as follows. Let
![]() $\mathcal {O}$
be the ring of integers of k,
$\mathcal {O}$
be the ring of integers of k,
![]() $\pi \in \mathcal {O}$
be a prime element and
$\pi \in \mathcal {O}$
be a prime element and
![]() $u\in \mathcal {O}$
be, such that the class of u in the residue field
$u\in \mathcal {O}$
be, such that the class of u in the residue field
![]() $\mathcal {O}/\pi $
is not a square. The quadratic form
$\mathcal {O}/\pi $
is not a square. The quadratic form
over k is the norm form for the quaternion algebra
![]() $(u,\pi )$
, hence, it is anisotropic over k. By [Reference Lam23, VI. Proposition 1.9], the quadratic form
$(u,\pi )$
, hence, it is anisotropic over k. By [Reference Lam23, VI. Proposition 1.9], the quadratic form
is anisotropic over
![]() $k(\!(t)\!)$
, hence, over
$k(\!(t)\!)$
, hence, over
![]() $k(t)$
. Let
$k(t)$
. Let
![]() $X\subset \mathbb {P}^4_{k(t)}$
be the smooth projective quadric hypersurface over
$X\subset \mathbb {P}^4_{k(t)}$
be the smooth projective quadric hypersurface over
![]() $k(t)$
defined by
$k(t)$
defined by
![]() $q=0$
. By [Reference Karpenko20, Theorem 5.3], we have
$q=0$
. By [Reference Karpenko20, Theorem 5.3], we have
![]() $CH^2(X)_{\operatorname {tors}}\simeq \mathbb {Z}/2$
(in the notation of [Reference Karpenko20, p. 120],
$CH^2(X)_{\operatorname {tors}}\simeq \mathbb {Z}/2$
(in the notation of [Reference Karpenko20, p. 120],
![]() $q=\left \langle {\!\left \langle {u,\pi }\right \rangle \!}\right \rangle \perp \left \langle {t}\right \rangle $
). We let
$q=\left \langle {\!\left \langle {u,\pi }\right \rangle \!}\right \rangle \perp \left \langle {t}\right \rangle $
). We let
![]() $\alpha \in CH^2(X)_{\operatorname {tors}}$
be the generator. The quadratic form q is a neighbor of the Pfister form
$\alpha \in CH^2(X)_{\operatorname {tors}}$
be the generator. The quadratic form q is a neighbor of the Pfister form
![]() $\left \langle {\!\left \langle {u,\pi ,-t}\right \rangle \!}\right \rangle $
, hence, X is a norm variety for the symbol
$\left \langle {\!\left \langle {u,\pi ,-t}\right \rangle \!}\right \rangle $
, hence, X is a norm variety for the symbol
![]() $(u)\cup (\pi )\cup (-t)\in H^3(k(t),\mathbb {Z}/2)$
.
$(u)\cup (\pi )\cup (-t)\in H^3(k(t),\mathbb {Z}/2)$
.
We are going to prove that
![]() $\operatorname {\mathrm {cl}}$
is not injective in codimension
$\operatorname {\mathrm {cl}}$
is not injective in codimension
![]() $2$
by showing that
$2$
by showing that
![]() $\operatorname {\mathrm {cl}}(\alpha )=0$
in
$\operatorname {\mathrm {cl}}(\alpha )=0$
in
![]() $H^4(X,\mathbb {Z}_{\ell }(2))$
. Consider the Hochschild-Serre spectral sequence in continuous
$H^4(X,\mathbb {Z}_{\ell }(2))$
. Consider the Hochschild-Serre spectral sequence in continuous
![]() $\ell $
-adic cohomology
$\ell $
-adic cohomology
It yields a filtration
where
![]() $F^i/F^{i+1}$
is a subquotient (respectively, a submodule) of
$F^i/F^{i+1}$
is a subquotient (respectively, a submodule) of
![]() $H^i(k,H^{4-i}(X_{k(t)_s},\mathbb {Z}_\ell (2)))$
for all
$H^i(k,H^{4-i}(X_{k(t)_s},\mathbb {Z}_\ell (2)))$
for all
![]() $0\leq i\leq 4$
(respectively, for
$0\leq i\leq 4$
(respectively, for
![]() $i=0,1$
). Let
$i=0,1$
). Let
![]() $\rho \colon M(X;\mathbb {Z}_{(\ell )})\to M(X;\mathbb {Z}_{(\ell )})$
be the projector onto the direct summand
$\rho \colon M(X;\mathbb {Z}_{(\ell )})\to M(X;\mathbb {Z}_{(\ell )})$
be the projector onto the direct summand
![]() $\mathcal {R}$
, so that
$\mathcal {R}$
, so that
![]() $\alpha \in \rho ^*CH^2(X)$
(when
$\alpha \in \rho ^*CH^2(X)$
(when
![]() $\ell =2$
and X is the quadric described above, we could also take
$\ell =2$
and X is the quadric described above, we could also take
![]() $\rho =\operatorname {id}$
in what follows). Since the Hochschild-Serre spectral sequence is natural with respect to correspondences,
$\rho =\operatorname {id}$
in what follows). Since the Hochschild-Serre spectral sequence is natural with respect to correspondences,
![]() $\rho $
and
$\rho $
and
![]() $1-\rho $
respect
$1-\rho $
respect
![]() $F^{\cdot }$
and determine a direct sum decomposition
$F^{\cdot }$
and determine a direct sum decomposition
![]() $F^{\cdot }=\rho ^*F^{\cdot }\oplus (1-\rho ^*)F^{\cdot }$
, where
$F^{\cdot }=\rho ^*F^{\cdot }\oplus (1-\rho ^*)F^{\cdot }$
, where
![]() $\rho ^*F^{i}/\rho ^*F^{i+1}$
is a subquotient (respectively, a submodule) of
$\rho ^*F^{i}/\rho ^*F^{i+1}$
is a subquotient (respectively, a submodule) of
![]() $H^i(k,\rho ^*H^{4-i}(X_{k(t)_s},\mathbb {Z}_\ell (2)))$
for all
$H^i(k,\rho ^*H^{4-i}(X_{k(t)_s},\mathbb {Z}_\ell (2)))$
for all
![]() $0\leq i\leq 4$
(respectively, for
$0\leq i\leq 4$
(respectively, for
![]() $i=0,1$
).
$i=0,1$
).
The Rost motive
![]() $\mathcal {R}_{k(t)_s}$
is a finite direct sum of powers of the Tate motive. Thus, for all
$\mathcal {R}_{k(t)_s}$
is a finite direct sum of powers of the Tate motive. Thus, for all
![]() $j\geq 0$
, we have
$j\geq 0$
, we have
![]() $\rho ^*H^{2j+1}(X_{k(t)_s},\mathbb {Z}_{\ell })=0$
and
$\rho ^*H^{2j+1}(X_{k(t)_s},\mathbb {Z}_{\ell })=0$
and
![]() $\rho ^*H^{2j}(X_{k(t)_s},\mathbb {Z}_{\ell })\simeq \mathbb {Z}_{\ell }(-j)^{\oplus r_{2j}}$
for some integers
$\rho ^*H^{2j}(X_{k(t)_s},\mathbb {Z}_{\ell })\simeq \mathbb {Z}_{\ell }(-j)^{\oplus r_{2j}}$
for some integers
![]() $r_{2j}\geq 0$
. It follows that
$r_{2j}\geq 0$
. It follows that
Since
![]() $H^0(X_{k(t)_s},\mathbb {Z}_{\ell }(2))\simeq \mathbb {Z}_{\ell }(2)$
, the direct summand
$H^0(X_{k(t)_s},\mathbb {Z}_{\ell }(2))\simeq \mathbb {Z}_{\ell }(2)$
, the direct summand
![]() $\rho ^*H^0(X_{k(t)_s},\mathbb {Z}_{\ell }(2))$
is either
$\rho ^*H^0(X_{k(t)_s},\mathbb {Z}_{\ell }(2))$
is either
![]() $0$
or
$0$
or
![]() $\mathbb {Z}_{\ell }(2)$
(as
$\mathbb {Z}_{\ell }(2)$
(as
![]() $CH^0(\mathcal {R})=\mathbb {Z}_{(\ell )}$
by [Reference Karpenko and Merkurjev21, Theorem RM.10], we actually have
$CH^0(\mathcal {R})=\mathbb {Z}_{(\ell )}$
by [Reference Karpenko and Merkurjev21, Theorem RM.10], we actually have
![]() $\rho ^*H^0(X_{k(t)_s},\mathbb {Z}_{\ell }(2))=\mathbb {Z}_{\ell }(2)$
). Thus, by Lemma 6.2,
$\rho ^*H^0(X_{k(t)_s},\mathbb {Z}_{\ell }(2))=\mathbb {Z}_{\ell }(2)$
). Thus, by Lemma 6.2,
We deduce that
![]() $\rho ^*F^1=\rho ^*F^2$
and
$\rho ^*F^1=\rho ^*F^2$
and
![]() $\rho ^*F^3=\rho ^*F^4=\rho ^*F^5=0$
. Therefore,
$\rho ^*F^3=\rho ^*F^4=\rho ^*F^5=0$
. Therefore,
![]() $\rho ^*F^1=\rho ^*F^2/\rho ^*F^3$
, that is, we have an exact sequence
$\rho ^*F^1=\rho ^*F^2/\rho ^*F^3$
, that is, we have an exact sequence
We know that
![]() $\rho ^*H^4(X_{k(t)_s},\mathbb {Z}_\ell (2))\simeq \mathbb {Z}_\ell ^{\oplus r_4}$
is torsion free. By Lemma 6.1, the group
$\rho ^*H^4(X_{k(t)_s},\mathbb {Z}_\ell (2))\simeq \mathbb {Z}_\ell ^{\oplus r_4}$
is torsion free. By Lemma 6.1, the group
is also torsion free. By [Reference Jannsen19, p. 262 and footnote 3] and [Reference Ekedahl16] (see also the announcement in [Reference Jannsen17, Remark 6.15(b)]), all differentials in (6.3) are torsion, hence,
![]() $\rho ^*F^2/\rho ^*F^3$
is torsion free. Now (6.4) implies that
$\rho ^*F^2/\rho ^*F^3$
is torsion free. Now (6.4) implies that
![]() $\rho ^*H^4(X,\mathbb {Z}_\ell (2))$
is torsion free. Since
$\rho ^*H^4(X,\mathbb {Z}_\ell (2))$
is torsion free. Since
![]() $\operatorname {\mathrm {cl}}(\alpha )\in \rho ^*H^4(X,\mathbb {Z}_\ell (2))$
and
$\operatorname {\mathrm {cl}}(\alpha )\in \rho ^*H^4(X,\mathbb {Z}_\ell (2))$
and
![]() $\ell \operatorname {\mathrm {cl}}(\alpha )=0$
, we conclude that
$\ell \operatorname {\mathrm {cl}}(\alpha )=0$
, we conclude that
![]() $\operatorname {\mathrm {cl}}(\alpha )=0$
.
$\operatorname {\mathrm {cl}}(\alpha )=0$
.
Remark 6.4 (Colliot-Thélène).
We sketch a more direct proof of the fact, used in the proof of Theorem 6.3, that the group
![]() $H^3(k(t),\mu _{\ell }^{\otimes 2})$
is nonzero. We first note that if a symbol
$H^3(k(t),\mu _{\ell }^{\otimes 2})$
is nonzero. We first note that if a symbol
![]() $(a,b)\in \operatorname {Br}(k)[\ell ]=H^2(k,\mu _\ell )$
is nonzero, then the residue of
$(a,b)\in \operatorname {Br}(k)[\ell ]=H^2(k,\mu _\ell )$
is nonzero, then the residue of
![]() $(a,b,t)\in H^3(k(t),\mu _{\ell }^{\otimes 2})$
is nonzero, hence,
$(a,b,t)\in H^3(k(t),\mu _{\ell }^{\otimes 2})$
is nonzero, hence,
![]() $(a,b,t)\neq 0$
. Therefore, it suffices to show that
$(a,b,t)\neq 0$
. Therefore, it suffices to show that
![]() $\operatorname {Br}(k)[\ell ]\neq 0$
for all global fields k.
$\operatorname {Br}(k)[\ell ]\neq 0$
for all global fields k.
One can show that
![]() $\operatorname {Br}(k)[2]\neq 0$
by constructing a conic
$\operatorname {Br}(k)[2]\neq 0$
by constructing a conic
![]() $X^2-aY^2-bT^2=0$
over k without rational points. If
$X^2-aY^2-bT^2=0$
over k without rational points. If
![]() $\ell $
is odd, one can construct a nonzero element of
$\ell $
is odd, one can construct a nonzero element of
![]() $\operatorname {Br}(k)[\ell ]$
by taking a cyclic extension
$\operatorname {Br}(k)[\ell ]$
by taking a cyclic extension
![]() $K/k$
of degree
$K/k$
of degree
![]() $\ell $
, a place v where
$\ell $
, a place v where
![]() $K/k$
is inert (using the Chebotarev density theorem [Reference Tschebotareff50]), an element
$K/k$
is inert (using the Chebotarev density theorem [Reference Tschebotareff50]), an element
![]() $c\in k_v^\times $
which is not a norm from
$c\in k_v^\times $
which is not a norm from
![]() $K_v^\times $
and approximating c by an element of
$K_v^\times $
and approximating c by an element of
![]() $k^\times $
.
$k^\times $
.
Remark 6.5. One might wonder if there exist a number field k, a prime number
![]() $\ell $
, a nontrivial mod
$\ell $
, a nontrivial mod
![]() $\ell $
symbol s of degree
$\ell $
symbol s of degree
![]() $n+1$
and a norm variety X for s for which
$n+1$
and a norm variety X for s for which
![]() $\operatorname {\mathrm {cl}}\colon CH^2(X)[\ell ]\to H^4(X,\mathbb {Z}_\ell (2))$
is not injective. If
$\operatorname {\mathrm {cl}}\colon CH^2(X)[\ell ]\to H^4(X,\mathbb {Z}_\ell (2))$
is not injective. If
![]() $\ell $
is odd, this is impossible, as
$\ell $
is odd, this is impossible, as
![]() $\operatorname {\mathrm {cd}}_{\ell }(k)=2$
. Suppose now that
$\operatorname {\mathrm {cd}}_{\ell }(k)=2$
. Suppose now that
![]() $\ell =2$
, so that X is the quadric hypersurface associated to a Pfister neighbor q of rank
$\ell =2$
, so that X is the quadric hypersurface associated to a Pfister neighbor q of rank
![]() $2^n+1$
. By [Reference Karpenko20, Theorem 6.1],
$2^n+1$
. By [Reference Karpenko20, Theorem 6.1],
![]() $CH^2(X)_{\operatorname {tors}}$
is either
$CH^2(X)_{\operatorname {tors}}$
is either
![]() $0$
or
$0$
or
![]() $\mathbb {Z}/2$
. Let
$\mathbb {Z}/2$
. Let
![]() $\mathcal {R}$
be the Rost motive of X: it is a direct summand of
$\mathcal {R}$
be the Rost motive of X: it is a direct summand of
![]() $M(X;\mathbb {Z}_{(2)})$
. By [Reference Karpenko and Merkurjev21, Theorem RM.10],
$M(X;\mathbb {Z}_{(2)})$
. By [Reference Karpenko and Merkurjev21, Theorem RM.10],
![]() $CH^2(\mathcal {R})[2]\neq 0$
if and only if there exists
$CH^2(\mathcal {R})[2]\neq 0$
if and only if there exists
![]() $1\leq i\leq n-1$
, such that
$1\leq i\leq n-1$
, such that
![]() $2^n-2^i=2$
, that is, if and only if
$2^n-2^i=2$
, that is, if and only if
![]() $n=2$
. If this is the case, then
$n=2$
. If this is the case, then
![]() $CH^2(X)_{\operatorname {tors}}\simeq \mathbb {Z}/2$
and
$CH^2(X)_{\operatorname {tors}}\simeq \mathbb {Z}/2$
and
![]() $\dim (X)=3$
.
$\dim (X)=3$
.
By definition of norm variety, for every field extension
![]() $F/k$
, we have
$F/k$
, we have
![]() $X(F)\neq \emptyset $
(that is,
$X(F)\neq \emptyset $
(that is,
![]() $q_F$
is isotropic) if and only if
$q_F$
is isotropic) if and only if
![]() $s_F$
is trivial. Therefore, by a theorem of Rost [Reference Rost35, Theorem 5] (see also [Reference Yagita52, Lemma 2.1], or follow the construction of the isomorphisms in [Reference Karpenko and Merkurjev21, Theorem RM.10]), the natural pullback map
$s_F$
is trivial. Therefore, by a theorem of Rost [Reference Rost35, Theorem 5] (see also [Reference Yagita52, Lemma 2.1], or follow the construction of the isomorphisms in [Reference Karpenko and Merkurjev21, Theorem RM.10]), the natural pullback map
![]() $CH^*(\mathcal {R})\to CH^*(\mathcal {R}_F)$
is injective for all field extensions
$CH^*(\mathcal {R})\to CH^*(\mathcal {R}_F)$
is injective for all field extensions
![]() $F/k$
, such that
$F/k$
, such that
![]() $q_F$
is anisotropic.
$q_F$
is anisotropic.
Recall that every form of degree
![]() $5$
over a p-adic field is isotropic (see [Reference Lam23, Chapter XI, Example 6.2(4)]). Thus, if q is isotropic at all real places of k, then q is isotropic at all places of k, and so it is isotropic by the Hasse-Minkowski principle [Reference Lam24, Chapter VI, Principle 3.1], hence,
$5$
over a p-adic field is isotropic (see [Reference Lam23, Chapter XI, Example 6.2(4)]). Thus, if q is isotropic at all real places of k, then q is isotropic at all places of k, and so it is isotropic by the Hasse-Minkowski principle [Reference Lam24, Chapter VI, Principle 3.1], hence,
![]() $CH^2(X)$
is torsion free by [Reference Karpenko20, Theorem 6.1]. Suppose now that there exists one real embedding
$CH^2(X)$
is torsion free by [Reference Karpenko20, Theorem 6.1]. Suppose now that there exists one real embedding
![]() $k\subset \mathbb {R}$
, such that
$k\subset \mathbb {R}$
, such that
![]() $q_{\mathbb {R}}$
is not isotropic. We have a commutative square
$q_{\mathbb {R}}$
is not isotropic. We have a commutative square

where the vertical maps are the cycle class maps in étale cohomology and the horizontal maps are induced by base change. The vertical map on the right is injective by [Reference Colliot-Thélène and Sujatha9, Proposition 2.5]. Since
![]() $CH^2(X)_{\operatorname {\mathrm {tors}}}\simeq \mathbb {Z}/2$
, we deduce that
$CH^2(X)_{\operatorname {\mathrm {tors}}}\simeq \mathbb {Z}/2$
, we deduce that
![]() $\operatorname {\mathrm {cl}}\colon CH^2(X)_{\operatorname {\mathrm {tors}}}\to H^4(X,\mathbb {Z}/2)$
is injective, and so
$\operatorname {\mathrm {cl}}\colon CH^2(X)_{\operatorname {\mathrm {tors}}}\to H^4(X,\mathbb {Z}/2)$
is injective, and so
![]() $\operatorname {\mathrm {cl}}\colon CH^2(X)_{\operatorname {\mathrm {tors}}}\rightarrow H^4(X,\mathbb {Z}_2(2))$
is also injective.
$\operatorname {\mathrm {cl}}\colon CH^2(X)_{\operatorname {\mathrm {tors}}}\rightarrow H^4(X,\mathbb {Z}_2(2))$
is also injective.
Acknowledgments
We thank Burt Totaro for telling us about Question 1.2. We thank Jean-Louis Colliot-Thélène, Stefan Schreieder, Burt Totaro and the referee for helpful comments and suggestions on this work.
Conflict of Interest
The authors have no conflict of interest to declare.