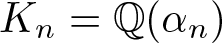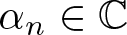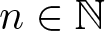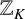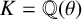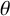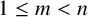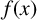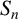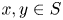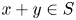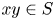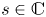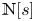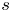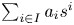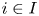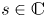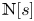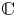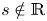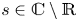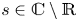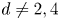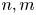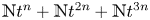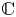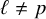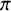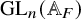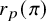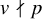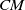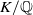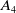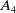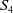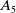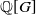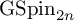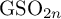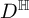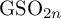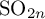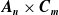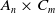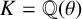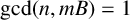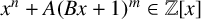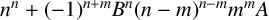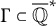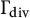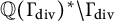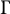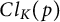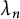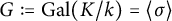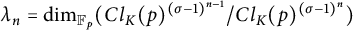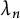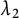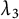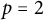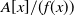308 results in 11Rxx
A solution to the Erdős–Sárközy–Sós problem on asymptotic Sidon bases of order 3
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1418-1432
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NORMAL BASES FOR FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1-12
-
- Article
- Export citation
Spectral decomposition of genuine cusp forms over global function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1194-1260
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discriminant and integral basis of number fields defined by exponential Taylor polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 528-541
-
- Article
- Export citation
CHARACTERISATION OF PRIMES DIVIDING THE INDEX OF A CLASS OF POLYNOMIALS AND ITS APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-8
-
- Article
- Export citation
NON-PÓLYA FIELDS WITH LARGE PÓLYA GROUPS ARISING FROM LEHMER QUINTICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-12
-
- Article
- Export citation
Invariant set generated by a nonreal number is everywhere dense
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local-global compatibility for regular algebraic cuspidal automorphic representations when
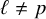 $\ell \neq p$
$\ell \neq p$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 12 February 2024, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kato’s main conjecture for potentially ordinary primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 26 January 2024, pp. 1-21
-
- Article
- Export citation
Leopoldt-type theorems for non-abelian extensions of
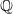 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Refinements of Katz–Sarnak theory for the number of points on curves over finite fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2024, pp. 1-26
-
- Article
- Export citation
On the root of unity ambiguity in a formula for the Brumer–Stark units
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 27 December 2023, pp. 1-13
-
- Article
- Export citation
GALOIS REPRESENTATIONS FOR EVEN GENERAL SPECIAL ORTHOGONAL GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 13 December 2023, pp. 1-92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On
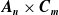 $\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
$\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 119-125
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A CONJECTURE OF LENNY JONES ABOUT CERTAIN MONOGENIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 November 2023, pp. 1-5
-
- Article
- Export citation
The tamely ramified geometric quantitative minimal ramification problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 21-51
- Print publication:
- January 2024
-
- Article
- Export citation
A new way to tackle a conjecture of Rémond
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 31 October 2023, pp. 1-24
-
- Article
- Export citation
Infinite families of Artin–Schreier function fields with any prescribed class group rank
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 October 2023, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Representatives of similarity classes of matrices over PIDs corresponding to ideal classes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 October 2023, pp. 88-103
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Thakur’s basis conjecture for multiple zeta values in positive characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 12 October 2023, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation