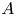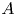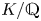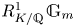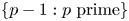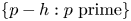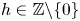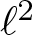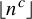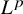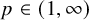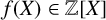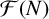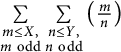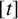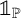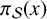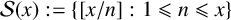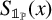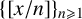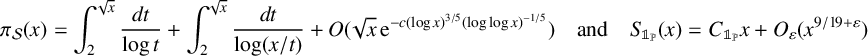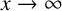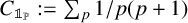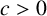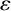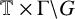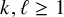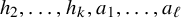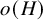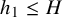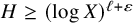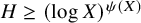125 results in 11Lxx
Weak approximation on the norm one torus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1304-1348
- Print publication:
- June 2024
-
- Article
- Export citation
BOUNDS FOR MOMENTS OF QUADRATIC DIRICHLET CHARACTER SUMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1-5
-
- Article
- Export citation
ON MATRICES ARISING IN FINITE FIELD HYPERGEOMETRIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-6
-
- Article
- Export citation
Unit fractions with shifted prime denominators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
L2 to Lp bounds for spectral projectors on the Euclidean two-dimensional torus
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 431-459
-
- Article
- Export citation
ENERGY BOUNDS FOR MODULAR ROOTS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bracket words along Hardy field sequences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 14 December 2023, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a multi-parameter variant of the Bellow–Furstenberg problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 September 2023, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete restriction estimates for forms in many variables
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 18 September 2023, pp. 923-939
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equidistribution of exponential sums indexed by a subgroup of fixed cardinality
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 65-94
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weil Sums over Small Subgroups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 39-53
- Print publication:
- January 2024
-
- Article
- Export citation
SHORT CHARACTER SUMS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 July 2023, pp. 339-340
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
ON QUADRATIC FIELDS GENERATED BY POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 29 June 2023, pp. 476-485
- Print publication:
- June 2024
-
- Article
- Export citation
Smooth numbers with few nonzero binary digits
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 20 June 2023, pp. 74-89
- Print publication:
- March 2024
-
- Article
- Export citation
Around Exponential-Algebraic Closedness
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 July 2023, p. 300
- Print publication:
- June 2023
-
- Article
-
- You have access
- Export citation
Mean value of real Dirichlet characters using a double Dirichlet series
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 22 March 2023, pp. 1135-1151
- Print publication:
- December 2023
-
- Article
- Export citation
ON THE PRIMES IN FLOOR FUNCTION SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 236-243
- Print publication:
- October 2023
-
- Article
- Export citation
AN AMAZING IDENTITY OF GAUSS AND JENKINS’ LEMMA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 08 November 2022, pp. 86-98
- Print publication:
- August 2023
-
- Article
- Export citation
A NOTE ON MÖBIUS DISJOINTNESS FOR SKEW PRODUCTS ON A CIRCLE AND A NILMANIFOLD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 471-482
- Print publication:
- June 2023
-
- Article
- Export citation
On the Hardy–Littlewood–Chowla conjecture on average
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 27 July 2022, e57
-
- Article
-
- You have access
- Open access
- HTML
- Export citation