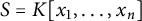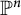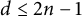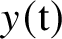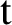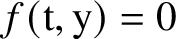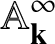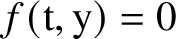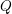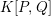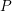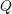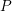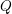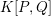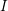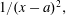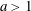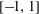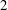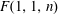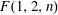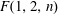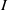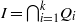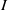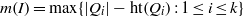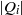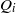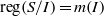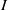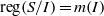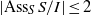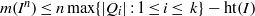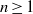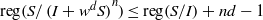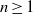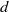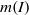24 results in 13Pxx
Ideals with componentwise linear powers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 12 March 2024, pp. 1-9
-
- Article
- Export citation
Toric degenerations of low-degree hypersurfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 1231-1236
- Print publication:
- December 2023
-
- Article
- Export citation
Arquile Varieties – Varieties Consisting of Power Series in a Single Variable
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 01 December 2021, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric vertex decomposition and liaison
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 19 October 2021, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOLVING DIFFERENCE EQUATIONS IN SEQUENCES: UNIVERSALITY AND UNDECIDABILITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e33
-
- Article
-
- You have access
- Open access
- Export citation
ON THE CONJECTURE OF VASCONCELOS FOR ARTINIAN ALMOST COMPLETE INTERSECTION MONOMIAL IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 10 December 2019, pp. 263-277
- Print publication:
- September 2021
-
- Article
- Export citation
ARITHMETIC ASPECTS OF SYMMETRIC EDGE POLYTOPES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 14 May 2019, pp. 763-784
- Print publication:
- 2019
-
- Article
- Export citation
BETTI NUMBERS FOR CERTAIN COHEN–MACAULAY TANGENT CONES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 68-77
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Grothendieck–Plücker Images of Hilbert Schemes are Degenerate
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 22 August 2018, pp. 47-60
-
- Article
- Export citation
Bounding the Number of Common Zeros of Multivariate Polynomials and Their Consecutive Derivatives
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 03 August 2018, pp. 253-279
-
- Article
- Export citation
LIFTINGS OF A MONOMIAL CURVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 05 July 2018, pp. 230-238
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
THE SHORT RESOLUTION OF A SEMIGROUP ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 29 August 2017, pp. 400-411
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
ISOTONIAN ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 08 March 2017, pp. 83-101
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
ON HILBERT FUNCTIONS OF GENERAL INTERSECTIONS OF IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 222 / Issue 1 / June 2016
- Published online by Cambridge University Press:
- 07 June 2016, pp. 61-73
- Print publication:
- June 2016
-
- Article
-
- You have access
- HTML
- Export citation
Irreducible decomposition of binomial ideals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1319-1332
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
A note on uniform approximation of functions having a double pole
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 233-244
-
- Article
-
- You have access
- Export citation
GROEBNER BASES AND NONEMBEDDINGS OF SOME FLAG MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 31 March 2014, pp. 338-353
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
ON A CLASS OF MONOMIAL IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 514-526
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Numerical-symbolic exact irreducible decomposition of cyclic-12
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 155-172
-
- Article
-
- You have access
- Export citation
An extension of Buchberger’s criteria for Gröbner basis decision
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 May 2010, pp. 111-129
-
- Article
-
- You have access
- Export citation