Article contents
BETTI NUMBERS FOR CERTAIN COHEN–MACAULAY TANGENT CONES
Published online by Cambridge University Press: 30 August 2018
Abstract
We compute Betti numbers for a Cohen–Macaulay tangent cone of a monomial curve in the affine 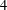 $4$-space corresponding to a pseudo-symmetric numerical semigroup. As a byproduct, we also show that for these semigroups, being of homogeneous type and homogeneous are equivalent properties.
$4$-space corresponding to a pseudo-symmetric numerical semigroup. As a byproduct, we also show that for these semigroups, being of homogeneous type and homogeneous are equivalent properties.
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
Footnotes
The authors were supported by the project 114F094 under the program 1001 of the Scientific and Technological Research Council of Turkey.
References
- 2
- Cited by


