No CrossRef data available.
Article contents
A note on uniform approximation of functions having a double pole
Published online by Cambridge University Press: 01 May 2014
Abstract
We consider the classical problem of finding the best uniform approximation by polynomials of 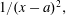 $1/(x-a)^2,$ where
$1/(x-a)^2,$ where 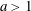 $a>1$ is given, on the interval
$a>1$ is given, on the interval 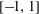 $[-\! 1,1]$. First, using symbolic computation tools we derive the explicit expressions of the polynomials of best approximation of low degrees and then give a parametric solution of the problem in terms of elliptic functions. Symbolic computation is invoked then once more to derive a recurrence relation for the coefficients of the polynomials of best uniform approximation based on a Pell-type equation satisfied by the solutions.
$[-\! 1,1]$. First, using symbolic computation tools we derive the explicit expressions of the polynomials of best approximation of low degrees and then give a parametric solution of the problem in terms of elliptic functions. Symbolic computation is invoked then once more to derive a recurrence relation for the coefficients of the polynomials of best uniform approximation based on a Pell-type equation satisfied by the solutions.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2014


