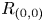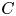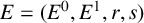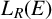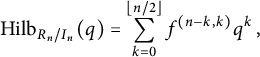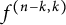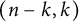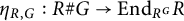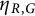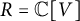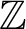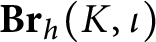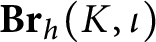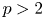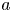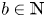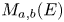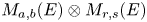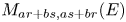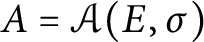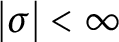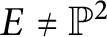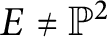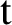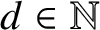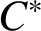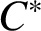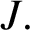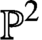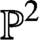77 results in 16Wxx
Pieri rules for skew dual immaculate functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Graphical methods and rings of invariants on the symmetric algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the representability of actions of Leibniz algebras and Poisson algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 22 November 2023, pp. 998-1021
-
- Article
- Export citation
Finite domination and Novikov homology over strongly $\mathbb {Z}^2$
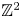 -graded rings
-graded rings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SIMPLICITY OF LEAVITT PATH ALGEBRAS VIA GRADED RING THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 03 March 2023, pp. 428-437
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasisymmetric harmonics of the exterior algebra
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 January 2023, pp. 997-1013
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twisted algebras of geometric algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 18 October 2022, pp. 715-730
- Print publication:
- September 2023
-
- Article
- Export citation
Graded comodule categories with enough projectives
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 257-271
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Auslander’s theorem for dihedral actions on preprojective algebras of type A
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 09 June 2022, pp. 324-339
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Casting light on shadow Somos sequences
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. S87-S101
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mixed Witt rings of algebras with involution
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 29 March 2022, pp. 608-644
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proper Lie automorphisms of incidence algebras
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 07 February 2022, pp. 702-715
- Print publication:
- September 2022
-
- Article
- Export citation
Graded identities for algebras with elementary gradings over an infinite field
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 146-166
-
- Article
- Export citation
Quantum projective planes finite over their centers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 January 2022, pp. 53-67
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arquile Varieties – Varieties Consisting of Power Series in a Single Variable
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 01 December 2021, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert’s 17th problem in free skew fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 06 September 2021, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EVERY GRADED IDEAL OF A LEAVITT PATH ALGEBRA IS GRADED ISOMORPHIC TO A LEAVITT PATH ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 August 2021, pp. 248-256
- Print publication:
- April 2022
-
- Article
- Export citation
AS-REGULARITY OF GEOMETRIC ALGEBRAS OF PLANE CUBIC CURVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 22 June 2021, pp. 193-217
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- Export citation
Two theorems on balanced braces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 05 May 2021, pp. 262-278
-
- Article
- Export citation
The Plectic Weight Filtration on Cohomology of Shimura Varieties and Partial Frobenius
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 12 April 2021, e30
-
- Article
-
- You have access
- Open access
- Export citation