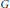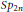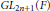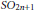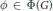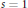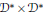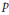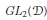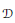25 results
Smith theory and cyclic base change functoriality
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 January 2024, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the derived category of the Iwahori–Hecke algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 04 May 2023, pp. 1042-1110
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Picard group of vertex affinoids in the first Drinfeld covering
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 13 April 2023, pp. 423-432
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The explicit Zelevinsky–Aubert duality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 20 February 2023, pp. 380-418
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Kottwitz conjecture for local shtuka spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 26 May 2022, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON SOME CONSEQUENCES OF A THEOREM OF J. LUDWIG
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 1067-1106
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
Diagrams in the mod p cohomology of Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 07 July 2021, pp. 1653-1723
- Print publication:
- August 2021
-
- Article
- Export citation
ON FORMAL DEGREES OF UNIPOTENT REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 19 March 2021, pp. 1947-1999
- Print publication:
- November 2022
-
- Article
- Export citation
CHARACTERIZING THE MOD-
 $\ell$ LOCAL LANGLANDS CORRESPONDENCE BY NILPOTENT GAMMA FACTORS
$\ell$ LOCAL LANGLANDS CORRESPONDENCE BY NILPOTENT GAMMA FACTORS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 12 May 2020, pp. 119-135
- Print publication:
- December 2021
-
- Article
- Export citation
Local Langlands correspondence and ramification for Carayol representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 10 / October 2019
- Published online by Cambridge University Press:
- 06 September 2019, pp. 1959-2038
- Print publication:
- October 2019
-
- Article
- Export citation
COHOMOLOGY AND OVERCONVERGENCE FOR REPRESENTATIONS OF POWERS OF GALOIS GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 11 April 2019, pp. 361-421
- Print publication:
- March 2021
-
- Article
- Export citation
Patching and the
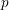 $p$
-adic Langlands program for
$p$
-adic Langlands program for
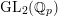 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 01 December 2017, pp. 503-548
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
On mod
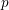 $p$ local-global compatibility for
$p$ local-global compatibility for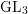 $\text{GL}_{3}$ in the ordinary case
$\text{GL}_{3}$ in the ordinary case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 25 August 2017, pp. 2215-2286
- Print publication:
- November 2017
-
- Article
-
- You have access
- HTML
- Export citation
Stable vectors in Moy–Prasad filtrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 09 February 2017, pp. 358-372
- Print publication:
- February 2017
-
- Article
-
- You have access
- HTML
- Export citation
TEMPERED SPECTRAL TRANSFER IN THE TWISTED ENDOSCOPY OF REAL GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 17 December 2014, pp. 569-612
- Print publication:
- July 2016
-
- Article
- Export citation
Lefschetz operator and local Langlands mod ℓ: The regular case
-
- Journal:
- Nagoya Mathematical Journal / Volume 208 / December 2012
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-38
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Simple wild
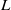 -packets
-packets
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 16 May 2012, pp. 43-75
- Print publication:
- January 2013
-
- Article
- Export citation
Decomposition of Splitting Invariants in Split Real Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 5 / 18 October 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1083-1106
- Print publication:
- 18 October 2011
-
- Article
-
- You have access
- Export citation
Genericity of Representations of p-Adic Sp2n and Local Langlands Parameters
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 5 / 18 October 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1107-1136
- Print publication:
- 18 October 2011
-
- Article
-
- You have access
- Export citation
On the Restriction to
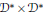 ${{\mathcal{D}}^{*}}\,\times \,{{\mathcal{D}}^{*}}$ of Representations of
${{\mathcal{D}}^{*}}\,\times \,{{\mathcal{D}}^{*}}$ of Representations of 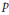 $p$-adic
$p$-adic 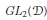 $G{{L}_{2}}(\mathcal{D})$
$G{{L}_{2}}(\mathcal{D})$
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 5 / 01 October 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1050-1068
- Print publication:
- 01 October 2007
-
- Article
-
- You have access
- Export citation



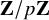
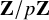
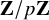
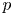
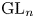
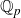
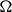
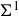
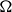
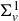
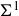
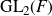
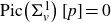
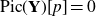
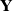
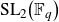
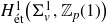
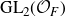
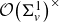
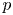
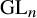
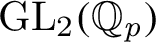
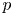
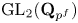
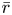
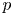
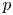
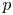
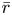
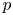
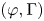
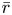
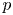
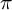
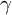
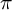
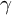

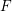
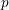
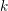
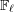

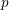
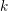
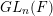
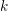


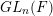
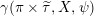
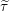
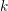

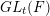


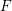
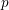
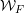

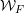

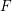

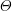


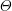

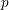

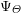
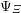
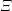

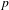
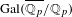
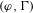
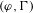
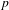
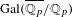
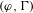
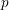
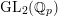
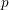
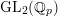
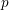
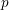
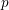
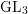
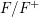
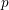
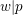
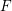
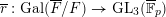
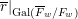

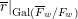
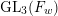
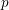



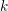
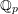
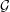
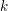
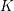
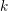
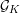
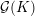
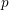
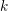
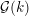
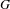
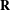
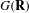
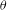
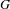

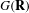
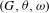
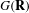
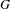
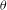
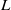 -packets
-packets
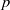 -adic groups, and they conjecture that a special class of these – the simple wild parameters – should correspond to
-adic groups, and they conjecture that a special class of these – the simple wild parameters – should correspond to 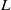 -packets consisting of simple supercuspidal representations. We provide a construction of this correspondence, and show that the simple wild
-packets consisting of simple supercuspidal representations. We provide a construction of this correspondence, and show that the simple wild 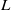 -packets satisfy many expected properties. In particular, they admit a description in terms of the Langlands dual group, and contain a unique generic element for a fixed Whittaker datum. Moreover, we prove their stability on an open subset of the regular semi-simple elements, and show that they satisfy a natural compatibility with respect to unramified base-change.
-packets satisfy many expected properties. In particular, they admit a description in terms of the Langlands dual group, and contain a unique generic element for a fixed Whittaker datum. Moreover, we prove their stability on an open subset of the regular semi-simple elements, and show that they satisfy a natural compatibility with respect to unramified base-change.