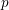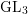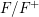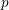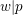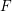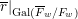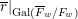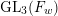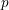1 Introduction
1.1 Motivation and statement of main results
Suppose that
$p$
is a prime and that
$\overline{\unicode[STIX]{x1D70C}}:\operatorname{Gal}(\overline{\mathbb{Q}}_{p}/\mathbb{Q}_{p})\rightarrow \operatorname{GL}_{n}(\overline{\mathbb{F}}_{p})$
is a continuous Galois representation. One would hope that there is a mod
$p$
Langlands correspondence that associates to
$\overline{\unicode[STIX]{x1D70C}}$
in a natural way a smooth representation
$\unicode[STIX]{x1D6F1}(\overline{\unicode[STIX]{x1D70C}})$
of
$\operatorname{GL}_{n}(\mathbb{Q}_{p})$
over
$\overline{\mathbb{F}}_{p}$
(or maybe a packet of such representations), and similarly for
$p$
-adic representations. Unfortunately, at this point, this is only known for
$n\leqslant 2$
[Reference BreuilBre03], [Reference ColmezCol10]. But suppose now that
$F/F^{+}$
is a CM extension of number fields in which
$p$
splits completely, and fix a place
$w|p$
. Even in the absence of a local mod
$p$
Langlands correspondence for
$n>2$
, given a global automorphic Galois representation
$\overline{r}:\operatorname{Gal}(\overline{F}/F)\rightarrow \operatorname{GL}_{n}(\overline{\mathbb{F}}_{p})$
we can define smooth representations
$\unicode[STIX]{x1D6F1}_{\text{glob}}(\overline{r})$
of
$\operatorname{GL}_{n}(\mathbb{Q}_{p})$
over
$\overline{\mathbb{F}}_{p}$
on spaces of mod
$p$
automorphic forms on a definite unitary group, that serve as candidates for
$\unicode[STIX]{x1D6F1}(\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})})$
(in the spirit of Emerton’s local-global compatibility [Reference EmertonEme11]; see also [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] in the
$p$
-adic setting). It is not known whether
$\unicode[STIX]{x1D6F1}_{\text{glob}}(\overline{r})$
depends only on
$\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})}$
. The motivating question of this paper is opposite to this: do the candidate representations
$\unicode[STIX]{x1D6F1}_{\text{glob}}(\overline{r})$
contain at least as much information as
$\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})}$
? We answer this question in the affirmative in many cases when
$n=3$
.
We fix a finite extension
$E/\mathbb{Q}_{p}$
with residue field
$\mathbb{F}$
, and consider absolutely irreducible Galois representations
$\overline{r}:\operatorname{Gal}(\overline{F}/F)\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
. We assume moreover that
$\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})}$
is upper-triangular, maximally non-split, and generic. This means that
$$\begin{eqnarray}\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})}\sim \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D714}^{a+1}\text{nr}_{\unicode[STIX]{x1D707}_{2}} & \ast _{1} & \ast \\ & \unicode[STIX]{x1D714}^{b+1}\text{nr}_{\unicode[STIX]{x1D707}_{1}} & \ast _{2}\\ & & \unicode[STIX]{x1D714}^{c+1}\text{nr}_{\unicode[STIX]{x1D707}_{0}}\end{array}\right),\end{eqnarray}$$
the extensions
$\ast _{1}$
,
$\ast _{2}$
are non-split, and
$a-b>2$
,
$b-c>2$
,
$a-c<p-3$
. (Here,
$\unicode[STIX]{x1D714}$
is the mod
$p$
cyclotomic character and
$\text{nr}_{\unicode[STIX]{x1D707}}$
denotes the unramified character taking value
$\unicode[STIX]{x1D707}\in \mathbb{F}^{\times }$
on geometric Frobenius elements.) It is not hard to see that once the diagonal characters are fixed, the isomorphism class of
$\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})}$
is determined by an invariant
$\text{FL}(\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})})$
that can take any value in
$\mathbb{P}^{1}(\mathbb{F})\setminus \{\unicode[STIX]{x1D707}_{1}\}$
. (We normalize this invariant using Fontaine–Laffaille theory, see Definition 2.1.10.)
To explain our results, we briefly describe our global setup, referring to § 4 for details. Fix a unitary group
$G_{/F^{+}}$
such that
$G\times F\cong \operatorname{GL}_{3}$
and
$G(F_{v}^{+})\cong U_{3}(\mathbb{R})$
for all
$v|\infty$
. Choose a model
${\mathcal{G}}_{/{\mathcal{O}}_{F^{+}}}$
of
$G$
such that
${\mathcal{G}}\times {\mathcal{O}}_{F_{v^{\prime }}^{+}}$
is reductive for all places
$v^{\prime }$
of
$F^{+}$
that split in
$F$
. Let
$v=w|_{F^{+}}$
. Choose a compact open subgroup
$U=U^{v}\times {\mathcal{G}}({\mathcal{O}}_{F_{v}^{+}})\leqslant G(\mathbb{A}_{F^{+}}^{\infty })$
that is sufficiently small, and unramified at all places dividing
$p$
. Let
$V^{\prime }$
denote an irreducible smooth representation of
$\prod _{v^{\prime }|p,v^{\prime }\neq v}{\mathcal{G}}({\mathcal{O}}_{F_{v^{\prime }}^{+}})$
over
$\mathbb{F}$
determined by a highest weight in the lowest alcove, and let
$\widetilde{V}^{\prime }$
denote a Weyl module of
$\prod _{v^{\prime }|p,v^{\prime }\neq v}{\mathcal{G}}({\mathcal{O}}_{F_{v^{\prime }}^{+}})$
over
${\mathcal{O}}_{E}$
of the same highest weight, so
$\widetilde{V}^{\prime }\otimes _{{\mathcal{O}}_{E}}\mathbb{F}\cong V^{\prime }$
. (Except for Theorem C below, the reader may assume for simplicity that
$V^{\prime }=\mathbb{F}$
and
$\widetilde{V}^{\prime }={\mathcal{O}}_{E}$
.) We can then define in the usual way spaces of mod
$p$
automorphic forms
$S(U^{v},V^{\prime })=\mathop{\varinjlim }\nolimits_{U_{v}\leqslant G(F_{v}^{+})}S(U^{v}U_{v},V^{\prime })$
and similarly
$S(U^{v},\widetilde{V}^{\prime })$
that are smooth representations of
$G(F_{v}^{+})\cong \operatorname{GL}_{3}(\mathbb{Q}_{p})$
(where this isomorphism depends on our chosen place
$w|v$
).
We fix a cofinite subset
${\mathcal{P}}$
of places
$w^{\prime }\nmid p$
of
$F$
that split over
$F^{+}$
, such that
$U$
is unramified at
$w^{\prime }|_{F^{+}}$
, and such that
$\overline{r}$
is unramified at
$w^{\prime }$
. Then the abstract Hecke algebra
$\mathbb{T}^{{\mathcal{P}}}$
generated over
${\mathcal{O}}_{E}$
by Hecke operators at all places in
${\mathcal{P}}$
acts on
$S(U^{v},V^{\prime })$
and
$S(U^{v},\widetilde{V}^{\prime })$
, commuting with the
$\operatorname{GL}_{3}(\mathbb{Q}_{p})$
-actions. Moreover,
$\overline{r}$
determines a maximal ideal
$\mathfrak{m}_{\overline{r}}$
of
$\mathbb{T}^{{\mathcal{P}}}$
. We assume that
$\overline{r}$
is automorphic in this setup, which means that
$S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]\neq 0$
(or equivalently,
$S(U^{v},V^{\prime })_{\mathfrak{m}_{\overline{r}}}\neq 0$
). These
$\operatorname{GL}_{3}(\mathbb{Q}_{p})$
-representations,
$S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]$
, are the natural candidates
$\unicode[STIX]{x1D6F1}_{\text{glob}}(\overline{r})$
that we mentioned above, at least if the level
$U^{v}$
is chosen optimally.
It is a consequence of earlier work of the first-named author and Breuil [Reference Breuil and HerzigBH15] that the
$\operatorname{GL}_{3}(\mathbb{Q}_{p})$
-representation
$S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]$
determines the ordered triple of diagonal characters
$(\unicode[STIX]{x1D714}^{a+1}\text{nr}_{\unicode[STIX]{x1D707}_{2}},\unicode[STIX]{x1D714}^{b+1}\text{nr}_{\unicode[STIX]{x1D707}_{1}},\unicode[STIX]{x1D714}^{c+1}\text{nr}_{\unicode[STIX]{x1D707}_{0}})$
of
$\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})}$
. In fact, the triple
$(a,b,c)$
can be recovered from the (ordinary part of the)
$\operatorname{GL}_{3}(\mathbb{Z}_{p})$
-socle, i.e., the Serre weights of
$\overline{r}$
, by [Reference Gee and GeraghtyGG12] and the
$\unicode[STIX]{x1D707}_{i}\in \mathbb{F}^{\times }$
are determined by the Hecke action at
$p$
on the
$\operatorname{GL}_{3}(\mathbb{Z}_{p})$
-socle. It therefore remains for us to show that
$S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]$
determines the invariant
$\text{FL}(\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})})$
. (We note that the representation
$\unicode[STIX]{x1D6F1}(\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})})^{\text{ord}}$
of [Reference Breuil and HerzigBH15] does not contain this information.)
Let
$I$
denote the Iwahori subgroup of
$\operatorname{GL}_{3}(\mathbb{Z}_{p})$
, which is the preimage of the upper-triangular matrices
$B(\mathbb{F}_{p})$
in
$\operatorname{GL}_{3}(\mathbb{F}_{p})$
. If
$V$
is a representation of
$\operatorname{GL}_{3}(\mathbb{Z}_{p})$
over
${\mathcal{O}}_{E}$
and
$a_{i}\in \mathbb{Z}$
we write
$$\begin{eqnarray}V^{I,(a_{2},a_{1},a_{0})}\stackrel{\text{def}}{=}\operatorname{Hom}_{I}({\mathcal{O}}_{E}(\widetilde{\unicode[STIX]{x1D714}}^{a_{2}}\otimes \widetilde{\unicode[STIX]{x1D714}}^{a_{1}}\otimes \widetilde{\unicode[STIX]{x1D714}}^{a_{0}}),V),\end{eqnarray}$$
where the character in the domain denotes the inflation to
$I$
of the homomorphism
$B(\mathbb{F}_{p})\rightarrow {\mathcal{O}}_{E}^{\times }$
,
$\Bigl(\!\begin{smallmatrix}x & y & z\\ & u & v\\ & & w\end{smallmatrix}\!\Bigr)\mapsto \widetilde{x}^{a_{2}}\widetilde{u}^{a_{1}}\widetilde{w}^{a_{0}}$
. If
$V$
is even a representation of
$\operatorname{GL}_{3}(\mathbb{Q}_{p})$
, then
$V^{I,(a_{2},a_{1},a_{0})}$
affords an action of
$U_{p}$
-operators
$U_{1}$
,
$U_{2}$
(see (3.1.10)). Define also
$\unicode[STIX]{x1D6F1}\stackrel{\text{def}}{=}\Bigl(\!\begin{smallmatrix} & 1 & \\ & & 1\\ p & & \end{smallmatrix}\!\Bigr)$
, which sends
$V^{I,(a_{2},a_{1},a_{0})}$
to
$V^{I,(a_{1},a_{0},a_{2})}$
.
Finally, and crucially, we define explicit group algebra operators
$S$
,
$S^{\prime }\in \mathbb{F}[\operatorname{GL}_{3}(\mathbb{F}_{p})]$
, see (4.5.1). We can now state our first main theorem.
Theorem A (Theorem 4.5.2).
We make the following additional assumptions:
-
(i)
$\text{FL}(\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})})\not \in \{0,\infty \}$
; -
(ii) the
${\mathcal{O}}_{E}$
-dual of
$S(U^{v},\widetilde{V}^{\prime })_{\mathfrak{m}_{\overline{r}}}^{I,(-b,-c,-a)}$
is free over
$\mathbb{T}$
, where
$\mathbb{T}$
denotes the
${\mathcal{O}}_{E}$
-subalgebra of
$\operatorname{End}\big(S(U^{v},\widetilde{V}^{\prime })_{\mathfrak{m}_{\overline{r}}}^{I,(-b,-c,-a)}\big)$
generated by
$\mathbb{T}^{{\mathcal{P}}}$
,
$U_{1}$
, and
$U_{2}$
.
Then we have the equality
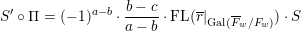$$\begin{eqnarray}S^{\prime }\circ \unicode[STIX]{x1D6F1}=(-1)^{a-b}\cdot \frac{b-c}{a-b}\cdot \text{FL}(\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})})\cdot S\end{eqnarray}$$
of maps
$$\begin{eqnarray}S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]^{I,(-b,-c,-a)}[U_{1},U_{2}]\rightarrow S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]^{I,(-c-1,-b,-a+1)}.\end{eqnarray}$$
Moreover, these maps are injective with non-zero domain. In particular,
$\text{FL}(\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})})$
is determined by the smooth
$\operatorname{GL}_{3}(\mathbb{Q}_{p})$
-representation
$S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]$
.
The first assumption is related to the surprising fact that the
$\operatorname{GL}_{3}(\mathbb{Z}_{p})$
-socle of
$S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]$
changes for the exceptional two invariants, see Theorem D below. (Incidentally, this means that even in the exceptional cases
$\text{FL}(\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})})$
is determined by
$S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]$
.)
We show that the second assumption is often a consequence of the first assumption. The second assumption is an analogue of Mazur’s ‘mod
$p$
multiplicity one’ result, and thus our result may be of independent interest. We have not tried to optimize our hypotheses, the most stringent of which is that
$U$
may be taken to be unramified at all finite places.
Theorem B (Theorem 5.1.1).
Assume hypotheses (i)–(ix) in § 5.1. If
$\text{FL}(\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})})\neq \infty$
, then assumption (ii) in Theorem A holds.
In fact we show that for any value of
$\text{FL}(\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})})$
either the second assumption or its dual holds (see Remark 5.3.6).
We also show, using results of [Reference Emerton and GeeEG14], that for any given local Galois representation as in (1.1.1) we can construct a globalization to which Theorem B applies.
Theorem C (Theorem 5.3.7).
Suppose that
$\overline{\unicode[STIX]{x1D70C}}:\operatorname{Gal}(\overline{\mathbb{Q}}_{p}/\mathbb{Q}_{p})\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
is upper-triangular, maximally non-split, and generic. Then, after possibly replacing
$\mathbb{F}$
by a finite extension, there exist a CM field
$F$
, a Galois representation
$\overline{r}:\operatorname{Gal}(\overline{F}/F)\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
, a place
$w|p$
of
$F$
, groups
$G_{/F^{+}}$
and
${\mathcal{G}}_{/{\mathcal{O}}_{F^{+}}}$
, and a compact open subgroup
$U^{v}$
(where
$v=w|_{F^{+}}$
) satisfying all hypotheses of the setup in § 5.1 such that
$\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})}\cong \overline{\unicode[STIX]{x1D70C}}$
. In particular, if
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})\not \in \{0,\infty \}$
, Theorem A applies to
$\overline{r}$
.
As a by-product of our methods we almost completely determine the set of Serre weights of
$\overline{r}$
. Here, the set
$W_{w}(\overline{r})$
is defined to be the set of irreducible
$\operatorname{GL}_{3}(\mathbb{Z}_{p})$
-representations whose duals occur in the
$\operatorname{GL}_{3}(\mathbb{Z}_{p})$
-socle of
$S(U^{v},V^{\prime })_{\mathfrak{m}_{\overline{r}}}$
(for some
$U^{v}$
and
${\mathcal{P}}$
as above). See § 4.2 for our notation for Serre weights.
Theorem D (Theorem 4.4.1).
Keep the assumptions on
$\overline{r}$
that precede Theorem A above.
-
(i) If
$\text{FL}(\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})})\notin \{0,\infty \}$
we have
$$\begin{eqnarray}\displaystyle & \{F(a-1,b,c+1)\}\subseteq W_{w}(\overline{r})\subseteq \{F(a-1,b,c+1),F(c+p-1,b,a-p+1)\}. & \displaystyle \nonumber\end{eqnarray}$$
-
(ii) If
$\text{FL}(\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})})=\infty$
we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \{F(a-1,b,c+1),F(a,c,b-p+1)\}\nonumber\\ \displaystyle & & \displaystyle \qquad \subseteq W_{w}(\overline{r})\subseteq \{F(a-1,b,c+1),F(c+p-1,b,a-p+1),F(a,c,b-p+1)\}.\nonumber\end{eqnarray}$$
-
(iii) If
$\text{FL}(\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})})=0$
we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \{F(a-1,b,c+1),F(b+p-1,a,c)\}\nonumber\\ \displaystyle & & \displaystyle \qquad \subseteq W_{w}(\overline{r})\subseteq \{F(a-1,b,c+1),F(c+p-1,b,a-p+1),F(b+p-1,a,c)\}.\nonumber\end{eqnarray}$$
This is one of the first Serre weight results in dimension 3. It was completed in early 2014, before the recent progress of [Reference Le, Hung, Levin and MorraLHLM15] (on Serre weights in dimension 3 in the generic semisimple case, using different methods). As we said above, the dependence on
$\text{FL}(\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})})$
in this theorem was unexpected, as there were no explicit Serre weight conjectures in the literature that apply to non-semisimple
$\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})}$
.
As a consequence of this theorem we also show the existence of an automorphic lift
$r$
of
$\overline{r}$
such that
$r|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})}$
is upper-triangular. It is in the same spirit as the main results of [Reference Barnet-Lamb, Gee and GeraghtyBLGG12] (which concerned two-dimensional representations).
Theorem E (Corollary 4.4.4).
In the setting of Theorem D,
$\overline{r}$
has an automorphic lift
$r:\operatorname{Gal}(\overline{F}/F)\rightarrow \operatorname{GL}_{3}({\mathcal{O}}_{E})$
(after possibly enlarging
$E$
) such that
$r|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})}$
is crystalline and ordinary of Hodge–Tate weights
$\{-a-1,-b-1,-c-1\}$
.
1.2 Methods used
Theorems A and B generalize earlier work of Breuil and Diamond [Reference Breuil and DiamondBD14] which treated the case of two-dimensional Galois representations of
$\operatorname{Gal}(\overline{F}/F)$
, where
$F$
is totally real and
$p$
is unramified in
$F$
. We follow the same general strategy: we lift the Hecke eigenvalues of
$\overline{r}$
to a well-chosen type in characteristic zero, use classical local-global compatibility at
$p$
, and then study carefully how both the Galois-side and the
$\operatorname{GL}_{3}$
-side reduce modulo
$p$
. However, it is significantly more difficult to carry out this strategy in the
$\operatorname{GL}_{3}$
-setting.
We first prove the upper bound in Theorem D by lifting to various types in characteristic zero and using integral
$p$
-adic Hodge theory to reduce modulo
$p$
. This is more involved in dimension 3, since we are no longer in the potentially Barsotti–Tate setting. We crucially use results of Caruso to filter our Breuil module (corresponding to
$\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})}$
) according to the socle filtration on
$\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})}$
, see Proposition 2.3.5.
The following theorem is our key local result on the Galois-side. Our chosen type is a tame principal series that contains in its reduction modulo
$p$
all elements of
$W_{w}(\overline{r})$
(unlike in [Reference Breuil and DiamondBD14], where the intersection always consisted of one element). In contrast to [Reference Breuil and DiamondBD14] we get away with a rough classification of the strongly divisible module corresponding to
$\unicode[STIX]{x1D70C}$
. (We do not need to determine Frobenius and monodromy operators.) We also note that the relevant information on the Galois-side is independent of the Hodge filtration, so that we can transfer this information to the
$\operatorname{GL}_{3}$
-side using classical local-global compatibility.
Theorem F (Theorem 2.5.1).
Let
$\unicode[STIX]{x1D70C}:\operatorname{Gal}(\overline{\mathbb{Q}}_{p}/\mathbb{Q}_{p})\rightarrow \text{GL}_{3}({\mathcal{O}}_{E})$
be a potentially semistable
$p$
-adic Galois representation of Hodge–Tate weights
$\{-2,-1,0\}$
and inertial type
$\widetilde{\unicode[STIX]{x1D714}}^{a}\oplus \widetilde{\unicode[STIX]{x1D714}}^{b}\oplus \widetilde{\unicode[STIX]{x1D714}}^{c}$
. Assume that the residual representation
$\overline{\unicode[STIX]{x1D70C}}:\operatorname{Gal}(\overline{\mathbb{Q}}_{p}/\mathbb{Q}_{p})\rightarrow \text{GL}_{3}(\mathbb{F})$
is upper-triangular, maximally non-split, and generic as in (1.1.1). Let
$\unicode[STIX]{x1D706}\in {\mathcal{O}}_{E}$
be the Frobenius eigenvalue on
$\text{D}_{\text{st}}^{\mathbb{Q}_{p},2}(\unicode[STIX]{x1D70C})^{I_{\mathbb{Q}_{p}}=\widetilde{\unicode[STIX]{x1D714}}^{b}}$
. Then the Fontaine–Laffaille invariant of
$\overline{\unicode[STIX]{x1D70C}}$
is given by
$$\begin{eqnarray}\text{FL}(\overline{\unicode[STIX]{x1D70C}})=\operatorname{red}(p\unicode[STIX]{x1D706}^{-1}),\end{eqnarray}$$
where
$\operatorname{red}$
denotes the specialization map
$\mathbb{P}^{1}({\mathcal{O}}_{E})\rightarrow \mathbb{P}^{1}(\mathbb{F})$
.
On the
$\operatorname{GL}_{3}$
-side our main innovation consists of the explicit group algebra operators
$S$
,
$S^{\prime }$
. The analogues of these operators for
$\operatorname{GL}_{2}$
show up in various contexts (see, for example, [Reference PaskunasPas07, Lemma 4.1], [Reference Breuil and PaškūnasBP12, Lemma 2.7], [Reference BreuilBre11, § 4], and [Reference Breuil and DiamondBD14, Proposition 2.6.1]). Our proof is specific to
$\operatorname{GL}_{3}$
. It would be interesting to find a more conceptual explanation for them. See also Question 3.1.3 for a further discussion of such operators.
Proposition G (Proposition 3.1.2).
-
(i) There is a unique non-split extension of irreducible
$\operatorname{GL}_{3}(\mathbb{F}_{p})$
-representations and
$$\begin{eqnarray}0\rightarrow F(-c-1,-b,-a+1)\rightarrow V\rightarrow F(-b+p-1,-c,-a)\rightarrow 0\end{eqnarray}$$
$S$
induces an isomorphism
$S:\,V^{I,(-b,-c,-a)}\stackrel{{\sim}}{\longrightarrow }V^{I,(-c-1,-b,-a+1)}$
of one-dimensional vector spaces.
-
(ii) There is a unique non-split extension of irreducible
$\operatorname{GL}_{3}(\mathbb{F}_{p})$
-representations and
$$\begin{eqnarray}0\rightarrow F(-c-1,-b,-a+1)\rightarrow V\rightarrow F(-c,-a,-b-p+1)\rightarrow 0\end{eqnarray}$$
$S^{\prime }$
induces an isomorphism
$S^{\prime }:\,V^{I,(-c,-a,-b)}\stackrel{{\sim}}{\longrightarrow }V^{I,(-c-1,-b,-a+1)}$
of one-dimensional vector spaces.
The result concerning reduction modulo
$p$
on the
$\operatorname{GL}_{3}$
-side is comparatively easier, see Proposition 3.2.2.
By combining the above results we deduce Theorem A. We note that assumption (ii) is needed for lifting elements of
$S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]^{I,(-b,-c,-a)}[U_{1},U_{2}]$
to suitable Iwahori eigenvectors in characteristic zero. The
$U_{i}$
-operators allow us to deal with the possible presence of the shadow weight
$F(c+p-1,b,a-p+1)$
in Theorem D. (The term ‘shadow weight’ is defined in [Reference Emerton, Gee and HerzigEGH13, § 6], and more generally in [Reference Gee, Herzig and SavittGHS16, §§ 1.5 and 7.2].) Namely, if
$v\in S(U^{v},V^{\prime })$
$[\mathfrak{m}_{\overline{r}}]^{I,(-b,-c,-a)}[U_{1},U_{2}]$
is non-zero, we show that it generates the representation of Proposition G(i) under the
$\operatorname{GL}_{3}(\mathbb{Z}_{p})$
-action. Similar comments apply to
$\unicode[STIX]{x1D6F1}v$
. Proposition G then allows us to deduce that the maps in Theorem A are well defined and injective. (We refer to Remark 4.5.8 for variations on assumption (ii). The stronger assumptions appearing in Remark 4.5.9 are analogous to the multiplicity one conditions appearing in [Reference Breuil and DiamondBD14].)
Interestingly, the argument proving Theorem A also lets us deduce the hardest part of Theorem D, namely the existence of the shadow weights
$F(a,c,b-p+1)$
,
$F(b+p-1,a,c)$
in the two exceptional cases. After [Reference Emerton, Gee and HerzigEGH13], this is only the second result in the literature proving the existence of shadow weights. (Again this precedes [Reference Le, Hung, Levin and MorraLHLM15].)
Finally, we establish Theorem B. As in [Reference Breuil and DiamondBD14] our method relies on the Taylor–Wiles method. However, as we do not know whether our local deformation ring at
$p$
is formally smooth (which in any case should be false if our chosen type intersects
$W_{w}(\overline{r})$
in more than one element) we cannot directly apply Diamond’s method [Reference DiamondDia97]. Instead we use the patched modules of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] that live over the universal deformation space at
$p$
and use ideas of [Reference Emerton, Gee and SavittEGS15] and [Reference LeLe15]. See Theorem 5.2.3 for our freeness result at infinite level from which we deduce Theorem B. Similarly to above, we add
$U_{p}$
-operators in order to deal with the possible presence of the shadow weight
$F(c+p-1,b,a-p+1)$
.
1.3 Notation
Let
$\overline{\mathbb{Q}}$
be an algebraic closure of
$\mathbb{Q}$
. All number fields
$F/\mathbb{Q}$
will be considered as subfields of
$\overline{\mathbb{Q}}$
and we write
$G_{F}\stackrel{\text{def}}{=}\operatorname{Gal}(\overline{\mathbb{Q}}/F)$
to denote the absolute Galois group of
$F$
. For any rational prime
$\ell \in \mathbb{Q}$
, we fix algebraic closures
$\overline{\mathbb{Q}}_{\ell }$
of
$\mathbb{Q}_{\ell }$
and embeddings
$\overline{\mathbb{Q}}{\hookrightarrow}\overline{\mathbb{Q}}_{\ell }$
(hence inclusions
$G_{\mathbb{Q}_{\ell }}{\hookrightarrow}G_{\mathbb{Q}}$
). The residue field of
$\overline{\mathbb{Q}}_{\ell }$
, which is an algebraic closure of
$\mathbb{F}_{\ell }$
, is denoted by
$\overline{\mathbb{F}}_{\ell }$
. As above, all algebraic extensions of
$\mathbb{Q}_{\ell }$
,
$\mathbb{F}_{\ell }$
will be considered as subfields of the fixed algebraic closures
$\overline{\mathbb{Q}}_{\ell }$
,
$\overline{\mathbb{F}}_{\ell }$
.
Let
$k/\mathbb{F}_{p}$
be a finite extension of degree
$f\geqslant 1$
, and let
$K_{0}\stackrel{\text{def}}{=}W(k)[1/p]$
be the unramified extension of
$\mathbb{Q}_{p}$
of degree
$f$
. Suppose that
$e\geqslant 1$
is any divisor of
$p^{f}-1$
. (Starting in § 2.4 we will assume
$e=p^{f}-1$
. However, in the appendix it will be convenient to allow more general
$e$
, in particular
$e=1$
.) We consider the Eisenstein polynomial
$E(u)\stackrel{\text{def}}{=}u^{e}+p\in \mathbb{Q}_{p}[u]$
and fix a root
$\unicode[STIX]{x1D71B}=\sqrt[e]{-p}\in \overline{\mathbb{Q}}_{p}$
. Let
$K\stackrel{\text{def}}{=}K_{0}(\unicode[STIX]{x1D71B})$
, a tamely totally ramified cyclic extension of
$K_{0}$
of degree
$e$
with uniformizer
$\unicode[STIX]{x1D71B}$
.
Let
$E$
be a finite extension of
$\mathbb{Q}_{p}$
. We write
${\mathcal{O}}_{E}$
for its ring of integers,
$\mathbb{F}$
for its residue field and
$\unicode[STIX]{x1D71B}_{E}\in {\mathcal{O}}_{E}$
to denote a uniformizer. We always assume that
$K\subseteq E$
.
The choice of
$\unicode[STIX]{x1D71B}\in K$
provides us with a homomorphism
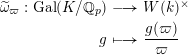$$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}\displaystyle \widetilde{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D71B}}:\operatorname{Gal}(K/\mathbb{Q}_{p})\ & \longrightarrow \ & W(k)^{\times }\\ \displaystyle g\ & \longmapsto \ & \displaystyle \frac{g(\unicode[STIX]{x1D71B})}{\unicode[STIX]{x1D71B}}\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
whose reduction modulo
$p$
will be denoted by
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}$
. Note that the inclusion
$k\subseteq \mathbb{F}$
induced by
$K\subseteq E$
provides us with a niveau
$f$
fundamental character
$\unicode[STIX]{x1D714}_{f}:\operatorname{Gal}(K/K_{0})\rightarrow \mathbb{F}^{\times }$
, namely
$\unicode[STIX]{x1D714}_{f}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}|_{\operatorname{Gal}(K/K_{0})}$
.
We denote by
$\unicode[STIX]{x1D714}:G_{\mathbb{Q}_{p}}\rightarrow \mathbb{F}_{p}^{\times }$
the mod
$p$
cyclotomic character, so
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{1}$
.
Write
$\unicode[STIX]{x1D711}$
for the
$p$
-power Frobenius on
$k$
. We recall the standard idempotent elements
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70E}}\in k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
defined for
$\unicode[STIX]{x1D70E}\in \operatorname{Hom}(k,\mathbb{F})$
, which verify
$(\unicode[STIX]{x1D711}\,\otimes \,1)(\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70E}})=\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D711}^{-1}}$
and
$(\unicode[STIX]{x1D706}\,\otimes \,1)\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70E}}=(1\,\otimes \,\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D706}))\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70E}}$
. We write
$\widehat{\unicode[STIX]{x1D716}}_{\unicode[STIX]{x1D70E}}\in W(k)\otimes _{\mathbb{Z}_{p}}{\mathcal{O}}_{E}$
for the standard idempotent elements; they reduce to
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70E}}$
modulo
$\unicode[STIX]{x1D71B}_{E}$
.
Our convention on Hodge–Tate weights is that the cyclotomic character
$\unicode[STIX]{x1D700}:G_{\mathbb{Q}_{p}}\rightarrow \mathbb{Q}_{p}^{\times }$
has Hodge–Tate weight
$-1$
.
Given a potentially semistable
$p$
-adic representation
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{n}(E)$
, we write
$\operatorname{WD}(\unicode[STIX]{x1D70C})$
to denote the associated Weil–Deligne representation as defined in [Reference Conrad, Diamond and TaylorCDT99, Appendix B.1]. Therefore,
$\unicode[STIX]{x1D70C}\mapsto \operatorname{WD}(\unicode[STIX]{x1D70C})$
is a covariant functor. We refer to
$\operatorname{WD}(\unicode[STIX]{x1D70C})|_{I_{\mathbb{Q}_{p}}}$
as the inertial type associated to
$\unicode[STIX]{x1D70C}$
.
2 The local Galois side
In this section we analyze the local Galois side. In particular, we establish Theorem F of the introduction.
2.1 Fontaine–Laffaille invariant
Let
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
be a continuous Galois representation. We assume that
$\overline{\unicode[STIX]{x1D70C}}$
is maximally non-split meaning that
$\overline{\unicode[STIX]{x1D70C}}$
is uniserial and the graded pieces in its socle filtration are at most one dimensional over
$\mathbb{F}$
. (Recall that a finite length module is uniserial if it has a unique composition series.) In other words,
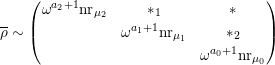$$\begin{eqnarray}\overline{\unicode[STIX]{x1D70C}}\sim \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D714}^{a_{2}+1}\text{nr}_{\unicode[STIX]{x1D707}_{2}} & \ast _{1} & \ast \\ & \unicode[STIX]{x1D714}^{a_{1}+1}\text{nr}_{\unicode[STIX]{x1D707}_{1}} & \ast _{2}\\ & & \unicode[STIX]{x1D714}^{a_{0}+1}\text{nr}_{\unicode[STIX]{x1D707}_{0}}\end{array}\right)\end{eqnarray}$$
for some
$a_{i}\in \mathbb{Z}$
,
$\unicode[STIX]{x1D707}_{i}\in \mathbb{F}^{\times }$
and where
$\ast _{1},\ast _{2}$
are non-split. Here,
$\text{nr}_{\unicode[STIX]{x1D707}}:G_{\mathbb{Q}_{p}}\rightarrow \mathbb{F}^{\times }$
denotes the unramified character taking the value
$\unicode[STIX]{x1D707}$
on a geometric Frobenius element of
$G_{\mathbb{Q}_{p}}$
.
2.1.1 Preliminaries on Fontaine–Laffaille theory
We begin by briefly recalling the theory of Fontaine–Laffaille modules with
$\mathbb{F}$
-coefficients and its relation with mod
$p$
Galois representations.
A Fontaine–Laffaille module
$(M,\operatorname{Fil}^{\bullet }M,\unicode[STIX]{x1D719}_{\bullet })$
over
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
is the datum of
-
(i) a finite free
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
-module
$M$
; -
(ii) a decreasing filtration
$\{\operatorname{Fil}^{j}M\}_{j\in \mathbb{Z}}$
on
$M$
by
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
-submodules such that
$\operatorname{Fil}^{0}M=M$
and
$\operatorname{Fil}^{p-1}M=0$
; -
(iii) a
$\unicode[STIX]{x1D711}$
-semilinear isomorphism
$\unicode[STIX]{x1D719}_{\bullet }:\text{gr}^{\bullet }M\rightarrow M$
.
Defining the morphisms in the obvious way, we obtain the abelian category
$\mathbb{F}\text{-}{\mathcal{F}}{\mathcal{L}}^{[0,p-2]}$
of Fontaine–Laffaille modules over
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
. Given a Fontaine–Laffaille module
$M$
and
$\unicode[STIX]{x1D70E}\in \operatorname{Hom}(k,\mathbb{F})$
, we define the Hodge–Tate weights of
$M$
with respect to
$\unicode[STIX]{x1D70E}$
:
$$\begin{eqnarray}\text{HT}_{\unicode[STIX]{x1D70E}}(M)\stackrel{\text{def}}{=}\biggl\{i\in \mathbb{N}:\dim _{\mathbb{F}}\biggl(\frac{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70E}}\operatorname{Fil}^{i}M}{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70E}}\operatorname{Fil}^{i+1}M}\biggr)\neq 0\biggr\}.\end{eqnarray}$$
In the remainder of this paper we focus on Fontaine–Laffaille modules with parallel Hodge–Tate weights, i.e. we assume that for all
$i\in \mathbb{N}$
, the submodules
$\operatorname{Fil}^{i}M$
are free over
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
.
Definition 2.1.2. Let
$M$
be a Fontaine–Laffaille module with parallel Hodge–Tate weights. A
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
-basis
$\text{}\underline{e}=(e_{0},\ldots ,e_{n-1})$
on
$M$
is compatible with the Hodge filtration if for all
$i\in \mathbb{N}$
there exists
$j_{i}\in \mathbb{N}$
such that
$\operatorname{Fil}^{i}M=\sum _{j=j_{i}}^{n}(k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F})\cdot e_{j}$
.
Note that if the graded pieces of the Hodge filtration have rank at most one, then any two compatible bases on
$M$
are related by a lower triangular matrix in
$\operatorname{GL}_{n}(k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F})$
.
Given a Fontaine–Laffaille module and a compatible basis
$\text{}\underline{e}$
, it is convenient to describe the Frobenius action via a matrix
$\text{Mat}_{\text{}\underline{e}}(\unicode[STIX]{x1D719}_{\bullet })\in \operatorname{GL}_{n}(k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F})$
, defined in the obvious way using the principal symbols
$(\text{gr}(e_{0}),\ldots ,\text{gr}(e_{n-1}))$
as a basis of
$\text{gr}^{\bullet }M$
.
Theorem 2.1.3. There is an exact, fully faithful contravariant functor
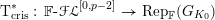$$\begin{eqnarray}\text{T}_{\text{cris}}^{\ast }:\,\mathbb{F}\text{-}{\mathcal{F}}{\mathcal{L}}^{[0,p-2]}\rightarrow \text{Rep}_{\mathbb{ F}}(G_{K_{0}})\end{eqnarray}$$
which is moreover compatible with base change: if
$K_{0}^{\prime }/K_{0}$
is finite unramified, with residue field
$k^{\prime }/k$
, then
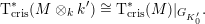$$\begin{eqnarray}\text{T}_{\text{cris}}^{\ast }(M\otimes _{k}k^{\prime })\cong \text{T}_{\text{cris}}^{\ast }(M)|_{G_{K_{0}^{\prime }}}.\end{eqnarray}$$
Also, the essential image of
$\text{T}_{\text{cris}}^{\ast }$
is closed under subquotients.
Proof. The statement with
$\mathbb{F}_{p}$
-coefficients is in [Reference Fontaine and LaffailleFL82, Théorème 6.1]; its analogue with
$\mathbb{F}$
-coefficient is a formal argument which is left to the reader (cf. also [Reference Gao and LiuGL14, Theorem 2.2.1]).◻
Lemma 2.1.4. Let
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
be as in (2.1.1). If the integers
$a_{i}$
verify
$a_{1}-a_{0}>1,a_{2}-a_{1}>1$
and
$p-2>a_{2}-a_{0}$
then
$\overline{\unicode[STIX]{x1D70C}}\,\otimes \,\unicode[STIX]{x1D714}^{-a_{0}}$
is Fontaine–Laffaille, i.e. it is in the essential image of
$\text{T}_{\text{cris}}^{\ast }$
.
Proof. This follows, for example, from [Reference Gee and GeraghtyGG12, Lemma 3.1.5]. ◻
In order to obtain the main results on Serre weights (§ 4.4) and local-global compatibility (§ 4.5), we must assume a stronger genericity condition on the integers
$a_{i}$
.
Definition 2.1.5. We say that a maximally non-split Galois representation
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
as in (2.1.1) is generic if the triple
$(a_{2},a_{1},a_{0})$
satisfies the condition
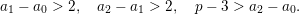$$\begin{eqnarray}a_{1}-a_{0}>2,\quad a_{2}-a_{1}>2,\quad p-3>a_{2}-a_{0}.\end{eqnarray}$$
2.1.2 The Fontaine–Laffaille invariant
Let
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
be as in Definition 2.1.5. By Lemma 2.1.4 there is a Fontaine–Laffaille module
$M$
with Hodge–Tate weights
$\{1,a_{1}-a_{0}+1,a_{2}-a_{0}+1\}$
such that
$\text{T}_{\text{cris}}^{\ast }(M)\cong \overline{\unicode[STIX]{x1D70C}}\,\otimes \,\unicode[STIX]{x1D714}^{-a_{0}}$
and which is moreover endowed with a filtration by Fontaine–Laffaille submodules
$0\subsetneq M_{0}\subsetneq M_{1}\subsetneq M_{2}=M$
induced via
$\text{T}_{\text{cris}}^{\ast }$
from the cosocle filtration on
$\overline{\unicode[STIX]{x1D70C}}$
(cf. Theorem 2.1.3).
Lemma 2.1.7. Let
$M\in \mathbb{F}\text{-}{\mathcal{F}}{\mathcal{L}}^{[0,p-2]}$
be such that
$\text{T}_{\text{cris}}^{\ast }(M)\cong \overline{\unicode[STIX]{x1D70C}}\,\otimes \,\unicode[STIX]{x1D714}^{-a_{0}}$
. There exists a basis
$\text{}\underline{e}=(e_{0},e_{1},e_{2})$
of
$M$
such that
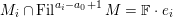$$\begin{eqnarray}M_{i}\cap \operatorname{Fil}^{a_{i}-a_{0}+1}M=\mathbb{F}\cdot e_{i}\end{eqnarray}$$
for all
$i\in \{0,1,2\}$
.
Proof. This follows by noting that
$M_{i}\,\cap \,\operatorname{Fil}^{a_{i}-a_{0}+1}M=\operatorname{Fil}^{a_{i}-a_{0}+1}M_{i}$
and that
$M_{i}$
has Hodge–Tate weights
$a_{j}-a_{0}+1$
with
$0\leqslant j\leqslant i$
.◻
Note that a basis
$\text{}\underline{e}$
as in Lemma 2.1.7 is compatible with the Hodge filtration. From Lemma 2.1.7 we deduce a useful observation on the Frobenius action on
$M$
.
Corollary 2.1.8. Let
$\overline{\unicode[STIX]{x1D70C}}$
,
$M$
,
$\text{}\underline{e}$
be as in Lemma 2.1.7. Then
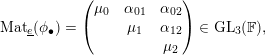$$\begin{eqnarray}\text{Mat}_{\text{}\underline{e}}(\unicode[STIX]{x1D719}_{\bullet })=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D707}_{0} & \unicode[STIX]{x1D6FC}_{01} & \unicode[STIX]{x1D6FC}_{02}\\ & \unicode[STIX]{x1D707}_{1} & \unicode[STIX]{x1D6FC}_{12}\\ & & \unicode[STIX]{x1D707}_{2}\end{array}\right)\in \operatorname{GL}_{3}(\mathbb{F}),\end{eqnarray}$$
where, moreover,
$\unicode[STIX]{x1D6FC}_{01},\unicode[STIX]{x1D6FC}_{12}\in \mathbb{F}^{\times }$
.
Proof. This follows from the lemma, by recalling that the Fontaine–Laffaille module associated to a
$G_{\mathbb{Q}_{p}}$
-character
$\unicode[STIX]{x1D714}^{r}\text{nr}_{\unicode[STIX]{x1D707}}$
has Hodge–Tate weight
$r$
and
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D707}$
. Note that
$\unicode[STIX]{x1D6FC}_{01},\unicode[STIX]{x1D6FC}_{12}\neq 0$
as
$\overline{\unicode[STIX]{x1D70C}}$
is maximally non-split.◻
Conversely, we also note that any such matrix defines a Fontaine–Laffaille module whose associated Galois representation is maximally non-split as in (2.1.1).
The Fontaine–Laffaille invariant
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})$
associated to
$\overline{\unicode[STIX]{x1D70C}}$
is defined in terms of
$\text{Mat}_{\text{}\underline{e}}(\unicode[STIX]{x1D719}_{\bullet })$
.
Lemma 2.1.9. Keep the hypotheses of Corollary 2.1.8. The element
$\unicode[STIX]{x1D6FC}_{02}/\unicode[STIX]{x1D6FC}_{01}\unicode[STIX]{x1D6FC}_{12}$
deduced from
$\text{Mat}_{\text{}\underline{e}}(\unicode[STIX]{x1D719}_{\bullet })$
does not depend on the choice of the basis
$\text{}\underline{e}$
.
Proof. By Lemma 2.1.7 any other such basis is of the form
$\unicode[STIX]{x1D6FD}_{i}e_{i}$
for
$\unicode[STIX]{x1D6FD}_{i}\in \mathbb{F}^{\times }$
. The lemma follows.◻
Definition 2.1.10. Let
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
be maximally non-split and generic as in Definition 2.1.5. Let
$M$
be the Fontaine–Laffaille module associated to
$\overline{\unicode[STIX]{x1D70C}}\,\otimes \,\unicode[STIX]{x1D714}^{-a_{0}}$
,
$\text{}\underline{e}=(e_{0},e_{1},e_{2})$
a basis of
$M$
as in Lemma 2.1.7 and let
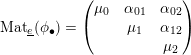$$\begin{eqnarray}\text{Mat}_{\text{}\underline{e}}(\unicode[STIX]{x1D719}_{\bullet })=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D707}_{0} & \unicode[STIX]{x1D6FC}_{01} & \unicode[STIX]{x1D6FC}_{02}\\ & \unicode[STIX]{x1D707}_{1} & \unicode[STIX]{x1D6FC}_{12}\\ & & \unicode[STIX]{x1D707}_{2}\end{array}\right)\end{eqnarray}$$
be the matrix of the Frobenius action on
$M$
.
The Fontaine–Laffaille invariant associated to
$\overline{\unicode[STIX]{x1D70C}}$
is defined as
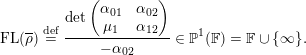$$\begin{eqnarray}\text{FL}(\overline{\unicode[STIX]{x1D70C}})\stackrel{\text{def}}{=}\frac{\det \left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{01} & \unicode[STIX]{x1D6FC}_{02}\\ \unicode[STIX]{x1D707}_{1} & \unicode[STIX]{x1D6FC}_{12}\end{array}\right)}{-\unicode[STIX]{x1D6FC}_{02}}\in \mathbb{P}^{1}(\mathbb{F})=\mathbb{F}\cup \{\infty \}.\end{eqnarray}$$
By Lemma 2.1.9 it is well defined.
Remark 2.1.11. Let
$\overline{\unicode[STIX]{x1D70C}}$
be maximally non-split as in (2.1.1). The isomorphism class of
$\overline{\unicode[STIX]{x1D70C}}$
is determined by the diagonal characters
$\unicode[STIX]{x1D714}^{a_{i}+1}\text{nr}_{\unicode[STIX]{x1D707}_{i}}$
and the Fontaine–Laffaille invariant
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})$
. Note that
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})$
can take any value in
$\mathbb{P}^{1}(\mathbb{F})$
except for
$\unicode[STIX]{x1D707}_{1}$
. (Similarly, a maximally non-split Galois representation
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{n}(\mathbb{F})$
is determined by the diagonal characters and
$\binom{n-1}{2}$
invariants.)
Remark 2.1.12. Note that in the situation of Definition 2.1.10, if
$\mathbb{F}^{\prime }/\mathbb{F}$
is a finite field extension, then
$\text{FL}(\overline{\unicode[STIX]{x1D70C}}\otimes _{\mathbb{F}}\mathbb{F}^{\prime })=\text{FL}(\overline{\unicode[STIX]{x1D70C}})$
.
Remark 2.1.13. We leave it to the reader to show that the Fontaine–Laffaille module associated to
$\overline{\unicode[STIX]{x1D70C}}^{\vee }\,\otimes \,\unicode[STIX]{x1D714}^{a_{2}+2}$
is described by
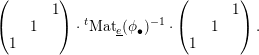$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}} & & 1\\ & 1 & \\ 1 & & \end{array}\right)\cdot ^{t}\text{Mat}_{\text{}\underline{e}}(\unicode[STIX]{x1D719}_{\bullet })^{-1}\cdot \left(\begin{array}{@{}ccc@{}} & & 1\\ & 1 & \\ 1 & & \end{array}\right).\end{eqnarray}$$
As a consequence,
$\text{FL}(\overline{\unicode[STIX]{x1D70C}}^{\vee })=\text{FL}(\overline{\unicode[STIX]{x1D70C}})^{-1}$
.
2.2
$p$
-adic Hodge theory
This section mainly consists of a review of some integral
$p$
-adic Hodge theory, although many of the results are not available in the literature in the form or generality that we need.
In the first subsection (§ 2.2.1) we define the categories of mod
$p$
objects we are going to work with (Breuil modules with descent data, étale
$\unicode[STIX]{x1D711}$
-modules, etc.). Moreover, we obtain a key result, Corollary 2.2.2, which provides a criterion for deciding when a given Breuil module with descent data and a Fontaine–Laffaille module have isomorphic Galois representations.
The second subsection (§ 2.2.2) is of a more technical nature. On the one hand we make two of the functors from § 2.2.1 (relating Breuil, Fontaine–Laffaille and étale
$\unicode[STIX]{x1D711}$
-modules) more explicit. We also provide a useful change-of-basis result for a Breuil module with descent data.
All missing proofs of this section are contained in § A.5. Our rationale is to state in this section all the results we need to prove our main results on the Galois side, and to relegate technical details to the appendix.
2.2.1 Breuil modules with tame descent data
Let
$K^{\prime }\subseteq K_{0}$
be a subfield containing
$\mathbb{Q}_{p}$
. The residual Breuil ring
$\overline{S}\stackrel{\text{def}}{=}(k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F})[u]/(u^{ep})$
is equipped with an action of
$\text{Gal}(K/K^{\prime })$
by
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
-semilinear automorphisms. Explicitly if
$g\in \text{Gal}(K/K^{\prime })$
and
$a\in k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
, we have
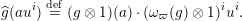$$\begin{eqnarray}\widehat{g}(au^{i})\stackrel{\text{def}}{=}(g\otimes 1)(a)\cdot (\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}(g)\otimes 1)^{i}u^{i}.\end{eqnarray}$$
If
$\overline{\unicode[STIX]{x1D712}}:\text{Gal}(K/K^{\prime })\rightarrow \mathbb{F}^{\times }$
is a character, we write
$\overline{S}_{\overline{\unicode[STIX]{x1D712}}}$
to denote the
$\overline{\unicode[STIX]{x1D712}}$
-isotypical component of
$\overline{S}$
for the action of
$\operatorname{Gal}(K/K^{\prime })$
.
We recall that
$\overline{S}$
is equipped with an
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
-linear derivation
$N\stackrel{\text{def}}{=}-u(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}u)$
and with a semilinear Frobenius
$\unicode[STIX]{x1D711}$
defined by
$u\mapsto u^{p}$
(semilinear with respect to the arithmetic Frobenius
$\unicode[STIX]{x1D711}\,\otimes \,1$
on
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
), which moreover commute with the action of
$\operatorname{Gal}(K/K^{\prime })$
on
$\overline{S}$
.
Fix
$r\in \{0,\ldots ,p-2\}$
. A Breuil module of weight
$r$
with descent data from
$K$
to
$K^{\prime }$
is a quintuple
$({\mathcal{M}},\operatorname{Fil}^{r}{\mathcal{M}},\unicode[STIX]{x1D711}_{r},N,\{\widehat{g}\})$
, consisting of the following data.
-
(i) A
$\bar{S}$
-module
${\mathcal{M}}$
that is finite free. -
(ii) A
$\bar{S}$
-submodule
$\operatorname{Fil}^{r}{\mathcal{M}}$
of
${\mathcal{M}}$
, verifying
$u^{er}{\mathcal{M}}\subseteq \operatorname{Fil}^{r}{\mathcal{M}}$
. -
(iii) A morphism
$\unicode[STIX]{x1D711}_{r}:\operatorname{Fil}^{r}{\mathcal{M}}\rightarrow {\mathcal{M}}$
which is
$\unicode[STIX]{x1D711}$
-semilinear and whose image generates
${\mathcal{M}}$
. -
(iv) An operator
$N:{\mathcal{M}}\rightarrow {\mathcal{M}}$
that is
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
-linear and satisfies certain axioms (see the beginning of [Reference Emerton, Gee and HerzigEGH13, § 3.2]). -
(v) An action of
$\text{Gal}(K/K^{\prime })$
on
${\mathcal{M}}$
by automorphisms
$\widehat{g}$
which are semilinear with respect to the Galois action on
$\overline{S}$
and which preserve
$\operatorname{Fil}^{r}{\mathcal{M}}$
and commute with
$\unicode[STIX]{x1D711}_{r}$
and
$N$
.
A morphism of Breuil modules is an
$\overline{S}$
-linear morphism which is compatible, in the evident sense, with the additional structures.
We write
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
to denote the category of Breuil modules of weight
$r$
with descent data from
$K$
to
$K^{\prime }$
; the field
$K^{\prime }$
will always be clear from the context (and will be specified in case of ambiguities). As we did for the coefficient ring
$\overline{S}$
, given a character
$\overline{\unicode[STIX]{x1D712}}:\text{Gal}(K/K^{\prime })\rightarrow \mathbb{F}^{\times }$
we write
${\mathcal{M}}_{\overline{\unicode[STIX]{x1D712}}}$
,
$(\operatorname{Fil}^{r}{\mathcal{M}})_{\overline{\unicode[STIX]{x1D712}}}$
to denote the
$\overline{\unicode[STIX]{x1D712}}$
-isotypical component of
${\mathcal{M}}$
,
$\operatorname{Fil}^{r}{\mathcal{M}}$
respectively.
We remark that the category
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
is additive and admits kernels and cokernels (cf. [Reference CarusoCar11, Théorème 4.2.4] and the Remarque following it). In particular a complex
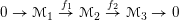$$\begin{eqnarray}0\rightarrow {\mathcal{M}}_{1}\stackrel{f_{1}}{\rightarrow }{\mathcal{M}}_{2}\stackrel{f_{2}}{\rightarrow }{\mathcal{M}}_{3}\rightarrow 0\end{eqnarray}$$
in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
is exact if the morphisms
$f_{i}$
induce exact sequences on the underlying
$\overline{S}$
-modules
${\mathcal{M}}_{j}$
and
$\operatorname{Fil}^{r}{\mathcal{M}}_{j}$
(
$j\in \{0,1,2\}$
). This endows
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
with the structure of an exact category (see Proposition 2.3.4 below).
We recall that we have an exact, faithful, contravariant functor
$$\begin{eqnarray}\displaystyle \text{T}_{\text{st}}^{\ast }:\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r} & \rightarrow & \displaystyle \text{Rep}_{\mathbb{F}}(G_{K^{\prime }})\nonumber\\ \displaystyle {\mathcal{M}} & \mapsto & \displaystyle \text{T}_{\text{st}}^{\ast }({\mathcal{M}})\stackrel{\text{def}}{=}\text{Hom}({\mathcal{M}},\widehat{A}),\nonumber\end{eqnarray}$$
where
$\widehat{A}$
is a certain period ring and homomorphisms respect all structures (cf. § A.3). We have
$\dim _{\mathbb{F}}\,\text{T}_{\text{st}}^{\ast }({\mathcal{M}})=\operatorname{rank}_{\overline{S}}{\mathcal{M}}$
(cf. [Reference CarusoCar11, Théorème 4.2.4], and the Remarque following it; see also [Reference Emerton, Gee and HerzigEGH13, Lemma 3.2.2]).
We will be mainly concerned with the covariant version
$\text{T}_{\text{st}}^{r}({\mathcal{M}})\stackrel{\text{def}}{=}(\text{T}_{\text{st}}^{\ast }({\mathcal{M}}))^{\vee }\,\otimes \,\unicode[STIX]{x1D714}^{r}$
of the functor
$\text{T}_{\text{st}}^{\ast }$
above. We remark that this is compatible with the notion of duality
${\mathcal{M}}\mapsto {\mathcal{M}}^{\ast }$
on
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
recalled in § A.4, namely
$\text{T}_{\text{st}}^{r}({\mathcal{M}})\cong \text{T}_{\text{st}}^{\ast }({\mathcal{M}}^{\ast })$
, cf. the discussion before [Reference Emerton, Gee and HerzigEGH13, Corollary 3.2.9].
We now move to the categories of étale
$\unicode[STIX]{x1D711}$
-modules. In the remainder of this subsection we will assume
$K^{\prime }=K_{0}$
, i.e. we will only consider descent data from
$K$
to
$K_{0}$
.
We fix the field of norms
$k((\text{}\underline{\unicode[STIX]{x1D71B}}))$
associated to a suitable Kummer extension
$K_{\infty }$
of
$K$
(see § A.1 for its precise definition). It is endowed with a
$p$
-power Frobenius endomorphism and with an action of
$\operatorname{Gal}(K/K_{0})$
.
An étale
$(\unicode[STIX]{x1D719},k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}((\text{}\underline{\unicode[STIX]{x1D71B}})))$
-module with descent data is the datum of a finite free
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}((\text{}\underline{\unicode[STIX]{x1D71B}}))$
-module
$\mathfrak{M}$
endowed with a semilinear injective Frobenius endomorphism
$\unicode[STIX]{x1D719}:\mathfrak{M}\rightarrow \mathfrak{M}$
and a semilinear action of
$\operatorname{Gal}(K/K_{0})$
, commuting with
$\unicode[STIX]{x1D719}$
. We write
$\mathbb{F}\text{-}\mathfrak{Mod}_{k((\text{}\underline{\unicode[STIX]{x1D71B}})),\text{dd}}$
to denote the category of étale
$(\unicode[STIX]{x1D719},k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}((\text{}\underline{\unicode[STIX]{x1D71B}})))$
-modules with descent data. In the special case when
$e=1$
this category is denoted by
$\mathbb{F}\text{-}\mathfrak{Mod}_{k((\text{}\underline{p}))}$
. (In this case
$k((\text{}\underline{p}))$
is also the field of norms associated to a suitable Kummer extension
$(K_{0})_{\infty }/K_{0}$
.) We remark that
$k((\text{}\underline{\unicode[STIX]{x1D71B}}))/k((\text{}\underline{p}))$
is a cyclic extension of degree
$e$
with Galois group
$\operatorname{Gal}(K/K_{0})$
, and we write
$k((\text{}\underline{p}))^{s}$
to denote a choice of separable closure of
$k((\text{}\underline{p}))$
containing
$k((\text{}\underline{\unicode[STIX]{x1D71B}}))$
. For details, see § A.1.
Finally, recall the category of Fontaine–Laffaille modules
$\mathbb{F}\text{-}{\mathcal{F}}{\mathcal{L}}^{[0,p-2]}$
over
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
(defined in § 2.1.1) and the category
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
of Breuil modules of weight
$r$
with descent data from
$K$
to
$K_{0}$
(defined in § 2.2.1).
The relations between the categories introduced so far are summarized in the following proposition. Its proof, as well as the definition of the functors
$M_{k((\text{}\underline{\unicode[STIX]{x1D71B}}))}$
,
${\mathcal{F}}$
, … can be found in Appendix A.
Proposition 2.2.1. Let
$0\leqslant r\leqslant p-2$
. We have the following commutative diagram:
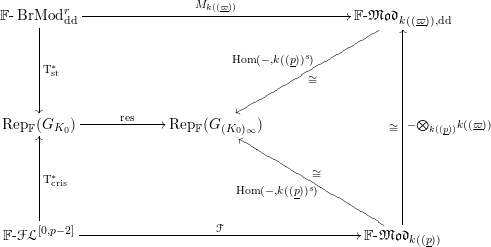
where the descent data is from
$K$
to
$K_{0}$
. Moreover, the functor
$\text{res}\circ \text{T}_{\text{cris}}^{\ast }$
is fully faithful.
We record the following immediate, yet crucial, corollary.
Corollary 2.2.2. Let
$0\leqslant r\leqslant p-2$
and let
${\mathcal{M}}$
,
$M$
be objects in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
and
$\mathbb{F}\text{-}{\mathcal{F}}{\mathcal{L}}^{[0,p-2]}$
respectively. Assume that
$\text{T}_{\text{st}}^{\ast }({\mathcal{M}})$
is Fontaine–Laffaille. If
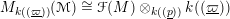$$\begin{eqnarray}M_{k((\text{}\underline{\unicode[STIX]{x1D71B}}))}({\mathcal{M}})\cong {\mathcal{F}}(M)\otimes _{k((\text{}\underline{p}))}k((\text{}\underline{\unicode[STIX]{x1D71B}}))\end{eqnarray}$$
then one has an isomorphism of
$G_{K_{0}}$
-representations
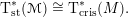$$\begin{eqnarray}\text{T}_{\text{st}}^{\ast }({\mathcal{M}})\cong \text{T}_{\text{cris}}^{\ast }(M).\end{eqnarray}$$
Let us explain the role that Corollary 2.2.2 plays in the proof of our main theorem on the Galois side (Theorem 2.5.1). Thus suppose that
$\unicode[STIX]{x1D70C}$
is potentially semistable of Hodge–Tate weights
$\{-2,-1,0\}$
with reduction
$\overline{\unicode[STIX]{x1D70C}}$
that is maximally non-split and generic as in Definition 2.1.5. Associated to
$\unicode[STIX]{x1D70C}$
is a strongly divisible module
$\widehat{{\mathcal{M}}}$
, whose reduction
${\mathcal{M}}\in \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
has Galois representation
$\overline{\unicode[STIX]{x1D70C}}$
. Corollary 2.2.2 will allow us to compute the Fontaine–Laffaille module
$M$
associated to
$\overline{\unicode[STIX]{x1D70C}}$
– and hence the invariant
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})$
– in terms of
$\widehat{{\mathcal{M}}}$
, so in terms of
$\unicode[STIX]{x1D70C}$
. In fact, we will start with
${\mathcal{M}}$
in the top left corner of the diagram and then go around it in a clockwise sense: first computing
$M_{k((\text{}\underline{\unicode[STIX]{x1D71B}}))}({\mathcal{M}})$
, then descending it to
$\mathbb{F}\text{-}\mathfrak{Mod}_{k((\text{}\underline{p}))}$
and finally to
$\mathbb{F}\text{-}{\mathcal{F}}{\mathcal{L}}^{[0,p-2]}$
. To obtain the precise result, Theorem 2.5.1, we will moreover need more information about
$\widehat{{\mathcal{M}}}$
, and this will be obtained in § 2.4.
2.2.2 Linear algebra with descent data
We continue to assume that
$K^{\prime }=K_{0}$
. It will be convenient to introduce bases
$\text{}\underline{e}$
(respectively generating sets
$\text{}\underline{f}$
) of a Breuil module
${\mathcal{M}}$
with descent data (respectively of
$\operatorname{Fil}^{r}{\mathcal{M}}$
) that are compatible with the action of
$\operatorname{Gal}(K/K_{0})$
, and to describe
$\operatorname{Fil}^{r}{\mathcal{M}}$
(respectively
$\unicode[STIX]{x1D711}_{r}$
) by matrices with respect to
$\text{}\underline{e}$
,
$\text{}\underline{f}$
. We then use this formalism to make the functors
$M_{k((\text{}\underline{\unicode[STIX]{x1D71B}}))}$
,
${\mathcal{F}}$
appearing in the diagram of Proposition 2.2.1 more explicit, as well as we obtain a change-of-basis result for a Breuil module with descent data. Proofs can be found in § A.5.
Definition 2.2.3. We say that a Breuil module
${\mathcal{M}}\in \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
is of type
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{0}}\oplus \ldots \oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{n-1}}$
(where
$a_{i}\in \mathbb{Z}$
) if
${\mathcal{M}}/u{\mathcal{M}}\cong \bigoplus _{i=0}^{n-1}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{i}}\,\otimes \,1)$
as
$(k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F})[\operatorname{Gal}(K/K_{0})]$
-modules. Equivalently,
${\mathcal{M}}$
has an
$\overline{S}$
-basis
$(e_{0},\ldots ,e_{n-1})$
such that
$\widehat{g}e_{i}=(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{i}}(g)\,\otimes \,1)e_{i}$
for all
$i$
and all
$g\in \operatorname{Gal}(K/K_{0})$
. We call such a basis a framed basis of
${\mathcal{M}}$
.
If
${\mathcal{M}}$
is of type
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{0}}\oplus \ldots \oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{n-1}}$
we say that
$(f_{0},\ldots ,f_{n-1})$
is a framed system of generators of
$\operatorname{Fil}^{r}{\mathcal{M}}$
if
$\operatorname{Fil}^{r}{\mathcal{M}}=\sum _{i=0}^{n-1}\overline{S}\cdot f_{i}$
and
$\widehat{g}f_{i}=(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{p^{-1}a_{i}}(g)\,\otimes \,1)f_{i}$
for all
$i$
and all
$g\in \operatorname{Gal}(K/K_{0})$
.
To justify the claim implicit in this definition, choose an
$\overline{S}/u$
-basis
$(\overline{e}_{1},\ldots ,\overline{e}_{n-1})$
of
${\mathcal{M}}/u{\mathcal{M}}$
such that
$\widehat{g}\cdot \overline{e}_{i}=(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{i}}(g)\,\otimes \,1)\overline{e}_{i}$
for all
$i$
and all
$g\in \operatorname{Gal}(K/K_{0})$
. Since
$(k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F})[\operatorname{Gal}(K/K_{0})]$
is a semisimple (commutative) ring we can pick a
$(k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F})[\operatorname{Gal}(K/K_{0})]$
-linear splitting of
${\mathcal{M}}{\twoheadrightarrow}{\mathcal{M}}/u{\mathcal{M}}$
and hence find
$e_{i}\in {\mathcal{M}}$
lifting
$\overline{e}_{i}$
such that
$\widehat{g}e_{i}=(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{i}}(g)\,\otimes \,1)e_{i}$
. By Nakayama’s lemma, the
$e_{i}$
form an
$\overline{S}$
-basis of
${\mathcal{M}}$
.
The notion of a framed basis (respectively a framed system of generators) depends on an ordering of the integers
$a_{i}$
. It will always be clear from the context which ordering we use.
Lemma 2.2.4. If
${\mathcal{M}}\in \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
is of type
$\bigoplus _{i=0}^{n-1}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{i}}$
, then
$\operatorname{Fil}^{r}{\mathcal{M}}$
admits a framed system of generators.
Definition 2.2.5. Let
${\mathcal{M}}\in \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
be of type
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{0}}\oplus \ldots \oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{n-1}}$
. Let
$\text{}\underline{e}$
,
$\text{}\underline{f}$
be a framed basis and a framed system of generators of
${\mathcal{M}}$
,
$\operatorname{Fil}^{r}{\mathcal{M}}$
respectively. The matrix of the filtration, with respect to
$\text{}\underline{e},\text{}\underline{f}$
, is the element
$\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\operatorname{Fil}^{r}{\mathcal{M}})\in \text{M}_{n}(\overline{S})$
verifying
$$\begin{eqnarray}\text{}\underline{f}=\text{}\underline{e}\cdot \text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\operatorname{Fil}^{r}{\mathcal{M}}).\end{eqnarray}$$
We define the matrix of Frobenius with respect to
$\text{}\underline{e}$
,
$\text{}\underline{f}$
as the element
$\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\unicode[STIX]{x1D711}_{r})\in \text{GL}_{n}(\overline{S})$
characterized by
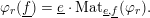$$\begin{eqnarray}\unicode[STIX]{x1D711}_{r}(\text{}\underline{f})=\text{}\underline{e}\cdot \text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\unicode[STIX]{x1D711}_{r}).\end{eqnarray}$$
As we require
$\text{}\underline{e},\text{}\underline{f}$
to be framed, the coefficients
$\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\operatorname{Fil}^{r}{\mathcal{M}})_{ij}$
verify the following conditions:
$$\begin{eqnarray}\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\operatorname{Fil}^{r}{\mathcal{M}})_{ij}\in \overline{S}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{p^{-1}a_{j}-a_{i}}}.\end{eqnarray}$$
Concretely
$\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\operatorname{Fil}^{r}{\mathcal{M}})_{ij}=u^{[p^{-1}a_{j}-a_{i}]}s_{ij}$
, where
$[x]\in \{0,\ldots ,e-1\}$
is defined by
$[x]\equiv x\,\text{mod}\,e$
for
$x\in \mathbb{Z}/e\mathbb{Z}$
and
$s_{ij}\in \overline{S}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{0}}=k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}[u^{e}]/(u^{ep})$
.
On the other hand,
$\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\unicode[STIX]{x1D711}_{r})\in \text{GL}_{n}^{\Box }(\overline{S})$
, where
$$\begin{eqnarray}\operatorname{GL}_{n}^{\Box }(\overline{S})\stackrel{\text{def}}{=}\{A\in \operatorname{GL}_{n}(\overline{S}):A_{ij}\in \overline{S}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{j}-a_{i}}}\,\,\text{for all}\,\,0\leqslant i,j\leqslant n-1\}.\end{eqnarray}$$
Lemma 2.2.6. Let
${\mathcal{M}}$
be a Breuil module of type
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{0}}\oplus \ldots \oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{n-1}}$
, and let
$\text{}\underline{e}$
be a framed basis of
${\mathcal{M}}$
and
$\text{}\underline{f}$
a framed system of generators of
$\operatorname{Fil}^{r}{\mathcal{M}}$
, respectively. Let
$V\stackrel{\text{def}}{=}\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\operatorname{Fil}^{r}{\mathcal{M}})\in \text{M}_{n}(\overline{S})$
and
$A\stackrel{\text{def}}{=}\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\unicode[STIX]{x1D711}_{r})\in \text{GL}_{n}^{\Box }(\overline{S})$
. Then there exists a basis
$\text{}\underline{\mathfrak{e}}$
of
$M_{k((\text{}\underline{\unicode[STIX]{x1D71B}}))}({\mathcal{M}}^{\ast })$
with
$\widehat{g}\cdot \mathfrak{e}_{i}=(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{-p^{-1}a_{i}}(g)\,\otimes \,1)\mathfrak{e}_{i}$
for all
$i$
and
$g\in \operatorname{Gal}(K/K_{0})$
, such that
$\text{Mat}_{\text{}\underline{\mathfrak{e}}}(\unicode[STIX]{x1D719})\in \text{M}_{n}(k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}[[\text{}\underline{\unicode[STIX]{x1D71B}}]])$
is given by any chosen lift of
$^{t}V\cdot ^{t}A^{-1}\in \text{M}_{n}(\overline{S})$
via the morphism
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}[[\text{}\underline{\unicode[STIX]{x1D71B}}]]{\twoheadrightarrow}\overline{S}$
sending
$\sum \unicode[STIX]{x1D706}_{i}\text{}\underline{\unicode[STIX]{x1D71B}}^{i}$
to
$\sum \unicode[STIX]{x1D706}_{i}u^{i}$
and such that
$(\text{Mat}_{\text{}\underline{\mathfrak{e}}}(\unicode[STIX]{x1D719}))_{ij}\in (k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}[[\text{}\underline{\unicode[STIX]{x1D71B}}]])_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{p^{-1}a_{i}-a_{j}}}$
for all
$0\leqslant i,j\leqslant n-1$
.
Lemma 2.2.7. Let
$M\in \mathbb{F}\text{-}{\mathcal{F}}{\mathcal{L}}^{[0,p-2]}$
be a rank
$n$
Fontaine–Laffaille module with parallel Hodge–Tate weights
$0\leqslant m_{0}\leqslant \ldots \leqslant m_{n-1}\leqslant p-2$
(counted with multiplicities).
Let
$\text{}\underline{e}=(e_{0},\ldots ,e_{n-1})$
be a
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
-basis of
$M_{i}$
that is compatible with the Hodge filtration
$\text{Fil}^{\bullet }M$
, and let
$F\in \operatorname{GL}_{n}(k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F})$
be the associated matrix of the Frobenius
$\unicode[STIX]{x1D719}_{\bullet }:\operatorname{gr}^{\bullet }M\xrightarrow[{}]{\,\sim \,}M$
.
Then there exists a basis
$\text{}\underline{\mathfrak{e}}$
of
$\mathfrak{M}\stackrel{\text{def}}{=}{\mathcal{F}}(M)$
in
$\mathbb{F}\text{-}\mathfrak{Mod}_{k((\text{}\underline{p}))}$
such that the Frobenius
$\unicode[STIX]{x1D719}$
on
$\mathfrak{M}$
is described by
$$\begin{eqnarray}\text{Mat}_{\text{}\underline{\mathfrak{e}}}(\unicode[STIX]{x1D719})=\text{Diag}(\text{}\underline{p}^{m_{0}}\ldots \text{}\underline{p}^{m_{n-1}})F.\end{eqnarray}$$
Lemma 2.2.8. Let
${\mathcal{M}}\in \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
be a Breuil module of type
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{0}}\oplus \ldots \oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{n-1}}$
and let
$\text{}\underline{e}$
,
$\text{}\underline{f}$
be a framed basis of
${\mathcal{M}}$
and a framed system of generators of
$\operatorname{Fil}^{r}{\mathcal{M}}$
respectively.
Write
$V\stackrel{\text{def}}{=}\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\operatorname{Fil}^{r}{\mathcal{M}})$
,
$A\stackrel{\text{def}}{=}\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\unicode[STIX]{x1D711}_{r})$
. Assume that there exist elements
$V^{\prime }\in \text{M}_{n}(\overline{S})$
,
$B\in \operatorname{GL}_{n}(\overline{S})$
such that
$V_{ij}^{\prime }\in \overline{S}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{p^{-1}a_{j}-a_{i}}}$
,
$B_{ij}\in \overline{S}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{p^{-1}(a_{j}-a_{i})}}$
and
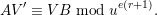$$\begin{eqnarray}AV^{\prime }\equiv VB\hspace{0.2em}{\rm mod}\hspace{0.2em}u^{e(r+1)}.\end{eqnarray}$$
Then
$\text{}\underline{e}^{\prime }\stackrel{\text{def}}{=}\text{}\underline{e}\cdot A$
is a framed basis of
${\mathcal{M}}$
,
$\text{}\underline{f}^{\prime }\stackrel{\text{def}}{=}\text{}\underline{e}^{\prime }\cdot V^{\prime }$
is a framed system of generators for
$\operatorname{Fil}^{r}{\mathcal{M}}$
, and
$\text{Mat}_{\text{}\underline{e}^{\prime },\text{}\underline{f}^{\prime }}(\unicode[STIX]{x1D711}_{r})=\unicode[STIX]{x1D711}(B)$
.
2.3 Breuil submodules and Galois representations
In this subsection we discuss some preliminaries on subobjects and quotients in the category
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
. Even though these notions are presumably well known to the experts, we did not find a suitable reference in the literature. The main result, Proposition 2.3.5, is a slight improvement of a result of Caruso [Reference CarusoCar11]. All missing proofs of this subsection are contained in § A.6.
In what follows, we let
$\overline{S}_{k}\stackrel{\text{def}}{=}k[u]/u^{ep}$
.
Definition 2.3.1. Let
${\mathcal{M}}$
be an object in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
. An
$\overline{S}$
-submodule
${\mathcal{N}}\subseteq {\mathcal{M}}$
is said to be a Breuil submodule if
${\mathcal{N}}$
fulfills the following conditions:
-
(i)
${\mathcal{N}}$
is an
$\overline{S}_{k}$
-direct summand of
${\mathcal{M}}$
; -
(ii)
$N({\mathcal{N}})\subseteq {\mathcal{N}}$
and
$\widehat{g}({\mathcal{N}})\subseteq {\mathcal{N}}$
for all
$g\in \operatorname{Gal}(K/K^{\prime })$
; -
(iii)
$\unicode[STIX]{x1D711}_{r}({\mathcal{N}}\,\cap \,\operatorname{Fil}^{r}{\mathcal{M}})\subseteq {\mathcal{N}}$
.
Lemma 2.3.2. Let
${\mathcal{M}}$
be an object in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
and let
${\mathcal{N}}\subseteq {\mathcal{M}}$
be a Breuil submodule. Then the
$\overline{S}$
-modules
${\mathcal{N}}$
,
${\mathcal{M}}/{\mathcal{N}}$
with their induced structures are objects of
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
and the sequence
$$\begin{eqnarray}0\rightarrow {\mathcal{N}}\rightarrow {\mathcal{M}}\rightarrow {\mathcal{M}}/{\mathcal{N}}\rightarrow 0\end{eqnarray}$$
is exact in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
. Conversely, given an exact sequence
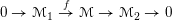$$\begin{eqnarray}0\rightarrow {\mathcal{M}}_{1}\stackrel{f}{\rightarrow }{\mathcal{M}}\rightarrow {\mathcal{M}}_{2}\rightarrow 0\end{eqnarray}$$
in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
, then
$f({\mathcal{M}}_{1})\subseteq {\mathcal{M}}$
is a Breuil submodule.
An immediate consequence of Lemma 2.3.2 is that the notion of Breuil submodule is transitive.
Lemma 2.3.3. Let
${\mathcal{M}}$
be an object in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
.
-
(i) If
${\mathcal{M}}_{1}\subseteq {\mathcal{M}}$
and
${\mathcal{M}}_{2}\subseteq {\mathcal{M}}_{1}$
are Breuil submodules, then so is
${\mathcal{M}}_{2}\subseteq {\mathcal{M}}$
. -
(ii) Let
${\mathcal{M}}_{1}$
,
${\mathcal{M}}_{2}$
be Breuil submodules of
${\mathcal{M}}$
, and assume that
${\mathcal{M}}_{2}\subseteq {\mathcal{M}}_{1}$
. Then
${\mathcal{M}}_{2}$
is a Breuil submodule of
${\mathcal{M}}_{1}$
, and the Breuil module structures on
${\mathcal{M}}_{2}$
inherited from
${\mathcal{M}}_{1}$
and
${\mathcal{M}}$
coincide. Similarly,
${\mathcal{M}}_{1}/{\mathcal{M}}_{2}\subseteq {\mathcal{M}}/{\mathcal{M}}_{2}$
is a Breuil submodule, and the Breuil module structures on
${\mathcal{M}}_{1}/{\mathcal{M}}_{2}$
, as a Breuil submodule of
${\mathcal{M}}/{\mathcal{M}}_{2}$
and as a quotient of
${\mathcal{M}}_{1}$
, coincide.
Proposition 2.3.4. With the above notion of exact sequence, the category
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
is an exact category in the sense of [Reference KellerKel90] and
$\text{T}_{\text{st}}^{r}$
is an exact functor.
We can now state a crucial result relating Breuil submodules of
${\mathcal{M}}$
and subrepresentations of
$\text{T}_{\text{st}}^{r}({\mathcal{M}})$
. It improves [Reference CarusoCar11, Proposition 2.2.5] (cf. also [Reference Emerton, Gee and HerzigEGH13, Corollary 3.2.9]).
Proposition 2.3.5. Let
${\mathcal{M}}$
be an object in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
. There is a natural order-preserving bijection
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}:\{\text{Breuil submodules in}\,\,{\mathcal{M}}\}\stackrel{{\sim}}{\longrightarrow }\{G_{K^{\prime }}\text{-subrepresentations of}\,\,\text{T}_{\text{st}}^{r}({\mathcal{M}})\}\end{eqnarray}$$
sending
${\mathcal{N}}\subseteq {\mathcal{M}}$
to the image of
$\text{T}_{\text{st}}^{r}({\mathcal{N}}){\hookrightarrow}\text{T}_{\text{st}}^{r}({\mathcal{M}})$
. Moreover, if
${\mathcal{M}}_{2}\subseteq {\mathcal{M}}_{1}$
are Breuil submodules of
${\mathcal{M}}$
, then
$\unicode[STIX]{x1D6E9}({\mathcal{M}}_{1})/\unicode[STIX]{x1D6E9}({\mathcal{M}}_{2})\cong \text{T}_{\text{st}}^{r}({\mathcal{M}}_{1}/{\mathcal{M}}_{2})$
.
2.4 On filtrations
Our goal is to give a rough classification of the filtration on certain strongly divisible modules
$\widehat{{\mathcal{M}}}$
of rank three whose associated
$p$
-adic Galois representation
$\unicode[STIX]{x1D70C}$
has maximally non-split and generic reduction
$\overline{\unicode[STIX]{x1D70C}}$
. The idea is to start with a simpler analysis in characteristic
$p$
(§ 2.4.1), using that the mod
$p$
reduction
${\mathcal{M}}$
of
$\widehat{{\mathcal{M}}}$
(a Breuil module) has associated mod
$p$
Galois representation
$\overline{\unicode[STIX]{x1D70C}}$
. The resulting Corollary 2.4.7 concerning
$\operatorname{Fil}^{2}{\mathcal{M}}$
helps us in our analysis of
$\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}$
in § 2.4.2. We obtain our classification in Proposition 2.4.10. This will be a key input into our main local result on the Galois side, Theorem 2.5.1.
Our conventions regarding strongly divisible modules will be explained at the start of § 2.4.2. For the remainder of § 2 we will assume that
$e=p^{f}-1$
.
2.4.1 Filtration on Breuil modules
We now obtain the first structure results for Breuil modules with descent data giving rise to maximally non-split
$\overline{\unicode[STIX]{x1D70C}}$
.
Proposition 2.4.1. Let
$K_{0}=\mathbb{Q}_{p}$
and suppose that
${\mathcal{M}}\in \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{2}$
is of type
$\unicode[STIX]{x1D714}^{a_{0}}\oplus \unicode[STIX]{x1D714}^{a_{1}}\oplus \unicode[STIX]{x1D714}^{a_{2}}$
. Assume that
$\overline{\unicode[STIX]{x1D70C}}\stackrel{\text{def}}{=}\text{T}_{\text{st}}^{2}({\mathcal{M}})$
is maximally non-split and generic as in Definition 2.1.5.
There is a framed basis
$\text{}\underline{e}=(e_{0},e_{1},e_{2})$
of
${\mathcal{M}}$
and a framed system of generators
$\text{}\underline{f}=(f_{0},f_{1},f_{2})$
for
$\operatorname{Fil}^{2}{\mathcal{M}}$
such that the coordinates of the elements in
$\text{}\underline{f}$
with respect to
$\text{}\underline{e}$
are described as follows:
$$\begin{eqnarray}f_{0}=\,\left(\begin{array}{@{}c@{}}u^{e}\\ \unicode[STIX]{x1D707}u^{e-(a_{1}-a_{0})}\\ \unicode[STIX]{x1D708}u^{e-(a_{2}-a_{0})}\end{array}\right),\quad f_{1}=\,\left(\begin{array}{@{}c@{}}0\\ u^{e}\\ \unicode[STIX]{x1D706}u^{e-(a_{2}-a_{1})}\end{array}\right),\quad f_{2}=\,\left(\begin{array}{@{}c@{}}0\\ 0\\ u^{e}\end{array}\right),\end{eqnarray}$$
where
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}\in \mathbb{F}$
verify, moreover,
$\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}\neq 0$
.
The proof of Proposition 2.4.1 will occupy the remainder of this subsection. We start with the following lemma. It gives a concrete criterion for the Galois representation associated to a rank-two Breuil module to split as a direct sum of characters.
Lemma 2.4.2. Assume
$K_{0}=\mathbb{Q}_{p}$
(so
$e=p-1$
) and let
$$\begin{eqnarray}0\rightarrow {\mathcal{M}}_{1}\rightarrow {\mathcal{M}}\rightarrow {\mathcal{M}}_{2}\rightarrow 0\end{eqnarray}$$
be an extension of rank-one objects in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{2}$
. For each
$i\in \{1,2\}$
, assume that
${\mathcal{M}}_{i}$
is of type
$\unicode[STIX]{x1D714}^{a_{i}}$
, with
$\unicode[STIX]{x1D714}^{a_{1}}\not \cong \unicode[STIX]{x1D714}^{a_{2}}$
and suppose
$\operatorname{Fil}^{2}{\mathcal{M}}_{i}=u^{\unicode[STIX]{x1D6FF}_{i}e}{\mathcal{M}}_{i}$
for
$0\leqslant \unicode[STIX]{x1D6FF}_{1}\leqslant \unicode[STIX]{x1D6FF}_{2}\leqslant 2$
. Finally, assume that
$\overline{\unicode[STIX]{x1D70C}}\stackrel{\text{def}}{=}\text{T}_{\text{st}}^{2}({\mathcal{M}})$
is Fontaine–Laffaille (possibly after a twist).
-
(i) If the extension of
$\overline{S}$
-modules (2.4.3)splits, then
$$\begin{eqnarray}0\rightarrow \operatorname{Fil}^{2}{\mathcal{M}}_{1}\rightarrow \operatorname{Fil}^{2}{\mathcal{M}}\rightarrow \operatorname{Fil}^{2}{\mathcal{M}}_{2}\rightarrow 0\end{eqnarray}$$
$\overline{\unicode[STIX]{x1D70C}}$
splits as a direct sum of two characters.
-
(ii) If
$\unicode[STIX]{x1D6FF}_{1}=1,\unicode[STIX]{x1D6FF}_{2}=2$
then
$\overline{\unicode[STIX]{x1D70C}}$
splits as a direct sum of two characters.
Proof. By assumption,
${\mathcal{M}}$
is of type
$\unicode[STIX]{x1D714}^{a_{1}}\oplus \unicode[STIX]{x1D714}^{a_{2}}$
. Let
$\text{}\underline{e}\stackrel{\text{def}}{=}(e_{1},e_{2})$
be a framed basis of
${\mathcal{M}}$
such that
${\mathcal{M}}_{1}=\overline{S}\cdot e_{1}$
. In what follows, we define
$[a_{2}-a_{1}]\in \{1,\ldots ,e-1\}$
by the requirement
$[a_{2}-a_{1}]\equiv a_{2}-a_{1}$
mod
$e$
.
From the exact sequence (2.4.3) we can find a framed system of generators of
$\operatorname{Fil}^{2}{\mathcal{M}}$
of the form
$f_{1}=u^{\unicode[STIX]{x1D6FF}_{1}e}e_{1}$
,
$f_{2}=u^{\unicode[STIX]{x1D6FF}_{2}e}e_{2}+xu^{[a_{2}-a_{1}]}e_{1}$
, where
$x\in \overline{S}_{\unicode[STIX]{x1D714}^{0}}$
. Moreover, we have
$$\begin{eqnarray}A\stackrel{\text{def}}{=}\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\unicode[STIX]{x1D711}_{2})=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FE}u^{[a_{2}-a_{1}]}\\ & \unicode[STIX]{x1D6FD}\end{array}\right)\in \operatorname{GL}_{2}(\overline{S})\end{eqnarray}$$
for some
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \overline{S}_{\unicode[STIX]{x1D714}^{0}}^{\times }$
and
$\unicode[STIX]{x1D6FE}\in \overline{S}_{\unicode[STIX]{x1D714}^{0}}$
.
Assume that the sequence (2.4.3) splits. Then we can fix a splitting
$s:\operatorname{Fil}^{2}{\mathcal{M}}_{2}\rightarrow \operatorname{Fil}^{2}{\mathcal{M}}$
which we can moreover assume to be
$\operatorname{Gal}(K/K_{0})$
-equivariant (by averaging). Let
$\overline{e}_{2}\in ({\mathcal{M}}_{2})_{\unicode[STIX]{x1D714}^{a_{2}}}$
be a generator of
${\mathcal{M}}_{2}$
. Then
$s(u^{e\unicode[STIX]{x1D6FF}_{2}}\overline{e}_{2})$
is killed by
$u^{e(p-\unicode[STIX]{x1D6FF}_{2})}$
and hence of the form
$u^{\unicode[STIX]{x1D6FF}_{2}e}e_{2}$
for some
$e_{2}\in {\mathcal{M}}$
. Without loss of generality,
$e_{2}\in {\mathcal{M}}_{\unicode[STIX]{x1D714}^{a_{2}}}$
. It is now easy to see that
$(e_{1},e_{2})$
is a framed basis of
${\mathcal{M}}$
and that
$(f_{1},f_{2})=(u^{\unicode[STIX]{x1D6FF}_{1}e}e_{1},u^{\unicode[STIX]{x1D6FF}_{2}e}e_{2})$
is a framed system of generators of
$\operatorname{Fil}^{2}{\mathcal{M}}$
. In other words, we can take
$x=0$
above.
From the obvious matrix equality
$$\begin{eqnarray}A\left(\begin{array}{@{}cc@{}}u^{\unicode[STIX]{x1D6FF}_{1}e} & \\ & u^{\unicode[STIX]{x1D6FF}_{2}e}\end{array}\right)=\left(\begin{array}{@{}cc@{}}u^{\unicode[STIX]{x1D6FF}_{1}e} & \\ & u^{\unicode[STIX]{x1D6FF}_{2}e}\end{array}\right)\underbrace{\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FE}u^{(\unicode[STIX]{x1D6FF}_{2}-\unicode[STIX]{x1D6FF}_{1})e+[a_{2}-a_{1}]}\\ & \unicode[STIX]{x1D6FD}\end{array}\right)}_{\stackrel{\text{def}}{=}B}\end{eqnarray}$$
and Lemma 2.2.8, we deduce that
$\text{}\underline{e}^{\prime }\stackrel{\text{def}}{=}\text{}\underline{e}\cdot A$
is a basis of
${\mathcal{M}}$
such that
${\mathcal{M}}_{1}=\overline{S}\cdot e_{1}^{\prime }$
, that
$\text{}\underline{f}^{\prime }\stackrel{\text{def}}{=}(u^{\unicode[STIX]{x1D6FF}_{1}e}e_{1}^{\prime },u^{\unicode[STIX]{x1D6FF}_{2}e}e_{2}^{\prime })$
is a system of generators for
$\operatorname{Fil}^{2}{\mathcal{M}}$
and that
$$\begin{eqnarray}\text{Mat}_{\text{}\underline{e}^{\prime },\text{}\underline{f}^{\prime }}(\unicode[STIX]{x1D711}_{2})=\unicode[STIX]{x1D711}(B)=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC}) & \unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FE})u^{[a_{2}-a_{1}]p}\\ & \unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FD})\end{array}\right).\end{eqnarray}$$
As
$[a_{2}-a_{1}]>0$
we can further assume that
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FE})=0$
, up to re-iterating the procedure above. Therefore
$M_{\mathbb{F}_{p}((\text{}\underline{\unicode[STIX]{x1D71B}}))}({\mathcal{M}})$
splits into a direct sum of rank-one
$(\unicode[STIX]{x1D711},\mathbb{F}((\text{}\underline{\unicode[STIX]{x1D71B}})))$
-modules (as can be immediately checked by Lemma 2.2.6), hence
$\overline{\unicode[STIX]{x1D70C}}|_{G_{(\mathbb{Q}_{p})_{\infty }}}$
splits as a direct sum of two characters. As
$\overline{\unicode[STIX]{x1D70C}}$
is Fontaine–Laffaille, we deduce from Proposition 2.2.1 that
$\overline{\unicode[STIX]{x1D70C}}$
splits into a direct sum of two characters, completing the proof of case (i).
Let us assume that
$\unicode[STIX]{x1D6FF}_{1}=1,\,\unicode[STIX]{x1D6FF}_{2}=2$
. We then have
$f_{2}=u^{2e}e_{2}+xu^{[a_{2}-a_{1}]}e_{1}$
and by adding a multiple of
$f_{1}$
we may assume
$x\in \mathbb{F}$
. If
$x\neq 0$
it follows that
$\operatorname{Fil}^{2}{\mathcal{M}}=\langle u^{[a_{2}-a_{1}]}e_{1},u^{3e-[a_{2}-a_{1}]}e_{2}\rangle$
, so
$u^{2e}e_{2}\not \in \operatorname{Fil}^{2}{\mathcal{M}}$
, which is a contradiction. Therefore
$x=0$
and we are in the situation of case (i).◻
Remark 2.4.4. The analogous statement of Lemma 2.4.2 holds when
$K_{0}\neq \mathbb{Q}_{p}$
. This will be described in detail in a particular case in the proof of Proposition 2.6.4, when
$[K_{0}:\mathbb{Q}_{p}]=2$
and developed in further generality in [Reference Morra and ParkMP14, Lemma 3.2].
We now make use of our knowledge of rank-one Breuil modules with descent data and their associated Galois representations to start to understand
$\operatorname{Fil}^{2}{\mathcal{M}}$
in Proposition 2.4.1.
Lemma 2.4.5. Assume
$K_{0}=\mathbb{Q}_{p}$
and let
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
be maximally non-split and generic as in Definition 2.1.5. Let
${\mathcal{M}}\in \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{2}$
be of type
$\unicode[STIX]{x1D714}^{a_{0}}\oplus \unicode[STIX]{x1D714}^{a_{1}}\oplus \unicode[STIX]{x1D714}^{a_{2}}$
and such that
$\text{T}_{\text{st}}^{2}({\mathcal{M}})\cong \overline{\unicode[STIX]{x1D70C}}$
and write
$0={\mathcal{M}}_{3}\subsetneq {\mathcal{M}}_{2}\subsetneq {\mathcal{M}}_{1}\subsetneq {\mathcal{M}}_{0}\stackrel{\text{def}}{=}{\mathcal{M}}$
to denote the Breuil submodule filtration on
${\mathcal{M}}$
deduced from the socle filtration on
$\overline{\unicode[STIX]{x1D70C}}$
(cf. Proposition 2.3.5).
Then for each
$i\in \{0,1,2\}$
the rank-one quotient
${\mathcal{M}}_{i}/{\mathcal{M}}_{i+1}\in \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{2}$
is of type
$\unicode[STIX]{x1D714}^{a_{i}}$
and its filtration is described by
$$\begin{eqnarray}\operatorname{Fil}^{2}({\mathcal{M}}_{i}/{\mathcal{M}}_{i+1})=u^{e}({\mathcal{M}}_{i}/{\mathcal{M}}_{i+1}).\end{eqnarray}$$
Proof. By Proposition 2.3.5, there exists a permutation
$\unicode[STIX]{x1D70E}\in S_{3}$
such that for any
$i\in \{0,1,2\}$
the rank-one module
${\mathcal{M}}_{i}/{\mathcal{M}}_{i+1}$
is of type
$\unicode[STIX]{x1D714}^{a_{\unicode[STIX]{x1D70E}(i)}}$
. This implies, by means of [Reference Emerton, Gee and HerzigEGH13], Lemma 3.3.2, that there exists
$\unicode[STIX]{x1D6FF}_{i}\in \{0,1,2\}$
such that
$\operatorname{Fil}^{2}({\mathcal{M}}_{i}/{\mathcal{M}}_{i+1})=u^{e\unicode[STIX]{x1D6FF}_{i}}({\mathcal{M}}_{i}/{\mathcal{M}}_{i+1})$
and
$\text{T}_{\text{st}}^{2}({\mathcal{M}}_{i}/{\mathcal{M}}_{i+1})|_{I_{\mathbb{Q}_{p}}}\cong \unicode[STIX]{x1D714}^{a_{\unicode[STIX]{x1D70E}(i)}+\unicode[STIX]{x1D6FF}_{i}}$
.
On the other hand we have
$\text{T}_{\text{st}}^{2}({\mathcal{M}}_{i}/{\mathcal{M}}_{i+1})|_{I_{\mathbb{Q}_{p}}}\cong \unicode[STIX]{x1D714}^{a_{i}+1}$
for all
$i$
, by the definition of the filtration
$\{{\mathcal{M}}_{i}\}_{i}$
. As
$\overline{\unicode[STIX]{x1D70C}}$
is generic (cf. Definition 2.1.5) we conclude that
$\unicode[STIX]{x1D70E}=\text{id}$
and that
$\unicode[STIX]{x1D6FF}_{i}=1$
for all
$i$
.◻
Proof of Proposition 2.4.1.
Let
$0\subsetneq {\mathcal{M}}_{2}\subsetneq {\mathcal{M}}_{1}\subsetneq {\mathcal{M}}_{0}\stackrel{\text{def}}{=}{\mathcal{M}}$
be the filtration by Breuil submodules on
${\mathcal{M}}$
, obtained from the socle filtration on
$\overline{\unicode[STIX]{x1D70C}}$
via Proposition 2.3.5. From Lemma 2.4.5 we obtain a framed basis
$(e_{0},e_{1},e_{2})$
of
${\mathcal{M}}$
with
$e_{i}\in {\mathcal{M}}_{i}$
such that
$$\begin{eqnarray}\operatorname{Fil}^{2}({\mathcal{M}}_{i}/{\mathcal{M}}_{i+1})=\langle u^{e}\overline{e}_{i}\rangle _{\overline{S}}\end{eqnarray}$$
for
$i\in \{0,1,2\}$
(with the obvious notation for the elements
$\overline{e}_{i}$
).
As the descent data acts semisimply on
${\mathcal{M}}_{1}$
, from the exact sequence
$$\begin{eqnarray}0\rightarrow \operatorname{Fil}^{2}{\mathcal{M}}_{2}\rightarrow \operatorname{Fil}^{2}{\mathcal{M}}_{1}\rightarrow \operatorname{Fil}^{2}({\mathcal{M}}_{1}/{\mathcal{M}}_{2})\rightarrow 0\end{eqnarray}$$
we see that
$$\begin{eqnarray}\operatorname{Fil}^{2}{\mathcal{M}}_{1}=\langle u^{e}e_{2},u^{e}e_{1}+se_{2}\rangle _{\overline{S}}\quad \text{for some}~s\in \overline{S}_{\unicode[STIX]{x1D714}^{a_{1}-a_{2}}}=u^{e-(a_{2}-a_{1})}\overline{S}_{\unicode[STIX]{x1D714}^{0}}.\end{eqnarray}$$
Without loss of generality, we can assume
$s=\unicode[STIX]{x1D706}u^{e-(a_{2}-a_{1})}$
for some
$\unicode[STIX]{x1D706}\in \mathbb{F}$
and, by Lemma 2.4.2 and the non-splitness assumption, we moreover have
$\unicode[STIX]{x1D706}\neq 0$
.
In a completely similar fashion we obtain
$$\begin{eqnarray}\operatorname{Fil}^{2}{\mathcal{M}}=\langle u^{e}e_{2},~u^{e}e_{1}+\unicode[STIX]{x1D706}u^{e-(a_{2}-a_{1})}e_{2},~u^{e}e_{0}+s_{1}e_{1}+s_{2}e_{2}\rangle _{\overline{S}},\end{eqnarray}$$
where
$s_{1}\in \overline{S}_{\unicode[STIX]{x1D714}^{a_{0}-a_{1}}},s_{2}\in \overline{S}_{\unicode[STIX]{x1D714}^{a_{0}-a_{2}}}$
. As above, we can assume without loss of generality that
$s_{1}=\unicode[STIX]{x1D707}u^{e-(a_{1}-a_{0})}$
and
$s_{2}=\unicode[STIX]{x1D708}u^{e-(a_{2}-a_{0})}$
and we furthermore deduce from Lemma 2.4.2 (applied to
${\mathcal{M}}/{\mathcal{M}}_{2}$
) that
$\unicode[STIX]{x1D708}\neq 0$
.◻
The following immediate corollary of Proposition 2.4.1 will play an important role in describing the filtration on certain strongly divisible
${\mathcal{O}}_{E}$
-modules, see § 2.4.2.
Corollary 2.4.7. Let
${\mathcal{M}}$
be a Breuil module and
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D708},\unicode[STIX]{x1D707}\in \mathbb{F}$
as in the statement of Proposition 2.4.1.
The elementary divisors for
${\mathcal{M}}/\!\operatorname{Fil}^{2}{\mathcal{M}}$
as an
$\mathbb{F}[u]$
-module are described by one of the following possibilities:
- (i)
-
if
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D708}-\unicode[STIX]{x1D706}\unicode[STIX]{x1D707})\neq 0$
, by
$(u^{e-(a_{2}-a_{0})},u^{e},u^{e+(a_{2}-a_{0})})$
; - (ii)
-
if
$\unicode[STIX]{x1D708}-\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}=0$
, by
$(u^{e-(a_{2}-a_{0})},u^{e+(a_{2}-a_{1})},u^{e+(a_{1}-a_{0})})$
; - (iii)
-
if
$\unicode[STIX]{x1D708}=0$
, by
$(u^{e-(a_{2}-a_{1})},u^{e-(a_{1}-a_{0})},u^{e+(a_{2}-a_{0})})$
.
We also have:
- (iv)
-
$\operatorname{Fil}^{2}{\mathcal{M}}\subseteq u^{e-(a_{2}-a_{0})}{\mathcal{M}}$
;
- (v)
-
$(\operatorname{Fil}^{2}{\mathcal{M}})_{\unicode[STIX]{x1D714}^{a_{0}}}\not \subseteq u^{e}{\mathcal{M}}$
;
- (vi)
-
$(\operatorname{Fil}^{2}{\mathcal{M}}\,\cap \,u^{e}{\mathcal{M}})_{\unicode[STIX]{x1D714}^{a_{0}}}\subseteq u^{2e-(a_{2}-a_{0})}{\mathcal{M}}$
;
- (vii)
-
$(\operatorname{Fil}^{2}{\mathcal{M}})_{\unicode[STIX]{x1D714}^{a_{2}}}\subseteq u^{e}{\mathcal{M}}$
.
2.4.2 Filtration on strongly divisible modules
In this section we pursue the analysis started in § 2.4.1. The main result of this section is Proposition 2.4.10.
As in § 2.2.1, we let
$K^{\prime }\subseteq K_{0}$
be a subfield containing
$\mathbb{Q}_{p}$
. The ring
$S_{W(k)}$
(cf. [Reference BreuilBre97, § 4.1]) is defined as the
$p$
-adic completion of
$W(k)[u,u^{ie}/i!]_{i\in \mathbb{N}}$
. The ring
$S_{W(k)}$
is endowed with a descending filtration
$\{\operatorname{Fil}^{i}S_{W(k)}\}_{i\in \mathbb{N}}$
, a semilinear Frobenius
$\unicode[STIX]{x1D711}$
, a
$W(k)$
-linear derivation
$N$
, and with a Galois action by
$W(k)$
-algebra endomorphisms defined by
$\widehat{g}(u)=\widetilde{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D71B}}(g)u$
for any
$g\in \text{Gal}(K/K^{\prime })$
. In particular, the action of any
$g\in \text{Gal}(K/K^{\prime })$
preserves the filtration and commutes with the Frobenius and the monodromy on
$S_{W(k)}$
. By extension of scalars, the ring
$S\stackrel{\text{def}}{=}S_{W(k)}\otimes _{\mathbb{Z}_{p}}{\mathcal{O}}_{E}$
is endowed with the additional structures inherited from
$S_{W(k)}$
. Note in particular that we have a natural map
$S{\twoheadrightarrow}\overline{S}$
, defined as the reduction modulo
$(\unicode[STIX]{x1D71B}_{E},\operatorname{Fil}^{p}S)$
. For more details, see [Reference Emerton, Gee and HerzigEGH13, § 3.1].
Fix
$r\in \{0,\ldots ,p-2\}$
. We refer to [Reference Emerton, Gee and HerzigEGH13, § 3.1] for the definition of the category
${\mathcal{O}}_{E}\text{-}\operatorname{Mod}_{\text{dd}}^{r}$
of strongly divisible
${\mathcal{O}}_{E}$
-modules of weight
$r$
and with descent data from
$K$
to
$K^{\prime }$
. The objects are certain quintuples
$(\widehat{{\mathcal{M}}},\operatorname{Fil}^{r}\widehat{{\mathcal{M}}},\unicode[STIX]{x1D711},N,\{\widehat{g}\})$
, where
$\widehat{{\mathcal{M}}}$
is a finite free
$S$
-module. There is a contravariant functor
$\text{T}_{\text{st}}^{\ast ,K^{\prime }}:{\mathcal{O}}_{E}\text{-}\operatorname{Mod}_{\text{dd}}^{r}\rightarrow \text{Rep}_{{\mathcal{O}}_{E}}(G_{K^{\prime }})$
, which by a theorem of Liu ([Reference LiuLiu08, Theorem 2.3.5], cf. also [Reference Emerton, Gee and HerzigEGH13, Proposition 3.1.4]) provides an equivalence of categories of
${\mathcal{O}}_{E}\text{-}\operatorname{Mod}_{\text{dd}}^{r}$
with the category of
$G_{K^{\prime }}$
-stable
${\mathcal{O}}_{E}$
-lattices in finite dimensional
$E$
-representations of
$G_{K^{\prime }}$
that become semistable over
$K$
and have Hodge–Tate weights in
$[-r,0]$
. As in the case of Breuil modules, we consider its covariant version defined by
$\text{T}_{\text{st}}^{K^{\prime },r}(\widehat{{\mathcal{M}}})\stackrel{\text{def}}{=}(\text{T}_{\text{st}}^{\ast ,K^{\prime }}(\widehat{{\mathcal{M}}}))^{\vee }\,\otimes \,\unicode[STIX]{x1D700}^{r}$
.
We also recall that if
$\widehat{{\mathcal{M}}}\in {\mathcal{O}}_{E}\text{-}\operatorname{Mod}_{\text{dd}}^{r}$
the base change
$\widehat{{\mathcal{M}}}\otimes _{S}\overline{S}$
is naturally an object of
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
and one has a natural isomorphism
$\text{T}_{\text{st}}^{\ast ,K^{\prime }}(\widehat{{\mathcal{M}}})\otimes _{{\mathcal{O}}_{E}}\mathbb{F}\cong \text{T}_{\text{st}}^{\ast }(\widehat{{\mathcal{M}}}\otimes _{S}\overline{S})$
of
$\mathbb{F}[G_{K^{\prime }}]$
-modules.
We write
$\text{Mod}_{E}^{\text{w.a.}}(\unicode[STIX]{x1D711},N,K/K^{\prime })$
for the category of weakly admissible filtered
$(\unicode[STIX]{x1D711},N,K/K^{\prime },E)$
-modules (see e.g. [Reference Emerton, Gee and HerzigEGH13, § 3.1]). In particular, the underlying objects are finite free
$K_{0}\otimes _{\mathbb{Q}_{p}}E$
-modules. We recall the contravariant equivalence of categories
$$\begin{eqnarray}\text{D}_{\text{st}}^{\ast ,K^{\prime }}:\text{Rep}_{E}^{K-\text{st}}(G_{K^{\prime }})\rightarrow \text{Mod}_{E}^{\text{w.a.}}(\unicode[STIX]{x1D711},N,K/K^{\prime }),\end{eqnarray}$$
where
$\text{Rep}_{E}^{K-\text{st}}(G_{K^{\prime }})$
denotes the category of finite dimensional
$E$
-representations of
$G_{K^{\prime }}$
that become semistable over
$K$
. If
$\unicode[STIX]{x1D70C}\in \text{Rep}_{E}^{K-\text{cris}}(G_{K^{\prime }})$
has Hodge–Tate weights in
$[-r,0]$
, we define
$\text{D}_{\text{st}}^{K^{\prime },r}(\unicode[STIX]{x1D70C})\stackrel{\text{def}}{=}\text{D}_{\text{st}}^{\ast ,K^{\prime }}(\unicode[STIX]{x1D70C}^{\vee }\,\otimes \,\unicode[STIX]{x1D700}^{r})$
.
As in the mod
$p$
setting, given an
${\mathcal{O}}_{E}[\operatorname{Gal}(K/K^{\prime })]$
-module
$X$
and a character
$\unicode[STIX]{x1D712}:\operatorname{Gal}(K/K^{\prime })\rightarrow {\mathcal{O}}_{E}^{\times }$
we let
$X_{\unicode[STIX]{x1D712}}$
denote its
$\unicode[STIX]{x1D712}$
-isotypical component.
We first require two lemmas.
Lemma 2.4.8. Assume that
$K^{\prime }=\mathbb{Q}_{p}$
and that the
$p$
-adic Galois representation
$\text{T}_{\text{st}}^{\mathbb{Q}_{p},r}(\widehat{{\mathcal{M}}})\otimes _{{\mathcal{O}}_{E}}E$
has inertial type
$\bigoplus _{i=0}^{n-1}\widetilde{\unicode[STIX]{x1D714}}_{f}^{a_{i}}$
. Then
$\widehat{{\mathcal{M}}}\otimes _{S}\overline{S}\in \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
is of type
$\bigoplus _{i=0}^{n-1}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{i}}$
.
Proof. The assumption that
$K^{\prime }=\mathbb{Q}_{p}$
implies that the multi-set
$\{\widetilde{\unicode[STIX]{x1D714}}_{f}^{a_{i}}\}_{i=0}^{n-1}$
(and hence the multi-set
$\{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{a_{i}}\}_{i=0}^{n-1}$
) is stable under the action of the
$p$
-power Frobenius. Together with [Reference Emerton, Gee and HerzigEGH13, Proposition 3.3.1], this is all we need to use the argument at the beginning of [Reference Emerton, Gee and HerzigEGH13, Proof of Theorem 3.3.13] to construct the required basis for
$\widehat{{\mathcal{M}}}\otimes _{S}\overline{S}$
.◻
Lemma 2.4.9. Assume
$K_{0}=\mathbb{Q}_{p}$
and let
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}(E)$
be a Galois representation, becoming semistable over
$K$
, with Hodge–Tate weights
$\{-2,-1,0\}$
. Let
$\widehat{{\mathcal{M}}}\in {\mathcal{O}}_{E}\text{-}\operatorname{Mod}_{\text{dd}}^{2}$
be such that
$\text{T}_{\text{st}}^{\mathbb{Q}_{p},2}(\widehat{{\mathcal{M}}})\otimes _{{\mathcal{O}}_{E}}E\cong \unicode[STIX]{x1D70C}$
and define
$$\begin{eqnarray}X\stackrel{\text{def}}{=}\biggl(\frac{\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}}{\operatorname{Fil}^{2}S\cdot \widehat{{\mathcal{M}}}}\biggr)\otimes _{{\mathcal{O}}_{E}}E\quad \text{and}\quad Y\stackrel{\text{def}}{=}\biggl(\frac{\operatorname{Fil}^{1}S\cdot \widehat{{\mathcal{M}}}}{\operatorname{Fil}^{2}S\cdot \widehat{{\mathcal{M}}}}\biggr)\otimes _{{\mathcal{O}}_{E}}E.\end{eqnarray}$$
Then for any character
$\unicode[STIX]{x1D712}:\operatorname{Gal}(K/\mathbb{Q}_{p})\rightarrow E^{\times }$
we have:
-
(i)
$\dim _{E}X_{\unicode[STIX]{x1D712}}=3$
; -
(ii)
$\dim _{E}(X\,\cap \,Y)_{\unicode[STIX]{x1D712}}=2$
.
Moreover, multiplication by
$u\in S$
induces an isomorphism
$X_{\unicode[STIX]{x1D712}}\stackrel{{\sim}}{\longrightarrow }X_{\unicode[STIX]{x1D712}\widetilde{\unicode[STIX]{x1D714}}}$
.
Proof. Let
$D\stackrel{\text{def}}{=}\text{D}_{\text{st}}^{\ast ,\mathbb{Q}_{p}}(\unicode[STIX]{x1D70C})$
. As
$\unicode[STIX]{x1D70C}|_{G_{K}}$
is semistable, with Hodge–Tate weights
$\{-2,-1,0\}$
, the
$E$
-linear spaces
$\operatorname{gr}^{i}(\operatorname{Fil}^{\bullet }D_{K})$
are at most one dimensional and they are non-zero if and only if
$i\in \{0,1,2\}$
.
Let
${\mathcal{D}}\stackrel{\text{def}}{=}D\,\otimes _{E}\,S_{E}$
. We then have
$X=\operatorname{Fil}^{2}{\mathcal{D}}/(\operatorname{Fil}^{2}S_{E}\cdot {\mathcal{D}})$
,
$Y=(\operatorname{Fil}^{1}S_{E}\cdot {\mathcal{D}})/(\operatorname{Fil}^{2}S_{E}\cdot {\mathcal{D}})$
and by the analogue with
$E$
-coefficients of [Reference BreuilBre97, Proposition A.4], we deduce that
$$\begin{eqnarray}\operatorname{Fil}^{1}{\mathcal{D}}=(\operatorname{Fil}^{1}S_{E})\widehat{f}_{0}\oplus S_{E}\widehat{f}_{1}\oplus S_{E}\widehat{f}_{2},\quad \operatorname{Fil}^{2}{\mathcal{D}}=(\operatorname{Fil}^{2}S_{E})\widehat{f}_{0}\oplus (\operatorname{Fil}^{1}S_{E})\widehat{f}_{1}\oplus S_{E}\widehat{f}_{2},\end{eqnarray}$$
for some
$S_{E}$
-basis
$\widehat{f}_{i}$
of
${\mathcal{D}}$
.
From the
$E$
-linear isomorphism
$$\begin{eqnarray}\frac{S}{\operatorname{Fil}^{m}S}\cong \bigoplus _{i=0}^{m-1_{}^{}\bigoplus }\langle u^{j}E(u)^{i}\rangle _{E}\end{eqnarray}$$
for
$m\leqslant p$
, we deduce that
$\dim _{E}X=3e$
,
$\dim _{E}(X\,\cap \,Y)=2e$
. We now note that
$\operatorname{Gal}(K/\mathbb{Q}_{p})$
acts semisimply and that multiplication by
$u$
defines an
$E$
-linear automorphism on
$S_{E}/\!\operatorname{Fil}^{p}S_{E}$
which cyclically permutes isotypical components. The result follows.◻
We can now state the main result of this section.
Proposition 2.4.10. Assume that
$K_{0}=\mathbb{Q}_{p}$
and let
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}({\mathcal{O}}_{E})$
be a semistable Galois representation, becoming crystalline over
$K$
, with inertial type
$\widetilde{\unicode[STIX]{x1D714}}^{a_{0}}\oplus \widetilde{\unicode[STIX]{x1D714}}^{a_{1}}\oplus \widetilde{\unicode[STIX]{x1D714}}^{a_{2}}$
and Hodge–Tate weights
$\{-2,-1,0\}$
. Let
$\widehat{{\mathcal{M}}}\in {\mathcal{O}}_{E}\text{-}\operatorname{Mod}_{\text{dd}}^{2}$
be a strongly divisible
${\mathcal{O}}_{E}$
-module such that
$\text{T}_{\text{st}}^{\mathbb{Q}_{p},2}(\widehat{{\mathcal{M}}})\cong \unicode[STIX]{x1D70C}$
. Assume that
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
is maximally non-split and generic as in Definition 2.1.5.
There exist a framed basis
$\widehat{\text{}\underline{e}}=(\widehat{e}_{0},\widehat{e}_{1},\widehat{e}_{2})$
of
$\widehat{{\mathcal{M}}}$
, with respect to
$\widetilde{\unicode[STIX]{x1D714}}^{a_{0}}\oplus \widetilde{\unicode[STIX]{x1D714}}^{a_{1}}\oplus \widetilde{\unicode[STIX]{x1D714}}^{a_{2}}$
, and a framed system of generators
$\widehat{\text{}\underline{f}}=(\widehat{f}_{0},\widehat{f}_{1},\widehat{f}_{2})$
for
$\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}/(\operatorname{Fil}^{p}S\cdot \widehat{{\mathcal{M}}})$
, whose coordinates with respect to
$\widehat{\text{}\underline{e}}$
are described by one of the following possibilities.
Case A.
$$\begin{eqnarray}\widehat{f}_{0}=\,\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}\\ 0\\ u^{e-(a_{2}-a_{0})}\end{array}\right),\quad \widehat{f}_{1}=\,E(u)\left(\begin{array}{@{}c@{}}0\\ 1\\ 0\end{array}\right),\quad \widehat{f}_{2}=\,\left(\begin{array}{@{}c@{}}(p+E(u))u^{a_{2}-a_{0}}\\ 0\\ -\frac{p^{2}}{\unicode[STIX]{x1D6FC}}\end{array}\right),\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{E}$
with
$0<\text{ord}_{p}(\unicode[STIX]{x1D6FC})<2$
.
Case B.
$$\begin{eqnarray}\widehat{f}_{0}=\,\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}\\ 0\\ u^{e-(a_{2}-a_{0})}\end{array}\right),\quad \widehat{f}_{1}=\,E(u)\left(\begin{array}{@{}c@{}}u^{a_{1}-a_{0}}\\ -\frac{p}{\unicode[STIX]{x1D6FD}}\\ 0\end{array}\right),\quad \widehat{f}_{2}=\,\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FD}u^{a_{2}-a_{0}}\\ E(u)u^{a_{2}-a_{1}}\\ -\frac{p\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6FC}}\end{array}\right),\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{E}$
with
$0<\text{ord}_{p}(\unicode[STIX]{x1D6FD})<1$
and
$0<\text{ord}_{p}(\unicode[STIX]{x1D6FC})<\text{ord}_{p}(\unicode[STIX]{x1D6FD})+1$
.
Case C.
$$\begin{eqnarray}\widehat{f}_{0}=\,\left(\begin{array}{@{}c@{}}-\frac{p\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FD}}\\ u^{e-(a_{1}-a_{0})}\\ \frac{p}{\unicode[STIX]{x1D6FD}}u^{e-(a_{2}-a_{0})}\end{array}\right),\quad \widehat{f}_{1}=\,\left(\begin{array}{@{}c@{}}-\unicode[STIX]{x1D6FC}u^{a_{1}-a_{0}}\\ -\unicode[STIX]{x1D6FD}\\ u^{e-(a_{2}-a_{1})}\end{array}\right),\quad \widehat{f}_{2}=\,\left(\begin{array}{@{}c@{}}(p+E(u))u^{a_{2}-a_{0}}\\ \frac{p\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6FC}}u^{a_{2}-a_{1}}\\ \frac{p^{2}}{\unicode[STIX]{x1D6FC}}\end{array}\right),\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{E}$
with
$0<\text{ord}_{p}(\unicode[STIX]{x1D6FD})<1$
and
$0<\text{ord}_{p}(\unicode[STIX]{x1D6FC})<\text{ord}_{p}(\unicode[STIX]{x1D6FD})+1$
.
Here, by a framed basis
$\text{}\underline{\widehat{e}}$
of
$\widehat{{\mathcal{M}}}$
we mean an
$S$
-basis such that
$\widehat{g}\cdot \widehat{e}_{i}=\widetilde{\unicode[STIX]{x1D714}}(g)^{a_{i}}\widehat{e}_{i}$
for all
$0\leqslant i\leqslant 2$
,
$g\in \operatorname{Gal}(K/K_{0})$
. Similarly, we mean that
$\text{}\underline{\widehat{f}}$
consists of elements of
$\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}$
that generate
$\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}/(\operatorname{Fil}^{p}S\cdot \widehat{{\mathcal{M}}})$
as
$S$
-module and such that
$\widehat{g}\cdot \widehat{f}_{i}=\widetilde{\unicode[STIX]{x1D714}}(g)^{a_{i}}\widehat{f}_{i}$
for all
$0\leqslant i\leqslant 2$
,
$g\in \operatorname{Gal}(K/K_{0})$
. Finally,
$\text{ord}_{p}$
is the valuation of
$E$
normalized by
$\text{ord}_{p}(p)=1$
.
Proof. Let
$\text{}\underline{e}\stackrel{\text{def}}{=}(e_{0},e_{1},e_{2})$
be a framed basis of
$\widehat{{\mathcal{M}}}$
. We write the elements of
$\widehat{{\mathcal{M}}}$
in terms of coordinates with respect to
$\text{}\underline{e}$
. Moreover, we let
${\mathcal{M}}\stackrel{\text{def}}{=}\widehat{{\mathcal{M}}}\otimes _{S}\overline{S}$
, define
${\mathcal{D}}\stackrel{\text{def}}{=}\widehat{{\mathcal{M}}}\otimes _{{\mathcal{O}}_{E}}S_{E}$
, and set
$X=(\operatorname{Fil}^{2}{\mathcal{M}}/\!\operatorname{Fil}^{2}S\cdot {\mathcal{M}})\otimes _{{\mathcal{O}}_{E}}E$
as in Lemma 2.4.9. In particular
${\mathcal{M}}\in \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{2}$
is of type
$\unicode[STIX]{x1D714}^{a_{0}}\oplus \unicode[STIX]{x1D714}^{a_{1}}\oplus \unicode[STIX]{x1D714}^{a_{2}}$
by Lemma 2.4.8.
By Lemma 2.4.9 we have a non-zero element
$f_{0}\in (\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}/\!\operatorname{Fil}^{2}S\cdot \widehat{{\mathcal{M}}})_{\widetilde{\unicode[STIX]{x1D714}}^{a_{0}}}$
of the form
$$\begin{eqnarray}f_{0}=\left(\begin{array}{@{}c@{}}x\\ yu^{e-(a_{1}-a_{0})}\\ zu^{e-(a_{2}-a_{0})}\end{array}\right)+E(u)\left(\begin{array}{@{}c@{}}x^{\prime }\\ y^{\prime }u^{e-(a_{1}-a_{0})}\\ z^{\prime }u^{e-(a_{2}-a_{0})}\end{array}\right),\end{eqnarray}$$
where
$x,y,z,x^{\prime },y^{\prime },z^{\prime }\in {\mathcal{O}}_{E}$
. As
$\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}/\!\operatorname{Fil}^{2}S\cdot \widehat{{\mathcal{M}}}$
is
$\unicode[STIX]{x1D71B}_{E}$
-torsion free, we may assume that one of
$x,y,z,x^{\prime },y^{\prime },z^{\prime }$
is in
${\mathcal{O}}_{E}^{\times }$
. If
$x,y,z\in \unicode[STIX]{x1D71B}_{E}{\mathcal{O}}_{E}$
for all choices of
$f_{0}$
, we get a contradiction from Corollary 2.4.7(v). On the other hand by Corollary 2.4.7(iv) we necessarily have
$x\in \unicode[STIX]{x1D71B}_{E}{\mathcal{O}}_{E}$
, and hence we may assume that
$y\in {\mathcal{O}}_{E}^{\times }$
or
$z\in {\mathcal{O}}_{E}^{\times }$
.
Case 1: assume
$z\in {\mathcal{O}}_{E}^{\times }$
. Let us define the element
$e_{2}^{\prime }\in \widehat{{\mathcal{M}}}$
by
$$\begin{eqnarray}e_{2}^{\prime }=\left(\begin{array}{@{}c@{}}x^{\prime }u^{a_{2}-a_{0}}\\ (y+y^{\prime }E(u))u^{a_{2}-a_{1}}\\ z+z^{\prime }E(u)\end{array}\right).\end{eqnarray}$$
As
$z\in {{\mathcal{O}}_{E}}^{\times }$
we deduce by Nakayama’s lemma that
$\text{}\underline{e}^{\prime }\stackrel{\text{def}}{=}(e_{0},e_{1},e_{2}^{\prime })$
is again a framed basis of
$\widehat{{\mathcal{M}}}$
. By letting
$\unicode[STIX]{x1D6FC}\stackrel{\text{def}}{=}x+px^{\prime }$
we therefore have the following coordinates for
$f_{0}$
in the basis
$\text{}\underline{e}^{\prime }$
:
$$\begin{eqnarray}f_{0}=\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}\\ 0\\ u^{e-(a_{2}-a_{0})}\end{array}\right),\end{eqnarray}$$
where
$\text{ord}_{p}(\unicode[STIX]{x1D6FC})>0$
. (Recall that
$E(u)=u^{e}+p$
.) From now on we use the basis
$\text{}\underline{e}^{\prime }$
to write the coordinates of the elements in
$\widehat{{\mathcal{M}}}$
.
By Lemma 2.4.9 we easily deduce that
$(\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}/\!\operatorname{Fil}^{2}S\cdot \widehat{{\mathcal{M}}})_{\widetilde{\unicode[STIX]{x1D714}}^{a_{0}}}$
equals
$$\begin{eqnarray}\left\langle \left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}\\ 0\\ u^{e-(a_{2}-a_{0})}\end{array}\right),E(u)\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}\\ 0\\ u^{e-(a_{2}-a_{0})}\end{array}\right),E(u)\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FD}\\ \unicode[STIX]{x1D6FE}u^{e-(a_{1}-a_{0})}\\ 0\end{array}\right)\right\rangle _{{\mathcal{O}}_{E}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in {\mathcal{O}}_{E}$
are such that either
$\unicode[STIX]{x1D6FD}\not \equiv 0$
or
$\unicode[STIX]{x1D6FE}\not \equiv 0$
modulo
$\unicode[STIX]{x1D71B}_{E}$
. Moreover, by Corollary 2.4.7(vi) we necessarily have
$\unicode[STIX]{x1D6FD}\equiv 0$
so that, without loss of generality, we may assume
$\unicode[STIX]{x1D6FE}=1$
. By Lemma 2.4.9 we obtain
$$\begin{eqnarray}X_{\widetilde{\unicode[STIX]{x1D714}}^{a_{1}}}=\left\langle \left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}u^{a_{1}-a_{0}}\\ 0\\ u^{e-(a_{2}-a_{1})}\end{array}\right),E(u)\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}u^{a_{1}-a_{0}}\\ 0\\ u^{e-(a_{2}-a_{1})}\end{array}\right),E(u)\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FD}u^{a_{1}-a_{0}}\\ -p\\ 0\end{array}\right)\right\rangle _{E}\end{eqnarray}$$
and we need to further distinguish two subcases according to the valuation of
$\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{E}$
.
Case 1a: assume
$\unicode[STIX]{x1D6FD}\in p{\mathcal{O}}_{E}$
. Then the element
$e_{1}^{\prime }$
defined by
$$\begin{eqnarray}e_{1}^{\prime }=\left(\begin{array}{@{}c@{}}-\frac{\unicode[STIX]{x1D6FD}}{p}u^{a_{1}-a_{0}}\\ 1\\ 0\end{array}\right)\end{eqnarray}$$
is in
$(\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}/\!\operatorname{Fil}^{2}S\cdot \widehat{{\mathcal{M}}})_{\widetilde{\unicode[STIX]{x1D714}}^{a_{1}}}$
and the family
$\text{}\underline{e}^{\prime \prime }\stackrel{\text{def}}{=}(e_{0},e_{1}^{\prime },e_{2}^{\prime })$
is again a framed basis of
$\widehat{{\mathcal{M}}}$
. Until the end of Case 1a we use the basis
$\text{}\underline{e}^{\prime \prime }$
to write the coordinates of the elements in
$\widehat{{\mathcal{M}}}$
.
Note that
$$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D6FC}}u^{a_{2}-a_{0}}(p+E(u))f_{0}=\left(\begin{array}{@{}c@{}}(p+E(u))u^{a_{2}-a_{0}}\\ 0\\ -\frac{p^{2}}{\unicode[STIX]{x1D6FC}}\end{array}\right)\in X_{\widetilde{\unicode[STIX]{x1D714}}^{a_{2}}}.\end{eqnarray}$$
By Corollary 2.4.7(vii) we necessarily have
$(p^{2}/\unicode[STIX]{x1D6FC})\in \unicode[STIX]{x1D71B}_{E}{\mathcal{O}}_{E}$
and therefore
$$\begin{eqnarray}\left\langle \left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}\\ 0\\ u^{e-(a_{2}-a_{0})}\end{array}\right),E(u)\left(\begin{array}{@{}c@{}}0\\ 1\\ 0\end{array}\right),\left(\begin{array}{@{}c@{}}(p+E(u))u^{a_{2}-a_{0}}\\ 0\\ -\frac{p^{2}}{\unicode[STIX]{x1D6FC}}\end{array}\right)\right\rangle _{S}\subseteq \operatorname{ Fil}^{2}\widehat{{\mathcal{M}}}/\!\operatorname{Fil}^{2}S\cdot \widehat{{\mathcal{M}}}.\end{eqnarray}$$
By Nakayama’s lemma, noticing that the left-hand side surjects onto
$\operatorname{Fil}^{2}{\mathcal{M}}/u^{2e}{\mathcal{M}}$
(e.g. by Corollary 2.4.7) we conclude that the inclusion is indeed an equality. We also see that the elementary divisors of
${\mathcal{M}}/\!\operatorname{Fil}^{2}{\mathcal{M}}$
are those described by Corollary 2.4.7(i). In fact, we can repeat the Nakayama argument to deduce that the same three elements generate the
$S$
-module
$\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}/\!\operatorname{Fil}^{p}S\cdot \widehat{{\mathcal{M}}}$
, since their images generate
$\operatorname{Fil}^{2}{\mathcal{M}}$
, so they form a framed system of generators of this module. (Alternatively there is a direct argument using
$\operatorname{Fil}^{2}S=(E(u)^{2},\operatorname{Fil}^{p}S)$
.) We therefore land in Case A.
Case 1b: assume
$p\in \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D71B}_{E}{\mathcal{O}}_{E}$
. As above we deduce
$$\begin{eqnarray}E(u)\left(\begin{array}{@{}c@{}}u^{a_{1}-a_{0}}\\ -\frac{p}{\unicode[STIX]{x1D6FD}}\\ 0\end{array}\right)\in (\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}/\!\operatorname{Fil}^{2}S\cdot \widehat{{\mathcal{M}}})_{\widetilde{\unicode[STIX]{x1D714}}^{a_{1}}}\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle & & \displaystyle \left\langle \left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}u^{a_{2}-a_{0}}\\ 0\\ -p\end{array}\right)+E(u)\left(\begin{array}{@{}c@{}}0\\ 0\\ 1\end{array}\right),E(u)\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}u^{a_{2}-a_{0}}\\ 0\\ -p\end{array}\right),E(u)\left(\begin{array}{@{}c@{}}u^{a_{2}-a_{0}}\\ -\frac{p}{\unicode[STIX]{x1D6FD}}u^{a_{2}-a_{1}}\\ 0\end{array}\right)\right\rangle _{{\mathcal{O}}_{E}}\nonumber\\ \displaystyle & & \displaystyle \qquad \subseteq (\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}/\!\operatorname{Fil}^{2}S\cdot \widehat{{\mathcal{M}}})_{\widetilde{\unicode[STIX]{x1D714}}^{a_{2}}}.\nonumber\end{eqnarray}$$
In particular
$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FD}u^{a_{2}-a_{0}}\\ u^{a_{2}-a_{1}}E(u)\\ -\frac{p\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6FC}}\end{array}\right)\in X_{\widetilde{\unicode[STIX]{x1D714}}^{a_{2}}}\end{eqnarray}$$
and, by Corollary 2.4.7(vii), we necessarily have
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D71B}_{E}{\mathcal{O}}_{E}$
and
$p\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D71B}_{E}{\mathcal{O}}_{E}$
.
We thus obtain
$$\begin{eqnarray}\left\langle \left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}\\ 0\\ u^{e-(a_{2}-a_{0})}\end{array}\right),E(u)\left(\begin{array}{@{}c@{}}u^{a_{1}-a_{0}}\\ -\frac{p}{\unicode[STIX]{x1D6FD}}\\ 0\end{array}\right),\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FD}u^{a_{2}-a_{0}}\\ u^{a_{2}-a_{1}}E(u)\\ -\frac{p\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6FC}}\end{array}\right)\right\rangle _{S}\subseteq \operatorname{ Fil}^{2}\widehat{{\mathcal{M}}}/\!\operatorname{Fil}^{2}S\cdot \widehat{{\mathcal{M}}}.\end{eqnarray}$$
It follows, as in Case 1a, that the inclusion is actually an equality and we land in Case B. We also see that the elementary divisors of
${\mathcal{M}}/\!\operatorname{Fil}^{2}{\mathcal{M}}$
are those described by Corollary 2.4.7(ii).
Case 2: assume
$y\in {\mathcal{O}}_{E}^{\times }$
and
$z\in \unicode[STIX]{x1D71B}_{E}{\mathcal{O}}_{E}$
. We note that the image of
$f_{0}$
in
$(\operatorname{Fil}^{2}{\mathcal{M}})_{\unicode[STIX]{x1D714}^{a_{0}}}$
is divisible by
$u^{e-(a_{1}-a_{0})}$
but not by
$u^{e}$
. From Proposition 2.4.1 we deduce that the elementary divisors of
${\mathcal{M}}/\!\operatorname{Fil}^{2}{\mathcal{M}}$
are those described by Corollary 2.4.7(iii). It is then not hard to see that Case B of the proposition applies to the dual strongly divisible module
$\widehat{{\mathcal{M}}}^{\ast }$
(see [Reference CarusoCar05, Chapitre V]) upon interchanging
$(a_{0},a_{1},a_{2})$
by
$(-a_{2},-a_{1},-a_{0})$
. We arrive at Case C by dualizing. Alternatively, Case 2 can be treated directly with some effort.◻
Corollary 2.4.11. Let
$\unicode[STIX]{x1D70C}$
and
$\widehat{{\mathcal{M}}}$
be as in Proposition 2.4.10. Write
$\unicode[STIX]{x1D706}_{i}$
for the Frobenius eigenvalue on
$\text{D}_{\text{st}}^{\mathbb{Q}_{p},2}(\unicode[STIX]{x1D70C})^{I_{\mathbb{Q}_{p}}=\widetilde{\unicode[STIX]{x1D714}}^{a_{i}}}$
. Then
$$\begin{eqnarray}(\text{ord}_{p}(\unicode[STIX]{x1D706}_{0}),\text{ord}_{p}(\unicode[STIX]{x1D706}_{1}),\text{ord}_{p}(\unicode[STIX]{x1D706}_{2}))=\left\{\begin{array}{@{}c@{}}(2-\text{ord}_{p}(\unicode[STIX]{x1D6FC}),1,\text{ord}_{p}(\unicode[STIX]{x1D6FC}))\\ (2-\text{ord}_{p}(\unicode[STIX]{x1D6FC}),\text{ord}_{p}(\unicode[STIX]{x1D6FD}),1+\text{ord}_{p}(\unicode[STIX]{x1D6FC})-\text{ord}_{p}(\unicode[STIX]{x1D6FD}))\\ (1+\text{ord}_{p}(\unicode[STIX]{x1D6FD})-\text{ord}_{p}(\unicode[STIX]{x1D6FC}),2-\text{ord}_{p}(\unicode[STIX]{x1D6FD}),\text{ord}_{p}(\unicode[STIX]{x1D6FC}))\end{array}\right.\end{eqnarray}$$
according to whether we are in Case A, B, or C of Proposition 2.4.10. In particular,
$\text{ord}_{p}(\unicode[STIX]{x1D706}_{i})\in (0,2)$
for all
$i$
and
$\sum _{i=0}^{2}\text{ord}_{p}(\unicode[STIX]{x1D706}_{i})=3$
.
Proof. We first note that the elements
$\unicode[STIX]{x1D711}_{2}(\widehat{f}_{i})$
span
$\widehat{{\mathcal{M}}}$
by Nakayama’s lemma, as
$\unicode[STIX]{x1D711}_{2}(\operatorname{Fil}^{p}S\cdot \widehat{{\mathcal{M}}})\subset p^{p-2}\widehat{M}\subset \mathfrak{m}_{S}\widehat{M}$
and
$p>2$
.
From the proof of [Reference Emerton, Gee and HerzigEGH13, Proposition 3.1.4] we have
$\text{D}_{\text{st}}^{\mathbb{Q}_{p},2}(\unicode[STIX]{x1D70C})\cong \widehat{{\mathcal{M}}}[1/p]\otimes _{S_{\mathbb{Q}_{p}},s_{0}}\mathbb{Q}_{p}$
where
$s_{0}:S_{\mathbb{Q}_{p}}\rightarrow \mathbb{Q}_{p}$
is defined by ‘
$u\mapsto 0$
’. We have
$\unicode[STIX]{x1D711}_{2}(\widehat{f}_{j})=\sum _{i=0}^{2}\widehat{\unicode[STIX]{x1D6FC}}_{ij}\widehat{e}_{i}$
where
$\widehat{\unicode[STIX]{x1D6FC}}_{ij}\in S_{\widetilde{\unicode[STIX]{x1D714}}^{a_{j}-a_{i}}}$
. Hence, as the elements
$\unicode[STIX]{x1D711}_{2}(\widehat{f}_{i})$
span
$\widehat{{\mathcal{M}}}$
, we see that
$\widehat{\unicode[STIX]{x1D6FC}}_{ii}\in S^{\times }$
for all
$0\leqslant i\leqslant 2$
. On the other hand note that
$S_{\widetilde{\unicode[STIX]{x1D714}}^{i}}\subseteq \ker (s_{0})$
for all
$i\not \equiv 0$
mod
$p-1$
. Let
$e_{i},f_{i}$
denote the images of
$\widehat{e}_{i},\widehat{f}_{i}$
in
$\text{D}_{\text{st}}^{\mathbb{Q}_{p},2}(\unicode[STIX]{x1D70C})$
. In Case A we now deduce that
$(\unicode[STIX]{x1D711}/p^{2})(f_{0})=\unicode[STIX]{x1D707}e_{0}$
where
$\unicode[STIX]{x1D707}\stackrel{\text{def}}{=}s_{0}(\widehat{\unicode[STIX]{x1D6FC}}_{00})\in {\mathcal{O}}_{E}^{\times }$
. In other words,
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D711}(e_{0})=p^{2}\unicode[STIX]{x1D707}e_{0}$
so that
$\unicode[STIX]{x1D706}_{0}=p^{2}\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}^{-1}$
with
$\text{ord}_{p}(\unicode[STIX]{x1D706}_{0})=2-\text{ord}_{p}(\unicode[STIX]{x1D6FC})$
. The other cases are deduced similarly.◻
2.5 From strongly divisible modules to Fontaine–Laffaille modules
The aim of this section is to explicitly determine the Fontaine–Laffaille module associated to the mod
$p$
reduction of a potentially semistable lift of a maximally non-split and generic Galois representation
$\overline{\unicode[STIX]{x1D70C}}$
. Using Proposition 2.4.10 we compute the étale
$\unicode[STIX]{x1D711}$
-modules associated to the mod
$p$
reduction of strongly divisible modules, letting us compare the Frobenius eigenvalues on the weakly admissible module of certain potentially semistable lifts of
$\overline{\unicode[STIX]{x1D70C}}$
with the Fontaine–Laffaille invariant
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})$
.
Let
$\operatorname{red}:\mathbb{P}^{1}({\mathcal{O}}_{E})\rightarrow \mathbb{P}^{1}(\mathbb{F})$
denote the specialization map. The main local result on the Galois side is the following theorem. It will be an important input for proving our global Theorem 4.5.2.
Theorem 2.5.1. Let
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}_{p}}\rightarrow \text{GL}_{3}({\mathcal{O}}_{E})$
be a potentially semistable
$p$
-adic Galois representation of Hodge–Tate weights
$\{-2,-1,0\}$
and inertial type
$\widetilde{\unicode[STIX]{x1D714}}^{a_{0}}\oplus \widetilde{\unicode[STIX]{x1D714}}^{a_{1}}\oplus \widetilde{\unicode[STIX]{x1D714}}^{a_{2}}$
. Assume that the residual representation
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}_{p}}\rightarrow \text{GL}_{3}(\mathbb{F})$
is maximally non-split and generic as in Definition 2.1.5. Let
$\unicode[STIX]{x1D706}_{i}\in {\mathcal{O}}_{E}$
be the Frobenius eigenvalue on
$\text{D}_{\text{st}}^{\mathbb{Q}_{p},2}(\unicode[STIX]{x1D70C})^{I_{\mathbb{Q}_{p}}=\widetilde{\unicode[STIX]{x1D714}}^{a_{i}}}$
. Then the Fontaine–Laffaille invariant of
$\overline{\unicode[STIX]{x1D70C}}$
is given by
$$\begin{eqnarray}\text{FL}(\overline{\unicode[STIX]{x1D70C}})=\operatorname{red}(p\unicode[STIX]{x1D706}_{1}^{-1}).\end{eqnarray}$$
We first determine the filtration and the Frobenius action on the Breuil modules obtained as the base change of strongly divisible
${\mathcal{O}}_{E}$
-modules corresponding to
${\mathcal{O}}_{E}$
-lattices inside
$\unicode[STIX]{x1D70C}$
.
Proposition 2.5.2. Let
$\widehat{{\mathcal{M}}}$
,
$\widehat{\text{}\underline{e}}$
,
$\widehat{\text{}\underline{f}}$
be as in the statement of Proposition 2.4.10. Define
$\unicode[STIX]{x1D6FC}_{i}\in \mathbb{F}^{\times }$
via the condition
$[\unicode[STIX]{x1D711}_{2}(\widehat{f}_{i})]=\unicode[STIX]{x1D6FC}_{i}[\widehat{e}_{i}]$
in
$\widehat{{\mathcal{M}}}/\mathfrak{m}_{S}\widehat{{\mathcal{M}}}$
and let
${\mathcal{M}}\in \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{2}$
be the base change of
$\widehat{{\mathcal{M}}}$
via
$S{\twoheadrightarrow}\overline{S}$
. Then
${\mathcal{M}}$
is of type
$\unicode[STIX]{x1D714}^{a_{0}}\oplus \unicode[STIX]{x1D714}^{a_{1}}\oplus \unicode[STIX]{x1D714}^{a_{2}}$
and there exist a framed basis
$\text{}\underline{e}$
of
${\mathcal{M}}$
and a framed system of generators
$\text{}\underline{f}$
for
$\operatorname{Fil}^{2}{\mathcal{M}}$
such that one of the following hold:
-
(i)
$\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}$
is as in Case
$A$
of Proposition 2.4.10 and for some
$$\begin{eqnarray}\displaystyle \text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\operatorname{Fil}^{2}{\mathcal{M}}) & = & \displaystyle \left(\begin{array}{@{}ccc@{}}c_{00}u^{e} & c_{01}u^{e+(a_{1}-a_{0})} & u^{e+(a_{2}-a_{0})}\\ c_{10}u^{e-(a_{1}-a_{0})} & u^{e} & \\ u^{e-(a_{2}-a_{0})} & & \end{array}\right);\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\unicode[STIX]{x1D711}_{2})\nonumber\\ \displaystyle & = & \displaystyle \text{Diag}(\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})\nonumber\end{eqnarray}$$
$c_{ij}\in \mathbb{F}$
.
-
(ii)
$\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}$
is as in Case
$B$
of Proposition 2.4.10 and for some
$$\begin{eqnarray}\displaystyle \text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\operatorname{Fil}^{2}{\mathcal{M}}) & = & \displaystyle \left(\begin{array}{@{}ccc@{}}c_{00}u^{e} & u^{e+(a_{1}-a_{0})} & \\ c_{10}u^{e-(a_{1}-a_{0})} & & u^{e+(a_{2}-a_{1})}\\ u^{e-(a_{2}-a_{0})} & & \end{array}\right);\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\unicode[STIX]{x1D711}_{2})\nonumber\\ \displaystyle & = & \displaystyle \text{Diag}(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{0})\nonumber\end{eqnarray}$$
$c_{ij}\in \mathbb{F}$
.
-
(iii)
$\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}$
is as in Case
$C$
of Proposition 2.4.10 and for some
$$\begin{eqnarray}\displaystyle \text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\operatorname{Fil}^{2}{\mathcal{M}}) & = & \displaystyle \left(\begin{array}{@{}ccc@{}}c_{00}u^{e} & c_{01}u^{e+(a_{1}-a_{0})} & u^{e+(a_{2}-a_{0})}\\ u^{e-(a_{1}-a_{0})} & & \\ & u^{e-(a_{2}-a_{1})} & \end{array}\right);\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\unicode[STIX]{x1D711}_{2})\nonumber\\ \displaystyle & = & \displaystyle \text{Diag}(\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1})\nonumber\end{eqnarray}$$
$c_{ij}\in \mathbb{F}$
.
Proof. We let
$a\stackrel{\text{def}}{=}a_{2}-a_{0}$
,
$b\stackrel{\text{def}}{=}a_{1}-a_{0}$
and define
$\text{}\underline{e}_{0}\stackrel{\text{def}}{=}\widehat{e}\,\otimes \,1$
,
$\text{}\underline{f}_{0}\stackrel{\text{def}}{=}\widehat{f}\,\otimes \,1$
. Then
${\mathcal{M}}$
is of type
$\unicode[STIX]{x1D714}^{a_{0}}\oplus \unicode[STIX]{x1D714}^{a_{1}}\oplus \unicode[STIX]{x1D714}^{a_{2}}$
,
$\text{}\underline{e}_{0}$
is a framed basis of
${\mathcal{M}}$
and
$\text{}\underline{f}_{0}$
is a framed system of generators of
$\operatorname{Fil}^{2}{\mathcal{M}}$
. We let
$$\begin{eqnarray}V_{0}\stackrel{\text{def}}{=}\text{Mat}_{\text{}\underline{e}_{0},\text{}\underline{f}_{0}}(\operatorname{Fil}^{2}{\mathcal{M}}),\quad A_{0}\stackrel{\text{def}}{=}\text{Mat}_{\text{}\underline{e}_{0},\text{}\underline{f}_{0}}(\unicode[STIX]{x1D711}_{2}).\end{eqnarray}$$
Note in particular that
$\unicode[STIX]{x1D6FC}_{i}\equiv (A_{0})_{ii}$
mod
$u^{e}$
for
$i=0,1,2$
, by construction.
We now treat separately each of the three cases (i), (ii) and (iii).
(i) From Case A of Proposition 2.4.10 we deduce that
$$\begin{eqnarray}V_{0}=\text{Mat}_{\text{}\underline{e}_{0},\text{}\underline{f}_{0}}(\operatorname{Fil}^{2}{\mathcal{M}})=\left(\begin{array}{@{}ccc@{}} & & u^{e+a}\\ & u^{e} & \\ u^{e-a} & & \end{array}\right).\end{eqnarray}$$
We can write
$V_{0}^{\text{adj}}=-u^{e}W_{0}$
for some
$W_{0}\in \text{M}_{3}(\overline{S})$
, which is uniquely defined modulo
$u^{e(p-1)}$
; in fact, we can and will take
$W_{0}=V_{0}$
. We claim that there exist
$b_{00},b_{01},b_{10}\in \mathbb{F}$
such that
$$\begin{eqnarray}W_{0}\cdot A_{0}\cdot \underbrace{\left(\begin{array}{@{}ccc@{}}b_{00}u^{e} & b_{01}u^{e+b} & u^{e+a}\\ b_{10}u^{e-b} & u^{e} & \\ u^{e-a} & & \end{array}\right)}_{\stackrel{\text{def}}{=}V_{1}}=u^{2e}B_{0}\end{eqnarray}$$
for some
$B_{0}\in \operatorname{GL}_{3}^{\Box }(\overline{S})$
. Indeed, if (2.5.3) holds, one obtains
$$\begin{eqnarray}V_{0}B_{0}\equiv A_{0}V_{1}\,\,\text{mod}\,u^{3e}\end{eqnarray}$$
(as
$p\geqslant 5$
) and by Lemma 2.2.8 we deduce that
$V_{1}=\text{Mat}_{\text{}\underline{e}_{1},\text{}\underline{f}_{1}}(\operatorname{Fil}^{2}{\mathcal{M}})$
is a matrix for
$\operatorname{Fil}^{2}{\mathcal{M}}$
with respect to the basis
$\text{}\underline{e}_{1}\stackrel{\text{def}}{=}\text{}\underline{e}_{0}\cdot A_{0}$
and a system of generators
$\text{}\underline{f}_{1}$
of
$\operatorname{Fil}^{2}{\mathcal{M}}$
, and that
$A_{1}\stackrel{\text{def}}{=}\text{Mat}_{\text{}\underline{e}_{1},\text{}\underline{f}_{1}}(\unicode[STIX]{x1D711}_{2})=\unicode[STIX]{x1D711}(B_{0})$
describes the Frobenius action on
${\mathcal{M}}$
with respect to
$(\text{}\underline{e}_{1},\text{}\underline{f}_{1})$
.
To prove the claim, for
$0\leqslant i,j\leqslant 2$
let us write
$(A_{0})_{ij}=u^{[a_{j}-a_{i}]}\unicode[STIX]{x1D6FC}_{ij}$
with
$\unicode[STIX]{x1D6FC}_{ij}\in \mathbb{F}[u^{e}]/u^{ep}$
. A computation, using the explicit description of the element
$W_{0}\in \text{M}_{3}^{\Box }(\overline{S})$
, gives
$$\begin{eqnarray}W_{0}\cdot A_{0}\cdot V_{1}\equiv \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FC}_{22}u^{2e} & & \\ xu^{e-b} & \unicode[STIX]{x1D6FC}_{11}u^{2e} & \\ yu^{e-a} & zu^{e-(a-b)} & \unicode[STIX]{x1D6FC}_{00}u^{2e}\end{array}\right)\,\,\text{mod}\,u^{3e},\end{eqnarray}$$
where
$x,y,z\in \mathbb{F}[u^{e}]/u^{ep}$
are defined by
$$\begin{eqnarray}\displaystyle & \displaystyle x=(\unicode[STIX]{x1D6FC}_{11}b_{10}+\unicode[STIX]{x1D6FC}_{12})u^{e}+\unicode[STIX]{x1D6FC}_{10}b_{00}u^{2e},\quad y=(\unicode[STIX]{x1D6FC}_{00}b_{00}+\unicode[STIX]{x1D6FC}_{01}b_{10}+\unicode[STIX]{x1D6FC}_{02})u^{e} & \displaystyle \nonumber\\ \displaystyle & \displaystyle z=(\unicode[STIX]{x1D6FC}_{00}b_{01}+\unicode[STIX]{x1D6FC}_{01})u^{e}. & \displaystyle \nonumber\end{eqnarray}$$
As
$\unicode[STIX]{x1D6FC}_{ij}\in \overline{S}_{\unicode[STIX]{x1D714}^{0}}$
and
$\unicode[STIX]{x1D6FC}_{ii}\in \overline{S}^{\times }$
we deduce the existence of unique
$b_{00},b_{10},b_{01}\in \mathbb{F}$
such that (2.5.3) holds and, what is more important,
$$\begin{eqnarray}B_{0}\equiv \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FC}_{2} & & \\ \unicode[STIX]{x1D6FD}_{10}u^{e-b} & \unicode[STIX]{x1D6FC}_{1} & \\ \unicode[STIX]{x1D6FD}_{20}u^{e-a} & \unicode[STIX]{x1D6FD}_{21}u^{e-(a-b)} & \unicode[STIX]{x1D6FC}_{0}\end{array}\right)\,\,\text{mod}\,u^{e}\end{eqnarray}$$
for some
$\unicode[STIX]{x1D6FD}_{ij}\in \mathbb{F}$
. In particular, we obtain
$$\begin{eqnarray}\displaystyle A_{1}\stackrel{\text{def}}{=}\text{Mat}_{\text{}\underline{e}_{1},\text{}\underline{f}_{1}}(\unicode[STIX]{x1D711}_{2}) & = & \displaystyle \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FC}_{2} & & \\ \unicode[STIX]{x1D6FD}_{10}u^{p(e-b)} & \unicode[STIX]{x1D6FC}_{1} & \\ \unicode[STIX]{x1D6FD}_{20}u^{p(e-a)} & \unicode[STIX]{x1D6FD}_{21}u^{p(e-(a-b))} & \unicode[STIX]{x1D6FC}_{0}\end{array}\right)\nonumber\\ \displaystyle & \equiv & \displaystyle \text{Diag}(\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{0})\,\,\text{mod}\,u^{3e}\nonumber\end{eqnarray}$$
by the genericity assumption (2.1.6).
Writing again
$V_{1}^{\text{adj}}=-u^{e}W_{1}$
for some
$W_{1}\in \text{M}_{3}(\overline{S})$
(uniquely defined modulo
$u^{e(p-1)}$
) we obtain
$$\begin{eqnarray}W_{1}\cdot A_{1}\equiv \left(\begin{array}{@{}ccc@{}} & & \unicode[STIX]{x1D6FC}_{0}u^{e+a}\\ & u^{e}\unicode[STIX]{x1D6FC}_{1} & -\unicode[STIX]{x1D6FC}_{0}b_{10}u^{e+(a-b)}\\ \unicode[STIX]{x1D6FC}_{2}u^{e-a} & -\unicode[STIX]{x1D6FC}_{1}b_{01}u^{e-(a-b)} & \unicode[STIX]{x1D6FC}_{0}(b_{10}b_{01}-b_{00})u^{e}\end{array}\right)\,\,\text{mod}\,u^{3e}\end{eqnarray}$$
and a computation shows that there exist uniquely determined elements
$c_{00},c_{10},c_{01}\in \mathbb{F}$
such that
$$\begin{eqnarray}W_{1}\cdot A_{1}\cdot \underbrace{\left(\begin{array}{@{}ccc@{}}c_{00}u^{e} & c_{01}u^{e+b} & u^{e+a}\\ c_{10}u^{e-b} & u^{e} & \\ u^{e-a} & & \end{array}\right)}_{\stackrel{\text{def}}{=}V_{2}}=u^{2e}B_{1},\end{eqnarray}$$
where now
$$\begin{eqnarray}B_{1}\equiv \text{Diag}(\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})\,\,\text{mod}\,u^{e}.\end{eqnarray}$$
By Lemma 2.2.8 one has
$V_{2}=\text{Mat}_{\text{}\underline{e}_{2},\text{}\underline{f}_{2}}(\operatorname{Fil}^{2}{\mathcal{M}})$
, where
$\text{}\underline{e}_{2}\stackrel{\text{def}}{=}\text{}\underline{e}_{1}\cdot A_{1}$
,
$\text{}\underline{f}_{2}$
is a system of generators for
$\operatorname{Fil}^{2}{\mathcal{M}}$
and the Frobenius action is now given by
$$\begin{eqnarray}A_{2}\stackrel{\text{def}}{=}\text{Mat}_{\text{}\underline{e}_{2},\text{}\underline{f}_{2}}(\unicode[STIX]{x1D711}_{2})=\unicode[STIX]{x1D711}(B_{1})=\text{Diag}(\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}).\end{eqnarray}$$
(ii) The proof is similar to case (i) and we content ourselves with giving the general argument, leaving the computational details to the scrupulous reader.
From Proposition 2.4.10 the filtration for
$\operatorname{Fil}^{2}{\mathcal{M}}$
now has the form
$$\begin{eqnarray}V_{0}\stackrel{\text{def}}{=}\left(\begin{array}{@{}ccc@{}} & u^{e+b} & \\ & & u^{e+(a-b)}\\ u^{e-a} & & \end{array}\right).\end{eqnarray}$$
Writing
$V_{0}^{\text{adj}}=u^{e}W_{0}$
for some
$W_{0}\in \text{M}_{3}(\overline{S})$
we claim that there exist
$b_{00},b_{10}\in \mathbb{F}$
and
$B_{0}\in \operatorname{GL}_{3}^{\Box }(\overline{S})$
such that
$$\begin{eqnarray}W_{0}\cdot A_{0}\cdot \underbrace{\left(\begin{array}{@{}ccc@{}}b_{00}u^{e} & u^{e+b} & \\ b_{10}u^{e-b} & & u^{e+(a-b)}\\ u^{e-a} & & \end{array}\right)}_{\stackrel{\text{def}}{=}V_{1}}=u^{2e}B_{0}.\end{eqnarray}$$
Indeed, using the same notation as in case (i), an easy computation now gives
$$\begin{eqnarray}W_{0}\cdot A_{0}\cdot V_{1}\equiv \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FC}_{22}u^{2e} & & \\ xu^{e-b} & \unicode[STIX]{x1D6FC}_{00}u^{2e} & \unicode[STIX]{x1D6FC}_{01}u^{2e+(a-b)}\\ yu^{e-a} & \unicode[STIX]{x1D6FC}_{10}u^{3e-(a-b)} & \unicode[STIX]{x1D6FC}_{11}u^{2e}\end{array}\right)\,\,\text{mod}\,u^{3e},\end{eqnarray}$$
where
$x,y\in \mathbb{F}[u^{e}]/u^{ep}$
are defined by
$$\begin{eqnarray}x=(\unicode[STIX]{x1D6FC}_{00}b_{00}+\unicode[STIX]{x1D6FC}_{01}b_{10}+\unicode[STIX]{x1D6FC}_{02})u^{e},\quad y=(\unicode[STIX]{x1D6FC}_{11}b_{10}+\unicode[STIX]{x1D6FC}_{12})u^{e}+\unicode[STIX]{x1D6FC}_{10}b_{00}u^{2e}.\end{eqnarray}$$
As
$\unicode[STIX]{x1D6FC}_{ii}\in \overline{S}^{\times }$
we find unique
$b_{00},b_{10}\in \mathbb{F}$
such that (2.5.5) holds and moreover
$$\begin{eqnarray}B_{0}\equiv \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FC}_{2} & & \\ \unicode[STIX]{x1D6FD}_{10}u^{e-b} & \unicode[STIX]{x1D6FC}_{0} & \unicode[STIX]{x1D6FD}_{12}u^{a-b}\\ \unicode[STIX]{x1D6FD}_{20}u^{e-a} & \unicode[STIX]{x1D6FD}_{21}u^{e-(a-b)} & \unicode[STIX]{x1D6FC}_{1}\end{array}\right)\,\text{mod}\,u^{e}\end{eqnarray}$$
for some
$\unicode[STIX]{x1D6FD}_{ij}\in \mathbb{F}$
. Note that
$$\begin{eqnarray}A_{1}\stackrel{\text{def}}{=}\text{Mat}_{\text{}\underline{e}_{1},\text{}\underline{f}_{1}}(\unicode[STIX]{x1D711}_{2})\equiv \text{Diag}(\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1})\,\,\text{mod}\,u^{3e}\end{eqnarray}$$
by the genericity assumption.
By means of Lemma 2.2.8 we can iterate the procedure: one finds an explicit element
$V_{2}=\text{Mat}_{\text{}\underline{e}_{2},\text{}\underline{f}_{2}}(\operatorname{Fil}^{2}{\mathcal{M}})\in \text{M}_{3}(\overline{S})$
, as in the statement of case (ii), which provides the filtration
$\operatorname{Fil}^{2}{\mathcal{M}}$
with respect to the basis
$\text{}\underline{e}_{2}\stackrel{\text{def}}{=}\text{}\underline{e}_{1}\cdot A_{1}$
and which verifies
$$\begin{eqnarray}\text{Mat}_{\text{}\underline{e}_{2},\text{}\underline{f}_{2}}(\unicode[STIX]{x1D711}_{2})=\text{Diag}(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{0}).\end{eqnarray}$$
(iii) This is analogous to case (ii). More succinctly, it can be obtained from case (ii) by duality. ◻
Thanks to Proposition 2.5.2 it is now straightforward to compute the Fontaine–Laffaille invariant of
$\overline{\unicode[STIX]{x1D70C}}$
.
Proposition 2.5.6. Let
$\widehat{{\mathcal{M}}}$
,
$\unicode[STIX]{x1D6FC}_{i}\in \mathbb{F}^{\times }$
be as in Proposition 2.5.2. Let
$\unicode[STIX]{x1D70C}\stackrel{\text{def}}{=}\text{T}_{\text{st}}^{\mathbb{Q}_{p},2}(\widehat{{\mathcal{M}}})$
. Then one of the following possibilities holds:
-
(i)
$\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}$
is as in Case
$A$
of Proposition 2.4.10 and
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})=\unicode[STIX]{x1D6FC}_{1}^{-1}$
; -
(ii)
$\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}$
is as in Case
$B$
of Proposition 2.4.10 and
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})=0$
; -
(iii)
$\operatorname{Fil}^{2}\widehat{{\mathcal{M}}}$
is as in Case
$C$
of Proposition 2.4.10 and
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})=\infty$
.
Proof. By twisting
$\unicode[STIX]{x1D70C}$
by
$\widetilde{\unicode[STIX]{x1D714}}^{-a_{0}}$
we may assume that
$a_{0}=0$
. Let
$a\stackrel{\text{def}}{=}a_{2}$
,
$b\stackrel{\text{def}}{=}a_{1}$
.
(i) Let
${\mathcal{M}}\in \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{2}$
be the base change of
$\widehat{{\mathcal{M}}}$
via
$S{\twoheadrightarrow}\overline{S}$
. By Proposition 2.5.2 and Lemma 2.2.6, the
$\unicode[STIX]{x1D719}$
-action on the
$(\unicode[STIX]{x1D719},\mathbb{F}((\text{}\underline{\unicode[STIX]{x1D71B}})))$
-module
$\mathfrak{M}\stackrel{\text{def}}{=}M_{\mathbb{F}_{p}((\text{}\underline{\unicode[STIX]{x1D71B}}))}({\mathcal{M}}^{\ast })$
is given by
$$\begin{eqnarray}\text{Mat}_{\text{}\underline{\mathfrak{e}}}(\unicode[STIX]{x1D719})=\left(\begin{array}{@{}ccc@{}}c_{00}\text{}\underline{\unicode[STIX]{x1D71B}}^{e} & c_{01}\text{}\underline{\unicode[STIX]{x1D71B}}^{e-b} & \unicode[STIX]{x1D6FC}_{2}^{-1}\text{}\underline{\unicode[STIX]{x1D71B}}^{e-a}\\ c_{10}\text{}\underline{\unicode[STIX]{x1D71B}}^{e+b} & \unicode[STIX]{x1D6FC}_{1}^{-1}\text{}\underline{\unicode[STIX]{x1D71B}}^{e} & \\ \unicode[STIX]{x1D6FC}_{0}^{-1}\text{}\underline{\unicode[STIX]{x1D71B}}^{e+a} & & \end{array}\right)\end{eqnarray}$$
for a framed basis
$\text{}\underline{\mathfrak{e}}$
(for the dual type
$\unicode[STIX]{x1D714}^{0}\oplus \unicode[STIX]{x1D714}^{-b}\oplus \unicode[STIX]{x1D714}^{-a}$
) of
$\mathfrak{M}$
and some
$c_{ij}\in \mathbb{F}$
(not those of Lemma 2.2.6). In the basis
$\text{}\underline{\mathfrak{e}}^{\prime }\stackrel{\text{def}}{=}\text{}\underline{\mathfrak{e}}\cdot \text{Diag}(1,\text{}\underline{\unicode[STIX]{x1D71B}}^{b},\text{}\underline{\unicode[STIX]{x1D71B}}^{a})$
, which is
$\operatorname{Gal}(K/K_{0})$
-invariant, one obtains
$$\begin{eqnarray}\text{Mat}_{\text{}\underline{\mathfrak{e}}^{\prime }}(\unicode[STIX]{x1D719})=\left(\begin{array}{@{}ccc@{}}c_{00}\text{}\underline{\unicode[STIX]{x1D71B}}^{e} & c_{01}\text{}\underline{\unicode[STIX]{x1D71B}}^{e(b+1)} & \unicode[STIX]{x1D6FC}_{2}^{-1}\text{}\underline{\unicode[STIX]{x1D71B}}^{e(a+1)}\\ c_{10}\text{}\underline{\unicode[STIX]{x1D71B}}^{e} & \unicode[STIX]{x1D6FC}_{1}^{-1}\text{}\underline{\unicode[STIX]{x1D71B}}^{e(b+1)} & \\ \unicode[STIX]{x1D6FC}_{0}^{-1}\text{}\underline{\unicode[STIX]{x1D71B}}^{e} & & \end{array}\right)\end{eqnarray}$$
proving that
$\mathfrak{M}$
is the base change to
$\mathbb{F}((\text{}\underline{\unicode[STIX]{x1D71B}}))$
of the
$(\unicode[STIX]{x1D719},\mathbb{F}((\text{}\underline{p})))$
-module
$\mathfrak{M}_{0}$
described by
$$\begin{eqnarray}\text{Mat}_{\text{}\underline{\mathfrak{e}}_{0}}(\unicode[STIX]{x1D719})=\underbrace{\left(\begin{array}{@{}ccc@{}}c_{00} & c_{01} & \unicode[STIX]{x1D6FC}_{2}^{-1}\\ c_{10} & \unicode[STIX]{x1D6FC}_{1}^{-1} & \\ \unicode[STIX]{x1D6FC}_{0}^{-1} & & \end{array}\right)}_{\stackrel{\text{def}}{=}F}\text{Diag}(\text{}\underline{p},\text{}\underline{p}^{b+1},\text{}\underline{p}^{a+1})\end{eqnarray}$$
for some basis
$\text{}\underline{\mathfrak{e}}_{0}$
of
$\mathfrak{M}_{0}$
. In the basis
$\text{}\underline{\mathfrak{e}}_{0}^{\prime }\stackrel{\text{def}}{=}\text{}\underline{\mathfrak{e}}_{0}\cdot F$
the matrix of
$\unicode[STIX]{x1D719}$
becomes
$\text{Diag}(\text{}\underline{p},\text{}\underline{p}^{b+1},\text{}\underline{p}^{a+1})F$
. We can now construct a Fontaine–Laffaille module
$M\in \mathbb{F}\text{-}{\mathcal{F}}{\mathcal{L}}^{[0,p-2]}$
with Hodge–Tate weights
$\{1,b+1,a+1\}$
endowed with a basis
$\text{}\underline{e}$
which is compatible with the Hodge filtration and satisfies
$\text{Mat}_{\text{}\underline{e}}(\unicode[STIX]{x1D719}_{\bullet })=F$
. By Lemma 2.2.7 we deduce that
$\mathfrak{M}_{0}\cong {\mathcal{F}}(M)$
.
On the other hand
$\text{T}_{\text{cris}}^{\ast }(M)\cong \text{T}_{\text{st}}^{\ast }({\mathcal{M}}^{\ast })\cong \overline{\unicode[STIX]{x1D70C}}$
by Corollary 2.2.2. As
$\overline{\unicode[STIX]{x1D70C}}$
is maximally non-split, there exists a basis
$\text{}\underline{e}^{\prime }$
of
$M$
compatible with the Hodge filtration and such that
$\text{Mat}_{\text{}\underline{e}^{\prime }}(\unicode[STIX]{x1D719}_{\bullet })$
is described as in Corollary 2.1.8. In other words
$\text{}\underline{e}$
,
$\text{}\underline{e}^{\prime }$
are related via a lower triangular unipotent matrix
$A\in \operatorname{GL}_{3}(\mathbb{F})$
in such a way that
$$\begin{eqnarray}\text{Mat}_{\text{}\underline{e}^{\prime }}(\unicode[STIX]{x1D719}_{\bullet })=A\cdot F=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D707}_{0} & x & z\\ & \unicode[STIX]{x1D707}_{1} & y\\ & & \unicode[STIX]{x1D707}_{2}\end{array}\right)\end{eqnarray}$$
for some
$x,y,\unicode[STIX]{x1D707}_{i}\in \mathbb{F}^{\times }$
,
$z\in \mathbb{F}$
. It follows that
$$\begin{eqnarray}\text{FL}(\overline{\unicode[STIX]{x1D70C}})=\frac{\det \left(\begin{array}{@{}cc@{}}x & z\\ \unicode[STIX]{x1D707}_{1} & y\end{array}\right)}{-z}=\frac{\det \left(\begin{array}{@{}cc@{}}c_{01} & \unicode[STIX]{x1D6FC}_{2}^{-1}\\ \unicode[STIX]{x1D6FC}_{1}^{-1} & \end{array}\right)}{-\unicode[STIX]{x1D6FC}_{2}^{-1}}=\unicode[STIX]{x1D6FC}_{1}^{-1}.\end{eqnarray}$$
(ii) The proof is similar to case (i). One checks that
$\mathfrak{M}\stackrel{\text{def}}{=}M_{\mathbb{F}_{p}((\text{}\underline{\unicode[STIX]{x1D71B}}))}({\mathcal{M}}^{\ast })\cong \mathfrak{M}_{0}\otimes _{\mathbb{F}_{p}((\text{}\underline{p}))}\mathbb{F}_{p}((\text{}\underline{\unicode[STIX]{x1D71B}}))$
, where the
$(\unicode[STIX]{x1D719},\mathbb{F}((\text{}\underline{p})))$
-module
$\mathfrak{M}_{0}$
is described by
$$\begin{eqnarray}\underbrace{\left(\begin{array}{@{}ccc@{}}c_{00} & c_{01} & \unicode[STIX]{x1D6FC}_{0}^{-1}\\ \unicode[STIX]{x1D6FC}_{1}^{-1} & & \\ & \unicode[STIX]{x1D6FC}_{2}^{-1} & \end{array}\right)}_{\stackrel{\text{def}}{=}F}\text{Diag}(\text{}\underline{p},\text{}\underline{p}^{b+1},\text{}\underline{p}^{a+1}).\end{eqnarray}$$
We deduce by Lemma 2.2.7 that
$\mathfrak{M}_{0}\cong {\mathcal{F}}(M)$
for the rank-three Fontaine–Laffaille module
$M\in \mathbb{F}\text{-}{\mathcal{F}}{\mathcal{L}}^{[0,p-2]}$
with Hodge–Tate weights
$\{1,b+1,a+1\}$
and
$\text{Mat}_{\text{}\underline{e}}(\unicode[STIX]{x1D719}_{\bullet })=F$
for some basis
$\text{}\underline{e}$
of
$M$
that is compatible with the Hodge filtration. As in case (i) we deduce that
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})=0$
.
(iii) Follows by a similar argument. ◻
Proof of Theorem 2.5.1.
Let
$\widehat{{\mathcal{M}}}\in {\mathcal{O}}_{E}\text{-}\operatorname{Mod}_{\text{dd}}^{2}$
be such that
$\text{T}_{\text{st}}^{\mathbb{Q}_{p},2}(\widehat{{\mathcal{M}}})\cong \unicode[STIX]{x1D70C}$
and let
$\text{}\underline{\widehat{e}}$
,
$\text{}\underline{\widehat{f}}$
be as in the statement of Proposition 2.4.10.
In Case A, from the proof of Corollary 2.4.11 we see that
$\unicode[STIX]{x1D706}_{1}=ps_{0}(\widehat{\unicode[STIX]{x1D6FC}}_{11})$
, where
$\widehat{\unicode[STIX]{x1D6FC}}_{ij}\in S$
are defined by
$\unicode[STIX]{x1D711}_{2}(\widehat{f}_{j})=\sum _{i=0}^{2}\widehat{\unicode[STIX]{x1D6FC}}_{ij}\widehat{e}_{i}$
, and
$p\unicode[STIX]{x1D706}_{1}^{-1}\in {\mathcal{O}}_{E}^{\times }$
. Hence
$\operatorname{red}(p\unicode[STIX]{x1D706}_{1}^{-1})=\overline{s_{0}(\widehat{\unicode[STIX]{x1D6FC}}_{11})}^{-1}\in \mathbb{F}^{\times }$
. The conclusion follows by Proposition 2.5.6, as
$\overline{s_{0}(\widehat{\unicode[STIX]{x1D6FC}}_{11})}=\unicode[STIX]{x1D6FC}_{1}$
in the notation of that proposition. In Case B the conclusion follows by Proposition 2.5.6, noting that
$\operatorname{red}(p\unicode[STIX]{x1D706}_{1}^{-1})=0$
, as
$\text{ord}_{p}(\unicode[STIX]{x1D706}_{1})<1$
. Case C is similar. ◻
2.6 Elimination of Galois types
The aim of this section is to perform a type elimination for a maximally non-split and generic representation
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
(cf. Definition 2.1.5), by means of integral
$p$
-adic Hodge theory. In other words we show for most tame inertial types
$\unicode[STIX]{x1D70F}:I_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}(E)$
(of niveau 1 or 2) that
$\overline{\unicode[STIX]{x1D70C}}$
cannot have a potentially crystalline lift with Hodge–Tate weights
$\{-2,-1,0\}$
and type
$\unicode[STIX]{x1D70F}$
.
The main results of this section (Propositions 2.6.1, 2.6.3 and 2.6.4) will be used to prove results about Serre weights in § 4.4.
2.6.1 Niveau 1 types
We first eliminate niveau 1 types. In particular, we have
$K_{0}=\mathbb{Q}_{p}$
,
$e=p-1$
, and
$K=\mathbb{Q}_{p}(\unicode[STIX]{x1D701}_{p})$
. The result is the following.
Proposition 2.6.1. Let
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}({\mathcal{O}}_{E})$
be a
$p$
-adic Galois representation, becoming semistable over
$K$
with Hodge–Tate weights
$\{-2,-1,0\}$
. Assume that
$\overline{\unicode[STIX]{x1D70C}}$
is maximally non-split and generic as in Definition 2.1.5. Then
$$\begin{eqnarray}\text{WD}(\unicode[STIX]{x1D70C})|_{I_{\mathbb{Q}_{p}}}\cong \widetilde{\unicode[STIX]{x1D714}}^{i}\oplus \widetilde{\unicode[STIX]{x1D714}}^{j}\oplus \widetilde{\unicode[STIX]{x1D714}}^{k},\end{eqnarray}$$
where either
$(i,j,k)\equiv (a_{2},a_{1},a_{0})\hspace{0.2em}{\rm mod}\hspace{0.2em}\!~p-1$
or
$(i,j,k)\equiv (a_{2}-1,a_{1},a_{0}+1)\hspace{0.2em}{\rm mod}\hspace{0.2em}\!~p-1$
.
Here and in the following the notation
$x\equiv y$
mod
$p-1$
for
$x,y\in \mathbb{Z}^{3}$
is shorthand for
$x_{i}\equiv y_{i}$
mod
$p-1$
for all
$i$
.
Proof. After twisting we may assume
$a_{0}=0$
and set
$a\stackrel{\text{def}}{=}a_{2}$
,
$b\stackrel{\text{def}}{=}a_{1}$
. Let
$\widehat{{\mathcal{M}}}$
be a strongly divisible
${\mathcal{O}}_{E}$
-module such that
$\text{T}_{\text{st}}^{\mathbb{Q}_{p},2}(\widehat{{\mathcal{M}}})=\unicode[STIX]{x1D70C}$
and let
${\mathcal{M}}$
be the Breuil module obtained by base change to
$\overline{S}$
. By Proposition 2.3.5
${\mathcal{M}}$
admits a unique filtration by Breuil submodules, with graded pieces described by
$$\begin{eqnarray}{\mathcal{M}}:{\mathcal{M}}_{2}\text{—}{\mathcal{M}}_{1}\text{—}{\mathcal{M}}_{0}\end{eqnarray}$$
(where the notation means that
${\mathcal{M}}_{2}$
is a submodule and
${\mathcal{M}}_{0}$
a quotient) and the rank-one Breuil submodules
${\mathcal{M}}_{i}$
verify
$\text{T}_{\text{st}}^{2}({\mathcal{M}}_{i})|_{I_{\mathbb{Q}_{p}}}\cong \unicode[STIX]{x1D714}^{a_{i}+1}$
for
$i=0,1,2$
. It follows from [Reference Emerton, Gee and HerzigEGH13, Lemma 3.3.2] that
${\mathcal{M}}_{i}$
is of type
$\unicode[STIX]{x1D714}^{k_{i}}$
, where
$k_{2}=a+1-\unicode[STIX]{x1D6FF}_{2}$
,
$k_{1}=b+1-\unicode[STIX]{x1D6FF}_{1}$
,
$k_{0}=1-\unicode[STIX]{x1D6FF}_{0}$
for some
$\unicode[STIX]{x1D6FF}_{i}\in \{0,1,2\}$
and
$$\begin{eqnarray}\operatorname{Fil}^{2}{\mathcal{M}}_{2}=u^{\unicode[STIX]{x1D6FF}_{2}e}{\mathcal{M}}_{2},\quad \operatorname{Fil}^{2}{\mathcal{M}}_{1}=u^{\unicode[STIX]{x1D6FF}_{1}e}{\mathcal{M}}_{1},\quad \operatorname{Fil}^{2}{\mathcal{M}}_{0}=u^{\unicode[STIX]{x1D6FF}_{0}e}{\mathcal{M}}_{0}.\end{eqnarray}$$
On the other hand we see that
$\text{WD}(\unicode[STIX]{x1D70C})|_{I_{\mathbb{Q}_{p}}}\cong \widetilde{\unicode[STIX]{x1D714}}^{k_{0}}\oplus \widetilde{\unicode[STIX]{x1D714}}^{k_{1}}\oplus \widetilde{\unicode[STIX]{x1D714}}^{k_{2}}$
(by Lemma 2.4.8) and hence
$\det \unicode[STIX]{x1D70C}=\widetilde{\unicode[STIX]{x1D714}}^{k_{0}+k_{1}+k_{2}}\unicode[STIX]{x1D700}^{3}$
, as
$\unicode[STIX]{x1D70C}$
has Hodge–Tate weights
$\{-2,-1,0\}$
. It follows that
$\unicode[STIX]{x1D6FF}_{0}+\unicode[STIX]{x1D6FF}_{1}+\unicode[STIX]{x1D6FF}_{2}=3$
.
We now use Lemma 2.4.2 to conclude the proof. In what follows, we write
$\overline{\unicode[STIX]{x1D70C}}_{21}$
to denote the unique two-dimensional sub-representation of
$\overline{\unicode[STIX]{x1D70C}}$
, and, similarly,
$\overline{\unicode[STIX]{x1D70C}}_{10}$
to denote its unique two-dimensional quotient. If
$(\unicode[STIX]{x1D6FF}_{2},\unicode[STIX]{x1D6FF}_{1})=(1,2)$
then
$\overline{\unicode[STIX]{x1D70C}}_{21}$
splits, by Lemma 2.4.2(ii). If
$\unicode[STIX]{x1D6FF}_{1}=0$
then
$\operatorname{Fil}^{2}({\mathcal{M}}_{1}\text{}\text{—}{\mathcal{M}}_{0})$
splits as an
$\overline{S}$
-module (as
$\operatorname{Fil}^{2}{\mathcal{M}}_{1}$
is an injective
$\overline{S}$
-module, cf. Lemma A.2.1), and hence
$\overline{\unicode[STIX]{x1D70C}}_{10}$
splits by Lemma 2.4.2(i). For the same reason, if
$\unicode[STIX]{x1D6FF}_{2}=0$
then
$\overline{\unicode[STIX]{x1D70C}}_{21}$
splits.
Therefore
$(\unicode[STIX]{x1D6FF}_{0},\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2})=(1,1,1)$
or
$(\unicode[STIX]{x1D6FF}_{0},\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2})=(0,1,2)$
, as claimed.◻
2.6.2 Niveau 2 types
We now eliminate niveau 2 types. In particular, we have
$k=\mathbb{F}_{p^{2}}$
,
$K_{0}=\mathbb{Q}_{p^{2}}$
is the degree-two unramified extension of
$\mathbb{Q}_{p}$
,
$e=p^{2}-1$
, and
$K=\mathbb{Q}_{p^{2}}(\sqrt[e]{-p})$
.
Lemma 2.6.2. Let
${\mathcal{M}}$
be a rank-one object in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{2}$
, with descent data from
$K$
to
$\mathbb{Q}_{p}$
. Then there exists a generator
$m\in {\mathcal{M}}$
such that:
-
(i)
$\operatorname{Fil}^{2}{\mathcal{M}}=u^{r(p-1)}{\mathcal{M}}$
, where
$0\leqslant r\leqslant 2(p+1)$
; -
(ii) there exists
$k\in \mathbb{Z}$
verifying
$k+pr\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}\!~p+1$
and such that
${\mathcal{M}}$
is of type
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{k}$
and
$m$
is a framed basis for
${\mathcal{M}}$
; -
(iii)
$N(m)=0$
.
Moreover, one has
$$\begin{eqnarray}\text{T}_{\text{st}}^{2}({\mathcal{M}})|_{I_{\mathbb{Q}_{p}}}=\unicode[STIX]{x1D714}_{2}^{k+pr}.\end{eqnarray}$$
Proof. Let
$\unicode[STIX]{x1D70E}\in \text{Gal}(K/\mathbb{Q}_{p})$
be the lift of the arithmetic Frobenius in
$\text{Gal}(k/\mathbb{F}_{p})$
that fixes
$\unicode[STIX]{x1D71B}$
, and hence
$\unicode[STIX]{x1D70E}^{2}=1$
. Then
$\unicode[STIX]{x1D70E}$
interchanges the two primitive idempotents
$\unicode[STIX]{x1D716}_{0}$
,
$\unicode[STIX]{x1D716}_{1}$
, and one has
$\unicode[STIX]{x1D70E}\circ g=g^{p}\circ \unicode[STIX]{x1D70E}$
for all
$g\in \text{Gal}(K/K_{0})$
.
By [Reference Emerton, Gee and HerzigEGH13, Lemma 3.3.2] there is a generator
$m\in {\mathcal{M}}$
such that:
-
(i)
$\unicode[STIX]{x1D716}_{i}\operatorname{Fil}^{2}{\mathcal{M}}=u^{r_{i}e}\unicode[STIX]{x1D716}_{i}{\mathcal{M}}$
for
$i=0,1$
; -
(ii)
$\widehat{g}(m)=(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}(g)^{k_{0}}\,\otimes \,1)\unicode[STIX]{x1D716}_{0}m+(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}(g)^{k_{1}}\,\otimes \,1)\unicode[STIX]{x1D716}_{1}m$
for all
$g\in \text{Gal}(K/K_{0})$
,
where the integers
$r_{i},k_{i}$
verify
$0\leqslant r_{i}\leqslant 2e$
,
$k_{i}\equiv p(k_{i-1}+r_{i-1})$
mod
$e$
.
As
$\unicode[STIX]{x1D70E}$
exchanges the idempotents
$\unicode[STIX]{x1D716}_{i}\in k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
we deduce that
$r\stackrel{\text{def}}{=}r_{0}=r_{1}$
. Let us consider
${\mathcal{M}}/(u\cdot {\mathcal{M}})$
. It is a rank-one module over
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
, endowed with a semilinear action of
$\text{Gal}(K/\mathbb{Q}_{p})$
. In particular
$\unicode[STIX]{x1D70E}\overline{m}=\unicode[STIX]{x1D707}\overline{m}$
for some
$\unicode[STIX]{x1D707}\in (k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F})^{\times }$
verifying
$\unicode[STIX]{x1D707}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D707})=1$
. We therefore deduce, by case (ii) above, that for all
$g\in \operatorname{Gal}(K/K_{0})$
,
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D70E}}\circ \widehat{g}(\overline{m}) & = & \displaystyle \widehat{\unicode[STIX]{x1D70E}}((\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{k_{0}}(g)\otimes 1)\unicode[STIX]{x1D716}_{0}\overline{m}+(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{k_{1}}(g)\otimes 1)\unicode[STIX]{x1D716}_{1}\overline{m})\nonumber\\ \displaystyle & = & \displaystyle [(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{pk_{0}}(g)\otimes 1)\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D707}\overline{m}+(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{pk_{1}}(g)\otimes 1)\unicode[STIX]{x1D716}_{0}\unicode[STIX]{x1D707}\overline{m}]\nonumber\end{eqnarray}$$
and
$$\begin{eqnarray}\widehat{g^{p}}\circ \widehat{\unicode[STIX]{x1D70E}}(\overline{m})=\unicode[STIX]{x1D707}[(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{pk_{0}}(g)\otimes 1)\unicode[STIX]{x1D716}_{0}\overline{m}+(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{pk_{1}}(g)\otimes 1)\unicode[STIX]{x1D716}_{1}\overline{m}].\end{eqnarray}$$
As
$\unicode[STIX]{x1D70E}\circ g=g^{p}\circ \unicode[STIX]{x1D70E}$
we conclude that
$k\stackrel{\text{def}}{=}k_{0}\equiv k_{1}$
mod
$e$
. We finally obtain
$k\equiv p(k+r)$
mod
$e$
, so that
$r\equiv 0$
mod
$p-1$
and
$k+pr/(p-1)\equiv 0$
mod
$p+1$
. The last statement on
$\text{T}_{\text{st}}^{2}({\mathcal{M}})$
follows again from [Reference Emerton, Gee and HerzigEGH13, Lemma 3.3.2] and the previous results on
$k_{i},r_{i}$
.◻
For the remainder of this section, all Breuil modules
${\mathcal{M}}\in \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{2}$
have descent data from
$K$
to
$\mathbb{Q}_{p}$
.
Proposition 2.6.3. Let
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}({\mathcal{O}}_{E})$
be a
$p$
-adic Galois representation, becoming semistable over
$K$
with Hodge–Tate weights
$\{-2,-1,0\}$
. Assume that
$\overline{\unicode[STIX]{x1D70C}}$
is maximally non-split and generic as in Definition 2.1.5 and that the inertial type of
$\unicode[STIX]{x1D70C}$
has niveau two, i.e.
$\unicode[STIX]{x1D70C}$
does not become semistable over
$\mathbb{Q}_{p}(\unicode[STIX]{x1D701}_{p})$
. Then
$$\begin{eqnarray}\text{WD}(\unicode[STIX]{x1D70C})|_{I_{\mathbb{Q}_{p}}}\cong \widetilde{\unicode[STIX]{x1D714}}^{x}\oplus \widetilde{\unicode[STIX]{x1D714}}_{2}^{y}\oplus \widetilde{\unicode[STIX]{x1D714}}_{2}^{py},\end{eqnarray}$$
where
$x,y\in \mathbb{Z}$
,
$y\not \equiv 0\,\text{mod}\,p+1$
and the pair
$(x,y)\in \mathbb{Z}^{2}$
verifies one of the following possibilities:
-
(i)
$x\equiv a_{0}-\unicode[STIX]{x1D6FF}\hspace{0.2em}{\rm mod}\hspace{0.2em}\!~p-1$
and
$y\equiv a_{2}+pa_{1}+\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D716}(p-1)\hspace{0.2em}{\rm mod}\hspace{0.2em}\!~e$
; -
(ii)
$x\equiv a_{1}-\unicode[STIX]{x1D6FF}\hspace{0.2em}{\rm mod}\hspace{0.2em}\!~p-1$
and
$y\equiv a_{2}+pa_{0}+\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D716}(p-1)\hspace{0.2em}{\rm mod}\hspace{0.2em}\!~e$
; -
(iii)
$x\equiv a_{2}-\unicode[STIX]{x1D6FF}\hspace{0.2em}{\rm mod}\hspace{0.2em}\!~p-1$
and
$y\equiv a_{1}+pa_{0}+\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D716}(p-1)\hspace{0.2em}{\rm mod}\hspace{0.2em}\!~e$
,
where
$\unicode[STIX]{x1D716}\in \{0,1\}$
,
$\unicode[STIX]{x1D6FF}\in \mathbb{Z}$
are such that
$\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D716}\in \{0,1\}$
.
Proof. As in the proof of Proposition 2.6.1 we may assume
$a_{0}=0$
and set
$a\stackrel{\text{def}}{=}a_{2}$
,
$b\stackrel{\text{def}}{=}a_{1}$
. Let
$\widehat{{\mathcal{M}}}$
be a strongly divisible
${\mathcal{O}}_{E}$
-module such that
$\text{T}_{\text{st}}^{\mathbb{Q}_{p},2}(\widehat{{\mathcal{M}}})\cong \unicode[STIX]{x1D70C}$
; let
${\mathcal{M}}$
be the Breuil module obtained by base change to
$\overline{S}$
. Then
${\mathcal{M}}$
is of type
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{x(p+1)}\oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{y}\oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{py}$
for some
$x,y\in \mathbb{Z}$
,
$y\not \equiv 0$
mod
$p+1$
(by Lemma 2.4.8). As
$\unicode[STIX]{x1D70C}$
has Hodge–Tate weights
$\{-2,-1,0\}$
we moreover have
$\det \unicode[STIX]{x1D70C}=\widetilde{\unicode[STIX]{x1D714}}^{x+y}\unicode[STIX]{x1D700}^{3}$
.
By Proposition 2.3.5,
${\mathcal{M}}$
has a unique filtration by Breuil submodules with graded pieces described by
$$\begin{eqnarray}{\mathcal{M}}:{\mathcal{M}}_{2}\text{—}{\mathcal{M}}_{1}\text{—}{\mathcal{M}}_{0},\end{eqnarray}$$
where
$\text{T}_{\text{st}}^{2}({\mathcal{M}}_{i})|_{I_{\mathbb{Q}_{p}}}=\unicode[STIX]{x1D714}^{a_{i}+1}$
. We conclude by Lemma 2.6.2 that one of the following three possibilities holds (up to interchanging
$y$
and
$py$
).
-
(i) The Breuil modules
$({\mathcal{M}}_{2},{\mathcal{M}}_{1},{\mathcal{M}}_{0})$
are respectively of type
$(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{y},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{py},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{x(p+1)})$
, where
$x\equiv 1-\unicode[STIX]{x1D6FF}$
mod
$p-1$
,
$y\equiv (a+1)(p+1)-rp$
mod
$e$
and
$py\equiv (p+1)(b+1)-sp$
mod
$e$
. -
(ii) The Breuil modules
$({\mathcal{M}}_{2},{\mathcal{M}}_{1},{\mathcal{M}}_{0})$
are respectively of type
$(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{y},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{x(p+1)},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{py})$
, where
$x\equiv b+1-\unicode[STIX]{x1D6FF}$
mod
$p-1$
,
$y\equiv (a+1)(p+1)-rp$
mod
$e$
and
$py\equiv (p+1)-sp$
mod
$p-1$
. -
(iii) The Breuil modules
$({\mathcal{M}}_{2},{\mathcal{M}}_{1},{\mathcal{M}}_{0})$
are respectively of type
$(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{x(p+1)},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{y},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{py})$
, where
$x\equiv a+1-\unicode[STIX]{x1D6FF}$
mod
$p-1$
,
$y\equiv (b+1)(p+1)-rp$
mod
$e$
and
$py\equiv (p+1)-sp$
mod
$e$
.
In each case, the integers
$\unicode[STIX]{x1D6FF},r,s$
verify
$\unicode[STIX]{x1D6FF}\in \{0,1,2\}$
,
$0\leqslant r,s\leqslant 2(p+1)$
and
$y+pr$
,
$y+s\equiv 0$
modulo
$p+1$
. Moreover,
$r\not \equiv 0$
mod
$p+1$
, as
$\unicode[STIX]{x1D70C}$
does not become semistable over
$\mathbb{Q}_{p}(\unicode[STIX]{x1D701}_{p})$
.
Assume we are in case (i). We deduce that
$pr-s\equiv (a-b)(p+1)$
mod
$e$
and hence
$r+s\equiv 0$
mod
$p+1$
. Provided the restrictions on
$r,s$
, we obtain
$r+s=\unicode[STIX]{x1D6FC}(p+1)$
for some
$\unicode[STIX]{x1D6FC}\in \{1,2,3\}$
and hence
$r\equiv \unicode[STIX]{x1D6FC}+(a-b)\,\,\text{mod}\,p-1$
. Considering the condition
$\det \unicode[STIX]{x1D70C}|_{I_{\mathbb{Q}_{p}}}\equiv \unicode[STIX]{x1D714}^{x+y}\unicode[STIX]{x1D714}^{3}$
, we see that the integers
$\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FF}$
verify moreover the relation
$\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D6FC}=3$
(as
$p>3$
).
As
$2<a-b<p-3$
, the condition
$0<r,s<2(p+1)$
implies that
$r\in \{1+(a-b),2+(a-b),p+1+(a-b),p+2+(a-b)\}$
and hence
$$\begin{eqnarray}(x,y)\in \{(-1,a+pb+1),(0,a+pb-(p-1)),(0,a+pb),(1,a+pb-p)\}.\end{eqnarray}$$
This concludes the analysis of case (i).
Cases (ii) and (iii) are strictly analogous. We remark that in cases (ii) and (iii) we obtain the condition
$r\equiv \unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D70E}$
for
$\unicode[STIX]{x1D70E}\in \{a,b\}$
; as
$2<\unicode[STIX]{x1D70E}<p-3$
this provides us with
$r\in \{\unicode[STIX]{x1D70E}+1+\unicode[STIX]{x1D716}+\unicode[STIX]{x1D701}p:\unicode[STIX]{x1D716},\unicode[STIX]{x1D701}\in \{0,1\}\}$
.◻
Proposition 2.6.4. Let
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}({\mathcal{O}}_{E})$
be a potentially semistable
$p$
-adic Galois representation with Hodge–Tate weights
$\{-2,-1,0\}$
. Assume that
$\overline{\unicode[STIX]{x1D70C}}$
is maximally non-split and generic as in Definition 2.1.5.
-
(i) If
$\text{WD}(\unicode[STIX]{x1D70C})|_{I_{\mathbb{Q}_{p}}}\cong \widetilde{\unicode[STIX]{x1D714}}^{a_{0}}\oplus \widetilde{\unicode[STIX]{x1D714}}_{2}^{a_{2}+1+p(a_{1}-1)}\oplus \widetilde{\unicode[STIX]{x1D714}}_{2}^{a_{1}-1+p(a_{2}+1)}$
, then
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})=\infty$
. -
(ii) If
$\text{WD}(\unicode[STIX]{x1D70C})|_{I_{\mathbb{Q}_{p}}}\cong \widetilde{\unicode[STIX]{x1D714}}^{a_{2}}\oplus \widetilde{\unicode[STIX]{x1D714}}_{2}^{a_{0}-1+p(a_{1}+1)}\oplus \widetilde{\unicode[STIX]{x1D714}}_{2}^{a_{1}+1+p(a_{0}-1)}$
, then
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})=0$
.
In order to prove Proposition 2.6.4 we follow the procedure used in § 2.5: we first diagonalize the Frobenius action on the Breuil module
${\mathcal{M}}$
and, subsequently, we compute
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})$
by extracting the Fontaine–Laffaille module from the datum of
${\mathcal{M}}$
(via the results of § 2.2).
The proof will occupy the remainder of this section.
Proof. We first note that part (ii) follows from part (i), replacing
$\unicode[STIX]{x1D70C}$
by
$\unicode[STIX]{x1D70C}^{\vee }$
and
$(a_{0},a_{1},a_{2})$
by
$(-a_{2},-a_{1},-a_{0})$
and keeping in mind Remark 2.1.13.
We will now explain the proof of part (i). By twisting we may assume that
$a_{0}=0$
. We set
$a\stackrel{\text{def}}{=}a_{2}$
,
$b\stackrel{\text{def}}{=}a_{1}$
and define
$$\begin{eqnarray}\displaystyle & \displaystyle k_{1}\stackrel{\text{def}}{=}a+1+p(b-1),\quad k_{2}\stackrel{\text{def}}{=}b-1+p(a+1), & \displaystyle \nonumber\\ \displaystyle & \displaystyle r_{1}\stackrel{\text{def}}{=}a-b+2,\quad r_{2}\stackrel{\text{def}}{=}2p-(a-b), & \displaystyle \nonumber\end{eqnarray}$$
so that
$\unicode[STIX]{x1D70F}\stackrel{\text{def}}{=}\text{WD}(\unicode[STIX]{x1D70C})|_{I_{\mathbb{Q}_{p}}}=\widetilde{\unicode[STIX]{x1D714}}^{0}\oplus \widetilde{\unicode[STIX]{x1D714}}_{2}^{k_{1}}\oplus \widetilde{\unicode[STIX]{x1D714}}_{2}^{k_{2}}$
. Note in particular that
$0<k_{1},k_{2}<e$
as well as the following relations, which will be useful for the computations below:
$$\begin{eqnarray}\displaystyle & \displaystyle r_{1}(p-1)<e,\quad (p-1)(r_{1}+r_{2})=2e, & \displaystyle \nonumber\\ \displaystyle & \displaystyle k_{1}+r_{1}(p-1)=k_{2},\quad k_{2}+r_{2}(p-1)=k_{1}+2e. & \displaystyle \nonumber\end{eqnarray}$$
Let
$\widehat{{\mathcal{M}}}\in {\mathcal{O}}_{E}\text{-}\operatorname{Mod}_{\text{dd}}^{2}$
be a strongly divisible
${\mathcal{O}}_{E}$
-module such that
$\text{T}_{\text{st}}^{\mathbb{Q}_{p},2}(\widehat{{\mathcal{M}}})=\unicode[STIX]{x1D70C}$
and let
${\mathcal{M}}\in \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{2}$
be the base change of
$\widehat{{\mathcal{M}}}$
via
$S{\twoheadrightarrow}\overline{S}$
. In particular by Lemma 2.4.8,
${\mathcal{M}}$
is of type
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{0}\oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{k_{1}}\oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{k_{2}}$
. The first step of the proof is to describe the filtration and the Frobenius action on
${\mathcal{M}}$
.
Claim 2.6.5. There is a framed basis
$\text{}\underline{e}$
of
${\mathcal{M}}$
and a framed system of generators
$\text{}\underline{f}$
for
$\operatorname{Fil}^{2}{\mathcal{M}}$
such that
$$\begin{eqnarray}\displaystyle \text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\operatorname{Fil}^{2}{\mathcal{M}})=\left(\begin{array}{@{}ccc@{}}u^{e} & & \\ & u^{r_{1}(p-1)} & z\\ yu^{2e-k_{2}} & & u^{r_{2}(p-1)}\end{array}\right),\quad \text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\unicode[STIX]{x1D711}_{2})=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D706} & & \\ & \unicode[STIX]{x1D707} & \\ & & \unicode[STIX]{x1D708}\end{array}\right), & & \displaystyle \nonumber\end{eqnarray}$$
where
$y,z\in k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
and
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}\in (k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F})^{\times }$
.
Proof. From Proposition 2.3.5, the proof of Proposition 2.6.3, and genericity, we see that
${\mathcal{M}}$
has a unique filtration by Breuil submodules
$$\begin{eqnarray}{\mathcal{M}}:{\mathcal{M}}_{1}\text{}\text{—}{\mathcal{M}}_{2}\text{}\text{—}{\mathcal{M}}_{0},\end{eqnarray}$$
where
${\mathcal{M}}_{1}$
(respectively
${\mathcal{M}}_{2}$
, respectively
${\mathcal{M}}_{0}$
) is a rank-one Breuil module of type
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{k_{1}}$
(respectively
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{k_{2}}$
, respectively
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{0}$
), and filtration described by
$\operatorname{Fil}^{2}{\mathcal{M}}_{1}=u^{r_{1}(p-1)}{\mathcal{M}}_{1}$
(respectively
$\operatorname{Fil}^{2}{\mathcal{M}}_{2}=u^{r_{2}(p-1)}{\mathcal{M}}_{1}$
, respectively
$\operatorname{Fil}^{2}{\mathcal{M}}_{0}=u^{e}{\mathcal{M}}_{0}$
).
We therefore deduce the existence of a framed basis
$\text{}\underline{e}_{0}\stackrel{\text{def}}{=}(e_{0},e_{1},e_{2})$
, and a framed system of generators
$\text{}\underline{f}_{0}=(f_{0},f_{1},f_{2})$
of
$\operatorname{Fil}^{2}{\mathcal{M}}$
such that
$$\begin{eqnarray}\displaystyle & \displaystyle V_{0}\stackrel{\text{def}}{=}\text{Mat}_{\text{}\underline{e}_{0},\text{}\underline{f}_{0}}(\operatorname{Fil}^{2}{\mathcal{M}})=\left(\begin{array}{@{}ccc@{}}u^{e} & & \\ x_{0}u^{e-k_{1}} & u^{r_{1}(p-1)} & z_{0}\\ y_{0}^{\prime }u^{e-k_{2}} & & u^{r_{2}(p-1)}\end{array}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle A_{0}\stackrel{\text{def}}{=}\text{Mat}_{\text{}\underline{e}_{0},\text{}\underline{f}_{0}}(\unicode[STIX]{x1D711}_{2})=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D706}_{0} & & \\ \unicode[STIX]{x1D6FC}_{0}u^{e-k_{1}} & \unicode[STIX]{x1D707}_{0} & \unicode[STIX]{x1D6FE}_{0}u^{r_{1}(p-1)}\\ \unicode[STIX]{x1D6FD}_{0}u^{e-k_{2}} & & \unicode[STIX]{x1D708}_{0}\end{array}\right), & \displaystyle \nonumber\end{eqnarray}$$
where
$x_{0},y_{0}^{\prime },z_{0},\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FD}_{0},\unicode[STIX]{x1D6FE}_{0}\in \overline{S}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{0}}$
and
$\unicode[STIX]{x1D706}_{0},\unicode[STIX]{x1D707}_{0},\unicode[STIX]{x1D708}_{0}\in \overline{S}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{0}}^{\times }$
.
Claim 2.6.6. We have
$y_{0}^{\prime }=u^{e}y_{0}$
for some
$y_{0}\in \overline{S}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{0}}$
.
Proof. Let
${\mathcal{N}}:{\mathcal{M}}_{2}\text{}\text{—}{\mathcal{M}}_{0}$
denote the rank-two quotient of
${\mathcal{M}}$
. By the previous analysis of
${\mathcal{M}}$
, we deduce that there is a basis
$(\overline{e}_{0},\overline{e}_{2})$
of
${\mathcal{N}}$
and a pair
$(\overline{f}_{0},\overline{f}_{1})$
of elements of
$\operatorname{Fil}^{2}{\mathcal{N}}$
such that
$$\begin{eqnarray}\operatorname{Fil}^{2}{\mathcal{N}}=\left\langle \overline{f}_{0}\stackrel{\text{def}}{=}\left(\begin{array}{@{}c@{}}u^{e}\\ y_{0}^{\prime }u^{e-k_{2}}\end{array}\right),\overline{f}_{1}\stackrel{\text{def}}{=}\left(\begin{array}{@{}c@{}}0\\ u^{r_{2}(p-1)}\end{array}\right)\right\rangle _{\overline{S}}\end{eqnarray}$$
(in terms of the basis
$(\overline{e}_{0},\overline{e}_{2})$
). If
$y_{0}^{\prime }\not \equiv 0$
mod
$u$
, then it is easy to see that
$u^{2e}\overline{e}_{0}\not \in \operatorname{Fil}^{2}{\mathcal{N}}$
, contradicting the Breuil module axioms. Therefore the claim follows.◻
We now complete the procedure to diagonalize the Frobenius action. An elementary computation shows that there exist
$y_{1},z_{1},\unicode[STIX]{x1D701}_{1}\in \overline{S}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{0}}$
such that the following equality holds:
$$\begin{eqnarray}A_{0}\left(\begin{array}{@{}ccc@{}}u^{e} & & \\ & u^{r_{1}(p-1)} & z_{1}\\ y_{1}u^{2e-k_{2}} & & u^{r_{2}(p-1)}\end{array}\right)\equiv V_{0}\underbrace{\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D706}_{0} & & \\ \unicode[STIX]{x1D701}_{1}u^{e-k_{2}} & \unicode[STIX]{x1D707}_{0} & \\ & & \unicode[STIX]{x1D708}_{0}\end{array}\right)}_{\stackrel{\text{def}}{=}B_{0}}\,\,\text{mod}\,u^{3e}.\end{eqnarray}$$
Indeed, it suffices to take
$y_{1}\equiv \unicode[STIX]{x1D708}_{0}^{-1}(\unicode[STIX]{x1D706}_{0}y_{0}-\unicode[STIX]{x1D6FD}_{0})$
modulo
$u^{2e}$
,
$z_{1}\equiv \unicode[STIX]{x1D707}_{0}^{-1}(\unicode[STIX]{x1D708}_{0}z_{0}-\unicode[STIX]{x1D6FE}_{0}u^{2e})$
modulo
$u^{3e}$
and
$\unicode[STIX]{x1D701}_{1}\equiv -\unicode[STIX]{x1D706}_{0}x_{0}+(\unicode[STIX]{x1D6FC}_{0}+y_{1}\unicode[STIX]{x1D6FE}_{0})u^{e}$
modulo
$u^{3e}$
.
We use now Lemma 2.2.8 to deduce that, in the basis
$\text{}\underline{e}_{1}\stackrel{\text{def}}{=}\text{}\underline{e}_{0}\cdot A_{0}$
, the filtration and the Frobenius action can respectively be described as
$$\begin{eqnarray}\displaystyle V_{1}\stackrel{\text{def}}{=}\left(\begin{array}{@{}ccc@{}}u^{e} & & \\ & u^{r_{1}(p-1)} & z_{1}\\ y_{1}u^{2e-k_{2}} & & u^{r_{2}(p-1)}\end{array}\right),\quad A_{1}\stackrel{\text{def}}{=}\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D706}_{0}) & & \\ \unicode[STIX]{x1D711}(\unicode[STIX]{x1D701}_{1})u^{p(e-k_{2})} & \unicode[STIX]{x1D711}(\unicode[STIX]{x1D707}_{0}) & \\ & & \unicode[STIX]{x1D711}(\unicode[STIX]{x1D708}_{0})\end{array}\right), & & \displaystyle \nonumber\end{eqnarray}$$
where
$y_{1},z_{1}\in \overline{S}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{0}}$
and
$A_{1}=\unicode[STIX]{x1D711}(B_{0})$
.
We write
$\text{}\underline{f}_{1}\stackrel{\text{def}}{=}\text{}\underline{e}_{1}\cdot V_{1}$
. As
$r_{1}(p-1)<e$
,
$(3e-k_{2})-r_{2}(p-1)=e-k_{1}>r_{1}(p-1)$
, we can find a matrix in
$\operatorname{GL}_{3}^{\Box }(\overline{S})$
of the form
$$\begin{eqnarray}C\stackrel{\text{def}}{=}\left(\begin{array}{@{}ccc@{}}1 & & \\ c_{10}u^{e-k_{1}-r_{1}(p-1)} & 1 & c_{12}u^{e-r_{1}(p-1)}\\ c_{20}u^{3e-k_{2}-r_{2}(p-1)} & & 1\end{array}\right)\end{eqnarray}$$
such that, relative to
$\text{}\underline{e}_{1}$
and
$\text{}\underline{f}_{1}^{\prime }\stackrel{\text{def}}{=}\text{}\underline{f}_{1}\cdot C$
, the filtration and the Frobenius action can be described by
$$\begin{eqnarray}V_{1}^{\prime }\stackrel{\text{def}}{=}\left(\begin{array}{@{}ccc@{}}u^{e} & & \\ & u^{r_{1}(p-1)} & z_{1}^{\prime }\\ y_{1}^{\prime }u^{2e-k_{2}} & & u^{r_{2}(p-1)}\end{array}\right),\quad A_{1}^{\prime }\stackrel{\text{def}}{=}\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D706}_{0}) & & \\ a_{10}^{\prime }u^{p(e-k_{2})} & \unicode[STIX]{x1D711}(\unicode[STIX]{x1D707}_{0}) & a_{12}^{\prime }u^{p(e-r_{1}(p-1))}\\ a_{20}^{\prime }u^{p(e-k_{1})} & & \unicode[STIX]{x1D711}(\unicode[STIX]{x1D708}_{0})\end{array}\right),\end{eqnarray}$$
where
$y_{1}^{\prime },z_{1}^{\prime }\in k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
and
$a_{ij}^{\prime }\in \overline{S}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{0}}$
. We can write
$a_{10}^{\prime }u^{p(e-k_{2})}=\unicode[STIX]{x1D6FC}_{1}^{\prime }u^{e-k_{1}}$
,
$a_{20}^{\prime }u^{p(e-k_{1})}=\unicode[STIX]{x1D6FD}_{1}^{\prime }u^{e-k_{2}}$
,
$a_{12}^{\prime }u^{p(e-r_{1}(p-1))}=\unicode[STIX]{x1D6FE}_{1}^{\prime }u^{r_{1}(p-1)}$
with
$\unicode[STIX]{x1D6FC}_{1}^{\prime },\unicode[STIX]{x1D6FD}_{1}^{\prime },\unicode[STIX]{x1D6FE}_{1}^{\prime }\in u^{2e}\overline{S}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{0}}$
by genericity. Writing
$\unicode[STIX]{x1D706}_{1}^{\prime }\stackrel{\text{def}}{=}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D706}_{0})$
,
$\unicode[STIX]{x1D707}_{1}^{\prime }\stackrel{\text{def}}{=}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D707}_{0})$
,
$\unicode[STIX]{x1D708}_{1}^{\prime }\stackrel{\text{def}}{=}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D708}_{0})$
, which all lie in
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
, we see that
$(V_{1}^{\prime },A_{1}^{\prime })$
is of the same form as
$(V_{0},A_{0})$
, so we can apply the above diagonalization procedure to obtain
$(V_{2},A_{2})$
as in the statement of the claim.◻
We now compute the Fontaine–Laffaille invariant of the Galois representation associated to
${\mathcal{M}}$
.
Claim 2.6.7. With the hypotheses and notation of Claim 2.6.5 we have
$$\begin{eqnarray}\text{FL}(\text{T}_{\text{st}}^{2}({\mathcal{M}}))=\infty .\end{eqnarray}$$
Proof. Consider the
$(\unicode[STIX]{x1D719},k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}((\text{}\underline{\unicode[STIX]{x1D71B}})))$
-module
$\mathfrak{M}\stackrel{\text{def}}{=}M_{k((\text{}\underline{\unicode[STIX]{x1D71B}}))}({\mathcal{M}}^{\ast })$
. From Claim 2.6.5 and Lemma 2.2.6
$\mathfrak{M}$
is endowed with a framed basis
$\text{}\underline{\mathfrak{e}}$
(for the type
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{0}\oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{-k_{1}}\oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{-k_{2}}$
) such that
$$\begin{eqnarray}\text{Mat}_{\text{}\underline{\mathfrak{e}}}(\unicode[STIX]{x1D719})=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D706}^{-1}\text{}\underline{\unicode[STIX]{x1D71B}}^{e} & y\unicode[STIX]{x1D708}^{-1}\text{}\underline{\unicode[STIX]{x1D71B}}^{2e-k_{2}} & \\ & \unicode[STIX]{x1D708}^{-1}\text{}\underline{\unicode[STIX]{x1D71B}}^{r_{2}(p-1)} & z\unicode[STIX]{x1D707}^{-1}\\ & & \unicode[STIX]{x1D707}^{-1}\text{}\underline{\unicode[STIX]{x1D71B}}^{r_{1}(p-1)}\end{array}\right),\end{eqnarray}$$
where
$y,z\in k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
,
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}\in (k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F})^{\times }$
.
By considering the
$\operatorname{Gal}(K/K_{0})$
-invariant basis
$\text{}\underline{\mathfrak{e}}^{\prime }\stackrel{\text{def}}{=}\text{}\underline{\mathfrak{e}}\cdot \text{Diag}(1,\text{}\underline{\unicode[STIX]{x1D71B}}^{k_{1}},\text{}\underline{\unicode[STIX]{x1D71B}}^{k_{2}})$
one deduces that
$\mathfrak{M}\cong \mathfrak{M}_{0}\otimes _{\mathbb{F}((\text{}\underline{p}))}\mathbb{F}((\text{}\underline{\unicode[STIX]{x1D71B}}))$
, where the
$(\unicode[STIX]{x1D719},k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}((\text{}\underline{p})))$
-module
$\mathfrak{M}_{0}$
is described (in some basis
$\text{}\underline{\mathfrak{e}}_{0}$
) by
$$\begin{eqnarray}\text{Mat}_{\text{}\underline{\mathfrak{e}}_{0}}(\unicode[STIX]{x1D719})=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D706}^{-1} & y\unicode[STIX]{x1D708}^{-1} & \\ & \unicode[STIX]{x1D708}^{-1} & z\unicode[STIX]{x1D707}^{-1}\\ & & \unicode[STIX]{x1D707}^{-1}\end{array}\right)\text{Diag}(\text{}\underline{p},\text{}\underline{p}^{b+1},\text{}\underline{p}^{a+1}).\end{eqnarray}$$
From (2.6.8), Lemma 2.2.7 (and a change of basis over
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
as in the proof of Proposition 2.5.6) we deduce that the Frobenius action on the Fontaine–Laffaille module
$M_{k}$
associated to
$\overline{\unicode[STIX]{x1D70C}}|_{G_{K_{0}}}$
is given by
$$\begin{eqnarray}F_{k}\stackrel{\text{def}}{=}\text{Mat}_{\text{}\underline{e}}(\unicode[STIX]{x1D719}_{\bullet })=\unicode[STIX]{x1D711}\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D706}^{-1} & y\unicode[STIX]{x1D708}^{-1} & \\ & \unicode[STIX]{x1D708}^{-1} & z\unicode[STIX]{x1D707}^{-1}\\ & & \unicode[STIX]{x1D707}^{-1}\end{array}\right)\in \operatorname{GL}_{3}(k\otimes _{\mathbb{F}_{p}}\mathbb{F})\end{eqnarray}$$
for some basis
$\text{}\underline{e}$
of
$M_{k}$
compatible with the Hodge filtration on
$M_{k}$
(and
$\unicode[STIX]{x1D711}$
denotes the relative Frobenius on
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
). By Corollary 2.2.2 we have
$\text{T}_{\text{cris}}^{\ast }(M_{k})\cong \overline{\unicode[STIX]{x1D70C}}|_{G_{K_{0}}}$
. In particular, we have
$M_{k}\cong M\,\otimes _{\mathbb{F}_{p}}\,k$
for some Fontaine–Laffaille module
$M\in \mathbb{F}\text{-}{\mathcal{F}}{\mathcal{L}}^{[p-2]}$
such that
$\text{T}_{\text{cris}}^{\ast }(M)\cong \overline{\unicode[STIX]{x1D70C}}$
as
$G_{\mathbb{Q}_{p}}$
-representations.
Since
$p>2$
,
$\overline{\unicode[STIX]{x1D70C}}|_{G_{K_{0}}}$
is still maximally non-split, and hence
$M_{k}$
is endowed with a unique filtration
$0\subsetneq M_{k,0}\subsetneq M_{k,1}\subsetneq M_{k,2}=M_{k}$
, obtained from the cosocle filtration on
$\overline{\unicode[STIX]{x1D70C}}|_{G_{K_{0}}}$
. By unicity, we have
$M_{k,i}=M_{i}\,\otimes _{\mathbb{F}_{p}}\,k$
for all
$i=0,1,2$
, where
$0\subsetneq M_{0}\subsetneq M_{1}\subsetneq M_{2}=M$
is the filtration on
$M$
obtained via
$\text{T}_{\text{cris}}^{\ast }$
from the cosocle filtration on
$\overline{\unicode[STIX]{x1D70C}}$
.
As
$\operatorname{Fil}^{1}M_{k}\,\cap \,M_{k,0}$
,
$\operatorname{Fil}^{b+1}M_{k}\,\cap \,M_{k,1}$
,
$\operatorname{Fil}^{a+1}M_{k}\,\cap \,M_{k,2}$
are all free of rank one over
$k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}$
it follows that any change of basis of
$M_{k}$
preserving both the Hodge and the submodule filtration needs to be diagonal.
Therefore, by letting
$F\in \operatorname{GL}_{3}(\mathbb{F})$
denote the matrix of the Frobenius action on
$M$
, we deduce that
$F_{02}=0$
if and only if
$(F_{k})_{02}=0$
, which shows that
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})=\infty$
, as claimed.◻
From the Claims 2.6.5, 2.6.7, the proof of Proposition 2.6.4(i) follows. ◻
3 The local automorphic side
In this section we analyze the
$\operatorname{GL}_{3}$
-side. In particular, we establish Proposition G of the introduction. We have [Reference JantzenJan03] as a main reference for the notation and terminology.
Let
$G\stackrel{\text{def}}{=}{\operatorname{GL}_{n}}_{/\mathbb{Z}_{p}}$
and let
$T$
be the maximal split torus consisting of diagonal matrices. We let
$\unicode[STIX]{x1D6F7}$
denote the set of roots with respect to
$T$
and
$B\supseteq T$
the Borel subgroup of upper-triangular matrices. We write
$\unicode[STIX]{x1D6E5}\subseteq \unicode[STIX]{x1D6F7}$
for the simple roots associated to the pair
$(B,T)$
and
$\langle \cdot ,\cdot \rangle$
for the natural pairing on
$X^{\ast }(T)\times X_{\ast }(T)$
. The character and cocharacter groups are identified with
$\mathbb{Z}^{n}$
in the usual way. We let
${\leqslant}$
denote the dominance order on
$X^{\ast }(T)$
. Finally, we let
$\overline{G},\overline{B},\ldots \,$
denote the base change of
$G,B,\ldots \,$
via
$\mathbb{Z}_{p}{\twoheadrightarrow}\mathbb{F}_{p}$
.
The Weyl group
$W_{G}$
of
$G$
is canonically isomorphic to the Weyl group of
$\overline{G}$
. We write
$w_{0}\in W_{G}$
for the longest element.
For any dominant character
$\unicode[STIX]{x1D706}\in X^{\ast }(\overline{T})$
let
$$\begin{eqnarray}H^{0}(\unicode[STIX]{x1D706})\stackrel{\text{def}}{=}(\operatorname{Ind}_{\overline{B}}^{\overline{G}}w_{0}\unicode[STIX]{x1D706})^{\text{alg}}\otimes _{\mathbb{ F}_{p}}\mathbb{F}\end{eqnarray}$$
be the associated dual Weyl module. It is an algebraic representation of
$\overline{G}$
(or more precisely of
$\overline{G}_{/\mathbb{F}}$
) and we write
$F(\unicode[STIX]{x1D706})\stackrel{\text{def}}{=}\text{soc}_{\overline{G}}(H^{0}(\unicode[STIX]{x1D706}))$
for its irreducible socle. If the weight
$\unicode[STIX]{x1D706}$
is, moreover,
$p$
-restricted, i.e. if
$0\leqslant \langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC}^{\vee }\rangle \leqslant p-1$
for all
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, then
$F(\unicode[STIX]{x1D706})$
is irreducible as
$\overline{G}(\mathbb{F}_{p})$
-representation (see, for example, [Reference HerzigHer09, Corollary 3.17]). If
$Q$
is an algebraic representation of
$\overline{G}$
and
$\unicode[STIX]{x1D708}\in X^{\ast }(T)$
we denote by
$Q_{\unicode[STIX]{x1D708}}$
the
$\unicode[STIX]{x1D708}$
-weight space for the action of
$\overline{T}$
on
$Q$
, as usual.
Note that if
$n=1$
and
$a\in \mathbb{Z}$
then
$F(a)\cong \unicode[STIX]{x1D714}^{a}$
, where
$\unicode[STIX]{x1D714}$
is seen as a character of
$\operatorname{GL}_{1}(\mathbb{F}_{p})$
via the Artin reciprocity map (so
$\unicode[STIX]{x1D714}$
is the inclusion
$\mathbb{F}_{p}^{\times }\rightarrow \mathbb{F}^{\times }$
).
Let us specialize to the case
$n=3$
. We set
$\unicode[STIX]{x1D6FC}_{1}\stackrel{\text{def}}{=}(1,-1,0)$
,
$\unicode[STIX]{x1D6FC}_{2}\stackrel{\text{def}}{=}(0,1,-1)$
, so that
$\unicode[STIX]{x1D6E5}=\{\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}\}$
, and we fix the following lifts
${\dot{s}}_{1},{\dot{s}}_{2}\in G(\mathbb{Z}_{p})$
of the simple reflections
$s_{1},s_{2}\in W_{G}$
corresponding to
$\unicode[STIX]{x1D6FC}_{1}$
,
$\unicode[STIX]{x1D6FC}_{2}$
:
$$\begin{eqnarray}{\dot{s}}_{1}\stackrel{\text{def}}{=}\left(\begin{array}{@{}ccc@{}} & 1 & \\ 1 & & \\ & & 1\end{array}\right),\quad {\dot{s}}_{2}\stackrel{\text{def}}{=}\left(\begin{array}{@{}ccc@{}}1 & & \\ & & 1\\ & 1 & \end{array}\right).\end{eqnarray}$$
Note that
${\dot{w}}_{0}\stackrel{\text{def}}{=}{\dot{s}}_{1}{\dot{s}}_{2}{\dot{s}}_{1}$
is then a lift of
$w_{0}\in W_{G}$
.
Finally, for each
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
we denote by
$U_{\unicode[STIX]{x1D6FC}}$
the associated root subgroup and by
$u_{\unicode[STIX]{x1D6FC}}:\mathbb{G}_{a}\stackrel{{\sim}}{\longrightarrow }U_{\unicode[STIX]{x1D6FC}}$
an isomorphism as in [Reference JantzenJan03], II.1.2. Explicitly we will take
$$\begin{eqnarray}u_{\unicode[STIX]{x1D6FC}_{1}}(x)=\left(\begin{array}{@{}ccc@{}}1 & x & \\ & 1 & \\ & & 1\end{array}\right),\quad u_{\unicode[STIX]{x1D6FC}_{2}}(x)=\left(\begin{array}{@{}ccc@{}}1 & & \\ & 1 & x\\ & & 1\end{array}\right),\quad u_{\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}(x)=\left(\begin{array}{@{}ccc@{}}1 & & x\\ & 1 & \\ & & 1\end{array}\right).\end{eqnarray}$$
Let
$K\stackrel{\text{def}}{=}G(\mathbb{Z}_{p})$
. (This should not cause any confusion with the field
$K$
of § 2 and Appendix A.) We write
$I$
for the Iwahori subgroup of
$K$
which is the preimage of
$\overline{B}(\mathbb{F}_{p})$
under the reduction map
$K{\twoheadrightarrow}\overline{G}(\mathbb{F}_{p})$
and similarly
$I_{1}\leqslant I$
for the pro-
$p$
Iwahori subgroup which is the preimage of
$\overline{U}(\mathbb{F}_{p})$
. If
$V$
is a representation of
$K$
over
${\mathcal{O}}_{E}$
and
$a_{i}\in \mathbb{Z}$
we write
$$\begin{eqnarray}V^{I,(a_{2},a_{1},a_{0})}\stackrel{\text{def}}{=}\operatorname{Hom}_{I}({\mathcal{O}}_{E}(\widetilde{\unicode[STIX]{x1D714}}^{a_{2}}\otimes \widetilde{\unicode[STIX]{x1D714}}^{a_{1}}\otimes \widetilde{\unicode[STIX]{x1D714}}^{a_{0}}),V),\end{eqnarray}$$
the largest
${\mathcal{O}}_{E}$
-submodule of
$V$
on which
$I$
acts via
$\widetilde{\unicode[STIX]{x1D714}}^{a_{2}}\,\otimes \,\widetilde{\unicode[STIX]{x1D714}}^{a_{1}}\,\otimes \,\widetilde{\unicode[STIX]{x1D714}}^{a_{0}}$
. In particular, this makes sense when
$V$
is killed by
$\unicode[STIX]{x1D71B}_{E}$
. Also, if
$V$
is a representation of
$\overline{G}(\mathbb{F}_{p})$
over
$\mathbb{F}$
we write
$V^{\overline{T}(\mathbb{F}_{p}),(a_{2},a_{1},a_{0})}$
to denote the largest subspace on which
$\overline{T}(\mathbb{F}_{p})$
acts as
$F(a_{2})\,\otimes \,F(a_{1})\,\otimes \,F(a_{0})$
, and we note that
$V^{I,(a_{2},a_{1},a_{0})}\subseteq V^{\overline{T}(\mathbb{F}_{p}),(a_{2},a_{1},a_{0})}$
.
3.1 Group algebra operators
We introduce certain mod
$p$
group algebra operators for
$\overline{G}(\mathbb{F}_{p})$
and study their effect on extensions of
$\overline{G}(\mathbb{F}_{p})$
-representations.
Let
$(a_{2},a_{1},a_{0})\in \mathbb{Z}^{3}$
be a triple verifying the genericity condition (2.1.6). Note that in this case the weight
$(a_{2},a_{1},a_{0})\in \mathbb{Z}^{3}$
is in particular
$p$
-restricted. We define the following elements of
$\mathbb{F}[\overline{G}(\mathbb{F}_{p})]$
:
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\displaystyle S\stackrel{\text{def}}{=}\underset{x,y,z\in \mathbb{F}_{p}}{\sum }x^{p-(a_{2}-a_{0})}z^{p-(a_{1}-a_{0})}\left(\begin{array}{@{}ccc@{}}1 & x & y\\ & 1 & z\\ & & 1\end{array}\right){\dot{w}}_{0},\\ \displaystyle S^{\prime }\stackrel{\text{def}}{=}\underset{x,y,z\in \mathbb{F}_{p}}{\sum }x^{p-(a_{2}-a_{1})}z^{p-(a_{2}-a_{0})}\left(\begin{array}{@{}ccc@{}}1 & x & y\\ & 1 & z\\ & & 1\end{array}\right){\dot{w}}_{0}.\end{array} & & \displaystyle\end{eqnarray}$$
In other words,
$S=\sum _{x,y,z\in \mathbb{F}_{p}}x^{p-(a_{2}-a_{0})}z^{p-(a_{1}-a_{0})}u_{\unicode[STIX]{x1D6FC}_{2}}(z)u_{\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}(y)u_{\unicode[STIX]{x1D6FC}_{1}}(x){\dot{w}}_{0}$
and similarly for
$S^{\prime }$
.
The following property of the operators
$S,S^{\prime }$
will be crucial for us.
Proposition 3.1.2. Let
$(a_{2},a_{1},a_{0})\in \mathbb{Z}^{3}$
be a triple satisfying (2.1.6). Consider the associated operators
$S,S^{\prime }\in \mathbb{F}[\overline{G}(\mathbb{F}_{p})]$
.
-
(i) There is a unique non-split extension of irreducible
$\overline{G}(\mathbb{F}_{p})$
-representations and
$$\begin{eqnarray}0\rightarrow F(a_{2}-1,a_{1},a_{0}+1)\rightarrow V\rightarrow F(a_{1}+p-1,a_{2},a_{0})\rightarrow 0\end{eqnarray}$$
$S$
induces an isomorphism
$S:\,V^{I,(a_{1},a_{2},a_{0})}\stackrel{{\sim}}{\longrightarrow }V^{I,(a_{2}-1,a_{1},a_{0}+1)}$
of one-dimensional vector spaces.
-
(ii) There is a unique non-split extension of irreducible
$\overline{G}(\mathbb{F}_{p})$
-representations and
$$\begin{eqnarray}0\rightarrow F(a_{2}-1,a_{1},a_{0}+1)\rightarrow V\rightarrow F(a_{2},a_{0},a_{1}-p+1)\rightarrow 0\end{eqnarray}$$
$S^{\prime }$
induces an isomorphism
$S^{\prime }:\,V^{I,(a_{2},a_{0},a_{1})}\stackrel{{\sim}}{\longrightarrow }V^{I,(a_{2}-1,a_{1},a_{0}+1)}$
of one-dimensional vector spaces.
More generally, one could ask the following (also for more general groups).
Question 3.1.3. Suppose that
$V$
is an
$\overline{G}(\mathbb{F}_{p})$
-representation that is generated by an
$I$
-eigenvector
$v\in V^{I,(b_{2},b_{1},b_{0})}$
. Given an
$I$
-eigenvector
$v^{\prime }\in V^{I,(c_{2},c_{1},c_{0})}$
, find an explicit element of
$\mathbb{F}[\overline{G}(\mathbb{F}_{p})]$
sending
$v$
to
$v^{\prime }$
.
By Frobenius reciprocity,
$V$
is a quotient of the principal series
$$\begin{eqnarray}\operatorname{Ind}_{\overline{B}(\mathbb{F}_{p})}^{\overline{G}(\mathbb{F}_{p})}(F(b_{2})\,\otimes \,F(b_{1})\,\otimes \,F(b_{0})),\end{eqnarray}$$
and an interesting special case of the above question is when
$V$
has irreducible socle that is moreover generated by
$v^{\prime }$
. Proposition 3.1.2 answers this in some instances. (See also the proof of [Reference Breuil and DiamondBD14, Proposition 2.6.1] for
$\operatorname{GL}_{2}$
.)
The proof of Proposition 3.1.2 requires a certain amount of preliminaries and will occupy the rest of this section.
Let
$\overline{P}\supseteq \overline{B}$
denote the standard parabolic associated to the simple root
$\unicode[STIX]{x1D6FC}_{1}$
. We consider the equivariant monomorphism
$$\begin{eqnarray}\unicode[STIX]{x1D70F}\stackrel{\text{def}}{=}\operatorname{Ind}_{\overline{P}(\mathbb{F}_{p})}^{\overline{G}(\mathbb{F}_{p})}(F(a_{1}+p-1,a_{2})\otimes F(a_{0})){\hookrightarrow}\operatorname{Ind}_{\overline{B}(\mathbb{F}_{p})}^{\overline{G}(\mathbb{F}_{p})}(F(a_{2})\otimes F(a_{1})\otimes F(a_{0}))\stackrel{\text{def}}{=}\unicode[STIX]{x1D70E}\end{eqnarray}$$
obtained by parabolically inducing the injection
$F(a_{1}+p-1,a_{2}){\hookrightarrow}\operatorname{Ind}_{B_{2}(\mathbb{F}_{p})}^{\operatorname{GL}_{2}(\mathbb{F}_{p})}(F(a_{2})\,\otimes \,F(a_{1}))$
coming from Frobenius reciprocity (where
$B_{2}\subseteq \operatorname{GL}_{2}$
denotes the upper-triangular Borel subgroup).
As in [Reference Emerton, Gee and HerzigEGH13, proof of Lemma 6.1.1] we check that
$$\begin{eqnarray}\text{soc}(\unicode[STIX]{x1D70F})\cong F(a_{0}+p-1,a_{1},a_{2}-p+1),\quad \text{cosoc}(\unicode[STIX]{x1D70F})\cong F(a_{1}+p-1,a_{2},a_{0})\end{eqnarray}$$
and, again by [Reference Emerton, Gee and HerzigEGH13, Lemma 6.1.1], we see that
$\text{rad}(\unicode[STIX]{x1D70F})/\text{soc}(\unicode[STIX]{x1D70F})$
has length 4, with constituents
$$\begin{eqnarray}\displaystyle F(a_{1},a_{0},a_{2}-p+1),\quad F(a_{0}+p-2,a_{2},a_{1}+1), & & \displaystyle \nonumber\\ \displaystyle F(a_{2}-1,a_{1},a_{0}+1),\quad F(a_{1}-1,a_{0},a_{2}-p+2). & & \displaystyle \nonumber\end{eqnarray}$$
By [Reference AndersenAnd87, § 4] we deduce that
$\text{rad}(\unicode[STIX]{x1D70F})/\text{soc}(\unicode[STIX]{x1D70F})$
is semisimple; in particular the extension
$V$
exists and we have a surjection
$\unicode[STIX]{x1D70F}{\twoheadrightarrow}V$
. Also, by [Reference AndersenAnd87, § 4], the extension
$V$
is unique, because
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{Ext}_{\overline{G}(\mathbb{F}_{p})}^{1}(F(a_{1}+p-1,a_{2},a_{0}),F(a_{2}-1,a_{1},a_{0}+1))\nonumber\\ \displaystyle & & \displaystyle \qquad \stackrel{{\sim}}{\longrightarrow }(\text{Ext}_{\text{SL}_{3}(\mathbb{F}_{p})}^{1}(F(a_{1}+p-1,a_{2},a_{0}),F(a_{2}-1,a_{1},a_{0}+1)))^{\mathbb{F}_{p}^{\times }}\nonumber\end{eqnarray}$$
has dimension at most one.
We also see by [Reference HerzigHer11, Lemma 2.3] that
$V^{I,(a_{2}-1,a_{1},a_{0}+1)}$
and
$V^{I,(a_{1},a_{2},a_{0})}\cong \unicode[STIX]{x1D70F}^{I,(a_{1},a_{2},a_{0})}\cong \unicode[STIX]{x1D70E}^{I,(a_{1},a_{2},a_{0})}$
are one dimensional.
Let
$W\stackrel{\text{def}}{=}H^{0}(\unicode[STIX]{x1D706})$
, where
$\unicode[STIX]{x1D706}\stackrel{\text{def}}{=}(a_{0}+p-1,a_{1},a_{2}-p+1)$
. We recall that
$0\rightarrow F(\unicode[STIX]{x1D706})\rightarrow W\rightarrow F(a_{2}-1,a_{1},a_{0}+1)\rightarrow 0$
(see [Reference HerzigHer09, Proposition 3.18]) and moreover that this sequence is non-split even on the level of
$\overline{G}(\mathbb{F}_{p})$
-representations (see [Reference HumphreysHum06, Theorem 5.9]). The natural
$\overline{G}(\mathbb{F}_{p})$
-linear evaluation map
$$\begin{eqnarray}f:W=(\operatorname{Ind}_{\overline{B}}^{\overline{G}}(w_{0}\unicode[STIX]{x1D706}))^{\text{alg}}\longrightarrow \operatorname{Ind}_{\overline{B}(\mathbb{F}_{p})}^{\overline{G}(\mathbb{F}_{p})}(w_{0}\unicode[STIX]{x1D706})=\unicode[STIX]{x1D70E}\end{eqnarray}$$
is injective. (To see this, it is enough to check that the restriction of
$f$
to
$\text{soc}_{\overline{G}(\mathbb{F}_{p})}(W)\cong F(\unicode[STIX]{x1D706})$
is injective, and hence enough to check that the composite of
$f$
followed by evaluation at
${\dot{w}}_{0}\in \overline{G}(\mathbb{F}_{p})$
is injective on the highest weight space of
$\text{soc}_{\overline{G}(\mathbb{F}_{p})}(W)$
. The last statement is true by the proof of [Reference JantzenJan03, Proposition II.2.2(a)].) As
$\unicode[STIX]{x1D70E}$
is multiplicity free we obtain an injection
$W{\hookrightarrow}\unicode[STIX]{x1D70F}$
.
Lemma 3.1.4. We have
$S(\unicode[STIX]{x1D70F}^{I,(a_{1},a_{2},a_{0})})\subseteq \text{rad}(\unicode[STIX]{x1D70F})$
.
Proof. It is equivalent to show that the operator
$S$
kills the highest weight space
$F(\unicode[STIX]{x1D708})^{I,(a_{1},a_{2},a_{0})}=F(\unicode[STIX]{x1D708})_{\unicode[STIX]{x1D708}}$
, where
$\unicode[STIX]{x1D708}\stackrel{\text{def}}{=}(a_{1}+p-1,a_{2},a_{0})$
.
Recall that if
$Q$
is an algebraic
$\overline{G}$
-module,
$v_{\unicode[STIX]{x1D708}}\in Q_{\unicode[STIX]{x1D708}}$
and
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
is a root then (cf. [Reference JantzenJan03, II.1.19, (5) and (6)])
$$\begin{eqnarray}u_{\unicode[STIX]{x1D6FC}}(t)v_{\unicode[STIX]{x1D708}}=\mathop{\sum }_{i\in \mathbb{N}}t^{i}v_{\unicode[STIX]{x1D708}+i\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
where
$v_{\unicode[STIX]{x1D708}+i\unicode[STIX]{x1D6FC}}\in Q_{\unicode[STIX]{x1D708}+i\unicode[STIX]{x1D6FC}}$
(and
$0^{0}=1$
).
Applying this with
$Q=F(\unicode[STIX]{x1D708})$
we obtain
$$\begin{eqnarray}S(v_{\unicode[STIX]{x1D708}})=\underset{i,j,k\geqslant 0}{\sum }\biggl(\mathop{\sum }_{x,y,z\in \mathbb{F}_{p}}x^{i+p-(a_{2}-a_{0})}y^{j}z^{k+p-(a_{1}-a_{0})}\biggr)v_{i,j,k},\end{eqnarray}$$
where
$v_{i,j,k}\in F(\unicode[STIX]{x1D708})_{(a_{0},a_{2},a_{1}+p-1)+(i+j,-i+k,-j-k)}$
. We deduce that if the inner sum is non-zero for a fixed triple
$(i,j,k)\in \mathbb{N}^{3}$
, then we necessarily have
$i\geqslant a_{2}-a_{0}-1$
,
$j\geqslant p-1$
and
$k\geqslant a_{1}-a_{0}-1$
. But then
$(a_{0},a_{2},a_{1}+p-1)+(i+j,-i+k,-j-k)\not \leqslant (a_{1}+p-1,a_{2},a_{0})$
and the corresponding weight space in
$F(\unicode[STIX]{x1D708})$
is zero.◻
Remark 3.1.5. An immediate computation shows that
$S(\unicode[STIX]{x1D70F}^{I,(a_{1},a_{2},a_{0})})\subseteq \unicode[STIX]{x1D70F}^{\overline{T}(\mathbb{F}_{p}),(a_{2}-1,a_{1},a_{0}+1)}$
.
Lemma 3.1.6. We have
$S(\unicode[STIX]{x1D70F}^{I,(a_{1},a_{2},a_{0})})\subseteq W$
.
Proof. By Lemma 3.1.4 and Remark 3.1.5, it is enough to show that the weight spaces of
$F(a_{1},a_{0},a_{2}-p+1)$
,
$F(a_{0}+p-2,a_{2},a_{1}+1)$
and
$F(a_{1}-1,a_{0},a_{2}-p+2)$
do not afford the
$\overline{T}(\mathbb{F}_{p})$
-character
$F(a_{2}-1)\,\otimes \,F(a_{1})\,\otimes \,F(a_{0}+1)$
.
By using the dominance order
${\leqslant}$
on
$X^{\ast }(\overline{T})$
we see that the weights in
$F(a_{1},a_{0},a_{2}-p+1)$
are of the form
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
with
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in \{a_{2}-p+1,\ldots ,a_{1}-1,a_{1}\}$
. Hence
$a_{2}-p<\unicode[STIX]{x1D6FC}<a_{2}-1$
and
$\unicode[STIX]{x1D6FC}\not \equiv a_{2}-1$
mod
$p-1$
. With a similar argument we see that any weight
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
appearing in
$F(a_{0}+p-2,a_{2},a_{1}+1)$
,
$F(a_{1}-1,a_{0},a_{2}-p+2)$
satisfies
$\unicode[STIX]{x1D6FD}\not \equiv a_{1}$
mod
$p-1$
.◻
Lemma 3.1.7. We have
$S(\unicode[STIX]{x1D70F}^{I,(a_{1},a_{2},a_{0})})\neq 0$
.
Proof. Consider
$\unicode[STIX]{x1D70F}{\hookrightarrow}\unicode[STIX]{x1D70E}$
. Then
$\unicode[STIX]{x1D70F}^{I,(a_{1},a_{2},a_{0})}$
consists of functions
$f\in \unicode[STIX]{x1D70E}$
such that
-
(i)
$\text{supp}(f)\subseteq \overline{B}(\mathbb{F}_{p}){\dot{s}}_{1}\overline{B}(\mathbb{F}_{p})$
; -
(ii)
$f$
is constant on
${\dot{s}}_{1}\Bigl(\!\begin{smallmatrix}1 & \ast & \ast \\ & 1 & \ast \\ & & 1\end{smallmatrix}\!\Bigr)$
.
Take any non-zero
$f\in \unicode[STIX]{x1D70F}^{I,(a_{1},a_{2},a_{0})}$
and let
$g\stackrel{\text{def}}{=}\Bigl(\!\begin{smallmatrix} & & 1\\ & 1 & -1\\ 1 & -1 & \end{smallmatrix}\!\Bigr)$
. It then follows immediately from the definitions that
$$\begin{eqnarray}S(f)(g)=\underset{x,y,z\in \mathbb{F}_{p}}{\sum }x^{p-(a_{2}-a_{0})}z^{p-(a_{1}-a_{0})}f\left(\begin{array}{@{}ccc@{}}1 & & \\ z-1 & 1 & \\ y-z & x-1 & 1\end{array}\right).\end{eqnarray}$$
We deduce from part (i) that the term inside the sum is non-zero if and only if
$x=1$
,
$z=y$
,
$z\neq 1$
. Hence,
$$\begin{eqnarray}\displaystyle S(f)(g) & = & \displaystyle \underset{z\in \mathbb{F}_{p}^{\times }}{\sum }(z+1)^{p-(a_{1}-a_{0})}f\left(\begin{array}{@{}ccc@{}}1 & & \\ z & 1 & \\ & & 1\end{array}\right)\nonumber\\ \displaystyle & = & \displaystyle (-1)^{a_{2}}\underset{z\in \mathbb{F}_{p}^{\times }}{\sum }(z+1)^{p-(a_{1}-a_{0})}z^{-(a_{2}-a_{1})}f({\dot{s}}_{1}),\nonumber\end{eqnarray}$$
where the last equality follows from parts (i) and (ii) via the relation
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}1 & & \\ z & 1 & \\ & & 1\end{array}\right)=\left(\begin{array}{@{}ccc@{}}-z^{-1} & 1 & \\ & z & \\ & & 1\end{array}\right){\dot{s}}_{1}\left(\begin{array}{@{}ccc@{}}1 & z^{-1} & \\ & 1 & \\ & & 1\end{array}\right).\end{eqnarray}$$
Note that the term inside the sum is a linear combination of monomials
$z^{i}$
with
$|i|<p-1$
. We easily deduce
$$\begin{eqnarray}S(f)(g)=(-1)^{a_{2}-1}\binom{p-(a_{1}-a_{0})}{a_{2}-a_{1}}f({\dot{s}}_{1})\neq 0.\square\end{eqnarray}$$
Lemma 3.1.8. We have
$S(V^{I,(a_{1},a_{2},a_{0})})\subseteq V^{I,(a_{2}-1,a_{1},a_{0}+1)}$
.
Proof. This is clear from Lemma 3.1.4 and Remark 3.1.5, as (just as in Lemma 3.1.6) we have
$\text{soc}(V)^{\overline{T}(\mathbb{F}_{p}),(a_{2}-1,a_{1},a_{0}+1)}=\text{soc}(V)^{\overline{U}(\mathbb{F}_{p})}$
.◻
Proof of Proposition 3.1.2.
We start by proving part (i). Recall that we defined
$W\stackrel{\text{def}}{=}H^{0}(\unicode[STIX]{x1D706})$
with
$\unicode[STIX]{x1D706}\stackrel{\text{def}}{=}(a_{0}+p-1,a_{1},a_{2}-p+1)$
. By Lemma 3.1.8 it is enough to show that
$S(V^{I,(a_{1},a_{2},a_{0})})\neq 0$
or, equivalently (cf. Lemma 3.1.6), that
$S(\unicode[STIX]{x1D70F}^{I,(a_{1},a_{2},a_{0})})\not \subseteq \text{soc}(W)$
.
Let us define
$X\stackrel{\text{def}}{=}\sum _{y\in \mathbb{F}_{p}}y^{p-2}\Bigl(\!\begin{smallmatrix}1 & & y\\ & 1 & \\ & & 1\end{smallmatrix}\!\Bigr)$
. We note that
$X$
kills
$S(\unicode[STIX]{x1D70F}^{I,(a_{1},a_{2},a_{0})})$
as the latter is easily checked to be fixed under
$\Bigl(\!\begin{smallmatrix}1 & & \mathbb{F}_{p}\\ & 1 & \\ & & 1\end{smallmatrix}\!\Bigr)$
; hence, to prove part (i), it is enough to show that
$X$
acts injectively on
$\text{soc}(W)^{\overline{T}(\mathbb{F}_{p}),(a_{2}-1,a_{1},a_{0}+1)}$
.
As in Lemma 3.1.6 we see that
$W^{\overline{T}(\mathbb{F}_{p}),(a_{2}-1,a_{1},a_{0}+1)}=W_{\unicode[STIX]{x1D707}}$
, where
$\unicode[STIX]{x1D707}\stackrel{\text{def}}{=}(a_{2}-1,a_{1},a_{0}+1)$
. Let
$\unicode[STIX]{x1D6FC}\stackrel{\text{def}}{=}(1,0,-1)\in \unicode[STIX]{x1D6F7}$
. By [Reference JantzenJan03, II.1.19, (5) and (6)], for
$v_{\unicode[STIX]{x1D707}}\in W_{\unicode[STIX]{x1D707}}$
we have
$$\begin{eqnarray}u_{\unicode[STIX]{x1D6FC}}(t)v_{\unicode[STIX]{x1D707}}=\underset{i\geqslant 0}{\sum }t^{i}(X_{\unicode[STIX]{x1D6FC},i}v_{\unicode[STIX]{x1D707}}),\end{eqnarray}$$
where
$X_{\unicode[STIX]{x1D6FC},i}\in \text{Dist}(\overline{U}_{\unicode[STIX]{x1D6FC}})$
and
$X_{\unicode[STIX]{x1D6FC},i}v_{\unicode[STIX]{x1D707}}\in W_{\unicode[STIX]{x1D707}+i\unicode[STIX]{x1D6FC}}$
(see [Reference JantzenJan03, II.1.12], for the definition of the operators
$X_{\unicode[STIX]{x1D6FC},i}$
). As
$\unicode[STIX]{x1D707}+i\unicode[STIX]{x1D6FC}\not \leqslant \unicode[STIX]{x1D706}$
if
$i\geqslant p$
we deduce that
$X=-X_{\unicode[STIX]{x1D6FC},1}$
on
$W_{\unicode[STIX]{x1D707}}$
.
To prove the proposition we will show that
$X_{\unicode[STIX]{x1D6FC},1}:W_{\unicode[STIX]{x1D707}}{\twoheadrightarrow}W_{\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}}$
is surjective, with a one-dimensional kernel not contained in
$\text{soc}(W)$
.
Let
$\overline{M}$
denote the Levi subgroup
$\Bigl(\!\begin{smallmatrix}\ast & & \ast \\ & \ast & \\ \ast & & \ast \end{smallmatrix}\!\Bigr)\subseteq \overline{G}$
. Any irreducible constituent of the restriction
$W|_{\overline{M}}$
has highest weight
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
with
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in \{a_{2}-p+1,\ldots ,a_{0}+p-1\}$
. As
$a_{0}+p>a_{0}+p-1$
, the Linkage Principle [Reference JantzenJan03, II.6.17] and [Reference JantzenJan03, II.2.12(1)] yield
$$\begin{eqnarray}W|_{\overline{M}}\cong F^{\oplus m}\oplus W^{\prime },\end{eqnarray}$$
where
$F$
is the irreducible
$\overline{M}$
-representation with highest weight
$\unicode[STIX]{x1D707}$
and no irreducible constituent of
$W^{\prime }$
has highest weight
$\unicode[STIX]{x1D707}$
.
Claim. The operator
$X_{\unicode[STIX]{x1D6FC},1}$
induces an isomorphism
$W_{\unicode[STIX]{x1D707}}^{\prime }\stackrel{{\sim}}{\longrightarrow }W_{\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}}^{\prime }$
.
Proof of the Claim.
By dévissage we may assume that
$W^{\prime }$
is irreducible. Let
$\unicode[STIX]{x1D708}\in X^{\ast }(\overline{T})$
be its highest weight, so in particular
$\unicode[STIX]{x1D708}\neq \unicode[STIX]{x1D707}$
. Then
$W^{\prime }{\hookrightarrow}H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})$
, where
$H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})$
denotes the dual Weyl module for
$\overline{M}$
of highest weight
$\unicode[STIX]{x1D708}$
. As
$\text{Dist}(\overline{M})$
preserves
$W^{\prime }{\hookrightarrow}H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})$
it is enough to show that
$X_{\unicode[STIX]{x1D6FC},1}:H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})_{\unicode[STIX]{x1D707}}\rightarrow H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})_{\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}}$
and
$X_{-\unicode[STIX]{x1D6FC},1}:H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})_{\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}}\rightarrow H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})_{\unicode[STIX]{x1D707}}$
are both injective.
Since
$M^{\text{der}}\cong \text{SL}_{2}$
and
$(\!\begin{smallmatrix}1 & t\\ & 1\end{smallmatrix}\!)X^{i}Y^{j}=X^{i}Y^{j}+tjX^{i+1}Y^{j-1}+\cdots \,$
, we see that
$X_{\unicode[STIX]{x1D6FC},1}:H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})_{\unicode[STIX]{x1D707}}\rightarrow H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})_{\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}}$
is injective provided that
${\textstyle \frac{1}{2}}(\langle \unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}^{\vee }\rangle -\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}^{\vee }\rangle )\not \equiv 0$
mod
$p$
. (This is because one has
$H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})|_{\overline{M}^{\text{der}}}\cong \operatorname{Sym}^{\langle \unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}^{\vee }\rangle }(\text{Std})$
and
$0\neq X^{(1/2)(\langle \unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}^{\vee }\rangle +\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}^{\vee }\rangle )}Y^{(1/2)(\langle \unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}^{\vee }\rangle -\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}^{\vee }\rangle )}\in H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})_{\unicode[STIX]{x1D707}}$
.) Similarly,
$X_{-\unicode[STIX]{x1D6FC},1}:H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})_{\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}}\rightarrow H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})_{\unicode[STIX]{x1D707}}$
is injective if
${\textstyle \frac{1}{2}}(\langle \unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}^{\vee }\rangle +\langle \unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}^{\vee }\rangle )\not \equiv 0$
mod
$p$
. As
$\unicode[STIX]{x1D6FC}^{\vee }$
is dominant and
$\unicode[STIX]{x1D708}\leqslant \unicode[STIX]{x1D706}$
(both relative to
$\overline{M}$
) we have
$$\begin{eqnarray}\langle \unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}^{\vee }\rangle \leqslant \langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC}^{\vee }\rangle =2(p-1)-(a_{2}-a_{0}).\end{eqnarray}$$
Similarly, if
$H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})_{\unicode[STIX]{x1D707}}\neq 0$
or
$H_{\overline{M}}^{0}(\unicode[STIX]{x1D708})_{\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}}\neq 0$
then
$$\begin{eqnarray}\langle \unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}^{\vee }\rangle >\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}^{\vee }\rangle =a_{2}-a_{0}-2\end{eqnarray}$$
(here we used that
$\unicode[STIX]{x1D708}\neq \unicode[STIX]{x1D707}$
). Now we can deduce the above two congruences, proving the claim.◻
From the claim we deduce that the morphism
$X_{\unicode[STIX]{x1D6FC},1}:W_{\unicode[STIX]{x1D707}}\rightarrow W_{\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}}$
is surjective, with kernel of dimension
$m$
. The Kostant multiplicity formula shows that
$$\begin{eqnarray}\displaystyle m & = & \displaystyle \dim _{\mathbb{F}}W_{\unicode[STIX]{x1D707}}-\dim _{\mathbb{F}}W_{\unicode[STIX]{x1D707}+\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle (p+1-(a_{2}-a_{0}))-(p-(a_{2}-a_{0}))=1.\nonumber\end{eqnarray}$$
Moreover,
$F(\unicode[STIX]{x1D707})\cong \text{cosoc}(W)$
contains the irreducible representation of
$\overline{M}$
of highest weight
$\unicode[STIX]{x1D707}$
. Hence
$\text{soc}(W)\subseteq W^{\prime }$
and
$X$
is indeed injective on
$\text{soc}(W)_{\unicode[STIX]{x1D707}}$
. This proves part (i) of the proposition.
For statement (ii) it is now enough to apply the automorphism
$g\mapsto \Bigl(\!\begin{smallmatrix} & & 1\\ & -1 & \\ 1 & & \end{smallmatrix}\!\Bigr)\cdot ^{t}g^{-1}\cdot \Bigl(\!\begin{smallmatrix} & & 1\\ & -1 & \\ 1 & & \end{smallmatrix}\!\Bigr)$
to part (i) and relabel
$(-a_{0},-a_{1},-a_{2})$
as
$(a_{2},a_{1},a_{0})$
.◻
Remark 3.1.9. In a similar fashion, there exists a unique non-split extension of irreducible
$\overline{G}(\mathbb{F}_{p})$
-representations
$$\begin{eqnarray}0\rightarrow F(a_{2}-1,a_{1},a_{0}+1)\rightarrow V\rightarrow F(a_{0}+p-1,a_{1},a_{2}-p+1)\rightarrow 0,\end{eqnarray}$$
namely
$V$
is the Weyl module of highest weight
$(a_{0}+p-1,a_{1},a_{2}-p+1)$
. The following operator induces an isomorphism
$V^{I,(a_{0},a_{1},a_{2})}\stackrel{{\sim}}{\longrightarrow }V^{I,(a_{2}-1,a_{1},a_{0}+1)}$
of one-dimensional vector spaces:
$$\begin{eqnarray}\underset{x,y,z\in \mathbb{F}_{p}}{\sum }\mathop{\sum }_{i=0}^{p-(a_{2}-a_{0})}\frac{(-1)^{i}}{i+1}\binom{p-(a_{1}-a_{0})}{p-(a_{2}-a_{0})-i}(xz)^{p-1-i}y^{i+1}\left(\begin{array}{@{}ccc@{}}1 & x & y\\ & 1 & z\\ & & 1\end{array}\right){\dot{w}}_{0}.\end{eqnarray}$$
We skip the somewhat lengthy proof, since we will not need it.
We conclude this section with a simple but important lemma concerning the action of
$U_{p}$
-operators on
$G(\mathbb{Q}_{p})$
-representations over
$\mathbb{F}$
. We define
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\displaystyle U_{1}\stackrel{\text{def}}{=}\underset{x,y\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}{\sum }\left(\begin{array}{@{}ccc@{}}p^{-1} & & \\ & 1 & \\ & & 1\end{array}\right)\left(\begin{array}{@{}ccc@{}}1 & & \\ x & 1 & \\ y & & 1\end{array}\right),\\ \displaystyle U_{2}\stackrel{\text{def}}{=}\underset{x,y\in \mathbb{Z}_{p}/p\mathbb{Z}_{p}}{\sum }\left(\begin{array}{@{}ccc@{}}p^{-1} & & \\ & p^{-1} & \\ & & 1\end{array}\right)\left(\begin{array}{@{}ccc@{}}1 & & \\ & 1 & \\ x & y & 1\end{array}\right),\end{array} & & \displaystyle\end{eqnarray}$$
so that for any
$G(\mathbb{Q}_{p})$
-representation
$\unicode[STIX]{x1D70E}$
over
${\mathcal{O}}_{E}$
and any
$(a_{2},a_{1},a_{0})\in \mathbb{Z}^{3}$
, both
$U_{1}$
and
$U_{2}$
preserve
$\unicode[STIX]{x1D70E}^{I,(a_{2},a_{1},a_{0})}$
.
Lemma 3.1.11. Let
$(a_{2},a_{1},a_{0})\in \mathbb{Z}^{3}$
be a triple with
$a_{2}-a_{1}>0$
,
$a_{1}-a_{0}>0$
and
$a_{2}-a_{0}<p-1$
. Let
$\overline{\unicode[STIX]{x1D70F}}\stackrel{\text{def}}{=}\operatorname{Ind}_{I}^{K}(\unicode[STIX]{x1D714}^{a_{1}}\,\otimes \,\unicode[STIX]{x1D714}^{a_{2}}\,\otimes \,\unicode[STIX]{x1D714}^{a_{0}})$
, and suppose that
$\unicode[STIX]{x1D70E}$
is a representation of
$G(\mathbb{Q}_{p})$
over
$\mathbb{F}$
.
Then
$\operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D70E})[U_{i}]=\operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70F}}/M_{i},\unicode[STIX]{x1D70E})$
for
$i\in \{1,2\}$
, where
$M_{1}$
(respectively
$M_{2}$
) is the minimal subrepresentation of
$\overline{\unicode[STIX]{x1D70F}}$
containing
$F(a_{2},a_{0},a_{1}-p+1)$
(respectively
$F(a_{0}+p-1,a_{1},a_{2}-p+1)$
) as subquotient. Concretely, both
$M_{i}$
are indecomposable of length 2 with socle
$F(a_{0}+p-1,a_{2},a_{1})$
.
Proof. Note that
$\overline{\unicode[STIX]{x1D70F}}^{I,(a_{1},a_{2},a_{0})}$
is spanned by a function
$f$
with
$\operatorname{supp}(f)=I$
and
$f(1)=1$
. Consider the case
$i=2$
, and suppose
$\unicode[STIX]{x1D711}\in \operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D70E})$
. Then
$U_{2}\unicode[STIX]{x1D711}=0$
if and only if
$U_{2}(\unicode[STIX]{x1D711}(f))=0$
. We note that
$\unicode[STIX]{x1D6F1}^{2}U_{2}=U_{2}^{\prime }$
, where
$U_{2}^{\prime }\stackrel{\text{def}}{=}\sum _{x,y\in \mathbb{F}_{p}}\Bigl(\!\begin{smallmatrix}1 & x & y\\ & 1 & \\ & & 1\end{smallmatrix}\!\Bigr)\Bigl(\!\begin{smallmatrix} & & 1\\ 1 & & \\ & 1 & \end{smallmatrix}\!\Bigr)$
, sending
$\unicode[STIX]{x1D70C}^{I,(a_{1},a_{2},a_{0})}$
to
$\unicode[STIX]{x1D70C}^{I,(a_{0},a_{1},a_{2})}$
for any
$K$
-representation
$\unicode[STIX]{x1D70C}$
over
$\mathbb{F}$
. We have that
$U_{2}^{\prime }f\neq 0$
, as
$(U_{2}^{\prime }f)\Bigl(\!\begin{smallmatrix} & 1 & \\ & & 1\\ 1 & & \end{smallmatrix}\!\Bigr)=1$
. Hence
$\langle K\cdot U_{2}^{\prime }f\rangle _{\mathbb{F}}$
is a quotient of
$\overline{\unicode[STIX]{x1D70F}}^{\prime }\stackrel{\text{def}}{=}\operatorname{Ind}_{I}^{K}(\unicode[STIX]{x1D714}^{a_{0}}\,\otimes \,\unicode[STIX]{x1D714}^{a_{1}}\,\otimes \,\unicode[STIX]{x1D714}^{a_{2}})$
that injects into
$\overline{\unicode[STIX]{x1D70F}}$
, so as the cosocle of
$\overline{\unicode[STIX]{x1D70F}}^{\prime }$
is
$F(a_{0}+p-1,a_{1},a_{2}-p+1)$
and
$\overline{\unicode[STIX]{x1D70F}}$
is multiplicity-free, we deduce that
$\langle K\cdot U_{2}^{\prime }f\rangle _{\mathbb{F}}=M_{2}$
. By [Reference LeLe15, Proposition 2.2.2],
$M_{2}$
is uniserial of shape
$F(a_{0}+p-1,a_{2},a_{1})\text{}\text{—}F(a_{0}+p-1,a_{1},a_{2}-p+1)$
. We have that
$$\begin{eqnarray}U_{2}\unicode[STIX]{x1D711}=0\Longleftrightarrow U_{2}^{\prime }(\unicode[STIX]{x1D711}(f))=0\Longleftrightarrow \unicode[STIX]{x1D711}(U_{2}^{\prime }f)=0\Longleftrightarrow \langle K\cdot U_{2}^{\prime }f\rangle _{\mathbb{ F}}\subseteq \ker \unicode[STIX]{x1D711}.\end{eqnarray}$$
The proof for the case
$i=1$
is analogous.◻
Corollary 3.1.12. Let
$(a_{2},a_{1},a_{0})\in \mathbb{Z}^{3}$
be a triple with
$a_{2}-a_{1}>0$
,
$a_{1}-a_{0}>0$
and
$a_{2}-a_{0}<p-1$
. Suppose
$\unicode[STIX]{x1D70E}$
is a representation of
$G(\mathbb{Q}_{p})$
over
$\mathbb{F}$
.
-
(i) If
$v\in \unicode[STIX]{x1D70E}^{I,(a_{1},a_{2},a_{0})}$
, then
$U_{2}v=0$
if and only if
$\langle Kv\rangle _{\mathbb{F}}$
does not contain
$F(a_{0}+p-1,a_{1},a_{2}-p+1)$
as subquotient. -
(ii) If
$v\in \unicode[STIX]{x1D70E}^{I,(a_{2},a_{0},a_{1})}$
, then
$U_{1}v=0$
if and only if
$\langle Kv\rangle _{\mathbb{F}}$
does not contain
$F(a_{0}+p-1,a_{1},a_{2}-p+1)$
as subquotient.
Proof. (i) In the notation of the proof of Lemma 3.1.11, by Frobenius reciprocity there is a unique
$\unicode[STIX]{x1D711}\in \operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D70E})$
such that
$v=\unicode[STIX]{x1D711}(f)$
. The claim follows, as
$\langle Kv\rangle _{\mathbb{F}}=\operatorname{im}\unicode[STIX]{x1D711}$
(since
$\langle Kf\rangle _{\mathbb{F}}=\overline{\unicode[STIX]{x1D70F}}$
). The proof of part (ii) is analogous.◻
3.2 Jacobi sums and characteristic zero principal series
In this section we consider certain group algebra operators with
${\mathcal{O}}_{E}$
-coefficients and study their effect on principal series representations.
We fix once and for all a triple
$(a_{2},a_{1},a_{0})\in \mathbb{Z}^{3}$
verifying (2.1.6). We define the following elements in the group algebra
${\mathcal{O}}_{E}[\overline{G}(\mathbb{F}_{p})]$
, lifting the mod
$p$
operators introduced in § 3.1:
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\displaystyle \widehat{S}\stackrel{\text{def}}{=}\underset{x,y,z\in \mathbb{F}_{p}}{\sum }\widetilde{x}^{p-(a_{2}-a_{0})}\widetilde{z}^{p-(a_{1}-a_{0})}\left(\begin{array}{@{}ccc@{}}1 & x & y\\ & 1 & z\\ & & 1\end{array}\right){\dot{w}}_{0},\\ \displaystyle \widehat{S}^{\prime }\stackrel{\text{def}}{=}\underset{x,y,z\in \mathbb{F}_{p}}{\sum }\widetilde{x}^{p-(a_{2}-a_{1})}\widetilde{z}^{p-(a_{2}-a_{0})}\left(\begin{array}{@{}ccc@{}}1 & x & y\\ & 1 & z\\ & & 1\end{array}\right){\dot{w}}_{0}.\end{array} & & \displaystyle\end{eqnarray}$$
The following relation between the actions of
$\widehat{S},\widehat{S}^{\prime }$
on certain principal series representations will be crucial later. To lighten notation, we set
$\unicode[STIX]{x1D6F1}\stackrel{\text{def}}{=}\Bigl(\!\begin{smallmatrix} & 1 & \\ & & 1\\ p & & \end{smallmatrix}\!\Bigr)\in N_{G(\mathbb{Q}_{p})}(I)$
.
Proposition 3.2.2. Let
$(a_{2},a_{1},a_{0})\in \mathbb{Z}^{3}$
be a triple verifying (2.1.6). Let
$\unicode[STIX]{x1D70B}_{p}\stackrel{\text{def}}{=}\operatorname{Ind}_{B(\mathbb{Q}_{p})}^{G(\mathbb{Q}_{p})}(\unicode[STIX]{x1D712}_{1}\,\otimes \,\unicode[STIX]{x1D712}_{2}\,\otimes \,\unicode[STIX]{x1D712}_{0})$
be a principal series representation, where the smooth characters
$\unicode[STIX]{x1D712}_{i}:\mathbb{Q}_{p}^{\times }\rightarrow E^{\times }$
verify
$\unicode[STIX]{x1D712}_{i}|_{\mathbb{Z}_{p}^{\times }}=\widetilde{\unicode[STIX]{x1D714}}^{a_{i}}$
for
$i\in \{0,1,2\}$
.
On the one-dimensional isotypical component
$\unicode[STIX]{x1D70B}_{p}^{I,(a_{1},a_{2},a_{0})}$
we have
$$\begin{eqnarray}\widehat{S}^{\prime }\circ \unicode[STIX]{x1D6F1}=p\unicode[STIX]{x1D712}_{1}(p)\unicode[STIX]{x1D705}\,\widehat{S},\end{eqnarray}$$
where
$\unicode[STIX]{x1D705}\in \mathbb{Z}_{p}^{\times }$
verifies
$\unicode[STIX]{x1D705}\equiv (-1)^{a_{1}-a_{0}}\cdot (a_{2}-a_{1})/(a_{1}-a_{0})$
mod
$p$
and is independent of the scalars
$\unicode[STIX]{x1D712}_{i}(p)$
.
Remark 3.2.4. Note that equation (3.2.3) makes sense, as both
$\widehat{S}$
and
$\widehat{S}^{\prime }$
act on
$\unicode[STIX]{x1D70B}^{K(1)}$
for any smooth
$K$
-representation
$\unicode[STIX]{x1D70B}$
, where
$K(1)\stackrel{\text{def}}{=}\ker (K{\twoheadrightarrow}\overline{G}(\mathbb{F}_{p}))$
.
The proof of Proposition 3.2.2 relies on certain direct manipulations on Jacobi sums and will occupy the rest of this section. Let us pick a non-zero element
$\widehat{v}$
in the one-dimensional isotypical component
$\unicode[STIX]{x1D70B}_{p}^{I,(a_{1},a_{2},a_{0})}$
. In particular,
$\widehat{v}$
is
$K(1)$
-fixed. We note that
$\text{supp}(\widehat{v})=B(\mathbb{Q}_{p})I$
and
$\widehat{v}(1)\neq 0$
.
Lemma 3.2.5. We have
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}\cdot \widehat{v}=\unicode[STIX]{x1D712}_{1}(p)\,\underset{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \mathbb{F}_{p}}{\sum }\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D706} & 1 & \\ \unicode[STIX]{x1D707} & & 1\\ 1 & & \end{array}\right)\cdot \widehat{v}.\end{eqnarray}$$
Proof. Noting that
$\unicode[STIX]{x1D6F1}U_{1}=\sum _{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \mathbb{F}_{p}}\Bigl(\!\begin{smallmatrix}\unicode[STIX]{x1D706} & 1 & \\ \unicode[STIX]{x1D707} & & 1\\ 1 & & \end{smallmatrix}\!\Bigr)$
, it suffices to show that
$U_{1}\cdot \widehat{v}=\unicode[STIX]{x1D712}_{1}(p)^{-1}\cdot \widehat{v}$
. As
$U_{1}\cdot \widehat{v}$
lies in the one-dimensional space
$\unicode[STIX]{x1D70B}_{p}^{I,(a_{1},a_{2},a_{0})}$
and
$\widehat{v}(1)\neq 0$
, it is enough to observe that
$$\begin{eqnarray}(U_{1}\widehat{v})(1)=\underset{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \mathbb{ Z}_{p}/p\mathbb{Z}_{p}}{\sum }\widehat{v}\left(\left(\begin{array}{@{}ccc@{}}p^{-1} & & \\ & 1 & \\ & & 1\end{array}\right)\left(\begin{array}{@{}ccc@{}}1 & & \\ \unicode[STIX]{x1D706} & 1 & \\ \unicode[STIX]{x1D707} & & 1\end{array}\right)\right)=\unicode[STIX]{x1D712}_{1}(p)^{-1}\,\cdot \,\widehat{v}(1).\square\end{eqnarray}$$
We now compute the action of the operator
$\widehat{S}^{\prime }$
on the element
$\unicode[STIX]{x1D6F1}\widehat{v}$
.
Lemma 3.2.6. We have
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \widehat{S}^{\prime }(\unicode[STIX]{x1D6F1}\widehat{v})\nonumber\\ \displaystyle & & \displaystyle ~~\displaystyle =(-1)^{a_{2}-a_{0}}\unicode[STIX]{x1D712}_{1}(p)\!\underset{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},x,y,z\in \mathbb{F}_{p}}{\sum }\!\widetilde{\unicode[STIX]{x1D706}}^{a_{2}-a_{1}}\widetilde{\unicode[STIX]{x1D707}}^{p-1-(a_{1}-a_{0})}\widetilde{(x-\unicode[STIX]{x1D707})}^{p-(a_{2}-a_{1})}\widetilde{(z-\unicode[STIX]{x1D706})}^{p-(a_{2}-a_{0})}\!\left(\begin{array}{@{}ccc@{}}1 & x & y\\ & 1 & z\\ & & 1\end{array}\right){\dot{w}}_{0}\widehat{v}.\nonumber\end{eqnarray}$$
Proof. In order to ease notation, we write
$a\stackrel{\text{def}}{=}a_{2}-a_{0}$
,
$b\stackrel{\text{def}}{=}a_{1}-a_{0}$
. An immediate computation using Lemma 3.2.5 gives
$$\begin{eqnarray}\widehat{S}^{\prime }(\unicode[STIX]{x1D6F1}\widehat{v})=\unicode[STIX]{x1D712}_{1}(p)\underset{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},x,y,z\in \mathbb{F}_{p}}{\sum }\widetilde{x}^{p-(a-b)}\widetilde{z}^{p-a}\underbrace{\left(\begin{array}{@{}ccc@{}}1+y\unicode[STIX]{x1D706}+x\unicode[STIX]{x1D707} & y & x\\ z\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707} & z & 1\\ \unicode[STIX]{x1D706} & 1 & \end{array}\right)}_{\stackrel{\text{def}}{=}A_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}}\widehat{v}.\end{eqnarray}$$
We now break up the sum (3.2.7) according to the values of
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \mathbb{F}_{p}$
.
Case 1. We have
$\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}=0$
. Suppose first that
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D707}=0$
. Then one has
$$\begin{eqnarray}A_{0,0}=\left(\begin{array}{@{}ccc@{}}1 & & \\ & 1 & z\\ & & 1\end{array}\right){\dot{s}}_{2}\left(\begin{array}{@{}ccc@{}}1 & y & x\\ & 1 & \\ & & 1\end{array}\right)\end{eqnarray}$$
and therefore, using that
$\widehat{v}$
is
$I_{1}$
-fixed, we obtain
$$\begin{eqnarray}\displaystyle \underset{x,y,z\in \mathbb{F}_{p}}{\sum }\widetilde{x}^{p-(a-b)}\widetilde{z}^{p-a}A_{0,0}\widehat{v} & = & \displaystyle \left(\underset{z\in \mathbb{F}_{p}}{\sum }\widetilde{z}^{p-a}\left(\begin{array}{@{}ccc@{}}1 & & \\ & 1 & z\\ & & 1\end{array}\right){\dot{s}}_{2}\widehat{v}\right)\biggl(\underset{x,y\in \mathbb{F}_{p}}{\sum }\widetilde{x}^{p-(a-b)}\biggr)\nonumber\\ \displaystyle & = & \displaystyle 0.\nonumber\end{eqnarray}$$
In an analogous fashion, if
$\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}\neq 0$
we have
$$\begin{eqnarray}\displaystyle & \displaystyle A_{\unicode[STIX]{x1D706},0}=\left(\begin{array}{@{}ccc@{}}1 & & y+\unicode[STIX]{x1D706}^{-1}\\ & 1 & z\\ & & 1\end{array}\right){\dot{s}}_{2}{\dot{s}}_{1}\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D706} & 1 & \\ & -\unicode[STIX]{x1D706}^{-1} & x\\ & & 1\end{array}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle A_{0,\unicode[STIX]{x1D707}}=\left(\begin{array}{@{}ccc@{}}1 & \unicode[STIX]{x1D707}^{-1}+x & y-z(\unicode[STIX]{x1D707}^{-1}+x)\\ & 1 & \\ & & 1\end{array}\right){\dot{s}}_{1}{\dot{s}}_{2}\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D707} & z & 1\\ & 1 & \\ & & -\unicode[STIX]{x1D707}^{-1}\end{array}\right), & \displaystyle \nonumber\end{eqnarray}$$
so, using that
$\widehat{v}$
is an eigenvector for the
$I$
-action, we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle \underset{x,y,z\in \mathbb{F}_{p}}{\sum }\,\underset{\unicode[STIX]{x1D706}\in \mathop{\mathbb{F}}_{p}^{\times }}{\sum }\widetilde{x}^{p-(a-b)}\widetilde{z}^{p-a}A_{\unicode[STIX]{x1D706},0}\widehat{v}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \underset{x,y,z\in \mathbb{F}_{p}}{\sum }\,\underset{\unicode[STIX]{x1D707}\in \mathop{\mathbb{F}}_{p}^{\times }}{\sum }\widetilde{x}^{p-(a-b)}\widetilde{z}^{p-a}A_{0,\unicode[STIX]{x1D707}}\widehat{v}=0 & \displaystyle \nonumber\end{eqnarray}$$
(in the first equation, the sum over
$x$
is zero; in the second equation the sum over
$z$
is zero, provided one first replaces
$y$
by
$y^{\prime }\stackrel{\text{def}}{=}y-z(\unicode[STIX]{x1D707}^{-1}+x)$
).
Case 2. We have
$\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}\neq 0$
. As before, a direct computation gives
$$\begin{eqnarray}A_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}=\left(\begin{array}{@{}ccc@{}}1 & \unicode[STIX]{x1D707}^{-1}+x & y+x\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{-1}+\unicode[STIX]{x1D706}^{-1}\\ & 1 & z+\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{-1}\\ & & 1\end{array}\right){\dot{w}}_{0}\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D706} & 1 & \\ & -\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{-1} & 1\\ & & -\unicode[STIX]{x1D707}^{-1}\end{array}\right)\end{eqnarray}$$
and, recalling that
$\widehat{v}$
lies in
$\unicode[STIX]{x1D70B}_{p}^{I,(a_{1},a_{2},a_{0})}$
, we obtain
$$\begin{eqnarray}\displaystyle & & \displaystyle \underset{x,y,z\in \mathbb{F}_{p}}{\sum }\,\underset{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \mathop{\mathbb{F}}_{p}^{\times }}{\sum }\widetilde{x}^{p-(a-b)}\widetilde{z}^{p-a}A_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}\widehat{v}\nonumber\\ \displaystyle & & \displaystyle \qquad =\underset{x,y,z\in \mathbb{F}_{p}}{\sum }\,\underset{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \mathop{\mathbb{F}}_{p}^{\times }}{\sum }(-1)^{a}\widetilde{\unicode[STIX]{x1D706}}^{-(a-b)}\widetilde{\unicode[STIX]{x1D707}}^{a}\widetilde{x}^{p-(a-b)}\widetilde{z}^{p-a}\left(\begin{array}{@{}ccc@{}}1 & \unicode[STIX]{x1D707}^{-1}+x & y+x\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{-1}+\unicode[STIX]{x1D706}^{-1}\\ & 1 & z+\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{-1}\\ & & 1\end{array}\right){\dot{w}}_{0}\widehat{v}.\nonumber\end{eqnarray}$$
We obtain the desired result by putting the two cases together and using the change of variables
$(x^{\prime },y^{\prime },z^{\prime },\unicode[STIX]{x1D706}^{\prime },\unicode[STIX]{x1D707}^{\prime })\stackrel{\text{def}}{=}(x+{\unicode[STIX]{x1D707}^{-1},y+x\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{-1}+\unicode[STIX]{x1D706}}^{-1},z+\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{-1},\unicode[STIX]{x1D707}\unicode[STIX]{x1D706}^{-1},\unicode[STIX]{x1D707}^{-1})$
.◻
Proof of Proposition 3.2.2.
Note that in the expression of Lemma 3.2.6 we may assume that
$x\neq 0$
(respectively
$z\neq 0$
) since otherwise the sum over
$\unicode[STIX]{x1D707}$
(respectively
$\unicode[STIX]{x1D706}$
) vanishes. Using the change of variables
$(\unicode[STIX]{x1D706}^{\prime },\unicode[STIX]{x1D707}^{\prime })\stackrel{\text{def}}{=}(\unicode[STIX]{x1D706}z^{-1},\unicode[STIX]{x1D707}x^{-1})$
we obtain
$$\begin{eqnarray}\widehat{S}^{\prime }(\unicode[STIX]{x1D6F1}\widehat{v})=(-1)^{a}\unicode[STIX]{x1D712}_{1}(p)\unicode[STIX]{x1D705}_{1}\unicode[STIX]{x1D705}_{2}\widehat{S}(\widehat{v}),\end{eqnarray}$$
where
$\unicode[STIX]{x1D705}_{1},\unicode[STIX]{x1D705}_{2}\in \mathbb{Z}_{p}$
are the following Jacobi sums:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}_{1}\stackrel{\text{def}}{=}\underset{\unicode[STIX]{x1D707}\in \mathbb{F}_{p}}{\sum }\widetilde{\unicode[STIX]{x1D707}}^{p-1-b}\widetilde{(1-\unicode[STIX]{x1D707})}^{p-(a-b)},\quad \unicode[STIX]{x1D705}_{2}\stackrel{\text{def}}{=}\underset{\unicode[STIX]{x1D706}\in \mathbb{F}_{p}}{\sum }\widetilde{\unicode[STIX]{x1D706}}^{a-b}\widetilde{(1-\unicode[STIX]{x1D706})}^{p-a}. & & \displaystyle \nonumber\end{eqnarray}$$
By Stickelberger’s theorem (see e.g. [Reference Breuil and DiamondBD14, Théorème 2.5.1]) one has
$\text{ord}_{p}(\unicode[STIX]{x1D705}_{1})=0,\text{ord}_{p}(\unicode[STIX]{x1D705}_{2})=1$
and
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}_{1}\equiv \frac{(p-1-b)!(p-(a-b))!}{(p-a)!},\quad \frac{\unicode[STIX]{x1D705}_{2}}{p}\equiv (-1)\frac{(a-b)!(p-a)!}{(p-b)!}~\text{mod}~p. & & \displaystyle \nonumber\end{eqnarray}$$
Therefore
$$\begin{eqnarray}\widehat{S}^{\prime }(\unicode[STIX]{x1D6F1}\widehat{v})=(-1)^{a}\unicode[STIX]{x1D712}_{1}(p)\unicode[STIX]{x1D705}\widehat{S}(\widehat{v}),\end{eqnarray}$$
where
$\text{ord}_{p}(\unicode[STIX]{x1D705})=1$
and
$\unicode[STIX]{x1D705}/p\equiv -(p-(a-b))!(a-b)!/(p-b)$
mod
$p$
.
As
$(p-(a-b))!(a-b)!\equiv (-1)^{p-(a-b)}(p-1)!(a-b)$
mod
$p$
we finally obtain
$$\begin{eqnarray}(-1)^{a}\frac{\unicode[STIX]{x1D705}}{p}\equiv (-1)^{b}\frac{a-b}{b},\end{eqnarray}$$
and the proof of Proposition 3.2.2 is now complete. ◻
Lemma 3.2.8. Suppose that
$\unicode[STIX]{x1D70B}_{p}\stackrel{\text{def}}{=}\operatorname{Ind}_{B(\mathbb{Q}_{p})}^{G(\mathbb{Q}_{p})}\big(\unicode[STIX]{x1D712}_{1}\,\otimes \,\unicode[STIX]{x1D712}_{2}\,\otimes \,\unicode[STIX]{x1D712}_{0}\big)$
is a principal series representation, where the smooth characters
$\unicode[STIX]{x1D712}_{i}:\mathbb{Q}_{p}^{\times }\rightarrow E^{\times }$
verify
$\unicode[STIX]{x1D712}_{i}|_{\mathbb{Z}_{p}^{\times }}=\widetilde{\unicode[STIX]{x1D714}}^{a_{i}}$
for
$i\in \{0,1,2\}$
and where
$a_{0},a_{1},a_{2}$
are distinct modulo
$p-1$
. On the one-dimensional isotypical component
$\unicode[STIX]{x1D70B}_{p}^{I,(a_{1},a_{2},a_{0})}$
we have
$U_{1}=\unicode[STIX]{x1D712}_{1}(p)^{-1}$
and
$U_{2}=\unicode[STIX]{x1D712}_{1}(p)^{-1}\unicode[STIX]{x1D712}_{2}(p)^{-1}$
.
Proof. For
$U_{1}$
this was observed in the proof of Lemma 3.2.5. The
$U_{2}$
-eigenvalue is computed similarly.◻
4 Local-global compatibility
In this section we establish most of our main results, namely Theorems A, D, and E of the introduction.
4.1 The space of automorphic forms on certain unitary groups
Let
$F/\mathbb{Q}$
be a CM field and
$F^{+}$
its maximal totally real subfield. Assume that
$F^{+}\neq \mathbb{Q}$
, and that
$p$
splits completely in
$F$
. We write
$c$
for the generator of
$\operatorname{Gal}(F/F^{+})$
. For
$w\nmid \infty$
(respectively
$v\nmid \infty$
) a place of
$F$
(respectively
$F^{+}$
) we denote by
$k_{w}$
(respectively
$k_{v}$
) the residue field of
$F_{w}$
(respectively
$F_{v}^{+}$
).
We let
$G_{/F^{+}}$
be a reductive group, which is an outer form of
$\operatorname{GL}_{3}$
which splits over
$F$
. We assume that
$G(F_{v}^{+})\cong U_{3}(\mathbb{R})$
for all
$v|\infty$
. By the argument of [Reference Clozel, Harris and TaylorCHT08, §3.3],
$G$
admits a model
${\mathcal{G}}$
over
${\mathcal{O}}_{F^{+}}$
such that
${\mathcal{G}}\times {\mathcal{O}}_{F_{v}^{+}}$
is reductive for all places
$v$
of
$F^{+}$
that split in
$F$
. For any such place
$v$
of
$F^{+}$
and
$w|v$
of
$F$
we get an isomorphism
$\unicode[STIX]{x1D704}_{w}:\,G(F_{v}^{+})\stackrel{{\sim}}{\longrightarrow }\operatorname{GL}_{3}(F_{w})$
which restricts moreover to an isomorphism
$\unicode[STIX]{x1D704}_{w}:\,{\mathcal{G}}({\mathcal{O}}_{F_{v}^{+}})\stackrel{{\sim}}{\longrightarrow }\operatorname{GL}_{3}({\mathcal{O}}_{F_{w}})$
.
Let
$F_{p}^{+}\stackrel{\text{def}}{=}F^{+}\otimes _{\mathbb{Q}}\mathbb{Q}_{p}$
and
${\mathcal{O}}_{F^{+},p}\stackrel{\text{def}}{=}{\mathcal{O}}_{F^{+}}\otimes _{\mathbb{Z}}\mathbb{Z}_{p}$
. If
$W$
is an
${\mathcal{O}}_{E}$
-module endowed with an action of
${\mathcal{G}}({\mathcal{O}}_{F^{+},p})$
and
$U\leqslant G(\mathbb{A}_{F^{+}}^{\infty ,p})\times {\mathcal{G}}({\mathcal{O}}_{F^{+},p})$
is a compact open subgroup, the space of algebraic automorphic forms on
$G$
of level
$U$
and coefficients in
$W$
is defined as the following
${\mathcal{O}}_{E}$
-module:
$$\begin{eqnarray}S(U,W)\stackrel{\text{def}}{=}\{f:\,G(F^{+})\backslash G(\mathbb{A}_{F^{+}}^{\infty })\rightarrow W\mid f(gu)=u_{p}^{-1}f(g)\,\,\forall g\in G(\mathbb{A}_{F^{+}}^{\infty }),u\in U\}\end{eqnarray}$$
(with the obvious notation
$u=u^{p}u_{p}$
for the elements in
$U$
).
We recall that the level
$U$
is said to be sufficiently small if for all
$t\in G(\mathbb{A}_{F^{+}}^{\infty })$
, the finite group
$t^{-1}G(F^{+})t\,\cap \,U$
is of order prime to
$p$
. For a finite place
$v$
of
$F^{+}$
we say that
$U$
is unramified at
$v$
if one has a decomposition
$U={\mathcal{G}}({\mathcal{O}}_{F_{v}^{+}})U^{v}$
for some compact open subgroup
$U^{v}\leqslant G(\mathbb{A}_{F^{+}}^{\infty ,v})$
.
Let
${\mathcal{P}}_{U}$
denote the set consisting of finite places
$w$
of
$F$
such that
$v\stackrel{\text{def}}{=}w|_{F^{+}}$
is split in
$F$
,
$v\nmid p$
and
$U$
is unramified at
$v$
. If
${\mathcal{P}}\subseteq {\mathcal{P}}_{U}$
is a subset of finite complement that is closed under complex conjugation, we write
$\mathbb{T}^{{\mathcal{P}}}={\mathcal{O}}_{E}[T_{w}^{(i)}:w\in {\mathcal{P}},\,i\in \{0,1,2,3\}]$
for the abstract Hecke algebra on
${\mathcal{P}}$
, where the Hecke operator
$T_{w}^{(i)}$
acts on the space
$S(U,W)$
as the usual double coset operator
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{w}^{-1}\left[\operatorname{GL}_{3}({\mathcal{O}}_{F_{w}})\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}_{w}\text{Id}_{i} & \\ & \text{Id}_{3-i}\end{array}\right)\operatorname{GL}_{3}({\mathcal{O}}_{F_{w}})\right],\end{eqnarray}$$
where
$\unicode[STIX]{x1D71B}_{w}$
denotes a uniformizer of
$F_{w}$
.
4.2 Serre weights
In this section we recall the notion of Serre weights, as well as define the set of Serre weights of a Galois representation
$\overline{r}:G_{F}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
.
Definition 4.2.1. A Serre weight for
${\mathcal{G}}$
(or just Serre weight if
${\mathcal{G}}$
is clear from the context) is an isomorphism class of a smooth, (absolutely) irreducible representation of
${\mathcal{G}}({\mathcal{O}}_{F^{+},p})$
over
$\mathbb{F}$
. If
$w|p$
is a place of
$F$
, a Serre weight at
$w$
is an isomorphism class of a smooth, (absolutely) irreducible representation of
$\operatorname{GL}_{3}({\mathcal{O}}_{F_{w}})$
over
$\mathbb{F}$
, or equivalently an isomorphism class of an (absolutely) irreducible representation of
$\operatorname{GL}_{3}(k_{w})$
over
$\mathbb{F}$
.
Let
$S_{p}^{+}$
(respectively
$S_{p}$
) denote the set of places of
$F^{+}$
(respectively
$F$
) that divide
$p$
. Suppose that for each
$w\in S_{p}$
we are given a
$p$
-restricted triple
$a_{w}=(a_{w,2},a_{w,1},a_{w,0})\in \mathbb{Z}^{3}$
such that
$a_{w,i}+a_{w^{c},2-i}=0$
for all
$0\leqslant i\leqslant 2$
and all
$w\in S_{p}$
. Let
$F_{a_{w}}$
denote the irreducible representation
$F(a_{w,2},a_{w,1},a_{w,0})$
of
$\operatorname{GL}_{3}(k_{w})$
over
$\mathbb{F}$
defined in § 3. Then
$F_{a_{v}}\stackrel{\text{def}}{=}F_{a_{w}}\circ \unicode[STIX]{x1D704}_{w}$
is an irreducible representation of
${\mathcal{G}}({\mathcal{O}}_{F_{v}^{+}})$
that is independent of the choice of place
$w$
dividing
$v$
, and we define the Serre weight
$F_{a}\stackrel{\text{def}}{=}\bigotimes _{v|p}F_{a_{v}}$
. By [Reference Emerton, Gee and HerzigEGH13, Lemma 7.3.4] any Serre weight is of this form.
Definition 4.2.2. Let
$\overline{r}:G_{F}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
be a continuous, absolutely irreducible Galois representation and let
$V$
be a Serre weight for
${\mathcal{G}}$
. We say that
$\overline{r}$
is automorphic of weight
$V$
or that
$V$
is a Serre weight of
$\overline{r}$
if there exist a compact open subgroup
$U$
of
$G(\mathbb{A}_{F}^{\infty ,p})\times {\mathcal{G}}({\mathcal{O}}_{F^{+},p})$
which is unramified at all places dividing
$p$
and a cofinite subset
${\mathcal{P}}$
of
${\mathcal{P}}_{U}$
such that
$\overline{r}$
is unramified at each place of
${\mathcal{P}}$
and
$S(U,V)_{\mathfrak{m}_{\overline{r}}}\neq 0$
, where
$\mathfrak{m}_{\overline{r}}$
is the maximal ideal of
$\mathbb{T}^{{\mathcal{P}}}$
with residue field
$\mathbb{F}$
defined by the formula
$$\begin{eqnarray}\det (1-\overline{r}^{\vee }(\text{Frob}_{w})X)=\mathop{\sum }_{j=0}^{3}(-1)^{j}(\mathbf{N}_{F/\mathbb{Q}}(w))^{\binom{j}{2}}(T_{w}^{(j)}\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{m}_{\overline{r}})X^{j}\quad \forall w\in {\mathcal{P}}\end{eqnarray}$$
(and
$\mathbf{N}_{F/\mathbb{Q}}(w)$
denotes the norm from
$F$
to
$\mathbb{Q}$
of the prime
$w$
). We write
$W(\overline{r})$
for the set of all Serre weights of
$\overline{r}$
.
From now on we fix a place
$w\in S_{p}$
and assume that
$\overline{r}$
is automorphic of weight
$F_{a}$
, where
$a_{w^{\prime }}$
lies in the lowest alcove, i.e.
$a_{w^{\prime },2}-a_{w^{\prime },0}<p-2$
, for all
$w^{\prime }\in S_{p}\setminus \{w,w^{c}\}$
.
Let
$v\stackrel{\text{def}}{=}w|_{F^{+}}$
and
$V^{\prime }\stackrel{\text{def}}{=}\bigotimes _{v^{\prime }\in S_{p}^{+}\setminus \{v\}}F_{a_{v^{\prime }}}$
. Now the construction in [Reference Emerton, Gee and HerzigEGH13, §7.1.4] (replacing the coefficients
$\overline{\mathbb{Z}}_{p}$
by
${\mathcal{O}}_{E}$
) gives a finite free
${\mathcal{O}}_{E}$
-module
$W_{a_{v^{\prime }}}$
with a linear action of
${\mathcal{G}}({\mathcal{O}}_{F_{v^{\prime }}^{+}})$
for any
$v^{\prime }\in S_{p}^{+}\setminus \{v\}$
, and we let
$\widetilde{V}^{\prime }\stackrel{\text{def}}{=}\bigotimes _{v^{\prime }\in S_{p}^{+}\setminus \{v\}}W_{a_{v^{\prime }}}$
. Note that since
$a_{w^{\prime }}$
lies in the lowest alcove for all
$w^{\prime }$
we have
$\widetilde{V}^{\prime }\otimes _{{\mathcal{O}}_{E}}\mathbb{F}\cong V^{\prime }$
.
Definition 4.2.3. We define
$$\begin{eqnarray}W_{w}(\overline{r})\stackrel{\text{def}}{=}\{F_{a_{w}}:a_{w}\in \mathbb{Z}^{3}\text{ is }p\text{-restricted and }(F_{a_{w}}\circ \unicode[STIX]{x1D704}_{w})\otimes _{\mathbb{F}}V^{\prime }\in W(\overline{r})\}.\end{eqnarray}$$
Note that by construction we have
$W_{w}(\overline{r})\neq \varnothing$
.
From now on we suppose that
$U$
is a compact open subgroup of
$G(\mathbb{A}_{F}^{\infty ,p})\times {\mathcal{G}}({\mathcal{O}}_{F^{+},p})$
that is sufficiently small, unramified at all places dividing
$p$
, and a subset
${\mathcal{P}}\subseteq {\mathcal{P}}_{U}$
as above such that
$S(U,(V\circ \unicode[STIX]{x1D704}_{w})\otimes _{\mathbb{F}}V^{\prime })_{\mathfrak{m}_{\overline{r}}}\neq 0$
for some Serre weight
$V$
at
$w$
. (Such a group
$U$
exists, since we are free to shrink
$U$
further to ensure it is sufficiently small, cf. [Reference Emerton, Gee and HerzigEGH13, Remark 7.3.6].)
Having fixed
$V^{\prime }$
, for any representation
$V$
of
$\operatorname{GL}_{3}({\mathcal{O}}_{F_{w}})=\operatorname{GL}_{3}(\mathbb{Z}_{p})$
over
${\mathcal{O}}_{E}$
, let
$$\begin{eqnarray}S(V)\stackrel{\text{def}}{=}S(U,(V\circ \unicode[STIX]{x1D704}_{w})\otimes _{{\mathcal{O}}_{E}}\widetilde{V}^{\prime }).\end{eqnarray}$$
In particular,
$W_{w}(\overline{r})\supseteq \{\text{Serre weights}~V~\text{at}~w:S(V)_{\mathfrak{m}_{\overline{r}}}\neq 0\}$
(and equality holds if we shrink
$U$
and
${\mathcal{P}}$
sufficiently).
4.3 Potentially semistable lifts
In this section we discuss the relationship between Serre weights and potentially semistable lifts. We start by recalling some facts about Deligne–Lusztig representations, referring to [Reference HerzigHer09, § 4] for details.
For any
$n\geqslant 1$
let
$k_{w,n}$
denote the extension of
$k_{w}$
of degree
$n$
. We write
$T$
for a maximal torus of
${\operatorname{GL}_{3}}_{/k_{w}}$
. We have an identification
$$\begin{eqnarray}T(k_{w})\stackrel{{\sim}}{\longrightarrow }\mathop{\prod }_{j=1}^{r}k_{w,n_{j}}^{\times },\end{eqnarray}$$
where
$1\leqslant n_{j}\leqslant 3$
and
$\sum _{j=1}^{r}n_{j}=3$
(cf. [Reference HerzigHer09, Lemma 4.7]), which is well defined up to
$\prod _{j=1}^{r}\operatorname{Gal}(k_{w,n_{j}}/k_{w})$
.
For any homomorphism
$\unicode[STIX]{x1D703}:T(k_{w})\rightarrow \overline{\mathbb{Q}}_{p}^{\times }$
we have a Deligne–Lusztig representation
$R_{T}^{\unicode[STIX]{x1D703}}$
of
$\operatorname{GL}_{3}(k_{w})$
over
$\overline{\mathbb{Q}}_{p}$
. Via the identification (4.3.1) we have
$\unicode[STIX]{x1D703}=\bigotimes _{j=1}^{r}\unicode[STIX]{x1D703}_{j}$
, where
$\unicode[STIX]{x1D703}_{j}:k_{w,n_{j}}^{\times }\rightarrow \overline{\mathbb{Q}}_{p}^{\times }$
. We say that
$\unicode[STIX]{x1D703}$
is primitive if for each
$j$
the
$\operatorname{Gal}(k_{w,n_{j}}/k_{w})$
-conjugates are pairwise distinct. By letting
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D703}_{j})$
be the cuspidal representation of
$\operatorname{GL}_{n_{j}}(k_{w})$
associated to the primitive character
$\unicode[STIX]{x1D703}_{j}$
via [Reference HerzigHer09, Lemma 4.7], we have
$$\begin{eqnarray}R_{T}^{\unicode[STIX]{x1D703}}\cong (-1)^{3-r}\operatorname{Ind}_{P_{\text{}\underline{n}}(k_{w})}^{\operatorname{GL}_{3}(k_{w})}\biggl(\bigotimes _{j}\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D703}_{j})\biggr),\end{eqnarray}$$
where
$P_{\text{}\underline{n}}$
is the standard parabolic subgroup containing the Levi
$\prod _{j}\operatorname{GL}_{n_{j}}$
.
Let
$F_{w,n}\stackrel{\text{def}}{=}W(k_{w,n})[1/p]$
be the unramified extension of
$F_{w}$
of degree
$n$
. We consider
$\unicode[STIX]{x1D703}_{j}$
as a character on
${\mathcal{O}}_{F_{w,n_{j}}}^{\times }$
by inflation and let
$\operatorname{Art}_{F_{w,n}}$
be the isomorphism
$F_{w,n}^{\times }\xrightarrow[{}]{\,\sim \,}W_{F_{w,n}}^{\text{ab}}$
of local class field theory, normalized so that geometric Frobenius elements correspond to uniformizers. We define the inertial type
$\operatorname{rec}(\unicode[STIX]{x1D703}):I_{F_{w}}\rightarrow \overline{\mathbb{Q}}_{p}^{\times }$
as follows:
-
(i)
$\operatorname{rec}(\unicode[STIX]{x1D703})\stackrel{\text{def}}{=}\bigoplus _{j=1}^{3}\unicode[STIX]{x1D703}_{j}\circ \operatorname{Art}_{F_{w}}^{-1}$
if
$\unicode[STIX]{x1D703}_{j}:k_{w}^{\times }\rightarrow \overline{\mathbb{Q}}_{p}^{\times }$
for all
$j=1,2,3$
; -
(ii)
$\operatorname{rec}(\unicode[STIX]{x1D703})\stackrel{\text{def}}{=}\unicode[STIX]{x1D703}_{1}\circ \operatorname{Art}_{F_{w}}^{-1}\,\oplus \,\,\bigoplus _{\unicode[STIX]{x1D70E}\in \operatorname{Gal}(k_{w,2}/k_{w})}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703}_{2}\circ \operatorname{Art}_{F_{w,2}}^{-1})$
if
$\unicode[STIX]{x1D703}_{1}:k_{w}^{\times }\rightarrow \overline{\mathbb{Q}}_{p}^{\times }$
and
$\unicode[STIX]{x1D703}_{2}:k_{w,2}^{\times }\rightarrow \overline{\mathbb{Q}}_{p}^{\times }$
are primitive characters; -
(iii)
$\operatorname{rec}(\unicode[STIX]{x1D703})\stackrel{\text{def}}{=}\bigoplus _{\unicode[STIX]{x1D70E}\in \operatorname{Gal}(k_{w,3}/k_{w})}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703}_{1}\circ \operatorname{Art}_{F_{w,3}}^{-1})$
if
$\unicode[STIX]{x1D703}_{1}:k_{w,3}^{\times }\rightarrow \overline{\mathbb{Q}}_{p}^{\times }$
is a primitive character.
Lemma 4.3.2. Let
$V_{w}$
be a Serre weight at
$w$
for the Galois representation
$\overline{r}:G_{F}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
and assume that
$V_{w}\otimes _{\mathbb{F}}\overline{\mathbb{F}}_{p}$
is a Jordan–Hölder constituent of the mod
$p$
reduction of a Deligne–Lusztig representation
$R_{T}^{\unicode[STIX]{x1D703}}$
of
$\operatorname{GL}_{3}(k_{w})$
, where
$T$
is a maximal torus of
${\operatorname{GL}_{3}}_{/k_{w}}$
and
$\unicode[STIX]{x1D703}:T(k_{w})\rightarrow \overline{\mathbb{Q}}_{p}^{\times }$
is a primitive character. Then
$\overline{r}|_{G_{F_{w}}}$
has a potentially semistable lift with Hodge–Tate weights
$\{-2,-1,0\}$
and inertial type
$\text{rec}(\unicode[STIX]{x1D703})$
.
Proof. This is proved in [Reference Morra and ParkMP14, Theorem 5.5] (cf. also [Reference Emerton, Gee and HerzigEGH13, Propositions 2.4.1 and 7.4.4 in cases (i), (iii)]), except when
$n_{i}=1$
for all
$i$
and some of the characters
$\unicode[STIX]{x1D703}_{i}$
are equal. The exceptional case follows in the same way, by using the lemma below, which is an extension of [Reference Emerton, Gee and HerzigEGH13, Proposition 2.4.1(ii)]. (We recall the idea: by the Deligne–Serre lifting lemma we obtain a global lift
$r$
of the dual
$\overline{r}^{\vee }$
which is attached to an automorphic representation in trivial weight and dual type
$(R_{T}^{\unicode[STIX]{x1D703}})^{\vee }$
. Classical local-global compatibility together with the lemma below shows that
$r^{\vee }|_{G_{F_{w}}}$
provides the required lift.)◻
Suppose
$n\geqslant 1$
and let
$B_{n}$
denote the Borel subgroup of
$\operatorname{GL}_{n}$
of upper-triangular matrices. Let
$\operatorname{rec}_{F_{w}}$
denote the local Langlands correspondence for
$\operatorname{GL}_{n}(F_{w})$
over
$\overline{\mathbb{Q}}_{p}$
, as in [Reference Emerton, Gee and HerzigEGH13, §1.3].
Lemma 4.3.3. Suppose that
$\unicode[STIX]{x1D70B}$
is an irreducible admissible representation of
$\operatorname{GL}_{n}(F_{w})$
over
$\overline{\mathbb{Q}}_{p}$
. Assume that
$\unicode[STIX]{x1D70B}|_{\operatorname{GL}_{n}({\mathcal{O}}_{F_{w}})}$
contains a Jordan–Hölder factor of the
$\operatorname{GL}_{n}({\mathcal{O}}_{F_{w}})$
-inflation of a principal series representation of the form
$$\begin{eqnarray}\operatorname{Ind}_{B_{n}(k_{w})}^{\operatorname{GL}_{n}(k_{w})}(\unicode[STIX]{x1D703}_{1}\otimes \cdots \otimes \unicode[STIX]{x1D703}_{n})\end{eqnarray}$$
for some characters
$\unicode[STIX]{x1D703}_{i}:k_{w}^{\times }\rightarrow \overline{\mathbb{Q}}_{p}^{\times }$
. Then
$\operatorname{rec}_{F_{w}}(\unicode[STIX]{x1D70B})|_{I_{F_{w}}}\cong \bigoplus _{i=1}^{n}\unicode[STIX]{x1D703}_{i}\circ \operatorname{Art}_{F_{w}}^{-1}$
.
Proof. We indicate how the proof of [Reference Emerton, Gee and HerzigEGH13, Proposition 2.4.1(ii)] needs to be adjusted. Recall the pair
$(I,\unicode[STIX]{x1D70C})$
described in that proof, which has the property that
$\operatorname{Ind}_{I}^{\operatorname{GL}_{n}({\mathcal{O}}_{F_{w}})}\unicode[STIX]{x1D70C}$
is isomorphic to the inflation of the representation (4.3.4) to
$\operatorname{GL}_{n}({\mathcal{O}}_{F_{w}})$
. Thus by assumption
$\operatorname{Hom}_{I}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70B})\neq 0$
. By [Reference RocheRoc98, Theorem 7.7] we deduce that
$\unicode[STIX]{x1D70B}$
is a subquotient of
$\operatorname{Ind}_{B_{n}(F_{w})}^{\operatorname{GL}_{n}(F_{w})}\widetilde{\unicode[STIX]{x1D703}}$
for some character
$\widetilde{\unicode[STIX]{x1D703}}=\widetilde{\unicode[STIX]{x1D703}}_{1}\,\otimes \,\cdots \,\otimes \,\widetilde{\unicode[STIX]{x1D703}}_{n}$
with
$\widetilde{\unicode[STIX]{x1D703}}_{i}|_{{\mathcal{O}}_{F_{w}}^{\times }}=\unicode[STIX]{x1D703}_{i}$
for all
$i$
. Now from [Reference HenniartHen02, §1.9] it follows that if
$\unicode[STIX]{x1D70B}^{\prime }$
is another irreducible admissible representation of
$\operatorname{GL}_{n}(F_{w})$
, then
$\unicode[STIX]{x1D70B}$
,
$\unicode[STIX]{x1D70B}^{\prime }$
have the same supercuspidal support if and only if
$\operatorname{rec}_{F_{w}}(\unicode[STIX]{x1D70B})|_{W_{F_{w}}}\cong \operatorname{rec}_{F_{w}}(\unicode[STIX]{x1D70B}^{\prime })|_{W_{F_{w}}}$
. The claim then follows from [Reference Harris and TaylorHT01, § VII.2 (pp. 251f)].◻
4.4 Serre weights of
$\overline{r}$
in the maximally non-split case
We keep the notation and assumptions of § 4.2. In particular,
$p$
splits completely in
$F$
, there is a distinguished place
$w\in S_{p}$
, and
$\overline{r}:G_{F}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
is an automorphic, absolutely irreducible Galois representation. The aim of this section is to almost completely determine the Serre weights of
$\overline{r}$
at
$w$
when
$\overline{r}|_{G_{F_{w}}}$
is maximally non-split and generic. The techniques of this section follow the strategy of [Reference Emerton, Gee and HerzigEGH13, § 5], and have been further pursued in [Reference Morra and ParkMP14] to cover other cases when
$\overline{r}$
is ordinary at
$w$
.
Theorem 4.4.1. Assume that
$\overline{r}|_{G_{F_{w}}}$
is maximally non-split and generic, of the form
$$\begin{eqnarray}\overline{r}|_{G_{F_{w}}}\sim \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D714}^{a+1}\text{nr}_{\unicode[STIX]{x1D707}_{2}} & \ast & \ast \\ & \unicode[STIX]{x1D714}^{b+1}\text{nr}_{\unicode[STIX]{x1D707}_{1}} & \ast \\ & & \unicode[STIX]{x1D714}^{c+1}\text{nr}_{\unicode[STIX]{x1D707}_{0}}\end{array}\right).\end{eqnarray}$$
-
(i) If
$\text{FL}(\overline{r}|_{G_{F_{w}}})\notin \{0,\infty \}$
, we have
$$\begin{eqnarray}\displaystyle \{F(a-1,b,c+1)\}\subseteq W_{w}(\overline{r})\subseteq \{F(a-1,b,c+1),\,F(c+p-1,b,a-p+1)\}. & & \displaystyle \nonumber\end{eqnarray}$$
-
(ii) If
$\text{FL}(\overline{r}|_{G_{F_{w}}})=\infty$
, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \{F(a-1,b,c+1),F(a,c,b-p+1)\}\nonumber\\ \displaystyle & & \displaystyle \qquad \subseteq W_{w}(\overline{r})\subseteq \{F(a-1,b,c+1),\,F(c+p-1,b,a-p+1),F(a,c,b-p+1)\}.\nonumber\end{eqnarray}$$
-
(iii) If
$\text{FL}(\overline{r}|_{G_{F_{w}}})=0$
, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \{F(a-1,b,c+1),F(b+p-1,a,c)\}\nonumber\\ \displaystyle & & \displaystyle \qquad \subseteq W_{w}(\overline{r})\subseteq \{F(a-1,b,c+1),\,F(c+p-1,b,a-p+1),F(b+p-1,a,c)\}.\nonumber\end{eqnarray}$$
Remark 4.4.2. In fact, the proof shows that the containments in parts (i)–(iii) hold if we replace
$W_{w}(\overline{r})$
by
$\{\text{Serre weights }~V~\text{at}~w:S(V)_{\mathfrak{m}_{\overline{r}}}\neq 0\}$
(for any group
$U$
and subset
${\mathcal{P}}\subseteq {\mathcal{P}}_{U}$
considered in § 4.2).
In the remainder of this section we will prove this theorem, except for showing the existence of the shadow weights
$F(a,c,b-p+1)$
,
$F(b+p-1,a,c)$
in parts (ii) and (iii). We will complete the proof in Proposition 4.5.10. We start with the following preliminary lemma.
Lemma 4.4.3. Let
$V\in W_{w}(\overline{r})$
be a Serre weight of
$\overline{r}$
at
$w$
. Then
$V$
is isomorphic to one of the weights in the following list:
$$\begin{eqnarray}\displaystyle & \displaystyle F(b+p-1,a-1,c+1),\quad F(a-1,c+1,b-p+1),\quad F(c+p,b,a-p), & \displaystyle \nonumber\\ \displaystyle & \displaystyle F(b+p-1,a,c),\quad F(a,c,b-p+1), & \displaystyle \nonumber\\ \displaystyle & \displaystyle F(c+p-1,b,a-p+1),\quad F(a-1,b,c+1). & \displaystyle \nonumber\end{eqnarray}$$
Proof. Let us write
$V\cong F(x,y,z)$
for a
$p$
-restricted weight
$(x,y,z)$
. By Frobenius reciprocity the weight
$F(x,y,z)$
is a constituent of the principal series
$\operatorname{Ind}_{\overline{B}(k_{w})}^{\overline{G}(k_{w})}(\unicode[STIX]{x1D714}^{x}\,\otimes \,\unicode[STIX]{x1D714}^{y}\,\otimes \,\unicode[STIX]{x1D714}^{z})$
. Hence, by Lemma 4.3.2,
$\overline{r}|_{G_{F_{w}}}$
admits a potentially semistable lift of Hodge–Tate weights
$\{-2,-1,0\}$
and inertial type
$\unicode[STIX]{x1D703}\stackrel{\text{def}}{=}\widetilde{\unicode[STIX]{x1D714}}^{x}\oplus \widetilde{\unicode[STIX]{x1D714}}^{y}\oplus \widetilde{\unicode[STIX]{x1D714}}^{z}$
. Proposition 2.6.1 implies
$\{x,y,z\}\equiv \{a,b,c\}$
or
$\{x,y,z\}\equiv \{a-1,b,c+1\}$
as subsets of
$\mathbb{Z}/(p-1)\mathbb{Z}$
.
If
$x-z\geqslant p-2$
, we conclude by genericity that
$V$
belongs to the following list:
$$\begin{eqnarray}\displaystyle & \displaystyle F(b+p-1,a-1,c+1),\quad F(a-1,c+1,b-p+1),\quad F(c+p,b,a-p), & \displaystyle \nonumber\\ \displaystyle & \displaystyle F(b+p-1,a,c),\quad F(a,c,b-p+1),\quad F(c+p-1,b,a-p+1). & \displaystyle \nonumber\end{eqnarray}$$
If
$x-z<p-2$
, then noting that
$x+1$
,
$y$
,
$z-1$
are distinct modulo
$p-1$
by above, the proof of [Reference Emerton, Gee and HerzigEGH13, Lemma 6.1.1], shows that
$V$
is also a constituent of the principal series
$\operatorname{Ind}_{\overline{B}(k_{w})}^{\overline{G}(k_{w})}(\unicode[STIX]{x1D714}^{z-1}\,\otimes \,\unicode[STIX]{x1D714}^{y}\,\otimes \,\unicode[STIX]{x1D714}^{x+1})$
, and hence
$\{x+1,y,z-1\}\equiv \{a,b,c\}$
or
$\{x+1,y,z-1\}\equiv \{a-1,b,c+1\}$
as subsets of
$\mathbb{Z}/(p-1)\mathbb{Z}$
. We deduce by genericity that
$V\cong F(a-1,b,c+1)$
.◻
Proof of Theorem 4.4.1 (Modulo the existence of shadows).
We first establish the upper bound on
$W_{w}(\overline{r})$
(this is sometimes called ‘weight elimination’). Let
$V\in W_{w}(\overline{r})$
. Then
$V$
is one of the weights appearing in the list of Lemma 4.4.3. We now prove that the weights
$F(a-1,c+1,b-p+1)$
,
$F(c+p,b,a-p)$
and
$F(b+p-1,a-1,c+1)$
cannot be Serre weights of
$\overline{r}$
at
$w$
. Indeed, by the proof of [Reference HerzigHer09, Proposition 7.4], it is easily checked that
$F(b+p-1,a-1,c+1)\otimes _{\mathbb{F}}\overline{\mathbb{F}}_{p}$
is an element of
$\text{JH}\big(\overline{R}_{T}^{\unicode[STIX]{x1D703}}\big)$
, where the maximal torus
$T$
verifies
$T(k_{w})\cong k_{w,2}^{\times }\times k_{w}^{\times }$
and
$\unicode[STIX]{x1D703}\cong \widetilde{\unicode[STIX]{x1D714}}_{2}^{a-1+pb}\,\otimes \,\widetilde{\unicode[STIX]{x1D714}}^{c+1}$
. If
$F(b+p-1,a-1,c+1)$
is a Serre weight of
$\overline{r}$
then by Lemma 4.3.2,
$\overline{r}|_{G_{F_{w}}}$
has a potentially semistable lift of Hodge–Tate weights
$\{-2,-1,0\}$
and inertial type
$\widetilde{\unicode[STIX]{x1D714}}_{2}^{a-1+pb}\oplus \widetilde{\unicode[STIX]{x1D714}}_{2}^{b+p(a-1)}\oplus \widetilde{\unicode[STIX]{x1D714}}^{c+1}$
, which is not possible by Proposition 2.6.3.
In a similar fashion, the weights
$F(a-1,c+1,b-p+1)\otimes _{\mathbb{F}}\overline{\mathbb{F}}_{p}$
,
$F(c+p,b,a-p)\otimes _{\mathbb{F}}\overline{\mathbb{F}}_{p}$
appear in
$\text{JH}\big(\overline{R}_{T}^{\unicode[STIX]{x1D703}}\big)$
, where now
$\unicode[STIX]{x1D703}\cong \widetilde{\unicode[STIX]{x1D714}}_{2}^{b+p(c+1)}\,\otimes \,\widetilde{\unicode[STIX]{x1D714}}^{a-1}$
, providing a contradiction with Proposition 2.6.3.
Assume now that
$\text{FL}(\overline{r}|_{G_{F_{w}}})\neq \infty$
; we claim that the weight
$F(a,c,b-p+1)$
cannot be a Serre weight of
$\overline{r}$
at
$w$
. Again, using [Reference HerzigHer09, proof of Proposition 7.4] we see that
$F(a,c,b-p+1)\otimes _{\mathbb{F}}\overline{\mathbb{F}}_{p}$
is an element of
$\text{JH}\big(\overline{R}_{T}^{\unicode[STIX]{x1D703}}\big)$
, where now
$\unicode[STIX]{x1D703}\cong \widetilde{\unicode[STIX]{x1D714}}_{2}^{a+1+p(b-1)}\,\otimes \,\widetilde{\unicode[STIX]{x1D714}}^{c}$
. By Lemma 4.3.2,
$\overline{r}|_{G_{F_{w}}}$
has a potentially semistable lift of Hodge–Tate weights
$\{-2,-1,0\}$
and inertial type
$\widetilde{\unicode[STIX]{x1D714}}_{2}^{a+1+p(b-1)}\oplus \widetilde{\unicode[STIX]{x1D714}}_{2}^{b-1+p(a+1)}\oplus \widetilde{\unicode[STIX]{x1D714}}^{c}$
, which implies
$\text{FL}(\overline{r}|_{G_{F_{w}}})=\infty$
by Proposition 2.6.4. By duality,
$F(b+p-1,a,c)$
cannot be a Serre weight of
$\overline{r}$
at
$w$
if
$\text{FL}(\overline{r}|_{G_{F_{w}}})\neq 0$
.
By weight cycling we will now deduce that
$F(a-1,b,c+1)\in W_{w}(\overline{r})$
. (We refer to the introduction of [Reference Emerton, Gee and HerzigEGH13] for the term ‘weight cycling’ as well as its history.) Recall the (commuting) Hecke operators
$\overline{T}_{1}$
,
$\overline{T}_{2}$
at
$w$
defined in [Reference Emerton, Gee and HerzigEGH13, §4.2]. They act on the finite-dimensional
$\mathbb{F}$
-vector space
$S(V)$
for any Serre weight
$V$
at
$w$
. If
$\overline{T}_{i}$
has a non-zero eigenvalue on
$S(F(c+p-1,b,a-p+1))_{\mathfrak{m}_{\overline{r}}}$
for some
$i$
, we deduce exactly as in the proof of [Reference Emerton, Gee and HerzigEGH13, Corollary 4.5.4] that
$\overline{r}|_{G_{F_{w}}}$
has a crystalline lift
$\unicode[STIX]{x1D70C}$
over
$E$
, where
$\unicode[STIX]{x1D70C}$
admits a subrepresentation of Hodge–Tate weight
$-(c+p+1)$
or a quotient of Hodge–Tate weight
$-(a-p+1)$
. This implies that
$\overline{r}|_{I_{F_{w}}}$
admits
$\unicode[STIX]{x1D714}^{c+2}$
as subrepresentation or
$\unicode[STIX]{x1D714}^{a}$
as quotient, contradicting our assumptions on
$\overline{r}|_{G_{F_{w}}}$
. Hence
$\overline{T}_{i}$
act nilpotently on
$S(V)_{\mathfrak{m}_{\overline{r}}}$
for
$V=F(c+p-1,b,a-p+1)$
. By a similar argument the same holds when
$V=F(b+p-1,a,c)$
or
$F(a,c,b-p+1)$
.
Suppose that
$F(a-1,b,c+1)\notin W_{w}(\overline{r})$
. If
$V\stackrel{\text{def}}{=}F(c+p-1,b,a-p+1)\in W_{w}(\overline{r})$
, then
$S(V)_{\mathfrak{m}_{\overline{r}}}\neq 0$
(for suitable
$U$
,
${\mathcal{P}}$
). By the previous paragraph we may apply weight cycling [Reference Emerton, Gee and HerzigEGH13, Proposition 6.1.3(ii)] to the smooth
$\operatorname{GL}_{3}(F_{w})$
-representation
$\unicode[STIX]{x1D70B}\stackrel{\text{def}}{=}S(U^{v},V^{\prime })_{\mathfrak{m}_{\overline{r}}}$
(defined just after (4.5.1)) and our weight
$V$
. Using the nilpotency of
$\overline{T}_{1}$
(respectively
$\overline{T}_{2}$
) we see that
$S(V^{\prime \prime })_{\mathfrak{m}_{\overline{r}}}\neq 0$
, hence
$V^{\prime \prime }\in W_{w}(\overline{r})$
, for at least one weight
$V^{\prime \prime }$
listed there. However, the genericity of
$\overline{r}|_{G_{F_{w}}}$
together with our upper bound for
$W_{w}(\overline{r})$
lets us rule out four out of five weights in each case and deduce that
$F(a,c,b-p+1)\in W_{w}(\overline{r})$
(respectively
$F(b+p-1,a,c)\in W_{w}(\overline{r})$
). But this contradicts the upper bound on
$W_{w}(\overline{r})$
we obtained above. Similarly, if
$F(b+p-1,a,c)\in W_{w}(\overline{r})$
, then weight cycling with
$\overline{T}_{2}$
and genericity imply that
$W_{w}(\overline{r})$
contains
$F(a,c,b-p+1)$
, contradicting our upper bound. We get a similar contradiction if
$F(a,c,b-p+1)\in W_{w}(\overline{r})$
. We conclude that
$F(a-1,b,c+1)\in W_{w}(\overline{r})$
.
This ends the proof of Theorem 4.4.1 modulo the existence of shadow weights. ◻
Corollary 4.4.4. In the setting of Theorem 4.4.1,
$\overline{r}$
has an automorphic lift
$r:G_{F}\rightarrow \operatorname{GL}_{3}({\mathcal{O}}_{E})$
(after possibly enlarging
$E$
) such that
$r|_{G_{F_{w}}}$
is crystalline and ordinary of Hodge–Tate weights
$\{-a-1,-b-1,-c-1\}$
.
Proof. Keeping our notation of the proof of Theorem 4.4.1, consider the Hecke operators
$\overline{T}_{1}$
,
$\overline{T}_{2}$
acting on
$S(F(a-1,b,c+1))_{\mathfrak{m}_{\overline{r}}}$
, which is non-zero by the proof above. If
$\overline{T}_{1}$
fails to be invertible on this vector space, then one of the weights
$F(c+p,a-1,b)$
,
$F(a-1,c+1,b-p+1)$
is contained in
$W_{w}(\overline{r})$
by [Reference Emerton, Gee and HerzigEGH13, Proposition 6.1.3(i)]. This contradicts the upper bound of Theorem 4.4.1 by genericity, hence
$\overline{T}_{1}$
is invertible on
$S(F(a-1,b,c+1))_{\mathfrak{m}_{\overline{r}}}$
. The same is true for
$\overline{T}_{2}$
. Enlarging
$E$
if necessary we can pick simultaneous eigenvalues
$\unicode[STIX]{x1D6FC}_{i}\in \mathbb{F}^{\times }$
of
$\overline{T}_{i}$
(
$i=1,2$
) on this space. Consider the double coset operators
$T_{w}^{(i)}$
(
$i=1,2$
) defined as in § 4.1 but for our fixed place
$w|p$
and let
$\widetilde{T}_{w}^{(1)}\stackrel{\text{def}}{=}p^{-c-1}T_{w}^{(1)}$
,
$\widetilde{T}_{w}^{(2)}\stackrel{\text{def}}{=}p^{-b-c-1}T_{w}^{(2)}$
. Let
$\mathbb{T}\stackrel{\text{def}}{=}\mathbb{T}^{{\mathcal{P}}}[\widetilde{T}_{w}^{(1)},\widetilde{T}_{w}^{(2)}]$
and consider the homomorphism
$\unicode[STIX]{x1D703}:\mathbb{T}\rightarrow \mathbb{F}$
whose kernel contains
$\mathfrak{m}_{\overline{r}}$
and which sends
$\widetilde{T}_{w}^{(i)}$
to
$\unicode[STIX]{x1D6FC}_{i}$
(
$i=1,2$
). Redefining
$a_{w}=(a-1,b,c+1)$
, the construction in [Reference Emerton, Gee and HerzigEGH13, §4.1.1] (replacing the coefficients
$\overline{\mathbb{Z}}_{p}$
by
${\mathcal{O}}_{E}$
) gives a finite free
${\mathcal{O}}_{E}$
-module
$W_{a_{w}}$
with a linear action of
$\operatorname{GL}_{3}({\mathcal{O}}_{F_{w}})$
. As
$a_{w}$
lies in the lowest alcove we have
$S(W_{a_{w}})\otimes _{{\mathcal{O}}_{E}}\mathbb{F}\cong S(F(a-1,b,c+1))$
. The commutative
${\mathcal{O}}_{E}$
-algebra
$\mathbb{T}$
acts naturally on both sides, with
$\widetilde{T}_{w}^{(i)}$
acting as
$\overline{T}_{i}$
on the right-hand side (see [Reference Emerton, Gee and HerzigEGH13, § 4.4]). Using the Deligne–Serre lifting lemma and enlarging
$E$
if necessary we can lift the Hecke eigenvalues
$\unicode[STIX]{x1D703}$
to
$S(W_{a_{w}})$
and obtain an automorphic lift
$r:G_{F}\rightarrow \operatorname{GL}_{3}({\mathcal{O}}_{E})$
of
$\overline{r}$
such that
$r|_{G_{F_{w}}}$
is crystalline of Hodge–Tate weights
$\{-a-1,-b-1,-c-1\}$
. It is, moreover, ordinary, i.e. its Hodge and Newton polygons coincide, using that
$\unicode[STIX]{x1D6FC}_{i}\neq 0$
for
$i=1,2$
(cf. the proof of [Reference Emerton, Gee and HerzigEGH13, Corollary 4.5.4]).◻
4.5 Local-global compatibility
We keep the notation and assumptions of § 4.2. Suppose that
$\overline{r}$
is as in Theorem 4.4.1. We recall the operators
$S,\,S^{\prime }\in \mathbb{F}[\operatorname{GL}_{3}(\mathbb{F}_{p})]$
obtained from (3.1.1) by setting
$(a_{2},a_{1},a_{0})=(-c,-b,-a)$
:
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\displaystyle S\stackrel{\text{def}}{=}\underset{x,y,z\in \mathbb{F}_{p}}{\sum }x^{p-(a-c)}z^{p-(a-b)}\left(\begin{array}{@{}ccc@{}}1 & x & y\\ & 1 & z\\ & & 1\end{array}\right){\dot{w}}_{0},\\ \displaystyle S^{\prime }\stackrel{\text{def}}{=}\underset{x,y,z\in \mathbb{F}_{p}}{\sum }x^{p-(b-c)}z^{p-(a-c)}\left(\begin{array}{@{}ccc@{}}1 & x & y\\ & 1 & z\\ & & 1\end{array}\right){\dot{w}}_{0}.\end{array} & & \displaystyle\end{eqnarray}$$
Since the compact open subgroup
$U$
we fixed is unramified at
$v$
, we can write
$U={\mathcal{G}}({\mathcal{O}}_{F_{v}^{+}})U^{v}$
for some compact open subgroup
$U^{v}\leqslant G(\mathbb{A}_{F^{+}}^{\infty ,v})$
. If
$W$
is an
${\mathcal{O}}_{E}$
-module endowed with an action of
$\prod _{v^{\prime }\in S_{p}^{+}\setminus \{v\}}{\mathcal{G}}({\mathcal{O}}_{F_{v^{\prime }}^{+}})$
we define
$S(U^{v},W)\stackrel{\text{def}}{=}\mathop{\varinjlim }\nolimits_{U_{v}}S(U^{v}\cdot U_{v},W)$
, where the limit runs over all compact open subgroups
$U_{v}\leqslant {\mathcal{G}}({\mathcal{O}}_{F_{v}^{+}})$
. Then
$S(U^{v},W)$
has a smooth action of
$G(F_{v}^{+})$
and hence via
$\unicode[STIX]{x1D704}_{w}$
of
$\operatorname{GL}_{3}(F_{w})=\operatorname{GL}_{3}(\mathbb{Q}_{p})$
. We also define
$\widetilde{S}(U^{v},W)\stackrel{\text{def}}{=}\mathop{\varprojlim }\nolimits_{s}S(U^{v},W/\unicode[STIX]{x1D71B}_{E}^{s})$
, which has a linear action of
$\operatorname{GL}_{3}(\mathbb{Q}_{p})$
. Note that
$\widetilde{S}(U^{v},W)$
is isomorphic to the
$p$
-adic completion of
$S(U^{v},W)$
, provided
$W$
is finitely generated.
We recall that in § 3 we defined an Iwahori subgroup
$I$
of
$K=\operatorname{GL}_{3}(\mathbb{Z}_{p})$
and the notation
$V^{I,(a_{2},a_{1},a_{0})}$
for any representation
$V$
of
$K$
over
${\mathcal{O}}_{E}$
and any triple
$(a_{2},a_{1},a_{0})\in \mathbb{Z}^{3}$
. We note that from the definitions it follows that
$\widetilde{S}(U^{v},\widetilde{V}^{\prime })^{I,(-b,-c,-a)}\cong S(U^{v},\widetilde{V}^{\prime })^{I,(-b,-c,-a)}$
, a finite free
${\mathcal{O}}_{E}$
-module. Recall furthermore that
$\unicode[STIX]{x1D6F1}=\Bigl(\!\begin{smallmatrix} & 1 & \\ & & 1\\ p & & \end{smallmatrix}\!\Bigr)$
.
Theorem 4.5.2. We make the following assumptions.
-
(i) The representation
$\overline{r}|_{G_{F_{w}}}$
is maximally non-split and generic, of the form
$$\begin{eqnarray}\overline{r}|_{G_{F_{w}}}\sim \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D714}^{a+1}\text{nr}_{\unicode[STIX]{x1D707}_{2}} & \ast & \ast \\ & \unicode[STIX]{x1D714}^{b+1}\text{nr}_{\unicode[STIX]{x1D707}_{1}} & \ast \\ & & \unicode[STIX]{x1D714}^{c+1}\text{nr}_{\unicode[STIX]{x1D707}_{0}}\end{array}\right).\end{eqnarray}$$
-
(ii) The invariant
$\text{FL}(\overline{r}|_{G_{F_{w}}})\not \in \{0,\infty \}$
. -
(iii) The
${\mathcal{O}}_{E}$
-dual of
$S(U^{v},\widetilde{V}^{\prime })_{\mathfrak{m}_{\overline{r}}}^{I,(-b,-c,-a)}$
is free over
$\mathbb{T}$
, where
$\mathbb{T}$
denotes the
${\mathcal{O}}_{E}$
-subalgebra of
$\operatorname{End}\big(S(U^{v},\widetilde{V}^{\prime })_{\mathfrak{m}_{\overline{r}}}^{I,(-b,-c,-a)}\big)$
generated by
$\mathbb{T}^{{\mathcal{P}}}$
,
$U_{1}$
, and
$U_{2}$
.
Then we have the equality
$$\begin{eqnarray}S^{\prime }\circ \unicode[STIX]{x1D6F1}=(-1)^{a-b}\cdot \frac{b-c}{a-b}\cdot \text{FL}(\overline{r}|_{G_{F_{w}}})\cdot S\end{eqnarray}$$
of maps
$$\begin{eqnarray}S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]^{I,(-b,-c,-a)}[U_{1},U_{2}]\rightarrow S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]^{I,(-c-1,-b,-a+1)}.\end{eqnarray}$$
Moreover, these maps are injective with non-zero domain. In particular,
$\text{FL}(\overline{r}|_{G_{F_{w}}})$
is determined by the smooth
$\operatorname{GL}_{3}(\mathbb{Q}_{p})$
-representation
$S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]$
.
Remark 4.5.4. The proof shows that for any non-zero
$v\in S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]^{I,(-b,-c,-a)}[U_{1},U_{2}]$
, the
$K$
-subrepresentation generated by
$v$
and
$\unicode[STIX]{x1D6F1}v$
is of the form
$$\begin{eqnarray}F(-c-1,-b,-a+1)\text{}\text{—}(F(-b+p-1,-c,-a)\oplus F(-c,-a,-b-p+1))\end{eqnarray}$$
with socle
$F(-c-1,-b,-a+1)$
. Together with Proposition 3.1.2 this explains why there exists a constant
$x\in \mathbb{F}^{\times }$
such that
$S^{\prime }\circ \unicode[STIX]{x1D6F1}=xS$
on
$S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]^{I,(-b,-c,-a)}[U_{1},U_{2}]$
.
Proof. Let
$\unicode[STIX]{x1D702}:I\rightarrow {\mathcal{O}}_{E}^{\times }$
denote the character
$\widetilde{\unicode[STIX]{x1D714}}^{b}\,\otimes \,\widetilde{\unicode[STIX]{x1D714}}^{c}\,\otimes \,\widetilde{\unicode[STIX]{x1D714}}^{a}$
and set
$$\begin{eqnarray}M\stackrel{\text{def}}{=}S(U^{v},\widetilde{V}^{\prime })_{\mathfrak{ m}_{\overline{r}}}^{I,(-b,-c,-a)}\cong S\big(U^{v}\cdot I,\unicode[STIX]{x1D702}\otimes \widetilde{V}^{\prime }\big)_{\mathfrak{m}_{\overline{r}}}.\end{eqnarray}$$
We remark that
$M\neq 0$
, as
$S(F(a-1,b,c+1))_{\mathfrak{m}_{\overline{r}}}\neq 0$
and
$F(a-1,b,c+1)$
is a Jordan–Hölder factor of
$\overline{\operatorname{Ind}_{I}^{K}\unicode[STIX]{x1D702}}$
, and also that
$M$
is a finite free
${\mathcal{O}}_{E}$
-module. For any
${\mathcal{O}}_{E}$
-algebra
$A$
we let
$M_{A}\stackrel{\text{def}}{=}M\otimes _{{\mathcal{O}}_{E}}A$
and
$\mathbb{T}_{A}\stackrel{\text{def}}{=}\mathbb{T}\otimes _{{\mathcal{O}}_{E}}A$
.
Picking a
$\mathbb{Q}_{p}$
-linear embedding
$E{\hookrightarrow}\overline{\mathbb{Q}}_{p}$
, as well as an isomorphism
$\imath :\overline{\mathbb{Q}}_{p}\xrightarrow[{}]{\,\sim \,}\mathbb{C}$
, we see that
$$\begin{eqnarray}M_{\overline{\mathbb{Q}}_{p}}\cong \underset{\unicode[STIX]{x1D70B}}{\bigoplus }m(\unicode[STIX]{x1D70B})\cdot \unicode[STIX]{x1D70B}_{v}^{I,(-b,-c,-a)}\otimes \big(\unicode[STIX]{x1D70B}^{\infty ,v}\big)^{U^{v}},\end{eqnarray}$$
where the sum runs over irreducible representations
$\unicode[STIX]{x1D70B}\cong \unicode[STIX]{x1D70B}_{\infty }\,\otimes \,\unicode[STIX]{x1D70B}_{v}\,\otimes \,\unicode[STIX]{x1D70B}^{\infty ,v}$
of
$G(\mathbb{A}_{F^{+}})$
such that
$\unicode[STIX]{x1D70B}\otimes _{\imath }\mathbb{C}$
is a cuspidal automorphic representation of multiplicity
$m(\unicode[STIX]{x1D70B})\in \mathbb{Z}_{{>}0}$
with
$\unicode[STIX]{x1D70B}_{\infty }\otimes _{\imath }\mathbb{C}$
determined by the algebraic representation
$(\widetilde{V}^{\prime })^{\vee }$
and with Galois representation
$r_{\unicode[STIX]{x1D70B}}$
lifting
$\overline{r}^{\vee }$
(cf. [Reference Emerton, Gee and HerzigEGH13, Lemma 7.1.6]). For any
$\unicode[STIX]{x1D70B}$
contributing to (4.5.5) we have the following.
-
(a) There is an isomorphism
$\unicode[STIX]{x1D70B}_{v}\cong \operatorname{Ind}_{B(\mathbb{Q}_{p})}^{G(\mathbb{Q}_{p})}\big(\unicode[STIX]{x1D713}_{b}|\cdot |^{2}\,\otimes \,\unicode[STIX]{x1D713}_{c}|\cdot |\,\otimes \,\unicode[STIX]{x1D713}_{a}\big)$
for some smooth characters
$\unicode[STIX]{x1D713}_{i}:\mathbb{Q}_{p}^{\times }\rightarrow \overline{\mathbb{Q}}_{p}^{\times }$
(depending on
$\unicode[STIX]{x1D70B}$
) with
$\unicode[STIX]{x1D713}_{i}|_{\mathbb{Z}_{p}^{\times }}=\widetilde{\unicode[STIX]{x1D714}}^{-i}$
for
$i\in \{a,b,c\}$
. -
(b) The Galois representation
$r_{\unicode[STIX]{x1D70B}}^{\vee }|_{G_{F_{w}}}$
is potentially crystalline with Hodge–Tate weights
$\{-2,-1,0\}$
; moreover one has
$\operatorname{WD}(r_{\unicode[STIX]{x1D70B}}^{\vee }|_{G_{F_{w}}})^{\text{F-ss}}\cong \unicode[STIX]{x1D713}_{b}^{-1}\oplus \unicode[STIX]{x1D713}_{c}^{-1}\oplus \unicode[STIX]{x1D713}_{a}^{-1}$
.
Here, part (a) follows from [Reference Emerton, Gee and HerzigEGH13, Propositions 2.4.1 and 7.4.4] and part (b) follows from classical local-global compatibility. In particular, from part (b) we deduce that
$p^{2}\unicode[STIX]{x1D713}_{b}(p)^{-1}\in \overline{\mathbb{Q}}_{p}$
is the
$\unicode[STIX]{x1D711}$
-eigenvalue on
$\text{D}_{\text{st}}^{\mathbb{Q}_{p},2}(r_{\unicode[STIX]{x1D70B}}^{\vee }|_{G_{F_{w}}})^{I_{F_{w}}=\widetilde{\unicode[STIX]{x1D714}}^{b}}$
, and so from Theorem 2.5.1 and assumptions (i), (ii) it follows that
$$\begin{eqnarray}\text{ord}_{p}(\unicode[STIX]{x1D713}_{b}(p))=1\quad \text{and}\quad \text{FL}(\overline{r}|_{G_{F_{w}}})=\biggl[\frac{\unicode[STIX]{x1D713}_{b}(p)}{p}\biggr].\end{eqnarray}$$
We also deduce from Corollary 2.4.11 that
$\text{ord}_{p}(p^{2}\unicode[STIX]{x1D713}_{i}(p)^{-1})\in (0,2)$
for
$i\in \{a,b,c\}$
, with sum equal to 3. In particular, the eigenvalue of
$U_{1}$
(respectively
$U_{2}$
) on
$\unicode[STIX]{x1D70B}_{v}^{I,(-b,-c,-a)}$
, which equals
$p^{2}\unicode[STIX]{x1D713}_{b}(p)^{-1}$
(respectively
$p^{3}\unicode[STIX]{x1D713}_{b}(p)^{-1}\unicode[STIX]{x1D713}_{c}(p)^{-1}$
) by Lemma 3.2.8, has positive valuation. (Note for later reference that this is true even if
$\text{FL}(\overline{r}|_{G_{F_{w}}})\in \{0,\infty \}$
.)
Note that the image
$\mathbb{T}_{a}$
of
$\mathbb{T}^{{\mathcal{P}}}$
in
$\operatorname{End}(M)$
is local with maximal ideal the image of
$\mathfrak{m}_{\overline{r}}$
. As
$\mathbb{T}_{a}\subseteq \mathbb{T}$
is a finite ring extension,
$\mathfrak{m}_{\overline{r}}\subseteq \operatorname{rad}(\mathbb{T})$
. Since all eigenvalues of
$U_{i}$
on
$M_{\overline{\mathbb{Q}}_{p}}$
have positive valuation, we deduce that
$U_{i}\in \operatorname{rad}(\mathbb{T})$
(
$i=1$
,
$2$
). It then follows that
$\mathbb{T}$
is local with maximal ideal
$\mathfrak{m}$
generated by
$\mathfrak{m}_{\overline{r}}$
,
$U_{1}$
, and
$U_{2}$
. As
$\mathbb{T}_{\overline{\mathbb{Q}}_{p}}$
acts faithfully and semisimply on
$M_{\overline{\mathbb{Q}}_{p}}$
(by (4.5.5)), we see that
$\mathbb{T}_{\overline{\mathbb{Q}}_{p}}$
is semisimple, hence reduced. In particular,
$\mathbb{T}$
is reduced.
As
$U$
is sufficiently small, our assumptions as well as the statement we want to prove is insensitive to a finite base change
$E\rightarrow E^{\prime }$
. Hence, by passing to a finite extension of
$E$
, we may assume that
$\mathbb{T}_{E}\cong E^{r}$
for some
$r>0$
.
We have
$M_{E}=\bigoplus _{\mathfrak{p}}M_{E}[\mathfrak{p}_{E}]$
, where the sum runs over the minimal primes of
$\mathbb{T}$
and
$\mathfrak{p}_{E}\stackrel{\text{def}}{=}\mathfrak{p}\mathbb{T}_{E}$
. Note that, by the above,
$\mathbb{T}_{E}/\mathfrak{p}_{E}=E$
for any such
$\mathfrak{p}$
. Then
$M_{E}[\mathfrak{p}_{E}]\otimes _{E}\overline{\mathbb{Q}}_{p}$
is a direct summand of (4.5.5), where
$\unicode[STIX]{x1D70B}$
runs over a subset of the automorphic representations in (4.5.5), and we claim that each
$\unicode[STIX]{x1D70B}_{v}$
occurring in this direct summand is the same. To see this, note that
$r_{\unicode[STIX]{x1D70B}}$
is determined by
$\mathfrak{p}$
, by using Cebotarev density and classical local-global compatibility at the places in
${\mathcal{P}}$
. (Note that classical local-global compatibility, which is known only up to Frobenius-semisimplification, determines
$\operatorname{tr}(r_{\unicode[STIX]{x1D70B}}|_{G_{F_{w^{\prime }}}})$
for
$w^{\prime }\in {\mathcal{P}}$
and that
$\operatorname{tr}(r_{\unicode[STIX]{x1D70B}})$
determines
$r_{\unicode[STIX]{x1D70B}}$
.) Then we deduce the claim from classical local-global compatibility at
$w$
.
By Proposition 3.2.2 we have
$$\begin{eqnarray}\widehat{S}^{\prime }\circ \unicode[STIX]{x1D6F1}=\frac{\unicode[STIX]{x1D713}_{b}(p)}{p}\unicode[STIX]{x1D705}\,\widehat{S}\end{eqnarray}$$
on
$M_{E}[\mathfrak{p}_{E}]$
, where
$\unicode[STIX]{x1D705}\in \mathbb{Z}_{p}^{\times }$
is such that
$\unicode[STIX]{x1D705}\equiv (-1)^{a-b}\cdot (b-c)/(a-b)$
mod
$p$
and where
$\widehat{S},\,\widehat{S}^{\prime }\in {\mathcal{O}}_{E}[\operatorname{GL}_{3}(\mathbb{F}_{p})]$
are obtained from (3.2.1) by setting
$(a_{2},a_{1},a_{0})=(-c,-b,-a)$
.
Let
$M^{\text{d}}\stackrel{\text{def}}{=}\operatorname{Hom}_{{\mathcal{O}}_{E}}(M,{\mathcal{O}}_{E})$
, which is finite free over
$\mathbb{T}$
by assumption (iii). Fix any minimal prime
$\mathfrak{p}$
of
$\mathbb{T}$
. As
$\mathbb{T}_{E}/\mathfrak{p}_{E}=E$
we have
$\mathbb{T}/\mathfrak{p}={\mathcal{O}}_{E}$
, so in particular
$M^{\text{d}}/\mathfrak{p}$
is a finite free
${\mathcal{O}}_{E}$
-module. The identity (4.5.7) holds also on
$M_{E}^{\text{d}}/\mathfrak{p}_{E}\cong \operatorname{Hom}_{E}(M_{E}[\mathfrak{p}_{E}],E)$
and on its submodule
$M^{\text{d}}/\mathfrak{p}$
. By (4.5.7) and (4.5.6), and since
$\mathfrak{p}+\unicode[STIX]{x1D71B}_{E}\mathbb{T}=\mathfrak{m}$
, we deduce the identity (4.5.3) on
$(M^{\text{d}}/\mathfrak{p})\otimes _{{\mathcal{O}}_{E}}\mathbb{F}\cong M^{\text{d}}/\mathfrak{m}$
, hence also on
$M_{\mathbb{F}}[\mathfrak{m}]\cong \operatorname{Hom}_{\mathbb{F}}(M^{\text{d}}/\mathfrak{m},\mathbb{F})$
. Now observe that
$M_{\mathbb{F}}\cong S(U^{v},V^{\prime })_{\mathfrak{m}_{\overline{r}}}^{I,(-b,-c,-a)}$
and hence
$M_{\mathbb{F}}[\mathfrak{m}]\cong S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]^{I,(-b,-c,-a)}[U_{1},U_{2}]$
.
We claim that
$U_{i}\unicode[STIX]{x1D6F1}(M_{\mathbb{F}}[\mathfrak{m}])=0$
for
$i=1$
,
$2$
. Let
$N\stackrel{\text{def}}{=}S(U^{v},\widetilde{V}^{\prime })_{\mathfrak{m}_{\overline{r}}}^{I,(-c,-a,-b)}$
and let
$\mathbb{T}^{\prime }\subseteq \operatorname{End}(N)$
be the
${\mathcal{O}}_{E}$
-subalgebra generated by
$\mathbb{T}^{{\mathcal{P}}}$
,
$U_{1}$
, and
$U_{2}$
. By above,
$\unicode[STIX]{x1D6F1}(M[\mathfrak{p}])\subseteq N[\mathfrak{p}^{\prime }]$
for the minimal prime
$\mathfrak{p}^{\prime }$
of
$\mathbb{T}^{\prime }$
lying over the same prime of
$\mathbb{T}^{{\mathcal{P}}}$
as
$\mathfrak{p}$
such that, moreover, the image of
$U_{i}$
in
$\mathbb{T}^{\prime }/\mathfrak{p}^{\prime }={\mathcal{O}}_{E}$
equals the eigenvalue of
$U_{i}$
on
$\unicode[STIX]{x1D70B}_{v}^{I,(-c,-a,-b)}$
. (In fact,
$\unicode[STIX]{x1D6F1}(M[\mathfrak{p}])=N[\mathfrak{p}^{\prime }]$
, by reversing the argument.) From the above, the natural injection
$M[\mathfrak{p}]\otimes _{{\mathcal{O}}_{E}}\mathbb{F}{\hookrightarrow}M_{\mathbb{F}}[\mathfrak{m}]$
is an isomorphism, so
$\unicode[STIX]{x1D6F1}(M_{\mathbb{F}}[\mathfrak{m}])$
is killed by the unique maximal ideal
$\mathfrak{m}^{\prime }$
of
$\mathbb{T}^{\prime }$
, which contains
$U_{1}$
,
$U_{2}$
by the same argument as for
$\mathbb{T}$
. This proves the claim. (In fact, if
$\operatorname{Hom}_{{\mathcal{O}}_{E}}(N,{\mathcal{O}}_{E})$
is, moreover, free as
$\mathbb{T}^{\prime }$
-module, which is true under the hypotheses of Theorem 5.1.1, then we even get that
$\unicode[STIX]{x1D6F1}$
induces an isomorphism
$M_{\mathbb{F}}[\mathfrak{m}]\xrightarrow[{}]{\,\sim \,}N_{\mathbb{F}}[\mathfrak{m}^{\prime }]$
.)
Now by Theorem 4.4.1(i) and [Reference Emerton, Gee and HerzigEGH13, Lemma 7.4.3] any irreducible
$K$
-subrepresentation of
$S(U^{v},V^{\prime })_{\mathfrak{m}_{\overline{r}}}$
is isomorphic to
$F(-c-1,-b,-a+1)$
or
$F(-a+p-1,-b,-c-p+1)$
. Thus by Corollary 3.1.12(i), if
$v\in M_{\mathbb{F}}[\mathfrak{m}]$
is non-zero, then
$\langle Kv\rangle _{\mathbb{F}}$
is the unique quotient of
$\operatorname{Ind}_{I}^{K}\big(\unicode[STIX]{x1D714}^{-b}\,\otimes \,\unicode[STIX]{x1D714}^{-c}\,\otimes \,\unicode[STIX]{x1D714}^{-a}\big)$
with socle
$F(-c-1,-b,-a+1)$
. By [Reference LeLe15, Proposition 2.2.2] we see that
$\langle Kv\rangle _{\mathbb{F}}$
is the uniserial length 2 representation of shape
$F(-c-1,-b,-a+1)\text{}\text{—}F(-b+p-1,-c,-a)$
. A similar argument shows that
$\langle K\unicode[STIX]{x1D6F1}v\rangle _{\mathbb{F}}$
is the uniserial length 2 representation of shape
$F(-c-1,-b,-a+1)\text{}\text{—}F(-c,-a,-b-p+1)$
. In particular,
$Sv\neq 0$
by Proposition 3.1.2.◻
Remark 4.5.8. Theorem 4.5.2 holds equally well if we replace
$\mathbb{T}$
in the statement and proof by the subalgebra
$\mathbb{T}_{2}\subseteq \mathbb{T}$
generated by
$\mathbb{T}^{{\mathcal{P}}}$
and
$U_{2}$
. Assumption (iii) will be verified in § 5 both for
$\mathbb{T}_{2}$
and for
$\mathbb{T}$
, under suitable hypotheses. The same comments apply for the subalgebra
$\mathbb{T}_{a}\subseteq \mathbb{T}$
, provided
$W_{w}(\overline{r})=\{F(a-1,b,c+1)\}$
(see Remark 5.3.5).
Remark 4.5.9. Theorem 4.5.2 holds if we replace assumption (iii) by either of the following two statements:
It suffices to note that (iii
$^{\prime \prime }$
)
$\Rightarrow$
(iii
$^{\prime }$
)
$\Rightarrow$
(iii). The first implication is obvious. For the second, we have
$\dim _{\mathbb{F}}M^{\text{d}}/\mathfrak{m}=\dim _{\mathbb{F}}M_{\mathbb{F}}[\mathfrak{m}]=1$
, in the notation of the proof. As in the proof, we may assume that
$\mathbb{T}/\mathfrak{m}=\mathbb{F}$
. By Nakayama’s lemma, we have a surjective
$\mathbb{T}$
-linear map
$\mathbb{T}{\twoheadrightarrow}M^{\text{d}}$
, which has to be an isomorphism, as
$M^{\text{d}}$
is a faithful
$\mathbb{T}$
-module. (Note that assumption (iii
$^{\prime \prime }$
) even implies that
$\mathbb{T}_{a}=\mathbb{T}$
.)
We now establish the existence of shadow weights in Theorem 4.4.1, thereby completing the proof of that theorem.
Proposition 4.5.10. Suppose
$\overline{r}$
satisfies assumption (i) of Theorem 4.5.2.
-
(i) If
$\text{FL}(\overline{r}|_{G_{F_{w}}})=\infty$
, then
$F(a,c,b-p+1)\in W_{w}(\overline{r})$
. -
(ii) If
$\text{FL}(\overline{r}|_{G_{F_{w}}})=0$
, then
$F(b+p-1,a,c)\in W_{w}(\overline{r})$
.
Remark 4.5.11. Suppose that
$\overline{r}$
is as in Proposition 4.5.10(i). Then the proof below shows that for some non-zero
$v\in S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]^{I,(-b,-c,-a)}[U_{1},U_{2}]$
, the
$K$
-subrepresentation generated by
$v$
and
$\unicode[STIX]{x1D6F1}v$
is of the form
$$\begin{eqnarray}F(-b+p-1,-c,-a)\oplus (F(-c-1,-b,-a+1)\text{}\text{—}F(-c,-a,-b-p+1)).\end{eqnarray}$$
In particular,
$Sv=0$
,
$S^{\prime }\unicode[STIX]{x1D6F1}v\neq 0$
. Similar remarks apply in case
$\text{FL}(\overline{r}|_{G_{F_{w}}})=0$
.
Proof. (i) We follow the proof of Theorem 4.5.2, noting that with our current assumption only three things change: (a) we get
$\text{ord}_{p}(\unicode[STIX]{x1D713}_{b}(p))<1$
instead of (4.5.6), (b) the natural injection
$M[\mathfrak{p}]\otimes _{{\mathcal{O}}_{E}}\mathbb{F}{\hookrightarrow}M_{\mathbb{F}}[\mathfrak{m}]$
need not be an isomorphism, and (c) we only know that
$\langle Kv\rangle _{\mathbb{F}}$
(for non-zero
$v\in M_{\mathbb{F}}[\mathfrak{m}]$
) is a quotient of the uniserial representation of shape
$F(-c-1,-b,-a+1)\text{}\text{—}F(-b+p-1,-c,-a)$
. From (a) we deduce that
$\widehat{S}=(p/\unicode[STIX]{x1D713}_{b}(p))\unicode[STIX]{x1D705}^{-1}\,\widehat{S}^{\prime }\circ \unicode[STIX]{x1D6F1}$
on
$M_{E}[\mathfrak{p}_{E}]$
, so
$Sv=0$
for some non-zero
$v\in M_{\mathbb{F}}[\mathfrak{m}]$
(but maybe not all, see (b)). Then (c) together with Proposition 3.1.2 implies that
$\langle Kv\rangle _{\mathbb{F}}\cong F(-b+p-1,-c,-a)$
for such
$v$
. In particular,
$F(a,c,b-p+1)\in W_{w}(\overline{r})$
. Part (ii) is analogous.◻
5 Freeness over the Hecke algebra
In this section, we prove Theorem 5.1.1, which states that the dual
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{O}}_{E}}(S(U^{v},\widetilde{V}^{\prime })_{\mathfrak{ m}_{\overline{r}}}^{I,(-b,-c,-a)},{\mathcal{O}}_{E})\end{eqnarray}$$
of the space of automorphic forms is free over a Hecke algebra under certain conditions on
$U^{v}$
and
$\overline{r}$
(and
$\widetilde{V}^{\prime }$
and
$\mathfrak{m}_{\overline{r}}$
are as defined in § 4.2).
5.1 The setup
As before, let
$F/\mathbb{Q}$
be a CM field in which
$p$
splits completely, and let
$F^{+}$
be its maximal totally real subfield. Assume moreover the following.
-
(i) The extension
$F/F^{+}$
is unramified at all finite places.
Fix a place
$w|p$
of
$F$
, and let
$v\stackrel{\text{def}}{=}w|_{F^{+}}$
. Let
$\overline{r}:G_{F}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
be a Galois representation with
$\overline{r}|_{G_{F_{w}}}$
maximally non-split and generic as in Theorem 4.5.2(i), satisfying the following additional properties:
-
(ii)
$\overline{r}$
is unramified at all finite places not dividing
$p$
; -
(iii)
$\overline{r}$
is Fontaine–Laffaille and regular at all places dividing
$p$
; -
(iv)
$\overline{r}$
has image containing
$\operatorname{GL}_{3}(k)$
for some
$k\subseteq \mathbb{F}$
with
$\#k>9$
; -
(v)
$\overline{F}^{\ker \operatorname{ad}\overline{r}}$
does not contain
$F(\unicode[STIX]{x1D701}_{p})$
.
Note that condition (iv), which is stronger than the usual condition of adequacy (see [Reference ThorneTho12, Definition 2.3]), allows us to choose a finite place
$v_{1}$
of
$F^{+}$
which is prime to
$p$
satisfying the following properties (see [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 2.3]):
-
∙
$v_{1}$
splits in
$F$
as
$v_{1}=w_{1}w_{1}^{c}$
; -
∙
$v_{1}$
does not split completely in
$F(\unicode[STIX]{x1D701}_{p})$
; -
∙
$\overline{r}(\operatorname{Frob}_{w_{1}})$
has distinct
$\mathbb{F}$
-rational eigenvalues, no two of which have ratio
$(\mathbf{N}v_{1})^{\pm 1}$
.
We choose a unitary group
$G_{/F^{+}}$
and a model
${\mathcal{G}}_{/{\mathcal{O}}_{F^{+}}}$
as in § 4.1. We note that
$G$
is automatically quasi-split, hence unramified by (i), at all finite places, as we are in odd rank. (See the proof of [Reference Bellaïche and ChenevierBC09, Lemma 6.2.4].) Let
$U^{v}=\prod _{v^{\prime }\neq v}U_{v^{\prime }}\leqslant G(\mathbb{A}_{F^{+}}^{\infty ,v})$
be a compact open subgroup satisfying the following properties:
-
(vi)
$U_{v^{\prime }}={\mathcal{G}}({\mathcal{O}}_{F_{v^{\prime }}^{+}})$
for all places
$v^{\prime }$
which split in
$F$
other than
$v_{1}$
and those dividing
$p$
; -
(vii)
$U_{v_{1}}$
is the preimage of the upper-triangular matrices under the map
$$\begin{eqnarray}{\mathcal{G}}({\mathcal{O}}_{F_{v_{1}}^{+}})\rightarrow {\mathcal{G}}(k_{v_{1}})\underset{\unicode[STIX]{x1D704}_{w_{1}}}{\stackrel{{\sim}}{\longrightarrow }}\operatorname{GL}_{3}(k_{w_{1}});\end{eqnarray}$$
-
(viii)
$U_{v^{\prime }}$
is a hyperspecial maximal compact open subgroup of
$G(F_{v^{\prime }}^{+})$
if
$v^{\prime }$
is inert in
$F$
.
The choice of
$U_{v_{1}}$
implies that
$U^{v}U_{v}$
is sufficiently small in the sense of § 4.1 for any compact open subgroup
$U_{v}$
of
$G(F_{v}^{+})$
.
As in § 4.2 suppose that for each
$w^{\prime }\in S_{p}\setminus \{w,w^{c}\}$
we are given a
$p$
-restricted triple
$a_{w^{\prime }}=(a_{w^{\prime },2},a_{w^{\prime },1},a_{w^{\prime },0})\in \mathbb{Z}^{3}$
such that
$a_{w^{\prime },i}+a_{{w^{\prime }}^{c},2-i}=0$
for all
$0\leqslant i\leqslant 2$
and all
$w^{\prime }\in S_{p}\setminus \{w,w^{c}\}$
. Suppose moreover that
$a_{w^{\prime },2}-a_{w^{\prime },0}<p-3$
, for all
$w^{\prime }\in S_{p}\setminus \{w,w^{c}\}$
, a slightly stronger condition than before. Recall that we defined
$V^{\prime }=\bigotimes _{v^{\prime }\in S_{p}^{+}\setminus \{v\}}F_{a_{v^{\prime }}}$
and
$\widetilde{V}^{\prime }=\bigotimes _{v^{\prime }\in S_{p}^{+}\setminus \{v\}}W_{a_{v^{\prime }}}$
.
Let
${\mathcal{P}}$
denote the set of finite places
$w^{\prime }$
of
$F$
that split over
$F^{+}$
and do not divide
$p$
or
$v_{1}$
, and define the maximal ideal
$\mathfrak{m}_{\overline{r}}$
of
$\mathbb{T}^{{\mathcal{P}}}$
as in § 4.2. We make the additional automorphy assumption:
-
(ix)
$S(U^{v},V^{\prime })_{\mathfrak{m}_{\overline{r}}}$
is non-zero.
By Theorem 4.4.1 this implies
$S(U^{v}{\mathcal{G}}({\mathcal{O}}_{F_{v}^{+}}),V^{\prime }\,\otimes \,F(a-1,b,c+1))_{\mathfrak{m}_{\overline{r}}}\neq 0$
and hence also assumptions (ii)–(iii) above. As in the proof of Theorem 4.5.2 this also implies that
$S(U^{v},\widetilde{V}^{\prime })_{\mathfrak{m}_{\overline{r}}}^{I,(-b,-c,-a)}$
is non-zero.
Let
$\mathbb{T}_{a}$
(respectively
$\mathbb{T}$
) denote the
${\mathcal{O}}_{E}$
-subalgebra of
$$\begin{eqnarray}\operatorname{End}(S(U^{v},\widetilde{V}^{\prime })_{\mathfrak{ m}_{\overline{r}}}^{I,(-b,-c,-a)})\cong \operatorname{End}((S(U^{v},\widetilde{V}^{\prime })_{\mathfrak{ m}_{\overline{r}}}^{I,(-b,-c,-a)})^{\text{d}})\end{eqnarray}$$
generated by
$\mathbb{T}^{{\mathcal{P}}}$
(respectively
$\mathbb{T}^{{\mathcal{P}}}$
,
$U_{1}$
, and
$U_{2}$
). Here the subscript ‘
$a$
’ stands for the ‘anemic’ Hecke algebra, and the superscript ‘
$\text{d}$
’ denotes the Schikhof dual (see [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 1.8]). Note that
$\mathbb{T}_{a}$
and
$\mathbb{T}$
are local
${\mathcal{O}}_{E}$
-algebras (see the proof of Theorem 4.5.2).
Theorem 5.1.1. Let
$\overline{r}$
be as in Theorem 4.5.2(i) with
$\text{FL}(\overline{r}|_{G_{F_{w}}})\neq \infty$
. Assume (i)–(ix) in the setup above. Then
$$\begin{eqnarray}(S(U^{v},\widetilde{V}^{\prime })_{\mathfrak{ m}_{\overline{r}}}^{I,(-b,-c,-a)})^{\text{d}}\end{eqnarray}$$
is free over
$\mathbb{T}$
.
Because of the following lemma, we may assume in the proof of Theorem 5.1.1 that
$E$
is as large as we like. (In fact, for the remainder of this section it will suffice to assume that
$E$
is large enough such that
$\mathbb{T}_{a}[1/p]\cong E^{r}$
for some
$r$
and that
$\mathbb{T}/\mathfrak{m}_{\mathbb{T}}=\mathbb{F}$
.)
Lemma 5.1.2. Suppose that
$M$
is a finite free
${\mathcal{O}}_{E}$
-module and that
$A$
is a local
${\mathcal{O}}_{E}$
-algebra acting faithfully on
$M$
with
$A/\mathfrak{m}_{A}=\mathbb{F}$
. If
$E^{\prime }/E$
is a finite extension and
$M\,\otimes _{{\mathcal{O}}_{E}}\,{\mathcal{O}}_{E^{\prime }}$
is free over
$A\,\otimes _{{\mathcal{O}}_{E}}\,{\mathcal{O}}_{E^{\prime }}$
, then
$M$
is free over
$A$
.
Proof. As
$A/\mathfrak{m}_{A}=\mathbb{F}$
we deduce that
$A\,\otimes _{{\mathcal{O}}_{E}}{\mathcal{O}}_{E^{\prime }}$
is local with residue field
${\mathcal{O}}_{E^{\prime }}/\mathfrak{m}_{E^{\prime }}$
. Pick any surjection
$f:A^{d}{\twoheadrightarrow}M$
with
$d$
minimal. It is easy to see that
$f\,\otimes _{{\mathcal{O}}_{E}}{\mathcal{O}}_{E^{\prime }}$
is an isomorphism, hence so is
$f$
.◻
5.2 The Taylor–Wiles method
Let
$S$
be the set of places
$S_{p}^{+}\cup \{v_{1}\}$
. For each place
$v^{\prime }$
in
$S$
, fix a place
$\widetilde{v}^{\prime }$
of
$F$
lying over
$v^{\prime }$
and let
$\widetilde{S}$
be the set of these places
$\widetilde{v}^{\prime }$
. We will assume that
$\widetilde{v}=w$
. For places
$w^{\prime }$
in
$F$
, let
$R_{w^{\prime }}^{\Box }$
be the universal
${\mathcal{O}}_{E}$
-lifting ring of
$\overline{r}|_{G_{F_{w^{\prime }}}}^{\vee }$
. For
$w^{\prime }\in S_{p}\setminus \{w,w^{c}\}$
let
$\unicode[STIX]{x1D713}_{w^{\prime }}=a_{w^{\prime }}\in \mathbb{Z}^{3}$
and let
$R_{w^{\prime }}^{\Box ,\unicode[STIX]{x1D713}_{w^{\prime }}}$
be the framed crystalline deformation ring for
$\overline{r}|_{G_{F_{w^{\prime }}}}^{\vee }$
of Hodge–Tate weights
$\unicode[STIX]{x1D713}_{w^{\prime }}+(2,1,0)$
. Let
$\unicode[STIX]{x1D6FF}_{F/F^{+}}$
denote the quadratic character of
$F/F^{+}$
. Consider the deformation problem
$$\begin{eqnarray}{\mathcal{S}}\stackrel{\text{def}}{=}(F/F^{+},S,\widetilde{S},{\mathcal{O}}_{E},\overline{r}^{\vee },\unicode[STIX]{x1D700}^{-2}\unicode[STIX]{x1D6FF}_{F/F^{+}},\{R_{\widetilde{v}_{1}}^{\Box }\}\cup \{R_{\widetilde{v}^{\prime }}^{\Box ,\unicode[STIX]{x1D713}_{\widetilde{v}^{\prime }}}\}_{v^{\prime }|p,v^{\prime }\neq v}\cup \{R_{\widetilde{v}}^{\Box }\})\end{eqnarray}$$
in the terminology of [Reference Clozel, Harris and TaylorCHT08, § 2.3]. There is a universal deformation ring
$R_{{\mathcal{S}}}^{\text{univ}}$
and a universal
$S$
-framed deformation ring
$R_{{\mathcal{S}}}^{\Box _{S}}$
in the sense of [Reference Clozel, Harris and TaylorCHT08, § 2.2]. (We work with deformations of
$\overline{r}^{\vee }$
to be consistent with [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16]. Note that
$\overline{r}^{\vee }(\operatorname{Frob}_{w})$
is used in our definition of
$\mathfrak{m}_{\overline{r}}$
in § 4.2.)
Let
$$\begin{eqnarray}R^{\text{loc}}\stackrel{\text{def}}{=}\widehat{\otimes }_{v^{\prime }|p,v^{\prime }\neq v}\,R_{\widetilde{v}^{\prime }}^{\Box ,\unicode[STIX]{x1D713}_{\widetilde{v}^{\prime }}}\,\widehat{\otimes }\,R_{\widetilde{v}}^{\Box }\,\widehat{\otimes }\,R_{\widetilde{v}_{1}}^{\Box },\end{eqnarray}$$
where all completed tensor products are taken over
${\mathcal{O}}_{E}$
. Choose an integer
$q\geqslant 3[F^{+}:\mathbb{Q}]$
as in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 2.6]. We introduce the local ring
$$\begin{eqnarray}R_{\infty }\stackrel{\text{def}}{=}R^{\text{loc}}[[x_{1},\ldots ,x_{q-3[F^{+}:\mathbb{Q}]}]],\end{eqnarray}$$
over which [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] constructs a patched module of automorphic forms. Let
$\unicode[STIX]{x1D70F}\stackrel{\text{def}}{=}\operatorname{Ind}_{I}^{K}(\widetilde{\unicode[STIX]{x1D714}}^{-b}\,\otimes \,\widetilde{\unicode[STIX]{x1D714}}^{-c}\,\otimes \,\widetilde{\unicode[STIX]{x1D714}}^{-a})\,\otimes _{\mathbb{Z}_{p}}\,{\mathcal{O}}_{E}$
be the natural
${\mathcal{O}}_{E}$
-lattice in a principal series type over
$E$
. In the following we will identify
$G(F_{v}^{+})$
with
$\operatorname{GL}_{3}(\mathbb{Q}_{p})$
and
${\mathcal{G}}({\mathcal{O}}_{F_{v}^{+}})$
with
$K=\operatorname{GL}_{3}(\mathbb{Z}_{p})$
via
$\unicode[STIX]{x1D704}_{w}$
. We collect some results from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16].
Theorem 5.2.1. There exist a map
$$\begin{eqnarray}S_{\infty }\stackrel{\text{def}}{=}{\mathcal{O}}_{E}[[z_{1},\ldots ,z_{9\#S},y_{1},\ldots ,y_{q}]]\rightarrow R_{\infty }\end{eqnarray}$$
and an
$R_{\infty }[[K]]$
-module
$M_{\infty }$
together with a compatible
$\operatorname{GL}_{3}(\mathbb{Q}_{p})$
-action, satisfying the following properties. For a finitely generated
${\mathcal{O}}_{E}$
-module
$W$
with continuous
$K$
-action, let
$M_{\infty }(W)$
denote
$\operatorname{Hom}_{K}^{\text{cont}}(W,M_{\infty }^{\vee })^{\vee }$
, where
$\cdot ^{\vee }$
denotes the Pontryagin dual.
-
(i) We have that
$M_{\infty }$
is a finitely generated projective
$S_{\infty }[[K]]$
-module. In particular, if
$W$
is
$p$
-torsion free, then
$M_{\infty }(W)$
is a finite free
$S_{\infty }$
-module. -
(ii) Suppose that
$W[1/p]$
is a locally algebraic type (as defined in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 4]). Assume that
$M_{\infty }(W)$
is non-zero and let
$\operatorname{Spec}R_{\infty }(W)$
be its support in
$\operatorname{Spec}R_{\infty }$
. Then
$M_{\infty }(W)$
is a maximal Cohen–Macaulay
$R_{\infty }(W)$
-module and
$M_{\infty }(W)[1/p]$
is a projective
$R_{\infty }(W)[1/p]$
-module. -
(iii) Let
$\mathfrak{a}\stackrel{\text{def}}{=}(z_{1},\ldots ,z_{9\#S},y_{1},\ldots ,y_{q})$
be the augmentation ideal of
$S_{\infty }$
. There is a natural
$\operatorname{GL}_{3}(\mathbb{Q}_{p})$
-equivariant identification which induces a
$$\begin{eqnarray}(M_{\infty }/\mathfrak{a})^{\text{d}}\cong \widetilde{S}(U^{v},\widetilde{V}^{\prime })_{\mathfrak{ m}_{\overline{r}}},\end{eqnarray}$$
$\operatorname{GL}_{3}(\mathbb{Q}_{p})$
-equivariant identification Furthermore, there is a surjection
$$\begin{eqnarray}(M_{\infty }(\unicode[STIX]{x1D70F})/\mathfrak{a})^{\text{d}}\cong S(U^{v},\widetilde{V}^{\prime })_{\mathfrak{ m}_{\overline{r}}}^{I,(-b,-c,-a)}.\end{eqnarray}$$
$R_{\infty }{\twoheadrightarrow}\mathbb{T}_{a}$
so that the latter identification is
$R_{\infty }$
-equivariant.
-
(iv) Let
${\wp}_{r}$
denote the prime ideal of
$R_{\infty }$
corresponding to an
${\mathcal{O}}_{E}$
-point of
$\operatorname{Spec}\mathbb{T}_{a}$
and by abuse, the corresponding prime ideal of
$\mathbb{T}^{{\mathcal{P}}}$
. By abuse, let
$\mathfrak{m}_{\overline{r}}$
also denote the maximal ideal of
$R_{\infty }$
. Then and
$$\begin{eqnarray}(M_{\infty }(\unicode[STIX]{x1D70F})/{\wp}_{r})^{\text{d}}\cong S(U^{v},\widetilde{V}^{\prime })[{\wp}_{r}]^{I,(-b,-c,-a)}\end{eqnarray}$$
$$\begin{eqnarray}(M_{\infty }(\unicode[STIX]{x1D70F})/\mathfrak{m}_{\overline{r}})^{\vee }\cong S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]^{I,(-b,-c,-a)}.\end{eqnarray}$$
Note that if
$W$
is
$p$
-torsion free, we have
$M_{\infty }(W)\cong \operatorname{Hom}_{K}^{\text{cont}}(W,M_{\infty }^{\text{d}})^{\text{d}}$
by [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Remark 4.15].
Proof. The construction of
$M_{\infty }$
is in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 2.8], except that we allow the Hodge–Tate weights
$\unicode[STIX]{x1D713}_{\widetilde{v}^{\prime }}$
to depend on
$v^{\prime }$
, and we do not include Hecke operators at
$v_{1}$
in our Hecke algebras. Without these Hecke operators, the rank of
$M_{\infty }(W)[1/p]$
as a projective
$R_{\infty }(W)[1/p]$
-module in part (ii) is greater than one. Otherwise, the necessary modifications are minor and straightforward. The map
$$\begin{eqnarray}S_{\infty }={\mathcal{O}}_{E}[[z_{1},\ldots ,z_{9\#S},y_{1},\ldots ,y_{q}]]\rightarrow R_{\infty }\end{eqnarray}$$
and the module
$M_{\infty }$
are defined in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 2.8]. Part (i) follows from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Proposition 2.10 and the proof of Lemma 4.18(1)]. Part (ii) follows from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Lemma 4.18(1)].
The first identification in part (iii) follows from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Corollary 2.11]. For the second identification, we have
$$\begin{eqnarray}\displaystyle (M_{\infty }(\unicode[STIX]{x1D70F})/\mathfrak{a})^{\text{d}}\cong \operatorname{Hom}_{K}^{\text{cont}}(\unicode[STIX]{x1D70F},M_{\infty }^{\text{d}})[\mathfrak{a}] & \cong & \displaystyle \operatorname{Hom}_{K}^{\text{cont}}(\unicode[STIX]{x1D70F},(M_{\infty }/\mathfrak{a})^{\text{d}})\nonumber\\ \displaystyle & \cong & \displaystyle ((M_{\infty }/\mathfrak{a})^{\text{d}})^{I,(-b,-c,-a)},\nonumber\end{eqnarray}$$
where the first isomorphism follows from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Remark 4.15] and the final isomorphism follows from Frobenius reciprocity.
We now define the map
$R_{\infty }{\twoheadrightarrow}\mathbb{T}_{a}$
. The surjection
$R_{\infty }{\twoheadrightarrow}\mathbb{T}_{a}$
comes from the construction in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 2.8], as we now explain. We will freely use the notation of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 2.8] with the caveat that we exclude the Hecke operators at
$v_{1}$
from our Hecke algebras (which allows us to deduce that the maps from
$R_{\infty }$
to our Hecke algebras are surjections). The patching argument produces compatible tuples
$(\unicode[STIX]{x1D719},M^{\Box },\unicode[STIX]{x1D713},\unicode[STIX]{x1D6FC})$
of all levels
$N\geqslant 1$
. Since the intersection
$\bigcap _{N}\mathfrak{d}_{N}$
is
$0$
, by completeness, the maps
$\unicode[STIX]{x1D719}:R_{\infty }{\twoheadrightarrow}R_{{\mathcal{S}}}^{\text{univ}}/\mathfrak{d}_{N}$
induce a surjection
$R_{\infty }{\twoheadrightarrow}R_{{\mathcal{S}}}^{\text{univ}}$
. Furthermore, in the paragraph before [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Corollary 2.11], a map
$R_{{\mathcal{S}}}^{\text{univ}}\rightarrow \mathbb{T}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}}^{S_{p}}(U^{\mathfrak{p}},{\mathcal{O}})_{\mathfrak{m}}$
is described as the inverse limit of maps
$R_{{\mathcal{S}}}^{\text{univ}}\rightarrow \mathbb{T}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}}^{S_{p}}(U_{m},{\mathcal{O}})_{\mathfrak{m}}$
(or equivalently of maps
$R_{{\mathcal{S}}}^{\text{univ}}\rightarrow \mathbb{T}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}}^{S_{p}}(U_{2N},{\mathcal{O}}/\unicode[STIX]{x1D71B}^{N})_{\mathfrak{m}}$
) at finite level. Using the explicit generators given by the surjection
$\mathbb{T}^{S_{p},\text{univ}}{\twoheadrightarrow}\mathbb{T}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}}^{S_{p}}(U^{\mathfrak{p}},{\mathcal{O}})_{\mathfrak{m}}$
(again for us with operators at
$v_{1}$
excluded) and [Reference Clozel, Harris and TaylorCHT08, Proposition 3.4.4(2)], each of these maps at finite level is surjective. By completeness, the map
$R_{{\mathcal{S}}}^{\text{univ}}\rightarrow \mathbb{T}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}}^{S_{p}}(U^{\mathfrak{p}},{\mathcal{O}})_{\mathfrak{m}}$
is surjective. We conclude that the composition
$R_{\infty }\rightarrow R_{{\mathcal{S}}}^{\text{univ}}\rightarrow \mathbb{T}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}}^{S_{p}}(U^{\mathfrak{p}},{\mathcal{O}})_{\mathfrak{m}}$
is surjective. Composing with the natural map
$\mathbb{T}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}}^{S_{p}}(U^{\mathfrak{p}},{\mathcal{O}})_{\mathfrak{m}}{\twoheadrightarrow}\mathbb{T}_{a}$
gives a surjective homomorphism
$R_{\infty }{\twoheadrightarrow}\mathbb{T}_{a}$
.
The proof of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Corollary 2.11] shows that the first identification of part (iii) is
$R_{\infty }$
-equivariant, with
$R_{\infty }$
acting via the map
$R_{{\mathcal{S}}}^{\text{univ}}\rightarrow \mathbb{T}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}}^{S_{p}}(U^{\mathfrak{p}},{\mathcal{O}})_{\mathfrak{m}}$
on the right-hand side, since at each finite level
$N$
, the map
$\unicode[STIX]{x1D713}:M^{\Box }/\mathfrak{a}\xrightarrow[{}]{\,\sim \,}\tilde{S}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}}(U_{2N},{\mathcal{O}}/\unicode[STIX]{x1D71B}^{N})_{\mathfrak{m}}$
is
$R_{\infty }$
-equivariant, with
$R_{\infty }$
acting via the map
$R_{{\mathcal{S}}}^{\text{univ}}\rightarrow \mathbb{T}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}}^{S_{p}}(U_{2N},{\mathcal{O}}/\unicode[STIX]{x1D71B}^{N})_{\mathfrak{m}}$
on the right-hand side. This shows that the second identification is also
$R_{\infty }$
-equivariant, with
$R_{\infty }$
acting on the right-hand side via the map
$R_{\infty }{\twoheadrightarrow}\mathbb{T}_{a}$
constructed above. Part (iv) follows from part (iii), noting that
$\mathfrak{a}\subseteq \ker (R_{\infty }\rightarrow \mathbb{T}_{a})$
by part (iii).◻
Let
$R$
be the
$R_{\infty }$
-subalgebra of
$\operatorname{End}_{R_{\infty }}(M_{\infty }(\unicode[STIX]{x1D70F}))$
generated by
$U_{1}$
and
$U_{2}$
.
Lemma 5.2.2. The ring
$R$
is local with maximal ideal
$(\mathfrak{m}_{\overline{r}},U_{1},U_{2})$
.
Here, by abuse,
$\mathfrak{m}_{\overline{r}}$
denotes the image of the maximal ideal of
$R_{\infty }$
in
$R$
.
Proof. As
$M_{\infty }(\unicode[STIX]{x1D70F})$
is a finitely generated
$R_{\infty }(\unicode[STIX]{x1D70F})$
-module, we deduce that the ring extension
$R_{\infty }(\unicode[STIX]{x1D70F})\subseteq R$
is finite, hence
$\mathfrak{m}_{\overline{r}}\subseteq \operatorname{rad}(R)$
. In particular,
$\mathfrak{a}\subseteq \operatorname{rad}(R)$
, and hence also
$\sqrt{\mathfrak{a}R}\subseteq \operatorname{rad}(R)$
. By Theorem 5.2.1(iii), the action of
$R_{\infty }/\mathfrak{a}$
on
$M_{\infty }(\unicode[STIX]{x1D70F})/\mathfrak{a}$
factors through
$\mathbb{T}_{a}$
, and hence the action of
$R/\mathfrak{a}$
on
$M_{\infty }(\unicode[STIX]{x1D70F})/\mathfrak{a}$
factors through
$\mathbb{T}$
, giving rise to a surjective homomorphism
$R/\mathfrak{a}{\twoheadrightarrow}\mathbb{T}$
. As the action of
$R$
on
$M_{\infty }(\unicode[STIX]{x1D70F})$
is faithful, the
$R/\mathfrak{a}$
-module
$M_{\infty }(\unicode[STIX]{x1D70F})/\mathfrak{a}$
has full support by [Reference TaylorTay08, Lemma 2.2] (i.e., is nearly faithful in the terminology of [Reference TaylorTay08]). Since
$\mathbb{T}$
is reduced, we get an induced isomorphism
$(R/\mathfrak{a})_{\operatorname{red}}\xrightarrow[{}]{\,\sim \,}\mathbb{T}$
. It follows that
$R$
is local, and
$U_{i}\in \mathfrak{m}_{R}$
, as
$U_{i}\in \mathfrak{m}_{\mathbb{T}}$
by the proof of Theorem 4.5.2 (
$i=1$
,
$2$
). It is then easy to see that
$\mathfrak{m}_{R}=(\mathfrak{m}_{\overline{r}},U_{1},U_{2})$
.◻
We now show that Theorem 5.1.1 follows from the following theorem.
Theorem 5.2.3. Let
$\overline{r}$
be as in Theorem 4.5.2(i) with
$\text{FL}(\overline{r}|_{G_{F_{w}}})\neq \infty$
. The module
$M_{\infty }(\unicode[STIX]{x1D70F})$
is finite free over
$R$
.
Proof of Theorem 5.1.1.
As
$M_{\infty }(\unicode[STIX]{x1D70F})$
is finite free over
$R$
by Theorem 5.2.3,
$M_{\infty }(\unicode[STIX]{x1D70F})/\mathfrak{a}$
is finite free over
$R/\mathfrak{a}$
. Hence the natural surjection
$R/\mathfrak{a}{\twoheadrightarrow}\mathbb{T}$
considered in the proof of Lemma 5.2.2 is an isomorphism. We complete the proof by Theorem 5.2.1(iii).◻
5.3 The Diamond–Fujiwara trick
In this section, we prove Theorem 5.2.3 using the method of Diamond and Fujiwara. Let
$B\subseteq {\operatorname{GL}_{3}}_{/\mathbb{Z}_{p}}$
be the algebraic subgroup of upper-triangular matrices. For a dominant character
$\unicode[STIX]{x1D706}$
of
$B$
, let
$W_{{\mathcal{O}}_{E}}(\unicode[STIX]{x1D706})$
be the algebraic induced module
$(\operatorname{Ind}_{B}^{\operatorname{GL}_{3}}w_{0}\unicode[STIX]{x1D706})^{\text{alg}}\otimes _{\mathbb{Z}_{p}}{\mathcal{O}}_{E}$
, considered as representation of
$K=\operatorname{GL}_{3}(\mathbb{Z}_{p})$
. (This is the characteristic
$0$
version of the module defined in § 3.) Let
$W\stackrel{\text{def}}{=}W_{{\mathcal{O}}_{E}}(-c-1,-b,-a+1)$
.
Proposition 5.3.1. The module
$M_{\infty }(W)$
is non-zero and finite free over its support in
$R_{\infty }$
.
Proof. Note that
$F(-c-1,-b,-a+1)\cong W\otimes _{{\mathcal{O}}_{E}}\mathbb{F}$
by [Reference HerzigHer09, Proposition 3.18(ii)]. Hence
$M_{\infty }(W)\neq 0$
by Theorems 4.4.1 and 5.2.1(iii), as well as [Reference LeLe15, Proposition 5.1.1]. Let
$\unicode[STIX]{x1D713}_{\widetilde{v}}\stackrel{\text{def}}{=}(a-1,b,c+1)$
and
$$\begin{eqnarray}R_{\infty }(W)^{\prime }\stackrel{\text{def}}{=}\widehat{\otimes }_{v^{\prime }|p}\,R_{\widetilde{v}^{\prime }}^{\Box ,\unicode[STIX]{x1D713}_{\widetilde{v}^{\prime }}}\,\widehat{\otimes }\,R_{\widetilde{v}_{1}}^{\Box }[[x_{1},\ldots ,x_{q-3[F^{+}:\mathbb{Q}]}]],\end{eqnarray}$$
where
$R_{\widetilde{v}}^{\Box ,\unicode[STIX]{x1D713}_{\widetilde{v}}}$
is the framed crystalline deformation ring for
$\overline{r}|_{G_{F_{\widetilde{v}}}}^{\vee }$
of Hodge–Tate weights
$\unicode[STIX]{x1D713}_{\widetilde{v}}+(2,1,0)$
. Then
$M_{\infty }(W)$
is supported on
$\operatorname{Spec}R_{\infty }(W)^{\prime }$
by [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Lemma 4.17(1)]. (Note the dual in the definition of ‘Hodge–Tate weights prescribed by
$\unicode[STIX]{x1D70E}_{\text{alg}}$
’ in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 4].) By the proof of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Lemma 4.18],
$M_{\infty }(W)$
is a maximal Cohen–Macaulay
$R_{\infty }(W)^{\prime }$
-module. By the choice of
$v_{1}$
,
$R_{\widetilde{v}_{1}}^{\Box }$
is formally smooth over
${\mathcal{O}}_{E}$
, see [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Lemma 2.5]. By [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.1],
$R_{\widetilde{v}^{\prime }}^{\Box ,\unicode[STIX]{x1D713}_{\widetilde{v}^{\prime }}}$
is formally smooth over
${\mathcal{O}}_{E}$
for all
$v^{\prime }|p$
. As
$R_{\infty }(W)^{\prime }$
is a regular local ring,
$M_{\infty }(W)$
is a projective and hence free
$R_{\infty }(W)^{\prime }$
-module by the Auslander–Buchsbaum–Serre theorem and the Auslander–Buchsbaum formula.◻
Let
$n$
be the (free) rank of
$M_{\infty }(W)$
over its support.
Lemma 5.3.2. Let
$\overline{r}$
be as in Theorem 4.5.2(i) with
$\text{FL}(\overline{r}|_{G_{F_{w}}})\neq \infty$
. The
$R$
-module
$M_{\infty }(\unicode[STIX]{x1D70F})$
is generated by
$n$
elements.
Proof. Let
$\overline{\unicode[STIX]{x1D70F}}\stackrel{\text{def}}{=}\unicode[STIX]{x1D70F}\otimes _{{\mathcal{O}}_{E}}\mathbb{F}$
. By Nakayama’s lemma, it suffices to show that
$M_{\infty }(\overline{\unicode[STIX]{x1D70F}})/(\mathfrak{m}_{\overline{r}},U_{1},U_{2})$
has dimension
$n$
. Consider
$$\begin{eqnarray}\displaystyle (M_{\infty }(\overline{\unicode[STIX]{x1D70F}})/(\mathfrak{m}_{\overline{r}},U_{1},U_{2}))^{\vee } & \cong & \displaystyle \operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70F}},M_{\infty }^{\vee })[\mathfrak{m}_{\overline{r}},U_{1},U_{2}]\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70F}},M_{\infty }^{\vee }[\mathfrak{m}_{\overline{r}}])[U_{1},U_{2}]\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70F}}/M,M_{\infty }^{\vee })[\mathfrak{m}_{\overline{r}}]\nonumber\\ \displaystyle & \cong & \displaystyle (M_{\infty }(\overline{\unicode[STIX]{x1D70F}}/M)/\mathfrak{m}_{\overline{r}})^{\vee },\nonumber\end{eqnarray}$$
where the third isomorphism holds by Lemma 3.1.11, and where
$M$
is the minimal subrepresentation of
$\overline{\unicode[STIX]{x1D70F}}$
containing
$F(-c,-a,-b-p+1)$
and
$F(-a+p-1,-b,-c-p+1)$
as Jordan–Hölder factors. By the isomorphism
$M_{\infty }(\overline{\unicode[STIX]{x1D70F}})/(\mathfrak{m}_{\overline{r}},U_{1},U_{2})\cong M_{\infty }(\overline{\unicode[STIX]{x1D70F}}/M)/\mathfrak{m}_{\overline{r}}$
, it suffices to show that
$M_{\infty }(\overline{\unicode[STIX]{x1D70F}}/M)/\mathfrak{m}_{\overline{r}}$
has dimension
$n$
. By [Reference LeLe15, Proposition 2.2.2] and Theorem 4.4.1,
$M$
is of length 3 and
$(\overline{\unicode[STIX]{x1D70F}}/M)^{\vee }$
contains no element of
$W_{w}(\overline{r})$
other than
$F(a-1,b,c+1)$
. Hence by [Reference LeLe15, Proposition 5.1.1], the natural inclusion
$M_{\infty }(F(-c-1,-b,-a+1)){\hookrightarrow}M_{\infty }(\overline{\unicode[STIX]{x1D70F}}/M)$
is an isomorphism. We conclude that the maps
$$\begin{eqnarray}M_{\infty }(W)/\mathfrak{m}_{\overline{r}}\rightarrow M_{\infty }(F(-c-1,-b,-a+1))/\mathfrak{m}_{\overline{r}}\rightarrow M_{\infty }(\overline{\unicode[STIX]{x1D70F}}/M)/\mathfrak{m}_{\overline{r}}\end{eqnarray}$$
are isomorphisms of
$n$
-dimensional
$\mathbb{F}$
-vector spaces, by definition of
$n$
.◻
Proof of Theorem 5.2.3.
By Lemma 5.3.2, we can and do fix a surjection
$R^{n}{\twoheadrightarrow}M_{\infty }(\unicode[STIX]{x1D70F})$
with kernel
$P$
. This induces an exact sequence
$$\begin{eqnarray}0\rightarrow P[1/p]\rightarrow (R[1/p])^{n}\rightarrow M_{\infty }(\unicode[STIX]{x1D70F})[1/p]\rightarrow 0.\end{eqnarray}$$
We now freely use the notation of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 4]. First, we note that
$R_{\infty }(\unicode[STIX]{x1D70F})[1/p]\rightarrow R[1/p]$
is an isomorphism by [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Theorem 4.1 and Lemma 4.17(2)]. Note that while the construction of
$M_{\infty }$
is slightly different in this paper, the proof of Lemma 4.17(2) still applies verbatim.
By [Reference Emerton, Gee and HerzigEGH13, Proposition 2.4.7] (and its easy converse)
$\unicode[STIX]{x1D70F}\otimes _{{\mathcal{O}}_{E}}\overline{\mathbb{Q}}_{p}$
is an irreducible smooth representation of
$K$
that is associated to the inertial type
$\widetilde{\unicode[STIX]{x1D714}}^{-b}\,\oplus \,\widetilde{\unicode[STIX]{x1D714}}^{-c}\,\oplus \,\widetilde{\unicode[STIX]{x1D714}}^{-a}$
by the inertial local Langlands correspondence [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Theorem 3.7]. Hence by Theorem 5.2.1(ii),
$M_{\infty }(\unicode[STIX]{x1D70F})[1/p]$
is a projective
$R_{\infty }(\unicode[STIX]{x1D70F})[1/p]$
-module. We claim that it is of constant rank
$n$
. The rank is clearly no larger than
$n$
by (5.3.3). Thus it suffices to show that each irreducible component of
$\operatorname{Spec}(R_{\infty }(\unicode[STIX]{x1D70F})[1/p])$
, or equivalently of
$\operatorname{Spec}R_{\infty }(\unicode[STIX]{x1D70F})$
, contains an
$E$
-point over which the fiber of
$M_{\infty }(\unicode[STIX]{x1D70F})[1/p]$
has
$E$
-dimension at least
$n$
.
First, we claim that each irreducible component
$Z$
of
$\operatorname{Spec}R_{\infty }(\unicode[STIX]{x1D70F})$
has an
$E$
-point in the closed subscheme
$\operatorname{Spec}\mathbb{T}_{a}$
. Indeed as
$M_{\infty }(\unicode[STIX]{x1D70F})$
is finite free over
$S_{\infty }$
by Theorem 5.2.1(i),
$R_{\infty }(\unicode[STIX]{x1D70F})$
is a subring of a matrix ring over
$S_{\infty }$
and hence a finite torsion-free
$S_{\infty }$
-module. From this, we see that
$R_{\infty }(\unicode[STIX]{x1D70F})$
is Cohen–Macaulay and in particular equidimensional. As
$Z\rightarrow \operatorname{Spec}S_{\infty }$
is a finite map between irreducible schemes of the same dimension, it is surjective. In particular, the base change
$Z\times _{\operatorname{Spec}S_{\infty }}\operatorname{Spec}(S_{\infty }/\mathfrak{a})\subseteq \operatorname{Spec}R_{\infty }(\unicode[STIX]{x1D70F})/\mathfrak{a}$
has a non-empty generic fibre. Just as in the proof of Lemma 5.2.2, we have an isomorphism
$(R_{\infty }(\unicode[STIX]{x1D70F})/\mathfrak{a})_{\text{red}}\xrightarrow[{}]{\,\sim \,}\mathbb{T}_{a}$
. Since
$E$
is sufficiently large,
$\operatorname{Spec}(\mathbb{T}_{a}[1/p])$
is a union of copies of
$\operatorname{Spec}E$
. We conclude that the underlying reduced subscheme of the generic fiber of
$Z\times _{\operatorname{Spec}S_{\infty }}\operatorname{Spec}(S_{\infty }/\mathfrak{a})$
is a non-empty union of copies of
$\operatorname{Spec}E$
in
$\operatorname{Spec}\mathbb{T}_{a}$
.
Second, we claim that for each
${\mathcal{O}}_{E}$
-point of
$\operatorname{Spec}\mathbb{T}_{a}$
with corresponding prime ideal
${\wp}_{r}$
,
$M_{\infty }(\unicode[STIX]{x1D70F})/{\wp}_{r}$
has generic rank at least
$n$
. Let
$M$
be the minimal subrepresentation of
$\overline{\unicode[STIX]{x1D70F}}$
containing
$F(-c-1,-b,-a+1)$
as a Jordan–Hölder factor. By [Reference LeLe15, Proposition 2.2.2] and Theorem 4.4.1,
$(\overline{\unicode[STIX]{x1D70F}}/M)^{\vee }$
contains no element of
$W_{w}(\overline{r})$
. By [Reference LeLe15, Proposition 5.1.1], the natural map
$M_{\infty }(M)\rightarrow M_{\infty }(\overline{\unicode[STIX]{x1D70F}})$
is an isomorphism. The natural surjection
$M_{\infty }(M){\twoheadrightarrow}M_{\infty }(F(-c-1,-b,-a+1))$
gives a surjection
$M_{\infty }(\overline{\unicode[STIX]{x1D70F}}){\twoheadrightarrow}M_{\infty }(F(-c-1,-b,-a+1))$
, and therefore a surjection
$M_{\infty }(\overline{\unicode[STIX]{x1D70F}})/\mathfrak{m}_{\overline{r}}{\twoheadrightarrow}M_{\infty }(F(-c-1,-b,-a+1))/\mathfrak{m}_{\overline{r}}$
. Since
$M_{\infty }(F(-c-1,-b,-a+1))/\mathfrak{m}_{\overline{r}}$
has dimension
$n$
by definition of
$n$
,
$M_{\infty }(\overline{\unicode[STIX]{x1D70F}})/\mathfrak{m}_{\overline{r}}$
has dimension at least
$n$
. For any
${\mathcal{O}}_{E}$
-point of
$\operatorname{Spec}\mathbb{T}_{a}$
with corresponding prime ideal
${\wp}_{r}$
,
$M_{\infty }(\unicode[STIX]{x1D70F})/{\wp}_{r}$
is
$p$
-torsion free by Theorem 5.2.1(iv) and so has generic rank at least
$n$
.
As
$M_{\infty }(\unicode[STIX]{x1D70F})[1/p]$
is projective of rank
$n$
over
$R[1/p]$
(
$\cong R_{\infty }(\unicode[STIX]{x1D70F})[1/p]$
), we conclude by (5.3.3) that
$P[1/p]$
is projective of rank zero and hence
$0$
. As
$R$
is
$p$
-torsion free,
$P$
is
$0$
.◻
Let
$R_{2}$
be the
$R_{\infty }$
-subalgebra of
$\operatorname{End}_{R_{\infty }}(M_{\infty }(\unicode[STIX]{x1D70F}))$
generated by
$U_{2}$
, and let
$\mathbb{T}_{2}$
be the
${\mathcal{O}}_{E}$
-subalgebra of
$\operatorname{End}(S(U^{v},\widetilde{V}^{\prime })_{\mathfrak{m}_{\overline{r}}}^{I,(-b,-c,-a)})$
generated by
$\mathbb{T}^{{\mathcal{P}}}$
and
$U_{2}$
.
Theorem 5.3.4. Let
$\overline{r}$
be as in Theorem 4.5.2(i)–(ii). We have
$R_{2}=R$
and
$\mathbb{T}_{2}=\mathbb{T}$
, i.e.
$U_{1}\in R_{2}$
and
$U_{1}\in \mathbb{T}_{2}$
. Moreover,
$S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]^{I,(-b,-c,-a)}[U_{2}]=S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]^{I,(-b,-c,-a)}[U_{1},U_{2}]$
.
Proof. The argument for Theorem 5.2.3 goes through to show that the module
$M_{\infty }(\unicode[STIX]{x1D70F})$
is also finite free over
$R_{2}$
, and the free rank is the same as for
$R$
. (The main thing that changes in the proof is that the analogue of
$M$
in the proof of Lemma 5.3.2 now has length 2, and we need that
$\text{FL}(\overline{r}|_{G_{F_{w}}})\not \in \{0,\infty \}$
in order to deduce that
$(\overline{\unicode[STIX]{x1D70F}}/M)^{\vee }$
contains no element of
$W_{w}(\overline{r})$
.) Now
$R_{2}\subseteq R$
is a finite ring extension, hence
$\mathfrak{m}_{R}\,\cap \,R_{2}=\mathfrak{m}_{R_{2}}$
. As
$E$
is sufficiently large, the residue fields of
$R_{2}$
and
$R$
are both equal to
$\mathbb{F}$
. It follows that the surjection
$M_{\infty }(\unicode[STIX]{x1D70F})/\mathfrak{m}_{R_{2}}{\twoheadrightarrow}M_{\infty }(\unicode[STIX]{x1D70F})/\mathfrak{m}_{R}$
is an isomorphism. Therefore any
$R_{2}$
-basis of
$M_{\infty }(\unicode[STIX]{x1D70F})$
is also an
$R$
-basis, so
$R_{2}=R$
. The other claims follow.◻
Remark 5.3.5. If
$W_{w}(\overline{r})=\{F(a-1,b,c+1)\}$
, then we even deduce (by the same argument) that
$R_{\infty }(\unicode[STIX]{x1D70F})=R$
,
$\mathbb{T}_{a}=\mathbb{T}$
, and that
$U_{1}$
,
$U_{2}$
annihilate
$S(U^{v},V^{\prime })[\mathfrak{m}_{\overline{r}}]^{I,(-b,-c,-a)}$
.
Remark 5.3.6. The analogues of all the above results in this section hold for the ‘dual’ lattice
$\unicode[STIX]{x1D70F}^{\prime }\stackrel{\text{def}}{=}\operatorname{Ind}_{I}^{K}(\widetilde{\unicode[STIX]{x1D714}}^{-c}\,\otimes \,\widetilde{\unicode[STIX]{x1D714}}^{-a}\,\otimes \,\widetilde{\unicode[STIX]{x1D714}}^{-b})\otimes _{\mathbb{Z}_{p}}{\mathcal{O}}_{E}$
, provided one interchanges
$U_{1}$
with
$U_{2}$
and the condition
$\text{FL}(\overline{r}|_{G_{F_{w}}})\neq \infty$
with
$\text{FL}(\overline{r}|_{G_{F_{w}}})\neq 0$
.
We now show that Theorem 4.5.2 applies to Galois representations of any possible invariant outside
$0$
,
$\infty$
.
Theorem 5.3.7. Suppose that
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
is upper-triangular, maximally non-split, and generic. Then, after possibly replacing
$\mathbb{F}$
by a finite extension, there exist a CM field
$F$
, a Galois representation
$\overline{r}:G_{F}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
, a place
$w|p$
of
$F$
, groups
$G_{/F^{+}}$
and
${\mathcal{G}}_{/{\mathcal{O}}_{F^{+}}}$
, and a compact open subgroup
$U^{v}$
(where
$v=w|_{F^{+}}$
) satisfying all hypotheses of the setup in § 5.1 such that
$\overline{r}|_{G_{F_{w}}}\cong \overline{\unicode[STIX]{x1D70C}}$
.
In particular, if
$\text{FL}(\overline{\unicode[STIX]{x1D70C}})\not \in \{0,\infty \}$
, Theorem 4.5.2 applies to
$\overline{r}$
.
Proof. We suppose that
$\overline{\unicode[STIX]{x1D70C}}$
is as in (2.1.1) with
$(a_{2},a_{1},a_{0})=(a,b,c)$
. We note that
$\overline{\unicode[STIX]{x1D70C}}$
satisfies the two hypotheses of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 2.1]:
$p\nmid 6$
by genericity, and
$\overline{\unicode[STIX]{x1D70C}}$
has a potentially diagonalizable lift of regular weight: for example, by Corollary 4.4.4 or by [Reference Gee and GeraghtyGG12, Lemma 3.1.5] there exists a crystalline lift with distinct Hodge–Tate weights in the Fontaine–Laffaille range. Therefore the procedure of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 2.1], building on [Reference Emerton and GeeEG14, § A], yields a ‘suitable globalization’
$\overline{r}:G_{F}\rightarrow \operatorname{GL}_{3}(\mathbb{F})$
(after possibly replacing
$\mathbb{F}$
) for a CM field
$F$
with
$F/F^{+}$
unramified at all finite places. For each place
$v^{\prime }\in S_{p}^{+}$
there exists a place
$\widetilde{v}^{\prime }$
of
$F$
lying over
$v^{\prime }$
with
$F_{\widetilde{v}^{\prime }}=\mathbb{Q}_{p}$
and
$\overline{r}|_{G_{F_{\widetilde{v}^{\prime }}}}\cong \overline{\unicode[STIX]{x1D70C}}$
, which is Fontaine–Laffaille and regular. We see that hypotheses (ii)–(v) in § 5.1 are satisfied.
Choose a unitary group
$G$
with integral model
${\mathcal{G}}$
as in § 5.1. Fix any
$v\in S_{p}^{+}$
, let
$w\stackrel{\text{def}}{=}\widetilde{v}$
, and define
$\widetilde{V}^{\prime }=\bigotimes _{v^{\prime }\in S_{p}^{+}\setminus \{v\}}W_{a_{v^{\prime }}}$
with
$a_{\widetilde{v}^{\prime }}=(a-1,b,c+1)$
for any
$v^{\prime }\in S_{p}^{+}\setminus \{v\}$
. There exists a compact open subgroup
$U=\prod _{v^{\prime }}U_{v^{\prime }}\leqslant G(\mathbb{A}_{F^{+}}^{\infty })$
with
$U_{v^{\prime }}={\mathcal{G}}({\mathcal{O}}_{F_{v^{\prime }}^{+}})$
(respectively
$U_{v^{\prime }}$
hyperspecial) for all places
$v^{\prime }$
which split (respectively are inert) in
$F$
such that
$S(U^{v},\widetilde{V}^{\prime })_{\mathfrak{m}_{\overline{r}}}\neq 0$
, where
${\mathcal{P}}$
and
$\mathfrak{m}_{\overline{r}}$
are defined as in § 5.1. (Note that a priori the proof of [Reference Emerton and GeeEG14, Corollary A.7] does not give us any information about the type
$(\unicode[STIX]{x1D706},\unicode[STIX]{x1D70F})$
in [Reference Emerton and GeeEG14, Definition 5.3.1]. However, we can get the desired type by choosing appropriate lifts locally at places dividing
$p$
in applying [Reference Barnet-Lamb, Gee, Geraghty and TaylorBLGGT14, Theorem 4.3.1] in the proof of [Reference Emerton and GeeEG14, Lemma A.5].) By choosing a place
$v_{1}$
and redefining
$U_{v_{1}}$
as in § 5.1, we see that hypothesis (ix) in § 5.1 is satisfied.◻
Acknowledgements
The debt that this paper owes to the work of Breuil and Diamond [Reference Breuil and DiamondBD14] should be obvious to the reader. We thank Christophe Breuil for a number of very helpful conversations as well as for his encouragement. We thank Guy Henniart for providing a reference for the proof of Lemma 4.3.3, Xavier Caruso for helpful correspondence regarding Appendix A, and John Enns for helpful remarks on an earlier version of this paper. Finally we are thankful to the referee for useful comments that in particular helped us to improve the exposition.
Appendix A Some integral
$p$
-adic Hodge theory
The first aim of this appendix is to collect some results in integral
$p$
-adic Hodge theory. Several of these are slight generalizations of known results in the literature, incorporating coefficients and descent data. The second aim of the appendix is to prove some lemmas and propositions of §§ 2.2 and 2.3.
A.1 On certain categories of torsion modules
The goal of this section is to recall the definition of various categories of
$p$
-torsion modules with additional structures (Breuil modules, Kisin modules,
$\unicode[STIX]{x1D719}$
-modules) and the relations between them.
Recall that
$K_{0}=W(k)[1/p]$
and that
$K=K_{0}(\unicode[STIX]{x1D71B})$
, where
$\unicode[STIX]{x1D71B}=\sqrt[e]{-p}$
and
$e\geqslant 1$
divides
$p^{[k:\mathbb{F}_{p}]}-1$
. Also recall our definitions of
$\overline{S}_{k}=k[u]/u^{ep}$
and
$S_{W(k)}$
in § 2.2. We will always suppose that
$0\leqslant r\leqslant p-2$
. For the purpose of establishing Proposition 2.2.1 we will consider general
$e$
, but sometimes we will specialize to
$e=1$
. We hope that this will not cause any confusion.
If
${\mathcal{A}}$
is any additive category we let
$\mathbb{F}\text{-}{\mathcal{A}}$
denote the
$\mathbb{F}$
-linear additive category whose objects consist of pairs
$(A,i)$
, where
$A\in {\mathcal{A}}$
and
$\mathbb{F}\rightarrow \operatorname{End}(A)$
is a ring homomorphism (the morphisms are the obvious ones). We will often use below, without further comment, that a functor
${\mathcal{A}}\rightarrow {\mathcal{B}}$
of additive categories gives rise to a functor
$\mathbb{F}\text{-}{\mathcal{A}}\rightarrow \mathbb{F}\text{-}{\mathcal{B}}$
.
We consider the general setting of § 2.2.1. In particular, we write
$\operatorname{BrMod}^{r}$
to denote the category of Breuil modules over
$\overline{S}_{k}$
and
$\operatorname{BrMod}_{0}^{r}$
for the category of Breuil modules without monodromy (also called quasi-Breuil modules), defined in the evident way. Note that these categories are respectively denoted by
$\widetilde{\text{}\underline{{\mathcal{M}}}}^{r}$
,
$\widetilde{\text{}\underline{{\mathcal{M}}}}_{0}^{r}$
in [Reference CarusoCar06, Reference BreuilBre99b].
In [Reference BreuilBre99a, § 2.2.1] (cf. also [Reference CarusoCar06, § 2.1]) the authors introduce certain categories of modules, noted as
$\text{}\underline{{\mathcal{M}}}^{r}$
,
$\text{}\underline{{\mathcal{M}}}_{0}^{r}$
. We actually only consider their full subcategories formed by
$p$
-torsion objects, though we keep the same notation. The objects of these subcategories are finite free modules over
$S_{W(k)}/pS_{W(k)}$
. We have the following commutative diagram:
where the functors
${\mathcal{T}}$
,
${\mathcal{T}}_{0}$
inducing equivalences of categories are defined in [Reference BreuilBre98, § 2.2.2] when
$e=1$
and [Reference CarusoCar06, § 2.3] in general, and the vertical arrows are forgetful functors. (Strictly speaking, this diagram and the ones that follow only commute up to equivalence.)
Choose a sequence
$(p_{n})_{n}\in \overline{\mathbb{Q}}_{p}^{\mathbb{N}}$
verifying
$p_{n+1}^{p}=(-1)^{p-1}p_{n}$
for all
$n$
and
$p_{0}\stackrel{\text{def}}{=}-p$
, so
$N_{K_{0}(p_{n+1})/K_{0}(p_{n})}(p_{n+1})=p_{n}$
. Let
$k((\text{}\underline{p}))$
be the field of norms associated to the field extension
$(K_{0})_{\infty }/K_{0}$
, where
$(K_{0})_{\infty }\stackrel{\text{def}}{=}\bigcup _{n\in \mathbb{N}}K_{0}(p_{n})$
, and let
$k[[\text{}\underline{p}]]$
be its ring of integers. In particular,
$\text{}\underline{p}$
is identified with the sequence
$(p_{n})_{n}$
. We write
$\mathfrak{Mod}_{k[[\text{}\underline{p}]]}^{r}$
for the category of
$(\unicode[STIX]{x1D719},k[[\text{}\underline{p}]])$
-modules of height less than or equal to
$r$
defined in [Reference BreuilBre99b, § 2.3].
We have an equivalence of categories:
$$\begin{eqnarray}M_{\mathfrak{S}}:\,\,\mathfrak{Mod}_{k[[\text{}\underline{p}]]}^{r}\stackrel{{\sim}}{\longrightarrow }\operatorname{BrMod}_{0}^{r}\end{eqnarray}$$
(cf. [Reference BreuilBre99b, §4], where the functor is noted by
$\tilde{\unicode[STIX]{x1D6E9}}_{r}$
).
We finally define the category
$\mathfrak{Mod}_{k((\text{}\underline{p}))}$
of étale
$(\unicode[STIX]{x1D719},k((\text{}\underline{p})))$
-modules as the category of finite-dimensional
$k((\text{}\underline{p}))$
-vector spaces
$\mathfrak{D}$
endowed with a semilinear map
$\unicode[STIX]{x1D719}:\mathfrak{D}\rightarrow \mathfrak{D}$
(with respect to the Frobenius on
$k((\text{}\underline{p}))$
) and inducing an isomorphism
$\unicode[STIX]{x1D719}^{\ast }\mathfrak{D}\rightarrow \mathfrak{D}$
(with obvious morphisms between objects).
By work of Fontaine [Reference FontaineFon90], we have an exact anti-equivalence
$$\begin{eqnarray}\displaystyle \mathbb{F}\text{-}\mathfrak{Mod}_{k((\text{}\underline{p}))} & \stackrel{{\sim}}{\longrightarrow } & \displaystyle \text{Rep}_{\mathbb{F}}(G_{(K_{0})_{\infty }})\nonumber\\ \displaystyle \mathfrak{D} & \longmapsto & \displaystyle \text{Hom}(\mathfrak{D},k((\text{}\underline{p}))^{\text{sep}}).\nonumber\end{eqnarray}$$
When
$e=1$
we have the fully faithful embedding
${\mathcal{F}}_{r}:{\mathcal{F}}{\mathcal{L}}^{[0,r]}\longrightarrow \operatorname{BrMod}_{0}^{r}$
of [Reference BreuilBre99b, § 5] (via the equivalence
${\mathcal{T}}_{0}$
above). By composition we obtain a fully faithful functor
where the last functor in the sequence is localization at
$\text{}\underline{p}$
(which is fully faithful by [Reference BreuilBre99b, Proposition 2.3.7]).
We are now going to define the analogous categories and functors with descent data. Recall that
$\unicode[STIX]{x1D71B}=\sqrt[e]{-p}\in K$
. There is a unique sequence
$(\unicode[STIX]{x1D71B}_{n})_{n}\in \overline{\mathbb{Q}}_{p}^{\mathbb{N}}$
such that
$\unicode[STIX]{x1D71B}_{n}^{e}=p_{n}$
,
$\unicode[STIX]{x1D71B}_{n+1}^{p}=(-1)^{p-1}\unicode[STIX]{x1D71B}_{n}$
for all
$n$
, and
$\unicode[STIX]{x1D71B}_{0}\stackrel{\text{def}}{=}\unicode[STIX]{x1D71B}$
. In particular,
$N_{K(\unicode[STIX]{x1D71B}_{n+1})/K(\unicode[STIX]{x1D71B}_{n})}(\unicode[STIX]{x1D71B}_{n+1})=\unicode[STIX]{x1D71B}_{n}$
. By letting
$K_{\infty }\stackrel{\text{def}}{=}\bigcup _{n\in \mathbb{N}}K(\unicode[STIX]{x1D71B}_{n})$
we have a canonical isomorphism
$\operatorname{Gal}(K_{\infty }/(K_{0})_{\infty })\xrightarrow[{}]{\,\sim \,}\operatorname{Gal}(K/K_{0})$
which lets us identify
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}$
with a character of
$\operatorname{Gal}(K_{\infty }/(K_{0})_{\infty })$
.
As
$\text{}\underline{\unicode[STIX]{x1D71B}}^{e}=\text{}\underline{p}$
and
$e$
divides
$|k^{\times }|$
, the field of norms
$k((\text{}\underline{\unicode[STIX]{x1D71B}}))$
associated to
$K_{\infty }/K$
is a cyclic extension of
$k((\text{}\underline{p}))$
of degree
$e$
. Note that
$\operatorname{Gal}(K_{\infty }/(K_{0})_{\infty })\cong \operatorname{Gal}(k((\text{}\underline{\unicode[STIX]{x1D71B}}))/k((\text{}\underline{p})))$
acts on
$k((\text{}\underline{\unicode[STIX]{x1D71B}}))$
; concretely this action is determined by
$g\cdot \text{}\underline{\unicode[STIX]{x1D71B}}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}(g)\text{}\underline{\unicode[STIX]{x1D71B}}$
for
$g\in \operatorname{Gal}(K_{\infty }/(K_{0})_{\infty })$
.
We write
$\mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]}^{r}$
for the category of
$(\unicode[STIX]{x1D719},k[[\text{}\underline{\unicode[STIX]{x1D71B}}]])$
-modules of height less than or equal to
$r$
, described in [Reference CarusoCar11, § 2.1] (where it is denoted by
$\text{Mod}_{/\tilde{\mathfrak{S}}}^{\unicode[STIX]{x1D719}}$
). By [Reference CarusoCar11, Théorème 2.1.2] (building on Breuil [Reference BreuilBre99b, Théorème 4.1.1]) we have an exact equivalence of categories
$$\begin{eqnarray}M_{\mathfrak{S}}:\,\,\mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]}^{r}\stackrel{{\sim}}{\longrightarrow }\operatorname{BrMod}_{0}^{r}.\end{eqnarray}$$
We define in the evident way the category
$\mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]],\,\text{dd}}^{r}$
consisting of
$(\unicode[STIX]{x1D719},k[[\text{}\underline{\unicode[STIX]{x1D71B}}]])$
-modules endowed with a descent data from
$K$
to
$K_{0}$
, i.e. a semilinear action of
$\operatorname{Gal}(K_{\infty }/(K_{0})_{\infty })$
that commutes with
$\unicode[STIX]{x1D719}$
(the morphisms now being required to be compatible with the descent datum).
Lemma A.1.1. There exists an exact covariant functor
$$\begin{eqnarray}M_{\mathfrak{S}}:\,\mathbb{F}\text{-}\mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]],\,\text{dd}}^{r}\rightarrow \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd},0}^{r}\end{eqnarray}$$
which establishes an equivalence of categories.
Here, the category
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd},0}^{r}$
has the same definition as
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
, except that we drop monodromy.
Proof. We may assume that
$\mathbb{F}=\mathbb{F}_{p}$
. By above we only need to check compatibility with the descent data. For this we follow the strategy outlined in [Reference Emerton, Gee and HerzigEGH13, proof of Proposition 3.2.6]. More precisely, given an object
$\mathfrak{M}\in \mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]],\,\text{dd}}^{r}$
and an element
$g\in \operatorname{Gal}(K/K_{0})$
we define its twist
$\mathfrak{M}^{(g)}$
as
$k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]\otimes _{g,k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]}\mathfrak{M}$
with
$\unicode[STIX]{x1D719}$
acting diagonally. It is easily checked that
$\mathfrak{M}^{(g)}\in \mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]}^{r}$
and that
$\widehat{g}:\mathfrak{M}\rightarrow \mathfrak{M}$
induces a morphism
$\widehat{g}:\mathfrak{M}^{(g)}\rightarrow \mathfrak{M}$
in
$\mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]}^{r}$
; moreover,
$\widehat{gh}=\widehat{g}\circ \widehat{h}^{(g)}$
for any
$g,h\in \operatorname{Gal}(K/K_{0})$
. It is formal to verify that the datum of a family of morphisms
$\widehat{g}:\mathfrak{M}^{(g)}\rightarrow \mathfrak{M}$
verifying the cocycle relation is equivalent to a descent datum on
$\mathfrak{M}$
from
$K$
to
$K_{0}$
.
Recall now that the functor
$M_{\mathfrak{S}}:\mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]}^{r}\rightarrow \operatorname{BrMod}_{0}^{r}$
is defined as the base change induced by the morphism
$k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]{\twoheadrightarrow}\overline{S}_{k}\stackrel{\unicode[STIX]{x1D711}}{\rightarrow }\overline{S}_{k}$
, where the first map sends
$\sum \unicode[STIX]{x1D706}_{i}\text{}\underline{\unicode[STIX]{x1D71B}}^{i}$
to
$\sum \unicode[STIX]{x1D706}_{i}u^{i}$
. Therefore
$M_{\mathfrak{S}}(\mathfrak{M}^{(g)})\cong (M_{\mathfrak{S}}(\mathfrak{M}))^{(g)}$
, where the twist in the right-hand side is the one defined in [Reference Emerton, Gee and HerzigEGH13, proof of Proposition 3.2.6].
By functoriality, the quasi-Breuil module
${\mathcal{M}}\stackrel{\text{def}}{=}M_{\mathfrak{S}}(\mathfrak{M})$
is thus endowed with a family of morphism
${\mathcal{M}}^{(g)}\rightarrow {\mathcal{M}}$
verifying the above cocycle relation, i.e.
${\mathcal{M}}$
is endowed with descent data from
$K$
to
$K_{0}$
. We conclude that the composite functor
$\mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]],\,\text{dd}}^{r}\rightarrow \mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]}^{r}\stackrel{{\sim}}{\longrightarrow }\operatorname{BrMod}_{0}^{r}$
factors though
$\operatorname{BrMod}_{\text{dd},0}^{r}\rightarrow \operatorname{BrMod}_{0}^{r}$
. Its exactness and the induced equivalence follow as a formal consequence of the analogous properties of
$M_{\mathfrak{S}}$
, cf. [Reference CarusoCar11, Théorème 2.1.2].◻
We can finally introduce the category
$\mathfrak{Mod}_{k((\text{}\underline{\unicode[STIX]{x1D71B}})),\text{dd}}$
of étale
$(\unicode[STIX]{x1D719},k((\text{}\underline{\unicode[STIX]{x1D71B}})))$
-modules with descent data: an object
$\mathfrak{D}$
is defined in the analogous way as for the category
$\mathfrak{Mod}_{k((\text{}\underline{p}))}$
, but we moreover require that
$\mathfrak{D}$
is endowed with a semilinear action of
$\operatorname{Gal}(K/K_{0})$
that commutes with
$\unicode[STIX]{x1D719}$
.
We can now define a functor by composition:
A.2 Some basic lemmas on Breuil modules
Lemma A.2.1. Let
${\mathcal{N}}$
be an
$\overline{S}$
-submodule of a Breuil module
${\mathcal{M}}\in \mathbb{F}\text{-}\text{BrMod}^{r}$
. Then
${\mathcal{N}}$
is an
$\overline{S}_{k}$
-direct summand of
${\mathcal{M}}$
if and only if
${\mathcal{N}}$
is free as
$\overline{S}$
-module.
Proof. By Baer’s criterion the noetherian ring
$\overline{S}_{k}$
is self-injective; in particular an
$\overline{S}_{k}$
-module is injective if and only if it is projective. As
$\overline{S}_{k}$
is local,
${\mathcal{N}}$
is an
$\overline{S}_{k}$
-direct summand of
${\mathcal{M}}$
if and only if
${\mathcal{N}}$
is free as
$\overline{S}_{k}$
-module. This is equivalent to
${\mathcal{N}}$
being free as
$\overline{S}$
-module by [Reference Emerton, Gee and HerzigEGH13, Remark 3.2.1].◻
Lemma A.2.2. If
${\mathcal{M}}\in \operatorname{BrMod}^{r}$
, then
$\operatorname{Fil}^{r}{\mathcal{M}}/u^{e}\operatorname{Fil}^{r}{\mathcal{M}}$
is a free
$k[u]/u^{e}$
-module of rank
$\operatorname{rank}_{\overline{S}_{k}}{\mathcal{M}}$
and the map
$$\begin{eqnarray}\overline{S}_{k}\otimes _{\unicode[STIX]{x1D711},k[u]/u^{e}}\operatorname{Fil}^{r}{\mathcal{M}}/u^{e}\operatorname{Fil}^{r}{\mathcal{M}}\rightarrow {\mathcal{M}}\end{eqnarray}$$
given by
$1\,\otimes \,\unicode[STIX]{x1D711}_{r}$
is an isomorphism.
Proof (Cf. [Reference BreuilBre98, Lemme 2.2.1.2] when
$e=1$
).
As
${\mathcal{M}}$
is finite free over
$\overline{S}_{k}$
and
$u^{er}{\mathcal{M}}\subseteq \operatorname{Fil}^{r}{\mathcal{M}}$
the first claim follows. Clearly the map (A.2.3) is well defined and surjective. It is an isomorphism for dimension reasons.◻
Corollary A.2.4. If
${\mathcal{M}}\in \text{}\underline{{\mathcal{M}}}^{r}$
, let
$$\begin{eqnarray}\operatorname{Fil}^{r+1}{\mathcal{M}}\stackrel{\text{def}}{=}(\operatorname{Fil}^{1}S_{W(k)})(\operatorname{Fil}^{r}{\mathcal{M}})+(\operatorname{Fil}^{r+1}S_{W(k)}){\mathcal{M}}.\end{eqnarray}$$
Then the natural map
$$\begin{eqnarray}\operatorname{Fil}^{r}{\mathcal{M}}/\operatorname{Fil}^{r+1}{\mathcal{M}}\rightarrow \operatorname{Fil}^{r}{\mathcal{T}}({\mathcal{M}})/u^{e}\operatorname{Fil}^{r}{\mathcal{T}}({\mathcal{M}})\end{eqnarray}$$
is an isomorphism of
$S_{W(k)}/(p,\operatorname{Fil}^{1}S_{W(k)})\cong k[u]/u^{e}$
-modules, and the map
$$\begin{eqnarray}S_{W(k)}/p\otimes _{\unicode[STIX]{x1D711},k[u]/u^{e}}\operatorname{Fil}^{r}{\mathcal{M}}/\operatorname{Fil}^{r+1}{\mathcal{M}}\rightarrow {\mathcal{M}}\end{eqnarray}$$
given by
$1\,\otimes \,\unicode[STIX]{x1D711}_{r}$
is an isomorphism.
Proof. The first claim follows, as
$\ker ({\mathcal{M}}\rightarrow {\mathcal{T}}({\mathcal{M}}))=(\operatorname{Fil}^{p}S_{W(k)}){\mathcal{M}}\subseteq \operatorname{Fil}^{r+1}{\mathcal{M}}$
. Thus by Lemma A.2.2 both sides of (A.2.5) are free
$S_{W(k)}/p$
-modules of the same rank. As
$S_{W(k)}$
is local, it suffices to check that (A.2.5) is an isomorphism after the base change
$S_{W(k)}/p{\twoheadrightarrow}\overline{S}_{k}$
, and hence we have finished by Lemma A.2.2.◻
A.3 Functors towards Galois representations
The aim of this section is to briefly recall the constructions of various functors towards Galois representations defined on the categories of § A.1.
The functors towards Galois representations are defined via certain period rings introduced in [Reference BreuilBre99a, § 2.2.2] (cf. also [Reference CarusoCar06, §§ 2.2 and 2.3]). We have a natural surjective morphism
$S_{W(k)}\rightarrow \overline{S}_{k}$
, as well as
$S_{W(k)}$
-algebras
$\widehat{A}_{\text{st}}$
,
$A_{\text{cris}}$
, which are endowed with an action of
$G_{K}$
. We have the following commutative diagram:
which becomes equivariant by endowing the ringsFootnote
1
$\widehat{A}$
,
$\widehat{A}_{0}$
with the actions of
$G_{K}$
,
$G_{K_{\infty }}$
inherited from
$\widehat{A}_{\text{st}}/p$
,
$A_{\text{cris}}/p$
, and
$\overline{S}_{k}$
. The choice of
$\text{}\underline{\unicode[STIX]{x1D71B}}$
lets us extend these actions to
$G_{K_{0}}$
(respectively
$G_{(K_{0})_{\infty }}$
in the case of
$\widehat{A}_{0}$
), as explained in [Reference Emerton, Gee and HerzigEGH13, § 3.1]. The horizontal maps in the diagram are then
$G_{K_{0}}$
-equivariant, while the vertical maps are
$G_{(K_{0})_{\infty }}$
-equivariant.
Let us consider the contravariant functors
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rcllcl@{}}\text{}\underline{{\mathcal{M}}}^{r}\ & \rightarrow \ & \text{Rep}_{\mathbb{F}_{p}}(G_{K}) & \qquad \qquad \text{}\underline{{\mathcal{M}}}_{0}^{r}\ & \rightarrow \ & \text{Rep}_{\mathbb{F}_{p}}(G_{K_{\infty }})\\ {\mathcal{M}}\ & \mapsto \ & \text{Hom}({\mathcal{M}},\widehat{A}_{\text{st}}/p) & \qquad \qquad {\mathcal{M}}_{0}\ & \mapsto \ & \text{Hom}({\mathcal{M}}_{0},A_{\text{cris}}/p)\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
(where homomorphisms, here and in the following, respect all structures) and their analogues on the categories
$\operatorname{BrMod}^{r}$
,
$\operatorname{BrMod}_{0}^{r}$
, defined by replacing the rings
$\widehat{A}_{\text{st}}/p$
,
$A_{\text{cris}}/p$
with
$\widehat{A}$
,
$\widehat{A}_{0}$
respectively. (The functor
$\text{Hom}(-,\widehat{A})$
on the category
$\operatorname{BrMod}^{r}$
is often denoted by
$\text{T}_{\text{st}}^{\ast }$
. This is compatible with the notation
$\text{T}_{\text{st}}^{\ast }$
in § 2.2 for the functor on the category
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
.)
These functors have been extensively studied in [Reference BreuilBre99a, § 2.3.1], [Reference BreuilBre99b, §§ 3.2 and 4], [Reference CarusoCar06, §§ 2.2 and 2.3] and the morphisms between the various period rings (A.3.1) induce natural transformation between the functors toward Galois representations. The following result provides us with a precise description of the relations between the categories and functors introduced above.
Proposition A.3.2. The natural maps (A.3.1) induce a commutative diagram
where the unlabeled morphisms are forgetful functors.
Proof. We may assume that
$\mathbb{F}=\mathbb{F}_{p}$
. The left square is commutative by above, and the external square is commutative by [Reference BreuilBre99a, Lemme 2.3.1.1].
We now indicate why the upper and lower triangles are commutative, completing the proof. For the upper triangle this follows from [Reference CarusoCar06, Proposition 2.3.4]. However, the second paragraph of the published proof needs to be fixed as follows. (We thank Xavier Caruso for the argument.) Given
$\overline{\unicode[STIX]{x1D713}}:{\mathcal{T}}({\mathcal{M}})\rightarrow \widehat{A}$
, we get an induced map
$\overline{\unicode[STIX]{x1D713}}:\operatorname{Fil}^{r}{\mathcal{T}}({\mathcal{M}})\rightarrow \operatorname{Fil}^{r}\widehat{A}$
. Also, as
$\unicode[STIX]{x1D711}_{r}$
kills the kernel of the map
$\widehat{A}_{\text{st}}/p\rightarrow \widehat{A}$
, we get an induced map
$\overline{\unicode[STIX]{x1D711}}_{r}:\operatorname{Fil}^{r}\widehat{A}\rightarrow \widehat{A}_{\text{st}}/p$
. The composite
$\overline{\unicode[STIX]{x1D711}}_{r}\circ \overline{\unicode[STIX]{x1D713}}$
induces a map
$\operatorname{Fil}^{r}{\mathcal{T}}({\mathcal{M}})/u^{e}\operatorname{Fil}^{r}{\mathcal{T}}({\mathcal{M}})\rightarrow \widehat{A}_{\text{st}}/p$
that is linear with respect to the homomorphism
$\unicode[STIX]{x1D711}:k[u]/u^{e}\rightarrow S_{W(k)}/p$
. Extending scalars, and using the isomorphisms of Corollary A.2.4, we get an
$S_{W(k)}$
-linear map
$\unicode[STIX]{x1D713}:{\mathcal{M}}\rightarrow \widehat{A}_{\text{st}}/p$
. It is now straightforward to check that
$\unicode[STIX]{x1D713}$
lifts
$\overline{\unicode[STIX]{x1D713}}$
and that
$\unicode[STIX]{x1D713}$
is compatible with all structures. (We note that the results of [Reference CarusoCar06] that we cite do not depend on the assumption
$er<p-1$
made there.)
The lower triangle is commutative by an analogous argument. ◻
Recall the rings
$k[[\text{}\underline{p}]]$
,
$k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]$
introduced in § A.1. The theory of the field of norms [Reference WintenbergerWin83] lets us endow the ring
$k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]^{s}\cong k[[\text{}\underline{p}]]^{s}$
with an action of
$G_{(K_{0})_{\infty }}$
in such a way that the natural morphism
$$\begin{eqnarray}k[[\text{}\underline{p}]]^{s}\rightarrow A_{\text{cris}}/p\end{eqnarray}$$
becomes
$G_{(K_{0})_{\infty }}$
-equivariant (cf. [Reference BreuilBre99b, § 4.2], where
$k[[\text{}\underline{p}]]^{s}$
is noted by
${\mathcal{X}}^{s}$
; note that we need to take the composite of
$\unicode[STIX]{x1D704}:{\mathcal{X}}^{s}\rightarrow R$
in [Reference BreuilBre99b, § 4.2] with the natural map
$R\rightarrow R^{DP}\cong A_{\text{cris}}/p$
).
We have an exact, contravariant functor
$\text{Hom}(-,k[[\text{}\underline{p}]]^{s})$
toward Galois representations (cf. [Reference BreuilBre99b, § 2.3], [Reference Caruso and LiuCL09, § 2.1]).
Proposition A.3.4. The morphism (A.3.3) and the equivalence
$M_{\mathfrak{S}}$
induce a commutative diagram as follows.
Proof. By Proposition A.3.2 the result follows from [Reference BreuilBre99b, Proposition 4.2.1] (which is stated for
$e=1$
but whose proof generalizes line by line to the case
$e>1$
).◻
We consider finally the category of
$(\unicode[STIX]{x1D719},k((\text{}\underline{\unicode[STIX]{x1D71B}})))$
-modules. By a classical result of Fontaine [Reference FontaineFon90], we have an anti-equivalence
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}\displaystyle \mathfrak{Mod}_{k((\text{}\underline{\unicode[STIX]{x1D71B}}))}\ & \stackrel{{\sim}}{\longrightarrow }\ & \text{Rep}_{\mathbb{F}_{p}}(G_{K_{\infty }})\\ \displaystyle \mathfrak{D}\ & \longmapsto \ & \text{Hom}(\mathfrak{D},k((\text{}\underline{p}))^{s})\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
and it is an exercise to prove that the composite functor
$$\begin{eqnarray}\mathfrak{Mod}_{k((\text{}\underline{\unicode[STIX]{x1D71B}})),\text{dd}}\rightarrow \mathfrak{Mod}_{k((\text{}\underline{\unicode[STIX]{x1D71B}}))}\rightarrow \text{Rep}_{\mathbb{F}_{p}}(G_{K_{\infty }})\end{eqnarray}$$
factors naturally through the restriction
$\text{Rep}_{\mathbb{F}_{p}}(G_{(K_{0})_{\infty }})\rightarrow \text{Rep}_{\mathbb{F}_{p}}(G_{K_{\infty }})$
. Indeed, for any
$g\in G_{(K_{0})_{\infty }}$
,
$f\in \text{Hom}(\mathfrak{D},k((\text{}\underline{p}))^{s})$
we define the element
$$\begin{eqnarray}g\cdot f\stackrel{\text{def}}{=}g\circ f\circ \widehat{\overline{g}}^{-1},\end{eqnarray}$$
where
$\widehat{\overline{g}}$
denotes the endomorphism of
$\mathfrak{D}$
associated to
$\overline{g}\in \operatorname{Gal}(K_{\infty }/(K_{0})_{\infty })$
via the descent data. It is easy to see that the assignment (A.3.5) is well defined and endows the former
$\text{Hom}$
-space with a continuous
$G_{(K_{0})_{\infty }}$
-action, thus providing us with the claimed factorization of functors.
Lemma A.3.6. The base change along
$k((\text{}\underline{p})){\hookrightarrow}k((\text{}\underline{\unicode[STIX]{x1D71B}}))$
induces a commutative diagram of equivalences of categories as follows.
Proof. We assume that
$\mathbb{F}=\mathbb{F}_{p}$
. For commutativity one just observes that for any
$(\unicode[STIX]{x1D719},k((\text{}\underline{p})))$
-module
$\mathfrak{D}_{0}$
, the natural isomorphism
$$\begin{eqnarray}\text{Hom}_{(\unicode[STIX]{x1D719},k((\text{}\underline{p})))}(\mathfrak{D}_{0},k((\text{}\underline{p}))^{s})\stackrel{{\sim}}{\longrightarrow }\text{Hom}_{(\unicode[STIX]{x1D719},k((\text{}\underline{\unicode[STIX]{x1D71B}})))}(\mathfrak{D}_{0}\otimes _{k((\text{}\underline{p}))}k((\text{}\underline{\unicode[STIX]{x1D71B}})),k((\text{}\underline{p}))^{s})\end{eqnarray}$$
is
$G_{(K_{0})_{\infty }}$
-equivariant once we endow the right-hand side with the
$G_{(K_{0})_{\infty }}$
-action induced by the descent data on
$\mathfrak{D}_{0}\otimes _{k((\text{}\underline{p}))}k((\text{}\underline{\unicode[STIX]{x1D71B}})).$
The vertical arrow is an equivalence by Galois descent for vector spaces.◻
As in the case of
$(\unicode[STIX]{x1D719},k((\text{}\underline{\unicode[STIX]{x1D71B}})))$
-modules, the contravariant functor
$\mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]],\text{dd}}^{r}\rightarrow \mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]}^{r}\rightarrow \text{Rep}_{\mathbb{F}_{p}}(G_{K_{\infty }})$
factors through the restriction
$\text{Rep}_{\mathbb{F}_{p}}(G_{(K_{0})_{\infty }})\rightarrow \text{Rep}_{\mathbb{F}_{p}}(G_{K_{\infty }})$
and we have the following lemma.
Lemma A.3.7. The functor
$\operatorname{BrMod}_{\text{dd}}^{r}\rightarrow \operatorname{BrMod}_{\text{dd},0}^{r}\stackrel{{\sim}}{\longrightarrow }\mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]],\,\text{dd}}^{r}$
fits into the following commutative diagram.
Proof. As usual we prove the result when
$\mathbb{F}=\mathbb{F}_{p}$
. Combining Propositions A.3.2 and A.3.4 we have a commutative diagram (the arrows being the evident ones):
where the natural functorial isomorphism on the right-hand side
$$\begin{eqnarray}\text{Hom}(M_{\mathfrak{S}}(-),\widehat{A}_{0})\stackrel{{\sim}}{\longrightarrow }\text{Hom}(-,k[[\text{}\underline{p}]]^{s})\end{eqnarray}$$
is induced by the morphisms between the period rings described by (A.3.1), (A.3.3). By using twists as in the proof of Lemma A.1.1 and the fact that the morphisms between period rings are
$G_{(K_{0})_{\infty }}$
-equivariant, it follows that (A.3.8) is compatible with the
$G_{(K_{0})_{\infty }}$
-action induced by the descent data assignment (A.3.5). An analogous argument applies to the left-hand side of the diagram.◻
In a similar fashion, we obtain the following.
Lemma A.3.9. The localization functor
$\mathbb{F}\text{-}\mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]],\,\text{dd}}^{r}\rightarrow \mathbb{F}\text{-}\mathfrak{Mod}_{k((\text{}\underline{\unicode[STIX]{x1D71B}})),\,\text{dd}}$
induces a commutative diagram as follows.
Proof. Without descent data this is [Reference BreuilBre99b, Lemme 2.3.3] (the latter being stated for
$e=1$
but its proof generalizes). The statement with descent data follows now as in the proof of Lemma A.3.7 (noting that
$k[[\text{}\underline{p}]]^{s}\rightarrow k((\text{}\underline{p}))^{s}$
is obviously
$G_{(K_{0})_{\infty }}$
-equivariant).◻
A.4 On dualities
We recall that we have a notion of duality on the category
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
; more precisely, there is an involutive contravariant functor
$$\begin{eqnarray}\displaystyle & \displaystyle \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}\rightarrow \mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r} & \displaystyle \nonumber\\ \displaystyle & \displaystyle {\mathcal{M}}\mapsto {\mathcal{M}}^{\ast } & \displaystyle \nonumber\end{eqnarray}$$
such that
$\text{T}_{\text{st}}^{r}({\mathcal{M}})\cong \text{T}_{\text{st}}^{\ast }({\mathcal{M}}^{\ast })$
. For details, see [Reference Emerton, Gee and HerzigEGH13, Definition 3.2.8] (building on work of Caruso [Reference CarusoCar05, Chapitre V]).
A.5 Proofs of some results in § 2.2
Proof of Proposition 2.2.1.
As usual we may assume that
$\mathbb{F}=\mathbb{F}_{p}$
. By Lemmas A.3.6, A.3.7 and A.3.9 the commutativity of the upper square and of the right triangle in the statement of Proposition 2.2.1 is clear. Concerning the lower square, we consider the fully faithful functor
${\mathcal{F}}_{p-2}:{\mathcal{F}}{\mathcal{L}}^{[0,p-2]}\rightarrow \operatorname{BrMod}^{p-2}$
defined in [Reference BreuilBre98, § 2.4], which extends the functor of the same name considered in § A.1. On the other hand, we have the functor
$M_{k((\text{}\underline{p}))}:\operatorname{BrMod}^{p-2}\rightarrow \mathfrak{Mod}_{k((\text{}\underline{p}))}$
obtained by specializing the functor
$M_{k((\text{}\underline{\unicode[STIX]{x1D71B}}))}$
of § A.1 to the case when
$e=1$
. The diagram
commutes: for the triangle, see [Reference BreuilBre98, Proposition 3.2.1.1], whereas the square is the specialization of the upper square of the statement of Proposition 2.2.1 to the case when
$e=1$
. The composite morphism
${\mathcal{F}}{\mathcal{L}}^{[0,p-2]}\rightarrow \text{Rep}_{\mathbb{F}_{p}}(G_{(K_{0})_{\infty }})$
is fully faithful, as the functor
${\mathcal{F}}$
in § A.1 has this property.◻
Proof of Lemma 2.2.4.
Lemma A.2.2 shows that
$\unicode[STIX]{x1D711}_{r}$
induces a
$\operatorname{Gal}(K/K_{0})$
-equivariant and
$\unicode[STIX]{x1D711}\,\otimes \,1$
-semilinear isomorphism
$\operatorname{Fil}^{r}{\mathcal{M}}/u\operatorname{Fil}^{r}{\mathcal{M}}\stackrel{{\sim}}{\longrightarrow }{\mathcal{M}}/u{\mathcal{M}}$
. We complete the proof by Nakayama’s lemma and the semisimplicity of
$(k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F})[\operatorname{Gal}(K/K_{0})]$
.◻
Proof of Lemma 2.2.6.
By passing to the new basis
$\text{}\underline{e}\cdot A$
we may assume, without loss of generality, that
$A=1$
. As
$u^{er}{\mathcal{M}}\subseteq \operatorname{Fil}^{r}{\mathcal{M}}$
we deduce that
$u^{er}=VV^{\prime }$
in
$\text{M}_{n}(\overline{S})$
for some
$V^{\prime }\in \text{M}_{n}(\overline{S})$
. Letting
$\widehat{V}\in \text{M}_{n}(k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}[[\text{}\underline{\unicode[STIX]{x1D71B}}]])$
denote any lift of
$V$
such that
$\widehat{V}_{ij}\in (k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}[[\text{}\underline{\unicode[STIX]{x1D71B}}]])_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{p^{-1}a_{j}-a_{i}}}$
we see that
$\text{}\underline{\unicode[STIX]{x1D71B}}^{er}=\widehat{V}\widehat{W}=\widehat{W}\widehat{V}$
for some
$\widehat{W}\in \text{M}_{n}(k\,\otimes _{\mathbb{F}_{p}}\,\mathbb{F}[[\text{}\underline{\unicode[STIX]{x1D71B}}]])$
. Let
$\text{}\underline{e}^{\ast }$
denote the basis of
${\mathcal{M}}^{\ast }$
that is dual to
$\text{}\underline{e}$
, and let
$\text{}\underline{f}^{\ast }\stackrel{\text{def}}{=}\text{}{\underline{e}^{\ast }\cdot }^{t}W$
, where
$W\in \text{M}_{n}(\overline{S})$
denotes the reduction of
$W$
. One easily computes that
$f_{i}^{\ast }\in \operatorname{Fil}^{r}{\mathcal{M}}$
and
$\unicode[STIX]{x1D711}_{r}(f_{i}^{\ast })=e_{i}^{\ast }$
for all
$i$
. As
$\unicode[STIX]{x1D711}_{r}$
induces an isomorphism
$\operatorname{Fil}^{r}{\mathcal{M}}^{\ast }/u\operatorname{Fil}^{r}{\mathcal{M}}^{\ast }\stackrel{{\sim}}{\longrightarrow }{\mathcal{M}}^{\ast }/u{\mathcal{M}}^{\ast }$
(cf. the proof of Lemma 2.2.4), it follows that
$\text{}\underline{f}^{\ast }$
generates
$\operatorname{Fil}^{r}{\mathcal{M}}$
as
$\overline{S}$
-module. Also,
$\widehat{g}e_{i}^{\ast }=(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{-a_{i}}(g)\,\otimes \,1)e_{i}^{\ast }$
.
Define
$\mathfrak{M}\in \mathbb{F}\text{-}\mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]],\,\text{dd}}^{r}$
of rank
$n$
by giving it basis
$\text{}\underline{\mathfrak{e}}$
and defining the maps
$\unicode[STIX]{x1D719}$
,
$\widehat{g}$
by
$\text{Mat}_{\text{}\underline{\mathfrak{e}}}(\unicode[STIX]{x1D719})=^{t}\widehat{V}$
and
$\widehat{g}\mathfrak{e}_{i}=(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{-p^{-1}a_{i}}(g)\,\otimes \,1)\mathfrak{e}_{i}$
. (It is easy to check that
$\mathfrak{M}$
is of height less than or equal to
$r$
, and the condition on
$\widehat{V}_{ij}$
above implies that
$\widehat{g}\circ \unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}\circ \widehat{g}$
.)
We can compute
${\mathcal{M}}^{\prime }\stackrel{\text{def}}{=}M_{\mathfrak{S}}(\mathfrak{M})$
without coefficients and descent data by the recipe in [Reference Caruso and LiuCL09, § 2.1], so
${\mathcal{M}}^{\prime }\cong \overline{S}_{k}\otimes _{\unicode[STIX]{x1D711},k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]}\mathfrak{M}$
. It has
$\overline{S}$
-basis
$\text{}\underline{e}^{\prime }\stackrel{\text{def}}{=}1\otimes _{\unicode[STIX]{x1D711}}\text{}\underline{\mathfrak{e}}$
. By functoriality,
${\mathcal{M}}^{\prime }$
has an
$\mathbb{F}$
-action with
$\unicode[STIX]{x1D706}\in \mathbb{F}$
acting as
$1\,\otimes \,\unicode[STIX]{x1D706}$
. By the twisting argument of the proof of Lemma A.1.1,
${\mathcal{M}}^{\prime }$
has descent data with
$g\in \operatorname{Gal}(K/K_{0})$
acting as
$g\,\otimes \,\widehat{g}$
. Letting
$\text{}\underline{f}^{\prime }\stackrel{\text{def}}{=}\text{}{\underline{e}^{\prime }\cdot }^{t}W$
, it is easy to check that
$f_{i}^{\prime }\in \operatorname{Fil}^{r}{\mathcal{M}}^{\prime }$
and
$\unicode[STIX]{x1D711}_{r}(f_{i}^{\prime })=e_{i}^{\prime }$
for all
$i$
. In particular, as above, we deduce that
$\text{}\underline{f}^{\prime }$
generates
$\operatorname{Fil}^{r}{\mathcal{M}}^{\prime }$
as
$\overline{S}$
-module. Also,
$\widehat{g}e_{i}^{\prime }=(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D71B}}^{-a_{i}}(g)\,\otimes \,1)e_{i}^{\prime }$
. Hence
${\mathcal{M}}^{\prime }\cong {\mathcal{M}}^{\ast }$
in
$\mathbb{F}\text{-}\text{BrMod}_{\text{dd},0}^{r}$
.◻
Proof of Lemma 2.2.7.
In the following
$e=1$
, so
$\overline{S}_{k}=k[u]/u^{p}$
. Note that
${\mathcal{N}}\stackrel{\text{def}}{=}{\mathcal{F}}_{p-2}(M)\in \mathbb{F}\text{-}\text{BrMod}_{0}^{p-2}$
has
$\overline{S}$
-basis
$\text{}\underline{e}$
(or more precisely
$1\,\otimes \,\text{}\underline{e}\in \overline{S}_{k}\otimes _{k}M$
). A computation shows that
$\operatorname{Fil}^{p-2}{\mathcal{N}}$
has generating set
$\text{}\underline{f}$
with
$\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\operatorname{Fil}^{p-2}{\mathcal{N}})=\text{Diag}(u^{p-2-m_{0}},\ldots ,u^{p-2-m_{n-1}})$
and
$\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\unicode[STIX]{x1D711}_{p-2})=F$
.
We now apply Lemma 2.2.6 with
$e=1$
and
${\mathcal{M}}={\mathcal{N}}^{\ast }$
, noting that
$M_{k((\text{}\underline{p}))}({\mathcal{N}})={\mathcal{F}}(M)$
in this case.◻
Proof of Lemma 2.2.8.
This is elementary. Indeed, by (2.2.9), one has
$$\begin{eqnarray}(V+u^{e(r+1)}M)B=AV^{\prime }\end{eqnarray}$$
for some element
$M\in \text{M}_{n}(\overline{S})$
. By considering descent data, we see that
$\text{}\underline{f}_{1}\stackrel{\text{def}}{=}\text{}\underline{e}\cdot (V+u^{e(r+1)}M)$
is a framed generating family of
$\operatorname{Fil}^{r}{\mathcal{M}}$
and one has
$$\begin{eqnarray}\text{Mat}_{\text{}\underline{e},\text{}\underline{f}_{1}}(\unicode[STIX]{x1D711}_{r})=\text{Mat}_{\text{}\underline{e},\text{}\underline{f}}(\unicode[STIX]{x1D711}_{r})=A.\end{eqnarray}$$
Note that
$\text{}\underline{f}^{\prime }=\text{}\underline{e}^{\prime }\,\cdot \,V^{\prime }=\text{}\underline{f}_{1}\cdot B$
. As
$B\in \operatorname{GL}_{n}(\overline{S})$
and by considering descent data, we see that
$\text{}\underline{f}^{\prime }$
is a framed system of generators for
$\operatorname{Fil}^{r}{\mathcal{M}}$
. The last statement follows from
$\unicode[STIX]{x1D711}_{r}(\text{}\underline{f}^{\prime })=\unicode[STIX]{x1D711}_{r}(\text{}\underline{f}_{1})\cdot \unicode[STIX]{x1D711}(B)=\text{}\underline{e}\cdot A\unicode[STIX]{x1D711}(B)=\text{}\underline{e}^{\prime }\cdot \unicode[STIX]{x1D711}(B)$
.◻
A.6 Proofs of some results in § 2.3
Recall that in Definition 2.3.1 we defined the notion of a Breuil submodule.
Proof of Lemma 2.3.2.
We note that
${\mathcal{N}}$
is a finite free
$\overline{S}$
-module by Lemma A.2.1. Let
$\operatorname{Fil}^{r}{\mathcal{N}}\stackrel{\text{def}}{=}\operatorname{Fil}^{r}{\mathcal{M}}\,\cap \,{\mathcal{N}}$
, so
$u^{er}{\mathcal{N}}\subseteq \operatorname{Fil}^{r}{\mathcal{N}}$
. The map
$\operatorname{Fil}^{r}{\mathcal{N}}/u^{e}\operatorname{Fil}^{r}{\mathcal{N}}\rightarrow \operatorname{Fil}^{r}{\mathcal{M}}/u^{e}\operatorname{Fil}^{r}{\mathcal{M}}$
is injective (as
${\mathcal{N}}$
is an
$\overline{S}_{k}$
-direct summand). It is in fact a split injection of
$k[u]/u^{e}$
-modules by Lemma A.2.2, as
$k[u]/u^{e}$
is self-injective. Thus, using again the same lemma, we have the following commutative diagram.
It follows that the left vertical map is injective, hence surjective by dimension reasons. It is now obvious that
${\mathcal{N}}$
inherits from
${\mathcal{M}}$
the structure of a Breuil module with descent data.
By defining
$\operatorname{Fil}^{r}({\mathcal{M}}/{\mathcal{N}})\stackrel{\text{def}}{=}(\operatorname{Fil}^{r}{\mathcal{M}}+{\mathcal{N}})/{\mathcal{N}}\cong \operatorname{Fil}^{r}{\mathcal{M}}/\!\operatorname{Fil}^{r}{\mathcal{N}}$
we see that the Frobenius
$\unicode[STIX]{x1D711}_{r}$
on
$\operatorname{Fil}^{r}{\mathcal{M}}$
naturally induces a semilinear morphism
$\unicode[STIX]{x1D711}_{r}:\operatorname{Fil}^{r}({\mathcal{M}}/{\mathcal{N}})\rightarrow {\mathcal{M}}/{\mathcal{N}}$
and it is immediate that the triple
$({\mathcal{M}}/{\mathcal{N}},\operatorname{Fil}^{r}({\mathcal{M}}/{\mathcal{N}}),\unicode[STIX]{x1D711}_{r})$
inherits the structure of a Breuil module with descent data.
By construction, the complex
$0\rightarrow {\mathcal{N}}\rightarrow {\mathcal{M}}\rightarrow {\mathcal{M}}/{\mathcal{N}}\rightarrow 0$
is an exact sequence in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
. The last statement in the lemma is obvious.◻
Recall that given an exact sequence
$$\begin{eqnarray}0\rightarrow {\mathcal{M}}_{1}\stackrel{f}{\rightarrow }{\mathcal{M}}\stackrel{g}{\rightarrow }{\mathcal{M}}_{2}\rightarrow 0\end{eqnarray}$$
in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
, the morphisms
$f$
and
$g$
are respectively said to be an admissible monomorphism and an admissible epimorphism.
Lemma A.6.1. Let
$f:{\mathcal{M}}\rightarrow {\mathcal{N}}$
be a morphism in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
. Then we have the following.
-
(i) The morphism
$f$
is an admissible epimorphism if and only if
$f$
induces
$\overline{S}$
-linear surjections
${\mathcal{M}}{\twoheadrightarrow}{\mathcal{N}}$
and
$\operatorname{Fil}^{r}{\mathcal{M}}{\twoheadrightarrow}\operatorname{Fil}^{r}{\mathcal{N}}$
. -
(ii) The morphism
$f$
is an admissible monomorphism if and only if
$f$
induces an
$\overline{S}$
-linear injection
${\mathcal{M}}{\hookrightarrow}{\mathcal{N}}$
and
$\operatorname{Fil}^{r}{\mathcal{M}}=f^{-1}(\operatorname{Fil}^{r}{\mathcal{N}})$
.
Proof. The ‘only if’ part, in both (i) and (ii), is obvious. Let us assume
$f:{\mathcal{M}}\rightarrow {\mathcal{N}}$
induces
$\overline{S}$
-linear surjections
${\mathcal{M}}{\twoheadrightarrow}{\mathcal{N}}$
and
$\operatorname{Fil}^{r}{\mathcal{M}}{\twoheadrightarrow}\operatorname{Fil}^{r}{\mathcal{N}}$
. Then
$\ker (f)$
is clearly a Breuil submodule of
${\mathcal{M}}$
; by Lemma 2.3.2 it is an object in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
and the complex
$0\rightarrow \ker (f)\rightarrow {\mathcal{M}}\rightarrow {\mathcal{N}}\rightarrow 0$
is an exact sequence in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
.
Assume now that
$f$
induces an
$\overline{S}$
-linear injection
${\mathcal{M}}{\hookrightarrow}{\mathcal{N}}$
and that
$\operatorname{Fil}^{r}{\mathcal{M}}=f^{-1}(\operatorname{Fil}^{r}{\mathcal{N}})$
. Then, using Lemma A.2.1 one sees that
$f({\mathcal{M}})$
is a Breuil submodule of
${\mathcal{N}}$
. As the map
$f:{\mathcal{M}}\rightarrow f({\mathcal{M}})$
is an isomorphism in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
, Lemma 2.3.2 implies that
$f$
is an admissible monomorphism, as required.◻
Recall from § A.4 that we have a duality on the category
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
.
Lemma A.6.2. The functor
${\mathcal{M}}\mapsto {\mathcal{M}}^{\ast }$
preserves exact sequences in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
.
Proof. By definition of
$\operatorname{Fil}^{r}({\mathcal{M}}^{\ast })$
and the self-injectivity of
$\overline{S}/u^{er}$
(cf. Lemma A.2.1) one has an exact sequence of
$\overline{S}$
-modules
$$\begin{eqnarray}0\rightarrow \operatorname{Fil}^{r}({\mathcal{M}}^{\ast })\rightarrow {\mathcal{M}}^{\ast }\rightarrow \text{Hom}_{\overline{S}/u^{er}}(\operatorname{Fil}^{r}{\mathcal{M}}/u^{er}{\mathcal{M}},\overline{S}/u^{er})\rightarrow 0,\end{eqnarray}$$
which is functorial in
${\mathcal{M}}$
. In order to prove the lemma it is enough to prove that the functor
${\mathcal{M}}\mapsto \operatorname{Fil}^{r}({\mathcal{M}}^{\ast })$
is exact (in
$\overline{S}$
-modules) which is in turn equivalent, thanks to the exact sequence above and the self-injectivity of
$\overline{S}/u^{er}$
, to the exactness of the functor
${\mathcal{M}}\mapsto \operatorname{Fil}^{r}{\mathcal{M}}/u^{er}{\mathcal{M}}$
(in
$\overline{S}$
-modules). But the exactness of
${\mathcal{M}}\mapsto \operatorname{Fil}^{r}{\mathcal{M}}/u^{er}{\mathcal{M}}$
is an easy consequence of the snake lemma.◻
We are now finally in a position to prove Propositions 2.3.4 and 2.3.5.
Proof of Proposition 2.3.4.
Clearly
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
is an additive category and the class of exact sequences is closed under isomorphism. Moreover, given an exact sequence
$$\begin{eqnarray}0\rightarrow {\mathcal{M}}_{1}\stackrel{f}{\rightarrow }{\mathcal{M}}\stackrel{g}{\rightarrow }{\mathcal{M}}_{2}\rightarrow 0\end{eqnarray}$$
in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
it is clear that
$f$
is the categorical kernel of
$g$
. By duality,
$g$
is the categorical cokernel of
$f$
.
We shall now check the axioms
$\text{Ex}0,\text{Ex}1,\text{Ex}2,\text{Ex}2^{op}$
of [Reference KellerKel90, Appendix A].
-
$(\text{Ex}0)$
:
-
It is obvious as
$0\rightarrow 0$
is an admissible epimorphism. -
$(\text{Ex}1)$
:
-
By Lemma A.6.1 a composition of admissible epimorphisms is an admissible epimorphism.
-
$(\text{Ex}2)$
:
-
Let
$\unicode[STIX]{x1D6FC}:{\mathcal{M}}\rightarrow {\mathcal{M}}_{2}$
be an admissible epimorphism and
$\unicode[STIX]{x1D6FD}:{\mathcal{N}}\rightarrow {\mathcal{M}}_{2}$
a morphism in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
. By Lemma A.6.1 the map
${\mathcal{M}}\,\oplus \,{\mathcal{N}}\rightarrow {\mathcal{M}}_{2}$
,
$(x,y)\mapsto \unicode[STIX]{x1D6FC}(x)-\unicode[STIX]{x1D6FD}(y)$
is an admissible epimorphism, so its kernel
${\mathcal{P}}$
is a Breuil submodule of
${\mathcal{M}}\,\oplus \,{\mathcal{N}}$
. The same lemma shows moreover that the natural map
${\mathcal{P}}\rightarrow {\mathcal{N}}$
is an admissible epimorphism. It is then clear that
${\mathcal{P}}$
is a categorical pullback of
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
. -
$(\text{Ex}2^{op})$
:
-
It follows from
$(\text{Ex}2)$
via the duality functor on
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
.
It remains to prove the exactness of the functor
$\text{T}_{\text{st}}^{r}$
. Let
$$\begin{eqnarray}0\rightarrow {\mathcal{M}}_{1}\stackrel{f}{\rightarrow }{\mathcal{M}}\stackrel{g}{\rightarrow }{\mathcal{M}}_{2}\rightarrow 0\end{eqnarray}$$
be an exact sequence in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
. Then, by forgetting monodromy, descent data and coefficients, we deduce that the exact sequence (A.6.3) arises from a sequence
$0\rightarrow \mathfrak{M}_{1}\rightarrow \mathfrak{M}\rightarrow \mathfrak{M}_{2}\rightarrow 0$
in
$\mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]}^{r}$
via the equivalence
$M_{\mathfrak{S}}$
. By [Reference Caruso and LiuCL09, Proposition 2.3.2] the latter sequence is exact. By Proposition A.3.4 and the exactness of the functor
$\text{Hom}(-,k[[\text{}\underline{p}]]^{s})$
we deduce that
$0\rightarrow \text{T}_{\text{st}}^{r}({\mathcal{M}}_{1})\rightarrow \text{T}_{\text{st}}^{r}({\mathcal{M}})\rightarrow \text{T}_{\text{st}}^{r}({\mathcal{M}}_{2})\rightarrow 0$
is an exact sequence in
$\text{Rep}_{\mathbb{F}_{p}}(G_{K_{\infty }})$
.◻
Proof of Proposition 2.3.5.
Let
$T^{\prime }\subseteq \text{T}_{\text{st}}^{r}({\mathcal{M}})\cong \text{T}_{\text{st}}^{\ast }({\mathcal{M}}^{\ast })$
. By the proof of [Reference Emerton, Gee and HerzigEGH13, Proposition 3.2.6] we get a unique (up to isomorphism) surjective homomorphism
$f:{\mathcal{M}}^{\ast }\rightarrow {\mathcal{N}}^{\prime }$
in
$\mathbb{F}\text{-}\operatorname{BrMod}_{\text{dd}}^{r}$
such that
$\text{im}(\text{T}_{\text{st}}^{\ast }(f))=T^{\prime }$
. We claim that
$f$
is an admissible epimorphism. We recall from [Reference Emerton, Gee and HerzigEGH13, proof of Proposition 3.2.6] and [Reference CarusoCar11, proof of Proposition 2.2.5] that
$f$
is obtained from a surjective homomorphism
$\mathfrak{f}:\mathfrak{M}^{\ast }\rightarrow \mathfrak{N}^{\prime }$
in
$\mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]}^{r}$
via the equivalence
$M_{\mathfrak{S}}$
, and that we have an exact sequence in
$\mathfrak{Mod}_{k[[\text{}\underline{\unicode[STIX]{x1D71B}}]]}^{r}$
given by
$0\rightarrow \ker (\mathfrak{f})\rightarrow \mathfrak{M}^{\ast }\rightarrow \mathfrak{N}^{\prime }\rightarrow 0.$
By the exactness of
$M_{\mathfrak{S}}$
we deduce that
$f$
is indeed an admissible epimorphism. By Lemma A.6.2 the image of
$({\mathcal{N}}^{\prime })^{\ast }$
inside
${\mathcal{M}}$
is the desired Breuil submodule in
${\mathcal{M}}$
mapping to
$T^{\prime }$
via
$\unicode[STIX]{x1D6E9}$
. It is unique by construction.
We still need to check that
$\unicode[STIX]{x1D6E9}$
is order preserving. Suppose that
${\mathcal{M}}_{2}$
,
${\mathcal{M}}_{1}$
are Breuil submodules of
${\mathcal{M}}$
such that
${\mathcal{M}}_{2}\subseteq {\mathcal{M}}_{1}$
. Then by Lemma 2.3.3 we have
$\unicode[STIX]{x1D6E9}({\mathcal{M}}_{2})\subseteq \unicode[STIX]{x1D6E9}({\mathcal{M}}_{1})$
. Moreover, we have a natural isomorphism
$\unicode[STIX]{x1D6E9}({\mathcal{M}}_{1})/\unicode[STIX]{x1D6E9}({\mathcal{M}}_{2})\cong \text{T}_{\text{st}}^{r}({\mathcal{M}}_{1}/{\mathcal{M}}_{2})$
by the exactness of
$\text{T}_{\text{st}}^{r}$
. Conversely, given
$T_{2}\subseteq T_{1}\subseteq \text{T}_{\text{st}}^{r}({\mathcal{M}})$
then, by the above, we have
$T_{1}=\text{im}(\text{T}_{\text{st}}^{r}(f_{1}))$
for some admissible monomorphism
$f_{1}:{\mathcal{M}}_{1}{\hookrightarrow}{\mathcal{M}}$
and, similarly,
$T_{2}=\text{im}(\text{T}_{\text{st}}^{r}(f_{2}))$
for some admissible monomorphism
$f_{2}:{\mathcal{M}}_{2}{\hookrightarrow}{\mathcal{M}}_{1}$
. Then
$f_{1}\circ f_{2}$
is an admissible monomorphism and, by uniqueness, we obtain finally
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}^{-1}(T_{2})=\text{im}(f_{1}\circ f_{2})\subseteq \text{im}(f_{1})=\unicode[STIX]{x1D6E9}^{-1}(T_{1}).\square\end{eqnarray}$$
