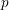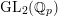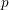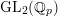1 Introduction
The primary goal of this paper is to explain how (under mild technical hypotheses) the patching construction of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16], when applied to the group
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
, gives rise to the
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
, gives rise to the
![]() $p$
-adic local Langlands correspondence for
$p$
-adic local Langlands correspondence for
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
, as constructed in [Reference ColmezCol10b] and as further analyzed in [Reference PaškūnasPaš13] and [Reference Colmez, Dospinescu and PaškūnasCDP14]. As a by-product, we obtain a new proof of many cases of the local–global compatibility theorem of [Reference EmertonEme11] (and of some cases not treated there).
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
, as constructed in [Reference ColmezCol10b] and as further analyzed in [Reference PaškūnasPaš13] and [Reference Colmez, Dospinescu and PaškūnasCDP14]. As a by-product, we obtain a new proof of many cases of the local–global compatibility theorem of [Reference EmertonEme11] (and of some cases not treated there).
1.1 Background
We start by recalling the main results of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] and the role we expect them to play in the (hypothetical)
![]() $p$
-adic local Langlands correspondence. Let
$p$
-adic local Langlands correspondence. Let
![]() $F$
be a finite extension of
$F$
be a finite extension of
![]() $\mathbb{Q}_{p}$
and let
$\mathbb{Q}_{p}$
and let
![]() $G_{F}$
be its absolute Galois group. One would like to have an analogue of the local Langlands correspondence for all finite-dimensional, continuous,
$G_{F}$
be its absolute Galois group. One would like to have an analogue of the local Langlands correspondence for all finite-dimensional, continuous,
![]() $p$
-adic representations of
$p$
-adic representations of
![]() $G_{F}$
. Let
$G_{F}$
. Let
![]() $E$
be another finite extension of
$E$
be another finite extension of
![]() $\mathbb{Q}_{p}$
, which will be our field of coefficients, assumed large enough, with ring of integers
$\mathbb{Q}_{p}$
, which will be our field of coefficients, assumed large enough, with ring of integers
![]() ${\mathcal{O}}$
, uniformizer
${\mathcal{O}}$
, uniformizer
![]() $\unicode[STIX]{x1D71B}$
and residue field
$\unicode[STIX]{x1D71B}$
and residue field
![]() $\mathbb{F}$
. To a continuous Galois representation
$\mathbb{F}$
. To a continuous Galois representation
 $r:G_{F}\rightarrow \operatorname{GL}_{n}(E)$
one would like to attach an admissible unitary
$r:G_{F}\rightarrow \operatorname{GL}_{n}(E)$
one would like to attach an admissible unitary
![]() $E$
-Banach space representation
$E$
-Banach space representation
![]() $\unicode[STIX]{x1D6F1}(r)$
of
$\unicode[STIX]{x1D6F1}(r)$
of
 $G:=\operatorname{GL}_{n}(F)$
(or possibly a family of such Banach space representations). Ideally, such a construction should be compatible with deformations, should encode the classical local Langlands correspondence and should be compatible with a global
$G:=\operatorname{GL}_{n}(F)$
(or possibly a family of such Banach space representations). Ideally, such a construction should be compatible with deformations, should encode the classical local Langlands correspondence and should be compatible with a global
![]() $p$
-adic correspondence, realized in the completed cohomology of locally symmetric spaces.
$p$
-adic correspondence, realized in the completed cohomology of locally symmetric spaces.
It is expected that the Banach spaces
![]() $\unicode[STIX]{x1D6F1}(r)$
should encode the classical local Langlands correspondence in the following way: if
$\unicode[STIX]{x1D6F1}(r)$
should encode the classical local Langlands correspondence in the following way: if
![]() $r$
is potentially semistable with regular Hodge–Tate weights, then the subspace of locally algebraic vectors
$r$
is potentially semistable with regular Hodge–Tate weights, then the subspace of locally algebraic vectors
 $\unicode[STIX]{x1D6F1}(r)^{\text{l.alg}}$
in
$\unicode[STIX]{x1D6F1}(r)^{\text{l.alg}}$
in
![]() $\unicode[STIX]{x1D6F1}(r)$
should be isomorphic to
$\unicode[STIX]{x1D6F1}(r)$
should be isomorphic to
 $\unicode[STIX]{x1D70B}_{\text{sm}}(r)\otimes \unicode[STIX]{x1D70B}_{\text{alg}}(r)$
as a
$\unicode[STIX]{x1D70B}_{\text{sm}}(r)\otimes \unicode[STIX]{x1D70B}_{\text{alg}}(r)$
as a
![]() $G$
-representation, where
$G$
-representation, where
![]() $\unicode[STIX]{x1D70B}_{\text{sm}}(r)$
is the smooth representation of
$\unicode[STIX]{x1D70B}_{\text{sm}}(r)$
is the smooth representation of
![]() $G$
corresponding via classical local Langlands to the Weil–Deligne representation obtained from
$G$
corresponding via classical local Langlands to the Weil–Deligne representation obtained from
![]() $r$
by Fontaine’s recipe, and
$r$
by Fontaine’s recipe, and
![]() $\unicode[STIX]{x1D70B}_{\text{alg}}(r)$
is an algebraic representation of
$\unicode[STIX]{x1D70B}_{\text{alg}}(r)$
is an algebraic representation of
![]() $G$
, whose highest-weight vector is determined by the Hodge–Tate weights of
$G$
, whose highest-weight vector is determined by the Hodge–Tate weights of
![]() $r$
.
$r$
.
Example 1.2. If
 $F=\mathbb{Q}_{p}$
,
$F=\mathbb{Q}_{p}$
,
![]() $n=2$
and
$n=2$
and
![]() $r$
is crystalline with Hodge–Tate weights
$r$
is crystalline with Hodge–Tate weights
![]() $a<b$
, then
$a<b$
, then
![]() $\unicode[STIX]{x1D70B}_{\text{sm}}(r)$
is a smooth unramified principal series representation, whose Satake parameters can be calculated in terms of the trace and determinant of Frobenius on
$\unicode[STIX]{x1D70B}_{\text{sm}}(r)$
is a smooth unramified principal series representation, whose Satake parameters can be calculated in terms of the trace and determinant of Frobenius on
![]() $D_{\text{cris}}(r)$
, and
$D_{\text{cris}}(r)$
, and
 $\unicode[STIX]{x1D70B}_{\text{alg}}(r)=\text{Sym}^{b-a-1}E^{2}\otimes \;\det ^{1-a}$
. (We note that in the literature different normalizations lead to different twists by a power of
$\unicode[STIX]{x1D70B}_{\text{alg}}(r)=\text{Sym}^{b-a-1}E^{2}\otimes \;\det ^{1-a}$
. (We note that in the literature different normalizations lead to different twists by a power of
![]() $\det$
.)
$\det$
.)
Such a correspondence has been established in the case of
![]() $n=2$
and
$n=2$
and
 $F=\mathbb{Q}_{p}$
by the works of Breuil, Colmez and others; see [Reference BreuilBre08, Reference ColmezCol10a] as well as the introduction to [Reference ColmezCol10b]. Moreover, when
$F=\mathbb{Q}_{p}$
by the works of Breuil, Colmez and others; see [Reference BreuilBre08, Reference ColmezCol10a] as well as the introduction to [Reference ColmezCol10b]. Moreover, when
![]() $n=2$
and
$n=2$
and
 $F=\mathbb{Q}_{p}$
, this correspondence has been proved (in most cases) to satisfy local–global compatibility with the
$F=\mathbb{Q}_{p}$
, this correspondence has been proved (in most cases) to satisfy local–global compatibility with the
![]() $p$
-adically completed cohomology of modular curves; see [Reference EmertonEme11]. However, not much is known beyond this case. In [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] we have constructed a candidate for such a correspondence using the Taylor–Wiles–Kisin patching method, which has been traditionally employed to prove modularity lifting theorems for Galois representations. We now describe the end product of the paper [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16].
$p$
-adically completed cohomology of modular curves; see [Reference EmertonEme11]. However, not much is known beyond this case. In [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] we have constructed a candidate for such a correspondence using the Taylor–Wiles–Kisin patching method, which has been traditionally employed to prove modularity lifting theorems for Galois representations. We now describe the end product of the paper [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16].
Let
 $\bar{r}:G_{F}\rightarrow \operatorname{GL}_{n}(\mathbb{F})$
be a continuous representation and let
$\bar{r}:G_{F}\rightarrow \operatorname{GL}_{n}(\mathbb{F})$
be a continuous representation and let
![]() $R_{p}^{\Box }$
be its universal framed deformation ring. Under the assumption that
$R_{p}^{\Box }$
be its universal framed deformation ring. Under the assumption that
![]() $p$
does not divide
$p$
does not divide
![]() $2n$
, we construct an
$2n$
, we construct an
![]() $R_{\infty }[G]$
-module
$R_{\infty }[G]$
-module
![]() $M_{\infty }$
, which is finitely generated as a module over the completed group algebra
$M_{\infty }$
, which is finitely generated as a module over the completed group algebra
 $R_{\infty }[[\operatorname{GL}_{n}({\mathcal{O}}_{F})]]$
, where
$R_{\infty }[[\operatorname{GL}_{n}({\mathcal{O}}_{F})]]$
, where
![]() $R_{\infty }$
is a complete local noetherian
$R_{\infty }$
is a complete local noetherian
![]() $R_{p}^{\Box }$
-algebra with residue field
$R_{p}^{\Box }$
-algebra with residue field
![]() $\mathbb{F}$
. If
$\mathbb{F}$
. If
 $y\in \operatorname{Spec}R_{\infty }$
is an
$y\in \operatorname{Spec}R_{\infty }$
is an
![]() $E$
-valued point, then
$E$
-valued point, then
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{y}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(M_{\infty }\otimes _{R_{\infty },y}{\mathcal{O}},E)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{y}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(M_{\infty }\otimes _{R_{\infty },y}{\mathcal{O}},E)\end{eqnarray}$$
is an admissible unitary
![]() $E$
-Banach space representation of
$E$
-Banach space representation of
![]() $G$
. The composition
$G$
. The composition
 $R_{p}^{\Box }\rightarrow R_{\infty }\overset{y}{\rightarrow }E$
defines an
$R_{p}^{\Box }\rightarrow R_{\infty }\overset{y}{\rightarrow }E$
defines an
![]() $E$
-valued point
$E$
-valued point
 $x\in \operatorname{Spec}R_{p}^{\Box }$
and thus a continuous Galois representation
$x\in \operatorname{Spec}R_{p}^{\Box }$
and thus a continuous Galois representation
 $r_{x}:G_{F}\rightarrow \operatorname{GL}_{n}(E)$
. We expect that the Banach space representation
$r_{x}:G_{F}\rightarrow \operatorname{GL}_{n}(E)$
. We expect that the Banach space representation
![]() $\unicode[STIX]{x1D6F1}_{y}$
depends only on
$\unicode[STIX]{x1D6F1}_{y}$
depends only on
![]() $x$
and that it should be related to
$x$
and that it should be related to
![]() $r_{x}$
by the hypothetical
$r_{x}$
by the hypothetical
![]() $p$
-adic Langlands correspondence; see [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 6] for a detailed discussion. We show in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Theorem 4.35] that if
$p$
-adic Langlands correspondence; see [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 6] for a detailed discussion. We show in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Theorem 4.35] that if
![]() $\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x})$
is generic and
$\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x})$
is generic and
![]() $x$
lies on an automorphic component of a potentially crystalline deformation ring of
$x$
lies on an automorphic component of a potentially crystalline deformation ring of
![]() $\bar{r}$
, then
$\bar{r}$
, then
 $\unicode[STIX]{x1D6F1}_{y}^{\text{l.alg}}\cong \unicode[STIX]{x1D70B}_{\text{sm}}(r_{x})\otimes \unicode[STIX]{x1D70B}_{\text{alg}}(r_{x})$
, as expected; moreover, the points
$\unicode[STIX]{x1D6F1}_{y}^{\text{l.alg}}\cong \unicode[STIX]{x1D70B}_{\text{sm}}(r_{x})\otimes \unicode[STIX]{x1D70B}_{\text{alg}}(r_{x})$
, as expected; moreover, the points
![]() $x$
such that
$x$
such that
![]() $\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x})$
is generic are Zariski dense in every irreducible component of a potentially crystalline deformation ring. (It is expected that every irreducible component of a potentially crystalline deformation ring is automorphic; this expectation is motivated by the Fontaine–Mazur and Breuil–Mézard conjectures. However, it is intrinsic to our method that we would not be able to access these non-automorphic components even if they existed.)
$\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x})$
is generic are Zariski dense in every irreducible component of a potentially crystalline deformation ring. (It is expected that every irreducible component of a potentially crystalline deformation ring is automorphic; this expectation is motivated by the Fontaine–Mazur and Breuil–Mézard conjectures. However, it is intrinsic to our method that we would not be able to access these non-automorphic components even if they existed.)
However, there are many natural questions regarding our construction for
 $\operatorname{GL}_{n}(F)$
that we cannot answer at the moment and that appear to be genuinely deep, as they are intertwined with questions about local–global compatibility for
$\operatorname{GL}_{n}(F)$
that we cannot answer at the moment and that appear to be genuinely deep, as they are intertwined with questions about local–global compatibility for
![]() $p$
-adically completed cohomology, with the Breuil–Mézard conjecture on the geometry of local deformation rings and with the Fontaine–Mazur conjecture for global Galois representations. For example, it is not clear that
$p$
-adically completed cohomology, with the Breuil–Mézard conjecture on the geometry of local deformation rings and with the Fontaine–Mazur conjecture for global Galois representations. For example, it is not clear that
![]() $\unicode[STIX]{x1D6F1}_{y}$
depends only on
$\unicode[STIX]{x1D6F1}_{y}$
depends only on
![]() $x$
, it is not clear that
$x$
, it is not clear that
![]() $\unicode[STIX]{x1D6F1}_{y}$
is non-zero for an arbitrary
$\unicode[STIX]{x1D6F1}_{y}$
is non-zero for an arbitrary
![]() $y$
and that furthermore
$y$
and that furthermore
![]() $\unicode[STIX]{x1D6F1}_{y}^{\text{l.alg}}$
is non-zero if
$\unicode[STIX]{x1D6F1}_{y}^{\text{l.alg}}$
is non-zero if
![]() $r_{x}$
is potentially semistable of regular weight and it is not at all clear that
$r_{x}$
is potentially semistable of regular weight and it is not at all clear that
![]() $M_{\infty }$
does not depend on the different choices made during the patching process.
$M_{\infty }$
does not depend on the different choices made during the patching process.
1.3 The present paper
In this paper, we specialize the construction of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] to the case
 $F=\mathbb{Q}_{p}$
and
$F=\mathbb{Q}_{p}$
and
![]() $n=2$
(so that
$n=2$
(so that
 $G:=\operatorname{GL}_{2}(\mathbb{Q}_{p})$
and
$G:=\operatorname{GL}_{2}(\mathbb{Q}_{p})$
and
 $K:=\operatorname{GL}_{2}(\mathbb{Z}_{p})$
from now on) to confirm our expectation that, firstly,
$K:=\operatorname{GL}_{2}(\mathbb{Z}_{p})$
from now on) to confirm our expectation that, firstly,
![]() $M_{\infty }$
does not depend on any of the choices made during the patching process and, secondly, that it does recover the
$M_{\infty }$
does not depend on any of the choices made during the patching process and, secondly, that it does recover the
![]() $p$
-adic local Langlands correspondence as constructed by Colmez.
$p$
-adic local Langlands correspondence as constructed by Colmez.
We achieve the first part without appealing to Colmez’s construction (which relies on the theory of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules). The proof that
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules). The proof that
![]() $M_{\infty }$
is uniquely determined highlights some key features of the
$M_{\infty }$
is uniquely determined highlights some key features of the
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
setting beyond the use of
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
setting beyond the use of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules: the classification of irreducible mod
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules: the classification of irreducible mod
![]() $p$
representations of
$p$
representations of
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
in terms of Serre weights and Hecke operators, and the fact that the Weil–Deligne representation and the Hodge–Tate weights determine a (irreducible) two-dimensional crystalline representation of
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
in terms of Serre weights and Hecke operators, and the fact that the Weil–Deligne representation and the Hodge–Tate weights determine a (irreducible) two-dimensional crystalline representation of
![]() $G_{\mathbb{Q}_{p}}$
uniquely (up to isomorphism).
$G_{\mathbb{Q}_{p}}$
uniquely (up to isomorphism).
When combined with the results of [Reference PaškūnasPaš13] (which do rely on Colmez’s functor
![]() $\check{\mathbf{V}}$
), we obtain that
$\check{\mathbf{V}}$
), we obtain that
![]() $M_{\infty }$
realizes the
$M_{\infty }$
realizes the
![]() $p$
-adic Langlands correspondence as constructed by Colmez.
$p$
-adic Langlands correspondence as constructed by Colmez.
We also obtain a new proof of local–global compatibility, which helps clarify the relationship between different perspectives and approaches to
![]() $p$
-adic local Langlands.
$p$
-adic local Langlands.
1.4 Arithmetic actions
In the body of the paper we restrict the representations
![]() $\bar{r}$
we consider by assuming that they have only scalar endomorphisms, so that
$\bar{r}$
we consider by assuming that they have only scalar endomorphisms, so that
 $\text{End}_{G_{\mathbb{Q}_{p}}}(\bar{r})=\mathbb{F}$
and that
$\text{End}_{G_{\mathbb{Q}_{p}}}(\bar{r})=\mathbb{F}$
and that
 $\bar{r}\not \cong \big(\!\begin{smallmatrix}\unicode[STIX]{x1D714} & \ast \\ 0 & 1\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
for any character
$\bar{r}\not \cong \big(\!\begin{smallmatrix}\unicode[STIX]{x1D714} & \ast \\ 0 & 1\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
for any character
 $\unicode[STIX]{x1D712}:G_{\mathbb{Q}_{p}}\rightarrow \mathbb{F}^{\times }$
. For simplicity, let us assume in this introduction that
$\unicode[STIX]{x1D712}:G_{\mathbb{Q}_{p}}\rightarrow \mathbb{F}^{\times }$
. For simplicity, let us assume in this introduction that
![]() $\bar{r}$
is irreducible and let
$\bar{r}$
is irreducible and let
![]() $R_{p}$
be its universal deformation ring. Then
$R_{p}$
be its universal deformation ring. Then
![]() $R_{p}^{\Box }$
is formally smooth over
$R_{p}^{\Box }$
is formally smooth over
![]() $R_{p}$
. Moreover (as
$R_{p}$
. Moreover (as
 $F=\mathbb{Q}_{p}$
and
$F=\mathbb{Q}_{p}$
and
![]() $n=2$
), we may also assume that
$n=2$
), we may also assume that
![]() $R_{\infty }$
is formally smooth over
$R_{\infty }$
is formally smooth over
![]() $R_{p}^{\Box }$
and thus over
$R_{p}^{\Box }$
and thus over
![]() $R_{p}$
.
$R_{p}$
.
The following definition is meant to axiomatize the key properties of the patched module
![]() $M_{\infty }$
.
$M_{\infty }$
.
Definition 1.5. Let
![]() $d$
be a non-negative integer, let
$d$
be a non-negative integer, let
 $R_{\infty }:=R_{p}[[x_{1},\ldots ,x_{d}]]$
and let
$R_{\infty }:=R_{p}[[x_{1},\ldots ,x_{d}]]$
and let
![]() $M$
be a non-zero
$M$
be a non-zero
![]() $R_{\infty }[G]$
-module. We say that the action of
$R_{\infty }[G]$
-module. We say that the action of
![]() $R_{\infty }$
on
$R_{\infty }$
on
![]() $M$
is arithmetic if the following conditions hold:
$M$
is arithmetic if the following conditions hold:
- (AA1)
 $M$
is a finitely generated module over the completed group algebra
$M$
is a finitely generated module over the completed group algebra
 $R_{\infty }[[K]]$
;
$R_{\infty }[[K]]$
;- (AA2)
 $M$
is projective in the category of pseudocompact
$M$
is projective in the category of pseudocompact
 ${\mathcal{O}}[[K]]$
-modules;
${\mathcal{O}}[[K]]$
-modules;- (AA3)
for each pair of integers
 $a<b$
, the action of
$a<b$
, the action of
 $R_{\infty }$
on
$R_{\infty }$
on  $$\begin{eqnarray}M(\unicode[STIX]{x1D70E}^{\circ }):=\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(M,(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\end{eqnarray}$$
$$\begin{eqnarray}M(\unicode[STIX]{x1D70E}^{\circ }):=\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(M,(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\end{eqnarray}$$
factors through the action of
 $R_{\infty }(\unicode[STIX]{x1D70E}):=R_{p}(\unicode[STIX]{x1D70E})[[x_{1},\ldots ,x_{d}]]$
. Here
$R_{\infty }(\unicode[STIX]{x1D70E}):=R_{p}(\unicode[STIX]{x1D70E})[[x_{1},\ldots ,x_{d}]]$
. Here
 $R_{p}(\unicode[STIX]{x1D70E})$
is the quotient of
$R_{p}(\unicode[STIX]{x1D70E})$
is the quotient of
 $R_{p}$
constructed by Kisin, which parameterizes crystalline representations with Hodge–Tate weights
$R_{p}$
constructed by Kisin, which parameterizes crystalline representations with Hodge–Tate weights
 $(a,b)$
,
$(a,b)$
,
 $\unicode[STIX]{x1D70E}^{\circ }$
is a
$\unicode[STIX]{x1D70E}^{\circ }$
is a
 $K$
-invariant
$K$
-invariant
 ${\mathcal{O}}$
-lattice in
${\mathcal{O}}$
-lattice in
 $\unicode[STIX]{x1D70E}:=\text{Sym}^{b-a-1}E^{2}\otimes \det ^{1-a}$
and
$\unicode[STIX]{x1D70E}:=\text{Sym}^{b-a-1}E^{2}\otimes \det ^{1-a}$
and
 $(\ast )^{d}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(\ast ,{\mathcal{O}})$
denotes the Schikhof dual.
$(\ast )^{d}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(\ast ,{\mathcal{O}})$
denotes the Schikhof dual.Moreover,
 $M(\unicode[STIX]{x1D70E}^{\circ })$
is maximal Cohen–Macaulay over
$M(\unicode[STIX]{x1D70E}^{\circ })$
is maximal Cohen–Macaulay over
 $R_{\infty }(\unicode[STIX]{x1D70E})$
and the
$R_{\infty }(\unicode[STIX]{x1D70E})$
and the
 $R_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
-module
$R_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
-module
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is locally free of rank
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is locally free of rank
 $1$
over its support;
$1$
over its support;- (AA4)
for each
 $\unicode[STIX]{x1D70E}$
as above and each maximal ideal
$\unicode[STIX]{x1D70E}$
as above and each maximal ideal
 $y$
of
$y$
of
 $R_{\infty }[1/p]$
in the support of
$R_{\infty }[1/p]$
in the support of
 $M(\unicode[STIX]{x1D70E}^{\circ })$
, there is a non-zero
$M(\unicode[STIX]{x1D70E}^{\circ })$
, there is a non-zero
 $G$
-equivariant map
$G$
-equivariant map  $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x})\otimes \unicode[STIX]{x1D70B}_{\text{alg}}(r_{x})\rightarrow \unicode[STIX]{x1D6F1}_{y}^{\text{l.alg}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x})\otimes \unicode[STIX]{x1D70B}_{\text{alg}}(r_{x})\rightarrow \unicode[STIX]{x1D6F1}_{y}^{\text{l.alg}},\end{eqnarray}$$
where
 $x$
is the image of
$x$
is the image of
 $y$
in
$y$
in
 $\operatorname{Spec}R_{p}$
.
$\operatorname{Spec}R_{p}$
.
The last condition says that
![]() $M$
encodes the classical local Langlands correspondence. This is what motivated us to call such actions arithmetic. (In fact in the main body of the paper we use a reformulation of condition (AA4); see § 3.1 and Remark 3.3.) To motivate (AA3), we note for the sake of the reader familiar with Kisin’s proof of the Fontaine–Mazur conjecture [Reference KisinKis09] that the modules
$M$
encodes the classical local Langlands correspondence. This is what motivated us to call such actions arithmetic. (In fact in the main body of the paper we use a reformulation of condition (AA4); see § 3.1 and Remark 3.3.) To motivate (AA3), we note for the sake of the reader familiar with Kisin’s proof of the Fontaine–Mazur conjecture [Reference KisinKis09] that the modules
![]() $M(\unicode[STIX]{x1D70E}^{\circ })$
are analogues of the patched modules denoted by
$M(\unicode[STIX]{x1D70E}^{\circ })$
are analogues of the patched modules denoted by
![]() $M_{\infty }$
in [Reference KisinKis09], except that Kisin patches algebraic automorphic forms for definite quaternion algebras and in this paper we will ultimately be making use of patching arguments for algebraic automorphic forms on forms of
$M_{\infty }$
in [Reference KisinKis09], except that Kisin patches algebraic automorphic forms for definite quaternion algebras and in this paper we will ultimately be making use of patching arguments for algebraic automorphic forms on forms of
![]() $U(2)$
.
$U(2)$
.
1.6 Uniqueness of
 $M_{\infty }$
$M_{\infty }$
As already mentioned, the patched module
![]() $M_{\infty }$
of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] carries an arithmetic action of
$M_{\infty }$
of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] carries an arithmetic action of
![]() $R_{\infty }$
for some
$R_{\infty }$
for some
![]() $d$
. In order to prove that
$d$
. In order to prove that
![]() $M_{\infty }$
is uniquely determined, it is enough to show that for any given
$M_{\infty }$
is uniquely determined, it is enough to show that for any given
![]() $d$
, any
$d$
, any
![]() $R_{\infty }[G]$
-module
$R_{\infty }[G]$
-module
![]() $M$
with an arithmetic action of
$M$
with an arithmetic action of
![]() $R_{\infty }$
is uniquely determined. The following is our main result, which for simplicity we state under the assumption that
$R_{\infty }$
is uniquely determined. The following is our main result, which for simplicity we state under the assumption that
![]() $\bar{r}$
is irreducible.
$\bar{r}$
is irreducible.
Theorem 1.7. Let
![]() $M$
be an
$M$
be an
![]() $R_{\infty }[G]$
-module with an arithmetic action of
$R_{\infty }[G]$
-module with an arithmetic action of
![]() $R_{\infty }$
.
$R_{\infty }$
.
(i) If
 $\unicode[STIX]{x1D70B}$
is any irreducible
$\unicode[STIX]{x1D70B}$
is any irreducible
 $G$
-subrepresentation of the Pontryagin dual
$G$
-subrepresentation of the Pontryagin dual
 $M^{\vee }$
of
$M^{\vee }$
of
 $M$
, then
$M$
, then
 $\unicode[STIX]{x1D70B}$
is isomorphic to the representation of
$\unicode[STIX]{x1D70B}$
is isomorphic to the representation of
 $G$
associated to
$G$
associated to
 $\bar{r}$
by the mod
$\bar{r}$
by the mod
 $p$
local Langlands correspondence for
$p$
local Langlands correspondence for
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
.
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
.(ii) Let
 $\unicode[STIX]{x1D70B}{\hookrightarrow}J$
be an injective envelope of the above
$\unicode[STIX]{x1D70B}{\hookrightarrow}J$
be an injective envelope of the above
 $\unicode[STIX]{x1D70B}$
in the category of smooth locally admissible representations of
$\unicode[STIX]{x1D70B}$
in the category of smooth locally admissible representations of
 $G$
on
$G$
on
 ${\mathcal{O}}$
-torsion modules. Let
${\mathcal{O}}$
-torsion modules. Let
 $\widetilde{P}$
be the Pontryagin dual of
$\widetilde{P}$
be the Pontryagin dual of
 $J$
. Then
$J$
. Then
 $\widetilde{P}$
carries a unique arithmetic action of
$\widetilde{P}$
carries a unique arithmetic action of
 $R_{p}$
and, moreover, as
$R_{p}$
and, moreover, as $$\begin{eqnarray}M\cong \widetilde{P}\;\operatorname{⊗̂}_{R_{p}}\,R_{\infty }\end{eqnarray}$$
$$\begin{eqnarray}M\cong \widetilde{P}\;\operatorname{⊗̂}_{R_{p}}\,R_{\infty }\end{eqnarray}$$
 $R_{\infty }[G]$
-modules.
$R_{\infty }[G]$
-modules.
The theorem completely characterizes modules with an arithmetic action and shows that
![]() $M_{\infty }$
does not depend on the choices made in the patching process. A further consequence is that the Banach space
$M_{\infty }$
does not depend on the choices made in the patching process. A further consequence is that the Banach space
![]() $\unicode[STIX]{x1D6F1}_{y}$
depends only on the image of
$\unicode[STIX]{x1D6F1}_{y}$
depends only on the image of
![]() $y$
in
$y$
in
 $\operatorname{Spec}R_{p}$
, as expected.
$\operatorname{Spec}R_{p}$
, as expected.
Let us sketch the proof of Theorem 1.7 assuming for simplicity that
![]() $d=0$
. The first step is to show that
$d=0$
. The first step is to show that
![]() $M^{\vee }$
is an injective object in the category of smooth locally admissible representations of
$M^{\vee }$
is an injective object in the category of smooth locally admissible representations of
![]() $G$
on
$G$
on
![]() ${\mathcal{O}}$
-torsion modules and that its
${\mathcal{O}}$
-torsion modules and that its
![]() $G$
-socle is isomorphic to
$G$
-socle is isomorphic to
![]() $\unicode[STIX]{x1D70B}$
. This is done by computing
$\unicode[STIX]{x1D70B}$
. This is done by computing
 $\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },M^{\vee })$
and showing that
$\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },M^{\vee })$
and showing that
 $\text{Ext}_{G}^{1}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })$
vanishes for all irreducible
$\text{Ext}_{G}^{1}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })$
vanishes for all irreducible
![]() $\mathbb{F}$
-representations
$\mathbb{F}$
-representations
![]() $\unicode[STIX]{x1D70B}^{\prime }$
of
$\unicode[STIX]{x1D70B}^{\prime }$
of
![]() $G$
; see Proposition 4.2 and Theorem 4.15. The arguments here use the foundational results of Barthel and Livné [Reference Barthel and LivnéBL94] and Breuil [Reference BreuilBre03a] on the classification of irreducible mod
$G$
; see Proposition 4.2 and Theorem 4.15. The arguments here use the foundational results of Barthel and Livné [Reference Barthel and LivnéBL94] and Breuil [Reference BreuilBre03a] on the classification of irreducible mod
![]() $p$
representations of
$p$
representations of
![]() $G$
, arguments related to the weight part of Serre’s conjecture and the fact that the rings
$G$
, arguments related to the weight part of Serre’s conjecture and the fact that the rings
![]() $R_{p}(\unicode[STIX]{x1D70E})$
are formally smooth over
$R_{p}(\unicode[STIX]{x1D70E})$
are formally smooth over
![]() ${\mathcal{O}}$
, whenever
${\mathcal{O}}$
, whenever
![]() $\unicode[STIX]{x1D70E}$
is of the form
$\unicode[STIX]{x1D70E}$
is of the form
 $\text{Sym}^{b-a-1}E^{2}\otimes \;\det ^{1-a}$
with
$\text{Sym}^{b-a-1}E^{2}\otimes \;\det ^{1-a}$
with
 $1\leqslant b-a\leqslant p$
.
$1\leqslant b-a\leqslant p$
.
This first step allows us to conclude that
![]() $M^{\vee }$
is an injective envelope of
$M^{\vee }$
is an injective envelope of
![]() $\unicode[STIX]{x1D70B}$
, which depends only on
$\unicode[STIX]{x1D70B}$
, which depends only on
![]() $\bar{r}$
. Since injective envelopes are unique up to isomorphism, we conclude that any two modules with an arithmetic action of
$\bar{r}$
. Since injective envelopes are unique up to isomorphism, we conclude that any two modules with an arithmetic action of
![]() $R_{p}$
are isomorphic as
$R_{p}$
are isomorphic as
![]() $G$
-representations. Therefore, it remains to show that any two arithmetic actions of
$G$
-representations. Therefore, it remains to show that any two arithmetic actions of
![]() $R_{p}$
on
$R_{p}$
on
![]() $\widetilde{P}$
coincide. As
$\widetilde{P}$
coincide. As
![]() $R_{p}$
is
$R_{p}$
is
![]() ${\mathcal{O}}$
-torsion free, it is enough to show that two such actions induce the same action on the unitary
${\mathcal{O}}$
-torsion free, it is enough to show that two such actions induce the same action on the unitary
![]() $E$
-Banach space
$E$
-Banach space
 $\unicode[STIX]{x1D6F1}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(M,E)$
. Since
$\unicode[STIX]{x1D6F1}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(M,E)$
. Since
![]() $M$
is a projective
$M$
is a projective
![]() ${\mathcal{O}}[[K]]$
-module by (AA2), one may show using the ‘capture’ arguments that appear in [Reference Colmez, Dospinescu and PaškūnasCDP14, § 2.4] and [Reference EmertonEme11, Proposition 5.4.1] that the subspace of
${\mathcal{O}}[[K]]$
-module by (AA2), one may show using the ‘capture’ arguments that appear in [Reference Colmez, Dospinescu and PaškūnasCDP14, § 2.4] and [Reference EmertonEme11, Proposition 5.4.1] that the subspace of
![]() $K$
-algebraic vectors in
$K$
-algebraic vectors in
![]() $\unicode[STIX]{x1D6F1}$
is dense. Since the actions of
$\unicode[STIX]{x1D6F1}$
is dense. Since the actions of
![]() $R_{p}$
on
$R_{p}$
on
![]() $\unicode[STIX]{x1D6F1}$
are continuous, it is enough to show that they agree on this dense subspace. Since the subspace of
$\unicode[STIX]{x1D6F1}$
are continuous, it is enough to show that they agree on this dense subspace. Since the subspace of
![]() $K$
-algebraic vectors is semisimple as a
$K$
-algebraic vectors is semisimple as a
![]() $K$
-representation, it is enough to show that the two actions agree on
$K$
-representation, it is enough to show that the two actions agree on
![]() $\unicode[STIX]{x1D70E}$
-isotypic subspaces in
$\unicode[STIX]{x1D70E}$
-isotypic subspaces in
![]() $\unicode[STIX]{x1D6F1}$
for all irreducible algebraic
$\unicode[STIX]{x1D6F1}$
for all irreducible algebraic
![]() $K$
-representations
$K$
-representations
![]() $\unicode[STIX]{x1D70E}$
. These are precisely the representations
$\unicode[STIX]{x1D70E}$
. These are precisely the representations
![]() $\unicode[STIX]{x1D70E}$
in axiom (AA3). Taking duals one more time, we are left with showing that any two arithmetic actions induce the same action of
$\unicode[STIX]{x1D70E}$
in axiom (AA3). Taking duals one more time, we are left with showing that any two arithmetic actions induce the same action of
![]() $R_{p}$
on
$R_{p}$
on
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
for all
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
for all
![]() $\unicode[STIX]{x1D70E}$
as above.
$\unicode[STIX]{x1D70E}$
as above.
At this point we use another special feature of two-dimensional crystalline representations of
![]() $G_{\mathbb{Q}_{p}}$
: the associated Weil–Deligne representation together with Hodge–Tate weights determine a two-dimensional crystalline representation of
$G_{\mathbb{Q}_{p}}$
: the associated Weil–Deligne representation together with Hodge–Tate weights determine a two-dimensional crystalline representation of
![]() $G_{\mathbb{Q}_{p}}$
up to isomorphism. Using this fact and axioms (AA3) and (AA4) for the arithmetic action, we show that the action of the Hecke algebra
$G_{\mathbb{Q}_{p}}$
up to isomorphism. Using this fact and axioms (AA3) and (AA4) for the arithmetic action, we show that the action of the Hecke algebra
 ${\mathcal{H}}(\unicode[STIX]{x1D70E}):=\text{End}_{G}(\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E})$
on
${\mathcal{H}}(\unicode[STIX]{x1D70E}):=\text{End}_{G}(\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E})$
on
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
completely determines the action of
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
completely determines the action of
![]() $R_{p}(\unicode[STIX]{x1D70E})$
on
$R_{p}(\unicode[STIX]{x1D70E})$
on
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
; see the proof of Theorem 4.30 as well as the key Proposition 2.13. Since the action of
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
; see the proof of Theorem 4.30 as well as the key Proposition 2.13. Since the action of
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
on
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
on
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
depends only on the
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
depends only on the
![]() $G$
-module structure of
$G$
-module structure of
![]() $M$
, we are able to conclude that the two arithmetic actions are the same. The reduction from the case when
$M$
, we are able to conclude that the two arithmetic actions are the same. The reduction from the case when
![]() $d$
is arbitrary to the case when
$d$
is arbitrary to the case when
![]() $d=0$
is carried out in § 4.16.
$d=0$
is carried out in § 4.16.
Remark 1.8. As we have already remarked, the arguments up to this point make no use of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules. Indeed, the proof of Theorem 1.7 does not use them. One of the objectives of this project was to find out how much of the
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules. Indeed, the proof of Theorem 1.7 does not use them. One of the objectives of this project was to find out how much of the
![]() $p$
-adic Langlands for
$p$
-adic Langlands for
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
correspondence can one recover from the patched module
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
correspondence can one recover from the patched module
![]() $M_{\infty }$
without using Colmez’s functors, as these constructions are not available for groups other than
$M_{\infty }$
without using Colmez’s functors, as these constructions are not available for groups other than
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
, while our patched module
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
, while our patched module
![]() $M_{\infty }$
is. Along the same lines, in § 5 we show that to a large extent we can recover a fundamental theorem of Berger and Breuil [Reference Berger and BreuilBB10] on the uniqueness of unitary completions of locally algebraic principal series without making use of
$M_{\infty }$
is. Along the same lines, in § 5 we show that to a large extent we can recover a fundamental theorem of Berger and Breuil [Reference Berger and BreuilBB10] on the uniqueness of unitary completions of locally algebraic principal series without making use of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules; see Theorem 5.1 and Remark 5.3.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules; see Theorem 5.1 and Remark 5.3.
Remark 1.9. As already explained, Theorem 1.7 implies that
![]() $\unicode[STIX]{x1D6F1}_{y}$
depends only on the image of
$\unicode[STIX]{x1D6F1}_{y}$
depends only on the image of
![]() $y$
in
$y$
in
 $\operatorname{Spec}R_{p}$
. However, we are still not able to deduce using only our methods that
$\operatorname{Spec}R_{p}$
. However, we are still not able to deduce using only our methods that
![]() $\unicode[STIX]{x1D6F1}_{y}$
is non-zero for an arbitrary
$\unicode[STIX]{x1D6F1}_{y}$
is non-zero for an arbitrary
 $y\in \operatorname{m - Spec}R_{\infty }[1/p]$
. Since
$y\in \operatorname{m - Spec}R_{\infty }[1/p]$
. Since
![]() $M_{\infty }$
is not a finitely generated module over
$M_{\infty }$
is not a finitely generated module over
![]() $R_{\infty }$
, theoretically it could happen that
$R_{\infty }$
, theoretically it could happen that
![]() $\unicode[STIX]{x1D6F1}_{y}\neq 0$
for a dense subset of
$\unicode[STIX]{x1D6F1}_{y}\neq 0$
for a dense subset of
 $\operatorname{m - Spec}R_{\infty }[1/p]$
, but
$\operatorname{m - Spec}R_{\infty }[1/p]$
, but
![]() $\unicode[STIX]{x1D6F1}_{y}=0$
at all other maximal ideals. We can only prove that this pathological situation does not occur after combining Theorem 1.7 with the results of [Reference PaškūnasPaš13].
$\unicode[STIX]{x1D6F1}_{y}=0$
at all other maximal ideals. We can only prove that this pathological situation does not occur after combining Theorem 1.7 with the results of [Reference PaškūnasPaš13].
In § 6 we relate the arithmetic action of
![]() $R_{p}$
on
$R_{p}$
on
![]() $\widetilde{P}$
to the results of [Reference PaškūnasPaš13], where an action of
$\widetilde{P}$
to the results of [Reference PaškūnasPaš13], where an action of
![]() $R_{p}$
on an injective envelope of
$R_{p}$
on an injective envelope of
![]() $\unicode[STIX]{x1D70B}$
in the subcategory of representations with a fixed central character is constructed using Colmez’s functor; see Theorem 6.18. Then by appealing to the results of [Reference PaškūnasPaš13] we show that
$\unicode[STIX]{x1D70B}$
in the subcategory of representations with a fixed central character is constructed using Colmez’s functor; see Theorem 6.18. Then by appealing to the results of [Reference PaškūnasPaš13] we show that
![]() $\unicode[STIX]{x1D6F1}_{y}$
and
$\unicode[STIX]{x1D6F1}_{y}$
and
![]() $r_{x}$
correspond to each other under the
$r_{x}$
correspond to each other under the
![]() $p$
-adic Langlands correspondence as defined by Colmez [Reference ColmezCol10b] for all
$p$
-adic Langlands correspondence as defined by Colmez [Reference ColmezCol10b] for all
 $y\in \operatorname{m - Spec}R_{\infty }[1/p]$
, where
$y\in \operatorname{m - Spec}R_{\infty }[1/p]$
, where
![]() $x$
denotes the image of
$x$
denotes the image of
![]() $y$
in
$y$
in
 $\operatorname{m - Spec}R_{p}[1/p]$
.
$\operatorname{m - Spec}R_{p}[1/p]$
.
It follows from the construction of
![]() $M_{\infty }$
that after quotienting out by a certain ideal of
$M_{\infty }$
that after quotienting out by a certain ideal of
![]() $R_{\infty }$
we obtain a dual of completed cohomology; see [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Corollary 2.11]. This property combined with Theorem 1.7 and with the results in § 6 enables us to obtain a new proof of local–global compatibility as in [Reference EmertonEme11] as well as obtaining a genuinely new result, when
$R_{\infty }$
we obtain a dual of completed cohomology; see [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Corollary 2.11]. This property combined with Theorem 1.7 and with the results in § 6 enables us to obtain a new proof of local–global compatibility as in [Reference EmertonEme11] as well as obtaining a genuinely new result, when
![]() $\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}}$
is isomorphic to
$\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}}$
is isomorphic to
 $\big(\!\begin{smallmatrix}1 & \ast \\ 0 & \unicode[STIX]{x1D714}\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
, where
$\big(\!\begin{smallmatrix}1 & \ast \\ 0 & \unicode[STIX]{x1D714}\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
, where
![]() $\unicode[STIX]{x1D714}$
is the cyclotomic character modulo
$\unicode[STIX]{x1D714}$
is the cyclotomic character modulo
![]() $p$
. (See Remark 7.7.)
$p$
. (See Remark 7.7.)
1.10 Prospects for generalization
Since our primary goal in this paper is to build some new connections between various existing ideas related to the
![]() $p$
-adic Langlands program, we have not striven for maximal generality, and we expect that some of our hypotheses on
$p$
-adic Langlands program, we have not striven for maximal generality, and we expect that some of our hypotheses on
 $\bar{r}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{F}}_{p})$
could be relaxed. In particular, it should be possible to prove results when
$\bar{r}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{F}}_{p})$
could be relaxed. In particular, it should be possible to prove results when
![]() $p=2$
by using results of Thorne [Reference ThorneTho17] to redo the patching in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16]. It may also be possible to extend our results to cover more general
$p=2$
by using results of Thorne [Reference ThorneTho17] to redo the patching in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16]. It may also be possible to extend our results to cover more general
![]() $\bar{r}$
(recall that we assume that
$\bar{r}$
(recall that we assume that
![]() $\bar{r}$
has only scalar endomorphisms, and that it is not a twist of an extension of the trivial character by the mod
$\bar{r}$
has only scalar endomorphisms, and that it is not a twist of an extension of the trivial character by the mod
![]() $p$
cyclotomic character). In § 6.27 we discuss the particular case where
$p$
cyclotomic character). In § 6.27 we discuss the particular case where
![]() $\bar{r}$
has scalar semisimplification; as this discussion (and the arguments of [Reference PaškūnasPaš13]) show, while it may well be possible to generalize our arguments, they will necessarily be considerably more involved in cases where
$\bar{r}$
has scalar semisimplification; as this discussion (and the arguments of [Reference PaškūnasPaš13]) show, while it may well be possible to generalize our arguments, they will necessarily be considerably more involved in cases where
![]() $\bar{r}$
does not satisfy the hypotheses that we have imposed.
$\bar{r}$
does not satisfy the hypotheses that we have imposed.
Since the patching construction in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] applies equally well to the case of
 $\operatorname{GL}_{2}(F)$
for any finite extension
$\operatorname{GL}_{2}(F)$
for any finite extension
![]() $F/\mathbb{Q}_{p}$
, or indeed to
$F/\mathbb{Q}_{p}$
, or indeed to
 $\operatorname{GL}_{n}(F)$
, it is natural to ask whether any of our arguments can be extended to such cases (where there is at present no construction of a
$\operatorname{GL}_{n}(F)$
, it is natural to ask whether any of our arguments can be extended to such cases (where there is at present no construction of a
![]() $p$
-adic local Langlands correspondence). As explained in Remark 3.2, the natural analogues of our axioms (AA1)–(AA4) hold, even in the generality of
$p$
-adic local Langlands correspondence). As explained in Remark 3.2, the natural analogues of our axioms (AA1)–(AA4) hold, even in the generality of
 $\operatorname{GL}_{n}(F)$
. Unfortunately, the prospects for proving analogues of our main theorems are less rosy, as it seems that none of the main inputs to our arguments will hold. Indeed, already for the case of
$\operatorname{GL}_{n}(F)$
. Unfortunately, the prospects for proving analogues of our main theorems are less rosy, as it seems that none of the main inputs to our arguments will hold. Indeed, already for the case of
 $\operatorname{GL}_{2}(\mathbb{Q}_{p^{2}})$
there is no analogue available of the classification in [Reference BreuilBre03a] of the irreducible
$\operatorname{GL}_{2}(\mathbb{Q}_{p^{2}})$
there is no analogue available of the classification in [Reference BreuilBre03a] of the irreducible
![]() $\mathbb{F}$
-representations of
$\mathbb{F}$
-representations of
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
, and it is clear from the results of [Reference Breuil and PaškūnasBP12] that any such classification would be much more complicated.
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
, and it is clear from the results of [Reference Breuil and PaškūnasBP12] that any such classification would be much more complicated.
Furthermore, beyond the case of
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
it is no longer the case that crystalline representations are (essentially) determined by their underlying Weil–Deligne representations, so there is no possibility of deducing that a
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
it is no longer the case that crystalline representations are (essentially) determined by their underlying Weil–Deligne representations, so there is no possibility of deducing that a
![]() $p$
-adic correspondence is uniquely determined by the classical correspondence in the way that we do here, and no hope that an analogue of the results of [Reference Berger and BreuilBB10] could hold. Finally, it is possible to use the constructions of [Reference PaškūnasPaš04] to show that for
$p$
-adic correspondence is uniquely determined by the classical correspondence in the way that we do here, and no hope that an analogue of the results of [Reference Berger and BreuilBB10] could hold. Finally, it is possible to use the constructions of [Reference PaškūnasPaš04] to show that for
 $\operatorname{GL}_{2}(\mathbb{Q}_{p^{2}})$
the patched module
$\operatorname{GL}_{2}(\mathbb{Q}_{p^{2}})$
the patched module
![]() $M_{\infty }$
is not a projective
$M_{\infty }$
is not a projective
 $\operatorname{GL}_{2}(\mathbb{Q}_{p^{2}})$
-module.
$\operatorname{GL}_{2}(\mathbb{Q}_{p^{2}})$
-module.
1.11 Outline of the paper
In § 2 we recall some well-known results about Hecke algebras and crystalline deformation rings for
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
. The main result in this section is Proposition 2.15, which describes the crystalline deformation rings corresponding to Serre weights as completions of the corresponding Hecke algebras. In § 3 we explain our axioms for a module with an arithmetic action, and show how the results of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] produce patched modules
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
. The main result in this section is Proposition 2.15, which describes the crystalline deformation rings corresponding to Serre weights as completions of the corresponding Hecke algebras. In § 3 we explain our axioms for a module with an arithmetic action, and show how the results of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] produce patched modules
![]() $M_{\infty }$
satisfying these axioms.
$M_{\infty }$
satisfying these axioms.
Section 4 proves that the axioms determine
![]() $M_{\infty }$
(essentially) uniquely, giving a new construction of the
$M_{\infty }$
(essentially) uniquely, giving a new construction of the
![]() $p$
-adic local Langlands correspondence for
$p$
-adic local Langlands correspondence for
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
. It begins by showing that
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
. It begins by showing that
![]() $M_{\infty }$
is a projective
$M_{\infty }$
is a projective
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
-module (Theorem 4.15), before making a category-theoretic argument that allows us to ‘factor out’ the patching variables (Proposition 4.22). We then use the ‘capture’ machinery to complete the proof.
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
-module (Theorem 4.15), before making a category-theoretic argument that allows us to ‘factor out’ the patching variables (Proposition 4.22). We then use the ‘capture’ machinery to complete the proof.
In § 5 we explain how our results can be used to give a new proof (not making use of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules) that certain locally algebraic principal series representations admit at most one unitary completion. Section 6 combines our results with those of [Reference PaškūnasPaš13] to show that our construction is compatible with Colmez’s correspondence, and as a by-product extends some results of [Reference PaškūnasPaš13] to a situation where the central character is not fixed.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules) that certain locally algebraic principal series representations admit at most one unitary completion. Section 6 combines our results with those of [Reference PaškūnasPaš13] to show that our construction is compatible with Colmez’s correspondence, and as a by-product extends some results of [Reference PaškūnasPaš13] to a situation where the central character is not fixed.
Finally, in § 7 we explain how our results give a new proof of the second author’s local–global compatibility theorem, and briefly explain how such results can be extended to quaternion algebras over totally real fields (Remark 7.8).
1.12 Notation
We fix an odd prime
![]() $p$
, an algebraic closure
$p$
, an algebraic closure
![]() $\overline{\mathbb{Q}}_{p}$
of
$\overline{\mathbb{Q}}_{p}$
of
![]() $\mathbb{Q}_{p}$
and a finite extension
$\mathbb{Q}_{p}$
and a finite extension
![]() $E/\mathbb{Q}_{p}$
in
$E/\mathbb{Q}_{p}$
in
![]() $\overline{\mathbb{Q}}_{p}$
, which will be our coefficient field. We write
$\overline{\mathbb{Q}}_{p}$
, which will be our coefficient field. We write
 ${\mathcal{O}}={\mathcal{O}}_{E}$
for the ring of integers in
${\mathcal{O}}={\mathcal{O}}_{E}$
for the ring of integers in
![]() $E$
,
$E$
,
 $\unicode[STIX]{x1D71B}=\unicode[STIX]{x1D71B}_{E}$
for a uniformizer and
$\unicode[STIX]{x1D71B}=\unicode[STIX]{x1D71B}_{E}$
for a uniformizer and
 $\mathbb{F}:={\mathcal{O}}/\unicode[STIX]{x1D71B}$
for the residue field. We will assume without comment that
$\mathbb{F}:={\mathcal{O}}/\unicode[STIX]{x1D71B}$
for the residue field. We will assume without comment that
![]() $E$
and
$E$
and
![]() $\mathbb{F}$
are sufficiently large, and in particular that if we are working with representations of the absolute Galois group of a
$\mathbb{F}$
are sufficiently large, and in particular that if we are working with representations of the absolute Galois group of a
![]() $p$
-adic field
$p$
-adic field
![]() $K$
, then the images of all embeddings
$K$
, then the images of all embeddings
 $K{\hookrightarrow}\overline{\mathbb{Q}}_{p}$
are contained in
$K{\hookrightarrow}\overline{\mathbb{Q}}_{p}$
are contained in
![]() $E$
.
$E$
.
1.12.1 Galois-theoretic notation
If
![]() $K$
is a field, we let
$K$
is a field, we let
![]() $G_{K}$
denote its absolute Galois group. Let
$G_{K}$
denote its absolute Galois group. Let
![]() $\unicode[STIX]{x1D700}$
denote the
$\unicode[STIX]{x1D700}$
denote the
![]() $p$
-adic cyclotomic character and
$p$
-adic cyclotomic character and
![]() $\overline{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D714}$
the mod
$\overline{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D714}$
the mod
![]() $p$
cyclotomic character. If
$p$
cyclotomic character. If
![]() $K$
is a finite extension of
$K$
is a finite extension of
![]() $\mathbb{Q}_{p}$
for some
$\mathbb{Q}_{p}$
for some
![]() $p$
, we write
$p$
, we write
![]() $I_{K}$
for the inertia subgroup of
$I_{K}$
for the inertia subgroup of
![]() $G_{K}$
. If
$G_{K}$
. If
![]() $R$
is a local ring, we write
$R$
is a local ring, we write
![]() $\mathfrak{m}_{R}$
for the maximal ideal of
$\mathfrak{m}_{R}$
for the maximal ideal of
![]() $R$
. If
$R$
. If
![]() $F$
is a number field and
$F$
is a number field and
![]() $v$
is a finite place of
$v$
is a finite place of
![]() $F$
, then we let
$F$
, then we let
![]() $\operatorname{Frob}_{v}$
denote a geometric Frobenius element of
$\operatorname{Frob}_{v}$
denote a geometric Frobenius element of
![]() $G_{F_{v}}$
.
$G_{F_{v}}$
.
If
![]() $K/\mathbb{Q}_{p}$
is a finite extension, we write
$K/\mathbb{Q}_{p}$
is a finite extension, we write
 $\operatorname{Art}_{K}:K^{\times }\stackrel{{\sim}}{\longrightarrow }W_{K}^{\text{ab}}$
for the Artin map normalized to send uniformizers to geometric Frobenius elements. To avoid cluttering up the notation, we will use
$\operatorname{Art}_{K}:K^{\times }\stackrel{{\sim}}{\longrightarrow }W_{K}^{\text{ab}}$
for the Artin map normalized to send uniformizers to geometric Frobenius elements. To avoid cluttering up the notation, we will use
![]() $\operatorname{Art}_{\mathbb{Q}_{p}}$
to regard characters of
$\operatorname{Art}_{\mathbb{Q}_{p}}$
to regard characters of
![]() $\mathbb{Q}_{p}^{\times }$
,
$\mathbb{Q}_{p}^{\times }$
,
![]() $\mathbb{Z}_{p}^{\times }$
as characters of
$\mathbb{Z}_{p}^{\times }$
as characters of
![]() $G_{\mathbb{Q}_{p}}$
,
$G_{\mathbb{Q}_{p}}$
,
![]() $I_{\mathbb{Q}_{p}}$
, respectively, without explicitly mentioning
$I_{\mathbb{Q}_{p}}$
, respectively, without explicitly mentioning
![]() $\operatorname{Art}_{\mathbb{Q}_{p}}$
when we do so.
$\operatorname{Art}_{\mathbb{Q}_{p}}$
when we do so.
If
![]() $K$
is a
$K$
is a
![]() $p$
-adic field and
$p$
-adic field and
![]() $\unicode[STIX]{x1D70C}$
a de Rham representation of
$\unicode[STIX]{x1D70C}$
a de Rham representation of
![]() $G_{K}$
over
$G_{K}$
over
![]() $E$
and if
$E$
and if
 $\unicode[STIX]{x1D70F}:K{\hookrightarrow}E$
, then we will write
$\unicode[STIX]{x1D70F}:K{\hookrightarrow}E$
, then we will write
![]() $\operatorname{HT}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D70C})$
for the multiset of Hodge–Tate numbers of
$\operatorname{HT}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D70C})$
for the multiset of Hodge–Tate numbers of
![]() $\unicode[STIX]{x1D70C}$
with respect to
$\unicode[STIX]{x1D70C}$
with respect to
![]() $\unicode[STIX]{x1D70F}$
. By definition, the multiset
$\unicode[STIX]{x1D70F}$
. By definition, the multiset
![]() $\operatorname{HT}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D70C})$
contains
$\operatorname{HT}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D70C})$
contains
![]() $i$
with multiplicity
$i$
with multiplicity
 $\dim _{E}(\unicode[STIX]{x1D70C}\otimes _{\unicode[STIX]{x1D70F},K}\widehat{\overline{K}}(i))^{G_{K}}$
. Thus for example
$\dim _{E}(\unicode[STIX]{x1D70C}\otimes _{\unicode[STIX]{x1D70F},K}\widehat{\overline{K}}(i))^{G_{K}}$
. Thus for example
 $\operatorname{HT}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D700})=\{-1\}$
. If
$\operatorname{HT}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D700})=\{-1\}$
. If
![]() $\unicode[STIX]{x1D70C}$
is moreover crystalline, then we have the associated filtered
$\unicode[STIX]{x1D70C}$
is moreover crystalline, then we have the associated filtered
![]() $\unicode[STIX]{x1D711}$
-module
$\unicode[STIX]{x1D711}$
-module
 $D_{\operatorname{cris}}(\unicode[STIX]{x1D70C}):=(\unicode[STIX]{x1D70C}\otimes _{\mathbb{Q}_{p}}B_{\text{cris}})^{G_{K}}$
, where
$D_{\operatorname{cris}}(\unicode[STIX]{x1D70C}):=(\unicode[STIX]{x1D70C}\otimes _{\mathbb{Q}_{p}}B_{\text{cris}})^{G_{K}}$
, where
![]() $B_{\text{cris}}$
is Fontaine’s crystalline period ring.
$B_{\text{cris}}$
is Fontaine’s crystalline period ring.
1.12.2 Local Langlands correspondence
Let
 $n\in \mathbb{Z}_{{\geqslant}1}$
, let
$n\in \mathbb{Z}_{{\geqslant}1}$
, let
![]() $K$
be a finite extension of
$K$
be a finite extension of
![]() $\mathbb{Q}_{p}$
and let
$\mathbb{Q}_{p}$
and let
![]() $\operatorname{rec}$
denote the local Langlands correspondence from isomorphism classes of irreducible smooth representations of
$\operatorname{rec}$
denote the local Langlands correspondence from isomorphism classes of irreducible smooth representations of
 $\operatorname{GL}_{n}(K)$
over
$\operatorname{GL}_{n}(K)$
over
![]() $\mathbb{C}$
to isomorphism classes of
$\mathbb{C}$
to isomorphism classes of
![]() $n$
-dimensional Frobenius semisimple Weil–Deligne representations of
$n$
-dimensional Frobenius semisimple Weil–Deligne representations of
![]() $W_{K}$
defined in [Reference Harris and TaylorHT01]. Fix an isomorphism
$W_{K}$
defined in [Reference Harris and TaylorHT01]. Fix an isomorphism
 $\imath :\overline{\mathbb{Q}}_{p}\rightarrow \mathbb{C}$
. We define the local Langlands correspondence
$\imath :\overline{\mathbb{Q}}_{p}\rightarrow \mathbb{C}$
. We define the local Langlands correspondence
![]() $\operatorname{rec}_{p}$
over
$\operatorname{rec}_{p}$
over
![]() $\overline{\mathbb{Q}}_{p}$
by
$\overline{\mathbb{Q}}_{p}$
by
 $\imath \circ \operatorname{rec}_{p}=\operatorname{rec}\circ \imath$
. Then
$\imath \circ \operatorname{rec}_{p}=\operatorname{rec}\circ \imath$
. Then
 $r_{p}(\unicode[STIX]{x1D70B}):=\operatorname{rec}_{p}(\unicode[STIX]{x1D70B}\otimes |\det |^{(1-n)/2})$
is independent of the choice of
$r_{p}(\unicode[STIX]{x1D70B}):=\operatorname{rec}_{p}(\unicode[STIX]{x1D70B}\otimes |\det |^{(1-n)/2})$
is independent of the choice of
![]() $\imath$
. In this paper we are mostly concerned with the case that
$\imath$
. In this paper we are mostly concerned with the case that
![]() $n=2$
and
$n=2$
and
 $K=\mathbb{Q}_{p}$
.
$K=\mathbb{Q}_{p}$
.
1.12.3 Notation for duals
If
![]() $A$
is a topological
$A$
is a topological
![]() ${\mathcal{O}}$
-module, we write
${\mathcal{O}}$
-module, we write
 $A^{\vee }:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A,E/{\mathcal{O}})$
for the Pontryagin dual of
$A^{\vee }:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A,E/{\mathcal{O}})$
for the Pontryagin dual of
![]() $A$
. We apply this to
$A$
. We apply this to
![]() ${\mathcal{O}}$
-modules that are either discrete or profinite, so that the usual formalism of Pontryagin duality applies.
${\mathcal{O}}$
-modules that are either discrete or profinite, so that the usual formalism of Pontryagin duality applies.
If
![]() $A$
is a pseudocompact
$A$
is a pseudocompact
![]() ${\mathcal{O}}$
-torsion-free
${\mathcal{O}}$
-torsion-free
![]() ${\mathcal{O}}$
-module, we write
${\mathcal{O}}$
-module, we write
 $A^{d}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A,{\mathcal{O}})$
for its Schikhof dual.
$A^{d}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A,{\mathcal{O}})$
for its Schikhof dual.
If
![]() $F$
is a free module of finite rank over a ring
$F$
is a free module of finite rank over a ring
![]() $R$
, then we write
$R$
, then we write
 $F^{\ast }:=\operatorname{Hom}_{R}(F,R)$
to denote its
$F^{\ast }:=\operatorname{Hom}_{R}(F,R)$
to denote its
![]() $R$
-linear dual, which is again a free
$R$
-linear dual, which is again a free
![]() $R$
-module of the same rank over
$R$
-module of the same rank over
![]() $R$
as
$R$
as
![]() $F$
.
$F$
.
If
![]() $R$
is a commutative
$R$
is a commutative
![]() ${\mathcal{O}}$
-algebra, and if
${\mathcal{O}}$
-algebra, and if
![]() $A$
is an
$A$
is an
![]() $R$
-module that is pseudocompact and
$R$
-module that is pseudocompact and
![]() ${\mathcal{O}}$
-torsion free as an
${\mathcal{O}}$
-torsion free as an
![]() ${\mathcal{O}}$
-module, then we may form its Schikhof dual
${\mathcal{O}}$
-module, then we may form its Schikhof dual
![]() $A^{d}$
, which has a natural
$A^{d}$
, which has a natural
![]() $R$
-module structure via the transpose action, extending its
$R$
-module structure via the transpose action, extending its
![]() ${\mathcal{O}}$
-module structure. If
${\mathcal{O}}$
-module structure. If
![]() $F$
is a finite-rank free
$F$
is a finite-rank free
![]() $R$
-module, then
$R$
-module, then
 $A\otimes _{R}F$
is again an
$A\otimes _{R}F$
is again an
![]() $R$
-module that is pseudocompact as an
$R$
-module that is pseudocompact as an
![]() ${\mathcal{O}}$
-module (if
${\mathcal{O}}$
-module (if
![]() $F$
has rank
$F$
has rank
![]() $n$
, then it is non-canonically isomorphic to a direct sum of
$n$
, then it is non-canonically isomorphic to a direct sum of
![]() $n$
copies of
$n$
copies of
![]() $A$
) and there is a canonical isomorphism of
$A$
) and there is a canonical isomorphism of
![]() $R$
-modules
$R$
-modules
 $(A\otimes _{R}F)^{d}\stackrel{{\sim}}{\longrightarrow }A^{d}\otimes _{R}F^{\ast }.$
$(A\otimes _{R}F)^{d}\stackrel{{\sim}}{\longrightarrow }A^{d}\otimes _{R}F^{\ast }.$
1.12.4 Group-theoretic notation
Throughout the paper we write
 $G=\operatorname{GL}_{2}(\mathbb{Q}_{p})$
and
$G=\operatorname{GL}_{2}(\mathbb{Q}_{p})$
and
 $K=\operatorname{GL}_{2}(\mathbb{Z}_{p})$
, and let
$K=\operatorname{GL}_{2}(\mathbb{Z}_{p})$
, and let
 $Z=Z(G)$
denote the centre of
$Z=Z(G)$
denote the centre of
![]() $G$
. We also let
$G$
. We also let
![]() $B$
denote the Borel subgroup of
$B$
denote the Borel subgroup of
![]() $G$
consisting of upper-triangular matrices, and
$G$
consisting of upper-triangular matrices, and
![]() $T$
denote the diagonal torus contained in
$T$
denote the diagonal torus contained in
![]() $B$
.
$B$
.
If
 $\unicode[STIX]{x1D712}:T\rightarrow E^{\times }$
is a continuous character, then we define the continuous induction
$\unicode[STIX]{x1D712}:T\rightarrow E^{\times }$
is a continuous character, then we define the continuous induction
 $(\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D712})_{\text{cont}}$
to be the
$(\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D712})_{\text{cont}}$
to be the
![]() $E$
-vector space of continuous functions
$E$
-vector space of continuous functions
 $f:G\rightarrow E$
satisfying the condition
$f:G\rightarrow E$
satisfying the condition
 $f(bg)=\unicode[STIX]{x1D712}(b)f(g)$
for all
$f(bg)=\unicode[STIX]{x1D712}(b)f(g)$
for all
![]() $b\in B$
and
$b\in B$
and
![]() $g\in G$
; it forms a
$g\in G$
; it forms a
![]() $G$
-representation with respect to the right regular action. If
$G$
-representation with respect to the right regular action. If
![]() $\unicode[STIX]{x1D712}$
is in fact a smooth character, then we may also form the smooth induction
$\unicode[STIX]{x1D712}$
is in fact a smooth character, then we may also form the smooth induction
 $(\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D712})_{\text{sm}}$
; this is the
$(\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D712})_{\text{sm}}$
; this is the
![]() $E$
-subspace of
$E$
-subspace of
 $(\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D712})_{\text{cont}}$
consisting of smooth functions, and is a
$(\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D712})_{\text{cont}}$
consisting of smooth functions, and is a
![]() $G$
-subrepresentation of the continuous induction.
$G$
-subrepresentation of the continuous induction.
If
![]() $\unicode[STIX]{x1D712}_{1}$
and
$\unicode[STIX]{x1D712}_{1}$
and
![]() $\unicode[STIX]{x1D712}_{2}$
are continuous characters of
$\unicode[STIX]{x1D712}_{2}$
are continuous characters of
![]() $\mathbb{Q}_{p}^{\times }$
, then the character
$\mathbb{Q}_{p}^{\times }$
, then the character
 $\unicode[STIX]{x1D712}_{1}\otimes \unicode[STIX]{x1D712}_{2}:T\rightarrow E^{\times }$
is defined via
$\unicode[STIX]{x1D712}_{1}\otimes \unicode[STIX]{x1D712}_{2}:T\rightarrow E^{\times }$
is defined via
 $\big(\!\begin{smallmatrix}a & 0\\ 0 & d\end{smallmatrix}\!\big)\mapsto \unicode[STIX]{x1D712}_{1}(a)\unicode[STIX]{x1D712}_{2}(d)$
. Any continuous
$\big(\!\begin{smallmatrix}a & 0\\ 0 & d\end{smallmatrix}\!\big)\mapsto \unicode[STIX]{x1D712}_{1}(a)\unicode[STIX]{x1D712}_{2}(d)$
. Any continuous
![]() $E$
-valued character
$E$
-valued character
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $T$
is of this form, and
$T$
is of this form, and
![]() $\unicode[STIX]{x1D712}$
is smooth if and only if
$\unicode[STIX]{x1D712}$
is smooth if and only if
![]() $\unicode[STIX]{x1D712}_{1}$
and
$\unicode[STIX]{x1D712}_{1}$
and
![]() $\unicode[STIX]{x1D712}_{2}$
are.
$\unicode[STIX]{x1D712}_{2}$
are.
2 Galois deformation rings and Hecke algebras
2.1 Galois deformation rings
Recall that we assume throughout the paper that
![]() $p$
is an odd prime. Fix a continuous representation
$p$
is an odd prime. Fix a continuous representation
 $\bar{r}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{2}(\mathbb{F})$
, where as before
$\bar{r}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{2}(\mathbb{F})$
, where as before
![]() $\mathbb{F}/\mathbb{F}_{p}$
is a finite extension. Possibly enlarging
$\mathbb{F}/\mathbb{F}_{p}$
is a finite extension. Possibly enlarging
![]() $\mathbb{F}$
, we fix a sufficiently large extension
$\mathbb{F}$
, we fix a sufficiently large extension
![]() $E/\mathbb{Q}_{p}$
with ring of integers
$E/\mathbb{Q}_{p}$
with ring of integers
![]() ${\mathcal{O}}$
and residue field
${\mathcal{O}}$
and residue field
![]() $\mathbb{F}$
.
$\mathbb{F}$
.
We will make the following assumption from now on.
Assumption 2.2. Assume that
 $\text{End}_{G_{\mathbb{Q}_{p}}}(\bar{r})=\mathbb{F}$
and that
$\text{End}_{G_{\mathbb{Q}_{p}}}(\bar{r})=\mathbb{F}$
and that
 $\bar{r}\not \cong \big(\!\begin{smallmatrix}\unicode[STIX]{x1D714} & \ast \\ 0 & 1\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
for any character
$\bar{r}\not \cong \big(\!\begin{smallmatrix}\unicode[STIX]{x1D714} & \ast \\ 0 & 1\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
for any character
 $\unicode[STIX]{x1D712}:G_{\mathbb{Q}_{p}}\rightarrow \mathbb{F}^{\times }$
.
$\unicode[STIX]{x1D712}:G_{\mathbb{Q}_{p}}\rightarrow \mathbb{F}^{\times }$
.
In particular this assumption implies that
![]() $\bar{r}$
has a universal deformation
$\bar{r}$
has a universal deformation
![]() ${\mathcal{O}}$
-algebra
${\mathcal{O}}$
-algebra
![]() $R_{p}$
, and that either
$R_{p}$
, and that either
![]() $\bar{r}$
is (absolutely) irreducible or that
$\bar{r}$
is (absolutely) irreducible or that
![]() $\bar{r}$
is a non-split extension of characters.
$\bar{r}$
is a non-split extension of characters.
We begin by recalling the relationship between crystalline deformation rings of
![]() $\bar{r}$
and the representation theory of
$\bar{r}$
and the representation theory of
 $G:=\operatorname{GL}_{2}(\mathbb{Q}_{p})$
and
$G:=\operatorname{GL}_{2}(\mathbb{Q}_{p})$
and
 $K:=\operatorname{GL}_{2}(\mathbb{Z}_{p})$
. Given a pair of integers
$K:=\operatorname{GL}_{2}(\mathbb{Z}_{p})$
. Given a pair of integers
![]() $a\in \mathbb{Z}$
and
$a\in \mathbb{Z}$
and
 $b\in \mathbb{Z}_{{\geqslant}0}$
, we let
$b\in \mathbb{Z}_{{\geqslant}0}$
, we let
![]() $\unicode[STIX]{x1D70E}_{a,b}$
be the absolutely irreducible
$\unicode[STIX]{x1D70E}_{a,b}$
be the absolutely irreducible
![]() $E$
-representation
$E$
-representation
 $\det ^{a}\otimes \;\text{Sym}^{b}E^{2}$
of
$\det ^{a}\otimes \;\text{Sym}^{b}E^{2}$
of
![]() $K$
. Note that this is just the algebraic representation of highest weight
$K$
. Note that this is just the algebraic representation of highest weight
 $(a+b,a)$
with respect to the Borel subgroup given by the upper-triangular matrices in
$(a+b,a)$
with respect to the Borel subgroup given by the upper-triangular matrices in
![]() $G$
.
$G$
.
We say that a representation
 $r:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{Q}}_{p})$
is crystalline of Hodge type
$r:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{Q}}_{p})$
is crystalline of Hodge type
 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
if it is crystalline with Hodge–Tate weights
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
if it is crystalline with Hodge–Tate weights
 $(1-a,-a-b)$
;Footnote
1
we write
$(1-a,-a-b)$
;Footnote
1
we write
![]() $R_{p}(\unicode[STIX]{x1D70E})$
for the reduced,
$R_{p}(\unicode[STIX]{x1D70E})$
for the reduced,
![]() $p$
-torsion-free quotient of
$p$
-torsion-free quotient of
![]() $R_{p}$
corresponding to crystalline deformations of Hodge type
$R_{p}$
corresponding to crystalline deformations of Hodge type
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
2.3 The morphism from the Hecke algebra to the deformation ring
We briefly recall some results from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 4], specialized to the case of crystalline representations of
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
.
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
.
Set
 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
and let
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
and let
 ${\mathcal{H}}(\unicode[STIX]{x1D70E}):=\text{End}_{G}(\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E})$
. The action of
${\mathcal{H}}(\unicode[STIX]{x1D70E}):=\text{End}_{G}(\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E})$
. The action of
![]() $K$
on
$K$
on
![]() $\unicode[STIX]{x1D70E}$
extends to the action of
$\unicode[STIX]{x1D70E}$
extends to the action of
![]() $G$
. This gives rise to the isomorphism of
$G$
. This gives rise to the isomorphism of
![]() $G$
-representations:
$G$
-representations:
 $$\begin{eqnarray}(\operatorname{c - Ind}_{K}^{G}\mathbf{1})\otimes \unicode[STIX]{x1D70E}\cong \operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E},\quad f\otimes v\mapsto [g\mapsto f(g)\unicode[STIX]{x1D70E}(g)v].\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{c - Ind}_{K}^{G}\mathbf{1})\otimes \unicode[STIX]{x1D70E}\cong \operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E},\quad f\otimes v\mapsto [g\mapsto f(g)\unicode[STIX]{x1D70E}(g)v].\end{eqnarray}$$
The map
 $$\begin{eqnarray}{\mathcal{H}}(\unicode[STIX]{x1D7D9})\rightarrow {\mathcal{H}}(\unicode[STIX]{x1D70E}),\quad \unicode[STIX]{x1D719}\mapsto \unicode[STIX]{x1D719}\otimes \text{id}_{\unicode[STIX]{x1D70E}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}(\unicode[STIX]{x1D7D9})\rightarrow {\mathcal{H}}(\unicode[STIX]{x1D70E}),\quad \unicode[STIX]{x1D719}\mapsto \unicode[STIX]{x1D719}\otimes \text{id}_{\unicode[STIX]{x1D70E}}\end{eqnarray}$$
is an isomorphism of
![]() $E$
-algebras by [Reference Schneider and TeitelbaumST06, Lemma 1.4]. Using the above isomorphism we will identify elements of
$E$
-algebras by [Reference Schneider and TeitelbaumST06, Lemma 1.4]. Using the above isomorphism we will identify elements of
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
with
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
with
![]() $E$
-valued
$E$
-valued
![]() $K$
-bi-invariant functions on
$K$
-bi-invariant functions on
![]() $G$
, supported on finitely many double cosets.
$G$
, supported on finitely many double cosets.
Proposition 2.5. Let
 $S\in {\mathcal{H}}(\unicode[STIX]{x1D70E})$
be the function supported on the double coset of
$S\in {\mathcal{H}}(\unicode[STIX]{x1D70E})$
be the function supported on the double coset of
![]() $\big(\!\begin{smallmatrix}p & 0\\ 0 & p\end{smallmatrix}\!\big)$
, with value
$\big(\!\begin{smallmatrix}p & 0\\ 0 & p\end{smallmatrix}\!\big)$
, with value
![]() $p^{2a+b}$
at
$p^{2a+b}$
at
![]() $\big(\!\begin{smallmatrix}p & 0\\ 0 & p\end{smallmatrix}\!\big)$
, and let
$\big(\!\begin{smallmatrix}p & 0\\ 0 & p\end{smallmatrix}\!\big)$
, and let
 $T\in {\mathcal{H}}(\unicode[STIX]{x1D70E})$
be the function supported on the double cosetFootnote
2
of
$T\in {\mathcal{H}}(\unicode[STIX]{x1D70E})$
be the function supported on the double cosetFootnote
2
of
![]() $\big(\!\begin{smallmatrix}p & 0\\ 0 & 1\end{smallmatrix}\!\big)$
, with value
$\big(\!\begin{smallmatrix}p & 0\\ 0 & 1\end{smallmatrix}\!\big)$
, with value
![]() $p^{a+b}$
at
$p^{a+b}$
at
![]() $\big(\!\begin{smallmatrix}p & 0\\ 0 & 1\end{smallmatrix}\!\big)$
. Then
$\big(\!\begin{smallmatrix}p & 0\\ 0 & 1\end{smallmatrix}\!\big)$
. Then
 ${\mathcal{H}}(\unicode[STIX]{x1D70E})=E[S^{\pm 1},T]$
as an
${\mathcal{H}}(\unicode[STIX]{x1D70E})=E[S^{\pm 1},T]$
as an
![]() $E$
-algebra.
$E$
-algebra.
Proof. This is immediate from (2.4) and the Satake isomorphism. ◻
Let
![]() $r,s$
be integers with
$r,s$
be integers with
![]() $r<s$
and let
$r<s$
and let
 $t,d\in E$
, with
$t,d\in E$
, with
![]() $d\in E^{\times }$
. We let
$d\in E^{\times }$
. We let
 $D:=D(r,s,t,d)$
be the two-dimensional filtered
$D:=D(r,s,t,d)$
be the two-dimensional filtered
![]() $\unicode[STIX]{x1D711}$
-module that has
$\unicode[STIX]{x1D711}$
-module that has
![]() $e_{1}$
,
$e_{1}$
,
![]() $e_{2}$
as a basis of its underlying
$e_{2}$
as a basis of its underlying
![]() $E$
-vector space, has its
$E$
-vector space, has its
![]() $E$
-linear Frobenius endomorphism
$E$
-linear Frobenius endomorphism
![]() $\unicode[STIX]{x1D711}$
given by
$\unicode[STIX]{x1D711}$
given by
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(e_{1})=e_{2},\quad \unicode[STIX]{x1D711}(e_{2})=-de_{1}+te_{2}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(e_{1})=e_{2},\quad \unicode[STIX]{x1D711}(e_{2})=-de_{1}+te_{2}\end{eqnarray}$$
and has its Hodge filtration given by
 $$\begin{eqnarray}\operatorname{Fil}^{i}D=D\quad \text{if }i\leqslant r,\quad \operatorname{Fil}^{i}D=Ee_{1}\quad \text{if }r+1\leqslant i\leqslant s\quad \text{and}\quad \operatorname{Fil}^{i}D=0\quad \text{if }i>s.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Fil}^{i}D=D\quad \text{if }i\leqslant r,\quad \operatorname{Fil}^{i}D=Ee_{1}\quad \text{if }r+1\leqslant i\leqslant s\quad \text{and}\quad \operatorname{Fil}^{i}D=0\quad \text{if }i>s.\end{eqnarray}$$
We note that
![]() $t$
is the trace and
$t$
is the trace and
![]() $d$
is the determinant of
$d$
is the determinant of
![]() $\unicode[STIX]{x1D711}$
on
$\unicode[STIX]{x1D711}$
on
![]() $D$
, and both are therefore determined uniquely by
$D$
, and both are therefore determined uniquely by
![]() $D$
. The same construction works if
$D$
. The same construction works if
![]() $E$
is replaced with an
$E$
is replaced with an
![]() $E$
-algebra
$E$
-algebra
![]() $A$
. We will still write
$A$
. We will still write
 $D(r,s,t,d)$
for the resulting
$D(r,s,t,d)$
for the resulting
![]() $\unicode[STIX]{x1D711}$
-module with
$\unicode[STIX]{x1D711}$
-module with
![]() $A$
-coefficients if the coefficient algebra is clear from the context.
$A$
-coefficients if the coefficient algebra is clear from the context.
Lemma 2.6. If
![]() $V$
is an indecomposable two-dimensional crystalline representation of
$V$
is an indecomposable two-dimensional crystalline representation of
![]() $G_{\mathbb{Q}_{p}}$
over
$G_{\mathbb{Q}_{p}}$
over
![]() $E$
with distinct Hodge–Tate weights
$E$
with distinct Hodge–Tate weights
![]() $(s,r)$
, then there exists a unique pair
$(s,r)$
, then there exists a unique pair
 $(t,d)\in E\times E^{\times }$
such that
$(t,d)\in E\times E^{\times }$
such that
 $D_{\operatorname{cris}}(V)\cong D(r,s,t,d)$
. Moreover,
$D_{\operatorname{cris}}(V)\cong D(r,s,t,d)$
. Moreover,
 $v_{p}(d)=r+s$
and
$v_{p}(d)=r+s$
and
 $v_{p}(t)\geqslant r$
.
$v_{p}(t)\geqslant r$
.
Proof. This is well known, and is a straightforward computation using the fact that
 $D_{\operatorname{cris}}(V)$
is weakly admissible. For the sake of completeness, we sketch the proof; the key fact one employs is that
$D_{\operatorname{cris}}(V)$
is weakly admissible. For the sake of completeness, we sketch the proof; the key fact one employs is that
 $V\mapsto D_{\operatorname{cris}}(V)$
is a fully faithful embedding of the category of crystalline representations of
$V\mapsto D_{\operatorname{cris}}(V)$
is a fully faithful embedding of the category of crystalline representations of
![]() $G_{\mathbb{Q}_{p}}$
into the category of weakly admissible filtered
$G_{\mathbb{Q}_{p}}$
into the category of weakly admissible filtered
![]() $\unicode[STIX]{x1D711}$
-modules. (Indeed, it induces an equivalence between these two categories, but that more difficult fact is not needed for this computation.) We choose
$\unicode[STIX]{x1D711}$
-modules. (Indeed, it induces an equivalence between these two categories, but that more difficult fact is not needed for this computation.) We choose
![]() $e_{1}$
to be a basis for
$e_{1}$
to be a basis for
 $\operatorname{Fil}^{s}D_{\operatorname{cris}}(V)$
; the assumption that
$\operatorname{Fil}^{s}D_{\operatorname{cris}}(V)$
; the assumption that
![]() $V$
is indecomposable implies that
$V$
is indecomposable implies that
 $\operatorname{Fil}^{s}D_{\operatorname{cris}}(V)$
is not stable under
$\operatorname{Fil}^{s}D_{\operatorname{cris}}(V)$
is not stable under
![]() $\unicode[STIX]{x1D711},$
and so if we write
$\unicode[STIX]{x1D711},$
and so if we write
 $e_{2}:=\unicode[STIX]{x1D711}(e_{1})$
then
$e_{2}:=\unicode[STIX]{x1D711}(e_{1})$
then
![]() $e_{1},e_{2}$
is a basis for
$e_{1},e_{2}$
is a basis for
 $D_{\operatorname{cris}}(V)$
, and
$D_{\operatorname{cris}}(V)$
, and
![]() $\unicode[STIX]{x1D711}$
has a matrix of the required form for a uniquely determined
$\unicode[STIX]{x1D711}$
has a matrix of the required form for a uniquely determined
![]() $t$
and
$t$
and
![]() $d$
. The asserted relations between
$d$
. The asserted relations between
![]() $v_{p}(t)$
,
$v_{p}(t)$
,
![]() $v_{p}(d)$
,
$v_{p}(d)$
,
![]() $r$
and
$r$
and
![]() $s$
follow from the weak admissibility of
$s$
follow from the weak admissibility of
 $D_{\operatorname{cris}}(V)$
.◻
$D_{\operatorname{cris}}(V)$
.◻
In fact, it will be helpful to state a generalization of the previous result to the context of finite-dimensional
![]() $E$
-algebras. (Note that the definition of
$E$
-algebras. (Note that the definition of
 $D(r,s,t,d)$
extends naturally to the case when
$D(r,s,t,d)$
extends naturally to the case when
![]() $t$
and
$t$
and
![]() $d$
are taken to lie in such a finite-dimensional algebra.)
$d$
are taken to lie in such a finite-dimensional algebra.)
Lemma 2.7. If
![]() $A$
is an Artinian local
$A$
is an Artinian local
![]() $E$
-algebra with residue field
$E$
-algebra with residue field
![]() $E^{\prime }$
, and if
$E^{\prime }$
, and if
![]() $V_{A}$
is a crystalline representation of rank
$V_{A}$
is a crystalline representation of rank
![]() $2$
over
$2$
over
![]() $A$
whose associated residual representation
$A$
whose associated residual representation
 $V_{E^{\prime }}:=E^{\prime }\otimes _{A}V_{A}$
is indecomposable with distinct Hodge–Tate weights
$V_{E^{\prime }}:=E^{\prime }\otimes _{A}V_{A}$
is indecomposable with distinct Hodge–Tate weights
![]() $(s,r)$
, and if
$(s,r)$
, and if
 $D_{\operatorname{cris}}(V_{A})$
denotes the filtered
$D_{\operatorname{cris}}(V_{A})$
denotes the filtered
![]() $\unicode[STIX]{x1D711}$
-module associated to
$\unicode[STIX]{x1D711}$
-module associated to
![]() $V_{A}$
, then there exists a unique pair
$V_{A}$
, then there exists a unique pair
 $(t,d)\in A\times A^{\times }$
such that
$(t,d)\in A\times A^{\times }$
such that
 $D_{\operatorname{cris}}(V_{A})\cong D(r,s,t,d)$
.
$D_{\operatorname{cris}}(V_{A})\cong D(r,s,t,d)$
.
Proof. Choose a basis
![]() $\overline{e}_{1}$
for
$\overline{e}_{1}$
for
 $\operatorname{Fil}^{s}D_{\operatorname{cris}}(V_{E^{\prime }})$
, and choose
$\operatorname{Fil}^{s}D_{\operatorname{cris}}(V_{E^{\prime }})$
, and choose
 $e_{1}\in \operatorname{Fil}^{s}D_{\operatorname{cris}}(V_{A})$
lifting
$e_{1}\in \operatorname{Fil}^{s}D_{\operatorname{cris}}(V_{A})$
lifting
![]() $\overline{e}_{1}$
. By Nakayama’s lemma,
$\overline{e}_{1}$
. By Nakayama’s lemma,
![]() $e_{1}$
generates
$e_{1}$
generates
 $\operatorname{Fil}^{s}D_{\operatorname{cris}}(V_{A})$
and, by considering the length of
$\operatorname{Fil}^{s}D_{\operatorname{cris}}(V_{A})$
and, by considering the length of
 $\operatorname{Fil}^{s}D_{\operatorname{cris}}(V_{A})$
as an
$\operatorname{Fil}^{s}D_{\operatorname{cris}}(V_{A})$
as an
![]() $E$
-vector space, we see that
$E$
-vector space, we see that
 $\operatorname{Fil}^{s}D_{\operatorname{cris}}(V_{A})$
is a free
$\operatorname{Fil}^{s}D_{\operatorname{cris}}(V_{A})$
is a free
![]() $A$
-module of rank
$A$
-module of rank
![]() $1$
.
$1$
.
Let
 $e_{2}=\unicode[STIX]{x1D719}(e_{1})$
and write
$e_{2}=\unicode[STIX]{x1D719}(e_{1})$
and write
![]() $\overline{e}_{2}$
for the image of
$\overline{e}_{2}$
for the image of
![]() $e_{2}$
in
$e_{2}$
in
 $D_{\operatorname{cris}}(V_{E^{\prime }})$
. As in the proof of Lemma 2.6,
$D_{\operatorname{cris}}(V_{E^{\prime }})$
. As in the proof of Lemma 2.6,
![]() $\overline{e}_{1},\overline{e}_{2}$
is a basis of
$\overline{e}_{1},\overline{e}_{2}$
is a basis of
 $D_{\operatorname{cris}}(V_{E^{\prime }})$
, and thus by another application of Nakayama’s lemma,
$D_{\operatorname{cris}}(V_{E^{\prime }})$
, and thus by another application of Nakayama’s lemma,
![]() $e_{1},e_{2}$
are an
$e_{1},e_{2}$
are an
![]() $A$
-basis of
$A$
-basis of
 $D_{\operatorname{cris}}(V_{A})$
. The matrix of
$D_{\operatorname{cris}}(V_{A})$
. The matrix of
![]() $\unicode[STIX]{x1D719}$
in this basis is evidently of the required form.◻
$\unicode[STIX]{x1D719}$
in this basis is evidently of the required form.◻
Corollary 2.8. If
![]() $V$
is an indecomposable two-dimensional crystalline representation of
$V$
is an indecomposable two-dimensional crystalline representation of
![]() $G_{\mathbb{Q}_{p}}$
over
$G_{\mathbb{Q}_{p}}$
over
![]() $E$
with distinct Hodge–Tate weights
$E$
with distinct Hodge–Tate weights
![]() $(s,r)$
, for which
$(s,r)$
, for which
 $D_{\operatorname{cris}}(V)\cong D(r,s,t_{0},d_{0})$
, then the formal crystalline deformation ring of
$D_{\operatorname{cris}}(V)\cong D(r,s,t_{0},d_{0})$
, then the formal crystalline deformation ring of
![]() $V$
is naturally isomorphic to
$V$
is naturally isomorphic to
 $E[[t-t_{0},d-d_{0}]].$
$E[[t-t_{0},d-d_{0}]].$
Proof. This is immediate from Lemma 2.7 and the fact that
 $V\mapsto D_{\operatorname{cris}}(V)$
is an equivalence of categories.◻
$V\mapsto D_{\operatorname{cris}}(V)$
is an equivalence of categories.◻
Suppose that
![]() $\bar{r}$
has a crystalline lift of Hodge type
$\bar{r}$
has a crystalline lift of Hodge type
![]() $\unicode[STIX]{x1D70E}$
. By [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Theorem 4.1], there is a natural
$\unicode[STIX]{x1D70E}$
. By [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Theorem 4.1], there is a natural
![]() $E$
-algebra homomorphism
$E$
-algebra homomorphism
 $\unicode[STIX]{x1D702}:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow R_{p}(\unicode[STIX]{x1D70E})[1/p]$
interpolating a normalized local Langlands correspondence
$\unicode[STIX]{x1D702}:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow R_{p}(\unicode[STIX]{x1D70E})[1/p]$
interpolating a normalized local Langlands correspondence
![]() $r_{p}$
(introduced in § 1.12). In order to characterize this map, one considers the composite
$r_{p}$
(introduced in § 1.12). In order to characterize this map, one considers the composite
 $$\begin{eqnarray}{\mathcal{H}}(\unicode[STIX]{x1D70E})\{R_{p}(\unicode[STIX]{x1D70E})[1/p]{\hookrightarrow}(R_{p}(\unicode[STIX]{x1D70E}))^{\text{an}},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}(\unicode[STIX]{x1D70E})\{R_{p}(\unicode[STIX]{x1D70E})[1/p]{\hookrightarrow}(R_{p}(\unicode[STIX]{x1D70E}))^{\text{an}},\end{eqnarray}$$
where
 $(R_{p}(\unicode[STIX]{x1D70E}))^{\text{an}}$
denotes the ring of rigid analytic functions on the rigid analytic generic fibre of
$(R_{p}(\unicode[STIX]{x1D70E}))^{\text{an}}$
denotes the ring of rigid analytic functions on the rigid analytic generic fibre of
 $\operatorname{Spf}R_{p}(\unicode[STIX]{x1D70E})$
. Over
$\operatorname{Spf}R_{p}(\unicode[STIX]{x1D70E})$
. Over
 $(R_{p}(\unicode[STIX]{x1D70E}))^{\text{an}}$
, we may consider the universal filtered
$(R_{p}(\unicode[STIX]{x1D70E}))^{\text{an}}$
, we may consider the universal filtered
![]() $\unicode[STIX]{x1D711}$
-module, and the underlying universal Weil group representation (given by forgetting the filtration). The trace and determinant of Frobenius on this representation are certain elements of
$\unicode[STIX]{x1D711}$
-module, and the underlying universal Weil group representation (given by forgetting the filtration). The trace and determinant of Frobenius on this representation are certain elements of
 $(R_{p}(\unicode[STIX]{x1D70E}))^{\text{an}}$
(which in fact lie in
$(R_{p}(\unicode[STIX]{x1D70E}))^{\text{an}}$
(which in fact lie in
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
), and
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
), and
![]() $\unicode[STIX]{x1D702}$
is characterized by the fact that it identifies appropriately chosen generators of
$\unicode[STIX]{x1D702}$
is characterized by the fact that it identifies appropriately chosen generators of
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
with these universal trace and determinant.
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
with these universal trace and determinant.
It is straightforward to give explicit formulas for these generators of
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
, but we have found it interesting (in part with an eye to making arguments in more general contexts) to also derive the facts that we need without using such explicit formulas.
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
, but we have found it interesting (in part with an eye to making arguments in more general contexts) to also derive the facts that we need without using such explicit formulas.
Regarding explicit formulas, we have the following result.
Proposition 2.9. The elements
 $\unicode[STIX]{x1D702}(S),\unicode[STIX]{x1D702}(T)\in R_{p}(\unicode[STIX]{x1D70E})[1/p]$
are characterized by the following property: if
$\unicode[STIX]{x1D702}(S),\unicode[STIX]{x1D702}(T)\in R_{p}(\unicode[STIX]{x1D70E})[1/p]$
are characterized by the following property: if
 $x:R_{p}(\unicode[STIX]{x1D70E})[1/p]\rightarrow \overline{\mathbb{Q}}_{p}$
is an
$x:R_{p}(\unicode[STIX]{x1D70E})[1/p]\rightarrow \overline{\mathbb{Q}}_{p}$
is an
![]() $E$
-algebra morphism, and
$E$
-algebra morphism, and
![]() $V_{x}$
is the corresponding two-dimensional
$V_{x}$
is the corresponding two-dimensional
![]() $\overline{\mathbb{Q}}_{p}$
-representation of
$\overline{\mathbb{Q}}_{p}$
-representation of
![]() $G_{\mathbb{Q}_{p}}$
, then
$G_{\mathbb{Q}_{p}}$
, then
 $x(\unicode[STIX]{x1D702}(T))=p^{a+b}t$
and
$x(\unicode[STIX]{x1D702}(T))=p^{a+b}t$
and
 $x(\unicode[STIX]{x1D702}(S))=p^{2a+b-1}d$
, where
$x(\unicode[STIX]{x1D702}(S))=p^{2a+b-1}d$
, where
![]() $t$
,
$t$
,
![]() $d$
are respectively the trace and the determinant of
$d$
are respectively the trace and the determinant of
![]() $\unicode[STIX]{x1D711}$
on
$\unicode[STIX]{x1D711}$
on
 $D_{\operatorname{cris}}(V_{x})$
.
$D_{\operatorname{cris}}(V_{x})$
.
Proof. Lemma 2.7 implies that there are uniquely determined
 $t,d\in \overline{\mathbb{Q}}_{p}$
such that
$t,d\in \overline{\mathbb{Q}}_{p}$
such that
 $$\begin{eqnarray}D_{\operatorname{cris}}(V_{x})\cong D(r,s,t,d),\end{eqnarray}$$
$$\begin{eqnarray}D_{\operatorname{cris}}(V_{x})\cong D(r,s,t,d),\end{eqnarray}$$
where
 $r=-a-b$
and
$r=-a-b$
and
 $s=1-a$
. The Weil–Deligne representation associated to
$s=1-a$
. The Weil–Deligne representation associated to
 $D(r,s,t,d)$
is an unramified two-dimensional representation of
$D(r,s,t,d)$
is an unramified two-dimensional representation of
![]() $W_{\mathbb{Q}_{p}}$
, on which the geometric Frobenius
$W_{\mathbb{Q}_{p}}$
, on which the geometric Frobenius
![]() $\operatorname{Frob}_{p}$
acts by the matrix of crystalline Frobenius on
$\operatorname{Frob}_{p}$
acts by the matrix of crystalline Frobenius on
 $D(r,s,t,d)$
, which is
$D(r,s,t,d)$
, which is
![]() $\big(\!\begin{smallmatrix}0 & -d\\ 1 & t\end{smallmatrix}\!\big)$
. Thus,
$\big(\!\begin{smallmatrix}0 & -d\\ 1 & t\end{smallmatrix}\!\big)$
. Thus,
 $$\begin{eqnarray}\text{WD}(D_{\operatorname{cris}}(V_{x}))=\operatorname{rec}_{p}(\unicode[STIX]{x1D712}_{1})\oplus \operatorname{rec}_{p}(\unicode[STIX]{x1D712}_{2}),\end{eqnarray}$$
$$\begin{eqnarray}\text{WD}(D_{\operatorname{cris}}(V_{x}))=\operatorname{rec}_{p}(\unicode[STIX]{x1D712}_{1})\oplus \operatorname{rec}_{p}(\unicode[STIX]{x1D712}_{2}),\end{eqnarray}$$
where
 $\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2}:\mathbb{Q}_{p}^{\times }\rightarrow \overline{\mathbb{Q}}_{p}^{\times }$
are unramified characters such that
$\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2}:\mathbb{Q}_{p}^{\times }\rightarrow \overline{\mathbb{Q}}_{p}^{\times }$
are unramified characters such that
 $\unicode[STIX]{x1D712}_{1}(p)+\unicode[STIX]{x1D712}_{2}(p)=t$
and
$\unicode[STIX]{x1D712}_{1}(p)+\unicode[STIX]{x1D712}_{2}(p)=t$
and
 $\unicode[STIX]{x1D712}_{1}(p)\unicode[STIX]{x1D712}_{2}(p)=d$
.
$\unicode[STIX]{x1D712}_{1}(p)\unicode[STIX]{x1D712}_{2}(p)=d$
.
If
 $\unicode[STIX]{x1D70B}=(\operatorname{Ind}_{B}^{G}|\centerdot |\unicode[STIX]{x1D712}_{1}\otimes \unicode[STIX]{x1D712}_{2})_{\text{sm}}$
, then
$\unicode[STIX]{x1D70B}=(\operatorname{Ind}_{B}^{G}|\centerdot |\unicode[STIX]{x1D712}_{1}\otimes \unicode[STIX]{x1D712}_{2})_{\text{sm}}$
, then
 $\unicode[STIX]{x1D70B}\otimes |\text{det}|^{-1/2}\cong \unicode[STIX]{x1D704}_{B}^{G}(\unicode[STIX]{x1D712}_{1}\otimes \unicode[STIX]{x1D712}_{2})$
, where
$\unicode[STIX]{x1D70B}\otimes |\text{det}|^{-1/2}\cong \unicode[STIX]{x1D704}_{B}^{G}(\unicode[STIX]{x1D712}_{1}\otimes \unicode[STIX]{x1D712}_{2})$
, where
![]() $\unicode[STIX]{x1D704}_{B}^{G}$
denotes smooth normalized parabolic induction. Then
$\unicode[STIX]{x1D704}_{B}^{G}$
denotes smooth normalized parabolic induction. Then
 $$\begin{eqnarray}r_{p}(\unicode[STIX]{x1D70B})=\operatorname{rec}_{p}(\unicode[STIX]{x1D704}_{B}^{G}(\unicode[STIX]{x1D712}_{1}\otimes \unicode[STIX]{x1D712}_{2}))=\operatorname{rec}_{p}(\unicode[STIX]{x1D712}_{1})\oplus \operatorname{rec}_{p}(\unicode[STIX]{x1D712}_{2}).\end{eqnarray}$$
$$\begin{eqnarray}r_{p}(\unicode[STIX]{x1D70B})=\operatorname{rec}_{p}(\unicode[STIX]{x1D704}_{B}^{G}(\unicode[STIX]{x1D712}_{1}\otimes \unicode[STIX]{x1D712}_{2}))=\operatorname{rec}_{p}(\unicode[STIX]{x1D712}_{1})\oplus \operatorname{rec}_{p}(\unicode[STIX]{x1D712}_{2}).\end{eqnarray}$$
The action of
![]() ${\mathcal{H}}(\mathbf{1})$
on
${\mathcal{H}}(\mathbf{1})$
on
![]() $\unicode[STIX]{x1D70B}^{K}$
is given by sending
$\unicode[STIX]{x1D70B}^{K}$
is given by sending
 $[K\big(\!\begin{smallmatrix}p & 0\\ 0 & 1\end{smallmatrix}\!\big)K]$
to
$[K\big(\!\begin{smallmatrix}p & 0\\ 0 & 1\end{smallmatrix}\!\big)K]$
to
 $p|p|\unicode[STIX]{x1D712}_{1}(p)+\unicode[STIX]{x1D712}_{2}(p)=t$
and
$p|p|\unicode[STIX]{x1D712}_{1}(p)+\unicode[STIX]{x1D712}_{2}(p)=t$
and
 $[K\big(\!\begin{smallmatrix}p & 0\\ 0 & p\end{smallmatrix}\!\big)K]$
to
$[K\big(\!\begin{smallmatrix}p & 0\\ 0 & p\end{smallmatrix}\!\big)K]$
to
 $|p|\unicode[STIX]{x1D712}_{1}(p)\unicode[STIX]{x1D712}_{2}(p)=p^{-1}d$
. By [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Theorem 4.1] and the fact that the evident isomorphism between
$|p|\unicode[STIX]{x1D712}_{1}(p)\unicode[STIX]{x1D712}_{2}(p)=p^{-1}d$
. By [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Theorem 4.1] and the fact that the evident isomorphism between
 $\unicode[STIX]{x1D70B}^{K}=\operatorname{Hom}_{K}(\mathbf{1},\mathbf{1}\otimes \unicode[STIX]{x1D70B})$
and
$\unicode[STIX]{x1D70B}^{K}=\operatorname{Hom}_{K}(\mathbf{1},\mathbf{1}\otimes \unicode[STIX]{x1D70B})$
and
 $\operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}\otimes \unicode[STIX]{x1D70B})$
is equivariant with respect to the actions by
$\operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}\otimes \unicode[STIX]{x1D70B})$
is equivariant with respect to the actions by
![]() ${\mathcal{H}}(\mathbf{1})$
and
${\mathcal{H}}(\mathbf{1})$
and
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
via the isomorphism (2.4), we see that
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
via the isomorphism (2.4), we see that
 $$\begin{eqnarray}x(\unicode[STIX]{x1D702}(T))=p^{-r}t=p^{a+b}t,\quad x(\unicode[STIX]{x1D702}(S))=p^{-r-s}d=p^{2a+b-1}d.\end{eqnarray}$$
$$\begin{eqnarray}x(\unicode[STIX]{x1D702}(T))=p^{-r}t=p^{a+b}t,\quad x(\unicode[STIX]{x1D702}(S))=p^{-r-s}d=p^{2a+b-1}d.\end{eqnarray}$$
Since
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
is a reduced Jacobson ring, the formulas determine
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
is a reduced Jacobson ring, the formulas determine
![]() $\unicode[STIX]{x1D702}(T)$
and
$\unicode[STIX]{x1D702}(T)$
and
![]() $\unicode[STIX]{x1D702}(S)$
uniquely.◻
$\unicode[STIX]{x1D702}(S)$
uniquely.◻
Corollary 2.11.
![]() $\unicode[STIX]{x1D702}(S)$
and
$\unicode[STIX]{x1D702}(S)$
and
![]() $\unicode[STIX]{x1D702}(T)$
are contained in the normalization of
$\unicode[STIX]{x1D702}(T)$
are contained in the normalization of
![]() $R_{p}(\unicode[STIX]{x1D70E})$
in
$R_{p}(\unicode[STIX]{x1D70E})$
in
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
.
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
.
Proof. It follows from (2.10) and Lemma 2.6 that for all closed points
 $x:R_{p}(\unicode[STIX]{x1D70E})[1/p]\rightarrow \overline{\mathbb{Q}}_{p}$
, we have
$x:R_{p}(\unicode[STIX]{x1D70E})[1/p]\rightarrow \overline{\mathbb{Q}}_{p}$
, we have
 $x(\unicode[STIX]{x1D702}(S)),x(\unicode[STIX]{x1D702}(T))\in \overline{\mathbb{Z}}_{p}$
. The result follows from [Reference de JongdeJ95, Proposition 7.3.6].◻
$x(\unicode[STIX]{x1D702}(S)),x(\unicode[STIX]{x1D702}(T))\in \overline{\mathbb{Z}}_{p}$
. The result follows from [Reference de JongdeJ95, Proposition 7.3.6].◻
A key fact that we will use, which is special to our context of two-dimensional crystalline representations of
![]() $G_{\mathbb{Q}_{p}}$
, is that the morphism
$G_{\mathbb{Q}_{p}}$
, is that the morphism
 $$\begin{eqnarray}(\operatorname{Spf}R(\unicode[STIX]{x1D70E}))^{\text{an}}\rightarrow (\operatorname{Spec}{\mathcal{H}}(\unicode[STIX]{x1D70E}))^{\text{an}}\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{Spf}R(\unicode[STIX]{x1D70E}))^{\text{an}}\rightarrow (\operatorname{Spec}{\mathcal{H}}(\unicode[STIX]{x1D70E}))^{\text{an}}\end{eqnarray}$$
induced by
![]() $\unicode[STIX]{x1D702}$
is an open immersion of rigid analytic spaces, where the superscript ‘an’ signifies the associated rigid analytic space. We prove this statement (in its infinitesimal form) in the following result.
$\unicode[STIX]{x1D702}$
is an open immersion of rigid analytic spaces, where the superscript ‘an’ signifies the associated rigid analytic space. We prove this statement (in its infinitesimal form) in the following result.
Lemma 2.12. Let
 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
, with
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
, with
![]() $a\in \mathbb{Z}$
and
$a\in \mathbb{Z}$
and
 $b\in \mathbb{Z}_{{\geqslant}0}$
. Then
$b\in \mathbb{Z}_{{\geqslant}0}$
. Then
 $$\begin{eqnarray}\dim _{\unicode[STIX]{x1D705}(y)}\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}R_{p}(\unicode[STIX]{x1D70E})[1/p]\leqslant 1,\quad \forall y\in \operatorname{m - Spec}{\mathcal{H}}(\unicode[STIX]{x1D70E}).\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\unicode[STIX]{x1D705}(y)}\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}R_{p}(\unicode[STIX]{x1D70E})[1/p]\leqslant 1,\quad \forall y\in \operatorname{m - Spec}{\mathcal{H}}(\unicode[STIX]{x1D70E}).\end{eqnarray}$$
Proof. Let us assume that
 $A:=\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}R_{p}(\unicode[STIX]{x1D70E})[1/p]$
is non-zero. If
$A:=\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}R_{p}(\unicode[STIX]{x1D70E})[1/p]$
is non-zero. If
 $x,x^{\prime }\in \operatorname{m - Spec}A$
, then the Frobenii on
$x,x^{\prime }\in \operatorname{m - Spec}A$
, then the Frobenii on
 $D_{\operatorname{cris}}(V_{x})$
and
$D_{\operatorname{cris}}(V_{x})$
and
 $D_{\operatorname{cris}}(V_{x^{\prime }})$
will have the same trace and determinant (since, by Proposition 2.9, these are determined by the images of
$D_{\operatorname{cris}}(V_{x^{\prime }})$
will have the same trace and determinant (since, by Proposition 2.9, these are determined by the images of
![]() $T$
and
$T$
and
![]() $S$
in
$S$
in
![]() $\unicode[STIX]{x1D705}(y)$
); denote them by
$\unicode[STIX]{x1D705}(y)$
); denote them by
![]() $t$
and
$t$
and
![]() $d$
. It follows from Lemma 2.6 that
$d$
. It follows from Lemma 2.6 that
 $D_{\operatorname{cris}}(V_{x})\cong D_{\operatorname{cris}}(V_{x^{\prime }})$
and hence
$D_{\operatorname{cris}}(V_{x})\cong D_{\operatorname{cris}}(V_{x^{\prime }})$
and hence
![]() $x=x^{\prime }$
. Since
$x=x^{\prime }$
. Since
 $D(r,s,t,d)$
can be constructed over
$D(r,s,t,d)$
can be constructed over
![]() $\unicode[STIX]{x1D705}(y)$
(as
$\unicode[STIX]{x1D705}(y)$
(as
![]() $t$
and
$t$
and
![]() $d$
lie in
$d$
lie in
![]() $\unicode[STIX]{x1D705}(y)$
), so can
$\unicode[STIX]{x1D705}(y)$
), so can
![]() $V_{x}$
and thus
$V_{x}$
and thus
 $\unicode[STIX]{x1D705}(x)=\unicode[STIX]{x1D705}(y)$
. To complete the proof of the lemma, it is enough to show that the map
$\unicode[STIX]{x1D705}(x)=\unicode[STIX]{x1D705}(y)$
. To complete the proof of the lemma, it is enough to show that the map
 $\mathfrak{m}_{y}\rightarrow \mathfrak{m}_{x}/\mathfrak{m}_{x}^{2}$
is surjective. Since we know that
$\mathfrak{m}_{y}\rightarrow \mathfrak{m}_{x}/\mathfrak{m}_{x}^{2}$
is surjective. Since we know that
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
is a regular ring of dimension
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
is a regular ring of dimension
![]() $2$
by [Reference KisinKis08, Theorem 3.3.8], it is enough to construct a two-dimensional family of deformations of
$2$
by [Reference KisinKis08, Theorem 3.3.8], it is enough to construct a two-dimensional family of deformations of
 $D_{\operatorname{cris}}(V_{x})$
to the ring of dual numbers
$D_{\operatorname{cris}}(V_{x})$
to the ring of dual numbers
![]() $\unicode[STIX]{x1D705}(y)[\unicode[STIX]{x1D716}]$
, which induces a non-trivial deformation of the images of
$\unicode[STIX]{x1D705}(y)[\unicode[STIX]{x1D716}]$
, which induces a non-trivial deformation of the images of
![]() $S,T$
. That this is possible is immediate from Corollary 2.8 and Proposition 2.9.◻
$S,T$
. That this is possible is immediate from Corollary 2.8 and Proposition 2.9.◻
Proposition 2.13. Let
 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
, with
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
, with
![]() $a\in \mathbb{Z}$
and
$a\in \mathbb{Z}$
and
 $b\in \mathbb{Z}_{{\geqslant}0}$
. Let
$b\in \mathbb{Z}_{{\geqslant}0}$
. Let
 $y\in \operatorname{m - Spec}{\mathcal{H}}(\unicode[STIX]{x1D70E})$
be the image of
$y\in \operatorname{m - Spec}{\mathcal{H}}(\unicode[STIX]{x1D70E})$
be the image of
 $x\in \operatorname{m - Spec}R_{p}(\unicode[STIX]{x1D70E})[1/p]$
under the morphism induced by
$x\in \operatorname{m - Spec}R_{p}(\unicode[STIX]{x1D70E})[1/p]$
under the morphism induced by
 $\unicode[STIX]{x1D702}:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow R_{p}(\unicode[STIX]{x1D70E})[1/p]$
. Then
$\unicode[STIX]{x1D702}:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow R_{p}(\unicode[STIX]{x1D70E})[1/p]$
. Then
![]() $\unicode[STIX]{x1D702}$
induces an isomorphism of completions:
$\unicode[STIX]{x1D702}$
induces an isomorphism of completions:
 $$\begin{eqnarray}\widehat{{\mathcal{H}}(\unicode[STIX]{x1D70E})}_{\mathfrak{m}_{y}}\overset{\cong }{\longrightarrow }\widehat{R_{p}(\unicode[STIX]{x1D70E})[1/p]}_{\mathfrak{m}_{x}}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\mathcal{H}}(\unicode[STIX]{x1D70E})}_{\mathfrak{m}_{y}}\overset{\cong }{\longrightarrow }\widehat{R_{p}(\unicode[STIX]{x1D70E})[1/p]}_{\mathfrak{m}_{x}}.\end{eqnarray}$$
Proof. This can be proved by explicit computation, taking into account Corollary 2.8 and Proposition 2.9.
We can also deduce it in more pure thought manner as follows: since
 ${\mathcal{H}}(\unicode[STIX]{x1D70E})\cong E[T,S^{\pm 1}]$
by Proposition 2.5 and
${\mathcal{H}}(\unicode[STIX]{x1D70E})\cong E[T,S^{\pm 1}]$
by Proposition 2.5 and
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
is a regular ring of dimension
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
is a regular ring of dimension
![]() $2$
as in the preceding proof, both completions are regular rings of dimension
$2$
as in the preceding proof, both completions are regular rings of dimension
![]() $2$
. It follows from Lemma 2.12 that
$2$
. It follows from Lemma 2.12 that
 $\unicode[STIX]{x1D705}(y)=\unicode[STIX]{x1D705}(x)$
and the map induces a surjection on tangent spaces. Hence, the map is an isomorphism.◻
$\unicode[STIX]{x1D705}(y)=\unicode[STIX]{x1D705}(x)$
and the map induces a surjection on tangent spaces. Hence, the map is an isomorphism.◻
If
 $0\leqslant b\leqslant p-1$
, then
$0\leqslant b\leqslant p-1$
, then
![]() $\unicode[STIX]{x1D70E}_{a,b}$
has a unique (up to homothety)
$\unicode[STIX]{x1D70E}_{a,b}$
has a unique (up to homothety)
![]() $K$
-invariant lattice
$K$
-invariant lattice
![]() $\unicode[STIX]{x1D70E}_{a,b}^{\circ }$
, which is isomorphic to
$\unicode[STIX]{x1D70E}_{a,b}^{\circ }$
, which is isomorphic to
 $\det ^{a}\otimes \;\text{Sym}^{b}{\mathcal{O}}^{2}$
as a
$\det ^{a}\otimes \;\text{Sym}^{b}{\mathcal{O}}^{2}$
as a
![]() $K$
-representation. We let
$K$
-representation. We let
![]() $\overline{\unicode[STIX]{x1D70E}}_{a,b}$
be its reduction modulo
$\overline{\unicode[STIX]{x1D70E}}_{a,b}$
be its reduction modulo
![]() $\unicode[STIX]{x1D71B}$
. Then
$\unicode[STIX]{x1D71B}$
. Then
![]() $\overline{\unicode[STIX]{x1D70E}}_{a,b}$
is the absolutely irreducible
$\overline{\unicode[STIX]{x1D70E}}_{a,b}$
is the absolutely irreducible
![]() $\mathbb{F}$
-representation
$\mathbb{F}$
-representation
 $\det ^{a}\otimes \;\text{Sym}^{b}\mathbb{F}^{2}$
of
$\det ^{a}\otimes \;\text{Sym}^{b}\mathbb{F}^{2}$
of
 $\operatorname{GL}_{2}(\mathbb{F}_{p})$
; note that every (absolutely) irreducible
$\operatorname{GL}_{2}(\mathbb{F}_{p})$
; note that every (absolutely) irreducible
![]() $\mathbb{F}$
-representation of
$\mathbb{F}$
-representation of
 $\operatorname{GL}_{2}(\mathbb{F}_{p})$
is of this form for some uniquely determined
$\operatorname{GL}_{2}(\mathbb{F}_{p})$
is of this form for some uniquely determined
![]() $a,b$
with
$a,b$
with
 $0\leqslant a<p-1$
. We refer to such representations as Serre weights.
$0\leqslant a<p-1$
. We refer to such representations as Serre weights.
If
 $\overline{\unicode[STIX]{x1D70E}}=\overline{\unicode[STIX]{x1D70E}}_{a,b}$
is a Serre weight with the property that
$\overline{\unicode[STIX]{x1D70E}}=\overline{\unicode[STIX]{x1D70E}}_{a,b}$
is a Serre weight with the property that
![]() $\bar{r}$
has a lift
$\bar{r}$
has a lift
 $r:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{Z}}_{p})$
that is crystalline of Hodge type
$r:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{Z}}_{p})$
that is crystalline of Hodge type
 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
, then we say that
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
, then we say that
![]() $\overline{\unicode[STIX]{x1D70E}}$
is a Serre weight of
$\overline{\unicode[STIX]{x1D70E}}$
is a Serre weight of
![]() $\bar{r}$
.
$\bar{r}$
.
Again we consider
 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
, with any
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
, with any
![]() $a\in \mathbb{Z}$
and
$a\in \mathbb{Z}$
and
 $b\in \mathbb{Z}_{{\geqslant}0}$
. Let
$b\in \mathbb{Z}_{{\geqslant}0}$
. Let
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}^{\circ }:=\det \!^{a}\otimes \;\text{Sym}^{b}{\mathcal{O}}^{2},\quad \overline{\unicode[STIX]{x1D70E}}:=\det \!^{a}\otimes \;\text{Sym}^{b}\mathbb{F}^{2},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}^{\circ }:=\det \!^{a}\otimes \;\text{Sym}^{b}{\mathcal{O}}^{2},\quad \overline{\unicode[STIX]{x1D70E}}:=\det \!^{a}\otimes \;\text{Sym}^{b}\mathbb{F}^{2},\end{eqnarray}$$
so that
 $\unicode[STIX]{x1D70E}^{\circ }/\unicode[STIX]{x1D71B}=\overline{\unicode[STIX]{x1D70E}}$
. We let
$\unicode[STIX]{x1D70E}^{\circ }/\unicode[STIX]{x1D71B}=\overline{\unicode[STIX]{x1D70E}}$
. We let
 $$\begin{eqnarray}{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ }):=\text{End}_{G}(\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ }),\quad {\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}):=\text{End}_{G}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ }):=\text{End}_{G}(\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ }),\quad {\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}):=\text{End}_{G}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}).\end{eqnarray}$$
Note that
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
is
${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
is
![]() $p$
-torsion free, since
$p$
-torsion free, since
 $\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ }$
is.
$\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ }$
is.
Lemma 2.14.
(1) For any
 $\unicode[STIX]{x1D70E}$
, there are a natural isomorphism
$\unicode[STIX]{x1D70E}$
, there are a natural isomorphism
 ${\mathcal{H}}(\unicode[STIX]{x1D70E})\cong {\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
and a natural inclusion
${\mathcal{H}}(\unicode[STIX]{x1D70E})\cong {\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
and a natural inclusion
 ${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })/\unicode[STIX]{x1D71B}{\hookrightarrow}{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}).$
Furthermore, the
${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })/\unicode[STIX]{x1D71B}{\hookrightarrow}{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}).$
Furthermore, the
 ${\mathcal{O}}$
-subalgebra
${\mathcal{O}}$
-subalgebra
 ${\mathcal{O}}[S^{\pm 1},T]$
of
${\mathcal{O}}[S^{\pm 1},T]$
of
 ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
is contained in
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
is contained in
 ${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
.
${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
.(2) If, in addition,
 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
, with
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
, with
 $0\leqslant b\leqslant p-1$
, then
$0\leqslant b\leqslant p-1$
, then
 ${\mathcal{O}}[S^{\pm 1},T]={\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
and there is a natural isomorphism
${\mathcal{O}}[S^{\pm 1},T]={\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
and there is a natural isomorphism
 ${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })/\unicode[STIX]{x1D71B}\cong {\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}).$
${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })/\unicode[STIX]{x1D71B}\cong {\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}).$
Proof. The isomorphism of (1) follows immediately from the fact that
 $\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ }$
is a finitely generated
$\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ }$
is a finitely generated
![]() ${\mathcal{O}}[G]$
-module. To see the claimed inclusion, apply
${\mathcal{O}}[G]$
-module. To see the claimed inclusion, apply
 $\operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ },-)$
to the exact sequence
$\operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ },-)$
to the exact sequence
 $$\begin{eqnarray}0\rightarrow \operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ }\overset{\unicode[STIX]{x1D71B}}{\rightarrow }\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ }\rightarrow \operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ }\overset{\unicode[STIX]{x1D71B}}{\rightarrow }\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ }\rightarrow \operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}\rightarrow 0\end{eqnarray}$$
so as to obtain an injective map
 $$\begin{eqnarray}{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })/\unicode[STIX]{x1D71B}{\hookrightarrow}\operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ },\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}})\cong {\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })/\unicode[STIX]{x1D71B}{\hookrightarrow}\operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ },\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}})\cong {\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}).\end{eqnarray}$$
To see the final claim of (1), we recall that from (2.4) and Frobenius reciprocity we have natural isomorphisms
 $$\begin{eqnarray}{\mathcal{H}}(\unicode[STIX]{x1D7D9})\simeq {\mathcal{H}}(\unicode[STIX]{x1D70E})\simeq \operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E});\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}(\unicode[STIX]{x1D7D9})\simeq {\mathcal{H}}(\unicode[STIX]{x1D70E})\simeq \operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E});\end{eqnarray}$$
the image of
 $\unicode[STIX]{x1D719}\in {\mathcal{H}}(\unicode[STIX]{x1D7D9})$
under the composite map sends
$\unicode[STIX]{x1D719}\in {\mathcal{H}}(\unicode[STIX]{x1D7D9})$
under the composite map sends
![]() $v\in \unicode[STIX]{x1D70E}$
to the function
$v\in \unicode[STIX]{x1D70E}$
to the function
 $g\mapsto \unicode[STIX]{x1D719}(g^{-1})\unicode[STIX]{x1D70E}(g)v$
. A direct computation of the actions of
$g\mapsto \unicode[STIX]{x1D719}(g^{-1})\unicode[STIX]{x1D70E}(g)v$
. A direct computation of the actions of
![]() $S,T$
on the standard basis of
$S,T$
on the standard basis of
![]() $\unicode[STIX]{x1D70E}^{\circ }$
then verifies that
$\unicode[STIX]{x1D70E}^{\circ }$
then verifies that
![]() $S^{\pm 1}$
and
$S^{\pm 1}$
and
![]() $T$
lie in the
$T$
lie in the
![]() ${\mathcal{O}}$
-submodule
${\mathcal{O}}$
-submodule
 $\operatorname{Hom}_{K}(\unicode[STIX]{x1D70E}^{\circ },\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ })$
of
$\operatorname{Hom}_{K}(\unicode[STIX]{x1D70E}^{\circ },\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E}^{\circ })$
of
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
.
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
.
To prove (2), we note that it follows from [Reference BreuilBre03b, § 2] and [Reference Barthel and LivnéBL94] that the composite
 $\mathbb{F}[S^{\pm 1},T]\rightarrow {\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })/\unicode[STIX]{x1D71B}\rightarrow {\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
is an isomorphism. Since the second of these maps is injective, by (1), we conclude that each of these maps is in fact an isomorphism, confirming the second claim of (2). Furthermore, this shows that the inclusion
$\mathbb{F}[S^{\pm 1},T]\rightarrow {\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })/\unicode[STIX]{x1D71B}\rightarrow {\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
is an isomorphism. Since the second of these maps is injective, by (1), we conclude that each of these maps is in fact an isomorphism, confirming the second claim of (2). Furthermore, this shows that the inclusion
 ${\mathcal{O}}[S^{\pm 1},T]{\hookrightarrow}{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
of (1) becomes an isomorphism both after reducing modulo
${\mathcal{O}}[S^{\pm 1},T]{\hookrightarrow}{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
of (1) becomes an isomorphism both after reducing modulo
![]() $\unicode[STIX]{x1D71B}$
as well as after inverting
$\unicode[STIX]{x1D71B}$
as well as after inverting
![]() $\unicode[STIX]{x1D71B}$
(because
$\unicode[STIX]{x1D71B}$
(because
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
is generated by
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
is generated by
![]() $S^{\pm 1}$
and
$S^{\pm 1}$
and
![]() $T$
by Proposition 2.5). Thus, it is an isomorphism, completing the proof of (2).◻
$T$
by Proposition 2.5). Thus, it is an isomorphism, completing the proof of (2).◻
The following lemma is well known, but for lack of a convenient reference we sketch a proof.
Lemma 2.15. Assume that
![]() $\bar{r}$
satisfies Assumption 2.2. Then
$\bar{r}$
satisfies Assumption 2.2. Then
![]() $\bar{r}$
has at most two Serre weights. Furthermore, if we let
$\bar{r}$
has at most two Serre weights. Furthermore, if we let
 $\overline{\unicode[STIX]{x1D70E}}=\overline{\unicode[STIX]{x1D70E}}_{a,b}$
be a Serre weight of
$\overline{\unicode[STIX]{x1D70E}}=\overline{\unicode[STIX]{x1D70E}}_{a,b}$
be a Serre weight of
![]() $\bar{r}$
, then the following hold.
$\bar{r}$
, then the following hold.
(i) The deformation ring
 $R_{p}(\unicode[STIX]{x1D70E})$
is formally smooth of relative dimension
$R_{p}(\unicode[STIX]{x1D70E})$
is formally smooth of relative dimension
 $2$
over
$2$
over
 ${\mathcal{O}}$
.
${\mathcal{O}}$
.(ii) The morphism of
 $E$
-algebras
$E$
-algebras
 $\unicode[STIX]{x1D702}:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow R_{p}(\unicode[STIX]{x1D70E})[1/p]$
induces a morphism of
$\unicode[STIX]{x1D702}:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow R_{p}(\unicode[STIX]{x1D70E})[1/p]$
induces a morphism of
 ${\mathcal{O}}$
-algebras
${\mathcal{O}}$
-algebras
 ${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })\rightarrow R_{p}(\unicode[STIX]{x1D70E})$
.
${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })\rightarrow R_{p}(\unicode[STIX]{x1D70E})$
.(iii) The character
 $\unicode[STIX]{x1D714}^{1-2a-b}\det \bar{r}$
is unramified and, if we let:
$\unicode[STIX]{x1D714}^{1-2a-b}\det \bar{r}$
is unramified and, if we let:–
 $\unicode[STIX]{x1D707}=(\unicode[STIX]{x1D714}^{1-2a-b}\det \bar{r})(\operatorname{Frob}_{p})$
; and
$\unicode[STIX]{x1D707}=(\unicode[STIX]{x1D714}^{1-2a-b}\det \bar{r})(\operatorname{Frob}_{p})$
; and– if
 $\bar{r}$
is irreducible, then
$\bar{r}$
is irreducible, then
 $\unicode[STIX]{x1D706}=0$
; and
$\unicode[STIX]{x1D706}=0$
; and– if
 $\bar{r}$
is reducible, then we can write
$\bar{r}$
is reducible, then we can write
 $\bar{r}\cong \unicode[STIX]{x1D714}^{a+b}\otimes (\!\begin{smallmatrix}\overline{\unicode[STIX]{x1D712}}_{1} & \ast \\ 0 & \overline{\unicode[STIX]{x1D712}}_{2}\unicode[STIX]{x1D714}^{-b-1}\end{smallmatrix}\!)$
for unramified characters
$\bar{r}\cong \unicode[STIX]{x1D714}^{a+b}\otimes (\!\begin{smallmatrix}\overline{\unicode[STIX]{x1D712}}_{1} & \ast \\ 0 & \overline{\unicode[STIX]{x1D712}}_{2}\unicode[STIX]{x1D714}^{-b-1}\end{smallmatrix}\!)$
for unramified characters
 $\overline{\unicode[STIX]{x1D712}}_{1}$
,
$\overline{\unicode[STIX]{x1D712}}_{1}$
,
 $\overline{\unicode[STIX]{x1D712}}_{2}$
and let
$\overline{\unicode[STIX]{x1D712}}_{2}$
and let
 $\unicode[STIX]{x1D706}=\overline{\unicode[STIX]{x1D712}}_{1}(\operatorname{Frob}_{p})$
,
$\unicode[STIX]{x1D706}=\overline{\unicode[STIX]{x1D712}}_{1}(\operatorname{Frob}_{p})$
,
then the composition
maps $$\begin{eqnarray}\unicode[STIX]{x1D6FC}:{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })\rightarrow R_{p}(\unicode[STIX]{x1D70E})\rightarrow \mathbb{F}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}:{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })\rightarrow R_{p}(\unicode[STIX]{x1D70E})\rightarrow \mathbb{F}\end{eqnarray}$$
 $T\mapsto \unicode[STIX]{x1D706}$
and
$T\mapsto \unicode[STIX]{x1D706}$
and
 $S\mapsto \unicode[STIX]{x1D707}$
.
$S\mapsto \unicode[STIX]{x1D707}$
.(iv) Let
 $\widehat{{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })}$
be the completion of
$\widehat{{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })}$
be the completion of
 ${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
with respect to the kernel of
${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
with respect to the kernel of
 $\unicode[STIX]{x1D6FC}$
. Then the map
$\unicode[STIX]{x1D6FC}$
. Then the map
 ${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })\rightarrow R_{p}(\unicode[STIX]{x1D70E})$
induces an isomorphism of local
${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })\rightarrow R_{p}(\unicode[STIX]{x1D70E})$
induces an isomorphism of local
 ${\mathcal{O}}$
-algebras
${\mathcal{O}}$
-algebras
 $\widehat{{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })}\overset{\cong }{\rightarrow }R_{p}(\unicode[STIX]{x1D70E})$
. In coordinates, we have
$\widehat{{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })}\overset{\cong }{\rightarrow }R_{p}(\unicode[STIX]{x1D70E})$
. In coordinates, we have
 $R_{p}(\unicode[STIX]{x1D70E})={\mathcal{O}}[[S-\widetilde{\unicode[STIX]{x1D707}},T-\widetilde{\unicode[STIX]{x1D706}}]]$
, where the tilde denotes the Teichmüller lift.
$R_{p}(\unicode[STIX]{x1D70E})={\mathcal{O}}[[S-\widetilde{\unicode[STIX]{x1D707}},T-\widetilde{\unicode[STIX]{x1D706}}]]$
, where the tilde denotes the Teichmüller lift.(v) If we set
 $\unicode[STIX]{x1D70B}:=(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}})\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),\unicode[STIX]{x1D6FC}}\mathbb{F}$
, then
$\unicode[STIX]{x1D70B}:=(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}})\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),\unicode[STIX]{x1D6FC}}\mathbb{F}$
, then
 $\unicode[STIX]{x1D70B}$
is an absolutely irreducible representation of
$\unicode[STIX]{x1D70B}$
is an absolutely irreducible representation of
 $G$
and is independent of the choice of Serre weight
$G$
and is independent of the choice of Serre weight
 $\overline{\unicode[STIX]{x1D70E}}$
of
$\overline{\unicode[STIX]{x1D70E}}$
of
 $\bar{r}$
.
$\bar{r}$
.
Proof. The claim that
![]() $\bar{r}$
has at most two Serre weights is immediate from the proof of [Reference Buzzard, Diamond and JarvisBDJ10, Theorem 3.17], which explicitly describes the Serre weights of
$\bar{r}$
has at most two Serre weights is immediate from the proof of [Reference Buzzard, Diamond and JarvisBDJ10, Theorem 3.17], which explicitly describes the Serre weights of
![]() $\bar{r}$
. Concretely, in the case at hand these weights are as follows (see also the discussion of [Reference EmertonEme11, § 3.5], which uses the same conventions as this paper). If
$\bar{r}$
. Concretely, in the case at hand these weights are as follows (see also the discussion of [Reference EmertonEme11, § 3.5], which uses the same conventions as this paper). If
![]() $\bar{r}$
is irreducible, then we may write
$\bar{r}$
is irreducible, then we may write
 $$\begin{eqnarray}\bar{r}|_{I_{\mathbb{Q}_{p}}}\cong \unicode[STIX]{x1D714}^{m-1}\otimes \left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D714}_{2}^{n+1} & 0\\ 0 & \unicode[STIX]{x1D714}_{2}^{p(n+1)}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\bar{r}|_{I_{\mathbb{Q}_{p}}}\cong \unicode[STIX]{x1D714}^{m-1}\otimes \left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D714}_{2}^{n+1} & 0\\ 0 & \unicode[STIX]{x1D714}_{2}^{p(n+1)}\end{array}\right),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D714}_{2}$
is a fundamental character of niveau
$\unicode[STIX]{x1D714}_{2}$
is a fundamental character of niveau
![]() $2$
, and
$2$
, and
 $0\leqslant m<p-1$
,
$0\leqslant m<p-1$
,
 $0\leqslant n\leqslant p-2$
. Then the Serre weights of
$0\leqslant n\leqslant p-2$
. Then the Serre weights of
![]() $\bar{r}$
are
$\bar{r}$
are
![]() $\overline{\unicode[STIX]{x1D70E}}_{m,n}$
and
$\overline{\unicode[STIX]{x1D70E}}_{m,n}$
and
 $\overline{\unicode[STIX]{x1D70E}}_{m+n,p-1-n}$
(with
$\overline{\unicode[STIX]{x1D70E}}_{m+n,p-1-n}$
(with
![]() $m+n$
taken modulo
$m+n$
taken modulo
![]() $p-1$
). If
$p-1$
). If
![]() $\bar{r}$
is reducible, then we may write
$\bar{r}$
is reducible, then we may write
 $$\begin{eqnarray}\bar{r}|_{I_{\mathbb{Q}_{p}}}\cong \unicode[STIX]{x1D714}^{m+n}\otimes \left(\begin{array}{@{}cc@{}}1 & \ast \\ 0 & \unicode[STIX]{x1D714}^{-n-1}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\bar{r}|_{I_{\mathbb{Q}_{p}}}\cong \unicode[STIX]{x1D714}^{m+n}\otimes \left(\begin{array}{@{}cc@{}}1 & \ast \\ 0 & \unicode[STIX]{x1D714}^{-n-1}\end{array}\right),\end{eqnarray}$$
where
 $0\leqslant m<p-1$
,
$0\leqslant m<p-1$
,
 $0\leqslant n<p-1$
. Then (under Assumption 2.2), if
$0\leqslant n<p-1$
. Then (under Assumption 2.2), if
![]() $n\neq 0$
, the unique Serre weight of
$n\neq 0$
, the unique Serre weight of
![]() $\bar{r}$
is
$\bar{r}$
is
![]() $\overline{\unicode[STIX]{x1D70E}}_{m,n}$
, while, if
$\overline{\unicode[STIX]{x1D70E}}_{m,n}$
, while, if
![]() $n=0$
, then
$n=0$
, then
![]() $\overline{\unicode[STIX]{x1D70E}}_{m,0}$
and
$\overline{\unicode[STIX]{x1D70E}}_{m,0}$
and
![]() $\overline{\unicode[STIX]{x1D70E}}_{m,p-1}$
are the two Serre weights of
$\overline{\unicode[STIX]{x1D70E}}_{m,p-1}$
are the two Serre weights of
![]() $\bar{r}$
.
$\bar{r}$
.
Part (2) follows from (1) by Lemma 2.14(2) and Corollary 2.11. We prove parts (1), (3) and (4) simultaneously. If
![]() $\overline{\unicode[STIX]{x1D70E}}$
is not of the form
$\overline{\unicode[STIX]{x1D70E}}$
is not of the form
![]() $\overline{\unicode[STIX]{x1D70E}}_{a,p-1}$
, the claims about
$\overline{\unicode[STIX]{x1D70E}}_{a,p-1}$
, the claims about
![]() $R_{p}(\unicode[STIX]{x1D70E})$
are a standard consequence of (unipotent) Fontaine–Laffaille theory; for example, the irreducible case with
$R_{p}(\unicode[STIX]{x1D70E})$
are a standard consequence of (unipotent) Fontaine–Laffaille theory; for example, the irreducible case with
![]() ${\mathcal{O}}=\mathbb{Z}_{p}$
is [Reference Fontaine and MazurFM95, Theorem B2], and the reducible case follows in the same way. The key point is that the corresponding weakly admissible modules are either reducible, or are uniquely determined by the trace and determinant of
${\mathcal{O}}=\mathbb{Z}_{p}$
is [Reference Fontaine and MazurFM95, Theorem B2], and the reducible case follows in the same way. The key point is that the corresponding weakly admissible modules are either reducible, or are uniquely determined by the trace and determinant of
![]() $\unicode[STIX]{x1D711}$
, by Lemma 2.6. Concretely, if
$\unicode[STIX]{x1D711}$
, by Lemma 2.6. Concretely, if
![]() $\bar{r}$
is irreducible, then the crystalline lifts of
$\bar{r}$
is irreducible, then the crystalline lifts of
![]() $\bar{r}$
of Hodge type
$\bar{r}$
of Hodge type
![]() $\unicode[STIX]{x1D70E}_{a,b}$
correspond exactly to the weakly admissible modules
$\unicode[STIX]{x1D70E}_{a,b}$
correspond exactly to the weakly admissible modules
 $D(-(a+b),1-a,t,d)$
, where
$D(-(a+b),1-a,t,d)$
, where
 $v_{p}(t)>-a-b$
and
$v_{p}(t)>-a-b$
and
 $\overline{p^{2a+b-1}d}=\unicode[STIX]{x1D707}$
. The claimed description of the deformation ring then follows.
$\overline{p^{2a+b-1}d}=\unicode[STIX]{x1D707}$
. The claimed description of the deformation ring then follows.
Similarly, if
![]() $\bar{r}$
is reducible, then it follows from Fontaine–Laffaille theory (and Assumption 2.2) that any crystalline lift of Hodge type
$\bar{r}$
is reducible, then it follows from Fontaine–Laffaille theory (and Assumption 2.2) that any crystalline lift of Hodge type
![]() $\overline{\unicode[STIX]{x1D70E}}_{a,b}$
is necessarily reducible and indecomposable, and one finds that these crystalline lifts correspond precisely to those weakly admissible modules with
$\overline{\unicode[STIX]{x1D70E}}_{a,b}$
is necessarily reducible and indecomposable, and one finds that these crystalline lifts correspond precisely to those weakly admissible modules with
 $D(-(a+b),1-a,t,d)$
, where
$D(-(a+b),1-a,t,d)$
, where
 $v_{p}(t)=-a-b$
,
$v_{p}(t)=-a-b$
,
 $\overline{p^{a+b}t}=\unicode[STIX]{x1D706}$
and
$\overline{p^{a+b}t}=\unicode[STIX]{x1D706}$
and
 $\overline{p^{2a+b-1}d}=\unicode[STIX]{x1D707}$
.
$\overline{p^{2a+b-1}d}=\unicode[STIX]{x1D707}$
.
This leaves only the case that
![]() $\overline{\unicode[STIX]{x1D70E}}$
is of the form
$\overline{\unicode[STIX]{x1D70E}}$
is of the form
![]() $\overline{\unicode[STIX]{x1D70E}}_{a,p-1}$
. In this case the result is immediate from the main result of [Reference Berger, Li and ZhuBLZ04], which shows that the above description of the weakly admissible modules continues to hold.
$\overline{\unicode[STIX]{x1D70E}}_{a,p-1}$
. In this case the result is immediate from the main result of [Reference Berger, Li and ZhuBLZ04], which shows that the above description of the weakly admissible modules continues to hold.
Finally, (5) is immediate from the main results of [Reference Barthel and LivnéBL94, Reference BreuilBre03a], together with the explicit description of
![]() $\overline{\unicode[STIX]{x1D70E}}$
and
$\overline{\unicode[STIX]{x1D70E}}$
and
![]() $\unicode[STIX]{x1D706}$
, established above. More precisely, in the case that
$\unicode[STIX]{x1D706}$
, established above. More precisely, in the case that
![]() $\bar{r}$
is irreducible, the absolute irreducibility of
$\bar{r}$
is irreducible, the absolute irreducibility of
![]() $\unicode[STIX]{x1D70B}$
is [Reference BreuilBre03a, Theorem 1.1] and its independence of the choice of
$\unicode[STIX]{x1D70B}$
is [Reference BreuilBre03a, Theorem 1.1] and its independence of the choice of
![]() $\overline{\unicode[STIX]{x1D70E}}$
is [Reference BreuilBre03a, Theorem 1.3]. If
$\overline{\unicode[STIX]{x1D70E}}$
is [Reference BreuilBre03a, Theorem 1.3]. If
![]() $\bar{r}$
is reducible and has only a single Serre weight, then the absolute irreducibility of
$\bar{r}$
is reducible and has only a single Serre weight, then the absolute irreducibility of
![]() $\unicode[STIX]{x1D70B}$
is [Reference Barthel and LivnéBL94, Theorem 33(2)]. In the remaining case that
$\unicode[STIX]{x1D70B}$
is [Reference Barthel and LivnéBL94, Theorem 33(2)]. In the remaining case that
![]() $\bar{r}$
is reducible and has two Serre weights, then Assumption 2.2 together with the explicit description of
$\bar{r}$
is reducible and has two Serre weights, then Assumption 2.2 together with the explicit description of
![]() $\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}$
above implies that
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}$
above implies that
![]() $\unicode[STIX]{x1D706}^{2}\neq \unicode[STIX]{x1D707}$
, and the absolute irreducibility of
$\unicode[STIX]{x1D706}^{2}\neq \unicode[STIX]{x1D707}$
, and the absolute irreducibility of
![]() $\unicode[STIX]{x1D70B}$
is again [Reference Barthel and LivnéBL94, Theorem 33(2)]. The independence of
$\unicode[STIX]{x1D70B}$
is again [Reference Barthel and LivnéBL94, Theorem 33(2)]. The independence of
![]() $\unicode[STIX]{x1D70B}$
of the choice of
$\unicode[STIX]{x1D70B}$
of the choice of
![]() $\overline{\unicode[STIX]{x1D70E}}$
is [Reference Barthel and LivnéBL94, Corollary 36(2)(b)].◻
$\overline{\unicode[STIX]{x1D70E}}$
is [Reference Barthel and LivnéBL94, Corollary 36(2)(b)].◻
Remark 2.16. It follows from the explicit description of
![]() $\unicode[STIX]{x1D70B}$
that it is either a principal series representation or supersingular, and neither one dimensional nor an element of the special series. (This would no longer be the case if we allowed
$\unicode[STIX]{x1D70B}$
that it is either a principal series representation or supersingular, and neither one dimensional nor an element of the special series. (This would no longer be the case if we allowed
![]() $\bar{r}$
to be a twist of an extension of the trivial character by the mod
$\bar{r}$
to be a twist of an extension of the trivial character by the mod
![]() $p$
cyclotomic character, when in fact
$p$
cyclotomic character, when in fact
![]() $\unicode[STIX]{x1D70B}$
would be an extension of a one-dimensional representation and a special representation, which would also depend on the Serre weight if
$\unicode[STIX]{x1D70B}$
would be an extension of a one-dimensional representation and a special representation, which would also depend on the Serre weight if
![]() $\bar{r}$
is peu ramifié.)
$\bar{r}$
is peu ramifié.)
Remark 2.17. If
![]() $\unicode[STIX]{x1D70B}$
has central character
$\unicode[STIX]{x1D70B}$
has central character
![]() $\unicode[STIX]{x1D713}$
, then
$\unicode[STIX]{x1D713}$
, then
 $\det \bar{r}=\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{-1}$
.
$\det \bar{r}=\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{-1}$
.
3 Patched modules and arithmetic actions
We now introduce the notion of an arithmetic action of (a power series ring over)
![]() $R_{p}$
on an
$R_{p}$
on an
![]() ${\mathcal{O}}[G]$
-module. It is not obvious from the definition that any examples exist, but we will explain later in this section how to deduce the existence of an example from the results of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] (that is, from the Taylor–Wiles patching method). The rest of the paper is devoted to showing a uniqueness result for such actions, and thus deducing that they encode the
${\mathcal{O}}[G]$
-module. It is not obvious from the definition that any examples exist, but we will explain later in this section how to deduce the existence of an example from the results of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] (that is, from the Taylor–Wiles patching method). The rest of the paper is devoted to showing a uniqueness result for such actions, and thus deducing that they encode the
![]() $p$
-adic local Langlands correspondence for
$p$
-adic local Langlands correspondence for
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
. We anticipate that the axiomatic approach taken here will be useful in other contexts (for example, for proving local–global compatibility in the
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
. We anticipate that the axiomatic approach taken here will be useful in other contexts (for example, for proving local–global compatibility in the
![]() $p$
-adic Langlands correspondence for
$p$
-adic Langlands correspondence for
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
in global settings other than those considered in [Reference EmertonEme11] or [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16]).
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
in global settings other than those considered in [Reference EmertonEme11] or [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16]).
3.1 Axioms
Fix an integer
![]() $d\geqslant 0$
and set
$d\geqslant 0$
and set
 $R_{\infty }:=R_{p}\;\widehat{\otimes }_{{\mathcal{O}}}\;{\mathcal{O}}[[x_{1},\ldots ,x_{d}]]$
. Then an
$R_{\infty }:=R_{p}\;\widehat{\otimes }_{{\mathcal{O}}}\;{\mathcal{O}}[[x_{1},\ldots ,x_{d}]]$
. Then an
![]() ${\mathcal{O}}[G]$
-module with an arithmetic action of
${\mathcal{O}}[G]$
-module with an arithmetic action of
![]() $R_{\infty }$
is by definition a non-zero
$R_{\infty }$
is by definition a non-zero
![]() $R_{\infty }[G]$
-module
$R_{\infty }[G]$
-module
![]() $M_{\infty }$
satisfying the following axioms.
$M_{\infty }$
satisfying the following axioms.
- (AA1)
 $M_{\infty }$
is a finitely generated
$M_{\infty }$
is a finitely generated
 $R_{\infty }[[K]]$
-module.
$R_{\infty }[[K]]$
-module.- (AA2)
 $M_{\infty }$
is projective in the category of pseudocompact
$M_{\infty }$
is projective in the category of pseudocompact
 ${\mathcal{O}}[[K]]$
-modules.
${\mathcal{O}}[[K]]$
-modules.
Let
![]() $\unicode[STIX]{x1D70E}^{\circ }$
be a
$\unicode[STIX]{x1D70E}^{\circ }$
be a
![]() $K$
-stable
$K$
-stable
![]() ${\mathcal{O}}$
-lattice in
${\mathcal{O}}$
-lattice in
 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
. Set
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
. Set
 $$\begin{eqnarray}M_{\infty }(\unicode[STIX]{x1D70E}^{\circ }):=(\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(M_{\infty },(\unicode[STIX]{x1D70E}^{\circ })^{d}))^{d},\end{eqnarray}$$
$$\begin{eqnarray}M_{\infty }(\unicode[STIX]{x1D70E}^{\circ }):=(\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(M_{\infty },(\unicode[STIX]{x1D70E}^{\circ })^{d}))^{d},\end{eqnarray}$$
where we are considering continuous homomorphisms for the profinite topology on
![]() $M_{\infty }$
and the
$M_{\infty }$
and the
![]() $p$
-adic topology on
$p$
-adic topology on
![]() $(\unicode[STIX]{x1D70E}^{\circ })^{d}$
. This is a finitely generated
$(\unicode[STIX]{x1D70E}^{\circ })^{d}$
. This is a finitely generated
![]() $R_{\infty }$
-module by (AA1) and [Reference PaškūnasPaš15, Corollary 2.5].
$R_{\infty }$
-module by (AA1) and [Reference PaškūnasPaš15, Corollary 2.5].
- (AA3)
For any
 $\unicode[STIX]{x1D70E}$
, the action of
$\unicode[STIX]{x1D70E}$
, the action of
 $R_{\infty }$
on
$R_{\infty }$
on
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
factors through
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
factors through
 $R_{\infty }(\unicode[STIX]{x1D70E}):=R_{p}(\unicode[STIX]{x1D70E})[[x_{1},\ldots ,x_{d}]]$
. Furthermore,
$R_{\infty }(\unicode[STIX]{x1D70E}):=R_{p}(\unicode[STIX]{x1D70E})[[x_{1},\ldots ,x_{d}]]$
. Furthermore,
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
is maximal Cohen–Macaulay over
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
is maximal Cohen–Macaulay over
 $R_{\infty }(\unicode[STIX]{x1D70E})$
, and the
$R_{\infty }(\unicode[STIX]{x1D70E})$
, and the
 $R_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
-module
$R_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
-module
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is locally free of rank
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is locally free of rank
 $1$
over its support.
$1$
over its support.
For each
![]() $\unicode[STIX]{x1D70E}^{\circ }$
, we have a natural action of
$\unicode[STIX]{x1D70E}^{\circ }$
, we have a natural action of
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
on
${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
on
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
and thus of
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
and thus of
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
on
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
on
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
.
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
.
- (AA4)
For any
 $\unicode[STIX]{x1D70E}$
, the action of
$\unicode[STIX]{x1D70E}$
, the action of
 ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
on
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
on
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is given by the composite
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is given by the composite  $$\begin{eqnarray}{\mathcal{H}}(\unicode[STIX]{x1D70E})\stackrel{\unicode[STIX]{x1D702}}{\rightarrow }R_{p}(\unicode[STIX]{x1D70E})[1/p]\rightarrow R_{p}(\unicode[STIX]{x1D70E})[[x_{1},\ldots ,x_{d}]][1/p],\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}(\unicode[STIX]{x1D70E})\stackrel{\unicode[STIX]{x1D702}}{\rightarrow }R_{p}(\unicode[STIX]{x1D70E})[1/p]\rightarrow R_{p}(\unicode[STIX]{x1D70E})[[x_{1},\ldots ,x_{d}]][1/p],\end{eqnarray}$$
where
 ${\mathcal{H}}(\unicode[STIX]{x1D70E})\stackrel{\unicode[STIX]{x1D702}}{\rightarrow }R_{p}(\unicode[STIX]{x1D70E})[1/p]$
is defined in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Theorem 4.1].
${\mathcal{H}}(\unicode[STIX]{x1D70E})\stackrel{\unicode[STIX]{x1D702}}{\rightarrow }R_{p}(\unicode[STIX]{x1D70E})[1/p]$
is defined in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Theorem 4.1].
Remark 3.2. While these axioms may appear somewhat mysterious, as we will see in the next subsection they arise very naturally in the constructions of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16]. (Indeed, those constructions give modules
![]() $M_{\infty }$
satisfying obvious analogues of the above conditions for
$M_{\infty }$
satisfying obvious analogues of the above conditions for
 $\operatorname{GL}_{n}(K)$
for any finite extension
$\operatorname{GL}_{n}(K)$
for any finite extension
![]() $K/\mathbb{Q}_{p}$
; however, our arguments in the rest of the paper will only apply to the case of
$K/\mathbb{Q}_{p}$
; however, our arguments in the rest of the paper will only apply to the case of
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
.)
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
.)
In these examples, axioms (AA1) and (AA2) essentially follow from the facts that spaces of automorphic forms are finite dimensional, and that the cohomology of zero-dimensional Shimura varieties is concentrated in a single degree (degree zero). Axioms (AA3) and (AA4) come from the existence of Galois representations attached to automorphic forms on unitary groups, and from local–global compatibility at
![]() $p$
for automorphic forms of level prime to
$p$
for automorphic forms of level prime to
![]() $p$
.
$p$
.
The following remark explains how axiom (AA4) is related to Breuil’s original formulation of the
![]() $p$
-adic Langlands correspondence in terms of unitary completions of locally algebraic vectors; see also the proof of Proposition 6.17 below.
$p$
-adic Langlands correspondence in terms of unitary completions of locally algebraic vectors; see also the proof of Proposition 6.17 below.
Remark 3.3. Axiom (AA4) is, in the presence of axioms (AA1)–(AA3), equivalent to an alternative axiom (AA4
![]() $^{\prime }$
), which expresses a pointwise compatibility with the classical local Langlands correspondence, as we now explain. Write
$^{\prime }$
), which expresses a pointwise compatibility with the classical local Langlands correspondence, as we now explain. Write
 $R_{\infty }(\unicode[STIX]{x1D70E}):=R_{p}(\unicode[STIX]{x1D70E})[[x_{1},\ldots ,x_{d}]]$
. If
$R_{\infty }(\unicode[STIX]{x1D70E}):=R_{p}(\unicode[STIX]{x1D70E})[[x_{1},\ldots ,x_{d}]]$
. If
![]() $y$
is a maximal ideal of
$y$
is a maximal ideal of
 $R_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
which lies in the support of
$R_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
which lies in the support of
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
, then we write
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
, then we write
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{y}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(M_{\infty }\otimes _{R_{\infty },y}{\mathcal{O}}_{\unicode[STIX]{x1D705}(y)},E).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{y}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(M_{\infty }\otimes _{R_{\infty },y}{\mathcal{O}}_{\unicode[STIX]{x1D705}(y)},E).\end{eqnarray}$$
We write
![]() $x$
for the corresponding maximal ideal of
$x$
for the corresponding maximal ideal of
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
,
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
,
![]() $r_{x}$
for the deformation of
$r_{x}$
for the deformation of
![]() $\bar{r}$
corresponding to
$\bar{r}$
corresponding to
![]() $x$
and set
$x$
and set
 $\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x}):=r_{p}^{-1}(\text{WD}(r_{x})^{F-\text{ss}})$
, which is the smooth representation of
$\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x}):=r_{p}^{-1}(\text{WD}(r_{x})^{F-\text{ss}})$
, which is the smooth representation of
![]() $G$
corresponding to the Weil–Deligne representation associated to
$G$
corresponding to the Weil–Deligne representation associated to
![]() $r_{x}$
by the classical Langlands correspondence
$r_{x}$
by the classical Langlands correspondence
![]() $r_{p}$
(normalized as in § 1.12). We write
$r_{p}$
(normalized as in § 1.12). We write
 $\unicode[STIX]{x1D70B}_{\text{alg}}(r_{x})$
for the algebraic representation of
$\unicode[STIX]{x1D70B}_{\text{alg}}(r_{x})$
for the algebraic representation of
![]() $G$
whose restriction to
$G$
whose restriction to
![]() $K$
is equal to
$K$
is equal to
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
- (AA4
 $^{\prime }$
)
$^{\prime }$
) For any
 $\unicode[STIX]{x1D70E}$
and for any
$\unicode[STIX]{x1D70E}$
and for any
 $y$
and
$y$
and
 $x$
as above, there is a non-zero
$x$
as above, there is a non-zero
 $G$
-equivariant map
$G$
-equivariant map  $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x})\otimes \unicode[STIX]{x1D70B}_{\text{alg}}(r_{x})\rightarrow \unicode[STIX]{x1D6F1}_{y}^{\text{l.alg}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x})\otimes \unicode[STIX]{x1D70B}_{\text{alg}}(r_{x})\rightarrow \unicode[STIX]{x1D6F1}_{y}^{\text{l.alg}}.\end{eqnarray}$$
That (AA1)–(AA4) imply (AA4
![]() $^{\prime }$
) is a straightforward consequence of the defining property of the map
$^{\prime }$
) is a straightforward consequence of the defining property of the map
![]() $\unicode[STIX]{x1D702}$
. Conversely, assume (AA1)–(AA3) and (AA4
$\unicode[STIX]{x1D702}$
. Conversely, assume (AA1)–(AA3) and (AA4
![]() $^{\prime }$
), and write
$^{\prime }$
), and write
 $$\begin{eqnarray}\overline{R}_{\infty }(\unicode[STIX]{x1D70E}):=R_{\infty }(\unicode[STIX]{x1D70E})/\text{Ann}(M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })).\end{eqnarray}$$
$$\begin{eqnarray}\overline{R}_{\infty }(\unicode[STIX]{x1D70E}):=R_{\infty }(\unicode[STIX]{x1D70E})/\text{Ann}(M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })).\end{eqnarray}$$
It follows from (AA3) that the natural map
 $\overline{R}_{\infty }(\unicode[STIX]{x1D70E})[1/p]\rightarrow \text{End}_{R_{\infty }(\unicode[STIX]{x1D70E})[1/p]}(M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })[1/p])$
is an isomorphism, as it is injective and the cokernel is not supported on any maximal ideal of
$\overline{R}_{\infty }(\unicode[STIX]{x1D70E})[1/p]\rightarrow \text{End}_{R_{\infty }(\unicode[STIX]{x1D70E})[1/p]}(M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })[1/p])$
is an isomorphism, as it is injective and the cokernel is not supported on any maximal ideal of
 $R_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
. In particular, the action of
$R_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
. In particular, the action of
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
on
${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
on
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
induces a homomorphism
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
induces a homomorphism
 $\unicode[STIX]{x1D702}^{\prime }:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow \overline{R}_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
. We have to show that this agrees with the map induced by
$\unicode[STIX]{x1D702}^{\prime }:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow \overline{R}_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
. We have to show that this agrees with the map induced by
![]() $\unicode[STIX]{x1D702}$
.
$\unicode[STIX]{x1D702}$
.
It follows from (AA4
![]() $^{\prime }$
) and the defining property of
$^{\prime }$
) and the defining property of
![]() $\unicode[STIX]{x1D702}$
that
$\unicode[STIX]{x1D702}$
that
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $\unicode[STIX]{x1D702}^{\prime }$
agree modulo every maximal ideal of
$\unicode[STIX]{x1D702}^{\prime }$
agree modulo every maximal ideal of
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
in the support of
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
in the support of
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
. It follows from (AA3) that
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
. It follows from (AA3) that
 $\overline{R}_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
is a union of irreducible components of
$\overline{R}_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
is a union of irreducible components of
 $R_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
. Since
$R_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
. Since
 $R_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
is reduced, we conclude that
$R_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
is reduced, we conclude that
 $\overline{R}_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
is reduced; thus, the intersection of all maximal ideals is equal to zero. Hence, (AA4) holds.
$\overline{R}_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
is reduced; thus, the intersection of all maximal ideals is equal to zero. Hence, (AA4) holds.
3.4 Existence of a patched module
 $M_{\infty }$
$M_{\infty }$
We now briefly recall some of the main results of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16], specialized to the case of two-dimensional representations. We emphasize that these results use only the Taylor–Wiles–Kisin patching method, and use nothing about the
![]() $p$
-adic Langlands correspondence for
$p$
-adic Langlands correspondence for
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
. (We should perhaps remark, though, that we do make implicit use of the results of [Reference Barnet-Lamb, Gee, Geraghty and TaylorB-LGGT14] in the globalization part of the argument, and thus of the Taylor–Wiles–Kisin method for unitary groups of rank
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
. (We should perhaps remark, though, that we do make implicit use of the results of [Reference Barnet-Lamb, Gee, Geraghty and TaylorB-LGGT14] in the globalization part of the argument, and thus of the Taylor–Wiles–Kisin method for unitary groups of rank
![]() $4$
, and not just for
$4$
, and not just for
![]() $U(2)$
.) We freely use the notation of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16].
$U(2)$
.) We freely use the notation of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16].
Enlarging
![]() $\mathbb{F}$
if necessary, we see from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Lemma 2.2] that the hypotheses on
$\mathbb{F}$
if necessary, we see from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Lemma 2.2] that the hypotheses on
![]() $\bar{r}$
at the start of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 2.1] are automatically satisfied. We fix the choice of weight
$\bar{r}$
at the start of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 2.1] are automatically satisfied. We fix the choice of weight
![]() $\unicode[STIX]{x1D709}$
and inertial type
$\unicode[STIX]{x1D709}$
and inertial type
![]() $\unicode[STIX]{x1D70F}$
in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 2.3] in the following way: we take
$\unicode[STIX]{x1D70F}$
in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 2.3] in the following way: we take
![]() $\unicode[STIX]{x1D70F}$
to be trivial, and we take
$\unicode[STIX]{x1D70F}$
to be trivial, and we take
![]() $\unicode[STIX]{x1D709}$
to be the weight corresponding to a Serre weight of
$\unicode[STIX]{x1D709}$
to be the weight corresponding to a Serre weight of
![]() $\bar{r}$
, as in Lemma 2.15.
$\bar{r}$
, as in Lemma 2.15.
With this choice, the modification of the Taylor–Wiles–Kisin method carried out in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, § 2.6] produces for some
![]() $d>0$
an
$d>0$
an
![]() $R_{\infty }$
-module
$R_{\infty }$
-module
![]() $M_{\infty }$
with an action of
$M_{\infty }$
with an action of
![]() $G$
. (Note that for our choice of
$G$
. (Note that for our choice of
![]() $\bar{r}$
,
$\bar{r}$
,
![]() $\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D709}$
and
![]() $\unicode[STIX]{x1D70F}$
, the various framed deformation rings appearing in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] are formal power series rings over
$\unicode[STIX]{x1D70F}$
, the various framed deformation rings appearing in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] are formal power series rings over
![]() ${\mathcal{O}}$
, and the framed deformation ring of
${\mathcal{O}}$
, and the framed deformation ring of
![]() $\bar{r}$
is formally smooth over
$\bar{r}$
is formally smooth over
![]() $R_{p}$
, so all of these rings are absorbed into the power series ring
$R_{p}$
, so all of these rings are absorbed into the power series ring
 ${\mathcal{O}}[[x_{1},\ldots ,x_{d}]]$
. The module
${\mathcal{O}}[[x_{1},\ldots ,x_{d}]]$
. The module
![]() $M_{\infty }$
is patched from the cohomology of a definite unitary group over some totally real field in which
$M_{\infty }$
is patched from the cohomology of a definite unitary group over some totally real field in which
![]() $p$
splits completely.)
$p$
splits completely.)
This
![]() $R_{\infty }[G]$
-module automatically satisfies the axioms (AA1)–(AA4) above. Indeed, (AA1) and (AA2) follow from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Proposition 2.10] and (AA3) follows from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Lemmas 4.17(1) and 4.18(1)]. Finally, (AA4) is [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Theorem 4.19].
$R_{\infty }[G]$
-module automatically satisfies the axioms (AA1)–(AA4) above. Indeed, (AA1) and (AA2) follow from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Proposition 2.10] and (AA3) follows from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Lemmas 4.17(1) and 4.18(1)]. Finally, (AA4) is [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Theorem 4.19].
4 Existence and uniqueness of arithmetic actions
We fix an
![]() ${\mathcal{O}}[G]$
-module
${\mathcal{O}}[G]$
-module
![]() $M_{\infty }$
with an arithmetic action of
$M_{\infty }$
with an arithmetic action of
![]() $R_{\infty }$
in the sense of § 3.1.
$R_{\infty }$
in the sense of § 3.1.
4.1 Serre weights and cosocles
Now let
 $\overline{\unicode[STIX]{x1D70E}}=\overline{\unicode[STIX]{x1D70E}}_{a,b}$
be a Serre weight and let
$\overline{\unicode[STIX]{x1D70E}}=\overline{\unicode[STIX]{x1D70E}}_{a,b}$
be a Serre weight and let
![]() $\unicode[STIX]{x1D70E}^{\circ }$
be a
$\unicode[STIX]{x1D70E}^{\circ }$
be a
![]() $K$
-stable
$K$
-stable
![]() ${\mathcal{O}}$
-lattice in
${\mathcal{O}}$
-lattice in
![]() $\unicode[STIX]{x1D70E}_{a,b}$
, so that
$\unicode[STIX]{x1D70E}_{a,b}$
, so that
 $\unicode[STIX]{x1D70E}^{\circ }/\unicode[STIX]{x1D71B}\unicode[STIX]{x1D70E}^{\circ }=\overline{\unicode[STIX]{x1D70E}}$
. We define
$\unicode[STIX]{x1D70E}^{\circ }/\unicode[STIX]{x1D71B}\unicode[STIX]{x1D70E}^{\circ }=\overline{\unicode[STIX]{x1D70E}}$
. We define
 $M_{\infty }(\overline{\unicode[STIX]{x1D70E}})=\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(M_{\infty },(\overline{\unicode[STIX]{x1D70E}})^{\vee })^{\vee }$
, so that by (AA2) we have
$M_{\infty }(\overline{\unicode[STIX]{x1D70E}})=\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(M_{\infty },(\overline{\unicode[STIX]{x1D70E}})^{\vee })^{\vee }$
, so that by (AA2) we have
 $M_{\infty }(\overline{\unicode[STIX]{x1D70E}})=M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })/\unicode[STIX]{x1D71B}M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
. By definition, the deformation ring
$M_{\infty }(\overline{\unicode[STIX]{x1D70E}})=M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })/\unicode[STIX]{x1D71B}M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
. By definition, the deformation ring
 $R_{p}(\unicode[STIX]{x1D70E})=R_{p}(\unicode[STIX]{x1D70E}_{a,b})$
is non-zero if and only if
$R_{p}(\unicode[STIX]{x1D70E})=R_{p}(\unicode[STIX]{x1D70E}_{a,b})$
is non-zero if and only if
![]() $\overline{\unicode[STIX]{x1D70E}}$
is a Serre weight of
$\overline{\unicode[STIX]{x1D70E}}$
is a Serre weight of
![]() $\bar{r}$
. Set
$\bar{r}$
. Set
 $R_{\infty }(\unicode[STIX]{x1D70E})=R_{p}(\unicode[STIX]{x1D70E})[[x_{1},\ldots ,x_{d}]]$
.
$R_{\infty }(\unicode[STIX]{x1D70E})=R_{p}(\unicode[STIX]{x1D70E})[[x_{1},\ldots ,x_{d}]]$
.
We let
![]() $\unicode[STIX]{x1D70B}$
denote the absolutely irreducible smooth
$\unicode[STIX]{x1D70B}$
denote the absolutely irreducible smooth
![]() $\mathbb{F}$
-representation of
$\mathbb{F}$
-representation of
![]() $G$
associated to
$G$
associated to
![]() $\bar{r}$
via Lemma 2.15(5).
$\bar{r}$
via Lemma 2.15(5).
Proposition 4.2. (i) We have
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })\neq 0$
if and only if
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })\neq 0$
if and only if
![]() $\overline{\unicode[STIX]{x1D70E}}$
is a Serre weight of
$\overline{\unicode[STIX]{x1D70E}}$
is a Serre weight of
![]() $\bar{r}$
, in which case
$\bar{r}$
, in which case
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
is a free
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
is a free
![]() $R_{\infty }(\unicode[STIX]{x1D70E})$
-module of rank
$R_{\infty }(\unicode[STIX]{x1D70E})$
-module of rank
![]() $1$
.
$1$
.
(ii) If
![]() $\overline{\unicode[STIX]{x1D70E}}$
is a Serre weight of
$\overline{\unicode[STIX]{x1D70E}}$
is a Serre weight of
![]() $\bar{r}$
, then the action of
$\bar{r}$
, then the action of
![]() ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
on
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
on
![]() $M_{\infty }(\overline{\unicode[STIX]{x1D70E}})$
factors through the natural map
$M_{\infty }(\overline{\unicode[STIX]{x1D70E}})$
factors through the natural map
 $R_{p}(\unicode[STIX]{x1D70E})/\unicode[STIX]{x1D71B}\rightarrow R_{\infty }(\unicode[STIX]{x1D70E})/\unicode[STIX]{x1D71B}$
, and
$R_{p}(\unicode[STIX]{x1D70E})/\unicode[STIX]{x1D71B}\rightarrow R_{\infty }(\unicode[STIX]{x1D70E})/\unicode[STIX]{x1D71B}$
, and
![]() $M_{\infty }(\overline{\unicode[STIX]{x1D70E}})$
is a flat
$M_{\infty }(\overline{\unicode[STIX]{x1D70E}})$
is a flat
![]() ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
-module.
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
-module.
(iii) If
![]() $\unicode[STIX]{x1D70B}^{\prime }$
is an irreducible smooth
$\unicode[STIX]{x1D70B}^{\prime }$
is an irreducible smooth
![]() $\mathbb{F}$
-representation of
$\mathbb{F}$
-representation of
![]() $G$
, then we have
$G$
, then we have
 $$\begin{eqnarray}\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })\neq 0\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })\neq 0\end{eqnarray}$$
if and only if
![]() $\unicode[STIX]{x1D70B}^{\prime }$
is isomorphic to
$\unicode[STIX]{x1D70B}^{\prime }$
is isomorphic to
![]() $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
Proof. It follows from (AA3) that
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })\neq 0$
only if
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })\neq 0$
only if
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]\neq 0$
, which is equivalent to
$R_{p}(\unicode[STIX]{x1D70E})[1/p]\neq 0$
, which is equivalent to
![]() $\overline{\unicode[STIX]{x1D70E}}$
being a Serre weight of
$\overline{\unicode[STIX]{x1D70E}}$
being a Serre weight of
![]() $\bar{r}$
. In this case, since
$\bar{r}$
. In this case, since
 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
with
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
with
 $0\leqslant b\leqslant p-1$
,
$0\leqslant b\leqslant p-1$
,
![]() $R_{\infty }(\unicode[STIX]{x1D70E})$
is formally smooth over
$R_{\infty }(\unicode[STIX]{x1D70E})$
is formally smooth over
![]() ${\mathcal{O}}$
by Lemma 2.15, so it follows from (AA3) and the Auslander–Buchsbaum theorem that
${\mathcal{O}}$
by Lemma 2.15, so it follows from (AA3) and the Auslander–Buchsbaum theorem that
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
is a free
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
is a free
![]() $R_{\infty }(\unicode[STIX]{x1D70E})$
-module of finite rank and that
$R_{\infty }(\unicode[STIX]{x1D70E})$
-module of finite rank and that
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is a locally free
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is a locally free
 $R_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
-module of rank
$R_{\infty }(\unicode[STIX]{x1D70E})[1/p]$
-module of rank
![]() $1$
. Thus,
$1$
. Thus,
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
is free of rank
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })$
is free of rank
![]() $1$
over
$1$
over
![]() $R_{\infty }(\unicode[STIX]{x1D70E})$
. This proves the ‘only if’ direction of (1).
$R_{\infty }(\unicode[STIX]{x1D70E})$
. This proves the ‘only if’ direction of (1).
For (2), note that
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })\neq 0$
if and only if
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })\neq 0$
if and only if
 $M_{\infty }(\overline{\unicode[STIX]{x1D70E}})\neq 0$
, so we may assume that
$M_{\infty }(\overline{\unicode[STIX]{x1D70E}})\neq 0$
, so we may assume that
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })\neq 0$
. The first part of (2) follows from (AA4) together with Lemmas 2.15(2) and 2.14(2). For the remaining part of (2), note that
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })\neq 0$
. The first part of (2) follows from (AA4) together with Lemmas 2.15(2) and 2.14(2). For the remaining part of (2), note that
 $R_{p}(\unicode[STIX]{x1D70E})/\unicode[STIX]{x1D71B}$
is flat over
$R_{p}(\unicode[STIX]{x1D70E})/\unicode[STIX]{x1D71B}$
is flat over
![]() ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
by Lemmas 2.14 and 2.15, and
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
by Lemmas 2.14 and 2.15, and
![]() $M_{\infty }(\overline{\unicode[STIX]{x1D70E}})$
is flat over
$M_{\infty }(\overline{\unicode[STIX]{x1D70E}})$
is flat over
 $R_{p}(\unicode[STIX]{x1D70E})/\unicode[STIX]{x1D71B}$
by the only if part of (1), as required.
$R_{p}(\unicode[STIX]{x1D70E})/\unicode[STIX]{x1D71B}$
by the only if part of (1), as required.
To prove (3), we first note that it is enough to prove the statement for absolutely irreducible
![]() $\unicode[STIX]{x1D70B}^{\prime }$
as we may enlarge the field
$\unicode[STIX]{x1D70B}^{\prime }$
as we may enlarge the field
![]() $\mathbb{F}$
. Let us assume that
$\mathbb{F}$
. Let us assume that
![]() $\unicode[STIX]{x1D70B}^{\prime }$
is absolutely irreducible and let
$\unicode[STIX]{x1D70B}^{\prime }$
is absolutely irreducible and let
![]() $\overline{\unicode[STIX]{x1D70E}}^{\prime }$
be an irreducible representation of
$\overline{\unicode[STIX]{x1D70E}}^{\prime }$
be an irreducible representation of
![]() $K$
contained in the socle of
$K$
contained in the socle of
![]() $\unicode[STIX]{x1D70B}^{\prime }$
. It follows from [Reference Barthel and LivnéBL94, Reference BreuilBre03a] that the surjection
$\unicode[STIX]{x1D70B}^{\prime }$
. It follows from [Reference Barthel and LivnéBL94, Reference BreuilBre03a] that the surjection
 $\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}^{\prime }{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\prime }$
factors through the map
$\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}^{\prime }{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\prime }$
factors through the map
 $$\begin{eqnarray}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}^{\prime })\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime }),\unicode[STIX]{x1D6FC}^{\prime }}\mathbb{F}{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}^{\prime })\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime }),\unicode[STIX]{x1D6FC}^{\prime }}\mathbb{F}{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\prime },\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6FC}^{\prime }:{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime })\rightarrow \mathbb{F}$
is given by the action of
$\unicode[STIX]{x1D6FC}^{\prime }:{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime })\rightarrow \mathbb{F}$
is given by the action of
![]() ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime })$
on the one-dimensional
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime })$
on the one-dimensional
![]() $\mathbb{F}$
-vector space
$\mathbb{F}$
-vector space
 $\operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70E}}^{\prime },\unicode[STIX]{x1D70B}^{\prime })$
. Moreover, (4.3) is an isomorphism unless
$\operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70E}}^{\prime },\unicode[STIX]{x1D70B}^{\prime })$
. Moreover, (4.3) is an isomorphism unless
![]() $\unicode[STIX]{x1D70B}^{\prime }$
is a character or special series. Since
$\unicode[STIX]{x1D70B}^{\prime }$
is a character or special series. Since
 $$\begin{eqnarray}M_{\infty }(\overline{\unicode[STIX]{x1D70E}}^{\prime })\cong \operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70E}}^{\prime },M_{\infty }^{\vee })^{\vee }\cong \operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}^{\prime },M_{\infty }^{\vee })^{\vee },\end{eqnarray}$$
$$\begin{eqnarray}M_{\infty }(\overline{\unicode[STIX]{x1D70E}}^{\prime })\cong \operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70E}}^{\prime },M_{\infty }^{\vee })^{\vee }\cong \operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}^{\prime },M_{\infty }^{\vee })^{\vee },\end{eqnarray}$$
from (4.3) we obtain a surjection of
![]() $R_{\infty }(\overline{\unicode[STIX]{x1D70E}}^{\prime })$
-modules
$R_{\infty }(\overline{\unicode[STIX]{x1D70E}}^{\prime })$
-modules
 $$\begin{eqnarray}M_{\infty }(\overline{\unicode[STIX]{x1D70E}}^{\prime })\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime }),\unicode[STIX]{x1D6FC}^{\prime }}\mathbb{F}\cong \operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}^{\prime }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime }),\unicode[STIX]{x1D6FC}^{\prime }}\mathbb{F},M_{\infty }^{\vee })^{\vee }{\twoheadrightarrow}\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })^{\vee },\end{eqnarray}$$
$$\begin{eqnarray}M_{\infty }(\overline{\unicode[STIX]{x1D70E}}^{\prime })\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime }),\unicode[STIX]{x1D6FC}^{\prime }}\mathbb{F}\cong \operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}^{\prime }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime }),\unicode[STIX]{x1D6FC}^{\prime }}\mathbb{F},M_{\infty }^{\vee })^{\vee }{\twoheadrightarrow}\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })^{\vee },\end{eqnarray}$$
which moreover is an isomorphism if
![]() $\unicode[STIX]{x1D70B}^{\prime }$
is not a character or special series. Thus, if
$\unicode[STIX]{x1D70B}^{\prime }$
is not a character or special series. Thus, if
 $\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })$
is non-zero, then we deduce from the previous displayed expression that
$\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })$
is non-zero, then we deduce from the previous displayed expression that
 $M_{\infty }(\overline{\unicode[STIX]{x1D70E}}^{\prime })\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime }),\unicode[STIX]{x1D6FC}^{\prime }}\mathbb{F}\neq 0.$
In particular,
$M_{\infty }(\overline{\unicode[STIX]{x1D70E}}^{\prime })\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime }),\unicode[STIX]{x1D6FC}^{\prime }}\mathbb{F}\neq 0.$
In particular,
 $M_{\infty }(\overline{\unicode[STIX]{x1D70E}}^{\prime })\neq 0$
and hence
$M_{\infty }(\overline{\unicode[STIX]{x1D70E}}^{\prime })\neq 0$
and hence
![]() $\overline{\unicode[STIX]{x1D70E}}^{\prime }$
is a Serre weight for
$\overline{\unicode[STIX]{x1D70E}}^{\prime }$
is a Serre weight for
![]() $\bar{r}$
by the only if part of (1).
$\bar{r}$
by the only if part of (1).
We claim that
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
coincides with the morphism
$\unicode[STIX]{x1D6FC}^{\prime }$
coincides with the morphism
![]() $\unicode[STIX]{x1D6FC}$
of Lemma 2.15(3) (with
$\unicode[STIX]{x1D6FC}$
of Lemma 2.15(3) (with
![]() $\overline{\unicode[STIX]{x1D70E}}^{\prime }$
in place of
$\overline{\unicode[STIX]{x1D70E}}^{\prime }$
in place of
![]() $\unicode[STIX]{x1D70E}$
). To see this, note that by the only if part of (1), we have that
$\unicode[STIX]{x1D70E}$
). To see this, note that by the only if part of (1), we have that
 $(R_{p}(\unicode[STIX]{x1D70E}^{\prime })/\unicode[STIX]{x1D71B})\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime }),\unicode[STIX]{x1D6FC}^{\prime }}\mathbb{F}\neq 0$
and hence by Lemma 2.15(4) we find that
$(R_{p}(\unicode[STIX]{x1D70E}^{\prime })/\unicode[STIX]{x1D71B})\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime }),\unicode[STIX]{x1D6FC}^{\prime }}\mathbb{F}\neq 0$
and hence by Lemma 2.15(4) we find that
 $\widehat{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime })}\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime }),\unicode[STIX]{x1D6FC}^{\prime }}\mathbb{F}\neq 0,$
where
$\widehat{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime })}\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime }),\unicode[STIX]{x1D6FC}^{\prime }}\mathbb{F}\neq 0,$
where
![]() $\widehat{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime })}$
denotes the completion of
$\widehat{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime })}$
denotes the completion of
![]() ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime })$
with respect to the kernel of the morphism
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime })$
with respect to the kernel of the morphism
![]() $\unicode[STIX]{x1D6FC}$
. This proves that
$\unicode[STIX]{x1D6FC}$
. This proves that
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
coincide.
$\unicode[STIX]{x1D6FC}^{\prime }$
coincide.
Part (5) of Lemma 2.15 now implies that
 $\unicode[STIX]{x1D70B}\cong (\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}^{\prime })\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime }),\unicode[STIX]{x1D6FC}^{\prime }}\mathbb{F}$
. Hence, (4.3) gives us a
$\unicode[STIX]{x1D70B}\cong (\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}^{\prime })\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}^{\prime }),\unicode[STIX]{x1D6FC}^{\prime }}\mathbb{F}$
. Hence, (4.3) gives us a
![]() $G$
-equivariant surjection
$G$
-equivariant surjection
![]() $\unicode[STIX]{x1D70B}{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\prime }$
, which is an isomorphism as
$\unicode[STIX]{x1D70B}{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\prime }$
, which is an isomorphism as
![]() $\unicode[STIX]{x1D70B}$
is irreducible.
$\unicode[STIX]{x1D70B}$
is irreducible.
Conversely, it follows from (AA1) that there is an irreducible smooth
![]() $\mathbb{F}$
-representation
$\mathbb{F}$
-representation
![]() $\unicode[STIX]{x1D70B}^{\prime }$
of
$\unicode[STIX]{x1D70B}^{\prime }$
of
![]() $G$
such that
$G$
such that
 $\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })$
is non-zero; we have just seen that
$\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })$
is non-zero; we have just seen that
![]() $\unicode[STIX]{x1D70B}\cong \unicode[STIX]{x1D70B}^{\prime }$
, so that
$\unicode[STIX]{x1D70B}\cong \unicode[STIX]{x1D70B}^{\prime }$
, so that
 $\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B},M_{\infty }^{\vee })\neq 0$
, as required.
$\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B},M_{\infty }^{\vee })\neq 0$
, as required.
Finally, suppose that
![]() $\overline{\unicode[STIX]{x1D70E}}$
is a Serre weight of
$\overline{\unicode[STIX]{x1D70E}}$
is a Serre weight of
![]() $\bar{r}$
. Then as above we have an isomorphism of
$\bar{r}$
. Then as above we have an isomorphism of
![]() $R_{\infty }(\overline{\unicode[STIX]{x1D70E}})$
-modules
$R_{\infty }(\overline{\unicode[STIX]{x1D70E}})$
-modules
 $$\begin{eqnarray}M_{\infty }(\overline{\unicode[STIX]{x1D70E}})\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),\unicode[STIX]{x1D6FC}}\mathbb{F}\cong \operatorname{Hom}_{G}(\unicode[STIX]{x1D70B},M_{\infty }^{\vee })^{\vee }\neq 0,\end{eqnarray}$$
$$\begin{eqnarray}M_{\infty }(\overline{\unicode[STIX]{x1D70E}})\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),\unicode[STIX]{x1D6FC}}\mathbb{F}\cong \operatorname{Hom}_{G}(\unicode[STIX]{x1D70B},M_{\infty }^{\vee })^{\vee }\neq 0,\end{eqnarray}$$
so that
 $M_{\infty }(\overline{\unicode[STIX]{x1D70E}})\neq 0$
. This completes the proof of the ‘if’ direction of (1).◻
$M_{\infty }(\overline{\unicode[STIX]{x1D70E}})\neq 0$
. This completes the proof of the ‘if’ direction of (1).◻
4.4 Smooth and admissible representations
We record a few definitions, following [Reference PaškūnasPaš13, § 2]. Let
![]() $(R,\mathfrak{m})$
be a complete local noetherian
$(R,\mathfrak{m})$
be a complete local noetherian
![]() ${\mathcal{O}}$
-algebra with residue field
${\mathcal{O}}$
-algebra with residue field
![]() $\mathbb{F}$
. Then
$\mathbb{F}$
. Then
 $\text{Mod}_{G}^{\text{sm}}(R)$
is the full subcategory of the category of
$\text{Mod}_{G}^{\text{sm}}(R)$
is the full subcategory of the category of
![]() $R[G]$
-modules consisting of smooth objects. More precisely, these are objects
$R[G]$
-modules consisting of smooth objects. More precisely, these are objects
![]() $V$
such that
$V$
such that
 $$\begin{eqnarray}V=\mathop{\bigcup }_{H,n}V^{H}[\mathfrak{m}^{n}],\end{eqnarray}$$
$$\begin{eqnarray}V=\mathop{\bigcup }_{H,n}V^{H}[\mathfrak{m}^{n}],\end{eqnarray}$$
where the union is taken over open compact subgroups
![]() $H\subset G$
and over positive integers
$H\subset G$
and over positive integers
![]() $n$
.
$n$
.
We say that an object
![]() $V$
of
$V$
of
 $\text{Mod}_{G}^{\text{sm}}(R)$
is admissible if
$\text{Mod}_{G}^{\text{sm}}(R)$
is admissible if
 $V^{H}[\mathfrak{m}^{n}]$
is a finitely generated
$V^{H}[\mathfrak{m}^{n}]$
is a finitely generated
![]() $R$
-module for every compact open subgroup
$R$
-module for every compact open subgroup
![]() $H\subset G$
and every
$H\subset G$
and every
![]() $n\geqslant 1$
. Moreover,
$n\geqslant 1$
. Moreover,
![]() $V$
is called locally admissible if, for every
$V$
is called locally admissible if, for every
![]() $v\in V$
, the smallest
$v\in V$
, the smallest
![]() $R[G]$
-submodule of
$R[G]$
-submodule of
![]() $V$
containing
$V$
containing
![]() $v$
is admissible. We let
$v$
is admissible. We let
 $\text{Mod}_{G}^{\text{l.adm}}(R)$
denote the full subcategory of
$\text{Mod}_{G}^{\text{l.adm}}(R)$
denote the full subcategory of
 $\text{Mod}_{G}^{\text{sm}}(R)$
consisting of locally admissible representations.
$\text{Mod}_{G}^{\text{sm}}(R)$
consisting of locally admissible representations.
The categories
 $\text{Mod}_{G}^{\text{sm}}(R)$
and
$\text{Mod}_{G}^{\text{sm}}(R)$
and
 $\text{Mod}_{G}^{\text{l.adm}}(R)$
are abelian (see [Reference EmertonEme10] for the second one) and have enough injectives.
$\text{Mod}_{G}^{\text{l.adm}}(R)$
are abelian (see [Reference EmertonEme10] for the second one) and have enough injectives.
Definition 4.5. (i) A monomorphism
 $\unicode[STIX]{x1D704}:N{\hookrightarrow}M$
in an abelian category is called essential if, for every non-zero subobject
$\unicode[STIX]{x1D704}:N{\hookrightarrow}M$
in an abelian category is called essential if, for every non-zero subobject
 $M^{\prime }\subset M$
,
$M^{\prime }\subset M$
,
 $\unicode[STIX]{x1D704}(N)\cap M^{\prime }$
is non-zero.
$\unicode[STIX]{x1D704}(N)\cap M^{\prime }$
is non-zero.
(ii) An injective envelope of an object
![]() $N$
of an abelian category is an essential monomorphism
$N$
of an abelian category is an essential monomorphism
 $\unicode[STIX]{x1D704}:N{\hookrightarrow}I$
with
$\unicode[STIX]{x1D704}:N{\hookrightarrow}I$
with
![]() $I$
an injective object of the abelian category.
$I$
an injective object of the abelian category.
If they exist, injective envelopes are unique up to (non-unique) isomorphism. By [Reference PaškūnasPaš13, Lemma 2.3], the category
 $\text{Mod}_{G}^{\text{sm}}(R)$
admits injective envelopes. The category
$\text{Mod}_{G}^{\text{sm}}(R)$
admits injective envelopes. The category
 $\text{Mod}_{G}^{\text{l.adm}}(R)$
also admits injective envelopes. (This follows from [Reference PaškūnasPaš10, Lemma 3.2] and the fact that the inclusion of
$\text{Mod}_{G}^{\text{l.adm}}(R)$
also admits injective envelopes. (This follows from [Reference PaškūnasPaš10, Lemma 3.2] and the fact that the inclusion of
 $\text{Mod}_{G}^{\text{l.adm}}(R)$
into
$\text{Mod}_{G}^{\text{l.adm}}(R)$
into
 $\text{Mod}_{G}^{\text{sm}}(R)$
has a right adjoint, namely the functor to which any smooth
$\text{Mod}_{G}^{\text{sm}}(R)$
has a right adjoint, namely the functor to which any smooth
![]() $G$
-representation associates its maximal locally admissible subrepresentation.)
$G$
-representation associates its maximal locally admissible subrepresentation.)
Lemma 4.6. If
![]() $V$
is a locally admissible representation of
$V$
is a locally admissible representation of
![]() $G$
, then the inclusion
$G$
, then the inclusion
 $\operatorname{soc}_{G}(V){\hookrightarrow}V$
is essential.
$\operatorname{soc}_{G}(V){\hookrightarrow}V$
is essential.
Proof. Any non-zero subrepresentation of
![]() $V$
contains a non-zero finitely generated subrepresentation. Thus, it suffices to show that any non-zero finitely generated subrepresentation
$V$
contains a non-zero finitely generated subrepresentation. Thus, it suffices to show that any non-zero finitely generated subrepresentation
![]() $W$
of
$W$
of
![]() $V$
has a non-zero intersection with
$V$
has a non-zero intersection with
 $\operatorname{soc}_{G}(V)$
. Since
$\operatorname{soc}_{G}(V)$
. Since
 $\operatorname{soc}_{G}(V)\cap W=\operatorname{soc}_{G}(W)$
, it suffices to show that any such subrepresentation has a non-zero socle. This follows from the fact that every finitely generated admissible representation of
$\operatorname{soc}_{G}(V)\cap W=\operatorname{soc}_{G}(W)$
, it suffices to show that any such subrepresentation has a non-zero socle. This follows from the fact that every finitely generated admissible representation of
![]() $G$
is of finite length by [Reference EmertonEme10, Theorem 2.3.8].◻
$G$
is of finite length by [Reference EmertonEme10, Theorem 2.3.8].◻
Definition 4.7. (i) An epimorphism
 $q:M{\twoheadrightarrow}N$
in an abelian category is called essential if a morphism
$q:M{\twoheadrightarrow}N$
in an abelian category is called essential if a morphism
 $s:M^{\prime }\rightarrow M$
is an epimorphism whenever
$s:M^{\prime }\rightarrow M$
is an epimorphism whenever
![]() $q\circ s$
is an epimorphism.
$q\circ s$
is an epimorphism.
(ii) A projective envelope of an object
![]() $N$
of an abelian category is an essential epimorphism
$N$
of an abelian category is an essential epimorphism
 $q:P{\twoheadrightarrow}N$
with
$q:P{\twoheadrightarrow}N$
with
![]() $P$
a projective object in the abelian category.
$P$
a projective object in the abelian category.
Pontryagin duality reverses arrows, so it exchanges injective and projective objects as well as injective and projective envelopes.
4.8 Projectivity of
 $M_{\infty }$
$M_{\infty }$
Our first aim is to show that
![]() $M_{\infty }^{\vee }$
is an injective locally admissible representation of
$M_{\infty }^{\vee }$
is an injective locally admissible representation of
![]() $G$
.
$G$
.
Lemma 4.9.
![]() $M_{\infty }^{\vee }$
is an admissible object of
$M_{\infty }^{\vee }$
is an admissible object of
 $\text{Mod}_{G}^{\text{sm}}(R_{\infty })$
and thus lies in
$\text{Mod}_{G}^{\text{sm}}(R_{\infty })$
and thus lies in
 $\text{Mod}_{G}^{\text{l.adm}}({\mathcal{O}})$
.
$\text{Mod}_{G}^{\text{l.adm}}({\mathcal{O}})$
.
Proof. Dually, it is enough by [Reference EmertonEme10, Lemma 2.2.11] to show that
![]() $M_{\infty }$
is a finitely generated
$M_{\infty }$
is a finitely generated
 $R_{\infty }[[K]]$
-module, which is (AA1).◻
$R_{\infty }[[K]]$
-module, which is (AA1).◻
Lemma 4.10. Let
![]() $\mathfrak{m}$
be a maximal ideal of
$\mathfrak{m}$
be a maximal ideal of
![]() ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
with residue field
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
with residue field
![]() $\unicode[STIX]{x1D705}(\mathfrak{m})$
. Then
$\unicode[STIX]{x1D705}(\mathfrak{m})$
. Then
 $$\begin{eqnarray}\operatorname{Tor}_{i}^{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D705}(\mathfrak{m}))=0,\quad \forall i>0.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Tor}_{i}^{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D705}(\mathfrak{m}))=0,\quad \forall i>0.\end{eqnarray}$$
Proof. Since the map
![]() $\mathbb{F}\rightarrow \overline{\mathbb{F}}$
is faithfully flat, we can and do assume that
$\mathbb{F}\rightarrow \overline{\mathbb{F}}$
is faithfully flat, we can and do assume that
![]() $\mathbb{F}$
is algebraically closed. Since
$\mathbb{F}$
is algebraically closed. Since
 ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})=\mathbb{F}[S^{\pm 1},T]$
, we have
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})=\mathbb{F}[S^{\pm 1},T]$
, we have
 $\mathfrak{m}=(S-\unicode[STIX]{x1D707},T-\unicode[STIX]{x1D706})$
for some
$\mathfrak{m}=(S-\unicode[STIX]{x1D707},T-\unicode[STIX]{x1D706})$
for some
![]() $\unicode[STIX]{x1D707}\in \mathbb{F}^{\times }$
,
$\unicode[STIX]{x1D707}\in \mathbb{F}^{\times }$
,
![]() $\unicode[STIX]{x1D706}\in \mathbb{F}$
. Since the sequence
$\unicode[STIX]{x1D706}\in \mathbb{F}$
. Since the sequence
 $S-\unicode[STIX]{x1D707},T-\unicode[STIX]{x1D706}$
is regular in
$S-\unicode[STIX]{x1D707},T-\unicode[STIX]{x1D706}$
is regular in
![]() ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
, the Koszul complex
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
, the Koszul complex
![]() $K_{\bullet }$
associated to it is a resolution of
$K_{\bullet }$
associated to it is a resolution of
![]() $\unicode[STIX]{x1D705}(\mathfrak{m})$
by free
$\unicode[STIX]{x1D705}(\mathfrak{m})$
by free
![]() ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
-modules [Reference MatsumuraMat89, Theorem 16.5(i)]. Thus, the complex
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
-modules [Reference MatsumuraMat89, Theorem 16.5(i)]. Thus, the complex
 $K_{\bullet }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
computes the
$K_{\bullet }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
computes the
![]() $\operatorname{Tor}$
-groups we are after, and to verify the claim it is enough to show that the sequence
$\operatorname{Tor}$
-groups we are after, and to verify the claim it is enough to show that the sequence
 $S-\unicode[STIX]{x1D707},T-\unicode[STIX]{x1D706}$
is regular on
$S-\unicode[STIX]{x1D707},T-\unicode[STIX]{x1D706}$
is regular on
 $\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
.
$\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
.
If
 $f\in \operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
, then
$f\in \operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
, then
 $(Sf)(g)=f(gz)$
, where
$(Sf)(g)=f(gz)$
, where
 $z=\big(\!\begin{smallmatrix}p & 0\\ 0 & p\end{smallmatrix}\!\big)$
. Since such an
$z=\big(\!\begin{smallmatrix}p & 0\\ 0 & p\end{smallmatrix}\!\big)$
. Since such an
![]() $f$
is supported only on finitely many cosets
$f$
is supported only on finitely many cosets
![]() $K\backslash G$
, we deduce that the map
$K\backslash G$
, we deduce that the map
 $$\begin{eqnarray}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}\overset{S-\unicode[STIX]{x1D707}}{\longrightarrow }\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}\overset{S-\unicode[STIX]{x1D707}}{\longrightarrow }\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}\end{eqnarray}$$
is injective. The quotient is isomorphic to
 $\operatorname{c - Ind}_{ZK}^{G}\overline{\unicode[STIX]{x1D70E}}$
, where
$\operatorname{c - Ind}_{ZK}^{G}\overline{\unicode[STIX]{x1D70E}}$
, where
![]() $z$
acts on
$z$
acts on
![]() $\overline{\unicode[STIX]{x1D70E}}$
by
$\overline{\unicode[STIX]{x1D70E}}$
by
![]() $\unicode[STIX]{x1D707}$
. It follows from the proof of [Reference Barthel and LivnéBL94, Theorem 19] that
$\unicode[STIX]{x1D707}$
. It follows from the proof of [Reference Barthel and LivnéBL94, Theorem 19] that
 $\operatorname{c - Ind}_{ZK}^{G}\overline{\unicode[STIX]{x1D70E}}$
is a free
$\operatorname{c - Ind}_{ZK}^{G}\overline{\unicode[STIX]{x1D70E}}$
is a free
![]() $\mathbb{F}[T]$
-module. Thus, the map
$\mathbb{F}[T]$
-module. Thus, the map
 $$\begin{eqnarray}\operatorname{c - Ind}_{ZK}^{G}\overline{\unicode[STIX]{x1D70E}}\overset{T-\unicode[STIX]{x1D706}}{\longrightarrow }\operatorname{c - Ind}_{ZK}^{G}\overline{\unicode[STIX]{x1D70E}}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{c - Ind}_{ZK}^{G}\overline{\unicode[STIX]{x1D70E}}\overset{T-\unicode[STIX]{x1D706}}{\longrightarrow }\operatorname{c - Ind}_{ZK}^{G}\overline{\unicode[STIX]{x1D70E}}\end{eqnarray}$$
is injective and the sequence
 $S-\unicode[STIX]{x1D707},T-\unicode[STIX]{x1D706}$
is regular on
$S-\unicode[STIX]{x1D707},T-\unicode[STIX]{x1D706}$
is regular on
 $\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
, as required.◻
$\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
, as required.◻
Lemma 4.11. Let
![]() $\mathfrak{m}$
be a maximal ideal of
$\mathfrak{m}$
be a maximal ideal of
![]() ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
. Then
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
. Then
 $$\begin{eqnarray}\text{Ext}_{G}^{i}(\unicode[STIX]{x1D705}(\mathfrak{m})\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee })=0,\quad \forall i\geqslant 1,\end{eqnarray}$$
$$\begin{eqnarray}\text{Ext}_{G}^{i}(\unicode[STIX]{x1D705}(\mathfrak{m})\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee })=0,\quad \forall i\geqslant 1,\end{eqnarray}$$
where the
![]() $\text{Ext}$
-groups are computed in
$\text{Ext}$
-groups are computed in
 $\text{Mod}_{G}^{\text{sm}}({\mathcal{O}})$
.
$\text{Mod}_{G}^{\text{sm}}({\mathcal{O}})$
.
Proof. We first prove that
 $\text{Ext}_{G}^{i}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee })=0$
for all
$\text{Ext}_{G}^{i}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee })=0$
for all
![]() $i\geqslant 1$
. Let
$i\geqslant 1$
. Let
 $M_{\infty }^{\vee }{\hookrightarrow}J^{\bullet }$
be an injective resolution of
$M_{\infty }^{\vee }{\hookrightarrow}J^{\bullet }$
be an injective resolution of
![]() $M_{\infty }^{\vee }$
in
$M_{\infty }^{\vee }$
in
 $\text{Mod}_{G}^{\text{sm}}({\mathcal{O}})$
. Since
$\text{Mod}_{G}^{\text{sm}}({\mathcal{O}})$
. Since
 $$\begin{eqnarray}\operatorname{Hom}_{K}(\unicode[STIX]{x1D70F},J|_{K})\cong \operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70F},J)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{K}(\unicode[STIX]{x1D70F},J|_{K})\cong \operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70F},J)\end{eqnarray}$$
and the functor
![]() $\operatorname{c - Ind}_{K}^{G}$
is exact, the restriction of an injective object in
$\operatorname{c - Ind}_{K}^{G}$
is exact, the restriction of an injective object in
 $\text{Mod}_{G}^{\text{sm}}({\mathcal{O}})$
to
$\text{Mod}_{G}^{\text{sm}}({\mathcal{O}})$
to
![]() $K$
is injective in
$K$
is injective in
 $\text{Mod}_{K}^{\text{sm}}({\mathcal{O}})$
. Thus,
$\text{Mod}_{K}^{\text{sm}}({\mathcal{O}})$
. Thus,
![]() $(J^{\bullet })|_{K}$
is an injective resolution of
$(J^{\bullet })|_{K}$
is an injective resolution of
![]() $M_{\infty }^{\vee }|_{K}$
in
$M_{\infty }^{\vee }|_{K}$
in
 $\text{Mod}_{K}^{\text{sm}}({\mathcal{O}})$
. Since
$\text{Mod}_{K}^{\text{sm}}({\mathcal{O}})$
. Since
 $\operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},J^{\bullet })\cong \operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70E}},(J^{\bullet })|_{K})$
, we conclude that we have natural isomorphisms
$\operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},J^{\bullet })\cong \operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70E}},(J^{\bullet })|_{K})$
, we conclude that we have natural isomorphisms
 $$\begin{eqnarray}\text{Ext}_{G}^{i}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee })\cong \text{Ext}_{K}^{i}(\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee }),\quad \forall i\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}\text{Ext}_{G}^{i}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee })\cong \text{Ext}_{K}^{i}(\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee }),\quad \forall i\geqslant 0.\end{eqnarray}$$
Since
![]() $M_{\infty }$
is a projective
$M_{\infty }$
is a projective
![]() ${\mathcal{O}}[[K]]$
-module by (AA2),
${\mathcal{O}}[[K]]$
-module by (AA2),
![]() $M_{\infty }^{\vee }$
is injective in
$M_{\infty }^{\vee }$
is injective in
 $\text{Mod}_{K}^{\text{sm}}({\mathcal{O}})$
and thus the
$\text{Mod}_{K}^{\text{sm}}({\mathcal{O}})$
and thus the
![]() $\text{Ext}$
-groups vanish, as claimed.
$\text{Ext}$
-groups vanish, as claimed.
Let
 $F_{\bullet }{\twoheadrightarrow}\unicode[STIX]{x1D705}(\mathfrak{m})$
be a resolution of
$F_{\bullet }{\twoheadrightarrow}\unicode[STIX]{x1D705}(\mathfrak{m})$
be a resolution of
![]() $\unicode[STIX]{x1D705}(\mathfrak{m})$
by finite free
$\unicode[STIX]{x1D705}(\mathfrak{m})$
by finite free
![]() ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
-modules. Lemma 4.10 implies that the complex
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
-modules. Lemma 4.10 implies that the complex
 $F_{\bullet }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
is a resolution of
$F_{\bullet }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
is a resolution of
 $\unicode[STIX]{x1D705}(\mathfrak{m})\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
by acyclic objects for the functor
$\unicode[STIX]{x1D705}(\mathfrak{m})\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
by acyclic objects for the functor
 $\operatorname{Hom}_{G}(\ast ,M_{\infty }^{\vee })$
. We conclude that the cohomology of the complex
$\operatorname{Hom}_{G}(\ast ,M_{\infty }^{\vee })$
. We conclude that the cohomology of the complex
 $$\begin{eqnarray}\operatorname{Hom}_{G}(F_{\bullet }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee })\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{G}(F_{\bullet }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee })\end{eqnarray}$$
computes the groups
 $\text{Ext}_{G}^{i}(\unicode[STIX]{x1D705}(\mathfrak{m})\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee })$
. We may think of the transition maps in
$\text{Ext}_{G}^{i}(\unicode[STIX]{x1D705}(\mathfrak{m})\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee })$
. We may think of the transition maps in
![]() $F_{\bullet }$
as matrices with entries in
$F_{\bullet }$
as matrices with entries in
![]() ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
. The functor
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
. The functor
 $\operatorname{Hom}_{G}(\ast ,M_{\infty }^{\vee })^{\vee }$
transposes these matrices twice; thus, we get an isomorphism of complexes:
$\operatorname{Hom}_{G}(\ast ,M_{\infty }^{\vee })^{\vee }$
transposes these matrices twice; thus, we get an isomorphism of complexes:
 $$\begin{eqnarray}\operatorname{Hom}_{G}(F_{\bullet }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee })^{\vee }\cong F_{\bullet }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee })^{\vee }\cong F_{\bullet }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}M_{\infty }(\overline{\unicode[STIX]{x1D70E}}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{G}(F_{\bullet }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee })^{\vee }\cong F_{\bullet }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee })^{\vee }\cong F_{\bullet }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}M_{\infty }(\overline{\unicode[STIX]{x1D70E}}).\end{eqnarray}$$
The above isomorphism induces a natural isomorphism
 $$\begin{eqnarray}(\text{Ext}_{G}^{i}(\unicode[STIX]{x1D705}(\mathfrak{m})\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee }))^{\vee }\cong \operatorname{Tor}_{i}^{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}(\unicode[STIX]{x1D705}(\mathfrak{m}),M_{\infty }(\overline{\unicode[STIX]{x1D70E}})),\quad \forall i\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}(\text{Ext}_{G}^{i}(\unicode[STIX]{x1D705}(\mathfrak{m})\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},M_{\infty }^{\vee }))^{\vee }\cong \operatorname{Tor}_{i}^{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}(\unicode[STIX]{x1D705}(\mathfrak{m}),M_{\infty }(\overline{\unicode[STIX]{x1D70E}})),\quad \forall i\geqslant 0.\end{eqnarray}$$
The isomorphism implies the assertion, as
![]() $M_{\infty }(\overline{\unicode[STIX]{x1D70E}})$
is a flat
$M_{\infty }(\overline{\unicode[STIX]{x1D70E}})$
is a flat
![]() ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
-module by Proposition 4.2(2).◻
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
-module by Proposition 4.2(2).◻
Lemma 4.12. Let
 $y:{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})\rightarrow \mathbb{F}^{\prime }$
be a homomorphism of
$y:{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})\rightarrow \mathbb{F}^{\prime }$
be a homomorphism of
![]() $\mathbb{F}$
-algebras, where
$\mathbb{F}$
-algebras, where
![]() $\mathbb{F}^{\prime }$
is a finite field extension of
$\mathbb{F}^{\prime }$
is a finite field extension of
![]() $\mathbb{F}$
. Let
$\mathbb{F}$
. Let
 $\unicode[STIX]{x1D706}^{\prime }:=\mathbb{F}^{\prime }\;\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),y}\;\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
and let
$\unicode[STIX]{x1D706}^{\prime }:=\mathbb{F}^{\prime }\;\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),y}\;\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
and let
![]() $\unicode[STIX]{x1D706}$
be an absolutely irreducible
$\unicode[STIX]{x1D706}$
be an absolutely irreducible
![]() $\mathbb{F}$
-representation of
$\mathbb{F}$
-representation of
![]() $G$
, which is either a principal series or supersingular. If
$G$
, which is either a principal series or supersingular. If
![]() $\unicode[STIX]{x1D706}$
is a subquotient of
$\unicode[STIX]{x1D706}$
is a subquotient of
![]() $\unicode[STIX]{x1D706}^{\prime }$
, then
$\unicode[STIX]{x1D706}^{\prime }$
, then
![]() $\unicode[STIX]{x1D706}^{\prime }$
is isomorphic to a direct sum of finitely many copies of
$\unicode[STIX]{x1D706}^{\prime }$
is isomorphic to a direct sum of finitely many copies of
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
Proof. In the course of the proof we will use the following fact repeatedly: if
![]() $A$
and
$A$
and
![]() $B$
are
$B$
are
![]() $\mathbb{F}$
-representations of
$\mathbb{F}$
-representations of
![]() $G$
and
$G$
and
![]() $A$
is finitely generated as an
$A$
is finitely generated as an
![]() $\mathbb{F}[G]$
-module, then
$\mathbb{F}[G]$
-module, then
 $$\begin{eqnarray}\operatorname{Hom}_{G}(A,B)\otimes _{\mathbb{F}}\overline{\mathbb{F}}\cong \operatorname{Hom}_{G}(A\otimes _{\mathbb{F}}\overline{\mathbb{F}},B\otimes _{\mathbb{F}}\overline{\mathbb{F}}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{G}(A,B)\otimes _{\mathbb{F}}\overline{\mathbb{F}}\cong \operatorname{Hom}_{G}(A\otimes _{\mathbb{F}}\overline{\mathbb{F}},B\otimes _{\mathbb{F}}\overline{\mathbb{F}}),\end{eqnarray}$$
where
![]() $\overline{\mathbb{F}}$
denotes the algebraic closure of
$\overline{\mathbb{F}}$
denotes the algebraic closure of
![]() $\mathbb{F}$
; see [Reference PaškūnasPaš13, Lemma 5.1]. Then
$\mathbb{F}$
; see [Reference PaškūnasPaš13, Lemma 5.1]. Then
 $$\begin{eqnarray}\overline{\mathbb{F}}\otimes _{\mathbb{F}}\unicode[STIX]{x1D706}^{\prime }\cong \overline{\mathbb{F}}\otimes _{\mathbb{ F}}\mathbb{F}^{\prime }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),y}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}\cong \bigoplus _{\unicode[STIX]{x1D704}:\mathbb{F}^{\prime }\rightarrow \overline{\mathbb{F}}}\overline{\mathbb{F}}\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),\unicode[STIX]{x1D704}\circ y}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},\end{eqnarray}$$
$$\begin{eqnarray}\overline{\mathbb{F}}\otimes _{\mathbb{F}}\unicode[STIX]{x1D706}^{\prime }\cong \overline{\mathbb{F}}\otimes _{\mathbb{ F}}\mathbb{F}^{\prime }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),y}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}\cong \bigoplus _{\unicode[STIX]{x1D704}:\mathbb{F}^{\prime }\rightarrow \overline{\mathbb{F}}}\overline{\mathbb{F}}\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),\unicode[STIX]{x1D704}\circ y}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},\end{eqnarray}$$
where the sum is taken over
![]() $\mathbb{F}$
-algebra homomorphisms
$\mathbb{F}$
-algebra homomorphisms
 $\unicode[STIX]{x1D704}:\mathbb{F}^{\prime }\rightarrow \overline{\mathbb{F}}$
. By the classification theorems of Barthel and Livné [Reference Barthel and LivnéBL94] and Breuil [Reference BreuilBre03a], each representation
$\unicode[STIX]{x1D704}:\mathbb{F}^{\prime }\rightarrow \overline{\mathbb{F}}$
. By the classification theorems of Barthel and Livné [Reference Barthel and LivnéBL94] and Breuil [Reference BreuilBre03a], each representation
 $\overline{\mathbb{F}}\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),\unicode[STIX]{x1D704}\circ y}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
is irreducible, an extension of a special series by a character or an extension of a character by a special series. Since
$\overline{\mathbb{F}}\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),\unicode[STIX]{x1D704}\circ y}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}$
is irreducible, an extension of a special series by a character or an extension of a character by a special series. Since
![]() $\unicode[STIX]{x1D706}$
is a subquotient of
$\unicode[STIX]{x1D706}$
is a subquotient of
![]() $\unicode[STIX]{x1D706}^{\prime }$
by assumption,
$\unicode[STIX]{x1D706}^{\prime }$
by assumption,
![]() $\unicode[STIX]{x1D706}\otimes _{\mathbb{F}}\overline{\mathbb{F}}$
is a subquotient of
$\unicode[STIX]{x1D706}\otimes _{\mathbb{F}}\overline{\mathbb{F}}$
is a subquotient of
![]() $\unicode[STIX]{x1D706}^{\prime }\otimes _{\mathbb{F}}\overline{\mathbb{F}}$
and, since
$\unicode[STIX]{x1D706}^{\prime }\otimes _{\mathbb{F}}\overline{\mathbb{F}}$
and, since
![]() $\unicode[STIX]{x1D706}$
is neither a special series nor a character, we deduce that
$\unicode[STIX]{x1D706}$
is neither a special series nor a character, we deduce that
 $$\begin{eqnarray}\unicode[STIX]{x1D706}\otimes _{\mathbb{F}}\overline{\mathbb{F}}\cong \overline{\mathbb{F}}\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),\unicode[STIX]{x1D704}\circ y}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}\otimes _{\mathbb{F}}\overline{\mathbb{F}}\cong \overline{\mathbb{F}}\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),\unicode[STIX]{x1D704}\circ y}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}\end{eqnarray}$$
for some embedding
 $\unicode[STIX]{x1D704}:\mathbb{F}^{\prime }{\hookrightarrow}\overline{\mathbb{F}}$
. For every
$\unicode[STIX]{x1D704}:\mathbb{F}^{\prime }{\hookrightarrow}\overline{\mathbb{F}}$
. For every
 $\unicode[STIX]{x1D70F}\in \text{Gal}(\overline{\mathbb{F}}/\mathbb{F})$
, we have
$\unicode[STIX]{x1D70F}\in \text{Gal}(\overline{\mathbb{F}}/\mathbb{F})$
, we have
 $$\begin{eqnarray}\overline{\mathbb{F}}\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),\unicode[STIX]{x1D70F}\circ \unicode[STIX]{x1D704}\circ y}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}\cong \overline{\mathbb{F}}\otimes _{\overline{\mathbb{F}},\unicode[STIX]{x1D70F}}(\overline{\mathbb{F}}\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),\unicode[STIX]{x1D704}\circ y}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}})\cong \overline{\mathbb{F}}\otimes _{\overline{\mathbb{F}},\unicode[STIX]{x1D70F}}(\overline{\mathbb{F}}\otimes _{\mathbb{F}}\unicode[STIX]{x1D706})\cong \overline{\mathbb{F}}\otimes _{\mathbb{F}}\unicode[STIX]{x1D706}.\end{eqnarray}$$
$$\begin{eqnarray}\overline{\mathbb{F}}\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),\unicode[STIX]{x1D70F}\circ \unicode[STIX]{x1D704}\circ y}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}\cong \overline{\mathbb{F}}\otimes _{\overline{\mathbb{F}},\unicode[STIX]{x1D70F}}(\overline{\mathbb{F}}\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),\unicode[STIX]{x1D704}\circ y}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}})\cong \overline{\mathbb{F}}\otimes _{\overline{\mathbb{F}},\unicode[STIX]{x1D70F}}(\overline{\mathbb{F}}\otimes _{\mathbb{F}}\unicode[STIX]{x1D706})\cong \overline{\mathbb{F}}\otimes _{\mathbb{F}}\unicode[STIX]{x1D706}.\end{eqnarray}$$
Hence, all the summands in (4.14) are isomorphic to
![]() $\unicode[STIX]{x1D706}\otimes _{\mathbb{F}}\overline{\mathbb{F}}$
. It follows from (4.13) that
$\unicode[STIX]{x1D706}\otimes _{\mathbb{F}}\overline{\mathbb{F}}$
. It follows from (4.13) that
![]() $\unicode[STIX]{x1D706}^{\prime }$
is isomorphic to a direct sum of copies of
$\unicode[STIX]{x1D706}^{\prime }$
is isomorphic to a direct sum of copies of
![]() $\unicode[STIX]{x1D706}$
, as required.◻
$\unicode[STIX]{x1D706}$
, as required.◻
Theorem 4.15.
![]() $M_{\infty }^{\vee }$
is an injective object in
$M_{\infty }^{\vee }$
is an injective object in
 $\text{Mod}_{G}^{\text{l.adm}}({\mathcal{O}})$
.
$\text{Mod}_{G}^{\text{l.adm}}({\mathcal{O}})$
.
Proof. Let
 $M_{\infty }^{\vee }{\hookrightarrow}J$
be an injective envelope of
$M_{\infty }^{\vee }{\hookrightarrow}J$
be an injective envelope of
![]() $M_{\infty }^{\vee }$
in
$M_{\infty }^{\vee }$
in
 $\text{Mod}_{G}^{\text{l.adm}}({\mathcal{O}})$
. Lemma 4.6 shows that the composition
$\text{Mod}_{G}^{\text{l.adm}}({\mathcal{O}})$
. Lemma 4.6 shows that the composition
 $\operatorname{soc}_{G}M_{\infty }^{\vee }{\hookrightarrow}M_{\infty }^{\vee }{\hookrightarrow}J$
is an essential monomorphism and thus induces an isomorphism between
$\operatorname{soc}_{G}M_{\infty }^{\vee }{\hookrightarrow}M_{\infty }^{\vee }{\hookrightarrow}J$
is an essential monomorphism and thus induces an isomorphism between
 $\operatorname{soc}_{G}M_{\infty }^{\vee }$
and
$\operatorname{soc}_{G}M_{\infty }^{\vee }$
and
![]() $\operatorname{soc}_{G}J$
. Proposition 4.2(3) shows that
$\operatorname{soc}_{G}J$
. Proposition 4.2(3) shows that
 $\operatorname{soc}_{G}M_{\infty }^{\vee }$
, and thus also
$\operatorname{soc}_{G}M_{\infty }^{\vee }$
, and thus also
![]() $\operatorname{soc}_{G}J$
, is isomorphic to a direct sum of copies of the representation
$\operatorname{soc}_{G}J$
, is isomorphic to a direct sum of copies of the representation
![]() $\unicode[STIX]{x1D70B}$
associated to
$\unicode[STIX]{x1D70B}$
associated to
![]() $\bar{r}$
via Lemma 2.15(5).
$\bar{r}$
via Lemma 2.15(5).
Let us assume that the quotient
![]() $J/M_{\infty }^{\vee }$
is non-zero; then there is a smooth irreducible
$J/M_{\infty }^{\vee }$
is non-zero; then there is a smooth irreducible
![]() $K$
-subrepresentation
$K$
-subrepresentation
 $\overline{\unicode[STIX]{x1D70E}}\subset J/M_{\infty }^{\vee }$
. Let
$\overline{\unicode[STIX]{x1D70E}}\subset J/M_{\infty }^{\vee }$
. Let
![]() $\unicode[STIX]{x1D705}$
be the
$\unicode[STIX]{x1D705}$
be the
![]() $G$
-subrepresentation of
$G$
-subrepresentation of
![]() $J/M_{\infty }^{\vee }$
generated by
$J/M_{\infty }^{\vee }$
generated by
![]() $\overline{\unicode[STIX]{x1D70E}}$
. Since
$\overline{\unicode[STIX]{x1D70E}}$
. Since
![]() $J/M_{\infty }^{\vee }$
is locally admissible, and
$J/M_{\infty }^{\vee }$
is locally admissible, and
![]() $\overline{\unicode[STIX]{x1D70E}}$
is finitely generated as a
$\overline{\unicode[STIX]{x1D70E}}$
is finitely generated as a
![]() $K$
-representation,
$K$
-representation,
![]() $\unicode[STIX]{x1D705}$
is an admissible representation of
$\unicode[STIX]{x1D705}$
is an admissible representation of
![]() $G$
. Thus,
$G$
. Thus,
 $\operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D705})\cong \operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D705})$
is a finite-dimensional
$\operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D705})\cong \operatorname{Hom}_{K}(\overline{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D705})$
is a finite-dimensional
![]() $\mathbb{F}$
-vector space.
$\mathbb{F}$
-vector space.
Let
![]() $\text{m}$
be any irreducible
$\text{m}$
be any irreducible
![]() ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
-submodule of
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
-submodule of
 $\operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D705})$
. Since
$\operatorname{Hom}_{G}(\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D705})$
. Since
![]() $\text{m}$
is finite dimensional over
$\text{m}$
is finite dimensional over
![]() $\mathbb{F}$
, Schur’s lemma implies that
$\mathbb{F}$
, Schur’s lemma implies that
 $\mathbb{F}^{\prime }:=\text{End}_{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}(\text{m})$
is a finite-dimensional division algebra over
$\mathbb{F}^{\prime }:=\text{End}_{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}(\text{m})$
is a finite-dimensional division algebra over
![]() $\mathbb{F}$
. Since
$\mathbb{F}$
. Since
![]() $\mathbb{F}$
is a finite field, we deduce that
$\mathbb{F}$
is a finite field, we deduce that
![]() $\mathbb{F}^{\prime }$
is a finite field extension of
$\mathbb{F}^{\prime }$
is a finite field extension of
![]() $\mathbb{F}$
. Since
$\mathbb{F}$
. Since
![]() ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
is commutative, we further deduce that
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})$
is commutative, we further deduce that
![]() $\text{m}$
is a one-dimensional
$\text{m}$
is a one-dimensional
![]() $\mathbb{F}^{\prime }$
-vector space and thus obtain a surjective homomorphism of
$\mathbb{F}^{\prime }$
-vector space and thus obtain a surjective homomorphism of
![]() $\mathbb{F}$
-algebras
$\mathbb{F}$
-algebras
 $y:{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}){\twoheadrightarrow}\mathbb{F}^{\prime }$
. Moreover, by the construction of
$y:{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}){\twoheadrightarrow}\mathbb{F}^{\prime }$
. Moreover, by the construction of
![]() $\text{m}$
, we obtain a non-zero
$\text{m}$
, we obtain a non-zero
![]() $G$
-equivariant map:
$G$
-equivariant map:
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\prime }:=\mathbb{F}^{\prime }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),y}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}\rightarrow \unicode[STIX]{x1D705}\subset J/M_{\infty }^{\vee }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\prime }:=\mathbb{F}^{\prime }\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}}),y}\operatorname{c - Ind}_{K}^{G}\overline{\unicode[STIX]{x1D70E}}\rightarrow \unicode[STIX]{x1D705}\subset J/M_{\infty }^{\vee }.\end{eqnarray}$$
Since
 $\text{Ext}_{G}^{1}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })=0$
by Lemma 4.11, by applying
$\text{Ext}_{G}^{1}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })=0$
by Lemma 4.11, by applying
 $\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },\ast )$
to the exact sequence
$\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },\ast )$
to the exact sequence
 $0\rightarrow M_{\infty }^{\vee }\rightarrow J\rightarrow J/M_{\infty }^{\vee }\rightarrow 0$
, we obtain a short exact sequence
$0\rightarrow M_{\infty }^{\vee }\rightarrow J\rightarrow J/M_{\infty }^{\vee }\rightarrow 0$
, we obtain a short exact sequence
 $$\begin{eqnarray}0\rightarrow \operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })\rightarrow \operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },J)\rightarrow \operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },J/M_{\infty }^{\vee })\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })\rightarrow \operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },J)\rightarrow \operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },J/M_{\infty }^{\vee })\rightarrow 0.\end{eqnarray}$$
Moreover, we know that
 $\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },J/M_{\infty }^{\vee })$
is non-zero. Hence,
$\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },J/M_{\infty }^{\vee })$
is non-zero. Hence,
 $\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },J)$
is non-zero.
$\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },J)$
is non-zero.
Fix a non-zero
![]() $G$
-equivariant map
$G$
-equivariant map
 $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D70B}^{\prime }\rightarrow J$
; then
$\unicode[STIX]{x1D711}:\unicode[STIX]{x1D70B}^{\prime }\rightarrow J$
; then
 $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70B}^{\prime })\cap \operatorname{soc}_{G}J\neq 0$
. Since
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70B}^{\prime })\cap \operatorname{soc}_{G}J\neq 0$
. Since
![]() $\operatorname{soc}_{G}J$
is isomorphic to a direct sum of copies of
$\operatorname{soc}_{G}J$
is isomorphic to a direct sum of copies of
![]() $\unicode[STIX]{x1D70B}$
, we find that
$\unicode[STIX]{x1D70B}$
, we find that
![]() $\unicode[STIX]{x1D70B}$
is an irreducible subquotient of
$\unicode[STIX]{x1D70B}$
is an irreducible subquotient of
![]() $\unicode[STIX]{x1D70B}^{\prime }$
. It follows from Lemma 4.12 that
$\unicode[STIX]{x1D70B}^{\prime }$
. It follows from Lemma 4.12 that
![]() $\unicode[STIX]{x1D70B}^{\prime }$
is then isomorphic to a finite direct sum of copies of
$\unicode[STIX]{x1D70B}^{\prime }$
is then isomorphic to a finite direct sum of copies of
![]() $\unicode[STIX]{x1D70B}$
and so in particular is semisimple. As we have already noted, the map
$\unicode[STIX]{x1D70B}$
and so in particular is semisimple. As we have already noted, the map
 $M_{\infty }^{\vee }{\hookrightarrow}J$
induces an isomorphism
$M_{\infty }^{\vee }{\hookrightarrow}J$
induces an isomorphism
 $\operatorname{soc}_{G}M_{\infty }^{\vee }\cong \operatorname{soc}_{G}J$
and so the map
$\operatorname{soc}_{G}M_{\infty }^{\vee }\cong \operatorname{soc}_{G}J$
and so the map
 $\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })\rightarrow \operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },J)$
is an isomorphism. This implies that
$\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },M_{\infty }^{\vee })\rightarrow \operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },J)$
is an isomorphism. This implies that
 $\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },J/M_{\infty }^{\vee })=0$
, contradicting the assumption
$\operatorname{Hom}_{G}(\unicode[STIX]{x1D70B}^{\prime },J/M_{\infty }^{\vee })=0$
, contradicting the assumption
 $J/M_{\infty }^{\vee }\neq 0$
. Hence,
$J/M_{\infty }^{\vee }\neq 0$
. Hence,
 $M_{\infty }^{\vee }=J$
is injective, as required.◻
$M_{\infty }^{\vee }=J$
is injective, as required.◻
4.16 Removing the patching variables
We now show that we can pass from
![]() $M_{\infty }$
to an arithmetic action of
$M_{\infty }$
to an arithmetic action of
![]() $R_{p}$
on a projective envelope of
$R_{p}$
on a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
, where as always
$\unicode[STIX]{x1D70B}^{\vee }$
, where as always
![]() $\unicode[STIX]{x1D70B}$
is the representation associated to
$\unicode[STIX]{x1D70B}$
is the representation associated to
![]() $\bar{r}$
via Lemma 2.15(5). Let
$\bar{r}$
via Lemma 2.15(5). Let
![]() $(A,\mathfrak{m})$
be a complete local noetherian
$(A,\mathfrak{m})$
be a complete local noetherian
![]() ${\mathcal{O}}$
-algebra. Let
${\mathcal{O}}$
-algebra. Let
![]() $\mathfrak{C}(A)$
be the Pontryagin dual of
$\mathfrak{C}(A)$
be the Pontryagin dual of
 $\text{Mod}_{G}^{\text{l.adm}}(A)$
, where, for the moment, we allow
$\text{Mod}_{G}^{\text{l.adm}}(A)$
, where, for the moment, we allow
![]() $G$
to be any
$G$
to be any
![]() $p$
-adic analytic group. There is a forgetful functor from
$p$
-adic analytic group. There is a forgetful functor from
![]() $\mathfrak{C}(A)$
to
$\mathfrak{C}(A)$
to
![]() $\mathfrak{C}({\mathcal{O}})$
. In this subsection we prove a structural result about objects
$\mathfrak{C}({\mathcal{O}})$
. In this subsection we prove a structural result about objects
![]() $P$
of
$P$
of
![]() $\mathfrak{C}(A)$
that are projective in
$\mathfrak{C}(A)$
that are projective in
![]() $\mathfrak{C}({\mathcal{O}})$
. We will apply this result to
$\mathfrak{C}({\mathcal{O}})$
. We will apply this result to
 $P=M_{\infty }$
and
$P=M_{\infty }$
and
 $G=\operatorname{GL}_{2}(\mathbb{Q}_{p})$
.
$G=\operatorname{GL}_{2}(\mathbb{Q}_{p})$
.
Lemma 4.17. Let
![]() $(A,\mathfrak{m})$
be a complete local noetherian
$(A,\mathfrak{m})$
be a complete local noetherian
![]() $\mathbb{F}$
-algebra with residue field
$\mathbb{F}$
-algebra with residue field
![]() $\mathbb{F}$
. Let
$\mathbb{F}$
. Let
 $P\in \mathfrak{C}(A)$
be such that
$P\in \mathfrak{C}(A)$
be such that
![]() $P$
is projective in
$P$
is projective in
![]() $\mathfrak{C}(\mathbb{F})$
and the map
$\mathfrak{C}(\mathbb{F})$
and the map
 $P{\twoheadrightarrow}\operatorname{cosoc}_{\mathfrak{C}(\mathbb{F})}P$
is essential. Assume that all irreducible subquotients of
$P{\twoheadrightarrow}\operatorname{cosoc}_{\mathfrak{C}(\mathbb{F})}P$
is essential. Assume that all irreducible subquotients of
 $\operatorname{cosoc}_{\mathfrak{C}(\mathbb{F})}P$
are isomorphic to some given object
$\operatorname{cosoc}_{\mathfrak{C}(\mathbb{F})}P$
are isomorphic to some given object
![]() $S$
, for which
$S$
, for which
 $\text{End}_{\mathfrak{C}(\mathbb{F})}(S)=\mathbb{F}$
. If
$\text{End}_{\mathfrak{C}(\mathbb{F})}(S)=\mathbb{F}$
. If
 $\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(P,S)^{\vee }$
is a free
$\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(P,S)^{\vee }$
is a free
![]() $A$
-module of rank
$A$
-module of rank
![]() $1$
, then there is an isomorphism
$1$
, then there is an isomorphism
 $A\operatorname{⊗̂}_{\mathbb{F}}\operatorname{Proj}(S)\cong P$
in
$A\operatorname{⊗̂}_{\mathbb{F}}\operatorname{Proj}(S)\cong P$
in
![]() $\mathfrak{C}(A)$
, where
$\mathfrak{C}(A)$
, where
 $\operatorname{Proj}(S){\twoheadrightarrow}S$
is a projective envelope of
$\operatorname{Proj}(S){\twoheadrightarrow}S$
is a projective envelope of
![]() $S$
in
$S$
in
![]() $\mathfrak{C}(\mathbb{F})$
.
$\mathfrak{C}(\mathbb{F})$
.
Proof. The assumption on the cosocle of
![]() $P$
implies that
$P$
implies that
 $(\operatorname{cosoc}P)^{\vee }$
is isomorphic to a direct sum of copies of
$(\operatorname{cosoc}P)^{\vee }$
is isomorphic to a direct sum of copies of
 $\unicode[STIX]{x1D706}:=S^{\vee }$
. This means that we have natural isomorphisms:
$\unicode[STIX]{x1D706}:=S^{\vee }$
. This means that we have natural isomorphisms:
 $$\begin{eqnarray}(\operatorname{cosoc}P)^{\vee }\cong \unicode[STIX]{x1D706}\otimes _{\mathbb{ F}}\operatorname{Hom}_{G}(\unicode[STIX]{x1D706},(\operatorname{cosoc}P)^{\vee })\cong \unicode[STIX]{x1D706}\otimes _{\mathbb{ F}}\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{cosoc}P,S).\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{cosoc}P)^{\vee }\cong \unicode[STIX]{x1D706}\otimes _{\mathbb{ F}}\operatorname{Hom}_{G}(\unicode[STIX]{x1D706},(\operatorname{cosoc}P)^{\vee })\cong \unicode[STIX]{x1D706}\otimes _{\mathbb{ F}}\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{cosoc}P,S).\end{eqnarray}$$
Taking Pontryagin duals, we get a natural isomorphism in
![]() $\mathfrak{C}(\mathbb{F})$
:
$\mathfrak{C}(\mathbb{F})$
:
 $$\begin{eqnarray}\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{cosoc}P,S)^{\vee }\operatorname{⊗̂}_{\mathbb{ F}}S\cong \operatorname{cosoc}P.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{cosoc}P,S)^{\vee }\operatorname{⊗̂}_{\mathbb{ F}}S\cong \operatorname{cosoc}P.\end{eqnarray}$$
Since the isomorphism is natural, it is an isomorphism in
![]() $\mathfrak{C}(A)$
with the trivial action of
$\mathfrak{C}(A)$
with the trivial action of
![]() $A$
on
$A$
on
![]() $S$
. Hence, we get a surjection in
$S$
. Hence, we get a surjection in
![]() $\mathfrak{C}(A)$
:
$\mathfrak{C}(A)$
:
 $$\begin{eqnarray}P{\twoheadrightarrow}\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{cosoc}P,S)^{\vee }\operatorname{⊗̂}_{\mathbb{ F}}S.\end{eqnarray}$$
$$\begin{eqnarray}P{\twoheadrightarrow}\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{cosoc}P,S)^{\vee }\operatorname{⊗̂}_{\mathbb{ F}}S.\end{eqnarray}$$
The surjection
 $\operatorname{Proj}(S){\twoheadrightarrow}S$
induces a surjection
$\operatorname{Proj}(S){\twoheadrightarrow}S$
induces a surjection
 $$\begin{eqnarray}\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{cosoc}P,S)^{\vee }\operatorname{⊗̂}_{\mathbb{ F}}\operatorname{Proj}(S){\twoheadrightarrow}\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{cosoc}P,S)^{\vee }\operatorname{⊗̂}_{\mathbb{ F}}S,\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{cosoc}P,S)^{\vee }\operatorname{⊗̂}_{\mathbb{ F}}\operatorname{Proj}(S){\twoheadrightarrow}\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{cosoc}P,S)^{\vee }\operatorname{⊗̂}_{\mathbb{ F}}S,\end{eqnarray}$$
with trivial
![]() $A$
-action on
$A$
-action on
 $\operatorname{Proj}(S)$
. The source of this surjection is projective in
$\operatorname{Proj}(S)$
. The source of this surjection is projective in
![]() $\mathfrak{C}(A)$
, since in general for a compact
$\mathfrak{C}(A)$
, since in general for a compact
![]() $A$
-module
$A$
-module
![]() $\text{m}$
,
$\text{m}$
,
 $$\begin{eqnarray}\operatorname{Hom}_{\mathfrak{C}(A)}(\text{m}\operatorname{⊗̂}_{\mathbb{F}}\operatorname{Proj}(S),-)\cong \operatorname{Hom}_{A}(\text{m},\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{Proj}(S),-)),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{\mathfrak{C}(A)}(\text{m}\operatorname{⊗̂}_{\mathbb{F}}\operatorname{Proj}(S),-)\cong \operatorname{Hom}_{A}(\text{m},\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{Proj}(S),-)),\end{eqnarray}$$
and
 $\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{cosoc}P,S)^{\vee }=\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(P,S)^{\vee }$
is projective since it is a free
$\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{cosoc}P,S)^{\vee }=\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(P,S)^{\vee }$
is projective since it is a free
![]() $A$
-module of rank
$A$
-module of rank
![]() $1$
.
$1$
.
Hence, there is a map
 $\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{cosoc}P,S)^{\vee }\operatorname{⊗̂}_{\mathbb{F}}\operatorname{Proj}(S)\rightarrow P$
in
$\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(\operatorname{cosoc}P,S)^{\vee }\operatorname{⊗̂}_{\mathbb{F}}\operatorname{Proj}(S)\rightarrow P$
in
![]() $\mathfrak{C}(A)$
such that the diagram
$\mathfrak{C}(A)$
such that the diagram

commutes. If we forget the
![]() $A$
-action, then we obtain a map in
$A$
-action, then we obtain a map in
![]() $\mathfrak{C}(\mathbb{F})$
between projective objects, which induces an isomorphism on their cosocles. Hence, the map is an isomorphism in
$\mathfrak{C}(\mathbb{F})$
between projective objects, which induces an isomorphism on their cosocles. Hence, the map is an isomorphism in
![]() $\mathfrak{C}(\mathbb{F})$
and hence also an isomorphism in
$\mathfrak{C}(\mathbb{F})$
and hence also an isomorphism in
![]() $\mathfrak{C}(A)$
.◻
$\mathfrak{C}(A)$
.◻
Proposition 4.19. Let
![]() $A$
be a complete local noetherian
$A$
be a complete local noetherian
![]() ${\mathcal{O}}$
-algebra with residue field
${\mathcal{O}}$
-algebra with residue field
![]() $\mathbb{F}$
, that is
$\mathbb{F}$
, that is
![]() ${\mathcal{O}}$
-flat. Let
${\mathcal{O}}$
-flat. Let
![]() $P$
in
$P$
in
![]() $\mathfrak{C}(A)$
be such that
$\mathfrak{C}(A)$
be such that
![]() $P$
is projective in
$P$
is projective in
![]() $\mathfrak{C}({\mathcal{O}})$
and the map
$\mathfrak{C}({\mathcal{O}})$
and the map
 $P{\twoheadrightarrow}\operatorname{cosoc}_{\mathfrak{C}({\mathcal{O}})}P$
is essential. Assume that all the irreducible subquotients of
$P{\twoheadrightarrow}\operatorname{cosoc}_{\mathfrak{C}({\mathcal{O}})}P$
is essential. Assume that all the irreducible subquotients of
 $\operatorname{cosoc}_{\mathfrak{C}({\mathcal{O}})}P$
are isomorphic to
$\operatorname{cosoc}_{\mathfrak{C}({\mathcal{O}})}P$
are isomorphic to
![]() $S$
, and
$S$
, and
 $\text{End}_{\mathfrak{C}({\mathcal{O}})}(S)=\mathbb{F}$
. If
$\text{End}_{\mathfrak{C}({\mathcal{O}})}(S)=\mathbb{F}$
. If
 $\operatorname{Hom}_{\mathfrak{C}({\mathcal{O}})}(P,S)^{\vee }$
is a free
$\operatorname{Hom}_{\mathfrak{C}({\mathcal{O}})}(P,S)^{\vee }$
is a free
![]() $A/\unicode[STIX]{x1D71B}A$
-module of rank
$A/\unicode[STIX]{x1D71B}A$
-module of rank
![]() $1$
, then there is an isomorphism in
$1$
, then there is an isomorphism in
![]() $\mathfrak{C}(A)$
:
$\mathfrak{C}(A)$
:
 $$\begin{eqnarray}A\operatorname{⊗̂}_{{\mathcal{O}}}\operatorname{Proj}(S)\cong P,\end{eqnarray}$$
$$\begin{eqnarray}A\operatorname{⊗̂}_{{\mathcal{O}}}\operatorname{Proj}(S)\cong P,\end{eqnarray}$$
where
 $\operatorname{Proj}(S){\twoheadrightarrow}S$
is a projective envelope of
$\operatorname{Proj}(S){\twoheadrightarrow}S$
is a projective envelope of
![]() $S$
in
$S$
in
![]() $\mathfrak{C}({\mathcal{O}})$
.
$\mathfrak{C}({\mathcal{O}})$
.
Proof. A special case of Lemma 4.17 implies that the reductions of
 $A\operatorname{⊗̂}_{{\mathcal{O}}}\operatorname{Proj}(S)$
and
$A\operatorname{⊗̂}_{{\mathcal{O}}}\operatorname{Proj}(S)$
and
![]() $P$
modulo
$P$
modulo
![]() $\unicode[STIX]{x1D71B}$
are isomorphic in
$\unicode[STIX]{x1D71B}$
are isomorphic in
![]() $\mathfrak{C}(\mathbb{F})$
. Arguing as in (4.18), we deduce that
$\mathfrak{C}(\mathbb{F})$
. Arguing as in (4.18), we deduce that
 $A\operatorname{⊗̂}_{{\mathcal{O}}}\operatorname{Proj}(S)$
is projective in
$A\operatorname{⊗̂}_{{\mathcal{O}}}\operatorname{Proj}(S)$
is projective in
![]() $\mathfrak{C}(A)$
. Thus, there is a map in
$\mathfrak{C}(A)$
. Thus, there is a map in
![]() $\mathfrak{C}(A)$
,
$\mathfrak{C}(A)$
,
 $$\begin{eqnarray}A\operatorname{⊗̂}_{{\mathcal{O}}}\operatorname{Proj}(S)\rightarrow P,\end{eqnarray}$$
$$\begin{eqnarray}A\operatorname{⊗̂}_{{\mathcal{O}}}\operatorname{Proj}(S)\rightarrow P,\end{eqnarray}$$
which is an isomorphism modulo
![]() $\unicode[STIX]{x1D71B}$
. If
$\unicode[STIX]{x1D71B}$
. If
![]() $V$
is a cokernel of this map, then
$V$
is a cokernel of this map, then
 $V/\unicode[STIX]{x1D71B}V=0$
, and Nakayama’s lemma for compact
$V/\unicode[STIX]{x1D71B}V=0$
, and Nakayama’s lemma for compact
![]() ${\mathcal{O}}$
-modules implies that
${\mathcal{O}}$
-modules implies that
![]() $V=0$
. Since
$V=0$
. Since
![]() $P$
is projective, this surjection must split. Since the map is an isomorphism modulo
$P$
is projective, this surjection must split. Since the map is an isomorphism modulo
![]() $\unicode[STIX]{x1D71B}$
, if
$\unicode[STIX]{x1D71B}$
, if
![]() $U$
is the kernel of this map then the decomposition
$U$
is the kernel of this map then the decomposition
 $A\operatorname{⊗̂}_{{\mathcal{O}}}\operatorname{Proj}(S)\cong U\oplus P$
implies that
$A\operatorname{⊗̂}_{{\mathcal{O}}}\operatorname{Proj}(S)\cong U\oplus P$
implies that
 $U/\unicode[STIX]{x1D71B}U=0$
and so
$U/\unicode[STIX]{x1D71B}U=0$
and so
![]() $U=0$
, as required.◻
$U=0$
, as required.◻
Corollary 4.20. Let
![]() $A$
,
$A$
,
![]() $P$
and
$P$
and
![]() $S$
be as in Proposition 4.19. Then, for any
$S$
be as in Proposition 4.19. Then, for any
![]() ${\mathcal{O}}$
-algebra homomorphism
${\mathcal{O}}$
-algebra homomorphism
 $x:A\rightarrow {\mathcal{O}}$
,
$x:A\rightarrow {\mathcal{O}}$
,
 $P\operatorname{⊗̂}_{A,x}{\mathcal{O}}$
is a projective envelope of
$P\operatorname{⊗̂}_{A,x}{\mathcal{O}}$
is a projective envelope of
![]() $S$
in
$S$
in
![]() $\mathfrak{C}({\mathcal{O}})$
.
$\mathfrak{C}({\mathcal{O}})$
.
Proof. It follows from Proposition 4.19 that
 $$\begin{eqnarray}P\operatorname{⊗̂}_{A,x}{\mathcal{O}}\cong (\operatorname{Proj}(S)\operatorname{⊗̂}_{{\mathcal{O}}}A)\operatorname{⊗̂}_{A,x}{\mathcal{O}}\cong \operatorname{Proj}(S).\square\end{eqnarray}$$
$$\begin{eqnarray}P\operatorname{⊗̂}_{A,x}{\mathcal{O}}\cong (\operatorname{Proj}(S)\operatorname{⊗̂}_{{\mathcal{O}}}A)\operatorname{⊗̂}_{A,x}{\mathcal{O}}\cong \operatorname{Proj}(S).\square\end{eqnarray}$$
Remark 4.21. If we replace the assumption in Proposition 4.19 that
 $\operatorname{Hom}_{\mathfrak{C}({\mathcal{O}})}(P,S)^{\vee }$
is a free
$\operatorname{Hom}_{\mathfrak{C}({\mathcal{O}})}(P,S)^{\vee }$
is a free
![]() $A/\unicode[STIX]{x1D71B}A$
-module of rank
$A/\unicode[STIX]{x1D71B}A$
-module of rank
![]() $1$
with the assumption that it is free of rank
$1$
with the assumption that it is free of rank
![]() $n$
, then we have an isomorphism
$n$
, then we have an isomorphism
 $A^{\oplus n}\operatorname{⊗̂}_{{\mathcal{O}}}\operatorname{Proj}(S)\cong P$
in
$A^{\oplus n}\operatorname{⊗̂}_{{\mathcal{O}}}\operatorname{Proj}(S)\cong P$
in
![]() $\mathfrak{C}(A)$
.
$\mathfrak{C}(A)$
.
Indeed, a generalization of Lemma 4.17 to the rank
![]() $n$
case gives an isomorphism in
$n$
case gives an isomorphism in
![]() $\mathfrak{C}(\mathbb{F})$
of
$\mathfrak{C}(\mathbb{F})$
of
 $A^{\oplus n}\operatorname{⊗̂}_{{\mathcal{O}}}\operatorname{Proj}(S)$
and
$A^{\oplus n}\operatorname{⊗̂}_{{\mathcal{O}}}\operatorname{Proj}(S)$
and
![]() $P$
modulo
$P$
modulo
![]() $\unicode[STIX]{x1D71B}$
. (In fact, the statement of Lemma 4.17 can be strengthened as follows: if
$\unicode[STIX]{x1D71B}$
. (In fact, the statement of Lemma 4.17 can be strengthened as follows: if
 $\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(P,S)^{\vee }$
is a projective object in the category of compact
$\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(P,S)^{\vee }$
is a projective object in the category of compact
![]() $A$
-modules, then we have an isomorphism
$A$
-modules, then we have an isomorphism
 $\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(P,S)^{\vee }\operatorname{⊗̂}_{\mathbb{F}}\operatorname{Proj}S\simeq P$
. The key is again the projectivity of the completed tensor product
$\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(P,S)^{\vee }\operatorname{⊗̂}_{\mathbb{F}}\operatorname{Proj}S\simeq P$
. The key is again the projectivity of the completed tensor product
 $\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(P,S)^{\vee }\operatorname{⊗̂}_{\mathbb{F}}\operatorname{Proj}S$
, which follows from our assumption and from (4.18).) We then upgrade the isomorphism modulo
$\operatorname{Hom}_{\mathfrak{C}(\mathbb{F})}(P,S)^{\vee }\operatorname{⊗̂}_{\mathbb{F}}\operatorname{Proj}S$
, which follows from our assumption and from (4.18).) We then upgrade the isomorphism modulo
![]() $\unicode[STIX]{x1D71B}$
to an isomorphism in
$\unicode[STIX]{x1D71B}$
to an isomorphism in
![]() $\mathfrak{C}(A)$
as in the proof of Proposition 4.19, again relying on (4.18).
$\mathfrak{C}(A)$
as in the proof of Proposition 4.19, again relying on (4.18).
We now apply the results above in the special case of
 $P=M_{\infty }$
and
$P=M_{\infty }$
and
 $G=\operatorname{GL}_{2}(\mathbb{Q}_{p})$
.
$G=\operatorname{GL}_{2}(\mathbb{Q}_{p})$
.
Proposition 4.22. Let
 $A={\mathcal{O}}[[x_{1},\ldots ,x_{d}]]$
and choose a homomorphism of local
$A={\mathcal{O}}[[x_{1},\ldots ,x_{d}]]$
and choose a homomorphism of local
![]() ${\mathcal{O}}$
-algebras
${\mathcal{O}}$
-algebras
 $A\rightarrow R_{\infty }$
that induces an isomorphism
$A\rightarrow R_{\infty }$
that induces an isomorphism
 $R_{p}\operatorname{⊗̂}_{{\mathcal{O}}}A\cong R_{\infty }$
. Then there is an isomorphism in
$R_{p}\operatorname{⊗̂}_{{\mathcal{O}}}A\cong R_{\infty }$
. Then there is an isomorphism in
![]() $\mathfrak{C}(A)$
:
$\mathfrak{C}(A)$
:
 $$\begin{eqnarray}M_{\infty }\cong \widetilde{P}\operatorname{⊗̂}_{{\mathcal{O}}}A,\end{eqnarray}$$
$$\begin{eqnarray}M_{\infty }\cong \widetilde{P}\operatorname{⊗̂}_{{\mathcal{O}}}A,\end{eqnarray}$$
where
 $\widetilde{P}{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\vee }$
is a projective envelope of
$\widetilde{P}{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\vee }$
is a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
in
$\unicode[STIX]{x1D70B}^{\vee }$
in
![]() $\mathfrak{C}({\mathcal{O}})$
.
$\mathfrak{C}({\mathcal{O}})$
.
Proof. Theorem 4.15 implies that
![]() $M_{\infty }$
is projective in
$M_{\infty }$
is projective in
![]() $\mathfrak{C}({\mathcal{O}})$
. As we already noted in the proof of that theorem, since
$\mathfrak{C}({\mathcal{O}})$
. As we already noted in the proof of that theorem, since
![]() $M_{\infty }^{\vee }$
is locally admissible, it follows from Lemma 4.6 that
$M_{\infty }^{\vee }$
is locally admissible, it follows from Lemma 4.6 that
 $\operatorname{soc}_{G}M_{\infty }^{\vee }{\hookrightarrow}M_{\infty }^{\vee }$
is essential and hence that
$\operatorname{soc}_{G}M_{\infty }^{\vee }{\hookrightarrow}M_{\infty }^{\vee }$
is essential and hence that
 $M_{\infty }{\twoheadrightarrow}\operatorname{cosoc}_{\mathfrak{C}({\mathcal{O}})}M_{\infty }$
is essential. Proposition 4.2(3) implies that all the irreducible subquotients of
$M_{\infty }{\twoheadrightarrow}\operatorname{cosoc}_{\mathfrak{C}({\mathcal{O}})}M_{\infty }$
is essential. Proposition 4.2(3) implies that all the irreducible subquotients of
 $\operatorname{cosoc}_{\mathfrak{C}({\mathcal{O}})}M_{\infty }$
are isomorphic to
$\operatorname{cosoc}_{\mathfrak{C}({\mathcal{O}})}M_{\infty }$
are isomorphic to
![]() $\unicode[STIX]{x1D70B}^{\vee }$
. It is therefore enough to show that
$\unicode[STIX]{x1D70B}^{\vee }$
. It is therefore enough to show that
 $$\begin{eqnarray}M_{\infty }(\unicode[STIX]{x1D70B}):=\operatorname{Hom}_{\mathfrak{C}({\mathcal{O}})}(M_{\infty },\unicode[STIX]{x1D70B}^{\vee })^{\vee }\cong \operatorname{Hom}_{G}(\unicode[STIX]{x1D70B},M_{\infty }^{\vee })^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}M_{\infty }(\unicode[STIX]{x1D70B}):=\operatorname{Hom}_{\mathfrak{C}({\mathcal{O}})}(M_{\infty },\unicode[STIX]{x1D70B}^{\vee })^{\vee }\cong \operatorname{Hom}_{G}(\unicode[STIX]{x1D70B},M_{\infty }^{\vee })^{\vee }\end{eqnarray}$$
is a free
![]() $A/\unicode[STIX]{x1D71B}$
-module of rank
$A/\unicode[STIX]{x1D71B}$
-module of rank
![]() $1$
, since the assertion then follows from Proposition 4.19.
$1$
, since the assertion then follows from Proposition 4.19.
As in the proof of Proposition 4.2, we have
 $$\begin{eqnarray}M_{\infty }(\unicode[STIX]{x1D70B})\cong \mathbb{F}\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}M_{\infty }(\overline{\unicode[STIX]{x1D70E}})\cong \mathbb{F}\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })}M_{\infty }(\unicode[STIX]{x1D70E}^{\circ }).\end{eqnarray}$$
$$\begin{eqnarray}M_{\infty }(\unicode[STIX]{x1D70B})\cong \mathbb{F}\otimes _{{\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})}M_{\infty }(\overline{\unicode[STIX]{x1D70E}})\cong \mathbb{F}\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })}M_{\infty }(\unicode[STIX]{x1D70E}^{\circ }).\end{eqnarray}$$
It follows from Proposition 4.2(1) that
![]() $M_{\infty }(\unicode[STIX]{x1D70B})$
is a free
$M_{\infty }(\unicode[STIX]{x1D70B})$
is a free
 $\mathbb{F}\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })}R_{\infty }(\unicode[STIX]{x1D70E})$
-module of rank
$\mathbb{F}\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })}R_{\infty }(\unicode[STIX]{x1D70E})$
-module of rank
![]() $1$
. Since
$1$
. Since
 $R_{\infty }(\unicode[STIX]{x1D70E})\cong R_{p}(\unicode[STIX]{x1D70E})\operatorname{⊗̂}_{{\mathcal{O}}}A$
and the map
$R_{\infty }(\unicode[STIX]{x1D70E})\cong R_{p}(\unicode[STIX]{x1D70E})\operatorname{⊗̂}_{{\mathcal{O}}}A$
and the map
 ${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})\rightarrow R_{\infty }(\unicode[STIX]{x1D70E})/\unicode[STIX]{x1D71B}$
factors through
${\mathcal{H}}(\overline{\unicode[STIX]{x1D70E}})\rightarrow R_{\infty }(\unicode[STIX]{x1D70E})/\unicode[STIX]{x1D71B}$
factors through
 $R_{p}(\unicode[STIX]{x1D70E})/\unicode[STIX]{x1D71B}$
by Proposition 4.2(2), we conclude that the map
$R_{p}(\unicode[STIX]{x1D70E})/\unicode[STIX]{x1D71B}$
by Proposition 4.2(2), we conclude that the map
 $A\rightarrow R_{\infty }$
induces an isomorphism
$A\rightarrow R_{\infty }$
induces an isomorphism
 $$\begin{eqnarray}A/\unicode[STIX]{x1D71B}\cong \mathbb{F}\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })}R_{\infty }(\unicode[STIX]{x1D70E}).\end{eqnarray}$$
$$\begin{eqnarray}A/\unicode[STIX]{x1D71B}\cong \mathbb{F}\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })}R_{\infty }(\unicode[STIX]{x1D70E}).\end{eqnarray}$$
(Recall that
 $\mathbb{F}\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })}R_{p}(\unicode[STIX]{x1D70E})/\unicode[STIX]{x1D71B}=\mathbb{F},$
by Lemma 2.15(4).) Thus,
$\mathbb{F}\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })}R_{p}(\unicode[STIX]{x1D70E})/\unicode[STIX]{x1D71B}=\mathbb{F},$
by Lemma 2.15(4).) Thus,
![]() $M_{\infty }(\unicode[STIX]{x1D70B})$
is a free
$M_{\infty }(\unicode[STIX]{x1D70B})$
is a free
![]() $A/\unicode[STIX]{x1D71B}$
-module of rank
$A/\unicode[STIX]{x1D71B}$
-module of rank
![]() $1$
, as required.◻
$1$
, as required.◻
Corollary 4.23. Let
 $A\rightarrow R_{\infty }$
be as in Proposition 4.22 and let
$A\rightarrow R_{\infty }$
be as in Proposition 4.22 and let
 $x:A\rightarrow {\mathcal{O}}$
be a homomorphism of local
$x:A\rightarrow {\mathcal{O}}$
be a homomorphism of local
![]() ${\mathcal{O}}$
-algebras. Then
${\mathcal{O}}$
-algebras. Then
 $M_{\infty }\operatorname{⊗̂}_{A,x}{\mathcal{O}}$
is a projective envelope of
$M_{\infty }\operatorname{⊗̂}_{A,x}{\mathcal{O}}$
is a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
in
$\unicode[STIX]{x1D70B}^{\vee }$
in
![]() $\mathfrak{C}({\mathcal{O}})$
with a continuous
$\mathfrak{C}({\mathcal{O}})$
with a continuous
 $R_{p}\cong R_{\infty }\otimes _{A,x}{\mathcal{O}}$
-action, which commutes with the action of
$R_{p}\cong R_{\infty }\otimes _{A,x}{\mathcal{O}}$
-action, which commutes with the action of
![]() $G$
.
$G$
.
Proof. This follows from Corollary 4.20. ◻
4.24 Uniqueness of arithmetic actions
As in the statement of Proposition 4.22, we let
 $\widetilde{P}{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\vee }$
be a projective envelope of
$\widetilde{P}{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\vee }$
be a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
in
$\unicode[STIX]{x1D70B}^{\vee }$
in
![]() $\mathfrak{C}({\mathcal{O}})$
.
$\mathfrak{C}({\mathcal{O}})$
.
Proposition 4.25.
![]() $\widetilde{P}$
can be endowed with an arithmetic action of
$\widetilde{P}$
can be endowed with an arithmetic action of
![]() $R_{p}$
(in the sense of § 3.1 when
$R_{p}$
(in the sense of § 3.1 when
![]() $d=0$
).
$d=0$
).
Proof. Making any choice of morphism
 $x:A\rightarrow {\mathcal{O}}$
in Corollary 4.23, we obtain an action of
$x:A\rightarrow {\mathcal{O}}$
in Corollary 4.23, we obtain an action of
![]() $R_{p}$
on
$R_{p}$
on
 $M_{\infty }\operatorname{⊗̂}_{A,x}{\mathcal{O}}\cong \widetilde{P}$
. Since the action of
$M_{\infty }\operatorname{⊗̂}_{A,x}{\mathcal{O}}\cong \widetilde{P}$
. Since the action of
![]() $R_{\infty }$
on
$R_{\infty }$
on
![]() $M_{\infty }$
is an arithmetic action, it follows immediately from the definitions that this induced action of
$M_{\infty }$
is an arithmetic action, it follows immediately from the definitions that this induced action of
![]() $R_{p}$
on
$R_{p}$
on
![]() $\widetilde{P}$
is also an arithmetic action.◻
$\widetilde{P}$
is also an arithmetic action.◻
4.26 Recapping capture
We now very briefly recall the theory of capture from [Reference Colmez, Dospinescu and PaškūnasCDP14, § 2.4], specialized to the case of interest to us. We note that analogues of these results are valid for general choices of
![]() $G$
, and in particular do not use either Colmez’s functor or
$G$
, and in particular do not use either Colmez’s functor or
![]() $p$
-adic Langlands correspondence for
$p$
-adic Langlands correspondence for
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
.
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
.
Let
![]() $M$
be a compact linear-topological
$M$
be a compact linear-topological
![]() ${\mathcal{O}}[[K]]$
-module, and let
${\mathcal{O}}[[K]]$
-module, and let
![]() $\{V_{i}\}_{i\in I}$
be a set of continuous
$\{V_{i}\}_{i\in I}$
be a set of continuous
![]() $K$
-representations on finite-dimensional
$K$
-representations on finite-dimensional
![]() $E$
-vector spaces.
$E$
-vector spaces.
Definition 4.27. We say that
![]() $\{V_{i}\}_{i\in I}$
captures
$\{V_{i}\}_{i\in I}$
captures
![]() $M$
if for any proper quotient
$M$
if for any proper quotient
 $M{\twoheadrightarrow}Q$
, we have
$M{\twoheadrightarrow}Q$
, we have
 $\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(M,V_{i}^{\ast })\neq \operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(Q,V_{i}^{\ast })$
for some
$\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(M,V_{i}^{\ast })\neq \operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(Q,V_{i}^{\ast })$
for some
![]() $i\in I$
.
$i\in I$
.
This definition is used only in the proof of the following result.
Proposition 4.28. Suppose that
 $\unicode[STIX]{x1D719}\in \text{End}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P})$
kills each
$\unicode[STIX]{x1D719}\in \text{End}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P})$
kills each
 $\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P},\unicode[STIX]{x1D70E}_{a,b}^{\ast })$
for
$\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P},\unicode[STIX]{x1D70E}_{a,b}^{\ast })$
for
![]() $a\in \mathbb{Z}$
and
$a\in \mathbb{Z}$
and
 $b\in \mathbb{Z}_{{\geqslant}0}$
. Then
$b\in \mathbb{Z}_{{\geqslant}0}$
. Then
![]() $\unicode[STIX]{x1D719}=0$
.
$\unicode[STIX]{x1D719}=0$
.
Proof. Since
![]() $\widetilde{P}$
is projective in
$\widetilde{P}$
is projective in
![]() $\mathfrak{C}({\mathcal{O}})$
, it follows from [Reference Colmez, Dospinescu and PaškūnasCDP14, Proposition 2.12] that the set
$\mathfrak{C}({\mathcal{O}})$
, it follows from [Reference Colmez, Dospinescu and PaškūnasCDP14, Proposition 2.12] that the set
![]() $\{\unicode[STIX]{x1D70E}_{a,b}\}$
captures
$\{\unicode[STIX]{x1D70E}_{a,b}\}$
captures
![]() $\widetilde{P}$
. The result follows from [Reference Colmez, Dospinescu and PaškūnasCDP14, Lemma 2.9] (that is, from an application of the definition of capture to the cokernel of
$\widetilde{P}$
. The result follows from [Reference Colmez, Dospinescu and PaškūnasCDP14, Lemma 2.9] (that is, from an application of the definition of capture to the cokernel of
![]() $\unicode[STIX]{x1D719}$
).◻
$\unicode[STIX]{x1D719}$
).◻
Set
 $M(\unicode[STIX]{x1D70E}^{\circ }):=(\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P},(\unicode[STIX]{x1D70E}^{\circ })^{d}))^{d}$
.
$M(\unicode[STIX]{x1D70E}^{\circ }):=(\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P},(\unicode[STIX]{x1D70E}^{\circ })^{d}))^{d}$
.
Lemma 4.29. Let
 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
with
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
with
![]() $a\in \mathbb{Z}$
and
$a\in \mathbb{Z}$
and
 $b\in \mathbb{Z}_{{\geqslant}0}$
and let
$b\in \mathbb{Z}_{{\geqslant}0}$
and let
![]() $\mathfrak{m}_{y}$
be a maximal ideal of
$\mathfrak{m}_{y}$
be a maximal ideal of
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
. Then
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
. Then
 $\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\neq 0$
if and only if
$\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\neq 0$
if and only if
 $\mathfrak{m}_{x}:=\unicode[STIX]{x1D702}(\mathfrak{m}_{y})R_{p}(\unicode[STIX]{x1D70E})[1/p]$
is a maximal ideal of
$\mathfrak{m}_{x}:=\unicode[STIX]{x1D702}(\mathfrak{m}_{y})R_{p}(\unicode[STIX]{x1D70E})[1/p]$
is a maximal ideal of
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
in the support of
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
in the support of
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
for some (equivalently, any) arithmetic action of
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
for some (equivalently, any) arithmetic action of
![]() $R_{p}$
on
$R_{p}$
on
![]() $\widetilde{P}$
.
$\widetilde{P}$
.
Proof. Since
![]() $M(\unicode[STIX]{x1D70E}^{\circ })$
is a finitely generated
$M(\unicode[STIX]{x1D70E}^{\circ })$
is a finitely generated
![]() $R_{p}(\unicode[STIX]{x1D70E})$
-module and the action of
$R_{p}(\unicode[STIX]{x1D70E})$
-module and the action of
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
on
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
on
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
factors through the action of
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
factors through the action of
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
via
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
via
![]() $\unicode[STIX]{x1D702}$
, we deduce that
$\unicode[STIX]{x1D702}$
, we deduce that
 $\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is a finitely generated
$\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is a finitely generated
 $\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}R_{p}(\unicode[STIX]{x1D70E})[1/p]$
-module. If
$\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}R_{p}(\unicode[STIX]{x1D70E})[1/p]$
-module. If
 $\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\neq 0$
, then we deduce from Lemma 2.12 that
$\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\neq 0$
, then we deduce from Lemma 2.12 that
![]() $\mathfrak{m}_{x}$
is a maximal ideal of
$\mathfrak{m}_{x}$
is a maximal ideal of
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
in the support of
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
in the support of
![]() $M(\unicode[STIX]{x1D70E}^{\circ })$
. Conversely, if
$M(\unicode[STIX]{x1D70E}^{\circ })$
. Conversely, if
![]() $y$
is the image of
$y$
is the image of
![]() $x$
then using Lemma 2.12 we obtain
$x$
then using Lemma 2.12 we obtain
 $\unicode[STIX]{x1D705}(x)=\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}R_{p}(\unicode[STIX]{x1D70E})[1/p]$
and hence:
$\unicode[STIX]{x1D705}(x)=\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}R_{p}(\unicode[STIX]{x1D70E})[1/p]$
and hence:
 $$\begin{eqnarray}\unicode[STIX]{x1D705}(x)\otimes _{R_{p}(\unicode[STIX]{x1D70E})[1/p]}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\cong \unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}M(\unicode[STIX]{x1D70E}^{\circ })[1/p],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}(x)\otimes _{R_{p}(\unicode[STIX]{x1D70E})[1/p]}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\cong \unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}M(\unicode[STIX]{x1D70E}^{\circ })[1/p],\end{eqnarray}$$
which implies that
 $\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is non-zero.◻
$\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is non-zero.◻
Theorem 4.30. There is a unique arithmetic action of
![]() $R_{p}$
on
$R_{p}$
on
![]() $\widetilde{P}$
.
$\widetilde{P}$
.
Proof. The existence of such an action follows from Proposition 4.25.
Let
 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
with
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
with
![]() $a\in \mathbb{Z}$
and
$a\in \mathbb{Z}$
and
 $b\in \mathbb{Z}_{{\geqslant}0}$
. Let
$b\in \mathbb{Z}_{{\geqslant}0}$
. Let
 $y\in \operatorname{m - Spec}{\mathcal{H}}(\unicode[STIX]{x1D70E})$
such that
$y\in \operatorname{m - Spec}{\mathcal{H}}(\unicode[STIX]{x1D70E})$
such that
 $\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\neq 0$
. Lemma 4.29 implies that
$\unicode[STIX]{x1D705}(y)\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E})}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\neq 0$
. Lemma 4.29 implies that
![]() $y$
is the image of
$y$
is the image of
 $x\in \operatorname{m - Spec}R_{p}(\unicode[STIX]{x1D70E})[1/p]$
, which lies in the support of
$x\in \operatorname{m - Spec}R_{p}(\unicode[STIX]{x1D70E})[1/p]$
, which lies in the support of
![]() $M(\unicode[STIX]{x1D70E}^{\circ })$
. Proposition 2.13 implies that
$M(\unicode[STIX]{x1D70E}^{\circ })$
. Proposition 2.13 implies that
 $$\begin{eqnarray}\widehat{M(\unicode[STIX]{x1D70E}^{\circ })[1/p]}_{\mathfrak{m}_{y}}=\widehat{M(\unicode[STIX]{x1D70E}^{\circ })[1/p]}_{\mathfrak{m}_{x}}\end{eqnarray}$$
$$\begin{eqnarray}\widehat{M(\unicode[STIX]{x1D70E}^{\circ })[1/p]}_{\mathfrak{m}_{y}}=\widehat{M(\unicode[STIX]{x1D70E}^{\circ })[1/p]}_{\mathfrak{m}_{x}}\end{eqnarray}$$
as
 $\widehat{R_{p}(\unicode[STIX]{x1D70E})[1/p]}_{\mathfrak{m}_{x}}$
-modules. Moreover, the action of
$\widehat{R_{p}(\unicode[STIX]{x1D70E})[1/p]}_{\mathfrak{m}_{x}}$
-modules. Moreover, the action of
 $\widehat{R_{p}(\unicode[STIX]{x1D70E})[1/p]}_{\mathfrak{m}_{x}}$
on
$\widehat{R_{p}(\unicode[STIX]{x1D70E})[1/p]}_{\mathfrak{m}_{x}}$
on
 $\widehat{M(\unicode[STIX]{x1D70E}^{\circ })[1/p]}_{\mathfrak{m}_{y}}$
does not depend on a given arithmetic action of
$\widehat{M(\unicode[STIX]{x1D70E}^{\circ })[1/p]}_{\mathfrak{m}_{y}}$
does not depend on a given arithmetic action of
![]() $R_{p}$
on
$R_{p}$
on
![]() $\widetilde{P}$
, as it acts via the isomorphism in Proposition 2.13. If
$\widetilde{P}$
, as it acts via the isomorphism in Proposition 2.13. If
![]() $M$
is a finitely generated module over a noetherian ring
$M$
is a finitely generated module over a noetherian ring
![]() $R$
, then we have injections:
$R$
, then we have injections:
 $$\begin{eqnarray}M{\hookrightarrow}\mathop{\prod }_{\mathfrak{m}}M_{\mathfrak{m}}{\hookrightarrow}\mathop{\prod }_{\mathfrak{m}}\widehat{M}_{\mathfrak{m}},\end{eqnarray}$$
$$\begin{eqnarray}M{\hookrightarrow}\mathop{\prod }_{\mathfrak{m}}M_{\mathfrak{m}}{\hookrightarrow}\mathop{\prod }_{\mathfrak{m}}\widehat{M}_{\mathfrak{m}},\end{eqnarray}$$
where the product is taken over all the maximal ideals in
![]() $R$
. In fact, it is enough to take the product over finitely many maximal ideals: if
$R$
. In fact, it is enough to take the product over finitely many maximal ideals: if
 $\mathfrak{p}_{1},\ldots ,\mathfrak{p}_{n}$
are minimal associated primes of
$\mathfrak{p}_{1},\ldots ,\mathfrak{p}_{n}$
are minimal associated primes of
![]() $M$
, just pick any maximal ideals
$M$
, just pick any maximal ideals
 $\mathfrak{m}_{1}\in V(\mathfrak{p}_{1}),\ldots ,\mathfrak{m}_{n}\in V(\mathfrak{p}_{n})$
. (The second injection follows from [Reference MatsumuraMat89, Theorem 8.9].) This observation applied to
$\mathfrak{m}_{1}\in V(\mathfrak{p}_{1}),\ldots ,\mathfrak{m}_{n}\in V(\mathfrak{p}_{n})$
. (The second injection follows from [Reference MatsumuraMat89, Theorem 8.9].) This observation applied to
 $R=R_{p}(\unicode[STIX]{x1D70E})[1/p]$
and
$R=R_{p}(\unicode[STIX]{x1D70E})[1/p]$
and
 $M=M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
together with Lemma 4.29 implies that we have an injection of
$M=M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
together with Lemma 4.29 implies that we have an injection of
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
-modules:
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
-modules:
 $$\begin{eqnarray}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]{\hookrightarrow}\mathop{\prod }_{y\in \operatorname{m-Spec}{\mathcal{H}}(\unicode[STIX]{x1D70E})}\widehat{M(\unicode[STIX]{x1D70E}^{\circ })[1/p]}_{\mathfrak{m}_{y}}.\end{eqnarray}$$
$$\begin{eqnarray}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]{\hookrightarrow}\mathop{\prod }_{y\in \operatorname{m-Spec}{\mathcal{H}}(\unicode[STIX]{x1D70E})}\widehat{M(\unicode[STIX]{x1D70E}^{\circ })[1/p]}_{\mathfrak{m}_{y}}.\end{eqnarray}$$
Since the map and the action of
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
on the right-hand side are independent of the arithmetic action of
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
on the right-hand side are independent of the arithmetic action of
![]() $R_{p}$
on
$R_{p}$
on
![]() $\widetilde{P}$
, we deduce that the action of
$\widetilde{P}$
, we deduce that the action of
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
on
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
on
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is also independent of the arithmetic action of
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is also independent of the arithmetic action of
![]() $R_{p}$
on
$R_{p}$
on
![]() $\widetilde{P}$
.
$\widetilde{P}$
.
If
 $\unicode[STIX]{x1D703}:R_{p}\rightarrow \text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
and
$\unicode[STIX]{x1D703}:R_{p}\rightarrow \text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
and
 $\unicode[STIX]{x1D703}^{\prime }:R_{p}\rightarrow \text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
are two arithmetic actions and
$\unicode[STIX]{x1D703}^{\prime }:R_{p}\rightarrow \text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
are two arithmetic actions and
![]() $r\in R_{p}$
, then it follows from the above that
$r\in R_{p}$
, then it follows from the above that
 $\unicode[STIX]{x1D703}(r)-\unicode[STIX]{x1D703}^{\prime }(r)$
will annihilate
$\unicode[STIX]{x1D703}(r)-\unicode[STIX]{x1D703}^{\prime }(r)$
will annihilate
 $M(\unicode[STIX]{x1D70E}_{a,b}^{\circ })$
for all
$M(\unicode[STIX]{x1D70E}_{a,b}^{\circ })$
for all
![]() $a\in \mathbb{Z}$
and
$a\in \mathbb{Z}$
and
 $b\in \mathbb{Z}_{{\geqslant}0}$
. Proposition 4.28 implies that
$b\in \mathbb{Z}_{{\geqslant}0}$
. Proposition 4.28 implies that
 $\unicode[STIX]{x1D703}(r)=\unicode[STIX]{x1D703}^{\prime }(r)$
.◻
$\unicode[STIX]{x1D703}(r)=\unicode[STIX]{x1D703}^{\prime }(r)$
.◻
Remark 4.31. A different proof of the theorem could be given using [Reference Colmez, Dospinescu and PaškūnasCDP14, Proposition 2.19].
Theorem 4.32. If
 $\widetilde{P}{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\vee }$
is a projective envelope of
$\widetilde{P}{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\vee }$
is a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
in
$\unicode[STIX]{x1D70B}^{\vee }$
in
![]() $\mathfrak{C}({\mathcal{O}})$
equipped with an arithmetic action of
$\mathfrak{C}({\mathcal{O}})$
equipped with an arithmetic action of
![]() $R_{p}$
, then there is an isomorphism in
$R_{p}$
, then there is an isomorphism in
![]() $\mathfrak{C}(R_{\infty })$
$\mathfrak{C}(R_{\infty })$
 $$\begin{eqnarray}\widetilde{P}\operatorname{⊗̂}_{R_{p}}R_{\infty }\cong M_{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{P}\operatorname{⊗̂}_{R_{p}}R_{\infty }\cong M_{\infty }.\end{eqnarray}$$
Proof. Let
 $A={\mathcal{O}}[[x_{1},\ldots ,x_{d}]]$
and choose a homomorphism of local
$A={\mathcal{O}}[[x_{1},\ldots ,x_{d}]]$
and choose a homomorphism of local
![]() ${\mathcal{O}}$
-algebras
${\mathcal{O}}$
-algebras
 $A\rightarrow R_{\infty }$
which induces an isomorphism
$A\rightarrow R_{\infty }$
which induces an isomorphism
 $R_{p}\operatorname{⊗̂}_{{\mathcal{O}}}A\cong R_{\infty }$
. Proposition 4.22 implies that there is an isomorphism
$R_{p}\operatorname{⊗̂}_{{\mathcal{O}}}A\cong R_{\infty }$
. Proposition 4.22 implies that there is an isomorphism
 $\widetilde{P}\operatorname{⊗̂}_{{\mathcal{O}}}A\cong M_{\infty }$
in
$\widetilde{P}\operatorname{⊗̂}_{{\mathcal{O}}}A\cong M_{\infty }$
in
![]() $\mathfrak{C}(A)$
; it is therefore enough to show that this isomorphism is
$\mathfrak{C}(A)$
; it is therefore enough to show that this isomorphism is
![]() $R_{p}$
-linear. Any
$R_{p}$
-linear. Any
![]() ${\mathcal{O}}$
-algebra homomorphism
${\mathcal{O}}$
-algebra homomorphism
 $x:A\rightarrow {\mathcal{O}}$
induces an isomorphism
$x:A\rightarrow {\mathcal{O}}$
induces an isomorphism
 $(\widetilde{P}\operatorname{⊗̂}_{{\mathcal{O}}}A)\operatorname{⊗̂}_{A,x}{\mathcal{O}}\cong M_{\infty }\operatorname{⊗̂}_{A,x}{\mathcal{O}}$
in
$(\widetilde{P}\operatorname{⊗̂}_{{\mathcal{O}}}A)\operatorname{⊗̂}_{A,x}{\mathcal{O}}\cong M_{\infty }\operatorname{⊗̂}_{A,x}{\mathcal{O}}$
in
![]() $\mathfrak{C}({\mathcal{O}})$
. We get two actions of
$\mathfrak{C}({\mathcal{O}})$
. We get two actions of
![]() $R_{p}$
on
$R_{p}$
on
 $M_{\infty }\operatorname{⊗̂}_{A,x}{\mathcal{O}}$
: one of them coming from the action of
$M_{\infty }\operatorname{⊗̂}_{A,x}{\mathcal{O}}$
: one of them coming from the action of
![]() $R_{p}$
on
$R_{p}$
on
![]() $M_{\infty }$
, the other transported by the isomorphism. Both actions are arithmetic: the first one by Proposition 4.25, the second one by assumption. Theorem 4.30 implies that the two actions coincide; thus, the isomorphism
$M_{\infty }$
, the other transported by the isomorphism. Both actions are arithmetic: the first one by Proposition 4.25, the second one by assumption. Theorem 4.30 implies that the two actions coincide; thus, the isomorphism
 $(\widetilde{P}\operatorname{⊗̂}_{{\mathcal{O}}}A)\operatorname{⊗̂}_{A,x}{\mathcal{O}}\cong M_{\infty }\operatorname{⊗̂}_{A,x}{\mathcal{O}}$
is
$(\widetilde{P}\operatorname{⊗̂}_{{\mathcal{O}}}A)\operatorname{⊗̂}_{A,x}{\mathcal{O}}\cong M_{\infty }\operatorname{⊗̂}_{A,x}{\mathcal{O}}$
is
![]() $R_{p}$
-linear.
$R_{p}$
-linear.
We have a commutative diagram in
![]() $\mathfrak{C}(A)$
:
$\mathfrak{C}(A)$
:

where the product is taken over all
![]() ${\mathcal{O}}$
-algebra homomorphisms
${\mathcal{O}}$
-algebra homomorphisms
 $x:A\rightarrow {\mathcal{O}}$
. We know that both vertical and the lower horizontal arrows are
$x:A\rightarrow {\mathcal{O}}$
. We know that both vertical and the lower horizontal arrows are
![]() $R_{p}$
-linear. The map
$R_{p}$
-linear. The map
 $A\rightarrow \prod _{x:A\rightarrow {\mathcal{O}}}{\mathcal{O}}$
is injective (see for example [Reference PaškūnasPaš13, Lemma 9.22]). Since
$A\rightarrow \prod _{x:A\rightarrow {\mathcal{O}}}{\mathcal{O}}$
is injective (see for example [Reference PaškūnasPaš13, Lemma 9.22]). Since
![]() $\widetilde{P}$
is
$\widetilde{P}$
is
![]() ${\mathcal{O}}$
-torsion free, the functor
${\mathcal{O}}$
-torsion free, the functor
 $\widetilde{P}\operatorname{⊗̂}_{{\mathcal{O}}}-$
is exact and hence the first vertical arrow is injective, which implies that the top horizontal arrow is
$\widetilde{P}\operatorname{⊗̂}_{{\mathcal{O}}}-$
is exact and hence the first vertical arrow is injective, which implies that the top horizontal arrow is
![]() $R_{p}$
-linear.◻
$R_{p}$
-linear.◻
Remark 4.33. The preceding result shows that, in particular, the construction of
![]() $M_{\infty }$
in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] is independent of the choices made in the case of
$M_{\infty }$
in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] is independent of the choices made in the case of
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
. More precisely, the isomorphism
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
. More precisely, the isomorphism
 $$\begin{eqnarray}\widetilde{P}\operatorname{⊗̂}_{R_{p}}R_{\infty }\cong M_{\infty }\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{P}\operatorname{⊗̂}_{R_{p}}R_{\infty }\cong M_{\infty }\end{eqnarray}$$
exhibits
![]() $M_{\infty }$
as the extension of scalars of
$M_{\infty }$
as the extension of scalars of
![]() $\widetilde{P}$
, and this latter object, with its arithmetic
$\widetilde{P}$
, and this latter object, with its arithmetic
![]() $R_{p}$
-action, is independent of all choices by Theorem 4.30. Thus, the only ambiguity in the construction of
$R_{p}$
-action, is independent of all choices by Theorem 4.30. Thus, the only ambiguity in the construction of
![]() $M_{\infty }$
is in the number of power series variables in
$M_{\infty }$
is in the number of power series variables in
![]() $R_{\infty }$
, and in their precise action. As one is free to choose as many Taylor–Wiles primes as one wishes in the patching construction, and as the presentations of global deformation rings as quotients of power series rings over local deformation rings are non-canonical, it is evident that this is the exact degree of ambiguity that the construction of
$R_{\infty }$
, and in their precise action. As one is free to choose as many Taylor–Wiles primes as one wishes in the patching construction, and as the presentations of global deformation rings as quotients of power series rings over local deformation rings are non-canonical, it is evident that this is the exact degree of ambiguity that the construction of
![]() $M_{\infty }$
is forced to permit.
$M_{\infty }$
is forced to permit.
5 Unitary completions of principal series representations
In this section, we record some arguments related to the paper [Reference Berger and BreuilBB10], which proves using
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module techniques that the locally algebraic representations associated to crystabelline Galois representations admit a unique unitary completion. We will use the machinery developed in the previous sections, namely the projective envelope
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module techniques that the locally algebraic representations associated to crystabelline Galois representations admit a unique unitary completion. We will use the machinery developed in the previous sections, namely the projective envelope
![]() $\widetilde{P}$
and the purely local map
$\widetilde{P}$
and the purely local map
 $R_{p}\rightarrow \text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
, to independently deduce (without using
$R_{p}\rightarrow \text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
, to independently deduce (without using
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module techniques) that the locally algebraic representations corresponding to crystalline types of regular weight admit at most one unitary completion satisfying certain properties, and that such a completion comes from some
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module techniques) that the locally algebraic representations corresponding to crystalline types of regular weight admit at most one unitary completion satisfying certain properties, and that such a completion comes from some
![]() $\widetilde{P}$
.
$\widetilde{P}$
.
We will use this result in § 7 below to show, assuming the existence results of [Reference Berger and BreuilBB10], that certain of these representations occur in completed cohomology. This gives an alternative approach to proving modularity results in the crystalline case.
As in § 2, we write
 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}=\det ^{a}\otimes \;\text{Sym}^{b}E^{2}$
. Let
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}=\det ^{a}\otimes \;\text{Sym}^{b}E^{2}$
. Let
 $\unicode[STIX]{x1D703}:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow E$
be a homomorphism, and set
$\unicode[STIX]{x1D703}:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow E$
be a homomorphism, and set
 $\unicode[STIX]{x1D6F9}:=(\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E})\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}),\unicode[STIX]{x1D703}}E$
; so
$\unicode[STIX]{x1D6F9}:=(\operatorname{c - Ind}_{K}^{G}\unicode[STIX]{x1D70E})\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}),\unicode[STIX]{x1D703}}E$
; so
![]() $\unicode[STIX]{x1D6F9}$
is a locally algebraic principal series representation of
$\unicode[STIX]{x1D6F9}$
is a locally algebraic principal series representation of
![]() $G$
.
$G$
.
Theorem 5.1. If
![]() $\unicode[STIX]{x1D6F9}$
is irreducible, then
$\unicode[STIX]{x1D6F9}$
is irreducible, then
![]() $\unicode[STIX]{x1D6F9}$
admits at most one non-zero admissible unitary completion
$\unicode[STIX]{x1D6F9}$
admits at most one non-zero admissible unitary completion
![]() $\widehat{\unicode[STIX]{x1D6F9}}$
with the following property: for an open bounded
$\widehat{\unicode[STIX]{x1D6F9}}$
with the following property: for an open bounded
![]() $G$
-invariant lattice
$G$
-invariant lattice
![]() $\unicode[STIX]{x1D6E9}$
in
$\unicode[STIX]{x1D6E9}$
in
![]() $\widehat{\unicode[STIX]{x1D6F9}}$
,
$\widehat{\unicode[STIX]{x1D6F9}}$
,
 $(\unicode[STIX]{x1D6E9}/\unicode[STIX]{x1D71B})\otimes _{\mathbb{F}}\overline{\mathbb{F}}_{p}$
contains no subquotient of the form
$(\unicode[STIX]{x1D6E9}/\unicode[STIX]{x1D71B})\otimes _{\mathbb{F}}\overline{\mathbb{F}}_{p}$
contains no subquotient of the form
 $(\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D712}\otimes \unicode[STIX]{x1D712}\unicode[STIX]{x1D714}^{-1})_{\text{sm}}$
, for any character
$(\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D712}\otimes \unicode[STIX]{x1D712}\unicode[STIX]{x1D714}^{-1})_{\text{sm}}$
, for any character
 $\unicode[STIX]{x1D712}:\mathbb{Q}_{p}^{\times }\rightarrow \overline{\mathbb{F}}_{p}^{\times }$
, and no special series or characters.
$\unicode[STIX]{x1D712}:\mathbb{Q}_{p}^{\times }\rightarrow \overline{\mathbb{F}}_{p}^{\times }$
, and no special series or characters.
If a completion satisfying this property exists, then it is absolutely irreducible.
Proof. Let
![]() $\unicode[STIX]{x1D6F1}$
be a non-zero admissible unitary completion of
$\unicode[STIX]{x1D6F1}$
be a non-zero admissible unitary completion of
![]() $\unicode[STIX]{x1D6F9}$
that satisfies the property in the statement of the theorem. We will first show that
$\unicode[STIX]{x1D6F9}$
that satisfies the property in the statement of the theorem. We will first show that
![]() $\unicode[STIX]{x1D6F1}$
is absolutely irreducible (and, indeed, most of the work of the proof will be in showing this). We note that in the course of the proof we are allowed to replace
$\unicode[STIX]{x1D6F1}$
is absolutely irreducible (and, indeed, most of the work of the proof will be in showing this). We note that in the course of the proof we are allowed to replace
![]() $E$
by a finite field extension
$E$
by a finite field extension
![]() $E^{\prime }$
, since if
$E^{\prime }$
, since if
 $\unicode[STIX]{x1D6F1}\otimes _{E}E^{\prime }$
is an absolutely irreducible
$\unicode[STIX]{x1D6F1}\otimes _{E}E^{\prime }$
is an absolutely irreducible
![]() $E^{\prime }$
-Banach space representation of
$E^{\prime }$
-Banach space representation of
![]() $G$
, then
$G$
, then
![]() $\unicode[STIX]{x1D6F1}$
is an absolutely irreducible
$\unicode[STIX]{x1D6F1}$
is an absolutely irreducible
![]() $E$
-Banach space representation of
$E$
-Banach space representation of
![]() $G$
.
$G$
.
Since
![]() $\unicode[STIX]{x1D6F1}$
is admissible, it will contain an irreducible closed sub-Banach space representation
$\unicode[STIX]{x1D6F1}$
is admissible, it will contain an irreducible closed sub-Banach space representation
![]() $\unicode[STIX]{x1D6F1}_{1}$
. If we let
$\unicode[STIX]{x1D6F1}_{1}$
. If we let
![]() $\unicode[STIX]{x1D6F1}^{\prime }$
denote the quotient
$\unicode[STIX]{x1D6F1}^{\prime }$
denote the quotient
![]() $\unicode[STIX]{x1D6F1}/\unicode[STIX]{x1D6F1}_{1}$
, then we must show that
$\unicode[STIX]{x1D6F1}/\unicode[STIX]{x1D6F1}_{1}$
, then we must show that
![]() $\unicode[STIX]{x1D6F1}^{\prime }$
is zero. For the moment, we note simply that if
$\unicode[STIX]{x1D6F1}^{\prime }$
is zero. For the moment, we note simply that if
![]() $\unicode[STIX]{x1D6F1}^{\prime }$
is non-zero, then since the composite
$\unicode[STIX]{x1D6F1}^{\prime }$
is non-zero, then since the composite
 $\unicode[STIX]{x1D6F9}\rightarrow \unicode[STIX]{x1D6F1}\rightarrow \unicode[STIX]{x1D6F1}^{\prime }$
has dense image, we see that
$\unicode[STIX]{x1D6F9}\rightarrow \unicode[STIX]{x1D6F1}\rightarrow \unicode[STIX]{x1D6F1}^{\prime }$
has dense image, we see that
![]() $\unicode[STIX]{x1D6F1}^{\prime }$
is another non-zero admissible unitary completion of
$\unicode[STIX]{x1D6F1}^{\prime }$
is another non-zero admissible unitary completion of
![]() $\unicode[STIX]{x1D6F9}$
.
$\unicode[STIX]{x1D6F9}$
.
Let
![]() $\unicode[STIX]{x1D6E9}$
be an open bounded
$\unicode[STIX]{x1D6E9}$
be an open bounded
![]() $G$
-invariant lattice in
$G$
-invariant lattice in
![]() $\unicode[STIX]{x1D6F1}$
and let
$\unicode[STIX]{x1D6F1}$
and let
 $\unicode[STIX]{x1D6E9}_{1}:=\unicode[STIX]{x1D6F1}_{1}\cap \unicode[STIX]{x1D6E9}$
. Since
$\unicode[STIX]{x1D6E9}_{1}:=\unicode[STIX]{x1D6F1}_{1}\cap \unicode[STIX]{x1D6E9}$
. Since
![]() $\unicode[STIX]{x1D6F1}_{1}$
is also admissible,
$\unicode[STIX]{x1D6F1}_{1}$
is also admissible,
![]() $\unicode[STIX]{x1D6E9}_{1}/\unicode[STIX]{x1D71B}$
will contain an irreducible subquotient
$\unicode[STIX]{x1D6E9}_{1}/\unicode[STIX]{x1D71B}$
will contain an irreducible subquotient
![]() $\unicode[STIX]{x1D70B}$
. Since we are allowed to enlarge
$\unicode[STIX]{x1D70B}$
. Since we are allowed to enlarge
![]() $E$
, we may assume that
$E$
, we may assume that
![]() $\unicode[STIX]{x1D70B}$
is absolutely irreducible. Let
$\unicode[STIX]{x1D70B}$
is absolutely irreducible. Let
 $\widetilde{P}{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\vee }$
be a projective envelope of
$\widetilde{P}{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\vee }$
be a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
in
$\unicode[STIX]{x1D70B}^{\vee }$
in
![]() $\mathfrak{C}({\mathcal{O}})$
. By the assumption on the subquotients of
$\mathfrak{C}({\mathcal{O}})$
. By the assumption on the subquotients of
![]() $\unicode[STIX]{x1D6E9}/\unicode[STIX]{x1D71B}$
, there is a Galois representation
$\unicode[STIX]{x1D6E9}/\unicode[STIX]{x1D71B}$
, there is a Galois representation
![]() $\bar{r}$
satisfying Assumption 2.2 that corresponds to
$\bar{r}$
satisfying Assumption 2.2 that corresponds to
![]() $\unicode[STIX]{x1D70B}$
via Lemma 2.15(5). We equip
$\unicode[STIX]{x1D70B}$
via Lemma 2.15(5). We equip
![]() $\widetilde{P}$
with the arithmetic action of
$\widetilde{P}$
with the arithmetic action of
![]() $R_{p}$
provided by Theorem 4.30.
$R_{p}$
provided by Theorem 4.30.
We let (for any admissible unitary
![]() $E$
-Banach space representation
$E$
-Banach space representation
![]() $\unicode[STIX]{x1D6F1}$
of
$\unicode[STIX]{x1D6F1}$
of
![]() $G$
)
$G$
)
 $$\begin{eqnarray}M(\unicode[STIX]{x1D6F1}):=\operatorname{Hom}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P},\unicode[STIX]{x1D6E9}^{d})^{d}[1/p]\cong \operatorname{Hom}_{G}^{\text{cont}}(\unicode[STIX]{x1D6F1},\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(\widetilde{P},E))^{d}.\end{eqnarray}$$
$$\begin{eqnarray}M(\unicode[STIX]{x1D6F1}):=\operatorname{Hom}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P},\unicode[STIX]{x1D6E9}^{d})^{d}[1/p]\cong \operatorname{Hom}_{G}^{\text{cont}}(\unicode[STIX]{x1D6F1},\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(\widetilde{P},E))^{d}.\end{eqnarray}$$
The projectivity of
![]() $\widetilde{P}$
implies that
$\widetilde{P}$
implies that
 $\unicode[STIX]{x1D6F1}\mapsto M(\unicode[STIX]{x1D6F1})$
is an exact covariant functor from the category of admissible unitary
$\unicode[STIX]{x1D6F1}\mapsto M(\unicode[STIX]{x1D6F1})$
is an exact covariant functor from the category of admissible unitary
![]() $E$
-Banach space representations of
$E$
-Banach space representations of
![]() $G$
to the category of
$G$
to the category of
![]() $R_{p}[1/p]$
-modules. In particular, we have an injection
$R_{p}[1/p]$
-modules. In particular, we have an injection
 $M(\unicode[STIX]{x1D6F1}_{1}){\hookrightarrow}M(\unicode[STIX]{x1D6F1})$
. Since
$M(\unicode[STIX]{x1D6F1}_{1}){\hookrightarrow}M(\unicode[STIX]{x1D6F1})$
. Since
![]() $\widetilde{P}$
is projective and
$\widetilde{P}$
is projective and
![]() $\unicode[STIX]{x1D70B}$
is a subquotient of
$\unicode[STIX]{x1D70B}$
is a subquotient of
![]() $\unicode[STIX]{x1D6E9}_{1}/\unicode[STIX]{x1D71B}$
, we have
$\unicode[STIX]{x1D6E9}_{1}/\unicode[STIX]{x1D71B}$
, we have
 $M(\unicode[STIX]{x1D6F1}_{1})\neq 0$
by [Reference PaškūnasPaš13, Lemma 4.13] and hence
$M(\unicode[STIX]{x1D6F1}_{1})\neq 0$
by [Reference PaškūnasPaš13, Lemma 4.13] and hence
 $M(\unicode[STIX]{x1D6F1})\neq 0$
.
$M(\unicode[STIX]{x1D6F1})\neq 0$
.
Similarly, we let
 $$\begin{eqnarray}M(\unicode[STIX]{x1D6F9}):=\operatorname{Hom}_{G}(\unicode[STIX]{x1D6F9},\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(\widetilde{P},E))^{d}\cong M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}),\unicode[STIX]{x1D703}}E.\end{eqnarray}$$
$$\begin{eqnarray}M(\unicode[STIX]{x1D6F9}):=\operatorname{Hom}_{G}(\unicode[STIX]{x1D6F9},\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(\widetilde{P},E))^{d}\cong M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}),\unicode[STIX]{x1D703}}E.\end{eqnarray}$$
Recall that
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
acts on
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
acts on
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
through the composite of the homomorphism
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
through the composite of the homomorphism
 ${\mathcal{H}}(\unicode[STIX]{x1D70E})\overset{\unicode[STIX]{x1D702}}{\longrightarrow }R_{p}(\unicode[STIX]{x1D70E})[1/p]$
and the
${\mathcal{H}}(\unicode[STIX]{x1D70E})\overset{\unicode[STIX]{x1D702}}{\longrightarrow }R_{p}(\unicode[STIX]{x1D70E})[1/p]$
and the
![]() $R_{p}[1/p]$
-action on
$R_{p}[1/p]$
-action on
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
and that, by Lemma 4.29, either the fibre module
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
and that, by Lemma 4.29, either the fibre module
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}),\unicode[STIX]{x1D703}}E$
vanishes or else
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}),\unicode[STIX]{x1D703}}E$
vanishes or else
![]() $\unicode[STIX]{x1D703}$
extends to a homomorphism
$\unicode[STIX]{x1D703}$
extends to a homomorphism
 $\widehat{\unicode[STIX]{x1D703}}:R_{p}(\unicode[STIX]{x1D70E})[1/p]\rightarrow E$
(so that then
$\widehat{\unicode[STIX]{x1D703}}:R_{p}(\unicode[STIX]{x1D70E})[1/p]\rightarrow E$
(so that then
 $\unicode[STIX]{x1D703}=\widehat{\unicode[STIX]{x1D703}}\circ \unicode[STIX]{x1D702}$
), in which case there is a natural isomorphism
$\unicode[STIX]{x1D703}=\widehat{\unicode[STIX]{x1D703}}\circ \unicode[STIX]{x1D702}$
), in which case there is a natural isomorphism
 $$\begin{eqnarray}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}),\unicode[STIX]{x1D703}}E\stackrel{{\sim}}{\longrightarrow }M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\otimes _{R_{p}(\unicode[STIX]{x1D70E})[1/p],\widehat{\unicode[STIX]{x1D703}}}E\end{eqnarray}$$
$$\begin{eqnarray}M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}),\unicode[STIX]{x1D703}}E\stackrel{{\sim}}{\longrightarrow }M(\unicode[STIX]{x1D70E}^{\circ })[1/p]\otimes _{R_{p}(\unicode[STIX]{x1D70E})[1/p],\widehat{\unicode[STIX]{x1D703}}}E\end{eqnarray}$$
of
![]() $E$
-vector spaces of dimension at most
$E$
-vector spaces of dimension at most
![]() $1$
.
$1$
.
The map
![]() $\unicode[STIX]{x1D6F9}\rightarrow \unicode[STIX]{x1D6F1}$
induces a continuous homomorphism
$\unicode[STIX]{x1D6F9}\rightarrow \unicode[STIX]{x1D6F1}$
induces a continuous homomorphism
 $$\begin{eqnarray}\operatorname{Hom}_{G}^{\text{cont}}(\unicode[STIX]{x1D6F1},\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(\widetilde{P},E))\rightarrow \operatorname{Hom}_{G}(\unicode[STIX]{x1D6F9},\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(\widetilde{P},E)).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{G}^{\text{cont}}(\unicode[STIX]{x1D6F1},\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(\widetilde{P},E))\rightarrow \operatorname{Hom}_{G}(\unicode[STIX]{x1D6F9},\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(\widetilde{P},E)).\end{eqnarray}$$
Since the image of
![]() $\unicode[STIX]{x1D6F9}$
in
$\unicode[STIX]{x1D6F9}$
in
![]() $\unicode[STIX]{x1D6F1}$
is dense, this map is injective and, by taking duals, we obtain a surjection of
$\unicode[STIX]{x1D6F1}$
is dense, this map is injective and, by taking duals, we obtain a surjection of
 $R_{p}[1/p]$
-modules
$R_{p}[1/p]$
-modules
 $$\begin{eqnarray}M(\unicode[STIX]{x1D6F9}){\twoheadrightarrow}M(\unicode[STIX]{x1D6F1}).\end{eqnarray}$$
$$\begin{eqnarray}M(\unicode[STIX]{x1D6F9}){\twoheadrightarrow}M(\unicode[STIX]{x1D6F1}).\end{eqnarray}$$
Since the target is non-zero, and the source is an
![]() $E$
-vector space of dimension at most
$E$
-vector space of dimension at most
![]() $1$
, this must be an isomorphism. Since
$1$
, this must be an isomorphism. Since
![]() $M(\unicode[STIX]{x1D6F1}_{1})$
is a non-zero subspace of
$M(\unicode[STIX]{x1D6F1}_{1})$
is a non-zero subspace of
![]() $M(\unicode[STIX]{x1D6F1})$
, we therefore have induced isomorphisms
$M(\unicode[STIX]{x1D6F1})$
, we therefore have induced isomorphisms
 $M(\unicode[STIX]{x1D6F1}_{1})\stackrel{{\sim}}{\longrightarrow }M(\unicode[STIX]{x1D6F1})\stackrel{{\sim}}{\longrightarrow }M(\unicode[STIX]{x1D6F9})$
. Since, as was noted above,
$M(\unicode[STIX]{x1D6F1}_{1})\stackrel{{\sim}}{\longrightarrow }M(\unicode[STIX]{x1D6F1})\stackrel{{\sim}}{\longrightarrow }M(\unicode[STIX]{x1D6F9})$
. Since, as was noted above,
![]() $M$
is an exact functor, we find that
$M$
is an exact functor, we find that
 $M(\unicode[STIX]{x1D6F1}^{\prime })=0$
.
$M(\unicode[STIX]{x1D6F1}^{\prime })=0$
.
We digress for a moment in order to establish that
![]() $\unicode[STIX]{x1D6F1}_{1}$
is in fact absolutely irreducible. Since it is irreducible and admissible, its endomorphism ring is a division algebra over
$\unicode[STIX]{x1D6F1}_{1}$
is in fact absolutely irreducible. Since it is irreducible and admissible, its endomorphism ring is a division algebra over
![]() $E$
. On the other hand, since
$E$
. On the other hand, since
![]() $M$
is a functor, and since
$M$
is a functor, and since
![]() $M(\unicode[STIX]{x1D6F1}_{1})$
is one dimensional over
$M(\unicode[STIX]{x1D6F1}_{1})$
is one dimensional over
![]() $E$
, we see that this division algebra admits a homomorphism to
$E$
, we see that this division algebra admits a homomorphism to
![]() $E$
. Thus, this division algebra is in fact equal to
$E$
. Thus, this division algebra is in fact equal to
![]() $E$
and this implies that
$E$
and this implies that
![]() $\unicode[STIX]{x1D6F1}_{1}$
is absolutely irreducible by [Reference PaškūnasPaš13, Lemma 4.2].
$\unicode[STIX]{x1D6F1}_{1}$
is absolutely irreducible by [Reference PaškūnasPaš13, Lemma 4.2].
Suppose now that
![]() $\unicode[STIX]{x1D6F1}^{\prime }\neq 0.$
We may then apply the above argument with
$\unicode[STIX]{x1D6F1}^{\prime }\neq 0.$
We may then apply the above argument with
![]() $\unicode[STIX]{x1D6F1}^{\prime }$
in place of
$\unicode[STIX]{x1D6F1}^{\prime }$
in place of
![]() $\unicode[STIX]{x1D6F1},$
and find an absolutely irreducible subrepresentation
$\unicode[STIX]{x1D6F1},$
and find an absolutely irreducible subrepresentation
![]() $\unicode[STIX]{x1D6F1}_{2}$
of
$\unicode[STIX]{x1D6F1}_{2}$
of
![]() $\unicode[STIX]{x1D6F1}^{\prime },$
a
$\unicode[STIX]{x1D6F1}^{\prime },$
a
![]() $G_{\mathbb{Q}_{p}}$
-representation
$G_{\mathbb{Q}_{p}}$
-representation
![]() $\bar{r}^{\prime }$
and an associated irreducible
$\bar{r}^{\prime }$
and an associated irreducible
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
-representation
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
-representation
![]() $\unicode[STIX]{x1D70B}^{\prime }$
, for which the projective envelope
$\unicode[STIX]{x1D70B}^{\prime }$
, for which the projective envelope
![]() $\widetilde{P}_{2}$
of
$\widetilde{P}_{2}$
of
![]() $(\unicode[STIX]{x1D70B}^{\prime })^{\vee }$
gives rise to an exact functor
$(\unicode[STIX]{x1D70B}^{\prime })^{\vee }$
gives rise to an exact functor
![]() $M^{\prime }$
such that
$M^{\prime }$
such that
 $M^{\prime }(\unicode[STIX]{x1D6F9})=M^{\prime }(\unicode[STIX]{x1D6F1}^{\prime })=M^{\prime }(\unicode[STIX]{x1D6F1}_{2})$
, with all three being one dimensional.
$M^{\prime }(\unicode[STIX]{x1D6F9})=M^{\prime }(\unicode[STIX]{x1D6F1}^{\prime })=M^{\prime }(\unicode[STIX]{x1D6F1}_{2})$
, with all three being one dimensional.
Since both
![]() $M(\unicode[STIX]{x1D6F9})$
and
$M(\unicode[STIX]{x1D6F9})$
and
![]() $M^{\prime }(\unicode[STIX]{x1D6F9})$
are non-zero, we find that each of
$M^{\prime }(\unicode[STIX]{x1D6F9})$
are non-zero, we find that each of
![]() $\bar{r}$
and
$\bar{r}$
and
![]() $\bar{r}^{\prime }$
admits a lift that is a lattice in a crystalline representation
$\bar{r}^{\prime }$
admits a lift that is a lattice in a crystalline representation
![]() $V$
of Hodge–Tate weights
$V$
of Hodge–Tate weights
 $(1-a,-(a+b))$
determined (via Lemma 2.6) by the homomorphism
$(1-a,-(a+b))$
determined (via Lemma 2.6) by the homomorphism
 $\hat{\unicode[STIX]{x1D703}}:R_{p}[1/p]\rightarrow E$
. (Strictly speaking, for this to make sense we need to know that
$\hat{\unicode[STIX]{x1D703}}:R_{p}[1/p]\rightarrow E$
. (Strictly speaking, for this to make sense we need to know that
![]() $V$
is indecomposable; but this is automatic, since each of
$V$
is indecomposable; but this is automatic, since each of
![]() $\bar{r}$
and
$\bar{r}$
and
![]() $\bar{r}^{\prime }$
is indecomposable and has non-scalar semisimplification.)
$\bar{r}^{\prime }$
is indecomposable and has non-scalar semisimplification.)
We note that
![]() $V$
is reducible if and only if
$V$
is reducible if and only if
![]() $\unicode[STIX]{x1D6F9}$
may be identified with the locally algebraic subrepresentation of a continuous induction
$\unicode[STIX]{x1D6F9}$
may be identified with the locally algebraic subrepresentation of a continuous induction
 $(\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D712})_{\text{cont}},$
for some unitary character
$(\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D712})_{\text{cont}},$
for some unitary character
 $\unicode[STIX]{x1D712}:T\rightarrow E^{\times }$
, where
$\unicode[STIX]{x1D712}:T\rightarrow E^{\times }$
, where
![]() $T$
denotes the diagonal torus contained in the upper-triangular Borel subgroup
$T$
denotes the diagonal torus contained in the upper-triangular Borel subgroup
![]() $B$
of
$B$
of
![]() $G$
. In this case it is well known that this continuous induction is the universal unitary completion of
$G$
. In this case it is well known that this continuous induction is the universal unitary completion of
![]() $\unicode[STIX]{x1D6F9}$
, see [Reference Breuil and EmertonBE10, Proposition 2.2.1], and the theorem is true in this case. Thus, for the remainder of the argument, we suppose that
$\unicode[STIX]{x1D6F9}$
, see [Reference Breuil and EmertonBE10, Proposition 2.2.1], and the theorem is true in this case. Thus, for the remainder of the argument, we suppose that
![]() $V$
is irreducible or, equivalently, that
$V$
is irreducible or, equivalently, that
![]() $\unicode[STIX]{x1D6F9}$
does not admit an embedding into the continuous parabolic induction of a unitary character.
$\unicode[STIX]{x1D6F9}$
does not admit an embedding into the continuous parabolic induction of a unitary character.
We now consider separately two cases, according to whether or not
![]() $\bar{r}$
and
$\bar{r}$
and
![]() $\bar{r}^{\prime }$
are themselves isomorphic. If they are, then
$\bar{r}^{\prime }$
are themselves isomorphic. If they are, then
![]() $M$
and
$M$
and
![]() $M^{\prime }$
are isomorphic functors, and we obtain a contradiction from the fact that
$M^{\prime }$
are isomorphic functors, and we obtain a contradiction from the fact that
 $M(\unicode[STIX]{x1D6F1}^{\prime })=0$
while
$M(\unicode[STIX]{x1D6F1}^{\prime })=0$
while
![]() $M^{\prime }(\unicode[STIX]{x1D6F1}^{\prime })$
is one dimensional, implying that in fact
$M^{\prime }(\unicode[STIX]{x1D6F1}^{\prime })$
is one dimensional, implying that in fact
![]() $\unicode[STIX]{x1D6F1}^{\prime }=0,$
as required.
$\unicode[STIX]{x1D6F1}^{\prime }=0,$
as required.
If
![]() $\bar{r}$
and
$\bar{r}$
and
![]() $\bar{r}^{\prime }$
are not isomorphic, but have isomorphic semisimplifications, then they must each consist of an extension of the same two characters, but in opposite directions. In this case
$\bar{r}^{\prime }$
are not isomorphic, but have isomorphic semisimplifications, then they must each consist of an extension of the same two characters, but in opposite directions. In this case
 $\unicode[STIX]{x1D70B}\cong (\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D714}\unicode[STIX]{x1D712}_{1}\otimes \unicode[STIX]{x1D712}_{2})_{\text{sm}}$
,
$\unicode[STIX]{x1D70B}\cong (\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D714}\unicode[STIX]{x1D712}_{1}\otimes \unicode[STIX]{x1D712}_{2})_{\text{sm}}$
,
 $\unicode[STIX]{x1D70B}^{\prime }\cong (\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D714}\unicode[STIX]{x1D712}_{2}\otimes \unicode[STIX]{x1D712}_{1})_{\text{sm}},$
for some smooth characters
$\unicode[STIX]{x1D70B}^{\prime }\cong (\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D714}\unicode[STIX]{x1D712}_{2}\otimes \unicode[STIX]{x1D712}_{1})_{\text{sm}},$
for some smooth characters
 $\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2}:{\mathbb{Q}_{p}}^{\times }\rightarrow \mathbb{F}^{\times }$
. In the terminology of [Reference ColmezCol10b],
$\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2}:{\mathbb{Q}_{p}}^{\times }\rightarrow \mathbb{F}^{\times }$
. In the terminology of [Reference ColmezCol10b],
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}^{\prime }$
are the two constituents of an atome automorphe, which by definition is the unique (up to isomorphism) non-split extension between
$\unicode[STIX]{x1D70B}^{\prime }$
are the two constituents of an atome automorphe, which by definition is the unique (up to isomorphism) non-split extension between
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}^{\prime }$
.
$\unicode[STIX]{x1D70B}^{\prime }$
.
We first show that
 $\unicode[STIX]{x1D6F1}_{2}=\unicode[STIX]{x1D6F1}^{\prime }.$
To this end, set
$\unicode[STIX]{x1D6F1}_{2}=\unicode[STIX]{x1D6F1}^{\prime }.$
To this end, set
 $\unicode[STIX]{x1D6F1}^{\prime \prime }:=\unicode[STIX]{x1D6F1}^{\prime }/\unicode[STIX]{x1D6F1}_{2}$
. If
$\unicode[STIX]{x1D6F1}^{\prime \prime }:=\unicode[STIX]{x1D6F1}^{\prime }/\unicode[STIX]{x1D6F1}_{2}$
. If
 $\unicode[STIX]{x1D6F1}^{\prime \prime }\neq 0,$
then, running through the above argument another time, we find
$\unicode[STIX]{x1D6F1}^{\prime \prime }\neq 0,$
then, running through the above argument another time, we find
![]() $\bar{r}^{\prime \prime }$
, etc, such that
$\bar{r}^{\prime \prime }$
, etc, such that
 $(\bar{r}^{\prime \prime })^{\operatorname{ss}}\cong (\bar{r}^{\prime })^{\operatorname{ss}}\cong \bar{r}^{\operatorname{ss}}$
, and such that
$(\bar{r}^{\prime \prime })^{\operatorname{ss}}\cong (\bar{r}^{\prime })^{\operatorname{ss}}\cong \bar{r}^{\operatorname{ss}}$
, and such that
 $M^{\prime \prime }(\unicode[STIX]{x1D6F1}^{\prime \prime })\neq 0.$
But either
$M^{\prime \prime }(\unicode[STIX]{x1D6F1}^{\prime \prime })\neq 0.$
But either
![]() $\bar{r}^{\prime \prime }\cong \bar{r}$
or
$\bar{r}^{\prime \prime }\cong \bar{r}$
or
![]() $\bar{r}^{\prime \prime }\cong \bar{r}^{\prime }$
. Thus, the functor
$\bar{r}^{\prime \prime }\cong \bar{r}^{\prime }$
. Thus, the functor
![]() $M^{\prime \prime }$
is isomorphic to either
$M^{\prime \prime }$
is isomorphic to either
![]() $M^{\prime }$
or to
$M^{\prime }$
or to
![]() $M$
. On the other hand,
$M$
. On the other hand,
 $M^{\prime }(\unicode[STIX]{x1D6F1}^{\prime \prime })=0$
and also
$M^{\prime }(\unicode[STIX]{x1D6F1}^{\prime \prime })=0$
and also
 $M(\unicode[STIX]{x1D6F1}^{\prime \prime })=0$
(since
$M(\unicode[STIX]{x1D6F1}^{\prime \prime })=0$
(since
![]() $\unicode[STIX]{x1D6F1}^{\prime \prime }$
is a quotient of
$\unicode[STIX]{x1D6F1}^{\prime \prime }$
is a quotient of
![]() $\unicode[STIX]{x1D6F1}^{\prime }$
and
$\unicode[STIX]{x1D6F1}^{\prime }$
and
 $M(\unicode[STIX]{x1D6F1}^{\prime })=0$
). This contradiction shows that
$M(\unicode[STIX]{x1D6F1}^{\prime })=0$
). This contradiction shows that
![]() $\unicode[STIX]{x1D6F1}^{\prime \prime }=0$
and thus that
$\unicode[STIX]{x1D6F1}^{\prime \prime }=0$
and thus that
 $\unicode[STIX]{x1D6F1}^{\prime }=\unicode[STIX]{x1D6F1}_{2}$
is absolutely irreducible.
$\unicode[STIX]{x1D6F1}^{\prime }=\unicode[STIX]{x1D6F1}_{2}$
is absolutely irreducible.
Since
 $M(\unicode[STIX]{x1D6F1}^{\prime })=0,$
we see that
$M(\unicode[STIX]{x1D6F1}^{\prime })=0,$
we see that
![]() $\unicode[STIX]{x1D6E9}^{\prime }/\unicode[STIX]{x1D71B}$
does not contain a copy of
$\unicode[STIX]{x1D6E9}^{\prime }/\unicode[STIX]{x1D71B}$
does not contain a copy of
![]() $\unicode[STIX]{x1D70B}$
as a subquotient (here
$\unicode[STIX]{x1D70B}$
as a subquotient (here
![]() $\unicode[STIX]{x1D6E9}^{\prime }$
denotes some choice of
$\unicode[STIX]{x1D6E9}^{\prime }$
denotes some choice of
![]() $G$
-invariant lattice in
$G$
-invariant lattice in
![]() $\unicode[STIX]{x1D6F1}^{\prime }$
). Since (as we have just shown)
$\unicode[STIX]{x1D6F1}^{\prime }$
). Since (as we have just shown)
![]() $\unicode[STIX]{x1D6F1}^{\prime }$
is absolutely irreducible, it follows from [Reference PaškūnasPaš13, Corollary 8.9] that
$\unicode[STIX]{x1D6F1}^{\prime }$
is absolutely irreducible, it follows from [Reference PaškūnasPaš13, Corollary 8.9] that
 $\unicode[STIX]{x1D6F1}^{\prime }\cong (\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D712})_{\text{cont}}$
for some unitary character
$\unicode[STIX]{x1D6F1}^{\prime }\cong (\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D712})_{\text{cont}}$
for some unitary character
 $\unicode[STIX]{x1D712}:T\rightarrow E^{\times }$
, where
$\unicode[STIX]{x1D712}:T\rightarrow E^{\times }$
, where
![]() $T$
denotes the diagonal torus contained in the upper-triangular Borel subgroup
$T$
denotes the diagonal torus contained in the upper-triangular Borel subgroup
![]() $B$
of
$B$
of
![]() $G$
. (The proof of this result uses various
$G$
. (The proof of this result uses various
![]() $\text{Ext}$
computations in
$\text{Ext}$
computations in
 $\text{Mod}_{G}^{\text{l.adm}}({\mathcal{O}})$
, but does not use either of Colmez’s functors. The basic idea is that the extension of
$\text{Mod}_{G}^{\text{l.adm}}({\mathcal{O}})$
, but does not use either of Colmez’s functors. The basic idea is that the extension of
![]() $\unicode[STIX]{x1D70B}^{\prime }$
by
$\unicode[STIX]{x1D70B}^{\prime }$
by
![]() $\unicode[STIX]{x1D70B}$
given by the atome automorphe induces an embedding
$\unicode[STIX]{x1D70B}$
given by the atome automorphe induces an embedding
 $\widetilde{P}{\hookrightarrow}\widetilde{P}^{\prime }$
whose cokernel is dual to the induction from
$\widetilde{P}{\hookrightarrow}\widetilde{P}^{\prime }$
whose cokernel is dual to the induction from
![]() $B$
to
$B$
to
![]() $G$
of a character; since
$G$
of a character; since
 $M(\unicode[STIX]{x1D6F1}^{\prime })=0$
, we see that
$M(\unicode[STIX]{x1D6F1}^{\prime })=0$
, we see that
![]() $\unicode[STIX]{x1D6E9}^{\prime }$
embeds into this induction and so is itself such an induction.) Thus,
$\unicode[STIX]{x1D6E9}^{\prime }$
embeds into this induction and so is itself such an induction.) Thus,
![]() $\unicode[STIX]{x1D6F9}$
admits an embedding into the continuous parabolic induction of a unitary character, contradicting our hypothesis that
$\unicode[STIX]{x1D6F9}$
admits an embedding into the continuous parabolic induction of a unitary character, contradicting our hypothesis that
![]() $V$
is irreducible. Thus, we conclude that in fact
$V$
is irreducible. Thus, we conclude that in fact
![]() $\unicode[STIX]{x1D6F1}^{\prime }=0$
, as required.
$\unicode[STIX]{x1D6F1}^{\prime }=0$
, as required.
If
![]() $\unicode[STIX]{x1D6F9}$
were to admit two non-isomorphic admissible irreducible unitary completions
$\unicode[STIX]{x1D6F9}$
were to admit two non-isomorphic admissible irreducible unitary completions
![]() $\unicode[STIX]{x1D6F1}_{1}$
and
$\unicode[STIX]{x1D6F1}_{1}$
and
![]() $\unicode[STIX]{x1D6F1}_{2}$
satisfying the assumptions of the theorem, the image of the diagonal map
$\unicode[STIX]{x1D6F1}_{2}$
satisfying the assumptions of the theorem, the image of the diagonal map
 $\unicode[STIX]{x1D6F9}\rightarrow \unicode[STIX]{x1D6F1}_{1}\oplus \unicode[STIX]{x1D6F1}_{2}$
would be dense in
$\unicode[STIX]{x1D6F9}\rightarrow \unicode[STIX]{x1D6F1}_{1}\oplus \unicode[STIX]{x1D6F1}_{2}$
would be dense in
 $\unicode[STIX]{x1D6F1}_{1}\oplus \unicode[STIX]{x1D6F1}_{2}$
. This yields a contradiction to what we have already proved, as
$\unicode[STIX]{x1D6F1}_{1}\oplus \unicode[STIX]{x1D6F1}_{2}$
. This yields a contradiction to what we have already proved, as
 $\unicode[STIX]{x1D6F1}_{1}\oplus \unicode[STIX]{x1D6F1}_{2}$
is not irreducible.◻
$\unicode[STIX]{x1D6F1}_{1}\oplus \unicode[STIX]{x1D6F1}_{2}$
is not irreducible.◻
Remark 5.2. It follows from the proof of Theorem 5.1 that if a completion
![]() $\widehat{\unicode[STIX]{x1D6F9}}$
of the kind considered there exists, then there is a Galois representation
$\widehat{\unicode[STIX]{x1D6F9}}$
of the kind considered there exists, then there is a Galois representation
![]() $\bar{r}$
satisfying Assumption 2.2 such that
$\bar{r}$
satisfying Assumption 2.2 such that
![]() $\unicode[STIX]{x1D703}$
extends to a homomorphism
$\unicode[STIX]{x1D703}$
extends to a homomorphism
 $\widehat{\unicode[STIX]{x1D703}}:R_{p}(\unicode[STIX]{x1D70E})[1/p]\rightarrow E$
. Furthermore, for any
$\widehat{\unicode[STIX]{x1D703}}:R_{p}(\unicode[STIX]{x1D70E})[1/p]\rightarrow E$
. Furthermore, for any
![]() $M_{\infty }$
as in § 3, we have
$M_{\infty }$
as in § 3, we have
 $M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })[1/p]\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}),\unicode[STIX]{x1D703}}E\neq 0$
.
$M_{\infty }(\unicode[STIX]{x1D70E}^{\circ })[1/p]\otimes _{{\mathcal{H}}(\unicode[STIX]{x1D70E}),\unicode[STIX]{x1D703}}E\neq 0$
.
Conversely, if there is an
![]() $\bar{r}$
satisfying Assumption 2.2 such that
$\bar{r}$
satisfying Assumption 2.2 such that
![]() $\unicode[STIX]{x1D703}$
extends to a homomorphism
$\unicode[STIX]{x1D703}$
extends to a homomorphism
 $\widehat{\unicode[STIX]{x1D703}}:R_{p}(\unicode[STIX]{x1D70E})[1/p]\rightarrow E$
, then the existence of a completion
$\widehat{\unicode[STIX]{x1D703}}:R_{p}(\unicode[STIX]{x1D70E})[1/p]\rightarrow E$
, then the existence of a completion
![]() $\widehat{\unicode[STIX]{x1D6F9}}$
is immediate from the main theorem of [Reference Berger and BreuilBB10] (which shows that some completion exists) together with the main theorem of [Reference BergerBer10] (which implies the required property of the subquotients).
$\widehat{\unicode[STIX]{x1D6F9}}$
is immediate from the main theorem of [Reference Berger and BreuilBB10] (which shows that some completion exists) together with the main theorem of [Reference BergerBer10] (which implies the required property of the subquotients).
Remark 5.3. As is true throughout this paper, the results of this section are equally valid for crystabelline representations, but for simplicity of notation we have restricted ourselves to the crystalline case.
6 Comparison to the local approach
We now examine the compatibility of our constructions with those of [Reference PaškūnasPaš13], which work with fixed central characters. The arguments of [Reference PaškūnasPaš13] make use of Colmez’s functor, and the results of this section therefore also depend on this functor. In § 6.24 we briefly discuss how to prove some of the more elementary statements in [Reference PaškūnasPaš13] using the results of the previous section (and in particular not using Colmez’s functor). We assume throughout this section that
![]() $p\geqslant 5$
, as this assumption is made in various of the results of [Reference PaškūnasPaš13] that we cite.
$p\geqslant 5$
, as this assumption is made in various of the results of [Reference PaškūnasPaš13] that we cite.
There are two approaches that we could take to this comparison. One would be to note that the axioms of § 3.1 and arguments of § 4 admit obvious analogues in the setting of a fixed central character, and thus show that if we pass to a quotient of
![]() $M_{\infty }$
with fixed central character, we obtain a uniquely determined
$M_{\infty }$
with fixed central character, we obtain a uniquely determined
![]() $p$
-adic Langlands correspondence. These axioms are satisfied by the purely local object constructed in [Reference PaškūnasPaš13] (which is a projective envelope of
$p$
-adic Langlands correspondence. These axioms are satisfied by the purely local object constructed in [Reference PaškūnasPaš13] (which is a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
in a category of representations with fixed central character), and this completes the comparison.
$\unicode[STIX]{x1D70B}^{\vee }$
in a category of representations with fixed central character), and this completes the comparison.
While this route would be shorter, we have preferred to take the second approach, and go in the opposite direction: we promote the projective envelope from [Reference PaškūnasPaš13] to a representation with non-constant central character by tensoring with the universal deformation of the trivial one-dimensional representation (which has a natural Galois action by local class field theory), and show that this satisfies the axioms of § 3.1. This requires us to make a careful study of various twisting constructions; the payoff is that we prove a stronger result than that which would follow from the first approach.
6.1 Deformation rings and twisting
Let
![]() $\unicode[STIX]{x1D6EC}$
be the universal deformation ring of the trivial one-dimensional representation of
$\unicode[STIX]{x1D6EC}$
be the universal deformation ring of the trivial one-dimensional representation of
![]() $G_{\mathbb{Q}_{p}}$
and let
$G_{\mathbb{Q}_{p}}$
and let
![]() $\mathbf{1}^{\operatorname{univ}}$
be the universal deformation. Then
$\mathbf{1}^{\operatorname{univ}}$
be the universal deformation. Then
![]() $\mathbf{1}^{\operatorname{univ}}$
is a free
$\mathbf{1}^{\operatorname{univ}}$
is a free
![]() $\unicode[STIX]{x1D6EC}$
-module of rank
$\unicode[STIX]{x1D6EC}$
-module of rank
![]() $1$
with a continuous
$1$
with a continuous
![]() $G_{\mathbb{Q}_{p}}$
-action. We let
$G_{\mathbb{Q}_{p}}$
-action. We let
![]() $G$
act on
$G$
act on
![]() $\mathbf{1}^{\operatorname{univ}}$
via the inverse determinant (composed with the Artin map). We let
$\mathbf{1}^{\operatorname{univ}}$
via the inverse determinant (composed with the Artin map). We let
![]() $\unicode[STIX]{x1D6EC}^{\text{ur}}$
be the quotient of
$\unicode[STIX]{x1D6EC}^{\text{ur}}$
be the quotient of
![]() $\unicode[STIX]{x1D6EC}$
unramified deformations. We note that
$\unicode[STIX]{x1D6EC}$
unramified deformations. We note that
![]() $\unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D6EC}$
and
![]() $\unicode[STIX]{x1D6EC}^{\text{ur}}$
are formally smooth over
$\unicode[STIX]{x1D6EC}^{\text{ur}}$
are formally smooth over
![]() ${\mathcal{O}}$
of relative dimensions
${\mathcal{O}}$
of relative dimensions
![]() $2$
and
$2$
and
![]() $1$
, respectively, and in particular are
$1$
, respectively, and in particular are
![]() ${\mathcal{O}}$
-torsion free.
${\mathcal{O}}$
-torsion free.
Let
 $\unicode[STIX]{x1D713}:G_{\mathbb{Q}_{p}}\rightarrow {\mathcal{O}}^{\times }$
be a continuous character such that
$\unicode[STIX]{x1D713}:G_{\mathbb{Q}_{p}}\rightarrow {\mathcal{O}}^{\times }$
be a continuous character such that
![]() $\unicode[STIX]{x1D713}\unicode[STIX]{x1D700}^{-1}$
is congruent to
$\unicode[STIX]{x1D713}\unicode[STIX]{x1D700}^{-1}$
is congruent to
![]() $\det \bar{r}$
modulo
$\det \bar{r}$
modulo
![]() $\unicode[STIX]{x1D71B}$
. (By Remark 2.17, this implies that
$\unicode[STIX]{x1D71B}$
. (By Remark 2.17, this implies that
![]() $\unicode[STIX]{x1D713}$
modulo
$\unicode[STIX]{x1D713}$
modulo
![]() $\unicode[STIX]{x1D71B}$
considered as a character of
$\unicode[STIX]{x1D71B}$
considered as a character of
![]() $\mathbb{Q}_{p}^{\times }$
coincides with the central character of
$\mathbb{Q}_{p}^{\times }$
coincides with the central character of
![]() $\unicode[STIX]{x1D70B}$
.) We let
$\unicode[STIX]{x1D70B}$
.) We let
![]() $R_{p}^{\unicode[STIX]{x1D713}}$
denote the quotient of
$R_{p}^{\unicode[STIX]{x1D713}}$
denote the quotient of
![]() $R_{p}$
parameterizing deformations with determinant
$R_{p}$
parameterizing deformations with determinant
![]() $\unicode[STIX]{x1D713}\unicode[STIX]{x1D700}^{-1}$
. Let
$\unicode[STIX]{x1D713}\unicode[STIX]{x1D700}^{-1}$
. Let
![]() $r^{\operatorname{univ},\unicode[STIX]{x1D713}}$
be the tautological deformation of
$r^{\operatorname{univ},\unicode[STIX]{x1D713}}$
be the tautological deformation of
![]() $\bar{r}$
to
$\bar{r}$
to
![]() $R_{p}^{\unicode[STIX]{x1D713}}$
. Then
$R_{p}^{\unicode[STIX]{x1D713}}$
. Then
 $r^{\operatorname{univ},\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is a deformation of
$r^{\operatorname{univ},\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is a deformation of
![]() $\bar{r}$
to
$\bar{r}$
to
 $R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
. Since
$R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
. Since
![]() $p>2$
, this induces an isomorphism of local
$p>2$
, this induces an isomorphism of local
![]() ${\mathcal{O}}$
-algebras
${\mathcal{O}}$
-algebras
 $$\begin{eqnarray}R_{p}\overset{\cong }{\longrightarrow }R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}.\end{eqnarray}$$
$$\begin{eqnarray}R_{p}\overset{\cong }{\longrightarrow }R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}.\end{eqnarray}$$
Let
![]() $R_{p}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
denote the quotient of
$R_{p}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
denote the quotient of
![]() $R_{p}(\unicode[STIX]{x1D70E})$
corresponding to deformations of determinant
$R_{p}(\unicode[STIX]{x1D70E})$
corresponding to deformations of determinant
![]() $\unicode[STIX]{x1D713}\unicode[STIX]{x1D700}^{-1}$
; note that
$\unicode[STIX]{x1D713}\unicode[STIX]{x1D700}^{-1}$
; note that
 $R_{p}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})=0$
unless
$R_{p}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})=0$
unless
![]() $\unicode[STIX]{x1D713}|_{\mathbb{Z}_{p}^{\times }}$
is equal to the central character of
$\unicode[STIX]{x1D713}|_{\mathbb{Z}_{p}^{\times }}$
is equal to the central character of
![]() $\unicode[STIX]{x1D70E}$
. If
$\unicode[STIX]{x1D70E}$
. If
![]() $\unicode[STIX]{x1D713}|_{\mathbb{Z}_{p}^{\times }}$
is equal to the central character of
$\unicode[STIX]{x1D713}|_{\mathbb{Z}_{p}^{\times }}$
is equal to the central character of
![]() $\unicode[STIX]{x1D70E}$
, then the isomorphism
$\unicode[STIX]{x1D70E}$
, then the isomorphism
 $R_{p}\overset{\cong }{\longrightarrow }R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
induces an isomorphism
$R_{p}\overset{\cong }{\longrightarrow }R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
induces an isomorphism
 $$\begin{eqnarray}R_{p}(\unicode[STIX]{x1D70E})\overset{\cong }{\longrightarrow }R_{p}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}}.\end{eqnarray}$$
$$\begin{eqnarray}R_{p}(\unicode[STIX]{x1D70E})\overset{\cong }{\longrightarrow }R_{p}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}}.\end{eqnarray}$$
Let
 $\unicode[STIX]{x1D6FF}:G_{\mathbb{Q}_{p}}\rightarrow {\mathcal{O}}^{\times }$
be a character that is trivial modulo
$\unicode[STIX]{x1D6FF}:G_{\mathbb{Q}_{p}}\rightarrow {\mathcal{O}}^{\times }$
be a character that is trivial modulo
![]() $\unicode[STIX]{x1D71B}$
. Twisting by
$\unicode[STIX]{x1D71B}$
. Twisting by
![]() $\unicode[STIX]{x1D6FF}$
induces isomorphisms of
$\unicode[STIX]{x1D6FF}$
induces isomorphisms of
![]() ${\mathcal{O}}$
-algebras
${\mathcal{O}}$
-algebras
 $$\begin{eqnarray}\text{tw}_{\unicode[STIX]{x1D6FF}}:R_{p}\stackrel{{\sim}}{\longrightarrow }R_{p},\quad \text{tw}_{\unicode[STIX]{x1D6FF}}:R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}\stackrel{{\sim}}{\longrightarrow }R_{p}^{\unicode[STIX]{x1D713}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{tw}_{\unicode[STIX]{x1D6FF}}:R_{p}\stackrel{{\sim}}{\longrightarrow }R_{p},\quad \text{tw}_{\unicode[STIX]{x1D6FF}}:R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}\stackrel{{\sim}}{\longrightarrow }R_{p}^{\unicode[STIX]{x1D713}}.\end{eqnarray}$$
(In terms of the deformation functor
![]() $D_{\bar{r}}$
pro-represented by
$D_{\bar{r}}$
pro-represented by
![]() $R_{p}$
, and the deformation functors
$R_{p}$
, and the deformation functors
![]() $D_{\bar{r}}^{\unicode[STIX]{x1D713}}$
and
$D_{\bar{r}}^{\unicode[STIX]{x1D713}}$
and
![]() $D_{\bar{r}}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}$
pro-represented by
$D_{\bar{r}}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}$
pro-represented by
![]() $R_{p}^{\unicode[STIX]{x1D713}}$
and
$R_{p}^{\unicode[STIX]{x1D713}}$
and
![]() $R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}$
, these isomorphisms are induced by the natural bijections
$R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}$
, these isomorphisms are induced by the natural bijections
 $$\begin{eqnarray}D_{\bar{r}}(A)\stackrel{{\sim}}{\longrightarrow }D_{\bar{r}}(A),\quad D_{\bar{r}}^{\unicode[STIX]{x1D713}}(A)\stackrel{{\sim}}{\longrightarrow }D_{\bar{r}}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(A)\end{eqnarray}$$
$$\begin{eqnarray}D_{\bar{r}}(A)\stackrel{{\sim}}{\longrightarrow }D_{\bar{r}}(A),\quad D_{\bar{r}}^{\unicode[STIX]{x1D713}}(A)\stackrel{{\sim}}{\longrightarrow }D_{\bar{r}}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(A)\end{eqnarray}$$
defined by
 $r_{A}\mapsto r_{A}\otimes \unicode[STIX]{x1D6FF}$
.) Similarly, we obtain isomorphisms
$r_{A}\mapsto r_{A}\otimes \unicode[STIX]{x1D6FF}$
.) Similarly, we obtain isomorphisms
 $$\begin{eqnarray}\text{tw}_{\unicode[STIX]{x1D6FF}}:\unicode[STIX]{x1D6EC}\stackrel{{\sim}}{\longrightarrow }\unicode[STIX]{x1D6EC},\quad \text{tw}_{\unicode[STIX]{x1D6FF}}:\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6FF})^{\text{ur}}\stackrel{{\sim}}{\longrightarrow }\unicode[STIX]{x1D6EC}^{\text{ur}}\end{eqnarray}$$
$$\begin{eqnarray}\text{tw}_{\unicode[STIX]{x1D6FF}}:\unicode[STIX]{x1D6EC}\stackrel{{\sim}}{\longrightarrow }\unicode[STIX]{x1D6EC},\quad \text{tw}_{\unicode[STIX]{x1D6FF}}:\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6FF})^{\text{ur}}\stackrel{{\sim}}{\longrightarrow }\unicode[STIX]{x1D6EC}^{\text{ur}}\end{eqnarray}$$
and we have a commutative diagram

6.5 Unfixing the central character
Let
 $\text{Mod}_{G}^{\text{l.adm},\unicode[STIX]{x1D713}}({\mathcal{O}})$
be the full subcategory of
$\text{Mod}_{G}^{\text{l.adm},\unicode[STIX]{x1D713}}({\mathcal{O}})$
be the full subcategory of
 $\text{Mod}_{G}^{\text{l.adm}}({\mathcal{O}})$
, consisting of those representations where
$\text{Mod}_{G}^{\text{l.adm}}({\mathcal{O}})$
, consisting of those representations where
![]() $Z$
acts by the central character
$Z$
acts by the central character
![]() $\unicode[STIX]{x1D713}$
. Let
$\unicode[STIX]{x1D713}$
. Let
![]() $\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
be the Pontryagin dual of
$\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
be the Pontryagin dual of
 $\text{Mod}_{G}^{\text{l.adm},\unicode[STIX]{x1D713}}({\mathcal{O}})$
, so that we can identify
$\text{Mod}_{G}^{\text{l.adm},\unicode[STIX]{x1D713}}({\mathcal{O}})$
, so that we can identify
![]() $\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
with a full subcategory of
$\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
with a full subcategory of
![]() $\mathfrak{C}({\mathcal{O}})$
consisting of those objects on which
$\mathfrak{C}({\mathcal{O}})$
consisting of those objects on which
![]() $Z$
acts by
$Z$
acts by
![]() $\unicode[STIX]{x1D713}^{-1}$
.
$\unicode[STIX]{x1D713}^{-1}$
.
Let
 $\widetilde{P}^{\unicode[STIX]{x1D713}}{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\vee }$
be a projective envelope of
$\widetilde{P}^{\unicode[STIX]{x1D713}}{\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\vee }$
be a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
in
$\unicode[STIX]{x1D70B}^{\vee }$
in
![]() $\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
. By [Reference PaškūnasPaš13, Proposition 6.3, Corollary 8.7 and Theorem 10.71], there is a natural isomorphism
$\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
. By [Reference PaškūnasPaš13, Proposition 6.3, Corollary 8.7 and Theorem 10.71], there is a natural isomorphism
 $$\begin{eqnarray}R_{p}^{\unicode[STIX]{x1D713}}\stackrel{{\sim}}{\longrightarrow }\text{End}_{\mathfrak{ C}({\mathcal{O}})}(\widetilde{P}^{\unicode[STIX]{x1D713}}).\end{eqnarray}$$
$$\begin{eqnarray}R_{p}^{\unicode[STIX]{x1D713}}\stackrel{{\sim}}{\longrightarrow }\text{End}_{\mathfrak{ C}({\mathcal{O}})}(\widetilde{P}^{\unicode[STIX]{x1D713}}).\end{eqnarray}$$
In Corollary 6.23 below, we will prove a version of the isomorphism (6.6) for
![]() $R_{p}$
.
$R_{p}$
.
Lemma 6.7. Let
 $\unicode[STIX]{x1D6FF}:G_{\mathbb{Q}_{p}}\rightarrow {\mathcal{O}}^{\times }$
be a character that is trivial modulo
$\unicode[STIX]{x1D6FF}:G_{\mathbb{Q}_{p}}\rightarrow {\mathcal{O}}^{\times }$
be a character that is trivial modulo
![]() $\unicode[STIX]{x1D71B}$
. There is an isomorphism in
$\unicode[STIX]{x1D71B}$
. There is an isomorphism in
![]() $\mathfrak{C}({\mathcal{O}})$
:
$\mathfrak{C}({\mathcal{O}})$
:
 $$\begin{eqnarray}\unicode[STIX]{x1D711}:\widetilde{P}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}\stackrel{{\sim}}{\longrightarrow }\widetilde{P}^{\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D6FF}^{-1}\circ \text{det}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}:\widetilde{P}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}\stackrel{{\sim}}{\longrightarrow }\widetilde{P}^{\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D6FF}^{-1}\circ \text{det}.\end{eqnarray}$$
Moreover, the following diagram commutes:

where the lower horizontal arrow is given by
 $\unicode[STIX]{x1D6FC}\mapsto \unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D711}^{-1}$
.
$\unicode[STIX]{x1D6FC}\mapsto \unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D711}^{-1}$
.
Proof. The claimed isomorphism follows from the fact that twisting by
 $\unicode[STIX]{x1D6FF}^{-1}\circ \det$
induces an equivalence of categories between
$\unicode[STIX]{x1D6FF}^{-1}\circ \det$
induces an equivalence of categories between
![]() $\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
and
$\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
and
 $\mathfrak{C}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}({\mathcal{O}})$
, so that the twist of a projective envelope of
$\mathfrak{C}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}({\mathcal{O}})$
, so that the twist of a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
in
$\unicode[STIX]{x1D70B}^{\vee }$
in
![]() $\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
is a projective envelope of
$\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
is a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
in
$\unicode[STIX]{x1D70B}^{\vee }$
in
 $\mathfrak{C}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}({\mathcal{O}}).$
The commutativity of the diagram follows from the compatibility of the constructions of [Reference PaškūnasPaš13], and in particular of the isomorphism (6.6), with twisting. (This comes down to the compatibility of the functor
$\mathfrak{C}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}({\mathcal{O}}).$
The commutativity of the diagram follows from the compatibility of the constructions of [Reference PaškūnasPaš13], and in particular of the isomorphism (6.6), with twisting. (This comes down to the compatibility of the functor
![]() $\check{\mathbf{V}}$
, discussed below, with twisting.)◻
$\check{\mathbf{V}}$
, discussed below, with twisting.)◻
Let
 $\unicode[STIX]{x1D6FF}:G_{\mathbb{Q}_{p}}\rightarrow {\mathcal{O}}^{\times }$
be a character that is trivial modulo
$\unicode[STIX]{x1D6FF}:G_{\mathbb{Q}_{p}}\rightarrow {\mathcal{O}}^{\times }$
be a character that is trivial modulo
![]() $\unicode[STIX]{x1D71B}$
. There is an evident isomorphism of pseudocompact
$\unicode[STIX]{x1D71B}$
. There is an evident isomorphism of pseudocompact
 ${\mathcal{O}}[[G_{\mathbb{Q}_{p}}]]$
-modules:
${\mathcal{O}}[[G_{\mathbb{Q}_{p}}]]$
-modules:
 $$\begin{eqnarray}\unicode[STIX]{x1D703}:\mathbf{1}^{\operatorname{univ}}\otimes \unicode[STIX]{x1D6FF}\stackrel{{\sim}}{\longrightarrow }\mathbf{1}^{\operatorname{univ}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}:\mathbf{1}^{\operatorname{univ}}\otimes \unicode[STIX]{x1D6FF}\stackrel{{\sim}}{\longrightarrow }\mathbf{1}^{\operatorname{univ}}\end{eqnarray}$$
and a commutative diagram

where the lower horizontal arrow is given by
 $\unicode[STIX]{x1D6FC}\mapsto \unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D703}^{-1}$
. (In terms of the deformation functor
$\unicode[STIX]{x1D6FC}\mapsto \unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D703}^{-1}$
. (In terms of the deformation functor
![]() $D_{\mathbf{1}}$
pro-represented by
$D_{\mathbf{1}}$
pro-represented by
![]() $\unicode[STIX]{x1D6EC}$
, the isomorphism
$\unicode[STIX]{x1D6EC}$
, the isomorphism
![]() $\text{tw}_{\unicode[STIX]{x1D6FF}^{-1}}$
is induced by the bijection
$\text{tw}_{\unicode[STIX]{x1D6FF}^{-1}}$
is induced by the bijection
 $D_{\mathbf{1}}(A)\stackrel{{\sim}}{\longrightarrow }D_{\mathbf{1}}(A)$
defined by
$D_{\mathbf{1}}(A)\stackrel{{\sim}}{\longrightarrow }D_{\mathbf{1}}(A)$
defined by
 $\unicode[STIX]{x1D712}\mapsto \unicode[STIX]{x1D712}\unicode[STIX]{x1D6FF}^{-1}$
.)
$\unicode[STIX]{x1D712}\mapsto \unicode[STIX]{x1D712}\unicode[STIX]{x1D6FF}^{-1}$
.)
Lemma 6.9. Let
 $\unicode[STIX]{x1D6FF}:\mathbb{Q}_{p}^{\times }\rightarrow {\mathcal{O}}^{\times }$
be a character that is trivial modulo
$\unicode[STIX]{x1D6FF}:\mathbb{Q}_{p}^{\times }\rightarrow {\mathcal{O}}^{\times }$
be a character that is trivial modulo
![]() $\unicode[STIX]{x1D71B}$
. Then there is an isomorphism
$\unicode[STIX]{x1D71B}$
. Then there is an isomorphism
 $$\begin{eqnarray}\widetilde{P}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}\stackrel{{\sim}}{\longrightarrow }\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{P}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}\stackrel{{\sim}}{\longrightarrow }\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}\end{eqnarray}$$
in the category
![]() $\mathfrak{C}(R_{p})$
, where
$\mathfrak{C}(R_{p})$
, where
![]() $R_{p}$
acts on both sides by the isomorphism of (6.2).
$R_{p}$
acts on both sides by the isomorphism of (6.2).
Proof. Using Lemma 6.7 and (6.8), we obtain isomorphisms in
![]() $\mathfrak{C}({\mathcal{O}})$
:
$\mathfrak{C}({\mathcal{O}})$
:
 $$\begin{eqnarray}\displaystyle \widetilde{P}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}} & \widehat{\longrightarrow } & \displaystyle (\widetilde{P}^{\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D6FF}^{-1}\circ \det )\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}\nonumber\\ \displaystyle & \stackrel{{\sim}}{\longrightarrow } & \displaystyle \widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}(\mathbf{1}^{\operatorname{univ}}\otimes \unicode[STIX]{x1D6FF}\circ \det )\widehat{\longrightarrow }\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{P}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}} & \widehat{\longrightarrow } & \displaystyle (\widetilde{P}^{\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D6FF}^{-1}\circ \det )\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}\nonumber\\ \displaystyle & \stackrel{{\sim}}{\longrightarrow } & \displaystyle \widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}(\mathbf{1}^{\operatorname{univ}}\otimes \unicode[STIX]{x1D6FF}\circ \det )\widehat{\longrightarrow }\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}.\nonumber\end{eqnarray}$$
The composition of these isomorphisms is equal to
 $\unicode[STIX]{x1D719}\operatorname{⊗̂}\unicode[STIX]{x1D703}:\widetilde{P}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}\stackrel{{\sim}}{\longrightarrow }\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
, which is an isomorphism in
$\unicode[STIX]{x1D719}\operatorname{⊗̂}\unicode[STIX]{x1D703}:\widetilde{P}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}\stackrel{{\sim}}{\longrightarrow }\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
, which is an isomorphism in
![]() $\mathfrak{C}({\mathcal{O}})$
. It follows from Lemma 6.7 and (6.8) that the following diagram commutes:
$\mathfrak{C}({\mathcal{O}})$
. It follows from Lemma 6.7 and (6.8) that the following diagram commutes:

where the lower horizontal arrow is given by
 $\unicode[STIX]{x1D6FC}\mapsto (\unicode[STIX]{x1D711}\operatorname{⊗̂}\unicode[STIX]{x1D703})\circ \unicode[STIX]{x1D6FC}\circ (\unicode[STIX]{x1D711}\operatorname{⊗̂}\unicode[STIX]{x1D703})^{-1}$
. It follows from the above diagram and (6.4) that
$\unicode[STIX]{x1D6FC}\mapsto (\unicode[STIX]{x1D711}\operatorname{⊗̂}\unicode[STIX]{x1D703})\circ \unicode[STIX]{x1D6FC}\circ (\unicode[STIX]{x1D711}\operatorname{⊗̂}\unicode[STIX]{x1D703})^{-1}$
. It follows from the above diagram and (6.4) that
![]() $\unicode[STIX]{x1D711}\operatorname{⊗̂}\unicode[STIX]{x1D703}$
is an isomorphism in
$\unicode[STIX]{x1D711}\operatorname{⊗̂}\unicode[STIX]{x1D703}$
is an isomorphism in
![]() $\mathfrak{C}(R_{p})$
.◻
$\mathfrak{C}(R_{p})$
.◻
Proposition 6.10.
 $\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is projective in the category of pseudocompact
$\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is projective in the category of pseudocompact
![]() ${\mathcal{O}}[[K]]$
-modules.
${\mathcal{O}}[[K]]$
-modules.
Proof. Let
 $I_{1}:=\{g\in K:g\equiv \big(\!\begin{smallmatrix}1 & \ast \\ 0 & 1\end{smallmatrix}\!\big)\hspace{0.6em}({\rm mod}\hspace{0.2em}\unicode[STIX]{x1D71B})\}$
. Then
$I_{1}:=\{g\in K:g\equiv \big(\!\begin{smallmatrix}1 & \ast \\ 0 & 1\end{smallmatrix}\!\big)\hspace{0.6em}({\rm mod}\hspace{0.2em}\unicode[STIX]{x1D71B})\}$
. Then
![]() $I_{1}$
is a pro-
$I_{1}$
is a pro-
![]() $p$
Sylow subgroup of
$p$
Sylow subgroup of
![]() $K$
and it is enough to show that
$K$
and it is enough to show that
 $\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is projective in the category of pseudocompact
$\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is projective in the category of pseudocompact
![]() ${\mathcal{O}}[[I_{1}]]$
-modules. Since
${\mathcal{O}}[[I_{1}]]$
-modules. Since
![]() $I_{1}$
is a pro-
$I_{1}$
is a pro-
![]() $p$
group, there is only one indecomposable projective object in the category, namely
$p$
group, there is only one indecomposable projective object in the category, namely
![]() ${\mathcal{O}}[[I_{1}]]$
, and thus a pseudocompact
${\mathcal{O}}[[I_{1}]]$
, and thus a pseudocompact
![]() ${\mathcal{O}}[[I_{1}]]$
-module is projective if and only if it is pro-free, which means that it is isomorphic to
${\mathcal{O}}[[I_{1}]]$
-module is projective if and only if it is pro-free, which means that it is isomorphic to
 $\prod _{j\in J}{\mathcal{O}}[[I_{1}]]$
for some indexing set
$\prod _{j\in J}{\mathcal{O}}[[I_{1}]]$
for some indexing set
![]() $J$
.
$J$
.
Let
 $\unicode[STIX]{x1D6E4}:=1+p\mathbb{Z}_{p}$
. We identify
$\unicode[STIX]{x1D6E4}:=1+p\mathbb{Z}_{p}$
. We identify
![]() $\unicode[STIX]{x1D6E4}$
with the image in
$\unicode[STIX]{x1D6E4}$
with the image in
![]() $G_{\mathbb{Q}_{p}}^{\text{ab}}$
of the wild inertia subgroup of
$G_{\mathbb{Q}_{p}}^{\text{ab}}$
of the wild inertia subgroup of
![]() $G_{\mathbb{Q}_{p}}$
. We may identify
$G_{\mathbb{Q}_{p}}$
. We may identify
![]() $\unicode[STIX]{x1D6EC}$
with the completed group algebra of the pro-
$\unicode[STIX]{x1D6EC}$
with the completed group algebra of the pro-
![]() $p$
completion of
$p$
completion of
![]() $G_{\mathbb{Q}_{p}}^{\text{ab}}$
, which is isomorphic to
$G_{\mathbb{Q}_{p}}^{\text{ab}}$
, which is isomorphic to
![]() $\unicode[STIX]{x1D6E4}\times \mathbb{Z}_{p}$
. There is an isomorphism of
$\unicode[STIX]{x1D6E4}\times \mathbb{Z}_{p}$
. There is an isomorphism of
![]() ${\mathcal{O}}$
-algebras
${\mathcal{O}}$
-algebras
 $\unicode[STIX]{x1D6EC}\cong {\mathcal{O}}[[\unicode[STIX]{x1D6E4}]][[x]]$
, and in particular
$\unicode[STIX]{x1D6EC}\cong {\mathcal{O}}[[\unicode[STIX]{x1D6E4}]][[x]]$
, and in particular
![]() $\mathbf{1}^{\operatorname{univ}}$
is a pro-free and hence projective
$\mathbf{1}^{\operatorname{univ}}$
is a pro-free and hence projective
![]() ${\mathcal{O}}[[\unicode[STIX]{x1D6E4}]]$
-module.
${\mathcal{O}}[[\unicode[STIX]{x1D6E4}]]$
-module.
The restriction of
![]() $\widetilde{P}^{\unicode[STIX]{x1D713}}$
to
$\widetilde{P}^{\unicode[STIX]{x1D713}}$
to
![]() $K$
is projective in the category of pseudocompact
$K$
is projective in the category of pseudocompact
![]() ${\mathcal{O}}[[K]]$
-modules on which
${\mathcal{O}}[[K]]$
-modules on which
![]() $Z\cap K$
acts by the central character
$Z\cap K$
acts by the central character
![]() $\unicode[STIX]{x1D713}^{-1}$
[Reference PaškūnasPaš15, Corollary 5.3]. By restricting further to
$\unicode[STIX]{x1D713}^{-1}$
[Reference PaškūnasPaš15, Corollary 5.3]. By restricting further to
![]() $I_{1}$
, we deduce that
$I_{1}$
, we deduce that
![]() $\widetilde{P}^{\unicode[STIX]{x1D713}}$
is projective in the category of pseudocompact
$\widetilde{P}^{\unicode[STIX]{x1D713}}$
is projective in the category of pseudocompact
![]() ${\mathcal{O}}[[I_{1}]]$
-modules, where
${\mathcal{O}}[[I_{1}]]$
-modules, where
 $Z_{1}:=I_{1}\cap Z$
acts by the central character
$Z_{1}:=I_{1}\cap Z$
acts by the central character
![]() $\unicode[STIX]{x1D713}^{-1}$
.
$\unicode[STIX]{x1D713}^{-1}$
.
Since
![]() $p>2$
, there is a character
$p>2$
, there is a character
 $\unicode[STIX]{x1D6FF}:\unicode[STIX]{x1D6E4}\rightarrow {\mathcal{O}}^{\times }$
such that
$\unicode[STIX]{x1D6FF}:\unicode[STIX]{x1D6E4}\rightarrow {\mathcal{O}}^{\times }$
such that
![]() $\unicode[STIX]{x1D6FF}^{2}=\unicode[STIX]{x1D713}$
. Twisting by characters preserves projectivity, so that
$\unicode[STIX]{x1D6FF}^{2}=\unicode[STIX]{x1D713}$
. Twisting by characters preserves projectivity, so that
 $\mathbf{1}^{\operatorname{univ}}\otimes \unicode[STIX]{x1D6FF}$
is projective in the category of pseudocompact
$\mathbf{1}^{\operatorname{univ}}\otimes \unicode[STIX]{x1D6FF}$
is projective in the category of pseudocompact
![]() ${\mathcal{O}}[[\unicode[STIX]{x1D6E4}]]$
-modules and
${\mathcal{O}}[[\unicode[STIX]{x1D6E4}]]$
-modules and
 $\widetilde{P}^{\unicode[STIX]{x1D713}}\otimes (\unicode[STIX]{x1D6FF}\circ \det )$
is projective in the category of pseudocompact
$\widetilde{P}^{\unicode[STIX]{x1D713}}\otimes (\unicode[STIX]{x1D6FF}\circ \det )$
is projective in the category of pseudocompact
![]() ${\mathcal{O}}[[I_{1}]]$
-modules on which
${\mathcal{O}}[[I_{1}]]$
-modules on which
![]() $Z_{1}$
acts trivially. We may identify this last category with the category of pseudocompact
$Z_{1}$
acts trivially. We may identify this last category with the category of pseudocompact
 ${\mathcal{O}}[[I_{1}/Z_{1}]]$
-modules.
${\mathcal{O}}[[I_{1}/Z_{1}]]$
-modules.
We have an isomorphism of
![]() $I_{1}$
-representations
$I_{1}$
-representations
 $$\begin{eqnarray}\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}\cong (\widetilde{P}^{\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D6FF}\circ \det )\operatorname{⊗̂}_{{\mathcal{O}}}(\mathbf{1}^{\operatorname{univ}}\otimes _{{\mathcal{O}}}\unicode[STIX]{x1D6FF}),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}\cong (\widetilde{P}^{\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D6FF}\circ \det )\operatorname{⊗̂}_{{\mathcal{O}}}(\mathbf{1}^{\operatorname{univ}}\otimes _{{\mathcal{O}}}\unicode[STIX]{x1D6FF}),\end{eqnarray}$$
where
![]() $I_{1}$
acts on
$I_{1}$
acts on
 $\mathbf{1}^{\operatorname{univ}}\otimes _{{\mathcal{O}}}\unicode[STIX]{x1D6FF}$
via the homomorphism
$\mathbf{1}^{\operatorname{univ}}\otimes _{{\mathcal{O}}}\unicode[STIX]{x1D6FF}$
via the homomorphism
![]() $I_{1}\rightarrow \unicode[STIX]{x1D6E4}$
,
$I_{1}\rightarrow \unicode[STIX]{x1D6E4}$
,
 $g\mapsto (\det g)^{-1}$
. We may therefore assume that
$g\mapsto (\det g)^{-1}$
. We may therefore assume that
![]() $\unicode[STIX]{x1D713}|_{Z_{1}}$
is trivial, so that
$\unicode[STIX]{x1D713}|_{Z_{1}}$
is trivial, so that
![]() $\widetilde{P}^{\unicode[STIX]{x1D713}}$
is projective in the category of pseudocompact
$\widetilde{P}^{\unicode[STIX]{x1D713}}$
is projective in the category of pseudocompact
 ${\mathcal{O}}[[I_{1}/Z_{1}]]$
-modules. Thus, there are indexing sets
${\mathcal{O}}[[I_{1}/Z_{1}]]$
-modules. Thus, there are indexing sets
![]() $J_{1}$
and
$J_{1}$
and
![]() $J_{2}$
such that
$J_{2}$
such that
 $$\begin{eqnarray}\widetilde{P}^{\unicode[STIX]{x1D713}}|_{I_{1}}\cong \mathop{\prod }_{j_{1}\in J}{\mathcal{O}}[[I_{1}/Z_{1}]],\quad \mathbf{1}^{\operatorname{univ}}\cong \mathop{\prod }_{j_{2}\in J_{2}}{\mathcal{O}}[[\unicode[STIX]{x1D6E4}]],\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{P}^{\unicode[STIX]{x1D713}}|_{I_{1}}\cong \mathop{\prod }_{j_{1}\in J}{\mathcal{O}}[[I_{1}/Z_{1}]],\quad \mathbf{1}^{\operatorname{univ}}\cong \mathop{\prod }_{j_{2}\in J_{2}}{\mathcal{O}}[[\unicode[STIX]{x1D6E4}]],\end{eqnarray}$$
where the first isomorphism is an isomorphism of pseudocompact
![]() ${\mathcal{O}}[[I_{1}]]$
-modules, and the second isomorphism is an isomorphism of pseudocompact
${\mathcal{O}}[[I_{1}]]$
-modules, and the second isomorphism is an isomorphism of pseudocompact
![]() ${\mathcal{O}}[[\unicode[STIX]{x1D6E4}]]$
-modules. Since completed tensor products commute with products, we obtain an isomorphism of pseudocompact
${\mathcal{O}}[[\unicode[STIX]{x1D6E4}]]$
-modules. Since completed tensor products commute with products, we obtain an isomorphism of pseudocompact
![]() ${\mathcal{O}}[[I_{1}]]$
-modules:
${\mathcal{O}}[[I_{1}]]$
-modules:
 $$\begin{eqnarray}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}})\cong \mathop{\prod }_{j_{1}\in J_{1}}\mathop{\prod }_{j_{2}\in J_{2}}{\mathcal{O}}[[I_{1}/Z_{1}]]\operatorname{⊗̂}_{{\mathcal{O}}}{\mathcal{O}}[[\unicode[STIX]{x1D6E4}]].\end{eqnarray}$$
$$\begin{eqnarray}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}})\cong \mathop{\prod }_{j_{1}\in J_{1}}\mathop{\prod }_{j_{2}\in J_{2}}{\mathcal{O}}[[I_{1}/Z_{1}]]\operatorname{⊗̂}_{{\mathcal{O}}}{\mathcal{O}}[[\unicode[STIX]{x1D6E4}]].\end{eqnarray}$$
Since
![]() $p>2$
, the determinant induces an isomorphism between
$p>2$
, the determinant induces an isomorphism between
![]() $Z_{1}$
and
$Z_{1}$
and
![]() $\unicode[STIX]{x1D6E4}$
. Thus, the map
$\unicode[STIX]{x1D6E4}$
. Thus, the map
 $I_{1}\rightarrow I_{1}/Z_{1}\times \unicode[STIX]{x1D6E4}$
,
$I_{1}\rightarrow I_{1}/Z_{1}\times \unicode[STIX]{x1D6E4}$
,
 $g\mapsto (gZ_{1},(\det g)^{-1})$
is an isomorphism of groups. The isomorphism induces a natural isomorphism of
$g\mapsto (gZ_{1},(\det g)^{-1})$
is an isomorphism of groups. The isomorphism induces a natural isomorphism of
![]() ${\mathcal{O}}[[I_{1}]]$
-modules,
${\mathcal{O}}[[I_{1}]]$
-modules,
 ${\mathcal{O}}[[I_{1}]]\cong {\mathcal{O}}[[I_{1}/Z_{1}]]\operatorname{⊗̂}_{{\mathcal{O}}}{\mathcal{O}}[[\unicode[STIX]{x1D6E4}]]$
. We conclude that
${\mathcal{O}}[[I_{1}]]\cong {\mathcal{O}}[[I_{1}/Z_{1}]]\operatorname{⊗̂}_{{\mathcal{O}}}{\mathcal{O}}[[\unicode[STIX]{x1D6E4}]]$
. We conclude that
 $\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is a pro-free and hence a projective
$\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is a pro-free and hence a projective
![]() ${\mathcal{O}}[[I_{1}]]$
-module.◻
${\mathcal{O}}[[I_{1}]]$
-module.◻
Remark 6.11. We will see in Theorem 6.18 below that in fact
 $\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is a projective object of
$\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is a projective object of
![]() $\mathfrak{C}({\mathcal{O}})$
. It is not so difficult to prove this directly, but we have found it more convenient to deduce it as part of the general formalism of arithmetic actions.
$\mathfrak{C}({\mathcal{O}})$
. It is not so difficult to prove this directly, but we have found it more convenient to deduce it as part of the general formalism of arithmetic actions.
Proposition 6.12. Let
 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
, and let
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{a,b}$
, and let
 $\unicode[STIX]{x1D6FF}:\mathbb{Q}_{p}^{\times }\rightarrow {\mathcal{O}}^{\times }$
be a character that is trivial modulo
$\unicode[STIX]{x1D6FF}:\mathbb{Q}_{p}^{\times }\rightarrow {\mathcal{O}}^{\times }$
be a character that is trivial modulo
![]() $\unicode[STIX]{x1D71B}$
, chosen so that
$\unicode[STIX]{x1D71B}$
, chosen so that
![]() $\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}|_{\mathbb{Z}_{p}^{\times }}$
is the central character of
$\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}|_{\mathbb{Z}_{p}^{\times }}$
is the central character of
![]() $\unicode[STIX]{x1D70E}^{\circ }$
. Then there is a natural isomorphism of
$\unicode[STIX]{x1D70E}^{\circ }$
. Then there is a natural isomorphism of
![]() $R_{p}$
-modules
$R_{p}$
-modules
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\overset{\cong }{\longrightarrow }\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\overset{\cong }{\longrightarrow }\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}},\end{eqnarray}$$
where
![]() $R_{p}$
acts on the left-hand side via the isomorphism
$R_{p}$
acts on the left-hand side via the isomorphism
 $R_{p}\cong R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
and on the right-hand side via the isomorphism
$R_{p}\cong R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
and on the right-hand side via the isomorphism
 $R_{p}\cong R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
.
$R_{p}\cong R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
.
Proof. Using Lemma 6.9, we may assume that
![]() $\unicode[STIX]{x1D713}|_{K\cap Z}$
is the central character of
$\unicode[STIX]{x1D713}|_{K\cap Z}$
is the central character of
![]() $\unicode[STIX]{x1D70E}$
. We note that
$\unicode[STIX]{x1D70E}$
. We note that
 $\mathbf{1}^{\operatorname{univ}}\otimes _{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D6EC}^{\text{ur}}$
is the largest quotient of
$\mathbf{1}^{\operatorname{univ}}\otimes _{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D6EC}^{\text{ur}}$
is the largest quotient of
![]() $\mathbf{1}^{\operatorname{univ}}$
on which
$\mathbf{1}^{\operatorname{univ}}$
on which
![]() $K\cap Z$
acts trivially. Since the central character of
$K\cap Z$
acts trivially. Since the central character of
![]() $(\unicode[STIX]{x1D70E}^{\circ })^{d}$
is
$(\unicode[STIX]{x1D70E}^{\circ })^{d}$
is
![]() $\unicode[STIX]{x1D713}^{-1}|_{\mathbb{Z}_{p}^{\times }}$
, and the central character of
$\unicode[STIX]{x1D713}^{-1}|_{\mathbb{Z}_{p}^{\times }}$
, and the central character of
![]() $\widetilde{P}^{\unicode[STIX]{x1D713}}$
is
$\widetilde{P}^{\unicode[STIX]{x1D713}}$
is
![]() $\unicode[STIX]{x1D713}^{-1}$
, we have a natural isomorphism
$\unicode[STIX]{x1D713}^{-1}$
, we have a natural isomorphism
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\overset{\cong }{\longrightarrow }\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}(\mathbf{1}^{\operatorname{univ}}\otimes _{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D6EC}^{\text{ur}}),(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\overset{\cong }{\longrightarrow }\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}(\mathbf{1}^{\operatorname{univ}}\otimes _{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D6EC}^{\text{ur}}),(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}.\end{eqnarray}$$
Since
![]() $K$
acts trivially on
$K$
acts trivially on
 $\mathbf{1}^{\operatorname{univ}}\otimes _{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D6EC}^{\text{ur}}$
, we have an isomorphism:
$\mathbf{1}^{\operatorname{univ}}\otimes _{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D6EC}^{\text{ur}}$
, we have an isomorphism:
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}(\mathbf{1}^{\operatorname{univ}}\otimes _{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D6EC}^{\text{ur}}),(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\cong \operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}(\mathbf{1}^{\operatorname{univ}}\otimes _{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D6EC}^{\text{ur}}),(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\cong \operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6EC}^{\text{ur}}$
carries a trivial
$\unicode[STIX]{x1D6EC}^{\text{ur}}$
carries a trivial
![]() $K$
-action and
$K$
-action and
![]() $R_{p}$
acts by the isomorphism
$R_{p}$
acts by the isomorphism
 $R_{p}\cong R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
. To finish the proof, we need to construct a natural isomorphism of
$R_{p}\cong R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
. To finish the proof, we need to construct a natural isomorphism of
 $R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
-modules:
$R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
-modules:
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\cong \operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\cong \operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}}.\end{eqnarray}$$
Both sides of (6.13) are finitely generated
 $R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}}$
-modules. The
$R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}}$
-modules. The
![]() $\mathfrak{m}$
-adic topology on
$\mathfrak{m}$
-adic topology on
 $R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}}$
induces a topology on them, and makes them into pseudocompact,
$R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}}$
induces a topology on them, and makes them into pseudocompact,
![]() ${\mathcal{O}}$
-torsion-free
${\mathcal{O}}$
-torsion-free
![]() ${\mathcal{O}}$
-modules. It is therefore enough to construct a natural isomorphism between the Schikhof duals of both sides of (6.13). To ease the notation, we let
${\mathcal{O}}$
-modules. It is therefore enough to construct a natural isomorphism between the Schikhof duals of both sides of (6.13). To ease the notation, we let
 $A=\widetilde{P}^{\unicode[STIX]{x1D713}}$
,
$A=\widetilde{P}^{\unicode[STIX]{x1D713}}$
,
 $B=\unicode[STIX]{x1D6EC}^{\text{ur}}$
,
$B=\unicode[STIX]{x1D6EC}^{\text{ur}}$
,
 $C=(\unicode[STIX]{x1D70E}^{\circ })^{d}$
. Since for a pseudocompact
$C=(\unicode[STIX]{x1D70E}^{\circ })^{d}$
. Since for a pseudocompact
![]() ${\mathcal{O}}$
-module
${\mathcal{O}}$
-module
![]() $D$
, we have
$D$
, we have
 $D^{d}=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(D,{\mathcal{O}})\cong \mathop{\varprojlim }\nolimits_{n}\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(D,{\mathcal{O}}/\unicode[STIX]{x1D71B}^{n})$
, using the adjointness between
$D^{d}=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(D,{\mathcal{O}})\cong \mathop{\varprojlim }\nolimits_{n}\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(D,{\mathcal{O}}/\unicode[STIX]{x1D71B}^{n})$
, using the adjointness between
![]() $\operatorname{⊗̂}_{{\mathcal{O}}}$
and
$\operatorname{⊗̂}_{{\mathcal{O}}}$
and
 $\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}$
(see [Reference BrumerBru66, Lemma 2.4]), we obtain natural isomorphisms
$\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}$
(see [Reference BrumerBru66, Lemma 2.4]), we obtain natural isomorphisms
 $$\begin{eqnarray}\displaystyle (\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A,C)^{d}\operatorname{⊗̂}_{{\mathcal{O}}}B)^{d} & \cong & \displaystyle \operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(B,(\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A,C)^{d})^{d})\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(B,\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A,C))\cong \operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A\operatorname{⊗̂}_{{\mathcal{O}}}B,C)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A,C)^{d}\operatorname{⊗̂}_{{\mathcal{O}}}B)^{d} & \cong & \displaystyle \operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(B,(\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A,C)^{d})^{d})\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(B,\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A,C))\cong \operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A\operatorname{⊗̂}_{{\mathcal{O}}}B,C)\nonumber\end{eqnarray}$$
and hence a natural isomorphism
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A\operatorname{⊗̂}_{{\mathcal{O}}}B,C)^{d}\cong \operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A,C)^{d}\operatorname{⊗̂}_{{\mathcal{O}}}B.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A\operatorname{⊗̂}_{{\mathcal{O}}}B,C)^{d}\cong \operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(A,C)^{d}\operatorname{⊗̂}_{{\mathcal{O}}}B.\end{eqnarray}$$
Since the isomorphism is natural and
![]() $K$
acts trivially on
$K$
acts trivially on
![]() $B$
, we obtain a natural isomorphism
$B$
, we obtain a natural isomorphism
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(A\operatorname{⊗̂}_{{\mathcal{O}}}B,C)^{d}\cong \operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(A,C)^{d}\operatorname{⊗̂}_{{\mathcal{O}}}B.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(A\operatorname{⊗̂}_{{\mathcal{O}}}B,C)^{d}\cong \operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(A,C)^{d}\operatorname{⊗̂}_{{\mathcal{O}}}B.\end{eqnarray}$$
Since the action of
![]() $R_{p}^{\unicode[STIX]{x1D713}}$
commutes with the action of
$R_{p}^{\unicode[STIX]{x1D713}}$
commutes with the action of
![]() $K$
and the isomorphism is natural, we deduce that (6.13) holds.◻
$K$
and the isomorphism is natural, we deduce that (6.13) holds.◻
Proposition 6.14. For any
![]() $\unicode[STIX]{x1D70E}$
, the action of
$\unicode[STIX]{x1D70E}$
, the action of
 $R_{p}\cong R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
on
$R_{p}\cong R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
on
 $$\begin{eqnarray}M^{\prime }(\unicode[STIX]{x1D70E}^{\circ }):=\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\end{eqnarray}$$
$$\begin{eqnarray}M^{\prime }(\unicode[STIX]{x1D70E}^{\circ }):=\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}\end{eqnarray}$$
factors through
![]() $R_{p}(\unicode[STIX]{x1D70E})$
. Moreover,
$R_{p}(\unicode[STIX]{x1D70E})$
. Moreover,
![]() $M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })$
is a maximal Cohen–Macaulay
$M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })$
is a maximal Cohen–Macaulay
![]() $R_{p}(\unicode[STIX]{x1D70E})$
-module and
$R_{p}(\unicode[STIX]{x1D70E})$
-module and
 $M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is a locally free
$M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is a locally free
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
-module of rank
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
-module of rank
![]() $1$
.
$1$
.
Remark 6.15. Recall that
![]() $M(\unicode[STIX]{x1D70E}^{\circ })$
was defined in the last section. Soon we will see from Theorem 6.18 below that
$M(\unicode[STIX]{x1D70E}^{\circ })$
was defined in the last section. Soon we will see from Theorem 6.18 below that
 $\widetilde{P}\stackrel{{\sim}}{\longrightarrow }\widetilde{P}^{\unicode[STIX]{x1D713}}\;\widehat{\otimes }_{{\mathcal{O}}}\;\mathbf{1}^{\operatorname{univ}}$
and thus also that
$\widetilde{P}\stackrel{{\sim}}{\longrightarrow }\widetilde{P}^{\unicode[STIX]{x1D713}}\;\widehat{\otimes }_{{\mathcal{O}}}\;\mathbf{1}^{\operatorname{univ}}$
and thus also that
 $M(\unicode[STIX]{x1D70E}^{\circ })\simeq M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })$
.
$M(\unicode[STIX]{x1D70E}^{\circ })\simeq M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })$
.
Proof. If the central character of
![]() $\unicode[STIX]{x1D70E}$
is not congruent to
$\unicode[STIX]{x1D70E}$
is not congruent to
![]() $\unicode[STIX]{x1D713}|_{\mathbb{Z}_{p}^{\times }}$
modulo
$\unicode[STIX]{x1D713}|_{\mathbb{Z}_{p}^{\times }}$
modulo
![]() $\unicode[STIX]{x1D71B}$
, then both
$\unicode[STIX]{x1D71B}$
, then both
![]() $R_{p}(\unicode[STIX]{x1D70E})$
and
$R_{p}(\unicode[STIX]{x1D70E})$
and
![]() $M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })$
are zero. Otherwise, there is a character
$M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })$
are zero. Otherwise, there is a character
 $\unicode[STIX]{x1D6FF}:{\mathbb{Q}_{p}}^{\times }\rightarrow {\mathcal{O}}^{\times }$
trivial modulo
$\unicode[STIX]{x1D6FF}:{\mathbb{Q}_{p}}^{\times }\rightarrow {\mathcal{O}}^{\times }$
trivial modulo
![]() $\unicode[STIX]{x1D71B}$
such that
$\unicode[STIX]{x1D71B}$
such that
 $(\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2})|_{\mathbb{Z}_{p}^{\times }}$
is equal to the central character of
$(\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2})|_{\mathbb{Z}_{p}^{\times }}$
is equal to the central character of
![]() $\unicode[STIX]{x1D70E}$
. Proposition 6.12 gives us an isomorphism of
$\unicode[STIX]{x1D70E}$
. Proposition 6.12 gives us an isomorphism of
![]() $R_{p}$
-modules
$R_{p}$
-modules
 $$\begin{eqnarray}M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })\cong M^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E}^{\circ })\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}},\end{eqnarray}$$
$$\begin{eqnarray}M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })\cong M^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E}^{\circ })\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}},\end{eqnarray}$$
where
 $M^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E}^{\circ }):=\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}$
, and the action of
$M^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E}^{\circ }):=\operatorname{Hom}_{{\mathcal{O}}[[K]]}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}},(\unicode[STIX]{x1D70E}^{\circ })^{d})^{d}$
, and the action of
![]() $R_{p}$
on the right-hand side is given by
$R_{p}$
on the right-hand side is given by
 $R_{p}\cong R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
. The action of
$R_{p}\cong R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
. The action of
![]() $R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}$
on
$R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}$
on
 $M^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E}^{\circ })$
factors through the action of
$M^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E}^{\circ })$
factors through the action of
 $R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E})$
and makes it into a maximal Cohen–Macaulay
$R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E})$
and makes it into a maximal Cohen–Macaulay
 $R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E})$
-module [Reference PaškūnasPaš15, Corollaries 6.4 and 6.5]. Since
$R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E})$
-module [Reference PaškūnasPaš15, Corollaries 6.4 and 6.5]. Since
 $\unicode[STIX]{x1D6EC}^{\text{ur}}\cong {\mathcal{O}}[[x]]$
, we conclude that
$\unicode[STIX]{x1D6EC}^{\text{ur}}\cong {\mathcal{O}}[[x]]$
, we conclude that
 $M^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E}^{\circ })\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}}$
is a maximal Cohen–Macaulay
$M^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E}^{\circ })\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}}$
is a maximal Cohen–Macaulay
 $R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E})\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}}$
-module. Using (6.3), we see that
$R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E})\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}^{\text{ur}}$
-module. Using (6.3), we see that
![]() $M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })$
is a maximal Cohen–Macaulay
$M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })$
is a maximal Cohen–Macaulay
![]() $R_{p}(\unicode[STIX]{x1D70E})$
-module. Since
$R_{p}(\unicode[STIX]{x1D70E})$
-module. Since
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
is a regular ring, a standard argument using the Auslander–Buchsbaum theorem shows that
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
is a regular ring, a standard argument using the Auslander–Buchsbaum theorem shows that
 $M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is a locally free
$M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is a locally free
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
-module. It follows from [Reference PaškūnasPaš15, Propositions 4.14 and 2.22] that
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
-module. It follows from [Reference PaškūnasPaš15, Propositions 4.14 and 2.22] that
 $$\begin{eqnarray}\dim _{\unicode[STIX]{x1D705}(x)}M^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E}^{\circ })\otimes _{R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}}\unicode[STIX]{x1D705}(x)=1,\quad \forall x\in \operatorname{m - Spec}R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E})[1/p].\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\unicode[STIX]{x1D705}(x)}M^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E}^{\circ })\otimes _{R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}}\unicode[STIX]{x1D705}(x)=1,\quad \forall x\in \operatorname{m - Spec}R_{p}^{\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}^{2}}(\unicode[STIX]{x1D70E})[1/p].\end{eqnarray}$$
This together with (6.16) gives us
 $$\begin{eqnarray}\dim _{\unicode[STIX]{x1D705}(x)}M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })\otimes _{R_{p}}\unicode[STIX]{x1D705}(x)=1,\quad \forall x\in \operatorname{m - Spec}R_{p}(\unicode[STIX]{x1D70E})[1/p].\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\unicode[STIX]{x1D705}(x)}M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })\otimes _{R_{p}}\unicode[STIX]{x1D705}(x)=1,\quad \forall x\in \operatorname{m - Spec}R_{p}(\unicode[STIX]{x1D70E})[1/p].\end{eqnarray}$$
Hence,
 $M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is a locally free
$M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is a locally free
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
-module of rank
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
-module of rank
![]() $1$
.◻
$1$
.◻
The natural action of
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
on
${\mathcal{H}}(\unicode[STIX]{x1D70E}^{\circ })$
on
![]() $M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })$
commutes with the action of
$M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })$
commutes with the action of
![]() $R_{p}(\unicode[STIX]{x1D70E})$
and hence induces an action of
$R_{p}(\unicode[STIX]{x1D70E})$
and hence induces an action of
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
on
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
on
 $M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
. Since
$M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
. Since
 $M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is locally free of rank
$M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is locally free of rank
![]() $1$
over
$1$
over
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
by Proposition 6.14, we obtain a homomorphism of
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
by Proposition 6.14, we obtain a homomorphism of
![]() $E$
-algebras:
$E$
-algebras:
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow \text{End}_{R_{p}(\unicode[STIX]{x1D70E})[1/p]}(M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })[1/p])\cong R_{p}(\unicode[STIX]{x1D70E})[1/p].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow \text{End}_{R_{p}(\unicode[STIX]{x1D70E})[1/p]}(M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })[1/p])\cong R_{p}(\unicode[STIX]{x1D70E})[1/p].\end{eqnarray}$$
Proposition 6.17. The map
 $\unicode[STIX]{x1D6FC}:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow R_{p}(\unicode[STIX]{x1D70E})[1/p]$
coincides with the map
$\unicode[STIX]{x1D6FC}:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow R_{p}(\unicode[STIX]{x1D70E})[1/p]$
coincides with the map
 $\unicode[STIX]{x1D702}:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow R_{p}(\unicode[STIX]{x1D70E})[1/p]$
constructed in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Theorem 4.1].
$\unicode[STIX]{x1D702}:{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow R_{p}(\unicode[STIX]{x1D70E})[1/p]$
constructed in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16, Theorem 4.1].
Proof. It is enough to show that the specializations of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D702}$
at
$\unicode[STIX]{x1D702}$
at
![]() $x$
coincide for
$x$
coincide for
![]() $x$
in a Zariski dense subset of
$x$
in a Zariski dense subset of
 $\operatorname{m - Spec}R_{p}(\unicode[STIX]{x1D70E})[1/p]$
. The isomorphism
$\operatorname{m - Spec}R_{p}(\unicode[STIX]{x1D70E})[1/p]$
. The isomorphism
 $R_{p}\cong R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
maps
$R_{p}\cong R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
maps
![]() $x$
to a pair
$x$
to a pair
![]() $(y,z)$
, where
$(y,z)$
, where
 $y\in \operatorname{m - Spec}R_{p}^{\unicode[STIX]{x1D713}}[1/p]$
and
$y\in \operatorname{m - Spec}R_{p}^{\unicode[STIX]{x1D713}}[1/p]$
and
 $z\in \operatorname{m - Spec}\unicode[STIX]{x1D6EC}[1/p]$
, so that if
$z\in \operatorname{m - Spec}\unicode[STIX]{x1D6EC}[1/p]$
, so that if
![]() $r_{x}^{\operatorname{univ}}$
,
$r_{x}^{\operatorname{univ}}$
,
![]() $r_{y}^{\operatorname{univ},\unicode[STIX]{x1D713}}$
and
$r_{y}^{\operatorname{univ},\unicode[STIX]{x1D713}}$
and
![]() $\mathbf{1}_{z}^{\operatorname{univ}}$
are Galois representations corresponding to
$\mathbf{1}_{z}^{\operatorname{univ}}$
are Galois representations corresponding to
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
, respectively, then
$z$
, respectively, then
 $$\begin{eqnarray}r_{x}^{\operatorname{univ}}\cong r_{y}^{\operatorname{univ},\unicode[STIX]{x1D713}}\otimes \mathbf{1}_{z}^{\operatorname{univ}}.\end{eqnarray}$$
$$\begin{eqnarray}r_{x}^{\operatorname{univ}}\cong r_{y}^{\operatorname{univ},\unicode[STIX]{x1D713}}\otimes \mathbf{1}_{z}^{\operatorname{univ}}.\end{eqnarray}$$
Let
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{x}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}((\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}})\operatorname{⊗̂}_{R_{p}}{\mathcal{O}}_{\unicode[STIX]{x1D705}(x)},E), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{y}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{R_{p}^{\unicode[STIX]{x1D713}}}{\mathcal{O}}_{\unicode[STIX]{x1D705}(y)},E). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{x}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}((\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}})\operatorname{⊗̂}_{R_{p}}{\mathcal{O}}_{\unicode[STIX]{x1D705}(x)},E), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{y}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{R_{p}^{\unicode[STIX]{x1D713}}}{\mathcal{O}}_{\unicode[STIX]{x1D705}(y)},E). & \displaystyle \nonumber\end{eqnarray}$$
Then both are unitary
![]() $G$
-Banach space representations and we have
$G$
-Banach space representations and we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{x}\cong \unicode[STIX]{x1D6F1}_{y}\otimes (\mathbf{1}_{z}^{\operatorname{univ}}\circ \det ).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{x}\cong \unicode[STIX]{x1D6F1}_{y}\otimes (\mathbf{1}_{z}^{\operatorname{univ}}\circ \det ).\end{eqnarray}$$
It follows from [Reference PaškūnasPaš15, Proposition 2.22] that
 $\operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F1}_{x})$
is a one-dimensional
$\operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F1}_{x})$
is a one-dimensional
![]() $\unicode[STIX]{x1D705}(x)$
-vector space, and the action of
$\unicode[STIX]{x1D705}(x)$
-vector space, and the action of
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
on it coincides with the specialization of
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
on it coincides with the specialization of
![]() $\unicode[STIX]{x1D6FC}$
at
$\unicode[STIX]{x1D6FC}$
at
![]() $x$
, which can be written as the composite
$x$
, which can be written as the composite
 $$\begin{eqnarray}{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow \text{End}_{\unicode[STIX]{x1D705}(x)}(M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })\otimes _{R_{p}}\unicode[STIX]{x1D705}(x))\cong \unicode[STIX]{x1D705}(x).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}(\unicode[STIX]{x1D70E})\rightarrow \text{End}_{\unicode[STIX]{x1D705}(x)}(M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })\otimes _{R_{p}}\unicode[STIX]{x1D705}(x))\cong \unicode[STIX]{x1D705}(x).\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D70E}$
is an algebraic representation of
$\unicode[STIX]{x1D70E}$
is an algebraic representation of
![]() $K$
, we have
$K$
, we have
 $$\begin{eqnarray}\operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F1}_{x})\cong \operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F1}_{x}^{\text{l.alg}}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F1}_{x})\cong \operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F1}_{x}^{\text{l.alg}}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6F1}_{x}^{\text{l.alg}}$
is the subspace of locally algebraic vectors in
$\unicode[STIX]{x1D6F1}_{x}^{\text{l.alg}}$
is the subspace of locally algebraic vectors in
![]() $\unicode[STIX]{x1D6F1}_{x}$
.
$\unicode[STIX]{x1D6F1}_{x}$
.
It follows from the main result of [Reference PaškūnasPaš13] that the specialization
![]() $\unicode[STIX]{x1D6F1}_{x}$
of
$\unicode[STIX]{x1D6F1}_{x}$
of
![]() $\widetilde{P}^{\unicode[STIX]{x1D713}}$
coincides with the Banach space representation attached to
$\widetilde{P}^{\unicode[STIX]{x1D713}}$
coincides with the Banach space representation attached to
![]() $r_{x}^{\operatorname{univ}}$
via the
$r_{x}^{\operatorname{univ}}$
via the
![]() $p$
-adic local Langlands correspondence. It is then a consequence of the construction of the appropriate cases of the
$p$
-adic local Langlands correspondence. It is then a consequence of the construction of the appropriate cases of the
![]() $p$
-adic local Langlands correspondence (that is, the construction of
$p$
-adic local Langlands correspondence (that is, the construction of
![]() $\unicode[STIX]{x1D6F1}_{x}$
) that there is an embedding
$\unicode[STIX]{x1D6F1}_{x}$
) that there is an embedding
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x}^{\operatorname{univ}})\otimes \unicode[STIX]{x1D70B}_{\text{alg}}(r_{x}^{\operatorname{univ}}){\hookrightarrow}\unicode[STIX]{x1D6F1}_{x}^{\text{l.alg}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x}^{\operatorname{univ}})\otimes \unicode[STIX]{x1D70B}_{\text{alg}}(r_{x}^{\operatorname{univ}}){\hookrightarrow}\unicode[STIX]{x1D6F1}_{x}^{\text{l.alg}},\end{eqnarray}$$
where
 $\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x}^{\operatorname{univ}})=r_{p}^{-1}(\text{WD}(r_{x}^{\operatorname{univ}})^{F-\text{ss}})$
is the smooth representation of
$\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x}^{\operatorname{univ}})=r_{p}^{-1}(\text{WD}(r_{x}^{\operatorname{univ}})^{F-\text{ss}})$
is the smooth representation of
![]() $G$
corresponding to the Weil–Deligne representation associated to
$G$
corresponding to the Weil–Deligne representation associated to
![]() $r_{x}^{\operatorname{univ}}$
by the classical Langlands correspondence
$r_{x}^{\operatorname{univ}}$
by the classical Langlands correspondence
![]() $r_{p}$
(normalized as in § 1.12), and
$r_{p}$
(normalized as in § 1.12), and
 $\unicode[STIX]{x1D70B}_{\text{alg}}(r_{x}^{\operatorname{univ}})$
is the algebraic representation of
$\unicode[STIX]{x1D70B}_{\text{alg}}(r_{x}^{\operatorname{univ}})$
is the algebraic representation of
![]() $G$
whose restriction to
$G$
whose restriction to
![]() $K$
is equal to
$K$
is equal to
![]() $\unicode[STIX]{x1D70E}$
. Indeed, if the representation
$\unicode[STIX]{x1D70E}$
. Indeed, if the representation
![]() $r_{x}^{\operatorname{univ}}$
is irreducible, then (for a Zariski dense set of
$r_{x}^{\operatorname{univ}}$
is irreducible, then (for a Zariski dense set of
![]() $x$
)
$x$
)
![]() $\unicode[STIX]{x1D6F1}_{x}$
is a completion of
$\unicode[STIX]{x1D6F1}_{x}$
is a completion of
 $\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x}^{\operatorname{univ}})\otimes \unicode[STIX]{x1D70B}_{\text{alg}}(r_{x}^{\operatorname{univ}})$
by the main result of [Reference Berger and BreuilBB10] (see in particular [Reference Berger and BreuilBB10, Theorem 4.3.1]), while in the case that
$\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x}^{\operatorname{univ}})\otimes \unicode[STIX]{x1D70B}_{\text{alg}}(r_{x}^{\operatorname{univ}})$
by the main result of [Reference Berger and BreuilBB10] (see in particular [Reference Berger and BreuilBB10, Theorem 4.3.1]), while in the case that
![]() $r_{x}^{\operatorname{univ}}$
is reducible, the result follows from the explicit description of
$r_{x}^{\operatorname{univ}}$
is reducible, the result follows from the explicit description of
![]() $\unicode[STIX]{x1D6F1}_{x}$
in [Reference Breuil and EmertonBE10].
$\unicode[STIX]{x1D6F1}_{x}$
in [Reference Breuil and EmertonBE10].
Since we have already noted that
 $\operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F1}_{x})$
is one dimensional, we find that in fact
$\operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F1}_{x})$
is one dimensional, we find that in fact
 $$\begin{eqnarray}\operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F1}_{x})\cong \operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x}^{\operatorname{univ}})\otimes \unicode[STIX]{x1D70B}_{\text{alg}}(r_{x}^{\operatorname{univ}}))\cong \unicode[STIX]{x1D70B}_{\text{sm}}(r_{x}^{\operatorname{univ}})^{K}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F1}_{x})\cong \operatorname{Hom}_{K}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70B}_{\text{sm}}(r_{x}^{\operatorname{univ}})\otimes \unicode[STIX]{x1D70B}_{\text{alg}}(r_{x}^{\operatorname{univ}}))\cong \unicode[STIX]{x1D70B}_{\text{sm}}(r_{x}^{\operatorname{univ}})^{K}\end{eqnarray}$$
and the right-hand side of this isomorphism is indeed a one-dimensional vector space on which
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
acts via the specialization of
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
acts via the specialization of
![]() $\unicode[STIX]{x1D702}$
.◻
$\unicode[STIX]{x1D702}$
.◻
Let
![]() $R_{p}$
act on
$R_{p}$
act on
 $\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
via the isomorphism
$\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
via the isomorphism
 $R_{p}\cong R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
, where (as throughout this section) the action of
$R_{p}\cong R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
, where (as throughout this section) the action of
![]() $R_{p}^{\unicode[STIX]{x1D713}}$
on
$R_{p}^{\unicode[STIX]{x1D713}}$
on
![]() $\widetilde{P}^{\unicode[STIX]{x1D713}}$
is via the isomorphism
$\widetilde{P}^{\unicode[STIX]{x1D713}}$
is via the isomorphism
 $R_{p}^{\unicode[STIX]{x1D713}}\cong \text{End}_{\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})}(\widetilde{P}^{\unicode[STIX]{x1D713}})$
constructed in [Reference PaškūnasPaš13].
$R_{p}^{\unicode[STIX]{x1D713}}\cong \text{End}_{\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})}(\widetilde{P}^{\unicode[STIX]{x1D713}})$
constructed in [Reference PaškūnasPaš13].
Theorem 6.18.
 $\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is a projective envelope of
$\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
in
$\unicode[STIX]{x1D70B}^{\vee }$
in
![]() $\mathfrak{C}({\mathcal{O}})$
, and the action of
$\mathfrak{C}({\mathcal{O}})$
, and the action of
![]() $R_{p}$
on
$R_{p}$
on
 $\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is arithmetic.
$\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is arithmetic.
Proof. We will show that the action of
![]() $R_{p}$
on
$R_{p}$
on
 $\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
satisfies the axioms (AA1)–(AA4) with
$\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
satisfies the axioms (AA1)–(AA4) with
![]() $d=0$
; then the action is arithmetic by definition, and
$d=0$
; then the action is arithmetic by definition, and
 $\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is a projective envelope of
$\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
in
$\unicode[STIX]{x1D70B}^{\vee }$
in
![]() $\mathfrak{C}({\mathcal{O}})$
by Theorem 4.32 (applied with
$\mathfrak{C}({\mathcal{O}})$
by Theorem 4.32 (applied with
![]() $d=0$
and with
$d=0$
and with
![]() $M_{\infty }$
taken to be
$M_{\infty }$
taken to be
 $\widetilde{P}^{\unicode[STIX]{x1D713}}\;\widehat{\otimes }_{{\mathcal{O}}}\,\mathbf{1}^{\operatorname{univ}}$
).
$\widetilde{P}^{\unicode[STIX]{x1D713}}\;\widehat{\otimes }_{{\mathcal{O}}}\,\mathbf{1}^{\operatorname{univ}}$
).
It is shown in [Reference PaškūnasPaš15, Proposition 6.1] that
 $\mathbb{F}\operatorname{⊗̂}_{R_{p}^{\unicode[STIX]{x1D713}}}\widetilde{P}^{\unicode[STIX]{x1D713}}$
is a finitely generated
$\mathbb{F}\operatorname{⊗̂}_{R_{p}^{\unicode[STIX]{x1D713}}}\widetilde{P}^{\unicode[STIX]{x1D713}}$
is a finitely generated
![]() ${\mathcal{O}}[[K]]$
-module, so the topological version of Nakayama’s lemma implies that
${\mathcal{O}}[[K]]$
-module, so the topological version of Nakayama’s lemma implies that
![]() $\widetilde{P}^{\unicode[STIX]{x1D713}}$
is a finitely generated
$\widetilde{P}^{\unicode[STIX]{x1D713}}$
is a finitely generated
 $R_{p}^{\unicode[STIX]{x1D713}}[[K]]$
-module. Since
$R_{p}^{\unicode[STIX]{x1D713}}[[K]]$
-module. Since
![]() $\mathbf{1}^{\operatorname{univ}}$
is a free
$\mathbf{1}^{\operatorname{univ}}$
is a free
![]() $\unicode[STIX]{x1D6EC}$
-module of rank
$\unicode[STIX]{x1D6EC}$
-module of rank
![]() $1$
,
$1$
,
 $\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is a finitely generated module over
$\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
is a finitely generated module over
 $(R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC})[[K]]$
and so (AA1) holds. Proposition 6.10 implies that (AA2) holds. Proposition 6.14 implies that (AA3) holds (indeed, it shows that the support of
$(R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC})[[K]]$
and so (AA1) holds. Proposition 6.10 implies that (AA2) holds. Proposition 6.14 implies that (AA3) holds (indeed, it shows that the support of
![]() $M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })$
is all of
$M^{\prime }(\unicode[STIX]{x1D70E}^{\circ })$
is all of
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
). Proposition 6.17 implies that (AA4) holds.◻
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
). Proposition 6.17 implies that (AA4) holds.◻
Recall that for each fixed central character
 $\unicode[STIX]{x1D713}:Z\rightarrow {\mathcal{O}}^{\times }$
, there is an exact functor
$\unicode[STIX]{x1D713}:Z\rightarrow {\mathcal{O}}^{\times }$
, there is an exact functor
![]() $\check{\mathbf{V}}$
from
$\check{\mathbf{V}}$
from
![]() $\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
to the category of continuous
$\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
to the category of continuous
![]() $G_{\mathbb{Q}_{p}}$
-representations on compact
$G_{\mathbb{Q}_{p}}$
-representations on compact
![]() ${\mathcal{O}}$
-modules. This is a modification of the functor introduced by Colmez in [Reference ColmezCol10b]; see [Reference PaškūnasPaš13, § 5.7] for details (we additionally have to twist the functor in [Reference PaškūnasPaš13] by the inverse of the cyclotomic character to get the desired relationship between the determinant of the Galois representations and the central character of
${\mathcal{O}}$
-modules. This is a modification of the functor introduced by Colmez in [Reference ColmezCol10b]; see [Reference PaškūnasPaš13, § 5.7] for details (we additionally have to twist the functor in [Reference PaškūnasPaš13] by the inverse of the cyclotomic character to get the desired relationship between the determinant of the Galois representations and the central character of
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
-representations.) If
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
-representations.) If
![]() $\unicode[STIX]{x1D6F1}$
is an admissible unitary
$\unicode[STIX]{x1D6F1}$
is an admissible unitary
![]() $E$
-Banach space representation of
$E$
-Banach space representation of
![]() $G$
with central character
$G$
with central character
![]() $\unicode[STIX]{x1D713}$
, and
$\unicode[STIX]{x1D713}$
, and
![]() $\unicode[STIX]{x1D6E9}$
is an open bounded
$\unicode[STIX]{x1D6E9}$
is an open bounded
![]() $G$
-invariant lattice in
$G$
-invariant lattice in
![]() $\unicode[STIX]{x1D6F1}$
, then the Schikhof dual of
$\unicode[STIX]{x1D6F1}$
, then the Schikhof dual of
![]() $\unicode[STIX]{x1D6E9}$
is an object of
$\unicode[STIX]{x1D6E9}$
is an object of
![]() $\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
and
$\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
and
 $\check{\mathbf{V}}(\unicode[STIX]{x1D6F1}):=\check{\mathbf{V}}(\unicode[STIX]{x1D6E9}^{d})[1/p]$
does not depend on the choice of
$\check{\mathbf{V}}(\unicode[STIX]{x1D6F1}):=\check{\mathbf{V}}(\unicode[STIX]{x1D6E9}^{d})[1/p]$
does not depend on the choice of
![]() $\unicode[STIX]{x1D6E9}$
.
$\unicode[STIX]{x1D6E9}$
.
The representation
![]() $\widetilde{P}^{\unicode[STIX]{x1D713}}$
satisfies the conditions (N0), (N1) and (N2) of [Reference PaškūnasPaš15, § 4] by [Reference PaškūnasPaš15, Proposition 6.1]. In particular, we have
$\widetilde{P}^{\unicode[STIX]{x1D713}}$
satisfies the conditions (N0), (N1) and (N2) of [Reference PaškūnasPaš15, § 4] by [Reference PaškūnasPaš15, Proposition 6.1]. In particular, we have
 $\check{\mathbf{V}}(\widetilde{P}^{\unicode[STIX]{x1D713}})\cong r^{\operatorname{univ},\unicode[STIX]{x1D713}}$
as
$\check{\mathbf{V}}(\widetilde{P}^{\unicode[STIX]{x1D713}})\cong r^{\operatorname{univ},\unicode[STIX]{x1D713}}$
as
 $R_{p}^{\unicode[STIX]{x1D713}}[[G_{\mathbb{Q}_{p}}]]$
-modules.
$R_{p}^{\unicode[STIX]{x1D713}}[[G_{\mathbb{Q}_{p}}]]$
-modules.
Let
 $R_{\infty }=R_{p}[[x_{1},\ldots ,x_{d}]]$
and let
$R_{\infty }=R_{p}[[x_{1},\ldots ,x_{d}]]$
and let
![]() $M_{\infty }$
be an
$M_{\infty }$
be an
![]() $R_{\infty }[G]$
-module satisfying the axioms (AA1)–(AA4). To
$R_{\infty }[G]$
-module satisfying the axioms (AA1)–(AA4). To
 $x\in \operatorname{m - Spec}R_{\infty }[1/p]$
we associate a unitary
$x\in \operatorname{m - Spec}R_{\infty }[1/p]$
we associate a unitary
![]() $\unicode[STIX]{x1D705}(x)$
-Banach space representation of
$\unicode[STIX]{x1D705}(x)$
-Banach space representation of
![]() $G$
,
$G$
,
 $\unicode[STIX]{x1D6F1}_{\infty ,x}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(M_{\infty }\operatorname{⊗̂}_{R_{\infty }}{\mathcal{O}}_{\unicode[STIX]{x1D705}(x)},E).$
The map
$\unicode[STIX]{x1D6F1}_{\infty ,x}:=\operatorname{Hom}_{{\mathcal{O}}}^{\text{cont}}(M_{\infty }\operatorname{⊗̂}_{R_{\infty }}{\mathcal{O}}_{\unicode[STIX]{x1D705}(x)},E).$
The map
 $R_{p}\rightarrow R_{\infty }$
induces a map
$R_{p}\rightarrow R_{\infty }$
induces a map
 $R_{p}\rightarrow \unicode[STIX]{x1D705}(x)$
and we let
$R_{p}\rightarrow \unicode[STIX]{x1D705}(x)$
and we let
 $r_{x}^{\operatorname{univ}}:=r^{\operatorname{univ}}\otimes _{R_{p}}\unicode[STIX]{x1D705}(x)$
.
$r_{x}^{\operatorname{univ}}:=r^{\operatorname{univ}}\otimes _{R_{p}}\unicode[STIX]{x1D705}(x)$
.
Corollary 6.19. We have an isomorphism of Galois representations
 $\check{\mathbf{V}}(\unicode[STIX]{x1D6F1}_{\infty ,x})\cong r_{x}^{\operatorname{univ}}$
. In particular,
$\check{\mathbf{V}}(\unicode[STIX]{x1D6F1}_{\infty ,x})\cong r_{x}^{\operatorname{univ}}$
. In particular,
 $\unicode[STIX]{x1D6F1}_{\infty ,x}\neq 0$
for all
$\unicode[STIX]{x1D6F1}_{\infty ,x}\neq 0$
for all
 $x\in \operatorname{m - Spec}R_{\infty }[1/p]$
.
$x\in \operatorname{m - Spec}R_{\infty }[1/p]$
.
Proof. Theorem 4.32 allows us to assume that
 $R_{\infty }=R_{p}$
and
$R_{\infty }=R_{p}$
and
 $M_{\infty }=\widetilde{P}$
is a projective envelope of
$M_{\infty }=\widetilde{P}$
is a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
in
$\unicode[STIX]{x1D70B}^{\vee }$
in
![]() $\mathfrak{C}({\mathcal{O}})$
. Since an arithmetic action of
$\mathfrak{C}({\mathcal{O}})$
. Since an arithmetic action of
![]() $R_{p}$
on
$R_{p}$
on
![]() $\widetilde{P}$
is unique by Theorem 4.30, using Theorem 6.18 we may assume that
$\widetilde{P}$
is unique by Theorem 4.30, using Theorem 6.18 we may assume that
 $R_{\infty }=R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
and
$R_{\infty }=R_{p}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\unicode[STIX]{x1D6EC}$
and
 $M_{\infty }=\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
. Then, with the notation introduced in the course of the proof of Proposition 6.17,
$M_{\infty }=\widetilde{P}^{\unicode[STIX]{x1D713}}\operatorname{⊗̂}_{{\mathcal{O}}}\mathbf{1}^{\operatorname{univ}}$
. Then, with the notation introduced in the course of the proof of Proposition 6.17,
![]() $x$
corresponds to a pair
$x$
corresponds to a pair
![]() $(y,z)$
,
$(y,z)$
,
 $\unicode[STIX]{x1D6F1}_{\infty ,x}=\unicode[STIX]{x1D6F1}_{x}\cong \unicode[STIX]{x1D6F1}_{y}\otimes (\mathbf{1}_{z}^{\operatorname{univ}}\circ \det )$
as in the proof of Proposition 6.17. It follows from [Reference PaškūnasPaš15, Lemma 4.3] that
$\unicode[STIX]{x1D6F1}_{\infty ,x}=\unicode[STIX]{x1D6F1}_{x}\cong \unicode[STIX]{x1D6F1}_{y}\otimes (\mathbf{1}_{z}^{\operatorname{univ}}\circ \det )$
as in the proof of Proposition 6.17. It follows from [Reference PaškūnasPaš15, Lemma 4.3] that
 $\check{\mathbf{V}}(\unicode[STIX]{x1D6F1}_{y})\cong r_{y}^{\operatorname{univ},\unicode[STIX]{x1D713}}$
. Since
$\check{\mathbf{V}}(\unicode[STIX]{x1D6F1}_{y})\cong r_{y}^{\operatorname{univ},\unicode[STIX]{x1D713}}$
. Since
![]() $\check{\mathbf{V}}$
is compatible with twisting by characters, we have
$\check{\mathbf{V}}$
is compatible with twisting by characters, we have
 $\check{\mathbf{V}}(\unicode[STIX]{x1D6F1}_{x})\cong \check{\mathbf{V}}(\unicode[STIX]{x1D6F1}_{y})\otimes \mathbf{1}_{z}^{\operatorname{univ}}\cong r_{x}^{\operatorname{univ}}$
, as required.◻
$\check{\mathbf{V}}(\unicode[STIX]{x1D6F1}_{x})\cong \check{\mathbf{V}}(\unicode[STIX]{x1D6F1}_{y})\otimes \mathbf{1}_{z}^{\operatorname{univ}}\cong r_{x}^{\operatorname{univ}}$
, as required.◻
Corollary 6.20.
![]() $R_{\infty }$
acts faithfully on
$R_{\infty }$
acts faithfully on
![]() $M_{\infty }$
.
$M_{\infty }$
.
Proof. It follows from Corollary 6.19 that
 $M_{\infty }\otimes _{R_{\infty }}\unicode[STIX]{x1D705}(x)$
is non-zero for all
$M_{\infty }\otimes _{R_{\infty }}\unicode[STIX]{x1D705}(x)$
is non-zero for all
 $x\in \operatorname{m - Spec}R_{\infty }[1/p]$
. Since
$x\in \operatorname{m - Spec}R_{\infty }[1/p]$
. Since
![]() $R_{p}$
and hence
$R_{p}$
and hence
![]() $R_{\infty }$
are reduced, we deduce that the action is faithful.◻
$R_{\infty }$
are reduced, we deduce that the action is faithful.◻
We now use the results of [Reference PaškūnasPaš13] to describe
 $\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P}$
. We will use this result in Corollary 7.5 below to describe the
$\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P}$
. We will use this result in Corollary 7.5 below to describe the
![]() $\mathfrak{m}$
-torsion in the completed cohomology of a modular curve, where
$\mathfrak{m}$
-torsion in the completed cohomology of a modular curve, where
![]() $\mathfrak{m}$
is a maximal ideal in a Hecke algebra.
$\mathfrak{m}$
is a maximal ideal in a Hecke algebra.
Proposition 6.21. The representation
![]() $\unicode[STIX]{x1D70B}^{\vee }$
occurs as a subquotient of
$\unicode[STIX]{x1D70B}^{\vee }$
occurs as a subquotient of
 $\,\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P}$
with multiplicity one. More precisely, if we let
$\,\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P}$
with multiplicity one. More precisely, if we let
 $\unicode[STIX]{x1D705}(\bar{r}):=(\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P})^{\vee }$
, then the
$\unicode[STIX]{x1D705}(\bar{r}):=(\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P})^{\vee }$
, then the
![]() $G$
-socle filtration of
$G$
-socle filtration of
![]() $\unicode[STIX]{x1D705}(\bar{r})$
is described as follows.
$\unicode[STIX]{x1D705}(\bar{r})$
is described as follows.
(i) If
 $\bar{r}$
is irreducible, then
$\bar{r}$
is irreducible, then
 $\unicode[STIX]{x1D705}(\bar{r})\cong \unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D705}(\bar{r})\cong \unicode[STIX]{x1D70B}$
.(ii) If
 $\bar{r}$
is a generic non-split extension of characters (so the ratio of the two characters is not
$\bar{r}$
is a generic non-split extension of characters (so the ratio of the two characters is not
 $1,\unicode[STIX]{x1D714}^{\pm 1}$
), the
$1,\unicode[STIX]{x1D714}^{\pm 1}$
), the
 $G$
-socle filtration of
$G$
-socle filtration of
 $\unicode[STIX]{x1D705}(\bar{r})$
has length two, with graded pieces consisting of
$\unicode[STIX]{x1D705}(\bar{r})$
has length two, with graded pieces consisting of
 $\unicode[STIX]{x1D70B}$
and of the other principal series representation in the block of
$\unicode[STIX]{x1D70B}$
and of the other principal series representation in the block of
 $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.(iii) If
 $\bar{r}\cong \big(\!\begin{smallmatrix}1 & \ast \\ 0 & \unicode[STIX]{x1D714}\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
, then the
$\bar{r}\cong \big(\!\begin{smallmatrix}1 & \ast \\ 0 & \unicode[STIX]{x1D714}\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
, then the
 $G$
-socle filtration of
$G$
-socle filtration of
 $\unicode[STIX]{x1D705}(\bar{r})$
has length three and the graded pieces are
$\unicode[STIX]{x1D705}(\bar{r})$
has length three and the graded pieces are
 $\unicode[STIX]{x1D70B}$
, the twist by
$\unicode[STIX]{x1D70B}$
, the twist by
 $\unicode[STIX]{x1D712}\circ \det$
of the Steinberg representation and two copies of the one-dimensional representation
$\unicode[STIX]{x1D712}\circ \det$
of the Steinberg representation and two copies of the one-dimensional representation
 $\unicode[STIX]{x1D712}\circ \det$
.
$\unicode[STIX]{x1D712}\circ \det$
.
Proof. We choose any continuous character
![]() $\unicode[STIX]{x1D713}$
such that
$\unicode[STIX]{x1D713}$
such that
![]() $\unicode[STIX]{x1D713}\unicode[STIX]{x1D700}^{-1}$
lifts
$\unicode[STIX]{x1D713}\unicode[STIX]{x1D700}^{-1}$
lifts
![]() $\det \bar{r}$
. It follows from Theorem 6.18 that
$\det \bar{r}$
. It follows from Theorem 6.18 that
 $\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P}\cong \mathbb{F}\operatorname{⊗̂}_{R_{p}^{\unicode[STIX]{x1D713}}}\widetilde{P}^{\unicode[STIX]{x1D713}}$
. Since we can identify the endomorphism ring of
$\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P}\cong \mathbb{F}\operatorname{⊗̂}_{R_{p}^{\unicode[STIX]{x1D713}}}\widetilde{P}^{\unicode[STIX]{x1D713}}$
. Since we can identify the endomorphism ring of
![]() $\widetilde{P}^{\unicode[STIX]{x1D713}}$
with
$\widetilde{P}^{\unicode[STIX]{x1D713}}$
with
![]() $R_{p}^{\unicode[STIX]{x1D713}}$
, see (6.6), it follows from [Reference PaškūnasPaš13, Lemma 3.7] applied with
$R_{p}^{\unicode[STIX]{x1D713}}$
, see (6.6), it follows from [Reference PaškūnasPaš13, Lemma 3.7] applied with
![]() $S=\unicode[STIX]{x1D70B}^{\vee }$
that any
$S=\unicode[STIX]{x1D70B}^{\vee }$
that any
![]() $Q$
in
$Q$
in
![]() $\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
satisfying the hypotheses (H1)–(H4) of [Reference PaškūnasPaš13, § 3] is isomorphic to
$\mathfrak{C}^{\unicode[STIX]{x1D713}}({\mathcal{O}})$
satisfying the hypotheses (H1)–(H4) of [Reference PaškūnasPaš13, § 3] is isomorphic to
 $\mathbb{F}\operatorname{⊗̂}_{R_{p}^{\unicode[STIX]{x1D713}}}\widetilde{P}^{\unicode[STIX]{x1D713}}$
, so that
$\mathbb{F}\operatorname{⊗̂}_{R_{p}^{\unicode[STIX]{x1D713}}}\widetilde{P}^{\unicode[STIX]{x1D713}}$
, so that
 $\unicode[STIX]{x1D705}(\bar{r})\cong Q^{\vee }$
. (We leave the reader to check that (H5) is not used to prove this part of [Reference PaškūnasPaš13, Lemma 3.7].) In all the cases
$\unicode[STIX]{x1D705}(\bar{r})\cong Q^{\vee }$
. (We leave the reader to check that (H5) is not used to prove this part of [Reference PaškūnasPaš13, Lemma 3.7].) In all the cases
![]() $Q$
has been constructed explicitly in [Reference PaškūnasPaš13] and it is immediate from the construction of
$Q$
has been constructed explicitly in [Reference PaškūnasPaš13] and it is immediate from the construction of
![]() $Q$
that the assertions about the socle filtration hold; see [Reference PaškūnasPaš13, Propositions 6.1 and 8.3 and Remark 10.33].◻
$Q$
that the assertions about the socle filtration hold; see [Reference PaškūnasPaš13, Propositions 6.1 and 8.3 and Remark 10.33].◻
Remark 6.22. In the first two cases of Proposition 6.21,
![]() $\unicode[STIX]{x1D705}(\bar{r})$
coincides with what Colmez calls the atome automorphe in [Reference ColmezCol10b, § VII.4]. In the last case,
$\unicode[STIX]{x1D705}(\bar{r})$
coincides with what Colmez calls the atome automorphe in [Reference ColmezCol10b, § VII.4]. In the last case,
![]() $\unicode[STIX]{x1D705}(\bar{r})$
has an extra copy of
$\unicode[STIX]{x1D705}(\bar{r})$
has an extra copy of
![]() $\unicode[STIX]{x1D712}\circ \det$
. This has to do with the fact that Colmez requires that his atome automorphe lift to irreducible unitary Banach space representations of
$\unicode[STIX]{x1D712}\circ \det$
. This has to do with the fact that Colmez requires that his atome automorphe lift to irreducible unitary Banach space representations of
![]() $G$
.
$G$
.
Corollary 6.23. There is a natural isomorphism
 $R_{p}\stackrel{{\sim}}{\longrightarrow }\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
.
$R_{p}\stackrel{{\sim}}{\longrightarrow }\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
.
Proof. Theorems 4.30 and 6.18 yield an isomorphism
 $\widetilde{P}\stackrel{{\sim}}{\longrightarrow }\widetilde{P}^{\unicode[STIX]{x1D713}}\;\widehat{\otimes }_{{\mathcal{O}}}\;\mathbf{1}^{\operatorname{univ}}$
as
$\widetilde{P}\stackrel{{\sim}}{\longrightarrow }\widetilde{P}^{\unicode[STIX]{x1D713}}\;\widehat{\otimes }_{{\mathcal{O}}}\;\mathbf{1}^{\operatorname{univ}}$
as
![]() $R_{p}[G]$
-modules via the isomorphism
$R_{p}[G]$
-modules via the isomorphism
 $R_{p}\stackrel{{\sim}}{\longrightarrow }R_{p}^{\unicode[STIX]{x1D713}}\;\widehat{\otimes }_{{\mathcal{O}}}\;\unicode[STIX]{x1D6EC}$
given by (6.2). Now
$R_{p}\stackrel{{\sim}}{\longrightarrow }R_{p}^{\unicode[STIX]{x1D713}}\;\widehat{\otimes }_{{\mathcal{O}}}\;\unicode[STIX]{x1D6EC}$
given by (6.2). Now
 $\text{End}_{G}^{\text{cont}}(\mathbf{1}^{\operatorname{univ}})=\unicode[STIX]{x1D6EC}$
, while (6.6) gives a natural isomorphism
$\text{End}_{G}^{\text{cont}}(\mathbf{1}^{\operatorname{univ}})=\unicode[STIX]{x1D6EC}$
, while (6.6) gives a natural isomorphism
 $R_{p}^{\unicode[STIX]{x1D713}}\stackrel{{\sim}}{\longrightarrow }\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P}^{\unicode[STIX]{x1D713}}).$
Thus, the corollary amounts to proving that the natural homomorphism
$R_{p}^{\unicode[STIX]{x1D713}}\stackrel{{\sim}}{\longrightarrow }\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P}^{\unicode[STIX]{x1D713}}).$
Thus, the corollary amounts to proving that the natural homomorphism
 $$\begin{eqnarray}\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P}^{\unicode[STIX]{x1D713}})\;\widehat{\otimes }_{{\mathcal{O}}}\;\text{End}_{G}^{\text{cont}}(\mathbf{1}^{\operatorname{univ}})\rightarrow \text{End}_{\mathfrak{ C}({\mathcal{O}})}(\widetilde{P}^{\unicode[STIX]{x1D713}}\;\widehat{\otimes }_{{\mathcal{O}}}\;\mathbf{1}^{\operatorname{univ}})\end{eqnarray}$$
$$\begin{eqnarray}\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P}^{\unicode[STIX]{x1D713}})\;\widehat{\otimes }_{{\mathcal{O}}}\;\text{End}_{G}^{\text{cont}}(\mathbf{1}^{\operatorname{univ}})\rightarrow \text{End}_{\mathfrak{ C}({\mathcal{O}})}(\widetilde{P}^{\unicode[STIX]{x1D713}}\;\widehat{\otimes }_{{\mathcal{O}}}\;\mathbf{1}^{\operatorname{univ}})\end{eqnarray}$$
is an isomorphism. The map is an injection of pseudocompact
![]() ${\mathcal{O}}$
-algebras. This makes the ring
${\mathcal{O}}$
-algebras. This makes the ring
 $\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
into a compact
$\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
into a compact
![]() $R_{p}$
-module. By the topological version of Nakayama’s lemma, in order to show that the map is surjective it is enough to show that
$R_{p}$
-module. By the topological version of Nakayama’s lemma, in order to show that the map is surjective it is enough to show that
 $\mathbb{F}\operatorname{⊗̂}_{R_{p}}\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
is a one-dimensional
$\mathbb{F}\operatorname{⊗̂}_{R_{p}}\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
is a one-dimensional
![]() $\mathbb{F}$
-vector space. Since
$\mathbb{F}$
-vector space. Since
![]() $\widetilde{P}$
is projective, we have an isomorphism:
$\widetilde{P}$
is projective, we have an isomorphism:
 $$\begin{eqnarray}\mathbb{F}\operatorname{⊗̂}_{R_{p}}\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})\cong \operatorname{Hom}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P},\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{F}\operatorname{⊗̂}_{R_{p}}\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})\cong \operatorname{Hom}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P},\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P}).\end{eqnarray}$$
By Proposition 6.21,
![]() $\unicode[STIX]{x1D70B}^{\vee }$
occurs as a subquotient of
$\unicode[STIX]{x1D70B}^{\vee }$
occurs as a subquotient of
 $\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P}$
with multiplicity one. Since
$\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P}$
with multiplicity one. Since
![]() $\widetilde{P}$
is a projective envelope of
$\widetilde{P}$
is a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
and
$\unicode[STIX]{x1D70B}^{\vee }$
and
 $\text{End}_{\mathfrak{C}({\mathcal{O}})}(\unicode[STIX]{x1D70B}^{\vee })=\mathbb{F}$
, this implies that
$\text{End}_{\mathfrak{C}({\mathcal{O}})}(\unicode[STIX]{x1D70B}^{\vee })=\mathbb{F}$
, this implies that
 $\operatorname{Hom}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P},\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P})$
is a one-dimensional
$\operatorname{Hom}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P},\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P})$
is a one-dimensional
![]() $\mathbb{F}$
-vector space, as required.◻
$\mathbb{F}$
-vector space, as required.◻
6.24 Endomorphism rings and deformation rings
We maintain the notation of the previous sections; in particular,
![]() $\widetilde{P}$
denotes a projective envelope of
$\widetilde{P}$
denotes a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
in
$\unicode[STIX]{x1D70B}^{\vee }$
in
![]() $\mathfrak{C}({\mathcal{O}})$
. If we write
$\mathfrak{C}({\mathcal{O}})$
. If we write
 $\widetilde{R}:=\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
, then the arithmetic action of
$\widetilde{R}:=\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
, then the arithmetic action of
![]() $R_{p}$
on
$R_{p}$
on
![]() $\widetilde{P}$
provided by Theorem 4.30 gives a morphism
$\widetilde{P}$
provided by Theorem 4.30 gives a morphism
 $R_{p}\rightarrow \widetilde{R}$
, which Corollary 6.23 shows is an isomorphism. The proof of that corollary uses the analogous statement proved in [Reference PaškūnasPaš13] (when the central character is fixed), a key input to the proof of which is Colmez’s functor from
$R_{p}\rightarrow \widetilde{R}$
, which Corollary 6.23 shows is an isomorphism. The proof of that corollary uses the analogous statement proved in [Reference PaškūnasPaš13] (when the central character is fixed), a key input to the proof of which is Colmez’s functor from
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
-representations to Galois representations. It is natural to ask (especially in light of possible generalizations) whether this isomorphism can be proved using just the methods of the present paper, without appealing to Colmez’s results. In this subsection we address this question, to the extent that we can.
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
-representations to Galois representations. It is natural to ask (especially in light of possible generalizations) whether this isomorphism can be proved using just the methods of the present paper, without appealing to Colmez’s results. In this subsection we address this question, to the extent that we can.
We begin by noting that since
![]() $\widetilde{P}$
is a projective envelope of the absolutely irreducible representation
$\widetilde{P}$
is a projective envelope of the absolutely irreducible representation
![]() $\unicode[STIX]{x1D70B}^{\vee }$
, the ring
$\unicode[STIX]{x1D70B}^{\vee }$
, the ring
![]() $\widetilde{R}$
is a local ring. We will furthermore give a proof that it is commutative, from the perspective of this paper. As already noted, this result is not new. Indeed, in addition to being a consequence of Corollary 6.23 (and thus, essentially, of the results of [Reference PaškūnasPaš13]), another proof is given in [Reference Colmez, Dospinescu and PaškūnasCDP14] (see Corollary 2.22 of that paper). This latter proof uses the capturing techniques that we are also employing in the present paper and (since it is easy to do so) we present a slightly rephrased version of the argument here, in order to illustrate how it fits naturally into our present perspective.
$\widetilde{R}$
is a local ring. We will furthermore give a proof that it is commutative, from the perspective of this paper. As already noted, this result is not new. Indeed, in addition to being a consequence of Corollary 6.23 (and thus, essentially, of the results of [Reference PaškūnasPaš13]), another proof is given in [Reference Colmez, Dospinescu and PaškūnasCDP14] (see Corollary 2.22 of that paper). This latter proof uses the capturing techniques that we are also employing in the present paper and (since it is easy to do so) we present a slightly rephrased version of the argument here, in order to illustrate how it fits naturally into our present perspective.
Proposition 6.25. The ring
![]() $\widetilde{R}$
is commutative.
$\widetilde{R}$
is commutative.
Proof. We first prove that the image of
![]() $R_{p}$
in
$R_{p}$
in
![]() $\widetilde{R}$
lies in the centre of
$\widetilde{R}$
lies in the centre of
![]() $\widetilde{R}$
. To see this, suppose that
$\widetilde{R}$
. To see this, suppose that
![]() $\unicode[STIX]{x1D719}\in \widetilde{R}$
. By Proposition 4.28, to show that
$\unicode[STIX]{x1D719}\in \widetilde{R}$
. By Proposition 4.28, to show that
![]() $\unicode[STIX]{x1D719}$
commutes with the action of
$\unicode[STIX]{x1D719}$
commutes with the action of
![]() $R_{p}$
, it suffices to show that
$R_{p}$
, it suffices to show that
![]() $\unicode[STIX]{x1D719}$
commutes with the action of
$\unicode[STIX]{x1D719}$
commutes with the action of
 $R_{p}(\unicode[STIX]{x1D70E})[1/p]$
on
$R_{p}(\unicode[STIX]{x1D70E})[1/p]$
on
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
for each
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
for each
![]() $\unicode[STIX]{x1D70E}$
. Since the action of
$\unicode[STIX]{x1D70E}$
. Since the action of
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
on
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
on
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
depends only on the
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
depends only on the
![]() $G$
-action on
$G$
-action on
![]() $\widetilde{P}$
, we see that
$\widetilde{P}$
, we see that
![]() $\unicode[STIX]{x1D719}$
commutes with the
$\unicode[STIX]{x1D719}$
commutes with the
![]() ${\mathcal{H}}(\unicode[STIX]{x1D70E})$
-action on
${\mathcal{H}}(\unicode[STIX]{x1D70E})$
-action on
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
. The desired result then follows from Proposition 2.13.
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
. The desired result then follows from Proposition 2.13.
To see that
![]() $\widetilde{R}$
is commutative, we again apply Proposition 4.28, by which it suffices to show that
$\widetilde{R}$
is commutative, we again apply Proposition 4.28, by which it suffices to show that
![]() $\widetilde{R}$
acts on each
$\widetilde{R}$
acts on each
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
through a commutative quotient. This follows from the fact that each
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
through a commutative quotient. This follows from the fact that each
 $M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is locally free of rank
$M(\unicode[STIX]{x1D70E}^{\circ })[1/p]$
is locally free of rank
![]() $1$
over its support in
$1$
over its support in
 $\operatorname{Spec}R_{p}(\unicode[STIX]{x1D70E})[1/p],$
and the fact that (by the result of the previous paragraph) the
$\operatorname{Spec}R_{p}(\unicode[STIX]{x1D70E})[1/p],$
and the fact that (by the result of the previous paragraph) the
![]() $\widetilde{R}$
-action commutes with the
$\widetilde{R}$
-action commutes with the
![]() $R_{p}$
-action.◻
$R_{p}$
-action.◻
Remark 6.26. As for proving the stronger result that the canonical map
 $R_{p}\rightarrow \widetilde{R}$
is an isomorphism, in a forthcoming paper two of us (M.E. and V.P.) will establish the injectivity of the morphism
$R_{p}\rightarrow \widetilde{R}$
is an isomorphism, in a forthcoming paper two of us (M.E. and V.P.) will establish the injectivity of the morphism
 $R_{p}\rightarrow \widetilde{R}$
. (In fact, we will prove a result in the more general context of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16]; in particular, our arguments will not rely on any special aspects of the
$R_{p}\rightarrow \widetilde{R}$
. (In fact, we will prove a result in the more general context of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16]; in particular, our arguments will not rely on any special aspects of the
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
situation, such as the existence of Colmez’s functors.) However, proving the surjectivity of this morphism seems to be more difficult, and we currently do not know a proof of this surjectivity that avoids appealing to the theory of Colmez’s functor from
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
situation, such as the existence of Colmez’s functors.) However, proving the surjectivity of this morphism seems to be more difficult, and we currently do not know a proof of this surjectivity that avoids appealing to the theory of Colmez’s functor from
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
-representations to
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
-representations to
![]() $G_{\mathbb{Q}_{p}}$
-representations.
$G_{\mathbb{Q}_{p}}$
-representations.
6.27 Speculations in the residually scalar semisimplification case
Suppose for the rest of this section that
 $\bar{r}\cong \big(\!\begin{smallmatrix}\unicode[STIX]{x1D712} & \ast \\ 0 & \unicode[STIX]{x1D712}\end{smallmatrix}\!\big)$
for some
$\bar{r}\cong \big(\!\begin{smallmatrix}\unicode[STIX]{x1D712} & \ast \\ 0 & \unicode[STIX]{x1D712}\end{smallmatrix}\!\big)$
for some
![]() $\unicode[STIX]{x1D712}$
; so in particular
$\unicode[STIX]{x1D712}$
; so in particular
![]() $\bar{r}$
does not satisfy Assumption 2.2. It is natural to ask what the modules
$\bar{r}$
does not satisfy Assumption 2.2. It is natural to ask what the modules
![]() $M_{\infty }$
constructed in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] look like in this case; we give a speculative answer below. By twisting, we may assume that
$M_{\infty }$
constructed in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] look like in this case; we give a speculative answer below. By twisting, we may assume that
![]() $\unicode[STIX]{x1D712}$
is the trivial character. Let
$\unicode[STIX]{x1D712}$
is the trivial character. Let
 $\unicode[STIX]{x1D70B}=(\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D714}\otimes \mathbf{1})_{\text{sm}}$
and let
$\unicode[STIX]{x1D70B}=(\operatorname{Ind}_{B}^{G}\unicode[STIX]{x1D714}\otimes \mathbf{1})_{\text{sm}}$
and let
![]() $\widetilde{P}$
be a projective envelope of
$\widetilde{P}$
be a projective envelope of
![]() $\unicode[STIX]{x1D70B}^{\vee }$
. We first give a conjectural description of
$\unicode[STIX]{x1D70B}^{\vee }$
. We first give a conjectural description of
 $\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
, under the assumption
$\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})$
, under the assumption
![]() $p>2$
.
$p>2$
.
Let
![]() $D^{\text{ps}}$
be a functor from the category
$D^{\text{ps}}$
be a functor from the category
![]() $\mathfrak{A}$
of complete local noetherian
$\mathfrak{A}$
of complete local noetherian
![]() ${\mathcal{O}}$
-algebras with residue field
${\mathcal{O}}$
-algebras with residue field
![]() $\mathbb{F}$
to the category of sets, that assigns to
$\mathbb{F}$
to the category of sets, that assigns to
![]() $A\in \mathfrak{A}$
the set of pairs of functions
$A\in \mathfrak{A}$
the set of pairs of functions
 $(t,d):G_{\mathbb{Q}_{p}}\rightarrow A$
, where:
$(t,d):G_{\mathbb{Q}_{p}}\rightarrow A$
, where:
–
 $d:G_{\mathbb{Q}_{p}}\rightarrow A^{\times }$
is a continuous group homomorphism, congruent to
$d:G_{\mathbb{Q}_{p}}\rightarrow A^{\times }$
is a continuous group homomorphism, congruent to
 $\det \bar{r}$
modulo
$\det \bar{r}$
modulo
 $\mathfrak{m}_{A}$
;
$\mathfrak{m}_{A}$
;–
 $t:G_{\mathbb{Q}_{p}}\rightarrow A$
is a continuous function with
$t:G_{\mathbb{Q}_{p}}\rightarrow A$
is a continuous function with
 $t(1)=2$
; and,
$t(1)=2$
; and,– for all
 $g,h\in G_{\mathbb{Q}_{p}}$
, we have:
$g,h\in G_{\mathbb{Q}_{p}}$
, we have:(i)
 $t(g)\equiv \operatorname{tr}\,\bar{r}(g)\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{m}_{A})$
;
$t(g)\equiv \operatorname{tr}\,\bar{r}(g)\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{m}_{A})$
;(ii)
 $t(gh)=t(hg)$
;
$t(gh)=t(hg)$
;(iii)
 $d(g)t(g^{-1}h)-t(g)t(h)+t(gh)=0$
.
$d(g)t(g^{-1}h)-t(g)t(h)+t(gh)=0$
.
(The ‘ps’ is for ‘pseudocharacter’. By [Reference ChenevierChe14, Lemma 1.9],
![]() $D^{\text{ps}}(A)$
is the set of pseudocharacters deforming the pseudocharacter
$D^{\text{ps}}(A)$
is the set of pseudocharacters deforming the pseudocharacter
 $(\operatorname{tr}\,\bar{r},\det \bar{r})$
associated to
$(\operatorname{tr}\,\bar{r},\det \bar{r})$
associated to
![]() $\bar{r}$
.) This functor is representable by a complete local noetherian
$\bar{r}$
.) This functor is representable by a complete local noetherian
![]() ${\mathcal{O}}$
-algebra
${\mathcal{O}}$
-algebra
![]() $R^{\text{ps}}$
. Let
$R^{\text{ps}}$
. Let
 $(t^{\operatorname{univ}},d^{\operatorname{univ}}):G_{\mathbb{Q}_{p}}\rightarrow R^{\text{ps}}$
be the universal object. We expect that there is a natural isomorphism of
$(t^{\operatorname{univ}},d^{\operatorname{univ}}):G_{\mathbb{Q}_{p}}\rightarrow R^{\text{ps}}$
be the universal object. We expect that there is a natural isomorphism of
![]() ${\mathcal{O}}$
-algebras
${\mathcal{O}}$
-algebras
 $$\begin{eqnarray}\widetilde{E}:=\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})\cong (R^{\text{ps}}[[G_{\mathbb{Q}_{p}}]]/J)^{\operatorname{op}},\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{E}:=\text{End}_{\mathfrak{C}({\mathcal{O}})}(\widetilde{P})\cong (R^{\text{ps}}[[G_{\mathbb{Q}_{p}}]]/J)^{\operatorname{op}},\end{eqnarray}$$
where
![]() $J$
is the closed two-sided ideal of
$J$
is the closed two-sided ideal of
 $R^{\text{ps}}[[G_{\mathbb{Q}_{p}}]]$
generated by all the elements of the form
$R^{\text{ps}}[[G_{\mathbb{Q}_{p}}]]$
generated by all the elements of the form
 $g^{2}-t^{\operatorname{univ}}(g)g+d^{\operatorname{univ}}(g)$
for all
$g^{2}-t^{\operatorname{univ}}(g)g+d^{\operatorname{univ}}(g)$
for all
 $g\in G_{\mathbb{Q}_{p}}$
, and the superscript ‘op’ indicates the opposite algebra. We note that such an isomorphism has been established in [Reference PaškūnasPaš13, § 9], when the central character is fixed, and we expect that one can deduce (6.28) from this using the twisting techniques of the previous subsection.
$g\in G_{\mathbb{Q}_{p}}$
, and the superscript ‘op’ indicates the opposite algebra. We note that such an isomorphism has been established in [Reference PaškūnasPaš13, § 9], when the central character is fixed, and we expect that one can deduce (6.28) from this using the twisting techniques of the previous subsection.
Let
![]() $R_{p}^{\Box }$
be the framed deformation ring of
$R_{p}^{\Box }$
be the framed deformation ring of
![]() $\bar{r}$
, let
$\bar{r}$
, let
![]() $M_{\infty }$
be the patched module constructed in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] (or the variant for the completed cohomology of modular curves that we briefly discuss in § 7 below) and let
$M_{\infty }$
be the patched module constructed in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] (or the variant for the completed cohomology of modular curves that we briefly discuss in § 7 below) and let
![]() $R_{\infty }$
be the patched ring. Then
$R_{\infty }$
be the patched ring. Then
![]() $R_{\infty }$
is an
$R_{\infty }$
is an
![]() $R_{p}^{\Box }$
-algebra, and the map
$R_{p}^{\Box }$
-algebra, and the map
 $R_{p}^{\Box }\rightarrow R_{\infty }$
gives rise to a Galois representation
$R_{p}^{\Box }\rightarrow R_{\infty }$
gives rise to a Galois representation
 $r_{\infty }:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{2}(R_{\infty })$
lifting
$r_{\infty }:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{2}(R_{\infty })$
lifting
![]() $\bar{r}$
. The pair
$\bar{r}$
. The pair
 $(\operatorname{tr}\,r_{\infty },\det r_{\infty })$
gives us a point in
$(\operatorname{tr}\,r_{\infty },\det r_{\infty })$
gives us a point in
 $D^{\text{ps}}(R_{\infty })$
and hence a map
$D^{\text{ps}}(R_{\infty })$
and hence a map
 $R^{\text{ps}}\rightarrow R_{\infty }$
. Hence, we obtain a homomorphism of
$R^{\text{ps}}\rightarrow R_{\infty }$
. Hence, we obtain a homomorphism of
![]() $R^{\text{ps}}$
-algebras
$R^{\text{ps}}$
-algebras
 $R^{\text{ps}}[[G_{\mathbb{Q}_{p}}]]\rightarrow M_{2\times 2}(R_{\infty })$
.
$R^{\text{ps}}[[G_{\mathbb{Q}_{p}}]]\rightarrow M_{2\times 2}(R_{\infty })$
.
The Cayley–Hamilton theorem implies that this map is zero on
![]() $J$
, so we obtain a left action of
$J$
, so we obtain a left action of
 $R^{\text{ps}}[[G_{\mathbb{Q}_{p}}]]/J$
on the standard module
$R^{\text{ps}}[[G_{\mathbb{Q}_{p}}]]/J$
on the standard module
 $R_{\infty }\oplus R_{\infty }$
. If we admit (6.28), then we get a right action of
$R_{\infty }\oplus R_{\infty }$
. If we admit (6.28), then we get a right action of
![]() $\widetilde{E}$
on
$\widetilde{E}$
on
 $R_{\infty }\oplus R_{\infty }$
. We expect that there are isomorphisms in
$R_{\infty }\oplus R_{\infty }$
. We expect that there are isomorphisms in
![]() $\mathfrak{C}(R_{\infty })$
:
$\mathfrak{C}(R_{\infty })$
:
 $$\begin{eqnarray}M_{\infty }\cong (R_{\infty }\oplus R_{\infty })\operatorname{⊗̂}_{\widetilde{E}}\widetilde{P}\cong R_{\infty }\operatorname{⊗̂}_{R_{p}^{\Box }}(R_{p}^{\Box }\oplus R_{p}^{\Box })\operatorname{⊗̂}_{\widetilde{E}}\widetilde{P}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\infty }\cong (R_{\infty }\oplus R_{\infty })\operatorname{⊗̂}_{\widetilde{E}}\widetilde{P}\cong R_{\infty }\operatorname{⊗̂}_{R_{p}^{\Box }}(R_{p}^{\Box }\oplus R_{p}^{\Box })\operatorname{⊗̂}_{\widetilde{E}}\widetilde{P}.\end{eqnarray}$$
We note that the representation appearing on the right-hand side of this equation has been studied by Sander in his thesis [Reference SanderSan16], in the setting where the central character is fixed. Motivated by [Reference SanderSan16, Theorem 2], we expect
 $(R_{\infty }\oplus R_{\infty })\operatorname{⊗̂}_{\widetilde{E}}\widetilde{P}$
to be projective in the category of pseudocompact
$(R_{\infty }\oplus R_{\infty })\operatorname{⊗̂}_{\widetilde{E}}\widetilde{P}$
to be projective in the category of pseudocompact
![]() ${\mathcal{O}}[[K]]$
-modules. We do not expect
${\mathcal{O}}[[K]]$
-modules. We do not expect
 $(R_{\infty }\oplus R_{\infty })\operatorname{⊗̂}_{\widetilde{E}}\widetilde{P}$
to be projective in
$(R_{\infty }\oplus R_{\infty })\operatorname{⊗̂}_{\widetilde{E}}\widetilde{P}$
to be projective in
![]() $\mathfrak{C}({\mathcal{O}})$
, so the methods of § 4 cannot directly be applied to this case. However, it might be possible to prove (6.29) using Colmez’s functor. This would show that
$\mathfrak{C}({\mathcal{O}})$
, so the methods of § 4 cannot directly be applied to this case. However, it might be possible to prove (6.29) using Colmez’s functor. This would show that
![]() $M_{\infty }$
does not depend on the choices made in the patching process.
$M_{\infty }$
does not depend on the choices made in the patching process.
7 Local–global compatibility
In this final section, we briefly explain how the results of this paper give a simple new proof of the local–global compatibility theorem of [Reference EmertonEme11] (under the hypotheses that we have imposed in this paper, which differ a little from those of [Reference EmertonEme11]: locally at
![]() $p$
, we have excluded the case of split
$p$
, we have excluded the case of split
![]() $\bar{r}$
, and have allowed a slightly different collection of indecomposable reducible representations
$\bar{r}$
, and have allowed a slightly different collection of indecomposable reducible representations
![]() $\bar{r}$
; and in the global context we consider below, we exclude the possibility of so-called vexing primes). Applying these considerations to the patched modules constructed in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] allows us to prove a local–global compatibility result for the completed cohomology of a compact unitary group, but, for ease of comparison to [Reference EmertonEme11], we instead briefly discuss the output of Taylor–Wiles patching for modular curves.
$\bar{r}$
; and in the global context we consider below, we exclude the possibility of so-called vexing primes). Applying these considerations to the patched modules constructed in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] allows us to prove a local–global compatibility result for the completed cohomology of a compact unitary group, but, for ease of comparison to [Reference EmertonEme11], we instead briefly discuss the output of Taylor–Wiles patching for modular curves.
Patching in this context goes back to [Reference Taylor and WilesTW95], but the precise construction we need is not in the literature. It is, however, essentially identical to that of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] (or the variant for Shimura curves presented in [Reference ScholzeSch15]), so to keep this paper at a reasonable length we simply recall the output of the construction here.
Let
 $\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\mathbb{F})$
be an absolutely irreducible odd (so modular, by Serre’s conjecture) representation and assume that
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\mathbb{F})$
be an absolutely irreducible odd (so modular, by Serre’s conjecture) representation and assume that
![]() $p\geqslant 5$
and that
$p\geqslant 5$
and that
![]() $\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}(\unicode[STIX]{x1D701}_{p})}}$
is irreducible. Write
$\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}(\unicode[STIX]{x1D701}_{p})}}$
is irreducible. Write
 $\bar{r}:=\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}}$
and assume that
$\bar{r}:=\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}}$
and assume that
![]() $\bar{r}$
satisfies Assumption 2.2. Write
$\bar{r}$
satisfies Assumption 2.2. Write
 $r^{\operatorname{univ}}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{2}(R_{p})$
for the universal deformation of
$r^{\operatorname{univ}}:G_{\mathbb{Q}_{p}}\rightarrow \operatorname{GL}_{2}(R_{p})$
for the universal deformation of
![]() $\bar{r}$
. Let
$\bar{r}$
. Let
![]() $N(\overline{\unicode[STIX]{x1D70C}})$
be the prime-to-
$N(\overline{\unicode[STIX]{x1D70C}})$
be the prime-to-
![]() $p$
conductor of
$p$
conductor of
![]() $\overline{\unicode[STIX]{x1D70C}}$
; that is, the level of
$\overline{\unicode[STIX]{x1D70C}}$
; that is, the level of
![]() $\overline{\unicode[STIX]{x1D70C}}$
in the sense of [Reference SerreSer87]. We assume that if
$\overline{\unicode[STIX]{x1D70C}}$
in the sense of [Reference SerreSer87]. We assume that if
![]() $q|N(\overline{\unicode[STIX]{x1D70C}})$
with
$q|N(\overline{\unicode[STIX]{x1D70C}})$
with
 $q\equiv -1\hspace{0.6em}({\rm mod}\hspace{0.2em}p)$
and
$q\equiv -1\hspace{0.6em}({\rm mod}\hspace{0.2em}p)$
and
![]() $\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{q}}}$
is irreducible, then
$\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{q}}}$
is irreducible, then
![]() $\overline{\unicode[STIX]{x1D70C}}|_{I_{\mathbb{Q}_{q}}}$
is also irreducible.
$\overline{\unicode[STIX]{x1D70C}}|_{I_{\mathbb{Q}_{q}}}$
is also irreducible.
Remark 7.1. The last condition we have imposed excludes the so-called vexing primes
![]() $q$
. The assumption that there are no vexing primes means that the Galois representations associated to modular forms of level
$q$
. The assumption that there are no vexing primes means that the Galois representations associated to modular forms of level
![]() $N(\overline{\unicode[STIX]{x1D70C}})$
are necessarily minimally ramified. This assumption can be removed by considering inertial types at such primes as in [Reference Conrad, Diamond and TaylorCDT99]. Since the arguments using types are standard and are orthogonal to the main concerns of this paper, we restrict ourselves to this simple case.
$N(\overline{\unicode[STIX]{x1D70C}})$
are necessarily minimally ramified. This assumption can be removed by considering inertial types at such primes as in [Reference Conrad, Diamond and TaylorCDT99]. Since the arguments using types are standard and are orthogonal to the main concerns of this paper, we restrict ourselves to this simple case.
We caution the reader that while the use of types would also allow us to work at certain non-minimal levels, the most naive analogues of Theorem 7.4 fail to hold at arbitrary tame levels. It seems that to formulate a clean statement, one should pass to infinite level at a finite set of primes, and formulate the compatibility statement in terms of the local Langlands correspondence in families of [Reference Emerton and HelmEH14], as is done in [Reference EmertonEme11].
However, it does not seem to be easy to prove this full local–global compatibility statement using only the methods of the present paper; indeed, the proof in [Reference EmertonEme11] ultimately makes use of mod
![]() $p$
multiplicity one theorems that rely on
$p$
multiplicity one theorems that rely on
![]() $q$
-expansions, whereas, in our approach, we are only using multiplicity one theorems that result from our patched modules being Cohen–Macaulay, and certain of our local deformation rings being regular (namely the minimal deformation rings at places not dividing
$q$
-expansions, whereas, in our approach, we are only using multiplicity one theorems that result from our patched modules being Cohen–Macaulay, and certain of our local deformation rings being regular (namely the minimal deformation rings at places not dividing
![]() $p$
, and the deformation rings considered in Lemma 2.15). Note that in general the (non-minimal) local deformation rings at places away from
$p$
, and the deformation rings considered in Lemma 2.15). Note that in general the (non-minimal) local deformation rings at places away from
![]() $p$
need not be regular (even after inverting
$p$
need not be regular (even after inverting
![]() $p$
), so that carrying out the patching construction below would result in a ring
$p$
), so that carrying out the patching construction below would result in a ring
![]() $R_{\infty }$
that was no longer formally smooth over
$R_{\infty }$
that was no longer formally smooth over
![]() $R_{p}$
, to which the results of § 4 would not apply.
$R_{p}$
, to which the results of § 4 would not apply.
Let
![]() $\mathbb{T}$
be the usual Hecke algebra acting on (completed) homology and cohomology of modular curves with (tame) level
$\mathbb{T}$
be the usual Hecke algebra acting on (completed) homology and cohomology of modular curves with (tame) level
 $\unicode[STIX]{x1D6E4}_{1}(N(\overline{\unicode[STIX]{x1D70C}}))$
and
$\unicode[STIX]{x1D6E4}_{1}(N(\overline{\unicode[STIX]{x1D70C}}))$
and
![]() ${\mathcal{O}}$
-coefficients; so
${\mathcal{O}}$
-coefficients; so
![]() $\mathbb{T}$
is an
$\mathbb{T}$
is an
![]() ${\mathcal{O}}$
-algebra, generated by the operators
${\mathcal{O}}$
-algebra, generated by the operators
![]() $T_{l}$
,
$T_{l}$
,
![]() $S_{l}$
with
$S_{l}$
with
![]() $l\nmid Np$
. Let
$l\nmid Np$
. Let
![]() $\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})$
be the maximal ideal of
$\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})$
be the maximal ideal of
![]() $\mathbb{T}$
corresponding to
$\mathbb{T}$
corresponding to
![]() $\overline{\unicode[STIX]{x1D70C}}$
(so that
$\overline{\unicode[STIX]{x1D70C}}$
(so that
 $T_{l}-\operatorname{tr}\,\overline{\unicode[STIX]{x1D70C}}(\operatorname{Frob}_{l})$
and
$T_{l}-\operatorname{tr}\,\overline{\unicode[STIX]{x1D70C}}(\operatorname{Frob}_{l})$
and
 $lS_{l}-\det \overline{\unicode[STIX]{x1D70C}}(\operatorname{Frob}_{l})$
are both zero in
$lS_{l}-\det \overline{\unicode[STIX]{x1D70C}}(\operatorname{Frob}_{l})$
are both zero in
![]() $\mathbb{T}/\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})$
). Let
$\mathbb{T}/\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})$
). Let
![]() $R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}$
be the universal deformation ring for deformations of
$R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}$
be the universal deformation ring for deformations of
![]() $\overline{\unicode[STIX]{x1D70C}}$
that are minimally ramified at primes
$\overline{\unicode[STIX]{x1D70C}}$
that are minimally ramified at primes
![]() $l\neq p$
, in the sense that they have the same conductor as
$l\neq p$
, in the sense that they have the same conductor as
![]() $\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{l}}}$
(and in particular are unramified if
$\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{l}}}$
(and in particular are unramified if
 $l\nmid N(\overline{\unicode[STIX]{x1D70C}})$
). Let
$l\nmid N(\overline{\unicode[STIX]{x1D70C}})$
). Let
 $\unicode[STIX]{x1D70C}_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}^{\operatorname{univ}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})})$
denote the corresponding universal deformation of
$\unicode[STIX]{x1D70C}_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}^{\operatorname{univ}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})})$
denote the corresponding universal deformation of
![]() $\overline{\unicode[STIX]{x1D70C}}$
.
$\overline{\unicode[STIX]{x1D70C}}$
.
We now use the notation introduced in § 3, so that in particular we write
 $R_{\infty }:=R_{p}\;\widehat{\otimes }_{{\mathcal{O}}}\;{\mathcal{O}}[[x_{1},\ldots ,x_{d}]]$
for some
$R_{\infty }:=R_{p}\;\widehat{\otimes }_{{\mathcal{O}}}\;{\mathcal{O}}[[x_{1},\ldots ,x_{d}]]$
for some
![]() $d\geqslant 0$
. Patching the completed étale homology of the modular curves
$d\geqslant 0$
. Patching the completed étale homology of the modular curves
 $Y_{1}(N(\overline{\unicode[STIX]{x1D70C}}))$
(and using an argument of Carayol [Reference CarayolCar94], as in [Reference EmertonEme11, § 5.5] and [Reference Emerton, Gee and SavittEGS15, §§ 6.2 and 6.3], to factor out the Galois action on the completed cohomology; see also [Reference ScholzeSch15, § 9] for the analogous patching construction for Shimura curves), we obtain (for some
$Y_{1}(N(\overline{\unicode[STIX]{x1D70C}}))$
(and using an argument of Carayol [Reference CarayolCar94], as in [Reference EmertonEme11, § 5.5] and [Reference Emerton, Gee and SavittEGS15, §§ 6.2 and 6.3], to factor out the Galois action on the completed cohomology; see also [Reference ScholzeSch15, § 9] for the analogous patching construction for Shimura curves), we obtain (for some
![]() $d\geqslant 0$
) an
$d\geqslant 0$
) an
![]() $R_{\infty }[G]$
-module
$R_{\infty }[G]$
-module
![]() $M_{\infty }$
with an arithmetic action, with the further property that there are an ideal
$M_{\infty }$
with an arithmetic action, with the further property that there are an ideal
![]() $\mathfrak{a}_{\infty }$
of
$\mathfrak{a}_{\infty }$
of
![]() $R_{\infty }$
, an isomorphism of local
$R_{\infty }$
, an isomorphism of local
![]() ${\mathcal{O}}$
-algebras
${\mathcal{O}}$
-algebras
 $R_{\infty }/\mathfrak{a}_{\infty }\stackrel{{\sim}}{\longrightarrow }R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}$
and an isomorphism of
$R_{\infty }/\mathfrak{a}_{\infty }\stackrel{{\sim}}{\longrightarrow }R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}$
and an isomorphism of
 $R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}[G\times G_{\mathbb{Q}}]$
-modules
$R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}[G\times G_{\mathbb{Q}}]$
-modules
 $$\begin{eqnarray}(M_{\infty }/\mathfrak{a}_{\infty })\otimes _{R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}}(\unicode[STIX]{x1D70C}_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}^{\operatorname{univ}})^{\ast }\stackrel{{\sim}}{\longrightarrow }\widetilde{H}_{1,\acute{\text{e}}\text{t}}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})_{\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})}.\end{eqnarray}$$
$$\begin{eqnarray}(M_{\infty }/\mathfrak{a}_{\infty })\otimes _{R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}}(\unicode[STIX]{x1D70C}_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}^{\operatorname{univ}})^{\ast }\stackrel{{\sim}}{\longrightarrow }\widetilde{H}_{1,\acute{\text{e}}\text{t}}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})_{\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})}.\end{eqnarray}$$
Here
 $\widetilde{H}_{1,\acute{\text{e}}\text{t}}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})$
denotes completed étale homology, as described for example in [Reference Calegari and EmertonCE12]. The action of
$\widetilde{H}_{1,\acute{\text{e}}\text{t}}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})$
denotes completed étale homology, as described for example in [Reference Calegari and EmertonCE12]. The action of
![]() $G_{\mathbb{Q}}$
on the left-hand side is via its action on
$G_{\mathbb{Q}}$
on the left-hand side is via its action on
 $(\unicode[STIX]{x1D70C}_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}^{\operatorname{univ}})^{\ast }$
, which as in (1.12.3) denotes the
$(\unicode[STIX]{x1D70C}_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}^{\operatorname{univ}})^{\ast }$
, which as in (1.12.3) denotes the
![]() $R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}$
-linear dual of
$R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}$
-linear dual of
![]() $\unicode[STIX]{x1D70C}_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}^{\operatorname{univ}}$
.
$\unicode[STIX]{x1D70C}_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}^{\operatorname{univ}}$
.
Remark 7.3. Here we have used implicitly that the minimally ramified local (framed) deformation rings are all smooth, which follows for example from [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.19]; this ensures that the ring
![]() $R_{\infty }$
occurring in the patching argument is formally smooth over
$R_{\infty }$
occurring in the patching argument is formally smooth over
![]() $R_{p}$
.
$R_{p}$
.
Theorem 7.4. Let
![]() $p>3$
be a prime, and let
$p>3$
be a prime, and let
 $\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\mathbb{F})$
be an absolutely irreducible odd representation, with the property that
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\mathbb{F})$
be an absolutely irreducible odd representation, with the property that
![]() $\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}(\unicode[STIX]{x1D701}_{p})}}$
is irreducible,
$\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}(\unicode[STIX]{x1D701}_{p})}}$
is irreducible,
![]() $N(\overline{\unicode[STIX]{x1D70C}})$
is not divisible by any vexing primes and
$N(\overline{\unicode[STIX]{x1D70C}})$
is not divisible by any vexing primes and
![]() $\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}}$
satisfies Assumption 2.2. Then there is an isomorphism of
$\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}}$
satisfies Assumption 2.2. Then there is an isomorphism of
 $R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}[G\times G_{\mathbb{Q}}]$
-modules
$R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}[G\times G_{\mathbb{Q}}]$
-modules
 $$\begin{eqnarray}\widetilde{H}_{1,\acute{\text{e}}\text{t}}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})_{\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})}\stackrel{{\sim}}{\longrightarrow }\widetilde{P}\;\widehat{\otimes }_{R_{p}}\;(\unicode[STIX]{x1D70C}_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}^{\operatorname{univ}})^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{H}_{1,\acute{\text{e}}\text{t}}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})_{\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})}\stackrel{{\sim}}{\longrightarrow }\widetilde{P}\;\widehat{\otimes }_{R_{p}}\;(\unicode[STIX]{x1D70C}_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}^{\operatorname{univ}})^{\ast },\end{eqnarray}$$
where the completed tensor product on the right-hand side is computed by regarding
 $(\unicode[STIX]{x1D70C}_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}^{\operatorname{univ}})^{\ast }$
as a
$(\unicode[STIX]{x1D70C}_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}^{\operatorname{univ}})^{\ast }$
as a
![]() $G_{\mathbb{Q}}$
-representation on an
$G_{\mathbb{Q}}$
-representation on an
![]() $R_{p}$
-module via the natural morphism
$R_{p}$
-module via the natural morphism
 $R_{p}\rightarrow R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}$
.
$R_{p}\rightarrow R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}$
.
Proof. As noted before Remark 7.1,
![]() $\overline{\unicode[STIX]{x1D70C}}$
is modular by Serre’s conjecture, so in particular
$\overline{\unicode[STIX]{x1D70C}}$
is modular by Serre’s conjecture, so in particular
![]() $M_{\infty }$
is not zero. By Theorem 4.32, there is an isomorphism of
$M_{\infty }$
is not zero. By Theorem 4.32, there is an isomorphism of
![]() $R_{\infty }[G]$
-modules
$R_{\infty }[G]$
-modules
 $$\begin{eqnarray}M_{\infty }\cong \widetilde{P}\operatorname{⊗̂}_{{\mathcal{O}}}{\mathcal{O}}[[x_{1},\ldots ,x_{d}]]\cong \widetilde{P}\operatorname{⊗̂}_{R_{p}}R_{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}M_{\infty }\cong \widetilde{P}\operatorname{⊗̂}_{{\mathcal{O}}}{\mathcal{O}}[[x_{1},\ldots ,x_{d}]]\cong \widetilde{P}\operatorname{⊗̂}_{R_{p}}R_{\infty }.\end{eqnarray}$$
Quotienting out by
![]() $\mathfrak{a}_{\infty }$
yields an isomorphism
$\mathfrak{a}_{\infty }$
yields an isomorphism
 $$\begin{eqnarray}M_{\infty }/\mathfrak{a}_{\infty }\cong \widetilde{P}\operatorname{⊗̂}_{R_{p}}R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\infty }/\mathfrak{a}_{\infty }\cong \widetilde{P}\operatorname{⊗̂}_{R_{p}}R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}.\end{eqnarray}$$
The result now follows by tensoring both sides with
 $(\unicode[STIX]{x1D70C}_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}^{\operatorname{univ}})^{\ast }$
and applying (7.2).◻
$(\unicode[STIX]{x1D70C}_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}^{\operatorname{univ}})^{\ast }$
and applying (7.2).◻
We now show how to compute the
![]() $\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})$
-torsion in the completed étale cohomology of modular curves
$\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})$
-torsion in the completed étale cohomology of modular curves
 $\widetilde{H}_{\acute{\text{e}}\text{t}}^{1}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})$
as a
$\widetilde{H}_{\acute{\text{e}}\text{t}}^{1}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})$
as a
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
-representation.
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
-representation.
Corollary 7.5. Under the assumptions of Theorem 7.4, we have an isomorphism of
 $\mathbb{F}[G\times G_{\mathbb{Q}}]$
-modules
$\mathbb{F}[G\times G_{\mathbb{Q}}]$
-modules
 $$\begin{eqnarray}\widetilde{H}_{\acute{\text{e}}\text{t}}^{1}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),\mathbb{F})[\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})]\simeq \unicode[STIX]{x1D705}(\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}})\otimes _{\mathbb{F}}\overline{\unicode[STIX]{x1D70C}},\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{H}_{\acute{\text{e}}\text{t}}^{1}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),\mathbb{F})[\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})]\simeq \unicode[STIX]{x1D705}(\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}})\otimes _{\mathbb{F}}\overline{\unicode[STIX]{x1D70C}},\end{eqnarray}$$
where
 $\unicode[STIX]{x1D705}(\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}})$
is the representation defined in Proposition 6.21.
$\unicode[STIX]{x1D705}(\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}})$
is the representation defined in Proposition 6.21.
Proof. The Pontryagin dual of the left-hand side is
 $\widetilde{H}_{1,\acute{\text{e}}\text{t}}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})\operatorname{⊗̂}_{R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}}\mathbb{F}$
. By Theorem 7.4, we have an isomorphism of
$\widetilde{H}_{1,\acute{\text{e}}\text{t}}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})\operatorname{⊗̂}_{R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}}\mathbb{F}$
. By Theorem 7.4, we have an isomorphism of
 $\mathbb{F}[G\times G_{\mathbb{Q}}]$
-modules
$\mathbb{F}[G\times G_{\mathbb{Q}}]$
-modules
 $$\begin{eqnarray}\widetilde{H}_{1,\acute{\text{e}}\text{t}}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})\operatorname{⊗̂}_{R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}}\mathbb{F}\simeq (\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P})\operatorname{⊗̂}_{\mathbb{F}}\overline{\unicode[STIX]{x1D70C}}^{\ast }\cong \unicode[STIX]{x1D705}(\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}})^{\vee }\operatorname{⊗̂}_{\mathbb{ F}}\overline{\unicode[STIX]{x1D70C}}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{H}_{1,\acute{\text{e}}\text{t}}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})\operatorname{⊗̂}_{R_{\mathbb{Q},N(\overline{\unicode[STIX]{x1D70C}})}}\mathbb{F}\simeq (\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P})\operatorname{⊗̂}_{\mathbb{F}}\overline{\unicode[STIX]{x1D70C}}^{\ast }\cong \unicode[STIX]{x1D705}(\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}})^{\vee }\operatorname{⊗̂}_{\mathbb{ F}}\overline{\unicode[STIX]{x1D70C}}^{\ast },\end{eqnarray}$$
the last isomorphism following from the definition of
 $\unicode[STIX]{x1D705}(\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}})$
. Passing to Pontryagin duals (and noting that since
$\unicode[STIX]{x1D705}(\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}})$
. Passing to Pontryagin duals (and noting that since
![]() $\overline{\unicode[STIX]{x1D70C}}$
is an
$\overline{\unicode[STIX]{x1D70C}}$
is an
![]() $\mathbb{F}$
-representation, we have
$\mathbb{F}$
-representation, we have
 $\overline{\unicode[STIX]{x1D70C}}^{\ast }=\overline{\unicode[STIX]{x1D70C}}^{\vee }$
) gives the result.◻
$\overline{\unicode[STIX]{x1D70C}}^{\ast }=\overline{\unicode[STIX]{x1D70C}}^{\vee }$
) gives the result.◻
Remark 7.6. Corollary 7.5 together with Proposition 6.21 gives a description of the
![]() $G$
-socle filtration of
$G$
-socle filtration of
 $\widetilde{H}_{\acute{\text{e}}\text{t}}^{1}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),\mathbb{F})[\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})]$
. Even more is true.
$\widetilde{H}_{\acute{\text{e}}\text{t}}^{1}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),\mathbb{F})[\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})]$
. Even more is true.
Since in Corollary 6.23 we have identified the endomorphism ring of
![]() $\widetilde{P}$
with
$\widetilde{P}$
with
![]() $R_{p}$
and
$R_{p}$
and
![]() $\unicode[STIX]{x1D705}(\bar{r})$
is by definition
$\unicode[STIX]{x1D705}(\bar{r})$
is by definition
 $\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P}$
, a completely formal argument (see the proof of [Reference PaškūnasPaš16, Proposition 2.8]) shows that
$\mathbb{F}\operatorname{⊗̂}_{R_{p}}\widetilde{P}$
, a completely formal argument (see the proof of [Reference PaškūnasPaš16, Proposition 2.8]) shows that
![]() $\unicode[STIX]{x1D705}(\bar{r})$
is up to isomorphism the unique representation in
$\unicode[STIX]{x1D705}(\bar{r})$
is up to isomorphism the unique representation in
 $\text{Mod}_{G}^{\text{l.adm}}({\mathcal{O}})$
that is maximal with respect to the following two properties:
$\text{Mod}_{G}^{\text{l.adm}}({\mathcal{O}})$
that is maximal with respect to the following two properties:
(i) the socle of
 $\unicode[STIX]{x1D705}(\bar{r})$
is
$\unicode[STIX]{x1D705}(\bar{r})$
is
 $\unicode[STIX]{x1D70B}$
;
$\unicode[STIX]{x1D70B}$
;(ii)
 $\unicode[STIX]{x1D70B}$
occurs as a subquotient of
$\unicode[STIX]{x1D70B}$
occurs as a subquotient of
 $\unicode[STIX]{x1D705}(\bar{r})$
with multiplicity one.
$\unicode[STIX]{x1D705}(\bar{r})$
with multiplicity one.
(It is maximal in the sense that it cannot be embedded into any other strictly larger representation in
 $\text{Mod}_{G}^{\text{l.adm}}({\mathcal{O}})$
satisfying these two properties.)
$\text{Mod}_{G}^{\text{l.adm}}({\mathcal{O}})$
satisfying these two properties.)
Corollary 7.5 shows that (after factoring out the
![]() $G_{\mathbb{Q}}$
-action) the same characterization carries over to
$G_{\mathbb{Q}}$
-action) the same characterization carries over to
 $\widetilde{H}_{\acute{\text{e}}\text{t}}^{1}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),\mathbb{F})[\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})]$
. However, we warn the reader that a simple-minded application of this recipe will not work in general, and in particular it fails if
$\widetilde{H}_{\acute{\text{e}}\text{t}}^{1}(Y_{1}(N(\overline{\unicode[STIX]{x1D70C}})),\mathbb{F})[\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})]$
. However, we warn the reader that a simple-minded application of this recipe will not work in general, and in particular it fails if
 $\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}}\cong \big(\!\begin{smallmatrix}\unicode[STIX]{x1D714} & \ast \\ 0 & 1\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
.
$\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}}\cong \big(\!\begin{smallmatrix}\unicode[STIX]{x1D714} & \ast \\ 0 & 1\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
.
More precisely, if Assumption 2.2 is in force, then
![]() $\bar{r}$
is determined up to isomorphism by the data of its determinant and its unique irreducible subrepresentation. This information can be recovered from
$\bar{r}$
is determined up to isomorphism by the data of its determinant and its unique irreducible subrepresentation. This information can be recovered from
![]() $\unicode[STIX]{x1D70B}$
, which in turn determines
$\unicode[STIX]{x1D70B}$
, which in turn determines
![]() $\unicode[STIX]{x1D705}(\bar{r})$
. If on the other hand
$\unicode[STIX]{x1D705}(\bar{r})$
. If on the other hand
 $\bar{r}\cong \big(\!\begin{smallmatrix}\unicode[STIX]{x1D714} & \ast \\ 0 & 1\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
and
$\bar{r}\cong \big(\!\begin{smallmatrix}\unicode[STIX]{x1D714} & \ast \\ 0 & 1\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
and
 $\text{End}_{G_{\mathbb{Q}_{p}}}(\bar{r})=\mathbb{F}$
, then the
$\text{End}_{G_{\mathbb{Q}_{p}}}(\bar{r})=\mathbb{F}$
, then the
![]() $G$
-socle of the atome automorphe associated by Colmez in [Reference ColmezCol10b, § VII.4] to
$G$
-socle of the atome automorphe associated by Colmez in [Reference ColmezCol10b, § VII.4] to
![]() $\bar{r}$
, which we still call
$\bar{r}$
, which we still call
![]() $\unicode[STIX]{x1D70B}$
, is the Steinberg representation twisted by
$\unicode[STIX]{x1D70B}$
, is the Steinberg representation twisted by
![]() $\unicode[STIX]{x1D712}\circ \det$
. This representation still carries the information about the irreducible subrepresentation of
$\unicode[STIX]{x1D712}\circ \det$
. This representation still carries the information about the irreducible subrepresentation of
![]() $\bar{r}$
and the determinant of
$\bar{r}$
and the determinant of
![]() $\bar{r}$
but it does not determine
$\bar{r}$
but it does not determine
![]() $\bar{r}$
up to isomorphism, as it does not carry the information about the extension class in
$\bar{r}$
up to isomorphism, as it does not carry the information about the extension class in
 $\text{Ext}_{G_{\mathbb{Q}_{p}}}^{1}(\unicode[STIX]{x1D712},\unicode[STIX]{x1D712}\unicode[STIX]{x1D714})$
corresponding to
$\text{Ext}_{G_{\mathbb{Q}_{p}}}^{1}(\unicode[STIX]{x1D712},\unicode[STIX]{x1D712}\unicode[STIX]{x1D714})$
corresponding to
![]() $\bar{r}$
. The maximal representation satisfying (1) and (2) above will contain the atome automorphe corresponding to
$\bar{r}$
. The maximal representation satisfying (1) and (2) above will contain the atome automorphe corresponding to
![]() $\bar{r}$
as a subrepresentation, but it will be strictly bigger. In fact, it can be shown that it is the smallest representation that contains all the atomes automorphes corresponding to different non-zero extensions in
$\bar{r}$
as a subrepresentation, but it will be strictly bigger. In fact, it can be shown that it is the smallest representation that contains all the atomes automorphes corresponding to different non-zero extensions in
 $\text{Ext}_{G_{\mathbb{Q}_{p}}}^{1}(\unicode[STIX]{x1D712},\unicode[STIX]{x1D712}\unicode[STIX]{x1D714})$
.
$\text{Ext}_{G_{\mathbb{Q}_{p}}}^{1}(\unicode[STIX]{x1D712},\unicode[STIX]{x1D712}\unicode[STIX]{x1D714})$
.
Remark 7.7. Theorem 7.4 and Corollary 7.5, when combined with Theorems 6.18 and 4.32 (which together show that
![]() $\widetilde{P}$
realizes the usual
$\widetilde{P}$
realizes the usual
![]() $p$
-adic local Langlands correspondence for
$p$
-adic local Langlands correspondence for
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
), prove a local–global compatibility result for completed cohomology. They are new in the case that
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
), prove a local–global compatibility result for completed cohomology. They are new in the case that
 $\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}}\cong \big(\!\begin{smallmatrix}1 & \ast \\ 0 & \unicode[STIX]{x1D714}\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
. In particular, they answer a question raised in Remark 1.2.9 in [Reference EmertonEme11] by confirming the expectation of Remark 6.1.23 of [Reference EmertonEme11]. In the other cases, Theorem 7.4 can be deduced from Theorem 6.4.6 in [Reference EmertonEme11] with
$\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}}\cong \big(\!\begin{smallmatrix}1 & \ast \\ 0 & \unicode[STIX]{x1D714}\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
. In particular, they answer a question raised in Remark 1.2.9 in [Reference EmertonEme11] by confirming the expectation of Remark 6.1.23 of [Reference EmertonEme11]. In the other cases, Theorem 7.4 can be deduced from Theorem 6.4.6 in [Reference EmertonEme11] with
![]() $\widetilde{P}$
replaced by a deformation of
$\widetilde{P}$
replaced by a deformation of
![]() $\unicode[STIX]{x1D705}(\bar{r})^{\vee }$
to
$\unicode[STIX]{x1D705}(\bar{r})^{\vee }$
to
![]() $R_{p}$
, such that one obtains the universal deformation of
$R_{p}$
, such that one obtains the universal deformation of
![]() $\bar{r}$
after applying Colmez’s functor
$\bar{r}$
after applying Colmez’s functor
![]() $\check{\mathbf{V}}$
to it. If
$\check{\mathbf{V}}$
to it. If
 $\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}}\cong \big(\!\begin{smallmatrix}1 & \ast \\ 0 & \unicode[STIX]{x1D714}\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
, then it can be shown that
$\overline{\unicode[STIX]{x1D70C}}|_{G_{\mathbb{Q}_{p}}}\cong \big(\!\begin{smallmatrix}1 & \ast \\ 0 & \unicode[STIX]{x1D714}\end{smallmatrix}\!\big)\otimes \unicode[STIX]{x1D712}$
, then it can be shown that
![]() $\widetilde{P}$
is not flat over
$\widetilde{P}$
is not flat over
![]() $R_{p}$
, and that is why the approach of [Reference EmertonEme11] does not work in this case.
$R_{p}$
, and that is why the approach of [Reference EmertonEme11] does not work in this case.
Remark 7.8. Theorem 7.4 and Corollary 7.5 have analogues in more general settings when the group at
![]() $p$
is essentially
$p$
is essentially
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
(or a product of copies of
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
(or a product of copies of
 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
). For example, taking
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
). For example, taking
![]() $M_{\infty }$
to be the patched module of § 3.4 (as constructed in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] for
$M_{\infty }$
to be the patched module of § 3.4 (as constructed in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEGGPS16] for
![]() $n=2$
), we obtain statements about the completed cohomology of unitary groups that are compact at infinity.
$n=2$
), we obtain statements about the completed cohomology of unitary groups that are compact at infinity.
Perhaps a case of greater interest is that of the completed cohomology of definite quaternion algebras over totally real fields. (One reason for this case to be of interest is its relationship to the cohomology of the Lubin–Tate tower as in [Reference ScholzeSch15, Theorem 6.2].) We expect that our results can be extended to this setting, although there is one wrinkle: in order to carry out Taylor–Wiles patching, we need to fix a central character and, as a consequence, our patched module has a fixed central character, and no longer satisfies the axioms of § 3. One approach to this difficulty would be to formulate analogues of those axioms with an arbitrary fixed central character, making use of the twisting constructions of § 6 and ‘capture’ arguments of [Reference PaškūnasPaš16, § 2.1], but this leads to ugly statements.
Instead, we content ourselves with considering the case that the fixed central character is the trivial character. In this case we can think of our patched modules as modules for
 $\operatorname{PGL}_{2}(\mathbb{Q}_{p})$
, and natural analogues of our axioms can be formulated in this setting; this is carried out in [Reference Gee and NewtonGN16, § 5], where an analogue of the results of § 4 is proved. In fact, the arguments there allow us to consider modules for a product of copies of
$\operatorname{PGL}_{2}(\mathbb{Q}_{p})$
, and natural analogues of our axioms can be formulated in this setting; this is carried out in [Reference Gee and NewtonGN16, § 5], where an analogue of the results of § 4 is proved. In fact, the arguments there allow us to consider modules for a product of copies of
 $\operatorname{PGL}_{2}(\mathbb{Q}_{p})$
, which is convenient when there is more than one place lying over
$\operatorname{PGL}_{2}(\mathbb{Q}_{p})$
, which is convenient when there is more than one place lying over
![]() $p$
; accordingly, we work below with cohomology that is completed at all primes above
$p$
; accordingly, we work below with cohomology that is completed at all primes above
![]() $p$
. (Of course, the case of cohomology that is completed at a single prime above
$p$
. (Of course, the case of cohomology that is completed at a single prime above
![]() $p$
can be deduced from this by returning to finite level via taking appropriate locally algebraic vectors.)
$p$
can be deduced from this by returning to finite level via taking appropriate locally algebraic vectors.)
As explained in Remark 7.1, one has to take some care with ramification at places away from
![]() $p$
, and we therefore content ourselves with considering quaternion algebras that split at all finite places. The reader wishing to prove extensions of these results to more general quaternion algebras is advised to examine the patching arguments of [Reference Gee and KisinGK14, § 4], which work in this setting. We further caution the reader that we have not attempted to check every detail of the expected result explained below.
$p$
, and we therefore content ourselves with considering quaternion algebras that split at all finite places. The reader wishing to prove extensions of these results to more general quaternion algebras is advised to examine the patching arguments of [Reference Gee and KisinGK14, § 4], which work in this setting. We further caution the reader that we have not attempted to check every detail of the expected result explained below.
Let
![]() $F$
be a totally real field in which
$F$
be a totally real field in which
![]() $p\geqslant 5$
splits completely, and let
$p\geqslant 5$
splits completely, and let
![]() $D$
be a quaternion algebra over
$D$
be a quaternion algebra over
![]() $F$
that is split at all finite places and definite at all infinite places (note that in particular this requires
$F$
that is split at all finite places and definite at all infinite places (note that in particular this requires
![]() $[F:\mathbb{Q}]$
to be even).
$[F:\mathbb{Q}]$
to be even).
Let
 $\overline{\unicode[STIX]{x1D70C}}:G_{F}\rightarrow \operatorname{GL}_{2}(\mathbb{F})$
be absolutely irreducible and assume that
$\overline{\unicode[STIX]{x1D70C}}:G_{F}\rightarrow \operatorname{GL}_{2}(\mathbb{F})$
be absolutely irreducible and assume that
![]() $\overline{\unicode[STIX]{x1D70C}}|_{G_{F(\unicode[STIX]{x1D701}_{p})}}$
is irreducible and that
$\overline{\unicode[STIX]{x1D70C}}|_{G_{F(\unicode[STIX]{x1D701}_{p})}}$
is irreducible and that
 $\det \overline{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D714}^{-1}$
. Suppose that
$\det \overline{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D714}^{-1}$
. Suppose that
![]() $\overline{\unicode[STIX]{x1D70C}}$
has no vexing primes; that is, if
$\overline{\unicode[STIX]{x1D70C}}$
has no vexing primes; that is, if
![]() $v\nmid p$
is a finite place at which
$v\nmid p$
is a finite place at which
![]() $\overline{\unicode[STIX]{x1D70C}}$
is ramified and
$\overline{\unicode[STIX]{x1D70C}}$
is ramified and
 $\mathbf{N}v\equiv -1\hspace{0.6em}({\rm mod}\hspace{0.2em}p)$
, and
$\mathbf{N}v\equiv -1\hspace{0.6em}({\rm mod}\hspace{0.2em}p)$
, and
![]() $\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}}$
is irreducible, then
$\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}}$
is irreducible, then
![]() $\overline{\unicode[STIX]{x1D70C}}|_{I_{F_{v}}}$
is also irreducible. Finally, suppose that for each place
$\overline{\unicode[STIX]{x1D70C}}|_{I_{F_{v}}}$
is also irreducible. Finally, suppose that for each place
![]() $v|p$
,
$v|p$
,
![]() $\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}}$
satisfies Assumption 2.2.
$\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}}$
satisfies Assumption 2.2.
Since
![]() $D$
splits at all finite places, we can consider the tame level subgroup
$D$
splits at all finite places, we can consider the tame level subgroup
 $U_{1}(N(\overline{\unicode[STIX]{x1D70C}}))\subset \operatorname{PGL}_{1}(D\otimes \mathbb{A}_{F}^{\infty ,p})\simeq \operatorname{PGL}_{2}(\mathbb{A}_{F}^{\infty ,p})$
given by the image of those matrices in
$U_{1}(N(\overline{\unicode[STIX]{x1D70C}}))\subset \operatorname{PGL}_{1}(D\otimes \mathbb{A}_{F}^{\infty ,p})\simeq \operatorname{PGL}_{2}(\mathbb{A}_{F}^{\infty ,p})$
given by the image of those matrices in
 $\operatorname{GL}_{2}(\mathbb{A}_{F}^{\infty ,p})$
that are unipotent and upper triangular modulo
$\operatorname{GL}_{2}(\mathbb{A}_{F}^{\infty ,p})$
that are unipotent and upper triangular modulo
![]() $N(\overline{\unicode[STIX]{x1D70C}})$
. Let
$N(\overline{\unicode[STIX]{x1D70C}})$
. Let
 $\widetilde{H}_{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})$
(respectively
$\widetilde{H}_{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})$
(respectively
 $\widetilde{H}^{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})$
) denote the completed homology (respectively cohomology) of the tower of locally symmetric spaces associated to
$\widetilde{H}^{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})$
) denote the completed homology (respectively cohomology) of the tower of locally symmetric spaces associated to
 $\operatorname{PGL}_{1}(D)$
with tame level
$\operatorname{PGL}_{1}(D)$
with tame level
 $U_{1}(N(\overline{\unicode[STIX]{x1D70C}}))$
. (Note that at finite level, the locally symmetric spaces are just finite sets of points.)
$U_{1}(N(\overline{\unicode[STIX]{x1D70C}}))$
. (Note that at finite level, the locally symmetric spaces are just finite sets of points.)
We assume that
![]() $\overline{\unicode[STIX]{x1D70C}}$
is modular, in the following sense:
$\overline{\unicode[STIX]{x1D70C}}$
is modular, in the following sense:
![]() $\overline{\unicode[STIX]{x1D70C}}$
determines a maximal ideal
$\overline{\unicode[STIX]{x1D70C}}$
determines a maximal ideal
![]() $\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})$
in the spherical Hecke algebra (generated by Hecke operators at places not dividing
$\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})$
in the spherical Hecke algebra (generated by Hecke operators at places not dividing
![]() $p$
at which
$p$
at which
![]() $\overline{\unicode[STIX]{x1D70C}}$
is unramified) acting on
$\overline{\unicode[STIX]{x1D70C}}$
is unramified) acting on
 $\widetilde{H}_{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})$
and we assume that
$\widetilde{H}_{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})$
and we assume that
 $\widetilde{H}_{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})_{\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})}\not =0$
.
$\widetilde{H}_{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})_{\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})}\not =0$
.
Let
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}$
be the universal deformation ring for deformations of
$R_{\overline{\unicode[STIX]{x1D70C}}}$
be the universal deformation ring for deformations of
![]() $\overline{\unicode[STIX]{x1D70C}}$
that are minimally ramified at places not dividing
$\overline{\unicode[STIX]{x1D70C}}$
that are minimally ramified at places not dividing
![]() $p$
, and which have determinant
$p$
, and which have determinant
![]() $\unicode[STIX]{x1D700}^{-1}$
. For each place
$\unicode[STIX]{x1D700}^{-1}$
. For each place
![]() $v|p$
, let
$v|p$
, let
![]() $R_{v}$
be the universal deformation ring for deformations of
$R_{v}$
be the universal deformation ring for deformations of
![]() $\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}}$
with determinant
$\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}}$
with determinant
![]() $\unicode[STIX]{x1D700}^{-1}$
, and set
$\unicode[STIX]{x1D700}^{-1}$
, and set
 $R_{p}:=\operatorname{⊗̂}_{v|p}R_{v}$
.
$R_{p}:=\operatorname{⊗̂}_{v|p}R_{v}$
.
Set
 $G=\prod _{v|p}\operatorname{PGL}_{1}(D_{v})$
, which we identify with
$G=\prod _{v|p}\operatorname{PGL}_{1}(D_{v})$
, which we identify with
 $\prod _{v|p}\operatorname{PGL}_{2}(\mathbb{Q}_{p})$
via a fixed isomorphism. By patching the completed homology
$\prod _{v|p}\operatorname{PGL}_{2}(\mathbb{Q}_{p})$
via a fixed isomorphism. By patching the completed homology
 $\widetilde{H}_{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})_{\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})}$
(with a variation of the argument in [Reference ScholzeSch15, § 9]), we obtainFootnote
3
a ring
$\widetilde{H}_{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})_{\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})}$
(with a variation of the argument in [Reference ScholzeSch15, § 9]), we obtainFootnote
3
a ring
![]() $R_{\infty }$
which is a power series ring over
$R_{\infty }$
which is a power series ring over
![]() $R_{p}$
, and an
$R_{p}$
, and an
![]() $R_{\infty }[G]$
-module
$R_{\infty }[G]$
-module
![]() $M_{\infty }$
with an arithmetic action in the sense of [Reference Gee and NewtonGN16, § 5.2], together with an ideal
$M_{\infty }$
with an arithmetic action in the sense of [Reference Gee and NewtonGN16, § 5.2], together with an ideal
 $\mathfrak{a}_{\infty }\subset R_{\infty }$
such that
$\mathfrak{a}_{\infty }\subset R_{\infty }$
such that
 $R_{\infty }/\mathfrak{a}_{\infty }\cong R_{\overline{\unicode[STIX]{x1D70C}}}$
as local
$R_{\infty }/\mathfrak{a}_{\infty }\cong R_{\overline{\unicode[STIX]{x1D70C}}}$
as local
![]() ${\mathcal{O}}$
-algebras and
${\mathcal{O}}$
-algebras and
 $M_{\infty }/\mathfrak{a}_{\infty }\cong \widetilde{H}_{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})_{\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})}$
as
$M_{\infty }/\mathfrak{a}_{\infty }\cong \widetilde{H}_{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})_{\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})}$
as
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}[G]$
-modules. (Note that we can ensure the smoothness of
$R_{\overline{\unicode[STIX]{x1D70C}}}[G]$
-modules. (Note that we can ensure the smoothness of
![]() $R_{\infty }$
over
$R_{\infty }$
over
![]() $R_{p}$
since we are assuming that
$R_{p}$
since we are assuming that
![]() $D$
splits at all finite places and that there are no vexing primes.)
$D$
splits at all finite places and that there are no vexing primes.)
Applying [Reference Gee and NewtonGN16, Proposition 5.2.2] now gives a
![]() $G$
-equivariant isomorphism
$G$
-equivariant isomorphism
 $$\begin{eqnarray}\widetilde{H}_{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})_{\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})}\simeq (\operatorname{⊗̂}_{v|p}\widetilde{P}^{1}(\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}}))\operatorname{⊗̂}_{R_{p}}R_{\overline{\unicode[STIX]{x1D70C}}},\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{H}_{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),{\mathcal{O}})_{\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})}\simeq (\operatorname{⊗̂}_{v|p}\widetilde{P}^{1}(\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}}))\operatorname{⊗̂}_{R_{p}}R_{\overline{\unicode[STIX]{x1D70C}}},\end{eqnarray}$$
where
 $\widetilde{P}^{1}(\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}})$
denotes the projective envelope considered in § 6 in the case that
$\widetilde{P}^{1}(\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}})$
denotes the projective envelope considered in § 6 in the case that
 $\bar{r}=\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}}$
and
$\bar{r}=\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}}$
and
![]() $\unicode[STIX]{x1D713}=1$
. Arguing as in the proof of Corollary 7.5, we obtain a
$\unicode[STIX]{x1D713}=1$
. Arguing as in the proof of Corollary 7.5, we obtain a
![]() $G$
-equivariant isomorphism
$G$
-equivariant isomorphism
 $$\begin{eqnarray}\widetilde{H}^{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),\mathbb{F})[\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})]\simeq \operatorname{⊗̂}_{v|p}\unicode[STIX]{x1D705}(\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}}),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{H}^{0}(U_{1}(N(\overline{\unicode[STIX]{x1D70C}})),\mathbb{F})[\mathfrak{m}(\overline{\unicode[STIX]{x1D70C}})]\simeq \operatorname{⊗̂}_{v|p}\unicode[STIX]{x1D705}(\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}}),\end{eqnarray}$$
where
 $\unicode[STIX]{x1D705}(\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}})$
denotes the representation defined in Proposition 6.21.
$\unicode[STIX]{x1D705}(\overline{\unicode[STIX]{x1D70C}}|_{G_{F_{v}}})$
denotes the representation defined in Proposition 6.21.
One can obtain analogous results in the case where
![]() $[F:\mathbb{Q}]$
is odd and
$[F:\mathbb{Q}]$
is odd and
![]() $D$
is split at one infinite place of
$D$
is split at one infinite place of
![]() $F$
and ramified at all the others. In this case, one works with a tower of Shimura curves. The main difference to the argument is to note that
$F$
and ramified at all the others. In this case, one works with a tower of Shimura curves. The main difference to the argument is to note that
![]() $\overline{\unicode[STIX]{x1D70C}}$
only contributes to completed homology (or cohomology) in degree
$\overline{\unicode[STIX]{x1D70C}}$
only contributes to completed homology (or cohomology) in degree
![]() $1$
(since the
$1$
(since the
 $D^{\times }(\mathbb{A}^{\infty })$
-action factors through the reduced norm in degree
$D^{\times }(\mathbb{A}^{\infty })$
-action factors through the reduced norm in degree
![]() $0$
), and the
$0$
), and the
![]() $G_{F}$
-action can be factored out by the same argument as for modular curves.
$G_{F}$
-action can be factored out by the same argument as for modular curves.
Acknowledgements
This paper has its germ in conversations between three of us (M.E., T.G. and V.P.) during the 2011 Durham Symposium on Automorphic Forms and Galois Representation, and we would like to thank the organizers Fred Diamond, Payman Kassaei and Minhyong Kim as well as Durham University, EPSRC and the LMS for providing a fertile atmosphere for discussion. The ideas of the paper were developed further when the six of us participated in focussed research groups on ‘The
![]() $p$
-adic Langlands program for non-split groups’ at the Banff Centre and AIM; we would like to thank AIM and BIRS for providing an excellent working atmosphere, and for their financial support. We would also like to thank the anonymous referees for their comments on the paper.
$p$
-adic Langlands program for non-split groups’ at the Banff Centre and AIM; we would like to thank AIM and BIRS for providing an excellent working atmosphere, and for their financial support. We would also like to thank the anonymous referees for their comments on the paper.