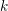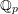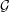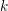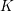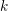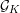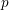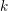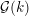1 Introduction
Let
![]() $k$
be a finite extension of
$k$
be a finite extension of
![]() $\mathbb{Q}_{p}$
and let
$\mathbb{Q}_{p}$
and let
![]() ${\mathcal{G}}$
be an absolutely simple split reductive group over
${\mathcal{G}}$
be an absolutely simple split reductive group over
![]() $k$
. In [Reference YuYu01], Yu gave a construction of supercuspidal representations of
$k$
. In [Reference YuYu01], Yu gave a construction of supercuspidal representations of
![]() ${\mathcal{G}}(k)$
with complex coefficients, generalizing earlier work of Adler [Reference AdlerAdl98]. For large primes
${\mathcal{G}}(k)$
with complex coefficients, generalizing earlier work of Adler [Reference AdlerAdl98]. For large primes
![]() $p$
, Yu’s construction yields all possible supercuspidal representations [Reference KimKim07]. However, the construction does not capture all supercuspidal representations when
$p$
, Yu’s construction yields all possible supercuspidal representations [Reference KimKim07]. However, the construction does not capture all supercuspidal representations when
![]() $p$
is small. In [Reference Reeder and YuRY14], Reeder and Yu gave a new construction of supercuspidal representations of lowest positive depth, which they called epipelagic representations. Their construction is uniform for all
$p$
is small. In [Reference Reeder and YuRY14], Reeder and Yu gave a new construction of supercuspidal representations of lowest positive depth, which they called epipelagic representations. Their construction is uniform for all
![]() $p$
, but requires as input stable vectors in a certain representation coming from a Moy–Prasad filtration, which we will describe below. For
$p$
, but requires as input stable vectors in a certain representation coming from a Moy–Prasad filtration, which we will describe below. For
![]() $p$
large enough, necessary and sufficient conditions for the existence of stable vectors were given in [Reference Reeder and YuRY14]. For small
$p$
large enough, necessary and sufficient conditions for the existence of stable vectors were given in [Reference Reeder and YuRY14]. For small
![]() $p$
, the existence of stable vectors, hence also of epipelagic representations, was previously unknown, except in the simple case of a torus action (see [Reference Gross and ReederGR10, § 9] and [Reference Reeder and YuRY14, § 2.6]).
$p$
, the existence of stable vectors, hence also of epipelagic representations, was previously unknown, except in the simple case of a torus action (see [Reference Gross and ReederGR10, § 9] and [Reference Reeder and YuRY14, § 2.6]).
In this paper, we show that the criterion of [Reference Reeder and YuRY14] for the existence of stable vectors is valid for all primes
![]() $p$
, uniformly. Thus, [Reference Reeder and YuRY14] can be used to construct supercuspidal representations uniformly for all
$p$
, uniformly. Thus, [Reference Reeder and YuRY14] can be used to construct supercuspidal representations uniformly for all
![]() $p$
.
$p$
.
Corollary 4.3
. Let
![]() ${\mathcal{G}}$
be an absolutely simple split reductive group over the local field
${\mathcal{G}}$
be an absolutely simple split reductive group over the local field
![]() $k$
. Then for each
$k$
. Then for each
![]() $m$
satisfying the conditions of Theorem 4.2, there exists a finite unramified extension
$m$
satisfying the conditions of Theorem 4.2, there exists a finite unramified extension
![]() $k^{\prime }$
of
$k^{\prime }$
of
![]() $k$
such that one can implement the construction of [Reference Reeder and YuRY14] to form supercuspidal epipelagic representations of
$k$
such that one can implement the construction of [Reference Reeder and YuRY14] to form supercuspidal epipelagic representations of
![]() ${\mathcal{G}}(k^{\prime })$
.
${\mathcal{G}}(k^{\prime })$
.
For small
![]() $p$
, we obtain previously unknown representations (see Remark 4.4).
$p$
, we obtain previously unknown representations (see Remark 4.4).
Let
![]() $K$
be a maximal unramified extension of
$K$
be a maximal unramified extension of
![]() $k$
with ring of integers
$k$
with ring of integers
![]() ${\mathcal{O}}$
and residue field
${\mathcal{O}}$
and residue field
![]() $\overline{\mathbb{F}}_{p}$
. In order to describe the input for the construction of [Reference Reeder and YuRY14], we choose a rational point
$\overline{\mathbb{F}}_{p}$
. In order to describe the input for the construction of [Reference Reeder and YuRY14], we choose a rational point
![]() $x$
in the Bruhat–Tits building
$x$
in the Bruhat–Tits building
![]() $\mathscr{B}(G,K)$
of
$\mathscr{B}(G,K)$
of
![]() $G:={\mathcal{G}}_{K}$
. Moy and Prasad defined in [Reference Moy and PrasadMP94, Reference Moy and PrasadMP96] a filtration of
$G:={\mathcal{G}}_{K}$
. Moy and Prasad defined in [Reference Moy and PrasadMP94, Reference Moy and PrasadMP96] a filtration of
![]() $G(K)$
by subgroups:
$G(K)$
by subgroups:
where
![]() $r_{1},r_{2},\ldots$
are rational numbers depending on
$r_{1},r_{2},\ldots$
are rational numbers depending on
![]() $x$
. The quotient
$x$
. The quotient
![]() $G(K)_{x,0}/G(K)_{x,r_{1}}$
can be identified with the
$G(K)_{x,0}/G(K)_{x,r_{1}}$
can be identified with the
![]() $\overline{\mathbb{F}}_{p}$
-points of a reductive group
$\overline{\mathbb{F}}_{p}$
-points of a reductive group
![]() $\mathbf{G}_{x}$
. The quotient
$\mathbf{G}_{x}$
. The quotient
![]() $\mathbf{V}_{x}:=$
$\mathbf{V}_{x}:=$
![]() $G(K)_{x,r_{1}}/G(K)_{x,r_{2}}$
forms an
$G(K)_{x,r_{1}}/G(K)_{x,r_{2}}$
forms an
![]() $\overline{\mathbb{F}}_{p}$
-vector space on which
$\overline{\mathbb{F}}_{p}$
-vector space on which
![]() $\mathbf{G}_{x}$
has an action induced by conjugation. A vector in the dual space
$\mathbf{G}_{x}$
has an action induced by conjugation. A vector in the dual space
![]() $\check{\mathbf{V}}_{x}$
is said to be stable under the action of
$\check{\mathbf{V}}_{x}$
is said to be stable under the action of
![]() $\mathbf{G}_{x}$
if its orbit is Zariski closed and its stabilizer in
$\mathbf{G}_{x}$
if its orbit is Zariski closed and its stabilizer in
![]() $\mathbf{G}_{x}$
is finite. The existence of such a stable vector over
$\mathbf{G}_{x}$
is finite. The existence of such a stable vector over
![]() $k$
is the only requirement for Reeder–Yu’s construction of epipelagic representations.
$k$
is the only requirement for Reeder–Yu’s construction of epipelagic representations.
Our main result, which is independent of
![]() $p$
, is the classification of all such
$p$
, is the classification of all such
![]() $x$
for which the representation of
$x$
for which the representation of
![]() $\mathbf{G}_{x}$
on
$\mathbf{G}_{x}$
on
![]() $\check{\mathbf{V}}_{x}$
contains stable vectors. To state the theorem, we fix an apartment
$\check{\mathbf{V}}_{x}$
contains stable vectors. To state the theorem, we fix an apartment
![]() $\mathscr{A}$
in
$\mathscr{A}$
in
![]() $\mathscr{B}(G,K)$
and a hyperspecial point
$\mathscr{B}(G,K)$
and a hyperspecial point
![]() $x_{0}\in \mathscr{A}$
. We use
$x_{0}\in \mathscr{A}$
. We use
![]() $\check{\unicode[STIX]{x1D70C}}$
to denote the half-sum of a set of positive coroots.
$\check{\unicode[STIX]{x1D70C}}$
to denote the half-sum of a set of positive coroots.
Theorem 4.2
. Let
![]() $x\in \mathscr{A}$
. Then the representation
$x\in \mathscr{A}$
. Then the representation
![]() $\check{\mathbf{V}}_{x}$
contains stable vectors under the action of
$\check{\mathbf{V}}_{x}$
contains stable vectors under the action of
![]() $\mathbf{G}_{x}$
if and only if
$\mathbf{G}_{x}$
if and only if
![]() $x$
is conjugate under the affine Weyl group
$x$
is conjugate under the affine Weyl group
![]() $W_{\text{aff}}$
to
$W_{\text{aff}}$
to
![]() $x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
, where
$x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
, where
![]() $m$
is the order of an elliptic,
$m$
is the order of an elliptic,
![]() $\mathbb{Z}$
-regular element in the Weyl group
$\mathbb{Z}$
-regular element in the Weyl group
![]() $W$
of
$W$
of
![]() $G$
.
$G$
.
For the definitions of elliptic and
![]() $\mathbb{Z}$
-regular, see § 4. We also obtain a similar result about the classification for semistable vectors (Proposition 4.5).
$\mathbb{Z}$
-regular, see § 4. We also obtain a similar result about the classification for semistable vectors (Proposition 4.5).
These results follow from a more general analysis of the relations between (semi)stable vectors in the special and geometric generic fibers of representations over
![]() ${\mathcal{O}}$
. More explicitly, let
${\mathcal{O}}$
. More explicitly, let
![]() $\mathscr{G}$
be a split reductive group over
$\mathscr{G}$
be a split reductive group over
![]() ${\mathcal{O}}$
acting on a free
${\mathcal{O}}$
acting on a free
![]() ${\mathcal{O}}$
-module
${\mathcal{O}}$
-module
![]() $\mathscr{V}$
and let
$\mathscr{V}$
and let
![]() $\overline{\mathbb{Q}}_{p}$
be an algebraic closure of
$\overline{\mathbb{Q}}_{p}$
be an algebraic closure of
![]() $K$
. We show that the representation of
$K$
. We show that the representation of
![]() $\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
on
$\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
on
![]() $\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
contains stable vectors if and only if the representation of
$\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
contains stable vectors if and only if the representation of
![]() $\mathscr{G}_{\overline{\mathbb{F}}_{p}}$
on
$\mathscr{G}_{\overline{\mathbb{F}}_{p}}$
on
![]() $\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
contains stable vectors (Corollary 2.4). The same statement is true with ‘stable’ replaced by ‘semistable’. Thus, we can transfer results about the existence of (semi)stable vectors in characteristic zero to arbitrary positive characteristics. This is a key step in the proof of Theorem 4.2.
$\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
contains stable vectors (Corollary 2.4). The same statement is true with ‘stable’ replaced by ‘semistable’. Thus, we can transfer results about the existence of (semi)stable vectors in characteristic zero to arbitrary positive characteristics. This is a key step in the proof of Theorem 4.2.
Structure of the paper
In § 2 we first recall basic definitions and properties related to stability. We then show that the special fiber of a representation of a split reductive group over
![]() ${\mathcal{O}}$
has (semi)stable vectors if and only if the geometric generic fiber of this representation admits (semi)stable vectors. In § 3 we review Moy–Prasad filtrations and define a split reductive group over
${\mathcal{O}}$
has (semi)stable vectors if and only if the geometric generic fiber of this representation admits (semi)stable vectors. In § 3 we review Moy–Prasad filtrations and define a split reductive group over
![]() ${\mathcal{O}}$
acting on a free
${\mathcal{O}}$
acting on a free
![]() ${\mathcal{O}}$
-module such that the special fiber of this action corresponds to the action of
${\mathcal{O}}$
-module such that the special fiber of this action corresponds to the action of
![]() $\mathbf{G}_{x}$
on
$\mathbf{G}_{x}$
on
![]() $\mathbf{V}_{x}$
. The generic fiber is isomorphic to a representation coming from Vinberg theory of graded Lie algebras, which we review in § 4. We finish the proof of Theorem 4.2 using results from [Reference Reeder, Levy, Yu and GrossRLYG12] on Vinberg theory in characteristic zero. In the final section, § 5, we give an example, classifying all stable vectors in
$\mathbf{V}_{x}$
. The generic fiber is isomorphic to a representation coming from Vinberg theory of graded Lie algebras, which we review in § 4. We finish the proof of Theorem 4.2 using results from [Reference Reeder, Levy, Yu and GrossRLYG12] on Vinberg theory in characteristic zero. In the final section, § 5, we give an example, classifying all stable vectors in
![]() $\check{\mathbf{V}}_{x}$
for the case of
$\check{\mathbf{V}}_{x}$
for the case of
![]() $G=G_{2}$
and
$G=G_{2}$
and
![]() $x=x_{0}+(1/2)\check{\unicode[STIX]{x1D70C}}$
. We then determine the Langlands parameter corresponding to the unique representation of
$x=x_{0}+(1/2)\check{\unicode[STIX]{x1D70C}}$
. We then determine the Langlands parameter corresponding to the unique representation of
![]() $G_{2}(\mathbb{Q}_{2})$
obtained using this choice of
$G_{2}(\mathbb{Q}_{2})$
obtained using this choice of
![]() $x$
in the construction of [Reference Reeder and YuRY14].
$x$
in the construction of [Reference Reeder and YuRY14].
Conventions and notation
Throughout the paper, we use the following conventions. If
![]() $A$
is a ring,
$A$
is a ring,
![]() $H$
a group scheme over
$H$
a group scheme over
![]() $\operatorname{Spec}A$
, and
$\operatorname{Spec}A$
, and
![]() $R$
an
$R$
an
![]() $A$
-algebra, we write
$A$
-algebra, we write
![]() $H(R)$
for the
$H(R)$
for the
![]() $\operatorname{Spec}R$
-points of
$\operatorname{Spec}R$
-points of
![]() $H$
and
$H$
and
![]() $H_{R}$
for
$H_{R}$
for
![]() $H\times _{\operatorname{Spec}A}\operatorname{Spec}R$
. For a free
$H\times _{\operatorname{Spec}A}\operatorname{Spec}R$
. For a free
![]() $A$
-module
$A$
-module
![]() $V$
, we write
$V$
, we write
![]() $V_{R}$
to denote the free
$V_{R}$
to denote the free
![]() $R$
-module
$R$
-module
![]() $V\otimes _{A}R$
. If
$V\otimes _{A}R$
. If
![]() $M$
is an
$M$
is an
![]() $A$
-module and there is no danger of confusion, we may also denote by
$A$
-module and there is no danger of confusion, we may also denote by
![]() $M$
the scheme corresponding to the functor of points
$M$
the scheme corresponding to the functor of points
![]() $R\mapsto M\otimes _{A}R$
for any
$R\mapsto M\otimes _{A}R$
for any
![]() $A$
-algebra
$A$
-algebra
![]() $R$
.
$R$
.
Throughout the paper, we consider reductive groups to be connected.
We maintain the following notation. Let
![]() $k$
be a finite field extension of
$k$
be a finite field extension of
![]() $\mathbb{Q}_{p}$
and let
$\mathbb{Q}_{p}$
and let
![]() $K$
be a maximal unramified extension of
$K$
be a maximal unramified extension of
![]() $k$
. We fix a discrete valuation
$k$
. We fix a discrete valuation
![]() $\mathsf{v}$
on
$\mathsf{v}$
on
![]() $K$
with image
$K$
with image
![]() $\mathbb{Z}\cup \{\infty \}$
. Let
$\mathbb{Z}\cup \{\infty \}$
. Let
![]() ${\mathcal{O}}$
denote the ring of integers of
${\mathcal{O}}$
denote the ring of integers of
![]() $K$
and let
$K$
and let
![]() $\unicode[STIX]{x1D71B}$
be a uniformizer of
$\unicode[STIX]{x1D71B}$
be a uniformizer of
![]() ${\mathcal{O}}$
. We fix an isomorphism between the residue field
${\mathcal{O}}$
. We fix an isomorphism between the residue field
![]() ${\mathcal{O}}/\unicode[STIX]{x1D71B}{\mathcal{O}}$
and
${\mathcal{O}}/\unicode[STIX]{x1D71B}{\mathcal{O}}$
and
![]() $\overline{\mathbb{F}}_{p}$
. We fix an algebraic closure
$\overline{\mathbb{F}}_{p}$
. We fix an algebraic closure
![]() $\overline{\mathbb{Q}}_{p}$
of
$\overline{\mathbb{Q}}_{p}$
of
![]() $K$
with ring of integers
$K$
with ring of integers
![]() $\mathbf{O}$
.
$\mathbf{O}$
.
2 Lifting and descent of stable vectors
Before describing our results about the lifting and descent of (semi)stable vectors, we will recall basic definitions and properties about stability, and introduce some notation.
If
![]() $G$
is a reductive group over an algebraically closed field
$G$
is a reductive group over an algebraically closed field
![]() $F$
and
$F$
and
![]() $V$
is a finite-dimensional algebraic representation of
$V$
is a finite-dimensional algebraic representation of
![]() $G$
, a vector
$G$
, a vector
![]() $v\in V$
is called semistable if its orbit under
$v\in V$
is called semistable if its orbit under
![]() $G(F)$
does not contain zero in its closure under the Zariski topology on
$G(F)$
does not contain zero in its closure under the Zariski topology on
![]() $V$
or, equivalently, if there exists a non-constant
$V$
or, equivalently, if there exists a non-constant
![]() $G(F)$
-invariant homogeneous polynomial
$G(F)$
-invariant homogeneous polynomial
![]() $f$
on
$f$
on
![]() $V$
such that
$V$
such that
![]() $f(v)\neq 0$
. A vector
$f(v)\neq 0$
. A vector
![]() $v\in V$
is called stable if its orbit is closed and its stabilizer in
$v\in V$
is called stable if its orbit is closed and its stabilizer in
![]() $G$
is finite. In particular, a stable vector is automatically semistable.
$G$
is finite. In particular, a stable vector is automatically semistable.
In this paper we are interested in (semi)stable vectors in the following setting. Let
![]() $\mathscr{G}$
be a split reductive group scheme over
$\mathscr{G}$
be a split reductive group scheme over
![]() ${\mathcal{O}}$
with split maximal torus
${\mathcal{O}}$
with split maximal torus
![]() $\mathscr{T}$
. Let
$\mathscr{T}$
. Let
![]() $\mathscr{V}$
be a free finite-dimensional
$\mathscr{V}$
be a free finite-dimensional
![]() ${\mathcal{O}}$
-module and let
${\mathcal{O}}$
-module and let
![]() $\mathscr{G}\rightarrow \operatorname{GL}(\mathscr{V})$
be a representation of
$\mathscr{G}\rightarrow \operatorname{GL}(\mathscr{V})$
be a representation of
![]() $\mathscr{G}$
, where, by abuse of notation,
$\mathscr{G}$
, where, by abuse of notation,
![]() $\operatorname{GL}(\mathscr{V})$
denotes the
$\operatorname{GL}(\mathscr{V})$
denotes the
![]() ${\mathcal{O}}$
-group scheme whose functor of points is given by
${\mathcal{O}}$
-group scheme whose functor of points is given by
![]() $A\mapsto \operatorname{GL}(\mathscr{V}_{A})$
. By base change, we obtain representations
$A\mapsto \operatorname{GL}(\mathscr{V}_{A})$
. By base change, we obtain representations
![]() $\mathscr{G}_{\overline{\mathbb{Q}}_{p}}\rightarrow \operatorname{GL}(\mathscr{V}_{\overline{\mathbb{Q}}_{p}})$
and
$\mathscr{G}_{\overline{\mathbb{Q}}_{p}}\rightarrow \operatorname{GL}(\mathscr{V}_{\overline{\mathbb{Q}}_{p}})$
and
![]() $\mathscr{G}_{\overline{\mathbb{F}}_{p}}\rightarrow \operatorname{GL}(\mathscr{V}_{\overline{\mathbb{F}}_{p}})$
. We will investigate the relationship between the geometric invariant theory of these two representations. To do this, we will make frequent use of the fact that since
$\mathscr{G}_{\overline{\mathbb{F}}_{p}}\rightarrow \operatorname{GL}(\mathscr{V}_{\overline{\mathbb{F}}_{p}})$
. We will investigate the relationship between the geometric invariant theory of these two representations. To do this, we will make frequent use of the fact that since
![]() $\mathscr{G}$
is smooth,
$\mathscr{G}$
is smooth,
![]() $\mathscr{G}({\mathcal{O}})$
(and thus
$\mathscr{G}({\mathcal{O}})$
(and thus
![]() $\mathscr{G}(\mathbf{O})$
) surjects onto
$\mathscr{G}(\mathbf{O})$
) surjects onto
![]() $\mathscr{G}(\overline{\mathbb{F}}_{p})$
. We denote the image of an element
$\mathscr{G}(\overline{\mathbb{F}}_{p})$
. We denote the image of an element
![]() $g\in \mathscr{G}(\mathbf{O})$
in
$g\in \mathscr{G}(\mathbf{O})$
in
![]() $\mathscr{G}(\overline{\mathbb{F}}_{p})$
by
$\mathscr{G}(\overline{\mathbb{F}}_{p})$
by
![]() $\overline{g}$
. Similarly, we denote the surjection
$\overline{g}$
. Similarly, we denote the surjection
![]() $\mathscr{V}_{\mathbf{O}}{\twoheadrightarrow}\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
by
$\mathscr{V}_{\mathbf{O}}{\twoheadrightarrow}\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
by
![]() $v\mapsto \overline{v}$
.
$v\mapsto \overline{v}$
.
Our other main tool is the Hilbert–Mumford criterion (see [Reference MumfordMum77, 1.1], which is based on [Reference MumfordMum65, Theorem 2.1]). Recall that for any
![]() ${\mathcal{O}}$
-algebra
${\mathcal{O}}$
-algebra
![]() $A$
and one-parameter subgroup
$A$
and one-parameter subgroup
![]() $\unicode[STIX]{x1D706}:\mathbb{G}_{m}\rightarrow \mathscr{G}_{A}$
, we obtain a weight decomposition
$\unicode[STIX]{x1D706}:\mathbb{G}_{m}\rightarrow \mathscr{G}_{A}$
, we obtain a weight decomposition
![]() $\mathscr{V}_{A}=\bigoplus _{i\in \mathbb{Z}}(\mathscr{V}_{A})_{i}$
, where
$\mathscr{V}_{A}=\bigoplus _{i\in \mathbb{Z}}(\mathscr{V}_{A})_{i}$
, where
![]() $\unicode[STIX]{x1D706}(t)\cdot v=t^{i}v$
for all
$\unicode[STIX]{x1D706}(t)\cdot v=t^{i}v$
for all
![]() $v\in (\mathscr{V}_{A})_{i}$
,
$v\in (\mathscr{V}_{A})_{i}$
,
![]() $t\in \mathbb{G}_{m}(A)\simeq A^{\times }$
. Given a vector
$t\in \mathbb{G}_{m}(A)\simeq A^{\times }$
. Given a vector
![]() $v\in \mathscr{V}_{A}$
, we let
$v\in \mathscr{V}_{A}$
, we let
![]() $I_{A}(\unicode[STIX]{x1D706},v)$
denote the set of negative weights for
$I_{A}(\unicode[STIX]{x1D706},v)$
denote the set of negative weights for
![]() $v$
: if we write
$v$
: if we write
![]() $v$
as a sum
$v$
as a sum
![]() $v=\sum v_{i}$
such that
$v=\sum v_{i}$
such that
![]() $v_{i}\in (\mathscr{V}_{A})_{i}$
, then
$v_{i}\in (\mathscr{V}_{A})_{i}$
, then
![]() $I_{A}(\unicode[STIX]{x1D706},v)=\{i<0\mid v_{i}\neq 0\}$
. If
$I_{A}(\unicode[STIX]{x1D706},v)=\{i<0\mid v_{i}\neq 0\}$
. If
![]() $A$
is an algebraically closed field, e.g.
$A$
is an algebraically closed field, e.g.
![]() $\overline{\mathbb{Q}}_{p}$
or
$\overline{\mathbb{Q}}_{p}$
or
![]() $\overline{\mathbb{F}}_{p}$
, the Hilbert–Mumford criterion says that a vector
$\overline{\mathbb{F}}_{p}$
, the Hilbert–Mumford criterion says that a vector
![]() $v\in \mathscr{V}_{A}$
is stable under
$v\in \mathscr{V}_{A}$
is stable under
![]() $\mathscr{G}_{A}$
if and only if for every non-trivial one-parameter subgroup
$\mathscr{G}_{A}$
if and only if for every non-trivial one-parameter subgroup
![]() $\unicode[STIX]{x1D706}:\mathbb{G}_{m}\rightarrow \mathscr{G}_{A}$
, we have
$\unicode[STIX]{x1D706}:\mathbb{G}_{m}\rightarrow \mathscr{G}_{A}$
, we have
![]() $I_{A}(\unicode[STIX]{x1D706},v)\neq \varnothing$
. We note for later use that if
$I_{A}(\unicode[STIX]{x1D706},v)\neq \varnothing$
. We note for later use that if
![]() $g\in \mathscr{G}(A)$
, then
$g\in \mathscr{G}(A)$
, then
![]() $I_{A}(g\unicode[STIX]{x1D706}g^{-1},v)=I_{A}(\unicode[STIX]{x1D706},g^{-1}v)$
.
$I_{A}(g\unicode[STIX]{x1D706}g^{-1},v)=I_{A}(\unicode[STIX]{x1D706},g^{-1}v)$
.
Lemma 2.1. If the representation
![]() $\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
contains stable vectors for the action of
$\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
contains stable vectors for the action of
![]() $\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
, then the representation
$\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
, then the representation
![]() $\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
contains stable vectors for the action of
$\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
contains stable vectors for the action of
![]() $\mathscr{G}_{\overline{\mathbb{F}}_{p}}$
.
$\mathscr{G}_{\overline{\mathbb{F}}_{p}}$
.
Proof. Suppose that the set
![]() $(\mathscr{V}_{\overline{\mathbb{Q}}_{p}})_{s}$
of stable vectors in
$(\mathscr{V}_{\overline{\mathbb{Q}}_{p}})_{s}$
of stable vectors in
![]() $\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
is non-empty. Since
$\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
is non-empty. Since
![]() $(\mathscr{V}_{\overline{\mathbb{Q}}_{p}})_{s}$
is open (see [Reference MumfordMum65, 1.4, p. 37]), there exists a non-zero polynomial
$(\mathscr{V}_{\overline{\mathbb{Q}}_{p}})_{s}$
is open (see [Reference MumfordMum65, 1.4, p. 37]), there exists a non-zero polynomial
![]() $P$
on
$P$
on
![]() $\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
such that if
$\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
such that if
![]() $v\notin (\mathscr{V}_{\overline{\mathbb{Q}}_{p}})_{s}$
, then
$v\notin (\mathscr{V}_{\overline{\mathbb{Q}}_{p}})_{s}$
, then
![]() $P(v)=0$
. Note that since
$P(v)=0$
. Note that since
![]() $0\in \mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
is not stable, we have
$0\in \mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
is not stable, we have
![]() $P(0)=0$
. Choosing a basis for
$P(0)=0$
. Choosing a basis for
![]() $\mathscr{V}$
(and thus for
$\mathscr{V}$
(and thus for
![]() $\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
), we may identify
$\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
), we may identify
![]() $P$
with an element of
$P$
with an element of
![]() $\overline{\mathbb{Q}}_{p}[x_{1},\ldots ,x_{n}]$
. We can assume without loss of generality that the minimum of the valuations of the coefficients of
$\overline{\mathbb{Q}}_{p}[x_{1},\ldots ,x_{n}]$
. We can assume without loss of generality that the minimum of the valuations of the coefficients of
![]() $P$
is zero. Let
$P$
is zero. Let
![]() $\overline{P}$
be the image of
$\overline{P}$
be the image of
![]() $P$
under the reduction map
$P$
under the reduction map
![]() $\mathbf{O}[x_{1},\ldots ,x_{n}]\rightarrow \overline{\mathbb{F}}_{p}[x_{1},\ldots ,x_{n}]$
. Then
$\mathbf{O}[x_{1},\ldots ,x_{n}]\rightarrow \overline{\mathbb{F}}_{p}[x_{1},\ldots ,x_{n}]$
. Then
![]() $\overline{P}\neq 0$
by choice of the coefficients, and
$\overline{P}\neq 0$
by choice of the coefficients, and
![]() $\overline{P}$
is not constant, because
$\overline{P}$
is not constant, because
![]() $P(0)=0$
. Thus, there exists
$P(0)=0$
. Thus, there exists
![]() $\overline{v}\in \mathscr{V}_{\overline{\mathbb{F}}_{p}}$
such that
$\overline{v}\in \mathscr{V}_{\overline{\mathbb{F}}_{p}}$
such that
![]() $\overline{P}(\overline{v})\neq 0$
. We claim that
$\overline{P}(\overline{v})\neq 0$
. We claim that
![]() $\overline{v}$
is a stable vector under the action of
$\overline{v}$
is a stable vector under the action of
![]() $\mathscr{G}_{\overline{\mathbb{F}}_{p}}$
. Assume that it is not. Then there exists a non-trivial one-parameter subgroup
$\mathscr{G}_{\overline{\mathbb{F}}_{p}}$
. Assume that it is not. Then there exists a non-trivial one-parameter subgroup
![]() $\overline{\unicode[STIX]{x1D706}}:\mathbb{G}_{m}\rightarrow \mathscr{G}_{\overline{\mathbb{F}}_{p}}$
such that
$\overline{\unicode[STIX]{x1D706}}:\mathbb{G}_{m}\rightarrow \mathscr{G}_{\overline{\mathbb{F}}_{p}}$
such that
![]() $I_{\overline{\mathbb{F}}_{p}}(\overline{\unicode[STIX]{x1D706}},\overline{v})=\varnothing$
. Choose an element
$I_{\overline{\mathbb{F}}_{p}}(\overline{\unicode[STIX]{x1D706}},\overline{v})=\varnothing$
. Choose an element
![]() $\overline{g}\in \mathscr{G}(\overline{\mathbb{F}}_{p})$
such that
$\overline{g}\in \mathscr{G}(\overline{\mathbb{F}}_{p})$
such that
![]() $\bar{\unicode[STIX]{x1D706}}_{1}:=\bar{g}\bar{\unicode[STIX]{x1D706}}\bar{g}^{-1}$
has image in
$\bar{\unicode[STIX]{x1D706}}_{1}:=\bar{g}\bar{\unicode[STIX]{x1D706}}\bar{g}^{-1}$
has image in
![]() $\mathscr{T}(\overline{\mathbb{F}}_{p})$
. We have
$\mathscr{T}(\overline{\mathbb{F}}_{p})$
. We have
![]() $I_{\overline{\mathbb{F}}_{p}}(\bar{\unicode[STIX]{x1D706}}_{1},\bar{g}\bar{v})=I_{\overline{\mathbb{F}}_{p}}(\bar{\unicode[STIX]{x1D706}},\overline{v})=\varnothing$
. Using the identification of the cocharacters of
$I_{\overline{\mathbb{F}}_{p}}(\bar{\unicode[STIX]{x1D706}}_{1},\bar{g}\bar{v})=I_{\overline{\mathbb{F}}_{p}}(\bar{\unicode[STIX]{x1D706}},\overline{v})=\varnothing$
. Using the identification of the cocharacters of
![]() $\mathscr{T}_{\overline{\mathbb{F}}_{p}}$
and the cocharacters of
$\mathscr{T}_{\overline{\mathbb{F}}_{p}}$
and the cocharacters of
![]() $\mathscr{T}_{\mathbf{O}}$
, we obtain a lift
$\mathscr{T}_{\mathbf{O}}$
, we obtain a lift
![]() $\unicode[STIX]{x1D706}_{1}:\mathbb{G}_{m}\rightarrow \mathscr{T}_{\overline{\mathbb{Q}}_{p}}{\hookrightarrow}\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
of
$\unicode[STIX]{x1D706}_{1}:\mathbb{G}_{m}\rightarrow \mathscr{T}_{\overline{\mathbb{Q}}_{p}}{\hookrightarrow}\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
of
![]() $\bar{\unicode[STIX]{x1D706}}_{1}$
. We also lift
$\bar{\unicode[STIX]{x1D706}}_{1}$
. We also lift
![]() $\overline{v}$
to an element
$\overline{v}$
to an element
![]() $v\in \mathscr{V}$
and lift
$v\in \mathscr{V}$
and lift
![]() $\overline{g}$
to an element
$\overline{g}$
to an element
![]() $g\in \mathscr{G}({\mathcal{O}})$
. Since
$g\in \mathscr{G}({\mathcal{O}})$
. Since
![]() $P(v)\neq 0$
,
$P(v)\neq 0$
,
![]() $v$
is stable, and so
$v$
is stable, and so
![]() $w:=gv$
is also stable. Using the decomposition
$w:=gv$
is also stable. Using the decomposition
![]() $\mathscr{V}=\bigoplus _{i\in \mathbb{Z}}\mathscr{V}_{i}$
coming from
$\mathscr{V}=\bigoplus _{i\in \mathbb{Z}}\mathscr{V}_{i}$
coming from
![]() $\unicode[STIX]{x1D706}_{1}$
, we write
$\unicode[STIX]{x1D706}_{1}$
, we write
![]() $w=w_{+}+w_{-}$
, where
$w=w_{+}+w_{-}$
, where
![]() $w_{+}\in \bigoplus _{m\in \mathbb{Z}_{{\geqslant}0}}\mathscr{V}_{m}$
and
$w_{+}\in \bigoplus _{m\in \mathbb{Z}_{{\geqslant}0}}\mathscr{V}_{m}$
and
![]() $w_{-}\in \bigoplus _{m\in \mathbb{Z}_{{<}0}}\mathscr{V}_{m}$
. Since
$w_{-}\in \bigoplus _{m\in \mathbb{Z}_{{<}0}}\mathscr{V}_{m}$
. Since
![]() $I_{\overline{\mathbb{F}}_{p}}(\bar{\unicode[STIX]{x1D706}}_{1},\overline{w})=I_{\overline{\mathbb{F}}_{p}}(\bar{\unicode[STIX]{x1D706}}_{1},\bar{g}\bar{v})=\varnothing$
, we have
$I_{\overline{\mathbb{F}}_{p}}(\bar{\unicode[STIX]{x1D706}}_{1},\overline{w})=I_{\overline{\mathbb{F}}_{p}}(\bar{\unicode[STIX]{x1D706}}_{1},\bar{g}\bar{v})=\varnothing$
, we have
![]() $\overline{w}_{-}=0$
, and so
$\overline{w}_{-}=0$
, and so
![]() $w_{+}$
is also a lift of
$w_{+}$
is also a lift of
![]() $\overline{w}$
in
$\overline{w}$
in
![]() $\mathscr{V}$
. Note that
$\mathscr{V}$
. Note that
![]() $I_{\overline{\mathbb{Q}}_{p}}(\unicode[STIX]{x1D706}_{1},w_{+})=\varnothing$
, so
$I_{\overline{\mathbb{Q}}_{p}}(\unicode[STIX]{x1D706}_{1},w_{+})=\varnothing$
, so
![]() $w_{+}$
is not stable as an element of
$w_{+}$
is not stable as an element of
![]() $\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
. Consider
$\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
. Consider
![]() $v^{\prime }:=g^{-1}(w_{+})$
. Since
$v^{\prime }:=g^{-1}(w_{+})$
. Since
![]() $\overline{g^{-1}(w_{+})}=\overline{g}^{-1}\overline{w}=\overline{g}^{-1}\bar{g}\bar{v}$
, we see that
$\overline{g^{-1}(w_{+})}=\overline{g}^{-1}\overline{w}=\overline{g}^{-1}\bar{g}\bar{v}$
, we see that
![]() $v^{\prime }$
is a lift of
$v^{\prime }$
is a lift of
![]() $\overline{v}$
. However,
$\overline{v}$
. However,
![]() $v^{\prime }$
is in the orbit of
$v^{\prime }$
is in the orbit of
![]() $w_{+}$
, so
$w_{+}$
, so
![]() $v^{\prime }$
is not stable, and so
$v^{\prime }$
is not stable, and so
![]() $P(v^{\prime })=0$
. But this implies that
$P(v^{\prime })=0$
. But this implies that
![]() $\overline{P}(\overline{v})=\overline{P(v^{\prime })}=0$
, contradicting our choice of
$\overline{P}(\overline{v})=\overline{P(v^{\prime })}=0$
, contradicting our choice of
![]() $\overline{v}$
.◻
$\overline{v}$
.◻
Lemma 2.2. Suppose that
![]() $v\in \mathscr{V}_{{\mathcal{O}}}$
is not stable for the action of
$v\in \mathscr{V}_{{\mathcal{O}}}$
is not stable for the action of
![]() $\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
on
$\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
on
![]() $\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
. Then the image
$\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
. Then the image
![]() $\overline{v}$
of
$\overline{v}$
of
![]() $v$
in
$v$
in
![]() $\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
is not stable for the action of
$\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
is not stable for the action of
![]() $\mathscr{G}_{\overline{\mathbb{F}}_{p}}$
. In particular, if
$\mathscr{G}_{\overline{\mathbb{F}}_{p}}$
. In particular, if
![]() $\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
contains stable vectors, then
$\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
contains stable vectors, then
![]() $\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
contains stable vectors.
$\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
contains stable vectors.
Proof. Since
![]() $v\in \mathscr{V}_{{\mathcal{O}}}$
is not stable as an element of
$v\in \mathscr{V}_{{\mathcal{O}}}$
is not stable as an element of
![]() $\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
, there exists a non-trivial one-parameter subgroup
$\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
, there exists a non-trivial one-parameter subgroup
![]() $\unicode[STIX]{x1D706}:\mathbb{G}_{m}\rightarrow \mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
such that
$\unicode[STIX]{x1D706}:\mathbb{G}_{m}\rightarrow \mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
such that
![]() $I_{\overline{\mathbb{Q}}_{p}}(\unicode[STIX]{x1D706},v)=\varnothing$
. Consider the parabolic subgroup
$I_{\overline{\mathbb{Q}}_{p}}(\unicode[STIX]{x1D706},v)=\varnothing$
. Consider the parabolic subgroup
![]() $P_{\unicode[STIX]{x1D706}}$
of
$P_{\unicode[STIX]{x1D706}}$
of
![]() $\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
defined by
$\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
defined by
 $$\begin{eqnarray}\displaystyle P_{\unicode[STIX]{x1D706}}(\overline{\mathbb{Q}}_{p}) & = & \displaystyle \Bigl\{g\in \mathscr{G}_{\overline{\mathbb{Q}}_{p}}(\overline{\mathbb{Q}}_{p})|\lim _{t\rightarrow 0}\unicode[STIX]{x1D706}(t)g\unicode[STIX]{x1D706}(t)^{-1}\text{ exists in }\mathscr{G}_{\overline{\mathbb{Q}}_{p}}(\overline{\mathbb{Q}}_{p})\Bigr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{g\in \mathscr{G}(\overline{\mathbb{Q}}_{p})\,\bigg|\,gv_{i}\in \bigoplus _{i\leqslant j}(\mathscr{V}_{\overline{\mathbb{Q}}_{p}})_{j}\text{ for all }v_{i}\in (\mathscr{V}_{\overline{\mathbb{Q}}_{p}})_{i}\biggr\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{\unicode[STIX]{x1D706}}(\overline{\mathbb{Q}}_{p}) & = & \displaystyle \Bigl\{g\in \mathscr{G}_{\overline{\mathbb{Q}}_{p}}(\overline{\mathbb{Q}}_{p})|\lim _{t\rightarrow 0}\unicode[STIX]{x1D706}(t)g\unicode[STIX]{x1D706}(t)^{-1}\text{ exists in }\mathscr{G}_{\overline{\mathbb{Q}}_{p}}(\overline{\mathbb{Q}}_{p})\Bigr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\{g\in \mathscr{G}(\overline{\mathbb{Q}}_{p})\,\bigg|\,gv_{i}\in \bigoplus _{i\leqslant j}(\mathscr{V}_{\overline{\mathbb{Q}}_{p}})_{j}\text{ for all }v_{i}\in (\mathscr{V}_{\overline{\mathbb{Q}}_{p}})_{i}\biggr\}.\nonumber\end{eqnarray}$$
Choose
![]() $g\in \mathscr{G}(\overline{\mathbb{Q}}_{p})$
such that
$g\in \mathscr{G}(\overline{\mathbb{Q}}_{p})$
such that
![]() $g\unicode[STIX]{x1D706}g^{-1}$
has image in
$g\unicode[STIX]{x1D706}g^{-1}$
has image in
![]() $\mathscr{T}$
. Using the Iwasawa decomposition, we write
$\mathscr{T}$
. Using the Iwasawa decomposition, we write
![]() $g=qp$
, where
$g=qp$
, where
![]() $q\in \mathscr{G}(\mathbf{O})$
and
$q\in \mathscr{G}(\mathbf{O})$
and
![]() $p\in P_{\unicode[STIX]{x1D706}}(\overline{\mathbb{Q}}_{p})$
, and we set
$p\in P_{\unicode[STIX]{x1D706}}(\overline{\mathbb{Q}}_{p})$
, and we set
![]() $\unicode[STIX]{x1D706}_{1}=p\unicode[STIX]{x1D706}p^{-1}$
. Note that
$\unicode[STIX]{x1D706}_{1}=p\unicode[STIX]{x1D706}p^{-1}$
. Note that
![]() $I_{\overline{\mathbb{Q}}_{p}}(\unicode[STIX]{x1D706}_{1},v)=I_{\overline{\mathbb{Q}}_{p}}(\unicode[STIX]{x1D706},p^{-1}v)=\varnothing$
because, by the definition of
$I_{\overline{\mathbb{Q}}_{p}}(\unicode[STIX]{x1D706}_{1},v)=I_{\overline{\mathbb{Q}}_{p}}(\unicode[STIX]{x1D706},p^{-1}v)=\varnothing$
because, by the definition of
![]() $P_{\unicode[STIX]{x1D706}}$
, the weights of
$P_{\unicode[STIX]{x1D706}}$
, the weights of
![]() $p^{-1}v$
with respect to
$p^{-1}v$
with respect to
![]() $\unicode[STIX]{x1D706}$
can only be larger than the weights of
$\unicode[STIX]{x1D706}$
can only be larger than the weights of
![]() $v$
with respect to
$v$
with respect to
![]() $\unicode[STIX]{x1D706}$
. Set
$\unicode[STIX]{x1D706}$
. Set
![]() $\unicode[STIX]{x1D707}:=g\unicode[STIX]{x1D706}g^{-1}=q\unicode[STIX]{x1D706}_{1}q^{-1}$
. By the identification of cocharacters
$\unicode[STIX]{x1D707}:=g\unicode[STIX]{x1D706}g^{-1}=q\unicode[STIX]{x1D706}_{1}q^{-1}$
. By the identification of cocharacters
![]() $\operatorname{Hom}_{\overline{\mathbb{Q}}_{p}}(\mathbb{G}_{m},\mathscr{T}_{\overline{\mathbb{Q}}_{p}})\simeq \operatorname{Hom}_{\mathbf{O}}(\mathbb{G}_{m},\mathscr{T})\simeq \operatorname{Hom}_{\overline{\mathbb{F}}_{p}}(\mathbb{G}_{m},\mathscr{T}_{\overline{\mathbb{F}}_{p}})$
, we obtain a non-trivial one-parameter subgroup
$\operatorname{Hom}_{\overline{\mathbb{Q}}_{p}}(\mathbb{G}_{m},\mathscr{T}_{\overline{\mathbb{Q}}_{p}})\simeq \operatorname{Hom}_{\mathbf{O}}(\mathbb{G}_{m},\mathscr{T})\simeq \operatorname{Hom}_{\overline{\mathbb{F}}_{p}}(\mathbb{G}_{m},\mathscr{T}_{\overline{\mathbb{F}}_{p}})$
, we obtain a non-trivial one-parameter subgroup
![]() $\overline{\unicode[STIX]{x1D707}}:\mathbb{G}_{m}\rightarrow \mathscr{G}_{\overline{\mathbb{F}}_{p}}$
corresponding to
$\overline{\unicode[STIX]{x1D707}}:\mathbb{G}_{m}\rightarrow \mathscr{G}_{\overline{\mathbb{F}}_{p}}$
corresponding to
![]() $\unicode[STIX]{x1D707}\in \operatorname{Hom}_{\overline{\mathbb{Q}}_{p}}(\mathbb{G}_{m},\mathscr{T}_{\overline{\mathbb{Q}}_{p}})$
.
$\unicode[STIX]{x1D707}\in \operatorname{Hom}_{\overline{\mathbb{Q}}_{p}}(\mathbb{G}_{m},\mathscr{T}_{\overline{\mathbb{Q}}_{p}})$
.
Next note that for all
![]() $w\in \mathscr{V}_{\mathbf{O}}$
,
$w\in \mathscr{V}_{\mathbf{O}}$
,
![]() $I_{\overline{\mathbb{F}}_{p}}(\overline{\unicode[STIX]{x1D707}},\overline{w})\subset I_{\overline{\mathbb{Q}}_{p}}(\unicode[STIX]{x1D707},w)$
; in particular,
$I_{\overline{\mathbb{F}}_{p}}(\overline{\unicode[STIX]{x1D707}},\overline{w})\subset I_{\overline{\mathbb{Q}}_{p}}(\unicode[STIX]{x1D707},w)$
; in particular,
![]() $I_{\overline{\mathbb{F}}_{p}}(\overline{\unicode[STIX]{x1D707}},\overline{qv})\,\subset \,I_{\overline{\mathbb{Q}}_{p}}(\unicode[STIX]{x1D707},qv)=I_{\overline{\mathbb{Q}}_{p}}(\unicode[STIX]{x1D706}_{1},v)=\varnothing$
. Hence,
$I_{\overline{\mathbb{F}}_{p}}(\overline{\unicode[STIX]{x1D707}},\overline{qv})\,\subset \,I_{\overline{\mathbb{Q}}_{p}}(\unicode[STIX]{x1D707},qv)=I_{\overline{\mathbb{Q}}_{p}}(\unicode[STIX]{x1D706}_{1},v)=\varnothing$
. Hence,
![]() $\overline{qv}$
is not stable. Since
$\overline{qv}$
is not stable. Since
![]() $\overline{qv}=\overline{q}\cdot \overline{v}$
is in the orbit of
$\overline{qv}=\overline{q}\cdot \overline{v}$
is in the orbit of
![]() $\overline{v}$
, we see that
$\overline{v}$
, we see that
![]() $\overline{v}$
is not stable.◻
$\overline{v}$
is not stable.◻
Remark 2.3. The above proof was inspired by the proof of [Reference Moy and PrasadMP94, Proposition 4.3]. Moy and Prasad showed that if
![]() $v\in \mathscr{V}_{{\mathcal{O}}}$
is an unstable, i.e. not semistable, vector of
$v\in \mathscr{V}_{{\mathcal{O}}}$
is an unstable, i.e. not semistable, vector of
![]() $\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
under the action of
$\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
under the action of
![]() $\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
, then the image
$\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
, then the image
![]() $\overline{v}$
of
$\overline{v}$
of
![]() $v$
in
$v$
in
![]() $\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
is unstable under the action of
$\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
is unstable under the action of
![]() $\mathscr{G}_{\overline{\mathbb{F}}_{p}}$
.
$\mathscr{G}_{\overline{\mathbb{F}}_{p}}$
.
Combining Lemmas 2.1 and 2.2, we obtain the following result.
Corollary 2.4. The representation
![]() $\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
contains stable vectors for the action of
$\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
contains stable vectors for the action of
![]() $\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
if and only if the representation
$\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
if and only if the representation
![]() $\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
contains stable vectors for the action of
$\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
contains stable vectors for the action of
![]() $\mathscr{G}_{\overline{\mathbb{F}}_{p}}$
.
$\mathscr{G}_{\overline{\mathbb{F}}_{p}}$
.
The same statement holds for semistability, as follows.
Lemma 2.5. The representation
![]() $\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
contains semistable vectors for the action of
$\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
contains semistable vectors for the action of
![]() $\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
if and only if the representation
$\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
if and only if the representation
![]() $\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
contains semistable vectors for the action of
$\mathscr{V}_{\overline{\mathbb{F}}_{p}}$
contains semistable vectors for the action of
![]() $\mathscr{G}_{\overline{\mathbb{F}}_{p}}$
.
$\mathscr{G}_{\overline{\mathbb{F}}_{p}}$
.
Proof. First suppose that
![]() $\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
contains semistable vectors under
$\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
contains semistable vectors under
![]() $\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
. As mentioned at the beginning of this section, this means that there exists a non-constant (hence non-zero)
$\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
. As mentioned at the beginning of this section, this means that there exists a non-constant (hence non-zero)
![]() $\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
-invariant homogeneous polynomial on
$\mathscr{G}_{\overline{\mathbb{Q}}_{p}}$
-invariant homogeneous polynomial on
![]() $\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
. As in the proof of Lemma 2.1, the choice of a basis of
$\mathscr{V}_{\overline{\mathbb{Q}}_{p}}$
. As in the proof of Lemma 2.1, the choice of a basis of
![]() $\mathscr{V}$
yields an identification of
$\mathscr{V}$
yields an identification of
![]() $f$
with an element of
$f$
with an element of
![]() $\overline{\mathbb{Q}}_{p}[x_{1},\ldots ,x_{n}]$
, and we may assume without loss of generality that the minimal valuation of the coefficients of
$\overline{\mathbb{Q}}_{p}[x_{1},\ldots ,x_{n}]$
, and we may assume without loss of generality that the minimal valuation of the coefficients of
![]() $f$
is zero. Thus, we can project
$f$
is zero. Thus, we can project
![]() $f$
to a non-constant homogeneous
$f$
to a non-constant homogeneous
![]() $\mathscr{G}(\overline{\mathbb{F}}_{p})$
-invariant element
$\mathscr{G}(\overline{\mathbb{F}}_{p})$
-invariant element
![]() $\overline{f}\in \operatorname{Sym}\check{\mathscr{V}}_{\overline{\mathbb{F}}_{p}}$
, and there exists
$\overline{f}\in \operatorname{Sym}\check{\mathscr{V}}_{\overline{\mathbb{F}}_{p}}$
, and there exists
![]() $\overline{v}\in \mathscr{V}_{\overline{\mathbb{F}}_{p}}$
such that
$\overline{v}\in \mathscr{V}_{\overline{\mathbb{F}}_{p}}$
such that
![]() $\overline{f}(\overline{v})\neq 0$
, i.e.
$\overline{f}(\overline{v})\neq 0$
, i.e.
![]() $\overline{v}$
is semistable.
$\overline{v}$
is semistable.
The converse follows from [Reference Moy and PrasadMP94, Proposition 4.3], as mentioned in Remark 2.3. ◻
3 Representations coming from Moy–Prasad filtrations
3.1 Moy–Prasad filtrations
Now we let
![]() $G$
be an absolutely simple algebraic group which is defined and split over
$G$
be an absolutely simple algebraic group which is defined and split over
![]() $K$
. Let
$K$
. Let
![]() $x$
be a point in the Bruhat–Tits building
$x$
be a point in the Bruhat–Tits building
![]() $\mathscr{B}(G,K)$
of
$\mathscr{B}(G,K)$
of
![]() $G$
over
$G$
over
![]() $K$
. Then
$K$
. Then
![]() $x$
is contained in some apartment
$x$
is contained in some apartment
![]() $\mathscr{A}$
corresponding to a maximal
$\mathscr{A}$
corresponding to a maximal
![]() $K$
-split torus
$K$
-split torus
![]() $T$
of
$T$
of
![]() $G$
. Let
$G$
. Let
![]() $\left(X=\operatorname{Hom}_{K}(T,\mathbb{G}_{m}),\unicode[STIX]{x1D6F7},\check{X},\check{\unicode[STIX]{x1D6F7}}\right)$
be the root datum of
$\left(X=\operatorname{Hom}_{K}(T,\mathbb{G}_{m}),\unicode[STIX]{x1D6F7},\check{X},\check{\unicode[STIX]{x1D6F7}}\right)$
be the root datum of
![]() $G$
and let
$G$
and let
![]() $\unicode[STIX]{x1D6E5}=\{\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\ldots ,\unicode[STIX]{x1D6FC}_{\ell }\}$
denote the set of simple roots of
$\unicode[STIX]{x1D6E5}=\{\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\ldots ,\unicode[STIX]{x1D6FC}_{\ell }\}$
denote the set of simple roots of
![]() $T$
corresponding to some Borel subgroup containing
$T$
corresponding to some Borel subgroup containing
![]() $T$
. For each
$T$
. For each
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
, let
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
, let
![]() $U_{\unicode[STIX]{x1D6FC}}$
be the unipotent subgroup of
$U_{\unicode[STIX]{x1D6FC}}$
be the unipotent subgroup of
![]() $G$
normalized by
$G$
normalized by
![]() $T$
and corresponding to
$T$
and corresponding to
![]() $\unicode[STIX]{x1D6FC}$
. We fix a Chevalley system
$\unicode[STIX]{x1D6FC}$
. We fix a Chevalley system
![]() $\{u_{\unicode[STIX]{x1D6FC}}:\mathbb{G}_{a}\rightarrow U_{\unicode[STIX]{x1D6FC}}\}_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}$
, which defines a Chevalley basis
$\{u_{\unicode[STIX]{x1D6FC}}:\mathbb{G}_{a}\rightarrow U_{\unicode[STIX]{x1D6FC}}\}_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}$
, which defines a Chevalley basis
![]() $\{e_{\unicode[STIX]{x1D6FC}},h_{i}\mid \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7},1\leqslant i\leqslant \ell \}$
of
$\{e_{\unicode[STIX]{x1D6FC}},h_{i}\mid \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7},1\leqslant i\leqslant \ell \}$
of
![]() $\mathfrak{g}=\operatorname{Lie}(G)$
by
$\mathfrak{g}=\operatorname{Lie}(G)$
by
![]() $e_{\unicode[STIX]{x1D6FC}}:=\operatorname{Lie}(u_{\unicode[STIX]{x1D6FC}})(1)$
and
$e_{\unicode[STIX]{x1D6FC}}:=\operatorname{Lie}(u_{\unicode[STIX]{x1D6FC}})(1)$
and
![]() $h_{i}=[e_{\unicode[STIX]{x1D6FC}_{i}},e_{-\unicode[STIX]{x1D6FC}_{i}}]$
. This choice yields a hyperspecial point
$h_{i}=[e_{\unicode[STIX]{x1D6FC}_{i}},e_{-\unicode[STIX]{x1D6FC}_{i}}]$
. This choice yields a hyperspecial point
![]() $x_{0}\in \mathscr{A}$
, i.e. the unique point in
$x_{0}\in \mathscr{A}$
, i.e. the unique point in
![]() $\mathscr{A}$
fixed by
$\mathscr{A}$
fixed by
![]() $u_{\unicode[STIX]{x1D6FC}}(-1)u_{-\unicode[STIX]{x1D6FC}}(1)u_{\unicode[STIX]{x1D6FC}}(-1)$
for all
$u_{\unicode[STIX]{x1D6FC}}(-1)u_{-\unicode[STIX]{x1D6FC}}(1)u_{\unicode[STIX]{x1D6FC}}(-1)$
for all
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
. Taking this point as the origin, we can identify the (
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
. Taking this point as the origin, we can identify the (
![]() $\mathbb{R}\otimes \check{X}$
)-torsor
$\mathbb{R}\otimes \check{X}$
)-torsor
![]() $\mathscr{A}$
with
$\mathscr{A}$
with
![]() $\mathbb{R}\otimes \check{X}$
. Elements of
$\mathbb{R}\otimes \check{X}$
. Elements of
![]() $X$
are then regarded as affine functions on
$X$
are then regarded as affine functions on
![]() $\mathscr{A}$
vanishing at
$\mathscr{A}$
vanishing at
![]() $x_{0}$
. The affine roots are precisely the affine functions
$x_{0}$
. The affine roots are precisely the affine functions
![]() $\unicode[STIX]{x1D713}:\mathscr{A}\rightarrow \mathbb{R}$
of the form
$\unicode[STIX]{x1D713}:\mathscr{A}\rightarrow \mathbb{R}$
of the form
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D6FC}+n$
, where
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D6FC}+n$
, where
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
and
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
and
![]() $n\in \mathbb{Z}$
. We denote the set of affine roots by
$n\in \mathbb{Z}$
. We denote the set of affine roots by
![]() $\unicode[STIX]{x1D6F9}$
and, for
$\unicode[STIX]{x1D6F9}$
and, for
![]() $\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}$
, denote by
$\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}$
, denote by
![]() $\dot{\unicode[STIX]{x1D713}}$
the gradient of
$\dot{\unicode[STIX]{x1D713}}$
the gradient of
![]() $\unicode[STIX]{x1D713}$
. We call
$\unicode[STIX]{x1D713}$
. We call
![]() $x$
rational if for every
$x$
rational if for every
![]() $\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}$
, we have
$\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}$
, we have
![]() $\unicode[STIX]{x1D713}(x)\in \mathbb{Q}$
. For rational
$\unicode[STIX]{x1D713}(x)\in \mathbb{Q}$
. For rational
![]() $x$
, the order of
$x$
, the order of
![]() $x$
is the smallest positive integer
$x$
is the smallest positive integer
![]() $m$
such that
$m$
such that
![]() $\unicode[STIX]{x1D713}(x)\in (1/m)\mathbb{Z}$
for all
$\unicode[STIX]{x1D713}(x)\in (1/m)\mathbb{Z}$
for all
![]() $\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}$
.
$\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}$
.
Given
![]() $\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}$
, we define the compact subgroup
$\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}$
, we define the compact subgroup
![]() $U_{\unicode[STIX]{x1D713}}$
of the root group
$U_{\unicode[STIX]{x1D713}}$
of the root group
![]() $U_{\dot{\unicode[STIX]{x1D713}}}\subset G(K)$
by
$U_{\dot{\unicode[STIX]{x1D713}}}\subset G(K)$
by
We let
![]() $T(K)_{0}$
denote the maximal bounded subgroup of
$T(K)_{0}$
denote the maximal bounded subgroup of
![]() $T(K)$
. Note that
$T(K)$
. Note that
For
![]() $r>0$
, we define the subgroups
$r>0$
, we define the subgroups
![]() $T(K)_{r}$
of
$T(K)_{r}$
of
![]() $T(K)_{0}$
by
$T(K)_{0}$
by
Then, for
![]() $r\geqslant 0$
, the Moy–Prasad filtration subgroups of
$r\geqslant 0$
, the Moy–Prasad filtration subgroups of
![]() $G$
are given by
$G$
are given by
We also set
The quotient
![]() $G(K)_{x,0}/G(K)_{x,0+}$
forms the
$G(K)_{x,0}/G(K)_{x,0+}$
forms the
![]() $\overline{\mathbb{F}}_{p}$
-points of a reductive group
$\overline{\mathbb{F}}_{p}$
-points of a reductive group
![]() $\mathbf{G}_{x}$
over
$\mathbf{G}_{x}$
over
![]() $\overline{\mathbb{F}}_{p}$
. If we let
$\overline{\mathbb{F}}_{p}$
. If we let
![]() $r(x)$
be the smallest positive value in the set
$r(x)$
be the smallest positive value in the set
![]() $\{\unicode[STIX]{x1D713}(x)\mid \unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}\}$
, then the quotient
$\{\unicode[STIX]{x1D713}(x)\mid \unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}\}$
, then the quotient
![]() $\mathbf{V}_{x}:=G(K)_{x,r(x)}/G(K)_{x,r(x)+}$
is an
$\mathbf{V}_{x}:=G(K)_{x,r(x)}/G(K)_{x,r(x)+}$
is an
![]() $\overline{\mathbb{F}}_{p}$
-vector space that admits a rational action of
$\overline{\mathbb{F}}_{p}$
-vector space that admits a rational action of
![]() $\mathbf{G}_{x}$
induced by conjugation in
$\mathbf{G}_{x}$
induced by conjugation in
![]() $G(K)$
. Similarly, one can define a filtration
$G(K)$
. Similarly, one can define a filtration
![]() $\mathfrak{g}_{x,r}$
(
$\mathfrak{g}_{x,r}$
(
![]() $r\in \mathbb{R}$
) of the Lie algebra
$r\in \mathbb{R}$
) of the Lie algebra
![]() $\mathfrak{g}$
such that
$\mathfrak{g}$
such that
![]() $G(K)_{x,r}/G(K)_{x,r+}\simeq \mathfrak{g}_{x,r}/\mathfrak{g}_{x,r+}$
as
$G(K)_{x,r}/G(K)_{x,r+}\simeq \mathfrak{g}_{x,r}/\mathfrak{g}_{x,r+}$
as
![]() $\mathbf{G}_{x}$
-representations. See [Reference Moy and PrasadMP94, Reference Moy and PrasadMP96] for details.
$\mathbf{G}_{x}$
-representations. See [Reference Moy and PrasadMP94, Reference Moy and PrasadMP96] for details.
Note that a slight variation of the proof of [Reference Reeder and YuRY14, Lemma 3.1] shows that if
![]() $\check{\mathbf{V}}_{x}$
contains semistable vectors, then
$\check{\mathbf{V}}_{x}$
contains semistable vectors, then
![]() $x$
is a barycenter of a facet (Reeder and Yu showed that if
$x$
is a barycenter of a facet (Reeder and Yu showed that if
![]() $G(K)_{x,(1/m)}/G(K)_{x,(1/m)+}$
contains semistable vectors, then
$G(K)_{x,(1/m)}/G(K)_{x,(1/m)+}$
contains semistable vectors, then
![]() $x$
is a barycenter, but their proof still holds after substituting ‘
$x$
is a barycenter, but their proof still holds after substituting ‘
![]() $r(x)$
’ for ‘
$r(x)$
’ for ‘
![]() $1/m$
’). If
$1/m$
’). If
![]() $x$
is a barycenter, then
$x$
is a barycenter, then
![]() $x$
is rational and
$x$
is rational and
![]() $r(x)=1/m$
, where
$r(x)=1/m$
, where
![]() $m$
is the order of
$m$
is the order of
![]() $x$
. Thus, for the rest of the paper, we assume that
$x$
. Thus, for the rest of the paper, we assume that
![]() $r(x)=1/m$
for some integer
$r(x)=1/m$
for some integer
![]() $m\geqslant 1$
and that
$m\geqslant 1$
and that
![]() $x$
is rational of order
$x$
is rational of order
![]() $m$
.
$m$
.
3.2 A reductive group associated to
 $x$
$x$
In order to study the action of
![]() $\mathbf{G}_{x}$
on
$\mathbf{G}_{x}$
on
![]() $\mathbf{V}_{x}$
using the results of § 2, we define an auxiliary reductive group as follows. Let
$\mathbf{V}_{x}$
using the results of § 2, we define an auxiliary reductive group as follows. Let
![]() $\unicode[STIX]{x1D6F7}_{x}$
be the sub-root system
$\unicode[STIX]{x1D6F7}_{x}$
be the sub-root system
![]() $\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}\mid \unicode[STIX]{x1D6FC}(x)\in \mathbb{Z}\}$
of
$\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}\mid \unicode[STIX]{x1D6FC}(x)\in \mathbb{Z}\}$
of
![]() $\unicode[STIX]{x1D6F7}$
, and define
$\unicode[STIX]{x1D6F7}$
, and define
![]() $H_{x}$
to be the reductive subgroup of
$H_{x}$
to be the reductive subgroup of
![]() $G$
whose
$G$
whose
![]() $K$
-points are given by
$K$
-points are given by
![]() $\left\langle T(K),U_{\unicode[STIX]{x1D6FC}}(K)\mid \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}_{x}\right\rangle$
. Note that
$\left\langle T(K),U_{\unicode[STIX]{x1D6FC}}(K)\mid \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}_{x}\right\rangle$
. Note that
![]() $H_{x}$
has root datum
$H_{x}$
has root datum
![]() $(X,\unicode[STIX]{x1D6F7}_{x},\check{X},\check{\unicode[STIX]{x1D6F7}}_{x})$
.
$(X,\unicode[STIX]{x1D6F7}_{x},\check{X},\check{\unicode[STIX]{x1D6F7}}_{x})$
.
Define
![]() $Q_{x}$
to be the parahoric subgroup of
$Q_{x}$
to be the parahoric subgroup of
![]() $H_{x}(K)$
generated by
$H_{x}(K)$
generated by
![]() $T(K)_{0}$
and
$T(K)_{0}$
and
![]() $\{U_{\unicode[STIX]{x1D713}}\mid \unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9},\unicode[STIX]{x1D713}(x)=0\}$
. Let
$\{U_{\unicode[STIX]{x1D713}}\mid \unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9},\unicode[STIX]{x1D713}(x)=0\}$
. Let
![]() $\mathscr{H}_{x}$
be the associated parahoric
$\mathscr{H}_{x}$
be the associated parahoric
![]() ${\mathcal{O}}$
-group scheme defined by [Reference Moy and PrasadMP96], whose generic fiber
${\mathcal{O}}$
-group scheme defined by [Reference Moy and PrasadMP96], whose generic fiber
![]() $\mathscr{H}_{x}\times _{{\mathcal{O}}}K$
is
$\mathscr{H}_{x}\times _{{\mathcal{O}}}K$
is
![]() $H_{x}$
and with
$H_{x}$
and with
![]() $\mathscr{H}_{x}({\mathcal{O}})=Q_{x}$
. By construction,
$\mathscr{H}_{x}({\mathcal{O}})=Q_{x}$
. By construction,
![]() $Q_{x}$
is hyperspecial in
$Q_{x}$
is hyperspecial in
![]() $H_{x}(K)$
, so
$H_{x}(K)$
, so
![]() $\mathscr{H}_{x}$
is a split reductive group over
$\mathscr{H}_{x}$
is a split reductive group over
![]() ${\mathcal{O}}$
[Reference TitsTit79, 3.4.2]. By comparing root data, we see that the special fiber
${\mathcal{O}}$
[Reference TitsTit79, 3.4.2]. By comparing root data, we see that the special fiber
![]() $\mathscr{H}_{x}\times _{{\mathcal{O}}}\overline{\mathbb{F}}_{p}$
of
$\mathscr{H}_{x}\times _{{\mathcal{O}}}\overline{\mathbb{F}}_{p}$
of
![]() $\mathscr{H}_{x}$
is isomorphic to
$\mathscr{H}_{x}$
is isomorphic to
![]() $\mathbf{G}_{x}$
. More precisely, we have an isomorphism
$\mathbf{G}_{x}$
. More precisely, we have an isomorphism
![]() $\unicode[STIX]{x1D704}$
, which on
$\unicode[STIX]{x1D704}$
, which on
![]() $\overline{\mathbb{F}}_{p}$
-points is induced by the inclusion
$\overline{\mathbb{F}}_{p}$
-points is induced by the inclusion
![]() $\mathscr{H}_{x}({\mathcal{O}})=Q_{x}{\hookrightarrow}G(K)_{x,0}$
:
$\mathscr{H}_{x}({\mathcal{O}})=Q_{x}{\hookrightarrow}G(K)_{x,0}$
:
Next we construct an
![]() ${\mathcal{O}}$
-module with an action of
${\mathcal{O}}$
-module with an action of
![]() $\mathscr{H}_{x}$
such that the action on the special fiber corresponds to the action of
$\mathscr{H}_{x}$
such that the action on the special fiber corresponds to the action of
![]() $\mathbf{G}_{x}$
on
$\mathbf{G}_{x}$
on
![]() $\mathbf{V}_{x}$
. Given
$\mathbf{V}_{x}$
. Given
![]() $0<r<1$
, we define the
$0<r<1$
, we define the
![]() ${\mathcal{O}}$
-submodule
${\mathcal{O}}$
-submodule
![]() $L_{x,r}$
of
$L_{x,r}$
of
![]() $\mathfrak{g}$
to be the free
$\mathfrak{g}$
to be the free
![]() ${\mathcal{O}}$
-submodule with basis
${\mathcal{O}}$
-submodule with basis
Then
![]() $L_{x,r}$
is a direct summand of the Moy–Prasad filtration lattice
$L_{x,r}$
is a direct summand of the Moy–Prasad filtration lattice
![]() $\mathfrak{g}_{x,r}$
, and the inclusion of
$\mathfrak{g}_{x,r}$
, and the inclusion of
![]() $L_{x,r}$
into
$L_{x,r}$
into
![]() $\mathfrak{g}_{x,r}$
induces an isomorphism
$\mathfrak{g}_{x,r}$
induces an isomorphism
of
![]() $\overline{\mathbb{F}}_{p}$
-modules.
$\overline{\mathbb{F}}_{p}$
-modules.
Lemma 3.1. The action of
![]() $Q_{x}$
on
$Q_{x}$
on
![]() $\mathfrak{g}$
by restriction of the adjoint action of
$\mathfrak{g}$
by restriction of the adjoint action of
![]() $G(K)$
stabilizes the
$G(K)$
stabilizes the
![]() ${\mathcal{O}}$
-module
${\mathcal{O}}$
-module
![]() $L_{x,r}$
.
$L_{x,r}$
.
Proof. Let us consider a basis element
![]() $e_{\unicode[STIX]{x1D6FE}}$
, where
$e_{\unicode[STIX]{x1D6FE}}$
, where
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D6FE}(x)=r$
. Note that an element of
$\unicode[STIX]{x1D6FE}(x)=r$
. Note that an element of
![]() $T(K)_{0}$
acts on
$T(K)_{0}$
acts on
![]() $e_{\unicode[STIX]{x1D6FE}}$
as multiplication by an element of
$e_{\unicode[STIX]{x1D6FE}}$
as multiplication by an element of
![]() ${\mathcal{O}}$
, so
${\mathcal{O}}$
, so
![]() $T(K)_{0}$
preserves
$T(K)_{0}$
preserves
![]() $L_{x,r}$
. Let
$L_{x,r}$
. Let
![]() $\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}$
with
$\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}$
with
![]() $\unicode[STIX]{x1D713}(x)=0$
. Since there exist integers
$\unicode[STIX]{x1D713}(x)=0$
. Since there exist integers
![]() $M_{\dot{\unicode[STIX]{x1D713}},\dot{\unicode[STIX]{x1D6FE}},i}$
such that for any
$M_{\dot{\unicode[STIX]{x1D713}},\dot{\unicode[STIX]{x1D6FE}},i}$
such that for any
![]() $t\in K$
, we have
$t\in K$
, we have
[Reference CarterCar89, p. 64], it is an easy calculation to check that
![]() $U_{\unicode[STIX]{x1D713}}\cdot e_{\unicode[STIX]{x1D6FE}}\subset L_{x,r}$
.◻
$U_{\unicode[STIX]{x1D713}}\cdot e_{\unicode[STIX]{x1D6FE}}\subset L_{x,r}$
.◻
As a corollary, the adjoint action of
![]() $G$
on
$G$
on
![]() $\mathfrak{g}$
restricts to an action of
$\mathfrak{g}$
restricts to an action of
![]() $H_{x}=\mathscr{H}_{x}\times _{{\mathcal{O}}}K$
on
$H_{x}=\mathscr{H}_{x}\times _{{\mathcal{O}}}K$
on
![]() $L_{x,r}\otimes K$
with the property that
$L_{x,r}\otimes K$
with the property that
![]() $\mathscr{H}_{x}({\mathcal{O}})$
preserves
$\mathscr{H}_{x}({\mathcal{O}})$
preserves
![]() $L_{x,r}$
. Thus, by [Reference Bruhat and TitsBT84, § 1.7], the action extends to a unique action of
$L_{x,r}$
. Thus, by [Reference Bruhat and TitsBT84, § 1.7], the action extends to a unique action of
![]() $\mathscr{H}_{x}$
on
$\mathscr{H}_{x}$
on
![]() $L_{x,r}$
.
$L_{x,r}$
.
Moreover, by construction, if
![]() $r(x)\neq 1$
, then the action of
$r(x)\neq 1$
, then the action of
![]() $\mathscr{H}_{x}\times \overline{\mathbb{F}}_{p}$
on
$\mathscr{H}_{x}\times \overline{\mathbb{F}}_{p}$
on
![]() $L_{x,r(x)}\otimes \overline{\mathbb{F}}_{p}$
corresponds via the isomorphisms in (1) and (2) to the action of
$L_{x,r(x)}\otimes \overline{\mathbb{F}}_{p}$
corresponds via the isomorphisms in (1) and (2) to the action of
![]() $\mathbf{G}_{x}$
on
$\mathbf{G}_{x}$
on
![]() $\mathbf{V}_{x}$
described in § 3.1. If
$\mathbf{V}_{x}$
described in § 3.1. If
![]() $r(x)=1$
, then
$r(x)=1$
, then
![]() $x$
is hyperspecial in
$x$
is hyperspecial in
![]() $\mathscr{A}$
and the
$\mathscr{A}$
and the
![]() $\mathbf{G}_{x}$
-representation
$\mathbf{G}_{x}$
-representation
![]() $\mathbf{V}_{x}$
is isomorphic to the adjoint representation of
$\mathbf{V}_{x}$
is isomorphic to the adjoint representation of
![]() $\mathbf{G}_{x}$
on
$\mathbf{G}_{x}$
on
![]() $\operatorname{Lie}(\mathbf{G}_{x})$
, with
$\operatorname{Lie}(\mathbf{G}_{x})$
, with
![]() $\operatorname{Lie}(\mathbf{G}_{x})\simeq \operatorname{Lie}(\mathscr{H}_{x})_{\overline{\mathbb{F}}_{p}}$
. Thus, we define
$\operatorname{Lie}(\mathbf{G}_{x})\simeq \operatorname{Lie}(\mathscr{H}_{x})_{\overline{\mathbb{F}}_{p}}$
. Thus, we define
Using Corollary 2.4 and Lemma 2.5, we conclude the following result.
Lemma 3.2. Let
![]() $H_{x}$
and
$H_{x}$
and
![]() $\mathscr{V}_{x}$
be as defined above. The action of
$\mathscr{V}_{x}$
be as defined above. The action of
![]() $(H_{x})_{\overline{\mathbb{Q}}_{p}}$
on
$(H_{x})_{\overline{\mathbb{Q}}_{p}}$
on
![]() $(\mathscr{V}_{x})_{\overline{\mathbb{Q}}_{p}}=\mathscr{V}_{x}\otimes _{{\mathcal{O}}}\overline{\mathbb{Q}}_{p}$
has stable (respectively semistable) vectors if and only if the action of
$(\mathscr{V}_{x})_{\overline{\mathbb{Q}}_{p}}=\mathscr{V}_{x}\otimes _{{\mathcal{O}}}\overline{\mathbb{Q}}_{p}$
has stable (respectively semistable) vectors if and only if the action of
![]() $\mathbf{G}_{x}$
on
$\mathbf{G}_{x}$
on
![]() $\mathbf{V}_{x}$
has stable (respectively semistable) vectors.
$\mathbf{V}_{x}$
has stable (respectively semistable) vectors.
Remark 3.3. By the same reasoning, the representation of
![]() $(H_{x})_{\overline{\mathbb{Q}}_{p}}$
on
$(H_{x})_{\overline{\mathbb{Q}}_{p}}$
on
![]() $(\check{\mathscr{V}}_{x})_{\overline{\mathbb{Q}}_{p}}$
has (semi)stable vectors if and only if the representation of
$(\check{\mathscr{V}}_{x})_{\overline{\mathbb{Q}}_{p}}$
has (semi)stable vectors if and only if the representation of
![]() $\mathbf{G}_{x}$
on
$\mathbf{G}_{x}$
on
![]() $\check{\mathbf{V}}_{x}$
does. Here
$\check{\mathbf{V}}_{x}$
does. Here
![]() $\check{\mathscr{V}}_{x}$
denotes the linear dual of
$\check{\mathscr{V}}_{x}$
denotes the linear dual of
![]() $\mathscr{V}_{x}$
over
$\mathscr{V}_{x}$
over
![]() ${\mathcal{O}}$
, and
${\mathcal{O}}$
, and
![]() $\check{\mathbf{V}}_{x}$
denotes the linear dual of
$\check{\mathbf{V}}_{x}$
denotes the linear dual of
![]() $\mathbf{V}_{x}$
over
$\mathbf{V}_{x}$
over
![]() $\overline{\mathbb{F}}_{p}$
. In fact, it is this case we are particularly interested in, since the construction of Reeder and Yu requires a stable vector in
$\overline{\mathbb{F}}_{p}$
. In fact, it is this case we are particularly interested in, since the construction of Reeder and Yu requires a stable vector in
![]() $\check{\mathbf{V}}_{x}$
.
$\check{\mathbf{V}}_{x}$
.
4 Vinberg gradings and stability
In this section we use results in Vinberg theory to classify all points
![]() $x$
of
$x$
of
![]() $\mathscr{B}(G,K)$
such that
$\mathscr{B}(G,K)$
such that
![]() $\check{\mathbf{V}}_{x}$
has stable vectors. First we show that the representations of
$\check{\mathbf{V}}_{x}$
has stable vectors. First we show that the representations of
![]() $(H_{x})_{\overline{\mathbb{Q}}_{p}}$
on
$(H_{x})_{\overline{\mathbb{Q}}_{p}}$
on
![]() $(\mathscr{V}_{x})_{\overline{\mathbb{Q}}_{p}}$
are those coming from Vinberg theory of graded Lie algebras. We keep the notation from the previous section. Let
$(\mathscr{V}_{x})_{\overline{\mathbb{Q}}_{p}}$
are those coming from Vinberg theory of graded Lie algebras. We keep the notation from the previous section. Let
![]() $G^{\text{ad}}$
be the adjoint group of
$G^{\text{ad}}$
be the adjoint group of
![]() $G$
. We have an isogeny
$G$
. We have an isogeny
![]() $\unicode[STIX]{x1D711}:G\rightarrow G^{\text{ad}}$
, and we denote the maximal torus
$\unicode[STIX]{x1D711}:G\rightarrow G^{\text{ad}}$
, and we denote the maximal torus
![]() $\unicode[STIX]{x1D711}(T)$
by
$\unicode[STIX]{x1D711}(T)$
by
![]() $T^{\text{ad}}$
. The isogeny
$T^{\text{ad}}$
. The isogeny
![]() $\unicode[STIX]{x1D711}$
induces an inclusion of cocharacters
$\unicode[STIX]{x1D711}$
induces an inclusion of cocharacters
![]() $\check{X}{\hookrightarrow}\check{X}^{\text{ad}}$
that yields an isomorphism
$\check{X}{\hookrightarrow}\check{X}^{\text{ad}}$
that yields an isomorphism
![]() $\check{X}\otimes \mathbb{R}\,\overset{{\sim}}{\longrightarrow }\,\check{X}^{\text{ad}}\otimes \mathbb{R}$
. Using this isomorphism to identify
$\check{X}\otimes \mathbb{R}\,\overset{{\sim}}{\longrightarrow }\,\check{X}^{\text{ad}}\otimes \mathbb{R}$
. Using this isomorphism to identify
![]() $\check{X}\otimes \mathbb{R}$
and
$\check{X}\otimes \mathbb{R}$
and
![]() $\check{X}^{\text{ad}}\otimes \mathbb{R}$
, we can write
$\check{X}^{\text{ad}}\otimes \mathbb{R}$
, we can write
![]() $x$
as
$x$
as
![]() $x_{0}-(1/m)\check{\unicode[STIX]{x1D706}}$
for some
$x_{0}-(1/m)\check{\unicode[STIX]{x1D706}}$
for some
![]() $\check{\unicode[STIX]{x1D706}}\in \check{X}^{\text{ad}}$
, where
$\check{\unicode[STIX]{x1D706}}\in \check{X}^{\text{ad}}$
, where
![]() $x_{0}$
is the hyperspecial point associated to our Chevalley system and
$x_{0}$
is the hyperspecial point associated to our Chevalley system and
![]() $m$
is the order of
$m$
is the order of
![]() $x$
, both as defined in § 3.1. Then
$x$
, both as defined in § 3.1. Then
![]() $x$
induces a homomorphism
$x$
induces a homomorphism
and the choice of a primitive
![]() $m$
th root of unity
$m$
th root of unity
![]() $\unicode[STIX]{x1D701}$
in
$\unicode[STIX]{x1D701}$
in
![]() $\overline{\mathbb{Q}}_{p}$
yields an automorphism
$\overline{\mathbb{Q}}_{p}$
yields an automorphism
![]() $\unicode[STIX]{x1D703}=\operatorname{Inn}(\check{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701}))$
of
$\unicode[STIX]{x1D703}=\operatorname{Inn}(\check{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701}))$
of
![]() $G_{\overline{\mathbb{Q}}_{p}}$
. The corresponding automorphism
$G_{\overline{\mathbb{Q}}_{p}}$
. The corresponding automorphism
![]() $d\unicode[STIX]{x1D703}:=\operatorname{Lie}(\unicode[STIX]{x1D703})$
of
$d\unicode[STIX]{x1D703}:=\operatorname{Lie}(\unicode[STIX]{x1D703})$
of
![]() $\mathfrak{g}_{\,\overline{\mathbb{Q}}_{p}}$
yields a grading
$\mathfrak{g}_{\,\overline{\mathbb{Q}}_{p}}$
yields a grading
where
![]() $\check{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\cdot v=\unicode[STIX]{x1D701}^{i}v$
for all
$\check{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})\cdot v=\unicode[STIX]{x1D701}^{i}v$
for all
![]() $v\in (\mathfrak{g}_{\,\overline{\mathbb{Q}}_{p}})_{i}$
.
$v\in (\mathfrak{g}_{\,\overline{\mathbb{Q}}_{p}})_{i}$
.
On the previously fixed Chevalley basis
![]() $\{e_{\unicode[STIX]{x1D6FC}},h_{i}\}_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7},1\leqslant i\leqslant \ell }$
, we can write the action of
$\{e_{\unicode[STIX]{x1D6FC}},h_{i}\}_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7},1\leqslant i\leqslant \ell }$
, we can write the action of
![]() $d\unicode[STIX]{x1D703}$
explicitly:
$d\unicode[STIX]{x1D703}$
explicitly:
We see that
![]() $(\mathfrak{g}_{\,\overline{\mathbb{Q}}_{p}})_{0}=\operatorname{Lie}(H_{x})_{\overline{\mathbb{Q}}_{p}}$
and hence
$(\mathfrak{g}_{\,\overline{\mathbb{Q}}_{p}})_{0}=\operatorname{Lie}(H_{x})_{\overline{\mathbb{Q}}_{p}}$
and hence
![]() $(H_{x})_{\overline{\mathbb{Q}}_{p}}$
is the connected component
$(H_{x})_{\overline{\mathbb{Q}}_{p}}$
is the connected component
![]() $(G_{\overline{\mathbb{Q}}_{p}}^{\unicode[STIX]{x1D703}})^{0}$
of the fixed-point subgroup of
$(G_{\overline{\mathbb{Q}}_{p}}^{\unicode[STIX]{x1D703}})^{0}$
of the fixed-point subgroup of
![]() $G_{\overline{\mathbb{Q}}_{p}}$
under the action of
$G_{\overline{\mathbb{Q}}_{p}}$
under the action of
![]() $\unicode[STIX]{x1D703}$
. Moreover,
$\unicode[STIX]{x1D703}$
. Moreover,
![]() $(\mathfrak{g}_{\,\overline{\mathbb{Q}}_{p}})_{-1}=(\mathscr{V}_{x})_{\overline{\mathbb{Q}}_{p}}$
and thus we have an isomorphism
$(\mathfrak{g}_{\,\overline{\mathbb{Q}}_{p}})_{-1}=(\mathscr{V}_{x})_{\overline{\mathbb{Q}}_{p}}$
and thus we have an isomorphism
of
![]() $(H_{x})_{\overline{\mathbb{Q}}_{p}}$
-modules, where the action of
$(H_{x})_{\overline{\mathbb{Q}}_{p}}$
-modules, where the action of
![]() $(G_{\overline{\mathbb{Q}}_{p}}^{\unicode[STIX]{x1D703}})^{0}$
on
$(G_{\overline{\mathbb{Q}}_{p}}^{\unicode[STIX]{x1D703}})^{0}$
on
![]() $(\mathfrak{g}_{\,\overline{\mathbb{Q}}_{p}})_{i}$
arises from the adjoint action of
$(\mathfrak{g}_{\,\overline{\mathbb{Q}}_{p}})_{i}$
arises from the adjoint action of
![]() $G$
on
$G$
on
![]() $\mathfrak{g}$
.
$\mathfrak{g}$
.
The benefit of relating our set-up to that of graded Lie algebras in characteristic zero is that those
![]() $(\mathfrak{g}_{\,\overline{\mathbb{Q}}_{p}})_{1}$
which contain stable vectors have been classified in [Reference Reeder, Levy, Yu and GrossRLYG12, Corollary 14]. Recall that an element
$(\mathfrak{g}_{\,\overline{\mathbb{Q}}_{p}})_{1}$
which contain stable vectors have been classified in [Reference Reeder, Levy, Yu and GrossRLYG12, Corollary 14]. Recall that an element
![]() $w$
in the Weyl group
$w$
in the Weyl group
![]() $W$
of
$W$
of
![]() $G$
is called elliptic if
$G$
is called elliptic if
![]() $w$
fixes no non-zero vector in
$w$
fixes no non-zero vector in
![]() $\check{X}$
, and
$\check{X}$
, and
![]() $w$
is
$w$
is
![]() $\mathbb{Z}$
-regular if the group generated by
$\mathbb{Z}$
-regular if the group generated by
![]() $w$
acts freely on
$w$
acts freely on
![]() $\unicode[STIX]{x1D6F7}$
.
$\unicode[STIX]{x1D6F7}$
.
Proposition 4.1. There exist stable vectors in
![]() $(\check{\mathscr{V}}_{x})_{\overline{\mathbb{Q}}_{p}}$
under the action of
$(\check{\mathscr{V}}_{x})_{\overline{\mathbb{Q}}_{p}}$
under the action of
![]() $(H_{x})_{\overline{\mathbb{Q}}_{p}}$
if and only if
$(H_{x})_{\overline{\mathbb{Q}}_{p}}$
if and only if
![]() $m$
is the order of an elliptic,
$m$
is the order of an elliptic,
![]() $\mathbb{Z}$
-regular element of the Weyl group
$\mathbb{Z}$
-regular element of the Weyl group
![]() $W$
of
$W$
of
![]() $G$
and
$G$
and
![]() $x$
is conjugate under the affine Weyl group
$x$
is conjugate under the affine Weyl group
![]() $W_{\text{aff}}$
to
$W_{\text{aff}}$
to
![]() $x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
.
$x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
.
Proof. By [Reference Reeder, Levy, Yu and GrossRLYG12, Corollary 14],
![]() $(\mathfrak{g}_{\,\overline{\mathbb{Q}}_{p}})_{1}$
contains stable vectors if and only if
$(\mathfrak{g}_{\,\overline{\mathbb{Q}}_{p}})_{1}$
contains stable vectors if and only if
![]() $W$
contains an elliptic,
$W$
contains an elliptic,
![]() $\mathbb{Z}$
-regular element of order
$\mathbb{Z}$
-regular element of order
![]() $m$
and
$m$
and
![]() $d\unicode[STIX]{x1D703}$
is principal, i.e.
$d\unicode[STIX]{x1D703}$
is principal, i.e.
![]() $\check{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})$
is conjugate by an element of
$\check{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})$
is conjugate by an element of
![]() $G^{\text{ad}}(\overline{\mathbb{Q}}_{p})$
to
$G^{\text{ad}}(\overline{\mathbb{Q}}_{p})$
to
![]() $\check{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D714})$
for some primitive
$\check{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D714})$
for some primitive
![]() $m$
th root of unity
$m$
th root of unity
![]() $\unicode[STIX]{x1D714}$
. (Note that [Reference Reeder, Levy, Yu and GrossRLYG12] formulates the result only for adjoint groups, but one can easily deduce that it holds in our setting as well.) In addition, the existence of an elliptic,
$\unicode[STIX]{x1D714}$
. (Note that [Reference Reeder, Levy, Yu and GrossRLYG12] formulates the result only for adjoint groups, but one can easily deduce that it holds in our setting as well.) In addition, the existence of an elliptic,
![]() $\mathbb{Z}$
-regular element of order
$\mathbb{Z}$
-regular element of order
![]() $m$
in
$m$
in
![]() $W$
implies that
$W$
implies that
![]() $\check{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D714})$
is conjugate to
$\check{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D714})$
is conjugate to
![]() $\check{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D701})$
[Reference Reeder, Levy, Yu and GrossRLYG12, Proposition 8]. But it is an easy exercise to check that
$\check{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D701})$
[Reference Reeder, Levy, Yu and GrossRLYG12, Proposition 8]. But it is an easy exercise to check that
![]() $\check{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})$
is conjugate to
$\check{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D701})$
is conjugate to
![]() $\check{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D701})$
if and only if
$\check{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D701})$
if and only if
![]() $x$
is conjugate to
$x$
is conjugate to
![]() $x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
under the extended affine Weyl group.
$x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
under the extended affine Weyl group.
To see that in this case
![]() $x$
is conjugate to
$x$
is conjugate to
![]() $x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
under the (unextended) affine Weyl group
$x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
under the (unextended) affine Weyl group
![]() $W_{\text{aff}}$
, we note that every element of the extended affine Weyl group can be written as a product
$W_{\text{aff}}$
, we note that every element of the extended affine Weyl group can be written as a product
![]() $ws$
, where
$ws$
, where
![]() $w\in W_{\text{aff}}$
and
$w\in W_{\text{aff}}$
and
![]() $s$
is in the stabilizer of an alcove whose closure contains
$s$
is in the stabilizer of an alcove whose closure contains
![]() $x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
. Checking the normalized Kac coordinates of all such
$x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
. Checking the normalized Kac coordinates of all such
![]() $x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
(see [Reference Reeder, Levy, Yu and GrossRLYG12] and [Reference Reeder and YuRY14]), one verifies that
$x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
(see [Reference Reeder, Levy, Yu and GrossRLYG12] and [Reference Reeder and YuRY14]), one verifies that
![]() $s$
fixes
$s$
fixes
![]() $x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
, and hence
$x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
, and hence
![]() $x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
and
$x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
and
![]() $x_{0}-(1/m)\check{\unicode[STIX]{x1D706}}$
are conjugated under
$x_{0}-(1/m)\check{\unicode[STIX]{x1D706}}$
are conjugated under
![]() $W_{\text{aff}}$
.◻
$W_{\text{aff}}$
.◻
4.1 Stable vectors
With all the pieces in place, we now come to the main purpose of our paper: the classification of points
![]() $x$
such that
$x$
such that
![]() $\check{\mathbf{V}}_{x}$
contains stable vectors for the action of
$\check{\mathbf{V}}_{x}$
contains stable vectors for the action of
![]() $\mathbf{G}_{x}$
.
$\mathbf{G}_{x}$
.
Theorem 4.2. Let
![]() $x\in \mathscr{A}$
. Then the representation
$x\in \mathscr{A}$
. Then the representation
![]() $\check{\mathbf{V}}_{x}$
contains stable vectors under the action of
$\check{\mathbf{V}}_{x}$
contains stable vectors under the action of
![]() $\mathbf{G}_{x}$
if and only if
$\mathbf{G}_{x}$
if and only if
![]() $x$
is conjugate under the affine Weyl group
$x$
is conjugate under the affine Weyl group
![]() $W_{\text{aff}}$
to
$W_{\text{aff}}$
to
![]() $x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
, where
$x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
, where
![]() $m$
is the order of an elliptic,
$m$
is the order of an elliptic,
![]() $\mathbb{Z}$
-regular element in the Weyl group
$\mathbb{Z}$
-regular element in the Weyl group
![]() $W$
of
$W$
of
![]() $G$
.
$G$
.
We would like to remark that Reeder and Yu have already given a proof of Theorem 4.2 for the case in which the characteristic
![]() $p$
of the residue field is sufficiently large (see [Reference Reeder and YuRY14, Corollary 5.1]). Because it uses Vinberg theory in characteristic
$p$
of the residue field is sufficiently large (see [Reference Reeder and YuRY14, Corollary 5.1]). Because it uses Vinberg theory in characteristic
![]() $p$
, their proof does not hold for some small primes, in particular, primes that divide
$p$
, their proof does not hold for some small primes, in particular, primes that divide
![]() $m$
.
$m$
.
Theorem 4.2 allows us to use the construction of [Reference Reeder and YuRY14] to form supercuspidal representations in a uniform way for all
![]() $p$
. We now briefly review the construction. For details, see [Reference Reeder and YuRY14, § 2.5]. Let
$p$
. We now briefly review the construction. For details, see [Reference Reeder and YuRY14, § 2.5]. Let
![]() ${\mathcal{G}}$
be an absolutely simple split reductive group over the local field
${\mathcal{G}}$
be an absolutely simple split reductive group over the local field
![]() $k$
and let
$k$
and let
![]() $=\mathbb{F}_{q}$
be the residue field of
$=\mathbb{F}_{q}$
be the residue field of
![]() $k$
. We set
$k$
. We set
![]() $G={\mathcal{G}}_{K}$
and let
$G={\mathcal{G}}_{K}$
and let
![]() $x\in \mathscr{B}(G,K)$
be a rational point that is fixed under the action of the Galois group
$x\in \mathscr{B}(G,K)$
be a rational point that is fixed under the action of the Galois group
![]() $\operatorname{Gal}(K/k)$
. By identifying the Bruhat–Tits building
$\operatorname{Gal}(K/k)$
. By identifying the Bruhat–Tits building
![]() $\mathscr{B}({\mathcal{G}},k)$
of
$\mathscr{B}({\mathcal{G}},k)$
of
![]() ${\mathcal{G}}$
over
${\mathcal{G}}$
over
![]() $k$
with the
$k$
with the
![]() $\operatorname{Gal}(K/k)$
-fixed points of
$\operatorname{Gal}(K/k)$
-fixed points of
![]() $\mathscr{B}(G,K)$
, we may view
$\mathscr{B}(G,K)$
, we may view
![]() $x$
as a point of
$x$
as a point of
![]() $\mathscr{B}({\mathcal{G}},k)$
. Then
$\mathscr{B}({\mathcal{G}},k)$
. Then
![]() $G(K)_{x,r}$
is
$G(K)_{x,r}$
is
![]() $\operatorname{Gal}(K/k)$
-stable for all
$\operatorname{Gal}(K/k)$
-stable for all
![]() $r$
; we denote its
$r$
; we denote its
![]() $\operatorname{Gal}(K/k)$
-fixed points
$\operatorname{Gal}(K/k)$
-fixed points
![]() $(G(K)_{x,r})^{\operatorname{Gal}(K/k)}$
by
$(G(K)_{x,r})^{\operatorname{Gal}(K/k)}$
by
![]() ${\mathcal{G}}(k)_{x,r}$
. Moreover, the action of
${\mathcal{G}}(k)_{x,r}$
. Moreover, the action of
![]() $\mathbf{G}_{x}$
on
$\mathbf{G}_{x}$
on
![]() $\mathbf{V}_{x}$
is defined over
$\mathbf{V}_{x}$
is defined over
![]() $\mathfrak{f}$
with
$\mathfrak{f}$
with
![]() $\mathbf{G}_{x}(\mathfrak{f})={\mathcal{G}}(k)_{x,0}/{\mathcal{G}}(k)_{x,r(x)}$
and
$\mathbf{G}_{x}(\mathfrak{f})={\mathcal{G}}(k)_{x,0}/{\mathcal{G}}(k)_{x,r(x)}$
and
![]() $\mathbf{V}_{x}(\mathfrak{f})={\mathcal{G}}(k)_{x,r(x)}/{\mathcal{G}}(k)_{x,r(x)+}$
. We call a vector
$\mathbf{V}_{x}(\mathfrak{f})={\mathcal{G}}(k)_{x,r(x)}/{\mathcal{G}}(k)_{x,r(x)+}$
. We call a vector
![]() $\unicode[STIX]{x1D706}\in \check{\mathbf{V}}_{x}(\mathfrak{f})$
stable if it is stable as a vector in
$\unicode[STIX]{x1D706}\in \check{\mathbf{V}}_{x}(\mathfrak{f})$
stable if it is stable as a vector in
![]() $\check{\mathbf{V}}_{x}$
under the action of
$\check{\mathbf{V}}_{x}$
under the action of
![]() $\mathbf{G}_{x}$
.
$\mathbf{G}_{x}$
.
Given a stable vector
![]() $\unicode[STIX]{x1D706}\in \check{\mathbf{V}}_{x}(\mathfrak{f})$
and a non-trivial character
$\unicode[STIX]{x1D706}\in \check{\mathbf{V}}_{x}(\mathfrak{f})$
and a non-trivial character
![]() $\unicode[STIX]{x1D712}:\mathfrak{f}^{+}\rightarrow \mathbb{C}^{\times }$
, we consider the composition
$\unicode[STIX]{x1D712}:\mathfrak{f}^{+}\rightarrow \mathbb{C}^{\times }$
, we consider the composition
![]() $\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D706}:\check{\mathbf{V}}_{x}(\mathfrak{f})\rightarrow \mathbb{C}^{\times }$
as a character of
$\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D706}:\check{\mathbf{V}}_{x}(\mathfrak{f})\rightarrow \mathbb{C}^{\times }$
as a character of
![]() ${\mathcal{G}}(k)_{x,r(x)}$
that is trivial on
${\mathcal{G}}(k)_{x,r(x)}$
that is trivial on
![]() ${\mathcal{G}}(k)_{x,r(x)+}$
. Then the compactly induced representation
${\mathcal{G}}(k)_{x,r(x)+}$
. Then the compactly induced representation
is a direct sum of irreducible supercuspidal representations of
![]() ${\mathcal{G}}(k)$
of depth
${\mathcal{G}}(k)$
of depth
![]() $r(x)$
[Reference Reeder and YuRY14, Proposition 2.4].
$r(x)$
[Reference Reeder and YuRY14, Proposition 2.4].
Corollary 4.3. Let
![]() ${\mathcal{G}}$
be an absolutely simple split reductive group over the local field
${\mathcal{G}}$
be an absolutely simple split reductive group over the local field
![]() $k$
. Then, for each
$k$
. Then, for each
![]() $m$
satisfying the conditions of Theorem 4.2, there exists a finite unramified extension
$m$
satisfying the conditions of Theorem 4.2, there exists a finite unramified extension
![]() $k^{\prime }$
of
$k^{\prime }$
of
![]() $k$
such that one can implement the construction of [Reference Reeder and YuRY14] to form supercuspidal epipelagic representations of
$k$
such that one can implement the construction of [Reference Reeder and YuRY14] to form supercuspidal epipelagic representations of
![]() ${\mathcal{G}}(k^{\prime })$
.
${\mathcal{G}}(k^{\prime })$
.
Proof. Let
![]() $G={\mathcal{G}}_{K}$
as above, let
$G={\mathcal{G}}_{K}$
as above, let
![]() $\mathscr{A}$
be an apartment of
$\mathscr{A}$
be an apartment of
![]() $\mathscr{B}(G,K)$
corresponding to a
$\mathscr{B}(G,K)$
corresponding to a
![]() $k$
-split maximal torus of
$k$
-split maximal torus of
![]() $G$
, i.e.
$G$
, i.e.
![]() $\mathscr{A}\subset \mathscr{B}(G,K)^{\operatorname{Gal}(K/k)}$
, and let
$\mathscr{A}\subset \mathscr{B}(G,K)^{\operatorname{Gal}(K/k)}$
, and let
![]() $x=x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
for some
$x=x_{0}+(1/m)\check{\unicode[STIX]{x1D70C}}$
for some
![]() $m$
satisfying the conditions of Theorem 4.2. By Theorem 4.2, the representation of
$m$
satisfying the conditions of Theorem 4.2. By Theorem 4.2, the representation of
![]() $\mathbf{G}_{x}$
on
$\mathbf{G}_{x}$
on
![]() $\check{\mathbf{V}}_{x}$
contains a stable vector; call it
$\check{\mathbf{V}}_{x}$
contains a stable vector; call it
![]() $\unicode[STIX]{x1D706}$
. Since
$\unicode[STIX]{x1D706}$
. Since
![]() $\mathbf{G}_{x}$
and
$\mathbf{G}_{x}$
and
![]() $\check{\mathbf{V}}_{x}$
are defined over
$\check{\mathbf{V}}_{x}$
are defined over
![]() $\mathfrak{f}=\mathbb{F}_{q}$
, we have that
$\mathfrak{f}=\mathbb{F}_{q}$
, we have that
![]() $\unicode[STIX]{x1D706}\in \check{\mathbf{V}}_{x}(\mathfrak{f}^{\prime })$
for some finite extension
$\unicode[STIX]{x1D706}\in \check{\mathbf{V}}_{x}(\mathfrak{f}^{\prime })$
for some finite extension
![]() $\mathfrak{f}^{\prime }$
of
$\mathfrak{f}^{\prime }$
of
![]() $\mathfrak{f}$
. Let
$\mathfrak{f}$
. Let
![]() $k^{\prime }$
be any finite extension of
$k^{\prime }$
be any finite extension of
![]() $k$
whose residue field is a finite extension of
$k$
whose residue field is a finite extension of
![]() $\mathfrak{f}^{\prime }$
. Then we can input
$\mathfrak{f}^{\prime }$
. Then we can input
![]() $\unicode[STIX]{x1D706}$
into the construction described above to form
$\unicode[STIX]{x1D706}$
into the construction described above to form
![]() $\unicode[STIX]{x1D70B}_{x}(\unicode[STIX]{x1D706})$
, which decomposes into a direct sum of supercuspidal epipelagic representations of
$\unicode[STIX]{x1D70B}_{x}(\unicode[STIX]{x1D706})$
, which decomposes into a direct sum of supercuspidal epipelagic representations of
![]() ${\mathcal{G}}(k^{\prime })$
.◻
${\mathcal{G}}(k^{\prime })$
.◻
Remark 4.4. Corollary 4.3 provides previously unknown representations for some small primes
![]() $p$
depending on the type of
$p$
depending on the type of
![]() ${\mathcal{G}}$
. In particular, the construction of [Reference YuYu01] requires a tameness assumption that fails for small
${\mathcal{G}}$
. In particular, the construction of [Reference YuYu01] requires a tameness assumption that fails for small
![]() $p$
.
$p$
.
4.2 Semistable vectors
In [Reference Reeder and YuRY14, Theorem 8.3], Reeder and Yu used results in Vinberg theory to classify those
![]() $x$
for which
$x$
for which
![]() $\check{\mathbf{V}}_{x}$
has semistable vectors in terms of conditions that are independent of the residue field characteristic
$\check{\mathbf{V}}_{x}$
has semistable vectors in terms of conditions that are independent of the residue field characteristic
![]() $p$
. Yet their proof only holds for
$p$
. Yet their proof only holds for
![]() $p$
sufficiently large: specifically, they assumed that
$p$
sufficiently large: specifically, they assumed that
![]() $p$
was larger than the Coxeter number of
$p$
was larger than the Coxeter number of
![]() $G$
. Let us call
$G$
. Let us call
![]() $x$
a semistability point if the prime-independent conditions in [Reference Reeder and YuRY14, Theorem 8.3] are satisfied. The proof of the theorem can be applied to the setting of graded Lie algebras in characteristic zero to show that
$x$
a semistability point if the prime-independent conditions in [Reference Reeder and YuRY14, Theorem 8.3] are satisfied. The proof of the theorem can be applied to the setting of graded Lie algebras in characteristic zero to show that
![]() $(\check{\mathscr{V}}_{x})_{\overline{\mathbb{Q}}_{p}}\simeq (\mathfrak{g}_{\overline{\mathbb{Q}}_{p}})_{1}$
contains semistable vectors under
$(\check{\mathscr{V}}_{x})_{\overline{\mathbb{Q}}_{p}}\simeq (\mathfrak{g}_{\overline{\mathbb{Q}}_{p}})_{1}$
contains semistable vectors under
![]() $(H_{x})_{\overline{\mathbb{Q}}_{p}}=(G_{\overline{\mathbb{Q}}_{p}}^{\unicode[STIX]{x1D703}})^{0}$
if and only if
$(H_{x})_{\overline{\mathbb{Q}}_{p}}=(G_{\overline{\mathbb{Q}}_{p}}^{\unicode[STIX]{x1D703}})^{0}$
if and only if
![]() $x$
is a semistability point. This allows us to extend their characterization to all primes
$x$
is a semistability point. This allows us to extend their characterization to all primes
![]() $p$
in the case when the number
$p$
in the case when the number
![]() $r$
appearing in [Reference Reeder and YuRY14, Theorem 8.3] is equal to
$r$
appearing in [Reference Reeder and YuRY14, Theorem 8.3] is equal to
![]() $r(x)$
.
$r(x)$
.
Proposition 4.5. Let
![]() $x\in \mathscr{A}$
be a rational point of order
$x\in \mathscr{A}$
be a rational point of order
![]() $m$
. Then the representation
$m$
. Then the representation
![]() $\check{\mathbf{V}}_{x}$
contains semistable vectors under the action of
$\check{\mathbf{V}}_{x}$
contains semistable vectors under the action of
![]() $\mathbf{G}_{x}$
if and only if
$\mathbf{G}_{x}$
if and only if
![]() $x$
is a semistability point.
$x$
is a semistability point.
5 Classifying stable vectors: an example for
 $G_{2}$
$G_{2}$
Theorem 4.2 gives necessary and sufficient conditions for the stable locus of
![]() $\mathbf{G}_{x}$
in
$\mathbf{G}_{x}$
in
![]() $\check{\mathbf{V}}_{x}$
to be non-empty. However, determining the stable locus itself is currently an ad hoc process that depends on an explicit realization of the representation of
$\check{\mathbf{V}}_{x}$
to be non-empty. However, determining the stable locus itself is currently an ad hoc process that depends on an explicit realization of the representation of
![]() $\mathbf{G}_{x}$
on
$\mathbf{G}_{x}$
on
![]() $\check{\mathbf{V}}_{x}$
in each case. Below we find the stable locus in the case when
$\check{\mathbf{V}}_{x}$
in each case. Below we find the stable locus in the case when
![]() $G=G_{2}$
and
$G=G_{2}$
and
![]() $x=x_{0}+(1/2)\check{\unicode[STIX]{x1D70C}}$
. Up to conjugation, this choice of
$x=x_{0}+(1/2)\check{\unicode[STIX]{x1D70C}}$
. Up to conjugation, this choice of
![]() $x$
determines a unique representation of
$x$
determines a unique representation of
![]() $G_{2}(\mathbb{Q}_{2})$
, for which we describe the Langlands parameter associated by the local Langlands correspondence. This Langlands parameter has characteristics which distinguish it from those corresponding to epipelagic representations of
$G_{2}(\mathbb{Q}_{2})$
, for which we describe the Langlands parameter associated by the local Langlands correspondence. This Langlands parameter has characteristics which distinguish it from those corresponding to epipelagic representations of
![]() $G(k)$
when
$G(k)$
when
![]() $p$
is large.
$p$
is large.
We start with a variation of the Hilbert–Mumford criterion. Let
![]() $H$
be a reductive group over an algebraically closed field
$H$
be a reductive group over an algebraically closed field
![]() $E$
and let
$E$
and let
![]() $V$
be a rational representation of
$V$
be a rational representation of
![]() $H$
over
$H$
over
![]() $E$
. Fix a maximal torus in
$E$
. Fix a maximal torus in
![]() $H$
and let
$H$
and let
![]() $\check{X}$
denote its cocharacter group. Let
$\check{X}$
denote its cocharacter group. Let
![]() $V_{s}$
be the set of stable vectors in
$V_{s}$
be the set of stable vectors in
![]() $V$
. Recall that
$V$
. Recall that
![]() $I_{E}(\unicode[STIX]{x1D706},v)$
is the set of negative weights for
$I_{E}(\unicode[STIX]{x1D706},v)$
is the set of negative weights for
![]() $v$
with respect to
$v$
with respect to
![]() $\unicode[STIX]{x1D706}$
(see § 2 for details).
$\unicode[STIX]{x1D706}$
(see § 2 for details).
Lemma 5.1. Suppose that
![]() $Y\subset V$
is an
$Y\subset V$
is an
![]() $H$
-invariant subset with the property that
$H$
-invariant subset with the property that
![]() $I_{E}(\unicode[STIX]{x1D707},y)\neq \varnothing$
for all non-trivial
$I_{E}(\unicode[STIX]{x1D707},y)\neq \varnothing$
for all non-trivial
![]() $\unicode[STIX]{x1D707}\in \check{X},y\in Y$
. Then
$\unicode[STIX]{x1D707}\in \check{X},y\in Y$
. Then
![]() $Y\subset V_{s}$
.
$Y\subset V_{s}$
.
Proof. Suppose that
![]() $y\in Y$
and let
$y\in Y$
and let
![]() $\unicode[STIX]{x1D706}:\mathbb{G}_{m}\rightarrow H$
be a non-trivial one-parameter subgroup. Then there exists
$\unicode[STIX]{x1D706}:\mathbb{G}_{m}\rightarrow H$
be a non-trivial one-parameter subgroup. Then there exists
![]() $g\in H(E)$
such that
$g\in H(E)$
such that
![]() $\unicode[STIX]{x1D707}:=g\unicode[STIX]{x1D706}g^{-1}\in \check{X}$
. By
$\unicode[STIX]{x1D707}:=g\unicode[STIX]{x1D706}g^{-1}\in \check{X}$
. By
![]() $H$
-invariance of
$H$
-invariance of
![]() $Y$
,
$Y$
,
![]() $gy\in Y$
, so
$gy\in Y$
, so
![]() $I_{E}(\unicode[STIX]{x1D706},y)=I_{E}(\unicode[STIX]{x1D707},gy)\neq \varnothing$
, and
$I_{E}(\unicode[STIX]{x1D706},y)=I_{E}(\unicode[STIX]{x1D707},gy)\neq \varnothing$
, and
![]() $y\in V_{s}$
by the usual Hilbert–Mumford criterion.◻
$y\in V_{s}$
by the usual Hilbert–Mumford criterion.◻
Remark 5.2. We will apply Lemma 5.1 in the following setting: let
![]() $f$
be an
$f$
be an
![]() $H$
-invariant polynomial on
$H$
-invariant polynomial on
![]() $V$
with the property that
$V$
with the property that
![]() $f(v)=0$
whenever there exists
$f(v)=0$
whenever there exists
![]() $\unicode[STIX]{x1D707}\in \check{X}$
such that
$\unicode[STIX]{x1D707}\in \check{X}$
such that
![]() $I_{E}(\unicode[STIX]{x1D707},v)=\varnothing$
. This means that
$I_{E}(\unicode[STIX]{x1D707},v)=\varnothing$
. This means that
![]() $f$
vanishes on vectors which are not stable for the action of the fixed maximal torus. By the lemma, if
$f$
vanishes on vectors which are not stable for the action of the fixed maximal torus. By the lemma, if
![]() $y\in V$
and
$y\in V$
and
![]() $f(y)\neq 0$
, then
$f(y)\neq 0$
, then
![]() $y$
is a stable vector for the action of
$y$
is a stable vector for the action of
![]() $H$
. Thus, the problem of finding stable vectors is reduced to finding such a polynomial
$H$
. Thus, the problem of finding stable vectors is reduced to finding such a polynomial
![]() $f$
.
$f$
.
For the rest of the section, we take the group
![]() $G$
to be the split form of
$G$
to be the split form of
![]() $G_{2}$
defined over
$G_{2}$
defined over
![]() $K$
. Applying Theorem 4.2 to this case, we see that
$K$
. Applying Theorem 4.2 to this case, we see that
![]() $\check{\mathbf{V}}_{x}$
has stable vectors under the action of
$\check{\mathbf{V}}_{x}$
has stable vectors under the action of
![]() $\mathbf{G}_{x}$
if and only if
$\mathbf{G}_{x}$
if and only if
![]() $x$
is conjugate under the affine Weyl group to
$x$
is conjugate under the affine Weyl group to
![]() $x_{0}+(1/2)\check{\unicode[STIX]{x1D70C}}$
,
$x_{0}+(1/2)\check{\unicode[STIX]{x1D70C}}$
,
![]() $x_{0}+(1/3)\check{\unicode[STIX]{x1D70C}}$
, or
$x_{0}+(1/3)\check{\unicode[STIX]{x1D70C}}$
, or
![]() $x_{0}+(1/6)\check{\unicode[STIX]{x1D70C}}$
. When
$x_{0}+(1/6)\check{\unicode[STIX]{x1D70C}}$
. When
![]() $x=x_{0}+(1/6)\check{\unicode[STIX]{x1D70C}}$
, we have that
$x=x_{0}+(1/6)\check{\unicode[STIX]{x1D70C}}$
, we have that
![]() $\mathbf{G}_{x}$
is a torus, and the stable vectors in
$\mathbf{G}_{x}$
is a torus, and the stable vectors in
![]() $\check{\mathbf{V}}_{x}$
are easily classified [Reference Reeder and YuRY14, § 2.6]. For
$\check{\mathbf{V}}_{x}$
are easily classified [Reference Reeder and YuRY14, § 2.6]. For
![]() $x=x_{0}+(1/3)\check{\unicode[STIX]{x1D70C}}$
, the stable vectors in
$x=x_{0}+(1/3)\check{\unicode[STIX]{x1D70C}}$
, the stable vectors in
![]() $\check{\mathbf{V}}_{x}$
are given in [Reference Reeder and YuRY14, § 7.5] in the case
$\check{\mathbf{V}}_{x}$
are given in [Reference Reeder and YuRY14, § 7.5] in the case
![]() $p\neq 3$
, and it is not hard to see that this classification extends to the case when
$p\neq 3$
, and it is not hard to see that this classification extends to the case when
![]() $p=3$
. In this section we will characterize all stable vectors when
$p=3$
. In this section we will characterize all stable vectors when
![]() $x=x_{0}+(1/2)\check{\unicode[STIX]{x1D70C}}$
.
$x=x_{0}+(1/2)\check{\unicode[STIX]{x1D70C}}$
.
Fix
![]() $x=x_{0}+(1/2)\check{\unicode[STIX]{x1D70C}}$
. We have that
$x=x_{0}+(1/2)\check{\unicode[STIX]{x1D70C}}$
. We have that
![]() $\mathbf{G}_{x}\simeq \operatorname{SO}_{4}\simeq (\operatorname{SL}_{2}\times \operatorname{SL}_{2})/\boldsymbol{\unicode[STIX]{x1D707}}_{2}$
, where
$\mathbf{G}_{x}\simeq \operatorname{SO}_{4}\simeq (\operatorname{SL}_{2}\times \operatorname{SL}_{2})/\boldsymbol{\unicode[STIX]{x1D707}}_{2}$
, where
![]() $\boldsymbol{\unicode[STIX]{x1D707}}_{2}$
is the diagonally embedded group of second roots of unity over
$\boldsymbol{\unicode[STIX]{x1D707}}_{2}$
is the diagonally embedded group of second roots of unity over
![]() $\overline{\mathbb{F}}_{p}$
. For any commutative ring
$\overline{\mathbb{F}}_{p}$
. For any commutative ring
![]() $A$
, let
$A$
, let
![]() $P_{n}(A)$
be the space of homogeneous degree-
$P_{n}(A)$
be the space of homogeneous degree-
![]() $n$
polynomials over
$n$
polynomials over
![]() $A$
in two variables, with natural action of
$A$
in two variables, with natural action of
![]() $\operatorname{SL}_{2}(A)$
by precomposition by the transpose, e.g.
$\operatorname{SL}_{2}(A)$
by precomposition by the transpose, e.g.
![]() $g=\left(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\right)$
acts by
$g=\left(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\right)$
acts by
![]() $g\cdot f(X,Y)=f(aX+cY,bX+dY)$
. Let
$g\cdot f(X,Y)=f(aX+cY,bX+dY)$
. Let
![]() $(P_{n}\boxtimes P_{l})(A)$
denote the
$(P_{n}\boxtimes P_{l})(A)$
denote the
![]() $A$
-span of the standard basis vectors
$A$
-span of the standard basis vectors
![]() $\{Z^{j}W^{n-j}\otimes X^{k}Y^{l-k}\}_{0\leqslant j\leqslant n,0\leqslant k\leqslant l}$
, with natural action of
$\{Z^{j}W^{n-j}\otimes X^{k}Y^{l-k}\}_{0\leqslant j\leqslant n,0\leqslant k\leqslant l}$
, with natural action of
![]() $\operatorname{SL}_{2}(A)\times \operatorname{SL}_{2}(A)$
, which induces an action of
$\operatorname{SL}_{2}(A)\times \operatorname{SL}_{2}(A)$
, which induces an action of
![]() $((\operatorname{SL}_{2}\times \operatorname{SL}_{2})/\boldsymbol{\unicode[STIX]{x1D707}}_{2})(A)$
whenever
$((\operatorname{SL}_{2}\times \operatorname{SL}_{2})/\boldsymbol{\unicode[STIX]{x1D707}}_{2})(A)$
whenever
![]() $n+l$
is even. By explicitly calculating the action of generators of
$n+l$
is even. By explicitly calculating the action of generators of
![]() $\mathscr{H}_{x}({\mathcal{O}})$
on basis vectors
$\mathscr{H}_{x}({\mathcal{O}})$
on basis vectors
![]() $e_{\unicode[STIX]{x1D6FE}}$
, one can check that as an
$e_{\unicode[STIX]{x1D6FE}}$
, one can check that as an
![]() $\mathscr{H}_{x}$
-module,
$\mathscr{H}_{x}$
-module,
![]() $\check{L}_{x,1/2}$
is isomorphic to
$\check{L}_{x,1/2}$
is isomorphic to
![]() $(P_{1}\boxtimes P_{3})({\mathcal{O}})$
and, as a
$(P_{1}\boxtimes P_{3})({\mathcal{O}})$
and, as a
![]() $\mathbf{G}_{x}$
-module,
$\mathbf{G}_{x}$
-module,
![]() $\check{\mathbf{V}}_{x}\simeq (P_{1}\boxtimes P_{3})(\overline{\mathbb{F}}_{p})$
.
$\check{\mathbf{V}}_{x}\simeq (P_{1}\boxtimes P_{3})(\overline{\mathbb{F}}_{p})$
.
5.1 An invariant of
 $P_{1}\boxtimes P_{3}$
$P_{1}\boxtimes P_{3}$
To use the strategy outlined in Remark 5.2, we will construct a homogeneous polynomial on
![]() $\check{\mathbf{V}}_{x}$
invariant under the action of
$\check{\mathbf{V}}_{x}$
invariant under the action of
![]() $\mathbf{G}_{x}$
. Using the isomorphism of
$\mathbf{G}_{x}$
. Using the isomorphism of
![]() ${\mathcal{O}}$
-modules
${\mathcal{O}}$
-modules
![]() ${\check{L}}_{x,1/2}\simeq (P_{1}\boxtimes P_{3})({\mathcal{O}})$
mentioned above, we see that it suffices to construct a polynomial on
${\check{L}}_{x,1/2}\simeq (P_{1}\boxtimes P_{3})({\mathcal{O}})$
mentioned above, we see that it suffices to construct a polynomial on
![]() $(P_{1}\otimes P_{3})({\mathcal{O}})$
invariant under the action of
$(P_{1}\otimes P_{3})({\mathcal{O}})$
invariant under the action of
![]() $\mathscr{H}_{x}({\mathcal{O}})\simeq (\operatorname{SL}_{2}\times \operatorname{SL}_{2})/\boldsymbol{\unicode[STIX]{x1D707}}_{2}({\mathcal{O}})$
. Working over integers initially will allow us to find a polynomial which works uniformly for all
$\mathscr{H}_{x}({\mathcal{O}})\simeq (\operatorname{SL}_{2}\times \operatorname{SL}_{2})/\boldsymbol{\unicode[STIX]{x1D707}}_{2}({\mathcal{O}})$
. Working over integers initially will allow us to find a polynomial which works uniformly for all
![]() $p$
.
$p$
.
First we consider an arbitrary element
of
![]() $(P_{1}\boxtimes P_{3})({\mathcal{O}})$
with
$(P_{1}\boxtimes P_{3})({\mathcal{O}})$
with
![]() $a,b,c,d,e,f,g,h\in {\mathcal{O}}$
as a homogeneous degree-three polynomial in the variables
$a,b,c,d,e,f,g,h\in {\mathcal{O}}$
as a homogeneous degree-three polynomial in the variables
![]() $X,Y$
with coefficients in
$X,Y$
with coefficients in
![]() $P_{1}({\mathcal{O}})$
. Then the cubic discriminant
$P_{1}({\mathcal{O}})$
. Then the cubic discriminant
![]() $\operatorname{disc}_{X,Y}$
may be written as
$\operatorname{disc}_{X,Y}$
may be written as
![]() $\operatorname{disc}_{X,Y}=AZ^{4}+BZ^{3}W+CZ^{2}W^{2}+DZW^{3}+EW^{4}$
, where
$\operatorname{disc}_{X,Y}=AZ^{4}+BZ^{3}W+CZ^{2}W^{2}+DZW^{3}+EW^{4}$
, where
 $$\begin{eqnarray}\displaystyle A & = & \displaystyle c^{2}e^{2}-4ae^{3}-4c^{3}g+18aceg-27a^{2}g^{2},\nonumber\\ \displaystyle B & = & \displaystyle 2cde^{2}-4be^{3}+2c^{2}ef-12ae^{2}f-12c^{2}dg+18bceg+18adeg+18acfg-54abg^{2}\nonumber\\ \displaystyle & & \displaystyle -\,4c^{3}h+18aceh-54a^{2}gh,\nonumber\\ \displaystyle C & = & \displaystyle d^{2}e^{2}+4cdef-12be^{2}f+c^{2}f^{2}-12aef^{2}-12cd^{2}g+18bdeg+18bcfg+18adfg\nonumber\\ \displaystyle & & \displaystyle -\,27b^{2}g^{2}-12c^{2}dh+18bceh+18adeh+18acfh-108abgh-27a^{2}h^{2},\nonumber\\ \displaystyle D & = & \displaystyle 2d^{2}ef+2cdf^{2}-12bef^{2}-4af^{3}-4d^{3}g+18bdfg-12cd^{2}h+18bdeh+18bcfh\nonumber\\ \displaystyle & & \displaystyle +\,18adfh-54b^{2}gh-54abh^{2},\nonumber\\ \displaystyle E & = & \displaystyle d^{2}f^{2}-4bf^{3}-4d^{3}h+18bdfh-27b^{2}h^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A & = & \displaystyle c^{2}e^{2}-4ae^{3}-4c^{3}g+18aceg-27a^{2}g^{2},\nonumber\\ \displaystyle B & = & \displaystyle 2cde^{2}-4be^{3}+2c^{2}ef-12ae^{2}f-12c^{2}dg+18bceg+18adeg+18acfg-54abg^{2}\nonumber\\ \displaystyle & & \displaystyle -\,4c^{3}h+18aceh-54a^{2}gh,\nonumber\\ \displaystyle C & = & \displaystyle d^{2}e^{2}+4cdef-12be^{2}f+c^{2}f^{2}-12aef^{2}-12cd^{2}g+18bdeg+18bcfg+18adfg\nonumber\\ \displaystyle & & \displaystyle -\,27b^{2}g^{2}-12c^{2}dh+18bceh+18adeh+18acfh-108abgh-27a^{2}h^{2},\nonumber\\ \displaystyle D & = & \displaystyle 2d^{2}ef+2cdf^{2}-12bef^{2}-4af^{3}-4d^{3}g+18bdfg-12cd^{2}h+18bdeh+18bcfh\nonumber\\ \displaystyle & & \displaystyle +\,18adfh-54b^{2}gh-54abh^{2},\nonumber\\ \displaystyle E & = & \displaystyle d^{2}f^{2}-4bf^{3}-4d^{3}h+18bdfh-27b^{2}h^{2}.\nonumber\end{eqnarray}$$
The polynomial
![]() $\operatorname{disc}_{X,Y}$
is invariant under the action of the second factor in
$\operatorname{disc}_{X,Y}$
is invariant under the action of the second factor in
![]() $\operatorname{SL}_{2}({\mathcal{O}})\times \operatorname{SL}_{2}({\mathcal{O}})$
. The first factor acts on
$\operatorname{SL}_{2}({\mathcal{O}})\times \operatorname{SL}_{2}({\mathcal{O}})$
. The first factor acts on
![]() $\operatorname{disc}_{X,Y}(F)$
via the usual action of
$\operatorname{disc}_{X,Y}(F)$
via the usual action of
![]() $\operatorname{SL}_{2}$
on
$\operatorname{SL}_{2}$
on
![]() $P_{4}$
.
$P_{4}$
.
Taking the discriminant of the quartic
![]() $\operatorname{disc}_{X,Y}(F)$
, we may form the composite discriminant
$\operatorname{disc}_{X,Y}(F)$
, we may form the composite discriminant
![]() $\operatorname{disc}_{Z,W}(\operatorname{disc}_{X,Y}F)$
. We set
$\operatorname{disc}_{Z,W}(\operatorname{disc}_{X,Y}F)$
. We set
![]() $\unicode[STIX]{x1D6E5}(F):=\frac{1}{2^{8}}\operatorname{disc}_{Z,W}(\operatorname{disc}_{X,Y}F)$
, which is a homogeneous polynomial in the variables
$\unicode[STIX]{x1D6E5}(F):=\frac{1}{2^{8}}\operatorname{disc}_{Z,W}(\operatorname{disc}_{X,Y}F)$
, which is a homogeneous polynomial in the variables
![]() $a,b,c,d,e,f,g,h$
that turns out to be a polynomial over
$a,b,c,d,e,f,g,h$
that turns out to be a polynomial over
![]() $\mathbb{Z}$
. We can write a formula for
$\mathbb{Z}$
. We can write a formula for
![]() $\unicode[STIX]{x1D6E5}$
over
$\unicode[STIX]{x1D6E5}$
over
![]() $\mathbb{Z}$
as follows. Define two degree-six homogeneous polynomials on
$\mathbb{Z}$
as follows. Define two degree-six homogeneous polynomials on
![]() $P_{1}\boxtimes P_{3}$
by
$P_{1}\boxtimes P_{3}$
by
 $$\begin{eqnarray}\displaystyle H_{6}(F) & = & \displaystyle -d^{3}e^{3}+3cd^{2}e^{2}f-3c^{2}def^{2}+c^{3}f^{3}+9bd^{2}e^{2}g+9bcdefg-27ad^{2}efg-27b^{2}e^{2}fg\nonumber\\ \displaystyle & & \displaystyle -\,18bc^{2}f^{2}g+27acdf^{2}g+54abef^{2}g-27a^{2}f^{3}g-27bcd^{2}g^{2}+27ad^{3}g^{2}+81b^{2}cfg^{2}\nonumber\\ \displaystyle & & \displaystyle -\,81abdfg^{2}-27bcde^{2}h+18ad^{2}e^{2}h+27b^{2}e^{3}h+27bc^{2}efh-9acdefh-54abe^{2}fh\nonumber\\ \displaystyle & & \displaystyle -\,9ac^{2}f^{2}h+27a^{2}ef^{2}h+54bc^{2}dgh-54acd^{2}gh-81b^{2}cegh+81abdegh-81abcfgh\nonumber\\ \displaystyle & & \displaystyle +\,81a^{2}dfgh-27bc^{3}h^{2}+27ac^{2}dh^{2}+81abceh^{2}-81a^{2}deh^{2}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{6}(F) & = & \displaystyle -d^{3}e^{3}+3cd^{2}e^{2}f-3c^{2}def^{2}+c^{3}f^{3}+9bd^{2}e^{2}g+9bcdefg-27ad^{2}efg-27b^{2}e^{2}fg\nonumber\\ \displaystyle & & \displaystyle -\,18bc^{2}f^{2}g+27acdf^{2}g+54abef^{2}g-27a^{2}f^{3}g-27bcd^{2}g^{2}+27ad^{3}g^{2}+81b^{2}cfg^{2}\nonumber\\ \displaystyle & & \displaystyle -\,81abdfg^{2}-27bcde^{2}h+18ad^{2}e^{2}h+27b^{2}e^{3}h+27bc^{2}efh-9acdefh-54abe^{2}fh\nonumber\\ \displaystyle & & \displaystyle -\,9ac^{2}f^{2}h+27a^{2}ef^{2}h+54bc^{2}dgh-54acd^{2}gh-81b^{2}cegh+81abdegh-81abcfgh\nonumber\\ \displaystyle & & \displaystyle +\,81a^{2}dfgh-27bc^{3}h^{2}+27ac^{2}dh^{2}+81abceh^{2}-81a^{2}deh^{2}\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle G_{6}(F) & = & \displaystyle bcdefg-ad^{2}efg-b^{2}e^{2}fg-bc^{2}f^{2}g+acdf^{2}g+2abef^{2}g-a^{2}f^{3}g-bcd^{2}g^{2}+ad^{3}g^{2}\nonumber\\ \displaystyle & & \displaystyle +\,b^{2}deg^{2}+2b^{2}cfg^{2}-3abdfg^{2}-b^{3}g^{3}-bcde^{2}h+ad^{2}e^{2}h+b^{2}e^{3}h+bc^{2}efh-acdefh\nonumber\\ \displaystyle & & \displaystyle -\,2abe^{2}fh+a^{2}ef^{2}h+2bc^{2}dgh-2acd^{2}gh-3b^{2}cegh+abdegh-abcfgh+3a^{2}dfgh\nonumber\\ \displaystyle & & \displaystyle +\,3ab^{2}g^{2}h-bc^{3}h^{2}+ac^{2}dh^{2}+3abceh^{2}-2a^{2}deh^{2}-a^{2}cfh^{2}-3a^{2}bgh^{2}+a^{3}h^{3}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G_{6}(F) & = & \displaystyle bcdefg-ad^{2}efg-b^{2}e^{2}fg-bc^{2}f^{2}g+acdf^{2}g+2abef^{2}g-a^{2}f^{3}g-bcd^{2}g^{2}+ad^{3}g^{2}\nonumber\\ \displaystyle & & \displaystyle +\,b^{2}deg^{2}+2b^{2}cfg^{2}-3abdfg^{2}-b^{3}g^{3}-bcde^{2}h+ad^{2}e^{2}h+b^{2}e^{3}h+bc^{2}efh-acdefh\nonumber\\ \displaystyle & & \displaystyle -\,2abe^{2}fh+a^{2}ef^{2}h+2bc^{2}dgh-2acd^{2}gh-3b^{2}cegh+abdegh-abcfgh+3a^{2}dfgh\nonumber\\ \displaystyle & & \displaystyle +\,3ab^{2}g^{2}h-bc^{3}h^{2}+ac^{2}dh^{2}+3abceh^{2}-2a^{2}deh^{2}-a^{2}cfh^{2}-3a^{2}bgh^{2}+a^{3}h^{3}.\nonumber\end{eqnarray}$$
Then one can check that
![]() $\unicode[STIX]{x1D6E5}(F)=H_{6}(F)^{3}G_{6}(F)$
. (In fact,
$\unicode[STIX]{x1D6E5}(F)=H_{6}(F)^{3}G_{6}(F)$
. (In fact,
![]() $H_{6}$
and
$H_{6}$
and
![]() $G_{6}$
are both invariant polynomials for the action of
$G_{6}$
are both invariant polynomials for the action of
![]() $\operatorname{SL}_{2}\times \operatorname{SL}_{2}$
on
$\operatorname{SL}_{2}\times \operatorname{SL}_{2}$
on
![]() $P_{1}\boxtimes P_{3}$
, though we will not need this fact here.) Let
$P_{1}\boxtimes P_{3}$
, though we will not need this fact here.) Let
![]() $\overline{\unicode[STIX]{x1D6E5}}$
be the reduction of
$\overline{\unicode[STIX]{x1D6E5}}$
be the reduction of
![]() $\unicode[STIX]{x1D6E5}$
mod
$\unicode[STIX]{x1D6E5}$
mod
![]() $p$
. It is easy to check that
$p$
. It is easy to check that
![]() $\overline{\unicode[STIX]{x1D6E5}}$
is a non-zero polynomial over
$\overline{\unicode[STIX]{x1D6E5}}$
is a non-zero polynomial over
![]() $\overline{\mathbb{F}}_{p}$
on
$\overline{\mathbb{F}}_{p}$
on
![]() $\check{\mathbf{V}}_{x}$
that is invariant under the action of
$\check{\mathbf{V}}_{x}$
that is invariant under the action of
![]() $\mathbf{G}_{x}$
.
$\mathbf{G}_{x}$
.
5.2 Characterization of stable vectors
Proposition 5.3. A vector
![]() $F\in (P_{1}\boxtimes P_{3})(\overline{\mathbb{F}}_{p})$
is stable for the action of
$F\in (P_{1}\boxtimes P_{3})(\overline{\mathbb{F}}_{p})$
is stable for the action of
![]() $\operatorname{SL}_{2}(\overline{\mathbb{F}}_{p})\times \operatorname{SL}_{2}(\overline{\mathbb{F}}_{p})$
if and only if
$\operatorname{SL}_{2}(\overline{\mathbb{F}}_{p})\times \operatorname{SL}_{2}(\overline{\mathbb{F}}_{p})$
if and only if
![]() $\overline{\unicode[STIX]{x1D6E5}}(F)\neq 0$
.
$\overline{\unicode[STIX]{x1D6E5}}(F)\neq 0$
.
Proof. Similar to above, we write an arbitrary vector
![]() $F\in (P_{1}\boxtimes P_{3})(\overline{\mathbb{F}}_{p})$
as
$F\in (P_{1}\boxtimes P_{3})(\overline{\mathbb{F}}_{p})$
as
![]() $F=(aZ+bW)\otimes X^{3}+(cZ+dW)\otimes X^{2}Y+(eZ+fW)\otimes XY^{2}+(gZ+hW)\otimes Y^{3}$
, but here we are taking the coefficients
$F=(aZ+bW)\otimes X^{3}+(cZ+dW)\otimes X^{2}Y+(eZ+fW)\otimes XY^{2}+(gZ+hW)\otimes Y^{3}$
, but here we are taking the coefficients
![]() $a,b,c,d,e,f,g,h$
in
$a,b,c,d,e,f,g,h$
in
![]() $\overline{\mathbb{F}}_{p}$
. Let
$\overline{\mathbb{F}}_{p}$
. Let
![]() $\unicode[STIX]{x1D706}(t)=\left(\!\begin{smallmatrix}t^{s} & 0\\ 0 & t^{-s}\end{smallmatrix}\!\right)\times \left(\!\begin{smallmatrix}t^{r} & 0\\ 0 & t^{-r}\end{smallmatrix}\!\right)$
be an arbitrary non-trivial cocharacter of the diagonal maximal torus. Note that
$\unicode[STIX]{x1D706}(t)=\left(\!\begin{smallmatrix}t^{s} & 0\\ 0 & t^{-s}\end{smallmatrix}\!\right)\times \left(\!\begin{smallmatrix}t^{r} & 0\\ 0 & t^{-r}\end{smallmatrix}\!\right)$
be an arbitrary non-trivial cocharacter of the diagonal maximal torus. Note that
![]() $\unicode[STIX]{x1D706}(t)$
acts on
$\unicode[STIX]{x1D706}(t)$
acts on
![]() $F$
with weights
$F$
with weights
![]() $3r+s,3r-s,r+s,r-s,-r+s,-r-s,-3r+s,-3r-s$
corresponding to
$3r+s,3r-s,r+s,r-s,-r+s,-r-s,-3r+s,-3r-s$
corresponding to
![]() $a,b,c,d,e,f,g,h$
.
$a,b,c,d,e,f,g,h$
.
First we show that if
![]() $\overline{\unicode[STIX]{x1D6E5}}(F)\neq 0$
, then
$\overline{\unicode[STIX]{x1D6E5}}(F)\neq 0$
, then
![]() $F$
is stable. Assume that
$F$
is stable. Assume that
![]() $I_{\overline{\mathbb{F}}_{p}}(\unicode[STIX]{x1D706},F)=\varnothing$
. First suppose that
$I_{\overline{\mathbb{F}}_{p}}(\unicode[STIX]{x1D706},F)=\varnothing$
. First suppose that
![]() $r+s=0$
and
$r+s=0$
and
![]() $3r-s>0$
. Then the weights corresponding to
$3r-s>0$
. Then the weights corresponding to
![]() $a,b,c,d,e,f,g,h$
are
$a,b,c,d,e,f,g,h$
are
![]() $2r,4r,0,2r,-2r,0,-4r,-2r$
, respectively, and
$2r,4r,0,2r,-2r,0,-4r,-2r$
, respectively, and
![]() $I_{\overline{\mathbb{F}}_{p}}(\unicode[STIX]{x1D706},F)=\varnothing$
implies that
$I_{\overline{\mathbb{F}}_{p}}(\unicode[STIX]{x1D706},F)=\varnothing$
implies that
![]() $e=g=h=0$
. Thus,
$e=g=h=0$
. Thus,
![]() $G_{6}(F)=0$
and so
$G_{6}(F)=0$
and so
![]() $\overline{\unicode[STIX]{x1D6E5}}(F)=0$
. Similarly, by considering all remaining possible cases given by taking
$\overline{\unicode[STIX]{x1D6E5}}(F)=0$
. Similarly, by considering all remaining possible cases given by taking
![]() $r+s$
and
$r+s$
and
![]() $3r-s$
to be positive, negative, or zero, one obtains that
$3r-s$
to be positive, negative, or zero, one obtains that
![]() $\overline{\unicode[STIX]{x1D6E5}}(F)=0$
, which is a contradiction. Thus,
$\overline{\unicode[STIX]{x1D6E5}}(F)=0$
, which is a contradiction. Thus,
![]() $I_{\overline{\mathbb{F}}_{p}}(\unicode[STIX]{x1D706},F)\neq \varnothing$
and, using Lemma 5.1 as outlined in Remark 5.2, we have that if
$I_{\overline{\mathbb{F}}_{p}}(\unicode[STIX]{x1D706},F)\neq \varnothing$
and, using Lemma 5.1 as outlined in Remark 5.2, we have that if
![]() $\overline{\unicode[STIX]{x1D6E5}}(F)\neq 0$
, then
$\overline{\unicode[STIX]{x1D6E5}}(F)\neq 0$
, then
![]() $F$
is stable.
$F$
is stable.
Next we claim that if
![]() $\overline{\unicode[STIX]{x1D6E5}}(F)=0$
, then
$\overline{\unicode[STIX]{x1D6E5}}(F)=0$
, then
![]() $F$
is not stable.
$F$
is not stable.
First assume that
![]() $p\neq 2$
. In this case,
$p\neq 2$
. In this case,
![]() $\overline{\unicode[STIX]{x1D6E5}}(F)=0$
if and only if the polynomial
$\overline{\unicode[STIX]{x1D6E5}}(F)=0$
if and only if the polynomial
![]() $\operatorname{disc}_{X,Y}F$
has a double root, i.e. there is a linear form
$\operatorname{disc}_{X,Y}F$
has a double root, i.e. there is a linear form
![]() $l$
in
$l$
in
![]() $Z$
and
$Z$
and
![]() $W$
such that
$W$
such that
![]() $l^{2}\mid \operatorname{disc}_{X,Y}F$
. Since the first factor of
$l^{2}\mid \operatorname{disc}_{X,Y}F$
. Since the first factor of
![]() $\operatorname{SL}_{2}(\overline{\mathbb{F}}_{p})\times \operatorname{SL}_{2}(\overline{\mathbb{F}}_{p})$
acts transitively on linear forms in
$\operatorname{SL}_{2}(\overline{\mathbb{F}}_{p})\times \operatorname{SL}_{2}(\overline{\mathbb{F}}_{p})$
acts transitively on linear forms in
![]() $Z$
and
$Z$
and
![]() $W$
, we can assume that
$W$
, we can assume that
![]() $Z^{2}\mid \operatorname{disc}_{X,Y}F$
, i.e.
$Z^{2}\mid \operatorname{disc}_{X,Y}F$
, i.e.
![]() $\overline{D}=\overline{E}=0$
(where
$\overline{D}=\overline{E}=0$
(where
![]() $\overline{D}$
and
$\overline{D}$
and
![]() $\overline{E}$
are the reductions mod
$\overline{E}$
are the reductions mod
![]() $p$
of the polynomials
$p$
of the polynomials
![]() $D$
and
$D$
and
![]() $E$
in § 5.1). If we write
$E$
in § 5.1). If we write
![]() $F$
as
$F$
as
![]() $F=Z\otimes F_{1}(X,Y)+W\otimes F_{2}(X,Y)$
for cubics
$F=Z\otimes F_{1}(X,Y)+W\otimes F_{2}(X,Y)$
for cubics
![]() $F_{1},F_{2}$
, then
$F_{1},F_{2}$
, then
![]() $\overline{E}=\operatorname{disc}_{X,Y}F_{2}$
. Since
$\overline{E}=\operatorname{disc}_{X,Y}F_{2}$
. Since
![]() $\overline{E}=0,F_{2}(X,Y)$
has a double root, i.e. there is a linear form
$\overline{E}=0,F_{2}(X,Y)$
has a double root, i.e. there is a linear form
![]() $l^{\prime }$
in
$l^{\prime }$
in
![]() $X$
and
$X$
and
![]() $Y$
such that
$Y$
such that
![]() $(l^{\prime })^{2}\mid F_{2}$
. Since the second factor of
$(l^{\prime })^{2}\mid F_{2}$
. Since the second factor of
![]() $\operatorname{SL}_{2}(\overline{\mathbb{F}}_{p})\times \operatorname{SL}_{2}(\overline{\mathbb{F}}_{p})$
acts transitively on linear forms in
$\operatorname{SL}_{2}(\overline{\mathbb{F}}_{p})\times \operatorname{SL}_{2}(\overline{\mathbb{F}}_{p})$
acts transitively on linear forms in
![]() $X$
and
$X$
and
![]() $Y$
, we can assume that
$Y$
, we can assume that
![]() $X^{2}\mid F_{2}$
, i.e.
$X^{2}\mid F_{2}$
, i.e.
![]() $f=h=0$
. Considering the formula for
$f=h=0$
. Considering the formula for
![]() $\overline{D}$
, we see that
$\overline{D}$
, we see that
![]() $dg=0$
. If
$dg=0$
. If
![]() $d=0$
, taking
$d=0$
, taking
![]() $r=1,s=3$
in
$r=1,s=3$
in
![]() $\unicode[STIX]{x1D706}$
above gives a one-parameter subgroup such that the weights for
$\unicode[STIX]{x1D706}$
above gives a one-parameter subgroup such that the weights for
![]() $F$
form a subset of
$F$
form a subset of
![]() $\{6,4,2,0\}$
, giving
$\{6,4,2,0\}$
, giving
![]() $I_{\overline{\mathbb{F}}_{p}}(\unicode[STIX]{x1D706},F)=\varnothing$
. If
$I_{\overline{\mathbb{F}}_{p}}(\unicode[STIX]{x1D706},F)=\varnothing$
. If
![]() $g=0$
, taking
$g=0$
, taking
![]() $r=s=1$
gives a one-parameter subgroup such that
$r=s=1$
gives a one-parameter subgroup such that
![]() $I_{\overline{\mathbb{F}}_{p}}(\unicode[STIX]{x1D706},F)=\varnothing$
. Thus,
$I_{\overline{\mathbb{F}}_{p}}(\unicode[STIX]{x1D706},F)=\varnothing$
. Thus,
![]() $F$
is not stable.
$F$
is not stable.
Now assume that
![]() $p=2$
. In this case, we use the fact that every stable orbit contains a vector of the form
$p=2$
. In this case, we use the fact that every stable orbit contains a vector of the form
to show that if
![]() $\overline{\unicode[STIX]{x1D6E5}}(F)=0$
, one can find a one-parameter subgroup
$\overline{\unicode[STIX]{x1D6E5}}(F)=0$
, one can find a one-parameter subgroup
![]() $\unicode[STIX]{x1D706}$
such that
$\unicode[STIX]{x1D706}$
such that
![]() $I_{\overline{\mathbb{F}}_{p}}(\unicode[STIX]{x1D706},F)=\varnothing$
. For detailed calculations, see the second author’s PhD thesis [Reference RomanoRom16, § 2.2].◻
$I_{\overline{\mathbb{F}}_{p}}(\unicode[STIX]{x1D706},F)=\varnothing$
. For detailed calculations, see the second author’s PhD thesis [Reference RomanoRom16, § 2.2].◻
Remark 5.4. Suppose that
![]() $k=\mathbb{Q}_{2}$
. Using Proposition 5.3, one may check that there exists a unique
$k=\mathbb{Q}_{2}$
. Using Proposition 5.3, one may check that there exists a unique
![]() $\mathbf{G}_{x}(\mathfrak{f})$
-orbit of stable vectors in
$\mathbf{G}_{x}(\mathfrak{f})$
-orbit of stable vectors in
![]() $\check{\mathbf{V}}_{x}(\mathfrak{f})$
(see § 4.1 for notation). It is easy to check that if
$\check{\mathbf{V}}_{x}(\mathfrak{f})$
(see § 4.1 for notation). It is easy to check that if
![]() $\unicode[STIX]{x1D706}\in \check{\mathbf{V}}(\mathfrak{f})$
is in this stable orbit, then the stabilizer
$\unicode[STIX]{x1D706}\in \check{\mathbf{V}}(\mathfrak{f})$
is in this stable orbit, then the stabilizer
![]() $\operatorname{Stab}_{\mathbf{G}_{x}(\mathfrak{f})}(\unicode[STIX]{x1D706})$
is trivial and, by [Reference Reeder and YuRY14, Proposition 2.4], the compactly induced representation
$\operatorname{Stab}_{\mathbf{G}_{x}(\mathfrak{f})}(\unicode[STIX]{x1D706})$
is trivial and, by [Reference Reeder and YuRY14, Proposition 2.4], the compactly induced representation
![]() $\unicode[STIX]{x1D70B}_{x}(\unicode[STIX]{x1D706})$
of
$\unicode[STIX]{x1D70B}_{x}(\unicode[STIX]{x1D706})$
of
![]() $G_{2}(\mathbb{Q}_{2})$
is irreducible. In what follows, we will describe the Langlands parameter associated to this representation.
$G_{2}(\mathbb{Q}_{2})$
is irreducible. In what follows, we will describe the Langlands parameter associated to this representation.
5.3 Langlands parameters
Let
![]() ${\mathcal{W}}_{k}$
be the Weil group of
${\mathcal{W}}_{k}$
be the Weil group of
![]() $k$
, and let
$k$
, and let
![]() ${\hat{G}}$
be the
${\hat{G}}$
be the
![]() $\mathbb{C}$
-points of the connected reductive group over
$\mathbb{C}$
-points of the connected reductive group over
![]() $\mathbb{C}$
whose root datum is dual to that of
$\mathbb{C}$
whose root datum is dual to that of
![]() ${\mathcal{G}}$
. According to the conjectural local Langlands correspondence, one should be able to attach to each irreducible representation
${\mathcal{G}}$
. According to the conjectural local Langlands correspondence, one should be able to attach to each irreducible representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() ${\mathcal{G}}(k)$
obtained through the construction of [Reference Reeder and YuRY14] a discrete Langlands parameter
${\mathcal{G}}(k)$
obtained through the construction of [Reference Reeder and YuRY14] a discrete Langlands parameter
such that certain properties, in particular the formal degree conjecture of [Reference Hiraga, Ichino and IkedaHII08], of the pair
![]() $(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D719})$
are satisfied (here ‘discrete’ is as defined in [Reference Gross and ReederGR10, § 3.2]). For
$(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D719})$
are satisfied (here ‘discrete’ is as defined in [Reference Gross and ReederGR10, § 3.2]). For
![]() $p\nmid |W|$
, [Reference Reeder and YuRY14, § 7] provides a template for the construction of such parameters. For
$p\nmid |W|$
, [Reference Reeder and YuRY14, § 7] provides a template for the construction of such parameters. For
![]() $p\nmid 2m$
, given certain ‘epipelagic’ parameters, [Reference KalethaKal15] gives a construction of
$p\nmid 2m$
, given certain ‘epipelagic’ parameters, [Reference KalethaKal15] gives a construction of
![]() $L$
-packets consisting of epipelagic representations of depth
$L$
-packets consisting of epipelagic representations of depth
![]() $1/m$
that satisfy many expected properties. However, parameters associated to epipelagic representations are not well understood when
$1/m$
that satisfy many expected properties. However, parameters associated to epipelagic representations are not well understood when
![]() $p$
is small, except in a few special cases (see [Reference Gross and ReederGR10, § 6.3] and [Reference Reeder and YuRY14, § 7.5]). Here we will explicitly describe the Langlands parameter associated to the representation discussed in Remark 5.4. We will see that in this case the formal degree conjecture of [Reference Hiraga, Ichino and IkedaHII08] is enough to determine a unique parameter. This parameter is not epipelagic in the sense of [Reference KalethaKal15, § 4.1] and, unlike parameters when
$p$
is small, except in a few special cases (see [Reference Gross and ReederGR10, § 6.3] and [Reference Reeder and YuRY14, § 7.5]). Here we will explicitly describe the Langlands parameter associated to the representation discussed in Remark 5.4. We will see that in this case the formal degree conjecture of [Reference Hiraga, Ichino and IkedaHII08] is enough to determine a unique parameter. This parameter is not epipelagic in the sense of [Reference KalethaKal15, § 4.1] and, unlike parameters when
![]() $p\nmid |W|$
, the image of the wild inertia subgroup of
$p\nmid |W|$
, the image of the wild inertia subgroup of
![]() ${\mathcal{W}}_{k}$
is not contained in a torus of
${\mathcal{W}}_{k}$
is not contained in a torus of
![]() ${\hat{G}}$
.
${\hat{G}}$
.
For the remainder of the section we fix
![]() $k=\mathbb{Q}_{2}$
, let
$k=\mathbb{Q}_{2}$
, let
![]() ${\mathcal{G}}$
be
${\mathcal{G}}$
be
![]() $G_{2}$
over
$G_{2}$
over
![]() $\mathbb{Q}_{2}$
, and let
$\mathbb{Q}_{2}$
, and let
![]() $\unicode[STIX]{x1D70B}_{x}(\unicode[STIX]{x1D706})$
be the representation of
$\unicode[STIX]{x1D70B}_{x}(\unicode[STIX]{x1D706})$
be the representation of
![]() $G_{2}(\mathbb{Q}_{2})$
discussed in Remark 5.4. For ease of notation, we let
$G_{2}(\mathbb{Q}_{2})$
discussed in Remark 5.4. For ease of notation, we let
![]() ${\mathcal{W}}={\mathcal{W}}_{\mathbb{Q}_{2}}$
. Suppose that
${\mathcal{W}}={\mathcal{W}}_{\mathbb{Q}_{2}}$
. Suppose that
is a discrete Langlands parameter. By [Reference Gross and ReederGR10, Lemma 3.1], the image
![]() $\unicode[STIX]{x1D719}({\mathcal{W}})$
of
$\unicode[STIX]{x1D719}({\mathcal{W}})$
of
![]() ${\mathcal{W}}$
is finite, so
${\mathcal{W}}$
is finite, so
![]() $\unicode[STIX]{x1D719}$
determines a finite, Galois field extension
$\unicode[STIX]{x1D719}$
determines a finite, Galois field extension
![]() $L_{\unicode[STIX]{x1D719}}/\mathbb{Q}_{2}$
such that
$L_{\unicode[STIX]{x1D719}}/\mathbb{Q}_{2}$
such that
![]() $L_{\unicode[STIX]{x1D719}}$
is the fixed field of
$L_{\unicode[STIX]{x1D719}}$
is the fixed field of
![]() $\ker \unicode[STIX]{x1D719}|_{{\mathcal{W}}}$
. We have
$\ker \unicode[STIX]{x1D719}|_{{\mathcal{W}}}$
. We have
![]() $D:=\operatorname{Gal}(L_{\unicode[STIX]{x1D719}}/\mathbb{Q}_{2})\simeq \unicode[STIX]{x1D719}({\mathcal{W}})$
, and the Lie algebra
$D:=\operatorname{Gal}(L_{\unicode[STIX]{x1D719}}/\mathbb{Q}_{2})\simeq \unicode[STIX]{x1D719}({\mathcal{W}})$
, and the Lie algebra
![]() $\hat{\mathfrak{g}}$
of
$\hat{\mathfrak{g}}$
of
![]() ${\hat{G}}=G_{2}(\mathbb{C})$
is a representation of
${\hat{G}}=G_{2}(\mathbb{C})$
is a representation of
![]() $D$
, via the composition of this isomorphism with the adjoint representation. The action of the lower ramification groups
$D$
, via the composition of this isomorphism with the adjoint representation. The action of the lower ramification groups
on
![]() $\hat{\mathfrak{g}}$
determines the Swan conductor
$\hat{\mathfrak{g}}$
determines the Swan conductor
of this representation, where
![]() $\hat{\mathfrak{g}}^{D_{j}}$
is the subspace of
$\hat{\mathfrak{g}}^{D_{j}}$
is the subspace of
![]() $\hat{\mathfrak{g}}$
fixed by
$\hat{\mathfrak{g}}$
fixed by
![]() $D_{j}$
. Recall that the Swan conductor of any representation of
$D_{j}$
. Recall that the Swan conductor of any representation of
![]() $D$
is an integer; in particular,
$D$
is an integer; in particular,
![]() $b(\unicode[STIX]{x1D719})\in \mathbb{Z}$
.
$b(\unicode[STIX]{x1D719})\in \mathbb{Z}$
.
Proposition 5.5. Up to
![]() $G_{2}(\mathbb{C})$
-conjugacy, there is a unique parameter
$G_{2}(\mathbb{C})$
-conjugacy, there is a unique parameter
![]() $\unicode[STIX]{x1D719}:{\mathcal{W}}_{\mathbb{Q}_{2}}\times \operatorname{SL}_{2}(\mathbb{C})\rightarrow G_{2}(\mathbb{C})$
such that the pair
$\unicode[STIX]{x1D719}:{\mathcal{W}}_{\mathbb{Q}_{2}}\times \operatorname{SL}_{2}(\mathbb{C})\rightarrow G_{2}(\mathbb{C})$
such that the pair
![]() $(\unicode[STIX]{x1D70B}_{x}(\unicode[STIX]{x1D706}),\unicode[STIX]{x1D719})$
satisfies the formal degree conjecture of [Reference Hiraga, Ichino and IkedaHII08]. The filtration of lower ramification groups of
$(\unicode[STIX]{x1D70B}_{x}(\unicode[STIX]{x1D706}),\unicode[STIX]{x1D719})$
satisfies the formal degree conjecture of [Reference Hiraga, Ichino and IkedaHII08]. The filtration of lower ramification groups of
![]() $D=\operatorname{Gal}(L_{\unicode[STIX]{x1D719}}/\mathbb{Q}_{2})$
is given by
$D=\operatorname{Gal}(L_{\unicode[STIX]{x1D719}}/\mathbb{Q}_{2})$
is given by
where, under the isomorphism
![]() $D\simeq \unicode[STIX]{x1D719}({\mathcal{W}})\subset G_{2}(\mathbb{C})$
,
$D\simeq \unicode[STIX]{x1D719}({\mathcal{W}})\subset G_{2}(\mathbb{C})$
,
![]() $D_{1}=D_{2}=D_{3}$
is the unique (up to conjugacy) subgroup of
$D_{1}=D_{2}=D_{3}$
is the unique (up to conjugacy) subgroup of
![]() $G_{2}(\mathbb{C})$
isomorphic to
$G_{2}(\mathbb{C})$
isomorphic to
![]() $(\mathbb{Z}/2\mathbb{Z})^{3}$
,
$(\mathbb{Z}/2\mathbb{Z})^{3}$
,
![]() $D_{0}$
is the unique subgroup of order
$D_{0}$
is the unique subgroup of order
![]() $56$
normalizing
$56$
normalizing
![]() $D_{1}$
, and
$D_{1}$
, and
![]() $D$
is the unique subgroup of order
$D$
is the unique subgroup of order
![]() $168$
normalizing
$168$
normalizing
![]() $D_{0}$
.
$D_{0}$
.
Proof. Suppose that the pair
![]() $(\unicode[STIX]{x1D70B}_{x}(\unicode[STIX]{x1D706}),\unicode[STIX]{x1D719})$
satisfies the formal degree conjecture of [Reference Hiraga, Ichino and IkedaHII08]. Then, from [Reference Reeder and YuRY14, § 7.1], we deduce that the following properties hold:
$(\unicode[STIX]{x1D70B}_{x}(\unicode[STIX]{x1D706}),\unicode[STIX]{x1D719})$
satisfies the formal degree conjecture of [Reference Hiraga, Ichino and IkedaHII08]. Then, from [Reference Reeder and YuRY14, § 7.1], we deduce that the following properties hold:
-
(a)
 $\unicode[STIX]{x1D719}$
is trivial on
$\unicode[STIX]{x1D719}$
is trivial on
 $\operatorname{SL}_{2}(\mathbb{C})$
;
$\operatorname{SL}_{2}(\mathbb{C})$
; -
(b)
 $b(\unicode[STIX]{x1D719})=\dim \mathbf{G}_{x}=6$
;
$b(\unicode[STIX]{x1D719})=\dim \mathbf{G}_{x}=6$
; -
(c) the centralizer
 $C_{G_{2}(\mathbb{C})}(\unicode[STIX]{x1D719}({\mathcal{W}}))$
of the image of
$C_{G_{2}(\mathbb{C})}(\unicode[STIX]{x1D719}({\mathcal{W}}))$
of the image of
 $\unicode[STIX]{x1D719}$
is trivial.
$\unicode[STIX]{x1D719}$
is trivial.
We identify the Galois group
![]() $D:=\operatorname{Gal}(L_{\unicode[STIX]{x1D719}}/\mathbb{Q}_{2})$
with
$D:=\operatorname{Gal}(L_{\unicode[STIX]{x1D719}}/\mathbb{Q}_{2})$
with
![]() $\unicode[STIX]{x1D719}({\mathcal{W}})\subset G_{2}(\mathbb{C})$
in order to determine its lower ramification groups. First we describe
$\unicode[STIX]{x1D719}({\mathcal{W}})\subset G_{2}(\mathbb{C})$
in order to determine its lower ramification groups. First we describe
![]() $D_{c}$
. Recall that, up to conjugacy,
$D_{c}$
. Recall that, up to conjugacy,
![]() $G_{2}(\mathbb{C})$
contains exactly three elementary abelian 2-groups, one of rank
$G_{2}(\mathbb{C})$
contains exactly three elementary abelian 2-groups, one of rank
![]() $r$
for each
$r$
for each
![]() $r\leqslant 3$
[Reference GriessGri91, Theorem 6.1]. The reader may refer to [Reference GriessGri91] to determine the normalizers and centralizers of these subgroups. If
$r\leqslant 3$
[Reference GriessGri91, Theorem 6.1]. The reader may refer to [Reference GriessGri91] to determine the normalizers and centralizers of these subgroups. If
![]() $D_{c}\simeq \mathbb{Z}/2\mathbb{Z}$
, then
$D_{c}\simeq \mathbb{Z}/2\mathbb{Z}$
, then
![]() $D\subset N_{G_{2}(\mathbb{C})}(D_{c})=C_{G_{2}(\mathbb{C})}(D_{c})$
and hence
$D\subset N_{G_{2}(\mathbb{C})}(D_{c})=C_{G_{2}(\mathbb{C})}(D_{c})$
and hence
![]() $D_{c}\subset C_{G_{2}(\mathbb{C})}(\unicode[STIX]{x1D719}({\mathcal{W}}))$
, contradicting (c).
$D_{c}\subset C_{G_{2}(\mathbb{C})}(\unicode[STIX]{x1D719}({\mathcal{W}}))$
, contradicting (c).
Now suppose that
![]() $D_{c}$
has rank 2. Then
$D_{c}$
has rank 2. Then
![]() $D_{c}$
is contained in a maximal torus
$D_{c}$
is contained in a maximal torus
![]() $S$
of
$S$
of
![]() $G_{2}(\mathbb{C})$
. Let
$G_{2}(\mathbb{C})$
. Let
![]() $\mathfrak{s}$
be the Lie algebra of
$\mathfrak{s}$
be the Lie algebra of
![]() $S$
and let
$S$
and let
![]() $\unicode[STIX]{x1D6FF}=\sum _{i=1}^{c}1/[D_{1}:D_{j}].$
Then
$\unicode[STIX]{x1D6FF}=\sum _{i=1}^{c}1/[D_{1}:D_{j}].$
Then
so
![]() $\unicode[STIX]{x1D6FF}/[D_{0}:D_{1}]\leqslant \frac{1}{2}$
. Since
$\unicode[STIX]{x1D6FF}/[D_{0}:D_{1}]\leqslant \frac{1}{2}$
. Since
![]() $D\subset N_{G_{2}(\mathbb{C})}(D_{c})=N_{G_{2}(\mathbb{C})}(S)$
stabilizes
$D\subset N_{G_{2}(\mathbb{C})}(D_{c})=N_{G_{2}(\mathbb{C})}(S)$
stabilizes
![]() $\mathfrak{s}$
, we have
$\mathfrak{s}$
, we have
![]() $b_{0}:=\sum _{j=1}^{c}(2-\mathfrak{s}^{D_{j}})/[D_{0}:D_{j}]\in \mathbb{Z}$
. We also have that
$b_{0}:=\sum _{j=1}^{c}(2-\mathfrak{s}^{D_{j}})/[D_{0}:D_{j}]\in \mathbb{Z}$
. We also have that
![]() $b_{0}<2\unicode[STIX]{x1D6FF}/[D_{0}:D_{1}]$
, so
$b_{0}<2\unicode[STIX]{x1D6FF}/[D_{0}:D_{1}]$
, so
![]() $b_{0}=0$
and
$b_{0}=0$
and
![]() $D_{1}\subset S$
. But
$D_{1}\subset S$
. But
![]() $D_{1}\subset S$
implies that
$D_{1}\subset S$
implies that
![]() $\unicode[STIX]{x1D6FF}\in \mathbb{Z}$
, contradicting
$\unicode[STIX]{x1D6FF}\in \mathbb{Z}$
, contradicting
![]() $b(\unicode[STIX]{x1D719})=6$
since
$b(\unicode[STIX]{x1D719})=6$
since
![]() $2\nmid [D_{0}:D_{1}]$
.
$2\nmid [D_{0}:D_{1}]$
.
Thus,
![]() $D_{c}$
must be the unique (up to
$D_{c}$
must be the unique (up to
![]() $G_{2}(\mathbb{C})$
-conjugacy) subgroup of
$G_{2}(\mathbb{C})$
-conjugacy) subgroup of
![]() $G_{2}(\mathbb{C})$
isomorphic to
$G_{2}(\mathbb{C})$
isomorphic to
![]() $(\mathbb{Z}/2\mathbb{Z})^{3}$
. Since
$(\mathbb{Z}/2\mathbb{Z})^{3}$
. Since
![]() $D_{1}\subset C_{G_{2}\mathbb{C}}(D_{c})=D_{c}$
, we must have
$D_{1}\subset C_{G_{2}\mathbb{C}}(D_{c})=D_{c}$
, we must have
![]() $D_{1}=D_{2}=\cdots =D_{c}$
. Using the facts that
$D_{1}=D_{2}=\cdots =D_{c}$
. Using the facts that
![]() $N_{G_{2}(\mathbb{C})}(D_{c})/D_{c}\simeq \operatorname{GL}_{3}(\mathbb{F}_{2})$
and that
$N_{G_{2}(\mathbb{C})}(D_{c})/D_{c}\simeq \operatorname{GL}_{3}(\mathbb{F}_{2})$
and that
![]() $D_{0}/D_{1}$
is cyclic of order prime to 2, we deduce that
$D_{0}/D_{1}$
is cyclic of order prime to 2, we deduce that
![]() $[D_{0}:D_{1}]=7$
and
$[D_{0}:D_{1}]=7$
and
![]() $[D:D_{0}]=3$
, which by (b) imply that
$[D:D_{0}]=3$
, which by (b) imply that
![]() $c=3$
. Thus, the lower ramification groups for
$c=3$
. Thus, the lower ramification groups for
![]() $D$
are as given in (5).
$D$
are as given in (5).
Next we will show that there is a unique finite, Galois field extension
![]() $L/\mathbb{Q}_{2}$
whose lower ramification groups are given by (5). Indeed, there is a unique Galois extension
$L/\mathbb{Q}_{2}$
whose lower ramification groups are given by (5). Indeed, there is a unique Galois extension
![]() $E/\mathbb{Q}_{2}$
with residue degree 3 and ramification degree 7. Fix a uniformizer
$E/\mathbb{Q}_{2}$
with residue degree 3 and ramification degree 7. Fix a uniformizer
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $E$
, let
$E$
, let
![]() ${\mathcal{O}}_{E}$
be the ring of integers of
${\mathcal{O}}_{E}$
be the ring of integers of
![]() $E$
, and, for
$E$
, and, for
![]() $j\geqslant 1$
, let
$j\geqslant 1$
, let
![]() $U_{j}=1+\unicode[STIX]{x1D70B}^{j}{\mathcal{O}}_{E}$
. We write
$U_{j}=1+\unicode[STIX]{x1D70B}^{j}{\mathcal{O}}_{E}$
. We write
![]() $\unicode[STIX]{x1D707}_{7}$
for the group of 7th roots of unity in
$\unicode[STIX]{x1D707}_{7}$
for the group of 7th roots of unity in
![]() $E$
. Suppose that
$E$
. Suppose that
![]() $L/\mathbb{Q}_{2}$
is a Galois field extension with ramification groups as in (5). We will show that the norm group
$L/\mathbb{Q}_{2}$
is a Galois field extension with ramification groups as in (5). We will show that the norm group
![]() $N_{L/E}(L^{\times })$
is uniquely determined.
$N_{L/E}(L^{\times })$
is uniquely determined.
We certainly have
![]() $\left\langle \unicode[STIX]{x1D70B}\right\rangle \times \unicode[STIX]{x1D707}_{7}\times U_{1}^{2}U_{4}\subset N_{L/E}(L^{\times })$
(see [Reference IwasawaIwa86, Theorem 7.12]). Let
$\left\langle \unicode[STIX]{x1D70B}\right\rangle \times \unicode[STIX]{x1D707}_{7}\times U_{1}^{2}U_{4}\subset N_{L/E}(L^{\times })$
(see [Reference IwasawaIwa86, Theorem 7.12]). Let
![]() $M/E$
be the abelian extension of local fields such that
$M/E$
be the abelian extension of local fields such that
![]() $N_{M/E}(M^{\times })=\left\langle \unicode[STIX]{x1D70B}\right\rangle \times \unicode[STIX]{x1D707}_{7}\times U_{1}^{2}U_{4}$
. Note that
$N_{M/E}(M^{\times })=\left\langle \unicode[STIX]{x1D70B}\right\rangle \times \unicode[STIX]{x1D707}_{7}\times U_{1}^{2}U_{4}$
. Note that
![]() $\unicode[STIX]{x1D6E4}:=\operatorname{Gal}(E/\mathbb{Q}_{2})$
preserves
$\unicode[STIX]{x1D6E4}:=\operatorname{Gal}(E/\mathbb{Q}_{2})$
preserves
![]() $N_{M/E}(M^{\times })$
, so
$N_{M/E}(M^{\times })$
, so
![]() $M/\mathbb{Q}_{2}$
is Galois. As a
$M/\mathbb{Q}_{2}$
is Galois. As a
![]() $\unicode[STIX]{x1D6E4}$
-module,
$\unicode[STIX]{x1D6E4}$
-module,
![]() $E^{\times }/N_{M/E}(M^{\times })$
decomposes as a sum of two irreducible submodules, each of order 8 (see [Reference RomanoRom16, § 5.3]), so there are exactly two non-trivial subextensions
$E^{\times }/N_{M/E}(M^{\times })$
decomposes as a sum of two irreducible submodules, each of order 8 (see [Reference RomanoRom16, § 5.3]), so there are exactly two non-trivial subextensions
![]() $E\subset M^{\prime }\subset M$
which are Galois over
$E\subset M^{\prime }\subset M$
which are Galois over
![]() $\mathbb{Q}_{2}$
. For one of these extensions
$\mathbb{Q}_{2}$
. For one of these extensions
![]() $M^{\prime }$
, the lower ramification groups
$M^{\prime }$
, the lower ramification groups
![]() $\operatorname{Gal}(M^{\prime }/\mathbb{Q}_{2})_{j}=1$
for
$\operatorname{Gal}(M^{\prime }/\mathbb{Q}_{2})_{j}=1$
for
![]() $j\geqslant 2$
. This extension was constructed in [Reference Gross and ReederGR10, Proposition 6.4] and corresponds under the local Langlands correspondence to the unique simple supercuspidal representation of
$j\geqslant 2$
. This extension was constructed in [Reference Gross and ReederGR10, Proposition 6.4] and corresponds under the local Langlands correspondence to the unique simple supercuspidal representation of
![]() $G_{2}(\mathbb{Q}_{2})$
. The other has lower ramification groups as given in (5), and so must be
$G_{2}(\mathbb{Q}_{2})$
. The other has lower ramification groups as given in (5), and so must be
![]() $L$
.
$L$
.
Since every automorphism of
![]() $D$
can be realized as conjugation by an element of
$D$
can be realized as conjugation by an element of
![]() $N_{G_{2}(\mathbb{C})}(D)$
, we see that properties (a), (b), and (c) determine a unique Langlands parameter
$N_{G_{2}(\mathbb{C})}(D)$
, we see that properties (a), (b), and (c) determine a unique Langlands parameter
![]() $\unicode[STIX]{x1D719}$
up to
$\unicode[STIX]{x1D719}$
up to
![]() $G_{2}(\mathbb{C})$
-conjugacy.◻
$G_{2}(\mathbb{C})$
-conjugacy.◻
Acknowledgements
The authors would like to thank their PhD advisors, Benedict Gross and Mark Reeder, for their support. Many of the results in this paper are adapted from the PhD dissertations of the authors. They also thank Mark Reeder for carefully reading an initial draft of the paper. The second author would like to thank Maksym Fedorchuk for a helpful conversation about the example in § 5. The authors also appreciate the referee’s detailed review and feedback.