Article contents
Local Langlands correspondence and ramification for Carayol representations
Published online by Cambridge University Press: 06 September 2019
Abstract
Let 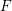 $F$ be a non-Archimedean locally compact field of residual characteristic
$F$ be a non-Archimedean locally compact field of residual characteristic 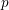 $p$ with Weil group
$p$ with Weil group 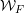 ${\mathcal{W}}_{F}$. Let
${\mathcal{W}}_{F}$. Let  $\unicode[STIX]{x1D70E}$ be an irreducible smooth complex representation of
$\unicode[STIX]{x1D70E}$ be an irreducible smooth complex representation of 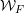 ${\mathcal{W}}_{F}$, realized as the Langlands parameter of an irreducible cuspidal representation
${\mathcal{W}}_{F}$, realized as the Langlands parameter of an irreducible cuspidal representation  $\unicode[STIX]{x1D70B}$ of a general linear group over
$\unicode[STIX]{x1D70B}$ of a general linear group over 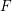 $F$. In an earlier paper we showed that the ramification structure of
$F$. In an earlier paper we showed that the ramification structure of  $\unicode[STIX]{x1D70E}$ is determined by the fine structure of the endo-class
$\unicode[STIX]{x1D70E}$ is determined by the fine structure of the endo-class 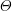 $\unicode[STIX]{x1D6E9}$ of the simple character contained in
$\unicode[STIX]{x1D6E9}$ of the simple character contained in  $\unicode[STIX]{x1D70B}$, in the sense of Bushnell and Kutzko. The connection is made via the Herbrand function
$\unicode[STIX]{x1D70B}$, in the sense of Bushnell and Kutzko. The connection is made via the Herbrand function  $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}}$ of
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}}$ of 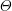 $\unicode[STIX]{x1D6E9}$. In this paper we concentrate on the fundamental Carayol case in which
$\unicode[STIX]{x1D6E9}$. In this paper we concentrate on the fundamental Carayol case in which  $\unicode[STIX]{x1D70E}$ is totally wildly ramified with Swan exponent not divisible by
$\unicode[STIX]{x1D70E}$ is totally wildly ramified with Swan exponent not divisible by 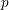 $p$. We show that, for such
$p$. We show that, for such  $\unicode[STIX]{x1D70E}$, the associated Herbrand function satisfies a certain functional equation, and that this property essentially characterizes this class of representations. We calculate
$\unicode[STIX]{x1D70E}$, the associated Herbrand function satisfies a certain functional equation, and that this property essentially characterizes this class of representations. We calculate 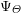 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}}$ explicitly, in terms of a classical Herbrand function arising naturally from the classification of simple characters. We describe exactly the class of functions arising as Herbrand functions
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}}$ explicitly, in terms of a classical Herbrand function arising naturally from the classification of simple characters. We describe exactly the class of functions arising as Herbrand functions 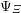 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6EF}}$, as
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6EF}}$, as 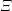 $\unicode[STIX]{x1D6EF}$ varies over the set of totally wild endo-classes of Carayol type. In a separate argument, we derive a complete description of the restriction of
$\unicode[STIX]{x1D6EF}$ varies over the set of totally wild endo-classes of Carayol type. In a separate argument, we derive a complete description of the restriction of  $\unicode[STIX]{x1D70E}$ to any ramification subgroup and hence a detailed interpretation of the Herbrand function. This gives concrete information concerning the Langlands correspondence.
$\unicode[STIX]{x1D70E}$ to any ramification subgroup and hence a detailed interpretation of the Herbrand function. This gives concrete information concerning the Langlands correspondence.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Authors 2019
References
- 1
- Cited by


