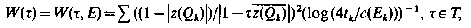Research Article
The determination of the surface impedance of an obstacle
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-15
-
- Article
-
- You have access
- Export citation
Lp-equivalence of a linear and a nonlinear impulsive differential equation in a Banach space
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 17-33
-
- Article
-
- You have access
- Export citation
The asymptotic distribution of the eigenvalues of right definite multiparameter Sturm-Liouville systems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 35-47
-
- Article
-
- You have access
- Export citation
Elements of finite order in Stone-Čech compactifications
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 49-54
-
- Article
-
- You have access
- Export citation
On semigroup presentations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 55-68
-
- Article
-
- You have access
- Export citation
On linear independence for integer translates of a finite number of functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 69-85
-
- Article
-
- You have access
- Export citation
On minimal thinness, reduced functions and Green potentials
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 87-106
-
- Article
-
- You have access
- Export citation
Classification of limits of triangular matrix algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 107-121
-
- Article
-
- You have access
- Export citation
Extreme n-positive linear maps
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 123-131
-
- Article
-
- You have access
- Export citation
Harmonic morphisms between spaces of constant curvature
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 133-143
-
- Article
-
- You have access
- Export citation
The squareroot of an ambiguous form in the principal genus
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 145-150
-
- Article
-
- You have access
- Export citation
On the deficiencies of composite entire functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 151-164
-
- Article
-
- You have access
- Export citation
Congruence permutable extensions of distributive double p-algebras*
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 165-168
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 36 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PEM volume 36 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 January 2009, p. b1
-
- Article
-
- You have access
- Export citation