Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-20T06:17:47.465Z Has data issue: false hasContentIssue false
  • English
  • Français

On minimal thinness, reduced functions and Green potentials

Published online by Cambridge University Press:  20 January 2009

Matts Essén
Matts Essén
Affiliation:
Uppsala UniversityDepartment of MathematicsBox 480S-75106 Uppsala, Sweden
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Ω be an open connected subset of the unit disc U, let E = U\Ω and let {Ωk} be a Whitney decomposition of U. If z(Q) is the centre of the “square” Q, if T is the unit circle and t = dist.(Q, T), we consider

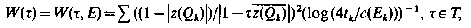
where Ek = E ∩ Qk and c(Ek) is the capacity of Ek. We prove that the set E is minimally thin at τ ∈ T in U if and only if W(τ)< ∞. We study functions of type W and discuss the relation between certain results of Naim on minimal thinness [15], a minimum principle of Beurling [3], related results due to Dahlberg [7] and Sjögren [16] and recent work of Hayman-Lyons [15] (cf. also Bonsall [4]) and Volberg [19]. For simplicity, we discuss our problems in the unit disc U in the plane. However, the same techniques work for analogous problems in higher dimensions and in more complicated regions.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 36 , Issue 1 , February 1993 , pp. 87 - 106
Copyright
Copyright © Edinburgh Mathematical Society 1993

References

REFERENCES

1.Ahlfors, L. V., Conformal invariants. Topics in Geometric Function Theory (McGraw-Hill, New York 1973).Google Scholar
2.Beardon, A. F., The geometry of discrete groups (Springer-Verlag, New York, 1983).CrossRefGoogle Scholar
3.Beurling, A., A minimum principle for positive harmonic functions, Ann. Acad. Sci. Fenn. Ser. A 1 Math. 372 (1965).Google Scholar
4.Bonsall, F. F., Domination of the supremum of a bounded harmonic function by its supremum over a countable subset, Proc. Edinburgh Math. Soc. 30 (1987), 471–477.CrossRefGoogle Scholar
5.Bonsall, F. F. and Walsh, D., Vanishing l 1-sums of the Poisson kernel, and sums with positive coefficients, Proc. Edinburgh Math. Soc. 32 (1989), 431–447.CrossRefGoogle Scholar
6.Collingwood, E. F. and Lohwater, A. J., The theory of cluster sets (Cambridge University Press, 1966).CrossRefGoogle Scholar
7.Dahlberg, B., A minimum principle for positive harmonic functions, Proc. London Math. Soc. 33 (1976), 238–250.CrossRefGoogle Scholar
8.Essén, M., On Wiener conditions for minimally thin and rarefied sets, in Complex Analysis (ed. Hersch, J. and Huber, A., Birkhäuser Verlag, Basel 1988), 41–50.CrossRefGoogle Scholar
9.Frostman, O., Sur les produits de Blaschke, K. Fysiogr. Sällsk, Lund Förh. 12 (1939), 1–14.Google Scholar
10.Garnett, J. B., Bounded Analytic Functions (Academic Press, New York, 1981).Google Scholar
11.Hayman, W. K. and Lyons, T. J., Bases for positive continuous functions, J. London Math. Soc. (2) 42 (1990), 292–308.CrossRefGoogle Scholar
12.Helms, L. L., Introduction to potential theory (Wiley-Interscience, New York-London 1969).Google Scholar
13.Hwang, J. S., On boundary behaviour of Blaschke products, Analysis 6 (1986), 317–338.CrossRefGoogle Scholar
14.Lelong-Ferrand, J., Étude au voisinage de la frontière des fonctions surharmoniques positives dans un demi-espace, Ann. Sci. École Norm. Sup. (3) 66 (1949), 125–159.CrossRefGoogle Scholar
15.Naim, L., Sur le rôle de la frontière de R. S. Martin dans la théorie du potentiel, Ann. Inst. Fourier 7 (1957), 183–281.CrossRefGoogle Scholar
16.Sjögren, P., Weak L1 characterizations of Poisson integrals, Green potentials and H p spaces, Trans. Amer. Math. Soc. 233 (1977), 179–196.Google Scholar
17.Stein, E. M., Singular integrals and differentiability properties of functions (Princeton University Press, 1970).Google Scholar
18.Tsuji, M., Potential theory in modern function theory (Maruzen, Tokyo, 1959).Google Scholar
19.Volberg, A. L., A criterion on a subdomain of the disc to have its harmonic measure comparable with Lebesgue measure (USSR Academy of Sciences. Steklov Mathematical Institute, Leningrad department, LOMI preprints E–2–89). Also Proc. Amer. Math. Soc., to appear.Google Scholar