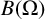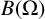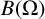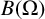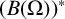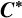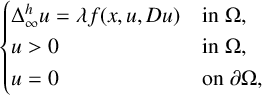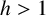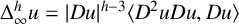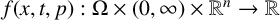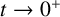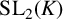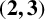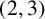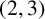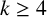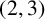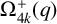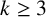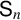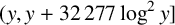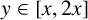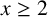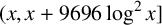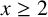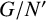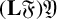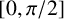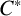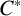FirstView articles
Research Article
EVALUATION FUNCTIONS AND REFLEXIVITY OF BANACH SPACES OF HOLOMORPHIC FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1-14
-
- Article
- Export citation
TWISTED ACTIONS ON COHOMOLOGIES AND BIMODULES
- Part of:
-
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1-52
-
- Article
- Export citation
SPHERICAL REPRESENTATIONS FOR
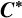 $\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
$\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1-34
-
- Article
- Export citation
VISCOSITY SOLUTIONS TO THE INFINITY LAPLACIAN EQUATION WITH SINGULAR NONLINEAR TERMS
- Part of:
-
- Published online by Cambridge University Press:
- 20 March 2024, pp. 1-30
-
- Article
- Export citation
BASIC NONARCHIMEDEAN JØRGENSEN THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 19 March 2024, pp. 1-15
-
- Article
- Export citation
FINITENESS OF CANONICAL QUOTIENTS OF DEHN QUANDLES OF SURFACES
-
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-18
-
- Article
- Export citation
RADU GROUPS ACTING ON TREES ARE CCR
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1-38
-
- Article
- Export citation
THE
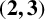 $\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
$\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 28 February 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE RIEFFEL CORRESPONDENCE FOR EQUIVALENT FELL BUNDLES
- Part of:
-
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BRATTELI–VERSHIKISABILITY OF POLYGONAL BILLIARDS ON THE HYPERBOLIC PLANE
- Part of:
-
- Published online by Cambridge University Press:
- 15 December 2023, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMMON ZEROS OF IRREDUCIBLE CHARACTERS
- Part of:
-
- Published online by Cambridge University Press:
- 11 December 2023, pp. 1-25
-
- Article
- Export citation
RODRIGUES FORMULA AND LINEAR INDEPENDENCE FOR VALUES OF HYPERGEOMETRIC FUNCTIONS WITH VARYING PARAMETERS
-
- Published online by Cambridge University Press:
- 05 December 2023, pp. 1-37
-
- Article
- Export citation
SOME GLOBAL EXISTENCE RESULTS ON LOCALLY FINITE GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1-17
-
- Article
- Export citation
FAITHFULNESS OF THE 2-BRAID GROUP VIA ZIGZAG ALGEBRA IN TYPE B
- Part of:
-
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1-18
-
- Article
- Export citation
AN EXPLICIT MEAN-VALUE ESTIMATE FOR THE PRIME NUMBER THEOREM IN INTERVALS
-
- Published online by Cambridge University Press:
- 19 September 2023, pp. 1-15
-
- Article
- Export citation
HALL CLASSES OF GROUPS WITH A LOCALLY FINITE OBSTRUCTION
- Part of:
-
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1-28
-
- Article
- Export citation
ON POSSIBLE VALUES OF THE INTERIOR ANGLE BETWEEN INTERMEDIATE SUBALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1-23
-
- Article
- Export citation
RETRACTED - THE KRONECKER–WEYL EQUIDISTRIBUTION THEOREM AND GEODESICS IN 3-MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2022, pp. 1-44
-
- Article
- Export citation