Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-25T00:35:42.121Z Has data issue: false hasContentIssue false
  • English
  • Français

RETRACTED - THE KRONECKER–WEYL EQUIDISTRIBUTION THEOREM AND GEODESICS IN 3-MANIFOLDS

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Low-dimensional dynamical systems

Published online by Cambridge University Press:  21 March 2022

J. BECK  and
W. W. L. CHEN Open the ORCID record for W. W. L. CHEN [Opens in a new window]
J. BECK
Affiliation:
Department of Mathematics, Hill Center for the Mathematical Sciences, Rutgers University, Piscataway, NJ08854, USA e-mail: jbeck@math.rutgers.edu
W. W. L. CHEN*
Affiliation:
Department of Mathematics and Statistics, Macquarie University, Sydney, NSW2109, Australia
*
e-mail: william.chen@mq.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

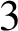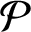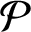Given any rectangular polyhedron $3$ -manifold $\mathcal {P}$ tiled with unit cubes, we find infinitely many explicit directions related to cubic algebraic numbers such that all half-infinite geodesics in these directions are uniformly distributed in $\mathcal {P}$ .

Keywords

geodesicsequidistributiondensity

MSC classification

Primary: 11K38: Irregularities of distribution, discrepancy
Secondary: 37E35: Flows on surfaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , First View , pp. 1 - 44
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Dzmitry Badziahin

References

Beck, J., Chen, W. W. L. and Yang, Y., ‘Quantitative behavior of non-integrable systems (III)’, Acta Math. Hungar. (to appear). arXiv:2006.06213.Google Scholar
Cassels, J. W. S., An Introduction to Diophantine Approximation (Cambridge University Press, Cambridge, 1957).Google Scholar
Furstenberg, H., Recurrence in Ergodic Theory and Combinatorial Number Theory (Princeton University Press, Princeton, NJ, 1981).CrossRefGoogle Scholar
Gutkin, E., ‘Billiards on almost integrable polyhedral surfaces’, Ergodic Theory Dynam. Systems 4 (1984), 569–584.CrossRefGoogle Scholar
Hubert, P. and Schmidt, T. A., ‘An introduction to Veech surfaces’, in: Handbook of Dynamical Systems, Vol. 1B (eds. Hasselblatt, B. and Katok, A.) (Elsevier, Amsterdam, 2006), 501–526.Google Scholar
König, D. and Szücs, A., ‘Mouvement d’un point abondonné à l’interieur d’un cube’, Rend. Circ. Mat. Palermo (2) 36 (1913), 79–90.CrossRefGoogle Scholar
Mahler, K., ‘Ein Übertragungsprinzip für lineare Ungleichungen’, Časopis Pěst. Math. Fys. 68 (1939), 85–92.CrossRefGoogle Scholar
Masur, H., ‘Ergodic theory of translation surfaces’, in: Handbook of Dynamical Systems, Vol. 1B (eds. Hasselblat, B. and Katok, A.) (Elsevier, Amsterdam, 2006), 527–547.Google Scholar
Masur, H. and Tabachnikov, S., ‘Rational billiards and flat surfaces’, in: Handbook of Dynamical Systems, Vol. 1A (eds. Hasselblat, B. and Katok, A.) (Elsevier, Amsterdam, 2006), 1015–1089.Google Scholar
Schmidt, W. M., Diophantine Approximation , Lecture Notes in Mathematics, 785 (Springer, Berlin, 1980).Google Scholar
Veech, W. A., ‘Boshernitzan’s criterion for unique ergodicity of an interval exchange transformation’, Ergodic Theory Dynam. Systems 7 (1987), 149–153.CrossRefGoogle Scholar
Weyl, H., ‘Über die Gleichverteilung von Zahlen mod. Eins’, Math. Ann. 77 (1916), 313–352.CrossRefGoogle Scholar
Zorich, A., ‘Flat surfaces’, in: Frontiers in Number Theory, Physics, and Geometry, Vol. 1 (eds. Cartier, P. E., Julia, B., Moussa, P. and Vanhove, P.) (Springer, Berlin, 2006), 439–586.CrossRefGoogle Scholar