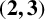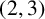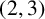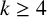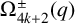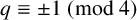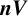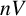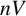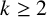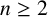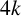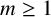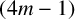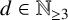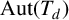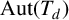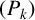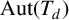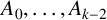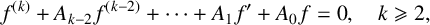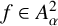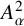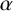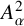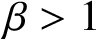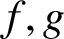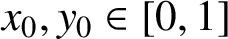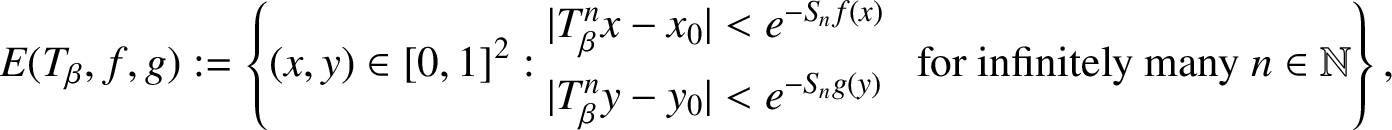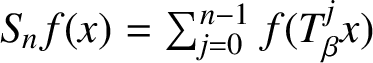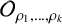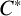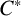Open access
Research Article
THE
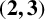 $\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
$\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 28 February 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE RIEFFEL CORRESPONDENCE FOR EQUIVALENT FELL BUNDLES
- Part of:
-
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BRATTELI–VERSHIKISABILITY OF POLYGONAL BILLIARDS ON THE HYPERBOLIC PLANE
- Part of:
-
- Published online by Cambridge University Press:
- 15 December 2023, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WIENER TAUBERIAN THEOREMS FOR CERTAIN BANACH ALGEBRAS ON REAL RANK ONE SEMISIMPLE LIE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 18 July 2023, pp. 68-95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONDITIONAL FLATNESS, FIBERWISE LOCALIZATIONS, AND ADMISSIBLE REFLECTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 23 June 2023, pp. 200-220
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RANK JUMPS AND GROWTH OF SHAFAREVICH–TATE GROUPS FOR ELLIPTIC CURVES IN
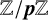 ${\mathbb {Z}}/\boldsymbol{p}{\mathbb {Z}}$-EXTENSIONS
${\mathbb {Z}}/\boldsymbol{p}{\mathbb {Z}}$-EXTENSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MULTIPLICATION TABLES AND WORD-HYPERBOLICITY IN FREE PRODUCTS OF SEMIGROUPS, MONOIDS AND GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 17 March 2023, pp. 396-430
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE NUMBER OF QUADRATIC ORTHOMORPHISMS THAT PRODUCE MAXIMALLY NONASSOCIATIVE QUASIGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2023, pp. 311-336
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN INCIDENCE RESULT FOR WELL-SPACED ATOMS IN ALL DIMENSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2023, pp. 58-72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ELLIPTIC COHOMOLOGY IS UNIQUE UP TO HOMOTOPY
- Part of:
-
- Published online by Cambridge University Press:
- 15 November 2022, pp. 99-118
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PERMUTATION-BASED PRESENTATIONS FOR BRIN’S HIGHER-DIMENSIONAL THOMPSON GROUPS
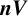 $\boldsymbol {nV}$
$\boldsymbol {nV}$
- Part of:
-
- Published online by Cambridge University Press:
- 15 November 2022, pp. 39-67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SIMPLY CONNECTED MANIFOLDS WITH LARGE HOMOTOPY STABLE CLASSES
- Part of:
-
- Published online by Cambridge University Press:
- 26 September 2022, pp. 172-203
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CHARACTER STACKS ARE PORC COUNT
- Part of:
-
- Published online by Cambridge University Press:
- 23 September 2022, pp. 289-310
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS ACTING ON TREES WITH PRESCRIBED LOCAL ACTION
- Part of:
-
- Published online by Cambridge University Press:
- 12 September 2022, pp. 240-288
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DESCRIPTION OF GROWTH AND OSCILLATION OF SOLUTIONS OF COMPLEX LDE’S
- Part of:
-
- Published online by Cambridge University Press:
- 16 June 2022, pp. 145-171
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDED COHOMOLOGY AND BINATE GROUPS
-
- Published online by Cambridge University Press:
- 10 May 2022, pp. 204-239
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REPRESENTING STRUCTURED SEMIGROUPS ON ÉTALE GROUPOID BUNDLES
- Part of:
-
- Published online by Cambridge University Press:
- 13 April 2022, pp. 1-49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPACT AND HILBERT–SCHMIDT WEIGHTED COMPOSITION OPERATORS ON WEIGHTED BERGMAN SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 22 March 2022, pp. 208-225
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HIGHER-DIMENSIONAL SHRINKING TARGET PROBLEM FOR BETA DYNAMICAL SYSTEMS
- Part of:
-
- Published online by Cambridge University Press:
- 22 March 2022, pp. 289-311
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
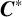 $\boldsymbol {C}^{*}$
-ALGEBRAS FROM
$\boldsymbol {C}^{*}$
-ALGEBRAS FROM 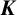 $\boldsymbol {K}$
GROUP REPRESENTATIONS
$\boldsymbol {K}$
GROUP REPRESENTATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2022, pp. 318-338
-
- Article
-
- You have access
- Open access
- HTML
- Export citation