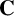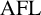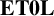Hyperbolic groups, being groups whose Cayley graphs are hyperbolic metric spaces, were introduced by Gromov in his seminal monograph [Reference Gromov62]. Subsequently, the theory of hyperbolic groups has grown to be one of the most influential areas of group theory. It is natural to wish to generalise hyperbolicity from groups to semigroups and monoids. This can be done in several ways. One way is to consider semigroups and monoids whose (right, undirected) Cayley graphs are hyperbolic as metric spaces. This approach is somewhat brittle: for a trivial example that illustrates this well, if G is any group whatsoever, then
![]() $G^0$
– the semigroup obtained from G by adjoining a zero – has a hyperbolic Cayley graph when this is considered as an undirected graph. A second, and somewhat more robust, approach is to use the methods of formal language theory, which is the starting point of the present article.
$G^0$
– the semigroup obtained from G by adjoining a zero – has a hyperbolic Cayley graph when this is considered as an undirected graph. A second, and somewhat more robust, approach is to use the methods of formal language theory, which is the starting point of the present article.
Language-theoretic methods in group theory have a rich history spanning the past half century, starting with Anīsīmov in 1969 [Reference Anīsīmov7] and continuing with the seminal [Reference Anīsīmov8]. It is in this latter article in which the ‘word problem’ of a group, being the formal language of words over a generating set representing the identity element, was introduced and studied. The connections between groups and context-free languages were explored further by Anīsīmov [Reference Anīsīmov4–Reference Anīsīmov and Seifert6, Reference Anīsīmov9, Reference Anīsīmov10]. Muller and Schupp [Reference Muller and Schupp86] (contingent on a weak form of a deep result by Dunwoody [Reference Dunwoody39]) subsequently proved a striking classification: a finitely generated group has context-free word problem if and only if it is virtually free. This decisively demonstrated the depth of the connection first uncovered by Anīsīmov.
With the importance of context-free languages to the theory of groups, it seems natural to desire a purely language-theoretic definition of hyperbolicity in groups. One such definition was given by Grunschlag [Reference Grunschlag63], who proved that a group is hyperbolic if and only if its word problem is generated by a terminating growing context-sensitive grammar. (A terminating grammar is one in which for every variable v, there is a sequence of productions that transforms v into a word over the terminals; see [Reference Grunschlag63, Section 1.8.5].) An arguably more elegant characterisation, using the weaker expressive power of context-free languages, was given by Gilman [Reference Gilman49]. This definition has the added benefit of being generalisable directly to semigroups, which was done by Duncan and Gilman [Reference Duncan and Gilman38]. To distinguish from the geometric variant, this form of hyperbolicity is called word-hyperbolicity. Loosely speaking, a semigroup S is word-hyperbolic if there exists a regular language of representatives (with no requirement of uniqueness) such that the multiplication table for S with respect to this language can be described by a context-free language. This definition (which is described formally in Section 1.3) is equivalent to geometric hyperbolicity for groups [Reference Duncan and Gilman38, Corollary 4.3] and for completely simple semigroups [Reference Fountain and Kambites46, Theorem 4.1]. In general, however, word-hyperbolic semigroups are a more restricted class than hyperbolic semigroups, and appear somewhat more amenable to general results than the geometric approach to hyperbolic semigroups. (Having said this – and as a paper on hyperbolicity of semigroups may be considered to be skewed without some references to the geometry of semigroups – there is a recent trend, pioneered by Gray and Kambites, in successfully handling the directed geometry of semigroups in a manner extending the usual geometric group theory (for example, the Milnor–Schwarz lemma [Reference Schwarz103]), see [Reference Gray and Kambites54–Reference Gray and Kambites58]; see also [Reference Garreta and Gray47, Reference Hoffmann and Thomas68, Reference Kuske and Lohrey76, Reference Silva and Steinberg101].) For example, just as in groups, there are links between word-hyperbolicity and automaticity in semigroups.
Whenever a generalisation (for example, of hyperbolicity in groups) is made, it is useful to ask: what properties should be desired to be retained, and which should not? For example, hyperbolicity in groups is independent of the generating set chosen, which is a rather (one may argue) essential and desirable property; this property holds also for word-hyperbolic semigroups [Reference Duncan and Gilman38, Theorem 3.4]. Furthermore, the word problem is well known to be decidable in all hyperbolic groups (in linear time); for word-hyperbolic semigroups, the word problem is also decidable [Reference Hoffmann, Kuske, Otto and Thomas67, Theorem 3.8], in fact in polynomial time [Reference Cain and Pfeiffer26, Theorem 7.1].
However, while hyperbolic groups are automatic [Reference Epstein, Cannon, Holt, Levy, Paterson and Thurston44, Theorem 3.4.5], it is not true that word-hyperbolic semigroups are always automatic [Reference Hoffmann, Kuske, Otto and Thomas67, Example 7.7]. Similarly, while the isomorphism problem is decidable for hyperbolic groups [Reference Dahmani and Guirardel34], it is undecidable in general for word-hyperbolic semigroups [Reference Cain and Pfeiffer26, Theorem 4.3]. When considering which properties are desired – and are reasonable to desire – if a definition is found to not satisfy one such desired property, then an amendment to the definition which forces this property to hold may be considered. (In fact, two amendments have already been proposed, by Hoffmann and Thomas [Reference Hoffmann and Thomas69], which recovers automaticity, and Cain and Pfeiffer [Reference Cain and Pfeiffer26], which has a word problem decidable in
![]() $O(n \log n$
)-time.) It is the view of the author that free products of word-hyperbolic semigroups ought to be word-hyperbolic; free products are free constructions, and free objects (for example, free semigroups) are word-hyperbolic. While we are not able to prove this result with exactly this statement, the main results of this article demonstrate that any possible counterexample to the general statement will be exceptional, rather than the norm.
$O(n \log n$
)-time.) It is the view of the author that free products of word-hyperbolic semigroups ought to be word-hyperbolic; free products are free constructions, and free objects (for example, free semigroups) are word-hyperbolic. While we are not able to prove this result with exactly this statement, the main results of this article demonstrate that any possible counterexample to the general statement will be exceptional, rather than the norm.
The outline of the paper is as follows. In Section 1, we give some background, necessary definitions and notation. In particular, in Section 1.8, we give a brief overview of the connections between substitutions in formal language theory (crucial to the arguments in subsequent sections) and
![]() $\mathbf {ET0L}$
systems. In Section 2, we prove the main result for semigroup free products, which is the following theorem.
$\mathbf {ET0L}$
systems. In Section 2, we prove the main result for semigroup free products, which is the following theorem.
Theorem A. Let
![]() $S_1, S_2$
be
$S_1, S_2$
be
![]() $1$
-extendable word-hyperbolic semigroups. Then the free product
$1$
-extendable word-hyperbolic semigroups. Then the free product
![]() $S_1 \ast S_2$
is word-hyperbolic.
$S_1 \ast S_2$
is word-hyperbolic.
The technical condition for a word-hyperbolic semigroup S to be
![]() $1$
-extendable is defined and explored in Section 1.3, and loosely speaking consists of a condition ensuring that the word-hyperbolic structure for S does not collapse if one adjoins an identity to S. In particular (see Lemma 1.6), any monoid and any (von Neumann) regular semigroup is
$1$
-extendable is defined and explored in Section 1.3, and loosely speaking consists of a condition ensuring that the word-hyperbolic structure for S does not collapse if one adjoins an identity to S. In particular (see Lemma 1.6), any monoid and any (von Neumann) regular semigroup is
![]() $1$
-extendable, so Theorem A applies when
$1$
-extendable, so Theorem A applies when
![]() $S_1$
and
$S_1$
and
![]() $S_2$
are from either of these classes.
$S_2$
are from either of these classes.
To deal with monoid free products (and, as a particular case, group free products), in Section 3, we first develop some technical purely language-theoretic tools which we call polypartisan ancestors. Loosely speaking, polypartisan ancestors model a form of sequential rewriting with respect to rules of the form
![]() $a \to W$
, where a is a single letter, and where the word w to which the rewriting is applied is divided into some fixed number k parts such that each part is rewritten using possibly different sets of rules. In Section 4, we first use our previous results on semigroup free products to prove the following main result.
$a \to W$
, where a is a single letter, and where the word w to which the rewriting is applied is divided into some fixed number k parts such that each part is rewritten using possibly different sets of rules. In Section 4, we first use our previous results on semigroup free products to prove the following main result.
Theorem B. Let
![]() $M_1, M_2$
be two word-hyperbolic monoids with
$M_1, M_2$
be two word-hyperbolic monoids with
![]() $1$
-uniqueness (with uniqueness). Then the monoid free product
$1$
-uniqueness (with uniqueness). Then the monoid free product
![]() $M_1 \ast M_2$
is word-hyperbolic with
$M_1 \ast M_2$
is word-hyperbolic with
![]() $1$
-uniqueness (with uniqueness).
$1$
-uniqueness (with uniqueness).
Here,
![]() $1$
-uniqueness (which is defined in Section 4.1) is the condition on a word-hyperbolic monoid M, with regular language of representatives R, saying the only word in R which represents the identity element is the empty word. In particular, one can show that hyperbolic groups are word-hyperbolic with
$1$
-uniqueness (which is defined in Section 4.1) is the condition on a word-hyperbolic monoid M, with regular language of representatives R, saying the only word in R which represents the identity element is the empty word. In particular, one can show that hyperbolic groups are word-hyperbolic with
![]() $1$
-uniqueness, and as a corollary, we derive, by language-theoretic means, the well-known group-theoretic result that the free product of hyperbolic groups is hyperbolic. Using polypartisan ancestors, we also deduce (Theorem 4.5) that the monoid free product of
$1$
-uniqueness, and as a corollary, we derive, by language-theoretic means, the well-known group-theoretic result that the free product of hyperbolic groups is hyperbolic. Using polypartisan ancestors, we also deduce (Theorem 4.5) that the monoid free product of
![]() $\star $
-word-hyperbolic monoids is
$\star $
-word-hyperbolic monoids is
![]() $\star $
-word-hyperbolic. Here,
$\star $
-word-hyperbolic. Here,
![]() $\star $
-word-hyperbolicity refers to a condition which can be seen, in a sense made precise in Section 4.3, as ‘complementary’ to
$\star $
-word-hyperbolicity refers to a condition which can be seen, in a sense made precise in Section 4.3, as ‘complementary’ to
![]() $1$
-uniqueness.
$1$
-uniqueness.
Finally, in Section 5, we use the language-theoretic generality in which the article is written to note that our results generalise immediately from context-free multiplication tables to much more general situations, including
![]() $\mathbf {ET0L}$
and indexed multiplication tables, leading to Theorems A′
and B′
, being more general versions of the main results of this article. In particular, we deduce (Corollary 5.2) that the free product of two groups, each having an
$\mathbf {ET0L}$
and indexed multiplication tables, leading to Theorems A′
and B′
, being more general versions of the main results of this article. In particular, we deduce (Corollary 5.2) that the free product of two groups, each having an
![]() $\mathbf {ET0L}$
multiplication table, again has an
$\mathbf {ET0L}$
multiplication table, again has an
![]() $\mathbf {ET0L}$
multiplication table; the analogous statement (Corollary 5.3) for groups with indexed multiplication tables is also deduced.
$\mathbf {ET0L}$
multiplication table; the analogous statement (Corollary 5.3) for groups with indexed multiplication tables is also deduced.
1 Introduction and notation
The paper also assumes familiarity with the basics of the theory of semigroup, monoid and group presentations, which is written as
![]() $\mathrm {Sgp} \langle A \mid \mathscr {R} \rangle $
,
$\mathrm {Sgp} \langle A \mid \mathscr {R} \rangle $
,
![]() $\mathrm {Mon} \langle A \mid \mathscr {R} \rangle $
and
$\mathrm {Mon} \langle A \mid \mathscr {R} \rangle $
and
![]() $\mathrm {Gp} \langle A \mid \mathscr {R} \rangle $
, respectively. For further background, see, for example, [Reference Adian1, Reference Campbell, Robertson, Ruškuc and Thomas27, Reference Lyndon and Schupp82, Reference Magnus, Karrass and Solitar83, Reference Neumann87].
$\mathrm {Gp} \langle A \mid \mathscr {R} \rangle $
, respectively. For further background, see, for example, [Reference Adian1, Reference Campbell, Robertson, Ruškuc and Thomas27, Reference Lyndon and Schupp82, Reference Magnus, Karrass and Solitar83, Reference Neumann87].
1.1 Formal language theory
We assume the reader is familiar with the fundamentals of formal language theory. In particular, a full
![]() $\operatorname {\mathrm {AFL}}$
(abstract family of languages) is a class of languages closed under homomorphism, inverse homomorphism, intersection with regular languages, union, concatenation and the Kleene star. Furthermore, a class
$\operatorname {\mathrm {AFL}}$
(abstract family of languages) is a class of languages closed under homomorphism, inverse homomorphism, intersection with regular languages, union, concatenation and the Kleene star. Furthermore, a class
![]() $\mathbf {C}$
is reversal-closed if for all
$\mathbf {C}$
is reversal-closed if for all
![]() $L \in \mathbf {C}$
, we have
$L \in \mathbf {C}$
, we have
![]() $L^{\text {rev}} \in \mathbf {C}$
. Here,
$L^{\text {rev}} \in \mathbf {C}$
. Here,
![]() $L^{\text {rev}}$
denotes the language of all words in L read backwards (see Section 1.2 for a formal definition). For some background on this, and other topics in formal language theory, we refer the reader to standard books on the subject [Reference Berstel20, Reference Harrison64, Reference Hopcroft and Ullman70, Reference Rozenberg and Salomaa96]. The class of context-free languages is denoted
$L^{\text {rev}}$
denotes the language of all words in L read backwards (see Section 1.2 for a formal definition). For some background on this, and other topics in formal language theory, we refer the reader to standard books on the subject [Reference Berstel20, Reference Harrison64, Reference Hopcroft and Ullman70, Reference Rozenberg and Salomaa96]. The class of context-free languages is denoted
![]() $\mathbf {CF}$
.
$\mathbf {CF}$
.
We also, in Sections 5 and 1.8, make reference to the class
![]() $\mathbf {IND}$
of indexed languages. The latter was introduced in Aho’s Ph.D. thesis [Reference Aho2], see also [Reference Aho3] as an extension of the context-free languages; we refer the reader to, for example, [Reference Gilman48, Reference Hayashi65, Reference Smith102] or [Reference Hopcroft and Ullman70, Ch. 14] for particularly readable definitions. Finally, we make some reference to the classes
$\mathbf {IND}$
of indexed languages. The latter was introduced in Aho’s Ph.D. thesis [Reference Aho2], see also [Reference Aho3] as an extension of the context-free languages; we refer the reader to, for example, [Reference Gilman48, Reference Hayashi65, Reference Smith102] or [Reference Hopcroft and Ullman70, Ch. 14] for particularly readable definitions. Finally, we make some reference to the classes
![]() $\mathbf {ET0L}$
and
$\mathbf {ET0L}$
and
![]() $\mathbf {EDT0L}$
in Section 5 (but not in the main sections of the paper). These are examples of
$\mathbf {EDT0L}$
in Section 5 (but not in the main sections of the paper). These are examples of
![]() $\mathbf {L}$
-languages, which arise from
$\mathbf {L}$
-languages, which arise from
![]() $\mathbf {L}$
-systems. The theory of
$\mathbf {L}$
-systems. The theory of
![]() $\mathbf {L}$
-systems originated in 1968 in the work of Lindenmayer [Reference Lindenmayer80, Reference Lindenmayer81] (whence the
$\mathbf {L}$
-systems originated in 1968 in the work of Lindenmayer [Reference Lindenmayer80, Reference Lindenmayer81] (whence the
![]() $\mathbf {L}$
) as a theory for the parallel branching of filamentous organisms in biology, but subsequently grew into a core branch of formal language theory [Reference Herman and Rozenberg66, Reference Rozenberg, Penttonen and Salomaa93–Reference Rozenberg and Salomaa95]. Because of this vast literature (and as we do not need the definitions), we do not define either
$\mathbf {L}$
) as a theory for the parallel branching of filamentous organisms in biology, but subsequently grew into a core branch of formal language theory [Reference Herman and Rozenberg66, Reference Rozenberg, Penttonen and Salomaa93–Reference Rozenberg and Salomaa95]. Because of this vast literature (and as we do not need the definitions), we do not define either
![]() $\mathbf {ET0L}$
or
$\mathbf {ET0L}$
or
![]() $\mathbf {EDT0L}$
, instead referring the reader to more recent articles on the subject (for example, especially [Reference Ciobanu, Elder and Ferov31], see also [Reference Brough, Ciobanu, Elder and Zetzsche24, Reference Istrate72, Reference Rabkin92]). The research topic remains very active; particularly, the connections between
$\mathbf {EDT0L}$
, instead referring the reader to more recent articles on the subject (for example, especially [Reference Ciobanu, Elder and Ferov31], see also [Reference Brough, Ciobanu, Elder and Zetzsche24, Reference Istrate72, Reference Rabkin92]). The research topic remains very active; particularly, the connections between
![]() $\mathbf {ET0L}$
and
$\mathbf {ET0L}$
and
![]() $\mathbf {EDT0L}$
languages and equations over groups and monoids have flourished in recent years; see, for example, [Reference Ciobanu and Elder30, Reference Ciobanu and Elder31, Reference Diekert and Elder35, Reference Evetts and Levine45]. There are also recent links with geometric group theory. For example, Bridson and Gilman [Reference Bridson and Gilman23] famously proved that any
$\mathbf {EDT0L}$
languages and equations over groups and monoids have flourished in recent years; see, for example, [Reference Ciobanu and Elder30, Reference Ciobanu and Elder31, Reference Diekert and Elder35, Reference Evetts and Levine45]. There are also recent links with geometric group theory. For example, Bridson and Gilman [Reference Bridson and Gilman23] famously proved that any
![]() $3$
-manifold group admits a combing which is an indexed language; in fact, their combing is an
$3$
-manifold group admits a combing which is an indexed language; in fact, their combing is an
![]() $\mathbf {ET0L}$
language [Reference Ciobanu, Elder and Ferov31] (note that
$\mathbf {ET0L}$
language [Reference Ciobanu, Elder and Ferov31] (note that
![]() $\mathbf {CF} \subsetneq \mathbf {ET0L} \subsetneq \mathbf {IND}$
).
$\mathbf {CF} \subsetneq \mathbf {ET0L} \subsetneq \mathbf {IND}$
).
A useful analogy to keep in mind is the following: the class
![]() $\mathbf {CF}$
can be seen as modelling closure under sequential recursion; the class
$\mathbf {CF}$
can be seen as modelling closure under sequential recursion; the class
![]() $\mathbf {ET0L}$
models closure under parallel recursion. See Section 1.8 for further details on this analogy, particularly Theorem 1.13, as well as [Reference Rozenberg and Vermeir97]. Finally,
$\mathbf {ET0L}$
models closure under parallel recursion. See Section 1.8 for further details on this analogy, particularly Theorem 1.13, as well as [Reference Rozenberg and Vermeir97]. Finally,
![]() $\mathbf {CF}, \mathbf {ET0L}$
and
$\mathbf {CF}, \mathbf {ET0L}$
and
![]() $\mathbf {IND}$
are all easily seen to be reversal-closed.
$\mathbf {IND}$
are all easily seen to be reversal-closed.
1.2 Rewriting systems
Let A be a finite alphabet, and let
![]() $A^{\ast }$
denote the free monoid on A, with identity element denoted
$A^{\ast }$
denote the free monoid on A, with identity element denoted
![]() $\varepsilon $
or
$\varepsilon $
or
![]() $1$
, depending on the context. Let
$1$
, depending on the context. Let
![]() $A^+$
denote the free semigroup on A, that is,
$A^+$
denote the free semigroup on A, that is,
![]() $A^+ = A^{\ast } - \{ \varepsilon \}$
. For
$A^+ = A^{\ast } - \{ \varepsilon \}$
. For
![]() $u, v \in A^{\ast }$
, by
$u, v \in A^{\ast }$
, by
![]() $u \equiv v$
, we mean that u and v are the same word. For
$u \equiv v$
, we mean that u and v are the same word. For
![]() $w \in A^{\ast }$
, we let
$w \in A^{\ast }$
, we let
![]() $|w|$
denote the length of w, that is, the number of letters in w. We have
$|w|$
denote the length of w, that is, the number of letters in w. We have
![]() $|\varepsilon | = 0$
. If
$|\varepsilon | = 0$
. If
![]() $w \equiv a_1 a_2 \cdots a_n$
for
$w \equiv a_1 a_2 \cdots a_n$
for
![]() $a_i \in A$
, then we let
$a_i \in A$
, then we let
![]() $w^{\text {rev}}$
denote the reverse of w, that is, the word
$w^{\text {rev}}$
denote the reverse of w, that is, the word
![]() $a_n a_{n-1} \cdots a_1$
. Note that
$a_n a_{n-1} \cdots a_1$
. Note that
![]() $^{\text {rev}} \colon A^{\ast } \to A^{\ast }$
is an anti-homomorphism, that is,
$^{\text {rev}} \colon A^{\ast } \to A^{\ast }$
is an anti-homomorphism, that is,
![]() $(uv)^{\text {rev}} \equiv v^{\text {rev}} u^{\text {rev}}$
for all
$(uv)^{\text {rev}} \equiv v^{\text {rev}} u^{\text {rev}}$
for all
![]() $u, v \in A^{\ast }$
. If
$u, v \in A^{\ast }$
. If
![]() $X \subseteq A^{\ast }$
, then we let
$X \subseteq A^{\ast }$
, then we let
![]() $X^{\text {rev}} = \{ x^{\text {rev}} \mid x \in X \}$
. If the words
$X^{\text {rev}} = \{ x^{\text {rev}} \mid x \in X \}$
. If the words
![]() $u, v \in A^{\ast }$
are equal in the monoid
$u, v \in A^{\ast }$
are equal in the monoid
![]() $M = \mathrm {Mon} \langle A \mid \mathscr {R} \rangle $
, then we denote this
$M = \mathrm {Mon} \langle A \mid \mathscr {R} \rangle $
, then we denote this
![]() $u =_M v$
. By
$u =_M v$
. By
![]() $M^{\text {rev}}$
, we mean the reversed monoid
$M^{\text {rev}}$
, we mean the reversed monoid
For
![]() $w_1, w_2 \in A^{\ast }$
,
$w_1, w_2 \in A^{\ast }$
,
![]() $w_1 =_M w_2$
if and only if
$w_1 =_M w_2$
if and only if
![]() $w_1^{\text {rev}} =_{M^{\text {rev}}} w_2^{\text {rev}}$
. That is, M and
$w_1^{\text {rev}} =_{M^{\text {rev}}} w_2^{\text {rev}}$
. That is, M and
![]() $M^{\text {rev}}$
are anti-isomorphic (if G is a group, then clearly
$M^{\text {rev}}$
are anti-isomorphic (if G is a group, then clearly
![]() $G \cong G^{\text {rev}}$
). Finally, when we say that a monoid M is generated by a set A, we mean that there exists a surjective homomorphism
$G \cong G^{\text {rev}}$
). Finally, when we say that a monoid M is generated by a set A, we mean that there exists a surjective homomorphism
![]() $\pi \colon A^{\ast } \to M$
. We use analogous terminology for semigroups and groups.
$\pi \colon A^{\ast } \to M$
. We use analogous terminology for semigroups and groups.
We give some notation for rewriting systems. For an in-depth treatment and further explanations of the terminology, see, for example, [Reference Book, Jantzen and Wrathall21, Reference Book and Otto22, Reference Jantzen73]. A rewriting system
![]() $\mathscr {R}$
on A is a subset of
$\mathscr {R}$
on A is a subset of
![]() $A^{\ast } \times A^{\ast }$
. We denote rewriting systems by script letters, for example,
$A^{\ast } \times A^{\ast }$
. We denote rewriting systems by script letters, for example,
![]() $\mathscr {R}, \mathscr {S}, \mathscr {T}$
. An element of
$\mathscr {R}, \mathscr {S}, \mathscr {T}$
. An element of
![]() $\mathscr {R}$
is called a rule. The system
$\mathscr {R}$
is called a rule. The system
![]() $\mathscr {R}$
induces several relations on
$\mathscr {R}$
induces several relations on
![]() $A^{\ast }$
. We write
$A^{\ast }$
. We write
if there exist
![]() $x, y \in A^{\ast }$
and a rule
$x, y \in A^{\ast }$
and a rule
![]() $(\ell , r) \in \mathscr {R}$
such that
$(\ell , r) \in \mathscr {R}$
such that
![]() $u \equiv x\ell y$
and
$u \equiv x\ell y$
and
![]() $v \equiv xry$
. We let
$v \equiv xry$
. We let
denote the reflexive and transitive closure of
. We denote by
the symmetric, reflexive and transitive closure of
. The relation
defines the least congruence on
![]() $A^{\ast }$
containing
$A^{\ast }$
containing
![]() $\mathscr {R}$
. For
$\mathscr {R}$
. For
![]() $X \subseteq A^{\ast }$
, we let
$X \subseteq A^{\ast }$
, we let
![]() $\nabla ^{\ast }_{\mathscr {R}}(X)$
denote the set of ancestors of X with respect to
$\nabla ^{\ast }_{\mathscr {R}}(X)$
denote the set of ancestors of X with respect to
![]() $\mathscr {R}$
, that is,
$\mathscr {R}$
, that is,
The monoid
![]() $\mathrm {Mon} \langle A \mid \mathscr {R} \rangle $
is identified with the quotient
$\mathrm {Mon} \langle A \mid \mathscr {R} \rangle $
is identified with the quotient
. For a rewriting system
![]() $\mathscr {T} \subseteq A^{\ast } \times A^{\ast }$
and a monoid
$\mathscr {T} \subseteq A^{\ast } \times A^{\ast }$
and a monoid
![]() $M = \mathrm {Mon} \langle A \mid \mathscr {R} \rangle $
, we say that
$M = \mathrm {Mon} \langle A \mid \mathscr {R} \rangle $
, we say that
![]() $\mathscr {T}$
is M-equivariant if for every rule
$\mathscr {T}$
is M-equivariant if for every rule
![]() $(u, v) \in \mathscr {T}$
, we have
$(u, v) \in \mathscr {T}$
, we have
![]() $u =_M v$
. That is,
$u =_M v$
. That is,
![]() $\mathscr {T}$
is M-equivariant if and only if every pair of words in the congruence
$\mathscr {T}$
is M-equivariant if and only if every pair of words in the congruence
also belongs to
, or, written symbolically,
.
Let
![]() $u, v \in A^{\ast }$
and let
$u, v \in A^{\ast }$
and let
![]() $n \geq 0$
. If there exist words
$n \geq 0$
. If there exist words
![]() $u_0, u_1, \ldots , u_n \in A^{\ast }$
such that
$u_0, u_1, \ldots , u_n \in A^{\ast }$
such that
then we denote this by
, that is, u rewrites to v in n steps. Thus,
.
A rewriting system
![]() $\mathscr {R} \subseteq A^{\ast } \times A^{\ast }$
is said to be monadic if
$\mathscr {R} \subseteq A^{\ast } \times A^{\ast }$
is said to be monadic if
![]() $(u, v) \in \mathscr {R}$
implies
$(u, v) \in \mathscr {R}$
implies
![]() $|u| \geq |v|$
and
$|u| \geq |v|$
and
![]() $v \in A \cup \{ \varepsilon \}$
. We say that
$v \in A \cup \{ \varepsilon \}$
. We say that
![]() $\mathscr {R}$
is special if
$\mathscr {R}$
is special if
![]() $(u, v) \in \mathscr {R}$
implies
$(u, v) \in \mathscr {R}$
implies
![]() $v \equiv \varepsilon $
. Every special system is monadic. Let
$v \equiv \varepsilon $
. Every special system is monadic. Let
![]() $\mathbf {C}$
be a class of languages. A monadic rewriting system
$\mathbf {C}$
be a class of languages. A monadic rewriting system
![]() $\mathscr {R}$
is said to be
$\mathscr {R}$
is said to be
![]() $\mathbf {C}$
if for every
$\mathbf {C}$
if for every
![]() $a \in A \cup \{ \varepsilon \}$
, the language
$a \in A \cup \{ \varepsilon \}$
, the language
![]() $\{ u \mid (u, a) \in \mathscr {R} \}$
is in
$\{ u \mid (u, a) \in \mathscr {R} \}$
is in
![]() $\mathbf {C}$
. Thus, we may speak of, for example,
$\mathbf {C}$
. Thus, we may speak of, for example,
![]() $\mathbf {C}$
-monadic rewriting systems or context-free monadic rewriting systems. Monadic rewriting systems are extensively treated in [Reference Book, Jantzen and Wrathall21].
$\mathbf {C}$
-monadic rewriting systems or context-free monadic rewriting systems. Monadic rewriting systems are extensively treated in [Reference Book, Jantzen and Wrathall21].
Definition 1.1. Let
![]() $\mathbf {C}$
be a class of languages. Let
$\mathbf {C}$
be a class of languages. Let
![]() $\mathscr {R} \subseteq A^{\ast } \times A^{\ast }$
be a rewriting system. Then we say that
$\mathscr {R} \subseteq A^{\ast } \times A^{\ast }$
be a rewriting system. Then we say that
![]() $\mathscr {R}$
is
$\mathscr {R}$
is
![]() $\mathbf {C}$
-ancestry preserving if for every
$\mathbf {C}$
-ancestry preserving if for every
![]() $L \subseteq A^{\ast }$
with
$L \subseteq A^{\ast }$
with
![]() $L \in \mathbf {C}$
, we have
$L \in \mathbf {C}$
, we have
![]() $\nabla ^{\ast }_{\mathscr {R}}(L) \in \mathbf {C}$
. If every
$\nabla ^{\ast }_{\mathscr {R}}(L) \in \mathbf {C}$
. If every
![]() $\mathbf {C}$
-monadic rewriting system is
$\mathbf {C}$
-monadic rewriting system is
![]() $\mathbf {C}$
-ancestry preserving, then we say that
$\mathbf {C}$
-ancestry preserving, then we say that
![]() $\mathbf {C}$
has the monadic ancestor property.
$\mathbf {C}$
has the monadic ancestor property.
The terminology monadic ancestor property was introduced by the author in [Reference Nyberg-Brodda91], and also appears in [Reference Nyberg-Brodda89, Reference Nyberg-Brodda90], but was treated implicitly already in [Reference Book, Jantzen and Wrathall21, Reference Jantzen73], see especially [Reference Jantzen73, Lemma 3.4]. The idea of defining classes of languages via ancestry in rewriting systems is not new, and can be traced back at least to, for example, McNaughton et al.’s Church–Rosser languages [Reference McNaughton, Narendran and Otto84] or Beaudry et al.’s McNaughton languages [Reference Beaudry, Holzer, Niemann and Otto17, Reference Beaudry, Holzer, Niemann and Otto18].
Example 1.2. If
![]() $\mathscr {R} \subseteq A^{\ast } \times A^{\ast }$
is a context-free monadic rewriting system, and
$\mathscr {R} \subseteq A^{\ast } \times A^{\ast }$
is a context-free monadic rewriting system, and
![]() $L \subseteq A^{\ast }$
is a context-free language, then
$L \subseteq A^{\ast }$
is a context-free language, then
![]() $\nabla ^{\ast }_{\mathscr {R}}(L)$
is a context-free language [Reference Book, Jantzen and Wrathall21, Theorem 2.2]. That is, every
$\nabla ^{\ast }_{\mathscr {R}}(L)$
is a context-free language [Reference Book, Jantzen and Wrathall21, Theorem 2.2]. That is, every
![]() $\mathbf {CF}$
-monadic rewriting system is
$\mathbf {CF}$
-monadic rewriting system is
![]() $\mathbf {CF}$
-ancestry preserving. Hence, the class of context-free languages has the monadic ancestor property.
$\mathbf {CF}$
-ancestry preserving. Hence, the class of context-free languages has the monadic ancestor property.
Having the monadic ancestor property is analogous to being closed under sequential recursion; see Section 1.8 for further elaboration on this. This gives rise to the notion of a super-
![]() $\operatorname {\mathrm {AFL}}$
.
$\operatorname {\mathrm {AFL}}$
.
Definition 1.3. Let
![]() $\mathbf {C}$
be a full
$\mathbf {C}$
be a full
![]() $\operatorname {\mathrm {AFL}}$
. Then
$\operatorname {\mathrm {AFL}}$
. Then
![]() $\mathbf {C}$
is said to be a super-
$\mathbf {C}$
is said to be a super-
![]() $\operatorname {\mathrm {AFL}}$
if it has the monadic ancestor property.
$\operatorname {\mathrm {AFL}}$
if it has the monadic ancestor property.
Hence, by Example 1.2,
![]() $\mathbf {CF}$
is a super-
$\mathbf {CF}$
is a super-
![]() $\operatorname {\mathrm {AFL}}$
. For the main body of the text, this is the only super-
$\operatorname {\mathrm {AFL}}$
. For the main body of the text, this is the only super-
![]() $\operatorname {\mathrm {AFL}}$
we deal with; see, however, Section 1.8 for a broader discussion, and Section 5 for generalisations of our results to all reversal-closed super-
$\operatorname {\mathrm {AFL}}$
we deal with; see, however, Section 1.8 for a broader discussion, and Section 5 for generalisations of our results to all reversal-closed super-
![]() $\operatorname {\mathrm {AFL}}$
s. The primary reason for dealing only with context-free languages comes from the importance of
$\operatorname {\mathrm {AFL}}$
s. The primary reason for dealing only with context-free languages comes from the importance of
![]() $\mathbf {CF}$
with regards to word-hyperbolicity.
$\mathbf {CF}$
with regards to word-hyperbolicity.
1.3 Word-hyperbolicity
Let S be a semigroup, finitely generated by some set A, with associated surjective homomorphism
![]() $\pi _S \colon A^+ \to S$
. Let
$\pi _S \colon A^+ \to S$
. Let
![]() $R \subseteq A^+$
be a regular language. If
$R \subseteq A^+$
be a regular language. If
![]() $\pi _S(R) = S$
, that is, every element of S is represented by some word from R, then we say that R is a regular combing of S. If
$\pi _S(R) = S$
, that is, every element of S is represented by some word from R, then we say that R is a regular combing of S. If
![]() $\pi _S$
is bijective when restricted to R, then we say that R is a regular combing with uniqueness. Let
$\pi _S$
is bijective when restricted to R, then we say that R is a regular combing with uniqueness. Let
![]() $\#_1, \#_2$
be two new symbols, and let
$\#_1, \#_2$
be two new symbols, and let
We say that
![]() $\mathcal {T}_R(S)$
is a multiplication table for S (with respect to R). If this table is context-free, that is, if
$\mathcal {T}_R(S)$
is a multiplication table for S (with respect to R). If this table is context-free, that is, if
![]() $\mathcal {T}_S(R) \in \mathbf {CF}$
, then we say that S is a word-hyperbolic semigroup (with respect to the combing R). If R is additionally a combing with uniqueness, then we say that
$\mathcal {T}_S(R) \in \mathbf {CF}$
, then we say that S is a word-hyperbolic semigroup (with respect to the combing R). If R is additionally a combing with uniqueness, then we say that
![]() $\mathcal {T}_S(R)$
is word-hyperbolic with uniqueness. Not every word-hyperbolic semigroup is word-hyperbolic with uniqueness [Reference Cain and Maltcev25].
$\mathcal {T}_S(R)$
is word-hyperbolic with uniqueness. Not every word-hyperbolic semigroup is word-hyperbolic with uniqueness [Reference Cain and Maltcev25].
The above notion of hyperbolicity was introduced by Duncan and Gilman [Reference Duncan and Gilman38]. One can show that if S is hyperbolic with respect to one choice of finite generating set, then it is hyperbolic with respect to every such choice [Reference Duncan and Gilman38, Theorem 3.4]. However, note that even if
![]() $\mathcal {T}_{S}(R_1) \in \mathbf {CF}$
for some regular combing
$\mathcal {T}_{S}(R_1) \in \mathbf {CF}$
for some regular combing
![]() $R_1$
, there may still be some regular combing
$R_1$
, there may still be some regular combing
![]() $R_2$
of S such that
$R_2$
of S such that
![]() $\mathcal {T}_S(R_2) \not \in \mathbf {CF}$
. For extensions of the condition
$\mathcal {T}_S(R_2) \not \in \mathbf {CF}$
. For extensions of the condition
![]() $\mathcal {T}_S(R) \in \mathbf {CF}$
to, for example,
$\mathcal {T}_S(R) \in \mathbf {CF}$
to, for example,
![]() $\mathcal {T}_S(R) \in \mathbf {ET0L}$
or
$\mathcal {T}_S(R) \in \mathbf {ET0L}$
or
![]() $\mathcal {T}_S(R) \in \mathbf {IND}$
, see Section 5.
$\mathcal {T}_S(R) \in \mathbf {IND}$
, see Section 5.
We extend this definition in the obvious way to monoids (and groups) by substituting
![]() $A^{\ast }$
for
$A^{\ast }$
for
![]() $A^+$
. Thus, a monoid M generated by A is word-hyperbolic ‘as a monoid’ if and only if there exists a regular combing
$A^+$
. Thus, a monoid M generated by A is word-hyperbolic ‘as a monoid’ if and only if there exists a regular combing
![]() $R \subseteq A^{\ast }$
such that
$R \subseteq A^{\ast }$
such that
![]() $\mathcal {T}_M(R) \in \mathbf {CF}$
. However, by [Reference Duncan and Gilman38, Theorem 3.5], a monoid is word-hyperbolic ‘as a monoid’ if and only if it is word-hyperbolic as a semigroup (in the above sense). We therefore speak of ‘word-hyperbolic monoids’ always referring to a regular combing
$\mathcal {T}_M(R) \in \mathbf {CF}$
. However, by [Reference Duncan and Gilman38, Theorem 3.5], a monoid is word-hyperbolic ‘as a monoid’ if and only if it is word-hyperbolic as a semigroup (in the above sense). We therefore speak of ‘word-hyperbolic monoids’ always referring to a regular combing
![]() $R \subseteq A^{\ast }$
. In fact, it is not difficult to see, by using a rational transduction, that if M is word-hyperbolic with respect to a combing
$R \subseteq A^{\ast }$
. In fact, it is not difficult to see, by using a rational transduction, that if M is word-hyperbolic with respect to a combing
![]() $R \subseteq A^+$
, then it is word-hyperbolic with respect to
$R \subseteq A^+$
, then it is word-hyperbolic with respect to
![]() $R \cup \{ \varepsilon \}$
(see, for example, the first paragraph in the proof of Lemma 1.5). We may thus assume without loss of generality that any regular combing for M includes the empty word (which necessarily represents the identity element). If M is word-hyperbolic with respect to the combing R, and the only word in R representing the identity element of M is the empty word, then we say that M is word-hyperbolic with
$R \cup \{ \varepsilon \}$
(see, for example, the first paragraph in the proof of Lemma 1.5). We may thus assume without loss of generality that any regular combing for M includes the empty word (which necessarily represents the identity element). If M is word-hyperbolic with respect to the combing R, and the only word in R representing the identity element of M is the empty word, then we say that M is word-hyperbolic with
![]() $1$
-uniqueness.
$1$
-uniqueness.
One can show that a group is word-hyperbolic if and only if it is hyperbolic in the usual sense, that is, the sense of Gromov [Reference Duncan and Gilman38, Theorem 4.3]. Furthermore, one can show that, due to the Muller–Schupp theorem, if G is a group generated by A, then
![]() $\mathcal {T}_{G}(A^{\ast })$
is context-free if and only if G is virtually free [Reference Gilman49, Theorem 2(2)], a condition which is significantly stronger than hyperbolicity. Indeed, more generally, it is not difficult to see that a semigroup S is word-hyperbolic with respect to the combing
$\mathcal {T}_{G}(A^{\ast })$
is context-free if and only if G is virtually free [Reference Gilman49, Theorem 2(2)], a condition which is significantly stronger than hyperbolicity. Indeed, more generally, it is not difficult to see that a semigroup S is word-hyperbolic with respect to the combing
![]() $A^+$
if and only if S has a context-free word problem (in the sense of Duncan and Gilman [Reference Duncan and Gilman38, Section 5]).
$A^+$
if and only if S has a context-free word problem (in the sense of Duncan and Gilman [Reference Duncan and Gilman38, Section 5]).
For brevity, for
![]() $i=1,2$
, we let
$i=1,2$
, we let
![]() $A_{\#_i} = A \cup \{ \#_i \}$
and let
$A_{\#_i} = A \cup \{ \#_i \}$
and let
![]() $A_{\#} = A \cup \{ \#_1, \#_2 \}$
.
$A_{\#} = A \cup \{ \#_1, \#_2 \}$
.
1.4 1-extendability
We now define a slightly technical condition, which proves useful in Section 2. Let S be a semigroup. We define
![]() to be the semigroup with an identity
to be the semigroup with an identity
![]() adjoined, regardless of whether S has an identity element already or not. (If S is a monoid, then defining
adjoined, regardless of whether S has an identity element already or not. (If S is a monoid, then defining
![]() in this manner (rather than simply taking
in this manner (rather than simply taking
![]() ) is only a technicality, but is used to avoid some other language-theoretic technicalities.)
) is only a technicality, but is used to avoid some other language-theoretic technicalities.)
Definition 1.4 (
 $1$
-extendable)
$1$
-extendable)
Let S be a word-hyperbolic semigroup with respect to a regular combing
![]() $R \subseteq A^+$
. We say that S is
$R \subseteq A^+$
. We say that S is
![]() $1$
-extendable if
$1$
-extendable if
![]() is word-hyperbolic with respect to the regular combing
is word-hyperbolic with respect to the regular combing
![]() $R \cup \{ \varepsilon \}$
.
$R \cup \{ \varepsilon \}$
.
Thus, if S is a
![]() $1$
-extendable word-hyperbolic semigroup, then
$1$
-extendable word-hyperbolic semigroup, then
![]() is word-hyperbolic. We do not know if the converse holds in general. Our main interest in
is word-hyperbolic. We do not know if the converse holds in general. Our main interest in
![]() $1$
-extendability is in the statement of Theorem A, in which we show that the free product of
$1$
-extendability is in the statement of Theorem A, in which we show that the free product of
![]() $1$
-extendable word-hyperbolic semigroups is again word-hyperbolic. We begin by showing that
$1$
-extendable word-hyperbolic semigroups is again word-hyperbolic. We begin by showing that
![]() $1$
-extendability is not particularly elusive.
$1$
-extendability is not particularly elusive.
Lemma 1.5 (Kambites)
Let S be a word-hyperbolic semigroup. If every element of S has a right stabiliser (that is, for every
![]() $s \in S$
, there exists some
$s \in S$
, there exists some
![]() $t \in S$
with
$t \in S$
with
![]() $st = s$
), then S is
$st = s$
), then S is
![]() $1$
-extendable.
$1$
-extendable.
Proof. Suppose S is generated by the finite set A, with
![]() $R \subseteq A^+$
a regular combing and
$R \subseteq A^+$
a regular combing and
![]() $\mathcal {T}_S(R)$
context-free. As noted by Duncan and Gilman [Reference Duncan and Gilman38, Question 1], to show that
$\mathcal {T}_S(R)$
context-free. As noted by Duncan and Gilman [Reference Duncan and Gilman38, Question 1], to show that
is word-hyperbolic, it suffices to show that the language
![]() $Q = \{ u \# v^{\text {rev}} \mid u, v \in R, u=_S v \}$
is context-free, as
$Q = \{ u \# v^{\text {rev}} \mid u, v \in R, u=_S v \}$
is context-free, as

that is, it is a union of
![]() $\mathcal {T}_S(R)$
and languages obtainable from Q by a rational transduction, and hence also context-free.
$\mathcal {T}_S(R)$
and languages obtainable from Q by a rational transduction, and hence also context-free.
For every
![]() $a \in A$
, let
$a \in A$
, let
![]() $a' \in R$
be a word such that
$a' \in R$
be a word such that
![]() $aa' =_S a$
, that is, a right stabiliser for a, which exists by assumption. Let
$aa' =_S a$
, that is, a right stabiliser for a, which exists by assumption. Let
![]() $A' = \{ a' \mid a \in A \}$
. Then for every
$A' = \{ a' \mid a \in A \}$
. Then for every
![]() $u \in R$
, say
$u \in R$
, say
![]() $u \equiv a_1 a_2 \cdots a_n$
, we have that
$u \equiv a_1 a_2 \cdots a_n$
, we have that
![]() $u a_n' =_S u$
. By partitioning R based on the final letters of words (which is well defined as
$u a_n' =_S u$
. By partitioning R based on the final letters of words (which is well defined as
![]() $\varepsilon \not \in R$
), we find that the language
$\varepsilon \not \in R$
), we find that the language
is a regular language, being a finite union of (pairwise disjoint) regular languages. Now,
 $$ \begin{align*} &\mathcal{T}_S(R) \cap (U \#_2 R^{\text{rev}})\\ &\quad= \{ u \#_1 v \#_2 w^{\text{rev}} \mid u, v, w \in R, uv =_S w, \text{there exists } a \in A \colon u \in A^{\ast} a, v \equiv a' \} \\ &\quad= \{ u \#_1 a' \#_2 w^{\text{rev}} \mid u, w \in R, \text{there exists } a \in A \colon u \in A^{\ast} a, u a' =_S w, u a' =_S u \} \\ &\quad= \{ u \#_1 a' \#_2 w^{\text{rev}} \mid u, w \in R, \text{there exists } a \in A \colon u \in A^{\ast} a, u =_S w \} =: L. \end{align*} $$
$$ \begin{align*} &\mathcal{T}_S(R) \cap (U \#_2 R^{\text{rev}})\\ &\quad= \{ u \#_1 v \#_2 w^{\text{rev}} \mid u, v, w \in R, uv =_S w, \text{there exists } a \in A \colon u \in A^{\ast} a, v \equiv a' \} \\ &\quad= \{ u \#_1 a' \#_2 w^{\text{rev}} \mid u, w \in R, \text{there exists } a \in A \colon u \in A^{\ast} a, u a' =_S w, u a' =_S u \} \\ &\quad= \{ u \#_1 a' \#_2 w^{\text{rev}} \mid u, w \in R, \text{there exists } a \in A \colon u \in A^{\ast} a, u =_S w \} =: L. \end{align*} $$
This latter language L is just given by
Now for every
![]() $a \in A$
, we have
$a \in A$
, we have
![]() $L_a = L \cap A^{\ast } \#_1 a' \#_2 A^{\ast }$
. Hence, as
$L_a = L \cap A^{\ast } \#_1 a' \#_2 A^{\ast }$
. Hence, as
![]() $\mathbf {CF}$
is closed under union and intersection with regular languages, we have that
$\mathbf {CF}$
is closed under union and intersection with regular languages, we have that
![]() $L \in \mathbf {CF}$
if and only if for all
$L \in \mathbf {CF}$
if and only if for all
![]() $a \in A$
,
$a \in A$
,
![]() $L_a \in \mathbf {CF}$
. As
$L_a \in \mathbf {CF}$
. As
![]() $\mathcal {T}_S(R) \in \mathbf {CF}$
, and
$\mathcal {T}_S(R) \in \mathbf {CF}$
, and
![]() $U \#_2 R^{\text {rev}}$
is regular, we have
$U \#_2 R^{\text {rev}}$
is regular, we have
![]() $L \in \mathbf {CF}$
, and thus also
$L \in \mathbf {CF}$
, and thus also
![]() $L_a \in \mathbf {CF}$
for all
$L_a \in \mathbf {CF}$
for all
![]() $a \in A$
.
$a \in A$
.
For every
![]() $a \in A$
, let
$a \in A$
, let
![]() $\varrho _a$
be the rational transduction of
$\varrho _a$
be the rational transduction of
![]() $L_a$
defined by deleting
$L_a$
defined by deleting
![]() $\#_1 a' \#_2$
in the input word and replacing it by
$\#_1 a' \#_2$
in the input word and replacing it by
![]() $\#$
in the output word, and fixing all other parts of the input word in
$\#$
in the output word, and fixing all other parts of the input word in
![]() $L_a$
. Then,
$L_a$
. Then,
As
![]() $\mathbf {CF}$
is closed under rational transduction, we have
$\mathbf {CF}$
is closed under rational transduction, we have
![]() $L_a' \in \mathbf {CF}$
for all
$L_a' \in \mathbf {CF}$
for all
![]() $a \in A$
. However, clearly
$a \in A$
. However, clearly
As
![]() $\mathbf {CF}$
is closed under finite unions, we have
$\mathbf {CF}$
is closed under finite unions, we have
![]() $Q \in \mathbf {CF}$
, as was to be shown.
$Q \in \mathbf {CF}$
, as was to be shown.
The author thanks Mark Kambites for suggesting Lemma 1.5 and its proof. We rephrase the above result to our current situation of
![]() $1$
-extendability, and note the following direct consequence.
$1$
-extendability, and note the following direct consequence.
Lemma 1.6. Let S be a word-hyperbolic semigroup. If S is either:
-
(1) a monoid;
-
(2) a (von Neumann) regular semigroup; or
-
(3) a word-hyperbolic semigroup with uniqueness,
then S is
![]() $1$
-extendable.
$1$
-extendable.
Proof. Parts (1) and (2) are direct corollaries of Lemma 1.5. Part (3) is immediate, and already noted by Duncan and Gilman [Reference Duncan and Gilman38, Question 1].
In particular, we find that hyperbolic groups are
![]() $1$
-extendable. On a philosophical note, we remark (for reasons not too dissimilar from those which are discussed in Section 4.3) that
$1$
-extendable. On a philosophical note, we remark (for reasons not too dissimilar from those which are discussed in Section 4.3) that
![]() $1$
-extendability strikes the author as a very natural condition for working with word-hyperbolic semigroups in the first place.
$1$
-extendability strikes the author as a very natural condition for working with word-hyperbolic semigroups in the first place.
1.5 Semigroup free products
Semigroup free products can be found described in, for example, [Reference Howie71, Ch. 8.2]. We give an overview of this theory here, with some additional terminology that simplifies later notation.
Let
![]() $S_1, S_2$
be semigroups defined by
$S_1, S_2$
be semigroups defined by
![]() $S_i = \mathrm {Sgp} \langle A_i \mid \mathscr {R}_i \rangle $
for
$S_i = \mathrm {Sgp} \langle A_i \mid \mathscr {R}_i \rangle $
for
![]() $i=1,2$
, assuming without loss of generality that
$i=1,2$
, assuming without loss of generality that
![]() $A_1 \cap A_2 = \varnothing $
. The semigroup free product
$A_1 \cap A_2 = \varnothing $
. The semigroup free product
![]() $S = S_1 \ast S_2$
is defined as
$S = S_1 \ast S_2$
is defined as
![]() $S = \mathrm {Sgp} \langle A_1 \cup A_2 \mid \mathscr {R}_1 \cup \mathscr {R}_2 \rangle $
. We identify S with the semigroup whose elements are all finite nonempty alternating sequences
$S = \mathrm {Sgp} \langle A_1 \cup A_2 \mid \mathscr {R}_1 \cup \mathscr {R}_2 \rangle $
. We identify S with the semigroup whose elements are all finite nonempty alternating sequences
![]() $(s_1, s_2, \ldots , s_n)$
of elements
$(s_1, s_2, \ldots , s_n)$
of elements
![]() $s_i \in S_1 \cup S_2$
, where alternating means that
$s_i \in S_1 \cup S_2$
, where alternating means that
![]() $s_i$
and
$s_i$
and
![]() $s_{i+1}$
come from different factors for
$s_{i+1}$
come from different factors for
![]() $1 \leq i < n$
. We write
$1 \leq i < n$
. We write
![]() $s_i \sim s_{j}$
if
$s_i \sim s_{j}$
if
![]() $s_i$
and
$s_i$
and
![]() $s_{j}$
come from the same factor, and
$s_{j}$
come from the same factor, and
![]() $s_i \not \sim s_j$
otherwise. We always have
$s_i \not \sim s_j$
otherwise. We always have
![]() $s_i \sim s_i$
and
$s_i \sim s_i$
and
![]() $s_i \not \sim s_{i+1}$
. Given any nonempty sequence
$s_i \not \sim s_{i+1}$
. Given any nonempty sequence
![]() $s = (s_1, s_2, \ldots , s_n)$
with
$s = (s_1, s_2, \ldots , s_n)$
with
![]() $s_i \in S_1 \cup S_2$
, we define the alternatisation
$s_i \in S_1 \cup S_2$
, we define the alternatisation
![]() $s'$
of s to simply be
$s'$
of s to simply be
![]() $s' = s$
if s is alternating; otherwise, if, say,
$s' = s$
if s is alternating; otherwise, if, say,
![]() $s_i \kern1.4pt{\sim}\kern1.4pt s_{i+1}$
, we define
$s_i \kern1.4pt{\sim}\kern1.4pt s_{i+1}$
, we define
![]() $s'$
as the alternatisation of
$s'$
as the alternatisation of
![]() ${(s_1, \ldots , s_i \cdot s_{i+1}, \ldots , s_n)}$
. Clearly, the alternatisation of s is a uniquely defined alternating sequence.
${(s_1, \ldots , s_i \cdot s_{i+1}, \ldots , s_n)}$
. Clearly, the alternatisation of s is a uniquely defined alternating sequence.
The product of two alternating sequences in S is given by the alternatisation of the concatenation of the sequences. That is, explicitly, multiplication in S is given by
 $$ \begin{align} (s_1, \ldots, s_n) \cdot (t_1, \ldots, t_m) = \begin{cases} (s_1, \ldots, s_n, t_1, \ldots, t_m) & \text{if } s_n \not\sim t_1,\\ (s_1,\ldots, s_n t_1, \ldots, t_m) & \text{otherwise.} \end{cases} \end{align} $$
$$ \begin{align} (s_1, \ldots, s_n) \cdot (t_1, \ldots, t_m) = \begin{cases} (s_1, \ldots, s_n, t_1, \ldots, t_m) & \text{if } s_n \not\sim t_1,\\ (s_1,\ldots, s_n t_1, \ldots, t_m) & \text{otherwise.} \end{cases} \end{align} $$
See, for example, [Reference Howie71, Eq. (8.2.1)]. Note that, in particular, the semigroup free product of two monoids is never a monoid. We now define monoid free products in a similar manner.
1.6 Monoid free products
Let
![]() $M_1, M_2$
be the monoids
$M_1, M_2$
be the monoids
![]() $M_i = \mathrm {Mon} \langle A_i \mid \mathscr {R}_i \rangle $
for
$M_i = \mathrm {Mon} \langle A_i \mid \mathscr {R}_i \rangle $
for
![]() $i=1,2$
, assuming without loss of generality that
$i=1,2$
, assuming without loss of generality that
![]() $A_1 \cap A_2 = \varnothing $
. The monoid free product
$A_1 \cap A_2 = \varnothing $
. The monoid free product
![]() $M = M_1 \ast M_2$
is defined as
$M = M_1 \ast M_2$
is defined as
![]() $M = \mathrm {Mon} \langle A_1 \cup A_2 \mid \mathscr {R}_1 \cup \mathscr {R}_2 \rangle $
. We identify M with the monoid whose elements are all finite reduced alternating sequences
$M = \mathrm {Mon} \langle A_1 \cup A_2 \mid \mathscr {R}_1 \cup \mathscr {R}_2 \rangle $
. We identify M with the monoid whose elements are all finite reduced alternating sequences
![]() $(m_1, m_2, \ldots , m_n)$
of elements
$(m_1, m_2, \ldots , m_n)$
of elements
![]() $m_i \in M_1 \cup M_2$
, where reduced means that
$m_i \in M_1 \cup M_2$
, where reduced means that
![]() $m_i \neq 1$
for all
$m_i \neq 1$
for all
![]() $1 \leq i \leq n$
. Given an alternating sequence
$1 \leq i \leq n$
. Given an alternating sequence
![]() $s = (s_1, s_2, \ldots , s_n)$
, we define the reduction
$s = (s_1, s_2, \ldots , s_n)$
, we define the reduction
![]() $s'$
of s to be s if s is already reduced; and, otherwise, define
$s'$
of s to be s if s is already reduced; and, otherwise, define
![]() $s'$
to be the reduction of the alternatisation of the subsequence
$s'$
to be the reduction of the alternatisation of the subsequence
![]() $(s_{i_1}, s_{i_2}, \ldots , s_{i_k})$
consisting of precisely those
$(s_{i_1}, s_{i_2}, \ldots , s_{i_k})$
consisting of precisely those
![]() $s_{i_j}$
that satisfy
$s_{i_j}$
that satisfy
![]() $s_{i_j} \neq 1$
. Clearly, the reduction
$s_{i_j} \neq 1$
. Clearly, the reduction
![]() $s'$
of s is a uniquely defined reduced alternating sequence.
$s'$
of s is a uniquely defined reduced alternating sequence.
The product of two reduced sequences in M is then defined as the reduction of the concatenation of the sequences. Hence, similar to Equation (1-1), we easily find an explicit expression for multiplication of elements in a monoid free product as
 $$ \begin{align} (s_1, \ldots, s_n) \cdot (t_1, \ldots, t_m) = \begin{cases} (s_1, \ldots, s_n, t_1, \ldots, t_m) & \text{if } s_n \not\sim t_1,\\ (s_1, \ldots, s_n t_1, \ldots, t_m) & \text{if } s_nt_1 \neq 1, \\ (s_1, \ldots, s_{n-1}) \cdot (t_2, \ldots, t_m) & \text{if } s_nt_1 = 1. \end{cases} \end{align} $$
$$ \begin{align} (s_1, \ldots, s_n) \cdot (t_1, \ldots, t_m) = \begin{cases} (s_1, \ldots, s_n, t_1, \ldots, t_m) & \text{if } s_n \not\sim t_1,\\ (s_1, \ldots, s_n t_1, \ldots, t_m) & \text{if } s_nt_1 \neq 1, \\ (s_1, \ldots, s_{n-1}) \cdot (t_2, \ldots, t_m) & \text{if } s_nt_1 = 1. \end{cases} \end{align} $$
See, for example, [Reference Howie71, page 266]. Unlike the case of the semigroup free product, the empty sequence is always an identity element for M, so the free product of two monoids is always (obviously) a monoid. We also remark on the recursive definition of multiplication in the third case of Equation (1-2). We may, of course, have that
![]() $s_{n-1} \cdot t_2 = 1$
, in which case we continue reducing. In particular, the monoid free product of two groups is a group, and hence the monoid free product of two groups coincides with the usual group free product of the same groups.
$s_{n-1} \cdot t_2 = 1$
, in which case we continue reducing. In particular, the monoid free product of two groups is a group, and hence the monoid free product of two groups coincides with the usual group free product of the same groups.
1.7 Alternating words and combings
We make the following definition of alternating words, which is useful in describing the language theory of free products. Let
![]() $R_1, R_2$
be regular languages over some alphabets
$R_1, R_2$
be regular languages over some alphabets
![]() $A_1, A_2$
, respectively, with
$A_1, A_2$
, respectively, with
![]() $A_1 \cap A_2 = \varnothing $
(and hence
$A_1 \cap A_2 = \varnothing $
(and hence
![]() $R_1 \cap R_2 = \varnothing $
or
$R_1 \cap R_2 = \varnothing $
or
![]() $R_1 \cap R_2 = \{ \varepsilon \}$
). Let
$R_1 \cap R_2 = \{ \varepsilon \}$
). Let
![]() $w \in (R_1 \cup R_2)^+$
be a nonempty word. Then we can factorise w – not necessarily uniquely! – as a product
$w \in (R_1 \cup R_2)^+$
be a nonempty word. Then we can factorise w – not necessarily uniquely! – as a product
![]() $w \equiv x_1 x_2 \cdots x_n$
, where for every
$w \equiv x_1 x_2 \cdots x_n$
, where for every
![]() $1 \leq i \leq n$
, we have
$1 \leq i \leq n$
, we have
![]() $x_i \in R_1 \cup R_2$
and
$x_i \in R_1 \cup R_2$
and
![]() $x_i \not \equiv \varepsilon $
. Any such factorisation
$x_i \not \equiv \varepsilon $
. Any such factorisation
![]() $x_1 x_2 \cdots x_n$
of w gives rise to a parametrisation
$x_1 x_2 \cdots x_n$
of w gives rise to a parametrisation
![]() $X \colon \mathbb {N} \to \{ 1, 2\}$
uniquely defined on
$X \colon \mathbb {N} \to \{ 1, 2\}$
uniquely defined on
![]() $\{ 1, \ldots , n \}$
(as
$\{ 1, \ldots , n \}$
(as
![]() $A_1 \cap A_2 = \varnothing $
) by
$A_1 \cap A_2 = \varnothing $
) by
![]() $X(i) = j$
when
$X(i) = j$
when
![]() $x_i \in X_j$
. If
$x_i \in X_j$
. If
![]() $X(i) = X(i+1)$
for some i, then we write this as
$X(i) = X(i+1)$
for some i, then we write this as
![]() $x_i \sim x_{i+1}$
(context will always make this slightly abusive notation clear). If X is such that
$x_i \sim x_{i+1}$
(context will always make this slightly abusive notation clear). If X is such that
![]() $x_i \not \sim x_{i+1}$
, that is,
$x_i \not \sim x_{i+1}$
, that is,
![]() $X(i) \neq X(i+1)$
, for all
$X(i) \neq X(i+1)$
, for all
![]() $1 \leq i < n$
, which is to say that X is a standard parametrisation when restricted to
$1 \leq i < n$
, which is to say that X is a standard parametrisation when restricted to
![]() $\{ 1, \ldots , n\}$
, then we say that the factorisation
$\{ 1, \ldots , n\}$
, then we say that the factorisation
![]() $x_1 x_2 \cdots x_n$
of w is alternating. In this case, we may without loss of generality assume X is a standard parametrisation.
$x_1 x_2 \cdots x_n$
of w is alternating. In this case, we may without loss of generality assume X is a standard parametrisation.
If w admits an alternating factorisation, then we say that w is an
![]() $(R_1, R_2)$
-alternating word (or simply alternating word, if context makes the regular languages
$(R_1, R_2)$
-alternating word (or simply alternating word, if context makes the regular languages
![]() $R_1, R_2$
clear). It is clear that w admits at most one alternating factorisation, and hence, if w is an alternating word, then we may speak of the alternating factorisation of w, with associated standard parametrisation X. We for convenience always also say that the empty word is alternating, with the ‘unique’ alternating factorisation
$R_1, R_2$
clear). It is clear that w admits at most one alternating factorisation, and hence, if w is an alternating word, then we may speak of the alternating factorisation of w, with associated standard parametrisation X. We for convenience always also say that the empty word is alternating, with the ‘unique’ alternating factorisation
![]() $\varepsilon $
(if
$\varepsilon $
(if
![]() $\varepsilon \in R_1 \cap R_2$
, then we simply for convenience choose
$\varepsilon \in R_1 \cap R_2$
, then we simply for convenience choose
![]() $\varepsilon \in R_1$
). Note that not every factorisation as a word over
$\varepsilon \in R_1$
). Note that not every factorisation as a word over
![]() $(R_1 \cup R_2)^+$
of an alternating word is alternating: for example, if
$(R_1 \cup R_2)^+$
of an alternating word is alternating: for example, if
![]() $R_1 = \{ x, xx\}$
and
$R_1 = \{ x, xx\}$
and
![]() $R_2 = \{ y \}$
, then the word
$R_2 = \{ y \}$
, then the word
![]() $xxy$
can be factorised as either
$xxy$
can be factorised as either
![]() $x \cdot x \cdot y$
or
$x \cdot x \cdot y$
or
![]() $xx \cdot y$
as a word over
$xx \cdot y$
as a word over
![]() $(R_1 \cup R_2)^+$
; only the latter of the two factorisations is alternating.
$(R_1 \cup R_2)^+$
; only the latter of the two factorisations is alternating.
The language of all
![]() $(R_1, R_2)$
-alternating words is regular, being the language
$(R_1, R_2)$
-alternating words is regular, being the language
We denote the language in Equation (1-3) as
![]() $\operatorname {\mathrm {Alt}}(R_1, R_2)$
. We denote by
$\operatorname {\mathrm {Alt}}(R_1, R_2)$
. We denote by
![]() $\operatorname {\mathrm {Alt}}^+(R_1, R_2)$
the language
$\operatorname {\mathrm {Alt}}^+(R_1, R_2)$
the language
![]() $\operatorname {\mathrm {Alt}}(R_1, R_2) - \{ \varepsilon \}$
of nonempty alternating words.
$\operatorname {\mathrm {Alt}}(R_1, R_2) - \{ \varepsilon \}$
of nonempty alternating words.
Lemma 1.7. Let
![]() $S_1, S_2$
be two semigroups, finitely generated by disjoint sets
$S_1, S_2$
be two semigroups, finitely generated by disjoint sets
![]() $A_1$
, respectively
$A_1$
, respectively
![]() $A_2$
, and with regular combings
$A_2$
, and with regular combings
![]() $R_1$
, respectively
$R_1$
, respectively
![]() $R_2$
. Then the language
$R_2$
. Then the language
![]() $\operatorname {\mathrm {Alt}}^+(R_1, R_2)$
is a regular combing of the semigroup free product
$\operatorname {\mathrm {Alt}}^+(R_1, R_2)$
is a regular combing of the semigroup free product
![]() $S = S_1 \ast S_2$
.
$S = S_1 \ast S_2$
.
Proof. Let
![]() $(s_1, s_2, \ldots , s_k) \in S$
be an alternating sequence, with associated parametrisation X, that is, so that
$(s_1, s_2, \ldots , s_k) \in S$
be an alternating sequence, with associated parametrisation X, that is, so that
![]() $s_i \in S_{X(i)}$
for all
$s_i \in S_{X(i)}$
for all
![]() $1 \leq i \leq k$
. For every
$1 \leq i \leq k$
. For every
![]() $1 \leq i \leq k$
, there is some
$1 \leq i \leq k$
, there is some
![]() $r_i \in R_{X(i)}$
such that
$r_i \in R_{X(i)}$
such that
![]() $\pi _{X(i)}(r_i) = s_i$
, as
$\pi _{X(i)}(r_i) = s_i$
, as
![]() $R_{X(i)}$
is a combing of
$R_{X(i)}$
is a combing of
![]() $S_{X(i)}$
. Hence,
$S_{X(i)}$
. Hence,
![]() $\pi (r_1 r_2 \cdots r_k) = (s_1, s_2, \ldots , s_k)$
, and as
$\pi (r_1 r_2 \cdots r_k) = (s_1, s_2, \ldots , s_k)$
, and as
![]() $r_1 r_2 \cdots r_k \in \operatorname {\mathrm {Alt}}^+(R_1, R_2)$
, we have the result.
$r_1 r_2 \cdots r_k \in \operatorname {\mathrm {Alt}}^+(R_1, R_2)$
, we have the result.
Now the following follows immediately from Lemma 1.7 and standard normal form lemmas for semigroup free products.
Lemma 1.8. Let
![]() $S_1$
and
$S_1$
and
![]() $S_2$
be as in Lemma 1.7. Let
$S_2$
be as in Lemma 1.7. Let
![]() $S= S_1 \ast S_2$
denote their semigroup free product, and let
$S= S_1 \ast S_2$
denote their semigroup free product, and let
![]() $u, v \in \operatorname {\mathrm {Alt}}^+(R_1, R_2)$
be such that
$u, v \in \operatorname {\mathrm {Alt}}^+(R_1, R_2)$
be such that
are the unique alternating factorisations of u and v, respectively, and with associated standard parametrisations X, respectively Y. Then,
![]() $u =_S v$
if and only if
$u =_S v$
if and only if
-
(1)
 $n = k$
and
$n = k$
and
 $X=Y$
;
$X=Y$
; -
(2)
 $u_i =_{S_{X(i)}} v_i$
for all
$u_i =_{S_{X(i)}} v_i$
for all
 $1 \leq i \leq n$
.
$1 \leq i \leq n$
.
Finally, we give an explicit expression for how multiplication works in semigroup free products with respect to the combing
![]() $\operatorname {\mathrm {Alt}}^+(R_1, R_2)$
. For brevity, we let
$\operatorname {\mathrm {Alt}}^+(R_1, R_2)$
. For brevity, we let
![]() $R = \operatorname {\mathrm {Alt}}^+(R_1, R_2)$
and
$R = \operatorname {\mathrm {Alt}}^+(R_1, R_2)$
and
![]() $S = S_1 \ast S_2$
.
$S = S_1 \ast S_2$
.
Lemma 1.9. Let
![]() $x \equiv x_1 x_2 \cdots x_n \in R$
be an alternating product such that
$x \equiv x_1 x_2 \cdots x_n \in R$
be an alternating product such that
![]() $x_i \in R_{X(i)}$
for some standard parametrisation X. Let
$x_i \in R_{X(i)}$
for some standard parametrisation X. Let
![]() $w_1, w_2 \in R$
be such that
$w_1, w_2 \in R$
be such that
![]() $w_1 \cdot w_2 = x$
in S. Then one of the following holds.
$w_1 \cdot w_2 = x$
in S. Then one of the following holds.
-
(1) For some
 $0 \leq k \leq n$
, we have
$0 \leq k \leq n$
, we have  $$ \begin{align*} w_1 \equiv \overline{x}_1 \overline{x}_2 \cdots \overline{x}_k, \quad \text{and} \quad w_2 \equiv \overline{x}_{k+1} \overline{x}_{k+2} \cdots \overline{x}_n, \end{align*} $$
$$ \begin{align*} w_1 \equiv \overline{x}_1 \overline{x}_2 \cdots \overline{x}_k, \quad \text{and} \quad w_2 \equiv \overline{x}_{k+1} \overline{x}_{k+2} \cdots \overline{x}_n, \end{align*} $$
where
 $\overline {x}_j \in R_{X(\,j)}$
and
$\overline {x}_j \in R_{X(\,j)}$
and
 $\overline {x}_j = x_j$
in
$\overline {x}_j = x_j$
in
 $S_{X(\,j)}$
for all
$S_{X(\,j)}$
for all
 $0 \leq j \leq n$
.
$0 \leq j \leq n$
. -
(2) For some
 $0 \leq k \leq n$
, we have
$0 \leq k \leq n$
, we have  $$ \begin{align*} w_1 \equiv \overline{x}_1 \overline{x}_2 \cdots \overline{x}_{k-1} x_k' \quad \text{and} \quad w_2 \equiv x_k'' \overline{x}_{k+1} \cdots \overline{x}_n, \end{align*} $$
$$ \begin{align*} w_1 \equiv \overline{x}_1 \overline{x}_2 \cdots \overline{x}_{k-1} x_k' \quad \text{and} \quad w_2 \equiv x_k'' \overline{x}_{k+1} \cdots \overline{x}_n, \end{align*} $$
where
 $x_k', x_k'' \in R_{X(k)}$
with
$x_k', x_k'' \in R_{X(k)}$
with
 $x_k = x_k' x_k''$
in
$x_k = x_k' x_k''$
in
 $S_{X(k)}$
, and
$S_{X(k)}$
, and
 $\overline {x}_j \in R_{X(\,j)}$
with
$\overline {x}_j \in R_{X(\,j)}$
with
 $\overline {x}_j = x_j$
in
$\overline {x}_j = x_j$
in
 $S_{X(\,j)}$
for all
$S_{X(\,j)}$
for all
 $0 \leq j < k$
and
$0 \leq j < k$
and
 $k < j \leq n$
.
$k < j \leq n$
.
Proof. This follows directly from Lemma 1.8 and the multiplication in Equation (1-1) in semigroup free products; case (1) corresponds to the first case of Equation (1-1), and case (2) corresponds to the second.
We give a similar treatment regarding combings and monoid free products. Let
![]() $M_1$
and
$M_1$
and
![]() $M_2$
be two monoids, generated by two finite disjoint sets
$M_2$
be two monoids, generated by two finite disjoint sets
![]() $A_1$
, respectively
$A_1$
, respectively
![]() $A_2$
. Let
$A_2$
. Let
![]() $M = M_1 \ast M_2$
denote their monoid free product, and let S denote their semigroup free product. (To emphasise just how different M and S are, we note that S is always (!) an infinite semigroup, even if
$M = M_1 \ast M_2$
denote their monoid free product, and let S denote their semigroup free product. (To emphasise just how different M and S are, we note that S is always (!) an infinite semigroup, even if
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are trivial monoids, whereas in this latter case, M would simply be trivial.) We let
$M_2$
are trivial monoids, whereas in this latter case, M would simply be trivial.) We let
![]() $A = A_1 \cup A_2$
. Let
$A = A_1 \cup A_2$
. Let
![]() $R_1, R_2$
be regular languages with
$R_1, R_2$
be regular languages with
![]() $R_1 \subseteq A_1^{\ast }$
and
$R_1 \subseteq A_1^{\ast }$
and
![]() $R_2 \subseteq A_2^{\ast }$
, and with
$R_2 \subseteq A_2^{\ast }$
, and with
![]() $R_1 \cap R_2 = \{ \varepsilon \}$
. We say that a nonempty word
$R_1 \cap R_2 = \{ \varepsilon \}$
. We say that a nonempty word
![]() $u \in \operatorname {\mathrm {Alt}}(R_1, R_2)$
, with alternating factorisation
$u \in \operatorname {\mathrm {Alt}}(R_1, R_2)$
, with alternating factorisation
![]() $u \equiv u_0 u_1 \cdots u_n$
and associated parametrisation X, is reduced if
$u \equiv u_0 u_1 \cdots u_n$
and associated parametrisation X, is reduced if
![]() $u_i \neq 1$
in
$u_i \neq 1$
in
![]() $M_{X(i)}$
for all
$M_{X(i)}$
for all
![]() $0 \leq i \leq n$
. The empty word is also declared to be reduced. Just as in the case of semigroup free products (Lemma 1.7), it is easy to see that if
$0 \leq i \leq n$
. The empty word is also declared to be reduced. Just as in the case of semigroup free products (Lemma 1.7), it is easy to see that if
![]() $R_1, R_2$
are regular combings of
$R_1, R_2$
are regular combings of
![]() $M_1$
, respectively
$M_1$
, respectively
![]() $M_2$
, then
$M_2$
, then
![]() $\operatorname {\mathrm {Alt}}(R_1, R_2)$
is a regular combing of M. We write, as before,
$\operatorname {\mathrm {Alt}}(R_1, R_2)$
is a regular combing of M. We write, as before,
![]() $R = \operatorname {\mathrm {Alt}}(R_1, R_2)$
. We have the following simple structural lemma, based on the identification of M with the semigroup free product of
$R = \operatorname {\mathrm {Alt}}(R_1, R_2)$
. We have the following simple structural lemma, based on the identification of M with the semigroup free product of
![]() $M_1$
by
$M_1$
by
![]() $M_2$
amalgamated over the trivial submonoid (see, for example, [Reference Howie71, page 266]).
$M_2$
amalgamated over the trivial submonoid (see, for example, [Reference Howie71, page 266]).
Lemma 1.10. Let
![]() $u, v \in R \setminus \{ \varepsilon \}$
be reduced words. Then
$u, v \in R \setminus \{ \varepsilon \}$
be reduced words. Then
![]() $u =_M v$
if and only if
$u =_M v$
if and only if
![]() $u =_S v$
.
$u =_S v$
.
Of course, this lemma would fail spectacularly if the reduced condition is removed. Despite this connection between M and S, there is one important distinction to make from the semigroup free product case: when multiplying the alternating word
![]() $u_0 u_1 \cdots u_k$
by the alternating word
$u_0 u_1 \cdots u_k$
by the alternating word
![]() $v_0 v_1 \cdots v_n$
in a monoid free product, if we are in the case
$v_0 v_1 \cdots v_n$
in a monoid free product, if we are in the case
![]() $u_k \sim v_0$
, we may, of course, have
$u_k \sim v_0$
, we may, of course, have
![]() $u_k v_0 =_{M_i} 1$
for
$u_k v_0 =_{M_i} 1$
for
![]() $i=1$
or
$i=1$
or
![]() $2$
. Unlike the case of semigroup free products, this now means that
$2$
. Unlike the case of semigroup free products, this now means that
![]() $u_k v_0 =_M 1$
. Hence, the multiplication table for M with respect to the regular combing R is mostly made up of the multiplication table for S, but with one additional case. We spell the above out in somewhat more technical language.
$u_k v_0 =_M 1$
. Hence, the multiplication table for M with respect to the regular combing R is mostly made up of the multiplication table for S, but with one additional case. We spell the above out in somewhat more technical language.
Lemma 1.11. Let
![]() $x \equiv x_1 x_2 \cdots x_n \in R$
be reduced, with
$x \equiv x_1 x_2 \cdots x_n \in R$
be reduced, with
![]() $x_i \in R_{X(i)}$
for some standard parametrisation X. Let
$x_i \in R_{X(i)}$
for some standard parametrisation X. Let
![]() $w_1, w_2 \in R$
be reduced with
$w_1, w_2 \in R$
be reduced with
![]() $w_1 \cdot w_2 = x$
in M. Then one of the following holds.
$w_1 \cdot w_2 = x$
in M. Then one of the following holds.
-
(1) For some
 $0 \leq k \leq n$
, we have where
$0 \leq k \leq n$
, we have where $$ \begin{align*} w_1 \equiv \overline{x}_1 \overline{x}_2 \cdots \overline{x}_k \quad \text{and} \quad w_2 \equiv \overline{x}_{k+1} \overline{x}_{k+2} \cdots \overline{x}_n, \end{align*} $$
$$ \begin{align*} w_1 \equiv \overline{x}_1 \overline{x}_2 \cdots \overline{x}_k \quad \text{and} \quad w_2 \equiv \overline{x}_{k+1} \overline{x}_{k+2} \cdots \overline{x}_n, \end{align*} $$
 $\overline {x}_j \in R_{X(\,j)}$
and
$\overline {x}_j \in R_{X(\,j)}$
and
 $\overline {x}_j = x_j$
in
$\overline {x}_j = x_j$
in
 $M_{X(\,j)}$
for all
$M_{X(\,j)}$
for all
 $0 \leq j \leq n$
.
$0 \leq j \leq n$
.
-
(2) For some
 $0 \leq k \leq n$
, we have where
$0 \leq k \leq n$
, we have where $$ \begin{align*} w_1 \equiv \overline{x}_1 \overline{x}_2 \cdots \overline{x}_{k-1} x_k' \quad \text{and} \quad w_2 \equiv x_k'' \overline{x}_{k+1} \cdots \overline{x}_n, \end{align*} $$
$$ \begin{align*} w_1 \equiv \overline{x}_1 \overline{x}_2 \cdots \overline{x}_{k-1} x_k' \quad \text{and} \quad w_2 \equiv x_k'' \overline{x}_{k+1} \cdots \overline{x}_n, \end{align*} $$
 $x_k', x_k'' \in R_{X(k)}$
with
$x_k', x_k'' \in R_{X(k)}$
with
 $1 \neq x_k = x_k' x_k''$
in
$1 \neq x_k = x_k' x_k''$
in
 $M_{X(k)}$
, and
$M_{X(k)}$
, and
 $\overline {x}_j \in R_{X(\,j)}$
with
$\overline {x}_j \in R_{X(\,j)}$
with
 $\overline {x}_j = x_j$
in
$\overline {x}_j = x_j$
in
 $M_{X(\,j)}$
for all
$M_{X(\,j)}$
for all
 $0 \leq j < k$
and
$0 \leq j < k$
and
 $k < j \leq n$
.
$k < j \leq n$
.
-
(3) For some
 $k \geq 0$
and
$k \geq 0$
and
 $m \geq n$
, we have where
$m \geq n$
, we have where $$ \begin{align*} w_1 \equiv \overline{x}_1 \overline{x}_2 \cdots \overline{x}_{k-1} x_k' \quad \text{and} \quad w_2 \equiv x_k'' \overline{x}_{k+1} \cdots \overline{x}_m, \end{align*} $$
$$ \begin{align*} w_1 \equiv \overline{x}_1 \overline{x}_2 \cdots \overline{x}_{k-1} x_k' \quad \text{and} \quad w_2 \equiv x_k'' \overline{x}_{k+1} \cdots \overline{x}_m, \end{align*} $$
 $x_k', x_k'' \in R_{X(k)}$
with
$x_k', x_k'' \in R_{X(k)}$
with
 $x_k' x_k'' = 1$
in
$x_k' x_k'' = 1$
in
 $M_{X(k)}$
. Furthermore, setting we have
$M_{X(k)}$
. Furthermore, setting we have $$ \begin{align*} w_1' \equiv \overline{x}_1 \overline{x}_2 \cdots \overline{x}_{k-1} \quad \text{and} \quad w_2' \equiv \overline{x}_{k+1} \overline{x}_{k+2} \cdots \overline{x}_m, \end{align*} $$
$$ \begin{align*} w_1' \equiv \overline{x}_1 \overline{x}_2 \cdots \overline{x}_{k-1} \quad \text{and} \quad w_2' \equiv \overline{x}_{k+1} \overline{x}_{k+2} \cdots \overline{x}_m, \end{align*} $$
 $w_1', w_2' \in R$
and
$w_1', w_2' \in R$
and
 $w_1' \cdot w_2' = x$
in M.
$w_1' \cdot w_2' = x$
in M.
Cases (1) and (2) are ‘inherited’ from S by combining Lemmas 1.9 and 1.10 in the case that the concatenation
![]() $w_1 w_2$
is reduced, while case (3) corresponds to case (3) in Lemma 1.10. This case (3) highlights the recursive nature of reduction in free products (see, for example, free reduction), and this recursion eventually terminates as
$w_1 w_2$
is reduced, while case (3) corresponds to case (3) in Lemma 1.10. This case (3) highlights the recursive nature of reduction in free products (see, for example, free reduction), and this recursion eventually terminates as
![]() $|w_j'|<|w_j|$
for
$|w_j'|<|w_j|$
for
![]() $j=1, 2$
. We give an example of an application of Lemma 1.11 below, in the case of the free product of two copies of the bicyclic monoid.
$j=1, 2$
. We give an example of an application of Lemma 1.11 below, in the case of the free product of two copies of the bicyclic monoid.
Example 1.12. Let
![]() $M_i = \mathrm {Mon} \langle b_i, c_i \mid b_ic_i = 1 \rangle $
for
$M_i = \mathrm {Mon} \langle b_i, c_i \mid b_ic_i = 1 \rangle $
for
![]() $i=1,2$
be two copies of the bicyclic monoid, and let
$i=1,2$
be two copies of the bicyclic monoid, and let
![]() $R_i = c_i^{\ast } b_i^{\ast }$
. Let
$R_i = c_i^{\ast } b_i^{\ast }$
. Let
![]() $x \equiv b_2^2$
, and let
$x \equiv b_2^2$
, and let
![]() $w_1 \equiv b_2 b_1$
,
$w_1 \equiv b_2 b_1$
,
![]() $w_2 \equiv c_1 b_2$
. Then,
$w_2 \equiv c_1 b_2$
. Then,
in M, so we can apply Lemma 1.11. Indeed, we find that we are in case (3), taking
![]() $k=2$
and
$k=2$
and
![]() $m=3$
,
$m=3$
,
![]() $\overline {x}_1 \equiv b_2, x_2' \equiv b_1$
and
$\overline {x}_1 \equiv b_2, x_2' \equiv b_1$
and
![]() $x_2'' \equiv c_1, \overline {x}_3 \equiv b_2$
, for then,
$x_2'' \equiv c_1, \overline {x}_3 \equiv b_2$
, for then,
in
![]() $M_1$
, and we have
$M_1$
, and we have
![]() $w_1' \equiv \overline {x}_1 \equiv b_2$
and
$w_1' \equiv \overline {x}_1 \equiv b_2$
and
![]() $w_2' \equiv \overline {x}_3 \equiv b_2$
, and this satisfies
$w_2' \equiv \overline {x}_3 \equiv b_2$
, and this satisfies
![]() $w_1' \cdot w_2' \equiv b_2^2 =_M~x$
. We may reapply Lemma 1.11, and find ourselves in case (1), taking
$w_1' \cdot w_2' \equiv b_2^2 =_M~x$
. We may reapply Lemma 1.11, and find ourselves in case (1), taking
![]() $\overline {x}_1 \equiv b_2$
and
$\overline {x}_1 \equiv b_2$
and
![]() $\overline {x}_n \equiv b_2$
.
$\overline {x}_n \equiv b_2$
.
These are all the statements we require about free products in the sequel.
1.8
 $\mathbf {ET0L}$
and substitutions
$\mathbf {ET0L}$
and substitutions
Word-hyperbolicity is connected with
![]() $\mathbf {CF}$
- multiplication tables. However, our results are true more generally, substituting, for example,
$\mathbf {CF}$
- multiplication tables. However, our results are true more generally, substituting, for example,
![]() $\mathbf {ET0L}$
or
$\mathbf {ET0L}$
or
![]() $\mathbf {IND}$
for
$\mathbf {IND}$
for
![]() $\mathbf {CF}$
, and we elaborate on this topic in Section 5. Specifically, the proofs of the main results about preservation properties in free products of word-hyperbolic algebraic structures (semigroups, monoids, or groups) in Sections 2 and 4 are all applicable to free products of algebraic structures with
$\mathbf {CF}$
, and we elaborate on this topic in Section 5. Specifically, the proofs of the main results about preservation properties in free products of word-hyperbolic algebraic structures (semigroups, monoids, or groups) in Sections 2 and 4 are all applicable to free products of algebraic structures with
![]() $\mathbf {C}$
-multiplication tables, where
$\mathbf {C}$
-multiplication tables, where
![]() $\mathbf {C}$
is some full
$\mathbf {C}$
is some full
![]() $\operatorname {\mathrm {AFL}}$
satisfying the monadic ancestor property. This includes the cases when
$\operatorname {\mathrm {AFL}}$
satisfying the monadic ancestor property. This includes the cases when
![]() $\mathbf {C}$
is one of
$\mathbf {C}$
is one of
![]() $\mathbf {CF}, \mathbf {IND}$
or
$\mathbf {CF}, \mathbf {IND}$
or
![]() $\mathbf {ET0L}$
. We give a brief overview of the strong historical connections between
$\mathbf {ET0L}$
. We give a brief overview of the strong historical connections between
![]() $\mathbf {ET0L}$
and the monadic ancestor property. This is a complex history; we cannot do it full justice here, and it will be expanded on in a future survey article.
$\mathbf {ET0L}$
and the monadic ancestor property. This is a complex history; we cannot do it full justice here, and it will be expanded on in a future survey article.
We give the definition of a substitution. Let A be an alphabet. For each
![]() $a \in A$
, let
$a \in A$
, let
![]() $\sigma (a)$
be a language (over any finite alphabet); let
$\sigma (a)$
be a language (over any finite alphabet); let
![]() $\sigma (\varepsilon ) = \{ \varepsilon \}$
; for every
$\sigma (\varepsilon ) = \{ \varepsilon \}$
; for every
![]() $x, y \in A^{\ast }$
, let
$x, y \in A^{\ast }$
, let
![]() $\sigma (xy) = \sigma (x)\sigma (y)$
; and for every
$\sigma (xy) = \sigma (x)\sigma (y)$
; and for every
![]() $L \subseteq A^{\ast }$
, let
$L \subseteq A^{\ast }$
, let
![]() $\sigma (L) = \bigcup _{w\in L} \sigma (w)$
. We then say that
$\sigma (L) = \bigcup _{w\in L} \sigma (w)$
. We then say that
![]() $\sigma $
is a substitution. For a class
$\sigma $
is a substitution. For a class
![]() $\mathbf {C}$
of languages, if for every
$\mathbf {C}$
of languages, if for every
![]() $a \in A$
we have
$a \in A$
we have
![]() $\sigma (a) \in \mathbf {C}$
, then we say that
$\sigma (a) \in \mathbf {C}$
, then we say that
![]() $\sigma $
is a
$\sigma $
is a
![]() $\mathbf {C}$
-substitution. Let A be an alphabet, and
$\mathbf {C}$
-substitution. Let A be an alphabet, and
![]() $\sigma $
a substitution on A. For every
$\sigma $
a substitution on A. For every
![]() $a \in A$
, let
$a \in A$
, let
![]() $A_a$
denote the smallest finite alphabet such that
$A_a$
denote the smallest finite alphabet such that
![]() $\sigma (a) \subseteq A_a^{\ast }$
. Extend
$\sigma (a) \subseteq A_a^{\ast }$
. Extend
![]() $\sigma $
to
$\sigma $
to
![]() $A \cup (\bigcup _{a \in A}A_a)$
by defining
$A \cup (\bigcup _{a \in A}A_a)$
by defining
![]() $\sigma (b) = \{ b \}$
whenever
$\sigma (b) = \{ b \}$
whenever
![]() $b \in (\bigcup _{a \in A} A_a) \setminus A$
. For
$b \in (\bigcup _{a \in A} A_a) \setminus A$
. For
![]() $L \subseteq A^{\ast }$
, let
$L \subseteq A^{\ast }$
, let
![]() $\sigma ^1(L) = \sigma (L)$
, and let
$\sigma ^1(L) = \sigma (L)$
, and let
![]() $\sigma ^{n+1}(L) = \sigma (\sigma ^n(L))$
for
$\sigma ^{n+1}(L) = \sigma (\sigma ^n(L))$
for
![]() $n \geq 1$
. Let
$n \geq 1$
. Let
![]() $\sigma ^{\infty }(L) = \bigcup _{n> 0} \sigma ^n(L)$
. Then we say that
$\sigma ^{\infty }(L) = \bigcup _{n> 0} \sigma ^n(L)$
. Then we say that
![]() $\sigma ^{\infty }$
is an iterated substitution. If for every
$\sigma ^{\infty }$
is an iterated substitution. If for every
![]() $b \in A \cup (\bigcup _a A_a)$
we have
$b \in A \cup (\bigcup _a A_a)$
we have
![]() $b \in \sigma (b)$
, then we say that
$b \in \sigma (b)$
, then we say that
![]() $\sigma ^{\infty }$
is a nested iterated substitution. Note that every nested iterated substitution is, of course, an example of an iterated substitution. If
$\sigma ^{\infty }$
is a nested iterated substitution. Note that every nested iterated substitution is, of course, an example of an iterated substitution. If
![]() $\sigma ^{\infty }$
is nested, then it is convenient for inductive purposes to set
$\sigma ^{\infty }$
is nested, then it is convenient for inductive purposes to set
![]() $\sigma ^0(L) := L$
. Note that the nested property ensures
$\sigma ^0(L) := L$
. Note that the nested property ensures
![]() $L \subseteq \sigma (L)$
, so
$L \subseteq \sigma (L)$
, so
![]() $\bigcup _{n \geq 0} \sigma ^n(L) = \bigcup _{n>0} \sigma ^n(L)$
. We say that
$\bigcup _{n \geq 0} \sigma ^n(L) = \bigcup _{n>0} \sigma ^n(L)$
. We say that
![]() $\mathbf {C}$
is closed under nested iterated substitution if for every
$\mathbf {C}$
is closed under nested iterated substitution if for every
![]() $\mathbf {C}$
-substitution
$\mathbf {C}$
-substitution
![]() $\sigma $
and every
$\sigma $
and every
![]() $L \in \mathbf {C}$
, we have: if
$L \in \mathbf {C}$
, we have: if
![]() $\sigma ^{\infty }$
is a nested iterated substitution, then
$\sigma ^{\infty }$
is a nested iterated substitution, then
![]() $\sigma ^{\infty }(L) \in \mathbf {C}$
. A similar definition yields closure under iterated substitutions. For the benefit of the reader, we mention two facts that can be useful to keep in mind, expanded on below: the class
$\sigma ^{\infty }(L) \in \mathbf {C}$
. A similar definition yields closure under iterated substitutions. For the benefit of the reader, we mention two facts that can be useful to keep in mind, expanded on below: the class
![]() $\mathbf {CF}$
is closed under nested iterated substitution (but not iterated substitution), and the class
$\mathbf {CF}$
is closed under nested iterated substitution (but not iterated substitution), and the class
![]() $\mathbf {ET0L}$
is closed under iterated substitution (and hence also nested iterated substitution).
$\mathbf {ET0L}$
is closed under iterated substitution (and hence also nested iterated substitution).
Substitutions are closely related to
![]() $\operatorname {\mathrm {AFL}}$
s. Indeed, the 1967 article by Greibach and Ginsburg which first defined
$\operatorname {\mathrm {AFL}}$
s. Indeed, the 1967 article by Greibach and Ginsburg which first defined
![]() $\operatorname {\mathrm {AFL}}$
s [Reference Ginsburg and Greibach50] (later expanded in [Reference Ginsburg and Greibach51]) included a proof about a form of substitution-closure for
$\operatorname {\mathrm {AFL}}$
s [Reference Ginsburg and Greibach50] (later expanded in [Reference Ginsburg and Greibach51]) included a proof about a form of substitution-closure for
![]() $\operatorname {\mathrm {AFL}}$
s (under
$\operatorname {\mathrm {AFL}}$
s (under
![]() $\varepsilon $
-free regular substitutions) and for full
$\varepsilon $
-free regular substitutions) and for full
![]() $\operatorname {\mathrm {AFL}}$
s (under regular substitutions). The closure of
$\operatorname {\mathrm {AFL}}$
s (under regular substitutions). The closure of
![]() $\mathbf {CF}$
under nested iterated substitution was proved by Král [Reference Král75] in 1970. Following some further results (for example, [Reference Ginsburg and Greibach52]), an abstract basis for substitution was developed by Ginsburg and Spanier [Reference Ginsburg and Spanier53]; one particular important notion developed there was treating the (nested) substitution-closure of a full
$\mathbf {CF}$
under nested iterated substitution was proved by Král [Reference Král75] in 1970. Following some further results (for example, [Reference Ginsburg and Greibach52]), an abstract basis for substitution was developed by Ginsburg and Spanier [Reference Ginsburg and Spanier53]; one particular important notion developed there was treating the (nested) substitution-closure of a full
![]() $\operatorname {\mathrm {AFL}}$
as a form of ‘algebraic closure’. In particular, it is proved that the substitution-closure of a full
$\operatorname {\mathrm {AFL}}$
as a form of ‘algebraic closure’. In particular, it is proved that the substitution-closure of a full
![]() $\operatorname {\mathrm {AFL}}$
is a full
$\operatorname {\mathrm {AFL}}$
is a full
![]() $\operatorname {\mathrm {AFL}}$
[Reference Ginsburg and Spanier53, Theorem 2.1]. Lewis [Reference Lewis, Fischer, Fabian, Ullman and Karp79] used substitution to define full
$\operatorname {\mathrm {AFL}}$
[Reference Ginsburg and Spanier53, Theorem 2.1]. Lewis [Reference Lewis, Fischer, Fabian, Ullman and Karp79] used substitution to define full
![]() $\operatorname {\mathrm {AFL}}$
s, and rediscover the aforementioned result by Ginsburg and Spanier, see [Reference Lewis, Fischer, Fabian, Ullman and Karp79, Theorem 1.13]. See also [Reference Asveld12, Reference Beauquier19].
$\operatorname {\mathrm {AFL}}$
s, and rediscover the aforementioned result by Ginsburg and Spanier, see [Reference Lewis, Fischer, Fabian, Ullman and Karp79, Theorem 1.13]. See also [Reference Asveld12, Reference Beauquier19].
Substitutions can be useful in studying full
![]() $\operatorname {\mathrm {AFL}}$
s for a number of reasons; for example, one can recover results of Ginsburg and Greibach [Reference Ginsburg and Greibach52] about principal
$\operatorname {\mathrm {AFL}}$
s for a number of reasons; for example, one can recover results of Ginsburg and Greibach [Reference Ginsburg and Greibach52] about principal
![]() $\operatorname {\mathrm {AFL}}$
s, see [Reference Lewis, Fischer, Fabian, Ullman and Karp79, Corollary 1.21]. One can also use substitution-based ideas to produce (see [Reference Christensen28, Corollary 4.13]) an infinite strict hierarchy
$\operatorname {\mathrm {AFL}}$
s, see [Reference Lewis, Fischer, Fabian, Ullman and Karp79, Corollary 1.21]. One can also use substitution-based ideas to produce (see [Reference Christensen28, Corollary 4.13]) an infinite strict hierarchy
of full
![]() $\operatorname {\mathrm {AFL}}$
-s
$\operatorname {\mathrm {AFL}}$
-s
![]() $\mathbf {C}_i$
between the classes
$\mathbf {C}_i$
between the classes
![]() $\mathbf {CF}$
and
$\mathbf {CF}$
and
![]() $\mathbf {ET0L}$
, see also [Reference Greibach60, Reference Latteux78] for related such hierarchies; for similar hierarchies between
$\mathbf {ET0L}$
, see also [Reference Greibach60, Reference Latteux78] for related such hierarchies; for similar hierarchies between
![]() $\mathbf {ET0L} \subset \mathbf {IND}$
, see [Reference Ehrenfeucht, Rozenberg and Skyum40, Reference Engelfriet43]; and for infinite hierarchies between
$\mathbf {ET0L} \subset \mathbf {IND}$
, see [Reference Ehrenfeucht, Rozenberg and Skyum40, Reference Engelfriet43]; and for infinite hierarchies between
![]() $\mathbf {IND} \subset \mathbf {CS}$
, see [Reference Asveld and van Leeuwen16, Reference Engelfriet42].
$\mathbf {IND} \subset \mathbf {CS}$
, see [Reference Asveld and van Leeuwen16, Reference Engelfriet42].
Because of the importance and utility of iterated substitution, Greibach [Reference Greibach59] (later expanded in [Reference Greibach61]) defined super-
![]() $\operatorname {\mathrm {AFL}}$
s as a full
$\operatorname {\mathrm {AFL}}$
s as a full
![]() $\operatorname {\mathrm {AFL}}$
closed under nested iterated substitution (by [Reference Nyberg-Brodda90, Proposition 2.2], this is equivalent to the definition of super-
$\operatorname {\mathrm {AFL}}$
closed under nested iterated substitution (by [Reference Nyberg-Brodda90, Proposition 2.2], this is equivalent to the definition of super-
![]() $\operatorname {\mathrm {AFL}}$
as defined in Section 1.2). Not long after, the notion of a hyper-
$\operatorname {\mathrm {AFL}}$
as defined in Section 1.2). Not long after, the notion of a hyper-
![]() $\operatorname {\mathrm {AFL}}$
was introduced, being any full
$\operatorname {\mathrm {AFL}}$
was introduced, being any full
![]() $\operatorname {\mathrm {AFL}}$
closed under iterated substitution [Reference Asveld11, Reference Salomaa99]. (Asveld [Reference Asveld14, page 1] on this point says the following: ‘Similar as in ordinary algebra – where one went from groups to semigroups, rings, and fields – full
$\operatorname {\mathrm {AFL}}$
closed under iterated substitution [Reference Asveld11, Reference Salomaa99]. (Asveld [Reference Asveld14, page 1] on this point says the following: ‘Similar as in ordinary algebra – where one went from groups to semigroups, rings, and fields – full
![]() $\operatorname {\mathrm {AFL}}$
s gave rise to weaker structures (full trios, full semi
$\operatorname {\mathrm {AFL}}$
s gave rise to weaker structures (full trios, full semi
![]() $\operatorname {\mathrm {AFL}}$
s) and more powerful ones: full substitution-closed
$\operatorname {\mathrm {AFL}}$
s) and more powerful ones: full substitution-closed
![]() $\operatorname {\mathrm {AFL}}$
s, full super-
$\operatorname {\mathrm {AFL}}$
s, full super-
![]() $\operatorname {\mathrm {AFL}}$
s, and full hyper-
$\operatorname {\mathrm {AFL}}$
s, and full hyper-
![]() $\operatorname {\mathrm {AFL}}$
s’. We cannot agree with this assessment of the historical development of ‘ordinary’ algebra. Finite fields and groups were intricately connected already in the early works of both Lagrange and Galois (see [Reference Neumann88]), whereas rings and semigroups would not appear as objects of study until half a century, respectively, a century later. Similarly, Klein initially posed an axiomatisation of group as what we today call a monoid, but as Lie ‘in his study of infinite groups saw it as necessary to expressly require [the existence of inverses]’, it was this axiomatisation that was chosen (‘
$\operatorname {\mathrm {AFL}}$
s’. We cannot agree with this assessment of the historical development of ‘ordinary’ algebra. Finite fields and groups were intricately connected already in the early works of both Lagrange and Galois (see [Reference Neumann88]), whereas rings and semigroups would not appear as objects of study until half a century, respectively, a century later. Similarly, Klein initially posed an axiomatisation of group as what we today call a monoid, but as Lie ‘in his study of infinite groups saw it as necessary to expressly require [the existence of inverses]’, it was this axiomatisation that was chosen (‘
![]() $\ldots $
sah sich Lie genötigt, ausdrücklich zu verlangen
$\ldots $
sah sich Lie genötigt, ausdrücklich zu verlangen
![]() $\ldots $
’, [Reference Klein74, page 335]). We strongly recommend the interested reader to consult Wußing [Reference Wussing103]. The above paragraph shows the difficulty in simplifying the development of ordinary algebra in a linear manner; and one may feel similarly about the linear narrative regarding
$\ldots $
’, [Reference Klein74, page 335]). We strongly recommend the interested reader to consult Wußing [Reference Wussing103]. The above paragraph shows the difficulty in simplifying the development of ordinary algebra in a linear manner; and one may feel similarly about the linear narrative regarding
![]() $\operatorname {\mathrm {AFL}}$
s.) Many fundamental results about hyper-
$\operatorname {\mathrm {AFL}}$
s.) Many fundamental results about hyper-
![]() $\operatorname {\mathrm {AFL}}$
s and substitution were developed by Christensen [Reference Christensen28], who also, along with Asveld [Reference Asveld11], fleshed out the connections between
$\operatorname {\mathrm {AFL}}$
s and substitution were developed by Christensen [Reference Christensen28], who also, along with Asveld [Reference Asveld11], fleshed out the connections between
![]() $\mathbf {ET0L}$
and hyper-
$\mathbf {ET0L}$
and hyper-
![]() $\operatorname {\mathrm {AFL}}$
s noted by for example Salomaa [Reference Salomaa98, Reference Salomaa99] and Čulík [Reference Čulik and Opatrny33]; see also [Reference Drewes and Engelfriet37, Reference Engelfriet41]. In particular, at this point, we arrive at the following rather pleasant result.
$\operatorname {\mathrm {AFL}}$
s noted by for example Salomaa [Reference Salomaa98, Reference Salomaa99] and Čulík [Reference Čulik and Opatrny33]; see also [Reference Drewes and Engelfriet37, Reference Engelfriet41]. In particular, at this point, we arrive at the following rather pleasant result.
Theorem 1.13
-
(1) [Reference Greibach61, Theorem 2.2] The class
 $\mathbf {CF}$
is the least super-
$\mathbf {CF}$
is the least super-
 $\operatorname {\mathrm {AFL}}$
.
$\operatorname {\mathrm {AFL}}$
. -
(2) [Reference Christensen28, Corollary 4.10] The class
 $\mathbf {ET0L}$
is the least hyper-
$\mathbf {ET0L}$
is the least hyper-
 $\operatorname {\mathrm {AFL}}$
.
$\operatorname {\mathrm {AFL}}$
.
Furthermore, one can also show that
![]() $\mathbf {IND}$
is a super-
$\mathbf {IND}$
is a super-
![]() $\operatorname {\mathrm {AFL}}$
[Reference Downey36].
$\operatorname {\mathrm {AFL}}$
[Reference Downey36].
As mentioned, the connections between substitutions and
![]() $\mathbf {ET0L}$
remain active research topics (if somewhat implicitly), but are far too numerous to recount here. While they will be given a proper treatment in the future, we mention a few. For example, one can give a complexity analysis of iterated substitutions, with applications to both
$\mathbf {ET0L}$
remain active research topics (if somewhat implicitly), but are far too numerous to recount here. While they will be given a proper treatment in the future, we mention a few. For example, one can give a complexity analysis of iterated substitutions, with applications to both
![]() $\mathbf {ET0L}$
and
$\mathbf {ET0L}$
and
![]() $\mathbf {EDT0L}$
languages [Reference Asveld13], and there are connections with fuzzy logic [Reference Asveld15]. One can also extend the notion of substitution to ‘deterministic substitution’ (which is not defined here), leading to a statement analogous to the fact that
$\mathbf {EDT0L}$
languages [Reference Asveld13], and there are connections with fuzzy logic [Reference Asveld15]. One can also extend the notion of substitution to ‘deterministic substitution’ (which is not defined here), leading to a statement analogous to the fact that
![]() $\mathbf {EDT0L}$
is the least dhyper-
$\mathbf {EDT0L}$
is the least dhyper-
![]() $\operatorname {\mathrm {AFL}}$
[Reference Asveld12, Corollary 4.5]; see also [Reference Latteux77] for more on
$\operatorname {\mathrm {AFL}}$
[Reference Asveld12, Corollary 4.5]; see also [Reference Latteux77] for more on
![]() $\mathbf {EDT0L}$
and substitutions. At this point, it bears mentioning that there is a great deal of involved and often obfuscating notation and abbreviations; as an example, we have that ‘if K is a pseudoid, then
$\mathbf {EDT0L}$
and substitutions. At this point, it bears mentioning that there is a great deal of involved and often obfuscating notation and abbreviations; as an example, we have that ‘if K is a pseudoid, then
![]() $\eta (K)$
is the smallest full dhyper-
$\eta (K)$
is the smallest full dhyper-
![]() $\operatorname {QAFL}$
containing K’ [Reference Asveld12, Theorem 4.5]. In addition, there are a great number of abbreviations for classes of languages associated with Lindenmayer systems (yielding the
$\operatorname {QAFL}$
containing K’ [Reference Asveld12, Theorem 4.5]. In addition, there are a great number of abbreviations for classes of languages associated with Lindenmayer systems (yielding the
![]() $\mathbf {L}$
); aside from
$\mathbf {L}$
); aside from
![]() $\mathbf {ET0L}$
and
$\mathbf {ET0L}$
and
![]() $\mathbf {EDT0L}$
, we have, for example,
$\mathbf {EDT0L}$
, we have, for example,
see for example [Reference Meduna and Švec85] for a large number of these. (Given the number of abbreviations, one may reasonably inquire about the language-theoretic properties of the language of all abbreviations of classes of languages.) We ensure the reader not familiar with this multitude of notation that most, if not all, such classes are generally defined (or definable) by relatively straightforward means; see, for example, the definition of
![]() $\mathbf {ET0L}$
as given by Theorem 1.13(2). Furthermore, the reader may notice, in the subsequent sections, the importance of substitution in dealing with free products – this link between the algebraic and the formal language theoretic runs deep, and there seems to be ample opportunity to develop it further.
$\mathbf {ET0L}$
as given by Theorem 1.13(2). Furthermore, the reader may notice, in the subsequent sections, the importance of substitution in dealing with free products – this link between the algebraic and the formal language theoretic runs deep, and there seems to be ample opportunity to develop it further.
2 Free products of word-hyperbolic semigroups
In this section, we prove the main result regarding semigroup free products and word-hyperbolicity (Theorem A).
Let
![]() $S_1, S_2$
be two semigroups, finitely generated by disjoint sets
$S_1, S_2$
be two semigroups, finitely generated by disjoint sets
![]() $A_1$
, respectively
$A_1$
, respectively
![]() $A_2$
, and with regular combings
$A_2$
, and with regular combings
![]() $R_1$
, respectively
$R_1$
, respectively
![]() $R_2$
. Let
$R_2$
. Let
![]() $S = S_1 \ast S_2$
denote the semigroup free product of
$S = S_1 \ast S_2$
denote the semigroup free product of
![]() $S_1$
and
$S_1$
and
![]() $S_2$
. We begin by recalling (Lemma 1.7) that the language
$S_2$
. We begin by recalling (Lemma 1.7) that the language
![]() $\operatorname {\mathrm {Alt}}^+(R_1, R_2)$
of alternating words is a combing for S. Let
$\operatorname {\mathrm {Alt}}^+(R_1, R_2)$
of alternating words is a combing for S. Let
![]() $R = \operatorname {\mathrm {Alt}}^+(R_1, R_2)$
. This is, in the following, our chosen combing for proving that the table
$R = \operatorname {\mathrm {Alt}}^+(R_1, R_2)$
. This is, in the following, our chosen combing for proving that the table
![]() $\mathcal {T}_S(R)$
is context-free when the factors
$\mathcal {T}_S(R)$
is context-free when the factors
![]() $S_1, S_2$
are word-hyperbolic.
$S_1, S_2$
are word-hyperbolic.
Theorem A. Let
![]() $S_1, S_2$
be
$S_1, S_2$
be
![]() $1$
-extendable word-hyperbolic semigroups. Then the free product
$1$
-extendable word-hyperbolic semigroups. Then the free product
![]() $S_1 \ast S_2$
is word-hyperbolic.
$S_1 \ast S_2$
is word-hyperbolic.
Proof. Suppose, for
![]() $i=1, 2$
, that
$i=1, 2$
, that
![]() $S_i$
is generated by the finite set
$S_i$
is generated by the finite set
![]() $A_i$
, and that
$A_i$
, and that
![]() $S_i$
is word-hyperbolic with respect to the regular combing
$S_i$
is word-hyperbolic with respect to the regular combing
![]() $R_i \subseteq A_i^+$
, with the multiplication table
$R_i \subseteq A_i^+$
, with the multiplication table
![]() $\mathcal {T}(R_i)$
context-free. We assume without loss of generality that
$\mathcal {T}(R_i)$
context-free. We assume without loss of generality that
![]() $A_1 \cap A_2 = \varnothing $
, and hence that
$A_1 \cap A_2 = \varnothing $
, and hence that
![]() $R_1 \cap R_2 = \varnothing $
. As
$R_1 \cap R_2 = \varnothing $
. As
![]() $S_i$
is
$S_i$
is
![]() $1$
-extendable, the semigroup
$1$
-extendable, the semigroup
![]() is word-hyperbolic with respect to the regular combing
is word-hyperbolic with respect to the regular combing
![]() $\overline {R_i} = R_i \cup \{ \varepsilon \}$
, where now
$\overline {R_i} = R_i \cup \{ \varepsilon \}$
, where now
![]() $\varepsilon $
is the unique word mapping to the identity element
$\varepsilon $
is the unique word mapping to the identity element
![]() of
of
![]() . Let
. Let
![]() $A = A_1 \cup A_2$
.
$A = A_1 \cup A_2$
.
For
![]() $i=1, 2$
, define the monadic rewriting system
$i=1, 2$
, define the monadic rewriting system
![]() $\mathscr {R}_i$
by
$\mathscr {R}_i$
by
Then, by assumption,
![]() $\mathscr {R}_i$
is a context-free monadic rewriting system. Note that for every
$\mathscr {R}_i$
is a context-free monadic rewriting system. Note that for every
![]() $x, x' \in R_i$
with
$x, x' \in R_i$
with
![]() $x =_{S_i} x'$
, we have that
$x =_{S_i} x'$
, we have that
![]() $x' \#_1 \#_2 x^{\text {rev}} \in \mathcal {T}(\overline {R_i})$
, as
$x' \#_1 \#_2 x^{\text {rev}} \in \mathcal {T}(\overline {R_i})$
, as
![]() , and thus also
, and thus also
![]() $(x' \#_1 \#_2 x^{\text {rev}}, \#_2) \in \mathscr {R}_i$
. Let
$(x' \#_1 \#_2 x^{\text {rev}}, \#_2) \in \mathscr {R}_i$
. Let
![]() $\mathscr {R}$
be the rewriting system
$\mathscr {R}$
be the rewriting system
![]() $\mathscr {R}_1 \cup \mathscr {R}_2$
. This is also a context-free monadic rewriting system. Recall that
$\mathscr {R}_1 \cup \mathscr {R}_2$
. This is also a context-free monadic rewriting system. Recall that
![]() $A_{\#} = A \cup \{ \#_1, \#_2 \}$
.
$A_{\#} = A \cup \{ \#_1, \#_2 \}$
.
Lemma 2.1. Let
![]() $w \in A^{\ast }_{\#}$
. Then
$w \in A^{\ast }_{\#}$
. Then
![]() $w \in \nabla ^{\ast }_{\mathscr {R}}(\#_1 \#_2)$
if and only if it is of the form
$w \in \nabla ^{\ast }_{\mathscr {R}}(\#_1 \#_2)$
if and only if it is of the form
 $$ \begin{align} w \equiv \#_1 \bigg( \prod_{i=1}^n x_i \#_1 y_i \bigg) \,\#_2\, \bigg(\prod_{i=1}^n z_i \bigg)^{\mathrm{rev}} \end{align} $$
$$ \begin{align} w \equiv \#_1 \bigg( \prod_{i=1}^n x_i \#_1 y_i \bigg) \,\#_2\, \bigg(\prod_{i=1}^n z_i \bigg)^{\mathrm{rev}} \end{align} $$
for some
![]() $n \geq 0$
, and where for every
$n \geq 0$
, and where for every
![]() $1 \leq i \leq n$
, we have
$1 \leq i \leq n$
, we have
![]() $x_i, y_i, z_i \in \overline {R}_{X(i)}$
with
$x_i, y_i, z_i \in \overline {R}_{X(i)}$
with
![]() $x_i y_i = z_i$
in
$x_i y_i = z_i$
in
![]() , where X is some parametrisation.
, where X is some parametrisation.
Proof. For ease of notation, we write
![]() for
for
![]() , and analogously for
, and analogously for
![]() , and so on.
, and so on.
![]() $(\!\!\impliedby \!\!)$
Suppose w is of the form of Equation (2-1). We prove the claim by induction on n. The case
$(\!\!\impliedby \!\!)$
Suppose w is of the form of Equation (2-1). We prove the claim by induction on n. The case
![]() $n=0$
is immediate. Suppose
$n=0$
is immediate. Suppose
![]() $n> 0$
. Then w contains exactly one occurrence of
$n> 0$
. Then w contains exactly one occurrence of
![]() $\#_2$
; to the left of this occurrence is an occurrence of the word
$\#_2$
; to the left of this occurrence is an occurrence of the word
![]() $x_n \#_1 y_n$
, and to the right is an occurrence of the word
$x_n \#_1 y_n$
, and to the right is an occurrence of the word
![]() $z_n^{\text {rev}}$
. As
$z_n^{\text {rev}}$
. As
![]() $x_n, y_n, z_n \in \overline {R}_{X(n)}$
and
$x_n, y_n, z_n \in \overline {R}_{X(n)}$
and
![]() $x_n y_n = z_n$
in
$x_n y_n = z_n$
in
, we have
![]() $(x_n \#_1 y_n \#_2 z_n^{\text {rev}}, \#_2) \in \mathscr {R}_{X(n)} \subseteq \mathscr {R}$
. Hence,
$(x_n \#_1 y_n \#_2 z_n^{\text {rev}}, \#_2) \in \mathscr {R}_{X(n)} \subseteq \mathscr {R}$
. Hence,

and the right-hand side now lies in
![]() $\nabla ^{\ast }_{\mathscr {R}}(\#_1 \#_2)$
by the inductive hypothesis.
$\nabla ^{\ast }_{\mathscr {R}}(\#_1 \#_2)$
by the inductive hypothesis.
![]() $(\!\!\implies \!\!)$
Suppose
$(\!\!\implies \!\!)$
Suppose
![]() , say
, say
![]() for some
for some
![]() $k \geq 0$
. The proof is by induction on k. The base case
$k \geq 0$
. The proof is by induction on k. The base case
![]() $k=0$
is trivial, for then
$k=0$
is trivial, for then
![]() $w \equiv \#_1 \#_2$
. Suppose
$w \equiv \#_1 \#_2$
. Suppose
![]() $k>0$
. Then there is some
$k>0$
. Then there is some
![]() $w' \in A^{\ast }_{\#}$
such that
$w' \in A^{\ast }_{\#}$
such that
![]() , and such that the rewriting is via some rule
, and such that the rewriting is via some rule
![]() $r \equiv (x\#_1 y \#_2 z^{\text {rev}}, \#_2) \in \mathscr {R}$
. Then, as
$r \equiv (x\#_1 y \#_2 z^{\text {rev}}, \#_2) \in \mathscr {R}$
. Then, as
![]() $r \in \mathscr {R}$
, we have
$r \in \mathscr {R}$
, we have
![]() $x, y, z \in \overline {R}_1 \cup \overline {R}_2$
and
$x, y, z \in \overline {R}_1 \cup \overline {R}_2$
and
![]() $x \cdot y = z$
in
$x \cdot y = z$
in
![]() for
for
![]() $j=1$
or
$j=1$
or
![]() $j=2$
. Now, by the inductive hypothesis,
$j=2$
. Now, by the inductive hypothesis,
 $$ \begin{align*} w' \equiv \#_1 \bigg( \prod_{i=1}^m x_i \#_1 y_i \bigg) \,\#_2\, \bigg( \prod_{i=1}^m z_i\bigg)^{\text{rev}}, \end{align*} $$
$$ \begin{align*} w' \equiv \#_1 \bigg( \prod_{i=1}^m x_i \#_1 y_i \bigg) \,\#_2\, \bigg( \prod_{i=1}^m z_i\bigg)^{\text{rev}}, \end{align*} $$
with some parametrisation
![]() $X'$
such that for every
$X'$
such that for every
![]() $1 \leq i \leq m$
, we have
$1 \leq i \leq m$
, we have
![]() $x_i' y_i' =_{} z^{\prime }_i$
in
$x_i' y_i' =_{} z^{\prime }_i$
in
![]() . As the right-hand side of r contains only one occurrence of
. As the right-hand side of r contains only one occurrence of
![]() $\#_2$
, and as
$\#_2$
, and as
![]() $w'$
contains only one occurrence of
$w'$
contains only one occurrence of
![]() $\#_2$
, it follows that
$\#_2$
, it follows that
 $$ \begin{align} w \equiv \#_1 \bigg( \prod_{i=1}^m x_i \#_1 y_i \bigg) (x \#_1 y \#_2 z^{\text{rev}}) \bigg( \prod_{i=1}^m z_i\bigg)^{\text{rev}}, \end{align} $$
$$ \begin{align} w \equiv \#_1 \bigg( \prod_{i=1}^m x_i \#_1 y_i \bigg) (x \#_1 y \#_2 z^{\text{rev}}) \bigg( \prod_{i=1}^m z_i\bigg)^{\text{rev}}, \end{align} $$
and hence, taking
![]() $n = m+1$
and defining the parametrisation
$n = m+1$
and defining the parametrisation
![]() $X(i) = X'(i)$
for
$X(i) = X'(i)$
for
![]() $i \neq n$
, and
$i \neq n$
, and
![]() $X(n) = j$
, the expression in Equation (2-2) is an expression of the form in Equation (2-1) for w.
$X(n) = j$
, the expression in Equation (2-2) is an expression of the form in Equation (2-1) for w.
We now show that a particular rational transduction of the language of all words of the form of Equation (2-1) equals
![]() $\mathcal {T}_S(R)$
. This yields the result. Let
$\mathcal {T}_S(R)$
. This yields the result. Let
![]() $\tau _0 \subseteq A_{\#}^{\ast } \times A_{\#}^{\ast }$
be the rational transduction defined by
$\tau _0 \subseteq A_{\#}^{\ast } \times A_{\#}^{\ast }$
be the rational transduction defined by
For any word
![]() $w \in A_{\#}^{\ast }$
, the language
$w \in A_{\#}^{\ast }$
, the language
![]() $\tau _0(w)$
consists of all words obtainable by erasing some (possibly zero) amount of
$\tau _0(w)$
consists of all words obtainable by erasing some (possibly zero) amount of
![]() $\#_1$
-symbols in w, while fixing all other symbols. Define the language
$\#_1$
-symbols in w, while fixing all other symbols. Define the language
Lemma 2.2. The language
![]() $\mathcal {L}_0$
is a context-free language.
$\mathcal {L}_0$
is a context-free language.
Proof. This is an immediate consequence of the expression in Equation (2-3), in combination with the facts that (i)
![]() $\mathscr {R}$
is a context-free monadic rewriting system; (ii) every singleton language is in
$\mathscr {R}$
is a context-free monadic rewriting system; (ii) every singleton language is in
![]() $\mathbf {CF}$
; (iii) the class
$\mathbf {CF}$
; (iii) the class
![]() $\mathbf {CF}$
has the monadic ancestor property; and (iv) the class
$\mathbf {CF}$
has the monadic ancestor property; and (iv) the class
![]() $\mathbf {CF}$
closed under rational transduction (and hence also, in particular, intersection with regular languages).
$\mathbf {CF}$
closed under rational transduction (and hence also, in particular, intersection with regular languages).
We now show that
![]() $\mathcal {L}_0 = \mathcal {T}_S(R)$
.
$\mathcal {L}_0 = \mathcal {T}_S(R)$
.
Lemma 2.3.
![]() $\mathcal {L}_0 \subseteq \mathcal {T}_S(R)$
.
$\mathcal {L}_0 \subseteq \mathcal {T}_S(R)$
.
Proof. Suppose
![]() $w \in \mathcal {L}_0$
. Then, (1) w is an element of
$w \in \mathcal {L}_0$
. Then, (1) w is an element of
![]() $\tau _0(w')$
, where
$\tau _0(w')$
, where
![]() $w'$
is of the form of Equation (2-1) (by Lemma 2.1); and (2)
$w'$
is of the form of Equation (2-1) (by Lemma 2.1); and (2)
![]() $w \in R \#_1 R \#_2 R^{\text {rev}}$
. As
$w \in R \#_1 R \#_2 R^{\text {rev}}$
. As
![]() $\tau _0(w')$
consists of all words obtainable from
$\tau _0(w')$
consists of all words obtainable from
![]() $w'$
by erasing some number of
$w'$
by erasing some number of
![]() $\#_1$
-symbols, and the words in
$\#_1$
-symbols, and the words in
![]() $R \#_1 R \#_2 R^{\text {rev}}$
contain exactly one
$R \#_1 R \#_2 R^{\text {rev}}$
contain exactly one
![]() $\#_1$
, it follows from the expression in Equation (2-1) for
$\#_1$
, it follows from the expression in Equation (2-1) for
![]() $w'$
that
$w'$
that
 $$ \begin{align*} w \equiv \bigg( \prod_{i=1}^k x_i y_i \bigg) \,\#_1\, \bigg( \prod_{i=k+1}^n x_i y_i \bigg) \,\#_2\, \bigg( \prod_{i=1}^n z_i \bigg)^{\text{rev}}, \end{align*} $$
$$ \begin{align*} w \equiv \bigg( \prod_{i=1}^k x_i y_i \bigg) \,\#_1\, \bigg( \prod_{i=k+1}^n x_i y_i \bigg) \,\#_2\, \bigg( \prod_{i=1}^n z_i \bigg)^{\text{rev}}, \end{align*} $$
where for every
![]() $1 \leq i \leq n$
, we have
$1 \leq i \leq n$
, we have
![]() $x_i, y_i, z_i \in \overline {R}_{X(i)}$
and
$x_i, y_i, z_i \in \overline {R}_{X(i)}$
and
![]() $x_i y_i = z_i$
in
$x_i y_i = z_i$
in
![]() , with X some parametrisation.
, with X some parametrisation.
Now
![]() $x_i \sim y_i$
for all
$x_i \sim y_i$
for all
![]() $1 \leq i \leq n$
. Furthermore,
$1 \leq i \leq n$
. Furthermore,
![]() $y_i \not \sim x_{i+1}$
for all
$y_i \not \sim x_{i+1}$
for all
![]() $1 \leq i < k$
and
$1 \leq i < k$
and
![]() $k< i \leq n$
, as
$k< i \leq n$
, as
![]() $\prod _{i=1}^k (x_iy_i)$
and
$\prod _{i=1}^k (x_iy_i)$
and
![]() $\prod _{i=k+1}^n (x_iy_i)$
are alternating words. It follows that we must have
$\prod _{i=k+1}^n (x_iy_i)$
are alternating words. It follows that we must have
![]() $x_iy_i \in R_{X(i)}$
for every
$x_iy_i \in R_{X(i)}$
for every
![]() $1 \leq i \leq n$
and that
$1 \leq i \leq n$
and that
![]() $z_i \not \sim z_{i+1}$
for every
$z_i \not \sim z_{i+1}$
for every
![]() $1 \leq i < n$
except possibly
$1 \leq i < n$
except possibly
![]() $i=k$
. We thus have two cases: (1)
$i=k$
. We thus have two cases: (1)
![]() $z_k \not \sim z_{k+1}$
; or else (2)
$z_k \not \sim z_{k+1}$
; or else (2)
![]() $z_k \sim z_{k+1}$
. In either case, let
$z_k \sim z_{k+1}$
. In either case, let
![]() $\overline {z}_i \equiv x_i y_i$
for
$\overline {z}_i \equiv x_i y_i$
for
![]() $1 \leq i \leq n$
. Then
$1 \leq i \leq n$
. Then
![]() $\overline {z}_i \in R_{X(i)}$
, and w is of the form
$\overline {z}_i \in R_{X(i)}$
, and w is of the form
 $$ \begin{align*} w \equiv \bigg( \prod_{i=1}^k \overline{z}_i \bigg) \,\#_1\, \bigg( \prod_{i=k+1}^n \overline{z}_i \bigg) \,\#_2\, \bigg( \prod_{i=1}^n z_i \bigg)^{\text{rev}}. \end{align*} $$
$$ \begin{align*} w \equiv \bigg( \prod_{i=1}^k \overline{z}_i \bigg) \,\#_1\, \bigg( \prod_{i=k+1}^n \overline{z}_i \bigg) \,\#_2\, \bigg( \prod_{i=1}^n z_i \bigg)^{\text{rev}}. \end{align*} $$
Suppose we are in case (1). As
![]() $\overline {z}_i \equiv x_iy_i$
, and
$\overline {z}_i \equiv x_iy_i$
, and
![]() $\overline {z}_i = z_i$
in
$\overline {z}_i = z_i$
in
![]() , we thus have that w is the element of the multiplication table
, we thus have that w is the element of the multiplication table
![]() $\mathcal {T}_S(R)$
corresponding to the product
$\mathcal {T}_S(R)$
corresponding to the product
which clearly holds in S.
In case (2), as
![]() , it follows that
, it follows that
![]() $z_k \sim z_{k+1}$
, and hence, as R consists of alternating words, that
$z_k \sim z_{k+1}$
, and hence, as R consists of alternating words, that
![]() $z_k z_{k+1} \in R_{X(k)}$
. Let
$z_k z_{k+1} \in R_{X(k)}$
. Let
![]() $z \equiv z_k z_{k+1}$
, and let
$z \equiv z_k z_{k+1}$
, and let
![]() $\overline {z} \equiv \overline {z}_k \overline {z}_{k+1}$
. Then,
$\overline {z} \equiv \overline {z}_k \overline {z}_{k+1}$
. Then,
![]() . Thus, w is the element of
. Thus, w is the element of
![]() $\mathcal {T}_S(R)$
corresponding to the product
$\mathcal {T}_S(R)$
corresponding to the product
which also clearly holds in S. Thus, in either case, we have that
![]() $w \in \mathcal {T}_S(R)$
.
$w \in \mathcal {T}_S(R)$
.
We hence have
![]() $\mathcal {L}_0 \subseteq \mathcal {T}_S(R)$
. We now prove the converse of Lemma 2.3.
$\mathcal {L}_0 \subseteq \mathcal {T}_S(R)$
. We now prove the converse of Lemma 2.3.
Lemma 2.4.
![]() $\mathcal {T}_S(R) \subseteq \mathcal {L}_0$
.
$\mathcal {T}_S(R) \subseteq \mathcal {L}_0$
.
Proof. Suppose that
![]() $w \equiv w_1 \#_1 w_2 \#_2 x^{\text {rev}} \in \mathcal {T}_S(R)$
, that is, that
$w \equiv w_1 \#_1 w_2 \#_2 x^{\text {rev}} \in \mathcal {T}_S(R)$
, that is, that
![]() $w_1, w_2, x \in R$
are such that
$w_1, w_2, x \in R$
are such that
![]() $w_1 \cdot w_2 =_S x$
. As
$w_1 \cdot w_2 =_S x$
. As
![]() $w_1, w_2, x \in R = \operatorname {\mathrm {Alt}}^+(R_1, R_2)$
, we have that
$w_1, w_2, x \in R = \operatorname {\mathrm {Alt}}^+(R_1, R_2)$
, we have that
where
![]() $x_i \in R_{X(i)}$
for some standard parametrisation X. By Lemma 1.9, we either fall in case (1) or (2) of the same lemma.
$x_i \in R_{X(i)}$
for some standard parametrisation X. By Lemma 1.9, we either fall in case (1) or (2) of the same lemma.
In case (1), we have, using the notation of that lemma, that
 $$ \begin{align*} w &\equiv w_1 \#_1 w_2 \#_2 x^{\text{rev}} \\ &\equiv \overline{x}_1 \overline{x}_2 \cdots \overline{x}_k \#_1 \overline{x}_{k+1} \overline{x}_{k+2} \cdots \overline{x}_{n} \#_2 x_n^{\text{rev}} x_{n-1}^{\text{rev}} \cdots x_1^{\text{rev}} \\ &\in \tau_0 \bigg[ \bigg( \prod_{i=1}^k \#_1 \overline{x}_i \bigg)\bigg( \prod_{i=k+1}^n \#_1 \overline{x}_i \bigg) \,\#_1\, \#_2\, \bigg( \prod_{i=i}^n x_i \bigg)^{\text{rev}} \bigg] \\ &= \tau_0 \bigg[ \bigg( \prod_{i=1}^n \#_1 \overline{x}_i \bigg) \,\#_1\, \#_2\, \bigg( \prod_{i=1}^n x_i \bigg)^{\text{rev}} \bigg]. \end{align*} $$
$$ \begin{align*} w &\equiv w_1 \#_1 w_2 \#_2 x^{\text{rev}} \\ &\equiv \overline{x}_1 \overline{x}_2 \cdots \overline{x}_k \#_1 \overline{x}_{k+1} \overline{x}_{k+2} \cdots \overline{x}_{n} \#_2 x_n^{\text{rev}} x_{n-1}^{\text{rev}} \cdots x_1^{\text{rev}} \\ &\in \tau_0 \bigg[ \bigg( \prod_{i=1}^k \#_1 \overline{x}_i \bigg)\bigg( \prod_{i=k+1}^n \#_1 \overline{x}_i \bigg) \,\#_1\, \#_2\, \bigg( \prod_{i=i}^n x_i \bigg)^{\text{rev}} \bigg] \\ &= \tau_0 \bigg[ \bigg( \prod_{i=1}^n \#_1 \overline{x}_i \bigg) \,\#_1\, \#_2\, \bigg( \prod_{i=1}^n x_i \bigg)^{\text{rev}} \bigg]. \end{align*} $$
Let
![]() $W \equiv ( \prod _{i=1}^n \#_1 \overline {x}_i ) \,\#_1\, \#_2\, ( \prod _{i=i}^n x_i )^{\text {rev}}$
. As
$W \equiv ( \prod _{i=1}^n \#_1 \overline {x}_i ) \,\#_1\, \#_2\, ( \prod _{i=i}^n x_i )^{\text {rev}}$
. As
![]() $w_1, w_2, x \in R$
, and hence
$w_1, w_2, x \in R$
, and hence
![]() $w \in R \#_1 R \#_2 R^{\text {rev}}$
, it suffices by the expression in Equation (2-3) to show that
$w \in R \#_1 R \#_2 R^{\text {rev}}$
, it suffices by the expression in Equation (2-3) to show that
![]() $W \in \nabla ^{\ast }_{\mathscr {R}}(\#_1 \#_2)$
. As
$W \in \nabla ^{\ast }_{\mathscr {R}}(\#_1 \#_2)$
. As
![]() $\overline {x}_i = x_i$
in
$\overline {x}_i = x_i$
in
![]() $S_{X(i)}$
, we have
$S_{X(i)}$
, we have
![]() $(\overline {x}_i \#_1 \#_2 x_i^{\text {rev}}, \#_2) \in \mathscr {R}$
for every
$(\overline {x}_i \#_1 \#_2 x_i^{\text {rev}}, \#_2) \in \mathscr {R}$
for every
![]() $1 \leq i \leq n$
. Hence,
$1 \leq i \leq n$
. Hence,

which is what was to be shown.
In case (2), the proof is almost the same as in case (1), but the reductions are no longer exclusively by rules of the form
![]() $(\overline {x}_i \#_1 \#_2 x_i^{\text {rev}}, \#_2)$
. In the same way as in case (1), however, we find that
$(\overline {x}_i \#_1 \#_2 x_i^{\text {rev}}, \#_2)$
. In the same way as in case (1), however, we find that
![]() $w \in \tau _0(W)$
, where
$w \in \tau _0(W)$
, where
 $$ \begin{align*} W \equiv \bigg( \prod_{i=1}^{k-1} \#_1 \overline{x}_i \bigg) \,\#_1\, (\overline{x}_k' \#_1 \overline{x}_k'') \bigg( \prod_{k+1}^n \#_1 \overline{x}_i\bigg) \,\#_2\, \bigg( \prod_{i=1}^n x_i \bigg)^{\text{rev}}. \end{align*} $$
$$ \begin{align*} W \equiv \bigg( \prod_{i=1}^{k-1} \#_1 \overline{x}_i \bigg) \,\#_1\, (\overline{x}_k' \#_1 \overline{x}_k'') \bigg( \prod_{k+1}^n \#_1 \overline{x}_i\bigg) \,\#_2\, \bigg( \prod_{i=1}^n x_i \bigg)^{\text{rev}}. \end{align*} $$
By applying the rules
![]() $(\overline {x}_i \#_1 \#_2 x_i^{\text {rev}} \to \#_2)$
to W, for
$(\overline {x}_i \#_1 \#_2 x_i^{\text {rev}} \to \#_2)$
to W, for
![]() $i = n, n-1, \ldots , k+1$
(all such rules are in
$i = n, n-1, \ldots , k+1$
(all such rules are in
![]() $\mathscr {R}$
as
$\mathscr {R}$
as
![]() $\overline {x}_i \cdot \varepsilon = x_i$
in
$\overline {x}_i \cdot \varepsilon = x_i$
in
), we find that

where in the final step, we use the rule
![]() $(\overline {x}_k' \#_1 \overline {x}_k'' \#_2 x_k^{\text {rev}}, \#_2)$
, which is in
$(\overline {x}_k' \#_1 \overline {x}_k'' \#_2 x_k^{\text {rev}}, \#_2)$
, which is in
![]() $\mathscr {R}$
as
$\mathscr {R}$
as
![]() $\overline {x}_k' \cdot \overline {x}_k'' = x_k^{\text {rev}}$
in
$\overline {x}_k' \cdot \overline {x}_k'' = x_k^{\text {rev}}$
in
![]() $S_{X(k)}$
(and hence also in
$S_{X(k)}$
(and hence also in
). The proof now proceeds just as in case (1), and we find that
![]() $W \in \nabla ^{\ast }_{\mathscr {R}}(\#_1 \#_2)$
, and as
$W \in \nabla ^{\ast }_{\mathscr {R}}(\#_1 \#_2)$
, and as
![]() $w \in \tau _0(W)$
and
$w \in \tau _0(W)$
and
![]() $w \in R \#_1 R \#_2 R^{\text {rev}}$
, we have
$w \in R \#_1 R \#_2 R^{\text {rev}}$
, we have
![]() $w \in \mathcal {L}_0$
.
$w \in \mathcal {L}_0$
.
Thus, we have
![]() $\mathcal {T}_S(R) = \mathcal {L}_0$
. As R is a regular combing of
$\mathcal {T}_S(R) = \mathcal {L}_0$
. As R is a regular combing of
![]() $S = S_1 \ast S_2$
by Lemma 1.7, and as
$S = S_1 \ast S_2$
by Lemma 1.7, and as
![]() $\mathcal {L}_0$
is context-free by Lemma 2.2, we conclude that
$\mathcal {L}_0$
is context-free by Lemma 2.2, we conclude that
![]() $(R, \mathcal {T}_S(R))$
is a word-hyperbolic structure for
$(R, \mathcal {T}_S(R))$
is a word-hyperbolic structure for
![]() $S = S_1 \ast S_2$
. This completes the proof of Theorem A.
$S = S_1 \ast S_2$
. This completes the proof of Theorem A.
By Lemma 1.6, we find the following explicit corollaries of Theorem A.
Corollary 2.5. The semigroup free product of two word-hyperbolic monoids is word-hyperbolic.
Corollary 2.6. The semigroup free product of two (von Neumann) regular word-hyperbolic semigroups is word-hyperbolic.
Corollary 2.7. The semigroup free product of two word-hyperbolic semigroups with uniqueness is word-hyperbolic with uniqueness.
The final ‘with uniqueness’ in the statement of Corollary 2.7 follows from the fact that the elements of
![]() $\operatorname {\mathrm {Alt}}^+(R_1, R_2)$
represent pairwise distinct elements of S. We now turn towards considering monoid free products. To do this, we first need to introduce a useful purely language-theoretic operation.
$\operatorname {\mathrm {Alt}}^+(R_1, R_2)$
represent pairwise distinct elements of S. We now turn towards considering monoid free products. To do this, we first need to introduce a useful purely language-theoretic operation.
3 Polypartisan ancestors
In this section, we generalise (in a fairly uncomplicated manner) the bipartisan ancestors introduced in [Reference Nyberg-Brodda90] to polypartisan ancestors, and prove that this construction preserves certain language-theoretic properties of the languages to which it is applied. We use this construction to obtain the multiplication table for a monoid free product from the table for a semigroup free product.
Let A be a finite alphabet, and let
![]() $k \geq 1$
. Let
$k \geq 1$
. Let
![]() $\#_1, \#_2, \ldots , \#_{k}$
be k new symbols, and let
$\#_1, \#_2, \ldots , \#_{k}$
be k new symbols, and let
![]() $A_{\#} = A \cup \bigcup _{i=1}^{k} \{ \#_i \}$
. We let
$A_{\#} = A \cup \bigcup _{i=1}^{k} \{ \#_i \}$
. We let
denote the language
We call
the full k-shuffled language (associated to A). Any subset of
is called a k-shuffled language (with respect to A). Thus, the ‘word problem’ in the sense of Duncan and Gilman [Reference Duncan and Gilman38] for a monoid generated by A is a
![]() $1$
-shuffled language, that is, a subset of
$1$
-shuffled language, that is, a subset of
, and its multiplication table is a
![]() $2$
-shuffled language, that is, a subset of
$2$
-shuffled language, that is, a subset of
. Furthermore, the solution set for a set of equations in k unknowns over a group is a k-shuffled language [Reference Ciobanu, Diekert and Elder29].
For elements
![]() , we introduce the notation
, we introduce the notation
To abbreviate even further, we write
![]() $[u_{(k)}]$
for
$[u_{(k)}]$
for
![]() $[u_0, u_1, \ldots , u_k]$
. Thus, the word problem for a monoid M consists of words
$[u_0, u_1, \ldots , u_k]$
. Thus, the word problem for a monoid M consists of words
![]() $[u_{(1)}]$
with
$[u_{(1)}]$
with
![]() $u_0 =_M u_1^{\text {rev}}$
, and a multiplication table for M consists of words of the form
$u_0 =_M u_1^{\text {rev}}$
, and a multiplication table for M consists of words of the form
![]() $[v_{(2)}]$
with
$[v_{(2)}]$
with
![]() $v_0 \cdot v_1 =_M v_2^{\text {rev}}$
.
$v_0 \cdot v_1 =_M v_2^{\text {rev}}$
.
Let
![]() $k \geq 1$
, and let
$k \geq 1$
, and let
![]() $\mathscr {R}_0, \mathscr {R}_1, \ldots , \mathscr {R}_k \subseteq A^{\ast } \times A^{\ast }$
be a collection of
$\mathscr {R}_0, \mathscr {R}_1, \ldots , \mathscr {R}_k \subseteq A^{\ast } \times A^{\ast }$
be a collection of
![]() $k+1$
rewriting systems. Let
$k+1$
rewriting systems. Let
![]() be any language. We define a new language
be any language. We define a new language
![]() as
as
We call
![]() $\mathscr {R}_{(k)}(L)$
the
$\mathscr {R}_{(k)}(L)$
the
![]() $(k+1)$
-partisan ancestor of L (with respect to
$(k+1)$
-partisan ancestor of L (with respect to
![]() $\mathscr {R}_0, \mathscr {R}_1, \ldots , \mathscr {R}_k$
).
$\mathscr {R}_0, \mathscr {R}_1, \ldots , \mathscr {R}_k$
).
Polypartisan ancestors generalise in an easy way the bipartisan ancestors introduced by the author in [Reference Nyberg-Brodda90]. It is clear that
![]() $\mathscr {R}_{(k)}(L)$
is a k-shuffled language. The use for polypartisan ancestors in this present article is in preserving language-theoretic properties, in the following sense.
$\mathscr {R}_{(k)}(L)$
is a k-shuffled language. The use for polypartisan ancestors in this present article is in preserving language-theoretic properties, in the following sense.
Proposition 3.1. Let
![]() $\mathbf {C}$
be a super-
$\mathbf {C}$
be a super-
![]() $\operatorname {\mathrm {AFL}}$
. Let
$\operatorname {\mathrm {AFL}}$
. Let
![]() $L \in \mathbf {C}$
, and let
$L \in \mathbf {C}$
, and let
![]() $\mathscr {R}_i \subseteq A^{\ast } \times A^{\ast }$
be
$\mathscr {R}_i \subseteq A^{\ast } \times A^{\ast }$
be
![]() $\mathbf {C}$
-monadic rewriting systems for
$\mathbf {C}$
-monadic rewriting systems for
![]() $0 \leq i \leq k$
. Then
$0 \leq i \leq k$
. Then
![]() $\mathscr {R}_{(k)}(L) \in \mathbf {C}$
.
$\mathscr {R}_{(k)}(L) \in \mathbf {C}$
.
The technique we use to prove Proposition 3.1 is a generalisation of a similar technique used to prove [Reference Nyberg-Brodda90, Proposition 2.5], but follows its ideas rather closely. We first prove a weaker form of Proposition 3.1 (namely Lemma 3.2). We then use a rational transduction to move from the general case to this weaker form.
Let
![]() $A_0, A_1, \ldots , A_k$
be
$A_0, A_1, \ldots , A_k$
be
![]() $k+1$
alphabets, with
$k+1$
alphabets, with
![]() $A \cap A_i = \varnothing $
for all i, and with
$A \cap A_i = \varnothing $
for all i, and with
![]() $A_i \cap A_j = \varnothing $
for
$A_i \cap A_j = \varnothing $
for
![]() $i \neq j$
. We define the language
$i \neq j$
. We define the language

and call
a separated k-shuffle. For separated k-shuffles, preservation properties are simple to prove.
Lemma 3.2. Let
![]() $\mathscr {R}_i \subseteq A_i^{\ast } \times A_i^{\ast }$
be
$\mathscr {R}_i \subseteq A_i^{\ast } \times A_i^{\ast }$
be
![]() $\mathbf {C}$
-monadic rewriting systems for
$\mathbf {C}$
-monadic rewriting systems for
![]() $0 \leq i \leq k$
. Let
$0 \leq i \leq k$
. Let
![]() $L \in \mathbf {C}$
be such that
$L \in \mathbf {C}$
be such that
![]() . Then
. Then
![]() $\mathscr {R}_{(k)}(L) \in \mathbf {C}$
.
$\mathscr {R}_{(k)}(L) \in \mathbf {C}$
.
Proof. This closely follows the proof of [Reference Nyberg-Brodda90, Lemma 2.4], which is the case for
![]() $k=1$
, so we only sketch the main idea. As
$k=1$
, so we only sketch the main idea. As
![]() , it suffices to show that
, it suffices to show that
![]() $\mathscr {R}_{(k)}(L) \in \mathbf {C}$
. It is not difficult to see that as the alphabets
$\mathscr {R}_{(k)}(L) \in \mathbf {C}$
. It is not difficult to see that as the alphabets
![]() $A_i$
are disjoint,
$A_i$
are disjoint,
![]() $\mathscr {R}_i \subseteq A_i^{\ast } \times A_i^{\ast }$
, and every word in L is of the form
$\mathscr {R}_i \subseteq A_i^{\ast } \times A_i^{\ast }$
, and every word in L is of the form
![]() $u_0 \#_1 u_1 \#_2 \cdots \#_k u_k$
, where
$u_0 \#_1 u_1 \#_2 \cdots \#_k u_k$
, where
![]() $u_i \in A_i^{\ast }$
, we have that
$u_i \in A_i^{\ast }$
, we have that
![]() $\mathscr {R}_{(k)}(L) =\nabla ^{\ast }_{\bigcup _{i=0}^k \mathscr {R}_i}(L)$
. As each
$\mathscr {R}_{(k)}(L) =\nabla ^{\ast }_{\bigcup _{i=0}^k \mathscr {R}_i}(L)$
. As each
![]() $\mathscr {R}_i$
is
$\mathscr {R}_i$
is
![]() $\mathbf {C}$
-monadic – and
$\mathbf {C}$
-monadic – and
![]() $\mathbf {C}$
is closed under unions being a super-
$\mathbf {C}$
is closed under unions being a super-
![]() $\operatorname {\mathrm {AFL}}$
– so too is
$\operatorname {\mathrm {AFL}}$
– so too is
![]() $\mathscr {R} := \bigcup _{i=0}^k \mathscr {R}_i$
. As
$\mathscr {R} := \bigcup _{i=0}^k \mathscr {R}_i$
. As
![]() $\mathbf {C}$
is a super-
$\mathbf {C}$
is a super-
![]() $\operatorname {\mathrm {AFL}}$
, it has the monadic ancestor property, whence we find that
$\operatorname {\mathrm {AFL}}$
, it has the monadic ancestor property, whence we find that
![]() $\nabla ^{\ast }_{\mathscr {R}}(L)$
is in
$\nabla ^{\ast }_{\mathscr {R}}(L)$
is in
![]() $\mathbf {C}$
.
$\mathbf {C}$
.
We, from this point on, assume that
![]() $|A_i| = |A|$
for all
$|A_i| = |A|$
for all
![]() $0 \leq i \leq k$
, and fix bijections
$0 \leq i \leq k$
, and fix bijections
![]() $\varphi _i \colon A \to A_i$
. We extend these to isomorphisms
$\varphi _i \colon A \to A_i$
. We extend these to isomorphisms
![]() $\varphi _i \colon A^{\ast } \to A_i^{\ast }$
of free monoids. We let
$\varphi _i \colon A^{\ast } \to A_i^{\ast }$
of free monoids. We let
![]() $A_{I} = \bigcup _{i=0}^k A_i$
, and let
$A_{I} = \bigcup _{i=0}^k A_i$
, and let
![]() $A_{I,\#} = A_I \cup \bigcup _{i=0}^k\{ \#_i \}$
. Further, we write
$A_{I,\#} = A_I \cup \bigcup _{i=0}^k\{ \#_i \}$
. Further, we write
![]() $\mathscr {R}^{\varphi }_{i} = \varphi _i( \mathscr {R}_i)$
, where the action of
$\mathscr {R}^{\varphi }_{i} = \varphi _i( \mathscr {R}_i)$
, where the action of
![]() $\varphi _i$
is entry-wise on the rules of
$\varphi _i$
is entry-wise on the rules of
![]() $\mathscr {R}_i$
. If
$\mathscr {R}_i$
. If
![]() $\mathscr {R}_i$
is a
$\mathscr {R}_i$
is a
![]() $\mathbf {C}$
-monadic rewriting system, then so too clearly is
$\mathbf {C}$
-monadic rewriting system, then so too clearly is
![]() $\mathscr {R}_i^{\varphi }$
.
$\mathscr {R}_i^{\varphi }$
.
We define a rational transduction
![]() $\mu _k \subseteq A_{\#}^{\ast } \times A_{I,\#}^{\ast }$
as
$\mu _k \subseteq A_{\#}^{\ast } \times A_{I,\#}^{\ast }$
as
 $$ \begin{align*} \mu_k = \bigg( \bigcup_{a \in A} (a, \varphi_k(a) )\bigg)^{\ast} \prod_{i=1}^k \bigg( \bigcup_{a \in A} (a, \varphi_i(a) )\bigg)^{\ast} (\#_i,\#_i). \end{align*} $$
$$ \begin{align*} \mu_k = \bigg( \bigcup_{a \in A} (a, \varphi_k(a) )\bigg)^{\ast} \prod_{i=1}^k \bigg( \bigcup_{a \in A} (a, \varphi_i(a) )\bigg)^{\ast} (\#_i,\#_i). \end{align*} $$
Then
![]() $\mu _k$
is indeed rational, as it is of the form
$\mu _k$
is indeed rational, as it is of the form
![]() $X_0^{\ast } x_1 X_1^{\ast } \cdots x_k X_k^{\ast }$
, where the subset
$X_0^{\ast } x_1 X_1^{\ast } \cdots x_k X_k^{\ast }$
, where the subset
![]() $X_i \subseteq A_{\#}^{\ast } \times A_{I,\#}^{\ast }$
is finite for
$X_i \subseteq A_{\#}^{\ast } \times A_{I,\#}^{\ast }$
is finite for
![]() $0 \leq i \leq k$
, and
$0 \leq i \leq k$
, and
![]() $x_j \in A_{\#}^{\ast } \times A_{I,\#}^{\ast }$
is a single element for
$x_j \in A_{\#}^{\ast } \times A_{I,\#}^{\ast }$
is a single element for
![]() $1 \leq i \leq k$
. Hence,
$1 \leq i \leq k$
. Hence,
![]() $\mu _k$
is a rational subset of
$\mu _k$
is a rational subset of
![]() $A_{\#}^{\ast } \times A_{I,\#}^{\ast }$
. If
$A_{\#}^{\ast } \times A_{I,\#}^{\ast }$
. If
![]() $\mu _k$
is applied to (the singleton language containing) exactly one word
$\mu _k$
is applied to (the singleton language containing) exactly one word
, it clearly produces (the singleton language containing) exactly one word from
, and
![]() $\mu _k$
is injective on
$\mu _k$
is injective on
. That is, if
where
![]() $u_i \in A^{\ast }$
, then
$u_i \in A^{\ast }$
, then
and if
, then
![]() $\mu _k(w_1) = \mu _k(w_2)$
if and only if
$\mu _k(w_1) = \mu _k(w_2)$
if and only if
![]() $w_1 \equiv w_2$
, as each
$w_1 \equiv w_2$
, as each
![]() $\varphi _i$
is an isomorphism of free monoids. Slightly abusively, we write the equality in Equation (3-2) as
$\varphi _i$
is an isomorphism of free monoids. Slightly abusively, we write the equality in Equation (3-2) as
![]() $\mu _k([u_{(k)}]) = [\varphi _k(u_{(k)})]$
. Let
$\mu _k([u_{(k)}]) = [\varphi _k(u_{(k)})]$
. Let
![]() $\mu _k^{-1}$
denote the inverse of the rational transduction
$\mu _k^{-1}$
denote the inverse of the rational transduction
![]() $\mu _k$
. Then the above amounts to saying that
$\mu _k$
. Then the above amounts to saying that
for every
.
Lemma 3.3. Let
![]() . Then
. Then
![]() $\mathscr {R}_{(k)}(L) = \mu _k^{-1}\mathscr {R}^{\varphi }_{(k)}(\,\mu _k(L))$
.
$\mathscr {R}_{(k)}(L) = \mu _k^{-1}\mathscr {R}^{\varphi }_{(k)}(\,\mu _k(L))$
.
Proof. By Equation (3-1),
![]() $[w_{(k)}] \in \mathscr {R}_{(k)}(L)$
if and only if there exists
$[w_{(k)}] \in \mathscr {R}_{(k)}(L)$
if and only if there exists
![]() $[u_{(k)}] \in L$
such that
$[u_{(k)}] \in L$
such that
![]() for all
for all
![]() $0 \leq i \leq k$
, which is true if and only if
$0 \leq i \leq k$
, which is true if and only if
![]() , that is,
, that is,
![]() $[\varphi _k(w_{(k)})] \in \mathscr {R}_{(k)}^{\varphi } (\varphi _k(u_{(k)}))$
. However, this is simply saying
$[\varphi _k(w_{(k)})] \in \mathscr {R}_{(k)}^{\varphi } (\varphi _k(u_{(k)}))$
. However, this is simply saying
![]() $\mu _k([w_{(k)}]) \in \mathscr {R}_{(k)}^{\varphi }(\,\mu _k([u_{(k)}]))$
, which by Equation (3-3) is equivalent to
$\mu _k([w_{(k)}]) \in \mathscr {R}_{(k)}^{\varphi }(\,\mu _k([u_{(k)}]))$
, which by Equation (3-3) is equivalent to
With less cumbersome notation, we have proved that
![]() $w \in \mathscr {R}_{(k)}(L)$
if and only if there is some
$w \in \mathscr {R}_{(k)}(L)$
if and only if there is some
![]() $u \in L$
such that
$u \in L$
such that
In other words, as w is arbitrary, we have
![]() $\mathscr {R}_{(k)}(L) = \mu _k^{-1}\mathscr {R}^{\varphi }_{(k)}(\,\mu _k(L))$
.
$\mathscr {R}_{(k)}(L) = \mu _k^{-1}\mathscr {R}^{\varphi }_{(k)}(\,\mu _k(L))$
.
Proof of Proposition 3.1
As
![]() $L \in \mathbf {C}$
, we have
$L \in \mathbf {C}$
, we have
![]() $\mu _k(L) \in \mathbf {C}$
, as the super-
$\mu _k(L) \in \mathbf {C}$
, as the super-
![]() $\operatorname {\mathrm {AFL}} \mathbf {C}$
is closed under rational transduction. As
$\operatorname {\mathrm {AFL}} \mathbf {C}$
is closed under rational transduction. As
![]() $\mathscr {R}_i$
is
$\mathscr {R}_i$
is
![]() $\mathbf {C}$
-monadic, so too is
$\mathbf {C}$
-monadic, so too is
![]() $\mathscr {R}_i^{\varphi }$
for
$\mathscr {R}_i^{\varphi }$
for
![]() $0 \leq i \leq k$
. As
$0 \leq i \leq k$
. As
![]() , we conclude by Lemma 3.2 that
, we conclude by Lemma 3.2 that
![]() $\mathscr {R}^{\varphi }_{(k)}(\,\mu _k(L))$
is in
$\mathscr {R}^{\varphi }_{(k)}(\,\mu _k(L))$
is in
![]() $\mathbf {C}$
. Finally, as
$\mathbf {C}$
. Finally, as
![]() $\mu _k^{-1}$
is a rational transduction, the language
$\mu _k^{-1}$
is a rational transduction, the language
![]() $\mu _k^{-1}\mathscr {R}^{\varphi }_{(k)}(\,\mu _k(L))$
is in
$\mu _k^{-1}\mathscr {R}^{\varphi }_{(k)}(\,\mu _k(L))$
is in
![]() $\mathbf {C}$
; by Lemma 3.3,
$\mathbf {C}$
; by Lemma 3.3,
![]() $\mathscr {R}_{(k)}(L)$
is hence in
$\mathscr {R}_{(k)}(L)$
is hence in
![]() $\mathbf {C}$
.
$\mathbf {C}$
.
This completes our discussion of polypartisan ancestors.
4 Monoid free products
In this section, we consider monoid free products. We begin by proving the main theorem for free products of word-hyperbolic monoids with
![]() $1$
-uniqueness (Theorem B). We then present a theorem which applies outside the
$1$
-uniqueness (Theorem B). We then present a theorem which applies outside the
![]() $1$
-uniqueness case, to the cases when the combings
$1$
-uniqueness case, to the cases when the combings
![]() $R_i$
of the factor monoids
$R_i$
of the factor monoids
![]() $M_i$
satisfy
$M_i$
satisfy
![]() $R_i^{\ast }~=~R_i$
(Theorem 4.5). We then argue that these two cases are, in a certain sense, complementary (Section 4.3).
$R_i^{\ast }~=~R_i$
(Theorem 4.5). We then argue that these two cases are, in a certain sense, complementary (Section 4.3).
4.1 The case of
 $1$
-uniqueness
$1$
-uniqueness
Suppose that
![]() $M_i$
(for
$M_i$
(for
![]() $i=1,2$
) is a word-hyperbolic monoid with
$i=1,2$
) is a word-hyperbolic monoid with
![]() $1$
-uniqueness, with respect to the regular combing
$1$
-uniqueness, with respect to the regular combing
![]() $R_i$
. By definition, the only word in
$R_i$
. By definition, the only word in
![]() $R_i$
that represents the identity of
$R_i$
that represents the identity of
![]() $M_i$
is
$M_i$
is
![]() $\varepsilon $
. Let
$\varepsilon $
. Let
![]() $R_i' = R_i - \{ \varepsilon \}$
. Then it is clear that every alternating word in
$R_i' = R_i - \{ \varepsilon \}$
. Then it is clear that every alternating word in
![]() $\operatorname {\mathrm {Alt}}(R_1', R_2')$
is reduced; for if
$\operatorname {\mathrm {Alt}}(R_1', R_2')$
is reduced; for if
![]() $u_0 u_1 \cdots u_n$
is the alternating factorisation of
$u_0 u_1 \cdots u_n$
is the alternating factorisation of
![]() $u \in \operatorname {\mathrm {Alt}}(R_1', R_2')$
, and u is not reduced, then
$u \in \operatorname {\mathrm {Alt}}(R_1', R_2')$
, and u is not reduced, then
![]() $u_i = 1$
in either
$u_i = 1$
in either
![]() $M_1$
or
$M_1$
or
![]() $M_2$
for some
$M_2$
for some
![]() $0 \leq i \leq n$
, and hence
$0 \leq i \leq n$
, and hence
![]() $u_i \equiv \varepsilon $
, a contradiction to
$u_i \equiv \varepsilon $
, a contradiction to
![]() $u_i \in R_1' \cup R_2'$
. Hence, by Lemma 1.8, monoid free products of monoids with
$u_i \in R_1' \cup R_2'$
. Hence, by Lemma 1.8, monoid free products of monoids with
![]() $1$
-uniqueness behave essentially as semigroup free products of the same monoids, up to the fact that the product of two reduced sequences may not be reduced.
$1$
-uniqueness behave essentially as semigroup free products of the same monoids, up to the fact that the product of two reduced sequences may not be reduced.
Using monadic ancestry, we may deal with this latter issue, and show the following main theorem.
Theorem B. Let
![]() $M_1, M_2$
be two word-hyperbolic monoids with
$M_1, M_2$
be two word-hyperbolic monoids with
![]() $1$
-uniqueness (with uniqueness). Then the monoid free product
$1$
-uniqueness (with uniqueness). Then the monoid free product
![]() $M_1 \ast M_2$
is word-hyperbolic with
$M_1 \ast M_2$
is word-hyperbolic with
![]() $1$
-uniqueness (with uniqueness).
$1$
-uniqueness (with uniqueness).
Proof. Suppose
![]() $M_1$
(respectively
$M_1$
(respectively
![]() $M_2$
) is word-hyperbolic with
$M_2$
) is word-hyperbolic with
![]() $1$
-uniqueness with respect to the regular combing
$1$
-uniqueness with respect to the regular combing
![]() $R_1$
(respectively
$R_1$
(respectively
![]() $R_2$
). As usual, we let
$R_2$
). As usual, we let
![]() $R = \operatorname {\mathrm {Alt}}(R_1, R_2)$
. If
$R = \operatorname {\mathrm {Alt}}(R_1, R_2)$
. If
![]() $M_1$
(respectively
$M_1$
(respectively
![]() $M_2$
) are word-hyperbolic with
$M_2$
) are word-hyperbolic with
![]() $1$
-uniqueness, then the only element of R representing the identity element is
$1$
-uniqueness, then the only element of R representing the identity element is
![]() $\varepsilon $
, as the only element of
$\varepsilon $
, as the only element of
![]() $R_1$
(respectively
$R_1$
(respectively
![]() $R_2$
) representing the identity element of
$R_2$
) representing the identity element of
![]() $M_1$
(respectively
$M_1$
(respectively
![]() $M_2$
) is
$M_2$
) is
![]() $\varepsilon $
. Analogously, if
$\varepsilon $
. Analogously, if
![]() $M_1, M_2$
are word-hyperbolic with uniqueness, then every alternating word is reduced, and hence every pair of distinct words in R represent distinct elements of M by Lemma 1.10. Hence, it suffices to show that M is word-hyperbolic with respect to R.
$M_1, M_2$
are word-hyperbolic with uniqueness, then every alternating word is reduced, and hence every pair of distinct words in R represent distinct elements of M by Lemma 1.10. Hence, it suffices to show that M is word-hyperbolic with respect to R.
For
![]() $i=1, 2$
, we define the monadic rewriting system
$i=1, 2$
, we define the monadic rewriting system
Now, the language of left-hand sides of
![]() $\#_1$
in
$\#_1$
in
![]() $\mathscr {S}_i$
is
$\mathscr {S}_i$
is
where
![]() $/$
denotes the right quotient, in this case by the regular language
$/$
denotes the right quotient, in this case by the regular language
![]() $\{ \#_2 \varepsilon \}$
. As
$\{ \#_2 \varepsilon \}$
. As
![]() $\mathcal {T}_{M_i}(R_i)$
is a context-free language, so too is the quotient of
$\mathcal {T}_{M_i}(R_i)$
is a context-free language, so too is the quotient of
![]() $\mathcal {T}_{M_i}$
by any regular language. We conclude that
$\mathcal {T}_{M_i}$
by any regular language. We conclude that
![]() $\mathscr {S}_i$
is a context-free monadic rewriting system. Hence, the union
$\mathscr {S}_i$
is a context-free monadic rewriting system. Hence, the union
![]() $\mathscr {S} = \mathscr {S}_1 \cup \mathscr {S}_2$
is also a context-free monadic system.
$\mathscr {S} = \mathscr {S}_1 \cup \mathscr {S}_2$
is also a context-free monadic system.
We define the language
We prove that
![]() $\mathcal {L}_1 = \mathcal {T}_M(R)$
, which suffices to prove the theorem (as a quick argument shows). This highlights that the language-theoretic properties of the monoid free product of word-hyperbolic monoids with
$\mathcal {L}_1 = \mathcal {T}_M(R)$
, which suffices to prove the theorem (as a quick argument shows). This highlights that the language-theoretic properties of the monoid free product of word-hyperbolic monoids with
![]() $1$
-uniqueness are not significantly more complicated than those of the semigroup free product of the same. One direction is easy, and depends on little more than the two facts that (i) if
$1$
-uniqueness are not significantly more complicated than those of the semigroup free product of the same. One direction is easy, and depends on little more than the two facts that (i) if
![]() $u \cdot v =_S w$
, then
$u \cdot v =_S w$
, then
![]() $u \cdot v =_M w$
for
$u \cdot v =_M w$
for
![]() $u, v, w \in R$
; and (ii) if
$u, v, w \in R$
; and (ii) if
![]() $u \cdot v =_{M_i} 1$
, then
$u \cdot v =_{M_i} 1$
, then
![]() $u \cdot v =_{M} 1$
for
$u \cdot v =_{M} 1$
for
![]() $u, v \in R_i$
.
$u, v \in R_i$
.
Lemma 4.1.
![]() $\mathcal {L}_1 \subseteq \mathcal {T}_M(R)$
.
$\mathcal {L}_1 \subseteq \mathcal {T}_M(R)$
.
Proof. The proof of this is entirely analogous to that of Lemma 2.3, with one minor addition: note that if
![]() $w_1 \#_1 w_2 \#_2 w_3^{\text {rev}} \in \mathcal {T}_S(R)$
, then we have
$w_1 \#_1 w_2 \#_2 w_3^{\text {rev}} \in \mathcal {T}_S(R)$
, then we have
![]() $w_1 \cdot w_2 =_S w_3$
and hence also
$w_1 \cdot w_2 =_S w_3$
and hence also
![]() $w_1 \cdot w_2 =_M w_3$
. If
$w_1 \cdot w_2 =_M w_3$
. If
![]() $u, v \in R_i$
are such that
$u, v \in R_i$
are such that
![]() $u \cdot v =_{M_i} 1$
for some
$u \cdot v =_{M_i} 1$
for some
![]() $i=1,2$
, then
$i=1,2$
, then
![]() $u \cdot v =_M 1$
, so also
$u \cdot v =_M 1$
, so also
![]() $w_1u \cdot vw_2 =_M w_3$
. Hence, if
$w_1u \cdot vw_2 =_M w_3$
. Hence, if
![]() $w_1 u, vw_2 \in R$
, then we conclude that
$w_1 u, vw_2 \in R$
, then we conclude that
![]() $w_1(u \#_1 v)w_2 \#_2 w_3^{\text {rev}} \in \mathcal {T}_M(R)$
, and
$w_1(u \#_1 v)w_2 \#_2 w_3^{\text {rev}} \in \mathcal {T}_M(R)$
, and
We leave the (simple) details to the reader.
We remark (as is needed in Section 4.2) that the assumption of
![]() $1$
-uniqueness is not needed to prove Lemma 4.1. The nontrivial part of the equality
$1$
-uniqueness is not needed to prove Lemma 4.1. The nontrivial part of the equality
![]() $\mathcal {T}_M(R) = \mathcal {L}_1$
is given by the following lemma.
$\mathcal {T}_M(R) = \mathcal {L}_1$
is given by the following lemma.
Lemma 4.2.
![]() $\mathcal {T}_M(R) \subseteq \mathcal {L}_1$
.
$\mathcal {T}_M(R) \subseteq \mathcal {L}_1$
.
Proof. Suppose
![]() $w \equiv w_1 \#_1 w_2 \#_2 x^{\text {rev}} \in \mathcal {T}_M(R)$
. Then
$w \equiv w_1 \#_1 w_2 \#_2 x^{\text {rev}} \in \mathcal {T}_M(R)$
. Then
![]() $w_1, w_2, x \in R$
, and
$w_1, w_2, x \in R$
, and
![]() $w_1 \cdot w_2 =_M x$
. By
$w_1 \cdot w_2 =_M x$
. By
![]() $1$
-uniqueness,
$1$
-uniqueness,
![]() $w_1, w_2$
, and x are all necessarily reduced (though
$w_1, w_2$
, and x are all necessarily reduced (though
![]() $w_1, w_2$
may not be). Hence, we can apply Lemma 1.11. If we are in case (1) or (2), then by Lemma 1.9, we have
$w_1, w_2$
may not be). Hence, we can apply Lemma 1.11. If we are in case (1) or (2), then by Lemma 1.9, we have
![]() $w_1 \cdot w_2 =_S x$
, and so
$w_1 \cdot w_2 =_S x$
, and so
![]() $w_1 \#_1 w_2 \#_2 x^{\text {rev}} \in \mathcal {T}_S(R)$
, and hence, using no rewritings, we find
$w_1 \#_1 w_2 \#_2 x^{\text {rev}} \in \mathcal {T}_S(R)$
, and hence, using no rewritings, we find
If we are instead in case (3), then we must use
![]() $\mathscr {S}$
nontrivially. As
$\mathscr {S}$
nontrivially. As
![]() $x^{\prime }_k, x_k'' \in R_{X'(k)}$
satisfy
$x^{\prime }_k, x_k'' \in R_{X'(k)}$
satisfy
![]() $x^{\prime }_k \cdot x^{\prime \prime }_k =_{M_{X'(k)}} 1$
, we have
$x^{\prime }_k \cdot x^{\prime \prime }_k =_{M_{X'(k)}} 1$
, we have
![]() $(x^{\prime }_k \#_1 x^{\prime \prime }_k, \#_1) \in \mathscr {S}_{X'(k)} \subseteq \mathscr {S}$
. Hence, also
$(x^{\prime }_k \#_1 x^{\prime \prime }_k, \#_1) \in \mathscr {S}_{X'(k)} \subseteq \mathscr {S}$
. Hence, also
As
![]() $w_1', w_2', x \in R$
satisfy
$w_1', w_2', x \in R$
satisfy
![]() $w_1' \cdot w_2' =_M x$
, and
$w_1' \cdot w_2' =_M x$
, and
![]() $|w_1'|+|w_2'| < |w_1|+|w_2|$
, we may use induction on the parameter
$|w_1'|+|w_2'| < |w_1|+|w_2|$
, we may use induction on the parameter
![]() $|w_1| + |w_2|$
(the base cases being cases (1) and (2) above), where the inductive hypothesis yields
$|w_1| + |w_2|$
(the base cases being cases (1) and (2) above), where the inductive hypothesis yields
![]() $w_1' \#_1 w_2' \#_2 x^{\text {rev}} \in \mathcal {L}_1$
. Thus,
$w_1' \#_1 w_2' \#_2 x^{\text {rev}} \in \mathcal {L}_1$
. Thus,
![]() $w_1' \#_1 w_2' \#_2 x^{\text {rev}} \in \nabla ^{\ast }_{\mathscr {S}}(\mathcal {T}_S(R))$
, so by Equation (4-2), we also have
$w_1' \#_1 w_2' \#_2 x^{\text {rev}} \in \nabla ^{\ast }_{\mathscr {S}}(\mathcal {T}_S(R))$
, so by Equation (4-2), we also have
![]() $w \in \nabla ^{\ast }_{\mathscr {S}}(\mathcal {T}_S(R))$
. We conclude by induction that
$w \in \nabla ^{\ast }_{\mathscr {S}}(\mathcal {T}_S(R))$
. We conclude by induction that
![]() $w \in \mathcal {L}_1$
, as desired.
$w \in \mathcal {L}_1$
, as desired.
Hence, we have found a regular combing R of M such that
![]() $\mathcal {T}_M(R)$
is given by the right-hand side of Equation (4-1). The right-hand side of Equation (4-1) is context-free, by the following chain of reasoning: (i)
$\mathcal {T}_M(R)$
is given by the right-hand side of Equation (4-1). The right-hand side of Equation (4-1) is context-free, by the following chain of reasoning: (i)
![]() $\mathcal {T}_S(R) \in \mathbf {CF}$
by Theorem A; and hence (ii)
$\mathcal {T}_S(R) \in \mathbf {CF}$
by Theorem A; and hence (ii)
![]() $\nabla ^{\ast }_{\mathscr {S}}(\mathcal {T}_S(R)) \in \mathbf {CF}$
, as the class of context-free languages has the monadic ancestor property and
$\nabla ^{\ast }_{\mathscr {S}}(\mathcal {T}_S(R)) \in \mathbf {CF}$
, as the class of context-free languages has the monadic ancestor property and
![]() $\mathscr {S}$
is a context-free monadic rewriting system; and (iii) thus,
$\mathscr {S}$
is a context-free monadic rewriting system; and (iii) thus,
![]() $\mathcal {T}_M(R) \in \mathbf {CF}$
as
$\mathcal {T}_M(R) \in \mathbf {CF}$
as
![]() $\mathbf {CF}$
is closed under intersection with regular languages. Hence,
$\mathbf {CF}$
is closed under intersection with regular languages. Hence,
![]() $(R, \mathcal {T}_M(R))$
is a word-hyperbolic structure for
$(R, \mathcal {T}_M(R))$
is a word-hyperbolic structure for
![]() $M = M_1 \ast M_2$
. This completes the proof of Theorem B.
$M = M_1 \ast M_2$
. This completes the proof of Theorem B.
Word-hyperbolicity with
![]() $1$
-uniqueness is not an unusual phenomenon. For example, it always holds in hyperbolic groups, so we find the following immediate corollary of Theorem B.
$1$
-uniqueness is not an unusual phenomenon. For example, it always holds in hyperbolic groups, so we find the following immediate corollary of Theorem B.
Corollary 4.3. The free product of two hyperbolic groups is hyperbolic.
Proof. By [Reference Gilman49, Theorem 1] (see also [Reference Duncan and Gilman38, Corollary 4.3]), a group is hyperbolic (in the geometric sense) if and only if it is word-hyperbolic (in the language-theoretic sense of this paper). Hence, as the monoid free product of two groups is the same as the (ordinary) free product of two groups, in view of Theorem B, it suffices to show that hyperbolic groups are word-hyperbolic with
![]() $1$
-uniqueness. However, every hyperbolic group G, generated by a finite set A, is word-hyperbolic with respect to the regular combing
$1$
-uniqueness. However, every hyperbolic group G, generated by a finite set A, is word-hyperbolic with respect to the regular combing
![]() $R \subseteq A^{\ast }$
given by the language of geodesics in the Cayley graph of G, and there is only one geodesic corresponding to the identity element, see [Reference Coornaert, Delzant and Papadopoulos32, Theorem 4.2].
$R \subseteq A^{\ast }$
given by the language of geodesics in the Cayley graph of G, and there is only one geodesic corresponding to the identity element, see [Reference Coornaert, Delzant and Papadopoulos32, Theorem 4.2].
Of course, Corollary 4.3 is well known in geometric group theory, and is not difficult to show geometrically. Our approach, via Theorem B, gives a proof which instead goes via formal language theory.
4.2
 $\star $
-word-hyperbolic monoids
$\star $
-word-hyperbolic monoids
In this section, we describe a stronger property than word-hyperbolicity. Let M be a word-hyperbolic monoid with respect to a regular combing R. If
![]() $R = R^{\ast }$
, then we say that M is
$R = R^{\ast }$
, then we say that M is
![]() $\star $
-word-hyperbolic (with respect to R). We do not know if every word-hyperbolic monoid is
$\star $
-word-hyperbolic (with respect to R). We do not know if every word-hyperbolic monoid is
![]() $\star $
-word-hyperbolic, but do not suspect this to be the case:
$\star $
-word-hyperbolic, but do not suspect this to be the case:
![]() $\star $
-word-hyperbolic monoids appear to inch too close to monoids with context-free word problem.
$\star $
-word-hyperbolic monoids appear to inch too close to monoids with context-free word problem.
Example 4.4. It is easy to see that the bicyclic monoid
![]() $B = \mathrm {Mon} \langle b,c \mid bc=~1~\rangle $
is word-hyperbolic with respect to the regular combing
$B = \mathrm {Mon} \langle b,c \mid bc=~1~\rangle $
is word-hyperbolic with respect to the regular combing
![]() $c^{\ast } b^{\ast }$
(as is shown explicitly in [Reference Duncan and Gilman38, Example 3.8]). Of course, for this combing, we have
$c^{\ast } b^{\ast }$
(as is shown explicitly in [Reference Duncan and Gilman38, Example 3.8]). Of course, for this combing, we have
![]() $(c^{\ast } b^{\ast })^{\ast } \neq c^{\ast } b^{\ast }$
. However, B is also word-hyperbolic with respect to the combing
$(c^{\ast } b^{\ast })^{\ast } \neq c^{\ast } b^{\ast }$
. However, B is also word-hyperbolic with respect to the combing
![]() $\{ b, c \}^{\ast }$
, as is easily seen by using the complete monadic rewriting system
$\{ b, c \}^{\ast }$
, as is easily seen by using the complete monadic rewriting system
![]() $(bc, 1)$
(see also the first few sentences of [Reference Cain and Maltcev25, Theorem 3.1], coupled with [Reference Book, Jantzen and Wrathall21, Corollary 3.8]). In particular, the bicyclic monoid is
$(bc, 1)$
(see also the first few sentences of [Reference Cain and Maltcev25, Theorem 3.1], coupled with [Reference Book, Jantzen and Wrathall21, Corollary 3.8]). In particular, the bicyclic monoid is
![]() $\star $
-word-hyperbolic.
$\star $
-word-hyperbolic.
In fact, this example is a consequence of the general fact that the group of units of the bicyclic monoid is trivial. Recall that a monoid is special if every defining relation is of the form
![]() $w_i = 1$
(see [Reference Adian1, Ch. III]). As proved by the author, a special monoid M has context-free word problem – in the sense of Duncan and Gilman [Reference Duncan and Gilman38, Section 5] – if and only if its group of units
$w_i = 1$
(see [Reference Adian1, Ch. III]). As proved by the author, a special monoid M has context-free word problem – in the sense of Duncan and Gilman [Reference Duncan and Gilman38, Section 5] – if and only if its group of units
![]() $U(M)$
is virtually free [Reference Nyberg-Brodda91]. Any monoid generated by a finite set A clearly has context-free word problem if and only if it is word-hyperbolic with respect to the regular combing
$U(M)$
is virtually free [Reference Nyberg-Brodda91]. Any monoid generated by a finite set A clearly has context-free word problem if and only if it is word-hyperbolic with respect to the regular combing
![]() $A^{\ast }$
(one direction is trivial by a rational transduction; the other is observed at the beginning of the proof of [Reference Cain and Maltcev25, Theorem 3.1]). See also [Reference Gilman49, Theorem 2(2)]. Thus, any context-free monoid is
$A^{\ast }$
(one direction is trivial by a rational transduction; the other is observed at the beginning of the proof of [Reference Cain and Maltcev25, Theorem 3.1]). See also [Reference Gilman49, Theorem 2(2)]. Thus, any context-free monoid is
![]() $\star $
-word-hyperbolic.
$\star $
-word-hyperbolic.
The main theorem of this section is the following, which uses polypartisan ancestors.
Theorem 4.5. Let
![]() $M_1, M_2$
be two
$M_1, M_2$
be two
![]() $\star $
-word-hyperbolic monoids. Then the monoid free product
$\star $
-word-hyperbolic monoids. Then the monoid free product
![]() $M_1 \ast M_2$
is
$M_1 \ast M_2$
is
![]() $\star $
-word-hyperbolic.
$\star $
-word-hyperbolic.
Proof. Suppose
![]() $M_1, M_2$
are
$M_1, M_2$
are
![]() $\star $
-word-hyperbolic monoids with respect to the regular combings
$\star $
-word-hyperbolic monoids with respect to the regular combings
![]() $R_1$
(respectively
$R_1$
(respectively
![]() $R_2$
). Then
$R_2$
). Then
![]() $R_1^{\ast } = R_1$
and
$R_1^{\ast } = R_1$
and
![]() $R_2^{\ast } = R_2$
. Let, as usual,
$R_2^{\ast } = R_2$
. Let, as usual,
![]() $R = \operatorname {\mathrm {Alt}}(R_1, R_2)$
, and let M denote the monoid free product
$R = \operatorname {\mathrm {Alt}}(R_1, R_2)$
, and let M denote the monoid free product
![]() $M_1 \ast M_2$
. However, note that, in this case, we can simplify
$M_1 \ast M_2$
. However, note that, in this case, we can simplify
![]() $\operatorname {\mathrm {Alt}}(R_1, R_2) = (R_1 \cup R_2)^{\ast }$
. It suffices to show that
$\operatorname {\mathrm {Alt}}(R_1, R_2) = (R_1 \cup R_2)^{\ast }$
. It suffices to show that
![]() $\mathcal {T}_M(R)$
is a context-free language, as R clearly combs M. We have done most of the heavy lifting in the proofs of Theorems A and B. However, unlike in the setting of these theorems, we cannot assume that every element of R is reduced. We remedy this with a context-free monadic rewriting system.
$\mathcal {T}_M(R)$
is a context-free language, as R clearly combs M. We have done most of the heavy lifting in the proofs of Theorems A and B. However, unlike in the setting of these theorems, we cannot assume that every element of R is reduced. We remedy this with a context-free monadic rewriting system.
We first define, for
![]() $i=1,2$
, the rewriting systems
$i=1,2$
, the rewriting systems
Then,
![]() $\mathscr {T}_i$
is a context-free monadic rewriting system, as the left-hand sides of
$\mathscr {T}_i$
is a context-free monadic rewriting system, as the left-hand sides of
![]() $1$
are obtained by taking a right quotient of the context-free multiplication table
$1$
are obtained by taking a right quotient of the context-free multiplication table
![]() $\mathcal {T}_{M_i}(R_i)$
by the regular language
$\mathcal {T}_{M_i}(R_i)$
by the regular language
![]() $\#_1\#_2$
. Note that for every rule
$\#_1\#_2$
. Note that for every rule
![]() $(w, 1) \in \mathscr {T}_i$
, we have
$(w, 1) \in \mathscr {T}_i$
, we have
![]() $w =_M 1$
, by the properties of the monoid free product. We let
$w =_M 1$
, by the properties of the monoid free product. We let
![]() $\mathscr {T} = \mathscr {T}_1 \cup \mathscr {T}_2$
, which is also a context-free monadic system. We let further
$\mathscr {T} = \mathscr {T}_1 \cup \mathscr {T}_2$
, which is also a context-free monadic system. We let further
![]() $\mathscr {T}^{\text {rev}}$
be the system consisting of all rules
$\mathscr {T}^{\text {rev}}$
be the system consisting of all rules
![]() $(w^{\text {rev}}, 1)$
such that
$(w^{\text {rev}}, 1)$
such that
![]() $(w, 1) \in \mathscr {T}$
. Then
$(w, 1) \in \mathscr {T}$
. Then
![]() $\mathscr {T}^{\text {rev}}$
is a context-free monadic rewriting system, as the class
$\mathscr {T}^{\text {rev}}$
is a context-free monadic rewriting system, as the class
![]() $\mathbf {CF}$
is closed under reversal.
$\mathbf {CF}$
is closed under reversal.
Note that for every word
![]() $w \in R$
, there exists some (not necessarily unique) reduced
$w \in R$
, there exists some (not necessarily unique) reduced
![]() $w' \in R$
such that
$w' \in R$
such that
![]() . Of course, as
. Of course, as
![]() $\mathscr {T}$
is M-equivariant, for such
$\mathscr {T}$
is M-equivariant, for such
![]() $w, w'$
, we have
$w, w'$
, we have
![]() $w =_M w'$
.
$w =_M w'$
.
Let
![]() $\mathscr {R}_1 = \mathscr {R}_2 = \mathscr {T}$
, and let
$\mathscr {R}_1 = \mathscr {R}_2 = \mathscr {T}$
, and let
![]() $\mathscr {R}_3 = \mathscr {T}^{\text {rev}}$
. Consider the polypartisan ancestor
$\mathscr {R}_3 = \mathscr {T}^{\text {rev}}$
. Consider the polypartisan ancestor
Recall the definition of
![]() $\mathcal {L}_1$
as Equation (4-1), and see Section 3 for notation pertaining to polypartisan ancestors. By Lemma 4.1 (and the remark following it), we have
$\mathcal {L}_1$
as Equation (4-1), and see Section 3 for notation pertaining to polypartisan ancestors. By Lemma 4.1 (and the remark following it), we have
![]() $\mathcal {L}_1 \subseteq \mathcal {T}_M(R)$
. Hence,
$\mathcal {L}_1 \subseteq \mathcal {T}_M(R)$
. Hence,
![]() $\mathcal {L}_2$
consists of some collection of words of the form
$\mathcal {L}_2$
consists of some collection of words of the form
![]() $w_1 \#_1 w_2 \#_2 x^{\text {rev}}$
with
$w_1 \#_1 w_2 \#_2 x^{\text {rev}}$
with
![]() $w_1, w_2, x \in R$
such that there exist words
$w_1, w_2, x \in R$
such that there exist words
![]() $w_1', w_2', x' \in R$
with
$w_1', w_2', x' \in R$
with
![]() $w_1' \cdot w_2' =_M x'$
. As the systems
$w_1' \cdot w_2' =_M x'$
. As the systems
![]() $\mathscr {R}_1$
and
$\mathscr {R}_1$
and
![]() $\mathscr {R}_2$
are M-equivariant, and
$\mathscr {R}_2$
are M-equivariant, and
![]() $\mathscr {R}_3$
is
$\mathscr {R}_3$
is
![]() $M^{\text {rev}}$
-equivariant, it follows easily that
$M^{\text {rev}}$
-equivariant, it follows easily that
![]() $w_1 =_M w_1', w_2 =_M w_2'$
, and
$w_1 =_M w_1', w_2 =_M w_2'$
, and
![]() $x =_M x'$
. Thus,
$x =_M x'$
. Thus,
![]() $w_1 \cdot w_2 =_M x$
, so it follows that
$w_1 \cdot w_2 =_M x$
, so it follows that
![]() $\mathcal {L}_2 \subseteq \mathcal {T}_M(R)$
. We show the reverse inclusion, which (by a simple argument) suffices to show that M is word-hyperbolic.
$\mathcal {L}_2 \subseteq \mathcal {T}_M(R)$
. We show the reverse inclusion, which (by a simple argument) suffices to show that M is word-hyperbolic.
Lemma 4.6.
![]() $\mathcal {T}_M(R) = \mathcal {L}_2$
.
$\mathcal {T}_M(R) = \mathcal {L}_2$
.
Proof. We have shown the inclusion
![]() $\mathcal {L}_2 \subseteq \mathcal {T}_M(R)$
above. For the inclusion
$\mathcal {L}_2 \subseteq \mathcal {T}_M(R)$
above. For the inclusion
![]() $\mathcal {T}_M(R) \subseteq \mathcal {L}_2$
, suppose that
$\mathcal {T}_M(R) \subseteq \mathcal {L}_2$
, suppose that
![]() $w \equiv w_1 \# w_2 \#_2 x^{\text {rev}} \in \mathcal {T}_M(R)$
. First,
$w \equiv w_1 \# w_2 \#_2 x^{\text {rev}} \in \mathcal {T}_M(R)$
. First,
![]() $w_1$
is an alternating product, say
$w_1$
is an alternating product, say
![]() $w_1 \equiv w_{1,0} w_{1,1} \cdots w_{1,k}$
, where
$w_1 \equiv w_{1,0} w_{1,1} \cdots w_{1,k}$
, where
![]() $w_{1,i} \in R_{X(i)}$
for some parametrisation X. Now,
$w_{1,i} \in R_{X(i)}$
for some parametrisation X. Now,
![]() $w_1$
may not be reduced; however, by removing each factor
$w_1$
may not be reduced; however, by removing each factor
![]() $w_{i,j}$
with
$w_{i,j}$
with
![]() $w_{i,j} =_{M_{X(i)}} = 1$
, we obtain a reduced word
$w_{i,j} =_{M_{X(i)}} = 1$
, we obtain a reduced word
![]() $w_1' \equiv w_{1,i_1} w_{1,i_2} \cdots w_{1,i_{\ell }}$
. Now, it may be the case that
$w_1' \equiv w_{1,i_1} w_{1,i_2} \cdots w_{1,i_{\ell }}$
. Now, it may be the case that
![]() $w_{1,i_j} \sim w_{1,i_{j+1}}$
, that is, that
$w_{1,i_j} \sim w_{1,i_{j+1}}$
, that is, that
![]() $w_{1,i_j}$
and
$w_{1,i_j}$
and
![]() $w_{1,i_{j+1}}$
come from the same factor, and that the factorisation of
$w_{1,i_{j+1}}$
come from the same factor, and that the factorisation of
![]() $w_1'$
is not alternating. However, and crucially, as
$w_1'$
is not alternating. However, and crucially, as
![]() $R_{X(i)}^{\ast } = R_{X(i)}$
, we can find some word
$R_{X(i)}^{\ast } = R_{X(i)}$
, we can find some word
![]() $w^{\prime \prime }_{1,i_j} \in R_{X(i)}$
such that
$w^{\prime \prime }_{1,i_j} \in R_{X(i)}$
such that
![]() $w^{\prime \prime }_{1,i_j} \equiv w^{\prime }_{1,i_j} w^{\prime }_{1,i_{j+1}}$
. By merging all terms in this way, we find an alternating factorisation of
$w^{\prime \prime }_{1,i_j} \equiv w^{\prime }_{1,i_j} w^{\prime }_{1,i_{j+1}}$
. By merging all terms in this way, we find an alternating factorisation of
![]() $w_1'$
, so
$w_1'$
, so
![]() $w_1' \in R$
. Thus there exists a word
$w_1' \in R$
. Thus there exists a word
![]() $w_1' \in R$
such that
$w_1' \in R$
such that
![]() . In exactly the same way, there are words
. In exactly the same way, there are words
![]() $w_2', x' \in R$
such that
$w_2', x' \in R$
such that
![]() and
and
![]() . In particular,
. In particular,
![]() . We note in passing that
. We note in passing that
![]() $w_1' \cdot w_2' =_M x'$
, by M-equivariance. It follows from the above that
$w_1' \cdot w_2' =_M x'$
, by M-equivariance. It follows from the above that
As the words
![]() $w_1', w_2', x' \in R$
are reduced and satisfy
$w_1', w_2', x' \in R$
are reduced and satisfy
![]() $w_1' \cdot w_2' =_M x'$
, we have
$w_1' \cdot w_2' =_M x'$
, we have
From Equations (4-4) and (4-5), we find immediately by the definition in Equation (4-3) that
![]() $w \in \mathcal {L}_2$
, which is what was to be shown.
$w \in \mathcal {L}_2$
, which is what was to be shown.
To finish our proof, we must simply conclude that
![]() $\mathcal {L}_2$
is context-free, which follows by combining the facts that (i)
$\mathcal {L}_2$
is context-free, which follows by combining the facts that (i)
![]() $\mathcal {L}_1$
is a context-free language (the proof of this uses nothing about
$\mathcal {L}_1$
is a context-free language (the proof of this uses nothing about
![]() $1$
-uniqueness); (ii)
$1$
-uniqueness); (ii)
![]() $\mathscr {R}_{(3)}(\mathcal {L}_1)$
is a context-free language by Proposition 3.1; and (iii) the intersection of a context-free language with a regular language is context-free. Hence, as
$\mathscr {R}_{(3)}(\mathcal {L}_1)$
is a context-free language by Proposition 3.1; and (iii) the intersection of a context-free language with a regular language is context-free. Hence, as
![]() $\mathcal {T}_M(R) = \mathcal {L}_2$
by Lemma 4.6, it follows that
$\mathcal {T}_M(R) = \mathcal {L}_2$
by Lemma 4.6, it follows that
![]() $(R, \mathcal {T}_M(R))$
is a word-hyperbolic structure for M; as
$(R, \mathcal {T}_M(R))$
is a word-hyperbolic structure for M; as
it follows that M is
![]() $\star $
-word-hyperbolic.
$\star $
-word-hyperbolic.
The reader may feel somewhat unsatisfied by the lack of a theorem stating simply that ‘the free product of two word-hyperbolic monoids is word-hyperbolic’ (see also Section 5). However, the combination of Theorems B and 4.5 essentially covers all cases of interest. We demonstrate this now, by showing that the
![]() $\star $
-word-hyperbolic case can be viewed as a ‘complement’ to the
$\star $
-word-hyperbolic case can be viewed as a ‘complement’ to the
![]() $1$
-uniqueness case treated in Section 4.1.
$1$
-uniqueness case treated in Section 4.1.
Proposition 4.7. Suppose
![]() $M_1, M_2$
are word-hyperbolic without
$M_1, M_2$
are word-hyperbolic without
![]() $1$
-uniqueness with respect to regular combings
$1$
-uniqueness with respect to regular combings
![]() $R_1$
(respectively
$R_1$
(respectively
![]() $R_2$
), and suppose further that the monoid free product
$R_2$
), and suppose further that the monoid free product
![]() $M = M_1 \ast M_2$
is word-hyperbolic with respect to some regular combing R. If
$M = M_1 \ast M_2$
is word-hyperbolic with respect to some regular combing R. If
![]() $\operatorname {\mathrm {Alt}}(R_1, R_2) \subseteq R$
, then
$\operatorname {\mathrm {Alt}}(R_1, R_2) \subseteq R$
, then
![]() $M_1, M_2$
, and M are all
$M_1, M_2$
, and M are all
![]() $\star $
-word-hyperbolic.
$\star $
-word-hyperbolic.
Proof. Suppose that
![]() $z \in R_1$
is a nonempty word such that
$z \in R_1$
is a nonempty word such that
![]() $z =_{M_1} 1$
. Then also
$z =_{M_1} 1$
. Then also
![]() $z =_M 1$
. Let
$z =_M 1$
. Let
be any words such that
Then certainly
Now the left-hand side of Equation (4-6) is of the form
![]() $r \cdot s$
, where
$r \cdot s$
, where
![]() $r, s \in \operatorname {\mathrm {Alt}}(R_1, R_2)$
, and the right-hand side is also an element of
$r, s \in \operatorname {\mathrm {Alt}}(R_1, R_2)$
, and the right-hand side is also an element of
![]() $\operatorname {\mathrm {Alt}}(R_1, R_2)$
. Hence, we have
$\operatorname {\mathrm {Alt}}(R_1, R_2)$
. Hence, we have
is an element of
![]() $\operatorname {\mathrm {Alt}}(R_1, R_2) \,\#_1\, \operatorname {\mathrm {Alt}}(R_1, R_2) \,\#_2\, \operatorname {\mathrm {Alt}}(R_1, R_2)^{\text {rev}}$
. As
$\operatorname {\mathrm {Alt}}(R_1, R_2) \,\#_1\, \operatorname {\mathrm {Alt}}(R_1, R_2) \,\#_2\, \operatorname {\mathrm {Alt}}(R_1, R_2)^{\text {rev}}$
. As
![]() $\operatorname {\mathrm {Alt}}(R_1, R_2) \subseteq R$
, we find that Equation (4-7) is an element of
$\operatorname {\mathrm {Alt}}(R_1, R_2) \subseteq R$
, we find that Equation (4-7) is an element of
![]() $R \#_1 R \#_2 R^{\text {rev}}$
, and hence in
$R \#_1 R \#_2 R^{\text {rev}}$
, and hence in
![]() $\mathcal {T}_M(R)$
.
$\mathcal {T}_M(R)$
.
We can thus simulate the multiplication table for
![]() $M_2$
with respect to
$M_2$
with respect to
![]() $R_2^{\ast }$
by using
$R_2^{\ast }$
by using
![]() $\mathcal {T}_M(R)$
, and inserting sufficiently many z-symbols between the words in
$\mathcal {T}_M(R)$
, and inserting sufficiently many z-symbols between the words in
![]() $R_2^{\ast }$
; rigorously, we perform a rational transduction of
$R_2^{\ast }$
; rigorously, we perform a rational transduction of
![]() $\mathcal {T}_M(R)$
to first obtain all words of the form Equation (4-7), and then kill all symbols z by a homomorphic image, and in this way obtain
$\mathcal {T}_M(R)$
to first obtain all words of the form Equation (4-7), and then kill all symbols z by a homomorphic image, and in this way obtain
![]() $\mathcal {T}_{M_2}(R_2^{\ast })$
, which is thus context-free. Thus,
$\mathcal {T}_{M_2}(R_2^{\ast })$
, which is thus context-free. Thus,
![]() $M_2$
is
$M_2$
is
![]() $\star $
-word-hyperbolic; by symmetry, so too is
$\star $
-word-hyperbolic; by symmetry, so too is
![]() $M_1$
. By Theorem 4.5, so too is M.
$M_1$
. By Theorem 4.5, so too is M.
We remark on why this proposition is useful. Assume the notation of the proposition. Given the ‘alternating’ nature of a free product, it is very natural to ask for a regular combing R of M to at least contain the alternating products of elements from
![]() $R_1$
and
$R_1$
and
![]() $R_2$
. Indeed, if it did not, then the regular combing of the free product could be seen as wholly artificial, and not in any way dependent on the structure of the free factors. In this natural setting, Proposition 4.7 then tells us: if
$R_2$
. Indeed, if it did not, then the regular combing of the free product could be seen as wholly artificial, and not in any way dependent on the structure of the free factors. In this natural setting, Proposition 4.7 then tells us: if
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are word-hyperbolic, but without
$M_2$
are word-hyperbolic, but without
![]() $1$
-uniqueness, then we must have that
$1$
-uniqueness, then we must have that
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are in fact
$M_2$
are in fact
![]() $\star $
-word-hyperbolic. We elaborate on this remark in Section 4.3, and use this to suggest that a new definition of word-hyperbolic monoid may be suitable. No new results are presented therein, and so may be skipped without losing any readability of Section 5.
$\star $
-word-hyperbolic. We elaborate on this remark in Section 4.3, and use this to suggest that a new definition of word-hyperbolic monoid may be suitable. No new results are presented therein, and so may be skipped without losing any readability of Section 5.
4.3
 $1$
-uniqueness as the norm
$1$
-uniqueness as the norm
The definition of word-hyperbolic semigroups by Duncan and Gilman has been noted by Cain and Maltcev [Reference Cain and Pfeiffer26] to lead to some minor technical issues to be fixed. Namely, Cain and Maltcev note the following: there exist a finite set A, a regular language
![]() $R \subseteq A^+$
and two non-isomorphic semigroups
$R \subseteq A^+$
and two non-isomorphic semigroups
![]() $S, T$
each generated by A such that
$S, T$
each generated by A such that
![]() $\mathcal {T}_S(R) = \mathcal {T}_T(R)$
. That is, the word-hyperbolic structure
$\mathcal {T}_S(R) = \mathcal {T}_T(R)$
. That is, the word-hyperbolic structure
![]() $(R, \mathcal {T}_S(R))$
does not necessarily determine the semigroup S up to isomorphism. (However, if considering monoids, this is not an issue, as the problem arises from the fact that some generators can be indecomposable in a semigroup, which never happens in monoids.) If, however, the associated homomorphism
$(R, \mathcal {T}_S(R))$
does not necessarily determine the semigroup S up to isomorphism. (However, if considering monoids, this is not an issue, as the problem arises from the fact that some generators can be indecomposable in a semigroup, which never happens in monoids.) If, however, the associated homomorphism
![]() $\pi \colon A^+ \to S$
is assumed to be injective on A, then one can show that uniqueness up to isomorphism does hold [Reference Cain and Pfeiffer26, Proposition 3.5], and that furthermore every word-hyperbolic semigroup admits a word-hyperbolic structure with this additional ‘injectivity on generators’ requirement [Reference Cain and Pfeiffer26, Proposition 3.6]. It is therefore no real restriction to impose the requirement on word-hyperbolic semigroups that
$\pi \colon A^+ \to S$
is assumed to be injective on A, then one can show that uniqueness up to isomorphism does hold [Reference Cain and Pfeiffer26, Proposition 3.5], and that furthermore every word-hyperbolic semigroup admits a word-hyperbolic structure with this additional ‘injectivity on generators’ requirement [Reference Cain and Pfeiffer26, Proposition 3.6]. It is therefore no real restriction to impose the requirement on word-hyperbolic semigroups that
![]() $\pi $
be injective on the generators.
$\pi $
be injective on the generators.
In a similar vein, we would like to suggest that for word-hyperbolic monoids, the earlier result (Proposition 4.7) demonstrates that
![]() $1$
-uniqueness in word-hyperbolic monoids is natural. This argument is based on three desired premises:
$1$
-uniqueness in word-hyperbolic monoids is natural. This argument is based on three desired premises:
-
(1) the free product of two word-hyperbolic monoids ought to be word-hyperbolic;
-
(2) a word-hyperbolic structure for a free product should reflect the structure of the free factors in an alternating manner; and
-
(3)
 $\star $
-word-hyperbolicity should be exceptional, rather than the norm.
$\star $
-word-hyperbolicity should be exceptional, rather than the norm.
If these premises are accepted, and premise (2) is interpreted as in the paragraph following Proposition 4.7, then we conclude from Proposition 4.7 that any given word-hyperbolic monoid ought to be either
![]() $\star $
-word-hyperbolic, or else is word-hyperbolic with
$\star $
-word-hyperbolic, or else is word-hyperbolic with
![]() $1$
-uniqueness. The third premise would therefore guide us to prescribing that word-hyperbolic monoids with
$1$
-uniqueness. The third premise would therefore guide us to prescribing that word-hyperbolic monoids with
![]() $1$
-uniqueness should be the norm. If the premises are accepted, a natural definition of word-hyperbolic monoid would thus be the following: a monoid M is word-hyperbolic if and only if it admits a finite generating set A and a regular combing R such that (i) the multiplication table
$1$
-uniqueness should be the norm. If the premises are accepted, a natural definition of word-hyperbolic monoid would thus be the following: a monoid M is word-hyperbolic if and only if it admits a finite generating set A and a regular combing R such that (i) the multiplication table
![]() $\mathcal {T}_M(R)$
is context-free; and (ii)
$\mathcal {T}_M(R)$
is context-free; and (ii)
![]() $\varepsilon \in R$
, and this is the only word in R that represents
$\varepsilon \in R$
, and this is the only word in R that represents
![]() $1 \in M$
. If this were the definition of word-hyperbolic monoid, then the free product of two word-hyperbolic monoids is again word-hyperbolic (Theorem B).
$1 \in M$
. If this were the definition of word-hyperbolic monoid, then the free product of two word-hyperbolic monoids is again word-hyperbolic (Theorem B).
Whether these premises (1)–(3) are acceptable or not depends on the reader. Ideally, we would like to bypass this definition-based argument and say that every word-hyperbolic monoid admits a word-hyperbolic structure with
![]() $1$
-uniqueness, but we do not know whether this is the case. Indeed, one might suspect that this is not the case, as there are word-hyperbolic monoids that do not admit any word-hyperbolic structure with uniqueness [Reference Cain and Maltcev25].
$1$
-uniqueness, but we do not know whether this is the case. Indeed, one might suspect that this is not the case, as there are word-hyperbolic monoids that do not admit any word-hyperbolic structure with uniqueness [Reference Cain and Maltcev25].
5 Super-AFLs and
 $\mathbf {C}$
-tabled groups
$\mathbf {C}$
-tabled groups
The observant reader may have noticed that, for all our usage of the properties of context-free languages, we have nowhere used the words ‘context-free grammar’ or ‘pushdown automaton’, or any of the usual specifications of context-free languages. Indeed, we have only used two properties of the class
![]() $\mathbf {CF}$
of context-free languages, namely:
$\mathbf {CF}$
of context-free languages, namely:
-
(1)
 $\mathbf {CF}$
is a reversal-closed full
$\mathbf {CF}$
is a reversal-closed full
 $\operatorname {\mathrm {AFL}}$
; and
$\operatorname {\mathrm {AFL}}$
; and -
(2)
 $\mathbf {CF}$
has the monadic ancestor property (see Section 1.2).
$\mathbf {CF}$
has the monadic ancestor property (see Section 1.2).
That is, in the terminology of Section 1.8, we have only used the property that
![]() $\mathbf {CF}$
is a reversal-closed super-
$\mathbf {CF}$
is a reversal-closed super-
![]() $\operatorname {\mathrm {AFL}}$
. (Similarly, general statements involving reversal-closed super-
$\operatorname {\mathrm {AFL}}$
. (Similarly, general statements involving reversal-closed super-
![]() $\operatorname {\mathrm {AFL}}$
s appear as the main results in previous work by the author [Reference Nyberg-Brodda89–Reference Nyberg-Brodda91].) Hence, the main results of this article (Theorems A, B, 4.5, and their corollaries) remain valid if
$\operatorname {\mathrm {AFL}}$
s appear as the main results in previous work by the author [Reference Nyberg-Brodda89–Reference Nyberg-Brodda91].) Hence, the main results of this article (Theorems A, B, 4.5, and their corollaries) remain valid if
![]() $\mathbf {CF}$
is replaced in the definition of word-hyperbolicity by any other reversal-closed super-
$\mathbf {CF}$
is replaced in the definition of word-hyperbolicity by any other reversal-closed super-
![]() $\operatorname {\mathrm {AFL}}$
, such as
$\operatorname {\mathrm {AFL}}$
, such as
![]() $\mathbf {IND}$
or
$\mathbf {IND}$
or
![]() $\mathbf {ET0L}$
. We have chosen not to state our theorems in this general form to maintain clarity; there does not, at present, seem to be a great deal of interest in the language-theoretic properties of multiplication tables outside the case of
$\mathbf {ET0L}$
. We have chosen not to state our theorems in this general form to maintain clarity; there does not, at present, seem to be a great deal of interest in the language-theoretic properties of multiplication tables outside the case of
![]() $\mathbf {CF}$
(that is, hyperbolicity). However, due to the recent interest in the class of
$\mathbf {CF}$
(that is, hyperbolicity). However, due to the recent interest in the class of
![]() $\mathbf {ET0L}$
-languages (see Section 1.8), which forms a super-
$\mathbf {ET0L}$
-languages (see Section 1.8), which forms a super-
![]() $\operatorname {\mathrm {AFL}}$
, we opt to include this discussion in this final section.
$\operatorname {\mathrm {AFL}}$
, we opt to include this discussion in this final section.
Let S be a semigroup, finitely generated by A. We say that a regular combing
![]() $R \subseteq A^+$
is a (language of) normal forms for S if every element of S is represented by exactly one word in S. We extend this in the natural way to monoids and groups. For example, the language
$R \subseteq A^+$
is a (language of) normal forms for S if every element of S is represented by exactly one word in S. We extend this in the natural way to monoids and groups. For example, the language
![]() $a^{\ast } b^{\ast }$
is a language of normal forms for the free commutative monoid
$a^{\ast } b^{\ast }$
is a language of normal forms for the free commutative monoid
![]() $\mathrm {Mon} \langle a,b \mid ab=ba \rangle $
, and the (regular) language of freely reduced words over
$\mathrm {Mon} \langle a,b \mid ab=ba \rangle $
, and the (regular) language of freely reduced words over
![]() $(A \cup A^{-1})^{\ast }$
is a language of normal forms for the free group on A.
$(A \cup A^{-1})^{\ast }$
is a language of normal forms for the free group on A.
Definition 5.1. Let S be a semigroup, finitely generated by A. Let
![]() $\mathbf {C}$
be a class of languages. We say that S is
$\mathbf {C}$
be a class of languages. We say that S is
![]() $\mathbf {C}$
-tabled if there exists a regular language
$\mathbf {C}$
-tabled if there exists a regular language
![]() $R \subseteq A^+$
of normal forms for S such that the multiplication table
$R \subseteq A^+$
of normal forms for S such that the multiplication table
![]() $\mathcal {T}_S(R)$
lies in
$\mathcal {T}_S(R)$
lies in
![]() $\mathbf {C}$
.
$\mathbf {C}$
.
For example, the condition of being
![]() $\mathbf {CF}$
-tabled is the same as being word-hyperbolic with uniqueness. The definition is extended in the obvious way to monoids and groups. Recently, Duncan, Evetts, Holt and Rees (private communication) have proved that the free product of two
$\mathbf {CF}$
-tabled is the same as being word-hyperbolic with uniqueness. The definition is extended in the obvious way to monoids and groups. Recently, Duncan, Evetts, Holt and Rees (private communication) have proved that the free product of two
![]() $\mathbf {EDT0L}$
-tabled groups is again
$\mathbf {EDT0L}$
-tabled groups is again
![]() $\mathbf {EDT0L}$
-tabled. We are in a place to complement these results since, as justified earlier, the statements of Theorems A, B, 4.5, and their corollaries, can be altered to replace ‘word-hyperbolic’ with ‘
$\mathbf {EDT0L}$
-tabled. We are in a place to complement these results since, as justified earlier, the statements of Theorems A, B, 4.5, and their corollaries, can be altered to replace ‘word-hyperbolic’ with ‘
![]() $\mathbf {C}$
-tabled’ for any reversal-closed super-
$\mathbf {C}$
-tabled’ for any reversal-closed super-
![]() $\operatorname {\mathrm {AFL}} \mathbf {C}$
without any loss of validity. Furthermore, the uniqueness of representatives in a normal form allows us to bypass the technical conditions of, for example,
$\operatorname {\mathrm {AFL}} \mathbf {C}$
without any loss of validity. Furthermore, the uniqueness of representatives in a normal form allows us to bypass the technical conditions of, for example,
![]() $1$
-uniqueness.
$1$
-uniqueness.
Theorem A′. Let
![]() $\mathbf {C}$
be a reversal-closed super-
$\mathbf {C}$
be a reversal-closed super-
![]() $\operatorname {\mathrm {AFL}}$
. Let
$\operatorname {\mathrm {AFL}}$
. Let
![]() $S_1, S_2$
be
$S_1, S_2$
be
![]() $\mathbf {C}$
-tabled semigroups. Then the semigroup free product
$\mathbf {C}$
-tabled semigroups. Then the semigroup free product
![]() $S_1 \ast S_2$
is
$S_1 \ast S_2$
is
![]() $\mathbf {C}$
-tabled.
$\mathbf {C}$
-tabled.
Theorem B′. Let
![]() $\mathbf {C}$
be a reversal-closed super-
$\mathbf {C}$
be a reversal-closed super-
![]() $\operatorname {\mathrm {AFL}}$
. Let
$\operatorname {\mathrm {AFL}}$
. Let
![]() $M_1, M_2$
be
$M_1, M_2$
be
![]() $\mathbf {C}$
-tabled monoids. Then the monoid free product
$\mathbf {C}$
-tabled monoids. Then the monoid free product
![]() $M_1 \ast M_2$
is
$M_1 \ast M_2$
is
![]() $\mathbf {C}$
-tabled.
$\mathbf {C}$
-tabled.
These theorems, which are quite elegant to state, demonstrate that the property of having unique normal forms ensures that free products behave very well, although many of the difficulties from words representing the identity being inserted into other words are bypassed in this way. Additionally, Theorem B′ yields the corresponding result for groups and group free products, too, as the monoid free product of two groups coincides with the group free product of the same groups. In particular, we find the following corollaries, both corresponding to Corollary 4.3:
Corollary 5.2. The free product of two
![]() $\mathbf {ET0L}$
-tabled groups is
$\mathbf {ET0L}$
-tabled groups is
![]() $\mathbf {ET0L}$
-tabled.
$\mathbf {ET0L}$
-tabled.
Corollary 5.3. The free product of two
![]() $\mathbf {IND}$
-tabled groups is
$\mathbf {IND}$
-tabled groups is
![]() $\mathbf {IND}$
-tabled.
$\mathbf {IND}$
-tabled.
This complements the aforementioned result by Duncan, Evetts, Holt and Rees for
![]() $\mathbf {EDT0L}$
-tabled groups.
$\mathbf {EDT0L}$
-tabled groups.
Acknowledgements
The author wishes to thank Zeph Grunschlag for providing access to and clarifying some points in [Reference Grunschlag63]. The author also wishes to thank the anonymous referee for several helpful suggestions, which helped improve the exposition of the article.