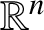1 Introduction
Bounded cohomology is defined via the topological dual of the simplicial resolution. It was introduced by Johnson and Trauber in the context of Banach algebras [Reference Johnson35], then extended by Gromov to topological spaces [Reference Gromov28]. Since then, it has become a fundamental tool in several fields, including the geometry of manifolds [Reference Gromov28], rigidity theory [Reference Burger and Monod13], the dynamics of circle actions [Reference Ghys25], and stable commutator length [Reference Calegari14].
Despite a good understanding in degree
![]() $2$
and a partial understanding in degree
$2$
and a partial understanding in degree
![]() $3$
, the full bounded cohomology of a group seems to be hard to compute [Reference Fournier-Facio, Löh and Moraschini22, Section 7]. Therefore, it is fundamental to produce alternative resolutions that compute the bounded cohomology of a group. In this respect, amenable groups played a fundamental role in the approach of Ivanov [Reference Ivanov32]. One can also exploit a larger class of groups for computing bounded cohomology, namely the class of boundedly acyclic groups [Reference Ivanov33, Reference Moraschini and Raptis48].
$3$
, the full bounded cohomology of a group seems to be hard to compute [Reference Fournier-Facio, Löh and Moraschini22, Section 7]. Therefore, it is fundamental to produce alternative resolutions that compute the bounded cohomology of a group. In this respect, amenable groups played a fundamental role in the approach of Ivanov [Reference Ivanov32]. One can also exploit a larger class of groups for computing bounded cohomology, namely the class of boundedly acyclic groups [Reference Ivanov33, Reference Moraschini and Raptis48].
Definition 1.1. Let
![]() $n \geq 1$
. A group
$n \geq 1$
. A group
![]() $\Gamma $
is said to be n-boundedly acyclic if
$\Gamma $
is said to be n-boundedly acyclic if
 $\operatorname {H}^{i}_{b}(\Gamma; {\mathbb {R}}) \cong ~0$
for all
$\operatorname {H}^{i}_{b}(\Gamma; {\mathbb {R}}) \cong ~0$
for all
![]() $i \in \{1,\ldots ,n\}$
. The group
$i \in \{1,\ldots ,n\}$
. The group
![]() $\Gamma $
is boundedly acyclic if it is n-boundedly acyclic for every
$\Gamma $
is boundedly acyclic if it is n-boundedly acyclic for every
![]() $n \geq 1$
.
$n \geq 1$
.
Amenable groups are boundedly acyclic [Reference Gromov28, Reference Johnson35]. The first nonamenable example, due to Matsumoto and Morita [Reference Matsumoto and Morita42], is the group
![]() $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
of compactly supported homeomorphisms of
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
of compactly supported homeomorphisms of
![]() $ {\mathbb {R}}^{n}$
. Their proof relies on the acyclicity of this group, which for the purposes of this paper will always be considered with respect to the integers.
$ {\mathbb {R}}^{n}$
. Their proof relies on the acyclicity of this group, which for the purposes of this paper will always be considered with respect to the integers.
Definition 1.2. A group
![]() $\Gamma $
is said to be acyclic if
$\Gamma $
is said to be acyclic if
![]() $\operatorname {H}_{n}(\Gamma; {\mathbb {Z}}) \cong 0$
for all
$\operatorname {H}_{n}(\Gamma; {\mathbb {Z}}) \cong 0$
for all
![]() $n \geq 1$
.
$n \geq 1$
.
It was shown by Mather that
![]() $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
is acyclic [Reference Mather40], and thus the proof of bounded acyclicity reduces to the proof of injectivity of the comparison map from bounded to ordinary cohomology. The same approach was employed by Löh to prove that mitotic groups are boundedly acyclic [Reference Löh39]. This class was introduced by Baumslag, Dyer and Heller [Reference Baumslag, Dyer and Heller1] to produce embedding results into finitely generated acyclic groups. Bounded acyclicity of mitotic groups, together with co-amenability of ascending HNN extensions, eventually led to finitely generated and finitely presented examples of nonamenable boundedly acyclic groups [Reference Fournier-Facio, Löh and Moraschini22].
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
is acyclic [Reference Mather40], and thus the proof of bounded acyclicity reduces to the proof of injectivity of the comparison map from bounded to ordinary cohomology. The same approach was employed by Löh to prove that mitotic groups are boundedly acyclic [Reference Löh39]. This class was introduced by Baumslag, Dyer and Heller [Reference Baumslag, Dyer and Heller1] to produce embedding results into finitely generated acyclic groups. Bounded acyclicity of mitotic groups, together with co-amenability of ascending HNN extensions, eventually led to finitely generated and finitely presented examples of nonamenable boundedly acyclic groups [Reference Fournier-Facio, Löh and Moraschini22].
The two bounded acyclicity results mentioned above are similar in spirit but independent of one another, since
![]() $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
is not mitotic [Reference Sankaran and Varadarajan49]. However, there is a larger framework that includes both
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
is not mitotic [Reference Sankaran and Varadarajan49]. However, there is a larger framework that includes both
![]() $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
and mitotic groups: binate groups (see Section 3 for the definition). This class was introduced by Berrick [Reference Berrick4] and independently by Varadarajan [Reference Varadarajan55], under the name pseudo-mitotic. They proved that binate groups are acyclic, and thus provided a unified approach to the proofs of Mather and Baumslag–Dyer–Heller, as well as several new and interesting examples of acyclic groups, mainly among groups of homeomorphisms (see Section 3.1). We adapt this unification to bounded cohomology.
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
and mitotic groups: binate groups (see Section 3 for the definition). This class was introduced by Berrick [Reference Berrick4] and independently by Varadarajan [Reference Varadarajan55], under the name pseudo-mitotic. They proved that binate groups are acyclic, and thus provided a unified approach to the proofs of Mather and Baumslag–Dyer–Heller, as well as several new and interesting examples of acyclic groups, mainly among groups of homeomorphisms (see Section 3.1). We adapt this unification to bounded cohomology.
Theorem 1.3 (Theorem 3.5)
All binate groups are boundedly acyclic.
We remark that, in general, binate groups are nonamenable, since they typically contain free subgroups. However, there are a few exceptions (Section 3.1.4).
Binate groups reflect enough of group theory to serve as a faithful testing class for open problems such as the Bass conjecture, a modified version of the Baum–Connes conjecture, or the Kervaire conjecture [Reference Berrick6]. By Theorem 1.3, boundedly acyclic groups also serve as conjecture testers. For instance, if the Bass conjecture holds for all boundedly acyclic groups, then it holds for all groups. This is especially interesting since amenable groups, which serve as the prototypical example of boundedly acyclic groups, are known to satisfy the Bass conjecture [Reference Berrick, Chatterji and Mislin7].
The bounded acyclicity of binate groups is a phenomenon that is not strictly linked to real coefficients. Indeed we prove the following theorem.
Theorem 1.4 (Corollary 5.4)
Binate groups are universally boundedly acyclic: if
![]() $\Gamma $
is a binate group, then for every complete valued field
$\Gamma $
is a binate group, then for every complete valued field
![]() $ {\mathbb {K}}$
and every
$ {\mathbb {K}}$
and every
![]() $n \geq 1$
, we have
$n \geq 1$
, we have
![]() $\operatorname {H}^{n}_{b}(\Gamma; {\mathbb {K}}) \cong 0$
.
$\operatorname {H}^{n}_{b}(\Gamma; {\mathbb {K}}) \cong 0$
.
More generally, we characterize universally boundedly acyclic groups as those groups that are simultaneously acyclic and boundedly acyclic (Theorem 5.2). In this sense, Theorem 1.4 is a combination of the acyclicity result of Berrick and Varadarajan, together with Theorem 1.3, but it also contains both results in its statement.
1.1 Hereditary properties of boundedly acyclic groups
By analogy with the amenable case, it is interesting to check which group-theoretic constructions preserve bounded acyclicity. It is known that extensions, as well as quotients with boundedly acyclic kernels, do [Reference Moraschini and Raptis48]. It is therefore natural to wonder whether these two results extend to a two-out-of-three property for bounded acyclicity and group extensions.
Using the fact that every group embeds
![]() $2$
-step subnormally into a binate group, we show that this cannot hold.
$2$
-step subnormally into a binate group, we show that this cannot hold.
Theorem 1.5 (Theorem 4.5)
There exists a boundedly acyclic group
![]() $\Gamma $
with a normal subgroup H such that
$\Gamma $
with a normal subgroup H such that
![]() $\Gamma /H$
is boundedly acyclic, but
$\Gamma /H$
is boundedly acyclic, but
![]() $\operatorname {H}^{n}_{b}(H; {\mathbb {R}})$
is continuum-dimensional for every
$\operatorname {H}^{n}_{b}(H; {\mathbb {R}})$
is continuum-dimensional for every
![]() $n \geq 2$
.
$n \geq 2$
.
We also look at directed unions of boundedly acyclic groups, and show that these are boundedly acyclic under an additional technical requirement (Proposition 4.13), which is however not needed in degree two (Corollary 4.16).
1.2 Application to Thompson groups
The advantage of Theorem 1.3 is that the class of binate groups is flexible enough that one can construct several concrete examples of boundedly acyclic groups. We use this to study the bounded cohomology of certain analogs of the classical Thompson groups F, T, and V. The amenability question for F is one of the most influential open questions in modern group theory. It is therefore natural to wonder whether F is at least boundedly acyclic. It is known that F is
![]() $2$
-boundedly acyclic, but nothing seems to be known in higher degrees. Using Theorem 1.3, we show that a countably singular analog of the Thompson group F is boundedly acyclic (Proposition 6.7).
$2$
-boundedly acyclic, but nothing seems to be known in higher degrees. Using Theorem 1.3, we show that a countably singular analog of the Thompson group F is boundedly acyclic (Proposition 6.7).
Moreover, we prove that if F is n-boundedly acyclic, then the bounded cohomology of T is generated by the real Euler class and its cup-powers, up to degree n (Corollary 6.17). In particular, we obtain the following theorem.
Theorem 1.6 (Corollaries 6.17 and 6.18)
If the Thompson group F is boundedly acyclic, then
![]() $\operatorname {H}^{*}_{b}(T; {\mathbb {R}})$
(with the cup-product structure) is isomorphic to the polynomial ring
$\operatorname {H}^{*}_{b}(T; {\mathbb {R}})$
(with the cup-product structure) is isomorphic to the polynomial ring
![]() $ {\mathbb {R}}[x]$
with
$ {\mathbb {R}}[x]$
with
![]() $|x| =2$
and the bounded Euler class of T is a polynomial generator of
$|x| =2$
and the bounded Euler class of T is a polynomial generator of
![]() $\operatorname {H}^{*}_{b}(T; {\mathbb {R}})$
. Moreover, the canonical semi-norm on
$\operatorname {H}^{*}_{b}(T; {\mathbb {R}})$
. Moreover, the canonical semi-norm on
![]() $\operatorname {H}_{b}^{*}(T; {\mathbb {R}})$
is a norm.
$\operatorname {H}_{b}^{*}(T; {\mathbb {R}})$
is a norm.
Therefore, the bounded acyclicity of F would make T into the first group of type
![]() $F_{\infty }$
that is not boundedly acyclic, and whose bounded cohomology ring can be completely and explicitly computed. Similarly, if F is boundedly acyclic, then the bounded cohomology ring of
$F_{\infty }$
that is not boundedly acyclic, and whose bounded cohomology ring can be completely and explicitly computed. Similarly, if F is boundedly acyclic, then the bounded cohomology ring of
![]() $T^{\times r}$
is a polynomial ring in r generators of degree two (Corollary 6.18).
$T^{\times r}$
is a polynomial ring in r generators of degree two (Corollary 6.18).
Independently, Monod and Nariman recently established analogous results for the bounded cohomology of the group of orientation-preserving homeomorphisms of
![]() $S^{1}$
[Reference Monod and Nariman46].
$S^{1}$
[Reference Monod and Nariman46].
1.3 A note from the future
After this paper was finished, Monod proved that the Thompson group F is boundedly acyclic [Reference Monod45]. Therefore, Theorem 1.6 shows that the bounded cohomology of the Thompson group T is isomorphic to the polynomial ring
![]() $ {\mathbb {R}}[x]$
with
$ {\mathbb {R}}[x]$
with
![]() $|x| =2$
and that the bounded Euler class of T is a polynomial generator of
$|x| =2$
and that the bounded Euler class of T is a polynomial generator of
![]() $\operatorname {H}^{*}_{b}(T; {\mathbb {R}})$
.
$\operatorname {H}^{*}_{b}(T; {\mathbb {R}})$
.
1.4 Organization of this article
We recall the definition of bounded cohomology and the uniform boundary condition in Section 2. Binate groups are surveyed in Section 3. In Section 4, we study hereditary properties of boundedly acyclic groups. Section 5 is devoted to universal bounded acyclicity. The applications to Thompson groups are discussed in Section 6. Finally, Appendix A contains the proof of Theorem 1.3.
2 Bounded cohomology
We quickly recall basic notions concerning bounded cohomology.
2.1 Definition of bounded cohomology
Let
![]() $\Gamma $
be a group and let
$\Gamma $
be a group and let
![]() $ {\mathbb {R}} \to \ell ^{\infty }(\Gamma ^{*+1})$
be the bounded simplicial
$ {\mathbb {R}} \to \ell ^{\infty }(\Gamma ^{*+1})$
be the bounded simplicial
![]() $\Gamma $
-resolution of
$\Gamma $
-resolution of
![]() $ {\mathbb {R}}$
. More generally, if V is a normed
$ {\mathbb {R}}$
. More generally, if V is a normed
![]() $\Gamma $
-module, we consider the complex
$\Gamma $
-module, we consider the complex
![]() $\ell ^{\infty }(\Gamma ^{*+1},V)$
and set
$\ell ^{\infty }(\Gamma ^{*+1},V)$
and set
 $$ \begin{align*} \operatorname{C}_{b}^{*}(\Gamma;V) := \ell^{\infty}(\Gamma^{*+1},V)^{\Gamma}. \end{align*} $$
$$ \begin{align*} \operatorname{C}_{b}^{*}(\Gamma;V) := \ell^{\infty}(\Gamma^{*+1},V)^{\Gamma}. \end{align*} $$
The bounded cohomology of
![]() $\Gamma $
with coefficients in V is defined as
$\Gamma $
with coefficients in V is defined as
The norm on
![]() $\operatorname {C}_{b}^{*}(\Gamma ;V)$
induces a semi-norm on
$\operatorname {C}_{b}^{*}(\Gamma ;V)$
induces a semi-norm on
![]() $\operatorname {H}_{b}^{*}(\Gamma ;V)$
, the so-called canonical semi-norm.
$\operatorname {H}_{b}^{*}(\Gamma ;V)$
, the so-called canonical semi-norm.
The canonical inclusion
![]() $\operatorname {C}_{b}^{*}(\Gamma ;V) \hookrightarrow \operatorname {C}^{*}(\Gamma ;V)$
induces a natural transformation between bounded cohomology and ordinary cohomology, the comparison map
$\operatorname {C}_{b}^{*}(\Gamma ;V) \hookrightarrow \operatorname {C}^{*}(\Gamma ;V)$
induces a natural transformation between bounded cohomology and ordinary cohomology, the comparison map
Further information on the bounded cohomology of groups (and spaces) can be found in the literature [Reference Frigerio24, Reference Gromov28, Reference Ivanov32].
In Section 5, we also deal with bounded cohomology over different valued fields. Recall that an absolute value on a field
![]() $ {\mathbb {K}}$
is a multiplicative map
$ {\mathbb {K}}$
is a multiplicative map
![]() $|\cdot | : {\mathbb {K}} \to {\mathbb {R}}$
such that
$|\cdot | : {\mathbb {K}} \to {\mathbb {R}}$
such that
![]() $|x| = 0$
if and only if
$|x| = 0$
if and only if
![]() $x = 0$
; and the triangle inequality holds:
$x = 0$
; and the triangle inequality holds:
![]() $|x + y| \leq |x| + |y|$
. We say that
$|x + y| \leq |x| + |y|$
. We say that
![]() $ {\mathbb {K}}$
is a complete valued field if the metric induced by the absolute value is complete. One can then define bounded cohomology over
$ {\mathbb {K}}$
is a complete valued field if the metric induced by the absolute value is complete. One can then define bounded cohomology over
![]() $ {\mathbb {K}}$
in exactly the same way.
$ {\mathbb {K}}$
in exactly the same way.
If the strong triangle inequality
![]() $|x + y| \leq \max \{ |x|, |y| \}$
holds for all
$|x + y| \leq \max \{ |x|, |y| \}$
holds for all
![]() $x,y \in {\mathbb {K}}$
, then
$x,y \in {\mathbb {K}}$
, then
![]() $ {\mathbb {K}}$
is said to be non-Archimedean. Concerning the bounded cohomology over non-Archimedean fields [Reference Fournier-Facio20], we only use the following result.
$ {\mathbb {K}}$
is said to be non-Archimedean. Concerning the bounded cohomology over non-Archimedean fields [Reference Fournier-Facio20], we only use the following result.
Lemma 2.1 [Reference Fournier-Facio20, Corollary 9.38]
Let
![]() $\Gamma $
be a group, let
$\Gamma $
be a group, let
![]() $n \geq 1$
, and suppose that
$n \geq 1$
, and suppose that
![]() $\operatorname {H}_{n-1}(\Gamma; {\mathbb {Z}})$
is finitely generated. Then the comparison map
$\operatorname {H}_{n-1}(\Gamma; {\mathbb {Z}})$
is finitely generated. Then the comparison map
is injective.
2.2 The uniform boundary condition
We recall the uniform boundary condition, originally due to Matsumoto and Morita [Reference Matsumoto and Morita42], and some of its variations [Reference Löh39].
Definition 2.2 (Uniform boundary condition)
Let
![]() $n \in {\mathbb {N}}$
and let
$n \in {\mathbb {N}}$
and let
![]() $\kappa \in {\mathbb {R}}_{> 0}$
. A group
$\kappa \in {\mathbb {R}}_{> 0}$
. A group
![]() $\Gamma $
satisfies the
$\Gamma $
satisfies the
![]() $(n, \kappa )$
-uniform boundary condition, or simply
$(n, \kappa )$
-uniform boundary condition, or simply
![]() $(n, \kappa )$
-
$(n, \kappa )$
-
![]() $\operatorname {\mathrm {UBC}}$
, if for every
$\operatorname {\mathrm {UBC}}$
, if for every
![]() $z \in \operatorname {\mathrm {im}} \partial _{n+1} \subset \operatorname {C}_{n}(\Gamma; {\mathbb {R}})$
, there exists a chain
$z \in \operatorname {\mathrm {im}} \partial _{n+1} \subset \operatorname {C}_{n}(\Gamma; {\mathbb {R}})$
, there exists a chain
![]() $c \in \operatorname {C}_{n+1}(\Gamma; {\mathbb {R}})$
with
$c \in \operatorname {C}_{n+1}(\Gamma; {\mathbb {R}})$
with
A group
![]() $\Gamma $
satisfies n-
$\Gamma $
satisfies n-
![]() $\operatorname {\mathrm {UBC}}$
if it satisfies
$\operatorname {\mathrm {UBC}}$
if it satisfies
![]() $(n, \kappa )$
-
$(n, \kappa )$
-
![]() $\operatorname {\mathrm {UBC}}$
for some
$\operatorname {\mathrm {UBC}}$
for some
![]() $\kappa \in {\mathbb {R}}_{> 0}$
.
$\kappa \in {\mathbb {R}}_{> 0}$
.
The uniform boundary condition can lead to bounded acyclicity.
Theorem 2.3 [Reference Matsumoto and Morita42, Theorem 2.8]
Let
![]() $\Gamma $
be a group and let
$\Gamma $
be a group and let
![]() $n \in {\mathbb {N}}$
. Then, the following are equivalent:
$n \in {\mathbb {N}}$
. Then, the following are equivalent:
-
(1) the group
 $\Gamma $
satisfies n-
$\Gamma $
satisfies n-
 $\operatorname {\mathrm {UBC}}$
;
$\operatorname {\mathrm {UBC}}$
; -
(2) the comparison map
 $\operatorname {\mathrm {comp}}_{\Gamma , {\mathbb {R}}}^{n+1} : \operatorname {H}_{b}^{n+1}(\Gamma; {\mathbb {R}}) \to \operatorname {H}^{n+1}(\Gamma; {\mathbb {R}})$
is injective.
$\operatorname {\mathrm {comp}}_{\Gamma , {\mathbb {R}}}^{n+1} : \operatorname {H}_{b}^{n+1}(\Gamma; {\mathbb {R}}) \to \operatorname {H}^{n+1}(\Gamma; {\mathbb {R}})$
is injective.
In particular: every acyclic group that satisfies
![]() $\operatorname {\mathrm {UBC}}$
in all positive degrees is boundedly acyclic.
$\operatorname {\mathrm {UBC}}$
in all positive degrees is boundedly acyclic.
In the proof of Theorem 1.3, it is useful to extend the definition of
![]() $\operatorname {\mathrm {UBC}}$
from groups to group homomorphisms [Reference Löh39, Definition 4.5].
$\operatorname {\mathrm {UBC}}$
from groups to group homomorphisms [Reference Löh39, Definition 4.5].
Definition 2.4 (
 $\operatorname {\mathrm {UBC}}$
for homomorphisms)
$\operatorname {\mathrm {UBC}}$
for homomorphisms)
Let
![]() $n \in {\mathbb {N}}$
and let
$n \in {\mathbb {N}}$
and let
![]() $\kappa \in {\mathbb {R}}_{> 0}$
. A group homomorphism
$\kappa \in {\mathbb {R}}_{> 0}$
. A group homomorphism
![]() $\varphi : H \to \Gamma $
satisfies the
$\varphi : H \to \Gamma $
satisfies the
![]() $(n, \kappa )$
-uniform boundary condition, or simply
$(n, \kappa )$
-uniform boundary condition, or simply
![]() $(n, \kappa )$
-
$(n, \kappa )$
-
![]() $\operatorname {\mathrm {UBC}}$
, if there exits a linear map
$\operatorname {\mathrm {UBC}}$
, if there exits a linear map
with
Here
is the operator norm of S with respect to the
![]() $\ell ^{1}$
-norms.
$\ell ^{1}$
-norms.
The uniform boundary condition will be more systematically reviewed in a forthcoming paper [Reference Li, Löh and Moraschini38].
3 Binate groups (alias pseudo-mitotic groups)
We recall basic notions, properties, and examples of binate (alias pseudo-mitotic) groups. We begin with the original definition given by Berrick [Reference Berrick4].
Definition 3.1 (Binate)
Let
![]() $\Gamma $
be a group. We say that
$\Gamma $
be a group. We say that
![]() $\Gamma $
is binate if for every finitely generated subgroup
$\Gamma $
is binate if for every finitely generated subgroup
![]() $H \leq \Gamma $
, there exists a homomorphism
$H \leq \Gamma $
, there exists a homomorphism
![]() $\varphi : H \to \Gamma $
and an element
$\varphi : H \to \Gamma $
and an element
![]() $g \in \Gamma $
such that for every
$g \in \Gamma $
such that for every
![]() $h \in H$
, we have
$h \in H$
, we have
We will rather work with the equivalent notion of pseudo-mitotic groups, introduced by Varadarajan [Reference Varadarajan55]; here an extra homomorphism
![]() $H \to \Gamma $
is taken as part of the structure, which leads to more transparent proofs. We refer the reader to the literature [Reference Berrick and Varadarajan8, Remark 2.3] for a proof of the equivalence, and point out that the terminology binate is more commonly used.
$H \to \Gamma $
is taken as part of the structure, which leads to more transparent proofs. We refer the reader to the literature [Reference Berrick and Varadarajan8, Remark 2.3] for a proof of the equivalence, and point out that the terminology binate is more commonly used.
Definition 3.2 (Pseudo-mitosis)
Let
![]() $\Gamma $
be a a group and let
$\Gamma $
be a a group and let
![]() $H \leq \Gamma $
be a subgroup. We say that H has a pseudo-mitosis in
$H \leq \Gamma $
be a subgroup. We say that H has a pseudo-mitosis in
![]() $\Gamma $
if there exist homomorphisms
$\Gamma $
if there exist homomorphisms
![]() $\psi _{0} : H \to \Gamma $
,
$\psi _{0} : H \to \Gamma $
,
![]() $\psi _{1} : H \to \Gamma $
and an element
$\psi _{1} : H \to \Gamma $
and an element
![]() $g \in \, \Gamma $
such that:
$g \in \, \Gamma $
such that:
-
(1) for every
 $h \in H$
, we have
$h \in H$
, we have
 $h \psi _{1}(h) = \psi _{0}(h)$
;
$h \psi _{1}(h) = \psi _{0}(h)$
; -
(2) for all
 $h, h^{\prime } \in \, H$
, we have
$h, h^{\prime } \in \, H$
, we have
 $[h, \psi _{1}(h^{\prime })] = 1$
;
$[h, \psi _{1}(h^{\prime })] = 1$
; -
(3) for every
 $h \in H$
, we have
$h \in H$
, we have
 $\psi _{1}(h) = g^{-1} \psi _{0}(h) g$
.
$\psi _{1}(h) = g^{-1} \psi _{0}(h) g$
.
Here is an intuitive interpretation of the definition. There exists a homomorphism
![]() $\psi _{1} : H \to \Gamma $
whose image commutes with H. This induces a homomorphism
$\psi _{1} : H \to \Gamma $
whose image commutes with H. This induces a homomorphism
Precomposing it with the diagonal inclusion
![]() $h \mapsto (h, h)$
, we get a second homomorphism
$h \mapsto (h, h)$
, we get a second homomorphism
![]() $\psi _{0} : h \mapsto h \psi _{1}(h)$
. In terms of acyclicity, the crucial condition is the third item:
$\psi _{0} : h \mapsto h \psi _{1}(h)$
. In terms of acyclicity, the crucial condition is the third item:
![]() $\psi _{0}$
and
$\psi _{0}$
and
![]() $\psi _{1}$
are conjugate inside
$\psi _{1}$
are conjugate inside
![]() $\Gamma $
.
$\Gamma $
.
Definition 3.3 (Pseudo-mitotic group)
A group
![]() $\Gamma $
is said to be pseudo-mitotic if all finitely generated subgroups of
$\Gamma $
is said to be pseudo-mitotic if all finitely generated subgroups of
![]() $\Gamma $
admit a pseudo-mitosis in
$\Gamma $
admit a pseudo-mitosis in
![]() $\Gamma $
.
$\Gamma $
.
Varadarajan [Reference Varadarajan55] and Berrick [Reference Berrick4] independently showed the following fundamental result.
Theorem 3.4 [Reference Varadarajan55, Theorem 1.7]
All pseudo-mitotic groups are acyclic.
In the present article, we prove that pseudo-mitotic groups are also examples of boundedly acyclic groups (Theorem 1.3).
Theorem 3.5. All pseudo-mitotic groups are boundedly acyclic.
Since the proof is rather technical and it closely follows those of Matsumoto– Morita [Reference Matsumoto and Morita42] and Löh [Reference Löh39], we postpone it to Appendix A.
Remark 3.6. It is an easy consequence of Theorem 3.4 that pseudo-mitotic groups are
![]() $2$
-boundedly acyclic, namely that if
$2$
-boundedly acyclic, namely that if
![]() $\Gamma $
is a pseudo-mitotic group, then
$\Gamma $
is a pseudo-mitotic group, then
 ${\operatorname {H}^{2}_{b}(\Gamma; {\mathbb {R}}) \cong 0}$
. Indeed, if
${\operatorname {H}^{2}_{b}(\Gamma; {\mathbb {R}}) \cong 0}$
. Indeed, if
![]() $\Gamma $
is a pseudo-mitotic group and
$\Gamma $
is a pseudo-mitotic group and
![]() $h \in \Gamma $
, by definition, there exist homomorphisms
$h \in \Gamma $
, by definition, there exist homomorphisms
![]() $\psi _{0}, \psi _{1} : \langle h \rangle \to \Gamma $
and an element
$\psi _{0}, \psi _{1} : \langle h \rangle \to \Gamma $
and an element
![]() $g \in \Gamma $
such that
$g \in \Gamma $
such that
In fact, this commutator expression is the one appearing in the definition of binate groups (Definition 3.1). Hence, every element in a pseudo-mitotic group is a commutator and so the second comparison map is injective [Reference Bavard2]. This shows that
 $\operatorname {H}^{2}_{b}(\Gamma; {\mathbb {R}})$
embeds into
$\operatorname {H}^{2}_{b}(\Gamma; {\mathbb {R}})$
embeds into
![]() $\operatorname {H}^{2}(\Gamma; {\mathbb {R}})$
, which vanishes by Theorem 3.4.
$\operatorname {H}^{2}(\Gamma; {\mathbb {R}})$
, which vanishes by Theorem 3.4.
3.1 Examples
We present several examples of pseudo-mitotic groups. A more detailed discussion of these examples can be found in Berrick’s work [Reference Berrick5].
We start with a combinatorial construction of pseudo-mitotic groups containing a given group.
Example 3.7 (Binate tower)
Let H be a group. Set
![]() $H_{0} := H$
, and construct
$H_{0} := H$
, and construct
![]() $H_{i+1}$
inductively by performing HNN extensions of
$H_{i+1}$
inductively by performing HNN extensions of
![]() $H_{i} \times H_{i}$
so that the embedding of
$H_{i} \times H_{i}$
so that the embedding of
![]() $H_{i}$
in the first coordinate is a pseudo-mitosis. More precisely, if
$H_{i}$
in the first coordinate is a pseudo-mitosis. More precisely, if
 $$ \begin{align*}H_{i+1} := \langle H_{i} \times H_{i}; g_{i+1} \mid g_{i+1}^{-1}(h, h) g_{i+1} = (1, h) : h \in H_{i} \rangle,\end{align*} $$
$$ \begin{align*}H_{i+1} := \langle H_{i} \times H_{i}; g_{i+1} \mid g_{i+1}^{-1}(h, h) g_{i+1} = (1, h) : h \in H_{i} \rangle,\end{align*} $$
then
![]() $h \mapsto (h, 1)$
is a pseudo-mitotic embedding of
$h \mapsto (h, 1)$
is a pseudo-mitotic embedding of
![]() $H_{i}$
in
$H_{i}$
in
![]() $H_{i+1}$
.
$H_{i+1}$
.
By construction, the direct limit of the
![]() $H_{i}$
is pseudo-mitotic. It is the initial object in a category of pseudo-mitotic groups containing H [Reference Berrick4].
$H_{i}$
is pseudo-mitotic. It is the initial object in a category of pseudo-mitotic groups containing H [Reference Berrick4].
This example shows that every group embeds into a pseudo-mitotic group. We see in the next section that a less canonical construction leads to embeddings with more special properties (Proposition 4.4).
The following example allows us to construct new binate groups from old ones.
Example 3.8. Let
![]() $(\Gamma _{i})_{i \in I}$
be a family of binate groups. Then their direct product
$(\Gamma _{i})_{i \in I}$
be a family of binate groups. Then their direct product
![]() $\prod \nolimits _{i \in I} G_{i}$
is binate [Reference Sankaran and Varadarajan49, Proposition 1.7].
$\prod \nolimits _{i \in I} G_{i}$
is binate [Reference Sankaran and Varadarajan49, Proposition 1.7].
We soon see that
![]() $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
is binate. Therefore, the previous example shows that
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
is binate. Therefore, the previous example shows that
![]() $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})^{ {\mathbb {N}}}$
is binate, whence boundedly acyclic. A direct proof of bounded acyclicity is given by Monod and Nariman [Reference Monod and Nariman46].
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})^{ {\mathbb {N}}}$
is binate, whence boundedly acyclic. A direct proof of bounded acyclicity is given by Monod and Nariman [Reference Monod and Nariman46].
For comparison, note that an arbitrary direct product of amenable groups need not be amenable. For instance, if
![]() $\Gamma $
is a nonamenable residually finite group, such as a nonabelian free group, then
$\Gamma $
is a nonamenable residually finite group, such as a nonabelian free group, then
![]() $\Gamma $
embeds into the direct product of its finite quotients, which is therefore not amenable.
$\Gamma $
embeds into the direct product of its finite quotients, which is therefore not amenable.
3.1.1 Dissipated groups
Let us move to more concrete examples. Varadarajan proved that the group
![]() $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
of compactly supported homeomorphisms of
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
of compactly supported homeomorphisms of
![]() $ {\mathbb {R}}^{n}$
is pseudo-mitotic [Reference Varadarajan55, Theorem 2.2]. Following Berrick [Reference Berrick5], we show here that this is just an instance of the behavior of a larger class of groups: dissipated boundedly supported transformation groups.
$ {\mathbb {R}}^{n}$
is pseudo-mitotic [Reference Varadarajan55, Theorem 2.2]. Following Berrick [Reference Berrick5], we show here that this is just an instance of the behavior of a larger class of groups: dissipated boundedly supported transformation groups.
Definition 3.9 (Boundedly supported group)
Let
![]() $\Gamma $
be a group acting faithfully on a set X, which is expressed as a directed union of subsets
$\Gamma $
be a group acting faithfully on a set X, which is expressed as a directed union of subsets
![]() $(X_{i})_{i \in I}$
. For each i, let
$(X_{i})_{i \in I}$
. For each i, let
![]() $\Gamma _{i} := \{ g \in \Gamma \mid g \text { is supported on } X_{i} \}$
. We say that
$\Gamma _{i} := \{ g \in \Gamma \mid g \text { is supported on } X_{i} \}$
. We say that
![]() $\Gamma $
is boundedly supported if
$\Gamma $
is boundedly supported if
![]() $\Gamma $
is the directed union of the
$\Gamma $
is the directed union of the
![]() $\Gamma _{i}$
.
$\Gamma _{i}$
.
The key property that makes certain boundedly supported groups pseudo-mitotic is the following.
Definition 3.10 (Dissipators)
Let
![]() $\Gamma \curvearrowright X$
and
$\Gamma \curvearrowright X$
and
![]() $(X_{i}, \Gamma _{i})_{i \in I}$
be as in Definition 3.9. Let
$(X_{i}, \Gamma _{i})_{i \in I}$
be as in Definition 3.9. Let
![]() $i \in I$
. A dissipator for
$i \in I$
. A dissipator for
![]() $\Gamma _{i}$
is an element
$\Gamma _{i}$
is an element
![]() $\varrho _{i} \in \Gamma $
such that:
$\varrho _{i} \in \Gamma $
such that:
-
(1)
 $\varrho _{i}^{k}(X_{i}) \cap X_{i} = \emptyset $
for all
$\varrho _{i}^{k}(X_{i}) \cap X_{i} = \emptyset $
for all
 $k \geq 1$
;
$k \geq 1$
; -
(2) for all
 $g \in \Gamma _{i}$
, the bijection of X defined by (*)is in
$g \in \Gamma _{i}$
, the bijection of X defined by (*)is in $$ \begin{align} \varphi_{i}(g) := \begin{cases} \varrho_{i}^{k} g \varrho_{i}^{-k} & \text{on } \varrho^{k}(X_{i}), \mbox{ for every } k \geq 1; \\ \operatorname{\mathrm{id}} & \text{elsewhere}, \end{cases} \end{align} $$
$$ \begin{align} \varphi_{i}(g) := \begin{cases} \varrho_{i}^{k} g \varrho_{i}^{-k} & \text{on } \varrho^{k}(X_{i}), \mbox{ for every } k \geq 1; \\ \operatorname{\mathrm{id}} & \text{elsewhere}, \end{cases} \end{align} $$
 $\Gamma $
.
$\Gamma $
.
If for each
![]() $i \in I$
there exists a dissipator for
$i \in I$
there exists a dissipator for
![]() $\Gamma _{i}$
, we say that
$\Gamma _{i}$
, we say that
![]() $\Gamma $
is dissipated.
$\Gamma $
is dissipated.
For
![]() $\varrho _{i}$
to be a dissipator, the element
$\varrho _{i}$
to be a dissipator, the element
![]() $\varphi _{i}(g)$
needs to belong to
$\varphi _{i}(g)$
needs to belong to
![]() $\Gamma $
, and the boundedly supported hypothesis implies that there exists
$\Gamma $
, and the boundedly supported hypothesis implies that there exists
![]() $j \in I$
such that
$j \in I$
such that
 $\varrho _{i}^{k}(X_{i}) \subset X_{j}$
for all
$\varrho _{i}^{k}(X_{i}) \subset X_{j}$
for all
![]() $k \geq 1$
. Figure 1 illustrates this situation.
$k \geq 1$
. Figure 1 illustrates this situation.

Figure 1 Dissipation, schematically: left, the subsets
![]() $\varrho ^{k}(X_{i})$
; right, the action of
$\varrho ^{k}(X_{i})$
; right, the action of
![]() $\varphi (g)$
.
$\varphi (g)$
.
The presence of dissipators is enough to ensure that the group is pseudo-mitotic.
Proposition 3.11 [Reference Berrick5, Section 3.1.6]
Dissipated groups are pseudo-mitotic.
Proof. Let
![]() $\Gamma \curvearrowright X$
and
$\Gamma \curvearrowright X$
and
![]() $(X_{i}, \Gamma _{i}, \varrho _{i})_{i \in I}$
be as in the definition of a dissipated group (Definition 3.10). Let
$(X_{i}, \Gamma _{i}, \varrho _{i})_{i \in I}$
be as in the definition of a dissipated group (Definition 3.10). Let
![]() $H \leq \Gamma $
be a finitely generated subgroup. Since
$H \leq \Gamma $
be a finitely generated subgroup. Since
![]() $\Gamma $
is boundedly supported, there exists an
$\Gamma $
is boundedly supported, there exists an
![]() $i \in I$
such that
$i \in I$
such that
![]() $H \leq \Gamma _{i}$
. Notice that H commutes with
$H \leq \Gamma _{i}$
. Notice that H commutes with
![]() $\varphi _{i}(H)$
(as defined in Equation (*)) since their supports are disjoint in X. Hence, if we define
$\varphi _{i}(H)$
(as defined in Equation (*)) since their supports are disjoint in X. Hence, if we define
![]() $\psi _{1} : H \to \Gamma $
as
$\psi _{1} : H \to \Gamma $
as
![]() $\psi _{1}(h) := \varphi _{i}(h)$
, it is immediate to check that
$\psi _{1}(h) := \varphi _{i}(h)$
, it is immediate to check that
![]() $\psi _{1}$
is a homomorphism and that
$\psi _{1}$
is a homomorphism and that
![]() $[h^{\prime }, \psi _{1}(h)] = 1$
for all
$[h^{\prime }, \psi _{1}(h)] = 1$
for all
![]() $h, h^{\prime } \in \, H$
. We then set
$h, h^{\prime } \in \, H$
. We then set
 $\psi _{0} := \varrho _{i}^{-1} \psi _{1} \varrho _{i} : H \to \Gamma $
and
$\psi _{0} := \varrho _{i}^{-1} \psi _{1} \varrho _{i} : H \to \Gamma $
and
 $g := \varrho _{i}^{-1} \in \Gamma $
. By construction, this implies that
$g := \varrho _{i}^{-1} \in \Gamma $
. By construction, this implies that
![]() $h \psi _{1}(h) = \psi _{0}(h)$
for all
$h \psi _{1}(h) = \psi _{0}(h)$
for all
![]() $h \in \, H$
. Hence,
$h \in \, H$
. Hence,
![]() $\psi _{0}, \psi _{1}$
and g are the witnesses of a pseudo-mitosis of H in
$\psi _{0}, \psi _{1}$
and g are the witnesses of a pseudo-mitosis of H in
![]() $\Gamma $
.
$\Gamma $
.
A more topological version of this criterion is described by Sankaran and Varadarajan [Reference Sankaran and Varadarajan50, Theorem 1.5]. Many boundedly supported groups are dissipated, and quite surprisingly, this is usually easy to check. We list some examples for which dissipators can be computed directly. More details and further constructions can be found in Berrick’s paper [Reference Berrick5, Section 3.1.6] and the references therein, as well as in that of Sankaran–Varadarajan [Reference Sankaran and Varadarajan50].
Example 3.12 (Dissipated groups)
The following groups are dissipated.
-
(1) The group
 $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
of compactly supported homeomorphisms of
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
of compactly supported homeomorphisms of
 $ {\mathbb {R}}^{n}$
is dissipated. This is already contained in a paper of Schreier and Ulam [Reference Schreier and Ulam52], where they study this phenomenon for the (isomorphic) group of homeomorphisms of the n-ball in
$ {\mathbb {R}}^{n}$
is dissipated. This is already contained in a paper of Schreier and Ulam [Reference Schreier and Ulam52], where they study this phenomenon for the (isomorphic) group of homeomorphisms of the n-ball in
 $ {\mathbb {R}}^{n}$
fixing a neighborhood of the boundary. Acyclicity was shown by Mather [Reference Mather40], and the proof serves as a model for the proof of acyclicity of pseudo-mitotic groups [Reference Varadarajan55].
$ {\mathbb {R}}^{n}$
fixing a neighborhood of the boundary. Acyclicity was shown by Mather [Reference Mather40], and the proof serves as a model for the proof of acyclicity of pseudo-mitotic groups [Reference Varadarajan55]. -
(2) The previous example generalizes to certain groups of boundedly supported homeomorphisms of topological manifolds [Reference Fisher19] and
 $C^{1}$
-manifolds [Reference Epstein18].
$C^{1}$
-manifolds [Reference Epstein18]. -
(3) Let C be the standard Cantor set, embedded in
 $[0, 1]$
. Then the group of homeomorphisms of C that are the identity in a neighborhood of
$[0, 1]$
. Then the group of homeomorphisms of C that are the identity in a neighborhood of
 $0$
and
$0$
and
 $1$
is dissipated [Reference Sankaran and Varadarajan50, Theorem 2.4].
$1$
is dissipated [Reference Sankaran and Varadarajan50, Theorem 2.4]. -
(4) Let
 $ {\mathbb {Q}}$
be endowed with the topology as a subspace of
$ {\mathbb {Q}}$
be endowed with the topology as a subspace of
 $ {\mathbb {R}}$
. Then, the group of homeomorphisms of
$ {\mathbb {R}}$
. Then, the group of homeomorphisms of
 $ {\mathbb {Q}}$
having support contained in some interval
$ {\mathbb {Q}}$
having support contained in some interval
 $[a, b]$
with
$[a, b]$
with
 $a < b \in {\mathbb {Q}}$
is dissipated. The same holds for the space of irrational numbers [Reference Sankaran and Varadarajan50, Theorem 1.13].
$a < b \in {\mathbb {Q}}$
is dissipated. The same holds for the space of irrational numbers [Reference Sankaran and Varadarajan50, Theorem 1.13]. -
(5) Forgetting the topology, denote by
 $\operatorname {\mathrm {Aut}}( {\mathbb {Q}})$
the group of bijections of
$\operatorname {\mathrm {Aut}}( {\mathbb {Q}})$
the group of bijections of
 $ {\mathbb {Q}}$
whose support is contained in some interval
$ {\mathbb {Q}}$
whose support is contained in some interval
 $(a, b)$
with
$(a, b)$
with
 $a < b \in {\mathbb {Q}}$
. Then
$a < b \in {\mathbb {Q}}$
. Then
 $\operatorname {\mathrm {Aut}}( {\mathbb {Q}})$
is dissipated [Reference Sankaran and Varadarajan49, Theorem 3.2]. The same holds for groups of bijections of infinite sets with similar properties.
$\operatorname {\mathrm {Aut}}( {\mathbb {Q}})$
is dissipated [Reference Sankaran and Varadarajan49, Theorem 3.2]. The same holds for groups of bijections of infinite sets with similar properties.
3.1.2 Flabby groups
Another source of examples are flabby groups.
Definition 3.13 (Flabby group)
A group
![]() $\Gamma $
is flabby if there exist homomorphisms
$\Gamma $
is flabby if there exist homomorphisms
![]() $\oplus : \Gamma \times \Gamma \to \Gamma $
and
$\oplus : \Gamma \times \Gamma \to \Gamma $
and
![]() $\tau : \Gamma \to \Gamma $
such that for every finitely generated subgroup
$\tau : \Gamma \to \Gamma $
such that for every finitely generated subgroup
![]() $H \leq \Gamma $
, there exist
$H \leq \Gamma $
, there exist
![]() $a, b, c \in \Gamma $
such that for all
$a, b, c \in \Gamma $
such that for all
![]() $h \in H$
:
$h \in H$
:
-
(1)
 $h \oplus 1 = a^{-1}ha$
;
$h \oplus 1 = a^{-1}ha$
; -
(2)
 $1 \oplus h = b^{-1}hb$
;
$1 \oplus h = b^{-1}hb$
; -
(3)
 $h \oplus \tau (h) = c^{-1}\tau (h)c$
.
$h \oplus \tau (h) = c^{-1}\tau (h)c$
.
Flabby groups were defined by Wagoner [Reference Wagoner56], who proved that they are acyclic. In fact, the following stronger result is true.
Lemma 3.14 [Reference Berrick4, Section 3.3]
Flabby groups are pseudo-mitotic.
Proof. Let
![]() $\Gamma $
be a flabby group and
$\Gamma $
be a flabby group and
![]() $H \leq \Gamma $
a finitely generated subgroup. Let
$H \leq \Gamma $
a finitely generated subgroup. Let
![]() $\oplus , \tau , a, b, c$
be as in the definition of a flabby group. We define
$\oplus , \tau , a, b, c$
be as in the definition of a flabby group. We define
![]() $\psi _{1}(h) := a(1 \oplus \tau (h))a^{-1}$
. Then, since
$\psi _{1}(h) := a(1 \oplus \tau (h))a^{-1}$
. Then, since
![]() $1 \oplus \Gamma $
commutes with
$1 \oplus \Gamma $
commutes with
![]() $\Gamma \oplus 1$
, we have
$\Gamma \oplus 1$
, we have
![]() $[h^{\prime }, \psi _{1}(h)] = 1$
for all
$[h^{\prime }, \psi _{1}(h)] = 1$
for all
![]() $h, h^{\prime } \in H$
. Let
$h, h^{\prime } \in H$
. Let
![]() $\psi _{0}(h) := h \psi _{1}(h)$
for every
$\psi _{0}(h) := h \psi _{1}(h)$
for every
![]() $h \in H$
. Then,
$h \in H$
. Then,
for every
![]() $h \in \, H$
. By setting
$h \in \, H$
. By setting
![]() $g := a c^{-1} b$
, we get the thesis.
$g := a c^{-1} b$
, we get the thesis.
The definition of a flabby group is more restrictive than that of a pseudo-mitotic group, since the homomorphisms
![]() $\oplus $
and
$\oplus $
and
![]() $\tau $
impose some uniformity in the choices of the homomorphisms
$\tau $
impose some uniformity in the choices of the homomorphisms
![]() $\psi _{0}$
and
$\psi _{0}$
and
![]() $\psi _{1}$
. Still, there are several examples of flabby groups in the literature.
$\psi _{1}$
. Still, there are several examples of flabby groups in the literature.
Example 3.15 (Flabby groups)
The following groups are flabby.
-
(1) To study the algebraic K theory of a ring R, Wagoner [Reference Wagoner56] embeds R into another ring
 $CR$
called the cone over R. Then the direct limit general linear group
$CR$
called the cone over R. Then the direct limit general linear group
 $\operatorname {\mathrm {GL}}(CR)$
is shown to be flabby, whence acyclic.
$\operatorname {\mathrm {GL}}(CR)$
is shown to be flabby, whence acyclic. -
(2) Building on the work of Wagoner, several other examples of flabby groups are exhibited by de la Harpe and McDuff [Reference de la Harpe and McDuff17], and they all have the following flavor. Let V be an (infinite-dimensional) Hilbert space, and let
be a chain of closed subspaces such that $$ \begin{align*}V = S_{0} \supset S_{1} \supset \cdots \supset S_{i} \supset \cdots\end{align*} $$
$$ \begin{align*}V = S_{0} \supset S_{1} \supset \cdots \supset S_{i} \supset \cdots\end{align*} $$
 $S_{i}/S_{i-1}$
is isomorphic to V for all i. Let
$S_{i}/S_{i-1}$
is isomorphic to V for all i. Let
 $\operatorname {\mathrm {GL}}(V)$
be the group of continuous linear isomorphisms of V, and let us define
$\operatorname {\mathrm {GL}}(V)$
be the group of continuous linear isomorphisms of V, and let us define
 $\Gamma _{i} := \{ g \in \operatorname {\mathrm {GL}}(V) \mid g(S_{i}^{\perp }) = S_{i}^{\perp } \}$
. Then the direct limit of the
$\Gamma _{i} := \{ g \in \operatorname {\mathrm {GL}}(V) \mid g(S_{i}^{\perp }) = S_{i}^{\perp } \}$
. Then the direct limit of the
 $\Gamma _{i}$
terms is flabby. The same holds if one restricts to unitary operators.
$\Gamma _{i}$
terms is flabby. The same holds if one restricts to unitary operators.
-
(3) Certain groups of automorphisms of measure spaces fall into the framework of the previous item, and thus are flabby [Reference de la Harpe and McDuff17].
3.1.3 Mitotic groups
Pseudo-mitotic groups were introduced by Varadarajan [Reference Varadarajan55] as a generalization of a more restricted class, that of mitotic groups, introduced by Baumslag et al. [Reference Baumslag, Dyer and Heller1]. Let us recall the following definition.
Definition 3.16 (Mitosis)
Let
![]() $\Gamma $
be a group and let
$\Gamma $
be a group and let
![]() $H \leq \Gamma $
be a subgroup. We say that H has a mitosis in
$H \leq \Gamma $
be a subgroup. We say that H has a mitosis in
![]() $\Gamma $
if there exist elements
$\Gamma $
if there exist elements
![]() $s, d \in \Gamma $
such that:
$s, d \in \Gamma $
such that:
-
(1’) for every
 $h \in \, H$
, we have
$h \in \, H$
, we have
 $h \cdot s^{-1} h s = d^{-1} h\, d$
;
$h \cdot s^{-1} h s = d^{-1} h\, d$
; -
(2’) for all
 $h, h^{\prime } \in \, H$
, we have
$h, h^{\prime } \in \, H$
, we have
 $[h, s^{-1} h^{\prime } s] = 1$
.
$[h, s^{-1} h^{\prime } s] = 1$
.
Definition 3.17 (Mitotic)
A group
![]() $\Gamma $
is said to be mitotic if all finitely generated subgroups of
$\Gamma $
is said to be mitotic if all finitely generated subgroups of
![]() $\Gamma $
admit a mitosis in
$\Gamma $
admit a mitosis in
![]() $\Gamma $
.
$\Gamma $
.
The main examples of mitotic groups are algebraically closed groups [Reference Baumslag, Dyer and Heller1, Theorem 4.3]; moreover, a functorial embedding analogous to Example 3.7 is also possible for mitotic groups.
If H has a mitosis in
![]() $\Gamma $
, then H also has a pseudo-mitosis in
$\Gamma $
, then H also has a pseudo-mitosis in
![]() $\Gamma $
: indeed, we can choose
$\Gamma $
: indeed, we can choose
![]() $\psi _{0}$
to be a conjugation by d,
$\psi _{0}$
to be a conjugation by d,
![]() $\psi _{1}$
to be a conjugation by s, and
$\psi _{1}$
to be a conjugation by s, and
![]() $g := s^{-1} d$
. Therefore, every mitotic group is pseudo-mitotic. However, the class of pseudo-mitotic groups is strictly larger, as proved by Sankaran and Varadarajan [Reference Sankaran and Varadarajan49]. Since Theorem 1.3 generalizes the bounded acyclicity of mitotic groups [Reference Löh39] to the class of pseudo-mitotic groups, let us show an explicit example of a group that is pseudo-mitotic but not mitotic.
$g := s^{-1} d$
. Therefore, every mitotic group is pseudo-mitotic. However, the class of pseudo-mitotic groups is strictly larger, as proved by Sankaran and Varadarajan [Reference Sankaran and Varadarajan49]. Since Theorem 1.3 generalizes the bounded acyclicity of mitotic groups [Reference Löh39] to the class of pseudo-mitotic groups, let us show an explicit example of a group that is pseudo-mitotic but not mitotic.
Lemma 3.18. The group
![]() $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}})$
is not mitotic.
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}})$
is not mitotic.
Proof. Let H be a finitely generated group acting minimally on
![]() $(0, 1)$
: for concreteness, one could take H to be the Thompson group F. We embed H inside
$(0, 1)$
: for concreteness, one could take H to be the Thompson group F. We embed H inside
![]() $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}})$
by letting H act trivially on
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}})$
by letting H act trivially on
![]() $ {\mathbb {R}} \setminus (0, 1)$
. Let
$ {\mathbb {R}} \setminus (0, 1)$
. Let
![]() $s \in \operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}})$
be an element such that H commutes with
$s \in \operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}})$
be an element such that H commutes with
![]() $s^{-1}Hs$
. Note that
$s^{-1}Hs$
. Note that
![]() $s^{-1}Hs$
is supported on
$s^{-1}Hs$
is supported on
![]() $s^{-1} (0, 1)$
and also acts minimally. So, to commute,
$s^{-1} (0, 1)$
and also acts minimally. So, to commute,
![]() $s^{-1}(0, 1)$
must be disjoint from
$s^{-1}(0, 1)$
must be disjoint from
![]() $(0, 1)$
.
$(0, 1)$
.
It follows that the diagonal group
![]() $\{ h s^{-1} h s \mid h \in H \}$
is supported on the disconnected set
$\{ h s^{-1} h s \mid h \in H \}$
is supported on the disconnected set
![]() $(0, 1) \cup s^{-1}(0, 1)$
, and therefore cannot be conjugate to H by an element in
$(0, 1) \cup s^{-1}(0, 1)$
, and therefore cannot be conjugate to H by an element in
![]() $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}})$
. This shows that
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}})$
. This shows that
![]() $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}})$
is not mitotic.
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}})$
is not mitotic.
With a little more work, this kind of argument can be applied to many of the groups from Example 3.12. Indeed, it is known that
![]() $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
is not mitotic [Reference Sankaran and Varadarajan49], but it is pseudo-mitotic (Example 3.12).
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
is not mitotic [Reference Sankaran and Varadarajan49], but it is pseudo-mitotic (Example 3.12).
3.1.4 Amenable examples
Most of the examples that we have seen so far are nonamenable, since they contain free subgroups. In particular, their bounded acyclicity does not follow from the classical result for amenable groups. However, there are some exceptions. The first one is due to Berrick.
Example 3.19. Hall’s countable universal locally finite group [Reference Hall29] is pseudo-mitotic [Reference Berrick4, Section 3.1]. Being locally finite, it is amenable.
Locally finite groups cannot be dissipated, since by construction, the dissipators must have infinite order. In the next example, we construct a dissipated amenable group.
Example 3.20. We start with
![]() $\Gamma _{1} = X_{1} = {\mathbb {Z}}$
, with the action given by left translation. Of course,
$\Gamma _{1} = X_{1} = {\mathbb {Z}}$
, with the action given by left translation. Of course,
![]() $\Gamma _{1}$
is amenable.
$\Gamma _{1}$
is amenable.
Next, let
![]() $X_{2}$
be the disjoint union of countably many copies of
$X_{2}$
be the disjoint union of countably many copies of
![]() $X_{1}$
indexed by
$X_{1}$
indexed by
![]() $ {\mathbb {Z}}$
, which contains a distinguished copy of
$ {\mathbb {Z}}$
, which contains a distinguished copy of
![]() $X_{1}$
, indexed by
$X_{1}$
, indexed by
![]() $0$
. The direct product
$0$
. The direct product
![]() $\Gamma _{1}^{ {\mathbb {Z}}}$
acts on
$\Gamma _{1}^{ {\mathbb {Z}}}$
acts on
![]() $X_{2}$
coordinate-wise. Let
$X_{2}$
coordinate-wise. Let
![]() $\varrho _{1}$
be the bijection of
$\varrho _{1}$
be the bijection of
![]() $X_{2}$
shifting the copies of
$X_{2}$
shifting the copies of
![]() $X_{1}$
. We set
$X_{1}$
. We set
![]() $\Gamma _{2}$
to be the group generated by the direct product
$\Gamma _{2}$
to be the group generated by the direct product
![]() $\Gamma _{1}^{ {\mathbb {Z}}}$
and
$\Gamma _{1}^{ {\mathbb {Z}}}$
and
![]() $\varrho _{1}$
. Note that
$\varrho _{1}$
. Note that
![]() $\Gamma _{2}$
splits as a semidirect product
$\Gamma _{2}$
splits as a semidirect product
 $\Gamma _{1}^{ {\mathbb {Z}}} \rtimes \langle \varrho _{1} \rangle $
, so it is
$\Gamma _{1}^{ {\mathbb {Z}}} \rtimes \langle \varrho _{1} \rangle $
, so it is
![]() $2$
-step-solvable. Moreover, given
$2$
-step-solvable. Moreover, given
![]() $g \in \Gamma _{1}$
, the element
$g \in \Gamma _{1}$
, the element
![]() $\varphi _{1}(g)$
from Definition 3.10 is just
$\varphi _{1}(g)$
from Definition 3.10 is just
 $(g_{n})_{n \in {\mathbb {Z}}} \in \Gamma _{1}^{ {\mathbb {Z}}} \leq \Gamma _{2}$
with
$(g_{n})_{n \in {\mathbb {Z}}} \in \Gamma _{1}^{ {\mathbb {Z}}} \leq \Gamma _{2}$
with
![]() $g_{n} = g$
for
$g_{n} = g$
for
![]() $n \geq 0$
and
$n \geq 0$
and
![]() $g_{n} = 0$
otherwise.
$g_{n} = 0$
otherwise.
By induction, if
![]() $\Gamma _{i}$
and
$\Gamma _{i}$
and
![]() $X_{i}$
have been constructed, we construct
$X_{i}$
have been constructed, we construct
![]() $X_{i+1}$
as the disjoint union of
$X_{i+1}$
as the disjoint union of
![]() $ {\mathbb {Z}}$
-many copies of
$ {\mathbb {Z}}$
-many copies of
![]() $X_{i}$
, we let
$X_{i}$
, we let
![]() $\varrho _{i}$
be the shift, and define
$\varrho _{i}$
be the shift, and define
![]() $\Gamma _{i+1}$
as the group generated by the direct product of the
$\Gamma _{i+1}$
as the group generated by the direct product of the
![]() $\Gamma _{i}$
and
$\Gamma _{i}$
and
![]() $\varrho _{i}$
. Then
$\varrho _{i}$
. Then
 $\Gamma _{i+1} \cong \Gamma _{i}^{ {\mathbb {Z}}} \rtimes {\mathbb {Z}}$
is
$\Gamma _{i+1} \cong \Gamma _{i}^{ {\mathbb {Z}}} \rtimes {\mathbb {Z}}$
is
![]() $(i+1)$
-step-solvable. Moreover, given
$(i+1)$
-step-solvable. Moreover, given
![]() $g \in \Gamma _{i}$
, the element
$g \in \Gamma _{i}$
, the element
![]() $\varphi _{i}(g)$
again belongs to
$\varphi _{i}(g)$
again belongs to
 $\Gamma _{i}^{ {\mathbb {Z}}} \leq \Gamma _{i+1}$
.
$\Gamma _{i}^{ {\mathbb {Z}}} \leq \Gamma _{i+1}$
.
The directed union
![]() $\Gamma $
of the
$\Gamma $
of the
![]() $\Gamma _{i}$
acts on the directed union X of the
$\Gamma _{i}$
acts on the directed union X of the
![]() $X_{i}$
. This action is boundedly supported by definition, and the
$X_{i}$
. This action is boundedly supported by definition, and the
![]() $\varrho _{i}$
are dissipators by construction. Finally,
$\varrho _{i}$
are dissipators by construction. Finally,
![]() $\Gamma $
is a directed union of solvable groups, so it is amenable.
$\Gamma $
is a directed union of solvable groups, so it is amenable.
Remark 3.21. In the construction in Example 3.20, we cannot pick any amenable group
![]() $\Gamma _{1}$
, since a direct power of amenable groups need not be amenable in general. Indeed, we strongly use the fact that a direct power of an i-step-solvable group is still i-step-solvable. By the same argument, we could have started with any group satisfying an amenable law.
$\Gamma _{1}$
, since a direct power of amenable groups need not be amenable in general. Indeed, we strongly use the fact that a direct power of an i-step-solvable group is still i-step-solvable. By the same argument, we could have started with any group satisfying an amenable law.
4 Hereditary properties of boundedly acyclic groups
In this section, we discuss the stability of bounded acyclicity under certain operations. We present new results concerning normal subgroups and directed unions. The case of normal subgroups makes use of pseudo-mitotic groups, showcasing their versatility compared with mitotic groups.
4.1 Extensions
We start with the operation of taking extensions of boundedly acyclic groups. This behaves particularly well.
Theorem 4.1 [Reference Moraschini and Raptis48, Corollary 4.2.2]
Let
![]() $1 \to N \to \Gamma \to Q \to 1$
be an exact sequence of groups, where
$1 \to N \to \Gamma \to Q \to 1$
be an exact sequence of groups, where
![]() $\varphi : \Gamma \to Q$
denotes the quotient map, and let
$\varphi : \Gamma \to Q$
denotes the quotient map, and let
![]() $n \in {\mathbb {N}}$
. Suppose that N is n-boundedly acyclic. Then
$n \in {\mathbb {N}}$
. Suppose that N is n-boundedly acyclic. Then
![]() $\Gamma $
is n-boundedly acyclic if and only if Q is n-boundedly acyclic.
$\Gamma $
is n-boundedly acyclic if and only if Q is n-boundedly acyclic.
In particular, the class of n-boundedly acyclic groups is closed under extensions. This generalizes the classical results for extensions with amenable kernels [Reference Gromov28] and amenable quotients [Reference Johnson35, Reference Monod and Popa47].
A natural question is then whether a
![]() $2$
-out-of-
$2$
-out-of-
![]() $3$
property holds.
$3$
property holds.
Question 4.2. In an extension
![]() $1 \to N \to \Gamma \to Q \to 1$
, suppose that
$1 \to N \to \Gamma \to Q \to 1$
, suppose that
![]() $\Gamma $
and Q are n-boundedly acyclic. Is N necessarily n-boundedly acyclic?
$\Gamma $
and Q are n-boundedly acyclic. Is N necessarily n-boundedly acyclic?
A characterization of when this occurs is available [Reference Moraschini and Raptis48, Corollary 4.2.1], but it is given in terms of a vanishing of bounded cohomology with a larger class of coefficients, and so it does not settle Question 4.2 in either direction. We answer Question 4.2 in the negative in Theorem 4.5.
4.2 Normal subgroups
Pseudo-mitotic groups are varied enough that they allow for several strong embedding constructions. The following is the most relevant one.
Example 4.3 (Cone over a group)
If
![]() $\Gamma $
is a group, let
$\Gamma $
is a group, let
![]() $\Gamma ^{ {\mathbb {Q}}}$
be the group of functions from
$\Gamma ^{ {\mathbb {Q}}}$
be the group of functions from
![]() $ {\mathbb {Q}}$
to
$ {\mathbb {Q}}$
to
![]() $\Gamma $
that map all numbers outside some finite interval to the neutral element. The group
$\Gamma $
that map all numbers outside some finite interval to the neutral element. The group
![]() $C\Gamma := \Gamma ^{ {\mathbb {Q}}} \rtimes \operatorname {\mathrm {Aut}}( {\mathbb {Q}})$
, where
$C\Gamma := \Gamma ^{ {\mathbb {Q}}} \rtimes \operatorname {\mathrm {Aut}}( {\mathbb {Q}})$
, where
![]() $\operatorname {\mathrm {Aut}}( {\mathbb {Q}})$
(defined in Example 3.12) acts on
$\operatorname {\mathrm {Aut}}( {\mathbb {Q}})$
(defined in Example 3.12) acts on
![]() $\Gamma ^{ {\mathbb {Q}}}$
by shifting the coordinates, is pseudo-mitotic, in fact dissipated [Reference Berrick4, Section 3.5]. The group
$\Gamma ^{ {\mathbb {Q}}}$
by shifting the coordinates, is pseudo-mitotic, in fact dissipated [Reference Berrick4, Section 3.5]. The group
![]() $C \Gamma $
is called the cone over
$C \Gamma $
is called the cone over
![]() $\Gamma $
, and was introduced by Kan and Thurston [Reference Kan and Thurston36] as a key step in the proof of their celebrated theorem.
$\Gamma $
, and was introduced by Kan and Thurston [Reference Kan and Thurston36] as a key step in the proof of their celebrated theorem.
Proposition 4.4 [Reference Berrick4, Section 3.5]
Every group embeds
![]() $2$
-step subnormally in a pseudo-mitotic group. More precisely, for every group
$2$
-step subnormally in a pseudo-mitotic group. More precisely, for every group
![]() $\Gamma $
, there exists a group
$\Gamma $
, there exists a group
![]() $\Gamma ^{0}$
such that
$\Gamma ^{0}$
such that
![]() $C\Gamma \cong (\Gamma \times \Gamma ^{0}) \rtimes \operatorname {\mathrm {Aut}}( {\mathbb {Q}})$
is pseudo-mitotic.
$C\Gamma \cong (\Gamma \times \Gamma ^{0}) \rtimes \operatorname {\mathrm {Aut}}( {\mathbb {Q}})$
is pseudo-mitotic.
Proof. By Example 4.3, it suffices to show that
![]() $\Gamma ^{ {\mathbb {Q}}} \cong \Gamma \times \Gamma ^{0}$
, for some group
$\Gamma ^{ {\mathbb {Q}}} \cong \Gamma \times \Gamma ^{0}$
, for some group
![]() $\Gamma ^{0}$
. The group
$\Gamma ^{0}$
. The group
![]() $\Gamma $
embeds normally in
$\Gamma $
embeds normally in
![]() $\Gamma ^{ {\mathbb {Q}}}$
as the subgroup of functions
$\Gamma ^{ {\mathbb {Q}}}$
as the subgroup of functions
![]() $ {\mathbb {Q}} \to \Gamma $
that map every nonzero rational to the identity. We then set
$ {\mathbb {Q}} \to \Gamma $
that map every nonzero rational to the identity. We then set
![]() $\Gamma ^{0}$
to be the subgroup of functions that map
$\Gamma ^{0}$
to be the subgroup of functions that map
![]() $0 \in {\mathbb {Q}}$
to
$0 \in {\mathbb {Q}}$
to
![]() $1 \in \Gamma $
.
$1 \in \Gamma $
.
In particular, every group embeds
![]() $2$
-step subnormally in a boundedly acyclic group. Embeddings into boundedly acyclic groups have been considered before [Reference Fournier-Facio, Löh and Moraschini22, Reference Löh39], but Proposition 4.4 goes one step further and provides a strong negative answer to Question 4.2.
$2$
-step subnormally in a boundedly acyclic group. Embeddings into boundedly acyclic groups have been considered before [Reference Fournier-Facio, Löh and Moraschini22, Reference Löh39], but Proposition 4.4 goes one step further and provides a strong negative answer to Question 4.2.
Theorem 4.5. There exists a boundedly acyclic group
![]() $\Gamma $
with a normal subgroup H such that
$\Gamma $
with a normal subgroup H such that
![]() $\Gamma /H$
is boundedly acyclic, but
$\Gamma /H$
is boundedly acyclic, but
![]() $\operatorname {H}^{n}_{b}(H; {\mathbb {R}})$
is continuum-dimensional for every
$\operatorname {H}^{n}_{b}(H; {\mathbb {R}})$
is continuum-dimensional for every
![]() $n \geq 2$
.
$n \geq 2$
.
Groups such as H above are said to have large bounded cohomology: countable [Reference Löh39] and even finitely presented [Reference Fournier-Facio, Löh and Moraschini22] examples are known to exist.
Proof. Let H be a group with large bounded cohomology. Then, for every group
![]() $\Lambda $
, the direct product
$\Lambda $
, the direct product
![]() $H \times \Lambda $
also has large bounded cohomology (as it retracts onto a group with large bounded cohomology). By Proposition 4.4 and Example 3.12, this implies that the pseudo-mitotic group
$H \times \Lambda $
also has large bounded cohomology (as it retracts onto a group with large bounded cohomology). By Proposition 4.4 and Example 3.12, this implies that the pseudo-mitotic group
![]() $\Gamma := C H$
provides the desired example.
$\Gamma := C H$
provides the desired example.
Even without the additional hypothesis on the quotient, it seems that Theorem 4.5 gives the first example of a nonboundedly acyclic normal subgroup of a boundedly acyclic group. Indeed, subgroups of amenable groups are amenable, and several of the nonamenable examples of boundedly acyclic groups available in the literature are simple, so they cannot provide counterexamples. For instance,
![]() $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
is simple, as are many other groups of boundedly supported homeomorphisms [Reference Epstein18].
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}}^{n})$
is simple, as are many other groups of boundedly supported homeomorphisms [Reference Epstein18].
4.3 Quotients
An intriguing open problem is whether boundedly acyclic groups are closed under passage to quotients [Reference Fournier-Facio, Löh and Moraschini22, Section 3.2]. One of the main difficulties about this problem is that mitotic groups behave extremely well with respect to quotients.
Lemma 4.6 [Reference Baumslag, Dyer and Heller1, page 16]
Mitotic groups are closed under passage to quotients.
However, the same behavior does not hold for pseudo-mitotic groups.
Lemma 4.7 [Reference Sankaran and Varadarajan49, Theorem 3.3]
Pseudo-mitotic groups are not closed under passage to quotients.
This suggests that pseudo-mitotic groups might be useful for constructing counterexamples for the problem above. However, the example considered by Sankaran and Varadarajan [Reference Sankaran and Varadarajan49, Theorem 3.3] still produces a boundedly acyclic quotient. Indeed, in this situation, the kernel of the epimorphism is the group of finitely supported permutations of
![]() $ {\mathbb {N}}$
, which is locally finite and therefore amenable. Hence, by Theorem 4.1 (or simply by Gromov’s mapping theorem [Reference Gromov28]), the quotient is a boundedly acyclic nonpseudo-mitotic group.
$ {\mathbb {N}}$
, which is locally finite and therefore amenable. Hence, by Theorem 4.1 (or simply by Gromov’s mapping theorem [Reference Gromov28]), the quotient is a boundedly acyclic nonpseudo-mitotic group.
A more interesting situation arises from the context of algebraic K-theory. Indeed, following Berrick [Reference Berrick3], given a (unital, associative) ring R, one can embed it into its cone
![]() $CR$
as a two-sided ideal. This leads to a short exact sequence
$CR$
as a two-sided ideal. This leads to a short exact sequence
where Q is the direct general linear group over the suspension of R, usually denoted by
![]() $\operatorname {\mathrm {GL}}(SR)$
[Reference Berrick3, page 85]. As discussed in Example 3.15(1), the group
$\operatorname {\mathrm {GL}}(SR)$
[Reference Berrick3, page 85]. As discussed in Example 3.15(1), the group
![]() $\operatorname {\mathrm {GL}}(CR)$
is a flabby group, whence pseudo-mitotic (in fact, this is also a dissipated group as proved by Berrick [Reference Berrick3, pages 84–85]). However, since one can compute the K-groups of the original ring R in terms of the plus construction over
$\operatorname {\mathrm {GL}}(CR)$
is a flabby group, whence pseudo-mitotic (in fact, this is also a dissipated group as proved by Berrick [Reference Berrick3, pages 84–85]). However, since one can compute the K-groups of the original ring R in terms of the plus construction over
![]() $\operatorname {\mathrm {GL}}(SR)$
, in general,
$\operatorname {\mathrm {GL}}(SR)$
, in general,
![]() $\operatorname {\mathrm {GL}}(SR)$
is far from being acyclic [Reference Berrick3]. Hence, the following is a natural question.
$\operatorname {\mathrm {GL}}(SR)$
is far from being acyclic [Reference Berrick3]. Hence, the following is a natural question.
Question 4.8. Let R be a ring. Is the group
![]() $\operatorname {\mathrm {GL}}(SR)$
boundedly acyclic?
$\operatorname {\mathrm {GL}}(SR)$
boundedly acyclic?
A negative answer to this question would show that boundedly acyclic groups are not closed under passage to quotients. However, here we prove the following proposition.
Proposition 4.9. Let R be a ring. Then, the group
![]() $\operatorname {\mathrm {GL}}(SR)$
is
$\operatorname {\mathrm {GL}}(SR)$
is
![]() $3$
-boundedly acyclic.
$3$
-boundedly acyclic.
Proof. Recall that a group extension provides an exact sequence in bounded cohomology in low degrees [Reference Monod43, Corollary 12.4.1 and Example 12.4.3], which in this case gives
 $$ \begin{align*} 0 \to \operatorname{H}^{2}_{b}(\operatorname{\mathrm{GL}}(SR); {\mathbb{R}}) &\to \operatorname{H}^{2}_{b}(\operatorname{\mathrm{GL}}(CR); {\mathbb{R}}) \to \operatorname{H}^{2}_{b}(\operatorname{\mathrm{GL}}(R); {\mathbb{R}})^{\operatorname{\mathrm{GL}}(SR)} \\ &\to \operatorname{H}^{3}_{b}(\operatorname{\mathrm{GL}}(SR); {\mathbb{R}}) \to \operatorname{H}^{3}_{b}(\operatorname{\mathrm{GL}}(CR); {\mathbb{R}}). \end{align*} $$
$$ \begin{align*} 0 \to \operatorname{H}^{2}_{b}(\operatorname{\mathrm{GL}}(SR); {\mathbb{R}}) &\to \operatorname{H}^{2}_{b}(\operatorname{\mathrm{GL}}(CR); {\mathbb{R}}) \to \operatorname{H}^{2}_{b}(\operatorname{\mathrm{GL}}(R); {\mathbb{R}})^{\operatorname{\mathrm{GL}}(SR)} \\ &\to \operatorname{H}^{3}_{b}(\operatorname{\mathrm{GL}}(SR); {\mathbb{R}}) \to \operatorname{H}^{3}_{b}(\operatorname{\mathrm{GL}}(CR); {\mathbb{R}}). \end{align*} $$
Using the fact that
![]() $\operatorname {\mathrm {GL}}(CR)$
is pseudo-mitotic, whence boundedly acyclic (Theorem 1.3), we then have
$\operatorname {\mathrm {GL}}(CR)$
is pseudo-mitotic, whence boundedly acyclic (Theorem 1.3), we then have
 $$ \begin{align*} \operatorname{H}^{2}_{b}(\operatorname{\mathrm{GL}}(SR); {\mathbb{R}}) \cong 0 \end{align*} $$
$$ \begin{align*} \operatorname{H}^{2}_{b}(\operatorname{\mathrm{GL}}(SR); {\mathbb{R}}) \cong 0 \end{align*} $$
and
 $$ \begin{align*} \operatorname{H}^{2}_{b}(\operatorname{\mathrm{GL}}(R); {\mathbb{R}})^{\operatorname{\mathrm{GL}}(SR)} \cong \operatorname{H}^{3}_{b}(\operatorname{\mathrm{GL}}(SR); {\mathbb{R}}). \end{align*} $$
$$ \begin{align*} \operatorname{H}^{2}_{b}(\operatorname{\mathrm{GL}}(R); {\mathbb{R}})^{\operatorname{\mathrm{GL}}(SR)} \cong \operatorname{H}^{3}_{b}(\operatorname{\mathrm{GL}}(SR); {\mathbb{R}}). \end{align*} $$
We show that
 $\operatorname {H}^{2}_{b}(\operatorname {\mathrm {GL}}(R); {\mathbb {R}}) \cong 0$
, whence the thesis.
$\operatorname {H}^{2}_{b}(\operatorname {\mathrm {GL}}(R); {\mathbb {R}}) \cong 0$
, whence the thesis.
It suffices to show that
![]() $\operatorname {\mathrm {GL}}(R)$
has commuting conjugates [Reference Fournier-Facio and Lodha21]; that is, for every finitely generated subgroup
$\operatorname {\mathrm {GL}}(R)$
has commuting conjugates [Reference Fournier-Facio and Lodha21]; that is, for every finitely generated subgroup
![]() $H \leq \operatorname {\mathrm {GL}}(R)$
, there exists
$H \leq \operatorname {\mathrm {GL}}(R)$
, there exists
![]() $g \in \operatorname {\mathrm {GL}}(R)$
such that H and
$g \in \operatorname {\mathrm {GL}}(R)$
such that H and
![]() $g^{-1} H g$
commute. Now let
$g^{-1} H g$
commute. Now let
![]() $H \leq \operatorname {\mathrm {GL}}(R)$
be finitely generated. Then there exists some
$H \leq \operatorname {\mathrm {GL}}(R)$
be finitely generated. Then there exists some
![]() $n \geq 1$
such that
$n \geq 1$
such that
![]() $H \leq \operatorname {\mathrm {GL}}_{n}(R)$
. Let
$H \leq \operatorname {\mathrm {GL}}_{n}(R)$
. Let
![]() $g \in \operatorname {\mathrm {GL}}_{2n}(R) \leq \operatorname {\mathrm {GL}}(R)$
be a permutation matrix that swaps the basis vectors
$g \in \operatorname {\mathrm {GL}}_{2n}(R) \leq \operatorname {\mathrm {GL}}(R)$
be a permutation matrix that swaps the basis vectors
![]() $e_{1}, \ldots , e_{n}$
with
$e_{1}, \ldots , e_{n}$
with
![]() $e_{n+1}, \ldots , e_{2n}$
. Then
$e_{n+1}, \ldots , e_{2n}$
. Then
![]() $g^{-1} H g$
acts trivially on the span of
$g^{-1} H g$
acts trivially on the span of
![]() $e_{1}, \ldots , e_{n}$
and H acts trivially on the span of
$e_{1}, \ldots , e_{n}$
and H acts trivially on the span of
![]() $e_{n+1}, \ldots , e_{2n}$
; therefore, these subgroups commute. We conclude that
$e_{n+1}, \ldots , e_{2n}$
; therefore, these subgroups commute. We conclude that
![]() $\operatorname {\mathrm {GL}}(R)$
has commuting conjugates and so it is
$\operatorname {\mathrm {GL}}(R)$
has commuting conjugates and so it is
![]() $2$
-boundedly acyclic [Reference Fournier-Facio and Lodha21]. This finishes the proof.
$2$
-boundedly acyclic [Reference Fournier-Facio and Lodha21]. This finishes the proof.
4.4 Directed unions
The operations we have looked at so far are known to preserve amenability. This is not surprising since amenable groups are the most illustrious examples of boundedly acyclic groups. One further operation that preserves amenability is that of directed unions. Here we study the behavior of bounded acyclicity under directed unions, and show that it is preserved under an additional technical requirement.
To proceed with the proof, it is convenient to consider the following dual version of UBC.
Definition 4.10. Let
![]() $n \in {\mathbb {N}}$
and let
$n \in {\mathbb {N}}$
and let
![]() $\Gamma $
be a group such that
$\Gamma $
be a group such that
![]() $\operatorname {H}^{n}_{b}(\Gamma; {\mathbb {R}}) \cong 0$
. We define the nth vanishing modulus of
$\operatorname {H}^{n}_{b}(\Gamma; {\mathbb {R}}) \cong 0$
. We define the nth vanishing modulus of
![]() $\Gamma $
as the minimal
$\Gamma $
as the minimal
![]() $K \in {\mathbb {R}}_{\geq 0} \cup \{\infty \}$
such that the following holds:
$K \in {\mathbb {R}}_{\geq 0} \cup \{\infty \}$
such that the following holds:
for each
![]() $c \in \ker (\delta ^{n}_{b})$
, there exists
$c \in \ker (\delta ^{n}_{b})$
, there exists
 $b \in \operatorname {C}^{n-1}_{b}(\Gamma; {\mathbb {R}})$
such that
$b \in \operatorname {C}^{n-1}_{b}(\Gamma; {\mathbb {R}})$
such that
 $$ \begin{align*}\delta^{n-1}_{b}(b) = c \quad\text{and}\quad |b|_{\infty} \leq K \cdot |c|_{\infty}.\end{align*} $$
$$ \begin{align*}\delta^{n-1}_{b}(b) = c \quad\text{and}\quad |b|_{\infty} \leq K \cdot |c|_{\infty}.\end{align*} $$
Example 4.11. Every amenable group
![]() $\Gamma $
has an nth vanishing modulus of
$\Gamma $
has an nth vanishing modulus of
![]() $1$
, for all
$1$
, for all
![]() $n \geq 1$
. Indeed, the proof of bounded acyclicity of amenable groups [Reference Frigerio24, Theorem 3.6] exhibits a contracting chain homotopy
$n \geq 1$
. Indeed, the proof of bounded acyclicity of amenable groups [Reference Frigerio24, Theorem 3.6] exhibits a contracting chain homotopy
![]() $\tau $
for the cochain complex
$\tau $
for the cochain complex
![]() $\operatorname {C}^{*}_{b}(\Gamma; {\mathbb {R}})$
, which has norm
$\operatorname {C}^{*}_{b}(\Gamma; {\mathbb {R}})$
, which has norm
![]() $1$
in every degree. Hence, given
$1$
in every degree. Hence, given
![]() $c \in \ker (\delta ^{n}_{b})$
, we can just set
$c \in \ker (\delta ^{n}_{b})$
, we can just set
![]() $b := \tau ^{n}(c)$
and obtain:
$b := \tau ^{n}(c)$
and obtain:
 $$ \begin{align*} \delta^{n-1}_{b}(b) = \delta^{n-1}_{b} \tau^{n}(c) + \tau^{n+1} \delta^{n}_{b}(c) = c. \end{align*} $$
$$ \begin{align*} \delta^{n-1}_{b}(b) = \delta^{n-1}_{b} \tau^{n}(c) + \tau^{n+1} \delta^{n}_{b}(c) = c. \end{align*} $$
In our definition, the vanishing modulus takes values in
![]() $ {\mathbb {R}}_{\geq 0} \cup \{\infty \}$
. It turns out that only finite values are possible.
$ {\mathbb {R}}_{\geq 0} \cup \{\infty \}$
. It turns out that only finite values are possible.
Lemma 4.12. Let
![]() $n \in {\mathbb {N}}$
and let
$n \in {\mathbb {N}}$
and let
![]() $\Gamma $
be such that
$\Gamma $
be such that
![]() $\operatorname {H}^{n}_{b}(\Gamma; {\mathbb {R}}) \cong 0$
. Then the nth vanishing modulus of
$\operatorname {H}^{n}_{b}(\Gamma; {\mathbb {R}}) \cong 0$
. Then the nth vanishing modulus of
![]() $\Gamma $
is finite.
$\Gamma $
is finite.
Proof. This is implicit in the work of Matsumoto and Morita [Reference Matsumoto and Morita42]: because of
![]() $\operatorname {H}_{b}^{n}(\Gamma; {\mathbb {R}}) \cong 0$
, we have
$\operatorname {H}_{b}^{n}(\Gamma; {\mathbb {R}}) \cong 0$
, we have
 $\operatorname {\mathrm {im}} \delta _{b}^{n-1} = \ker \delta _{b}^{n}$
. Hence, the bounded linear map
$\operatorname {\mathrm {im}} \delta _{b}^{n-1} = \ker \delta _{b}^{n}$
. Hence, the bounded linear map
 $\delta _{b}^{n-1}$
has closed range; by the open mapping theorem,
$\delta _{b}^{n-1}$
has closed range; by the open mapping theorem,
 $\delta _{b}^{n-1}$
induces a Banach space isomorphism
$\delta _{b}^{n-1}$
induces a Banach space isomorphism
 $$ \begin{align*} \overline\delta_{b}^{n-1} : \operatorname{C}_{b}^{n-1}(\Gamma; {\mathbb{R}}) / \ker \delta_{b}^{n-1} \to \ker \delta_{b}^{n}. \end{align*} $$
$$ \begin{align*} \overline\delta_{b}^{n-1} : \operatorname{C}_{b}^{n-1}(\Gamma; {\mathbb{R}}) / \ker \delta_{b}^{n-1} \to \ker \delta_{b}^{n}. \end{align*} $$
Let
![]() $\varphi ^{n}$
be the inverse of
$\varphi ^{n}$
be the inverse of
 $\overline \delta _{b}^{n-1}$
. If
$\overline \delta _{b}^{n-1}$
. If
![]() $c \in \ker \delta _{b}^{n}$
, then the definition of the quotient norm on
$c \in \ker \delta _{b}^{n}$
, then the definition of the quotient norm on
 $\operatorname {C}_{b}^{n-1}(\Gamma; {\mathbb {R}}) / \ker \delta _{b}^{n-1}$
shows that there exists a
$\operatorname {C}_{b}^{n-1}(\Gamma; {\mathbb {R}}) / \ker \delta _{b}^{n-1}$
shows that there exists a
 $b \in \operatorname {C}_{b}^{n-1}(\Gamma; {\mathbb {R}})$
with
$b \in \operatorname {C}_{b}^{n-1}(\Gamma; {\mathbb {R}})$
with
 $$ \begin{align*} \delta_{b}^{n-1}(b) = c \qquad\text{and}\qquad |b|_{\infty} \leq 2 \cdot \|\varphi^{n}\| \cdot |c|_{\infty}. \end{align*} $$
$$ \begin{align*} \delta_{b}^{n-1}(b) = c \qquad\text{and}\qquad |b|_{\infty} \leq 2 \cdot \|\varphi^{n}\| \cdot |c|_{\infty}. \end{align*} $$
Thus, the constant
![]() $2 \cdot \|\varphi ^{n}\|$
is a finite upper bound for the nth vanishing modulus.
$2 \cdot \|\varphi ^{n}\|$
is a finite upper bound for the nth vanishing modulus.
Proposition 4.13. Let
![]() $\Gamma $
be a group that is the directed union of a directed family
$\Gamma $
be a group that is the directed union of a directed family
![]() $(\Gamma _{i})_{i \in I}$
of subgroups. Moreover, let
$(\Gamma _{i})_{i \in I}$
of subgroups. Moreover, let
![]() $n \in {\mathbb {N}}$
and suppose that
$n \in {\mathbb {N}}$
and suppose that
![]() $\operatorname {H}^{n}_{b}(\Gamma _{i}; {\mathbb {R}}) \cong 0$
for all i, and that there is a uniform, finite upper bound for the nth vanishing moduli of all the
$\operatorname {H}^{n}_{b}(\Gamma _{i}; {\mathbb {R}}) \cong 0$
for all i, and that there is a uniform, finite upper bound for the nth vanishing moduli of all the
![]() $\Gamma _{i}$
terms. Then
$\Gamma _{i}$
terms. Then
![]() $\operatorname {H}^{n}_{b}(\Gamma; {\mathbb {R}}) \cong 0$
.
$\operatorname {H}^{n}_{b}(\Gamma; {\mathbb {R}}) \cong 0$
.
Proof. Let
![]() $K < +\infty $
be a common upper bound for the nth vanishing moduli of the
$K < +\infty $
be a common upper bound for the nth vanishing moduli of the
![]() $\Gamma _{i}$
terms. We show that the nth vanishing modulus of
$\Gamma _{i}$
terms. We show that the nth vanishing modulus of
![]() $\Gamma $
is at most K. Let
$\Gamma $
is at most K. Let
![]() $c \in \operatorname {C}_{b}^{n}(\Gamma; {\mathbb {R}})$
be a bounded cocycle. For each
$c \in \operatorname {C}_{b}^{n}(\Gamma; {\mathbb {R}})$
be a bounded cocycle. For each
![]() $i \in I$
, we set
$i \in I$
, we set
 $$ \begin{align*} B_{i} := \{ b \in \operatorname{C}_{b}^{n-1}(\Gamma; {\mathbb{R}}) \mid \delta_{b}^{n-1}(b|_{\Gamma_{i}}) = c|_{\Gamma_{i}} \text{ and } |b|_{\infty} \leq K \cdot |c|_{\infty} \}. \end{align*} $$
$$ \begin{align*} B_{i} := \{ b \in \operatorname{C}_{b}^{n-1}(\Gamma; {\mathbb{R}}) \mid \delta_{b}^{n-1}(b|_{\Gamma_{i}}) = c|_{\Gamma_{i}} \text{ and } |b|_{\infty} \leq K \cdot |c|_{\infty} \}. \end{align*} $$
It suffices to show that
![]() $\bigcap _{i \in I} B_{i} \neq \emptyset $
. To this end, we use the Banach–Alaoglu theorem: by construction, each
$\bigcap _{i \in I} B_{i} \neq \emptyset $
. To this end, we use the Banach–Alaoglu theorem: by construction, each
![]() $B_{i}$
is a bounded weak
$B_{i}$
is a bounded weak
![]() $*$
-closed subset of
$*$
-closed subset of
 $\operatorname {C}_{b}^{n-1}(\Gamma; {\mathbb {R}})$
and
$\operatorname {C}_{b}^{n-1}(\Gamma; {\mathbb {R}})$
and
![]() $B_{j} \subset B_{i}$
for all
$B_{j} \subset B_{i}$
for all
![]() $j \in I$
with
$j \in I$
with
![]() $i \leq j$
. Moreover,
$i \leq j$
. Moreover,
![]() $B_{i} \neq \emptyset $
: by hypothesis, there exists
$B_{i} \neq \emptyset $
: by hypothesis, there exists
 $b_{i} \in \operatorname {C}_{b}^{n-1}(\Gamma _{i}; {\mathbb {R}})$
with
$b_{i} \in \operatorname {C}_{b}^{n-1}(\Gamma _{i}; {\mathbb {R}})$
with
 $\delta _{b}^{n-1}(b_{i}) = c|_{\Gamma _{i}}$
and
$\delta _{b}^{n-1}(b_{i}) = c|_{\Gamma _{i}}$
and
![]() $|b_{i}|_{\infty } \leq K \cdot |c|_{\infty }$
. We now extend
$|b_{i}|_{\infty } \leq K \cdot |c|_{\infty }$
. We now extend
![]() $b_{i}$
by
$b_{i}$
by
![]() $0$
; this extension lies in
$0$
; this extension lies in
![]() $B_{i}$
.
$B_{i}$
.
Because the system is directed, the family
![]() $(B_{i})_{i\in I}$
satisfies the finite intersection property; by the Banach–Alaoglu theorem, therefore, the whole intersection
$(B_{i})_{i\in I}$
satisfies the finite intersection property; by the Banach–Alaoglu theorem, therefore, the whole intersection
![]() $\bigcap _{i \in I} B_{i}$
is nonempty.
$\bigcap _{i \in I} B_{i}$
is nonempty.
The following special case is used when studying the Thompson group F (Lemma 6.5).
Corollary 4.14. Let
![]() $\Gamma $
be a group that is the directed union of a directed family
$\Gamma $
be a group that is the directed union of a directed family
![]() $(\Gamma _{i})_{i \in I}$
of subgroups. Suppose that the
$(\Gamma _{i})_{i \in I}$
of subgroups. Suppose that the
![]() $\Gamma _{i}$
’s are pairwise isomorphic and n-boundedly acyclic. Then
$\Gamma _{i}$
’s are pairwise isomorphic and n-boundedly acyclic. Then
![]() $\Gamma $
is n-boundedly acyclic.
$\Gamma $
is n-boundedly acyclic.
In degree two, we may get rid of the uniformity condition in Proposition 4.13, thanks to the following surprising fact.
Proposition 4.15. Let
![]() $\Gamma $
be a
$\Gamma $
be a
![]() $2$
-boundedly acyclic group. Then the second vanishing modulus of
$2$
-boundedly acyclic group. Then the second vanishing modulus of
![]() $\Gamma $
is
$\Gamma $
is
![]() $1$
.
$1$
.
Proof. This is essentially a dual version of a result by Matsumoto and Morita [Reference Matsumoto and Morita42, Corollary 2.7]. First, the map
![]() $\delta _{b}^{1}$
is injective, since the only bounded homomorphism
$\delta _{b}^{1}$
is injective, since the only bounded homomorphism
![]() $\Gamma \to {\mathbb {R}}$
is the trivial one. We consider the map
$\Gamma \to {\mathbb {R}}$
is the trivial one. We consider the map
 $$ \begin{align*} \psi : \ker\delta_{b}^{2} = \operatorname{\mathrm{im}} \delta_{b}^{1} & \to \operatorname{C}^{1}_{b}(\Gamma; {\mathbb{R}}) \\ c & \mapsto \bigg( (g_{0},g_{1}) \mapsto \sum_{k=0}^{\infty} 2^{-(k+1)} \cdot c (1, g_{01}^{2^{k}}, g_{01}^{2^{k+1}}) \bigg), \end{align*} $$
$$ \begin{align*} \psi : \ker\delta_{b}^{2} = \operatorname{\mathrm{im}} \delta_{b}^{1} & \to \operatorname{C}^{1}_{b}(\Gamma; {\mathbb{R}}) \\ c & \mapsto \bigg( (g_{0},g_{1}) \mapsto \sum_{k=0}^{\infty} 2^{-(k+1)} \cdot c (1, g_{01}^{2^{k}}, g_{01}^{2^{k+1}}) \bigg), \end{align*} $$
where we use the abbreviation
 $g_{01} := g_{0}^{-1} \cdot g_{1}$
, and claim that
$g_{01} := g_{0}^{-1} \cdot g_{1}$
, and claim that
![]() $\psi $
is the inverse of
$\psi $
is the inverse of
![]() $\delta _{b}^{1}$
. By definition,
$\delta _{b}^{1}$
. By definition,
![]() $\|\psi \| \leq 1$
; moreover,
$\|\psi \| \leq 1$
; moreover,
![]() $\|\psi \| =1$
because
$\|\psi \| =1$
because
![]() $\delta _{b}^{1}$
sends constant functions to constant functions.
$\delta _{b}^{1}$
sends constant functions to constant functions.
We are left to prove the claim. Let
 $c \in \operatorname {\mathrm {im}} \delta _{b}^{1}$
, say
$c \in \operatorname {\mathrm {im}} \delta _{b}^{1}$
, say
 $c = \delta _{b}^{1}(b)$
. We need to show that
$c = \delta _{b}^{1}(b)$
. We need to show that
![]() $\psi (c) = b$
: Using
$\psi (c) = b$
: Using
![]() $\Gamma $
-invariance, we obtain for all
$\Gamma $
-invariance, we obtain for all
![]() $g_{0},g_{1} \in \Gamma $
:
$g_{0},g_{1} \in \Gamma $
:
 $$ \begin{align*} (\psi(c))(g_{0},g_{1}) & = \sum_{k=0}^{\infty} 2^{-(k+1)} \cdot ( b(g_{01}^{2^{k}}, g_{01}^{2^{k+1}}) - b (1, g_{01}^{2^{k+1}}) + b(1, g_{01}^{2^{k}})) \\ & = \sum_{k=0}^{\infty} 2^{-(k+1)} \cdot ( b(1, g_{01}^{2^{k}}) - b (1, g_{01}^{2^{k+1}}) + b(1, g_{01}^{2^{k}})) \\ & = \sum_{k=0}^{\infty} 2^{-k} \cdot b(1,g_{01}^{2^{k}}) - \sum_{k=0}^{\infty} 2^{-(k+1)} \cdot b(1,g_{01}^{2^{k+1}}) \\ & = b(1, g_{01}) = b(g_{0},g_{1}). \end{align*} $$
$$ \begin{align*} (\psi(c))(g_{0},g_{1}) & = \sum_{k=0}^{\infty} 2^{-(k+1)} \cdot ( b(g_{01}^{2^{k}}, g_{01}^{2^{k+1}}) - b (1, g_{01}^{2^{k+1}}) + b(1, g_{01}^{2^{k}})) \\ & = \sum_{k=0}^{\infty} 2^{-(k+1)} \cdot ( b(1, g_{01}^{2^{k}}) - b (1, g_{01}^{2^{k+1}}) + b(1, g_{01}^{2^{k}})) \\ & = \sum_{k=0}^{\infty} 2^{-k} \cdot b(1,g_{01}^{2^{k}}) - \sum_{k=0}^{\infty} 2^{-(k+1)} \cdot b(1,g_{01}^{2^{k+1}}) \\ & = b(1, g_{01}) = b(g_{0},g_{1}). \end{align*} $$
Note that all series involved are absolutely convergent because b is bounded, which is what allows us to change the order of summation.
Corollary 4.16. A directed union of
![]() $2$
-boundedly acyclic groups is
$2$
-boundedly acyclic groups is
![]() $2$
-boundedly acyclic.
$2$
-boundedly acyclic.
![]() $\square $
$\square $
Proposition 4.15 is essentially equivalent to the fact that the canonical semi-norm in degree two is always a norm [Reference Matsumoto and Morita42, Corollary 2.7]. This fails already in degree three [Reference Franceschini, Frigerio, Pozzetti and Sisto23, Reference Soma53], but such examples also have large bounded cohomology and so are difficult to control. Therefore, we ask the following question.
Question 4.17. Does the analog of Proposition 4.15 hold in higher degrees?
One can use Lemma 4.12 to show that a direct sum of n-boundedly acyclic groups with unbounded vanishing modulus cannot be n-boundedly acyclic. Therefore, a negative answer to this question would imply that, in higher degrees, the uniformity assumption in Proposition 4.13 is necessary.
5 Universal bounded acyclicity
In this section, we show that the bounded acyclicity of pseudo-mitotic groups is not a phenomenon confined to real coefficients. Since several different coefficients are involved in this section, we will be explicit and talk about
![]() $ {\mathbb {Z}}$
-acyclic groups (Definition 1.2) and
$ {\mathbb {Z}}$
-acyclic groups (Definition 1.2) and
![]() $ {\mathbb {R}}$
-boundedly acyclic groups (Definition 1.1).
$ {\mathbb {R}}$
-boundedly acyclic groups (Definition 1.1).
Definition 5.1. Let
![]() $ {\mathbb {K}}$
be a complete valued field, and let
$ {\mathbb {K}}$
be a complete valued field, and let
![]() $\Gamma $
be a group. We say that
$\Gamma $
be a group. We say that
![]() $\Gamma $
is
$\Gamma $
is
![]() $ {\mathbb {K}}$
-boundedly acyclic if
$ {\mathbb {K}}$
-boundedly acyclic if
![]() $\operatorname {H}^{n}_{b}(\Gamma; {\mathbb {K}}) \cong 0$
for all
$\operatorname {H}^{n}_{b}(\Gamma; {\mathbb {K}}) \cong 0$
for all
![]() $n \geq 1$
. If this holds for all complete valued fields
$n \geq 1$
. If this holds for all complete valued fields
![]() $ {\mathbb {K}}$
, we say that
$ {\mathbb {K}}$
, we say that
![]() $\Gamma $
is universally boundedly acyclic.
$\Gamma $
is universally boundedly acyclic.
We can characterize universal bounded acyclicity in very simple terms.
Theorem 5.2. Let
![]() $\Gamma $
be a group. Then
$\Gamma $
be a group. Then
![]() $\Gamma $
is universally boundedly acyclic if and only if it is
$\Gamma $
is universally boundedly acyclic if and only if it is
![]() $ {\mathbb {R}}$
-boundedly acyclic and
$ {\mathbb {R}}$
-boundedly acyclic and
![]() $ {\mathbb {Z}}$
-acyclic.
$ {\mathbb {Z}}$
-acyclic.
Remark 5.3. In fact, Theorem 5.2 even holds degree-wise. More precisely, for a group
![]() $\Gamma $
and an integer
$\Gamma $
and an integer
![]() $n \geq 1$
, the following are equivalent:
$n \geq 1$
, the following are equivalent:
-
(1)
 $\operatorname {H}^{i}_{b}(\Gamma; {\mathbb {R}}) \cong 0$
and
$\operatorname {H}^{i}_{b}(\Gamma; {\mathbb {R}}) \cong 0$
and
 $\operatorname {H}_{i}(\Gamma; {\mathbb {Z}}) \cong 0$
for all
$\operatorname {H}_{i}(\Gamma; {\mathbb {Z}}) \cong 0$
for all
 $i \in \{1, \ldots , n\}$
;
$i \in \{1, \ldots , n\}$
; -
(2)
 $\operatorname {H}^{i}_{b}(\Gamma; {\mathbb {K}}) \cong 0$
for every complete valued field
$\operatorname {H}^{i}_{b}(\Gamma; {\mathbb {K}}) \cong 0$
for every complete valued field
 $ {\mathbb {K}}$
and all
$ {\mathbb {K}}$
and all
 $i \in \{1, \ldots , n\}$
.
$i \in \{1, \ldots , n\}$
.
This will be apparent from the proof, but we prefer to state the theorem in global terms to simplify the notation.
Before giving the proof, we note the following consequence.
Corollary 5.4. Pseudo-mitotic groups are universally boundedly acyclic.
Proof. Pseudo-mitotic groups are both acyclic (Theorem 3.4) and boundedly acyclic (Theorem 3.5). Therefore, we can apply Theorem 5.2.
The proof of Theorem 5.2 is carried out in two steps: the Archimedean and the non-Archimedean case.
Lemma 5.5. Let
![]() $\Gamma $
be a group. Then
$\Gamma $
be a group. Then
![]() $\Gamma $
is
$\Gamma $
is
![]() $ {\mathbb {R}}$
-boundedly acyclic if and only if
$ {\mathbb {R}}$
-boundedly acyclic if and only if
![]() $\Gamma $
is
$\Gamma $
is
![]() $ {\mathbb {C}}$
-boundedly acyclic.
$ {\mathbb {C}}$
-boundedly acyclic.
Proof. Because we have
![]() $ {\mathbb {C}} \cong {\mathbb {R}}^{2}$
as normed
$ {\mathbb {C}} \cong {\mathbb {R}}^{2}$
as normed
![]() $ {\mathbb {R}}$
-vector spaces, the cochain complex
$ {\mathbb {R}}$
-vector spaces, the cochain complex
![]() $\operatorname {C}_{b}^{*}(\Gamma; {\mathbb {C}})$
splits as the direct sum
$\operatorname {C}_{b}^{*}(\Gamma; {\mathbb {C}})$
splits as the direct sum
 $\operatorname {C}_{b}^{*}(\Gamma; {\mathbb {R}})^{\oplus 2}$
. Therefore, we obtain the isomorphism
$\operatorname {C}_{b}^{*}(\Gamma; {\mathbb {R}})^{\oplus 2}$
. Therefore, we obtain the isomorphism
 $\operatorname {H}_{b}^{*}(\Gamma; {\mathbb {C}}) \cong \operatorname {H}_{b}^{*}(\Gamma; {\mathbb {R}})^{\oplus 2} $
(over
$\operatorname {H}_{b}^{*}(\Gamma; {\mathbb {C}}) \cong \operatorname {H}_{b}^{*}(\Gamma; {\mathbb {R}})^{\oplus 2} $
(over
![]() $ {\mathbb {R}}$
). The claim easily follows.
$ {\mathbb {R}}$
). The claim easily follows.
Lemma 5.6. Let
![]() $\Gamma $
be a group. Then
$\Gamma $
be a group. Then
![]() $\Gamma $
is
$\Gamma $
is
![]() $ {\mathbb {K}}$
-boundedly acyclic for every non-Archimedean field
$ {\mathbb {K}}$
-boundedly acyclic for every non-Archimedean field
![]() $ {\mathbb {K}}$
if and only if it is
$ {\mathbb {K}}$
if and only if it is
![]() $ {\mathbb {Z}}$
-acyclic.
$ {\mathbb {Z}}$
-acyclic.
Proof. Suppose that
![]() $\Gamma $
is
$\Gamma $
is
![]() $ {\mathbb {K}}$
-boundedly acyclic for every non-Archimedean field
$ {\mathbb {K}}$
-boundedly acyclic for every non-Archimedean field
![]() $ {\mathbb {K}}$
. Endowing an arbitrary field
$ {\mathbb {K}}$
. Endowing an arbitrary field
![]() $ {\mathbb {K}}$
with the trivial norm, we deduce that
$ {\mathbb {K}}$
with the trivial norm, we deduce that
![]() $\operatorname {H}^{n}(\Gamma; {\mathbb {K}}) \cong 0$
for every field
$\operatorname {H}^{n}(\Gamma; {\mathbb {K}}) \cong 0$
for every field
![]() $ {\mathbb {K}}$
. It then follows from the universal coefficient theorem [Reference Brown10, Ch. I] that
$ {\mathbb {K}}$
. It then follows from the universal coefficient theorem [Reference Brown10, Ch. I] that
![]() $\Gamma $
is
$\Gamma $
is
![]() $ {\mathbb {K}}$
-acyclic for every field
$ {\mathbb {K}}$
-acyclic for every field
![]() $ {\mathbb {K}}$
, that is,
$ {\mathbb {K}}$
, that is,
![]() $\operatorname {H}_{n}(\Gamma; {\mathbb {K}}) \cong 0$
for all
$\operatorname {H}_{n}(\Gamma; {\mathbb {K}}) \cong 0$
for all
![]() $n \geq 1$
. In particular,
$n \geq 1$
. In particular,
![]() $\Gamma $
is
$\Gamma $
is
![]() $ {\mathbb {Q}}$
-acyclic and
$ {\mathbb {Q}}$
-acyclic and
![]() $ {\mathbb {F}_{p}}$
-acyclic for every prime p; so
$ {\mathbb {F}_{p}}$
-acyclic for every prime p; so
![]() $\Gamma $
is
$\Gamma $
is
![]() $ {\mathbb {Z}}$
-acyclic [Reference Hatcher30, Corollary 3A.7].
$ {\mathbb {Z}}$
-acyclic [Reference Hatcher30, Corollary 3A.7].
Conversely, let us suppose that
![]() $\Gamma $
is
$\Gamma $
is
![]() $ {\mathbb {Z}}$
-acyclic, and let
$ {\mathbb {Z}}$
-acyclic, and let
![]() $ {\mathbb {K}}$
be a non-Archimedean field
$ {\mathbb {K}}$
be a non-Archimedean field
![]() $ {\mathbb {K}}$
. By Lemma 2.1, the comparison map
$ {\mathbb {K}}$
. By Lemma 2.1, the comparison map
![]() $\operatorname {H}^{n}_{b}(\Gamma; {\mathbb {K}}) \to \operatorname {H}^{n}(\Gamma; {\mathbb {K}})$
is injective. So it suffices to show that
$\operatorname {H}^{n}_{b}(\Gamma; {\mathbb {K}}) \to \operatorname {H}^{n}(\Gamma; {\mathbb {K}})$
is injective. So it suffices to show that
![]() $\operatorname {H}^{n}(\Gamma; {\mathbb {K}}) \cong 0$
. This follows immediately from the universal coefficient theorem; hence,
$\operatorname {H}^{n}(\Gamma; {\mathbb {K}}) \cong 0$
. This follows immediately from the universal coefficient theorem; hence,
![]() $\Gamma $
is
$\Gamma $
is
![]() $ {\mathbb {K}}$
-boundedly acyclic.
$ {\mathbb {K}}$
-boundedly acyclic.
Proof of Theorem 5.2
By Ostrowski’s theorem [Reference Cassels16, Ch. 3], every complete valued field is either non-Archimedean or isomorphic to
![]() $ {\mathbb {R}}$
or
$ {\mathbb {R}}$
or
![]() $ {\mathbb {C}}$
. So Theorem 5.2 follows from Lemmas 5.5 and 5.6.□
$ {\mathbb {C}}$
. So Theorem 5.2 follows from Lemmas 5.5 and 5.6.□
Remark 5.7. Corollary 5.4 provides many examples of groups that are universally boundedly acyclic. One could ask whether something similar could be said for the stronger notion of universal amenability, defined analogously using the general notion of
![]() $ {\mathbb {K}}$
-amenability for valued fields defined by Shikhof [Reference Schikhof51]. However, it turns out that if
$ {\mathbb {K}}$
-amenability for valued fields defined by Shikhof [Reference Schikhof51]. However, it turns out that if
![]() $\Gamma $
is
$\Gamma $
is
![]() $ {\mathbb {F}_{p}}$
-amenable in the sense of Shikhof for every prime p, then
$ {\mathbb {F}_{p}}$
-amenable in the sense of Shikhof for every prime p, then
![]() $\Gamma $
is trivial [Reference Fournier-Facio20, Example 5.5 and Theorem 6.2]. The same holds for the weaker notion of normed
$\Gamma $
is trivial [Reference Fournier-Facio20, Example 5.5 and Theorem 6.2]. The same holds for the weaker notion of normed
![]() $ {\mathbb {K}}$
-amenability [Reference Fournier-Facio20], which also implies bounded
$ {\mathbb {K}}$
-amenability [Reference Fournier-Facio20], which also implies bounded
![]() $ {\mathbb {K}}$
-acyclicity [Reference Fournier-Facio20, Theorem 1.3].
$ {\mathbb {K}}$
-acyclicity [Reference Fournier-Facio20, Theorem 1.3].
Corollary 5.8. Let
![]() $\Gamma $
be a universally boundedly acyclic group. Then, for all
$\Gamma $
be a universally boundedly acyclic group. Then, for all
![]() $n \geq 1$
, we have
$n \geq 1$
, we have
![]() $\operatorname {H}_{b}^{n}(\Gamma; {\mathbb {Z}}) \cong 0$
, with the standard absolute value on
$\operatorname {H}_{b}^{n}(\Gamma; {\mathbb {Z}}) \cong 0$
, with the standard absolute value on
![]() $ {\mathbb {Z}}$
.
$ {\mathbb {Z}}$
.
Proof. The short exact sequence
![]() $0 \to {\mathbb {Z}} \to {\mathbb {R}} \to {\mathbb {R}}/ {\mathbb {Z}} \to 0$
induces a long exact sequence [Reference Frigerio24, proof of Proposition 2.13]
$0 \to {\mathbb {Z}} \to {\mathbb {R}} \to {\mathbb {R}}/ {\mathbb {Z}} \to 0$
induces a long exact sequence [Reference Frigerio24, proof of Proposition 2.13]
 $$ \begin{align*} \cdots \to \operatorname{H}_{b}^{n-1} (\Gamma; {\mathbb{R}}) \to \operatorname{H}^{n-1}(\Gamma; {\mathbb{R}}/ {\mathbb{Z}}) \to \operatorname{H}_{b}^{n}(\Gamma; {\mathbb{Z}}) \to \operatorname{H}_{b}^{n}(\Gamma; {\mathbb{R}}) \to \dotsm. \end{align*} $$
$$ \begin{align*} \cdots \to \operatorname{H}_{b}^{n-1} (\Gamma; {\mathbb{R}}) \to \operatorname{H}^{n-1}(\Gamma; {\mathbb{R}}/ {\mathbb{Z}}) \to \operatorname{H}_{b}^{n}(\Gamma; {\mathbb{Z}}) \to \operatorname{H}_{b}^{n}(\Gamma; {\mathbb{R}}) \to \dotsm. \end{align*} $$
By Theorem 5.2, the group
![]() $\Gamma $
is
$\Gamma $
is
![]() $ {\mathbb {R}}$
-boundedly acyclic and
$ {\mathbb {R}}$
-boundedly acyclic and
![]() $ {\mathbb {Z}}$
-acyclic. The universal coefficient theorem and
$ {\mathbb {Z}}$
-acyclic. The universal coefficient theorem and
![]() $ {\mathbb {Z}}$
-acyclicity give
$ {\mathbb {Z}}$
-acyclicity give
![]() $\operatorname {H}^{k}(\Gamma; {\mathbb {R}}/ {\mathbb {Z}}) \cong 0$
for all
$\operatorname {H}^{k}(\Gamma; {\mathbb {R}}/ {\mathbb {Z}}) \cong 0$
for all
![]() $k>0$
. Therefore, the long exact sequence and surjectivitiy of the induced map
$k>0$
. Therefore, the long exact sequence and surjectivitiy of the induced map
 $\operatorname {H}_{b}^{0}(\Gamma; {\mathbb {R}}) \to \operatorname {H}^{0}(\Gamma; {\mathbb {R}}/ {\mathbb {Z}})$
show that
$\operatorname {H}_{b}^{0}(\Gamma; {\mathbb {R}}) \to \operatorname {H}^{0}(\Gamma; {\mathbb {R}}/ {\mathbb {Z}})$
show that
![]() $\operatorname {H}_{b}^{n}(\Gamma; {\mathbb {Z}}) \cong 0$
for all
$\operatorname {H}_{b}^{n}(\Gamma; {\mathbb {Z}}) \cong 0$
for all
![]() $n\geq 1$
.
$n\geq 1$
.
6 Thompson groups and their siblings
The groups F, T, and V were introduced by Richard Thompson in 1965; they are some of the most important groups in geometric and dynamical group theory. These groups can be realized as groups of homeomorphisms of the interval, the circle, and the Cantor set respectively; these realizations exhibit inclusions
![]() $F \leq T \leq V$
. We refer the reader to the literature [Reference Cannon, Floyd and Parry15] for a detailed discussion.
$F \leq T \leq V$
. We refer the reader to the literature [Reference Cannon, Floyd and Parry15] for a detailed discussion.
The groups F, T, and V are finitely presented, even of type
![]() $F_{\infty }$
. Moreover, T and V are simple (in fact, they were the first examples of infinite finitely presented simple groups). However, F has abelianization
$F_{\infty }$
. Moreover, T and V are simple (in fact, they were the first examples of infinite finitely presented simple groups). However, F has abelianization
![]() $ {\mathbb {Z}}^{2}$
, but its derived subgroup
$ {\mathbb {Z}}^{2}$
, but its derived subgroup
![]() $F^{\prime }$
is simple, and infinitely generated.
$F^{\prime }$
is simple, and infinitely generated.
The rational cohomology [Reference Brown9, Reference Ghys and Sergiescu26] and, with the exception of T, the integral cohomology [Reference Brown and Geoghegan11, Reference Ghys and Sergiescu26, Reference Szymik and Wahl54] of these groups has been computed. However, little is known about their real bounded cohomology. We formulate one question for each group.
Question 6.1. Is the Thompson group F boundedly acyclic?
Question 6.1 is usually attributed to Grigorchuk [Reference Grigorchuk27, page 131, Problem 3.19].
Question 6.2. Does the following hold?
The bounded cohomology of the Thompson group T is given by
 $$ \begin{align*}\operatorname{H}^{n}_{b}(T; {\mathbb{R}}) \cong \begin{cases} 0 & \text{if } n \text{ is odd}, \\ {\mathbb{R}} & \text{if } n \text{ is even}, \end{cases}\end{align*} $$
$$ \begin{align*}\operatorname{H}^{n}_{b}(T; {\mathbb{R}}) \cong \begin{cases} 0 & \text{if } n \text{ is odd}, \\ {\mathbb{R}} & \text{if } n \text{ is even}, \end{cases}\end{align*} $$
where the nontrivial classes are spanned by cup-powers of the bounded real Euler class.
Question 6.3. Is the Thompson group V boundedly acyclic?
The rest of this section is devoted to discussing these three questions, how they relate to each other, and providing some evidence towards positive answers.
One may also formulate corresponding questions for every degree, namely whether the previous descriptions hold up to degree n. We see that all three questions have a positive answer up to degree two, while to our knowledge, nothing is known from degree three onwards.
6.1 On the bounded cohomology of F
We recall the definition of F.
Definition 6.4. The Thompson group F is the group of orientation-preserving piecewise linear homeomorphisms f of the interval
![]() $[0, 1]$
with the following properties:
$[0, 1]$
with the following properties:
-
(1) f has finitely many breakpoints, all of which lie in
 $ {\mathbb {Z}}[1/2]$
;
$ {\mathbb {Z}}[1/2]$
; -
(2) away from the breakpoints, the slope of f is a power of
 $2$
.
$2$
.
The map
![]() $F \to {\mathbb {Z}}, f \mapsto \log _{2}(f_{0})$
, where
$F \to {\mathbb {Z}}, f \mapsto \log _{2}(f_{0})$
, where
![]() $f_{0}$
is the slope of f at
$f_{0}$
is the slope of f at
![]() $0$
, is a surjective homomorphism, called the germ at
$0$
, is a surjective homomorphism, called the germ at
![]() $0$
. Similarly, there is a germ at
$0$
. Similarly, there is a germ at
![]() $1$
, leading to a surjective homomorphism
$1$
, leading to a surjective homomorphism
![]() $F \to {\mathbb {Z}}^{2}$
. This is the abelianization of F, so the derived subgroup
$F \to {\mathbb {Z}}^{2}$
. This is the abelianization of F, so the derived subgroup
![]() $F^{\prime }$
coincides with the subgroup of homeomorphisms that are compactly supported in
$F^{\prime }$
coincides with the subgroup of homeomorphisms that are compactly supported in
![]() $(0, 1)$
.
$(0, 1)$
.
The most important open question about F is whether F is amenable or not. Since amenable groups are boundedly acyclic, a negative answer to Question 6.1 would disprove its amenability. The general philosophy is that F is very close to being amenable, and so it is likely to satisfy most properties that are somewhat weaker than amenability.
For example: the group F is
![]() $2$
-boundedly acyclic. This can be deduced from the explicit description of its rational cohomology [Reference Ghys and Sergiescu26], by using arguments analogous to those of Heuer and Löh for the computation of the second bounded cohomology of T [Reference Heuer and Löh31] (although a direct approach is possible [Reference Fournier-Facio and Lodha21]). To our knowledge, nothing is known about the bounded cohomology of F with trivial real coefficients in higher degrees, although vanishing is known in every degree with mixing coefficients [Reference Monod44].
$2$
-boundedly acyclic. This can be deduced from the explicit description of its rational cohomology [Reference Ghys and Sergiescu26], by using arguments analogous to those of Heuer and Löh for the computation of the second bounded cohomology of T [Reference Heuer and Löh31] (although a direct approach is possible [Reference Fournier-Facio and Lodha21]). To our knowledge, nothing is known about the bounded cohomology of F with trivial real coefficients in higher degrees, although vanishing is known in every degree with mixing coefficients [Reference Monod44].
The connection between pseudo-mitotic groups and F is more transparent when passing to the derived subgroup. The following equivalent formulation is relevant.
Lemma 6.5. Let
![]() $n \in {\mathbb {N}}$
. Then the Thompson group F is n-boundedly acyclic if and only if
$n \in {\mathbb {N}}$
. Then the Thompson group F is n-boundedly acyclic if and only if
![]() $F^{\prime }$
is n-boundedly acyclic.
$F^{\prime }$
is n-boundedly acyclic.
Proof. If
![]() $F^{\prime }$
is n-boundedly acyclic, then F is also boundedly acyclic by Theorem 4.1, or more simply by co-amenability [Reference Monod and Popa47].
$F^{\prime }$
is n-boundedly acyclic, then F is also boundedly acyclic by Theorem 4.1, or more simply by co-amenability [Reference Monod and Popa47].
Conversely, let us suppose that F is n-boundedly acyclic. Let
![]() $(a_{i})_{i \geq 1}$
and
$(a_{i})_{i \geq 1}$
and
![]() $(b_{i})_{i \geq 1}$
be sequences of dyadic rationals in
$(b_{i})_{i \geq 1}$
be sequences of dyadic rationals in
![]() $(0, 1)$
that converge to
$(0, 1)$
that converge to
![]() $0$
and
$0$
and
![]() $1$
, respectively. Then
$1$
, respectively. Then
![]() $F^{\prime }$
may be expressed as the directed union of the subgroups
$F^{\prime }$
may be expressed as the directed union of the subgroups
![]() $F_{i}$
consisting of elements supported in
$F_{i}$
consisting of elements supported in
![]() $[a_{i}, b_{i}]$
. Since each group
$[a_{i}, b_{i}]$
. Since each group
![]() $F_{i}$
is isomorphic to F, the group
$F_{i}$
is isomorphic to F, the group
![]() $F^{\prime }$
is a directed union of pairwise isomorphic n-boundedly acyclic groups. It follows from Corollary 4.14 that
$F^{\prime }$
is a directed union of pairwise isomorphic n-boundedly acyclic groups. It follows from Corollary 4.14 that
![]() $F^{\prime }$
is n-boundedly acyclic.
$F^{\prime }$
is n-boundedly acyclic.
The derived subgroup
![]() $F^{\prime }$
is a group of boundedly supported homeomorphisms of the interval. In analogy with Example 3.12, one may ask whether
$F^{\prime }$
is a group of boundedly supported homeomorphisms of the interval. In analogy with Example 3.12, one may ask whether
![]() $F^{\prime }$
is pseudo-mitotic. This is not the case, because
$F^{\prime }$
is pseudo-mitotic. This is not the case, because
![]() $F^{\prime }$
is not acyclic [Reference Ghys and Sergiescu26]. Intuitively,
$F^{\prime }$
is not acyclic [Reference Ghys and Sergiescu26]. Intuitively,
![]() $F^{\prime }$
cannot be dissipated, since a dissipator could not possibly have finitely many breakpoints. However, a countably singular analog of
$F^{\prime }$
cannot be dissipated, since a dissipator could not possibly have finitely many breakpoints. However, a countably singular analog of
![]() $F^{\prime }$
is dissipated.
$F^{\prime }$
is dissipated.
Definition 6.6. Let
![]() $\Omega F$
be the group of orientation-preserving homeomorphisms f of the interval
$\Omega F$
be the group of orientation-preserving homeomorphisms f of the interval
![]() $[0, 1]$
with the following properties:
$[0, 1]$
with the following properties:
-
(1) there exists a closed and countable set
 $K \subset (0, 1) \cap {\mathbb {Z}}[1/2]$
such that f is linear on each component of
$K \subset (0, 1) \cap {\mathbb {Z}}[1/2]$
such that f is linear on each component of
 $[0, 1] \setminus K$
;
$[0, 1] \setminus K$
; -
(2) away from K, the slope of f is a power of 2.
Since the set of breakpoints of each element is contained in
![]() $(0, 1)$
, the germs at
$(0, 1)$
, the germs at
![]() $0$
and
$0$
and
![]() $1$
are still defined, and
$1$
are still defined, and
![]() $\Omega F^{\prime }$
is the subgroup of homeomorphisms that are compactly supported in
$\Omega F^{\prime }$
is the subgroup of homeomorphisms that are compactly supported in
![]() $(0, 1)$
.
$(0, 1)$
.
Proposition 6.7. The groups
![]() $\Omega F$
and
$\Omega F$
and
![]() $\Omega F^{\prime }$
are boundedly acyclic.
$\Omega F^{\prime }$
are boundedly acyclic.
Proof. Once again, the bounded acyclicity of
![]() $\Omega F$
follows from that of
$\Omega F$
follows from that of
![]() $\Omega F^{\prime }$
by Theorem 4.1.
$\Omega F^{\prime }$
by Theorem 4.1.
We show that
![]() $\Omega F^{\prime }$
is dissipated. Let
$\Omega F^{\prime }$
is dissipated. Let
![]() $(a_{i})_{i \geq 1}$
and
$(a_{i})_{i \geq 1}$
and
![]() $(b_{i})_{i \geq 1}$
be sequences of dyadic rationals in
$(b_{i})_{i \geq 1}$
be sequences of dyadic rationals in
![]() $(0, 1)$
converging to
$(0, 1)$
converging to
![]() $0$
and
$0$
and
![]() $1$
, respectively. For every
$1$
, respectively. For every
![]() $i \geq 1$
, let
$i \geq 1$
, let
![]() $H_{i} \leq \Omega F^{\prime }$
be the subgroup consisting of homeomorphisms supported in
$H_{i} \leq \Omega F^{\prime }$
be the subgroup consisting of homeomorphisms supported in
![]() $(a_{i}, b_{i})$
. We show that there exists a dissipator
$(a_{i}, b_{i})$
. We show that there exists a dissipator
![]() $\varrho _{i} \in \Omega F^{\prime }$
for
$\varrho _{i} \in \Omega F^{\prime }$
for
![]() $H_{i}$
, that is:
$H_{i}$
, that is:
-
(1) for every
 $k \geq 1$
, we have
$k \geq 1$
, we have
 $\varrho _{i}^{k}((a_{i}, b_{i})) \cap (a_{i}, b_{i}) = \emptyset $
;
$\varrho _{i}^{k}((a_{i}, b_{i})) \cap (a_{i}, b_{i}) = \emptyset $
; -
(2) for every
 $g \in H_{i}$
, the element is in
$g \in H_{i}$
, the element is in $$ \begin{align*}\varphi_{i}(g) := \begin{cases} \varrho_{i}^{k} g \varrho_{i}^{-k} & \text{on } \varrho^{k}(a_{i}, b_{i}),\ \text{for every } k \geq 1, \\ \operatorname{\mathrm{id}} & \text{elsewhere} \end{cases} \end{align*} $$
$$ \begin{align*}\varphi_{i}(g) := \begin{cases} \varrho_{i}^{k} g \varrho_{i}^{-k} & \text{on } \varrho^{k}(a_{i}, b_{i}),\ \text{for every } k \geq 1, \\ \operatorname{\mathrm{id}} & \text{elsewhere} \end{cases} \end{align*} $$
 $\Omega F^{\prime }$
.
$\Omega F^{\prime }$
.
To this end, let us set
![]() $x_{0} := a_{i}$
and
$x_{0} := a_{i}$
and
![]() $x_{1} := b_{i}$
. We then pick a dyadic rational
$x_{1} := b_{i}$
. We then pick a dyadic rational
![]() $x_{-1}$
in
$x_{-1}$
in
![]() $(0, x_{0})$
such that
$(0, x_{0})$
such that
 $$ \begin{align*} \frac{x_{1} - x_{-1}}{x_{0} - x_{-1}} \end{align*} $$
$$ \begin{align*} \frac{x_{1} - x_{-1}}{x_{0} - x_{-1}} \end{align*} $$
is a power of 2. Moreover, given a dyadic rational
![]() $x \in \, (x_{1}, 1)$
, we can extend
$x \in \, (x_{1}, 1)$
, we can extend
![]() $x_{-1}, x_{0}, x_{1}$
to a sequence
$x_{-1}, x_{0}, x_{1}$
to a sequence
![]() $(x_{j})_{j \geq -1}$
of dyadic rationals converging to x and such that for every
$(x_{j})_{j \geq -1}$
of dyadic rationals converging to x and such that for every
![]() $j \geq 1$
, the ratio
$j \geq 1$
, the ratio
 $$ \begin{align*} \frac{x_{j+1}- x_{j}}{x_{j} - x_{j-1}} \end{align*} $$
$$ \begin{align*} \frac{x_{j+1}- x_{j}}{x_{j} - x_{j-1}} \end{align*} $$
is a power of 2.
Now we define
![]() $\varrho _{i} : [0, 1] \to [0, 1]$
piecewise as follows:
$\varrho _{i} : [0, 1] \to [0, 1]$
piecewise as follows:
 $$ \begin{align*} \varrho_{i} |_{[0, x_{-1}] \cup [x, 1]} & := \operatorname{\mathrm{id}}|_{[0, x_{-1}] \cup [x, 1]},\\ \varrho_{i}([x_{-1}, x_{0}]) & := [x_{-1}, x_{1}], \\ \varrho_{i}([x_{j-1}, x_{j}]) & := [x_{j}, x_{j+1}] \quad\text{for } j \geq 1, \end{align*} $$
$$ \begin{align*} \varrho_{i} |_{[0, x_{-1}] \cup [x, 1]} & := \operatorname{\mathrm{id}}|_{[0, x_{-1}] \cup [x, 1]},\\ \varrho_{i}([x_{-1}, x_{0}]) & := [x_{-1}, x_{1}], \\ \varrho_{i}([x_{j-1}, x_{j}]) & := [x_{j}, x_{j+1}] \quad\text{for } j \geq 1, \end{align*} $$
and let
![]() $\varrho _{i}$
be the unique affine isomorphism on each of these pieces. Notice that
$\varrho _{i}$
be the unique affine isomorphism on each of these pieces. Notice that
![]() $\varrho _{i}$
is supported in
$\varrho _{i}$
is supported in
![]() $[x_{-1}, x] \subset (0,1)$
, and the set
$[x_{-1}, x] \subset (0,1)$
, and the set
![]() $\{ x, x_{-1}, x_{0}, x_{1}, \ldots \}$
of breakpoints is closed, countable, and consists only of dyadic rationals. Since all the slopes are powers of 2, this implies that
$\{ x, x_{-1}, x_{0}, x_{1}, \ldots \}$
of breakpoints is closed, countable, and consists only of dyadic rationals. Since all the slopes are powers of 2, this implies that
![]() $\varrho _{i} \in \Omega F^{\prime }$
.
$\varrho _{i} \in \Omega F^{\prime }$
.
We claim that
![]() $\varrho _{i}$
is a dissipator for
$\varrho _{i}$
is a dissipator for
![]() $H_{i}$
. First, notice that by construction and the definition of
$H_{i}$
. First, notice that by construction and the definition of
![]() $x_{0}$
and
$x_{0}$
and
![]() $x_{1}$
, we have
$x_{1}$
, we have
 $$ \begin{align*} \varrho_{i}^{k}(a_{i}, b_{i}) \cap (a_{i}, b_{i}) = (x_{k}, x_{k+1}) \cap (x_{0}, x_{1}) = \emptyset \end{align*} $$
$$ \begin{align*} \varrho_{i}^{k}(a_{i}, b_{i}) \cap (a_{i}, b_{i}) = (x_{k}, x_{k+1}) \cap (x_{0}, x_{1}) = \emptyset \end{align*} $$
for every
![]() $k \geq 1$
. This shows that
$k \geq 1$
. This shows that
![]() $\varrho _{i}$
satisfies property (1).
$\varrho _{i}$
satisfies property (1).
Finally, for every
![]() $g \in \, H_{i}$
, the support of the homeomorphism
$g \in \, H_{i}$
, the support of the homeomorphism
![]() $\varphi _{i}(g)$
is contained in
$\varphi _{i}(g)$
is contained in
![]() $[x_{0}, x]$
. Moreover, the set of breakpoints of
$[x_{0}, x]$
. Moreover, the set of breakpoints of
![]() $\varphi _{i}(g)$
is still a closed, countable set consisting only of dyadic rationals. Hence,
$\varphi _{i}(g)$
is still a closed, countable set consisting only of dyadic rationals. Hence,
![]() $\varrho _{i}$
also satisfies property (2).
$\varrho _{i}$
also satisfies property (2).
This shows that
![]() $\Omega F^{\prime }$
is dissipated, whence pseudo-mitotic by Proposition 3.11. The thesis now follows from Theorem 3.5.
$\Omega F^{\prime }$
is dissipated, whence pseudo-mitotic by Proposition 3.11. The thesis now follows from Theorem 3.5.
We believe that a careful study of the embedding
![]() $F^{\prime } \hookrightarrow \Omega F^{\prime }$
could lead to some understanding of the bounded cohomology of
$F^{\prime } \hookrightarrow \Omega F^{\prime }$
could lead to some understanding of the bounded cohomology of
![]() $F^{\prime }$
.
$F^{\prime }$
.
6.2 On the bounded cohomology of T
We recall the definition of T.
Definition 6.8. The Thompson group T is the group of orientation-preserving piecewise linear homeomorphisms f of the circle
![]() $ {\mathbb {R}}/ {\mathbb {Z}}$
with the following properties:
$ {\mathbb {R}}/ {\mathbb {Z}}$
with the following properties:
-
(1) f has finitely many breakpoints, all of which lie in
 $ {\mathbb {Z}}[1/2]/ {\mathbb {Z}}$
;
$ {\mathbb {Z}}[1/2]/ {\mathbb {Z}}$
; -
(2) away from the breakpoints, the slope of f is a power of 2;
-
(3) f preserves
 $ {\mathbb {Z}}[1/2]/ {\mathbb {Z}}$
.
$ {\mathbb {Z}}[1/2]/ {\mathbb {Z}}$
.
The stabilizer of
![]() $0$
for the canonical T-action on the circle is canonically isomorphic to the Thompson group F.
$0$
for the canonical T-action on the circle is canonically isomorphic to the Thompson group F.
Since T acts minimally on the circle, it admits a second bounded cohomology class, namely the real Euler class [Reference Bucher, Frigerio and Hartnick12, Reference Matsumoto41]. The bounded Euler class is a refinement of the classical Euler class. All cup-powers of the classical Euler class are nontrivial in cohomology [Reference Ghys and Sergiescu26]; and thus, also the cup-powers of the bounded Euler class are nontrivial in
![]() $\operatorname {H}_{b}^{*}(T; {\mathbb {R}})$
; this was first noticed by Burger and Monod [Reference Burger and Monod13]. Therefore, Question 6.2 is asking whether these are the only bounded cohomology classes. In degree two, this is known to be true [Reference Heuer and Löh31], but again, to our knowledge, nothing is known in higher degrees.
$\operatorname {H}_{b}^{*}(T; {\mathbb {R}})$
; this was first noticed by Burger and Monod [Reference Burger and Monod13]. Therefore, Question 6.2 is asking whether these are the only bounded cohomology classes. In degree two, this is known to be true [Reference Heuer and Löh31], but again, to our knowledge, nothing is known in higher degrees.
The main goal of this section is to show that a positive answer to Question 6.1 implies a positive answer to Question 6.2, and this implication holds degree-wise. To do this, we prove the following general criterion for computing the bounded cohomology of groups acting highly transitively on the circle with boundedly acyclic stabilizers.
Proposition 6.9. Let
![]() $n \in {\mathbb {N}}_{\geq 2}$
. Let
$n \in {\mathbb {N}}_{\geq 2}$
. Let
![]() $\Gamma $
be a group acting orientation-preservingly on the circle, let S be an orbit of
$\Gamma $
be a group acting orientation-preservingly on the circle, let S be an orbit of
![]() $\Gamma $
with
$\Gamma $
with
![]() $|S| \geq n+1$
. Suppose that the following hold:
$|S| \geq n+1$
. Suppose that the following hold:
-
(1) for all
 $k \in \{1,\ldots ,n+1\}$
, the action of
$k \in \{1,\ldots ,n+1\}$
, the action of
 $\Gamma $
on the set of circularly ordered k-tuples in S is transitive;
$\Gamma $
on the set of circularly ordered k-tuples in S is transitive; -
(2) for all
 $k \in \{1,\ldots ,n\}$
, the stabilizer of a circularly ordered k-tuple is n-boundedly acyclic.
$k \in \{1,\ldots ,n\}$
, the stabilizer of a circularly ordered k-tuple is n-boundedly acyclic.
Then
 $\operatorname {H}_{b}^{2}(\Gamma; {\mathbb {R}})$
is generated by the bounded Euler class of this circle action of
$\operatorname {H}_{b}^{2}(\Gamma; {\mathbb {R}})$
is generated by the bounded Euler class of this circle action of
![]() $\Gamma $
and
$\Gamma $
and
 $$ \begin{align*}\operatorname{H}^{i}_{b}(\Gamma; {\mathbb{R}}) \cong \begin{cases} 0 & \text{if }\textit{i}\text{ is odd},\\ {\mathbb{R}} & \text{if }\textit{i}\text{ is even}, \end{cases}\end{align*} $$
$$ \begin{align*}\operatorname{H}^{i}_{b}(\Gamma; {\mathbb{R}}) \cong \begin{cases} 0 & \text{if }\textit{i}\text{ is odd},\\ {\mathbb{R}} & \text{if }\textit{i}\text{ is even}, \end{cases}\end{align*} $$
for all
![]() $i \in \{1, \ldots , n\}$
, generated by the cup-powers of Euler class.
$i \in \{1, \ldots , n\}$
, generated by the cup-powers of Euler class.
Recall that a k-tuple
![]() $(s_{1}, \ldots , s_{k})$
in
$(s_{1}, \ldots , s_{k})$
in
![]() $S^{1}$
is circularly ordered if there exists a point
$S^{1}$
is circularly ordered if there exists a point
![]() $p \in S^{1} \setminus \{s_{1}, \ldots , s_{k}\}$
such that
$p \in S^{1} \setminus \{s_{1}, \ldots , s_{k}\}$
such that
![]() $(s_{1}, \ldots , s_{k}) \in S^{1} \setminus \{p\} \cong (0,1)$
is an ordered k-tuple in the interval. We follow the convention that circularly ordered tuples are nondegenerate, that is, they consist of pairwise distinct entries.
$(s_{1}, \ldots , s_{k}) \in S^{1} \setminus \{p\} \cong (0,1)$
is an ordered k-tuple in the interval. We follow the convention that circularly ordered tuples are nondegenerate, that is, they consist of pairwise distinct entries.
For the proof, we follow the general principle of computing bounded cohomology through boundedly acyclic actions. Boundedly acyclic stabilizers lead to boundedly acyclic modules.
Lemma 6.10. Let
![]() $\Gamma $
be a group and let
$\Gamma $
be a group and let
![]() $\Gamma \curvearrowright X$
be an action of
$\Gamma \curvearrowright X$
be an action of
![]() $\Gamma $
on a set X that has only finitely many orbits
$\Gamma $
on a set X that has only finitely many orbits
![]() $(X_{i})_{i \in I}$
. Let
$(X_{i})_{i \in I}$
. Let
![]() $n \in {\mathbb {N}}$
. If each of the orbits has n-boundedly acyclic stabilizer, then we have for all
$n \in {\mathbb {N}}$
. If each of the orbits has n-boundedly acyclic stabilizer, then we have for all
![]() $k \in \{1,\ldots ,n\}$
that
$k \in \{1,\ldots ,n\}$
that
 $$ \begin{align*} \operatorname{H}_{b}^{k}(\Gamma; \ell^{\infty} (X) ) \cong 0. \end{align*} $$
$$ \begin{align*} \operatorname{H}_{b}^{k}(\Gamma; \ell^{\infty} (X) ) \cong 0. \end{align*} $$
Proof. Let
![]() $k \in \{1,\ldots ,n\}$
. Because I is finite, we have
$k \in \{1,\ldots ,n\}$
. Because I is finite, we have
 $\ell ^{\infty } (X) \cong \bigoplus _{i \in I} \ell ^{\infty }(X_{i})$
and
$\ell ^{\infty } (X) \cong \bigoplus _{i \in I} \ell ^{\infty }(X_{i})$
and
 $$ \begin{align*} \operatorname{H}_{b}^{k}(\Gamma;\ell^{\infty} (X) ) \cong \operatorname{H}_{b}^{k}\bigg(\Gamma;\bigoplus_{i \in I} \ell^{\infty}(X_{i}) \bigg) \cong \bigoplus_{i \in I} \operatorname{H}_{b}^{k}(\Gamma;\ell^{\infty}(X_{i})). \end{align*} $$
$$ \begin{align*} \operatorname{H}_{b}^{k}(\Gamma;\ell^{\infty} (X) ) \cong \operatorname{H}_{b}^{k}\bigg(\Gamma;\bigoplus_{i \in I} \ell^{\infty}(X_{i}) \bigg) \cong \bigoplus_{i \in I} \operatorname{H}_{b}^{k}(\Gamma;\ell^{\infty}(X_{i})). \end{align*} $$
We show that each of the summands is trivial. Let
![]() $i \in I$
and let
$i \in I$
and let
![]() $H_{i} \subset \Gamma $
be the stabilizer of a point in
$H_{i} \subset \Gamma $
be the stabilizer of a point in
![]() $X_{i}$
. Then, by the Eckmann–Shapiro lemma in bounded cohomology [Reference Monod43, Proposition 10.13], we obtain
$X_{i}$
. Then, by the Eckmann–Shapiro lemma in bounded cohomology [Reference Monod43, Proposition 10.13], we obtain
 $$ \begin{align*} \operatorname{H}_{b}^{k}(\Gamma;\ell^{\infty}(X_{i})) \cong \operatorname{H}_{b}^{k}(\Gamma;\ell^{\infty}(\Gamma)^{H_{i}}) \cong \operatorname{H}_{b}^{k}(H_{i}; {\mathbb{R}}); \end{align*} $$
$$ \begin{align*} \operatorname{H}_{b}^{k}(\Gamma;\ell^{\infty}(X_{i})) \cong \operatorname{H}_{b}^{k}(\Gamma;\ell^{\infty}(\Gamma)^{H_{i}}) \cong \operatorname{H}_{b}^{k}(H_{i}; {\mathbb{R}}); \end{align*} $$
the last term is trivial, because
![]() $H_{i}$
is n-boundedly acyclic by hypothesis.
$H_{i}$
is n-boundedly acyclic by hypothesis.
The effect of boundedly acyclic stabilizers is studied more systematically in a forthcoming article on boundedly acyclic covers and relative simplicial volume [Reference Li, Löh and Moraschini38].
Proof of Proposition 6.9
The given
![]() $\Gamma $
-action on S gives a simplicial
$\Gamma $
-action on S gives a simplicial
![]() $\Gamma $
-resolution
$\Gamma $
-resolution
![]() $ {\mathbb {R}} \to \ell ^{\infty } (S^{*+1})$
[Reference Frigerio24, Lemma 4.21].
$ {\mathbb {R}} \to \ell ^{\infty } (S^{*+1})$
[Reference Frigerio24, Lemma 4.21].
Claim 6.11. The
![]() $\Gamma $
-resolution
$\Gamma $
-resolution
![]() $ {\mathbb {R}} \to \ell ^{\infty } (S^{*+1})$
is boundedly acylic up to degree n, that is, for all
$ {\mathbb {R}} \to \ell ^{\infty } (S^{*+1})$
is boundedly acylic up to degree n, that is, for all
![]() $k \in \{0,\ldots ,n\}$
and all
$k \in \{0,\ldots ,n\}$
and all
![]() $i \in \{1,\ldots ,n\}$
, we have
$i \in \{1,\ldots ,n\}$
, we have
 $$ \begin{align*} \operatorname{H}_{b}^{i}(\Gamma;\ell^{\infty} (S^{k+1})) \cong 0. \end{align*} $$
$$ \begin{align*} \operatorname{H}_{b}^{i}(\Gamma;\ell^{\infty} (S^{k+1})) \cong 0. \end{align*} $$
To prove Claim 6.11, first note that the
![]() $\Gamma $
-space
$\Gamma $
-space
![]() $S^{k+1}$
consists only of finitely many
$S^{k+1}$
consists only of finitely many
![]() $\Gamma $
-orbits. Indeed, every tuple can be permuted to be circularly ordered (possibly with repetitions), and only finitely many permutations and repetition patterns are possible. Moreover,
$\Gamma $
-orbits. Indeed, every tuple can be permuted to be circularly ordered (possibly with repetitions), and only finitely many permutations and repetition patterns are possible. Moreover,
![]() $\Gamma $
acts transitively on circularly ordered tuples of every given size
$\Gamma $
acts transitively on circularly ordered tuples of every given size
![]() $\leq k+1$
.
$\leq k+1$
.
The stabilizer groups of the
![]() $\Gamma $
-space
$\Gamma $
-space
![]() $S^{k+1}$
are all n-boundedly acyclic by hypothesis. Thus, Lemma 6.10 shows the claim.
$S^{k+1}$
are all n-boundedly acyclic by hypothesis. Thus, Lemma 6.10 shows the claim.
Therefore, we can apply the fact that boundedly acyclic resolutions compute bounded cohomology [Reference Moraschini and Raptis48, Proposition 2.5.4] and symmetrization [Reference Frigerio24, Section 4.10] to conclude that
 $$ \begin{align} \operatorname{H}_{b}^{i}(\Gamma; {\mathbb{R}}) \cong \operatorname{H}^{i} ( \ell^{\infty}(S^{*+1})^{\Gamma} ) \cong \operatorname{H}^{i} ( \ell^{\infty}_{\operatorname{\mathrm{alt}}}(S^{*+1})^{\Gamma} ) \end{align} $$
$$ \begin{align} \operatorname{H}_{b}^{i}(\Gamma; {\mathbb{R}}) \cong \operatorname{H}^{i} ( \ell^{\infty}(S^{*+1})^{\Gamma} ) \cong \operatorname{H}^{i} ( \ell^{\infty}_{\operatorname{\mathrm{alt}}}(S^{*+1})^{\Gamma} ) \end{align} $$
for all
![]() $i \in \{1,\ldots ,n\}$
. Here,
$i \in \{1,\ldots ,n\}$
. Here,
 $\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{*+1})$
denotes the subcomplex of alternating cochains, that is, functions f with
$\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{*+1})$
denotes the subcomplex of alternating cochains, that is, functions f with
for all
![]() $(s_{0}, \ldots , s_{k}) \in S^{k+1}$
and all permutations
$(s_{0}, \ldots , s_{k}) \in S^{k+1}$
and all permutations
![]() $\sigma $
of
$\sigma $
of
![]() $\{0, \ldots , k\}$
.
$\{0, \ldots , k\}$
.
Claim 6.12. Let
![]() $k \in \{0,\ldots ,n\}$
.
$k \in \{0,\ldots ,n\}$
.
-
(1) If k is odd, then
 $\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{k+1})^{\Gamma } \cong 0$
.
$\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{k+1})^{\Gamma } \cong 0$
. -
(2) If k is even, then
 $\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{k+1})^{\Gamma } \cong {\mathbb {R}}$
, generated by the function
$\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{k+1})^{\Gamma } \cong {\mathbb {R}}$
, generated by the function
 $f_{k}$
constructed in the proof below.
$f_{k}$
constructed in the proof below.
To prove Claim 6.12, let
 $f \in \ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{k+1})$
. We first show that f is determined by its value on a single circularly ordered tuple: indeed, f vanishes on tuples with a repetition; all other tuples may be permuted to be circularly ordered. Moreover, since
$f \in \ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{k+1})$
. We first show that f is determined by its value on a single circularly ordered tuple: indeed, f vanishes on tuples with a repetition; all other tuples may be permuted to be circularly ordered. Moreover, since
![]() $\Gamma $
acts transitively on the set of circularly ordered tuples, f is constant on the set of all circularly ordered tuples. In particular,
$\Gamma $
acts transitively on the set of circularly ordered tuples, f is constant on the set of all circularly ordered tuples. In particular,
 $\dim _ {\mathbb {R}} \ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{k+1})^{\Gamma } \leq 1$
.
$\dim _ {\mathbb {R}} \ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{k+1})^{\Gamma } \leq 1$
.
As
![]() $|S| \geq n+1$
, there exists a circularly ordered tuple
$|S| \geq n+1$
, there exists a circularly ordered tuple
![]() $(s_{0}, \ldots , s_{k}) \in S^{k+1}$
.
$(s_{0}, \ldots , s_{k}) \in S^{k+1}$
.
Let k be odd. It suffices to show that
![]() $f(s_{0}, \ldots , s_{k})=0$
. With
$f(s_{0}, \ldots , s_{k})=0$
. With
![]() $(s_{0}, \ldots , s_{k})$
, also
$(s_{0}, \ldots , s_{k})$
, also
![]() $(s_{k}, s_{0}, \ldots , s_{k-1})$
is circularly ordered. Because k is odd, these two tuples differ by an odd permutation. As f is both constant on all circulary ordered tuples and alternating, we obtain
$(s_{k}, s_{0}, \ldots , s_{k-1})$
is circularly ordered. Because k is odd, these two tuples differ by an odd permutation. As f is both constant on all circulary ordered tuples and alternating, we obtain
and thus
![]() $f(s_{0},\ldots ,s_{k}) =0$
. Therefore,
$f(s_{0},\ldots ,s_{k}) =0$
. Therefore,
 $\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{k+1})^{\Gamma } \cong 0$
.
$\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{k+1})^{\Gamma } \cong 0$
.
Let k be even. We define
![]() $f_{k} : S^{k+1} \to {\mathbb {R}}$
as follows: on tuples with a repetition, we define
$f_{k} : S^{k+1} \to {\mathbb {R}}$
as follows: on tuples with a repetition, we define
![]() $f_{k}$
to vanish. If
$f_{k}$
to vanish. If
![]() $(t_{0}, \ldots , t_{k}) \in S^{k+1}$
has no repetition, we set
$(t_{0}, \ldots , t_{k}) \in S^{k+1}$
has no repetition, we set
where
![]() $\sigma $
is a permutation such that
$\sigma $
is a permutation such that
![]() $(t_{\sigma (0)}, \ldots , t_{\sigma (k)})$
is circularly ordered; this permutation
$(t_{\sigma (0)}, \ldots , t_{\sigma (k)})$
is circularly ordered; this permutation
![]() $\sigma $
is only unique up to a
$\sigma $
is only unique up to a
![]() $(k+1)$
-cycle, but since k is even,
$(k+1)$
-cycle, but since k is even,
![]() $\operatorname {\mathrm {sgn}}(\sigma )$
is well defined. Because
$\operatorname {\mathrm {sgn}}(\sigma )$
is well defined. Because
![]() $\Gamma $
acts orientation-preservingly and because there exists at least one circularly ordered
$\Gamma $
acts orientation-preservingly and because there exists at least one circularly ordered
![]() $(k+1)$
-tuple, this gives a well-defined nontrivial element in
$(k+1)$
-tuple, this gives a well-defined nontrivial element in
 $\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{k+1})^{\Gamma }$
. Therefore,
$\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{k+1})^{\Gamma }$
. Therefore,
 $\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{k+1})^{\Gamma } \cong {\mathbb {R}}$
. This proves our claim.
$\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{k+1})^{\Gamma } \cong {\mathbb {R}}$
. This proves our claim.
In view of Claim 6.12, the cochain complex
 $\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{*+1})^{\Gamma }$
is (up to degree n) isomorphic to the cochain complex
$\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{*+1})^{\Gamma }$
is (up to degree n) isomorphic to the cochain complex
(whose coboundary operator is necessarily trivial) and if
![]() $k \in \{0,\ldots , n\}$
is even, then
$k \in \{0,\ldots , n\}$
is even, then
![]() $[f_{k}]$
is nontrivial in
$[f_{k}]$
is nontrivial in
 $\operatorname {H}^{k}(\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{*+1})^{\Gamma })$
. In particular, we obtain
$\operatorname {H}^{k}(\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{*+1})^{\Gamma })$
. In particular, we obtain
 $$ \begin{align*} \operatorname{H}_{b}^{i}(\Gamma; {\mathbb{R}}) \cong \operatorname{H}^{i}(\ell^{\infty}_{\operatorname{\mathrm{alt}}}(S^{*+1})^{\Gamma} ) \cong \begin{cases} 0 & \text{if }\textit{i}\text{ is odd},\\ {\mathbb{R}} & \text{if }\textit{i}\text{ is even}, \end{cases} \end{align*} $$
$$ \begin{align*} \operatorname{H}_{b}^{i}(\Gamma; {\mathbb{R}}) \cong \operatorname{H}^{i}(\ell^{\infty}_{\operatorname{\mathrm{alt}}}(S^{*+1})^{\Gamma} ) \cong \begin{cases} 0 & \text{if }\textit{i}\text{ is odd},\\ {\mathbb{R}} & \text{if }\textit{i}\text{ is even}, \end{cases} \end{align*} $$
for all
![]() $i \in \{0,\ldots , n-1\}$
.
$i \in \{0,\ldots , n-1\}$
.
As for degree n, under our assumptions, we cannot show that
 $\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{n+1})$
follows the same periodic pattern. However, we still have the following claim.
$\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{n+1})$
follows the same periodic pattern. However, we still have the following claim.
Claim 6.13. The differential
 $\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{n+1})^{\Gamma } \to \ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{n+2})^{\Gamma }$
is trivial.
$\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{n+1})^{\Gamma } \to \ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{n+2})^{\Gamma }$
is trivial.
To prove Claim 6.13, first note that this is obvious if n is odd, since then,
 $\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{n+1})^{\Gamma } \cong 0$
by Claim 6.12.
$\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{n+1})^{\Gamma } \cong 0$
by Claim 6.12.
Suppose instead that n is even, and let
 $f \in \ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{n+1})^{\Gamma }$
be a function that takes the constant value
$f \in \ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{n+1})^{\Gamma }$
be a function that takes the constant value
![]() $\lambda $
on circularly ordered tuples. Then, if
$\lambda $
on circularly ordered tuples. Then, if
![]() $(s_{0}, \ldots , s_{n+1})$
is a circularly ordered tuple, we have
$(s_{0}, \ldots , s_{n+1})$
is a circularly ordered tuple, we have
 $$ \begin{align*}\delta^{n+1}_{b}(f)(s_{0}, \ldots, s_{n+1}) = \sum\limits_{i = 0}^{n+1} (-1)^{i} \cdot \lambda = 0,\end{align*} $$
$$ \begin{align*}\delta^{n+1}_{b}(f)(s_{0}, \ldots, s_{n+1}) = \sum\limits_{i = 0}^{n+1} (-1)^{i} \cdot \lambda = 0,\end{align*} $$
since n is even. This proves our claim.
Therefore,
 $$ \begin{align*} \operatorname{H}_{b}^{n}(\Gamma; {\mathbb{R}}) \cong \begin{cases} 0 & \text{if }\textit{n}\text{ is odd},\\ {\mathbb{R}} & \text{if }\textit{n}\text{ is even}, \end{cases} \end{align*} $$
$$ \begin{align*} \operatorname{H}_{b}^{n}(\Gamma; {\mathbb{R}}) \cong \begin{cases} 0 & \text{if }\textit{n}\text{ is odd},\\ {\mathbb{R}} & \text{if }\textit{n}\text{ is even}, \end{cases} \end{align*} $$
as well. It remains to deal with the bounded Euler class and its powers.
Claim 6.14. The bounded Euler class
 $\operatorname {\mathrm {eu}}_{b}^{\Gamma } \in \operatorname {H}_{b}^{2}(\Gamma; {\mathbb {R}})$
is nontrivial.
$\operatorname {\mathrm {eu}}_{b}^{\Gamma } \in \operatorname {H}_{b}^{2}(\Gamma; {\mathbb {R}})$
is nontrivial.
To prove Claim 6.14, we first make the isomorphism in Equation (6-1) more explicit. Let
![]() $x_{0} \in S$
. For
$x_{0} \in S$
. For
![]() $k\in {\mathbb {N}}$
, we consider the map
$k\in {\mathbb {N}}$
, we consider the map
 $$ \begin{align*} \varphi^{k} : \ell^{\infty}(S^{*+1}) & \to \ell^{\infty}(\Gamma^{*+1}) \\ f & \mapsto ((\gamma_{0}, \ldots, \gamma_{k}) \mapsto f(\gamma_{0}x_{0}, \ldots, \gamma_{k} x_{0})). \end{align*} $$
$$ \begin{align*} \varphi^{k} : \ell^{\infty}(S^{*+1}) & \to \ell^{\infty}(\Gamma^{*+1}) \\ f & \mapsto ((\gamma_{0}, \ldots, \gamma_{k}) \mapsto f(\gamma_{0}x_{0}, \ldots, \gamma_{k} x_{0})). \end{align*} $$
Then
![]() $\varphi ^{*} : \ell ^{\infty }(S^{*+1}) \to \ell ^{\infty }(\Gamma ^{*+1})$
is a degree-wise bounded
$\varphi ^{*} : \ell ^{\infty }(S^{*+1}) \to \ell ^{\infty }(\Gamma ^{*+1})$
is a degree-wise bounded
![]() $\Gamma $
-cochain map that extends the identity on the resolved module
$\Gamma $
-cochain map that extends the identity on the resolved module
![]() $ {\mathbb {R}}$
. Because the resolution
$ {\mathbb {R}}$
. Because the resolution
![]() $\ell ^{\infty }(S^{*+1})$
is strong [Reference Frigerio24, Lemma 4.21],
$\ell ^{\infty }(S^{*+1})$
is strong [Reference Frigerio24, Lemma 4.21],
![]() $(\varphi ^{*})^{\Gamma }$
induces an isomorphism
$(\varphi ^{*})^{\Gamma }$
induces an isomorphism
 $\operatorname {H}_{b}^{i}(\Gamma; {\mathbb {R}}) \cong \operatorname {H}^{i}(\ell ^{\infty }(S^{*+1})^{\Gamma })$
for all
$\operatorname {H}_{b}^{i}(\Gamma; {\mathbb {R}}) \cong \operatorname {H}^{i}(\ell ^{\infty }(S^{*+1})^{\Gamma })$
for all
![]() $i \in \{0,\ldots , n\}$
[Reference Moraschini and Raptis48, Proposition 2.5.4 and Remark 2.5.5].
$i \in \{0,\ldots , n\}$
[Reference Moraschini and Raptis48, Proposition 2.5.4 and Remark 2.5.5].
As the inclusion
 $i^{*} : \ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{*+1}) \to \ell ^{\infty }(S^{*+1})$
is a
$i^{*} : \ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{*+1}) \to \ell ^{\infty }(S^{*+1})$
is a
![]() $\Gamma $
-cochain map that induces an isomorphism
$\Gamma $
-cochain map that induces an isomorphism
 $\operatorname {H}^{*}(\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{*+1})^{\Gamma }) \cong \operatorname {H}^{*}(\ell ^{\infty }(S^{*+1})^{\Gamma })$
, we conclude that
$\operatorname {H}^{*}(\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{*+1})^{\Gamma }) \cong \operatorname {H}^{*}(\ell ^{\infty }(S^{*+1})^{\Gamma })$
, we conclude that
![]() $\varphi _{\operatorname {\mathrm {alt}}}^{*} := \varphi ^{*} \circ i^{*}$
induces an isomorphism
$\varphi _{\operatorname {\mathrm {alt}}}^{*} := \varphi ^{*} \circ i^{*}$
induces an isomorphism
 $\operatorname {H}_{b}^{i}(\Gamma; {\mathbb {R}}) \cong \operatorname {H}^{i}(\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{*+1})^{\Gamma })$
.
$\operatorname {H}_{b}^{i}(\Gamma; {\mathbb {R}}) \cong \operatorname {H}^{i}(\ell ^{\infty }_{\operatorname {\mathrm {alt}}}(S^{*+1})^{\Gamma })$
.
By construction,
 $(\varphi _{\operatorname {\mathrm {alt}}}^{2})^{\Gamma }(f_{2})$
gives the orientation cocycle
$(\varphi _{\operatorname {\mathrm {alt}}}^{2})^{\Gamma }(f_{2})$
gives the orientation cocycle
![]() $\operatorname {\mathrm {or}}^{\Gamma }$
of the
$\operatorname {\mathrm {or}}^{\Gamma }$
of the
![]() $\Gamma $
-action. Because of
$\Gamma $
-action. Because of
![]() $[f_{2}] \neq 0$
, we know that the bounded Euler class
$[f_{2}] \neq 0$
, we know that the bounded Euler class
 $$ \begin{align*} \operatorname{\mathrm{eu}}_{b}^{\Gamma} = \tfrac12 \cdot [\operatorname{\mathrm{or}}^{\Gamma}] = \tfrac12 \cdot \operatorname{H}^{2}((\varphi_{\operatorname{\mathrm{alt}}}^{*})^{\Gamma})[f_{2}] \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{eu}}_{b}^{\Gamma} = \tfrac12 \cdot [\operatorname{\mathrm{or}}^{\Gamma}] = \tfrac12 \cdot \operatorname{H}^{2}((\varphi_{\operatorname{\mathrm{alt}}}^{*})^{\Gamma})[f_{2}] \end{align*} $$
is nonzero in
 $\operatorname {H}_{b}^{2}(\Gamma; {\mathbb {R}})$
. This proves our claim.
$\operatorname {H}_{b}^{2}(\Gamma; {\mathbb {R}})$
. This proves our claim.
Because of Claim 6.14 and
 $\operatorname {H}_{b}^{2}(\Gamma; {\mathbb {R}}) \cong {\mathbb {R}}$
, we conclude that
$\operatorname {H}_{b}^{2}(\Gamma; {\mathbb {R}}) \cong {\mathbb {R}}$
, we conclude that
 $\operatorname {H}_{b}^{2}(\Gamma; {\mathbb {R}})$
is generated by the bounded Euler class.
$\operatorname {H}_{b}^{2}(\Gamma; {\mathbb {R}})$
is generated by the bounded Euler class.
Claim 6.15. For all
![]() $k \in \{0,\ldots , n/2\}$
, the cup-power
$k \in \{0,\ldots , n/2\}$
, the cup-power
 $(\operatorname {\mathrm {eu}}_{b}^{\Gamma })^{\cup k} \in \operatorname {H}_{b}^{2k}(\Gamma; {\mathbb {R}})$
is nontrivial.
$(\operatorname {\mathrm {eu}}_{b}^{\Gamma })^{\cup k} \in \operatorname {H}_{b}^{2k}(\Gamma; {\mathbb {R}})$
is nontrivial.
To prove Claim 6.15, in view of the relation between
 $\operatorname {\mathrm {eu}}_{b}^{\Gamma }$
and
$\operatorname {\mathrm {eu}}_{b}^{\Gamma }$
and
![]() $[f_{2}]$
(proof of Claim 6.14) and the above description of
$[f_{2}]$
(proof of Claim 6.14) and the above description of
 $\operatorname {H}_{b}^{2k}(\Gamma; {\mathbb {R}})$
, it suffices to show that
$\operatorname {H}_{b}^{2k}(\Gamma; {\mathbb {R}})$
, it suffices to show that
![]() $\operatorname {\mathrm {alt}}(f_{2}{}^{\cup k})$
is nontrivial, where
$\operatorname {\mathrm {alt}}(f_{2}{}^{\cup k})$
is nontrivial, where
![]() $\;\cdot \;\cup \;\cdot \;$
denotes the standard cup-product on the cochain level (notice that even if
$\;\cdot \;\cup \;\cdot \;$
denotes the standard cup-product on the cochain level (notice that even if
![]() $f_{2}$
is alternating, the nontrivial cup-product
$f_{2}$
is alternating, the nontrivial cup-product
![]() $f_{2}{}^{\cup k}$
is not so). Indeed, we have
$f_{2}{}^{\cup k}$
is not so). Indeed, we have
 $$ \begin{align*} \operatorname{\mathrm{alt}}(f_{2}{}^{\cup k}) = \frac{2^{k} \cdot k!}{(2k)!} \cdot f_{2k} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{alt}}(f_{2}{}^{\cup k}) = \frac{2^{k} \cdot k!}{(2k)!} \cdot f_{2k} \end{align*} $$
(Appendix B), which is nontrivial (Claim 6.12). This proves our claim.
This completes the proof of Proposition 6.9.
Remark 6.16. The second hypothesis in Proposition 6.9 is used to show that the modules
![]() $\ell ^{\infty }(S^{k+1})$
are n-boundedly acyclic, which in turn is used to apply the computation of bounded cohomology through acyclic resolutions [Reference Moraschini and Raptis48, Proposition 2.5.4]. Note however that this result does not require n-bounded acyclicity of all stabilizers. Indeed, it is enough to ask that the stabilizer of a circularly ordered k-tuple is
$\ell ^{\infty }(S^{k+1})$
are n-boundedly acyclic, which in turn is used to apply the computation of bounded cohomology through acyclic resolutions [Reference Moraschini and Raptis48, Proposition 2.5.4]. Note however that this result does not require n-bounded acyclicity of all stabilizers. Indeed, it is enough to ask that the stabilizer of a circularly ordered k-tuple is
![]() $(n - k + 1)$
boundedly acyclic, for
$(n - k + 1)$
boundedly acyclic, for
![]() $k \in \{ 1, \ldots , n \}$
. To keep the notation simple, we chose to state Proposition 6.9 with the stronger hypothesis.
$k \in \{ 1, \ldots , n \}$
. To keep the notation simple, we chose to state Proposition 6.9 with the stronger hypothesis.
We apply this to
![]() $\Gamma = T$
, to show that if F is n-boundedly acyclic, then Question 6.2 has a positive answer up to degree n.
$\Gamma = T$
, to show that if F is n-boundedly acyclic, then Question 6.2 has a positive answer up to degree n.
Corollary 6.17. If F is boundedly acyclic, then
![]() $\operatorname {H}^{*}_{b}(T; {\mathbb {R}})$
(with the cup-product structure) is isomorphic to the polynomial ring
$\operatorname {H}^{*}_{b}(T; {\mathbb {R}})$
(with the cup-product structure) is isomorphic to the polynomial ring
![]() $ {\mathbb {R}}[x]$
with
$ {\mathbb {R}}[x]$
with
![]() $|x| =2$
, and the bounded Euler class of T is a polynomial generator of
$|x| =2$
, and the bounded Euler class of T is a polynomial generator of
![]() $\operatorname {H}^{*}_{b}(T; {\mathbb {R}})$
.
$\operatorname {H}^{*}_{b}(T; {\mathbb {R}})$
.
Proof. For each
![]() $k \geq 1$
, the group T acts transitively on the set of circularly ordered k-tuples in
$k \geq 1$
, the group T acts transitively on the set of circularly ordered k-tuples in
![]() $ {\mathbb {Z}}[1/2]/ {\mathbb {Z}}$
; the stabilizers of this action are isomorphic to direct powers of F [Reference Cannon, Floyd and Parry15]. In particular, the stabilizers are boundedly acyclic by Theorem 4.1. Therefore, Proposition 6.9 is applicable and we obtain that
$ {\mathbb {Z}}[1/2]/ {\mathbb {Z}}$
; the stabilizers of this action are isomorphic to direct powers of F [Reference Cannon, Floyd and Parry15]. In particular, the stabilizers are boundedly acyclic by Theorem 4.1. Therefore, Proposition 6.9 is applicable and we obtain that
![]() $\operatorname {H}_{b}^{*}(T; {\mathbb {R}})$
is isomorphic as a graded
$\operatorname {H}_{b}^{*}(T; {\mathbb {R}})$
is isomorphic as a graded
![]() $ {\mathbb {R}}$
-algebra to
$ {\mathbb {R}}$
-algebra to
![]() $ {\mathbb {R}}[x]$
with x corresponding to the bounded Euler class
$ {\mathbb {R}}[x]$
with x corresponding to the bounded Euler class
 $\operatorname {\mathrm {eu}}_{b}^{T}$
.
$\operatorname {\mathrm {eu}}_{b}^{T}$
.
Alternatively, in this case, the nontriviality of the powers of the bounded Euler class is already known through the computations of Ghys–Sergiescu and Burger–Monod [Reference Burger and Monod13].
Corollary 6.17 also holds in a range up to n (with the same proof).
Corollary 6.18. If F is boundedly acyclic and
![]() $r \in {\mathbb {N}}_{\geq 1}$
, then
$r \in {\mathbb {N}}_{\geq 1}$
, then
 $$ \begin{align*} {\mathbb{R}}[x_{1},\ldots,x_{r}] & \to \operatorname{H}_{b}^{*}(T^{\times r}; {\mathbb{R}}) \\ x_{j} & \mapsto \operatorname{H}_{b}^{2}(\pi_{j}; {\mathbb{R}}) (\operatorname{\mathrm{eu}}_{b}^{T}) \end{align*} $$
$$ \begin{align*} {\mathbb{R}}[x_{1},\ldots,x_{r}] & \to \operatorname{H}_{b}^{*}(T^{\times r}; {\mathbb{R}}) \\ x_{j} & \mapsto \operatorname{H}_{b}^{2}(\pi_{j}; {\mathbb{R}}) (\operatorname{\mathrm{eu}}_{b}^{T}) \end{align*} $$
defines an isomorphism of graded
![]() $ {\mathbb {R}}$
-algebras; here,
$ {\mathbb {R}}$
-algebras; here,
![]() $\operatorname {H}_{b}^{*}(T^{\times r}; {\mathbb {R}})$
carries the cup-product structure,
$\operatorname {H}_{b}^{*}(T^{\times r}; {\mathbb {R}})$
carries the cup-product structure,
![]() $|x_{j}| =2 $
, and
$|x_{j}| =2 $
, and
![]() $\pi _{j} : T^{\times r} \to T$
denotes the projection onto the jth factor for each
$\pi _{j} : T^{\times r} \to T$
denotes the projection onto the jth factor for each
![]() $j \in \{1,\ldots , r\}$
. Moreover, the canonical semi-norm on
$j \in \{1,\ldots , r\}$
. Moreover, the canonical semi-norm on
![]() $\operatorname {H}_{b}^{*}(T^{\times r}; {\mathbb {R}})$
then is a norm.
$\operatorname {H}_{b}^{*}(T^{\times r}; {\mathbb {R}})$
then is a norm.
Proof. We combine Corollary 6.17 with suitable Künneth arguments. As usual in bounded cohomology, some care is necessary to execute this.
We first show that the polynomial ring embeds into
![]() $\operatorname {H}_{b}^{*}(T; {\mathbb {R}})$
: the
$\operatorname {H}_{b}^{*}(T; {\mathbb {R}})$
: the
![]() $ {\mathbb {R}}$
-algebra homomorphism
$ {\mathbb {R}}$
-algebra homomorphism
![]() $ {\mathbb {R}}[x] \to \operatorname {H}^{*}(T; {\mathbb {R}})$
given by
$ {\mathbb {R}}[x] \to \operatorname {H}^{*}(T; {\mathbb {R}})$
given by
is injective [Reference Ghys and Sergiescu26]. Therefore, the Künneth theorem shows that
 $$ \begin{align*} x_{j} \mapsto \operatorname{H}^{2}(\pi_{j}; {\mathbb{R}})(\operatorname{\mathrm{eu}}^{T}) \end{align*} $$
$$ \begin{align*} x_{j} \mapsto \operatorname{H}^{2}(\pi_{j}; {\mathbb{R}})(\operatorname{\mathrm{eu}}^{T}) \end{align*} $$
yields an injective
![]() $ {\mathbb {R}}$
-algebra homomorphism
$ {\mathbb {R}}$
-algebra homomorphism
![]() $\Phi ^{r} : {\mathbb {R}}[x_{1},\ldots ,x_{r}] \to \operatorname {H}^{*}(T^{\times r}; {\mathbb {R}})$
. In combination with the universal coefficient theorem, we obtain: for every polynomial
$\Phi ^{r} : {\mathbb {R}}[x_{1},\ldots ,x_{r}] \to \operatorname {H}^{*}(T^{\times r}; {\mathbb {R}})$
. In combination with the universal coefficient theorem, we obtain: for every polynomial
![]() $p \in {\mathbb {R}}[x_{1},\ldots ,x_{r}] \setminus \{0\}$
, there exists a class
$p \in {\mathbb {R}}[x_{1},\ldots ,x_{r}] \setminus \{0\}$
, there exists a class
![]() $\alpha _{p} \in \operatorname {H}_{*}(T^{\times r}; {\mathbb {R}})$
with
$\alpha _{p} \in \operatorname {H}_{*}(T^{\times r}; {\mathbb {R}})$
with
These nontrivial evaluations show that also the bounded version
 $$ \begin{align*} \Phi_{b}^{r} : {\mathbb{R}}[x_{1},\ldots,x_{r}] & \to \operatorname{H}_{b}^{*}(T^{\times r}; {\mathbb{R}}) \\ x_{j} & \mapsto \operatorname{H}_{b}^{2}(\pi_{j}; {\mathbb{R}})(\operatorname{\mathrm{eu}}_{b}^{T}) \end{align*} $$
$$ \begin{align*} \Phi_{b}^{r} : {\mathbb{R}}[x_{1},\ldots,x_{r}] & \to \operatorname{H}_{b}^{*}(T^{\times r}; {\mathbb{R}}) \\ x_{j} & \mapsto \operatorname{H}_{b}^{2}(\pi_{j}; {\mathbb{R}})(\operatorname{\mathrm{eu}}_{b}^{T}) \end{align*} $$
is injective; even more, for each
![]() $p \in {\mathbb {R}}[x_{1},\ldots ,x_{r}]\setminus \{0\}$
, we have
$p \in {\mathbb {R}}[x_{1},\ldots ,x_{r}]\setminus \{0\}$
, we have
and thus
![]() $\|\Phi _{b}^{r}(p)\|_{\infty } \neq 0$
. So far, we did not use the postulated bounded acyclicity of F.
$\|\Phi _{b}^{r}(p)\|_{\infty } \neq 0$
. So far, we did not use the postulated bounded acyclicity of F.
It remains to show that
![]() $\Phi _{b}^{r}$
is surjective. To this end, it suffices to inductively (on r) establish that
$\Phi _{b}^{r}$
is surjective. To this end, it suffices to inductively (on r) establish that
 $\dim _ {\mathbb {R}} \operatorname {H}_{b}^{k}(T^{\times r}; {\mathbb {R}}) \leq \dim _ {\mathbb {R}} ( {\mathbb {R}}[x_{1},\ldots ,x_{r}])_{k}$
holds for all
$\dim _ {\mathbb {R}} \operatorname {H}_{b}^{k}(T^{\times r}; {\mathbb {R}}) \leq \dim _ {\mathbb {R}} ( {\mathbb {R}}[x_{1},\ldots ,x_{r}])_{k}$
holds for all
![]() $k \in {\mathbb {N}}$
.
$k \in {\mathbb {N}}$
.
The base case is handled in Corollary 6.17; moreover, the evaluation argument above shows that the canonical semi-norm on
![]() $\operatorname {H}_{b}^{*}(T; {\mathbb {R}})$
indeed is a norm.
$\operatorname {H}_{b}^{*}(T; {\mathbb {R}})$
indeed is a norm.
For the induction step, let us assume that the claim holds for
![]() $r-1$
. We recall that for group extensions
$r-1$
. We recall that for group extensions
![]() $1 \to N \to \Gamma \to Q \to 1$
, there is a Hochschild–Serre spectral sequence
$1 \to N \to \Gamma \to Q \to 1$
, there is a Hochschild–Serre spectral sequence
 $$ \begin{align*} E_{2}^{pq} = \operatorname{H}_{b}^{p}(Q; \operatorname{H}_{b}^{q}(N; {\mathbb{R}}) ) \Longrightarrow \operatorname{H}_{b}^{p+q}(\Gamma; {\mathbb{R}}) \end{align*} $$
$$ \begin{align*} E_{2}^{pq} = \operatorname{H}_{b}^{p}(Q; \operatorname{H}_{b}^{q}(N; {\mathbb{R}}) ) \Longrightarrow \operatorname{H}_{b}^{p+q}(\Gamma; {\mathbb{R}}) \end{align*} $$
in bounded cohomology, whenever the canonical semi-norm on
![]() $\operatorname {H}_{b}^{*}(N; {\mathbb {R}})$
is a norm [Reference Monod43, Proposition 12.2.1]. Applying this spectral sequence to the trivial product extension
$\operatorname {H}_{b}^{*}(N; {\mathbb {R}})$
is a norm [Reference Monod43, Proposition 12.2.1]. Applying this spectral sequence to the trivial product extension
shows that the degree-wise dimensions of
![]() $\operatorname {H}_{b}^{*}(T^{\times r}; {\mathbb {R}})$
are at most the degree-wise dimensions of
$\operatorname {H}_{b}^{*}(T^{\times r}; {\mathbb {R}})$
are at most the degree-wise dimensions of
![]() $ {\mathbb {R}}[x_{1},\ldots ,x_{r}]$
(with
$ {\mathbb {R}}[x_{1},\ldots ,x_{r}]$
(with
![]() $|x_{i}| = 2$
for all
$|x_{i}| = 2$
for all
![]() $i\in \{1,\ldots ,r\}$
). Hence,
$i\in \{1,\ldots ,r\}$
). Hence,
![]() $\Phi _{b}^{r}$
is surjective. In particular, again by the evaluation argument above, the canonical semi-norm on all of
$\Phi _{b}^{r}$
is surjective. In particular, again by the evaluation argument above, the canonical semi-norm on all of
![]() $\operatorname {H}_{b}^{*}(T^{\times r}; {\mathbb {R}})$
is a norm.
$\operatorname {H}_{b}^{*}(T^{\times r}; {\mathbb {R}})$
is a norm.
Remark 6.19. Analogous results are obtained by Monod and Nariman [Reference Monod and Nariman46], who computed the full bounded cohomology of the groups of orientation-preserving homeomorphisms of the circle and the
![]() $2$
-disc. In fact, in Proposition 6.9, one can replace orbits by fat orbits (that is, orbits of fat points [Reference Monod and Nariman46]). This allows to compute the full bounded cohomology of
$2$
-disc. In fact, in Proposition 6.9, one can replace orbits by fat orbits (that is, orbits of fat points [Reference Monod and Nariman46]). This allows to compute the full bounded cohomology of
![]() $\operatorname {\mathrm {Homeo}}^{+}(S^{1})$
from the bounded acyclicity of
$\operatorname {\mathrm {Homeo}}^{+}(S^{1})$
from the bounded acyclicity of
![]() $\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}})$
. Moreover, again using fat orbits, one can deduce from Proposition 6.7 a positive answer to Question 6.2 for a natural countably singular analog of Thompson’s group T.
$\operatorname {\mathrm {Homeo}}_{c}( {\mathbb {R}})$
. Moreover, again using fat orbits, one can deduce from Proposition 6.7 a positive answer to Question 6.2 for a natural countably singular analog of Thompson’s group T.
6.3 On the bounded cohomology of V
We recall the definition of V.
Definition 6.20. The Thompson group V is the group of piecewise linear right-continuous bijections f of the circle
![]() $ {\mathbb {R}}/ {\mathbb {Z}}$
with the following properties:
$ {\mathbb {R}}/ {\mathbb {Z}}$
with the following properties:
-
(1) f has finitely many breakpoints, all of which lie in
 $ {\mathbb {Z}}[1/2]/ {\mathbb {Z}}$
;
$ {\mathbb {Z}}[1/2]/ {\mathbb {Z}}$
; -
(2) away from the breakpoints, f is orientation-preserving and the slope of f is a power of
 $2$
;
$2$
; -
(3) f preserves
 $ {\mathbb {Z}}[1/2]/ {\mathbb {Z}}$
.
$ {\mathbb {Z}}[1/2]/ {\mathbb {Z}}$
.
It was recently proved that V is acyclic [Reference Szymik and Wahl54]: this had been conjectured by Brown [Reference Brown9], who already proved that V is rationally acyclic. Moreover, V is uniformly perfect [Reference Cannon, Floyd and Parry15]; so, using the same argument as in Remark 3.6, we deduce that V is
![]() $2$
-boundedly acyclic.
$2$
-boundedly acyclic.
While the proof of acyclicity of V is involved, the proof of rational acyclicity is much simpler and only relies on standard arguments in equivariant homology. A bounded analog of equivariant homology theory has recently been developed [Reference Li37], but it does not seem possible to directly translate Brown’s proof to bounded cohomology.
A positive answer to Question 6.3 would make V the first example of a nonamenable boundedly acyclic group of type
![]() $F_{\infty }$
. Moreover, it would make V the first tractable example of a nonamenable boundedly acyclic finitely presented group: the only known example [Reference Fournier-Facio, Löh and Moraschini22] is very implicit.
$F_{\infty }$
. Moreover, it would make V the first tractable example of a nonamenable boundedly acyclic finitely presented group: the only known example [Reference Fournier-Facio, Löh and Moraschini22] is very implicit.
Acknowledgements
We wish to thank Jon Berrick, Jonathan Bowden, Amir Khodayan Karim, Kevin Li, Yash Lodha, Antonio López Neumann, Nicolas Monod, Sam Nariman, and George Raptis for helpful discussions.
Appendix A Pseudo-mitotic groups are boundedly acyclic
We prove Theorem 1.3. The proof is an adaption of the original proofs for ordinary cohomology [Reference Berrick4, Reference Varadarajan55] to the setting of bounded cohomology. In bounded cohomology, we keep additional control on primitives, similar to Matsumoto and Morita for certain homeomorphism groups [Reference Matsumoto and Morita42] and similarly to the case of mitotic groups [Reference Löh39].
The main ingredient in the proof is the following proposition which is an adaptation for the pseudo-mitotic setting of the mitotic case [Reference Löh39, Proposition 4.6].
Proposition A.1. Let
![]() $n \in {\mathbb {N}}$
and let
$n \in {\mathbb {N}}$
and let
![]() $\kappa \in {\mathbb {R}}_{> 0}$
. Let
$\kappa \in {\mathbb {R}}_{> 0}$
. Let
 $$ \begin{align*} H \xrightarrow{\varphi} H^{\prime} \xrightarrow{\varphi^{\prime}} K \xrightarrow{\psi} \Gamma \xrightarrow{i} P \end{align*} $$
$$ \begin{align*} H \xrightarrow{\varphi} H^{\prime} \xrightarrow{\varphi^{\prime}} K \xrightarrow{\psi} \Gamma \xrightarrow{i} P \end{align*} $$
be a chain of group homomorphisms such that:
-
(1) the homomorphism
 $i : \Gamma \to P$
is a pseudomitosis of
$i : \Gamma \to P$
is a pseudomitosis of
 $\Gamma $
in P;
$\Gamma $
in P; -
(2) for every
 $s \in \{1, \ldots , n-1\}$
, we have
$s \in \{1, \ldots , n-1\}$
, we have
 $\operatorname {H}_{s}(\varphi ^{\prime }) = 0$
;
$\operatorname {H}_{s}(\varphi ^{\prime }) = 0$
; -
(3) for every
 $s \in \{0, \ldots , n-1\}$
, the homomorphisms
$s \in \{0, \ldots , n-1\}$
, the homomorphisms
 $\varphi $
and
$\varphi $
and
 $\psi $
satisfy
$\psi $
satisfy
 $(s, \kappa )$
-
$(s, \kappa )$
-
 $\operatorname {\mathrm {UBC}}$
.
$\operatorname {\mathrm {UBC}}$
.
Then, for all
![]() $s \in \{1, \ldots , n\}$
, we have
$s \in \{1, \ldots , n\}$
, we have
Moreover, there exists a constant
![]() $c_{n, \kappa } \in {\mathbb {R}}_{>0}$
(depending only on n and
$c_{n, \kappa } \in {\mathbb {R}}_{>0}$
(depending only on n and
![]() $\kappa $
) such that the composition
$\kappa $
) such that the composition
![]() $i \circ \psi \circ \varphi ^{\prime } \circ \varphi $
satisfies
$i \circ \psi \circ \varphi ^{\prime } \circ \varphi $
satisfies
![]() $(s, c_{n, \kappa })$
-
$(s, c_{n, \kappa })$
-
![]() $\operatorname {\mathrm {UBC}}$
for every
$\operatorname {\mathrm {UBC}}$
for every
![]() $s \in \{0, \ldots , n\}$
.
$s \in \{0, \ldots , n\}$
.
We give the proof of Proposition A.1 in Appendix A.1. Following the mitotic case [Reference Löh39], we show first how to deduce Theorem 1.3 from this result.
Proof of Theorem 1.3
Let P be a pseudo-mitotic group. According to Theorems 2.3 and 3.4, it is sufficient to show that for every
![]() $n \in {\mathbb {N}}_{>0}$
, the group P satisfies n-
$n \in {\mathbb {N}}_{>0}$
, the group P satisfies n-
![]() $\operatorname {\mathrm {UBC}}$
.
$\operatorname {\mathrm {UBC}}$
.
Let
![]() $n \in {\mathbb {N}}_{>0}$
and let
$n \in {\mathbb {N}}_{>0}$
and let
![]() $z \in \operatorname {C}_{n}(P; {\mathbb {R}})$
be a boundary, that is,
$z \in \operatorname {C}_{n}(P; {\mathbb {R}})$
be a boundary, that is,
![]() $\partial_{n+1} c = z\ \text{for some}\ {c \in C_{n+1}(P; {\mathbb {R}})}$
. Since both z and c involve only finitely many elements of P, there exists a finitely generated subgroup
$\partial_{n+1} c = z\ \text{for some}\ {c \in C_{n+1}(P; {\mathbb {R}})}$
. Since both z and c involve only finitely many elements of P, there exists a finitely generated subgroup
![]() $\Gamma _{0}$
of P such that both z and c are supported on
$\Gamma _{0}$
of P such that both z and c are supported on
![]() $\Gamma_0$
. We show that the inclusion
$\Gamma_0$
. We show that the inclusion
![]() $\Gamma _{0} \hookrightarrow P$
satisfies
$\Gamma _{0} \hookrightarrow P$
satisfies
![]() $(n, \kappa _{n})$
-
$(n, \kappa _{n})$
-
![]() $\operatorname {\mathrm {UBC}}$
, where
$\operatorname {\mathrm {UBC}}$
, where
![]() $\kappa _{n} \in {\mathbb {R}}_{>0}$
only depends on n. This condition readily implies that P satisfies n-
$\kappa _{n} \in {\mathbb {R}}_{>0}$
only depends on n. This condition readily implies that P satisfies n-
![]() $\operatorname {\mathrm {UBC}}$
, whence the thesis.
$\operatorname {\mathrm {UBC}}$
, whence the thesis.
Since P is pseudo-mitotic,
![]() $\Gamma _{0}$
has a mitosis into P. Let
$\Gamma _{0}$
has a mitosis into P. Let
![]() $\psi _{0}, \psi _{1} : \Gamma _{0} \to P$
and
$\psi _{0}, \psi _{1} : \Gamma _{0} \to P$
and
![]() $g \in P$
be witnesses of such a pseudo-mitosis. Then,
$g \in P$
be witnesses of such a pseudo-mitosis. Then,
![]() $\Gamma _{0}$
also admits a pseudo-mitosis into the following finitely generated subgroup of P:
$\Gamma _{0}$
also admits a pseudo-mitosis into the following finitely generated subgroup of P:
By iterating this construction, we get a sequence
![]() $\Gamma _{0} \leq \Gamma _{1} \leq \cdots \leq P$
of finitely generated groups such that at each step, the inclusion
$\Gamma _{0} \leq \Gamma _{1} \leq \cdots \leq P$
of finitely generated groups such that at each step, the inclusion
![]() $\Gamma _{j} \hookrightarrow \Gamma _{j+1}$
is a pseudo-mitosis.
$\Gamma _{j} \hookrightarrow \Gamma _{j+1}$
is a pseudo-mitosis.
Following verbatim the proof of the mitotic case [Reference Löh39, Theorem 1.2], by induction on
![]() $n \geq 1$
and using Proposition A.1, one can show that the inclusion of
$n \geq 1$
and using Proposition A.1, one can show that the inclusion of
![]() $\Gamma $
into a sufficiently large
$\Gamma $
into a sufficiently large
![]() $\Gamma _{j_{n}}$
satisfies
$\Gamma _{j_{n}}$
satisfies
![]() $(n, \kappa _{n})$
-
$(n, \kappa _{n})$
-
![]() $\operatorname {\mathrm {UBC}}$
, where
$\operatorname {\mathrm {UBC}}$
, where
![]() $\kappa _{n}$
only depends on n.
$\kappa _{n}$
only depends on n.
Using the fact that
![]() $\Gamma _{j_{n}} \leq P$
, this implies that there exists
$\Gamma _{j_{n}} \leq P$
, this implies that there exists
![]() $c^{\prime } \in \operatorname {C}_{n+1}(P; {\mathbb {R}})$
with
$c^{\prime } \in \operatorname {C}_{n+1}(P; {\mathbb {R}})$
with
This shows that P satisfies n-
![]() $\operatorname {\mathrm {UBC}}$
for all positive degrees n; whence, P is boundedly acyclic (Theorem 2.3).
$\operatorname {\mathrm {UBC}}$
for all positive degrees n; whence, P is boundedly acyclic (Theorem 2.3).
A.1 Proof of Proposition A.1
This section is devoted to the proof of Proposition A.1. The proof is based on a refinement of Varadarajan’s proof [Reference Varadarajan55, Proposition 1.4], additionally taking the norm of the morphisms involved into account. Our approach closely follows the mitotic case [Reference Löh39, Appendix A].
Proof of Proposition A.1
We prove the statement in degree
![]() $n \in {\mathbb {N}}$
. For convenience, we write
$n \in {\mathbb {N}}$
. For convenience, we write
Since
![]() $\operatorname {H}_{s}(\varphi ^{\prime }) = 0$
for every
$\operatorname {H}_{s}(\varphi ^{\prime }) = 0$
for every
![]() $s \in \{1, \ldots , n-1\}$
, also
$s \in \{1, \ldots , n-1\}$
, also
![]() $\operatorname {H}_{s}(f) = 0$
in the same degrees. The fact that
$\operatorname {H}_{s}(f) = 0$
in the same degrees. The fact that
![]() $\operatorname {H}_{s}(i \circ f) = 0$
for every
$\operatorname {H}_{s}(i \circ f) = 0$
for every
![]() $s \in \, \{1, \ldots , n\}$
was already proved by Varadarajan [Reference Varadarajan55, Proposition 1.4]. To adapt the mitosis proof [Reference Löh39, Appendix A] to the case of pseudo-mitoses, it is convenient to recall Varadarajan’s argument.
$s \in \, \{1, \ldots , n\}$
was already proved by Varadarajan [Reference Varadarajan55, Proposition 1.4]. To adapt the mitosis proof [Reference Löh39, Appendix A] to the case of pseudo-mitoses, it is convenient to recall Varadarajan’s argument.
Let
![]() $\psi _{0}, \psi _{1} : \Gamma \to P$
and
$\psi _{0}, \psi _{1} : \Gamma \to P$
and
![]() $g \in \, P$
be witnesses of the pseudo-mitosis
$g \in \, P$
be witnesses of the pseudo-mitosis
![]() $i : \Gamma \to P$
. Then, we define the map
$i : \Gamma \to P$
. Then, we define the map
 $$ \begin{align*} \mu : \Gamma \times \Gamma &\to P \\ (g^{\prime}, g) &\mapsto g^{\prime} \cdot \psi_{1}(g). \end{align*} $$
$$ \begin{align*} \mu : \Gamma \times \Gamma &\to P \\ (g^{\prime}, g) &\mapsto g^{\prime} \cdot \psi_{1}(g). \end{align*} $$
Notice that
![]() $\mu $
is a group homomorphism by condition (2) of the definition of pseudo-mitosis [Reference Varadarajan55, proof of Proposition 1.4].
$\mu $
is a group homomorphism by condition (2) of the definition of pseudo-mitosis [Reference Varadarajan55, proof of Proposition 1.4].
Let
![]() $j_{1} : H \to H \times H$
and
$j_{1} : H \to H \times H$
and
![]() $j_{2} : H \to H \times H$
be the inclusions into the first and the second factor, respectively. Let
$j_{2} : H \to H \times H$
be the inclusions into the first and the second factor, respectively. Let
![]() $\gamma _{g}$
denote the conjugation with respect to g, that is,
$\gamma _{g}$
denote the conjugation with respect to g, that is,
 $\gamma _{g}(g^{\prime }) = g g^{\prime } g^{-1}$
for every
$\gamma _{g}(g^{\prime }) = g g^{\prime } g^{-1}$
for every
![]() $g^{\prime } \in P$
. Moreover, let
$g^{\prime } \in P$
. Moreover, let
![]() $\Delta _{H} : H \to H \times H$
denote the diagonal homomorphism. Then, for every
$\Delta _{H} : H \to H \times H$
denote the diagonal homomorphism. Then, for every
![]() $h \in H$
,
$h \in H$
,
 $$ \begin{align*} \gamma_{g} \circ \psi_{1} \circ f (h) = \psi_{0} \circ f (h) &= \psi_{0}(f(h)) \\ &= f(h) \cdot \psi_{1}(f(h)) \\ &= \mu(f(h), f(h)) \\ &= \mu \circ (f \times f) \circ \Delta_{H} (h). \end{align*} $$
$$ \begin{align*} \gamma_{g} \circ \psi_{1} \circ f (h) = \psi_{0} \circ f (h) &= \psi_{0}(f(h)) \\ &= f(h) \cdot \psi_{1}(f(h)) \\ &= \mu(f(h), f(h)) \\ &= \mu \circ (f \times f) \circ \Delta_{H} (h). \end{align*} $$
However,
 $$ \begin{align*} \mu \circ (f \times f) \circ j_{1} & = \mu (f, 1) = f = i \circ f \quad\text{and} \\ \mu \circ (f \times f) \circ j_{2} & = \mu(1, f) = \psi_{1}(f) = \psi_{1} \circ f. \end{align*} $$
$$ \begin{align*} \mu \circ (f \times f) \circ j_{1} & = \mu (f, 1) = f = i \circ f \quad\text{and} \\ \mu \circ (f \times f) \circ j_{2} & = \mu(1, f) = \psi_{1}(f) = \psi_{1} \circ f. \end{align*} $$
Hence, the Künneth formula (and its naturality) together with the assumption that
![]() $\operatorname {H}_{s}(f) = 0$
for all
$\operatorname {H}_{s}(f) = 0$
for all
![]() $s \in \{1, \ldots , n-1\}$
imply that the following diagram commutes (similarly to the mitotic case [Reference Löh39, page 729]):
$s \in \{1, \ldots , n-1\}$
imply that the following diagram commutes (similarly to the mitotic case [Reference Löh39, page 729]):

where
![]() $p_{1}, p_{2} : H \times H \to H$
denote the projections and
$p_{1}, p_{2} : H \times H \to H$
denote the projections and
![]() $i_{1}, i_{2} : \Gamma \to \Gamma \times \Gamma $
the inclusions. The commutativity of the previous diagram leads to
$i_{1}, i_{2} : \Gamma \to \Gamma \times \Gamma $
the inclusions. The commutativity of the previous diagram leads to
 $$ \begin{align*} \operatorname{H}_{n}(\gamma_{g}) \circ \operatorname{H}_{n} (\psi_{1} \circ f) &= \operatorname{H}_{n} (\mu \circ (f \times f) \circ \Delta_{H}) \\ &= \operatorname{H}_{n} (i \circ f) + \operatorname{H}_{n}(\psi_{1} \circ f). \end{align*} $$
$$ \begin{align*} \operatorname{H}_{n}(\gamma_{g}) \circ \operatorname{H}_{n} (\psi_{1} \circ f) &= \operatorname{H}_{n} (\mu \circ (f \times f) \circ \Delta_{H}) \\ &= \operatorname{H}_{n} (i \circ f) + \operatorname{H}_{n}(\psi_{1} \circ f). \end{align*} $$
Since the conjugation
![]() $\gamma _{g}$
is trivial in homology, that is,
$\gamma _{g}$
is trivial in homology, that is,
![]() $\operatorname {H}_{n}(\gamma _{g}) = \operatorname {\mathrm {id}}$
, we obtain
$\operatorname {H}_{n}(\gamma _{g}) = \operatorname {\mathrm {id}}$
, we obtain
We are thus reduced to showing that the previous construction can be controlled in such a way that
![]() $i \circ f$
satisfies the required
$i \circ f$
satisfies the required
![]() $\operatorname {\mathrm {UBC}}$
condition.
$\operatorname {\mathrm {UBC}}$
condition.
Let
![]() $z \in \partial _{n+1}(\operatorname {C}_{n+1}(H; {\mathbb {R}}))$
. We construct a controlled
$z \in \partial _{n+1}(\operatorname {C}_{n+1}(H; {\mathbb {R}}))$
. We construct a controlled
![]() $\partial _{n+1}$
-primitive for
$\partial _{n+1}$
-primitive for
![]() $\operatorname {C}_{n}(i \circ f)$
. Following the mitotic case [Reference Löh39, page 731], we have
$\operatorname {C}_{n}(i \circ f)$
. Following the mitotic case [Reference Löh39, page 731], we have
on the chain level, where
![]() $E^{\prime }$
is bounded and
$E^{\prime }$
is bounded and
![]() $\|E^{\prime }\|$
admits a bound that only depends on the given
$\|E^{\prime }\|$
admits a bound that only depends on the given
![]() $\kappa \in {\mathbb {R}}_{>0}$
and n (the proof uses hypothesis (3) in the statement).
$\kappa \in {\mathbb {R}}_{>0}$
and n (the proof uses hypothesis (3) in the statement).
To complete the construction of a controlled
![]() $\partial _{n+1}$
-primitive for
$\partial _{n+1}$
-primitive for
![]() $\operatorname {C}_{n}(i \circ f)$
, we consider the following chain homotopy:
$\operatorname {C}_{n}(i \circ f)$
, we consider the following chain homotopy:
 $$ \begin{align*} \Theta_{n} : \operatorname{C}_{n}(P; {\mathbb{R}}) &\to \operatorname{C}_{n+1}(P; {\mathbb{R}}) \\ (g_{1}, \ldots, g_{n}) &\mapsto \sum_{j = 1}^{n+1} (-1)^{j+1} \cdot (g_{1}, \ldots, g_{j-1}, g, g^{-1} g_{j} g, \ldots, g^{-1} g_{n} g) \end{align*} $$
$$ \begin{align*} \Theta_{n} : \operatorname{C}_{n}(P; {\mathbb{R}}) &\to \operatorname{C}_{n+1}(P; {\mathbb{R}}) \\ (g_{1}, \ldots, g_{n}) &\mapsto \sum_{j = 1}^{n+1} (-1)^{j+1} \cdot (g_{1}, \ldots, g_{j-1}, g, g^{-1} g_{j} g, \ldots, g^{-1} g_{n} g) \end{align*} $$
between
![]() $\operatorname {C}_{*}(\gamma _{g})$
and the identity. The previous map is in fact such a chain homotopy and
$\operatorname {C}_{*}(\gamma _{g})$
and the identity. The previous map is in fact such a chain homotopy and
![]() $\|\Theta _{n}\| \leq n+1$
is proved as in the mitotic case [Reference Löh39, Lemma A.2] (notice that for convenience we changed the sign of
$\|\Theta _{n}\| \leq n+1$
is proved as in the mitotic case [Reference Löh39, Lemma A.2] (notice that for convenience we changed the sign of
![]() $\Theta $
). We then have:
$\Theta $
). We then have:
 $$ \begin{align*} (i \circ f)_{*}(z) &= (\mu \circ (f \times f) \circ j_{1})_{*} (z) \\ &= (\mu \circ (f \times f) \circ \Delta_{H})_{*}(z) \\ & \quad - (\mu \circ (f \times f) \circ j_{2})_{*}(z) - \mu_{*} \circ \partial_{n+1} \circ E^{\prime}(z) \\ &= (\gamma_{g})_{*} \circ (\psi_{1} \circ f)_{*} (z) \\ & \quad - (\psi_{1} \circ f)_{*}(z) - \partial_{n+1} \circ \mu_{*} \circ E^{\prime}(z) \\ &= (\partial_{n+1} \circ \Theta + \Theta \circ \partial_{n}) \circ (\psi_{1} \circ f)_{*}(z) - \partial_{n+1} \circ \mu_{*} \circ E^{\prime}(z) \\ &= \partial_{n+1} (\Theta \circ (\psi_{1} \circ f)_{*}(z) - \mu_{*} \circ E^{\prime}(z)), \end{align*} $$
$$ \begin{align*} (i \circ f)_{*}(z) &= (\mu \circ (f \times f) \circ j_{1})_{*} (z) \\ &= (\mu \circ (f \times f) \circ \Delta_{H})_{*}(z) \\ & \quad - (\mu \circ (f \times f) \circ j_{2})_{*}(z) - \mu_{*} \circ \partial_{n+1} \circ E^{\prime}(z) \\ &= (\gamma_{g})_{*} \circ (\psi_{1} \circ f)_{*} (z) \\ & \quad - (\psi_{1} \circ f)_{*}(z) - \partial_{n+1} \circ \mu_{*} \circ E^{\prime}(z) \\ &= (\partial_{n+1} \circ \Theta + \Theta \circ \partial_{n}) \circ (\psi_{1} \circ f)_{*}(z) - \partial_{n+1} \circ \mu_{*} \circ E^{\prime}(z) \\ &= \partial_{n+1} (\Theta \circ (\psi_{1} \circ f)_{*}(z) - \mu_{*} \circ E^{\prime}(z)), \end{align*} $$
where we moved from the first line to the second one using the Equation (A-1) and the last equality holds because z is a cycle. Moreover, using the fact that group homomorphisms induce norm nonincreasing chain maps, we have that the norm
is bounded from above by a quantity
![]() $c_{n, \kappa } \in {\mathbb {R}}_{>0}$
depending only on n and
$c_{n, \kappa } \in {\mathbb {R}}_{>0}$
depending only on n and
![]() $\kappa $
(since this is true for
$\kappa $
(since this is true for
![]() $E^{\prime }$
and
$E^{\prime }$
and
![]() $\Theta $
). This shows that
$\Theta $
). This shows that
![]() $i \circ f$
satisfies
$i \circ f$
satisfies
![]() $(n, c_{n, \kappa })$
-
$(n, c_{n, \kappa })$
-
![]() $\operatorname {\mathrm {UBC}}$
, as claimed.□
$\operatorname {\mathrm {UBC}}$
, as claimed.□
Appendix B Computation of cup-powers
In the following, we give the combinatorial part of the proof of Claim 6.15 in the proof of Proposition 6.9. We use the notation established in the proof of Proposition 6.9.
Lemma B.1. For all
![]() $k \in \{0,\ldots , n/2\}$
, we have
$k \in \{0,\ldots , n/2\}$
, we have
 $$ \begin{align*} \operatorname{\mathrm{alt}}(f_{2}{}^{\cup k}) = \frac{2^{k} \cdot k!}{(2k)!} \cdot f_{2k}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{alt}}(f_{2}{}^{\cup k}) = \frac{2^{k} \cdot k!}{(2k)!} \cdot f_{2k}. \end{align*} $$
Proof. Proceeding inductively, it suffices to show that
 $$ \begin{align*} \operatorname{\mathrm{alt}}(f_{2} \cup f_{2(k-1)}) = \frac1{2k-1} \cdot f_{2k}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{alt}}(f_{2} \cup f_{2(k-1)}) = \frac1{2k-1} \cdot f_{2k}. \end{align*} $$
This is a purely combinatorial statement. Let
![]() $(s_{0}, \ldots , s_{2k})$
be a circularly ordered
$(s_{0}, \ldots , s_{2k})$
be a circularly ordered
![]() ${(2k+1)}$
-tuple over S. To simplify notation, we write
${(2k+1)}$
-tuple over S. To simplify notation, we write
![]() $f(i_{0},\ldots , i_{p})$
for
$f(i_{0},\ldots , i_{p})$
for
![]() $f(s_{i_{0}}, \ldots , s_{i_{p}})$
, and so on. In this notation, since
$f(s_{i_{0}}, \ldots , s_{i_{p}})$
, and so on. In this notation, since
![]() $(s_{0}, \ldots , s_{2k})$
is circularly ordered, it suffices to show that
$(s_{0}, \ldots , s_{2k})$
is circularly ordered, it suffices to show that
![]() $A := \operatorname {\mathrm {alt}}(f_{2} \cup f_{2(k-1)}) (0,\ldots , 2k)$
is equal to
$A := \operatorname {\mathrm {alt}}(f_{2} \cup f_{2(k-1)}) (0,\ldots , 2k)$
is equal to
 $$ \begin{align*} \frac1{2k-1}. \end{align*} $$
$$ \begin{align*} \frac1{2k-1}. \end{align*} $$
By definition of
![]() $\operatorname {\mathrm {alt}}$
and the cup-product on simplicial cochains, we have
$\operatorname {\mathrm {alt}}$
and the cup-product on simplicial cochains, we have
 $$ \begin{align*} A = \frac1{(2k +1)!} \cdot \sum_{\sigma \in \Sigma(0,\ldots, 2k)} \operatorname{\mathrm{sgn}}(\sigma) & \cdot f_{2}(\sigma(0),\sigma(1),\sigma(2)) \\[-.5em] & \cdot f_{2(k-1)} (\sigma(2), \ldots, \sigma(2k) ). \end{align*} $$
$$ \begin{align*} A = \frac1{(2k +1)!} \cdot \sum_{\sigma \in \Sigma(0,\ldots, 2k)} \operatorname{\mathrm{sgn}}(\sigma) & \cdot f_{2}(\sigma(0),\sigma(1),\sigma(2)) \\[-.5em] & \cdot f_{2(k-1)} (\sigma(2), \ldots, \sigma(2k) ). \end{align*} $$
Because
![]() $2k$
is even, we can fix one position and obtain via cyclic permutations that
$2k$
is even, we can fix one position and obtain via cyclic permutations that
 $$ \begin{align*} A = \frac{2k+1}{(2k +1)!} \cdot \sum_{\sigma \in \Sigma(0,\ldots, 2k-1)} \operatorname{\mathrm{sgn}}(\sigma) & \cdot f_{2}(\sigma(0),\sigma(1),2k) \\[-.5em] & \cdot f_{2(k-1)} (2k,\sigma(2), \ldots, \sigma(2k-1) ). \end{align*} $$
$$ \begin{align*} A = \frac{2k+1}{(2k +1)!} \cdot \sum_{\sigma \in \Sigma(0,\ldots, 2k-1)} \operatorname{\mathrm{sgn}}(\sigma) & \cdot f_{2}(\sigma(0),\sigma(1),2k) \\[-.5em] & \cdot f_{2(k-1)} (2k,\sigma(2), \ldots, \sigma(2k-1) ). \end{align*} $$
Flipping
![]() $\sigma (0)$
and
$\sigma (0)$
and
![]() $\sigma (1)$
changes both the sign of
$\sigma (1)$
changes both the sign of
![]() $\sigma $
and that of
$\sigma $
and that of
![]() $f_{2}(\sigma (0), \sigma (1),2k)$
. Therefore, we obtain
$f_{2}(\sigma (0), \sigma (1),2k)$
. Therefore, we obtain
 $$ \begin{align*} A & = \frac{2}{(2k)!} \cdot \sum_{i=0}^{2k-2}\sum_{j=i+1}^{2k-1} \sum_{\sigma \in \Sigma(X_{i,j})} \operatorname{\mathrm{sgn}}([i,j]*\sigma) \cdot f_{2}(i,j,2k) \cdot f_{2(k-1)} ([2k]*\sigma ) \\ & = \frac{2}{(2k)!} \cdot \sum_{i=0}^{2k-2}\sum_{j=i+1}^{2k-1} \sum_{\sigma \in \Sigma(X_{i,j})} \operatorname{\mathrm{sgn}}([i,j]*\sigma) \cdot 1 \cdot \operatorname{\mathrm{sgn}}(\sigma). \end{align*} $$
$$ \begin{align*} A & = \frac{2}{(2k)!} \cdot \sum_{i=0}^{2k-2}\sum_{j=i+1}^{2k-1} \sum_{\sigma \in \Sigma(X_{i,j})} \operatorname{\mathrm{sgn}}([i,j]*\sigma) \cdot f_{2}(i,j,2k) \cdot f_{2(k-1)} ([2k]*\sigma ) \\ & = \frac{2}{(2k)!} \cdot \sum_{i=0}^{2k-2}\sum_{j=i+1}^{2k-1} \sum_{\sigma \in \Sigma(X_{i,j})} \operatorname{\mathrm{sgn}}([i,j]*\sigma) \cdot 1 \cdot \operatorname{\mathrm{sgn}}(\sigma). \end{align*} $$
Here, we use the following notation:
![]() $X_{i,j} := \{0,\ldots ,2k-1\} \setminus \{i,j\}$
; the permutation/tuple
$X_{i,j} := \{0,\ldots ,2k-1\} \setminus \{i,j\}$
; the permutation/tuple
![]() $[i,j]*\sigma $
on
$[i,j]*\sigma $
on
![]() $\{0,\ldots ,2k-1\}$
is obtained by using i, j in the first two positions, and then filling up with
$\{0,\ldots ,2k-1\}$
is obtained by using i, j in the first two positions, and then filling up with
![]() $\sigma $
, and so on.
$\sigma $
, and so on.
Let
![]() $[X_{i,j}]$
be the sequence of elements in
$[X_{i,j}]$
be the sequence of elements in
![]() $X_{i,j}$
, in order. Then
$X_{i,j}$
, in order. Then
for all
![]() $i \in \{0,\ldots ,2k-2\}$
,
$i \in \{0,\ldots ,2k-2\}$
,
![]() $j \in \{i+1,\ldots ,2k-1\}$
; here, we set
$j \in \{i+1,\ldots ,2k-1\}$
; here, we set
![]() $\operatorname {\mathrm {sgn}}(x)$
of
$\operatorname {\mathrm {sgn}}(x)$
of
![]() $x \in {\mathbb {N}}$
to
$x \in {\mathbb {N}}$
to
![]() $+1$
if x is even, and to
$+1$
if x is even, and to
![]() $-1$
if x is odd. We distinguish two cases.
$-1$
if x is odd. We distinguish two cases.
-
• If i is odd, then
 $\sum _{j=i+1}^{2k-1} \operatorname {\mathrm {sgn}}(\kern1.5pt j-1)$
is zero, because there are equally many even and odd numbers in
$\sum _{j=i+1}^{2k-1} \operatorname {\mathrm {sgn}}(\kern1.5pt j-1)$
is zero, because there are equally many even and odd numbers in
 $\{i+1, \ldots , 2k-1\}$
.
$\{i+1, \ldots , 2k-1\}$
. -
• If i is even, then
 $\{i+1,\ldots , 2k-1\}$
contains one more odd number than even numbers, whence
$\{i+1,\ldots , 2k-1\}$
contains one more odd number than even numbers, whence  $$ \begin{align*} \operatorname{\mathrm{sgn}}(i) \cdot \sum_{j=i+1}^{2k-1} \operatorname{\mathrm{sgn}}(\kern1.5pt j-1) = 1. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{sgn}}(i) \cdot \sum_{j=i+1}^{2k-1} \operatorname{\mathrm{sgn}}(\kern1.5pt j-1) = 1. \end{align*} $$
Therefore, since there are k even numbers inside
![]() $\{0, \ldots , 2k -2\}$
, we obtain
$\{0, \ldots , 2k -2\}$
, we obtain
 $$ \begin{align*} A & = \frac{2}{(2k)!} \cdot k \cdot |X_{i,j}| ! = \frac{2}{(2k)!} \cdot k \cdot (2k-2)! = \frac{1}{2k-1}, \end{align*} $$
$$ \begin{align*} A & = \frac{2}{(2k)!} \cdot k \cdot |X_{i,j}| ! = \frac{2}{(2k)!} \cdot k \cdot (2k-2)! = \frac{1}{2k-1}, \end{align*} $$
as claimed.
Similar computations can also be found in the literature [Reference Jekel34].