No CrossRef data available.
Article contents
BASIC NONARCHIMEDEAN JØRGENSEN THEORY
Published online by Cambridge University Press: 19 March 2024
Abstract
We prove a nonarchimedean analogue of Jørgensen’s inequality, and use it to deduce several algebraic convergence results. As an application, we show that every dense subgroup of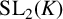 
${\mathrm {SL}_2}(K)$, where K is a p-adic field, contains two elements that generate a dense subgroup of 
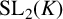${\mathrm {SL}_2}(K)$, which is a special case of a result by Breuillard and Gelander [‘On dense free subgroups of Lie groups’, J. Algebra 261(2) (2003), 448–467]. We also list several other related results, which are well known to experts, but not easy to locate in the literature; for example, we show that a nonelementary subgroup of 
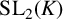${\mathrm {SL}_2}(K)$ over a nonarchimedean local field K is discrete if and only if each of its two-generator subgroups is discrete.
MSC classification
Primary:
20E08: Groups acting on trees
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by George Willis
The first and third author are supported by the New Zealand Marsden Fund. The first author is also supported by the Rutherford Foundation.
References
Armitage, J. V. and Parker, J. R., ‘Jørgensen’s inequality for non-archimedean metric spaces’, in: Geometry and Dynamics of Groups and Spaces (eds. Kapranov, M., Manin, Y. I., Moree, P., Kolyada, S. and Potyagailo, L.) (Birkhäuser, Basel, 2008), 97–111.CrossRefGoogle Scholar
Beardon, A., The Geometry of Discrete Groups, Graduate Texts in Mathematics, 91 (Springer-Verlag, New York, 1995).Google Scholar
Bourbaki, N., Elements of Mathematics: General Topology. Part 2 (Hermann, Paris, 1966).Google Scholar
Breuillard, E. and Gelander, T., ‘On dense free subgroups of Lie groups’, J. Algebra 261(2) (2003), 448–467.CrossRefGoogle Scholar
Bridson, M. and Haefliger, A., Metric Spaces of Non-Positive Curvature, Grundlehren der mathematischen Wissenschaften, 319 (Springer-Verlag, Berlin, 1999).CrossRefGoogle Scholar
Bruhat, F. and Tits, J., ‘Groupes réductifs sur un corps local. I. Données radicielles valuées’, Publ. Math. Inst. Hautes Études Sci. 41 (1972), 5–251.CrossRefGoogle Scholar
Caprace, P. E. and De Medts, T., ‘Simple locally compact groups acting on trees and their germs of automorphisms’, Transform. Groups 16(2) (2011), 375–411.CrossRefGoogle Scholar
Cassels, J. W. S., Local Fields (Cambridge University Press, Cambridge, 1986).CrossRefGoogle Scholar
Conder, M. J. and Schillewaert, J., ‘Discrete two-generator subgroups of
$\mathrm{PSL}_2$
over non-archimedean local fields’, Preprint, 2023, arXiv:2208.12404.Google Scholar
$\mathrm{PSL}_2$
over non-archimedean local fields’, Preprint, 2023, arXiv:2208.12404.Google ScholarCuller, M. and Morgan, J. W., ‘Group actions on
$\mathbb{R}$
-trees’, Proc. Lond. Math. Soc. (3) 55(3) (1987), 571–604.CrossRefGoogle Scholar
$\mathbb{R}$
-trees’, Proc. Lond. Math. Soc. (3) 55(3) (1987), 571–604.CrossRefGoogle ScholarGilman, J., ‘Two-generator discrete subgroups of
${}\mathrm{PSL}_2\left(\mathbb{R}\right)$
’, Mem. Amer. Math. Soc. 117 (1995), 561.Google Scholar
${}\mathrm{PSL}_2\left(\mathbb{R}\right)$
’, Mem. Amer. Math. Soc. 117 (1995), 561.Google ScholarGromov, M., ‘Hyperbolic groups’, in: Essays in Group Theory, Mathematical Sciences Research Institute Publications, 8 (ed. Gersten, S. M.) (Springer, New York, 1987), 75–263.CrossRefGoogle Scholar
Jørgensen, T., ‘On discrete groups of Möbius transformations’, Amer. J. Math. 98(3) (1976), 739–749.CrossRefGoogle Scholar
Jørgensen, T., ‘A note on subgroups of
$\mathrm{SL}_2\left(\mathbb{C}\right)$
’, Quart. J. Math. Oxford Ser. (2) 28(110) (1977), 209–211.CrossRefGoogle Scholar
$\mathrm{SL}_2\left(\mathbb{C}\right)$
’, Quart. J. Math. Oxford Ser. (2) 28(110) (1977), 209–211.CrossRefGoogle ScholarJørgensen, T. and Kiikka, M., ‘Some extreme discrete groups’, Ann. Acad. Sci. Fenn. Ser. A I Math. 1(2) (1975), 245–248.CrossRefGoogle Scholar
Jørgensen, T. and Klein, P., ‘Algebraic convergence of finitely generated Kleinian groups’, Quart. J. Math. Oxford Ser. (2) 33(131) (1982), 325–332.CrossRefGoogle Scholar
Kato, F., ‘Non-archimedean orbifolds covered by Mumford curves’, J. Algebraic Geom. 14(1 (2005), 1–34.CrossRefGoogle Scholar
Kramer, L., ‘Some remarks on proper actions, proper metric spaces, and buildings’, Adv. Geom. 22(4) (2022), 541–559.CrossRefGoogle Scholar
Kuranishi, M., ‘On everywhere dense imbedding of free groups in Lie groups’, Nagoya Math. J. 2 (1951), 63–71.CrossRefGoogle Scholar
Lubotzky, A., ‘Lattices of minimal covolume in
$\mathrm{SL}_2$
: a nonarchimedean analogue of Siegel’s Theorem
$\mu \ge \pi /21$
’, J. Amer. Math. Soc. 3(4) (1990), 961–975.Google Scholar
$\mathrm{SL}_2$
: a nonarchimedean analogue of Siegel’s Theorem
$\mu \ge \pi /21$
’, J. Amer. Math. Soc. 3(4) (1990), 961–975.Google ScholarMartin, G. J., ‘On discrete Möbius groups in all dimensions: a generalization of Jørgensen’s inequality’, Acta Math. 163(3–4) (1989), 253–289.CrossRefGoogle Scholar
Morgan, J. W. and Shalen, P. B., ‘Valuations, trees, and degenerations of hyperbolic structures I’, Ann. of Math. (2) 120(3) (1984), 401–476.CrossRefGoogle Scholar
Qiu, W. Y., Yang, J. H. and Yin, Y. C., ‘The discrete subgroups and Jørgensen’s inequality for
$(m,{\mathbb{C}}_p)$
’, Acta Math. Sin. 29(3) (2013), 417–428.CrossRefGoogle Scholar
$(m,{\mathbb{C}}_p)$
’, Acta Math. Sin. 29(3) (2013), 417–428.CrossRefGoogle ScholarScott, G. P., ‘Finitely generated 3-manifold groups are finitely presented’, J. Lond. Math. Soc. (2) 6 (1973), 437–440.CrossRefGoogle Scholar
Serre, J.-P., Local Fields (Springer-Verlag, New York, 1979); translated by M. J. Greenberg.CrossRefGoogle Scholar
Serre, J.-P., Trees (Springer-Verlag, Berlin, 1980); translated by J. Stillwell.CrossRefGoogle Scholar
Tits, J., ‘A theorem of Lie–Kolchin for trees’, in: Contributions to Algebra: A Collection of Papers Dedicated to Ellis-Kolchin (eds. Bass, H., Cassidy, P. J. and Kovacic, J.) (Academic Press, New York, 1977), 377–388.CrossRefGoogle Scholar