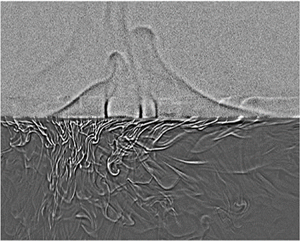
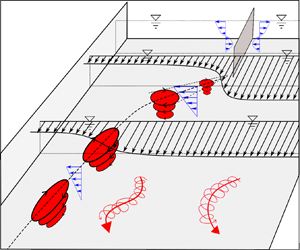
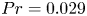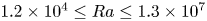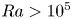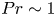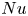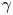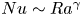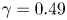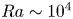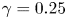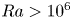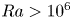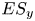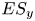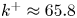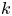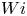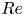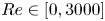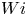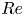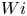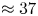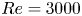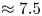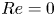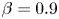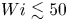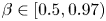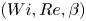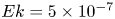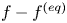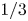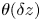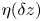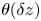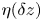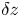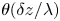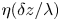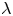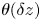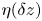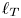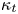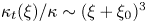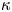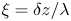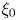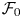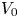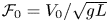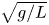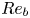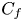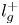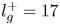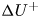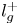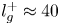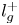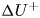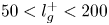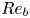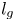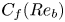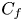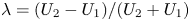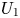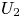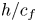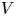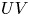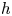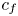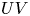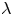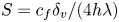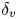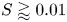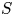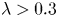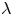Graphical abstract from Veltkamp, B., Velikov, K. & Bonn, D. 2022 High velocity impact on a thin (non-Newtonian) fluid layer. J. Fluid Mech. 951, A40. doi:10.1017/jfm.2022.884.
JFM Rapids
Flow states and heat transport in liquid metal convection
-
- Published online by Cambridge University Press:
- 28 October 2022, R1
-
- Article
-
- You have access
- HTML
- Export citation
Tandem droplet locomotion in a uniform electric field
-
- Published online by Cambridge University Press:
- 10 November 2022, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weakly nonlinear evolution of stochastically driven non-normal systems
-
- Published online by Cambridge University Press:
- 14 November 2022, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Impact of spanwise effective slope upon rough-wall turbulent channel flow
-
- Published online by Cambridge University Press:
- 28 October 2022, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A spectral inspection for turbulence amplification in oblique shock wave/turbulent boundary layer interaction
-
- Published online by Cambridge University Press:
- 28 October 2022, A2
-
- Article
- Export citation
Finite-amplitude elastic waves in viscoelastic channel flow from large to zero Reynolds number
-
- Published online by Cambridge University Press:
- 28 October 2022, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the analytic explanation of experiments where turbulence vanishes in pipe flow
-
- Published online by Cambridge University Press:
- 02 November 2022, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bénard convection in a slowly rotating penny-shaped cylinder subject to constant heat flux boundary conditions
-
- Published online by Cambridge University Press:
- 02 November 2022, A5
-
- Article
- Export citation
Computational analysis of experiments on shock detachment in hypersonic flow of nitrogen and carbon dioxide over a wedge
-
- Published online by Cambridge University Press:
- 08 November 2022, A6
-
- Article
- Export citation
Effects of kinematic and magnetic boundary conditions on the dynamics of convection-driven plane layer dynamos
-
- Published online by Cambridge University Press:
- 02 November 2022, A7
-
- Article
- Export citation
Discrete Boltzmann multi-scale modelling of non-equilibrium multiphase flows
-
- Published online by Cambridge University Press:
- 03 November 2022, A8
-
- Article
- Export citation
Instabilities in three-dimensional boundary-layer flows with a highly non-ideal fluid
-
- Published online by Cambridge University Press:
- 03 November 2022, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fluctuation-induced slip of thermal boundary layers at a stable liquid–liquid interface
-
- Published online by Cambridge University Press:
- 08 November 2022, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Richtmyer–Meshkov instability of thermal, isotope and species interfaces in a five-moment multi-fluid plasma
-
- Published online by Cambridge University Press:
- 03 November 2022, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A tractable mathematical model for rectified diffusion
-
- Published online by Cambridge University Press:
- 03 November 2022, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vibration-induced ‘anti-gravity’ tames thermal turbulence at high Rayleigh numbers
-
- Published online by Cambridge University Press:
- 03 November 2022, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Viscous effects on real gases in quasi-one-dimensional supersonic convergent divergent nozzle flows
-
- Published online by Cambridge University Press:
- 03 November 2022, A14
-
- Article
- Export citation
Wave drag during an unsteady motion
-
- Published online by Cambridge University Press:
- 04 November 2022, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
From drag-reducing riblets to drag-increasing ridges
-
- Published online by Cambridge University Press:
- 04 November 2022, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shallow mixing layers over hydraulically smooth bottom in a tilted open channel
-
- Published online by Cambridge University Press:
- 08 November 2022, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation