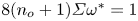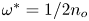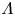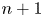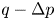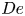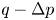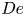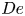Open access
Limited time 'free to read' article collections
Impact Metrics - 10 highest cited articles contributing to the current Impact factor
JFM Papers
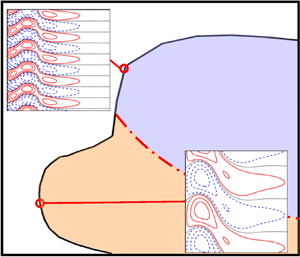
Lattice Boltzmann modelling and study of droplet equatorial streaming in an electric field
-
- Published online by Cambridge University Press:
- 26 July 2024, A40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the relevance of lift force modelling in turbulent wall flows with small inertial particles
-
- Published online by Cambridge University Press:
- 25 July 2024, A47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of a magnetic particle in an oscillating magnetic field subject to a shear flow
-
- Published online by Cambridge University Press:
- 25 July 2024, A49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A model for frequency scaling of flow oscillations in high-speed double cones
-
- Published online by Cambridge University Press:
- 25 July 2024, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-Oberbeck–Boussinesq effects on the linear stability of a vertical natural convection boundary layer
-
- Published online by Cambridge University Press:
- 24 July 2024, A44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flow regimes in emptying–filling boxes with two buoyancy sources of differing strengths and elevations
-
- Published online by Cambridge University Press:
- 24 July 2024, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Investigation of free surface effect on the cavity expansion and contraction in high-speed water entry
-
- Published online by Cambridge University Press:
- 24 July 2024, A53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics-augmented cluster-based network model
-
- Published online by Cambridge University Press:
- 24 July 2024, A48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Long-range two-dimensional hydrodynamic interaction between a pair of mutually repellent disks
-
- Published online by Cambridge University Press:
- 26 June 2024, A39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The characteristics of bubbly shock waves in a cavitating axisymmetric venturi via time-resolved X-ray densitometry
-
- Published online by Cambridge University Press:
- 26 June 2024, A34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Capillary rise in partially saturated rigid porous media
-
- Published online by Cambridge University Press:
- 04 June 2024, A36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A critical transition of two-dimensional flow in toroidal geometry
-
- Published online by Cambridge University Press:
- 04 June 2024, A33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Connections between propulsive efficiency and wake structure via modal decomposition
-
- Published online by Cambridge University Press:
- 04 June 2024, A35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two-interface and thin-filament approximation in Hele-Shaw channel flow
-
- Published online by Cambridge University Press:
- 03 June 2024, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A continuum model of discrete granular avalanches
-
- Published online by Cambridge University Press:
- 03 June 2024, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flow of an Oldroyd-B fluid in a slowly varying contraction: theoretical results for arbitrary values of Deborah number in the ultra-dilute limit
-
- Published online by Cambridge University Press:
- 31 May 2024, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fluctuation covariance-based study of roll-streak dynamics in Poiseuille flow turbulence
-
- Published online by Cambridge University Press:
- 31 May 2024, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the dynamics of aligned inertial particles settling in a quiescent, stratified two-layer medium
-
- Published online by Cambridge University Press:
- 31 May 2024, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite-size inertial spherical particles in turbulence
-
- Published online by Cambridge University Press:
- 31 May 2024, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spreading dynamics of droplets impacting on oscillating hydrophobic substrates
-
- Published online by Cambridge University Press:
- 31 May 2024, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation