Research Article
Characterizations of Schützenberger graphs in terms of their automorphism groups and fundamental groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 275-291
-
- Article
-
- You have access
- Export citation
Proper left type-A monoids revisited
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 293-306
-
- Article
-
- You have access
- Export citation
Eta-products which are simultaneous eigenforms of Hecke operators
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 307-323
-
- Article
-
- You have access
- Export citation
Interpolation and inequalities for functions of exponential type: the Arens irregularity of an extremal algebra
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 325-326
-
- Article
-
- You have access
- Export citation
Some characterizations of the hereditary pretorsion class of semigroup automata
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 327-337
-
- Article
-
- You have access
- Export citation
Metacyclic p-groups and their conjugacy classes of subgroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 339-344
-
- Article
-
- You have access
- Export citation
On injectives in some varieties of Ockham algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 345-351
-
- Article
-
- You have access
- Export citation
Isomorphisms between endomorphism rings of projective modules
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 353-355
-
- Article
-
- You have access
- Export citation
Some characterizations of semiprime Goldie rings
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 357-365
-
- Article
-
- You have access
- Export citation
Units of group rings of groups of order 16
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 367-379
-
- Article
-
- You have access
- Export citation
An identity for the Fibonacci and Lucas numbers
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 381-384
-
- Article
-
- You have access
- Export citation
On congruences of double p-algebras with nonvoid core
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 385-394
-
- Article
-
- You have access
- Export citation
Pythagorean ratios in arithmetic progression, part i. three Pythagorean ratios
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 395-407
-
- Article
-
- You have access
- Export citation
Corrigendum
On frattini-like subgroups
-
- Published online by Cambridge University Press:
- 18 May 2009, p. 408
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 35 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f8
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 35 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation



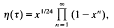

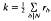 is an integer. Using the Legendre-Jacobi symbol (—), we define a Dirichlet character ∈ by
is an integer. Using the Legendre-Jacobi symbol (—), we define a Dirichlet character ∈ by
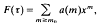
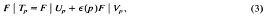
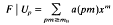

 (Z
(Z