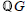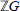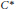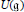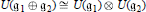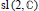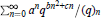Research Article
Derivations and Invariant Forms of Lie Algebras Graded by Finite Root Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-241
-
- Article
-
- You have access
- Export citation
Intégration Du Sous-Différentiel Proximal: Un Contre Exemple
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 242-265
-
- Article
-
- You have access
- Export citation
The Torsion Free Pieri Formula
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 266-289
-
- Article
-
- You have access
- Export citation
Noncommutative Disc Algebras for Semigroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 290-311
-
- Article
-
- You have access
- Export citation
Units in Group Rings of Free Products of Prime Cyclic Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 312-322
-
- Article
-
- You have access
- Export citation
Purely Infinite, Simple C*-Algebras Arising From Free Product Constructions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 323-341
-
- Article
-
- You have access
- Export citation
Shape Fibrations, Multivalued Maps and Shape Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 342-355
-
- Article
-
- You have access
- Export citation
Some Norms on Universal Enveloping Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 356-377
-
- Article
-
- You have access
- Export citation
Equivariant Polynomial Automorphisms Of Θ-Representations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 378-400
-
- Article
-
- You have access
- Export citation
The Hypercentre and the n-Centre of the Unit Group of an Integral Group Ring
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 401-411
-
- Article
-
- You have access
- Export citation
Asymptotic Transformations of q-Series
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 412-425
-
- Article
-
- You have access
- Export citation
The Groups of the Regular Star-Polytopes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 426-448
-
- Article
-
- You have access
- Export citation