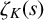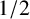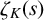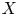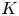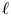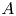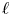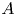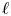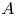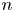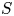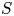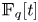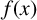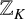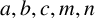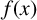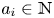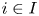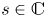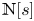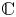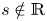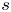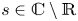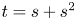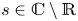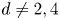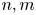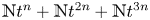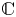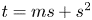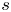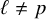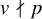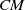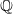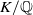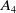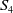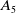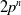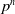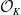318 results in 11Rxx
Zagier–Hoffman’s Conjectures in Positive Characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 22 October 2024, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE LOWEST ZERO OF THE DEDEKIND ZETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 22 October 2024, pp. 1-9
-
- Article
-
- You have access
- HTML
- Export citation
MONOGENIC QUARTIC POLYNOMIALS AND THEIR GALOIS GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
Gassmann triples with special cycle types and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 October 2024, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CONJECTURE OF ZHI-WEI SUN ON MATRICES CONCERNING MULTIPLICATIVE SUBGROUPS OF FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 September 2024, pp. 1-7
-
- Article
-
- You have access
- HTML
- Export citation
Multiplicative dependence of rational values modulo approximate finitely generated groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-17
-
- Article
-
- You have access
- HTML
- Export citation
MONOGENIC EVEN QUARTIC TRINOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-6
-
- Article
-
- You have access
- HTML
- Export citation
Cyclic base change of cuspidal automorphic representations over function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1959-2004
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
On the integral part of A-motivic cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 16 September 2024, pp. 1715-1783
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
Minimal subfields of elliptic curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A solution to the Erdős–Sárközy–Sós problem on asymptotic Sidon bases of order 3
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1418-1432
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NORMAL BASES FOR FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 44-55
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
Spectral decomposition of genuine cusp forms over global function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1194-1260
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discriminant and integral basis of number fields defined by exponential Taylor polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 528-541
-
- Article
-
- You have access
- HTML
- Export citation
CHARACTERISATION OF PRIMES DIVIDING THE INDEX OF A CLASS OF POLYNOMIALS AND ITS APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-8
-
- Article
-
- You have access
- HTML
- Export citation
NON-PÓLYA FIELDS WITH LARGE PÓLYA GROUPS ARISING FROM LEHMER QUINTICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
Invariant set generated by a nonreal number is everywhere dense
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local-global compatibility for regular algebraic cuspidal automorphic representations when
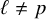 $\ell \neq p$
$\ell \neq p$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 12 February 2024, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kato’s main conjecture for potentially ordinary primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 26 January 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
Leopoldt-type theorems for non-abelian extensions of
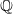 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation