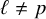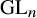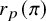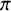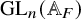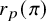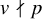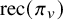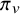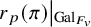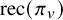1 Introduction
Let F be an imaginary CM (or totally real) field, and let
![]() $\pi $
be a regular algebraic (i.e.,
$\pi $
be a regular algebraic (i.e.,
![]() $\pi _\infty $
has the same infinitesimal character as an irreducible algebraic representation
$\pi _\infty $
has the same infinitesimal character as an irreducible algebraic representation
![]() $\rho _\pi $
of
$\rho _\pi $
of
![]() $\operatorname {RS}^F_{\mathbb {Q}} \operatorname {GL}_n$
) cuspidal automorphic representation of
$\operatorname {RS}^F_{\mathbb {Q}} \operatorname {GL}_n$
) cuspidal automorphic representation of
![]() $\operatorname {GL}_n(\mathbb {A}_F)$
. In Harris-Lan-Taylor-Thorne [Reference Harris, Lan, Taylor and Thorne10] and in Scholze [Reference Scholze18], the authors construct a continuous semisimple representation (depending on a choice of a rational prime p and an isomorphism
$\operatorname {GL}_n(\mathbb {A}_F)$
. In Harris-Lan-Taylor-Thorne [Reference Harris, Lan, Taylor and Thorne10] and in Scholze [Reference Scholze18], the authors construct a continuous semisimple representation (depending on a choice of a rational prime p and an isomorphism
![]() $\imath : \overline {\mathbb {Q}}_p \stackrel {\sim }{\longrightarrow } \mathbb {C}$
)
$\imath : \overline {\mathbb {Q}}_p \stackrel {\sim }{\longrightarrow } \mathbb {C}$
)
which satisfies the following: For every finite place
![]() $v \nmid p$
of F such that
$v \nmid p$
of F such that
![]() $\pi $
and F are both unramified at v,
$\pi $
and F are both unramified at v,
![]() $r_{p,\imath }(\pi )$
is unramified at v and
$r_{p,\imath }(\pi )$
is unramified at v and
Here,
![]() $\operatorname {rec}_{F_v}$
as normalized in [Reference Harris and Taylor11] denotes the local Langlands correspondence for
$\operatorname {rec}_{F_v}$
as normalized in [Reference Harris and Taylor11] denotes the local Langlands correspondence for
![]() $F_v$
, and
$F_v$
, and
![]() $\operatorname {WD}(r_v)$
denotes the Weil-Deligne representation associated to the the p-adic Galois representation
$\operatorname {WD}(r_v)$
denotes the Weil-Deligne representation associated to the the p-adic Galois representation
![]() $r_v$
of the decomposition group
$r_v$
of the decomposition group
![]() $G_{F_v} := \operatorname {Gal}(\overline {F_v}/F_v)$
. In this paper, we extend local-global compatibility up to semisimplification (1.1) to all primes
$G_{F_v} := \operatorname {Gal}(\overline {F_v}/F_v)$
. In this paper, we extend local-global compatibility up to semisimplification (1.1) to all primes
![]() $v \nmid p$
of F. In particular, we prove the following theorem:
$v \nmid p$
of F. In particular, we prove the following theorem:
Theorem 1. Keeping the notation of the previous paragraph, let
![]() $v \nmid p$
be a prime of F. Then
$v \nmid p$
be a prime of F. Then
In fact, our methods allow us to ‘bound’ the monodromy of
![]() $\operatorname {WD}(\left .r_{p,\imath }(\pi )\right |{}_{G_{F_v}})^{\operatorname {Frob}-ss}$
by the monodromy of
$\operatorname {WD}(\left .r_{p,\imath }(\pi )\right |{}_{G_{F_v}})^{\operatorname {Frob}-ss}$
by the monodromy of
![]() $\operatorname {rec}_{F_v}(\pi _v|\operatorname {det}|_v^{(1-n)/2})$
. In the past, such versions of local-global compatibility have been used for proving the nonvanishing of certain Selmer groups (see, for example, Bellaiche-Chenevier [Reference Bellaiche and Chenevier3]). Using the notation introduced in Definition 8.2, we can generalize the above theorem to the following:
$\operatorname {rec}_{F_v}(\pi _v|\operatorname {det}|_v^{(1-n)/2})$
. In the past, such versions of local-global compatibility have been used for proving the nonvanishing of certain Selmer groups (see, for example, Bellaiche-Chenevier [Reference Bellaiche and Chenevier3]). Using the notation introduced in Definition 8.2, we can generalize the above theorem to the following:
Theorem 2. Keeping the notation of the first paragraph, let
![]() $v \nmid p$
be a prime of F. Then
$v \nmid p$
be a prime of F. Then
where ‘
![]() $\operatorname {Frob}$
-ss’ denotes Frobenius semisimplification.
$\operatorname {Frob}$
-ss’ denotes Frobenius semisimplification.
The above theorems are already known when such
![]() $\pi $
are conjugate self-dual, by work of Caraiani [Reference Caraiani6], Shin [Reference Shin19] and Chenevier-Harris [Reference Chenevier and Harris9]. In particular, in [Reference Caraiani6, Reference Shin19], the authors prove the stronger statement that the monodromy of
$\pi $
are conjugate self-dual, by work of Caraiani [Reference Caraiani6], Shin [Reference Shin19] and Chenevier-Harris [Reference Chenevier and Harris9]. In particular, in [Reference Caraiani6, Reference Shin19], the authors prove the stronger statement that the monodromy of
![]() $\operatorname {WD}(\left .r_{p,\imath }(\pi )\right |{}_{G_{F_v}})^{\operatorname {Frob}-ss}$
is equal to that of
$\operatorname {WD}(\left .r_{p,\imath }(\pi )\right |{}_{G_{F_v}})^{\operatorname {Frob}-ss}$
is equal to that of
![]() $\operatorname {rec}_{F_v}(\pi _v \otimes |\operatorname {det}|_v^{(1-n)/2})$
under the added hypothesis that
$\operatorname {rec}_{F_v}(\pi _v \otimes |\operatorname {det}|_v^{(1-n)/2})$
under the added hypothesis that
![]() $\pi $
is conjugate self-dual. When removing the ‘conjugate self-dual’ hypothesis for a given
$\pi $
is conjugate self-dual. When removing the ‘conjugate self-dual’ hypothesis for a given
![]() $\pi $
, one can no longer expect to find the corresponding Galois representations in the etale cohomology of Shimura varieties, and so the authors of [Reference Harris, Lan, Taylor and Thorne10] construct
$\pi $
, one can no longer expect to find the corresponding Galois representations in the etale cohomology of Shimura varieties, and so the authors of [Reference Harris, Lan, Taylor and Thorne10] construct
![]() $r_{p,\imath }(\pi )$
instead using an p-adic interpolation argument. To prove Theorem 1, we must reconstruct the Galois representations
$r_{p,\imath }(\pi )$
instead using an p-adic interpolation argument. To prove Theorem 1, we must reconstruct the Galois representations
![]() $r_{p,\imath }(\pi )$
as in [Reference Harris, Lan, Taylor and Thorne10] while studying the Hecke action at all primes
$r_{p,\imath }(\pi )$
as in [Reference Harris, Lan, Taylor and Thorne10] while studying the Hecke action at all primes
![]() $v \nmid p$
. We summarize the argument below.
$v \nmid p$
. We summarize the argument below.
Let
![]() $\pi $
be a regular algebraic cuspidal automorphic representation on
$\pi $
be a regular algebraic cuspidal automorphic representation on
![]() $\operatorname {GL}_n(\mathbb {A}_F)$
. Let G denote the quasisplit unitary similitude group of signature
$\operatorname {GL}_n(\mathbb {A}_F)$
. Let G denote the quasisplit unitary similitude group of signature
![]() $(n,n)$
associated to
$(n,n)$
associated to
![]() $F^{2n}$
and alternating form
$F^{2n}$
and alternating form
![]() $\left (\begin {smallmatrix} 0 & 1_n \\-1_n & 0\end {smallmatrix}\right )$
, where the similitude factor
$\left (\begin {smallmatrix} 0 & 1_n \\-1_n & 0\end {smallmatrix}\right )$
, where the similitude factor
![]() $\operatorname {GL}_1$
is defined over
$\operatorname {GL}_1$
is defined over
![]() $\mathbb {Q}$
(not F). It has a maximal parabolic
$\mathbb {Q}$
(not F). It has a maximal parabolic
![]() $P = \{\operatorname {GL}_1 \times \left (\begin {smallmatrix}\ast & \ast \\0 & \ast \end {smallmatrix}\right )\} \subset G$
with Levi
$P = \{\operatorname {GL}_1 \times \left (\begin {smallmatrix}\ast & \ast \\0 & \ast \end {smallmatrix}\right )\} \subset G$
with Levi
![]() $L = \{\operatorname {GL}_1 \times \left (\begin {smallmatrix}\ast & 0 \\0 & \ast \end {smallmatrix}\right )\} \subset P$
. However, note that
$L = \{\operatorname {GL}_1 \times \left (\begin {smallmatrix}\ast & 0 \\0 & \ast \end {smallmatrix}\right )\} \subset P$
. However, note that
![]() $L \cong \operatorname {GL}_1 \times \operatorname {RS}^F_{\mathbb {Q}}\operatorname {GL}_n$
. For all sufficiently large positive integers M, let
$L \cong \operatorname {GL}_1 \times \operatorname {RS}^F_{\mathbb {Q}}\operatorname {GL}_n$
. For all sufficiently large positive integers M, let
(where
![]() $\operatorname {Ind}$
denotes unnormalized induction). The authors of [Reference Harris, Lan, Taylor and Thorne10] prove that
$\operatorname {Ind}$
denotes unnormalized induction). The authors of [Reference Harris, Lan, Taylor and Thorne10] prove that
![]() $\Pi (M)$
is a subrepresentation of the space of overconvergent p-adic automorphic forms on G of some possibly nonclassical weight and finite slope. Classical cusp forms on this space base change via the trace formula to
$\Pi (M)$
is a subrepresentation of the space of overconvergent p-adic automorphic forms on G of some possibly nonclassical weight and finite slope. Classical cusp forms on this space base change via the trace formula to
![]() $\operatorname {GL}_{2n}$
to isobaric sums of conjugate self-dual cuspidal automorphic representations, and they have Galois representations satisfying full local-global compatibility. Now, at all primes
$\operatorname {GL}_{2n}$
to isobaric sums of conjugate self-dual cuspidal automorphic representations, and they have Galois representations satisfying full local-global compatibility. Now, at all primes
![]() $v \nmid p$
of F which split over
$v \nmid p$
of F which split over
![]() $F^+$
(equivalently, at all primes away from p where G splits), take the Bernstein centers associated to a finite union of Bernstein components containing
$F^+$
(equivalently, at all primes away from p where G splits), take the Bernstein centers associated to a finite union of Bernstein components containing
![]() $\Pi (M)_v$
as the Hecke algebras acting on spaces of p-adic and classical cusp forms on G of arbitrary integral (not necessarily classical) weight. For each
$\Pi (M)_v$
as the Hecke algebras acting on spaces of p-adic and classical cusp forms on G of arbitrary integral (not necessarily classical) weight. For each
![]() $\sigma \in W_{F_v}$
, the image of the Bernstein centers contains Hecke operators whose eigenvalue on a p-adic cusp form
$\sigma \in W_{F_v}$
, the image of the Bernstein centers contains Hecke operators whose eigenvalue on a p-adic cusp form
![]() $\Pi ^{\prime }$
of G is equal to
$\Pi ^{\prime }$
of G is equal to
If
![]() $\Pi ^{\prime }$
is classical, then local-global compatibility is already known, and so the eigenvalue is also equal to
$\Pi ^{\prime }$
is classical, then local-global compatibility is already known, and so the eigenvalue is also equal to
where
![]() $r_p(\Pi ^{\prime }): G_F \rightarrow \operatorname {GL}_{2n}(\overline {\mathbb {Q}}_p)$
denotes the Galois representation associated to
$r_p(\Pi ^{\prime }): G_F \rightarrow \operatorname {GL}_{2n}(\overline {\mathbb {Q}}_p)$
denotes the Galois representation associated to
![]() $\Pi ^{\prime }$
. By showing that there are linear combinations of classical cusp forms of G whose Hecke eigenvalues are congruent mod
$\Pi ^{\prime }$
. By showing that there are linear combinations of classical cusp forms of G whose Hecke eigenvalues are congruent mod
![]() $p^k$
to those of
$p^k$
to those of
![]() $\Pi (M)$
for each positive k, we are able to construct a continuous pseudorepresentation
$\Pi (M)$
for each positive k, we are able to construct a continuous pseudorepresentation
![]() $T: G_F \rightarrow \overline {\mathbb {Q}}_p$
satisfying the following: for every place
$T: G_F \rightarrow \overline {\mathbb {Q}}_p$
satisfying the following: for every place
![]() $v \nmid p$
of F which is split over
$v \nmid p$
of F which is split over
![]() $F^+$
and each
$F^+$
and each
![]() $\sigma _v \in W_{F_v}$
,
$\sigma _v \in W_{F_v}$
,
This implies that there is a continuous semisimple Galois representation
![]() $r_{p,\imath }(\Pi (M)): G_F \rightarrow \operatorname {GL}_{2n}(\overline {\mathbb {Q}}_p)$
whose trace is equal to T, and so for all primes v of F which are split over
$r_{p,\imath }(\Pi (M)): G_F \rightarrow \operatorname {GL}_{2n}(\overline {\mathbb {Q}}_p)$
whose trace is equal to T, and so for all primes v of F which are split over
![]() $F^+$
and lie above any rational prime other than p,
$F^+$
and lie above any rational prime other than p,
Thus, if
![]() $\epsilon _p$
denotes the p-adic cyclotomic character, then
$\epsilon _p$
denotes the p-adic cyclotomic character, then
![]() $\operatorname {WD}(\left .r_{p,\imath }(\Pi (M)) \otimes \epsilon _p^{-M}\right |{}_{G_{F_v}})^{ss}$
is isomorphic to
$\operatorname {WD}(\left .r_{p,\imath }(\Pi (M)) \otimes \epsilon _p^{-M}\right |{}_{G_{F_v}})^{ss}$
is isomorphic to
Because we construct
![]() $r_{p,\imath }(\Pi (M))$
for each sufficiently large positive integer M, it is now group theory to isolate an n-dimensional subquotient
$r_{p,\imath }(\Pi (M))$
for each sufficiently large positive integer M, it is now group theory to isolate an n-dimensional subquotient
![]() $r_{p,\imath }(\pi ): G_F \rightarrow \operatorname {GL}_{n}(\overline {\mathbb {Q}}_p)$
satisfying
$r_{p,\imath }(\pi ): G_F \rightarrow \operatorname {GL}_{n}(\overline {\mathbb {Q}}_p)$
satisfying
when
![]() $v \nmid p$
is a prime of F which is split over
$v \nmid p$
is a prime of F which is split over
![]() $F^+$
. Using the patching lemma of Sorensen [Reference Sorensen21], we can remove the assumption that v must split over
$F^+$
. Using the patching lemma of Sorensen [Reference Sorensen21], we can remove the assumption that v must split over
![]() $F^+$
and therefore conclude Theorem 1
$F^+$
and therefore conclude Theorem 1
![]() $^{ss}$
. We then use idempotents constructed by Schneider-Zink [Reference Schneider and Zink17] and properties of
$^{ss}$
. We then use idempotents constructed by Schneider-Zink [Reference Schneider and Zink17] and properties of
![]() $\wedge ^k r_{p,\imath }(\Pi (M))$
and
$\wedge ^k r_{p,\imath }(\Pi (M))$
and
![]() $\wedge ^k \operatorname {rec}_{F_v}(\operatorname {BC}(\Pi (M))_v)$
to ‘bound’ the monodromy of
$\wedge ^k \operatorname {rec}_{F_v}(\operatorname {BC}(\Pi (M))_v)$
to ‘bound’ the monodromy of
![]() $\operatorname {WD}(r_{p,\imath }(\pi ))^{\operatorname {Frob}-ss}$
by the monodromy of
$\operatorname {WD}(r_{p,\imath }(\pi ))^{\operatorname {Frob}-ss}$
by the monodromy of
![]() $\operatorname {rec}_{F_v}(\pi _v \otimes |\operatorname {det}|_v^{(1-n)/2})$
.
$\operatorname {rec}_{F_v}(\pi _v \otimes |\operatorname {det}|_v^{(1-n)/2})$
.
Notation and conventions
Let
![]() $F^+$
be a totally real field, and let
$F^+$
be a totally real field, and let
![]() $F_0$
denote an imaginary quadratic field. We set
$F_0$
denote an imaginary quadratic field. We set
![]() $F = F_0F^+$
, and c will denote the nontrivial element of
$F = F_0F^+$
, and c will denote the nontrivial element of
![]() $\operatorname {Gal}(F/F^+)$
. Let p denote a rational prime that splits in
$\operatorname {Gal}(F/F^+)$
. Let p denote a rational prime that splits in
![]() $F_0$
. Let n denote a positive integer, and if
$F_0$
. Let n denote a positive integer, and if
![]() $F^+ = \mathbb {Q}$
, assume
$F^+ = \mathbb {Q}$
, assume
![]() $n> 2$
. In the sequel,
$n> 2$
. In the sequel,
![]() $\ell $
will always denote a rational prime such that
$\ell $
will always denote a rational prime such that
![]() $\ell \neq p$
. Fix
$\ell \neq p$
. Fix
![]() $\imath : \overline {\mathbb {Q}}_p \stackrel {\sim }{\longrightarrow } \mathbb {C}$
.
$\imath : \overline {\mathbb {Q}}_p \stackrel {\sim }{\longrightarrow } \mathbb {C}$
.
For any field K, we will once and for all choose an algebraic closure
![]() $\overline {K}$
of K, and
$\overline {K}$
of K, and
![]() $G_K$
will denote the absolute Galois group of
$G_K$
will denote the absolute Galois group of
![]() $\overline {K}$
over K. If
$\overline {K}$
over K. If
![]() $K_0 \subset K$
is a subfield and S is a finite set of primes of
$K_0 \subset K$
is a subfield and S is a finite set of primes of
![]() $K_0$
, then we will denote by
$K_0$
, then we will denote by
![]() $G_K^S$
the maximal continuous quotient of
$G_K^S$
the maximal continuous quotient of
![]() $G_K$
in which all primes of K not lying above an element of S are unramified.
$G_K$
in which all primes of K not lying above an element of S are unramified.
If K is an arbitrary number field and v is a finite place of K, let
![]() $\varpi _v$
denote the uniformizer of
$\varpi _v$
denote the uniformizer of
![]() $K_v$
and
$K_v$
and
![]() $k(v)$
is the residue field of v. Denote the absolute value on K associated to v by
$k(v)$
is the residue field of v. Denote the absolute value on K associated to v by
![]() $|\cdot |_v$
, which is normalized so that
$|\cdot |_v$
, which is normalized so that
![]() $|\varpi _{v}|_v = (\#k(v))^{-1}$
. If v is a real place of K, then
$|\varpi _{v}|_v = (\#k(v))^{-1}$
. If v is a real place of K, then
![]() $|x|_v := \pm x$
, and if v is complex, then
$|x|_v := \pm x$
, and if v is complex, then
![]() $|x|_v = {}^cxx.$
Let
$|x|_v = {}^cxx.$
Let
If
![]() $r: G_{K_v} \rightarrow \operatorname {GL}_n(\overline {\mathbb {Q}}_{p})$
denotes a continuous representation of
$r: G_{K_v} \rightarrow \operatorname {GL}_n(\overline {\mathbb {Q}}_{p})$
denotes a continuous representation of
![]() $G_{K_v}$
where
$G_{K_v}$
where
![]() $v \nmid p$
is finite, then we will write
$v \nmid p$
is finite, then we will write
![]() $\operatorname {WD}(r)$
for the corresponding Weil-Deligne representation of the Weil group
$\operatorname {WD}(r)$
for the corresponding Weil-Deligne representation of the Weil group
![]() $W_{K_v}$
of
$W_{K_v}$
of
![]() $K_v$
(see section 1 of Taylor-Yoshida [Reference Taylor and Yoshida24]). A Weil-Deligne representation is denoted as
$K_v$
(see section 1 of Taylor-Yoshida [Reference Taylor and Yoshida24]). A Weil-Deligne representation is denoted as
![]() $(r,V,N) = (r,N) = (V,N)$
, where V is a finite-dimensional vector space over
$(r,V,N) = (r,N) = (V,N)$
, where V is a finite-dimensional vector space over
![]() $\overline {\mathbb {Q}}_p$
,
$\overline {\mathbb {Q}}_p$
,
![]() $r: W_{F_v} \rightarrow \operatorname {GL}(V)$
is a representation with open kernel and
$r: W_{F_v} \rightarrow \operatorname {GL}(V)$
is a representation with open kernel and
![]() $N(r) = N: V \rightarrow V$
is a nilpotent endomorphism satisfying
$N(r) = N: V \rightarrow V$
is a nilpotent endomorphism satisfying
(here,
![]() $\operatorname {Art}_{F_v}: F_v^\times \stackrel {\sim }{\longrightarrow } W_{F_v}^{ab}$
denotes the local Artin map, normalized as in [Reference Taylor and Yoshida24]). We say
$\operatorname {Art}_{F_v}: F_v^\times \stackrel {\sim }{\longrightarrow } W_{F_v}^{ab}$
denotes the local Artin map, normalized as in [Reference Taylor and Yoshida24]). We say
![]() $(r,V,N)$
is Frobenius semisimple if r is semisimple. We denote the Frobenius semisimplification of
$(r,V,N)$
is Frobenius semisimple if r is semisimple. We denote the Frobenius semisimplification of
![]() $(r,V,N)$
by
$(r,V,N)$
by
![]() $(r,V,N)^{\operatorname {Frob}-ss}$
, and the semisimplification of
$(r,V,N)^{\operatorname {Frob}-ss}$
, and the semisimplification of
![]() $(r,V,N)$
is
$(r,V,N)$
is
![]() $(r,V,N)^{ss} = (r^{ss},V,0)$
(see section 1 of [Reference Taylor and Yoshida24]).
$(r,V,N)^{ss} = (r^{ss},V,0)$
(see section 1 of [Reference Taylor and Yoshida24]).
If
![]() $\pi $
is an irreducible smooth representation of
$\pi $
is an irreducible smooth representation of
![]() $\operatorname {GL}_n(K_v)$
over
$\operatorname {GL}_n(K_v)$
over
![]() $\mathbb {C}$
, we will write
$\mathbb {C}$
, we will write
![]() $\operatorname {rec}_{K_v}(\pi )$
for the Weil-Deligne representation of
$\operatorname {rec}_{K_v}(\pi )$
for the Weil-Deligne representation of
![]() $W_{K_v}$
corresponding to
$W_{K_v}$
corresponding to
![]() $\pi $
by the local Langlands correspondence (see Harris-Taylor [Reference Harris and Taylor11] or Henniart [Reference Henniart12]). If
$\pi $
by the local Langlands correspondence (see Harris-Taylor [Reference Harris and Taylor11] or Henniart [Reference Henniart12]). If
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
are irreducible smooth representations of
$\pi _2$
are irreducible smooth representations of
![]() $\operatorname {GL}_{n_1}(K_v)$
(resp.
$\operatorname {GL}_{n_1}(K_v)$
(resp.
![]() $\operatorname {GL}_{n_2}(K_v)$
), then there is an irreducible smooth representation
$\operatorname {GL}_{n_2}(K_v)$
), then there is an irreducible smooth representation
![]() $\pi _1 \boxplus \pi _2$
of
$\pi _1 \boxplus \pi _2$
of
![]() $\operatorname {GL}_{n_1 + n_2}(K_v)$
over
$\operatorname {GL}_{n_1 + n_2}(K_v)$
over
![]() $\mathbb {C}$
satisfying
$\mathbb {C}$
satisfying
Let G be a reductive group over
![]() $K_v$
, and let P be a parabolic subgroup of G with unipotent radical N and Levi L. For a smooth representation
$K_v$
, and let P be a parabolic subgroup of G with unipotent radical N and Levi L. For a smooth representation
![]() $\pi $
of
$\pi $
of
![]() $L(K_v)$
on a vector space
$L(K_v)$
on a vector space
![]() $V_{\pi }$
over a field
$V_{\pi }$
over a field
![]() $\Omega $
of characteristic 0, we define
$\Omega $
of characteristic 0, we define
![]() $\operatorname {Ind}_{P(K_v)}^{G(K_v)} \pi $
to be the representation of
$\operatorname {Ind}_{P(K_v)}^{G(K_v)} \pi $
to be the representation of
![]() $G(K_v)$
by right translation on the set of locally constant functions
$G(K_v)$
by right translation on the set of locally constant functions
![]() $\varphi : G(K_v) \rightarrow V_{\pi }$
such that
$\varphi : G(K_v) \rightarrow V_{\pi }$
such that
![]() $\varphi (hg) = \pi (h)\varphi (g)$
for all
$\varphi (hg) = \pi (h)\varphi (g)$
for all
![]() $h \in P(F_v)$
and
$h \in P(F_v)$
and
![]() $g \in G(K_v)$
. When
$g \in G(K_v)$
. When
![]() $\Omega = \mathbb {C}$
, define normalized induction as
$\Omega = \mathbb {C}$
, define normalized induction as
2 Recollections
We recall the setup of Harris-Lan-Taylor-Thorne [Reference Harris, Lan, Taylor and Thorne10], including the unitary similitude group, and the Shimura variety (and various compactifications) associated to the unitary group, as well as their integral models. This will allow us to define automorphic vector bundles defined on these integral models, whose global sections will be the space of classical and p-adic automorphic forms.
2.1 Unitary group
We define an integral unitary similitude group, which is associated to the following data. If
![]() $\Psi _n$
denotes the
$\Psi _n$
denotes the
![]() $n \times n$
matrix with
$n \times n$
matrix with
![]() $1$
’s on the anti-diagonal and
$1$
’s on the anti-diagonal and
![]() $0$
’s elsewhere, then let
$0$
’s elsewhere, then let
![]() $J_n$
denote the following element of
$J_n$
denote the following element of
![]() $\operatorname {GL}_{2n}(\mathbb {Z})$
:
$\operatorname {GL}_{2n}(\mathbb {Z})$
:
 $$ \begin{align*}J_n = \left(\begin{array}{cc}0 & \Psi_n \\-\Psi_n & 0\end{array}\right).\end{align*} $$
$$ \begin{align*}J_n = \left(\begin{array}{cc}0 & \Psi_n \\-\Psi_n & 0\end{array}\right).\end{align*} $$
Let
![]() $\mathcal {D}_F^{-1}$
denote the inverse different of
$\mathcal {D}_F^{-1}$
denote the inverse different of
![]() $\mathcal {O}_F$
, and define the
$\mathcal {O}_F$
, and define the
![]() $2n$
-dimensional lattice
$2n$
-dimensional lattice
![]() $\Lambda = (\mathcal {D}_F^{-1})^{n} \oplus \mathcal {O}_F^n$
. Let G be the group scheme over
$\Lambda = (\mathcal {D}_F^{-1})^{n} \oplus \mathcal {O}_F^n$
. Let G be the group scheme over
![]() $\mathbb {Z}$
defined by
$\mathbb {Z}$
defined by
for any ring R. Over
![]() $\mathbb {Z}[1/\operatorname {Disc}(F/\mathbb {Q})]$
, it is a quasi-split connected reductive group which splits over
$\mathbb {Z}[1/\operatorname {Disc}(F/\mathbb {Q})]$
, it is a quasi-split connected reductive group which splits over
![]() $\mathcal {O}_{\widetilde {F}}[1/\operatorname {Disc}(F/\mathbb {Q})]$
, where
$\mathcal {O}_{\widetilde {F}}[1/\operatorname {Disc}(F/\mathbb {Q})]$
, where
![]() $\widetilde {F}$
denotes the normal closure of
$\widetilde {F}$
denotes the normal closure of
![]() $F/\mathbb {Q}$
. Let
$F/\mathbb {Q}$
. Let
![]() $\nu : G \rightarrow \operatorname {GL}_1$
be the multiplier character sending
$\nu : G \rightarrow \operatorname {GL}_1$
be the multiplier character sending
![]() $(g,\mu ) \mapsto \mu $
.
$(g,\mu ) \mapsto \mu $
.
If
![]() $R = \Omega $
is an algebraically closed field of characteristic 0, then
$R = \Omega $
is an algebraically closed field of characteristic 0, then
Fix the lattice
![]() $\Lambda _{(n)} \cong (\mathcal {D}_F^{-1})^n$
consisting of elements of
$\Lambda _{(n)} \cong (\mathcal {D}_F^{-1})^n$
consisting of elements of
![]() $\Lambda $
whose last n coordinates are equal to 0, and define
$\Lambda $
whose last n coordinates are equal to 0, and define
![]() $\Lambda _{(n)}^{\prime } \cong \mathcal {O}_F^n$
consisting of elements of
$\Lambda _{(n)}^{\prime } \cong \mathcal {O}_F^n$
consisting of elements of
![]() $\Lambda $
whose first n coordinates are equal to
$\Lambda $
whose first n coordinates are equal to
![]() $0$
. Let
$0$
. Let
![]() $P^+_{(n)}$
denote the subgroup of G preserving
$P^+_{(n)}$
denote the subgroup of G preserving
![]() $\Lambda _{(n)}$
. Write
$\Lambda _{(n)}$
. Write
![]() $L_{(n),\operatorname {lin}}$
for the subgroup of
$L_{(n),\operatorname {lin}}$
for the subgroup of
![]() $P_{(n)}^+$
consisting of elements with
$P_{(n)}^+$
consisting of elements with
![]() $\nu = 1$
which preserve
$\nu = 1$
which preserve
![]() $\Lambda _{(n)}^{\prime }$
, and write
$\Lambda _{(n)}^{\prime }$
, and write
![]() $L_{(n),\operatorname {herm}}$
for the subgroup of
$L_{(n),\operatorname {herm}}$
for the subgroup of
![]() $P_{(n)}^+$
which act trivially on
$P_{(n)}^+$
which act trivially on
![]() $\Lambda /\Lambda _{(n)}$
and preserve
$\Lambda /\Lambda _{(n)}$
and preserve
![]() $\Lambda _{(n)}^{\prime }$
. Then
$\Lambda _{(n)}^{\prime }$
. Then
![]() $L_{(n),\operatorname {lin}} \cong \operatorname {RS}^{\mathcal {O}_F}_{\mathbb {Z}} \operatorname {GL}_n$
and
$L_{(n),\operatorname {lin}} \cong \operatorname {RS}^{\mathcal {O}_F}_{\mathbb {Z}} \operatorname {GL}_n$
and
![]() $L_{(n),\operatorname {herm}} \cong \mathbb {G}_m$
, and we can define
$L_{(n),\operatorname {herm}} \cong \mathbb {G}_m$
, and we can define
![]() $L_{(n)} := L_{(n),\operatorname {lin}} \times L_{(n),\operatorname {herm}}$
.
$L_{(n)} := L_{(n),\operatorname {lin}} \times L_{(n),\operatorname {herm}}$
.
Finally, let
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord},\times } := G(\mathbb {A}^{p,\infty }) \times P^+_{(n)}(\mathbb {Z}_p)$
, and
$G(\mathbb {A}^\infty )^{\operatorname {ord},\times } := G(\mathbb {A}^{p,\infty }) \times P^+_{(n)}(\mathbb {Z}_p)$
, and
![]() $G(\mathbb {A}^{\infty })^{\operatorname {ord}} = G(\mathbb {A}^{p,\infty }) \times \varsigma _p^{\mathbb {Z}_{\geq 0}} P_{(n)}^+(\mathbb {Z}_p),$
where
$G(\mathbb {A}^{\infty })^{\operatorname {ord}} = G(\mathbb {A}^{p,\infty }) \times \varsigma _p^{\mathbb {Z}_{\geq 0}} P_{(n)}^+(\mathbb {Z}_p),$
where
![]() $\varsigma _p \in L_{(n),\operatorname {herm}}(\mathbb {Q}_p) \cong \mathbb {Q}_p^\times $
denotes the unique element with multiplier
$\varsigma _p \in L_{(n),\operatorname {herm}}(\mathbb {Q}_p) \cong \mathbb {Q}_p^\times $
denotes the unique element with multiplier
![]() $p^{-1}$
.
$p^{-1}$
.
2.2 Level structure
If
![]() $N_2 \geq N_1 \geq 0$
are integers, then let
$N_2 \geq N_1 \geq 0$
are integers, then let
![]() $U_p(N_1,N_2)$
be the subgroup of elements of
$U_p(N_1,N_2)$
be the subgroup of elements of
![]() $G(\mathbb {Z}_p)$
which
$G(\mathbb {Z}_p)$
which
![]() ${\operatorname {mod}} p^{N_2}$
lie in
${\operatorname {mod}} p^{N_2}$
lie in
![]() $P^+_{(n)}(\mathbb {Z}/p^{N_2}\mathbb {Z})$
and map to 1 in
$P^+_{(n)}(\mathbb {Z}/p^{N_2}\mathbb {Z})$
and map to 1 in
![]() $L_{(n),\operatorname {lin}}(\mathbb {Z}/p^{N_1}\mathbb {Z})$
. If
$L_{(n),\operatorname {lin}}(\mathbb {Z}/p^{N_1}\mathbb {Z})$
. If
![]() $U^p$
is an open compact subgroup of
$U^p$
is an open compact subgroup of
![]() $G(\mathbb {A}^{p,\infty })$
, we write
$G(\mathbb {A}^{p,\infty })$
, we write
![]() $U^p(N_1, N_2)$
for
$U^p(N_1, N_2)$
for
![]() $U^p \times U_p(N_1,N_2)$
.
$U^p \times U_p(N_1,N_2)$
.
If
![]() $N \geq 0$
is an integer, we write
$N \geq 0$
is an integer, we write
![]() $U_p(N)$
for the kernel of the map
$U_p(N)$
for the kernel of the map
![]() $P^{+}_{(n)}(\mathbb {Z}_p) \rightarrow L_{(n),\operatorname {lin}}(\mathbb {Z}/p^N\mathbb {Z})$
. In addition,
$P^{+}_{(n)}(\mathbb {Z}_p) \rightarrow L_{(n),\operatorname {lin}}(\mathbb {Z}/p^N\mathbb {Z})$
. In addition,
![]() $U_p(N)$
will also denote the image of this kernel inside
$U_p(N)$
will also denote the image of this kernel inside
![]() $L_{(n),\operatorname {lin}}(\mathbb {Z}_p)$
.
$L_{(n),\operatorname {lin}}(\mathbb {Z}_p)$
.
2.3 Shimura variety
Fix a neat open compact subgroup U (as defined in section 0.6 of Pink [Reference Pink16]), and let S be a locally noetherian scheme over
![]() $\mathbb {Q}$
. Recall from §3.1 in [Reference Harris, Lan, Taylor and Thorne10] that a polarized G-abelian scheme with U-level structure is an abelian scheme A over S of relative dimension
$\mathbb {Q}$
. Recall from §3.1 in [Reference Harris, Lan, Taylor and Thorne10] that a polarized G-abelian scheme with U-level structure is an abelian scheme A over S of relative dimension
![]() $n\cdot [F:\mathbb {Q}]$
along with the following data:
$n\cdot [F:\mathbb {Q}]$
along with the following data:
-
• An embedding
 $\imath : F \hookrightarrow \operatorname {End}^0(A)$
such that
$\imath : F \hookrightarrow \operatorname {End}^0(A)$
such that
 $\operatorname {Lie} A$
is locally free of rank n over
$\operatorname {Lie} A$
is locally free of rank n over
 $F \otimes _{\mathbb {Q}} \mathcal {O}_S$
.
$F \otimes _{\mathbb {Q}} \mathcal {O}_S$
. -
• A polarization
 $\lambda : A \rightarrow A^\vee $
$\lambda : A \rightarrow A^\vee $
-
• U-level structure
 $[\eta ]$
.
$[\eta ]$
.
For more precise definitions, see §3.1.1 of [Reference Harris, Lan, Taylor and Thorne10]. Denote by
![]() $X_{U}$
the smooth quasi-projective scheme over
$X_{U}$
the smooth quasi-projective scheme over
![]() $\mathbb {Q}$
which represents the functor that sends a locally noetherian scheme
$\mathbb {Q}$
which represents the functor that sends a locally noetherian scheme
![]() $S/\mathbb {Q}$
to the set of quasi-isogeny classes of polarized G-abelian schemes with U-level structure. Let
$S/\mathbb {Q}$
to the set of quasi-isogeny classes of polarized G-abelian schemes with U-level structure. Let
![]() $[(A^{\operatorname {univ}},\imath ^{\operatorname {univ}},\lambda ^{\operatorname {univ}},[\eta ^{\operatorname {univ}}])]$
denote the universal equivalence class of polarized G-abelian varieties with U-level structure. Allowing U to vary, the inverse system
$[(A^{\operatorname {univ}},\imath ^{\operatorname {univ}},\lambda ^{\operatorname {univ}},[\eta ^{\operatorname {univ}}])]$
denote the universal equivalence class of polarized G-abelian varieties with U-level structure. Allowing U to vary, the inverse system
![]() $\{X_{U}\}$
has a right
$\{X_{U}\}$
has a right
![]() $G(\mathbb {A}^\infty )$
action, with finite etale transition maps
$G(\mathbb {A}^\infty )$
action, with finite etale transition maps
![]() $g: X_{U} \rightarrow X_{U^{\prime }}$
whenever
$g: X_{U} \rightarrow X_{U^{\prime }}$
whenever
![]() $U^{\prime } \supset g^{-1}Ug$
.
$U^{\prime } \supset g^{-1}Ug$
.
For each U, denote by
![]() $\Omega ^1_{A^{\operatorname {univ}}/X_{U}}$
the sheaf of relative differentials on
$\Omega ^1_{A^{\operatorname {univ}}/X_{U}}$
the sheaf of relative differentials on
![]() $A^{\operatorname {univ}}$
. Let
$A^{\operatorname {univ}}$
. Let
![]() $\Omega _U$
denote the Hodge bundle (i.e., the pullback by the identity section of
$\Omega _U$
denote the Hodge bundle (i.e., the pullback by the identity section of
![]() $\Omega ^1_{A^{\operatorname {univ}}/X_U}$
). It is locally free of rank
$\Omega ^1_{A^{\operatorname {univ}}/X_U}$
). It is locally free of rank
![]() $n\cdot [F:\mathbb {Q}]$
and does not depend on
$n\cdot [F:\mathbb {Q}]$
and does not depend on
![]() $A^{\operatorname {univ}}$
.
$A^{\operatorname {univ}}$
.
For each neat open compact subgroup
![]() $U \subset G(\mathbb {A}^\infty )$
, there is a normal projective scheme
$U \subset G(\mathbb {A}^\infty )$
, there is a normal projective scheme
![]() $X^{\operatorname {min}}_{U}$
over
$X^{\operatorname {min}}_{U}$
over
![]() $\operatorname {Spec} \mathbb {Q}$
together with a
$\operatorname {Spec} \mathbb {Q}$
together with a
![]() $G(\mathbb {A}^\infty )$
-equivariant dense open embedding
$G(\mathbb {A}^\infty )$
-equivariant dense open embedding
which is known as the minimal compactification of
![]() $X_U$
. Let the boundary be denoted by
$X_U$
. Let the boundary be denoted by
![]() $\partial X^{\operatorname {min}}_U = X^{\operatorname {min}}_U \smallsetminus j_{U} X_{U}$
. The inverse system
$\partial X^{\operatorname {min}}_U = X^{\operatorname {min}}_U \smallsetminus j_{U} X_{U}$
. The inverse system
![]() $\{X^{\operatorname {min}}_U\}$
also has a right
$\{X^{\operatorname {min}}_U\}$
also has a right
![]() $G(\mathbb {A}^\infty )$
-action. Furthermore, there is a normal projective flat
$G(\mathbb {A}^\infty )$
-action. Furthermore, there is a normal projective flat
![]() $\mathbb {Z}_{(p)}$
scheme
$\mathbb {Z}_{(p)}$
scheme
![]() $\mathcal {X}^{\operatorname {min}}_{U}$
whose generic fiber is
$\mathcal {X}^{\operatorname {min}}_{U}$
whose generic fiber is
![]() $X^{\operatorname {min}}_U$
. We will denote the ample line bundle on
$X^{\operatorname {min}}_U$
. We will denote the ample line bundle on
![]() $\mathcal {X}^{\operatorname {min}}_{U}$
constructed in Propositions 2.2.1.2 and 2.2.3.1 in Lan [Reference Lan14] by
$\mathcal {X}^{\operatorname {min}}_{U}$
constructed in Propositions 2.2.1.2 and 2.2.3.1 in Lan [Reference Lan14] by
![]() $\omega _U$
. Its pullback to
$\omega _U$
. Its pullback to
![]() $X_U$
is identified with
$X_U$
is identified with
![]() $\wedge ^{n[F:\mathbb {Q}]}\Omega _U$
, and the system
$\wedge ^{n[F:\mathbb {Q}]}\Omega _U$
, and the system
![]() $\{\omega _U\}$
over
$\{\omega _U\}$
over
![]() $\{\mathcal {X}_{U}^{\operatorname {min}}\}$
has an action of
$\{\mathcal {X}_{U}^{\operatorname {min}}\}$
has an action of
![]() $G(\mathbb {A}^{p,\infty } \times \mathbb {Z}_p)$
. If we let
$G(\mathbb {A}^{p,\infty } \times \mathbb {Z}_p)$
. If we let
![]() $\overline {X}_U^{\operatorname {min}} = \mathcal {X}_U^{\operatorname {min}} \otimes _{\mathbb {Z}_{(p)}} \mathbb {F}_p$
, there is a canonical
$\overline {X}_U^{\operatorname {min}} = \mathcal {X}_U^{\operatorname {min}} \otimes _{\mathbb {Z}_{(p)}} \mathbb {F}_p$
, there is a canonical
![]() $G(\mathbb {A}^{p,\infty })$
-invariant section
$G(\mathbb {A}^{p,\infty })$
-invariant section
![]() $\operatorname {Hasse}_U \in H^0(\overline {X}_U^{\operatorname {min}}, \omega _U^{\otimes (p-1)})$
constructed in Corollaries 6.3.1.7-8 in [Reference Lan14] satisfying
$\operatorname {Hasse}_U \in H^0(\overline {X}_U^{\operatorname {min}}, \omega _U^{\otimes (p-1)})$
constructed in Corollaries 6.3.1.7-8 in [Reference Lan14] satisfying
Denote by
![]() $\overline {X}^{\operatorname {min} n-\operatorname {ord}}_U$
the zero locus in
$\overline {X}^{\operatorname {min} n-\operatorname {ord}}_U$
the zero locus in
![]() $\overline {X}^{\operatorname {min}}_U$
of
$\overline {X}^{\operatorname {min}}_U$
of
![]() $\operatorname {Hasse}_U$
.
$\operatorname {Hasse}_U$
.
Lemma 2.1. The nonzero locus
![]() $\overline {X}^{\operatorname {min}}_U \backslash \overline {X}^{\operatorname {min} n-\operatorname {ord}}_U$
is relatively affine over
$\overline {X}^{\operatorname {min}}_U \backslash \overline {X}^{\operatorname {min} n-\operatorname {ord}}_U$
is relatively affine over
![]() $\overline {X}^{\operatorname {min}}_U$
. Furthermore, it is affine over
$\overline {X}^{\operatorname {min}}_U$
. Furthermore, it is affine over
![]() $\mathbb {F}_p$
.
$\mathbb {F}_p$
.
Proof. The nonzero locus over
![]() $\overline {X}^{\operatorname {min}}_U$
is associated to the sheaf of algebras
$\overline {X}^{\operatorname {min}}_U$
is associated to the sheaf of algebras
Over
![]() $\mathbb {F}_p$
, it is associated to the algebra
$\mathbb {F}_p$
, it is associated to the algebra
We conclude the lemma.
2.4 Ordinary locus
Now let
![]() $\mathcal {S}$
denote a locally Noetherian scheme over
$\mathcal {S}$
denote a locally Noetherian scheme over
![]() $\mathbb {Z}_{(p)}$
, and fix a neat open compact subgroup
$\mathbb {Z}_{(p)}$
, and fix a neat open compact subgroup
![]() $U^p$
along with two positive integers
$U^p$
along with two positive integers
![]() $N_2 \geq N_1$
. Then the ordinary locus is a smooth quasi-projective scheme
$N_2 \geq N_1$
. Then the ordinary locus is a smooth quasi-projective scheme
![]() $\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2)}$
over
$\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2)}$
over
![]() $\mathbb {Z}_{(p)}$
representing the functor which sends
$\mathbb {Z}_{(p)}$
representing the functor which sends
![]() $\mathcal {S}$
to the the set of prime-to-p quasi-isogeny classes of ordinary, prime-to-p quasi-polarized G-abelian schemes with
$\mathcal {S}$
to the the set of prime-to-p quasi-isogeny classes of ordinary, prime-to-p quasi-polarized G-abelian schemes with
![]() $U^p(N_1,N_2)$
-level structure as defined in §3.1 of [Reference Harris, Lan, Taylor and Thorne10]. It is a partial integral model of
$U^p(N_1,N_2)$
-level structure as defined in §3.1 of [Reference Harris, Lan, Taylor and Thorne10]. It is a partial integral model of
![]() $X_{U^p(N_1,N_2)}$
. Let
$X_{U^p(N_1,N_2)}$
. Let
![]() $[\mathcal {A}^{\operatorname {univ}},\imath ^{\operatorname {univ}},\lambda ^{\operatorname {univ}},[\eta ^{\operatorname {univ}}]]/\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2)}$
denote the universal equivalence class of ordinary prime-to-p quasi-polarized G-abelian schemes with
$[\mathcal {A}^{\operatorname {univ}},\imath ^{\operatorname {univ}},\lambda ^{\operatorname {univ}},[\eta ^{\operatorname {univ}}]]/\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2)}$
denote the universal equivalence class of ordinary prime-to-p quasi-polarized G-abelian schemes with
![]() $U^p(N_1,N_2)$
-level structure up to quasi-isogeny. Finally, let
$U^p(N_1,N_2)$
-level structure up to quasi-isogeny. Finally, let
![]() $\overline {X}^{\operatorname {ord}}_{U^p(N_1,N_2)} = \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2)} \otimes _{\mathbb {Z}_{(p)}} \mathbb {F}_p$
, which forms an inverse system each with a right
$\overline {X}^{\operatorname {ord}}_{U^p(N_1,N_2)} = \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2)} \otimes _{\mathbb {Z}_{(p)}} \mathbb {F}_p$
, which forms an inverse system each with a right
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-action. Furthermore, the map
$G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-action. Furthermore, the map
is the absolute Frobenius map composed with the forgetful map
![]() $\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2+1)} \rightarrow \mathcal {X}^{\operatorname {ord}}_{U^p(N_2,N_2)}$
for any
$\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2+1)} \rightarrow \mathcal {X}^{\operatorname {ord}}_{U^p(N_2,N_2)}$
for any
![]() $N_2 \geq N_1 \geq 0$
. If
$N_2 \geq N_1 \geq 0$
. If
![]() $N_2> 0$
, then
$N_2> 0$
, then
![]() $\varsigma _p$
defines a finite flat map
$\varsigma _p$
defines a finite flat map
with fibers of degree
![]() $p^{n^2[F^+:\mathbb {Q}]}$
(see §3.1 of [Reference Harris, Lan, Taylor and Thorne10]).
$p^{n^2[F^+:\mathbb {Q}]}$
(see §3.1 of [Reference Harris, Lan, Taylor and Thorne10]).
For each
![]() $U^p(N_1,N_2)$
such that
$U^p(N_1,N_2)$
such that
![]() $U^p$
is neat, there is a partial minimal compactification of the ordinary locus
$U^p$
is neat, there is a partial minimal compactification of the ordinary locus
![]() $\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2)}$
denoted by
$\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2)}$
denoted by
![]() $\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)}$
. By Theorem 6.2.1.1 in [Reference Lan14], this compactification of the ordinary locus is a normal quasi-projective scheme over
$\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)}$
. By Theorem 6.2.1.1 in [Reference Lan14], this compactification of the ordinary locus is a normal quasi-projective scheme over
![]() $\mathbb {Z}_{(p)}$
together with a dense open
$\mathbb {Z}_{(p)}$
together with a dense open
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-equivariant embedding
$G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-equivariant embedding
Its generic fiber is
![]() $X^{\operatorname {min}}_{U^p(N_1,N_2)}$
, but unlike
$X^{\operatorname {min}}_{U^p(N_1,N_2)}$
, but unlike
![]() $\mathcal {X}^{\operatorname {min}}_{U^p(N_1,N_2)}$
, it is not proper. Furthermore, by Proposition 6.2.2.1 in [Reference Lan14], the induced action of
$\mathcal {X}^{\operatorname {min}}_{U^p(N_1,N_2)}$
, it is not proper. Furthermore, by Proposition 6.2.2.1 in [Reference Lan14], the induced action of
![]() $g \in G(\mathbb {A}^\infty )^{\operatorname {ord}}$
on
$g \in G(\mathbb {A}^\infty )^{\operatorname {ord}}$
on
![]() $\{\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)}\}$
is quasi-finite. Write
$\{\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)}\}$
is quasi-finite. Write
![]() $\partial \mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)} = \mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)} - j_{U^p(N_1,N_2)} \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2)}$
for the boundary, and let
$\partial \mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)} = \mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)} - j_{U^p(N_1,N_2)} \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2)}$
for the boundary, and let
![]() $\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)}$
be the formal completion along the special fiber of
$\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)}$
be the formal completion along the special fiber of
![]() $\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)}$
. Note that by Corollary 6.2.2.8 and Example 3.4.5.5 in [Reference Lan14], the natural map
$\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)}$
. Note that by Corollary 6.2.2.8 and Example 3.4.5.5 in [Reference Lan14], the natural map
is an isomorphism, and so we will drop
![]() $N_2$
from notation. Define
$N_2$
from notation. Define
For each
![]() $U^p(N_1,N_2)$
, note that there are
$U^p(N_1,N_2)$
, note that there are
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-equivariant open embeddings
$G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-equivariant open embeddings
This induces a map on the special fibers
which is both an open and closed embedding by Proposition 6.3.2.2 of [Reference Lan14]. Note that only when the level is prime-to-p is the nonzero locus of
![]() $\operatorname {Hasse}_{U^p(N_1,N_2)}$
isomorphic to the special fiber of the minimally compactified ordinary locus. When
$\operatorname {Hasse}_{U^p(N_1,N_2)}$
isomorphic to the special fiber of the minimally compactified ordinary locus. When
![]() $N_2> 0$
, the map in (2.1) is not an isomorphism.
$N_2> 0$
, the map in (2.1) is not an isomorphism.
2.5 Toroidal compactifications
We now introduce toroidal compactifications of
![]() $X_U$
and
$X_U$
and
![]() $\mathcal {X}_{U^p(N_1,N_2)}$
, which are parametrized by neat open compact subgroups of
$\mathcal {X}_{U^p(N_1,N_2)}$
, which are parametrized by neat open compact subgroups of
![]() $G(\mathbb {A}^\infty )$
and certain cone decompositions defined in [Reference Lan14] and [Reference Harris, Lan, Taylor and Thorne10]. Let
$G(\mathbb {A}^\infty )$
and certain cone decompositions defined in [Reference Lan14] and [Reference Harris, Lan, Taylor and Thorne10]. Let
![]() $\mathcal {J}^{\operatorname {tor}}$
be the indexing set of pairs
$\mathcal {J}^{\operatorname {tor}}$
be the indexing set of pairs
![]() $(U,\Delta )$
defined in Proposition 7.1.1.21 in [Reference Lan14] or on pages 169–170 in [Reference Harris, Lan, Taylor and Thorne10], where U is a neat open compact subgroup and
$(U,\Delta )$
defined in Proposition 7.1.1.21 in [Reference Lan14] or on pages 169–170 in [Reference Harris, Lan, Taylor and Thorne10], where U is a neat open compact subgroup and
![]() $\Delta $
is a U-admissible cone decomposition as defined in §5.2 of [Reference Harris, Lan, Taylor and Thorne10]. We will not recall the definition here as it is not necessary for any argument.
$\Delta $
is a U-admissible cone decomposition as defined in §5.2 of [Reference Harris, Lan, Taylor and Thorne10]. We will not recall the definition here as it is not necessary for any argument.
If
![]() $(U,\Delta ) \in \mathcal {J}^{\operatorname {tor}}$
, then by Theorem 1.3.3.15 of [Reference Lan14], there is a smooth projective scheme
$(U,\Delta ) \in \mathcal {J}^{\operatorname {tor}}$
, then by Theorem 1.3.3.15 of [Reference Lan14], there is a smooth projective scheme
![]() $X_{U,\Delta }$
and a divisor with simple normal crossings
$X_{U,\Delta }$
and a divisor with simple normal crossings
![]() $\partial X_{U,\Delta } \subset X_{U,\Delta }$
equipped with an isomorphism
$\partial X_{U,\Delta } \subset X_{U,\Delta }$
equipped with an isomorphism
and a projection
![]() $\pi _{\operatorname {tor}/\operatorname {min}}: X_{U,\Delta } \rightarrow X^{\operatorname {min}}_U$
such that the following diagram commutes:
$\pi _{\operatorname {tor}/\operatorname {min}}: X_{U,\Delta } \rightarrow X^{\operatorname {min}}_U$
such that the following diagram commutes:
 $$ \begin{align*} \begin{aligned} X_{U} &\hookrightarrow X_{U,\Delta} \\ \downarrow & \ \ \ \ \ \ \downarrow \\ X_U & \hookrightarrow X_U^{\operatorname{min}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} X_{U} &\hookrightarrow X_{U,\Delta} \\ \downarrow & \ \ \ \ \ \ \downarrow \\ X_U & \hookrightarrow X_U^{\operatorname{min}}. \end{aligned} \end{align*} $$
The collection
![]() $\{X_{U,\Delta }\}_{\mathcal {J}^{\operatorname {tor}}}$
becomes a system of schemes with a right
$\{X_{U,\Delta }\}_{\mathcal {J}^{\operatorname {tor}}}$
becomes a system of schemes with a right
![]() $G(\mathbb {A}^\infty )$
-action via the maps
$G(\mathbb {A}^\infty )$
-action via the maps
![]() $\pi _{(U,\Delta )/(U^{\prime },\Delta ^{\prime })}: X_{U,\Delta } \rightarrow X_{U^{\prime },\Delta ^{\prime }}$
whenever
$\pi _{(U,\Delta )/(U^{\prime },\Delta ^{\prime })}: X_{U,\Delta } \rightarrow X_{U^{\prime },\Delta ^{\prime }}$
whenever
![]() $(U,\Delta ) \geq (U^{\prime },\Delta ^{\prime })$
(see page 166 of [Reference Harris, Lan, Taylor and Thorne10] for the definition of
$(U,\Delta ) \geq (U^{\prime },\Delta ^{\prime })$
(see page 166 of [Reference Harris, Lan, Taylor and Thorne10] for the definition of
![]() $\geq $
in this context).
$\geq $
in this context).
If
![]() $(U^p(N_1,N_2),\Delta ) \in \mathcal {J}^{\operatorname {tor}}$
, then by Theorem 7.1.4.1 of [Reference Lan14], there is a smooth quasi-projective scheme
$(U^p(N_1,N_2),\Delta ) \in \mathcal {J}^{\operatorname {tor}}$
, then by Theorem 7.1.4.1 of [Reference Lan14], there is a smooth quasi-projective scheme
![]() $\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
and a divisor with simple normal crossings
$\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
and a divisor with simple normal crossings
![]() $\partial \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta } \subset \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
equipped with an isomorphism
$\partial \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta } \subset \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
equipped with an isomorphism
such that the following diagram commutes:
 $$ \begin{align*} \begin{aligned} \mathcal{X}^{\operatorname{ord}}_{U^p(N_1,N_2)} &\hookrightarrow \mathcal{X}^{\operatorname{ord}}_{U^p(N_1,N_2),\Delta} \\ \downarrow & \ \ \ \ \ \ \downarrow \\ \mathcal{X}^{\operatorname{ord}}_{U^p)N_1,N_2)}& \hookrightarrow \mathcal{X}^{\operatorname{ord},\operatorname{min}}_{U^p(N_1,N_2)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathcal{X}^{\operatorname{ord}}_{U^p(N_1,N_2)} &\hookrightarrow \mathcal{X}^{\operatorname{ord}}_{U^p(N_1,N_2),\Delta} \\ \downarrow & \ \ \ \ \ \ \downarrow \\ \mathcal{X}^{\operatorname{ord}}_{U^p)N_1,N_2)}& \hookrightarrow \mathcal{X}^{\operatorname{ord},\operatorname{min}}_{U^p(N_1,N_2)}. \end{aligned} \end{align*} $$
The collection
![]() $\{\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }\}_{\mathcal {J}^{\operatorname {tor}}}$
becomes a system of schemes with a right
$\{\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }\}_{\mathcal {J}^{\operatorname {tor}}}$
becomes a system of schemes with a right
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-action via the maps
$G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-action via the maps
![]() $\pi _{(U^p(N_1,N_2),\Delta )/(U^{p^{\prime }}(N_1^{\prime },N_2^{\prime }),\Delta ^{\prime })}: \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta } \rightarrow \mathcal {X}^{\operatorname {ord}}_{U^{p^{\prime }}(N_1^{\prime },N_2),\Delta ^{\prime }}$
whenever
$\pi _{(U^p(N_1,N_2),\Delta )/(U^{p^{\prime }}(N_1^{\prime },N_2^{\prime }),\Delta ^{\prime })}: \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta } \rightarrow \mathcal {X}^{\operatorname {ord}}_{U^{p^{\prime }}(N_1^{\prime },N_2),\Delta ^{\prime }}$
whenever
![]() $(U^p(N_1,N_2),\Delta ) \geq (U^{p^{\prime }}(N_1^{\prime },N_2),\Delta ^{\prime })$
(see page 167 of [Reference Harris, Lan, Taylor and Thorne10] for the definition of
$(U^p(N_1,N_2),\Delta ) \geq (U^{p^{\prime }}(N_1^{\prime },N_2),\Delta ^{\prime })$
(see page 167 of [Reference Harris, Lan, Taylor and Thorne10] for the definition of
![]() $\geq $
in this context).
$\geq $
in this context).
3 Automorphic bundles
We first define the coherent sheaves on
![]() $\mathcal {X}^{\operatorname {min}}$
whose global sections are what we consider to be the finite part of classical cuspidal automorphic forms on G. They are sheaves originally defined over the toroidal compactifications
$\mathcal {X}^{\operatorname {min}}$
whose global sections are what we consider to be the finite part of classical cuspidal automorphic forms on G. They are sheaves originally defined over the toroidal compactifications
![]() $X_{U,\Delta }$
(where they are locally free) and are then pushed forward to
$X_{U,\Delta }$
(where they are locally free) and are then pushed forward to
![]() $X^{\operatorname {min}}$
via
$X^{\operatorname {min}}$
via
![]() $\pi _{\operatorname {tor},\operatorname {min}}$
. We start by recalling some differential sheaves that have already been defined.
$\pi _{\operatorname {tor},\operatorname {min}}$
. We start by recalling some differential sheaves that have already been defined.
3.1 Automorphic bundles on compactifications of the Shimura variety
Recall from the previous section that we have a locally free sheaf
![]() $\Omega _U$
on
$\Omega _U$
on
![]() $X_U$
, which is the pullback by the identity section of the sheaf of relative differentials from
$X_U$
, which is the pullback by the identity section of the sheaf of relative differentials from
![]() $A^{\operatorname {univ}}$
, the universal abelian variety over
$A^{\operatorname {univ}}$
, the universal abelian variety over
![]() $X_U$
. On
$X_U$
. On
![]() $\mathcal {X}^{\operatorname {min}}_U$
, the normal integral model of the minimal compactification of
$\mathcal {X}^{\operatorname {min}}_U$
, the normal integral model of the minimal compactification of
![]() $X_U$
, there is an ample line bundle
$X_U$
, there is an ample line bundle
![]() $\omega _U$
whose pullback to
$\omega _U$
whose pullback to
![]() $X_U$
is identified with
$X_U$
is identified with
![]() $\wedge ^{n[F:\mathbb {Q}]} \Omega _U$
.
$\wedge ^{n[F:\mathbb {Q}]} \Omega _U$
.
Any universal abelian variety
![]() $A^{\operatorname {univ}}/X_{U}$
extends to a semi-abelian variety
$A^{\operatorname {univ}}/X_{U}$
extends to a semi-abelian variety
![]() $A_\Delta /X_{U,\Delta }$
(see remarks 1.1.2.1 and 1.3.1.4 of [Reference Lan14]). Define
$A_\Delta /X_{U,\Delta }$
(see remarks 1.1.2.1 and 1.3.1.4 of [Reference Lan14]). Define
![]() $\Omega _{U,\Delta }$
as the pullback by the identity section of the sheaf of relative differentials on
$\Omega _{U,\Delta }$
as the pullback by the identity section of the sheaf of relative differentials on
![]() $A_{\Delta }$
. Note that when restricting to the Shimura variety
$A_{\Delta }$
. Note that when restricting to the Shimura variety
![]() $X_U$
, the sheaf
$X_U$
, the sheaf
![]() $\left .\Omega _{U,\Delta }\right |{}_{X_U}$
is canonically isomorphic to
$\left .\Omega _{U,\Delta }\right |{}_{X_U}$
is canonically isomorphic to
![]() $\Omega _U$
. Let
$\Omega _U$
. Let
![]() $\mathcal {O}_{X_{U,\Delta }}(||\nu ||)$
denote the structure sheaf with
$\mathcal {O}_{X_{U,\Delta }}(||\nu ||)$
denote the structure sheaf with
![]() $G(\mathbb {A}^\infty )$
-action twisted by
$G(\mathbb {A}^\infty )$
-action twisted by
![]() $||\nu ||$
.
$||\nu ||$
.
Let
![]() $\mathcal {E}^{\operatorname {can}}_{U,\Delta }$
denote the principal
$\mathcal {E}^{\operatorname {can}}_{U,\Delta }$
denote the principal
![]() $L_{(n)}$
-bundle on
$L_{(n)}$
-bundle on
![]() $X_{U,\Delta }$
, defined as follows: For a Zariski open W,
$X_{U,\Delta }$
, defined as follows: For a Zariski open W,
![]() $\mathcal {E}^{\operatorname {can}}_{U,\Delta }(W)$
is the set of pairs of isomorphisms
$\mathcal {E}^{\operatorname {can}}_{U,\Delta }(W)$
is the set of pairs of isomorphisms
where
![]() $V = \Lambda \otimes \mathbb {Q} = F^{2n}$
and
$V = \Lambda \otimes \mathbb {Q} = F^{2n}$
and
![]() $V_{(n)} = \Lambda _{(n)} \otimes \mathbb {Q} \cong F^{n}$
. There is an action of
$V_{(n)} = \Lambda _{(n)} \otimes \mathbb {Q} \cong F^{n}$
. There is an action of
![]() $h \in L_{(n)}$
on
$h \in L_{(n)}$
on
![]() $\mathcal {E}^{\operatorname {can}}_{U,\Delta }$
by
$\mathcal {E}^{\operatorname {can}}_{U,\Delta }$
by
The inverse system
![]() $\{\mathcal {E}^{\operatorname {can}}_{U,\Delta }\}$
has an action of
$\{\mathcal {E}^{\operatorname {can}}_{U,\Delta }\}$
has an action of
![]() $G(\mathbb {A}^\infty )$
.
$G(\mathbb {A}^\infty )$
.
Let R be any
![]() $\mathbb {Q}$
-algebra. Fix a representation
$\mathbb {Q}$
-algebra. Fix a representation
![]() $\rho $
of
$\rho $
of
![]() $L_{(n)}$
on a finite, locally free R-module
$L_{(n)}$
on a finite, locally free R-module
![]() $W_{\rho }$
. Define the locally free sheaf
$W_{\rho }$
. Define the locally free sheaf
![]() $\mathcal {E}^{\operatorname {can}}_{U,\Delta ,\rho }$
over
$\mathcal {E}^{\operatorname {can}}_{U,\Delta ,\rho }$
over
![]() $X_{U,\Delta } \times \operatorname {Spec} R$
as follows: For a Zariski open W, let
$X_{U,\Delta } \times \operatorname {Spec} R$
as follows: For a Zariski open W, let
![]() $\mathcal {E}^{\operatorname {can}}_{U,\Delta ,\rho }(W)$
be the set of
$\mathcal {E}^{\operatorname {can}}_{U,\Delta ,\rho }(W)$
be the set of
![]() $L_{(n)}(\mathcal {O}_W)$
-equivariant maps of Zariski sheaves of sets,
$L_{(n)}(\mathcal {O}_W)$
-equivariant maps of Zariski sheaves of sets,
With fixed
![]() $\rho $
, the system of sheaves
$\rho $
, the system of sheaves
![]() $\{\mathcal {E}^{\operatorname {can}}_{U,\Delta ,\rho }\}$
has a
$\{\mathcal {E}^{\operatorname {can}}_{U,\Delta ,\rho }\}$
has a
![]() $G(\mathbb {A}^\infty )$
-action. If
$G(\mathbb {A}^\infty )$
-action. If
![]() $\operatorname {Std}$
denotes the representation over
$\operatorname {Std}$
denotes the representation over
![]() $\mathbb {Z}$
of
$\mathbb {Z}$
of
![]() $L_{(n)}$
on
$L_{(n)}$
on
![]() $\Lambda /\Lambda _{(n)}$
, then let
$\Lambda /\Lambda _{(n)}$
, then let
![]() $\omega _{U,\Delta } := \mathcal {E}^{\operatorname {can}}_{U,\Delta ,\wedge ^{n[F:\mathbb {Q}]}\operatorname {Std}^\vee }.$
We will write
$\omega _{U,\Delta } := \mathcal {E}^{\operatorname {can}}_{U,\Delta ,\wedge ^{n[F:\mathbb {Q}]}\operatorname {Std}^\vee }.$
We will write
![]() $\mathcal {I}_{\partial X_{U,\Delta }}$
for the ideal sheaf in
$\mathcal {I}_{\partial X_{U,\Delta }}$
for the ideal sheaf in
![]() $\mathcal {O}_{X_{U,\Delta }}$
, defining the boundary
$\mathcal {O}_{X_{U,\Delta }}$
, defining the boundary
![]() $\partial X_{U,\Delta }$
. Define the subcanonical extension
$\partial X_{U,\Delta }$
. Define the subcanonical extension
Recall the projection
![]() $\pi _{\operatorname {tor}/\operatorname {min}}: X_{U,\Delta } \rightarrow X^{\operatorname {min}}_U$
, and define
$\pi _{\operatorname {tor}/\operatorname {min}}: X_{U,\Delta } \rightarrow X^{\operatorname {min}}_U$
, and define
![]() $\mathcal {E}^{\operatorname {sub}}_{U,\rho } = \pi _{\operatorname {tor}/\operatorname {min}\ast } \mathcal {E}^{\operatorname {sub}}_{U,\Delta ,\rho }.$
The coherent sheaves defined on
$\mathcal {E}^{\operatorname {sub}}_{U,\rho } = \pi _{\operatorname {tor}/\operatorname {min}\ast } \mathcal {E}^{\operatorname {sub}}_{U,\Delta ,\rho }.$
The coherent sheaves defined on
![]() $X^{\operatorname {min}}_U$
are independent of the choice of
$X^{\operatorname {min}}_U$
are independent of the choice of
![]() $\Delta $
. If we fix
$\Delta $
. If we fix
![]() $\rho $
, there is an action of
$\rho $
, there is an action of
![]() $G(\mathbb {A}^\infty )$
on the system
$G(\mathbb {A}^\infty )$
on the system
![]() $\{\mathcal {E}^{\operatorname {sub}}_{U,\rho }\}$
indexed by neat open compact subgroups.
$\{\mathcal {E}^{\operatorname {sub}}_{U,\rho }\}$
indexed by neat open compact subgroups.
Now let
![]() $\rho _0$
be a representation of
$\rho _0$
be a representation of
![]() $L_{(n)}$
on a finite locally free
$L_{(n)}$
on a finite locally free
![]() $\mathbb {Z}_{(p)}$
-module. By Definition 8.3.5.1 of [Reference Lan14], there is a system of coherent sheaves associated to
$\mathbb {Z}_{(p)}$
-module. By Definition 8.3.5.1 of [Reference Lan14], there is a system of coherent sheaves associated to
![]() $\rho _0$
over
$\rho _0$
over
![]() $\{\mathcal {X}^{\operatorname {min}}_U\}$
with
$\{\mathcal {X}^{\operatorname {min}}_U\}$
with
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-action whose pullback to
$G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-action whose pullback to
![]() $\{X^{\operatorname {min}}_U\}$
is
$\{X^{\operatorname {min}}_U\}$
is
![]() $G(\mathbb {A}^\infty )$
-equivariantly identified with
$G(\mathbb {A}^\infty )$
-equivariantly identified with
![]() $\{\mathcal {E}^{\operatorname {sub}}_{U,\rho _0 \otimes \mathbb {Q}}\}$
. We will also refer to these sheaves by
$\{\mathcal {E}^{\operatorname {sub}}_{U,\rho _0 \otimes \mathbb {Q}}\}$
. We will also refer to these sheaves by
![]() $\mathcal {E}^{\operatorname {sub}}_{U,\rho _0}$
. Note that over
$\mathcal {E}^{\operatorname {sub}}_{U,\rho _0}$
. Note that over
![]() $\mathcal {X}^{\operatorname {min}}_U$
,
$\mathcal {X}^{\operatorname {min}}_U$
,
where
![]() $\omega _U$
denotes the ample line bundle defined on
$\omega _U$
denotes the ample line bundle defined on
![]() $\mathcal {X}^{\operatorname {min}}_U$
.
$\mathcal {X}^{\operatorname {min}}_U$
.
3.2 Automorphic bundles on the ordinary locus
We now define automorphic vector bundles on the system of integral models of the minimally compactified ordinary locus
![]() $\{\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)}\}$
as well as its formal completion along the special fiber
$\{\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)}\}$
as well as its formal completion along the special fiber
![]() $\{\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)}\}$
. The global sections of these coherent sheaves will consist of what we consider cuspidal p-adic automorphic forms. We first recall some definitions of sheaves defined on
$\{\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)}\}$
. The global sections of these coherent sheaves will consist of what we consider cuspidal p-adic automorphic forms. We first recall some definitions of sheaves defined on
![]() $\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
.
$\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
.
Any universal abelian variety
![]() $\mathcal {A}^{\operatorname {univ}}/\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2)}$
extends uniquely to a semi-abelian variety
$\mathcal {A}^{\operatorname {univ}}/\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2)}$
extends uniquely to a semi-abelian variety
![]() $\mathcal {A}_\Delta /\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
by Remarks 1.1.2.1 and 1.3.1.4 of [Reference Lan14]. Define
$\mathcal {A}_\Delta /\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
by Remarks 1.1.2.1 and 1.3.1.4 of [Reference Lan14]. Define
![]() $\Omega ^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
as the pullback by the identity section of the sheaf of relative differentials on
$\Omega ^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
as the pullback by the identity section of the sheaf of relative differentials on
![]() $\mathcal {A}_{\Delta }$
. The inverse system
$\mathcal {A}_{\Delta }$
. The inverse system
![]() $\{\Omega ^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }\}$
has an action of
$\{\Omega ^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }\}$
has an action of
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
. There is also a natural map
$G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
. There is also a natural map
Denote by
![]() $\mathcal {O}_{\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }}(||\nu ||)$
the structure sheaf
$\mathcal {O}_{\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }}(||\nu ||)$
the structure sheaf
![]() $\mathcal {O}_{\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }}$
with
$\mathcal {O}_{\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }}$
with
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-action twisted by
$G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-action twisted by
![]() $||\nu ||$
(recall that
$||\nu ||$
(recall that
![]() $\{\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }\}$
has a right
$\{\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }\}$
has a right
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-action).
$G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-action).
Let
![]() $\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta }$
denote the principal
$\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta }$
denote the principal
![]() $L_{(n)}$
-bundle on
$L_{(n)}$
-bundle on
![]() $\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
in the Zariski topology defined as follows: For a Zariski open W,
$\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
in the Zariski topology defined as follows: For a Zariski open W,
![]() $\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta }(W))$
is the set of pairs of isomorphisms
$\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta }(W))$
is the set of pairs of isomorphisms
 $$ \begin{align*}\xi_0:\left.\mathcal{O}_{\mathcal{X}^{\operatorname{ord}}_{U^p(N_1,N_2),\Delta}}(||\nu||)\right|_W \stackrel{\sim}{\longrightarrow} \mathcal{O}_W \qquad \text{and} \qquad \xi_1:\Omega^{\operatorname{ord}}_{U^p(N_1,N_2),\Delta} \stackrel{\sim}{\longrightarrow} \operatorname{Hom}_{\mathbb{Z}}(\Lambda/\Lambda_{(n)}, \mathcal{O}_W).\end{align*} $$
$$ \begin{align*}\xi_0:\left.\mathcal{O}_{\mathcal{X}^{\operatorname{ord}}_{U^p(N_1,N_2),\Delta}}(||\nu||)\right|_W \stackrel{\sim}{\longrightarrow} \mathcal{O}_W \qquad \text{and} \qquad \xi_1:\Omega^{\operatorname{ord}}_{U^p(N_1,N_2),\Delta} \stackrel{\sim}{\longrightarrow} \operatorname{Hom}_{\mathbb{Z}}(\Lambda/\Lambda_{(n)}, \mathcal{O}_W).\end{align*} $$
(Recall that
![]() $\Lambda _{(n)}$
is the sublattice of
$\Lambda _{(n)}$
is the sublattice of
![]() $\Lambda = (\mathcal {D}_F^{-1})^n \oplus \mathcal {O}_F^n$
consisting of elements whose last n coordinates are equal to
$\Lambda = (\mathcal {D}_F^{-1})^n \oplus \mathcal {O}_F^n$
consisting of elements whose last n coordinates are equal to
![]() $0$
.) There is an action of
$0$
.) There is an action of
![]() $h \in L_{(n)}$
on
$h \in L_{(n)}$
on
![]() $\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta }$
by
$\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta }$
by
The inverse system
![]() $\{\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta }\}$
has an action of
$\{\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta }\}$
has an action of
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord}}$
. Let R be a
$G(\mathbb {A}^\infty )^{\operatorname {ord}}$
. Let R be a
![]() $\mathbb {Z}_{(p)}$
-algebra. Fix a representation
$\mathbb {Z}_{(p)}$
-algebra. Fix a representation
![]() $\rho $
of
$\rho $
of
![]() $L_{n,(n)}$
on a finite, locally free R-module
$L_{n,(n)}$
on a finite, locally free R-module
![]() $W_\rho $
. Denote the canonical extension to
$W_\rho $
. Denote the canonical extension to
![]() $\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta ,\rho } \times \operatorname {Spec} R$
of the automorphic vector bundle on
$\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta ,\rho } \times \operatorname {Spec} R$
of the automorphic vector bundle on
![]() $\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2)}$
associated to
$\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2)}$
associated to
![]() $\rho $
by
$\rho $
by
![]() $\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta ,\rho }$
, which is defined as follows: For any Zariski open W,
$\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta ,\rho }$
, which is defined as follows: For any Zariski open W,
![]() $\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta ,\rho }(W)$
is the set of
$\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta ,\rho }(W)$
is the set of
![]() $L_{(n)}(\mathcal {O}_W)$
-equivariant maps of Zariski sheaves of sets
$L_{(n)}(\mathcal {O}_W)$
-equivariant maps of Zariski sheaves of sets
When
![]() $\rho $
is fixed, the system of sheaves
$\rho $
is fixed, the system of sheaves
![]() $\{\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta ,\rho }\}$
has an action of
$\{\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta ,\rho }\}$
has an action of
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord}}$
. Furthermore, the inverse of
$G(\mathbb {A}^\infty )^{\operatorname {ord}}$
. Furthermore, the inverse of
![]() $\varsigma _p^{\ast }$
gives a map
$\varsigma _p^{\ast }$
gives a map
Composing
![]() $(\varsigma _p^{\ast })^{-1}$
with
$(\varsigma _p^{\ast })^{-1}$
with
![]() $1 \otimes \operatorname {tr}_{\varsigma _p}: \mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2 -1),\Delta ,\rho } \otimes {\varsigma _p}_{\ast } \mathcal {O}_{\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }} \rightarrow \mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2 -1),\Delta ,\rho }$
gives a
$1 \otimes \operatorname {tr}_{\varsigma _p}: \mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2 -1),\Delta ,\rho } \otimes {\varsigma _p}_{\ast } \mathcal {O}_{\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }} \rightarrow \mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2 -1),\Delta ,\rho }$
gives a
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-equivariant map
$G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-equivariant map
satisfying
![]() $\operatorname {tr}_F \circ \varsigma _p^{\ast } = p^{n^2[F^+:\mathbb {Q}]}$
. If
$\operatorname {tr}_F \circ \varsigma _p^{\ast } = p^{n^2[F^+:\mathbb {Q}]}$
. If
![]() $\operatorname {Std}$
denotes the representation over
$\operatorname {Std}$
denotes the representation over
![]() $\mathbb {Z}$
of
$\mathbb {Z}$
of
![]() $L_{(n)}$
on
$L_{(n)}$
on
![]() $\Lambda /\Lambda _{(n)}$
, then let
$\Lambda /\Lambda _{(n)}$
, then let
![]() $\omega _{U^p(N_1,N_2),\Delta } := \mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta ,\wedge ^{n[F:\mathbb {Q}]}\operatorname {Std}^\vee }$
denote the pullback of
$\omega _{U^p(N_1,N_2),\Delta } := \mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2),\Delta ,\wedge ^{n[F:\mathbb {Q}]}\operatorname {Std}^\vee }$
denote the pullback of
![]() $\omega _{U}$
to
$\omega _{U}$
to
![]() $\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
. We will write
$\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
. We will write
![]() $\mathcal {I}_{\partial \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }}$
for the ideal sheaf in
$\mathcal {I}_{\partial \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }}$
for the ideal sheaf in
![]() $\mathcal {O}_{\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }}$
defining the boundary
$\mathcal {O}_{\mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }}$
defining the boundary
![]() $\partial \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
. Define the subcanonical extension as
$\partial \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }$
. Define the subcanonical extension as
Again, the inverse of
![]() $\varsigma _p^{\ast }$
gives a map
$\varsigma _p^{\ast }$
gives a map
Composing
![]() $(\varsigma _p^{\ast })^{-1}$
with
$(\varsigma _p^{\ast })^{-1}$
with
![]() $1 \otimes \operatorname {tr}_{\varsigma _p}: \mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2-1),\Delta ,\rho } \otimes {\varsigma _p}_{\ast }\mathcal {I}_{\partial \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }} \rightarrow \mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2-1),\Delta ,\rho }$
gives another
$1 \otimes \operatorname {tr}_{\varsigma _p}: \mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2-1),\Delta ,\rho } \otimes {\varsigma _p}_{\ast }\mathcal {I}_{\partial \mathcal {X}^{\operatorname {ord}}_{U^p(N_1,N_2),\Delta }} \rightarrow \mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U^p(N_1,N_2-1),\Delta ,\rho }$
gives another
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-equivariant map
$G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-equivariant map
satisfying
![]() $\operatorname {tr}_F \circ \varsigma _p^{\ast } = p^{n^2[F^+:\mathbb {Q}]}$
and compatible with the analogous map defined on
$\operatorname {tr}_F \circ \varsigma _p^{\ast } = p^{n^2[F^+:\mathbb {Q}]}$
and compatible with the analogous map defined on
![]() $\{\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U,\Delta ,\rho }\}_{U}$
.
$\{\mathcal {E}^{\operatorname {ord},\operatorname {can}}_{U,\Delta ,\rho }\}_{U}$
.
Denote the pushforward by
![]() $\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1,N_2),\rho } = \pi ^{\operatorname {ord}}_{\operatorname {tor}/\operatorname {min}\ast } \mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1,N_2),\Delta ,\rho }.$
These coherent sheaves defined on
$\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1,N_2),\rho } = \pi ^{\operatorname {ord}}_{\operatorname {tor}/\operatorname {min}\ast } \mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1,N_2),\Delta ,\rho }.$
These coherent sheaves defined on
![]() $\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)}$
are independent of the choice of
$\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)}$
are independent of the choice of
![]() $\Delta $
by Proposition 1.4.3.1 and Lemma 8.3.5.2 in [Reference Lan14]. Note that
$\Delta $
by Proposition 1.4.3.1 and Lemma 8.3.5.2 in [Reference Lan14]. Note that
and by Lemma 5.5 in [Reference Harris, Lan, Taylor and Thorne10], the pullback of
![]() $\mathcal {E}^{\operatorname {sub}}_{U^p(N_1,N_2),\rho }$
to
$\mathcal {E}^{\operatorname {sub}}_{U^p(N_1,N_2),\rho }$
to
![]() $\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2),\rho }$
is
$\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2),\rho }$
is
![]() $\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1,N_2),\rho }.$
$\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1,N_2),\rho }.$
Abusing notation, denote the pullback of
![]() $\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1,N_2),\rho }$
to
$\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1,N_2),\rho }$
to
![]() $\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)}$
by
$\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)}$
by
![]() $\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1),\rho }$
. It is independent of
$\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1),\rho }$
. It is independent of
![]() $N_2$
, and thus,
$N_2$
, and thus,
![]() $\operatorname {tr}_F$
induces a
$\operatorname {tr}_F$
induces a
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-equivariant map
$G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-equivariant map
over
![]() $\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)}$
, and also induces an endomorphism on global sections.
$\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)}$
, and also induces an endomorphism on global sections.
4 Classical and p-adic automorphic forms
Before we define cuspidal automorphic representations on
![]() $G(\mathbb {A}^\infty )$
,
$G(\mathbb {A}^\infty )$
,
![]() $L_{(n)}(\mathbb {A})$
and
$L_{(n)}(\mathbb {A})$
and
![]() $\operatorname {GL}_m(\mathbb {A}_F)$
, we first recall some facts about highest weights of algebraic representations of
$\operatorname {GL}_m(\mathbb {A}_F)$
, we first recall some facts about highest weights of algebraic representations of
![]() $L_{(n)}$
and G.
$L_{(n)}$
and G.
4.1 Weights
For each integer
![]() $0 \leq i \leq n$
, let
$0 \leq i \leq n$
, let
![]() $\Lambda _{(i)}$
denote the elements of
$\Lambda _{(i)}$
denote the elements of
![]() $\Lambda $
for which the last
$\Lambda $
for which the last
![]() $2n - i$
coordinates are zero, and let
$2n - i$
coordinates are zero, and let
![]() $B_n$
denote the Borel of G preserving the chain
$B_n$
denote the Borel of G preserving the chain
![]() $\Lambda _{(n)}\supset \Lambda _{(n-1)} \supset ... \supset \Lambda _{(0)}.$
Let
$\Lambda _{(n)}\supset \Lambda _{(n-1)} \supset ... \supset \Lambda _{(0)}.$
Let
![]() $T_n$
denote the subgroup of diagonal matrices of G.
$T_n$
denote the subgroup of diagonal matrices of G.
Let
![]() $X^{\ast }(T_{n/\Omega }) := \operatorname {Hom}(T_n \times \operatorname {Spec} \Omega , \mathbb {G}_m \times \operatorname {Spec} \Omega )$
, and denote by
$X^{\ast }(T_{n/\Omega }) := \operatorname {Hom}(T_n \times \operatorname {Spec} \Omega , \mathbb {G}_m \times \operatorname {Spec} \Omega )$
, and denote by
![]() $\Phi _n \subset X^{\ast }(T_{n/\Omega })$
the set of roots of
$\Phi _n \subset X^{\ast }(T_{n/\Omega })$
the set of roots of
![]() $T_n$
on
$T_n$
on
![]() $\operatorname {Lie} G$
. The subset of positive roots with respect to
$\operatorname {Lie} G$
. The subset of positive roots with respect to
![]() $B_n$
will be denoted
$B_n$
will be denoted
![]() $\Phi ^+_n$
, and
$\Phi ^+_n$
, and
![]() $\Delta _n$
will denote the set of simple positive roots. For any ring
$\Delta _n$
will denote the set of simple positive roots. For any ring
![]() $R\subset \mathbb {R}$
, let
$R\subset \mathbb {R}$
, let
![]() $X^\ast (T_{n/\Omega })^+_R$
denote the subset of elements
$X^\ast (T_{n/\Omega })^+_R$
denote the subset of elements
![]() $X^\ast (T_n/\Omega ) \otimes _{\mathbb {Z}} R$
which pair nonnegatively with the simple coroots
$X^\ast (T_n/\Omega ) \otimes _{\mathbb {Z}} R$
which pair nonnegatively with the simple coroots
![]() $\check {\alpha } \in X_{\ast }(T_n/\Omega ) = \operatorname {Hom}(\mathbb {G}_m \times \operatorname {Spec} \Omega , T_n \times \operatorname {Spec} \Omega )$
corresponding to the elements of
$\check {\alpha } \in X_{\ast }(T_n/\Omega ) = \operatorname {Hom}(\mathbb {G}_m \times \operatorname {Spec} \Omega , T_n \times \operatorname {Spec} \Omega )$
corresponding to the elements of
![]() $\alpha \in \Delta _n$
.
$\alpha \in \Delta _n$
.
Let
![]() $\Phi _{(n)} \subset \Phi _n$
denote the set of roots of
$\Phi _{(n)} \subset \Phi _n$
denote the set of roots of
![]() $T_n$
on
$T_n$
on
![]() $\operatorname {Lie} L_{(n)}$
, and set
$\operatorname {Lie} L_{(n)}$
, and set
![]() $\Phi _{(n)}^+ = \Phi _{(n)} \cap \Phi _n^+$
as well as
$\Phi _{(n)}^+ = \Phi _{(n)} \cap \Phi _n^+$
as well as
![]() $\Delta _{(n)} = \Delta _n \cap \Phi _{(n)}$
. If
$\Delta _{(n)} = \Delta _n \cap \Phi _{(n)}$
. If
![]() $R \subset \mathbb {R}$
is a subring, then
$R \subset \mathbb {R}$
is a subring, then
![]() $X^{\ast }(T_{n/\Omega })^+_{(n),R}$
will denote the subset of
$X^{\ast }(T_{n/\Omega })^+_{(n),R}$
will denote the subset of
![]() $X^{\ast }(T_{n/\Omega })_{(n)} \otimes _{\mathbb {Z}} R$
consisting of elements which pair nonnegatively with the simple coroot
$X^{\ast }(T_{n/\Omega })_{(n)} \otimes _{\mathbb {Z}} R$
consisting of elements which pair nonnegatively with the simple coroot
![]() $\check {\alpha } \in X_{\ast }(T_{n/\Omega })_{(n)}$
corresponding to each
$\check {\alpha } \in X_{\ast }(T_{n/\Omega })_{(n)}$
corresponding to each
![]() $\alpha \in \Delta _{(n)}$
.
$\alpha \in \Delta _{(n)}$
.
Recall that
![]() $L_{(n)} \times \operatorname {Spec} \Omega \cong \operatorname {GL}_1 \times \operatorname {GL}_n^{\operatorname {Hom}(F,\Omega )}$
, which induces an identification
$L_{(n)} \times \operatorname {Spec} \Omega \cong \operatorname {GL}_1 \times \operatorname {GL}_n^{\operatorname {Hom}(F,\Omega )}$
, which induces an identification
and hence,
![]() $X^{\ast }(T_{n/\Omega }) \cong \mathbb {Z} \bigoplus (\mathbb {Z}^n)^{\operatorname {Hom}(F,\Omega )}.$
Under this isomorphism, the image of
$X^{\ast }(T_{n/\Omega }) \cong \mathbb {Z} \bigoplus (\mathbb {Z}^n)^{\operatorname {Hom}(F,\Omega )}.$
Under this isomorphism, the image of
![]() $X^{\ast }(T_{n/\Omega })^+_{(n)}$
is the set
$X^{\ast }(T_{n/\Omega })^+_{(n)}$
is the set
Furthermore,
![]() $X^{\ast }(T_{n/\Omega })^+$
is identified with
$X^{\ast }(T_{n/\Omega })^+$
is identified with
Denote by
![]() $\operatorname {Std}$
the representation of
$\operatorname {Std}$
the representation of
![]() $L_{(n)}$
on
$L_{(n)}$
on
![]() $\Lambda /\Lambda _{(n)}$
over
$\Lambda /\Lambda _{(n)}$
over
![]() $\mathbb {Z}$
. Note that the representation
$\mathbb {Z}$
. Note that the representation
![]() $\wedge ^{n[F:\mathbb {Q}]} \operatorname {Std}^{\vee }$
is irreducible with highest weight
$\wedge ^{n[F:\mathbb {Q}]} \operatorname {Std}^{\vee }$
is irreducible with highest weight ![]() . If
. If
![]() $\rho $
is an irreducible algebraic representation of
$\rho $
is an irreducible algebraic representation of
![]() $L_{(n)}$
over
$L_{(n)}$
over
![]() $\overline {\mathbb {Q}}_p$
, then its highest weight lies in
$\overline {\mathbb {Q}}_p$
, then its highest weight lies in
![]() $X^{\ast }(T_{n/\overline {\mathbb {Q}}_p})_{(n)}^+$
and uniquely up to isomorphism identifies
$X^{\ast }(T_{n/\overline {\mathbb {Q}}_p})_{(n)}^+$
and uniquely up to isomorphism identifies
![]() $\rho $
. Thus, for any
$\rho $
. Thus, for any
![]() $\underline {b} \in X^{\ast }(T_{n/\overline {\mathbb {Q}}_p})_{(n)}^+$
, let
$\underline {b} \in X^{\ast }(T_{n/\overline {\mathbb {Q}}_p})_{(n)}^+$
, let
![]() $\rho _{\underline {b}}$
denote the
$\rho _{\underline {b}}$
denote the
![]() $L_{(n)}$
-representation over
$L_{(n)}$
-representation over
![]() $\overline {\mathbb {Q}}_p$
with highest weight
$\overline {\mathbb {Q}}_p$
with highest weight
![]() $\underline {b}$
.
$\underline {b}$
.
Define the set of classical highest weights
![]() $X^{\ast }(T_{n/\overline {\mathbb {Q}}_p})_{\operatorname {cl}}^+$
as any
$X^{\ast }(T_{n/\overline {\mathbb {Q}}_p})_{\operatorname {cl}}^+$
as any
![]() $\underline {b} = (b_0,(b_{\tau ,i})_{\tau \in \operatorname {Hom}(F,\overline {\mathbb {Q}}_p)}) \in X^{\ast }(T_{n/\overline {\mathbb {Q}}_p})^+_{(n)}$
such that
$\underline {b} = (b_0,(b_{\tau ,i})_{\tau \in \operatorname {Hom}(F,\overline {\mathbb {Q}}_p)}) \in X^{\ast }(T_{n/\overline {\mathbb {Q}}_p})^+_{(n)}$
such that
![]() $b_{\tau ,1} + b_{\tau c, 1} \leq -2n$
.
$b_{\tau ,1} + b_{\tau c, 1} \leq -2n$
.
We next turn to local components of automorphic representations (i.e., smooth representations of
![]() $G(\mathbb {Q}_\ell )$
when
$G(\mathbb {Q}_\ell )$
when
![]() $\ell \neq p$
). We relate them to smooth representations of
$\ell \neq p$
). We relate them to smooth representations of
![]() $\operatorname {GL}_{2n}(\mathbb {Q}_\ell )$
via local base change defined below.
$\operatorname {GL}_{2n}(\mathbb {Q}_\ell )$
via local base change defined below.
4.2 Local base change
For a rational prime
![]() $\ell \neq p$
, denote the primes of
$\ell \neq p$
, denote the primes of
![]() $F^+$
above
$F^+$
above
![]() $\mathbb {Q}$
as
$\mathbb {Q}$
as
![]() $u_1, \cdots , u_r, v_1 \cdots v_s$
, where each
$u_1, \cdots , u_r, v_1 \cdots v_s$
, where each
![]() $u_i = w_i{}^cw_i$
splits in F and none of the
$u_i = w_i{}^cw_i$
splits in F and none of the
![]() $v_j$
split in F. Note that
$v_j$
split in F. Note that
 $$ \begin{align*}G(\mathbb{Q}_{\ell}) \cong \prod_{i=1}^r \operatorname{GL}_{2n}(F_{w_i}) \times H,\end{align*} $$
$$ \begin{align*}G(\mathbb{Q}_{\ell}) \cong \prod_{i=1}^r \operatorname{GL}_{2n}(F_{w_i}) \times H,\end{align*} $$
where
 $$ \begin{align*}H = \left\{ (\mu,g_i) \in \mathbb{Q}_\ell^\times \times \prod_{i=1}^s \operatorname{GL}_{2n}(F_{v_i}) : {}^tg_i J_n {}^c g_i = \mu J_n \quad \forall i\right\}.\end{align*} $$
$$ \begin{align*}H = \left\{ (\mu,g_i) \in \mathbb{Q}_\ell^\times \times \prod_{i=1}^s \operatorname{GL}_{2n}(F_{v_i}) : {}^tg_i J_n {}^c g_i = \mu J_n \quad \forall i\right\}.\end{align*} $$
Here, H contains a product
![]() $\prod _{i=1}^s G^1(F_{v_i}^+),$
where
$\prod _{i=1}^s G^1(F_{v_i}^+),$
where
![]() $G^1$
denotes the group scheme over
$G^1$
denotes the group scheme over
![]() $\mathcal {O}_{F^+}$
defined by
$\mathcal {O}_{F^+}$
defined by
Note that
![]() $\operatorname {ker} \nu \cong \operatorname {RS}^{\mathcal {O}_{F^+}}_{\mathbb {Z}} G^1.$
If
$\operatorname {ker} \nu \cong \operatorname {RS}^{\mathcal {O}_{F^+}}_{\mathbb {Z}} G^1.$
If
![]() $\Pi $
is an irreducible smooth representation of
$\Pi $
is an irreducible smooth representation of
![]() $G(\mathbb {Q}_\ell )$
, then
$G(\mathbb {Q}_\ell )$
, then
Define
![]() $\operatorname {BC}(\Pi )_{w_i} := \Pi _{w_i}$
and
$\operatorname {BC}(\Pi )_{w_i} := \Pi _{w_i}$
and
![]() $\operatorname {BC}(\Pi )_{cw_i} := \Pi _{w_i}^{c,\vee }$
. This does not depend on the choice of
$\operatorname {BC}(\Pi )_{cw_i} := \Pi _{w_i}^{c,\vee }$
. This does not depend on the choice of
![]() $w_i$
. We call
$w_i$
. We call
![]() $\Pi $
unramified at
$\Pi $
unramified at
![]() $v_i$
if
$v_i$
if
![]() $v_i$
is unramified over
$v_i$
is unramified over
![]() $F^+$
and
$F^+$
and
Let
![]() $B^1$
denote the Borel subgroup of
$B^1$
denote the Borel subgroup of
![]() $G^1$
consisting of upper triangular matrices and
$G^1$
consisting of upper triangular matrices and
![]() $T^1$
the torus subgroup consisting of diagonal matrices.
$T^1$
the torus subgroup consisting of diagonal matrices.
If
![]() $\Pi $
is unramified at
$\Pi $
is unramified at
![]() $v_i$
, then there is a character
$v_i$
, then there is a character
![]() $\chi $
of
$\chi $
of
![]() $T^1(F_{v_i}^+)/T^1(\mathcal {O}_{F^+,v_i})$
such that
$T^1(F_{v_i}^+)/T^1(\mathcal {O}_{F^+,v_i})$
such that
![]() $\left .\Pi \right |{}_{G^1(F_{v_i}^+)}$
and
$\left .\Pi \right |{}_{G^1(F_{v_i}^+)}$
and
![]() $\operatorname {n-Ind}_{B^1(F_{v_i}^+)}^{G^1(F_{v_i}^+)} \chi $
share an irreducible subquotient with a
$\operatorname {n-Ind}_{B^1(F_{v_i}^+)}^{G^1(F_{v_i}^+)} \chi $
share an irreducible subquotient with a
![]() $G^1(\mathcal {O}_{F^+,v_i})$
-fixed vector. Define a map between the torus of diagonal matrices of
$G^1(\mathcal {O}_{F^+,v_i})$
-fixed vector. Define a map between the torus of diagonal matrices of
![]() $\operatorname {GL}_{2n}(F_{v_i})$
and
$\operatorname {GL}_{2n}(F_{v_i})$
and
![]() $G^1(\mathcal {O}_{F^+,v_i})$
:
$G^1(\mathcal {O}_{F^+,v_i})$
:
 $$ \begin{align}\qquad\quad\!\!\! \left(\begin{array}{ccc}t_1 & 0 & 0 \\0 & \ddots & 0 \\0 & 0 & t_{2n}\end{array}\right) & \mapsto \left(\begin{array}{ccc}t_1/{}^c t_{2n} & 0 & 0 \\0 & \ddots & 0 \\0 & 0 & t_{2n}/{}^ct_1\end{array}\right). \end{align} $$
$$ \begin{align}\qquad\quad\!\!\! \left(\begin{array}{ccc}t_1 & 0 & 0 \\0 & \ddots & 0 \\0 & 0 & t_{2n}\end{array}\right) & \mapsto \left(\begin{array}{ccc}t_1/{}^c t_{2n} & 0 & 0 \\0 & \ddots & 0 \\0 & 0 & t_{2n}/{}^ct_1\end{array}\right). \end{align} $$
We define
![]() $\operatorname {BC}(\Pi )_{v_i}$
to be the unique subquotient of
$\operatorname {BC}(\Pi )_{v_i}$
to be the unique subquotient of
with a
![]() $\operatorname {GL}_{2n}(\mathcal {O}_{F,v_i})$
-fixed vector, where
$\operatorname {GL}_{2n}(\mathcal {O}_{F,v_i})$
-fixed vector, where
![]() $B_{\operatorname {GL}_{2n}}(F_{v_i})$
denote the Borel subgroup of upper triangular matrices.
$B_{\operatorname {GL}_{2n}}(F_{v_i})$
denote the Borel subgroup of upper triangular matrices.
Lemma 4.1 (Lemma 1.1 in [Reference Harris, Lan, Taylor and Thorne10]).
Suppose that
![]() $\psi \otimes \pi $
is an irreducible smooth representation of
$\psi \otimes \pi $
is an irreducible smooth representation of
-
1. If v is unramified over
 $F^+$
and
$F^+$
and
 $\pi _v$
is unramified, then
$\pi _v$
is unramified, then
 $\operatorname {n-Ind}_{P_{(n)}(\mathbb {Q}_q)}^{G(\mathbb {Q}_q)}(\psi \otimes \pi )$
has a subquotient
$\operatorname {n-Ind}_{P_{(n)}(\mathbb {Q}_q)}^{G(\mathbb {Q}_q)}(\psi \otimes \pi )$
has a subquotient
 $\Pi $
which is unramified at v. Moreover,
$\Pi $
which is unramified at v. Moreover,
 $\operatorname {BC}(\Pi )_v$
is the unramified irreducible subquotient of
$\operatorname {BC}(\Pi )_v$
is the unramified irreducible subquotient of
 $\operatorname {n-Ind}_{B_{\operatorname {GL}_{2n}}(F_v)}^{\operatorname {GL}_{2n}(F_v)} (\pi _v^{c,\vee } \otimes \pi _v)$
.
$\operatorname {n-Ind}_{B_{\operatorname {GL}_{2n}}(F_v)}^{\operatorname {GL}_{2n}(F_v)} (\pi _v^{c,\vee } \otimes \pi _v)$
. -
2. If v is split over
 $F^+$
and
$F^+$
and
 $\Pi $
is an irreducible subquotient of the normalized induction
$\Pi $
is an irreducible subquotient of the normalized induction
 $\operatorname {n-Ind}_{P_{(n)}(\mathbb {Q}_q)}^{G(\mathbb {Q}_q)} (\psi \otimes \pi )$
, then
$\operatorname {n-Ind}_{P_{(n)}(\mathbb {Q}_q)}^{G(\mathbb {Q}_q)} (\psi \otimes \pi )$
, then
 $\operatorname {BC}(\Pi )_v$
is an irreducible subquotient of
$\operatorname {BC}(\Pi )_v$
is an irreducible subquotient of
 $\operatorname {n-Ind}_{B_{\operatorname {GL}_{2n}}(F_v)}^{\operatorname {GL}_{2n}(F_v)} (\pi _{{}^cv}^{c,\vee } \otimes \pi _v)$
.
$\operatorname {n-Ind}_{B_{\operatorname {GL}_{2n}}(F_v)}^{\operatorname {GL}_{2n}(F_v)} (\pi _{{}^cv}^{c,\vee } \otimes \pi _v)$
.
Note that in both cases,
![]() $\operatorname {BC}(\Pi _v)$
does not depend on v.
$\operatorname {BC}(\Pi _v)$
does not depend on v.
4.3 Cuspidal automorphic representations
Here, we define automorphic representations on
![]() $G(\mathbb {A})$
whose finite parts will be realized in the space of global sections of
$G(\mathbb {A})$
whose finite parts will be realized in the space of global sections of
![]() $\mathcal {E}^{\operatorname {sub}}_{U,\rho }$
on
$\mathcal {E}^{\operatorname {sub}}_{U,\rho }$
on
![]() $X^{\operatorname {min}}_{U,\rho }$
. We first recall a few definitions. Let
$X^{\operatorname {min}}_{U,\rho }$
. We first recall a few definitions. Let
![]() $U(n) \subset \operatorname {GL}_n(\mathbb {C})$
denote the subgroup of matrices g satisfying
$U(n) \subset \operatorname {GL}_n(\mathbb {C})$
denote the subgroup of matrices g satisfying
![]() ${}^tg{}^cg = 1_n$
. Define
${}^tg{}^cg = 1_n$
. Define
where
![]() $S_2$
acts by permuting
$S_2$
acts by permuting
![]() $U(n) \times U(n)$
. We can embed
$U(n) \times U(n)$
. We can embed
![]() $\mathcal {K}_{n,\infty }$
in
$\mathcal {K}_{n,\infty }$
in
via the map sending
 $$ \begin{align*}(g_{\tau},h_{\tau})_{\tau \in\operatorname{Hom}(F^+,\mathbb{R})} \mapsto \left( 1, \left( \begin{array}{cc} {(g_\tau+h_\tau)/2} & {(g_\tau-h_\tau)\Psi_n/2i} \\ {\Psi_n(g_\tau-h_\tau)/2i} & {\Psi_n(g_\tau+h_\tau)\Psi_n/2} \end{array} \right)_{\tau \in \operatorname{Hom}(F^+,\mathbb{R})} \right),\end{align*} $$
$$ \begin{align*}(g_{\tau},h_{\tau})_{\tau \in\operatorname{Hom}(F^+,\mathbb{R})} \mapsto \left( 1, \left( \begin{array}{cc} {(g_\tau+h_\tau)/2} & {(g_\tau-h_\tau)\Psi_n/2i} \\ {\Psi_n(g_\tau-h_\tau)/2i} & {\Psi_n(g_\tau+h_\tau)\Psi_n/2} \end{array} \right)_{\tau \in \operatorname{Hom}(F^+,\mathbb{R})} \right),\end{align*} $$
and sending the nontrivial element of
![]() $S_2$
to
$S_2$
to
 $\left (-1,\left (\begin {smallmatrix} -1_n & 0 \\ 0 & 1_n \end {smallmatrix}\right )_{\tau \in \operatorname {Hom}(F^+,\mathbb {R})}\right ).$
This forces
$\left (-1,\left (\begin {smallmatrix} -1_n & 0 \\ 0 & 1_n \end {smallmatrix}\right )_{\tau \in \operatorname {Hom}(F^+,\mathbb {R})}\right ).$
This forces
![]() $\mathcal {K}_{n,\infty }$
to be a maximal compact subgroup of
$\mathcal {K}_{n,\infty }$
to be a maximal compact subgroup of
![]() $G(\mathbb {R})$
such that
$G(\mathbb {R})$
such that
![]() $\mathcal {K}_{n,\infty } \cap P_{(n)}(\mathbb {R})$
is a maximal compact of
$\mathcal {K}_{n,\infty } \cap P_{(n)}(\mathbb {R})$
is a maximal compact of
![]() $L_{(n)}(\mathbb {R})$
. Let
$L_{(n)}(\mathbb {R})$
. Let
![]() $\mathfrak {g} = (\operatorname {Lie} G(\mathbb {R}))_{\mathbb {C}}$
, and denote by
$\mathfrak {g} = (\operatorname {Lie} G(\mathbb {R}))_{\mathbb {C}}$
, and denote by
![]() $A_n$
the image of
$A_n$
the image of
![]() $\mathbb {G}_m$
in G via the embedding
$\mathbb {G}_m$
in G via the embedding
![]() $t \mapsto t \cdot 1_{2n}$
. We define a cuspidal automorphic representation of
$t \mapsto t \cdot 1_{2n}$
. We define a cuspidal automorphic representation of
![]() $G(\mathbb {A})$
to be an irreducible admissible
$G(\mathbb {A})$
to be an irreducible admissible
![]() $G(\mathbb {A}^\infty ) \times (\mathfrak {g}, \mathcal {K}_{n,\infty })$
-submodule of the space of cuspidal automorphic forms on the double coset space
$G(\mathbb {A}^\infty ) \times (\mathfrak {g}, \mathcal {K}_{n,\infty })$
-submodule of the space of cuspidal automorphic forms on the double coset space
![]() $G(\mathbb {Q})\backslash G(\mathbb {A})/A_n(\mathbb {R})^0$
. Furthermore, a square-integrable automorphic representation of
$G(\mathbb {Q})\backslash G(\mathbb {A})/A_n(\mathbb {R})^0$
. Furthermore, a square-integrable automorphic representation of
![]() $G(\mathbb {A})$
is the twist by a character on
$G(\mathbb {A})$
is the twist by a character on
![]() $\mathbb {Q}^\times \backslash \mathbb {A}^\times /\mathbb {R}_{>0}^\times $
of an irreducible admissible
$\mathbb {Q}^\times \backslash \mathbb {A}^\times /\mathbb {R}_{>0}^\times $
of an irreducible admissible
![]() $G(\mathbb {A}^\infty ) \times (\mathfrak {g},\mathcal {K}_{n,\infty })$
-module that occurs discretely in the space of square integrable automorphic forms on
$G(\mathbb {A}^\infty ) \times (\mathfrak {g},\mathcal {K}_{n,\infty })$
-module that occurs discretely in the space of square integrable automorphic forms on
![]() $G(\mathbb {A})\backslash G(\mathbb {A})/A_n(\mathbb {R})^0$
.
$G(\mathbb {A})\backslash G(\mathbb {A})/A_n(\mathbb {R})^0$
.
Now let
![]() $\mathfrak {l} = (\operatorname {Lie} L_{(n)}(\mathbb {R}))_{\mathbb {C}}$
, and let
$\mathfrak {l} = (\operatorname {Lie} L_{(n)}(\mathbb {R}))_{\mathbb {C}}$
, and let
![]() $A_{(n)}$
denote the maximal split torus in the center of
$A_{(n)}$
denote the maximal split torus in the center of
![]() $L_{(n)}$
. A cuspidal automorphic representation of
$L_{(n)}$
. A cuspidal automorphic representation of
![]() $L_{(n)}(\mathbb {A})$
is an irreducible admissible
$L_{(n)}(\mathbb {A})$
is an irreducible admissible
![]() $L_{(n)}(\mathbb {A}^\infty ) \times (\mathfrak {l}, \mathcal {K}_{n,\infty } \cap L_{(n)}(\mathbb {R}))$
-submodule of the space of cuspidal automorphic forms of
$L_{(n)}(\mathbb {A}^\infty ) \times (\mathfrak {l}, \mathcal {K}_{n,\infty } \cap L_{(n)}(\mathbb {R}))$
-submodule of the space of cuspidal automorphic forms of
![]() $L_{(n)}(\mathbb {A})$
on the double coset space
$L_{(n)}(\mathbb {A})$
on the double coset space
![]() $L_{(n)}(\mathbb {Q})\backslash L_{(n)}(\mathbb {A})/A_{(n)}(\mathbb {R})^0$
.
$L_{(n)}(\mathbb {Q})\backslash L_{(n)}(\mathbb {A})/A_{(n)}(\mathbb {R})^0$
.
For a number field K and any positive integer m, let
![]() $\mathcal {K}_{K,\infty }$
denote a maximal compact subgroup of
$\mathcal {K}_{K,\infty }$
denote a maximal compact subgroup of
![]() $\operatorname {GL}_m(K_{\infty })$
, and let
$\operatorname {GL}_m(K_{\infty })$
, and let
![]() $\mathfrak {g}\mathfrak {l} = (\operatorname {Lie} \operatorname {GL}_m(K_{\infty }))_{\mathbb {C}}$
. Define a cuspidal automorphic representation of
$\mathfrak {g}\mathfrak {l} = (\operatorname {Lie} \operatorname {GL}_m(K_{\infty }))_{\mathbb {C}}$
. Define a cuspidal automorphic representation of
![]() $\operatorname {GL}_m(\mathbb {A}_K)$
as an irreducible admissible
$\operatorname {GL}_m(\mathbb {A}_K)$
as an irreducible admissible
![]() $\operatorname {GL}_m(\mathbb {A}^\infty _K) \times (\mathfrak {g}\mathfrak {l}, \mathcal {K}_{K,\infty })$
-submodule of the space of cuspidal automorphic forms on the double coset space
$\operatorname {GL}_m(\mathbb {A}^\infty _K) \times (\mathfrak {g}\mathfrak {l}, \mathcal {K}_{K,\infty })$
-submodule of the space of cuspidal automorphic forms on the double coset space
![]() $\operatorname {GL}_m(K)\backslash \operatorname {GL}_m(\mathbb {A}_K)/\mathbb {R}^\times _{>0}$
. Finally, by a square-integrable automorphic representation of
$\operatorname {GL}_m(K)\backslash \operatorname {GL}_m(\mathbb {A}_K)/\mathbb {R}^\times _{>0}$
. Finally, by a square-integrable automorphic representation of
![]() $\operatorname {GL}_m(\mathbb {A}_K)$
, we shall mean the twist by a continuous character on
$\operatorname {GL}_m(\mathbb {A}_K)$
, we shall mean the twist by a continuous character on
![]() $K^\times /\mathbb {A}_K^\times /\mathbb {R}_{>0}^\times $
of an irreducible admissible
$K^\times /\mathbb {A}_K^\times /\mathbb {R}_{>0}^\times $
of an irreducible admissible
![]() $\operatorname {GL}_m(\mathbb {A}_K^\infty ) \times (\mathfrak {g}\mathfrak {l},\mathcal {K}_{K,\infty })$
-module that occurs discretely in the space of square integrable automorphic forms on
$\operatorname {GL}_m(\mathbb {A}_K^\infty ) \times (\mathfrak {g}\mathfrak {l},\mathcal {K}_{K,\infty })$
-module that occurs discretely in the space of square integrable automorphic forms on
![]() $\operatorname {GL}_m(\mathbb {A}_K)$
.
$\operatorname {GL}_m(\mathbb {A}_K)$
.
We will now relate the finite parts of these automorphic representations to the global sections of the automorphic bundles defined previously.
4.4 Global sections of automorphic bundles over the Shimura variety
Let
![]() $\rho $
be a representation of
$\rho $
be a representation of
![]() $L_{(n)}$
on a finite
$L_{(n)}$
on a finite
![]() $\mathbb {Q}$
-vector space. Define the admissible
$\mathbb {Q}$
-vector space. Define the admissible
![]() $G(\mathbb {A}^\infty )$
-module
$G(\mathbb {A}^\infty )$
-module
Note that for any neat open compact U,
![]() $H^0(X^{\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\rho })^{U} = H^0(X^{\operatorname {min}}_U,\mathcal {E}^{\operatorname {sub}}_{U,\rho })$
(see Lemma 5.5 of [Reference Harris, Lan, Taylor and Thorne10] or Proposition 8.3.6.9 of [Reference Lan14].
$H^0(X^{\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\rho })^{U} = H^0(X^{\operatorname {min}}_U,\mathcal {E}^{\operatorname {sub}}_{U,\rho })$
(see Lemma 5.5 of [Reference Harris, Lan, Taylor and Thorne10] or Proposition 8.3.6.9 of [Reference Lan14].
Proposition 4.2 (Corollary 5.12 in [Reference Harris, Lan, Taylor and Thorne10]).
Suppose that
![]() $\underline {b} \in X^{\ast }(T_{n/\overline {\mathbb {Q}}_p})_{\operatorname {cl}}^+$
, and
$\underline {b} \in X^{\ast }(T_{n/\overline {\mathbb {Q}}_p})_{\operatorname {cl}}^+$
, and
![]() $\rho _{\underline {b}}$
is the irreducible representation of
$\rho _{\underline {b}}$
is the irreducible representation of
![]() $L_{(n)}$
with highest weight
$L_{(n)}$
with highest weight
![]() $\underline {b}$
. Then
$\underline {b}$
. Then
![]() $H^0(X^{\operatorname {min}}, \mathcal {E}^{\operatorname {sub}}_{\rho _{\underline {b}}})$
is a semisimple
$H^0(X^{\operatorname {min}}, \mathcal {E}^{\operatorname {sub}}_{\rho _{\underline {b}}})$
is a semisimple
![]() $G(\mathbb {A}^\infty )$
module, and if
$G(\mathbb {A}^\infty )$
module, and if
![]() $\Pi $
is an irreducible subquotient of
$\Pi $
is an irreducible subquotient of
![]() $H^0(X^{\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\rho _{\underline {b}}})$
, then there is a continuous representation
$H^0(X^{\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\rho _{\underline {b}}})$
, then there is a continuous representation
which is de Rham above p and has the following property: Suppose that
![]() $v \nmid p$
is a prime of F above a rational prime
$v \nmid p$
is a prime of F above a rational prime
![]() $\ell $
such that
$\ell $
such that
-
• either
 $\ell $
splits in
$\ell $
splits in
 $F_0$
,
$F_0$
, -
• or F and
 $\Pi $
are unramified above
$\Pi $
are unramified above
 $\ell $
;
$\ell $
;
then
where
![]() $\ell $
is the rational prime below v.
$\ell $
is the rational prime below v.
Proof. Each irreducible subquotient
![]() $\Pi $
of
$\Pi $
of
![]() $H^0(X^{\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\rho _{\underline {b}}})$
is the finite part of a cohomological cuspidal
$H^0(X^{\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\rho _{\underline {b}}})$
is the finite part of a cohomological cuspidal
![]() $G(\mathbb {A})$
-automorphic representation
$G(\mathbb {A})$
-automorphic representation
![]() $\pi $
by Lemma 5.11 in [Reference Harris, Lan, Taylor and Thorne10], and furthermore,
$\pi $
by Lemma 5.11 in [Reference Harris, Lan, Taylor and Thorne10], and furthermore,
![]() $H^0(X^{\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\rho _{\underline {b}}})$
is a semisimple
$H^0(X^{\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\rho _{\underline {b}}})$
is a semisimple
![]() $G(\mathbb {A}^\infty )$
-module. For such
$G(\mathbb {A}^\infty )$
-module. For such
![]() $\pi $
, by Shin [Reference Shin20] and Moeglin-Waldspurger [Reference Moeglin and Waldspurger15], there is a decomposition into positive integers
$\pi $
, by Shin [Reference Shin20] and Moeglin-Waldspurger [Reference Moeglin and Waldspurger15], there is a decomposition into positive integers
and cuspidal conjugate self-dual automorphic representations
![]() $\tilde {\pi }_i$
of
$\tilde {\pi }_i$
of
![]() $\operatorname {GL}_{m_i}(\mathbb {A}_F)$
such that for each
$\operatorname {GL}_{m_i}(\mathbb {A}_F)$
such that for each
![]() $i \in [1,r]$
,
$i \in [1,r]$
,
![]() $\tilde {\pi }_i ||\operatorname {det}||^{(m_i + n_i - 1)/2}$
is cohomological and satisfies the following at all primes v of F which are split over
$\tilde {\pi }_i ||\operatorname {det}||^{(m_i + n_i - 1)/2}$
is cohomological and satisfies the following at all primes v of F which are split over
![]() $F^+$
:
$F^+$
:
These
![]() $\tilde {\pi }_i$
are automorphic representations which have Galois representations associated to them satisfying full local-global compatibility – results due to many people including [Reference Chenevier and Harris9, Reference Shin19, Reference Caraiani6, Reference Barnet-Lamb, Geraghty, Harris and Taylor2] (for a summary, see [Reference Barnet-Lamb, Gee, Geraghty and Taylor1]).
$\tilde {\pi }_i$
are automorphic representations which have Galois representations associated to them satisfying full local-global compatibility – results due to many people including [Reference Chenevier and Harris9, Reference Shin19, Reference Caraiani6, Reference Barnet-Lamb, Geraghty, Harris and Taylor2] (for a summary, see [Reference Barnet-Lamb, Gee, Geraghty and Taylor1]).
We will refer to irreducible subquotients of
![]() $H^0(X^{\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\rho _{\overline {b}}})$
as classical cuspidal G-automorphic forms of weight
$H^0(X^{\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\rho _{\overline {b}}})$
as classical cuspidal G-automorphic forms of weight
![]() $\rho _{\underline {b}}$
.
$\rho _{\underline {b}}$
.
4.5 p-adic (cuspidal) G-automorphic forms
Now let
![]() $\rho $
be a representation of
$\rho $
be a representation of
![]() $L_{(n)}$
on a finite locally free
$L_{(n)}$
on a finite locally free
![]() $\mathbb {Z}_{(p)}$
-module. Let
$\mathbb {Z}_{(p)}$
-module. Let
![]() $H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{\rho })$
denote the smooth
$H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{\rho })$
denote the smooth
![]() $G(\mathbb {A}^{\infty })^{\operatorname {ord}}$
-module defined as
$G(\mathbb {A}^{\infty })^{\operatorname {ord}}$
-module defined as
For each positive integer r, define
It is a smooth
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-module of p-adic cuspidal G-automorphic forms of weight
$G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-module of p-adic cuspidal G-automorphic forms of weight
![]() $\rho $
, with the property that
$\rho $
, with the property that
Note that mod
![]() $p^M$
, and there is a
$p^M$
, and there is a
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-equivariant embedding
$G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-equivariant embedding
Fix a neat open compact subgroup
![]() $U^p \subset G(\mathbb {A}^{p,\infty })$
and integers
$U^p \subset G(\mathbb {A}^{p,\infty })$
and integers
![]() $N_2 \geq N_1 \geq 0$
, and recall that there is a canonical section
$N_2 \geq N_1 \geq 0$
, and recall that there is a canonical section
![]() $\operatorname {Hasse}_U \in H^0(\overline {X}^{\operatorname {min}}_U, \omega _U^{\otimes (p-1)})$
which is
$\operatorname {Hasse}_U \in H^0(\overline {X}^{\operatorname {min}}_U, \omega _U^{\otimes (p-1)})$
which is
![]() $G(\mathbb {A}^{p,\infty } \times \mathbb {Z}_p)$
-invariant. Let
$G(\mathbb {A}^{p,\infty } \times \mathbb {Z}_p)$
-invariant. Let
![]() $\widetilde {\operatorname {Hasse}}_U$
denote the noncanonical lift of
$\widetilde {\operatorname {Hasse}}_U$
denote the noncanonical lift of
![]() $\operatorname {Hasse}_U$
over an open subset of
$\operatorname {Hasse}_U$
over an open subset of
![]() $\mathcal {X}^{\operatorname {min}}_U$
. For each positive integer M, the powers
$\mathcal {X}^{\operatorname {min}}_U$
. For each positive integer M, the powers
![]() $\widetilde {\operatorname {Hasse}}_U^{p^{M-1}} {\operatorname {mod}} p^M$
are canonical despite the noncanonical choice of
$\widetilde {\operatorname {Hasse}}_U^{p^{M-1}} {\operatorname {mod}} p^M$
are canonical despite the noncanonical choice of
![]() $\widetilde {\operatorname {Hasse}}_U$
, and hence, they glue with each other and give a canonical
$\widetilde {\operatorname {Hasse}}_U$
, and hence, they glue with each other and give a canonical
![]() $G(\mathbb {A}^{\infty ,p} \times \mathbb {Z}_p)$
-invariant section
$G(\mathbb {A}^{\infty ,p} \times \mathbb {Z}_p)$
-invariant section
![]() $\operatorname {Hasse}_{U,M}$
of
$\operatorname {Hasse}_{U,M}$
of
![]() $\omega ^{\otimes (p-1)p^{M-1}}$
over
$\omega ^{\otimes (p-1)p^{M-1}}$
over
![]() $\mathcal {X}^{\operatorname {min}}_U \times \operatorname {Spec} \mathbb {Z}/p^M\mathbb {Z}$
.
$\mathcal {X}^{\operatorname {min}}_U \times \operatorname {Spec} \mathbb {Z}/p^M\mathbb {Z}$
.
Fix
![]() $\rho $
a representation of
$\rho $
a representation of
![]() $L_{(n)}$
on a finite free
$L_{(n)}$
on a finite free
![]() $\mathbb {Z}_{(p)}$
-module. Then for each integer i, define the
$\mathbb {Z}_{(p)}$
-module. Then for each integer i, define the
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-equivariant map,
$G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-equivariant map,
 $$ \begin{align*} H^0(\mathcal{X}^{\operatorname{min}}_{U^p(N_1,N_2)}, \mathcal{E}^{\operatorname{sub}}_{\rho} \otimes \omega_U^{ip^{M-1}(p-1)}) &\rightarrow H^0(\mathcal{X}^{\operatorname{ord},\operatorname{min}}_{U^p(N_1,N_2)}, \mathcal{E}^{\operatorname{ord},\operatorname{sub}}_{\rho} \otimes \mathbb{Z}/p^M\mathbb{Z}), \\f &\mapsto (\left.f\right|{}_{\mathcal{X}^{\operatorname{ord},\operatorname{min}}_{U^p(N_1,N_2)}})/\operatorname{Hasse}^i_{U^p(N_1,N_2),M}. \end{align*} $$
$$ \begin{align*} H^0(\mathcal{X}^{\operatorname{min}}_{U^p(N_1,N_2)}, \mathcal{E}^{\operatorname{sub}}_{\rho} \otimes \omega_U^{ip^{M-1}(p-1)}) &\rightarrow H^0(\mathcal{X}^{\operatorname{ord},\operatorname{min}}_{U^p(N_1,N_2)}, \mathcal{E}^{\operatorname{ord},\operatorname{sub}}_{\rho} \otimes \mathbb{Z}/p^M\mathbb{Z}), \\f &\mapsto (\left.f\right|{}_{\mathcal{X}^{\operatorname{ord},\operatorname{min}}_{U^p(N_1,N_2)}})/\operatorname{Hasse}^i_{U^p(N_1,N_2),M}. \end{align*} $$
Using the map defined above, Harris-Lan-Taylor-Thorne [Reference Harris, Lan, Taylor and Thorne10] prove the following density theorem relating p-adic and classical cuspidal automorphic forms.
Lemma 4.3 (Lemma 6.1 in [Reference Harris, Lan, Taylor and Thorne10]).
Let
![]() $\rho $
be an irreducible representation of
$\rho $
be an irreducible representation of
![]() $L_{(n)}$
on a finite free
$L_{(n)}$
on a finite free
![]() $\mathbb {Z}_p$
-module. The induced map
$\mathbb {Z}_p$
-module. The induced map
 $$ \begin{align*}\bigoplus_{j = r}^\infty H^0(\mathcal{X}^{\operatorname{min}}_{U^p(N_1,N_2)},\mathcal{E}^{\operatorname{sub}}_{U^p(N_1,N_2),\rho \otimes (\wedge^{n[F:\mathbb{Q}]} \operatorname{Std}^{\vee})^{jp^{M-1}(p-1)}}) \rightarrow H^0(\mathcal{X}^{\operatorname{ord},\operatorname{min}}_{U^p(N_1,N_2),\rho}, \mathcal{E}^{\operatorname{sub},\operatorname{ord}}_{U^p(N_1,N_2),\rho}\otimes \mathbb{Z}/p^M\mathbb{Z})\end{align*} $$
$$ \begin{align*}\bigoplus_{j = r}^\infty H^0(\mathcal{X}^{\operatorname{min}}_{U^p(N_1,N_2)},\mathcal{E}^{\operatorname{sub}}_{U^p(N_1,N_2),\rho \otimes (\wedge^{n[F:\mathbb{Q}]} \operatorname{Std}^{\vee})^{jp^{M-1}(p-1)}}) \rightarrow H^0(\mathcal{X}^{\operatorname{ord},\operatorname{min}}_{U^p(N_1,N_2),\rho}, \mathcal{E}^{\operatorname{sub},\operatorname{ord}}_{U^p(N_1,N_2),\rho}\otimes \mathbb{Z}/p^M\mathbb{Z})\end{align*} $$
is surjective for any integer r.
5 The
 $U_p$
-operator and the main theorem of [Reference Harris, Lan, Taylor and Thorne10]
$U_p$
-operator and the main theorem of [Reference Harris, Lan, Taylor and Thorne10]
The map
![]() $\operatorname {tr}_F: {\varsigma _p}_{\ast } \mathcal {E}^{\operatorname {sub}}_{U^p(N_1),\rho } \rightarrow \mathcal {E}^{\operatorname {sub}}_{U^p(N_1),\rho }$
over
$\operatorname {tr}_F: {\varsigma _p}_{\ast } \mathcal {E}^{\operatorname {sub}}_{U^p(N_1),\rho } \rightarrow \mathcal {E}^{\operatorname {sub}}_{U^p(N_1),\rho }$
over
![]() $\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)}$
induces an endomorphism
$\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)}$
induces an endomorphism
![]() $U_p = \operatorname {tr}_F$
in the endomorphism algebra of
$U_p = \operatorname {tr}_F$
in the endomorphism algebra of
![]() $H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1),\rho })_{\overline {\mathbb {Q}}_p} := H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1),\rho })\otimes \overline {\mathbb {Q}}_p$
satisfying
$H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1),\rho })_{\overline {\mathbb {Q}}_p} := H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1),\rho })\otimes \overline {\mathbb {Q}}_p$
satisfying
![]() $U_p \circ \varsigma _p = p^{n^2[F^+:\mathbb {Q}]}$
. The subspace of overconvergent automorphic forms
$U_p \circ \varsigma _p = p^{n^2[F^+:\mathbb {Q}]}$
. The subspace of overconvergent automorphic forms
![]() $H^\dagger $
in
$H^\dagger $
in
![]() $H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1),\rho })_{\overline {\mathbb {Q}}_p}$
defined in §6.4 of [Reference Harris, Lan, Taylor and Thorne10] admits a slope decomposition for
$H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1),\rho })_{\overline {\mathbb {Q}}_p}$
defined in §6.4 of [Reference Harris, Lan, Taylor and Thorne10] admits a slope decomposition for
![]() $U_p$
in the sense of §6.2 of [Reference Harris, Lan, Taylor and Thorne10]. This means that for each
$U_p$
in the sense of §6.2 of [Reference Harris, Lan, Taylor and Thorne10]. This means that for each
![]() $a \in \mathbb {Q}$
, there is a
$a \in \mathbb {Q}$
, there is a
![]() $U_p$
-preserving decomposition
$U_p$
-preserving decomposition
such that
![]() $H^\dagger _{ \leq a}$
is finite-dimensional and satisfies the following:
$H^\dagger _{ \leq a}$
is finite-dimensional and satisfies the following:
-
1. There is a nonzero polynomial
 $f(X) \in \overline {\mathbb {Q}}_p[X]$
with slopes
$f(X) \in \overline {\mathbb {Q}}_p[X]$
with slopes
 $\leq a$
(i.e.,
$\leq a$
(i.e.,
 $f(x) \neq 0$
and every root of
$f(x) \neq 0$
and every root of
 $f(x)$
has p-adic valuation at most equal to a) such that the endomorphism
$f(x)$
has p-adic valuation at most equal to a) such that the endomorphism
 $f(U_p)$
restricts to
$f(U_p)$
restricts to
 $0$
on
$0$
on
 $H^{\dagger }_{\leq a}$
;
$H^{\dagger }_{\leq a}$
; -
2. If the roots of
 $f(X) \in \overline {\mathbb {Q}}_p[X]$
have slopes
$f(X) \in \overline {\mathbb {Q}}_p[X]$
have slopes
 $\leq a$
, then the endomorphism
$\leq a$
, then the endomorphism
 $f(U_p)$
restricts to an automorphism of
$f(U_p)$
restricts to an automorphism of
 $H^{\dagger }_{> a}$
.
$H^{\dagger }_{> a}$
.
Additionally,
![]() $H^\dagger _{ \leq a}$
is an admissible
$H^\dagger _{ \leq a}$
is an admissible
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-module. Fix an isomorphism
$G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-module. Fix an isomorphism
![]() $\overline {\mathbb {Q}}_p \cong \mathbb {C}$
.
$\overline {\mathbb {Q}}_p \cong \mathbb {C}$
.
Theorem 5.1. Assume that
![]() $n> 1$
and that
$n> 1$
and that
![]() $\rho $
is an irreducible algebraic representation of
$\rho $
is an irreducible algebraic representation of
![]() $L_{(n),\operatorname {lin}}$
on a finite-dimensional
$L_{(n),\operatorname {lin}}$
on a finite-dimensional
![]() $\overline {\mathbb {Q}}_p$
-vector space. Suppose that
$\overline {\mathbb {Q}}_p$
-vector space. Suppose that
![]() $\pi $
is a cuspidal automorphic representation of
$\pi $
is a cuspidal automorphic representation of
![]() $L_{(n),\operatorname {lin}}(\mathbb {A})$
such that
$L_{(n),\operatorname {lin}}(\mathbb {A})$
such that
![]() $\pi _\infty $
has the same infinitesimal character as
$\pi _\infty $
has the same infinitesimal character as
![]() $\rho ^{\vee }$
, and suppose also that
$\rho ^{\vee }$
, and suppose also that
![]() $\psi $
is a continuous
$\psi $
is a continuous
![]() $\overline {\mathbb {Q}}_p$
-character of
$\overline {\mathbb {Q}}_p$
-character of
![]() $\mathbb {Q}^\times \backslash \mathbb {A}^\times /\mathbb {R}^\times _{>0}$
such that
$\mathbb {Q}^\times \backslash \mathbb {A}^\times /\mathbb {R}^\times _{>0}$
such that
![]() $\left. \psi \right |{}_{\mathbb {Z}_p^\times } = 1$
. Then for all
$\left. \psi \right |{}_{\mathbb {Z}_p^\times } = 1$
. Then for all
![]() $M \in \mathbb {Z}_{>0}$
sufficiently large and for each irreducible subquotient
$M \in \mathbb {Z}_{>0}$
sufficiently large and for each irreducible subquotient
![]() $\pi _j$
of
$\pi _j$
of
![]() $\operatorname {Ind}_{P_{(n)}^+(\mathbb {A}^{p,\infty })}^{G(\mathbb {A}^{p,\infty })} (\pi ^\infty ||\operatorname {det}||^M \times \psi ^{\infty })$
, there exist a representation
$\operatorname {Ind}_{P_{(n)}^+(\mathbb {A}^{p,\infty })}^{G(\mathbb {A}^{p,\infty })} (\pi ^\infty ||\operatorname {det}||^M \times \psi ^{\infty })$
, there exist a representation
![]() $\rho (M)$
of
$\rho (M)$
of
![]() $L_{(n)}$
over
$L_{(n)}$
over
![]() $\mathbb {Z}_{(p)}$
, a corresponding scalar
$\mathbb {Z}_{(p)}$
, a corresponding scalar
![]() $a(M) \in \mathbb {Q}$
and an admissible representation
$a(M) \in \mathbb {Q}$
and an admissible representation
![]() $\Pi ^{\prime }$
of
$\Pi ^{\prime }$
of
![]() $H^{\dagger }_{\leq a} \subseteq H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\rho (M)})_{\overline {\mathbb {Q}}_p}$
such that
$H^{\dagger }_{\leq a} \subseteq H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\rho (M)})_{\overline {\mathbb {Q}}_p}$
such that
![]() $\pi _j$
is a subquotient of
$\pi _j$
is a subquotient of
![]() $\Pi ^{\prime }$
.
$\Pi ^{\prime }$
.
Proof. Combine Corollary 1.9, Lemma 6.12, Corollary 6.17, Lemma 6.20 and Corollary 6.25 in [Reference Harris, Lan, Taylor and Thorne10].
Our next step is to consider properties of the Galois representations associated to the irreducible
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-subquotients of
$G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-subquotients of
![]() $H^\dagger _{\leq a}$
, as constructed in Corollary 6.13 in [Reference Harris, Lan, Taylor and Thorne10]. In order to prove local-global compatibility at all primes above
$H^\dagger _{\leq a}$
, as constructed in Corollary 6.13 in [Reference Harris, Lan, Taylor and Thorne10]. In order to prove local-global compatibility at all primes above
![]() $\ell $
such that
$\ell $
such that
![]() $\ell \neq p$
, we strengthen the construction of Galois representations associated to irreducible admissible
$\ell \neq p$
, we strengthen the construction of Galois representations associated to irreducible admissible
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-subquotients of
$G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-subquotients of
![]() $H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\rho })_{\overline {\mathbb {Q}}_p}$
(i.e., Galois representations associated to p-adic cuspidal G-automorphic forms of weight
$H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\rho })_{\overline {\mathbb {Q}}_p}$
(i.e., Galois representations associated to p-adic cuspidal G-automorphic forms of weight
![]() $\rho $
) (see Proposition 6.5 of [Reference Harris, Lan, Taylor and Thorne10]). These Galois representations are constructed using the following two facts we have already recalled:
$\rho $
) (see Proposition 6.5 of [Reference Harris, Lan, Taylor and Thorne10]). These Galois representations are constructed using the following two facts we have already recalled:
-
1. Proposition 4.2: Classical cuspidal G-automorphic forms of classical weight
 $\rho $
have Galois representations associated to them; furthermore, they satisfy full local-global compatibility at all primes
$\rho $
have Galois representations associated to them; furthermore, they satisfy full local-global compatibility at all primes
 $\ell $
such that
$\ell $
such that
 $\ell \neq p$
.
$\ell \neq p$
. -
2. Lemma 4.3: For any integer M, every p-adic cuspidal G-automorphic form of any weight
 $\rho $
‘is congruent mod
$\rho $
‘is congruent mod
 $p^M$
to’ some classical cuspidal G automorphic form of classical weight
$p^M$
to’ some classical cuspidal G automorphic form of classical weight
 $\rho ^{\prime }$
which is of the form
$\rho ^{\prime }$
which is of the form
 $\rho ^{\prime } = \rho \otimes (\wedge ^{n[F:\mathbb {Q}]} \operatorname {Std}^{\vee })^{(p-1)p^{M-1}j}$
for some integer j.
$\rho ^{\prime } = \rho \otimes (\wedge ^{n[F:\mathbb {Q}]} \operatorname {Std}^{\vee })^{(p-1)p^{M-1}j}$
for some integer j.
To prove local-global compatibility when
![]() $\ell \neq p$
, we will use these two results to reconstruct the Galois representations associated to p-adic cuspidal automorphic forms on G of weight
$\ell \neq p$
, we will use these two results to reconstruct the Galois representations associated to p-adic cuspidal automorphic forms on G of weight
![]() $\rho $
, but we will consider the action of a larger Hecke algebra than in [Reference Harris, Lan, Taylor and Thorne10] on the p-adic automorphic spaces
$\rho $
, but we will consider the action of a larger Hecke algebra than in [Reference Harris, Lan, Taylor and Thorne10] on the p-adic automorphic spaces
![]() $H^0(\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{\rho } \otimes \mathbb {Z}/p^M\mathbb {Z})$
and
$H^0(\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{\rho } \otimes \mathbb {Z}/p^M\mathbb {Z})$
and
![]() $H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{\rho })$
as well as the classical automorphic spaces
$H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{\rho })$
as well as the classical automorphic spaces
![]() $H^0(\mathcal {X}^{\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {sub}}_{\rho })$
.
$H^0(\mathcal {X}^{\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {sub}}_{\rho })$
.
6 Hecke algebras away from p
Let S denote the set of ‘bad’ rational primes consisting of p and the primes
![]() $\ell $
which ramify in F but do not split in
$\ell $
which ramify in F but do not split in
![]() $F_0$
. Let
$F_0$
. Let
![]() $S_{\operatorname {ram}}$
denote the set of rational primes
$S_{\operatorname {ram}}$
denote the set of rational primes
![]() $\ell \,(\neq p)$
that ramify in F and split in
$\ell \,(\neq p)$
that ramify in F and split in
![]() $F_0$
. Let
$F_0$
. Let
![]() $S_{\mathrm {ur}}$
denote the set of rational primes
$S_{\mathrm {ur}}$
denote the set of rational primes
![]() $\ell \,(\neq p)$
that are unramified in F and split in
$\ell \,(\neq p)$
that are unramified in F and split in
![]() $F_0$
; note that
$F_0$
; note that
![]() $S_{\operatorname {spl}} := S_{\mathrm {ur}} \sqcup S_{\operatorname {ram}}$
contains all rational primes away from p that split in
$S_{\operatorname {spl}} := S_{\mathrm {ur}} \sqcup S_{\operatorname {ram}}$
contains all rational primes away from p that split in
![]() $F_0$
. Let
$F_0$
. Let
![]() $Q = S_{\mathrm {ur}} \sqcup S_{\operatorname {ram}} \sqcup S$
, and let
$Q = S_{\mathrm {ur}} \sqcup S_{\operatorname {ram}} \sqcup S$
, and let
![]() $Q^p = Q \backslash \{p\}$
. Finally, let
$Q^p = Q \backslash \{p\}$
. Finally, let
![]() $S^p = S \backslash \{p\}$
.
$S^p = S \backslash \{p\}$
.
For each conjugate pair of primes
![]() $\{v,{}^cv\}$
of F above a rational prime
$\{v,{}^cv\}$
of F above a rational prime
![]() $\ell \in S_{\operatorname {spl}}$
, choose exactly one of
$\ell \in S_{\operatorname {spl}}$
, choose exactly one of
![]() $\{v,{}^cv\}$
to put into a set
$\{v,{}^cv\}$
to put into a set
![]() $\underline {\mathcal {S}}_{\operatorname {spl}}$
and the other in
$\underline {\mathcal {S}}_{\operatorname {spl}}$
and the other in
![]() $\underline {\mathcal {S}}^c_{\operatorname {spl}}$
. For
$\underline {\mathcal {S}}^c_{\operatorname {spl}}$
. For
![]() $\ell \in S_{\operatorname {spl}}$
, identify
$\ell \in S_{\operatorname {spl}}$
, identify
 $$ \begin{align*}G(\mathbb{Q}_\ell) \cong \prod_{\substack{v \in \underline{\mathcal{S}}_{\operatorname{spl}}\\ v \mid \ell}} \operatorname{GL}_{2n}(F_v).\end{align*} $$
$$ \begin{align*}G(\mathbb{Q}_\ell) \cong \prod_{\substack{v \in \underline{\mathcal{S}}_{\operatorname{spl}}\\ v \mid \ell}} \operatorname{GL}_{2n}(F_v).\end{align*} $$
6.1 At unramified primes
We recall the definition of the unramified Hecke algebra. Fix a neat open compact subgroup
![]() $U^p = G(\widehat {\mathbb {Z}}^Q) \times U_{Q^p} \subset G(\mathbb {A}^{p,\infty })$
. Suppose that v is a place of F above a rational prime
$U^p = G(\widehat {\mathbb {Z}}^Q) \times U_{Q^p} \subset G(\mathbb {A}^{p,\infty })$
. Suppose that v is a place of F above a rational prime
![]() $\ell \notin S$
, and let
$\ell \notin S$
, and let
![]() $i \in \mathbb {Z}$
.
$i \in \mathbb {Z}$
.
By work of Bernstein-Deligne [Reference Bernstein and Deligne4] building on Satake, there is an element
![]() $T_v^{(i)} \in \mathbb {Q}[G(\mathbb {Z}_\ell )\backslash G(\mathbb {Q}_\ell )/G(\mathbb {Z}_\ell )]$
such that if
$T_v^{(i)} \in \mathbb {Q}[G(\mathbb {Z}_\ell )\backslash G(\mathbb {Q}_\ell )/G(\mathbb {Z}_\ell )]$
such that if
![]() $\Pi _\ell $
is an unramified representation of
$\Pi _\ell $
is an unramified representation of
![]() $G(\mathbb {Q}_\ell )$
, then its eigenvalue on
$G(\mathbb {Q}_\ell )$
, then its eigenvalue on
![]() $\Pi _\ell ^{G(\mathbb {Z}_\ell )}$
is equal to
$\Pi _\ell ^{G(\mathbb {Z}_\ell )}$
is equal to
(For more details on this construction, see pages 196–197 in [Reference Harris, Lan, Taylor and Thorne10].) If v is an unramified prime of F which splits over
![]() $F^+$
, then we can write the Hecke operator
$F^+$
, then we can write the Hecke operator
![]() $T_v^{(1)}$
as the double coset
$T_v^{(1)}$
as the double coset
 $$ \begin{align*}G(\mathbb{Z}_\ell)\left(\begin{array}{cccc}1 & & & \\ & \ddots & & \\ & & 1 & \\ & \ & & \varpi_v\end{array}\right)G(\mathbb{Z}_\ell),\end{align*} $$
$$ \begin{align*}G(\mathbb{Z}_\ell)\left(\begin{array}{cccc}1 & & & \\ & \ddots & & \\ & & 1 & \\ & \ & & \varpi_v\end{array}\right)G(\mathbb{Z}_\ell),\end{align*} $$
where
![]() $\varpi _v$
denotes a uniformizer of
$\varpi _v$
denotes a uniformizer of
![]() $F_v$
.
$F_v$
.
For each unramified prime v of F and each integer
![]() $i \in \mathbb {Z}$
, there exists an integer
$i \in \mathbb {Z}$
, there exists an integer
![]() $d_v^{(i)} \in \mathbb {Z}$
such that
$d_v^{(i)} \in \mathbb {Z}$
such that
Let
![]() $\mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p} := \mathbb {Z}_p[G(\widehat {\mathbb {Z}}^{Q})\backslash G(\mathbb {A}^{Q})/G(\widehat {\mathbb {Z}}^Q)]$
denote the abstract unramified Hecke algebra. Let
$\mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p} := \mathbb {Z}_p[G(\widehat {\mathbb {Z}}^{Q})\backslash G(\mathbb {A}^{Q})/G(\widehat {\mathbb {Z}}^Q)]$
denote the abstract unramified Hecke algebra. Let
![]() $N_1$
and
$N_1$
and
![]() $N_2$
be two integers
$N_2$
be two integers
![]() $N_2 \geq N_1 \geq 0$
, and let
$N_2 \geq N_1 \geq 0$
, and let
![]() $\rho $
be a representation of
$\rho $
be a representation of
![]() $L_{(n)}$
over
$L_{(n)}$
over
![]() $\mathbb {Z}_{(p)}$
. The Hecke algebra
$\mathbb {Z}_{(p)}$
. The Hecke algebra
![]() $\mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p}$
has an action on the classical and p-adic spaces
$\mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p}$
has an action on the classical and p-adic spaces
![]() $H^0(\mathcal {X}^{\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {sub}}_{U^p(N_1,N_2),\rho })$
,
$H^0(\mathcal {X}^{\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {sub}}_{U^p(N_1,N_2),\rho })$
,
![]() $H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1),\rho })$
and
$H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1),\rho })$
and
![]() $H^0(\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1,N_2),\rho } \otimes \mathbb {Z}/p^M\mathbb {Z})$
induced from the action of
$H^0(\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1,N_2),\rho } \otimes \mathbb {Z}/p^M\mathbb {Z})$
induced from the action of
![]() $G(\mathbb {A}^S)$
. Denote by
$G(\mathbb {A}^S)$
. Denote by
![]() $\mathbb {T}^{\mathrm {ur}}_{U^p(N_1,N_2),\rho }$
the image of
$\mathbb {T}^{\mathrm {ur}}_{U^p(N_1,N_2),\rho }$
the image of
![]() $\mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p}$
in the endomorphism algebra
$\mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p}$
in the endomorphism algebra
Furthermore, if
![]() $W \subset H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1),\rho })$
(respectively, if
$W \subset H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1),\rho })$
(respectively, if
![]() $W \subset H^0(\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1,N_2),\rho } \otimes \mathbb {Z}/p^M\mathbb {Z})$
) is a finitely-generated
$W \subset H^0(\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1,N_2),\rho } \otimes \mathbb {Z}/p^M\mathbb {Z})$
) is a finitely-generated
![]() $\mathbb {Z}_p$
-submodule invariant under the action of the algebra
$\mathbb {Z}_p$
-submodule invariant under the action of the algebra
![]() $\mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p}$
, then let
$\mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p}$
, then let
![]() $\mathbb {T}^{\operatorname {ord},\mathrm {ur}}_{U^p(N_1,N_2),\rho }(W)$
(respectively, let
$\mathbb {T}^{\operatorname {ord},\mathrm {ur}}_{U^p(N_1,N_2),\rho }(W)$
(respectively, let
![]() $\mathbb {T}^{\operatorname {ord},\mathrm {ur}}_{U^p(N_1,N_2),\rho ,M}(W)$
) denote the image of
$\mathbb {T}^{\operatorname {ord},\mathrm {ur}}_{U^p(N_1,N_2),\rho ,M}(W)$
) denote the image of
![]() $\mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p}$
in
$\mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p}$
in
![]() $\operatorname {End}_{\mathbb {Z}_p}(W)$
.
$\operatorname {End}_{\mathbb {Z}_p}(W)$
.
For each v, let
![]() $\tilde {T}_v^{(i)}$
denote the image of
$\tilde {T}_v^{(i)}$
denote the image of
![]() $d_{v}^{(i)} T_v^{(i)}$
in any
$d_{v}^{(i)} T_v^{(i)}$
in any
![]() $\mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p}$
-algebra
$\mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p}$
-algebra
![]() $\mathbb {T}$
via the canonical map
$\mathbb {T}$
via the canonical map
![]() $\mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p} \rightarrow \mathbb {T}$
.
$\mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p} \rightarrow \mathbb {T}$
.
6.2 At primes which are split in
 $F_0$
$F_0$
Suppose that
![]() $v \in \underline {\mathcal {S}}_{\operatorname {spl}} \sqcup \underline {\mathcal {S}}^c_{\operatorname {spl}}$
is a place of F above a rational prime
$v \in \underline {\mathcal {S}}_{\operatorname {spl}} \sqcup \underline {\mathcal {S}}^c_{\operatorname {spl}}$
is a place of F above a rational prime
![]() $\ell $
, and let
$\ell $
, and let
![]() $\sigma _v$
denote an element of
$\sigma _v$
denote an element of
![]() $W_{F_v}$
, the Weil group of
$W_{F_v}$
, the Weil group of
![]() $F_v$
. Let
$F_v$
. Let
![]() $\mathcal {B}$
denote a fixed Bernstein component; it is a subcategory of the smooth representations of
$\mathcal {B}$
denote a fixed Bernstein component; it is a subcategory of the smooth representations of
![]() $\operatorname {GL}_{2n}(F_v)$
. Every component
$\operatorname {GL}_{2n}(F_v)$
. Every component
![]() $\mathcal {B}$
is uniquely associated to an inertial equivalence class
$\mathcal {B}$
is uniquely associated to an inertial equivalence class
![]() $(M,\omega )$
, where M denotes a Levi subgroup of
$(M,\omega )$
, where M denotes a Levi subgroup of
![]() $\operatorname {GL}_{2n}(F_v)$
and
$\operatorname {GL}_{2n}(F_v)$
and
![]() $\omega $
is a supercuspidal representation of M. (Recall that two inertial classes
$\omega $
is a supercuspidal representation of M. (Recall that two inertial classes
![]() $(M,\omega )$
and
$(M,\omega )$
and
![]() $(M^{\prime },\omega ^{\prime })$
are equivalent if there exists
$(M^{\prime },\omega ^{\prime })$
are equivalent if there exists
![]() $g \in G$
and an unramified character
$g \in G$
and an unramified character
![]() $\chi $
of
$\chi $
of
![]() $M^{\prime }$
such that
$M^{\prime }$
such that
![]() $M = g^{-1}Mg$
and
$M = g^{-1}Mg$
and
![]() $\omega ^{\prime } = \chi \otimes \omega (g\cdot g^{-1}).$
) Then,
$\omega ^{\prime } = \chi \otimes \omega (g\cdot g^{-1}).$
) Then,
![]() $\mathcal {B}$
is defined to be the full subcategory of smooth representations of
$\mathcal {B}$
is defined to be the full subcategory of smooth representations of
![]() $\operatorname {GL}_{2n}(F_v)$
consisting of those representations all of whose irreducible subquotients have inertial support equivalent to
$\operatorname {GL}_{2n}(F_v)$
consisting of those representations all of whose irreducible subquotients have inertial support equivalent to
![]() $(M,\omega )$
. This implies that there exists some
$(M,\omega )$
. This implies that there exists some
![]() $(M^{\prime },\omega ^{\prime }) \sim (M,\omega )$
such that
$(M^{\prime },\omega ^{\prime }) \sim (M,\omega )$
such that
![]() $\pi $
occurs as a composition factor of the parabolic induction
$\pi $
occurs as a composition factor of the parabolic induction
![]() $\operatorname {Ind}_{P_M}^{\operatorname {GL}_{2n}(F_v)}(\omega ^{\prime })$
where
$\operatorname {Ind}_{P_M}^{\operatorname {GL}_{2n}(F_v)}(\omega ^{\prime })$
where
![]() $\omega ^{\prime }$
is an irreducible supercuspidal representation and
$\omega ^{\prime }$
is an irreducible supercuspidal representation and
![]() $P_M$
is a parabolic subgroup of
$P_M$
is a parabolic subgroup of
![]() $\operatorname {GL}_{2n}(F_v)$
with Levi M.
$\operatorname {GL}_{2n}(F_v)$
with Levi M.
Let
![]() $\mathfrak {z}_{\mathcal {B}} = \mathfrak {z}_{[M,\omega ]}$
denote the Bernstein center of
$\mathfrak {z}_{\mathcal {B}} = \mathfrak {z}_{[M,\omega ]}$
denote the Bernstein center of
![]() $\mathcal {B}$
, which is the image under the idempotent
$\mathcal {B}$
, which is the image under the idempotent
![]() $e_{\mathcal {B}}$
associated to
$e_{\mathcal {B}}$
associated to
![]() $\mathcal {B}$
of
$\mathcal {B}$
of
the inverse limit over open compact subgroup K of the centers of the complex Hecke algebra for
![]() $\operatorname {GL}_{2n}(F_v).$
$\operatorname {GL}_{2n}(F_v).$
Proposition 6.1 (Proposition 3.11 in Chenevier [Reference Chenevier8]).
For an inertial equivalence class
![]() $[M,\omega ]$
, there is a representative
$[M,\omega ]$
, there is a representative
![]() $(M,\omega )$
which can be defined over
$(M,\omega )$
which can be defined over
![]() $\overline {\mathbb {Q}}$
. Let
$\overline {\mathbb {Q}}$
. Let
![]() $E \subset \overline {\mathbb {Q}}$
denote a sufficiently large finite-degree normal field over which
$E \subset \overline {\mathbb {Q}}$
denote a sufficiently large finite-degree normal field over which
![]() $\omega $
,
$\omega $
,
![]() $\operatorname {rec}(\omega )$
,
$\operatorname {rec}(\omega )$
,
![]() $\mathcal {B}_{[M,\omega ]}$
,
$\mathcal {B}_{[M,\omega ]}$
,
![]() $\mathfrak {z}_{[M,\omega ]}$
are all defined over E. Let
$\mathfrak {z}_{[M,\omega ]}$
are all defined over E. Let
![]() $E[\mathcal {B}_{[M,\omega ]}]$
denote the affine coordinate ring of the variety associated to
$E[\mathcal {B}_{[M,\omega ]}]$
denote the affine coordinate ring of the variety associated to
![]() $\mathcal {B}_{[M,\omega ]}$
. Then there exists a unique pseudocharacter of dimension
$\mathcal {B}_{[M,\omega ]}$
. Then there exists a unique pseudocharacter of dimension
![]() $2n$
$2n$
such that for all irreducible smooth representations
![]() $\pi $
of
$\pi $
of
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\sigma _v \in W_{F_v}$
,
$\sigma _v \in W_{F_v}$
,
For a Bernstein component
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\sigma \in W_{F_v}$
, let
$\sigma \in W_{F_v}$
, let
![]() $T_{v,\mathcal {B},\sigma }$
denote the twist of
$T_{v,\mathcal {B},\sigma }$
denote the twist of
![]() $T^{\mathcal {B}}(\sigma )$
such that
$T^{\mathcal {B}}(\sigma )$
such that
![]() $T_{v,\mathcal {B},\sigma }(\pi ) = \operatorname {tr} \operatorname {rec}_{F_v}(\pi |\operatorname {det}|_v^{(1-2n)/2})(\sigma )$
if
$T_{v,\mathcal {B},\sigma }(\pi ) = \operatorname {tr} \operatorname {rec}_{F_v}(\pi |\operatorname {det}|_v^{(1-2n)/2})(\sigma )$
if
![]() $\pi $
is a smooth irreducible representation in
$\pi $
is a smooth irreducible representation in
![]() $\mathcal {B}$
. Multiplying
$\mathcal {B}$
. Multiplying
![]() $T_{v,\mathcal {B},\sigma }$
by
$T_{v,\mathcal {B},\sigma }$
by
![]() $e_{\mathcal {B}}$
if necessary, we may suppose that
$e_{\mathcal {B}}$
if necessary, we may suppose that
![]() $T_{v,\mathcal {B},\sigma }$
acts as
$T_{v,\mathcal {B},\sigma }$
acts as
![]() $0$
on all irreducible
$0$
on all irreducible
![]() $\pi \notin \mathcal {B}$
.
$\pi \notin \mathcal {B}$
.
Theorem 6.2 (Bernstein [Reference Bernstein and Deligne4]).
For each prime
![]() $v \in \underline {\mathcal {S}}_{\operatorname {spl}}$
. Let
$v \in \underline {\mathcal {S}}_{\operatorname {spl}}$
. Let
![]() $\mathcal {B}_v = \mathcal {B}$
be a Bernstein component, and let
$\mathcal {B}_v = \mathcal {B}$
be a Bernstein component, and let
![]() $e_{\mathcal {B}}$
denote the projector element such that for any smooth irreducible representation
$e_{\mathcal {B}}$
denote the projector element such that for any smooth irreducible representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {GL}_{2n}(F_v)$
,
$\operatorname {GL}_{2n}(F_v)$
,
![]() $e_{\mathcal {B}}(\pi ) = \pi $
if and only if
$e_{\mathcal {B}}(\pi ) = \pi $
if and only if
![]() $\pi \in \mathcal {B}$
.
$\pi \in \mathcal {B}$
.
There is a compact open subgroup K of
![]() $\operatorname {GL}_{2n}(F_v)$
for which we may find a finite union of Bernstein components
$\operatorname {GL}_{2n}(F_v)$
for which we may find a finite union of Bernstein components
![]() $\mathfrak {B} = \mathfrak {B}_v$
containing
$\mathfrak {B} = \mathfrak {B}_v$
containing
![]() $\mathcal {B}_v$
with the following property: If
$\mathcal {B}_v$
with the following property: If
![]() $\pi _v$
is an irreducible smooth representation of
$\pi _v$
is an irreducible smooth representation of
![]() $\operatorname {GL}_{2n}(F_v)$
, then
$\operatorname {GL}_{2n}(F_v)$
, then
![]() $\pi _v^K$
is nonzero if and only if
$\pi _v^K$
is nonzero if and only if
![]() $\pi _v$
belongs to one of the Bernstein components in
$\pi _v$
belongs to one of the Bernstein components in
![]() $\mathfrak {B}$
.
$\mathfrak {B}$
.
Proof. For the first statement, see Proposition 2.10 in [Reference Bernstein and Deligne4]. For the second statement, see Proposition 3.8 and Corollary 3.9(i) of [Reference Bernstein and Deligne4]. Also, see §2.3 and 2.5 of [Reference Bernstein, Deligne and Kazhdan5].
We will denote this compact open subgroup by
![]() $K_{\mathfrak {B}} = K_{\mathfrak {B}_v}$
; note that all irreducible smooth representations inside
$K_{\mathfrak {B}} = K_{\mathfrak {B}_v}$
; note that all irreducible smooth representations inside
![]() $\mathcal {B}$
have a fixed vector under
$\mathcal {B}$
have a fixed vector under
![]() $K_{\mathfrak {B}}$
. More generally, for every
$K_{\mathfrak {B}}$
. More generally, for every
![]() $\mathcal {B}^{\prime } \subset \mathfrak {B}$
,
$\mathcal {B}^{\prime } \subset \mathfrak {B}$
,
![]() $\mathfrak {z}_{\mathcal {B}^{\prime }}$
embeds in the center of
$\mathfrak {z}_{\mathcal {B}^{\prime }}$
embeds in the center of
![]() $\mathcal {H}(\operatorname {GL}_{2n},K_{\mathfrak {B}})_{\mathbb {C}} = \mathbb {C}[K_{\mathfrak {B}}\backslash \operatorname {GL}_{2n}(F_v) /K_{\mathfrak {B}}]$
via multiplication by the characteristic function of
$\mathcal {H}(\operatorname {GL}_{2n},K_{\mathfrak {B}})_{\mathbb {C}} = \mathbb {C}[K_{\mathfrak {B}}\backslash \operatorname {GL}_{2n}(F_v) /K_{\mathfrak {B}}]$
via multiplication by the characteristic function of
![]() $K_{\mathfrak {B}}$
. Let
$K_{\mathfrak {B}}$
. Let
![]() $\mathfrak {z}_{\mathfrak {B}_v} = \mathfrak {z}_{\mathfrak {B}} := \operatorname {im}(\prod _{\mathcal {B}^{\prime } \subset \mathfrak {B}} \mathfrak {z}_{\mathcal {B}^{\prime }} \hookrightarrow \mathcal {H}(\operatorname {GL}_{2n},K_{\mathfrak {B}})_{\mathbb {C}})$
. Note that
$\mathfrak {z}_{\mathfrak {B}_v} = \mathfrak {z}_{\mathfrak {B}} := \operatorname {im}(\prod _{\mathcal {B}^{\prime } \subset \mathfrak {B}} \mathfrak {z}_{\mathcal {B}^{\prime }} \hookrightarrow \mathcal {H}(\operatorname {GL}_{2n},K_{\mathfrak {B}})_{\mathbb {C}})$
. Note that
![]() $\mathfrak {z}_{\mathfrak {B}}$
is the center of
$\mathfrak {z}_{\mathfrak {B}}$
is the center of
![]() $\mathcal {H}(\operatorname {GL}_{2n},K_{\mathfrak {B}})_{\mathbb {C}}$
.
$\mathcal {H}(\operatorname {GL}_{2n},K_{\mathfrak {B}})_{\mathbb {C}}$
.
For
![]() $\ell \in S_{\operatorname {spl}}$
, assume
$\ell \in S_{\operatorname {spl}}$
, assume
![]() $K_\ell $
is an open compact subgroup of
$K_\ell $
is an open compact subgroup of
![]() $G(\mathbb {Q}_\ell )$
such that under the identification
$G(\mathbb {Q}_\ell )$
such that under the identification
![]() $G(\mathbb {Q}_\ell ) \cong \prod _{\underline {\mathcal {S}}_{\operatorname {spl}} \ni v \mid \ell } \operatorname {GL}_{2n}(F_v),$
we can decompose
$G(\mathbb {Q}_\ell ) \cong \prod _{\underline {\mathcal {S}}_{\operatorname {spl}} \ni v \mid \ell } \operatorname {GL}_{2n}(F_v),$
we can decompose
 $$ \begin{align*}K_\ell = \prod_{\underline{\mathcal{S}}_{\operatorname{spl}} \ni v \mid \ell} K_{\mathfrak{B}_v}.\end{align*} $$
$$ \begin{align*}K_\ell = \prod_{\underline{\mathcal{S}}_{\operatorname{spl}} \ni v \mid \ell} K_{\mathfrak{B}_v}.\end{align*} $$
If
![]() $v \in \underline {\mathcal {S}}_{\operatorname {spl}}$
divides the rational prime
$v \in \underline {\mathcal {S}}_{\operatorname {spl}}$
divides the rational prime
![]() $\ell $
and
$\ell $
and
![]() $\mathfrak {B}$
is a Bernstein component, then for any
$\mathfrak {B}$
is a Bernstein component, then for any
![]() $\sigma \in W_{F_v}$
, we can find an element of
$\sigma \in W_{F_v}$
, we can find an element of
![]() $\mathfrak {z}_{\mathfrak {B}}$
, which we will denote by
$\mathfrak {z}_{\mathfrak {B}}$
, which we will denote by
![]() $T_{v,\mathfrak {B},\sigma }$
, such that its eigenvalue on the
$T_{v,\mathfrak {B},\sigma }$
, such that its eigenvalue on the
![]() $K_{\ell }$
-fixed vectors of an irreducible representation
$K_{\ell }$
-fixed vectors of an irreducible representation
![]() $\pi $
of
$\pi $
of
![]() $G(\mathbb {Q}_\ell )$
in
$G(\mathbb {Q}_\ell )$
in
![]() $\mathcal {B}$
is
$\mathcal {B}$
is
(However, if
![]() $\pi _v \notin \mathfrak {B}$
, then
$\pi _v \notin \mathfrak {B}$
, then
![]() $\pi ^{K_\ell }$
is trivial and
$\pi ^{K_\ell }$
is trivial and
![]() $T_{v,\mathfrak {B},\sigma }$
acts as 0.) This element
$T_{v,\mathfrak {B},\sigma }$
acts as 0.) This element
![]() $T_{v,\mathfrak {B},\sigma }$
is the image in
$T_{v,\mathfrak {B},\sigma }$
is the image in
![]() $\mathfrak {z}_{\mathfrak {B}}$
of
$\mathfrak {z}_{\mathfrak {B}}$
of
![]() $\prod _{\mathcal {B}^{\prime } \subset \mathfrak {B}} T_{v,\mathcal {B}^{\prime },\sigma } \in \prod _{\mathcal {B}^{\prime }\subset \mathfrak {B}} \mathfrak {z}_{\mathcal {B}^{\prime }}$
. It is independent of
$\prod _{\mathcal {B}^{\prime } \subset \mathfrak {B}} T_{v,\mathcal {B}^{\prime },\sigma } \in \prod _{\mathcal {B}^{\prime }\subset \mathfrak {B}} \mathfrak {z}_{\mathcal {B}^{\prime }}$
. It is independent of
![]() $\pi $
. Furthermore, for each
$\pi $
. Furthermore, for each
![]() $\varphi \in \operatorname {Aut}(\mathbb {C})$
, we have that
$\varphi \in \operatorname {Aut}(\mathbb {C})$
, we have that
![]() ${}^{\varphi }\mathfrak {B} = \mathfrak {B}$
and additionally,
${}^{\varphi }\mathfrak {B} = \mathfrak {B}$
and additionally,
Thus, we have that
![]() ${}^\varphi T_{v,\mathfrak {B},\sigma } = T_{v,\mathfrak {B},\sigma }$
, and so
${}^\varphi T_{v,\mathfrak {B},\sigma } = T_{v,\mathfrak {B},\sigma }$
, and so
![]() $T_{v,\mathfrak {B},\sigma } \in \mathbb {Q}[K_\ell \backslash G(\mathbb {Q}_\ell )/K_\ell ].$
$T_{v,\mathfrak {B},\sigma } \in \mathbb {Q}[K_\ell \backslash G(\mathbb {Q}_\ell )/K_\ell ].$
Define
 $$ \begin{align*}\mathfrak{z}_\ell^0 := \prod_{\underline{\mathcal{S}}_{\operatorname{spl}} \ni v \mid \ell} (\mathfrak{z}_{\mathfrak{B}_v} \cap \mathbb{Z}[K_{\mathfrak{B}}\backslash \operatorname{GL}_{2n}(F_v) /K_{\mathfrak{B}}]).\end{align*} $$
$$ \begin{align*}\mathfrak{z}_\ell^0 := \prod_{\underline{\mathcal{S}}_{\operatorname{spl}} \ni v \mid \ell} (\mathfrak{z}_{\mathfrak{B}_v} \cap \mathbb{Z}[K_{\mathfrak{B}}\backslash \operatorname{GL}_{2n}(F_v) /K_{\mathfrak{B}}]).\end{align*} $$
Then
![]() $\mathfrak {z}_\ell ^0$
lies in the center of
$\mathfrak {z}_\ell ^0$
lies in the center of
![]() $\mathbb {Z}[K_\ell \backslash G(\mathbb {Q}_\ell )/K_\ell ]$
. Note that for any element
$\mathbb {Z}[K_\ell \backslash G(\mathbb {Q}_\ell )/K_\ell ]$
. Note that for any element
![]() $T \in \mathfrak {z}_{\mathfrak {B}} \cap \mathbb {Q}[K_\ell G(\mathbb {Q}_\ell )/K_{\ell }]$
, there exists a nonzero integer
$T \in \mathfrak {z}_{\mathfrak {B}} \cap \mathbb {Q}[K_\ell G(\mathbb {Q}_\ell )/K_{\ell }]$
, there exists a nonzero integer
![]() $d(T) \in \mathbb {Z} $
such that
$d(T) \in \mathbb {Z} $
such that
![]() $d(T)T\in \mathfrak {z}_\ell ^0,$
where
$d(T)T\in \mathfrak {z}_\ell ^0,$
where
![]() $v \mid \ell $
. Thus, we can choose
$v \mid \ell $
. Thus, we can choose
![]() $d(T_{v,\mathfrak {B},\sigma }) \in \mathbb {Z} \smallsetminus \{0\}$
such that
$d(T_{v,\mathfrak {B},\sigma }) \in \mathbb {Z} \smallsetminus \{0\}$
such that
so
![]() $d(T_{v,\mathfrak {B},\sigma })T_{v,\mathfrak {B},\sigma } \in \mathfrak {z}_\ell ^0$
.
$d(T_{v,\mathfrak {B},\sigma })T_{v,\mathfrak {B},\sigma } \in \mathfrak {z}_\ell ^0$
.
For each
![]() $v \in \underline {\mathcal {S}}_{\operatorname {spl}}$
, fix a Bernstein component
$v \in \underline {\mathcal {S}}_{\operatorname {spl}}$
, fix a Bernstein component
![]() $\mathcal {B}_v$
, and let
$\mathcal {B}_v$
, and let
![]() $\mathfrak {B}_v$
be the disjoint union as defined in Theorem 6.2. We will make the further assumption that
$\mathfrak {B}_v$
be the disjoint union as defined in Theorem 6.2. We will make the further assumption that
![]() $U^p = \prod _{\ell \neq p} U_\ell $
is a neat open compact subgroup of
$U^p = \prod _{\ell \neq p} U_\ell $
is a neat open compact subgroup of
![]() $G(\mathbb {A}^{p,\infty })$
such that
$G(\mathbb {A}^{p,\infty })$
such that
 $$ \begin{align} U_\ell = \prod_{\substack{v \in \underline{\mathcal{S}}_{\operatorname{spl}} \\ v \mid \ell}} K_{\mathfrak{B}_v}. \end{align} $$
$$ \begin{align} U_\ell = \prod_{\substack{v \in \underline{\mathcal{S}}_{\operatorname{spl}} \\ v \mid \ell}} K_{\mathfrak{B}_v}. \end{align} $$
Let
![]() $\mathcal {H}_{\operatorname {spl}, \mathbb {Z}_p} := \left (\bigotimes _{\ell \in S_{\operatorname {spl}}} \mathfrak {z}_\ell ^0\right )$
be the abstract ramified Hecke algebra. For any two integers
$\mathcal {H}_{\operatorname {spl}, \mathbb {Z}_p} := \left (\bigotimes _{\ell \in S_{\operatorname {spl}}} \mathfrak {z}_\ell ^0\right )$
be the abstract ramified Hecke algebra. For any two integers
![]() $N_2 \geq N_1 \geq 0$
and any algebraic representation
$N_2 \geq N_1 \geq 0$
and any algebraic representation
![]() $\rho $
of
$\rho $
of
![]() $L_{(n)}$
over
$L_{(n)}$
over
![]() $\mathbb {Z}_{(p)}$
, recall that the classical space
$\mathbb {Z}_{(p)}$
, recall that the classical space
![]() $H^0(\mathcal {X}^{\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {sub}}_{U^p(N_1,N_2),\rho })$
has an action of
$H^0(\mathcal {X}^{\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {sub}}_{U^p(N_1,N_2),\rho })$
has an action of
![]() $G(\mathbb {A}^{p,\infty })$
which induces an action of
$G(\mathbb {A}^{p,\infty })$
which induces an action of
![]() $\mathcal {H}_{\operatorname {spl},\mathbb {Z}_p}$
, and similarly, the p-adic spaces
$\mathcal {H}_{\operatorname {spl},\mathbb {Z}_p}$
, and similarly, the p-adic spaces
![]() $H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{\rho },\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{\rho })$
and
$H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{\rho },\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{\rho })$
and
![]() $H^0(\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{\rho },\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{\rho } \otimes \mathbb {Z}/p^M\mathbb {Z})$
have an action of
$H^0(\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{\rho },\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{\rho } \otimes \mathbb {Z}/p^M\mathbb {Z})$
have an action of
![]() $G(\mathbb {A}^{p,\infty })$
, which similarly induces an action of
$G(\mathbb {A}^{p,\infty })$
, which similarly induces an action of
![]() $\mathcal {H}_{\operatorname {spl},\mathbb {Z}_p}$
. Let
$\mathcal {H}_{\operatorname {spl},\mathbb {Z}_p}$
. Let
![]() $\mathbb {T}^p_{U^p(N_1,N_2),\rho }$
denote the image of
$\mathbb {T}^p_{U^p(N_1,N_2),\rho }$
denote the image of
![]() $\mathcal {H}^p_{\mathbb {Z}_p} := \mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p} \otimes \mathcal {H}_{\operatorname {spl},\mathbb {Z}_p}$
in
$\mathcal {H}^p_{\mathbb {Z}_p} := \mathcal {H}^{\mathrm {ur}}_{\mathbb {Z}_p} \otimes \mathcal {H}_{\operatorname {spl},\mathbb {Z}_p}$
in
Furthermore, if
![]() $W \subset H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1),\rho })$
(resp.,
$W \subset H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1),\rho })$
(resp.,
![]() $W \subset H^0(\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1,N_2),\rho } \otimes \mathbb {Z}/p^M\mathbb {Z})$
) is a finitely generated
$W \subset H^0(\mathcal {X}^{\operatorname {ord},\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{U^p(N_1,N_2),\rho } \otimes \mathbb {Z}/p^M\mathbb {Z})$
) is a finitely generated
![]() $\mathbb {Z}_p$
-submodule invariant under the action of the algebra
$\mathbb {Z}_p$
-submodule invariant under the action of the algebra
![]() $\mathcal {H}^p_{\mathbb {Z}_p}$
, then let
$\mathcal {H}^p_{\mathbb {Z}_p}$
, then let
![]() $\mathbb {T}^{\operatorname {ord},p}_{U^p(N_1,N_2),\rho }(W)$
(resp.
$\mathbb {T}^{\operatorname {ord},p}_{U^p(N_1,N_2),\rho }(W)$
(resp.
![]() $\mathbb {T}^{\operatorname {ord},p}_{U^p(N_1,N_2),\rho ,M}(W)$
) denote the image of
$\mathbb {T}^{\operatorname {ord},p}_{U^p(N_1,N_2),\rho ,M}(W)$
) denote the image of
![]() $\mathcal {H}^p_{\mathbb {Z}_p}$
in
$\mathcal {H}^p_{\mathbb {Z}_p}$
in
![]() $\operatorname {End}_{\mathbb {Z}_p}(W)$
.
$\operatorname {End}_{\mathbb {Z}_p}(W)$
.
For each
![]() $v \in \underline {\mathcal {S}}_{\operatorname {spl}} \sqcup \underline {\mathcal {S}}^c_{\operatorname {spl}}$
, let
$v \in \underline {\mathcal {S}}_{\operatorname {spl}} \sqcup \underline {\mathcal {S}}^c_{\operatorname {spl}}$
, let
![]() $\tilde {T}_{v,\mathfrak {B},\sigma }$
denote the image of
$\tilde {T}_{v,\mathfrak {B},\sigma }$
denote the image of
![]() $d(T_{v,\mathfrak {B},\sigma })T_{v,\mathfrak {B},\sigma }$
in any
$d(T_{v,\mathfrak {B},\sigma })T_{v,\mathfrak {B},\sigma }$
in any
![]() $\mathcal {H}^p_{\mathbb {Z}_p}$
-algebra
$\mathcal {H}^p_{\mathbb {Z}_p}$
-algebra
![]() $\mathbb {T}$
.
$\mathbb {T}$
.
7 Interpolating the Hecke action
The main goal of this section is to prove the following proposition.
Proposition 7.1. Let
![]() $\rho $
be an algebraic representation of
$\rho $
be an algebraic representation of
![]() $L_{(n)}$
over
$L_{(n)}$
over
![]() $\mathbb {Z}_{(p)}$
. Suppose that
$\mathbb {Z}_{(p)}$
. Suppose that
![]() $\Pi $
is an irreducible quotient of an admissible
$\Pi $
is an irreducible quotient of an admissible
![]() $G(\mathbb {A}^{\infty })^{\operatorname {ord},\times }$
-submodule
$G(\mathbb {A}^{\infty })^{\operatorname {ord},\times }$
-submodule
![]() $\Pi ^{\prime }$
of
$\Pi ^{\prime }$
of
![]() $H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{\rho }) \otimes \overline {\mathbb {Q}}_p$
. Then there is a continuous semisimple representation
$H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}},\mathcal {E}^{\operatorname {ord},\operatorname {sub}}_{\rho }) \otimes \overline {\mathbb {Q}}_p$
. Then there is a continuous semisimple representation
with the following property: If
![]() $\ell \neq p$
is a rational prime such that either
$\ell \neq p$
is a rational prime such that either
![]() $\ell $
splits in
$\ell $
splits in
![]() $F_0$
, or both F and
$F_0$
, or both F and
![]() $\Pi $
are unramified above
$\Pi $
are unramified above
![]() $\ell $
, and
$\ell $
, and
![]() $v \mid \ell $
is a prime of F, then
$v \mid \ell $
is a prime of F, then
Proposition 6.5 in [Reference Harris, Lan, Taylor and Thorne10] proves the existence of
![]() $R_p(\Pi )$
and its local-global compatibility at primes above
$R_p(\Pi )$
and its local-global compatibility at primes above
![]() $\ell \notin S_{\operatorname {ram}} \sqcup S$
such that
$\ell \notin S_{\operatorname {ram}} \sqcup S$
such that
![]() $\Pi $
is unramified at
$\Pi $
is unramified at
![]() $\ell $
. We extend the local-global compatibility results to primes above
$\ell $
. We extend the local-global compatibility results to primes above
![]() $\ell \in S_{\operatorname {ram}} \sqcup S_{\mathrm {ur}}$
.
$\ell \in S_{\operatorname {ram}} \sqcup S_{\mathrm {ur}}$
.
Fix
![]() $\rho $
,
$\rho $
,
![]() $\Pi $
and
$\Pi $
and
![]() $\Pi ^{\prime }$
as in the proposition. For each
$\Pi ^{\prime }$
as in the proposition. For each
![]() $v \in \underline {\mathcal {S}}_{\operatorname {spl}}$
, let
$v \in \underline {\mathcal {S}}_{\operatorname {spl}}$
, let
![]() $\mathcal {B}_v$
denote the Bernstein component containing
$\mathcal {B}_v$
denote the Bernstein component containing
![]() $\operatorname {BC}(\Pi _\ell )_v$
. Let
$\operatorname {BC}(\Pi _\ell )_v$
. Let
![]() $\mathfrak {B}_v$
be a disjoint union of Bernstein components containing
$\mathfrak {B}_v$
be a disjoint union of Bernstein components containing
![]() $\mathcal {B}_v$
such that there is an open compact subgroup
$\mathcal {B}_v$
such that there is an open compact subgroup
![]() $K_{\mathfrak {B}_v}$
of
$K_{\mathfrak {B}_v}$
of
![]() $\operatorname {GL}_{2n}(F_v)$
and an irreducible representation of
$\operatorname {GL}_{2n}(F_v)$
and an irreducible representation of
![]() $\operatorname {GL}_{2n}(F_v)$
with a nontrivial
$\operatorname {GL}_{2n}(F_v)$
with a nontrivial
![]() $K_{\mathfrak {B}_v}$
-fixed vector is contained in
$K_{\mathfrak {B}_v}$
-fixed vector is contained in
![]() $\mathfrak {B}_v$
. Choose a neat open compact subgroup
$\mathfrak {B}_v$
. Choose a neat open compact subgroup
![]() $U^p = \prod _{\ell \neq p} U_\ell $
of
$U^p = \prod _{\ell \neq p} U_\ell $
of
![]() $G(\mathbb {A}^{p,\infty })$
such that
$G(\mathbb {A}^{p,\infty })$
such that
![]() $U_\ell = K_\ell $
for each
$U_\ell = K_\ell $
for each
![]() $\ell \in S_{\operatorname {spl}}$
as well as an integer N such that
$\ell \in S_{\operatorname {spl}}$
as well as an integer N such that
![]() $\Pi ^{U^p(N)} \neq (0)$
. Recall that
$\Pi ^{U^p(N)} \neq (0)$
. Recall that
![]() $\mathcal {H}_{\operatorname {spl},\mathbb {Z}_p} := (\bigotimes _{\ell \in S_{\operatorname {spl}}} \mathfrak {z}_\ell ^0)$
, where
$\mathcal {H}_{\operatorname {spl},\mathbb {Z}_p} := (\bigotimes _{\ell \in S_{\operatorname {spl}}} \mathfrak {z}_\ell ^0)$
, where
![]() $\mathfrak {z}_{\ell }^0$
is associated to the Bernstein components
$\mathfrak {z}_{\ell }^0$
is associated to the Bernstein components
![]() $\mathcal {B}_v$
and disjoint unions
$\mathcal {B}_v$
and disjoint unions
![]() $\mathfrak {B}_v$
and open compact subgroups
$\mathfrak {B}_v$
and open compact subgroups
![]() $K_{\mathfrak {B}_v}$
fixed above, for each
$K_{\mathfrak {B}_v}$
fixed above, for each
![]() $v \in \underline {\mathcal {S}}_{\operatorname {spl}}$
, and let
$v \in \underline {\mathcal {S}}_{\operatorname {spl}}$
, and let
![]() $\mathcal {H}^p_{\mathbb {Z}_p} = \mathbb {Z}_p[G(\widehat {\mathbb {Z}}^Q)\backslash G(\mathbb {A}^Q) / G(\widehat {\mathbb {Z}}^Q)] \otimes _{\mathbb {Z}_p} \mathcal {H}_{\operatorname {spl},\mathbb {Z}_p}$
as before.
$\mathcal {H}^p_{\mathbb {Z}_p} = \mathbb {Z}_p[G(\widehat {\mathbb {Z}}^Q)\backslash G(\mathbb {A}^Q) / G(\widehat {\mathbb {Z}}^Q)] \otimes _{\mathbb {Z}_p} \mathcal {H}_{\operatorname {spl},\mathbb {Z}_p}$
as before.
We first show the existence and local-global compatibility of a Galois representations associated to irreducible subquotients of the classical space
![]() $H^0(\mathcal {X}^{\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {sub}}_{\rho \otimes (\wedge ^{n[F:\mathbb {Q}]} \operatorname {Std}^{\vee })^{\otimes (p-1) t}})$
for t sufficiently large. It will be most relevant to write this result in terms of pseudorepresentations.
$H^0(\mathcal {X}^{\operatorname {min}}_{U^p(N_1,N_2)},\mathcal {E}^{\operatorname {sub}}_{\rho \otimes (\wedge ^{n[F:\mathbb {Q}]} \operatorname {Std}^{\vee })^{\otimes (p-1) t}})$
for t sufficiently large. It will be most relevant to write this result in terms of pseudorepresentations.
Lemma 7.2. For t sufficiently large, there is a continuous pseudorepresentation
where if
![]() $v \mid \ell \notin S,$
$v \mid \ell \notin S,$
 $$ \begin{align*}\begin{cases} d(T_{v,\mathfrak{B}_v,\sigma})T_t(\sigma) = \tilde{T}_{v,\mathfrak{B}_v,\sigma} \text{ for all } \sigma \in W_{F_v} & \text{if } v \mid \ell \in S_{\operatorname{spl}} \\d_v^{(i)}T_t(\operatorname{Frob}_v^i) = \tilde{T}_v^{(i)} \text{ for all } i \geq 0 & \text{ if } v \mid \ell \notin Q \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} d(T_{v,\mathfrak{B}_v,\sigma})T_t(\sigma) = \tilde{T}_{v,\mathfrak{B}_v,\sigma} \text{ for all } \sigma \in W_{F_v} & \text{if } v \mid \ell \in S_{\operatorname{spl}} \\d_v^{(i)}T_t(\operatorname{Frob}_v^i) = \tilde{T}_v^{(i)} \text{ for all } i \geq 0 & \text{ if } v \mid \ell \notin Q \end{cases}\end{align*} $$
for all positive integers i and for all
![]() $\sigma \in W_{F_v}$
.
$\sigma \in W_{F_v}$
.
Proof. First, assume that
![]() $\rho \otimes \overline {\mathbb {Q}}_p$
is irreducible. Let
$\rho \otimes \overline {\mathbb {Q}}_p$
is irreducible. Let
![]() $(b_0,(b_{\tau ,i})) \in X^\ast (T_{n/\overline {\mathbb {Q}}_p})_{(n)}^+$
denote the highest weight of
$(b_0,(b_{\tau ,i})) \in X^\ast (T_{n/\overline {\mathbb {Q}}_p})_{(n)}^+$
denote the highest weight of
![]() $\rho \otimes \overline {\mathbb {Q}}_p$
. If
$\rho \otimes \overline {\mathbb {Q}}_p$
. If
![]() $t \in \mathbb {Z}$
satisfies the inequality
$t \in \mathbb {Z}$
satisfies the inequality
and
![]() $\rho _t := \rho \otimes (\wedge ^{n[F:\mathbb {Q}]} \operatorname {Std})^{\otimes (p-1)t}$
, then by Lemma 5.11 of [Reference Harris, Lan, Taylor and Thorne10],
$\rho _t := \rho \otimes (\wedge ^{n[F:\mathbb {Q}]} \operatorname {Std})^{\otimes (p-1)t}$
, then by Lemma 5.11 of [Reference Harris, Lan, Taylor and Thorne10],
where the sum runs over irreducible admissible representations of
![]() $G(\mathbb {A}^\infty )$
with
$G(\mathbb {A}^\infty )$
with
![]() $\Pi ^{U^p(N_1,N_2)} \neq (0)$
that occur in
$\Pi ^{U^p(N_1,N_2)} \neq (0)$
that occur in
![]() $H^0(X^{\operatorname {min}} \times \operatorname {Spec} \overline {\mathbb {Q}}_p, \mathcal {E}^{\operatorname {sub}}_{\rho _t})$
. Further, from Proposition 4.2, we deduce that there is a continuous representation
$H^0(X^{\operatorname {min}} \times \operatorname {Spec} \overline {\mathbb {Q}}_p, \mathcal {E}^{\operatorname {sub}}_{\rho _t})$
. Further, from Proposition 4.2, we deduce that there is a continuous representation
satisfying for
![]() $v \mid \ell \notin S$
,
$v \mid \ell \notin S$
,
 $$ \begin{align} \begin{cases} \operatorname{tr} r_{\rho_t}(\operatorname{Frob}_v^i) = T_v^{(i)} \text{ for all } i \geq 0 & \text{ if } v \mid \ell \in S_{\operatorname{spl}}\\\operatorname{tr} r_{\rho_t}(\sigma) = T_{v,\mathfrak{B},\sigma} \text{ for all } \sigma \in W_{F_v} & \text{ if } v \mid \ell \notin Q. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \operatorname{tr} r_{\rho_t}(\operatorname{Frob}_v^i) = T_v^{(i)} \text{ for all } i \geq 0 & \text{ if } v \mid \ell \in S_{\operatorname{spl}}\\\operatorname{tr} r_{\rho_t}(\sigma) = T_{v,\mathfrak{B},\sigma} \text{ for all } \sigma \in W_{F_v} & \text{ if } v \mid \ell \notin Q. \end{cases} \end{align} $$
Let
![]() $T_t := \operatorname {tr} r_{\rho _t}$
. Note that if
$T_t := \operatorname {tr} r_{\rho _t}$
. Note that if
![]() $v\mid \ell \notin S$
, then
$v\mid \ell \notin S$
, then
![]() $T_t(\operatorname {Frob}_v) = T_v^{(1)} \in \mathbb {T}^p_{U^p(N_1,N_2),\rho _t}$
. Thus, by Cebotarev density theorem,
$T_t(\operatorname {Frob}_v) = T_v^{(1)} \in \mathbb {T}^p_{U^p(N_1,N_2),\rho _t}$
. Thus, by Cebotarev density theorem,
![]() $T_t: G_F^S \rightarrow \mathbb {T}^p_{U^p(N_1,N_2),\rho _t}$
.
$T_t: G_F^S \rightarrow \mathbb {T}^p_{U^p(N_1,N_2),\rho _t}$
.
For general
![]() $\rho $
, recall that algebraic representations of
$\rho $
, recall that algebraic representations of
![]() $L_{(n)}(\mathbb {Z}_p)$
over
$L_{(n)}(\mathbb {Z}_p)$
over
![]() $\overline {\mathbb {Q}}_p$
are semisimple, and so we can construct from the Galois representations associated to the irreducible constituents of
$\overline {\mathbb {Q}}_p$
are semisimple, and so we can construct from the Galois representations associated to the irreducible constituents of
![]() $\rho \otimes \overline {\mathbb {Q}}_p$
a continuous representation
$\rho \otimes \overline {\mathbb {Q}}_p$
a continuous representation
![]() $r: G_F^S \rightarrow \operatorname {GL}_{2n}(\mathbb {T}^p_{U^p(N_1,N_2),\rho \otimes (\wedge ^{n[F:\mathbb {Q}]} \operatorname {Std})^{\otimes (p-1) t}} \otimes \overline {\mathbb {Q}}_p)$
for sufficiently large t whose trace satisfies the desired properties.
$r: G_F^S \rightarrow \operatorname {GL}_{2n}(\mathbb {T}^p_{U^p(N_1,N_2),\rho \otimes (\wedge ^{n[F:\mathbb {Q}]} \operatorname {Std})^{\otimes (p-1) t}} \otimes \overline {\mathbb {Q}}_p)$
for sufficiently large t whose trace satisfies the desired properties.
Combining the above lemma with the congruences properties established in Lemma 4.3, we have the following corollaries.
Corollary 7.3. If W is a finitely generated
![]() $\mathcal {H}^p_{\mathbb {Z}_p}$
-invariant submodule of either
$\mathcal {H}^p_{\mathbb {Z}_p}$
-invariant submodule of either
then there is a continuous pseudorepresentation
such that
 $$ \begin{align*}\begin{cases} d(T_{v,\mathfrak{B}_v,\sigma})T(\sigma) = \tilde{T}_{v,\mathfrak{B}_v,\sigma} \text{ for all } \sigma \in W_{F_v} & \text{ if } v \mid \ell \in S_{\operatorname{spl}}, \text{ and} \\d_v^{(i)}T(\operatorname{Frob}_v^i) = \tilde{T}_v^{(i)} \text{ for all } i \geq 0 & \text{ if } v\mid \ell \notin Q. \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} d(T_{v,\mathfrak{B}_v,\sigma})T(\sigma) = \tilde{T}_{v,\mathfrak{B}_v,\sigma} \text{ for all } \sigma \in W_{F_v} & \text{ if } v \mid \ell \in S_{\operatorname{spl}}, \text{ and} \\d_v^{(i)}T(\operatorname{Frob}_v^i) = \tilde{T}_v^{(i)} \text{ for all } i \geq 0 & \text{ if } v\mid \ell \notin Q. \end{cases}\end{align*} $$
Proof. It suffices to show that for finitely generated
such a pseudorepresentation exists since there is an
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-equivariant embedding
$G(\mathbb {A}^\infty )^{\operatorname {ord}}$
-equivariant embedding
Since W is finitely generated, there exists
![]() $k \in \mathbb {Z}$
such that
$k \in \mathbb {Z}$
such that
 $$ \begin{align*}W \subset \operatorname{Im}\bigl(\bigoplus_{j = r}^k H^0(\mathcal{X}^{\operatorname{min}}_{U^p(N_1,N_2)},\mathcal{E}^{\operatorname{sub}}_{U^p(N_1,N_2),\rho_{jp^{M-1}(p-1)}}) \rightarrow H^0(\mathcal{X}^{\operatorname{ord},\operatorname{min}}_{U^p(N_1,N_2)}, \mathcal{E}^{\operatorname{sub},\operatorname{ord}}_{U^p(N_1,N_2),\rho} \otimes \mathbb{Z}/p^M\mathbb{Z})\bigr).\end{align*} $$
$$ \begin{align*}W \subset \operatorname{Im}\bigl(\bigoplus_{j = r}^k H^0(\mathcal{X}^{\operatorname{min}}_{U^p(N_1,N_2)},\mathcal{E}^{\operatorname{sub}}_{U^p(N_1,N_2),\rho_{jp^{M-1}(p-1)}}) \rightarrow H^0(\mathcal{X}^{\operatorname{ord},\operatorname{min}}_{U^p(N_1,N_2)}, \mathcal{E}^{\operatorname{sub},\operatorname{ord}}_{U^p(N_1,N_2),\rho} \otimes \mathbb{Z}/p^M\mathbb{Z})\bigr).\end{align*} $$
Since the above map is
![]() $G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-equivariant, we see that for r sufficiently large, by Lemma 4.3, there is a continuous pseudorepresentation
$G(\mathbb {A}^\infty )^{\operatorname {ord},\times }$
-equivariant, we see that for r sufficiently large, by Lemma 4.3, there is a continuous pseudorepresentation
![]() $T_r: G_F^S \rightarrow \mathbb {T}^p_{U^p(N_1,N_2),\rho _{rp^{M-1}(p-1)}}$
. If we take r to be sufficiently large, then we can compose to get
$T_r: G_F^S \rightarrow \mathbb {T}^p_{U^p(N_1,N_2),\rho _{rp^{M-1}(p-1)}}$
. If we take r to be sufficiently large, then we can compose to get
such that
 $$ \begin{align*}\begin{cases} d(T_{v,\mathfrak{B}_v,\sigma})T(\sigma) = \tilde{T}_{v,\mathfrak{B}_v,\sigma} \text{ for all } \sigma \in W_{F_v} & \text{ if } v \in \underline{\mathcal{S}}_{\operatorname{spl}}, \text{ and} \\ d_v^{(i)}T(\operatorname{Frob}_v^i) = \tilde{T}_v^{(i)} \text{ for all}\ i \geq 0 & \text{ if } v\mid \ell \notin Q. \end{cases}\\[-42pt]\end{align*} $$
$$ \begin{align*}\begin{cases} d(T_{v,\mathfrak{B}_v,\sigma})T(\sigma) = \tilde{T}_{v,\mathfrak{B}_v,\sigma} \text{ for all } \sigma \in W_{F_v} & \text{ if } v \in \underline{\mathcal{S}}_{\operatorname{spl}}, \text{ and} \\ d_v^{(i)}T(\operatorname{Frob}_v^i) = \tilde{T}_v^{(i)} \text{ for all}\ i \geq 0 & \text{ if } v\mid \ell \notin Q. \end{cases}\\[-42pt]\end{align*} $$
We use the pseudorepresentations constructed in Lemma 7.3 to finish the proof of Proposition 7.1.
Proof of Proposition 7.1.
Since
![]() $(\Pi ^{\prime })^{U^p(N)}$
is finite dimensional, it is a closed subspace of
$(\Pi ^{\prime })^{U^p(N)}$
is finite dimensional, it is a closed subspace of
that is preserved by the action of
![]() $\mathcal {H}^p_{\mathbb {Z}_p}$
; thus, we have by Corollary 7.3 that there is a continuous pseudorepresentation
$\mathcal {H}^p_{\mathbb {Z}_p}$
; thus, we have by Corollary 7.3 that there is a continuous pseudorepresentation
such that
 $$ \begin{align*}\begin{cases} d(T_{v,\mathfrak{B}_v,\sigma})T(\sigma) = \tilde{T}_{v,\mathfrak{B}_v,\sigma} \text{ for all } \sigma \in W_{F_v} & \text{ if } v \in \underline{\mathcal{S}}_{\operatorname{spl}}, \text{ and} \\d_v^{(i)}T(\operatorname{Frob}_v^i) = \tilde{T}_v^{(i)} \text{ for all } i \geq 0 & \text{ if } v\mid \ell \notin Q. \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} d(T_{v,\mathfrak{B}_v,\sigma})T(\sigma) = \tilde{T}_{v,\mathfrak{B}_v,\sigma} \text{ for all } \sigma \in W_{F_v} & \text{ if } v \in \underline{\mathcal{S}}_{\operatorname{spl}}, \text{ and} \\d_v^{(i)}T(\operatorname{Frob}_v^i) = \tilde{T}_v^{(i)} \text{ for all } i \geq 0 & \text{ if } v\mid \ell \notin Q. \end{cases}\end{align*} $$
Since there is a
![]() $\mathcal {H}^p_{\mathbb {Z}_p}$
-equivariant map
$\mathcal {H}^p_{\mathbb {Z}_p}$
-equivariant map ![]() , there is a map
, there is a map
sending a Hecke operator to its eigenvalue on
![]() $(\Pi )^{U^p(N_1,N_2)}$
. Composing
$(\Pi )^{U^p(N_1,N_2)}$
. Composing
![]() $\varphi _{\Pi } \circ T =: T_\Pi $
gives a pseudorepresentation
$\varphi _{\Pi } \circ T =: T_\Pi $
gives a pseudorepresentation
which by work of Taylor [Reference Taylor23] is the trace of a continuous semisimple Galois representation satisfying the semisimplified local-global compatibility at the primes away from
![]() $\underline {\mathcal {S}}^{\operatorname {nspl}}$
(and away from the primes above p). The proposition then follows from the main theorem on pseudorepresentations (see again [Reference Taylor23]).
$\underline {\mathcal {S}}^{\operatorname {nspl}}$
(and away from the primes above p). The proposition then follows from the main theorem on pseudorepresentations (see again [Reference Taylor23]).
8 Bounding the monodromy
Let
![]() $\ell \neq p$
be distinct prime that splits in
$\ell \neq p$
be distinct prime that splits in
![]() $F_0$
and v a prime of F above
$F_0$
and v a prime of F above
![]() $\ell $
(i.e.,
$\ell $
(i.e.,
![]() $\ell \in S_{\operatorname {spl}}$
and
$\ell \in S_{\operatorname {spl}}$
and
![]() $v \in \underline {\mathcal {S}}_{\operatorname {spl}} \sqcup \underline {\mathcal {S}}^c_{\operatorname {spl}}).$
The main result of this section is as follows.
$v \in \underline {\mathcal {S}}_{\operatorname {spl}} \sqcup \underline {\mathcal {S}}^c_{\operatorname {spl}}).$
The main result of this section is as follows.
Proposition 8.1. Suppose
![]() $\rho $
is an algebraic representation of
$\rho $
is an algebraic representation of
![]() $L_{(n)}$
over
$L_{(n)}$
over
![]() $\mathbb {Z}_{(p)}$
and that
$\mathbb {Z}_{(p)}$
and that
![]() $\Pi $
is an irreducible quotient of an admissible
$\Pi $
is an irreducible quotient of an admissible
![]() $G(\mathbb {A}^{\infty })^{\operatorname {ord},\times }$
-submodule
$G(\mathbb {A}^{\infty })^{\operatorname {ord},\times }$
-submodule
![]() $\Pi ^{\prime }$
of
$\Pi ^{\prime }$
of
![]() $H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}, \mathcal {E}_{\rho }^{\operatorname {ord},\operatorname {sub}})\otimes _{\mathbb {Q}_p} \overline {\mathbb {Q}}_p$
. Then the continuous semisimple representation
$H^0(\mathfrak {X}^{\operatorname {ord},\operatorname {min}}, \mathcal {E}_{\rho }^{\operatorname {ord},\operatorname {sub}})\otimes _{\mathbb {Q}_p} \overline {\mathbb {Q}}_p$
. Then the continuous semisimple representation
![]() $R_{p,\imath }(\Pi )$
satisfies for
$R_{p,\imath }(\Pi )$
satisfies for
![]() $v \mid \ell \in S_{\operatorname {spl}}$
(i.e., for all primes of F above
$v \mid \ell \in S_{\operatorname {spl}}$
(i.e., for all primes of F above
![]() $\ell $
(away from p) which splits in
$\ell $
(away from p) which splits in
![]() $F_0$
),
$F_0$
),
where
![]() $\prec $
is defined below.
$\prec $
is defined below.
Let
![]() $(\sigma ,N)$
be a Weil-Deligne representation of
$(\sigma ,N)$
be a Weil-Deligne representation of
![]() $W_{F_v}$
over
$W_{F_v}$
over
![]() $\overline {\mathbb {Q}}_p$
, where
$\overline {\mathbb {Q}}_p$
, where
![]() $\sigma : W_{F_v} \rightarrow \operatorname {GL}(V)$
and
$\sigma : W_{F_v} \rightarrow \operatorname {GL}(V)$
and
![]() $N \in \operatorname {End}(V)$
. Let
$N \in \operatorname {End}(V)$
. Let
![]() $\mathcal {W}$
denote the set of equivalence classes of irreducible representations of
$\mathcal {W}$
denote the set of equivalence classes of irreducible representations of
![]() $W_{F_v}$
over
$W_{F_v}$
over
![]() $\overline {\mathbb {Q}}_p$
with open kernel, where two representations
$\overline {\mathbb {Q}}_p$
with open kernel, where two representations
![]() $s,s^{\prime }$
of
$s,s^{\prime }$
of
![]() $W_{F_v}$
are in the same equivalence if
$W_{F_v}$
are in the same equivalence if
![]() $s \cong s^{\prime } \otimes \chi $
for some unramified character
$s \cong s^{\prime } \otimes \chi $
for some unramified character
![]() $\chi $
. We can decompose any Weil-Deligne representation into isotypic components indexed by these equivalence classes of
$\chi $
. We can decompose any Weil-Deligne representation into isotypic components indexed by these equivalence classes of
![]() $\mathcal {W}$
– that is,
$\mathcal {W}$
– that is,
where
![]() $\sigma [\omega ]: W_{F_v} \rightarrow \operatorname {GL}(V[\omega ])$
is a Weil representation with all irreducible subquotients lying in
$\sigma [\omega ]: W_{F_v} \rightarrow \operatorname {GL}(V[\omega ])$
is a Weil representation with all irreducible subquotients lying in
![]() $\omega \in \mathcal {W}$
. The operator N preserves isotypic components of
$\omega \in \mathcal {W}$
. The operator N preserves isotypic components of
![]() $\sigma $
; thus, it preserves
$\sigma $
; thus, it preserves
![]() $V[\omega ]$
. If
$V[\omega ]$
. If
![]() $N[\omega ]$
denotes N restricted to
$N[\omega ]$
denotes N restricted to
![]() $V[\omega ]$
, then
$V[\omega ]$
, then
![]() $(\sigma [\omega ], N[\omega ])$
is a Weil-Deligne representation. Recall from Tate [Reference Tate22] that there is an indecomposable Weil-Deligne representation
$(\sigma [\omega ], N[\omega ])$
is a Weil-Deligne representation. Recall from Tate [Reference Tate22] that there is an indecomposable Weil-Deligne representation
![]() $\operatorname {Sp}(m)$
of dimension m with nilpotent matrix of degree exactly m. Explicitly, we have for all
$\operatorname {Sp}(m)$
of dimension m with nilpotent matrix of degree exactly m. Explicitly, we have for all
![]() $\tau \in W_{F_v}$
,
$\tau \in W_{F_v}$
,
 $$ \begin{align*}\operatorname{Sp}(m)(\tau) = \left(\begin{array}{ccccc}|\tau|^{\frac{m-1}{2}} & & & & \\ & |\tau|^{\frac{m-3}{2}} & & & \\ & & \ddots & & \\ & & & |\tau|^{\frac{3-m}{2}} & \\ & & & & |\tau|^{\frac{1-m}{2}}\end{array}\right),\end{align*} $$
$$ \begin{align*}\operatorname{Sp}(m)(\tau) = \left(\begin{array}{ccccc}|\tau|^{\frac{m-1}{2}} & & & & \\ & |\tau|^{\frac{m-3}{2}} & & & \\ & & \ddots & & \\ & & & |\tau|^{\frac{3-m}{2}} & \\ & & & & |\tau|^{\frac{1-m}{2}}\end{array}\right),\end{align*} $$
where
 $$ \begin{align*}N(\operatorname{Sp}(m)) = \left(\begin{array}{ccccc}0 & 1 & & & \\ & 0 & 1 & & \\ & & \ddots & \ddots & \\ & & & 0 & 1 \\ & & & & 0\end{array}\right).\end{align*} $$
$$ \begin{align*}N(\operatorname{Sp}(m)) = \left(\begin{array}{ccccc}0 & 1 & & & \\ & 0 & 1 & & \\ & & \ddots & \ddots & \\ & & & 0 & 1 \\ & & & & 0\end{array}\right).\end{align*} $$
It is well known that every indecomposable Frobenius-semisimple Weil-Deligne representation is isomorphic to one of the form
![]() $s \otimes \operatorname {Sp}(m)$
, where s is an irreducible representation of
$s \otimes \operatorname {Sp}(m)$
, where s is an irreducible representation of
![]() $W_{F_v}$
and
$W_{F_v}$
and
![]() $N(s) = 0$
(see [Reference Tate22, 4.1.5]). If
$N(s) = 0$
(see [Reference Tate22, 4.1.5]). If
![]() $(\sigma ,N)$
and
$(\sigma ,N)$
and
![]() $(\sigma ^{\prime },N^{\prime })$
are two Weil-Deligne representations of the same dimension, then for each
$(\sigma ^{\prime },N^{\prime })$
are two Weil-Deligne representations of the same dimension, then for each
![]() $\omega \in \mathcal {W}$
, we can compare the dimensions of
$\omega \in \mathcal {W}$
, we can compare the dimensions of
![]() $\operatorname {Sp}(\cdot )$
in the decomposition of
$\operatorname {Sp}(\cdot )$
in the decomposition of
![]() $\sigma [\omega ]^{\operatorname {Frob}-ss}$
and
$\sigma [\omega ]^{\operatorname {Frob}-ss}$
and
![]() $\sigma ^{\prime }[\omega ]^{\operatorname {Frob}-ss}$
into indecomposable representations using the following ordering:
$\sigma ^{\prime }[\omega ]^{\operatorname {Frob}-ss}$
into indecomposable representations using the following ordering:
Definition 8.2. For each
![]() $\omega \in \mathcal {W}$
, and for each Weil-Deligne representation
$\omega \in \mathcal {W}$
, and for each Weil-Deligne representation
![]() $(\sigma ,N)$
, there exists a unique decreasing sequence of nonnegative integers
$(\sigma ,N)$
, there exists a unique decreasing sequence of nonnegative integers ![]() with an associated sequence of
with an associated sequence of ![]() such that
such that
The sequence
![]() $(m_{i,\omega }(\sigma ,N))_i$
is a partition of the integer
$(m_{i,\omega }(\sigma ,N))_i$
is a partition of the integer
![]() $\operatorname {dim}(\sigma [\omega ])/\operatorname {dim}(s_i)$
for any
$\operatorname {dim}(\sigma [\omega ])/\operatorname {dim}(s_i)$
for any
![]() $s_i \in \omega $
. If
$s_i \in \omega $
. If
![]() $(\sigma ^{\prime },N^{\prime })$
is another Weil-Deligne representation, then we say
$(\sigma ^{\prime },N^{\prime })$
is another Weil-Deligne representation, then we say
if and only if
![]() $\forall \omega \in \mathcal {W}$
and
$\forall \omega \in \mathcal {W}$
and
![]() $i \geq 1$
,
$i \geq 1$
,
In particular,
![]() $(\sigma ,N) \prec (\sigma ^{\prime },N^{\prime })$
if and only if
$(\sigma ,N) \prec (\sigma ^{\prime },N^{\prime })$
if and only if
![]() $N[\omega ]$
is ‘more nilpotent’ than
$N[\omega ]$
is ‘more nilpotent’ than
![]() $N^{\prime }[\omega ]$
for each
$N^{\prime }[\omega ]$
for each
![]() $\omega \in \mathcal {W}$
. Denote by
$\omega \in \mathcal {W}$
. Denote by
![]() $I_v$
the inertia subgroup of the Weil group
$I_v$
the inertia subgroup of the Weil group
![]() $W_{F_v}$
at v, and let
$W_{F_v}$
at v, and let
![]() $\mathcal {I}$
denote the set of isomorphism classes of irreducible representations of
$\mathcal {I}$
denote the set of isomorphism classes of irreducible representations of
![]() $I_v$
with open kernel. For every
$I_v$
with open kernel. For every
![]() $\theta \in \mathcal {I}$
, define
$\theta \in \mathcal {I}$
, define
![]() $\sigma [\theta ]$
to be the isotypic component of
$\sigma [\theta ]$
to be the isotypic component of
![]() $\left .\sigma \right |{}_{I_v}$
, whose irreducible subquotients are isomorphic to
$\left .\sigma \right |{}_{I_v}$
, whose irreducible subquotients are isomorphic to
![]() $\theta $
. Since N commutes with the image of
$\theta $
. Since N commutes with the image of
![]() $I_v$
, these isotypic components are preserved by the monodromy operator; thus, we can define
$I_v$
, these isotypic components are preserved by the monodromy operator; thus, we can define
![]() $N[\theta ]$
as the restriction of N to
$N[\theta ]$
as the restriction of N to
![]() $V[\theta ]$
.
$V[\theta ]$
.
Definition 8.3. Let
![]() $(\sigma ,N)$
be a Weil-Deligne representations of
$(\sigma ,N)$
be a Weil-Deligne representations of
![]() $W_{F_v}$
over
$W_{F_v}$
over
![]() $\overline {\mathbb {Q}}_p$
. For each
$\overline {\mathbb {Q}}_p$
. For each
![]() $\theta \in \mathcal {I}$
, we can define a unique decreasing sequence of nonnegative integers
$\theta \in \mathcal {I}$
, we can define a unique decreasing sequence of nonnegative integers ![]() which determines the conjugacy class of the monodromy operator
which determines the conjugacy class of the monodromy operator
![]() $N[\theta ]$
. It is a partition of the integer
$N[\theta ]$
. It is a partition of the integer
![]() $\operatorname {dim}(r[\theta ])/\operatorname {dim}(\theta )$
. If
$\operatorname {dim}(r[\theta ])/\operatorname {dim}(\theta )$
. If
![]() $(\sigma ^{\prime },N^{\prime })$
is another Weil-Deligne representation, then we say
$(\sigma ^{\prime },N^{\prime })$
is another Weil-Deligne representation, then we say
if and only if
![]() $\left .\sigma \right |{}_{I_v} \cong \left .\sigma ^{\prime }\right |{}_{I_v}$
and
$\left .\sigma \right |{}_{I_v} \cong \left .\sigma ^{\prime }\right |{}_{I_v}$
and
![]() $\forall \theta \in \mathcal {I}$
and
$\forall \theta \in \mathcal {I}$
and
![]() $i \geq 1$
,
$i \geq 1$
,
We have the following lemma relating the two dominance relations
![]() $\prec $
and
$\prec $
and
![]() $\prec _I$
defined above. For any sequence of integers
$\prec _I$
defined above. For any sequence of integers
![]() $(m_i)_{i \in \mathbb {Z}_{> 0}}$
and
$(m_i)_{i \in \mathbb {Z}_{> 0}}$
and
![]() $d \in \mathbb {Z}_{>0}$
, let
$d \in \mathbb {Z}_{>0}$
, let
![]() $d\cdot (m_i)_i$
be the sequence of integers
$d\cdot (m_i)_i$
be the sequence of integers ![]() where each
where each
![]() $m_i$
occurs d times.
$m_i$
occurs d times.
Lemma 8.4 (Lemma 6.5.3 in [Reference Bellaiche and Chenevier3]).
Let
![]() $(\sigma ,N)$
be a Weil-Deligne representation of
$(\sigma ,N)$
be a Weil-Deligne representation of
![]() $W_{F_v}$
.
$W_{F_v}$
.
-
1. Let
 $\omega \in \mathcal {W}$
and
$\omega \in \mathcal {W}$
and
 $\theta $
an irreducible constituent of
$\theta $
an irreducible constituent of
 $\left .s\right |{}_{I_v}$
for any
$\left .s\right |{}_{I_v}$
for any
 $s \in \omega $
. Then
$s \in \omega $
. Then
 $\sigma [s^{\prime }] \cap \sigma [\theta ] = 0$
if
$\sigma [s^{\prime }] \cap \sigma [\theta ] = 0$
if
 $s^{\prime }$
is not an unramified twist of s. Furthermore, if
$s^{\prime }$
is not an unramified twist of s. Furthermore, if
 $d = \operatorname {dim}(s)/\operatorname {dim}(\theta )$
, then
$d = \operatorname {dim}(s)/\operatorname {dim}(\theta )$
, then 
-
2. If
 $(\sigma ^{\prime },N^{\prime })$
is another Weil-Deligne representation of
$(\sigma ^{\prime },N^{\prime })$
is another Weil-Deligne representation of
 $F_v$
such that
$F_v$
such that
 $\sigma ^{ss} \cong \sigma ^{\prime }{ss}$
, then
$\sigma ^{ss} \cong \sigma ^{\prime }{ss}$
, then
 $(\sigma ,N) \prec (\sigma ^{\prime },N^{\prime }) \Leftrightarrow (\sigma ,N) \prec _I (\sigma ^{\prime },N^{\prime }).$
$(\sigma ,N) \prec (\sigma ^{\prime },N^{\prime }) \Leftrightarrow (\sigma ,N) \prec _I (\sigma ^{\prime },N^{\prime }).$
From Lemma 8.4 and Proposition 7.1, it suffices to prove that
in order to conclude the proposition. We start by characterizing irreducible representations of
![]() $I_v$
with open kernel.
$I_v$
with open kernel.
Definition 8.5. If
![]() $(\theta ,V)$
is a representation of
$(\theta ,V)$
is a representation of
![]() $I_v$
and
$I_v$
and
![]() $\tau $
is an irreducible representation of a subgroup H of
$\tau $
is an irreducible representation of a subgroup H of
![]() $I_v$
, set
$I_v$
, set
![]() $(\theta [\tau ],V[\tau ])$
to be the
$(\theta [\tau ],V[\tau ])$
to be the
![]() $\tau $
-isotypical component of the H-representation
$\tau $
-isotypical component of the H-representation
![]() $(\left .\theta \right |{}_H,\left. V\right |{}_H)$
. Furthermore, if N is a commuting nilpotent endomorphism of V, then set
$(\left .\theta \right |{}_H,\left. V\right |{}_H)$
. Furthermore, if N is a commuting nilpotent endomorphism of V, then set
![]() $N[\tau ] = N \cap V[\tau ]$
.
$N[\tau ] = N \cap V[\tau ]$
.
Let P denote a Sylow pro-p-subgroup of
![]() $I_v$
. Recall that there is a map
$I_v$
. Recall that there is a map
![]() $t_p: I_v \rightarrow \mathbb {Z}_p$
since
$t_p: I_v \rightarrow \mathbb {Z}_p$
since
![]() $v \nmid p$
and let
$v \nmid p$
and let
![]() $I_v^p := \operatorname {ker} t_p$
. Recall that there is also an identification of P with
$I_v^p := \operatorname {ker} t_p$
. Recall that there is also an identification of P with
![]() $I_v/I_v^{p}$
. Let
$I_v/I_v^{p}$
. Let
![]() $\mathcal {I}^p$
denote the set of isomorphism classes of representations of
$\mathcal {I}^p$
denote the set of isomorphism classes of representations of
![]() $I_v^p$
with open kernel; there is a canonical action on
$I_v^p$
with open kernel; there is a canonical action on
![]() $\mathcal {I}^p$
by
$\mathcal {I}^p$
by
![]() $I_v/I_v^p$
acting by conjugation. For
$I_v/I_v^p$
acting by conjugation. For
![]() $i \in I_v$
, let
$i \in I_v$
, let
![]() $c_i$
denote the conjugation map
$c_i$
denote the conjugation map
![]() $I_v \rightarrow I_v$
where
$I_v \rightarrow I_v$
where
![]() $x \mapsto ixi^{-1}$
, and abusing notation, we let
$x \mapsto ixi^{-1}$
, and abusing notation, we let
![]() $c_i$
also denote restrictions of
$c_i$
also denote restrictions of
![]() $c_i$
to certain subgroups of
$c_i$
to certain subgroups of
![]() $I_v$
.
$I_v$
.
Let
![]() $\mathcal {I}^p_0$
denote the subset of elements of
$\mathcal {I}^p_0$
denote the subset of elements of
![]() $\mathcal {I}^p$
with open stabilizer in
$\mathcal {I}^p$
with open stabilizer in
![]() $I_v/I_v^p$
. For
$I_v/I_v^p$
. For
![]() $\eta \in \mathcal {I}^p_0$
, set
$\eta \in \mathcal {I}^p_0$
, set
![]() $I^\eta = \operatorname {Stab}_{I_v}(\eta )= \{ i \in I_v: \eta \circ c_i \cong \eta \}$
, which is open in
$I^\eta = \operatorname {Stab}_{I_v}(\eta )= \{ i \in I_v: \eta \circ c_i \cong \eta \}$
, which is open in
![]() $I_v$
. Additionally, fix a choice of topological generator
$I_v$
. Additionally, fix a choice of topological generator
![]() $g_{\eta }$
of
$g_{\eta }$
of
![]() $P \cap I^{\eta }$
such that
$P \cap I^{\eta }$
such that
![]() $I^{\eta } = \overline {\langle I_v^p , g_{\eta }\rangle }.$
Note that
$I^{\eta } = \overline {\langle I_v^p , g_{\eta }\rangle }.$
Note that
![]() $g_{\eta }$
has pro-p-order and can be chosen so that
$g_{\eta }$
has pro-p-order and can be chosen so that
![]() $g_{\eta \circ c_g} = g_{\eta }$
for all
$g_{\eta \circ c_g} = g_{\eta }$
for all
![]() $g \in P$
.
$g \in P$
.
Lemma 8.6. If
![]() $\eta \in \mathcal {I}^p_0$
, there exists an irreducible representation
$\eta \in \mathcal {I}^p_0$
, there exists an irreducible representation
![]() $\tilde {\eta }$
of
$\tilde {\eta }$
of
![]() $I^{\eta }$
with open kernel such that
$I^{\eta }$
with open kernel such that
![]() $\left .\tilde {\eta }\right |{}_{I^p_v} \cong \eta .$
$\left .\tilde {\eta }\right |{}_{I^p_v} \cong \eta .$
Proof. Since
![]() $\eta \in \mathcal {I}^p_0$
, we have that
$\eta \in \mathcal {I}^p_0$
, we have that
![]() $I^p_v/\operatorname {ker}(\eta )$
is finite order, and conjugation by
$I^p_v/\operatorname {ker}(\eta )$
is finite order, and conjugation by
![]() $g_{\eta }$
induces an automorphism of the quotient. This automorphism must have finite order as well, and since
$g_{\eta }$
induces an automorphism of the quotient. This automorphism must have finite order as well, and since
![]() $g_{\eta }$
has pro-p-order in
$g_{\eta }$
has pro-p-order in
![]() $I_v$
, conjugating by g must have p-power order as an automorphism of
$I_v$
, conjugating by g must have p-power order as an automorphism of
![]() $I^p_v/\operatorname {ker}(\eta )$
. This implies that there is some nonnegative integer n such that
$I^p_v/\operatorname {ker}(\eta )$
. This implies that there is some nonnegative integer n such that
![]() $g_{\eta }^{p^n}$
centralizes
$g_{\eta }^{p^n}$
centralizes
![]() $I^p_v/\operatorname {ker}(\eta )$
. Let
$I^p_v/\operatorname {ker}(\eta )$
. Let
![]() $A_{g_{\eta }}$
be an invertible matrix such that
$A_{g_{\eta }}$
be an invertible matrix such that
![]() $\eta \circ c_{g_\eta } = A_{g_{\eta }}\circ \eta \circ A_{g_{\eta }}^{-1}$
. Then
$\eta \circ c_{g_\eta } = A_{g_{\eta }}\circ \eta \circ A_{g_{\eta }}^{-1}$
. Then
![]() $A_{g_\eta }^{p^n}$
centralizes
$A_{g_\eta }^{p^n}$
centralizes
![]() $\eta $
and therefore must be a scalar since
$\eta $
and therefore must be a scalar since
![]() $\eta $
is irreducible; thus, we may suppose that
$\eta $
is irreducible; thus, we may suppose that
![]() $A_{g_{\eta }}^{p^n} = 1$
. We can then define the representation
$A_{g_{\eta }}^{p^n} = 1$
. We can then define the representation
![]() $\tilde {\eta }: I^\eta \rightarrow \operatorname {GL}_{\operatorname {dim} \eta }(\overline {\mathbb {Q}}_p)$
sending
$\tilde {\eta }: I^\eta \rightarrow \operatorname {GL}_{\operatorname {dim} \eta }(\overline {\mathbb {Q}}_p)$
sending
Furthermore, since
![]() $\eta $
is irreducible,
$\eta $
is irreducible,
![]() $\tilde {\eta }$
is also irreducible.
$\tilde {\eta }$
is also irreducible.
For each
![]() $\eta \in \mathcal {I}^p_0$
, choose once and for all a lift
$\eta \in \mathcal {I}^p_0$
, choose once and for all a lift
![]() $\tilde {\eta }$
to
$\tilde {\eta }$
to
![]() $I^{\eta }$
such that
$I^{\eta }$
such that
![]() $\widetilde {\eta \circ c_g} = \tilde {\eta } \circ c_g$
for all
$\widetilde {\eta \circ c_g} = \tilde {\eta } \circ c_g$
for all
![]() $g \in P$
. If
$g \in P$
. If
![]() $\eta \in \mathcal {I}^p_0$
and
$\eta \in \mathcal {I}^p_0$
and
![]() $\chi $
is a character of
$\chi $
is a character of
![]() $I^{\eta }$
with open kernel containing
$I^{\eta }$
with open kernel containing
![]() $I_v^p$
, set
$I_v^p$
, set
![]() $\theta _{\eta ,\chi } := \operatorname {Ind}^{I_v}_{I^{\eta }} (\tilde {\eta } \otimes \chi $
).
$\theta _{\eta ,\chi } := \operatorname {Ind}^{I_v}_{I^{\eta }} (\tilde {\eta } \otimes \chi $
).
Lemma 8.7. If
![]() $\eta \in \mathcal {I}^p_0$
and
$\eta \in \mathcal {I}^p_0$
and
![]() $\chi $
is a character of
$\chi $
is a character of
![]() $I^{\eta }$
with open kernel containing
$I^{\eta }$
with open kernel containing
![]() $I^p_v$
, then
$I^p_v$
, then
-
1.
 $\theta _{\eta ,\chi }$
is irreducible and
$\theta _{\eta ,\chi }$
is irreducible and
 $\left. \theta _{\eta ,\chi }\right |{}_{I^\eta } \cong \displaystyle {\bigoplus _{[i] \in I_v/I^\eta }}\tilde {\eta }\circ c_i \otimes \chi .$
$\left. \theta _{\eta ,\chi }\right |{}_{I^\eta } \cong \displaystyle {\bigoplus _{[i] \in I_v/I^\eta }}\tilde {\eta }\circ c_i \otimes \chi .$
-
2.
 $\theta _{\eta ,\chi } \cong \theta _{\eta ^{\prime },\chi ^{\prime }}$
if and only if
$\theta _{\eta ,\chi } \cong \theta _{\eta ^{\prime },\chi ^{\prime }}$
if and only if
 $\chi = \chi ^{\prime }$
and
$\chi = \chi ^{\prime }$
and
 $\eta ^{\prime } \cong \eta \circ c_i$
for some
$\eta ^{\prime } \cong \eta \circ c_i$
for some
 $i \in I_v$
.
$i \in I_v$
. -
3. Every irreducible representation of
 $I_v$
with open kernel arises in this way.
$I_v$
with open kernel arises in this way.
Proof. 1. For any character
![]() $\chi : I^\eta \rightarrow \overline {\mathbb {Q}}_p^\times $
with open kernel containing
$\chi : I^\eta \rightarrow \overline {\mathbb {Q}}_p^\times $
with open kernel containing
![]() $I^p_v$
,
$I^p_v$
,
![]() $\tilde {\eta } \otimes \chi $
is irreducible since
$\tilde {\eta } \otimes \chi $
is irreducible since
![]() $\eta $
is. Thus, we can prove that
$\eta $
is. Thus, we can prove that
![]() $\theta _{\eta ,\chi }$
is irreducible using Mackey’s Criterion. Consider some element
$\theta _{\eta ,\chi }$
is irreducible using Mackey’s Criterion. Consider some element
![]() $i \in I_v \smallsetminus I^\eta $
. We want to show that
$i \in I_v \smallsetminus I^\eta $
. We want to show that
![]() $\theta _{\eta ,\chi }$
and
$\theta _{\eta ,\chi }$
and
![]() $\theta _{\eta ,\chi } \circ c_i$
are disjoint representations of
$\theta _{\eta ,\chi } \circ c_i$
are disjoint representations of
![]() $I^\eta $
(i.e., have no irreducible component in common). It is enough to see that they are disjoint on
$I^\eta $
(i.e., have no irreducible component in common). It is enough to see that they are disjoint on
![]() $I_v^p$
. Since
$I_v^p$
. Since
![]() $\left .\theta _{\eta ,\chi } \circ \operatorname {id}\right |{}_{I_v^p} = \eta $
and
$\left .\theta _{\eta ,\chi } \circ \operatorname {id}\right |{}_{I_v^p} = \eta $
and
![]() $\left .\theta _{\eta ,\chi } \circ c_i\right |{}_{I_v^p} = \eta \circ c_i$
for
$\left .\theta _{\eta ,\chi } \circ c_i\right |{}_{I_v^p} = \eta \circ c_i$
for
![]() $i \notin I^{\eta }$
, these are not isomorphic irreducible representations; thus, they must be disjoint. The second part follows from Frobenius reciprocity and the definition of
$i \notin I^{\eta }$
, these are not isomorphic irreducible representations; thus, they must be disjoint. The second part follows from Frobenius reciprocity and the definition of
![]() $\theta _{\eta ,\chi }$
as an induced representation from the stabilizer of
$\theta _{\eta ,\chi }$
as an induced representation from the stabilizer of
![]() $\eta $
in
$\eta $
in
![]() $I_v$
to
$I_v$
to
![]() $I_v$
.
$I_v$
.
2. Next, we prove that
![]() $\theta _{\eta ,\chi }$
and
$\theta _{\eta ,\chi }$
and
![]() $\theta _{\eta ^{\prime },\chi ^{\prime }}$
are isomorphic if and only if for some
$\theta _{\eta ^{\prime },\chi ^{\prime }}$
are isomorphic if and only if for some
![]() $i \in I_v$
,
$i \in I_v$
,
![]() $\eta \cong \eta ^{\prime }\circ c_i$
and
$\eta \cong \eta ^{\prime }\circ c_i$
and
![]() $\chi = \chi ^{\prime }$
. One direction follows from the first part of the lemma. To prove the converse, assume
$\chi = \chi ^{\prime }$
. One direction follows from the first part of the lemma. To prove the converse, assume
![]() $\theta _{\eta ,\chi }$
and
$\theta _{\eta ,\chi }$
and
![]() $\theta _{\eta ^{\prime },\chi ^{\prime }}$
are isomorphic. Restricting to
$\theta _{\eta ^{\prime },\chi ^{\prime }}$
are isomorphic. Restricting to
![]() $I_v^p$
, we have
$I_v^p$
, we have
 $$ \begin{align*}\bigoplus_{[i] \in I_v/I^\eta} \eta \circ c_i \cong \left.\theta_{\eta,\chi}\right|{}_{I_v^p} \cong \left.\theta_{\eta^{\prime},\chi^{\prime}}\right|{}_{I_v^p} \cong \bigoplus_{[i] \in I_v/I^{\eta^{\prime}}} \eta^{\prime}\circ c_i.\end{align*} $$
$$ \begin{align*}\bigoplus_{[i] \in I_v/I^\eta} \eta \circ c_i \cong \left.\theta_{\eta,\chi}\right|{}_{I_v^p} \cong \left.\theta_{\eta^{\prime},\chi^{\prime}}\right|{}_{I_v^p} \cong \bigoplus_{[i] \in I_v/I^{\eta^{\prime}}} \eta^{\prime}\circ c_i.\end{align*} $$
Thus,
![]() $\eta \cong \eta ^{\prime } \circ c_i$
for some
$\eta \cong \eta ^{\prime } \circ c_i$
for some
![]() $[i] \in I_v/I_v^p$
. This further implies
$[i] \in I_v/I_v^p$
. This further implies
![]() $I^\eta \cong I^{\eta ^{\prime }}$
, where the isomorphism is given by conjugation by i since for any element
$I^\eta \cong I^{\eta ^{\prime }}$
, where the isomorphism is given by conjugation by i since for any element
![]() $g \in I^\eta $
,
$g \in I^\eta $
,
In fact, since
![]() $I_v/I_v^p$
is abelian, we have proven that
$I_v/I_v^p$
is abelian, we have proven that
![]() $I^\eta = I^{\eta ^{\prime }}$
.
$I^\eta = I^{\eta ^{\prime }}$
.
It remains to show that
![]() $\chi \cong \chi ^{\prime }$
. By Frobenius reciprocity,
$\chi \cong \chi ^{\prime }$
. By Frobenius reciprocity,
 $$ \begin{align*}\operatorname{Hom}_{I_v}(\theta_{\eta,\chi^{\prime}},\theta_{\eta,\chi}) = \operatorname{Hom}_{I^{\eta}}(\tilde{\eta} \otimes \chi^{\prime}, \bigoplus_{[i] \in I_v/I^\eta}\tilde{\eta} \circ c_i \otimes \chi).\end{align*} $$
$$ \begin{align*}\operatorname{Hom}_{I_v}(\theta_{\eta,\chi^{\prime}},\theta_{\eta,\chi}) = \operatorname{Hom}_{I^{\eta}}(\tilde{\eta} \otimes \chi^{\prime}, \bigoplus_{[i] \in I_v/I^\eta}\tilde{\eta} \circ c_i \otimes \chi).\end{align*} $$
Since
![]() $\tilde {\eta }\circ c_i \otimes \chi $
is irreducible, it remains to check that
$\tilde {\eta }\circ c_i \otimes \chi $
is irreducible, it remains to check that
![]() $\tilde {\eta } \otimes \chi \not \cong \tilde {\eta }$
as representations of
$\tilde {\eta } \otimes \chi \not \cong \tilde {\eta }$
as representations of
![]() $I^\eta $
for nontrivial
$I^\eta $
for nontrivial
![]() $\chi $
. Let
$\chi $
. Let
![]() $\chi (g_{\eta }) = \lambda _{g_{\eta }}$
, and note that if
$\chi (g_{\eta }) = \lambda _{g_{\eta }}$
, and note that if
![]() $\tilde {\eta }(g_{\eta }) = (\tilde {\eta }\otimes \chi )(g_\eta ) = \lambda _{g_\eta } \tilde {\eta }(g_\eta )$
, then either
$\tilde {\eta }(g_{\eta }) = (\tilde {\eta }\otimes \chi )(g_\eta ) = \lambda _{g_\eta } \tilde {\eta }(g_\eta )$
, then either
![]() $\lambda _{g_\eta } = 1$
or
$\lambda _{g_\eta } = 1$
or
![]() $\operatorname {tr}(\tilde {\eta }(g_{\eta }))$
is zero; however, since
$\operatorname {tr}(\tilde {\eta }(g_{\eta }))$
is zero; however, since
![]() $\tilde {\eta }$
is irreducible, for any
$\tilde {\eta }$
is irreducible, for any
![]() $h \in I^p_v$
, we have
$h \in I^p_v$
, we have
![]() $\tilde {\eta }(g_{\eta }h) = \lambda _{g_{\eta }}\tilde {\eta }(g_{\eta } h)$
, and for some h,
$\tilde {\eta }(g_{\eta }h) = \lambda _{g_{\eta }}\tilde {\eta }(g_{\eta } h)$
, and for some h,
![]() $\operatorname {tr}(\tilde {\eta }(g_{\eta }h)) \neq 0$
. Thus,
$\operatorname {tr}(\tilde {\eta }(g_{\eta }h)) \neq 0$
. Thus,
![]() $\operatorname {tr}(\tilde {\eta }(g_{\eta })) \neq 0$
, and so we must have that
$\operatorname {tr}(\tilde {\eta }(g_{\eta })) \neq 0$
, and so we must have that
![]() $\lambda _{g_\eta } = 1$
. Thus, we conclude that
$\lambda _{g_\eta } = 1$
. Thus, we conclude that
![]() $\theta _{\eta ,\chi } \neq \theta _{\eta ^{\prime },\chi ^{\prime }}$
when
$\theta _{\eta ,\chi } \neq \theta _{\eta ^{\prime },\chi ^{\prime }}$
when
![]() $\chi \neq \chi ^{\prime }$
or
$\chi \neq \chi ^{\prime }$
or
![]() $\eta $
and
$\eta $
and
![]() $\eta ^{\prime }$
are not in the same orbit of
$\eta ^{\prime }$
are not in the same orbit of
![]() $\mathcal {I}^p_0$
under the action of
$\mathcal {I}^p_0$
under the action of
![]() $I_v/I_v^p$
(or equivalently,
$I_v/I_v^p$
(or equivalently,
![]() $I_v/I^\eta $
).
$I_v/I^\eta $
).
3. Finally, we show that any irreducible (finite-dimensional) representation of
![]() $I_v$
arises as
$I_v$
arises as
![]() $\theta _{\eta ,\chi }$
for some
$\theta _{\eta ,\chi }$
for some
![]() $\eta $
and
$\eta $
and
![]() $\chi $
. Let
$\chi $
. Let
![]() $\theta : I \rightarrow \operatorname {GL}(V)$
be an irreducible representation, and restrict to
$\theta : I \rightarrow \operatorname {GL}(V)$
be an irreducible representation, and restrict to
![]() $I_v^p$
. Let
$I_v^p$
. Let
![]() $\oplus _{\eta \in \mathcal {I}^p_0} V[\eta ]$
denote the decomposition of
$\oplus _{\eta \in \mathcal {I}^p_0} V[\eta ]$
denote the decomposition of
![]() $\left .\theta \right |{}_{I_v^p}$
into its isotypic components. For each
$\left .\theta \right |{}_{I_v^p}$
into its isotypic components. For each
![]() $\eta $
,
$\eta $
,
![]() $I^{\eta } = \operatorname {Stab}_I(\eta )$
acts on
$I^{\eta } = \operatorname {Stab}_I(\eta )$
acts on
![]() $V[\eta ]$
, and furthermore, each
$V[\eta ]$
, and furthermore, each
![]() $i \in I$
induces an identification of
$i \in I$
induces an identification of
![]() $V[\eta ]$
and
$V[\eta ]$
and
![]() $V[\eta \circ c_i]$
. This implies that
$V[\eta \circ c_i]$
. This implies that
![]() $\operatorname {Ind}_{I^{\eta }}^I V[\eta ] \cong V$
, and thus as a representation of
$\operatorname {Ind}_{I^{\eta }}^I V[\eta ] \cong V$
, and thus as a representation of
![]() $I^{\eta }$
,
$I^{\eta }$
,
![]() $V[\eta ]$
is irreducible. There is an isomorphism as
$V[\eta ]$
is irreducible. There is an isomorphism as
![]() $\overline {\mathbb {Q}}_p$
-vector spaces,
$\overline {\mathbb {Q}}_p$
-vector spaces,
The space
![]() $\operatorname {Hom}_{I^p_v}(\left .\tilde {\eta }\right |{}_{I^p_v},\left .V[\eta ]\right |{}_{I^p_v})$
has an action of
$\operatorname {Hom}_{I^p_v}(\left .\tilde {\eta }\right |{}_{I^p_v},\left .V[\eta ]\right |{}_{I^p_v})$
has an action of
![]() $i \in I^{\eta }$
by conjugation, and
$i \in I^{\eta }$
by conjugation, and
![]() $I^p_v$
acts trivially. With this action, (8.1) is indeed an isomorphism of
$I^p_v$
acts trivially. With this action, (8.1) is indeed an isomorphism of
![]() $I^{\eta }$
-representations. However, since
$I^{\eta }$
-representations. However, since
![]() $V[\eta ]$
is irreducible,
$V[\eta ]$
is irreducible,
![]() $\operatorname {Hom}_{I^p_v}(\left .\tilde {\eta }\right |{}_{I^p_v},\left .V[\eta ]\right |{}_{I^p_v})$
must be irreducible over
$\operatorname {Hom}_{I^p_v}(\left .\tilde {\eta }\right |{}_{I^p_v},\left .V[\eta ]\right |{}_{I^p_v})$
must be irreducible over
![]() $I^{\eta }/I^p_v$
, which is abelian. Letting
$I^{\eta }/I^p_v$
, which is abelian. Letting
![]() $\chi = \operatorname {Hom}_{I^p_v}(\left .\tilde {\eta }\right |{}_{I^p_v},\left .V[\eta ]\right |{}_{I^p_v})$
, we conclude that
$\chi = \operatorname {Hom}_{I^p_v}(\left .\tilde {\eta }\right |{}_{I^p_v},\left .V[\eta ]\right |{}_{I^p_v})$
, we conclude that
![]() $\theta = \theta _{\eta ,\chi }$
.
$\theta = \theta _{\eta ,\chi }$
.
We now consider a more useful version of Definition 8.3 to all representations of
![]() $I_v$
with open kernel and commuting nilpotent endomorphism.
$I_v$
with open kernel and commuting nilpotent endomorphism.
Proposition 8.8. If
![]() $(\sigma ,V,N)$
and
$(\sigma ,V,N)$
and
![]() $(\sigma ^{\prime },V^{\prime },N^{\prime })$
are two Weil-Deligne representations, then
$(\sigma ^{\prime },V^{\prime },N^{\prime })$
are two Weil-Deligne representations, then
![]() $(\sigma ,V,N) \prec _I (\sigma ^{\prime },V^{\prime },N)$
if and only if
$(\sigma ,V,N) \prec _I (\sigma ^{\prime },V^{\prime },N)$
if and only if
![]() $\left .\sigma \right |{}_{I_v} \cong \left .\sigma ^{\prime }\right |{}_{I_v}$
and
$\left .\sigma \right |{}_{I_v} \cong \left .\sigma ^{\prime }\right |{}_{I_v}$
and
for all
![]() $j \in \mathbb {Z}_{>0}$
,
$j \in \mathbb {Z}_{>0}$
,
![]() $\eta \in \mathcal {I}^p_0$
, and
$\eta \in \mathcal {I}^p_0$
, and
![]() $\chi $
a character of
$\chi $
a character of
![]() $I^\eta /I^p_v$
with open kernel.
$I^\eta /I^p_v$
with open kernel.
Proof. Note that for any
![]() $\theta \in \mathcal {I}$
, the conjugacy class of
$\theta \in \mathcal {I}$
, the conjugacy class of
![]() $N[\theta ]$
(resp.
$N[\theta ]$
(resp.
![]() $N^{\prime }[\theta ]$
) is determined by the partition of
$N^{\prime }[\theta ]$
) is determined by the partition of
![]() $\operatorname {dim}(\sigma [\theta ])/\operatorname {dim}(\theta )$
(resp.
$\operatorname {dim}(\sigma [\theta ])/\operatorname {dim}(\theta )$
(resp.
![]() $\operatorname {dim}(\sigma ^{\prime }[\theta ])/\operatorname {dim}(\theta )$
) given by
$\operatorname {dim}(\sigma ^{\prime }[\theta ])/\operatorname {dim}(\theta )$
) given by
![]() $(n_{i,\theta }(\sigma ,N))_{i \geq 1}$
(resp.
$(n_{i,\theta }(\sigma ,N))_{i \geq 1}$
(resp.
![]() $(n_{i,\theta }(\sigma ^{\prime },N^{\prime }))_{i \geq 1}$
). The condition
$(n_{i,\theta }(\sigma ^{\prime },N^{\prime }))_{i \geq 1}$
). The condition
is equivalent to the condition
Since we require
![]() $\left .\sigma \right |{}_{I_v} \cong \left .\sigma ^{\prime }\right |{}_{I_v}$
in both definitions, we have that their dimensions are equal; thus,
$\left .\sigma \right |{}_{I_v} \cong \left .\sigma ^{\prime }\right |{}_{I_v}$
in both definitions, we have that their dimensions are equal; thus,
![]() $\operatorname {rk} N[\theta ]^j \leq \operatorname {rk} (N^{\prime }[\theta ])^j$
is equivalent to
$\operatorname {rk} N[\theta ]^j \leq \operatorname {rk} (N^{\prime }[\theta ])^j$
is equivalent to
By Lemma 8.7, we know that all
![]() $\theta \in \mathcal {I}$
are of the form
$\theta \in \mathcal {I}$
are of the form
![]() $\theta _{\eta ,\chi }$
where
$\theta _{\eta ,\chi }$
where
![]() $\eta \in \mathcal {I}^p_0$
and
$\eta \in \mathcal {I}^p_0$
and
![]() $\chi $
is a character of
$\chi $
is a character of
![]() $I^{\eta }$
with open kernel containing
$I^{\eta }$
with open kernel containing
![]() $I^p_v$
, and so we are done.
$I^p_v$
, and so we are done.
Furthermore, given
![]() $j \in \mathbb {Z}_{>0}$
,
$j \in \mathbb {Z}_{>0}$
,
![]() $\eta \in \mathcal {I}^p_0$
, and
$\eta \in \mathcal {I}^p_0$
, and
![]() $\chi $
a character of
$\chi $
a character of
![]() $I^{\eta }/I^p_v$
with open kernel, then using the fact that
$I^{\eta }/I^p_v$
with open kernel, then using the fact that
![]() $\operatorname {dim} \operatorname {ker} N = [I:I^\eta ]\operatorname {dim} \operatorname {ker} \left. N \right |{}_{\theta _{\eta ,\chi }[\tilde {\eta } \otimes \chi ]}$
(coming from the Lemma 8.7(1)), we can conclude
$\operatorname {dim} \operatorname {ker} N = [I:I^\eta ]\operatorname {dim} \operatorname {ker} \left. N \right |{}_{\theta _{\eta ,\chi }[\tilde {\eta } \otimes \chi ]}$
(coming from the Lemma 8.7(1)), we can conclude
 $$ \begin{align*}&\operatorname{dim}(\operatorname{ker} N^j \cap V[\theta_{\eta,\chi}]) \geq \operatorname{dim}(\operatorname{ker} {N^{\prime}}^j \cap V^{\prime}[\theta_{\eta,\chi}]) \\&\quad\Leftrightarrow \operatorname{dim}(\operatorname{ker} N^j \cap V [\tilde{\eta} \otimes \chi]) \geq \operatorname{dim} (\operatorname{ker} {N^{\prime}}^j \cap V^{\prime}[\tilde{\eta} \otimes \chi]).\end{align*} $$
$$ \begin{align*}&\operatorname{dim}(\operatorname{ker} N^j \cap V[\theta_{\eta,\chi}]) \geq \operatorname{dim}(\operatorname{ker} {N^{\prime}}^j \cap V^{\prime}[\theta_{\eta,\chi}]) \\&\quad\Leftrightarrow \operatorname{dim}(\operatorname{ker} N^j \cap V [\tilde{\eta} \otimes \chi]) \geq \operatorname{dim} (\operatorname{ker} {N^{\prime}}^j \cap V^{\prime}[\tilde{\eta} \otimes \chi]).\end{align*} $$
If
![]() $\eta $
denotes a representation of
$\eta $
denotes a representation of
![]() $I_v^p$
with open kernel and
$I_v^p$
with open kernel and
![]() $f:I_v^p \rightarrow \overline {\mathbb {Q}}_p$
is a locally constant function, then let
$f:I_v^p \rightarrow \overline {\mathbb {Q}}_p$
is a locally constant function, then let
![]() $\eta (f) := \int _{I_v^p} f(i)\eta (i)di,$
where
$\eta (f) := \int _{I_v^p} f(i)\eta (i)di,$
where
![]() $di$
denotes the Haar measure on
$di$
denotes the Haar measure on
![]() $I_v^p$
(normalized so that vol(
$I_v^p$
(normalized so that vol(
![]() $I_v^p$
) = 1). Since
$I_v^p$
) = 1). Since
![]() $I^p_v$
is compact, this integral is in fact a finite sum. Recall that for each
$I^p_v$
is compact, this integral is in fact a finite sum. Recall that for each
![]() $\eta $
, we fixed a choice of topological generator
$\eta $
, we fixed a choice of topological generator
![]() $g_{\eta }$
of
$g_{\eta }$
of
![]() $P \cap I^{\eta }$
such that
$P \cap I^{\eta }$
such that
![]() $I^{\eta } = \overline {\langle I_v^p , g_{\eta }\rangle }.$
The following lemma describes the existence of projection operators for representations of
$I^{\eta } = \overline {\langle I_v^p , g_{\eta }\rangle }.$
The following lemma describes the existence of projection operators for representations of
![]() $I_v^p$
and the relationship between the image of
$I_v^p$
and the relationship between the image of
![]() $\tilde {\eta }$
and
$\tilde {\eta }$
and
![]() $\eta $
(both irreducible).
$\eta $
(both irreducible).
Lemma 8.9. If
![]() $(\eta ,V)$
and
$(\eta ,V)$
and
![]() $(\eta ^{\prime },V^{\prime }) \in \mathcal {I}^p_0$
, then
$(\eta ^{\prime },V^{\prime }) \in \mathcal {I}^p_0$
, then
-
1. There exists a locally constant function
 $\epsilon _{\eta }: I_v^p \rightarrow \overline {\mathbb {Q}}_p$
sending
$\epsilon _{\eta }: I_v^p \rightarrow \overline {\mathbb {Q}}_p$
sending
 $i \mapsto \frac {\operatorname {tr}(\eta ^{\vee }(i))}{\operatorname {dim} \eta }$
(where
$i \mapsto \frac {\operatorname {tr}(\eta ^{\vee }(i))}{\operatorname {dim} \eta }$
(where
 $\eta ^{\vee }$
denotes the dual representation) such that
$\eta ^{\vee }$
denotes the dual representation) such that
 $\eta (\epsilon _\eta ) = 1$
, but
$\eta (\epsilon _\eta ) = 1$
, but
 $\eta ^{\prime }(\epsilon _\eta ) = 0$
for all
$\eta ^{\prime }(\epsilon _\eta ) = 0$
for all
 $\eta ^{\prime } \not \cong \eta $
.
$\eta ^{\prime } \not \cong \eta $
. -
2. There exists a locally constant function
 $a_{\eta }: I_v^p \rightarrow \overline {\mathbb {Q}}_p$
such that
$a_{\eta }: I_v^p \rightarrow \overline {\mathbb {Q}}_p$
such that
 $\tilde {\eta }(g_{\eta }) = \eta (a_{\eta })$
, but
$\tilde {\eta }(g_{\eta }) = \eta (a_{\eta })$
, but
 $\eta ^{\prime }(a_{\eta }) = 0$
if
$\eta ^{\prime }(a_{\eta }) = 0$
if
 $\eta \not \cong \eta ^{\prime }$
.
$\eta \not \cong \eta ^{\prime }$
.
Proof. The first part is clear. As for the second part, since
![]() $\eta $
has open kernel, there is a finite quotient
$\eta $
has open kernel, there is a finite quotient
![]() $I^v_p/\operatorname {ker}(\eta )$
through which it factors. Furthermore,
$I^v_p/\operatorname {ker}(\eta )$
through which it factors. Furthermore,
![]() $\eta $
is irreducible, and thus the matrix
$\eta $
is irreducible, and thus the matrix
![]() $\tilde {\eta }(g_{\eta }) \in \operatorname {Hom}(V)$
can be written as a sum
$\tilde {\eta }(g_{\eta }) \in \operatorname {Hom}(V)$
can be written as a sum
![]() $\sum _{g \in I^v_p/\operatorname {ker}(\eta )} a_{\eta ,g} \eta (g)$
. Define
$\sum _{g \in I^v_p/\operatorname {ker}(\eta )} a_{\eta ,g} \eta (g)$
. Define
![]() $a_\eta $
by sending
$a_\eta $
by sending
![]() $g \mapsto a_{\eta ,g}$
. By orthogonality, we have that
$g \mapsto a_{\eta ,g}$
. By orthogonality, we have that
![]() $\eta ^{\prime }(a_{\eta }) = 0$
for
$\eta ^{\prime }(a_{\eta }) = 0$
for
![]() $\eta ^{\prime } \not \equiv \eta $
. Recall that the Peter-Weyl theorem gives an isomorphism
$\eta ^{\prime } \not \equiv \eta $
. Recall that the Peter-Weyl theorem gives an isomorphism
 $$ \begin{align*}\operatorname{Hom}(I^v_p/\operatorname{ker}(\eta),\overline{\mathbb{Q}}_p) \stackrel{\sim}{\longrightarrow} \bigoplus_{(r,V) \in \mathrm{Irr}(I^v_p/\operatorname{ker}(\eta))} \operatorname{End}_{\overline{\mathbb{Q}}_p}(V),\end{align*} $$
$$ \begin{align*}\operatorname{Hom}(I^v_p/\operatorname{ker}(\eta),\overline{\mathbb{Q}}_p) \stackrel{\sim}{\longrightarrow} \bigoplus_{(r,V) \in \mathrm{Irr}(I^v_p/\operatorname{ker}(\eta))} \operatorname{End}_{\overline{\mathbb{Q}}_p}(V),\end{align*} $$
and thus
![]() $a_{\eta }$
pulls back to a locally constant function of
$a_{\eta }$
pulls back to a locally constant function of
![]() $I^p_v$
.
$I^p_v$
.
For each
![]() $\eta \in \mathcal {I}^p_0$
, fix a choice of
$\eta \in \mathcal {I}^p_0$
, fix a choice of
![]() $\epsilon _{\eta }$
and
$\epsilon _{\eta }$
and
![]() $a_{\eta }$
as described in Lemma 8.9. If
$a_{\eta }$
as described in Lemma 8.9. If
![]() $(\sigma ,V,N)$
(resp.
$(\sigma ,V,N)$
(resp.
![]() $(\sigma ^{\prime },V^{\prime },N^{\prime })$
) uniquely determine (local) Galois representations
$(\sigma ^{\prime },V^{\prime },N^{\prime })$
) uniquely determine (local) Galois representations
![]() $\rho _v$
(resp.
$\rho _v$
(resp.
![]() $\rho _v^{\prime }$
) of
$\rho _v^{\prime }$
) of
![]() $G_{F_v}$
acting on the same underlying vector space V (resp.
$G_{F_v}$
acting on the same underlying vector space V (resp.
![]() $V^{\prime }$
), then recall that the defining relation between
$V^{\prime }$
), then recall that the defining relation between
![]() $\rho _v$
and
$\rho _v$
and
![]() $(\sigma ,V,N)$
is
$(\sigma ,V,N)$
is
If
![]() $i \in I_v$
is an element such that
$i \in I_v$
is an element such that
![]() $t_p(g)$
is nonzero, then we can write
$t_p(g)$
is nonzero, then we can write
![]() $\operatorname {log} (\sigma (i)^{-1}\rho _v(i)) = t_p(i)N$
. Additionally, for all positive j,
$\operatorname {log} (\sigma (i)^{-1}\rho _v(i)) = t_p(i)N$
. Additionally, for all positive j,
![]() $\operatorname {rk}(t_p(i)N)^j = \operatorname {rk} N^j$
, and for any unipotent matrix U,
$\operatorname {rk}(t_p(i)N)^j = \operatorname {rk} N^j$
, and for any unipotent matrix U,
![]() $\operatorname {rk}(\operatorname {log} U)^j = \operatorname {rk}(U - 1)^j$
. Thus,
$\operatorname {rk}(\operatorname {log} U)^j = \operatorname {rk}(U - 1)^j$
. Thus,
This implies that
and we have that
![]() $(\sigma ,N) \prec _I (\sigma ^{\prime },N^{\prime })$
if and only if
$(\sigma ,N) \prec _I (\sigma ^{\prime },N^{\prime })$
if and only if
![]() $\left. \sigma \right |{}_{I_v} \cong \left .\sigma ^{\prime }\right |{}_{I_v}$
and for all
$\left. \sigma \right |{}_{I_v} \cong \left .\sigma ^{\prime }\right |{}_{I_v}$
and for all
![]() $j \in \mathbb {Z}_{>0}$
,
$j \in \mathbb {Z}_{>0}$
,
![]() $\eta \in \mathcal {I}^p_0$
, and
$\eta \in \mathcal {I}^p_0$
, and
![]() $\chi $
a character of
$\chi $
a character of
![]() $I^{\eta }/I^p_v$
with open kernel,
$I^{\eta }/I^p_v$
with open kernel,
Additionally, since
![]() $\operatorname {ker} \left .(\rho (g_{\eta }) - \sigma (g_{\eta }))^j\right |{}_{V[\tilde {\eta } \otimes \chi ]} = \operatorname {ker}(\rho (g_{\eta }) - \rho (a_{\eta })\chi (g_{\eta }))^j,$
we can then conclude the following:
$\operatorname {ker} \left .(\rho (g_{\eta }) - \sigma (g_{\eta }))^j\right |{}_{V[\tilde {\eta } \otimes \chi ]} = \operatorname {ker}(\rho (g_{\eta }) - \rho (a_{\eta })\chi (g_{\eta }))^j,$
we can then conclude the following:
Lemma 8.10. If
![]() $(\rho ,V),(\rho ,V^{\prime })$
are two continuous m-dimensional representations of
$(\rho ,V),(\rho ,V^{\prime })$
are two continuous m-dimensional representations of
![]() $I_v$
(arising from continuous
$I_v$
(arising from continuous
![]() $G_{F_v}$
-representations), then
$G_{F_v}$
-representations), then
![]() $(\sigma _\rho ,N) \prec _I (\sigma _{\rho ^{\prime }},N^{\prime })$
if and only if
$(\sigma _\rho ,N) \prec _I (\sigma _{\rho ^{\prime }},N^{\prime })$
if and only if
![]() $\left. \rho \right |{}_{I_v^p} \cong \left .\rho ^{\prime }\right |{}_{I_v^p}$
and
$\left. \rho \right |{}_{I_v^p} \cong \left .\rho ^{\prime }\right |{}_{I_v^p}$
and
for all
![]() $j,k \in \mathbb {Z}_{>0}$
,
$j,k \in \mathbb {Z}_{>0}$
,
![]() $\eta \in \mathcal {I}^p_0$
, and p-power root of unity
$\eta \in \mathcal {I}^p_0$
, and p-power root of unity
![]() $\zeta $
.
$\zeta $
.
Proof. This follows from (8.2) and the fact that for any
![]() $A \in \operatorname {End}(V)$
,
$A \in \operatorname {End}(V)$
,
![]() $\operatorname {dim} \operatorname {ker} A = \operatorname {dim} V + 1 - \operatorname {min}\{k \in \mathbb {Z}_{>0} : \wedge ^k A = 0\}.$
$\operatorname {dim} \operatorname {ker} A = \operatorname {dim} V + 1 - \operatorname {min}\{k \in \mathbb {Z}_{>0} : \wedge ^k A = 0\}.$
Suppose
![]() $\rho _v^{\prime }$
is a local p-adic
$\rho _v^{\prime }$
is a local p-adic
![]() $G_{F_v}$
-Galois representation of dimension m, and
$G_{F_v}$
-Galois representation of dimension m, and
![]() $\rho $
is a semisimple continuous m-dimensional global Galois representations of
$\rho $
is a semisimple continuous m-dimensional global Galois representations of
![]() $G_{F} \supset I_v$
. Then
$G_{F} \supset I_v$
. Then
![]() $\wedge ^k \rho $
is also semisimple, and
$\wedge ^k \rho $
is also semisimple, and
![]() $\operatorname {WD}(\left .\rho \right |{}_{G_{F_v}})^{\operatorname {Frob}-ss} \prec _I \operatorname {WD}(\rho _v^{\prime })^{\operatorname {Frob}-ss}$
if and only if for all
$\operatorname {WD}(\left .\rho \right |{}_{G_{F_v}})^{\operatorname {Frob}-ss} \prec _I \operatorname {WD}(\rho _v^{\prime })^{\operatorname {Frob}-ss}$
if and only if for all
![]() $j,k \in \mathbb {Z}_{>0}$
,
$j,k \in \mathbb {Z}_{>0}$
,
![]() $\eta \in \mathcal {I}^p_0$
,
$\eta \in \mathcal {I}^p_0$
,
![]() $\zeta $
a p-power root of unity,
$\zeta $
a p-power root of unity,
because trace is a non-degenerate bilinear form on the image of semisimple representation. For any
![]() $\rho $
, we can extend it by linearity to
$\rho $
, we can extend it by linearity to
![]() $\rho : \overline {\mathbb {Q}}_p[G_F] \rightarrow \operatorname {GL}(V)$
, and let
$\rho : \overline {\mathbb {Q}}_p[G_F] \rightarrow \operatorname {GL}(V)$
, and let
![]() $b_{\eta ,\zeta } := g_{\eta } - \zeta \cdot a_{\eta } \in \overline {\mathbb {Q}}_p[G_F]$
. Then
$b_{\eta ,\zeta } := g_{\eta } - \zeta \cdot a_{\eta } \in \overline {\mathbb {Q}}_p[G_F]$
. Then
![]() $\operatorname {WD}(\rho )^{\operatorname {Frob}-ss} \prec _I \operatorname {WD}(\rho ^{\prime })^{\operatorname {Frob}-ss}$
if and only if for all
$\operatorname {WD}(\rho )^{\operatorname {Frob}-ss} \prec _I \operatorname {WD}(\rho ^{\prime })^{\operatorname {Frob}-ss}$
if and only if for all
![]() $k,j \in \mathbb {Z}_{>0}$
,
$k,j \in \mathbb {Z}_{>0}$
,
![]() $\eta \in \mathcal {I}^p_0$
, and p-power roots of unity
$\eta \in \mathcal {I}^p_0$
, and p-power roots of unity
![]() $\zeta $
,
$\zeta $
,
Now, if T denotes a
![]() $2n$
-dimensional continuous pseudocharacter of
$2n$
-dimensional continuous pseudocharacter of
![]() $G_{F}$
, then by extending linearly and using the recursive formula for a matrix A,
$G_{F}$
, then by extending linearly and using the recursive formula for a matrix A,
![]() $\operatorname {tr} \wedge ^k A = \frac {1}{k} \sum _{m=1}^k (-1)^{m-1} \operatorname {tr}(A^m) \operatorname {tr} \wedge ^{k-m}(A)$
, we can define
$\operatorname {tr} \wedge ^k A = \frac {1}{k} \sum _{m=1}^k (-1)^{m-1} \operatorname {tr}(A^m) \operatorname {tr} \wedge ^{k-m}(A)$
, we can define
 $$ \begin{align*}\wedge^k T: \overline{\mathbb{Q}}_p[G_{F}] \rightarrow \overline{\mathbb{Q}}_p \quad \text{by} \quad g \mapsto \frac{1}{k} \sum_{m=1}^k (-1)^{m-1} T(g^m) \wedge^{k-m}T(g)\end{align*} $$
$$ \begin{align*}\wedge^k T: \overline{\mathbb{Q}}_p[G_{F}] \rightarrow \overline{\mathbb{Q}}_p \quad \text{by} \quad g \mapsto \frac{1}{k} \sum_{m=1}^k (-1)^{m-1} T(g^m) \wedge^{k-m}T(g)\end{align*} $$
for
![]() $k \leq 2n$
. In the sequel, we will be interested in whether the following function
$k \leq 2n$
. In the sequel, we will be interested in whether the following function
is identically zero.
8.1 Proof of
 $\prec $
$\prec $
In this section, we prove Proposition 8.1.
Proof. Fix
![]() $\ell \in S_{\operatorname {spl}}$
and let
$\ell \in S_{\operatorname {spl}}$
and let
![]() $v \mid \ell $
be a prime of F in
$v \mid \ell $
be a prime of F in
![]() $\underline {\mathcal {S}}_{\operatorname {spl}} \sqcup {\underline {\mathcal {S}}}^c_{\operatorname {spl}}$
. We have already seen that for
$\underline {\mathcal {S}}_{\operatorname {spl}} \sqcup {\underline {\mathcal {S}}}^c_{\operatorname {spl}}$
. We have already seen that for
![]() $\Pi $
satisfying the hypothesis of the proposition,
$\Pi $
satisfying the hypothesis of the proposition,
By Lemma 8.4, it therefore remains to show that
For ease of notation, let the p-adic local Galois representation associated to the Frobenius semisimple Weil-Deligne representation
![]() $\operatorname {rec}_{F_v}(\operatorname {BC}(\Pi _\ell )_v |\operatorname {det}|_v^{(1-2n)/2})$
be denoted
$\operatorname {rec}_{F_v}(\operatorname {BC}(\Pi _\ell )_v |\operatorname {det}|_v^{(1-2n)/2})$
be denoted
![]() $\rho _{\Pi ,v}^{\operatorname {rec}}$
. We want to show that for all
$\rho _{\Pi ,v}^{\operatorname {rec}}$
. We want to show that for all
![]() $\eta \in \mathcal {I}^p_0$
, p-power roots of unity
$\eta \in \mathcal {I}^p_0$
, p-power roots of unity
![]() $\zeta $
, and
$\zeta $
, and
![]() $j,k \in \mathbb {Z}_{>0}$
,
$j,k \in \mathbb {Z}_{>0}$
,
Recall from (7.3) that for
![]() $T_{\Pi } := \varphi _{\Pi } \circ T$
constructed in the proof of Proposition 7.1, there is a function
$T_{\Pi } := \varphi _{\Pi } \circ T$
constructed in the proof of Proposition 7.1, there is a function
![]() $B^{k,j}_{\eta ,\zeta }$
for each
$B^{k,j}_{\eta ,\zeta }$
for each
![]() $j,k \in \mathbb {Z}_{>0}$
,
$j,k \in \mathbb {Z}_{>0}$
,
![]() $\eta \in \mathcal {I}^p_0$
, and p-power root of unity
$\eta \in \mathcal {I}^p_0$
, and p-power root of unity
![]() $\zeta $
such that
$\zeta $
such that
By (8.4), we want to show that
Let
![]() $\mathcal {B}_v$
denote the Bernstein component containing
$\mathcal {B}_v$
denote the Bernstein component containing
![]() $\operatorname {BC}(\Pi _\ell )_v.$
By Proposition 6.2 in [Reference Schneider and Zink17], associated to
$\operatorname {BC}(\Pi _\ell )_v.$
By Proposition 6.2 in [Reference Schneider and Zink17], associated to
![]() $\Pi $
, there exists an idempotent
$\Pi $
, there exists an idempotent
![]() $e_{\Pi ,\mathcal {B}_v}$
inside the Bernstein center
$e_{\Pi ,\mathcal {B}_v}$
inside the Bernstein center
![]() $\mathfrak {z}_{\mathcal {B}_v}$
associated to
$\mathfrak {z}_{\mathcal {B}_v}$
associated to
![]() $\mathcal {B}_v$
such that
$\mathcal {B}_v$
such that
-
•
 $e_{\Pi ,\mathcal {B}_v}(\operatorname {BC}(\Pi _\ell )_v) \neq 0$
$e_{\Pi ,\mathcal {B}_v}(\operatorname {BC}(\Pi _\ell )_v) \neq 0$
-
•
 $e_{\Pi ,\mathcal {B}_v}(\Pi _0) \neq 0 \Rightarrow \operatorname {rec}(\Pi _0) \prec _I \operatorname {rec}(\operatorname {BC}(\Pi _\ell )_v)$
for all irreducible
$e_{\Pi ,\mathcal {B}_v}(\Pi _0) \neq 0 \Rightarrow \operatorname {rec}(\Pi _0) \prec _I \operatorname {rec}(\operatorname {BC}(\Pi _\ell )_v)$
for all irreducible
 $\Pi _0$
of
$\Pi _0$
of
 $\operatorname {GL}_{2n}(F_v)$
.
$\operatorname {GL}_{2n}(F_v)$
.
If
![]() $e_{\Pi }$
denotes the image of
$e_{\Pi }$
denotes the image of
![]() $e_{\Pi ,\mathcal {B}_v} \in \mathfrak {z}_{\mathfrak {B}_v}$
, where
$e_{\Pi ,\mathcal {B}_v} \in \mathfrak {z}_{\mathfrak {B}_v}$
, where
![]() $\mathfrak {B}_v$
is the disjoint union of Bernstein components containing
$\mathfrak {B}_v$
is the disjoint union of Bernstein components containing
![]() $\mathcal {B}_v$
defined in Theorem 6.2, let
$\mathcal {B}_v$
defined in Theorem 6.2, let
![]() $\tilde {e}_{\Pi } := d(e_{\Pi })e_{\Pi } \in \mathfrak {z}_\ell ^0$
, and abusing notation, let
$\tilde {e}_{\Pi } := d(e_{\Pi })e_{\Pi } \in \mathfrak {z}_\ell ^0$
, and abusing notation, let
![]() $\tilde {e}_{\Pi }$
also denote its own image in
$\tilde {e}_{\Pi }$
also denote its own image in
![]() $\mathcal {H}^{\operatorname {spl}}_{\mathbb {Z}_p}$
and
$\mathcal {H}^{\operatorname {spl}}_{\mathbb {Z}_p}$
and
![]() $\operatorname {End}(H^0(\mathcal {X}^{\operatorname {min}}_U, \mathcal {E}^{\operatorname {sub}}_{U,\rho _{\underline {b}}}))$
for any
$\operatorname {End}(H^0(\mathcal {X}^{\operatorname {min}}_U, \mathcal {E}^{\operatorname {sub}}_{U,\rho _{\underline {b}}}))$
for any
![]() $\underline {b} \in X^\ast (T_{n/\overline {\mathbb {Q}}_p})_{\operatorname {cl}}^+$
and any neat open compact
$\underline {b} \in X^\ast (T_{n/\overline {\mathbb {Q}}_p})_{\operatorname {cl}}^+$
and any neat open compact
![]() $U = \prod U_\ell $
such that
$U = \prod U_\ell $
such that
![]() $U_v = K_{\mathfrak {B}_v}$
.
$U_v = K_{\mathfrak {B}_v}$
.
Lemma 8.11. Let
![]() $\underline {b} \in X^\ast (T_{n/\overline {\mathbb {Q}}_p})_{\operatorname {cl}}^+$
, and let
$\underline {b} \in X^\ast (T_{n/\overline {\mathbb {Q}}_p})_{\operatorname {cl}}^+$
, and let
![]() $\mathbb {T}^p_{U,\underline {b}}$
denote the image in
$\mathbb {T}^p_{U,\underline {b}}$
denote the image in
![]() $\mathcal {H}^p_{\mathbb {Z}_p}$
in
$\mathcal {H}^p_{\mathbb {Z}_p}$
in
where
![]() $U = \prod U_\ell $
and
$U = \prod U_\ell $
and
![]() $U_\ell $
satisfies (6.1) for every
$U_\ell $
satisfies (6.1) for every
![]() $\ell \in S_{\operatorname {spl}}$
. There is a continuous representation
$\ell \in S_{\operatorname {spl}}$
. There is a continuous representation
![]() $r_{\underline {b}}:G_F^S \rightarrow \operatorname {GL}_{2n}(\mathbb {T}_{\underline {b}} \otimes \overline {\mathbb {Q}}_p)$
described in (7.1) for every
$r_{\underline {b}}:G_F^S \rightarrow \operatorname {GL}_{2n}(\mathbb {T}_{\underline {b}} \otimes \overline {\mathbb {Q}}_p)$
described in (7.1) for every
![]() $\underline {b}$
, and let
$\underline {b}$
, and let
![]() $T_{\underline {b}} = \operatorname {tr} r_{\underline {b}}$
. Assume that
$T_{\underline {b}} = \operatorname {tr} r_{\underline {b}}$
. Assume that
![]() $\eta \in \mathcal {I}^p_0$
,
$\eta \in \mathcal {I}^p_0$
,
![]() $\zeta $
a p-power root of unity, and
$\zeta $
a p-power root of unity, and
![]() $k,j \in \mathbb {Z}_{>0}$
are such that
$k,j \in \mathbb {Z}_{>0}$
are such that
For each
![]() ${\underline {b}}$
, the map
${\underline {b}}$
, the map
![]() $\tilde {e}_{\Pi }B^{k,j}_{\eta ,\zeta }(T_{\underline {b}}): G_F^S \rightarrow \mathbb {T}_{\underline {b}}$
is identically zero.
$\tilde {e}_{\Pi }B^{k,j}_{\eta ,\zeta }(T_{\underline {b}}): G_F^S \rightarrow \mathbb {T}_{\underline {b}}$
is identically zero.
Proof. Recall that
![]() $\mathbb {T}_{\underline {b}} \cong \oplus _{\Pi _0} \overline {\mathbb {Q}}_p$
, where the sum runs over irreducible admissible representations of
$\mathbb {T}_{\underline {b}} \cong \oplus _{\Pi _0} \overline {\mathbb {Q}}_p$
, where the sum runs over irreducible admissible representations of
![]() $G(\mathbb {A}^{p,\infty } \times \mathbb {Z}_p)$
with
$G(\mathbb {A}^{p,\infty } \times \mathbb {Z}_p)$
with
![]() $\Pi _0^U \neq (0)$
which occur in
$\Pi _0^U \neq (0)$
which occur in
![]() $H^0(\mathcal {X}^{\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\underline {b}})$
. We will prove that for each
$H^0(\mathcal {X}^{\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\underline {b}})$
. We will prove that for each
![]() $\Pi _0$
, the composition
$\Pi _0$
, the composition
is zero. Assume
![]() $\tilde {e}_{\Pi }(\operatorname {BC}(\Pi _{0,\ell })_v) \neq 0$
for some
$\tilde {e}_{\Pi }(\operatorname {BC}(\Pi _{0,\ell })_v) \neq 0$
for some
![]() $\Pi _0 \in H^0(\mathcal {X}^{\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\underline {b}})$
. Then
$\Pi _0 \in H^0(\mathcal {X}^{\operatorname {min}},\mathcal {E}^{\operatorname {sub}}_{\underline {b}})$
. Then
![]() $\operatorname {rec}(\operatorname {BC}(\Pi _{0,\ell })_v) \prec _I \operatorname {rec}(\operatorname {BC}(\Pi _{\ell })_v)$
, and so by Lemma 8.10, for
$\operatorname {rec}(\operatorname {BC}(\Pi _{0,\ell })_v) \prec _I \operatorname {rec}(\operatorname {BC}(\Pi _{\ell })_v)$
, and so by Lemma 8.10, for
![]() $\eta \in \mathcal {I}^p_0$
,
$\eta \in \mathcal {I}^p_0$
,
By Corollary 7.1 and Lemma 8.10, we know this implies that
Thus,
![]() $\varphi _{\Pi _0} \circ \tilde {e}_{\Pi } B_{\eta ,\zeta }^{k,j}(T_{\underline {b}}) = 0$
.
$\varphi _{\Pi _0} \circ \tilde {e}_{\Pi } B_{\eta ,\zeta }^{k,j}(T_{\underline {b}}) = 0$
.
Continuing the proof of the proposition, since
![]() $T_{\Pi }$
is constructed in terms of
$T_{\Pi }$
is constructed in terms of
![]() $T_{\underline {b}}$
, if
$T_{\underline {b}}$
, if
![]() $\tilde {e}_\Pi (\operatorname {BC}(\Pi _{\ell })_v)B_{\eta ,\zeta }^{k,j}(T_{\underline {b}})$
is identically zero for all
$\tilde {e}_\Pi (\operatorname {BC}(\Pi _{\ell })_v)B_{\eta ,\zeta }^{k,j}(T_{\underline {b}})$
is identically zero for all
![]() $\underline {b} \in X^{\ast }(T_{n/\overline {\mathbb {Q}}_p})_{\operatorname {cl}}^+$
, then
$\underline {b} \in X^{\ast }(T_{n/\overline {\mathbb {Q}}_p})_{\operatorname {cl}}^+$
, then
![]() $\tilde {e}_{\Pi }B_{\eta ,\zeta }^{k,j}(T_{\Pi })$
is also identically zero. Since
$\tilde {e}_{\Pi }B_{\eta ,\zeta }^{k,j}(T_{\Pi })$
is also identically zero. Since
![]() $\tilde {e}_{\Pi }(\operatorname {BC}(\Pi _{\ell })_v) \neq 0$
, we can conclude that
$\tilde {e}_{\Pi }(\operatorname {BC}(\Pi _{\ell })_v) \neq 0$
, we can conclude that
![]() $B_{\eta ,\zeta }^{k,j}(T_\Pi ) = 0$
if
$B_{\eta ,\zeta }^{k,j}(T_\Pi ) = 0$
if
![]() $\eta \in \mathcal {I}^p_0$
,
$\eta \in \mathcal {I}^p_0$
,
![]() $\zeta $
a p-power root of unity, and
$\zeta $
a p-power root of unity, and
![]() $k,j \in \mathbb {Z}_{>0}$
are such that
$k,j \in \mathbb {Z}_{>0}$
are such that
This implies that
![]() $\operatorname {WD}(\left .R_{p,\imath }(\Pi )\right |{}_{W_{F_v}})^{\operatorname {Frob}-ss} \prec _{I} \operatorname {rec}_{F_v}(\operatorname {BC}(\Pi _\ell )_v |\operatorname {det}|_v^{(1-2n)/2})$
. Thus, we conclude
$\operatorname {WD}(\left .R_{p,\imath }(\Pi )\right |{}_{W_{F_v}})^{\operatorname {Frob}-ss} \prec _{I} \operatorname {rec}_{F_v}(\operatorname {BC}(\Pi _\ell )_v |\operatorname {det}|_v^{(1-2n)/2})$
. Thus, we conclude
Proposition 8.1 in conjunction with Theorem 5.1 then allows us to conclude the following:
Corollary 8.12. Assume that
![]() $n> 1$
and that
$n> 1$
and that
![]() $\rho $
is an irreducible algebraic representation of
$\rho $
is an irreducible algebraic representation of
![]() $L_{(n),\operatorname {lin}}$
on a finite-dimensional
$L_{(n),\operatorname {lin}}$
on a finite-dimensional
![]() $\overline {\mathbb {Q}}_p$
-vector space. Suppose that
$\overline {\mathbb {Q}}_p$
-vector space. Suppose that
![]() $\pi $
is a cuspidal automorphic representation of
$\pi $
is a cuspidal automorphic representation of
![]() $L_{(n),\operatorname {lin}}(\mathbb {A})$
such that
$L_{(n),\operatorname {lin}}(\mathbb {A})$
such that
![]() $\pi _\infty $
has the same infinitesimal character as
$\pi _\infty $
has the same infinitesimal character as
![]() $\rho ^\vee $
. Then, for all sufficiently large integers M, there is a continuous semisimple representation
$\rho ^\vee $
. Then, for all sufficiently large integers M, there is a continuous semisimple representation
with the following property: if
![]() $\ell \neq p$
is a rational prime in
$\ell \neq p$
is a rational prime in
![]() $S_{\operatorname {spl}}$
, then for all primes
$S_{\operatorname {spl}}$
, then for all primes
![]() $v \mid \ell $
,
$v \mid \ell $
,
Proof. Let
![]() $\Pi $
be an irreducible subquotient of the induced representation
$\Pi $
be an irreducible subquotient of the induced representation
![]() $\operatorname {Ind}_{P_{(n)}^+(\mathbb {A}^{p,\infty })}^{G(\mathbb {A}^{p,\infty })} (\pi ^\infty ||\operatorname {det}||^M \times 1)$
with the property that at any
$\operatorname {Ind}_{P_{(n)}^+(\mathbb {A}^{p,\infty })}^{G(\mathbb {A}^{p,\infty })} (\pi ^\infty ||\operatorname {det}||^M \times 1)$
with the property that at any
![]() $v \mid \ell \in S_{\operatorname {spl}}$
,
$v \mid \ell \in S_{\operatorname {spl}}$
,
Then set
9 Group theory
Let
![]() $\Gamma $
be a topological group, and let
$\Gamma $
be a topological group, and let
![]() $\frak {F}$
be a dense set of elements of
$\frak {F}$
be a dense set of elements of
![]() $\Gamma $
. Let k be an algebraically closed, topological field of characteristic 0, and let
$\Gamma $
. Let k be an algebraically closed, topological field of characteristic 0, and let
![]() $d \in \mathbb {Z}_{>0}$
. Let
$d \in \mathbb {Z}_{>0}$
. Let
![]() $\mu : \Gamma \rightarrow k^\times $
be a continuous homomorphism such that
$\mu : \Gamma \rightarrow k^\times $
be a continuous homomorphism such that
![]() $\mu (f)$
has infinite order for all
$\mu (f)$
has infinite order for all
![]() $f \in \mathfrak {F}$
. For
$f \in \mathfrak {F}$
. For
![]() $f \in \mathfrak {F}$
, let
$f \in \mathfrak {F}$
, let
![]() $\mathcal {E}^1_f$
and
$\mathcal {E}^1_f$
and
![]() $\mathcal {E}^2_f$
be two d-elements multiset of elements of
$\mathcal {E}^2_f$
be two d-elements multiset of elements of
![]() $k^\times $
. Let
$k^\times $
. Let
![]() $\mathcal {M}$
be an infinite subset of
$\mathcal {M}$
be an infinite subset of
![]() $\mathbb {Z}$
. For
$\mathbb {Z}$
. For
![]() $m\in \mathcal {M}$
, suppose that
$m\in \mathcal {M}$
, suppose that
is a continuous semisimple representation such that for every
![]() $f \in \mathfrak {F}$
, the multiset of roots of the characteristic polynomial of
$f \in \mathfrak {F}$
, the multiset of roots of the characteristic polynomial of
![]() $\rho _m(f)$
equals
$\rho _m(f)$
equals
Proposition 9.1 (Proposition 7.12 in [Reference Harris, Lan, Taylor and Thorne10]).
There are continuous semisimple representations
for
![]() $i = 1,2$
such that for all
$i = 1,2$
such that for all
![]() $f \in \mathfrak {F}$
, the multiset of roots of the characteristic polynomial of
$f \in \mathfrak {F}$
, the multiset of roots of the characteristic polynomial of
![]() $\rho ^i(f)$
equals
$\rho ^i(f)$
equals
![]() $\mathcal {E}^i_f$
.
$\mathcal {E}^i_f$
.
Theorem 9.2. Suppose that
![]() $\pi $
is a cuspidal automorphic representation of
$\pi $
is a cuspidal automorphic representation of
![]() $\operatorname {GL}_n(\mathbb {A}_F)$
such that
$\operatorname {GL}_n(\mathbb {A}_F)$
such that
![]() $\pi _\infty $
has the same infinitesimal character as an algebraic representation of
$\pi _\infty $
has the same infinitesimal character as an algebraic representation of
![]() $\operatorname {RS}^F_{\mathbb {Q}} \operatorname {GL}_n$
. Then there is a continuous semisimple representation
$\operatorname {RS}^F_{\mathbb {Q}} \operatorname {GL}_n$
. Then there is a continuous semisimple representation
such that if
![]() $v \nmid p$
is a prime of F above a rational prime
$v \nmid p$
is a prime of F above a rational prime
![]() $\ell $
satisfying either
$\ell $
satisfying either
-
1.
 $\ell $
is split over
$\ell $
is split over
 $F_0$
, or
$F_0$
, or -
2.
 $\pi $
and F are unramified at all primes above
$\pi $
and F are unramified at all primes above
 $\ell $
,
$\ell $
,
then
In particular, if
![]() $\pi $
and F are unramified at v, then
$\pi $
and F are unramified at v, then
![]() $r_{p,\imath }(\pi )$
is unramified.
$r_{p,\imath }(\pi )$
is unramified.
Proof. Assume that
![]() $n> 1$
. Recall that S contains p and the rational primes that are not split in
$n> 1$
. Recall that S contains p and the rational primes that are not split in
![]() $F_0$
but ramified in F; and let
$F_0$
but ramified in F; and let
![]() $G_{F}^{S}$
denote the Galois group over F of the maximal extension of F unramified outside S. Let
$G_{F}^{S}$
denote the Galois group over F of the maximal extension of F unramified outside S. Let
![]() $\Gamma = G_{F,S}$
,
$\Gamma = G_{F,S}$
,
![]() $k = \overline {\mathbb {Q}}_p$
, and
$k = \overline {\mathbb {Q}}_p$
, and
![]() $\mu = \epsilon _p^{-2}$
, and let
$\mu = \epsilon _p^{-2}$
, and let
![]() $\mathcal {M}$
consist of all sufficiently large integers m. Choose an irreducible subquotient
$\mathcal {M}$
consist of all sufficiently large integers m. Choose an irreducible subquotient
![]() $\Pi $
of the induced representation
$\Pi $
of the induced representation
![]() $\operatorname {Ind}_{P_{(n)}^+(\mathbb {A}^{p,\infty })}^{G(\mathbb {A}^{p,\infty })} (\pi ^\infty ||\operatorname {det}||^m \times 1)$
satisfying for
$\operatorname {Ind}_{P_{(n)}^+(\mathbb {A}^{p,\infty })}^{G(\mathbb {A}^{p,\infty })} (\pi ^\infty ||\operatorname {det}||^m \times 1)$
satisfying for
![]() $v \mid \ell \in S_{\operatorname {spl}}$
,
$v \mid \ell \in S_{\operatorname {spl}}$
,
Then we set
for each v and let
![]() $k(v)$
denote the residue field of
$k(v)$
denote the residue field of
![]() $F_v$
. Let
$F_v$
. Let
![]() $\mathfrak {F}$
contain all elements
$\mathfrak {F}$
contain all elements
![]() $\sigma _v \in W_{F_v}$
which projects to a power of Frobenius under the map
$\sigma _v \in W_{F_v}$
which projects to a power of Frobenius under the map
![]() $W_{F_v} \rightarrow \operatorname {Gal}(\overline {k(v)}/k(v))$
, where
$W_{F_v} \rightarrow \operatorname {Gal}(\overline {k(v)}/k(v))$
, where
![]() $v \notin S^{\prime }$
. Denote by
$v \notin S^{\prime }$
. Denote by
![]() $\sigma _{{}^cv}$
the image of
$\sigma _{{}^cv}$
the image of
![]() $\sigma _v$
under the isomorphism
$\sigma _v$
under the isomorphism
![]() $W_{F_v} \cong W_{F_{{}^cv}}$
induced by conjugation c. Define
$W_{F_v} \cong W_{F_{{}^cv}}$
induced by conjugation c. Define
![]() $\mathcal {E}^1_{\sigma _v}$
to be the multiset of roots of the characteristic polynomial
$\mathcal {E}^1_{\sigma _v}$
to be the multiset of roots of the characteristic polynomial
![]() $\imath ^{-1}\operatorname {rec}_{F_v}(\pi _v|\operatorname {det}|_v^{(1-n)/2})(\sigma _v)$
and
$\imath ^{-1}\operatorname {rec}_{F_v}(\pi _v|\operatorname {det}|_v^{(1-n)/2})(\sigma _v)$
and
![]() $\mathcal {E}^2_{\sigma _v}$
equal to the multiset of roots of the characteristic polynomial of
$\mathcal {E}^2_{\sigma _v}$
equal to the multiset of roots of the characteristic polynomial of
![]() $\imath ^{-1}\operatorname {rec}_{F_{{}^cv}}(\pi _{{}^cv}|\operatorname {det}|_{{}^cv}^{(-1+3n)/2})(\sigma _{{}^cv}^{-1}).$
We can then conclude
$\imath ^{-1}\operatorname {rec}_{F_{{}^cv}}(\pi _{{}^cv}|\operatorname {det}|_{{}^cv}^{(-1+3n)/2})(\sigma _{{}^cv}^{-1}).$
We can then conclude
By Proposition 9.1, we have that for a sufficiently large integer M in the sense of Theorem 5.1,
Now choose a finite order Hecke character
![]() $\psi $
on
$\psi $
on
![]() $\mathbb {A}_F^\times $
such that
$\mathbb {A}_F^\times $
such that
-
•
 $\psi $
is unramified at v,
$\psi $
is unramified at v, -
•
 $\psi $
highly ramified at
$\psi $
highly ramified at
 $v^c$
, and
$v^c$
, and -
•
 $\operatorname {rec}_{F_v}((\pi \otimes \psi )_v|\operatorname {det}|_v^{(1-n)/2})$
and
$\operatorname {rec}_{F_v}((\pi \otimes \psi )_v|\operatorname {det}|_v^{(1-n)/2})$
and
 $\operatorname {rec}_{F_{v}}((\pi \otimes \psi )_{{}^cv}|\operatorname {det}|_{{}^cv}^{(1-n)/2})^{c,\vee }$
have no common irreducible constituents, even after restricting to
$\operatorname {rec}_{F_{v}}((\pi \otimes \psi )_{{}^cv}|\operatorname {det}|_{{}^cv}^{(1-n)/2})^{c,\vee }$
have no common irreducible constituents, even after restricting to
 $I_v$
.
$I_v$
.
From (9.2) applied to
![]() $\pi \otimes \psi $
in conjunction with Corollary 8.12, after untwisting, we obtain
$\pi \otimes \psi $
in conjunction with Corollary 8.12, after untwisting, we obtain
 $$ \begin{align*}&\operatorname{WD}(\left.r_{p,\iota}(\pi \otimes \psi)\right|{}_{W_{F_v}})^{\operatorname{Frob}-ss} \oplus \operatorname{WD}(\left.r_{p,\iota}({}^c\pi \otimes {}^c\psi)^{c, \vee}\right|{}_{W_{F_v}})^{\operatorname{Frob}-ss} \\&\quad\prec \operatorname{rec}_{F_v}((\pi \otimes \psi)_v|\operatorname{det}|_v^{(1-n)/2}) \oplus \operatorname{rec}_{F_{{}^cv}}((\pi\otimes \psi)_{{}^cv}|\operatorname{det}|_{{}^cv}^{(1-n)/2})^{c,\vee}.\end{align*} $$
$$ \begin{align*}&\operatorname{WD}(\left.r_{p,\iota}(\pi \otimes \psi)\right|{}_{W_{F_v}})^{\operatorname{Frob}-ss} \oplus \operatorname{WD}(\left.r_{p,\iota}({}^c\pi \otimes {}^c\psi)^{c, \vee}\right|{}_{W_{F_v}})^{\operatorname{Frob}-ss} \\&\quad\prec \operatorname{rec}_{F_v}((\pi \otimes \psi)_v|\operatorname{det}|_v^{(1-n)/2}) \oplus \operatorname{rec}_{F_{{}^cv}}((\pi\otimes \psi)_{{}^cv}|\operatorname{det}|_{{}^cv}^{(1-n)/2})^{c,\vee}.\end{align*} $$
Additionally, by (9.1),
Since
![]() $\prec $
is defined component-by-component, we can conclude
$\prec $
is defined component-by-component, we can conclude
Since the relation
![]() $\prec $
is compatible with twisting, we conclude the theorem.
$\prec $
is compatible with twisting, we conclude the theorem.
Corollary 9.3. Suppose that E is a totally real or CM field and that
![]() $\pi $
is a cuspidal automorphic representation such that
$\pi $
is a cuspidal automorphic representation such that
![]() $\pi _\infty $
has the same infinitesimal character as an algebraic representation of
$\pi _\infty $
has the same infinitesimal character as an algebraic representation of
![]() $\operatorname {RS}^{E}_{\mathbb {Q}} \operatorname {GL}_n$
. Then there is a continuous semisimple representation
$\operatorname {RS}^{E}_{\mathbb {Q}} \operatorname {GL}_n$
. Then there is a continuous semisimple representation
such that, if
![]() $\ell \neq p$
is a prime and if
$\ell \neq p$
is a prime and if
![]() $v \mid \ell $
is a prime of E, then
$v \mid \ell $
is a prime of E, then
Proof. This can be deduced from Theorem 9.2 in conjunction with Lemma 1 of [Reference Sorensen21] using the same argument as in Theorem VII.1.9 of [Reference Harris and Taylor11].
Acknowledgments
The author would like to thank Richard Taylor for suggesting this problem and for his invaluable assistance throughout this project; she would also like to thank Ana Caraiani, Gaetan Chenevier, David Geraghty and Jay Pottharst for answering questions. The author would like to thank the anonymous referees for their careful suggestions and patience, especially with the proof of Theorem 9.2.